Что такое магнитный гистерезис. Как проявляется магнитный гистерезис в ферромагнетиках. Какие материалы обладают свойством магнитного гистерезиса. Где применяется явление магнитного гистерезиса. Как используется магнитный гистерезис в одномолекулярных магнитах.
Что такое магнитный гистерезис и как он проявляется
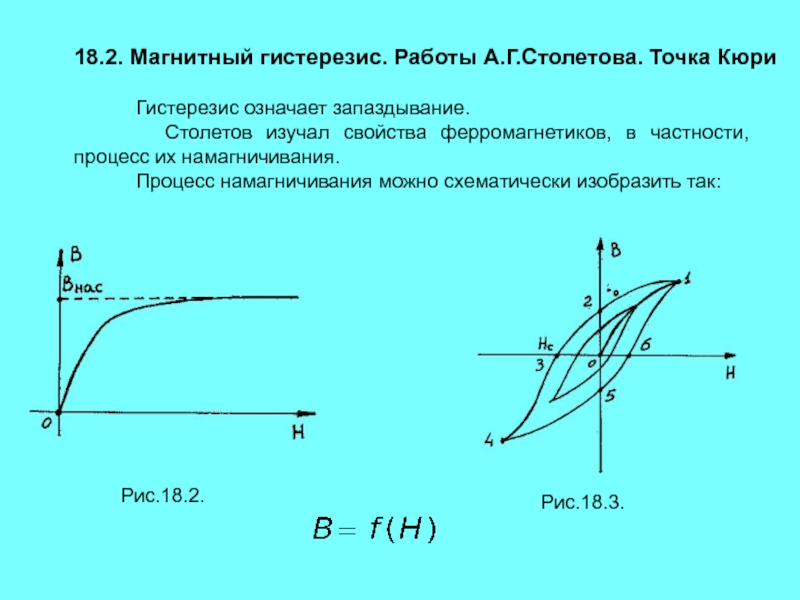
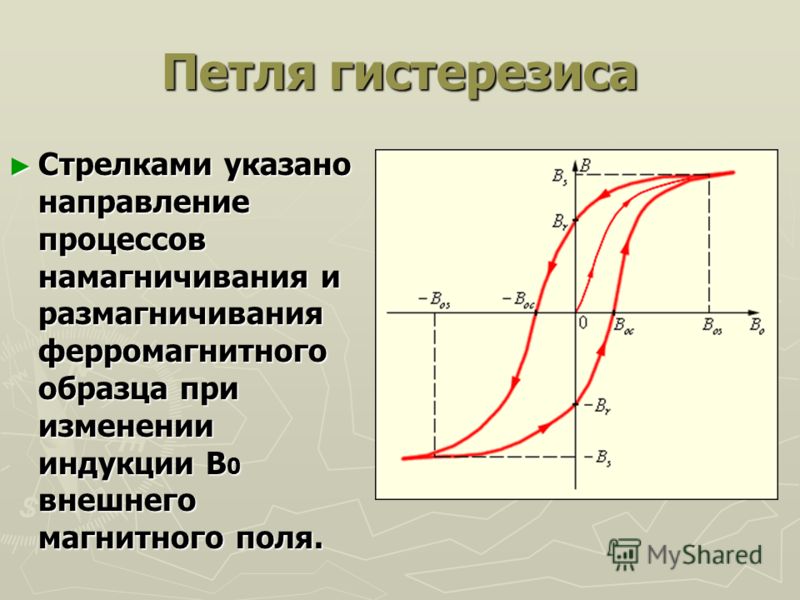
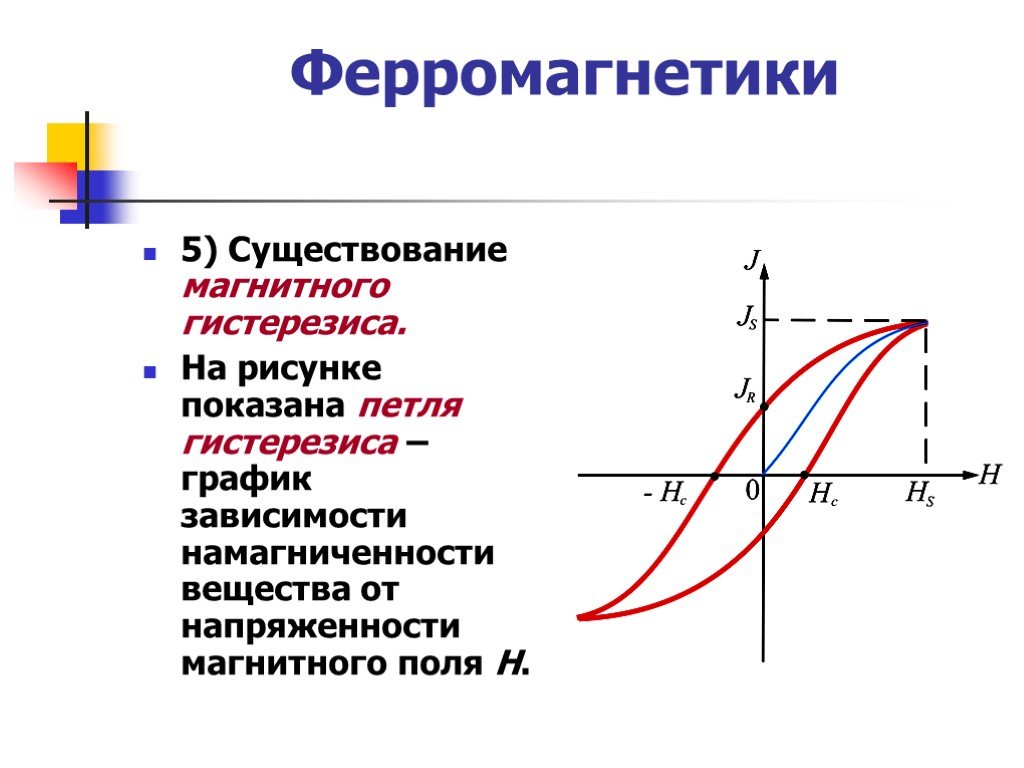
Магнитный гистерезис — это явление, при котором намагниченность ферромагнитного материала зависит не только от приложенного в данный момент магнитного поля, но и от предыстории намагничивания образца. Проявляется магнитный гистерезис следующим образом:
- При увеличении внешнего магнитного поля намагниченность материала растет нелинейно
- При уменьшении поля намагниченность уменьшается, но не по той же кривой
- При нулевом внешнем поле сохраняется остаточная намагниченность
- Для размагничивания требуется приложить поле противоположного направления
- График зависимости намагниченности от поля имеет характерную петлеобразную форму — петлю гистерезиса
Такое поведение обусловлено особенностями магнитной доменной структуры ферромагнетиков и процессами смещения доменных границ при намагничивании.
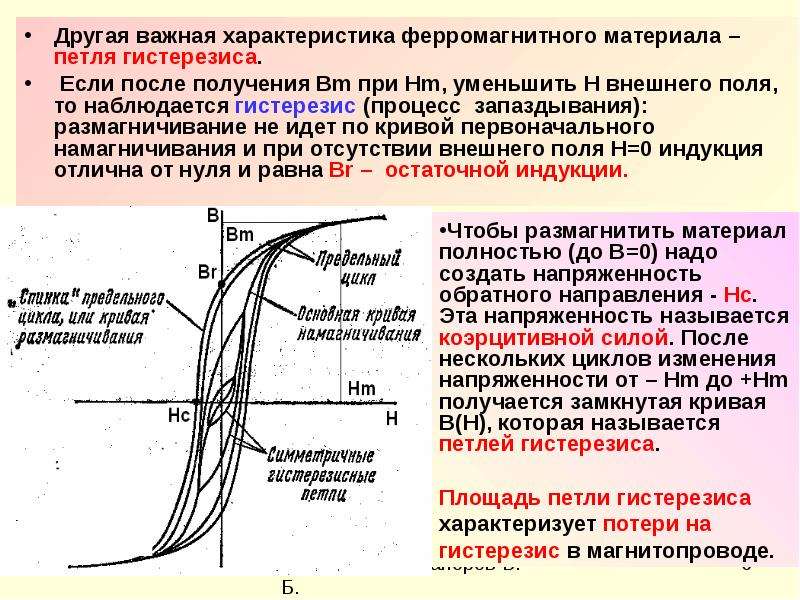
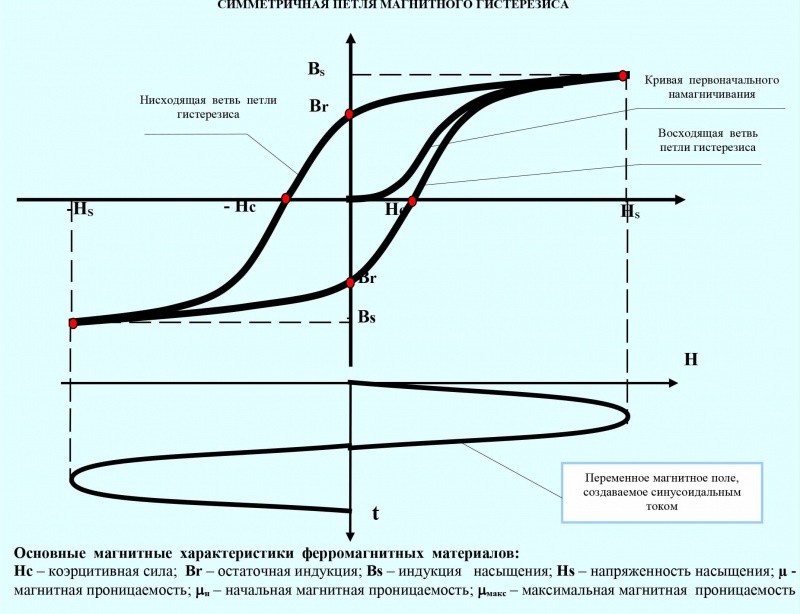
Основные характеристики петли магнитного гистерезиса
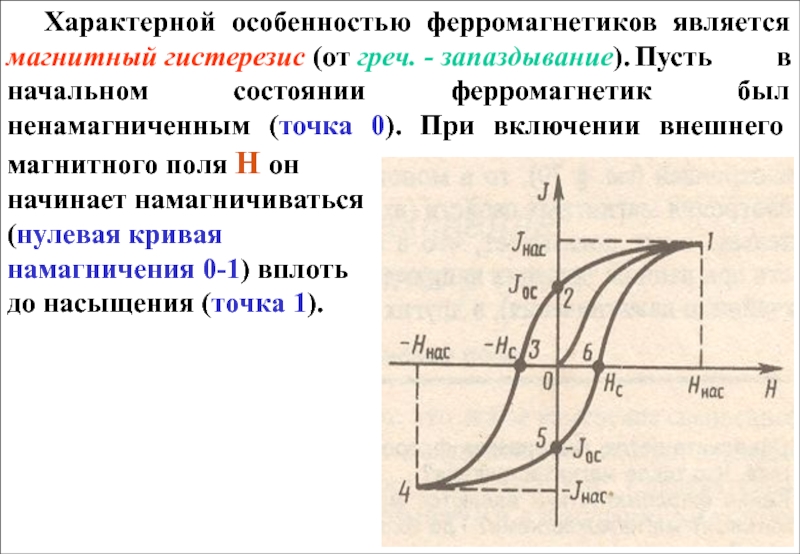
Петля магнитного гистерезиса имеет ряд важных характеристик:
- Остаточная намагниченность — намагниченность, сохраняющаяся при нулевом внешнем поле
- Коэрцитивная сила — величина размагничивающего поля, необходимого для снятия остаточной намагниченности
- Магнитная проницаемость — отношение индукции к напряженности поля в образце
- Площадь петли гистерезиса — пропорциональна энергии перемагничивания
Форма и параметры петли гистерезиса зависят от состава и структуры материала, а также режимов намагничивания.
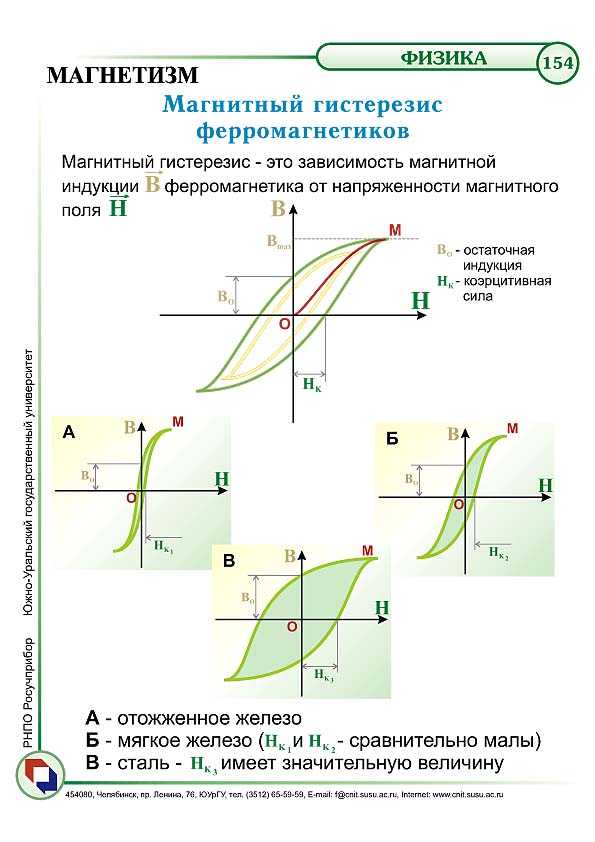
Материалы, обладающие магнитным гистерезисом
Магнитный гистерезис наиболее ярко проявляется в ферромагнитных материалах, таких как:
- Железо и его сплавы (сталь, чугун)
- Никель и кобальт
- Редкоземельные металлы (неодим, самарий)
- Ферриты
- Аморфные магнитные сплавы
Также гистерезис наблюдается в некоторых антиферромагнетиках и ферримагнетиках. Степень выраженности гистерезиса зависит от магнитной структуры вещества.
Применение явления магнитного гистерезиса
Магнитный гистерезис находит широкое практическое применение в различных областях:
- Создание постоянных магнитов
- Магнитная запись информации
- Магнитные системы памяти
- Трансформаторы и электродвигатели
- Магнитные экраны
- Датчики магнитного поля
- Устройства СВЧ-электроники
При этом в одних устройствах стремятся максимально использовать гистерезисные свойства, а в других — минимизировать потери на гистерезис.
Магнитный гистерезис в одномолекулярных магнитах
Одномолекулярные магниты (Single-Molecule Magnets, SMM) — это класс координационных соединений, способных сохранять намагниченность на молекулярном уровне. Их ключевые особенности:
- Проявляют магнитный гистерезис молекулярного происхождения
- Обладают большой магнитной анизотропией
- Имеют высокий спин основного состояния
- Демонстрируют медленную релаксацию намагниченности
Наличие гистерезиса в SMM открывает перспективы их применения для хранения информации на молекулярном уровне.

Рекордные показатели магнитного гистерезиса в SMM
За последние годы в области одномолекулярных магнитов достигнут значительный прогресс:
- Температура блокировки намагниченности повышена с 4 К до 60 К
- Высота барьера анизотропии увеличена до 1837 К
- Получены SMM, работающие при температуре жидкого азота (77 К)
- Синтезированы соединения с временем релаксации более года при 2 К
Это приближает одномолекулярные магниты к практическому применению в устройствах спинтроники и квантовых вычислений.
Факторы, влияющие на магнитный гистерезис в SMM
На магнитные свойства одномолекулярных магнитов влияет ряд факторов:
- Природа центрального иона (чаще всего лантаноиды)
- Симметрия координационного окружения
- Тип лигандов
- Межмолекулярные взаимодействия
- Спин-орбитальное взаимодействие
- Спин-решеточная релаксация
Оптимизация этих параметров позволяет повысить температуру проявления гистерезиса и улучшить магнитные характеристики SMM.
Перспективы применения одномолекулярных магнитов
Уникальные магнитные свойства SMM открывают широкие перспективы их практического использования:

- Сверхплотная магнитная запись информации
- Квантовые компьютеры на основе молекулярных кубитов
- Спинтронные устройства молекулярного масштаба
- Высокочувствительные магнитные сенсоры
- МРТ-контрастные агенты нового поколения
Однако для практической реализации этих применений необходимо дальнейшее повышение рабочих температур и стабильности одномолекулярных магнитов.
Магнитный гистерезис, теория и примеры задач
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Физика Магнитный гистерезис
Основные понятия магнитного гистерезиса
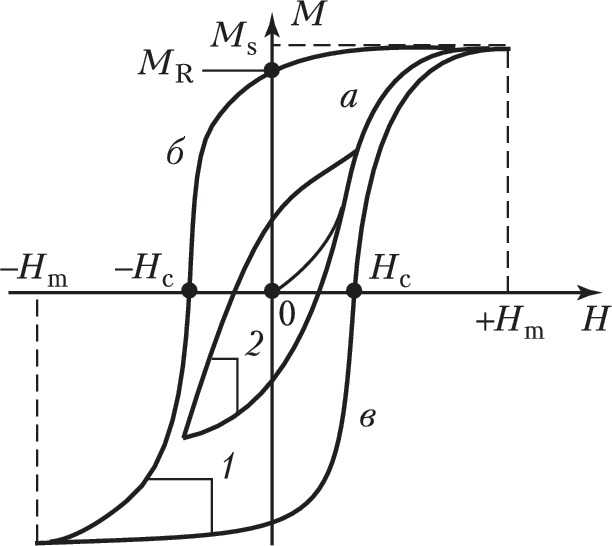
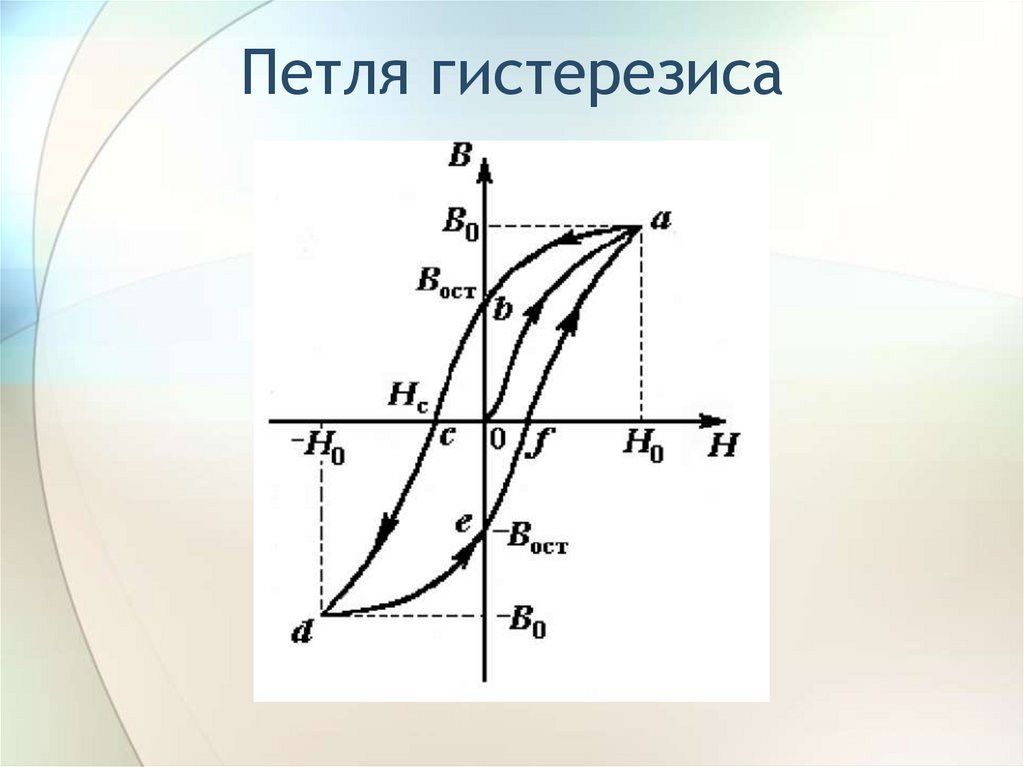
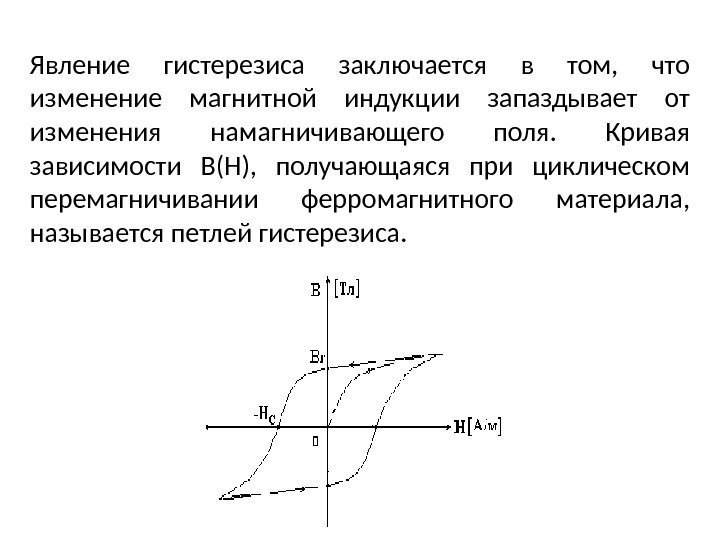
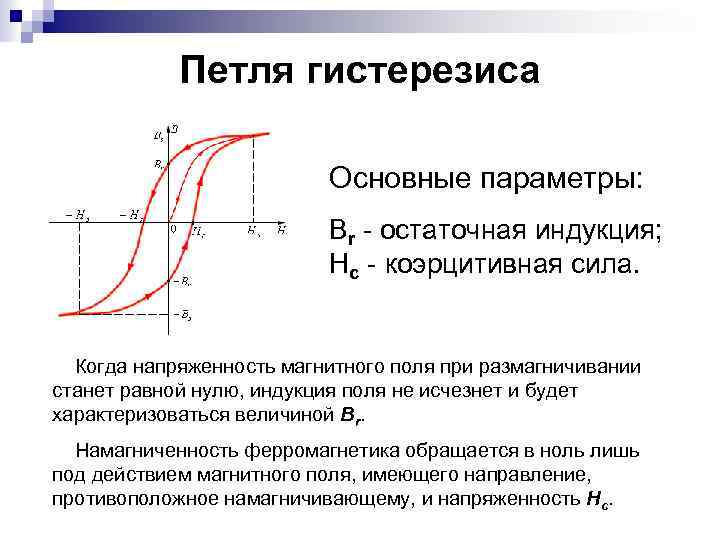
Если взять ферромагнетик в ненамагниченном состоянии, поместить его в магнитное поле, напряженность которого можно постепенно изменять, увеличивать величину H от нуля до некоторого значения . Зависимость (рис.1 (б)) будет отображать отрезок ОА. Потом будем постепенно уменьшать напряженность внешнего магнитного поля. При этом кривая намагничивания пойдет не по тому же пути (AO), что шла наверх, а по кривой, которая на рис. 1(б) обозначена как ACD. Если от величины напряжения изменять магнитное поле снова до H, то кривая намагничивания пройдет ниже и вернется в точку А (см. рис.1). Получается замкнутая кривая, которая называется петлей гистерезиса. Из рис.1 видно, что при индукция пол ферромагнетика (и его намагниченность) не становятся равными нулю. Из рис. 1(б) видно, что модуль магнитной индукции равен длине отрезка ОС. Этому отрезку соответствует остаточное намагничивание. С существованием остаточного намагничивания связано наличие постоянных магнитов. Для размагничивания ферромагнетика его следует поместить в обратное магнитное поле, величина которого равна так называемой коэрцитивной силе ферромагнетика ().
1(б) обозначена как ACD. Если от величины напряжения изменять магнитное поле снова до H, то кривая намагничивания пройдет ниже и вернется в точку А (см. рис.1). Получается замкнутая кривая, которая называется петлей гистерезиса. Из рис.1 видно, что при индукция пол ферромагнетика (и его намагниченность) не становятся равными нулю. Из рис. 1(б) видно, что модуль магнитной индукции равен длине отрезка ОС. Этому отрезку соответствует остаточное намагничивание. С существованием остаточного намагничивания связано наличие постоянных магнитов. Для размагничивания ферромагнетика его следует поместить в обратное магнитное поле, величина которого равна так называемой коэрцитивной силе ферромагнетика ().
Рис. 1(a)
Рис. 1(б)
Петля магнитного гистерезиса
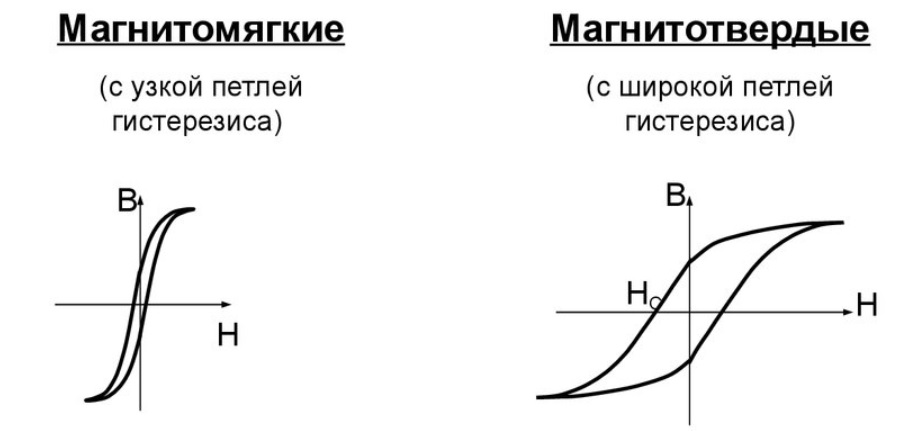
Величины остаточного намагничивания и коэрцитивной силы могут испытывать большие вариации для разных ферромагнетиков. Так, для мягких ферромагнетиков петля гистерезиса узкая, соответственно коэрцитивная сила небольшая. Для материалов, которые применяют при изготовлении постоянных магнитов петля гистерезиса широкая.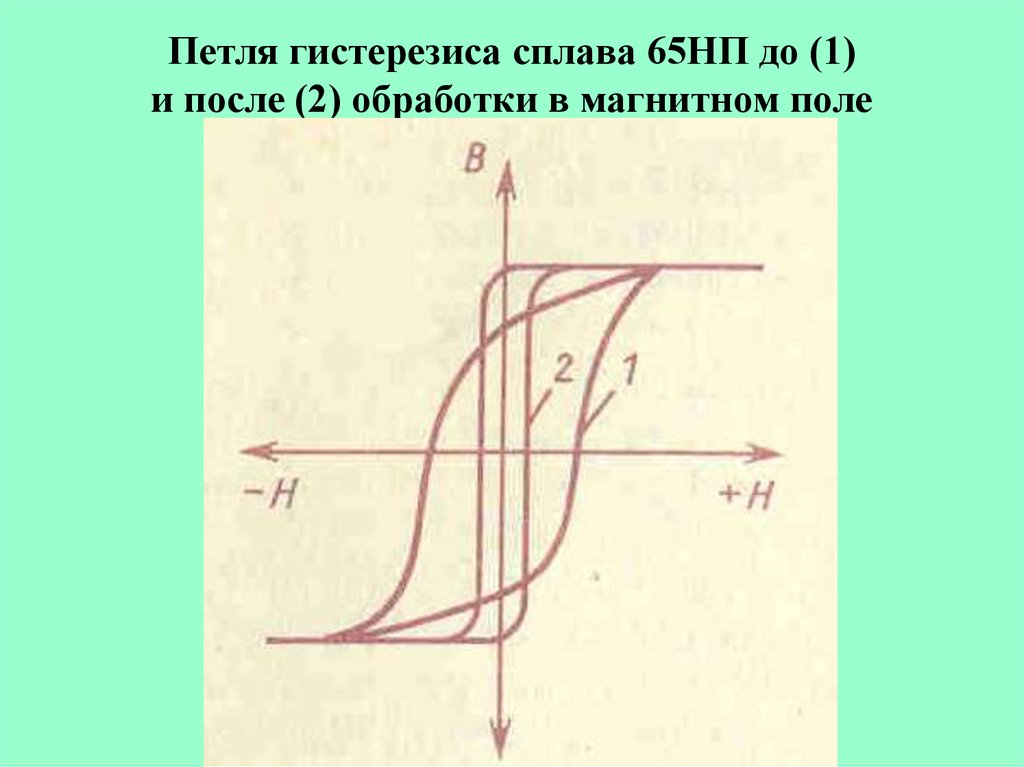 Петля гистерезиса для зависимости имеет подобную форму (рис.1 (а)).
Петля гистерезиса для зависимости имеет подобную форму (рис.1 (а)).
Следует отметить, что при увеличении внешнего магнитного поля намагниченность ферромагнетиков растет быстро, затем ее скорость ее роста уменьшается и при некоторой величине, которую называют магнитным насыщением, остается постоянной и не зависит от напряженности внешнего поля. Аналогичный процесс происходит и со связью магнитной индукции ферромагнетика и внешнего магнитного поля. Такую зависимость объясняют тем, что магнитные моменты молекул при увеличении напряженности внешнего поля ориентируются по полю, так растет степень ориентации моментов. Когда неориентированных моментов остается все меньше и меньше, увеличение J прекращается и происходит магнитное насыщение. На рис. 1 точка А – является точкой насыщения.
Мы получили, что величина магнитной индукции (или величина намагниченности) в ферромагнетике определяется не только существующим внешним магнитным полем, но еще зависит от предыдущих состояний намагничивания, при этом происходит некоторое отставание изменения индукции (намагничивания) от изменений напряженности поля. Магнитный гистерезис подобен диэлектрическому гистерезису в сегнетоэлектриках. Гистерезис очень сильно зависит от состава ферромагнетика и способов его обработки.
Магнитный гистерезис подобен диэлектрическому гистерезису в сегнетоэлектриках. Гистерезис очень сильно зависит от состава ферромагнетика и способов его обработки.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Магнитный гистерезис | это… Что такое Магнитный гистерезис?
Петля гистерезиса. Подобная зависимость величин характерна для всех видов гистерезиса
Гистере́зис (греч. ὑστέρησις — «отстающий») — свойство систем (обычно физических), которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть системы зависят от собственной истории.
|
Содержание
|
В физике
Наибольший интерес представляют магнитный гистерезис, сегнетоэлектрический гистерезис и упругий гистерезис.
Магнитный гистерезис
Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженности магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов.
Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H. Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H.
Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания.
Петля гистерезиса для триггера Шмитта имеет прямоугольный вид.
В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M. Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений). Благодаря анизотропии, M как бы удерживается некоторым внутренним полем HA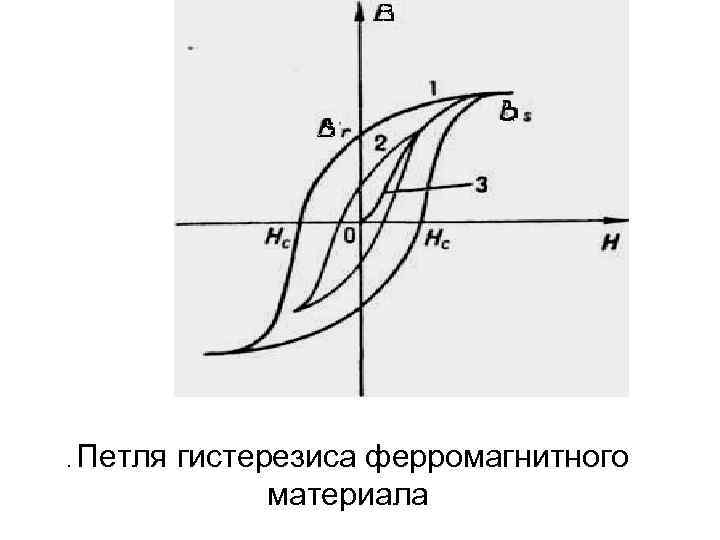 При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H, Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила . Более универсальным является механизм неоднородного вращения M. Однако наибольшее влияние на Hc он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом
Hc может быть существенно меньше эффективного поля анизотропии формы.
При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H, Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила . Более универсальным является механизм неоднородного вращения M. Однако наибольшее влияние на Hc он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом
Hc может быть существенно меньше эффективного поля анизотропии формы.
В электронике и электротехнике используются устройства, обладающие магнитным — различные магнитные носители информации, или электрическим гистерезисом, например, триггер Шмитта или гистерезисный двигатель.
Сегнетоэлектрический гистерезис
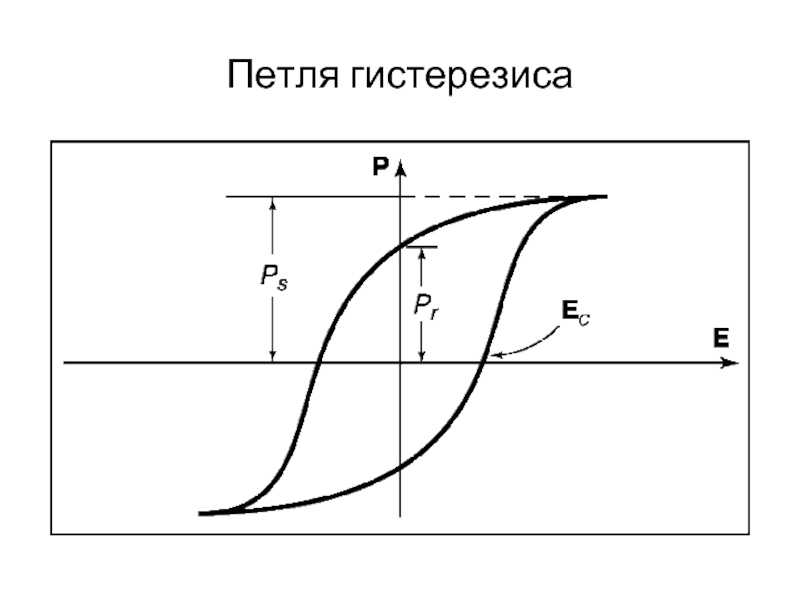
Сегнетоэлектрический гистерезис — неоднозначная петлеобразная зависимость поляризации P сегнетоэлектриков от внешнего электрического поля E при его циклическом изменении. Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией Pc. Направление поляризации может быть изменено электрическим полем. При этом зависимость
Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией Pc. Направление поляризации может быть изменено электрическим полем. При этом зависимость
- остаточная поляризация кристалла Pост, при E = 0
- значение поля EKt(коэрцитивное поле) при котором происходит переполяризация
Упругий гистерезис
В теории упругости явление гистерезиса наблюдается в поведении упругих материалов, которые под воздействием больших давлений способны сохранять деформацию и утрачивать её при воздействии обратного давления (например, вытягивание сжатого стержня).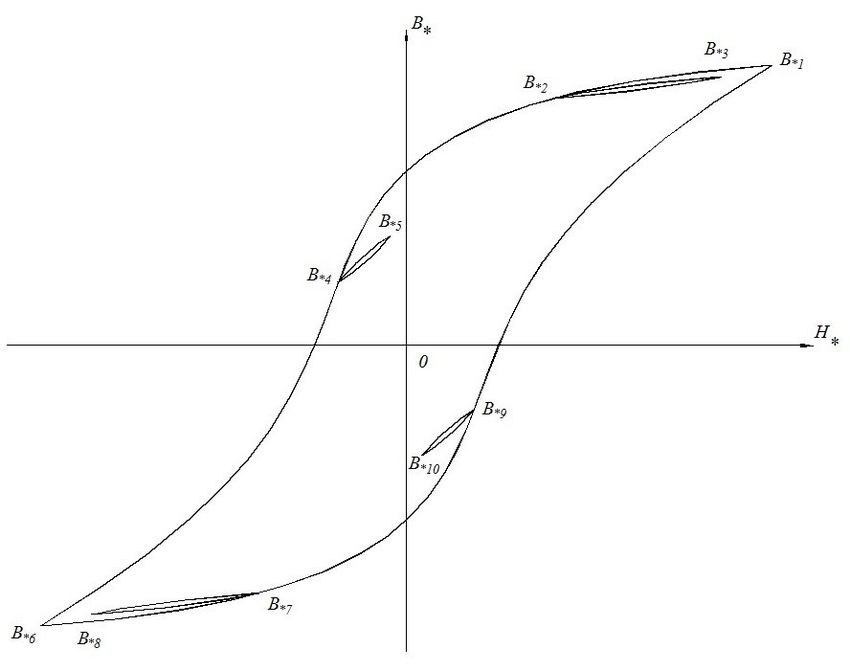 Во многом именно это явление объясняет анизотропию механических характеристик кованых изделий, а также их высокие механические качества.
Во многом именно это явление объясняет анизотропию механических характеристик кованых изделий, а также их высокие механические качества.
Различают два вида упругого гистерезиса — динамический и статический.
Динамический гистерезис наблюдают при циклически изменяющихся напряжениях, максимальная амплитуда которых существенно ниже предела упругости. Причиной этого вида гистерезиса является неупругость либо вязкоупругость. При неупругости, помимо чисто упругой деформации (отвечающей закону Гука), имеется составляющая, которая полностью исчезает при снятии напряжений, но с некоторым запаздыванием, а при вязкоупругости эта составляющая полностью со временем не исчезает. Как при неупругом, так и вязкоупругом поведении величина ΔU — энергия упругой деформации не зависит от амплитуды деформации и меняется с частотой изменения нагрузки. Также динамический гистерезис возникает в результате термоупругости, магнитоупругих явлений и изменения положения точечных дефектов и растворённых атомов в кристаллической решётке тела под влиянием приложенных напряжений.
В биологии
Гистерезисные свойства характерны для скелетных мышц млекопитающих.
В почвоведении
Основная гидрофизическая характеристика почвы обладает гистерезисом.
В гидрологии
Зависимость Q=f(H) — связь расходов и уровней воды в реках — имеет петлеобразную форму.
В экономике
Некоторые экономические системы проявляют признаки гистерезиса: например, могут потребоваться значительные усилия, чтобы начать экспорт в какой-либо отрасли, но для его поддержания на постоянном уровне — небольшие.
В теории игр эффект гистерезиса проявляется в том, что небольшие отличия по одному или нескольким параметрам приводят две системы в противоположные стабильные равновесия, например, «хорошее» — доверие, честность и высокое благосостояние; и «плохое» — воровство, недоверие, коррупция и бедность. Несмотря на небольшие первоначальные различия, системы требуют огромных усилий для перехода из одного равновесия в другое.
Эффект гистерезиса — состояние безработицы; достигнув достаточно высокого уровня, она может в определенной мере самовоспроизводиться и удерживаться на нем. Экономические причины гистерезиса (долгосрочной негибкости рынка труда) неоднозначны. Некоторые институциональные факторы ведут к гистерезису. Например, социальное страхование, особенно страхование по безработице, может через налоговую систему снижать спрос фирм на рабочую силу в официальной экономике. Безработица может вести к потере человеческого капитала и к «помечиванию» тех, кто долгое время остается безработным. Профсоюзы могут вести переговоры с целью поддерживать благосостояние их настоящих членов, игнорируя интересы аутсайдеров, оказавшихся безработными. Фиксированные издержки, связанные со сменой должности, места работы или отрасли, также могут приводит к гистерезису. Наконец, возможны трудности при различении реальных и кажущихся явлений гистерезиса, когда конечное состояние системы определяется, ее текущей динамикой или ее начальным состоянием. В первом случае гистерезис отражает наше незнание: добавив недостающие переменные и информацию, можно более полно описать эволюцию изучаемой системы.
Экономические причины гистерезиса (долгосрочной негибкости рынка труда) неоднозначны. Некоторые институциональные факторы ведут к гистерезису. Например, социальное страхование, особенно страхование по безработице, может через налоговую систему снижать спрос фирм на рабочую силу в официальной экономике. Безработица может вести к потере человеческого капитала и к «помечиванию» тех, кто долгое время остается безработным. Профсоюзы могут вести переговоры с целью поддерживать благосостояние их настоящих членов, игнорируя интересы аутсайдеров, оказавшихся безработными. Фиксированные издержки, связанные со сменой должности, места работы или отрасли, также могут приводит к гистерезису. Наконец, возможны трудности при различении реальных и кажущихся явлений гистерезиса, когда конечное состояние системы определяется, ее текущей динамикой или ее начальным состоянием. В первом случае гистерезис отражает наше незнание: добавив недостающие переменные и информацию, можно более полно описать эволюцию изучаемой системы.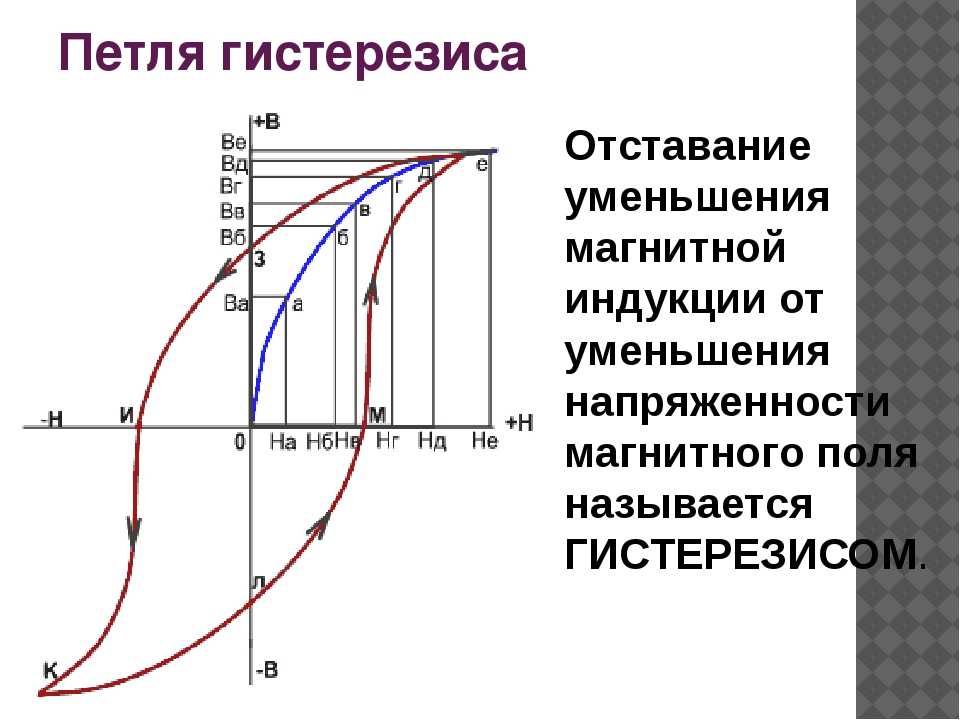 Др. интерпретация явления гистерезиса — простое существование нескольких состояний равновесия, когда невидимые воздействия перемещают экономику из одного состояния равновесия в др.
Др. интерпретация явления гистерезиса — простое существование нескольких состояний равновесия, когда невидимые воздействия перемещают экономику из одного состояния равновесия в др.
Математические модели гистерезиса
Появление математических моделей гистерезисных явлений обуславливалось достаточно богатым набором прикладных задач (прежде всего в теории автоматического регулирования), в которых носители гистерезиса нельзя рассматривать изолированно, поскольку они являлись частью некоторой системы. Создание математической теории гистерезиса относится к 60-м годам XX-го века, когда в Воронежском университете начал работать семинар под руководством М. А. Красносельского, «гистерезисной» тематики. Позднее, в 1983 году появилась монография [1], в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния как от параметра, определенные на достаточно богатом функциональном пространстве(напр. пространстве непрерывных функций), действующие в некоторое функциональное пространство.
пространстве непрерывных функций), действующие в некоторое функциональное пространство.
Свойства
Простое параметрическое описание различных петель гистерезиса можно найти в работе[2]. Замена гармонических функций на прямоугольные, треугольные или трапецеидальные импульсы позволяет получить кусочно-линейные петли гистерезиса, часто встречающиеся в дискретной автоматике.
Литература
- ↑ М.А. Красносельский,А.В.Покровский. Системы с гистерезисом М., Наука, 1983. 271 стр.
- ↑ R. V. Lapshin, “Analytical model for the approximation of hysteresis loop and its application to the scanning tunneling microscope”, Review of Scientific Instruments, volume 66, number 9, pages 4718-4730, 1995.(англ.)
См. также
Обменное смещение — как особенность петель гистерезиса.
Молекулярный магнитный гистерезис при 60 кельвинах в диспроцоцении
- Опубликовано:
- Conrad A. P. Goodwin 1 ,
- Fabrizio Ortu 1 ,
- Daniel Reta 1 ,
- Nicholas F. Chilton 1 и
- …
- David P. Mills 1 и
- …
- David P. Mills 1 и
- …
- David P. Mills 1 и
- …
- David P. Mills 1 и
- …
- .
Природа том 548 , страницы 439–442 (2017)Процитировать эту статью
-
26 тыс. обращений
-
1240 цитирований
-
265 Альтметрический
-
Сведения о показателях
Предметы
- Химическая физика
- Металлоорганическая химия
- Физическая химия
Abstract
Лантаноиды широко исследовались на предмет потенциального применения в квантовой обработке информации и хранении данных с высокой плотностью на молекулярном и атомном уровне.
 Экспериментальные достижения включают чтение и манипулирование отдельными ядерными спинами 1,2 , используя переходы атомных часов для надежных кубитов 3 и, совсем недавно, магнитное хранилище данных в отдельных атомах 4,5 . Одномолекулярные магниты демонстрируют магнитный гистерезис молекулярного происхождения 6 — эффект магнитной памяти и необходимое условие хранения данных — и до сих пор образцы лантаноидов демонстрировали это явление при самых высоких температурах. Однако за почти 25 лет, прошедших с момента открытия мономолекулярных магнитов 7 , температуры гистерезиса увеличились с 4 кельвинов до примерно 14 кельвинов 8,9,10 с использованием постоянной скорости развертки магнитного поля около 20 эрстед в секунду, хотя более высокие температуры были достигнуты за счет использования очень высокой скорости развертки 11,12 (например, 30 кельвинов с 200 эрстед в секунду) 12 . Здесь мы сообщаем о комплексе Hexa- TERT -ButyLydysProsocenium — [DY (CP TTT ) 2 ] [B (C 6 F 5 ) 4 ], с CP TTT = {C C C C C C C.
Экспериментальные достижения включают чтение и манипулирование отдельными ядерными спинами 1,2 , используя переходы атомных часов для надежных кубитов 3 и, совсем недавно, магнитное хранилище данных в отдельных атомах 4,5 . Одномолекулярные магниты демонстрируют магнитный гистерезис молекулярного происхождения 6 — эффект магнитной памяти и необходимое условие хранения данных — и до сих пор образцы лантаноидов демонстрировали это явление при самых высоких температурах. Однако за почти 25 лет, прошедших с момента открытия мономолекулярных магнитов 7 , температуры гистерезиса увеличились с 4 кельвинов до примерно 14 кельвинов 8,9,10 с использованием постоянной скорости развертки магнитного поля около 20 эрстед в секунду, хотя более высокие температуры были достигнуты за счет использования очень высокой скорости развертки 11,12 (например, 30 кельвинов с 200 эрстед в секунду) 12 . Здесь мы сообщаем о комплексе Hexa- TERT -ButyLydysProsocenium — [DY (CP TTT ) 2 ] [B (C 6 F 5 ) 4 ], с CP TTT = {C C C C C C C. C C C C. 5 Н 2 т Bu 3 -1,2,4} и t Bu = C(CH 3 ) 3 — который проявляет магнитный гистерезис при температурах до 60 кельвинов2 при скорости вращения в секунду. Мы наблюдаем четкое изменение динамики релаксации при этой температуре, которое сохраняется в образцах, разбавленных магнитным полем, что позволяет предположить, что источником гистерезиса являются локализованные колебательные моды металл-лиганд, которые являются уникальными для диспрозоцения. Ab initio расчеты спиновой динамики показывают, что магнитная релаксация при высоких температурах обусловлена локальными молекулярными колебаниями. Эти результаты показывают, что при разумном молекулярном дизайне хранение магнитных данных в отдельных молекулах при температурах выше жидкого азота должно быть возможным.
C C C C. 5 Н 2 т Bu 3 -1,2,4} и t Bu = C(CH 3 ) 3 — который проявляет магнитный гистерезис при температурах до 60 кельвинов2 при скорости вращения в секунду. Мы наблюдаем четкое изменение динамики релаксации при этой температуре, которое сохраняется в образцах, разбавленных магнитным полем, что позволяет предположить, что источником гистерезиса являются локализованные колебательные моды металл-лиганд, которые являются уникальными для диспрозоцения. Ab initio расчеты спиновой динамики показывают, что магнитная релаксация при высоких температурах обусловлена локальными молекулярными колебаниями. Эти результаты показывают, что при разумном молекулярном дизайне хранение магнитных данных в отдельных молекулах при температурах выше жидкого азота должно быть возможным. Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Соответствующие статьи
Статьи открытого доступа со ссылками на эту статью.

-
Проектирование молекулярных наномагнитов на основе данных
- Ян Дуан
- , Лорена Э. Розалени
- … Алехандро Гаита-Ариньо
Связь с природой Открытый доступ 09 декабря 2022 г.
-
Атомарно-точный контроль динамики вращения в заряженных редкоземельных комплексах на поверхности металла
- Толулоп Майкл Аджайи
- , Виджай Сингх
- … Сав Вай Хла
Связь с природой Открытый доступ 22 октября 2022 г.
-
Интерметаллический молекулярный наномагнетик с лантаноидом, координированным только переходными металлами.
- Михал Маготт
- , Мария Бжозовска
- … Давид Пинкович
Связь с природой Открытый доступ 19 апреля 2022 г.
Варианты доступа
Подписаться на журнал
Получить полный доступ к журналу на 1 год
199,00 €
всего 3,90 € за номер
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Рисунок 1: Синтез и структура [Dy(Cp ttt ) 2 ][B(C 6 F 5 ) 4 ] (1). Рис. 2: Магнитный гистерезис 1. Рис. 3: Динамика релаксации 1. Рис. 4: Ab initio спиновая динамика.Ссылки
-
Винсент Р., Кляцкая С., Рубен М., Вернсдорфер В. и Балестро Ф. Электронное считывание одиночного ядерного спина с использованием молекулярного спинового транзистора. Природа 488 , 357–360 (2012)
Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Тиле, С.
 и др. Электрически управляемый ядерный спиновый резонанс в одномолекулярных магнитах. Наука 344 , 1135–1138 (2014)
и др. Электрически управляемый ядерный спиновый резонанс в одномолекулярных магнитах. Наука 344 , 1135–1138 (2014) Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Шиддик, М. и др. Повышение когерентности в молекулярных спиновых кубитах с помощью переходов атомных часов. Природа 531 , 348–351 (2016)
Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Донати, Ф. и др. Магнитная остаточная намагниченность в одиночных атомах. Наука 352 , 318–321 (2016)
Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Natterer, F.D. et al. Чтение и запись одноатомных магнитов. Природа 543 , 226–228 (2017)
Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Гаттески Д .
 , Сессоли Р . & Villain, J. Molecular Nanomagnets (Oxford Univ. Press, 2006)
, Сессоли Р . & Villain, J. Molecular Nanomagnets (Oxford Univ. Press, 2006) -
Сессоли Р., Гаттески Д., Канески А. и Новак М. А. Магнитная бистабильность в металлоионном кластере. Природа 365 , 141–143 (1993)
Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Rinehart, J.D., Fang, M., Evans, W.J. & Long, J.R. N2 3– комплекс тербия с радикальным мостиком, проявляющий магнитный гистерезис при 14 K. J. Am. хим. соц. 133 , 14236–14239 (2011)
Статья КАС Google Scholar
-
Лю, Дж. и др. Стабильный пентагональный бипирамидальный одноионный магнит Dy(III) с рекордным барьером перемагничивания свыше 1000 К. Дж. Ам. хим. соц. 138 , 5441–5450 (2016)
Артикул КАС Google Scholar
-
Дин, Ю.
 -С., Чилтон, Н.Ф., Винпенни, Р.Е.П. и Чжэн, Ю.-З. О приближении к пределу молекулярной магнитной анизотропии: почти идеальный пятиугольный бипирамидальный магнетик из одной молекулы диспрозия (III). Анжю. хим. Междунар. Эд. 55 , 16071–16074 (2016)
-С., Чилтон, Н.Ф., Винпенни, Р.Е.П. и Чжэн, Ю.-З. О приближении к пределу молекулярной магнитной анизотропии: почти идеальный пятиугольный бипирамидальный магнетик из одной молекулы диспрозия (III). Анжю. хим. Междунар. Эд. 55 , 16071–16074 (2016) Артикул КАС Google Scholar
-
Чен Ю.-К. и другие. Поддерживаемая симметрией магнитная блокировка при 20 К в пятиугольных бипирамидальных одноионных магнитах Dy(III). Дж. Ам. хим. соц. 138 , 2829–2837 (2016)
Статья КАС Google Scholar
-
Гупта С.К., Раджешкумар Т., Раджараман Г. и Муругавел Р. Стабильный на воздухе одноионный магнит Dy(III) с высоким барьером анизотропии и температурой блокировки. Хим. науч. 7 , 5181–5191 (2016)
Артикул КАС Google Scholar
-
Эванс, В.
 Дж., Перотти, Дж. М., Брэди, Дж. К. и Зиллер, Дж. В. Исследования связанных олефинов координации алкена по сравнению с тетрафенилборатом и взаимодействия олефинов лантанидов в металлоценах. Дж. Ам. хим. соц. 125 , 5204–5212 (2003)
Дж., Перотти, Дж. М., Брэди, Дж. К. и Зиллер, Дж. В. Исследования связанных олефинов координации алкена по сравнению с тетрафенилборатом и взаимодействия олефинов лантанидов в металлоценах. Дж. Ам. хим. соц. 125 , 5204–5212 (2003) Артикул КАС Google Scholar
-
Berkefeld, A. et al. Активация монооксида углерода через O-связанный CO с использованием ионных пар декаметилскандоциний-гидридоборат. Дж. Ам. хим. соц. 134 , 10843–10851 (2012)
Артикул КАС Google Scholar
-
Kaita, S. et al. В конечном итоге специфическая 1,4-цис-полимеризация 1,3-бутадиена с новым гадолиниевым катализатором. Макромоль. Быстрое общение. 24 , 179–184 (2003)
Артикул КАС Google Scholar
-
Демир, С.
 , Задрозный, Дж. М., Ниппе, М. и Лонг, Дж. Р. Обменное связывание и магнитное блокирование в дилантанидных комплексах с бипиримидильными мостиками. Дж. Ам. хим. соц. 134 , 18546–18549 (2012)
, Задрозный, Дж. М., Ниппе, М. и Лонг, Дж. Р. Обменное связывание и магнитное блокирование в дилантанидных комплексах с бипиримидильными мостиками. Дж. Ам. хим. соц. 134 , 18546–18549 (2012) Артикул КАС Google Scholar
-
Демир С., Задрозный Дж. М. и Лонг Дж. Р. Большие барьеры спиновой релаксации для низкосимметричных лантанидорганических комплексов [Cp*2Ln(BPh5)] (Cp*=пентаметилциклопентадиенил; Ln=Tb, Dy). Хим. Евро. J. 20 , 9524–9529 (2014)
Статья КАС Google Scholar
-
Мэн, Ю.-С., Чжан, Ю.-К., Ван, З.-М., Ван, Б.-В. и Гао, С. Влияние вспомогательных лигандов на слабое поле лиганда на повышение производительности одноионного магнита. Хим. Евро. J. 22 , 12724–12731 (2016)
Статья КАС Google Scholar
-
Райнхарт, Дж.
 Д. и Лонг, Дж. Р. Использование одноионной анизотропии в конструкции одномолекулярных магнитов f-элемента. Хим. науч. 2 , 2078–2085 (2011)
Д. и Лонг, Дж. Р. Использование одноионной анизотропии в конструкции одномолекулярных магнитов f-элемента. Хим. науч. 2 , 2078–2085 (2011) Статья КАС Google Scholar
-
Чилтон, Н. Ф., Коллисон, Д., Макиннес, Э. Дж. Л., Винпенни, Р. Е. П. и Сончини, А. Электростатическая модель для определения магнитной анизотропии в комплексах диспрозия. Нац. коммун. 4 , 2551 (2013)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
-
Цзян, С.-Д., Ван, Б.-В., Сунь, Х.-Л., Ван, З.-М. & Gao, S. Металлоорганический одноионный магнит. Дж. Ам. хим. соц. 133 , 4730–4733 (2011)
Артикул КАС Google Scholar
-
Цзян С.-Д. и другие. Серия лантанидорганических одноионных магнитов. Неорг. хим. 51 , 3079–3087 (2012)
Статья КАС Google Scholar
-
Джелетич, М.
 и др. Металлоорганический сэндвич-лантаноидный одноионный магнит с необычным механизмом множественной релаксации. Дж. Ам. хим. соц. 133 , 19286–19289 (2011)
и др. Металлоорганический сэндвич-лантаноидный одноионный магнит с необычным механизмом множественной релаксации. Дж. Ам. хим. соц. 133 , 19286–19289 (2011) Артикул КАС Google Scholar
-
Чжан, П. и др. Одноионные магниты из лантанидов с экваториальной координацией. Дж. Ам. хим. соц. 136 , 4484–4487 (2014)
Статья КАС Google Scholar
-
Стоянов Е. С., Стоянова И. В. и Рид С. А. Основность ненасыщенных углеводородов по способности акцептора водородной связи: раздвоенная водородная связь N–H + ···π. Хим. Евро. J. 14 , 7880–7891 (2008)
Статья КАС Google Scholar
-
Го, Ф.-С. и другие. Одномолекулярный магнит из металлоцена диспрозия, работающий на осевом пределе.
 Анжю. хим. Междунар. Эд. http://dx.doi.org/10.1002/anie.201705426 (2017)
Анжю. хим. Междунар. Эд. http://dx.doi.org/10.1002/anie.201705426 (2017) -
Абрагам, А. и Блини, Б. Электронный парамагнитный резонанс переходных ионов Гл. 10 (Oxford Univ. Press, 1970)
-
Лунги А., Тотти Ф., Сессоли Р. и Санвито С. Роль ангармонических фононов в подбарьерной спиновой релаксации одномолекулярных магнитов. Нац. коммун. 8 , 14620 (2017)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
-
Эскалера-Морено, Л., Суауд, Н., Гаита-Ариньо, А. и Коронадо, Э. Определение ключевых локальных колебаний при релаксации молекулярных спиновых кубитов и одномолекулярных магнитов. J. Phys. хим. лат. 8 , 1695–1700 (2017)
Артикул КАС Google Scholar
-
Шривастава К. Н. Теория спин-решеточной релаксации. Физ.
 Status Solidi B 117 , 437–458 (1983)
Status Solidi B 117 , 437–458 (1983) Статья КАС ОБЪЯВЛЕНИЯ Google Scholar
-
Грегсон, М. и др. Монометаллический лантанид-бис(метандиид) магнит с одной молекулой с большим энергетическим барьером и сложным поведением спиновой релаксации. Хим. науч. 7 , 155–165 (2016)
Статья КАС Google Scholar
Загрузить ссылки
Благодарности
Мы выражаем признательность Исследовательскому совету по инженерным и физическим наукам (стипендия в C.A.P.G. и EP/P002560/1 для F.O. и DR), Мемориальному фонду стипендий Рамзи (стипендия NFC) и Университет Манчестера. Мы благодарим Манчестерский университет за доступ к магнитометру SQUID и Computational Shared Facility, а также REP Winpenny, EJL McInnes и D. Collison за комментарии.
Информация об авторе
Авторы и организации
-
Химическая школа Манчестерского университета, Оксфорд-роуд, Манчестер, M13 9PL, Великобритания
Конрад А.
 П. Гудвин, Фабрицио Орту, Даниэль П. Рета, Николас Ф. Миллс
П. Гудвин, Фабрицио Орту, Даниэль П. Рета, Николас Ф. Миллс
Авторы
- Conrad A. P. Goodwin
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Fabrizio Ortu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Daniel Reta
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Николас Ф. Чилтон
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Дэвид П. Миллс
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
C.A.P.G. и Д.П.М. представил оригинальную концепцию. К.
 А.П.Г. синтезированы и охарактеризованы соединения. Ф.О. выполнил рентгеноструктурный анализ монокристалла и вспомогательную работу по синтезу/характеристике. NFC собраны и интерпретированы магнитные данные. NFC разработал модель динамики релаксации и написал компьютерные программы для выполнения этих расчетов. Д.Р. и Н.Ф.С. выполнил расчеты. Д.П.М. и Н.Ф.С. написал рукопись с участием всех авторов. Д.П.М. и Н.Ф.С. курировал проект.
А.П.Г. синтезированы и охарактеризованы соединения. Ф.О. выполнил рентгеноструктурный анализ монокристалла и вспомогательную работу по синтезу/характеристике. NFC собраны и интерпретированы магнитные данные. NFC разработал модель динамики релаксации и написал компьютерные программы для выполнения этих расчетов. Д.Р. и Н.Ф.С. выполнил расчеты. Д.П.М. и Н.Ф.С. написал рукопись с участием всех авторов. Д.П.М. и Н.Ф.С. курировал проект. Авторы переписки
Переписка с Николас Ф. Чилтон или Дэвид П. Миллс.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих финансовых интересов.
Дополнительная информация
Информация для рецензентов Nature благодарит Р. Сессоли, П. Чжана и других анонимных рецензентов за их вклад в рецензирование этой работы.
Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
Дополнительная информация
Этот файл содержит дополнительные методы, обсуждение, данные и уравнения, дополнительные таблицы 1-21, дополнительные рисунки 1-64. Он включает подробную информацию о методах синтеза, кристаллографии, ЯМР, УФ-видимом-БИК, колебательных спектрах, магнитных данных, теоретическом анализе и дополнительных ссылках. Этот файл был заменен 4 сентября 2017 г. для исправления повреждения файла в уравнениях . (PDF 26419 КБ)
Дополнительные данные
Файл кристаллографической информации для 1 и 5-7 . (CIF 4576 KB)
PowerPoint Slide
PowerPoint Slide для рис.
Исходные данные
Исходные данные к рис. 1
Исходные данные к рис. 2
Исходные данные к рис. 3
Права и разрешения
Перепечатки и разрешения
Об этой статье
Эта статья цитируется
-
Приближение к одноосности магнитной анизотропии в одномолекулярных магнетиках
- Чен Ван
- Инь-Шань Мэн
- Сун Гао
Наука Китай Химия (2023)
-
Вычислительный дизайн магнитных молекул и их окружения с использованием квантовой химии, машинного обучения и многомасштабного моделирования
- Алессандро Лунги
- Стефано Санвито
Nature Reviews Chemistry (2022)
-
Проектирование молекулярных наномагнитов на основе данных
- Ян Дуан
- Лорена Э.
 Розалени
Розалени - Алехандро Гаита-Ариньо
Nature Communications (2022)
-
Интерметаллический молекулярный наномагнетик с лантаноидом, координированным только переходными металлами.
- Михал Магот
- Мария Бжозовска
- Давид Пинкович
Nature Communications (2022)
-
Анализ вибронной связи в молекулярном магнетике 4f с помощью FIRMS
- Джон Г.
 К. Крагскоу
К. Крагскоу - Джонатан Марби
- Николас Ф. Чилтон
Nature Communications (2022)
- Джон Г.
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Моделирование и симуляция нелинейного магнитного гистерезиса – x-engineer.org
Внутренние магнитные поля присутствуют во всех материалах, но с разной интенсивностью. В некоторых материалах влияние магнитного поля слабое, но в ферромагнитных материалах напряженность магнитного поля выражена хорошо. Намагниченность материала или вещества характеризуется магнитной индукцией Б [Тл] и напряженностью магнитного поля 9{-7} \frac{Wb}{A \cdot m}\]
Гистерезис наблюдается в ферромагнитных материалах как тенденция оставаться намагниченными после того, как приложенная сила поля была удалена.
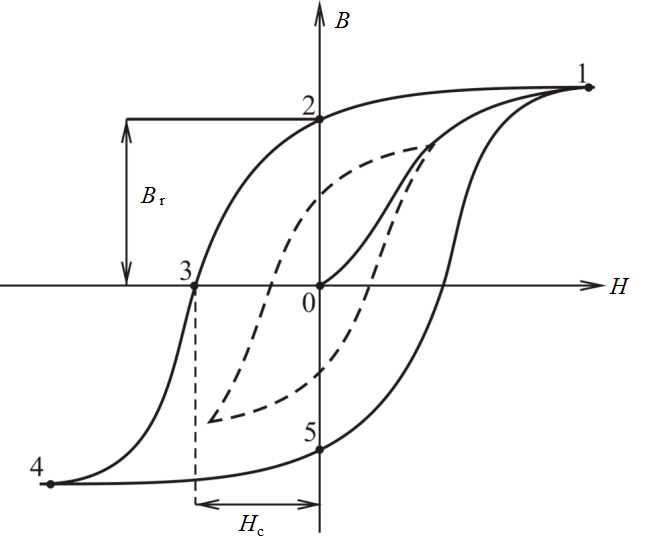
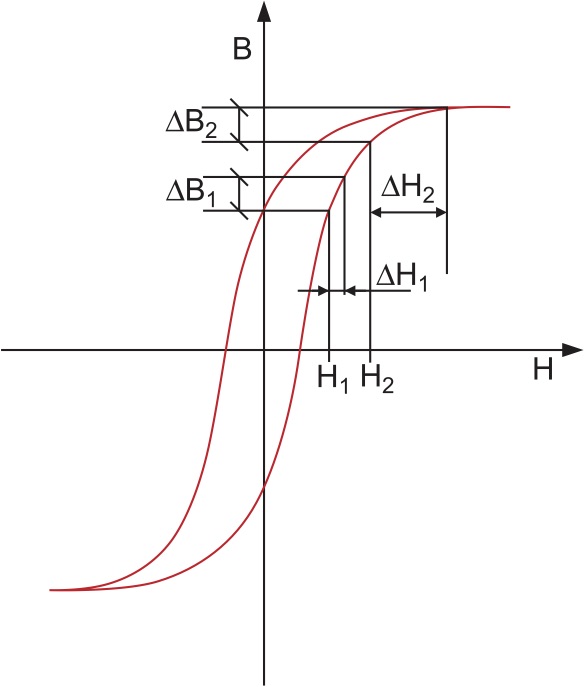
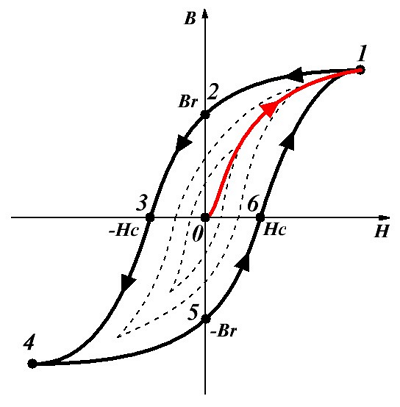
 Общее поведение магнитного сердечника, описанное в терминах B и H , показано на изображении ниже.
Общее поведение магнитного сердечника, описанное в терминах B и H , показано на изображении ниже. Изображение: Магнитный гистерезис B(H)
Наиболее важными параметрами кривой магнитного гистерезиса B(H) являются: уровень насыщения (B sat ), остаточная магнитная намагниченность (также называемая сохраняющей способностью ) и коэрцитивная сила (также называемая коэрцитивной силой ). Эти параметры имеют следующий физический смысл:
- Уровень насыщения : максимальная плотность поля, поддерживаемая магнитным материалом;
- Сохраняемость : это уровень намагниченности, который остается в материале после того, как напряженность магнитного поля установлена на ноль;
- Коэрцитивность : представляет собой значение напряженности магнитного поля, необходимое для возврата намагниченности материала к нулю.
Математическая модель, предложенная в этой статье, будет имитировать магнитный материал, который имеет кривую B(H) , аналогичную кривой на изображении выше. Эту модель можно рассматривать в контексте приложений управления, которые требуют точной характеристики взаимосвязи между входными токами и магнитным полем.
Модель Jiles-Atherton
Явление ферромагнитного гистерезиса может быть представлено моделью компании Jiles-Atherton (JA) . Модель JA использует магнитное поле H в качестве независимой переменной, что означает, что вход в модель равен H , а выход равен B . Уравнения , описывающие модель JA , представляют собой набор дифференциальных и алгебраических уравнений (2):
\[\left\{\begin{matrix}
H_{eff} &= H+ \alpha \cdot M\\
M_{anh} &= M_{sat} \cdot \text{tanh} \left ( \frac{H_{eff}}{\alpha} \right )\\
\frac{dM_{irr}}{dt} &= \frac{dH}{dt} \cdot \frac{M_{anh}-M_{irr}}{k \cdot \delta – \alpha (M_{anh}-M_{irr})} \\
M_ {rev} &= c \cdot (M_{anh}-M_{irr})\\
M &= M_{rev}+M_{irr}
\end{matrix}\right.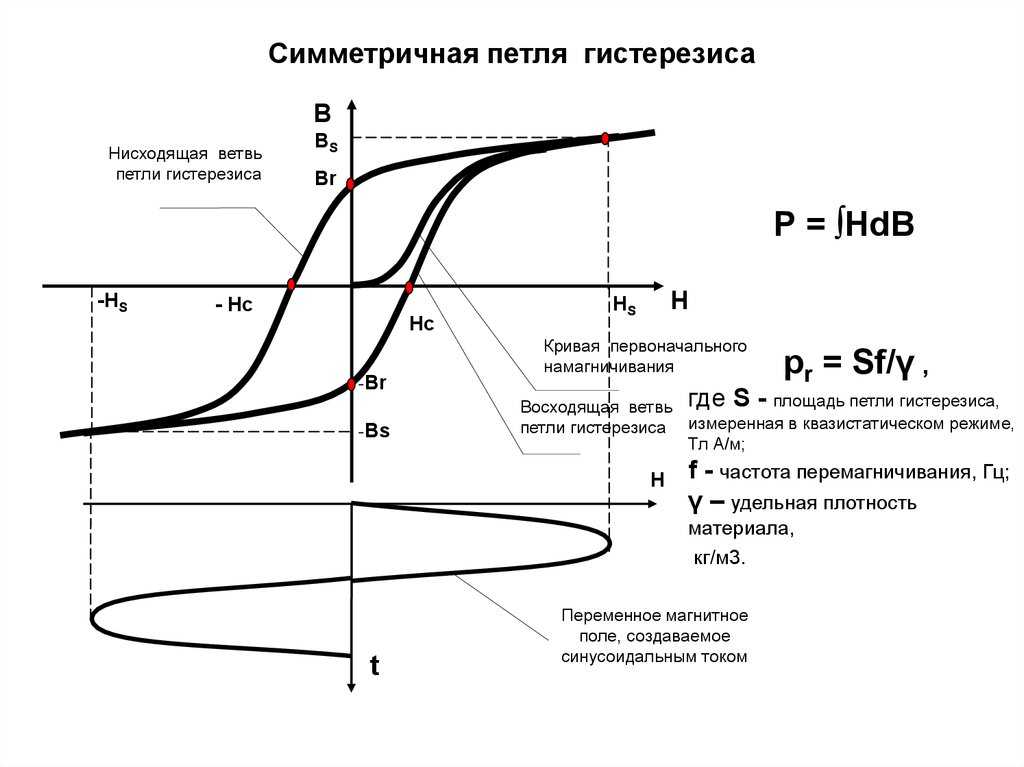 \]
\] Намагниченность ( M ) разлагается на обратимый ( M rev ) и необратимый компонент ( M irr ), соответствующие соответственно обратимой и необратимой деформации магнитных доменов. Связь между этими двумя компонентами и безгистерезисной намагниченностью ( M и ) основана на физических соображениях процесса намагничивания. Эффективная напряженность поля ( H eff ) учитывает как напряженность магнитного поля, так и уровень намагниченности ( М ).
Гистерезис реализован с помощью:
\[\delta = \text{sgn} \left ( \frac{dH}{dt} \right )\]
, который принимает значение 1 или -1 в зависимости от того, является ли это положительным или отрицательным полупериодом кривой гистерезиса .
Преимущество модели JA заключается в малом количестве требуемых параметров для определения математической модели.
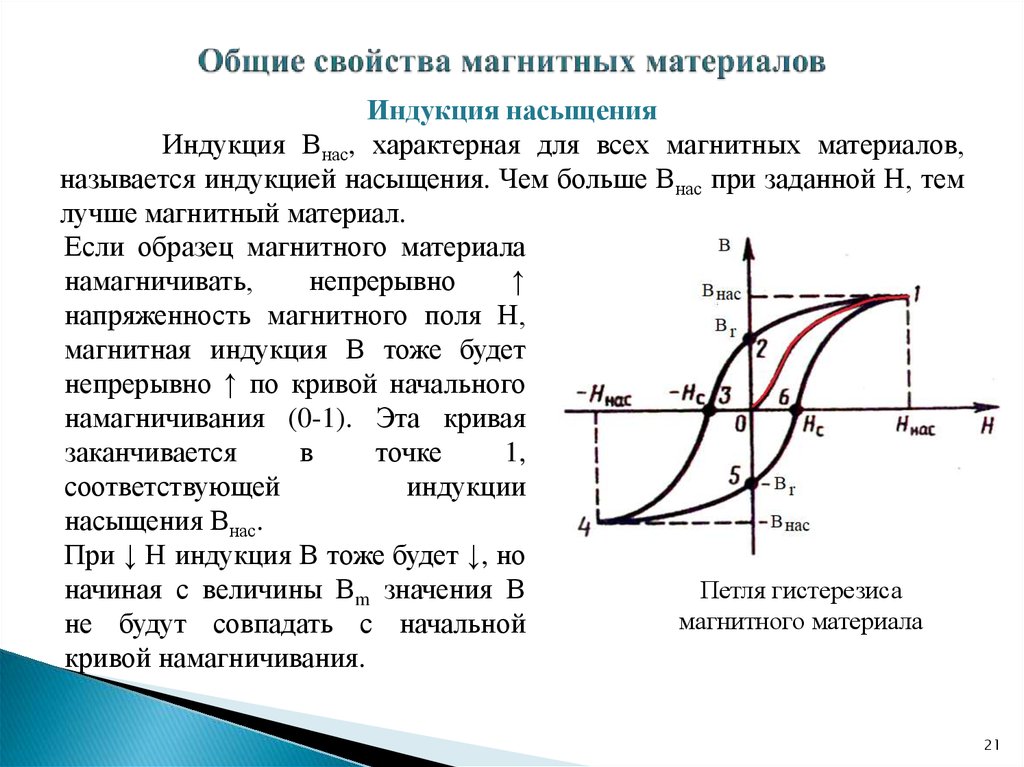
 Символ параметров, название, описание и эффекты на 9Кривая 0749 B(H) описана в таблице ниже.
Символ параметров, название, описание и эффекты на 9Кривая 0749 B(H) описана в таблице ниже. Symbol Physical property Effects on the B(H) characteristic M sat [A/m] Saturation magnetization Higher value leads к большим значениям насыщения кривой намагничивания a [А/м] Параметр формы M AN Более высокое значение приводит к снижению м AN наклона A [-] QUANTIFIEST DOMINESISTARICAITION 9089 898.SERELESTERESTERESTERESTERESTERESTERESTERESTERESTERISISISISMISIS .c [-] Коэффициент обратимости Более высокое значение приводит к более узкой кривой гистерезиса k [А/м] Средняя энергия, необходимая для разрыва точек закрепления Более высокое значение приводит к более широкой кривой гистрезиса Параметры JA-модели можно определить с помощью нескольких методов, таких как методы наименьших квадратов, генетические алгоритмы или расширенные процедуры оптимизации.
Модель блок-схемы магнитного гистерезиса Xcos
Набор уравнений (2) реализован в Scilab/Xcos для моделирования явления магнитного гистерезиса . Строится модель непрерывного времени, и моделирование выполняется с использованием различных методов интеграции. Все решатели должны выводить одинаковые результаты, чтобы доказать численную устойчивость модели.
Реализация Xcos уравнения (1) выглядит следующим образом:
Изображение: Нелинейный магнитный гистерезис Модель блок-диаграммы Xcos
Напряженность магнитного поля H подается в качестве входных данных в модель. Модель JA вычисляет намагниченность M , которая используется для расчета магнитной индукции B . Сила магнитного поля и магнитная индукция сохраняются в рабочей области Scilab как структурные переменные
Hsimи 9.0989 Бсим .The magnetic field strength H is generated through a
Signal Builderwith the following setup:Spline method (0 … 7) 1x x_timey y_HПериодический сигнал (д/н)? nЗапустить графическое окно (д/н)? nЗначения напряженности магнитного поля H и времени определены в сценарии Scilab (
*.) как: sce
sce x_time = [ 0,1,1050 4,5,6,7,8,9,10,11,12,13,14,15,.. 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]; y_H = [0.0E+00,0.0E+00,5.0E+02,-5.0E+02,1.0E+03,-1.0E+03,.. 2.0E+03,-2.0E+03,3.0E+03,-3.0E+03,4.0E+03,-4.0E+03,.. 5.0E+03,-5.0E+03,6.0E+03,-6.0E+03,7.0E+03,-7.0E+03,.. 8.0Е+03,-8.0Е+03,9.0E+03,-9.0E+03,1.0E+04,-1.0E+04,.. 1.1E+04,-1.1E+04,1.2E+04,-1.2E+04,1.3E+04,-1.3E+04,0.0E+00];Мы можем использовать функцию plot() , чтобы визуализировать изменение напряженности магнитного поля во времени.
Изображение: Изменение напряженности магнитного поля во времени H(t)
Даже если мы определим напряженность магнитного поля в качестве входных данных, мы сохраним ее в блоке
В рабочее пространство, чтобы иметь то же количество точек, что и переменная магнитная индукция. ПериодБлок часовустановлен на0,01 с.Детали модели блок-схемы JA можно увидеть на изображении ниже.
 Эта модель реализует набор уравнений (2), определенных выше.
Эта модель реализует набор уравнений (2), определенных выше. Изображение: модель блок-схемы Jiles-Atherton Xcos
Результаты моделирования Xcos
Смоделированная магнитная характеристика вычисляет инициализацию (первая кривая намагничивания), начиная с ненамагниченного состояния, за которой следует ее насыщенная петля гистерезиса . Для первого моделирования используются следующие параметры: M sat = 76500 А/м, a = 7012 А/м, α = 0,01, c = 0,18 и k = 3942 .
Параметры могут быть определены в консоли Scilab или в меню
Set contextв Xcos.Мс=76500;
а=7012;
альфа=0,01;
с=0,18;
k=3942;
miu0=1,2566e-5;Выполняется несколько симуляций для разных значений параметра формы ( α ) и средней энергии, необходимой для разрыва участков закрепления ( k ), чтобы подчеркнуть их влияние на кривую B(H) .

После запуска модели Xcos для
30 смы можем использовать следующие инструкции Scilab для построения кривой магнитного гистерезиса:plot(Hsim.values,Bsim.values) xlabel('Ч [А/м]','Размер шрифта',3) ylabel('B [T]','Размер шрифта',3) title('x-engineer.org','FontSize',3)Первый запуск с вышеуказанными параметрами дает следующую кривую намагничивания:
Изображение: Кривая намагничивания B(H) – результаты моделирования 1
Второй запуск с k = 2000 и α = 0,01 .
Изображение: Кривая намагничивания B(H) – результаты моделирования 2
Третий запуск с k = 3942 и α = 0,1 .
Изображение: Кривая намагничивания B(H) – результаты моделирования 3
Преимущество этой модели заключается в том, что ее можно использовать для целей моделирования, а также интегрировать в более сложные модели приводов или двигателей благодаря ее простоте и быстрому расчету. Чтобы иметь полную и проверенную модель нашего привода или двигателя, параметры JA должны быть идентифицированы одним из методов, упомянутых выше.
 Результаты моделирования показывают, что JA-модель является гибкой и может использоваться при разных значениях параметров ( М сб , а, α, с и к ).
Результаты моделирования показывают, что JA-модель является гибкой и может использоваться при разных значениях параметров ( М сб , а, α, с и к ). Модель нуждается в дальнейших улучшениях из-за того, что здесь наблюдается неожиданное увеличение общей намагниченности ( M ) сразу после изменения направления входного тока (около кончиков контура). Причиной был неправильный расчет общей намагниченности между точкой, в которой ток изменил направление, и точкой, где кривая намагничивания пересекает кривую без истерики. Было решено, что
намагниченность на этом участке кривой должна быть полностью обратимой. Это оправдано, поскольку доменные стенки, однажды деформированные в определенном направлении приложенным полем, должны сначала релаксировать до равновесия, а затем деформироваться в противоположном направлении, прежде чем произойдет какое-либо дальнейшее необратимое изменение. Чтобы учесть это изменение в уравнениях, необходимо включить дополнительный условный пункт, чтобы получить правильный расчет общей намагниченности.
-

 также
также