Множимое множитель произведение: Умножение чисел. Множимое, множитель и произведение

Умножение чисел. Множимое, множитель и произведение

• Множимое, множитель и произведение
• Проверка умножения

Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.

Пример. Во дворе посадили  3  ряда ёлок, по  4  ёлки в каждом ряду. Сколько ёлок посадили во дворе?

Чтобы ответить на этот вопрос, надо найти сумму  3  слагаемых, каждое из которых равно  4.

4 + 4 + 4 = 12.

Складывая  3  раза по  4  ёлки, мы получим общее количество ёлок во всех трёх рядах.

Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.

Для записи умножения используется знак  х  (косой крест)  или  ·  (точка),  который ставится между числами. Например:

4 х 3   или   4 · 3

Эта запись означает, что  4  надо умножить на  3.  Справа от записи умножения ставится знак  =  (равно),  после которого записывается полученный результат:

4 · 3 = 12.

Умножение – это краткая запись сложения одинаковых слагаемых.

Пример. Умножить  6  на  5  — это значит найти сумму пяти слагаемых, каждое из которых равно шести:

6 + 6 + 6 + 6 + 6 = 30.

Сократим запись, заменив сложение на умножение:

6 · 5 = 30.

Оба выражения равны:

6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,

но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.

Множимое, множитель и произведение

Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:

4 · 3,

4  — это множимое,  3  — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.

Произведение — это число, которое получается в результате умножения. Например, в записи:

4 · 3 = 12,

12  — это произведение.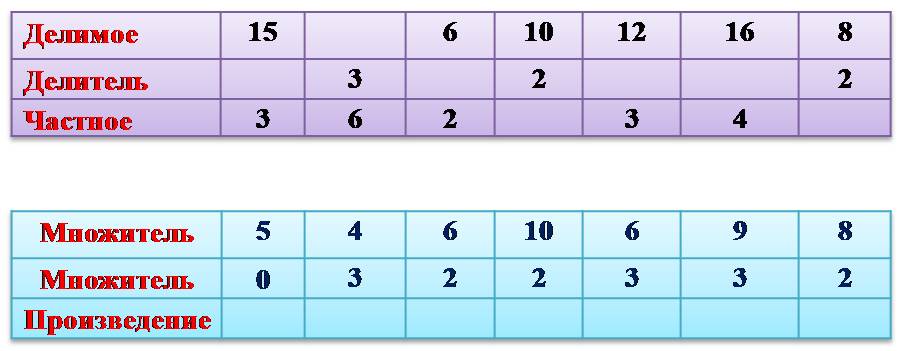 При этом сама запись  4 · 3  тоже называется произведением.

Эту запись можно прочитать так:  произведение четырёх и трёх равно двенадцати,  четыре умножить на три равно двенадцати,  по четыре взять три раза, получится двенадцать.

Множимое и множитель иначе называются множителями или сомножителями.

Проверка умножения

Рассмотрим выражение:

4 · 3 = 12,

где  4  — это множимое,  3  — это множитель, а  12  — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:

1. Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:

   12 : 3 = 4.

2. Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно:
   12 : 4 = 3.

Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.

Умножение | Математика

Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Основное свойство произведения

Произведение не изменяется от перемены порядка производителей.

Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:

Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.

Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.

Умножение однозначных чисел. Таблица Пифагора

Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.

Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).

Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:

1, 2, 3, 4, 5, 6, 7, 8, 9.

Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.

Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде

Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.

Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.

Умножение многозначного числа на однозначное

Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.

При этом ход вычислений выражают словесно:

1. Начинаем умножение с единиц

   : 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).

2. Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.

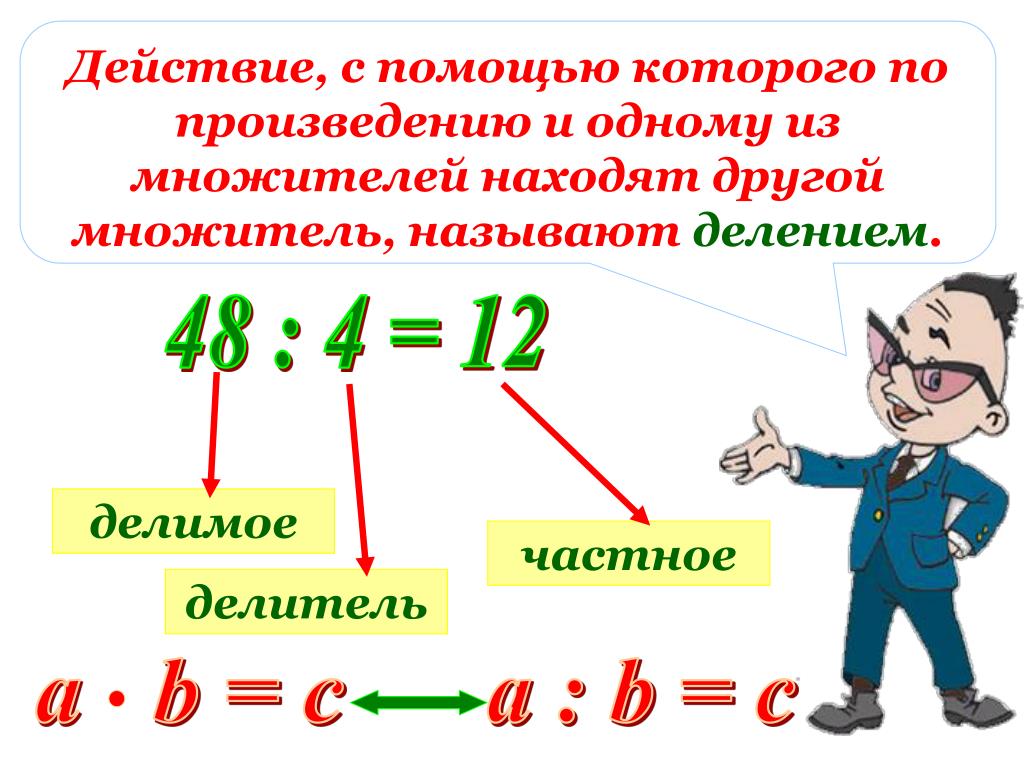
3. Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.

4. Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.

Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:

1. Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.

2. Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.

3. Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.

4. Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.

5. Умножение продолжается до тех пор, пока не получат полного произведения.

Умножение чисел на 10, 100, 1000 …

Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.

Этого достигают, приписывая к числу два нуля.

Отсюда заключаем:

Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.

Умножение числа 6035 на 1000 выразится письменно:

Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.

Умножение на число с нулями в конце

Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.

Ход вычисления выразится письменно:

Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4,    3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Выучить определение, факты и примеры

В математике есть четыре основных действия: сложение, вычитание, умножение и деление. Итак, умножение — одна из элементарных вычислительных операций в математике. В процессе умножения число, которое нужно умножить, называется множимым, а число, на которое мы умножаем, называется множителем. Произведение есть результат умножения. В приведенном ниже примере выполняется умножение 8 и 5, где 8 — множитель, 5 — множимое, а 40 — произведение. Для обозначения умножения используется знак «».

Изображение: Пример умножения

Свойства умножения

Существуют следующие свойства умножения:

1. Переместительное свойство умножения

продукт не меняется.

Например: 4 × 3 = 12 или 3 × 4 = 12

Итак, 4 × 3 = 3 × 4.

2. Ассоциативное свойство умножения

Согласно ассоциативному свойству умножения произведение трех или более чисел не изменится, если мы изменим группировку чисел .

Например: (4 × 7) × 5 = 28 × 5 = 140

или (7 × 5) × 4 = 35 × 4 = 140

или (4 × 5) × 7 = 20 × 7 = 140

3. Одно свойство умножения

Согласно одному свойству умножения произведение числа на 1 есть само число.

Например:

18 × 1 = 18

75 × 1 = 75

54 × 1 = 54

21 × 1 = 21

4. Zero Свойство умножения

в зависимости от свойства Zero. умножения результат умножения любого числа на ноль равен нулю.

Например:

5 × 0 = 0

0 × 15 = 0

24 × 0 = 0

90 × 0 = 0

5. Распределительное свойство умножения

Согласно распределительному свойству умножения произведение числа на сумму двух чисел всегда равно сумме произведения чисел.

Например:

4 × (3 + 5) = 4 × 8 = 32

4 × 3 + 4 × 5 = 32

Итак, 4 × (3 + 5) = 4 × 3 + 4 × 5 = 32

Точно так же произведение числа на разность двух чисел также всегда равно разности произведения чисел.

Например:

4 × (6 − 5) = 4

4 × 6 − 4 × 5 = 24 − 20 = 4

Итак, 4 × (6 − 5) = 4 × 6 − 4 × 5 = 4

Заключение

Учащимся важно четко понимать понятия множителя и множимого. Свойства умножения основаны на множителе и множимом. Каждое свойство умножения объясняется примерами в статье выше.

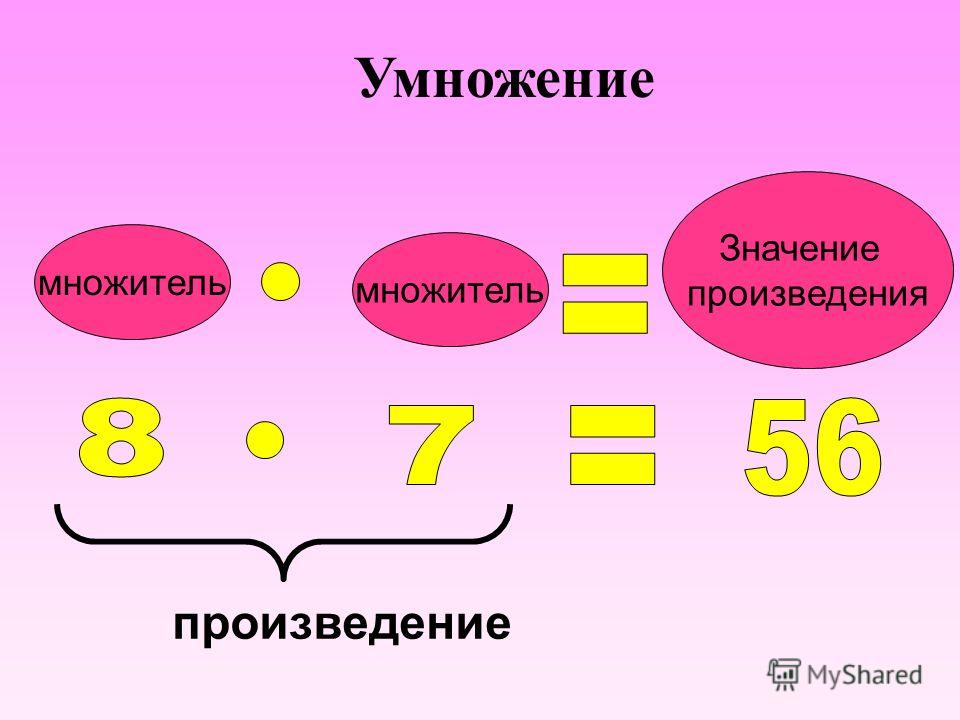
Умножитель — Cuemath

В математике умножение означает прибавление числа к самому себе определенное количество раз.

Умножение можно рассматривать как процесс многократного сложения.

Например, \(4 \times 3\) равно \(3+3+3+3=12\)

В этом коротком уроке мы узнаем о множителе и множимом. .

План урока

1.	Что означает множитель?
2.	Важные примечания по мультипликатору
3.	Решенные примеры на множителе
4.	Нестандартное мышление!
5.	Интерактивные вопросы по множителю

Что означает множитель?

Значение множителя в математике

Посмотрите на 3 группы по 7 кексов.

Вместо того, чтобы прибавлять семь три раза, мы можем записать это как \( 7 \times 3 =21\)

Это означает, что всего 21 кекс.

Здесь 7 — это множитель, а 3 — множимое.

Множитель и множимое являются частями оператора умножения.

---

Как найти продукт с помощью множителя?

Когда мы записываем оператор умножения по горизонтали, самое левое число является множителем.

Когда мы записываем оператор умножения вертикально, число сверху является множителем.

Посмотрите на сетку, показанную ниже.

Все прямоугольники, содержащиеся в сетке, соответствуют произведению множителя и множимого.

Это один из самых простых методов, используемых для чисел с меньшим количеством.

Поэкспериментируйте с приведенной ниже симуляцией, используя ползунки для изменения множителя и множимого, и посмотрите, как изменится произведение.

Важные примечания

1. Если множитель равен 1, то значения произведения и множимого равны.

2. Если множитель или множимое равно 0 в операторе умножения, то произведение всегда равно 0.

3. Изменение порядка множителя и множимого в операторе умножения не влияет на произведение.

4. Значения множителя и множимого всегда меньше или равны произведению.

Решенные примеры

Пример 1

 

 

Том получил 3 пачки коллекционных карточек, и в каждой пачке было по 5 карточек.

Итак, сколько всего карточек получил Том?

Выразите это как оператор умножения и укажите множитель и множимое.

Решение

Количество карточек в одной колоде коллекционных карточек = 5

Количество карточек в 3 колодах коллекционных карточек = \(5 \умножить на 3=15\)

Итак, у Тома всего 15 карточек.

Множитель и множимое равны 5 и 3 соответственно.

Пример 2

 

 

Лягушка должна прыгать на каждую третью плитку, не наступая ни на одно число между ними.

Начинает прыгать с цифры 3

Можете ли вы перечислить плитки, на которые он прыгает?

Какой здесь множитель?

Решение

Раскрасим каждую третью плитку, когда лягушка прыгает по дорожке.

Заметим, что плитки, на которые прыгает лягушка, кратны 3: 3, 6, 9, 12, 15, 18,…

Итак, множитель равен 3

 

Аналитический центр

1.	Следующая карта содержит неполную сетку из 5 столбцов. Выполните соответствующие вычисления, чтобы найти пропущенные числа. Наконец, в каждой сетке есть пять выбранных чисел. Перенесите их в последний столбец, и последняя задача — найти сумму всех этих чисел.

Интерактивные вопросы 

Вот несколько заданий для практики.

Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

 

 

 

---

Подведем итоги

Этот мини-урок посвящен увлекательной концепции умножения. Математическое путешествие по Multiplier начинается с того, что студент уже знает, и продолжается творческим созданием новой концепции в умах молодых. Сделано таким образом, что это не только понятно и понятно, но и останется с ними навсегда. В этом заключается магия Cuemath.

Надеемся, вам понравилось изучение значения множителя в математике.

О Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.

---

Часто задаваемые вопросы (FAQ)

1.