Мощность через сопротивление. Мощность, напряжение и сопротивление в электрических цепях: основные понятия и формулы

Что такое электрическое напряжение и как оно связано с током. Как рассчитать мощность в электрической цепи. Какую роль играет сопротивление проводников. Как применять закон Ома на практике.

Основные понятия электрического тока

Электрический ток представляет собой упорядоченное движение заряженных частиц в проводнике. Для возникновения тока необходимо создать электрическое поле, которое приводит заряженные частицы в движение. Появление свободных зарядов возможно при контакте двух различных веществ.

Вещества, в которых заряды могут свободно перемещаться, называются проводниками. Вещества, в которых заряды неподвижны, называются изоляторами или диэлектриками. Однако эта классификация условна, так как способность проводить электрические заряды у разных веществ различна — они обладают разным электрическим сопротивлением.

Сила тока и ее характеристики

Основной характеристикой электрического тока является сила тока. Она равна количеству заряженных частиц, проходящих через поперечное сечение проводника за единицу времени:

I = dq / dt,

где dq — количество заряда, dt — время.

Электрические заряды бывают положительными и отрицательными. В наэлектризованном теле ток будет протекать некоторое время, пока заряд не иссякнет. Для обеспечения длительного существования тока необходимо поддерживать разность потенциалов с помощью источника тока.

Напряжение в электрической цепи

Напряжение — один из основных параметров, характеризующих электрический ток. Оно показывает работу электрического поля по перемещению единичного заряда между двумя точками цепи. Напряжение измеряется в вольтах (В).

Для возникновения напряжения необходим источник тока. В разомкнутой цепи напряжение есть только на клеммах источника. При замыкании цепи напряжение и ток появляются на ее участках.

Напряжение измеряют вольтметром, подключая его параллельно к исследуемому участку цепи.

Мощность в электрических цепях

Мощность характеризует скорость совершения работы электрическим полем. Она равна произведению силы тока на напряжение:

P = IU,

где P — мощность, I — сила тока, U — напряжение.

Физически мощность показывает интенсивность передачи электрической энергии. Для измерения мощности используются ваттметры.

Мощность работы электроприборов зависит от силы тока и напряжения, при которых они работают. Чем выше эти параметры, тем больше мощность.

Активная и реактивная мощность

Различают активную и реактивную мощность:

• Активная мощность преобразуется в механическую, тепловую, световую и другие виды энергии.
• Реактивная мощность характеризует нагрузку на индуктивные и емкостные элементы, вызванную колебательным характером энергии электромагнитного поля.

Электрическое сопротивление проводников

Электрическое сопротивление определяет силу тока, протекающего при заданном напряжении в цепи. Сопротивление элемента цепи равно отношению напряжения на нем к силе протекающего тока:

R = U / I,

<где R - сопротивление, U - напряжение, I - сила тока.

Знание сопротивлений элементов необходимо для расчета напряжений и токов в цепи.

Виды источников питания

Источники питания бывают двух основных видов:

• Источники постоянного тока (батарейки, аккумуляторы и др.) — электродвижущая сила постоянна.
• Источники переменного тока (генераторы и др.) — электродвижущая сила меняется по синусоидальному закону с определенной частотой.

Активное и реактивное сопротивление

Различают активное и реактивное сопротивление:

• Активное сопротивление не зависит от частоты тока. В цепях переменного тока сила тока на активном сопротивлении меняется синхронно с напряжением.
• Реактивное сопротивление характерно для емкостных и индуктивных элементов. На реактивной нагрузке ток отстает или опережает напряжение по фазе.

Особенности реактивных элементов

Реактивные элементы имеют ряд особенностей:

• В емкостном элементе ток опережает напряжение.
• В индуктивном элементе ток отстает от напряжения.
• При подключении разряженного конденсатора к источнику постоянного тока в начальный момент наблюдается максимальный ток при минимальном напряжении. По мере зарядки ток уменьшается, а напряжение растет.
• При подключении конденсатора к источнику переменного тока происходит его постоянная перезарядка с частотой сети. Увеличение тока происходит раньше, чем рост напряжения.

Закон Ома для участка цепи

Закон Ома устанавливает связь между напряжением, силой тока и сопротивлением участка цепи:

I = U / R

Этот закон позволяет рассчитать любую из трех величин, зная две другие. Он справедлив для участков цепи, не содержащих источников тока.

Последовательное и параллельное соединение проводников

При последовательном соединении проводников:

• Общее сопротивление равно сумме сопротивлений отдельных проводников
• Сила тока одинакова во всех проводниках
• Общее напряжение равно сумме напряжений на отдельных проводниках

При параллельном соединении:

• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных проводников
• Напряжение одинаково на всех проводниках
• Общий ток равен сумме токов в отдельных проводниках

Работа и мощность электрического тока

Работа электрического тока равна произведению напряжения, силы тока и времени:

A = UIt

Мощность электрического тока можно рассчитать по формулам:

P = UI = I^2R = U^2/R

Эти формулы позволяют определить мощность, зная различные параметры цепи.

Тепловое действие тока

При протекании электрического тока проводники нагреваются. Количество теплоты, выделяемое проводником с током, определяется законом Джоуля-Ленца:

Q = I^2Rt

где Q — количество теплоты, I — сила тока, R — сопротивление, t — время.

Этот закон лежит в основе работы многих нагревательных электроприборов.

Что такое напряжение, ток, сопротивление: разбираемся на примерах

Содержание

Не имея определенных начальных знаний об электричестве, тяжело себе представить, как работают электрические приборы, почему вообще они работают, почему надо включать телевизор в розетку, чтобы он заработал, а фонарику хватает маленькой батарейки, чтобы он светил в темноте.

И так будем разбираться во всем по порядку.

Электричество

Электричество – это природное явление, подтверждающее существование, взаимодействие и движение электрических зарядов. Электричество впервые было обнаружено еще в VII веке до н.э. греческим философом Фалесом. Фалес обратил внимание на то, что если кусочек янтаря потереть о шерсть, он начинает притягивать к себе легкие предметы. Янтарь на древнегреческом – электрон.

Вот так и представляю себе, сидит Фалес, трет кусок янтаря о свой гиматий (это шерстяная верхняя одежда у древних греков), а затем с озадаченным видом смотрит, как к янтарю притягиваются волосы, обрывки ниток, перья и клочки бумаги.

Данное явление называется статическим электричеством. Вы можете повторить данный опыт. Для этого хорошенько потрите шерстяной тканью обычную пластмассовую линейку и поднесите ее к мелким бумажным кусочкам.

Следует отметить, что долгое время это явление не изучалось. И только в 1600 году в своем сочинении «О магните, магнитных телах и о большом магните – Земле» английский естествоиспытатель Уильям Гилберт ввел термин – электричество. В своей работе он описал свои опыты с наэлектризованными предметами, а также установил, что наэлектризовываться могут и другие вещества.

Далее на протяжении трех веков самые передовые ученые мира исследуют электричество, пишут трактаты, формулируют законы, изобретают электрические машины и только в 1897 году Джозеф Томсон открывает первый материальный носитель электричества – электрон, частицу, благодаря которой возможны электрические процессы в веществах.

Электрон – это элементарная частица, имеет отрицательный заряд примерно равный -1,602·10^-19 Кл (Кулон). Обозначается е или е^–.

Напряжение

Чтобы заставить перемещаться заряженные частицы от одного полюса к другому необходимо создать между полюсами разность потенциалов или – Напряжение. Единица измерения напряжения – Вольт (В или V). В формулах и расчетах напряжение обозначается буквой V. Чтобы получить напряжение величиной 1 В нужно передать между полюсами заряд в 1 Кл, совершив при этом работу в 1 Дж (Джоуль).

Для наглядности представим резервуар с водой расположенный на некоторой высоте. Из резервуара выходит труба. Вода под естественным давлением покидает резервуар через трубу. Давайте условимся, что вода – это электрический заряд, высота водяного столба (давление) – это напряжение, а скорость потока воды – это электрический ток.

Таким образом, чем больше воды в баке, тем выше давление. Аналогично с электрической точки зрения, чем больше заряд, тем выше напряжение.

Начнем сливать воду, давление при этом будет уменьшаться. Т.е. уровень заряда опускается – величина напряжения уменьшается. Такое явление можно наблюдать в фонарике, лампочка светит все тусклее по мере того как разряжаются батарейки. Обратите внимание, чем меньше давление воды (напряжение), тем меньше поток воды (ток).

 

Электрический ток

Электрический ток – это физический процесс направленного движения заряженных частиц под действием электромагнитного поля от одного полюса замкнутой электрической цепи к другому. В качестве частиц, переносящих заряд, могут выступать электроны, протоны, ионы и дырки. При отсутствии замкнутой цепи ток невозможен. Частицы способные переносить электрические заряды существуют не во всех веществах, те в которых они есть, называются проводниками и полупроводниками. А вещества, в которых таких частиц нет – диэлектриками.

Принято считать направление тока от плюса к минусу, при этом электроны движутся от минуса к плюсу!

Единица измерения силы тока – Ампер (А). В формулах и расчетах сила тока обозначается буквой I. Ток в 1 Ампер образуется при прохождении через точку электрической цепи заряда в 1 Кулон (6,241·10¹⁸ электронов) за 1 секунду.

 

Вновь обратимся к нашей аналогии вода – электричество. Только теперь возьмем два резервуара и наполним их равным количеством воды. Отличие между баками в диаметре выходной трубы.

Откроем краны и убедимся, что поток воды из левого бака больше (диаметр трубы больше), чем из правого. Такой опыт – явное доказательство зависимости скорости потока от диаметра трубы. Теперь попробуем уравнять два потока. Для этого добавим в правый бак воды (заряд). Это даст большее давление (напряжение) и увеличит скорость потока (ток). В электрической цепи в роли диаметра трубы выступает сопротивление.

Проведенные эксперименты наглядно демонстрируют взаимосвязь между напряжением, током и сопротивлением. Подробнее о сопротивлении поговорим чуть позже, а сейчас еще несколько слов о свойствах электрического тока.

Если напряжение не меняет свою полярность, плюс на минус, и ток течет в одном направлении, то – это постоянный ток и соответственно постоянное напряжение. Если источник напряжения меняет свою полярность и ток течет то в одном направлении, то в другом – это уже переменный ток и переменное напряжение. Максимальные и минимальные значения (на графике обозначены как Io) – это амплитудные или пиковые значения силы тока. В домашних розетках напряжение меняет свою полярность 50 раз в секунду, т.е. ток колеблется то туда, то сюда, получается, что частота этих колебаний составляет 50 Герц или сокращенно 50 Гц. В некоторых странах, например в США принята частота 60 Гц.

Сопротивление

Электрическое сопротивление – физическая величина, определяющая свойство проводника препятствовать (сопротивляться) прохождению тока. Единица измерения сопротивления – Ом (обозначается Ом или греческой буквой омега Ω). В формулах и расчетах сопротивление обозначается буквой R. Сопротивлением в 1 Ом обладает проводник к полюсам которого приложено напряжение 1 В и протекает ток 1 А.

Проводники по-разному проводят ток. Их проводимость зависит, в первую очередь, от материала проводника, а также от сечения и длины. Чем больше сечение, тем выше проводимость, но, чем больше длина, тем проводимость ниже. Сопротивление – это обратное понятие проводимости.

На примере водопроводной модели сопротивление можно представить как диаметр трубы. Чем он меньше, тем хуже проводимость и выше сопротивление.

Сопротивление проводника проявляется, например, в нагреве проводника при протекании в нем тока. Причем, чем больше ток и меньше сечение проводника – тем сильнее нагрев.

 

Мощность

Электрическая мощность – это физическая величина, определяющая скорость преобразования электроэнергии. Например, вы не раз слышали: «лампочка на столько-то ватт». Это и есть мощность потребляемая лампочкой за единицу времени во время работы, т.е. преобразовании одного вида энергии в другой с некоторой скоростью.

Источники электроэнергии, например генераторы, также характеризуется мощностью, но уже вырабатываемой в единицу времени.

Единица измерения мощности – Ватт (обозначается Вт или W). В формулах и расчетах мощность обозначается буквой P. Для цепей переменного тока применяется термин Полная мощность, единица измерения – Вольт-ампер (В·А или V·A), обозначается буквой S.

И в завершение про Электрическую цепь. Данная цепь представляет собой некоторый набор электрических компонентов, способных проводить электрический ток и соединенных между собой соответствующим образом.

Что мы видим на этом изображении – элементарный электроприбор (фонарик). Под действием напряжения U (В) источника электроэнергии (батарейки) по проводникам и другим компонентам обладающих разными сопротивлениями R (Ом) от плюса к минусу течет электрический ток I (А) заставляющий светиться лампочку мощностью P (Вт). Не обращайте внимания на яркость лампы, это из-за плохого давления и малого потока воды батареек.

Фонарик, что представлен на фотографии, собран на базе конструктора «Знаток». Данный конструктор позволяет ребенку в игровой форме познать основы электроники и принцип работы электронных компонентов. Поставляется в виде наборов с разным количеством схем и разного уровня сложности.

Напряжение, мощность и 📙 сопротивление в электрической цепи

1. Напряжение электрических цепей
2. Мощность электрических цепей
3. Сопротивление электрических цепей

Электрическая цепь – это комплекс устройств, соединенных проводами с целью передачи, распределения и сохранения электроэнергии. Основными параметрами электроцепей есть сила тока и напряжение. Электрическая схема – это графическое изображение электроцепи при помощи соответствующих обозначений.

Для начала стоит обозначить, чем является электрический ток. Электрически током есть упорядоченное перемещение заряженных частиц в проводнике. Для того, чтобы заряженные частички начали двигаться, создается электрическое поле, которое определенным образом приводит их в движение. При этом появление заряженных частиц возможно при тесном контакте двух разных веществ. В отдельных веществах заряды свободно перемещаются по их объему, в других – вовсе неподвижны. Вещества, в которых заряды свободно движутся, – это проводники, а те, в которых заряды не перемещаются – изоляторы или диэлектрики. Такая классификация считается условной, так как способность проводить электрические заряды различным веществам свойственна в разной мере, то есть они обладают различным сопротивлением прохождению электрических частичек.

Электрический ток характеризует сила тока, которая равна количеству заряженных частиц, перемещающемуся за единицу времени через поперечное сечение вещества:

\(i={dq\over dt},\)

где \(dq\) – количество заряда;

       \(dt\) – время.

Электрические заряды бывают положительные и отрицательные. Если наэлектризовать какое-либо тело, ток в нем будет протекать некоторое время, пока заряд не угаснет сам собой. Для обеспечения его длительного существования необходимо действие электрического поля, то есть разности потенциалов.

Такое поле может быть сформировано источником электрического тока.

Самый простой пример протекания электрического тока – это соединение заряженного тела при помощи проводника с землей.

Основными величинам, характеризующими электрический ток, считаются сила тока, напряжение и сопротивление. Они взаимосвязаны между собой и характеризуют основные процессы, протекающие в электроцепях.

Напряжение является одним из главных параметров, описывающих электрический ток. Электрический ток в физическом смысле – это упорядоченное перемещение электронов. Электрическое поле, которое формирует данное перемещение, выполняет для этого определенную работу. Работа электрического поля будет тем больше, чем большее количество заряда перемещается в единицу времени.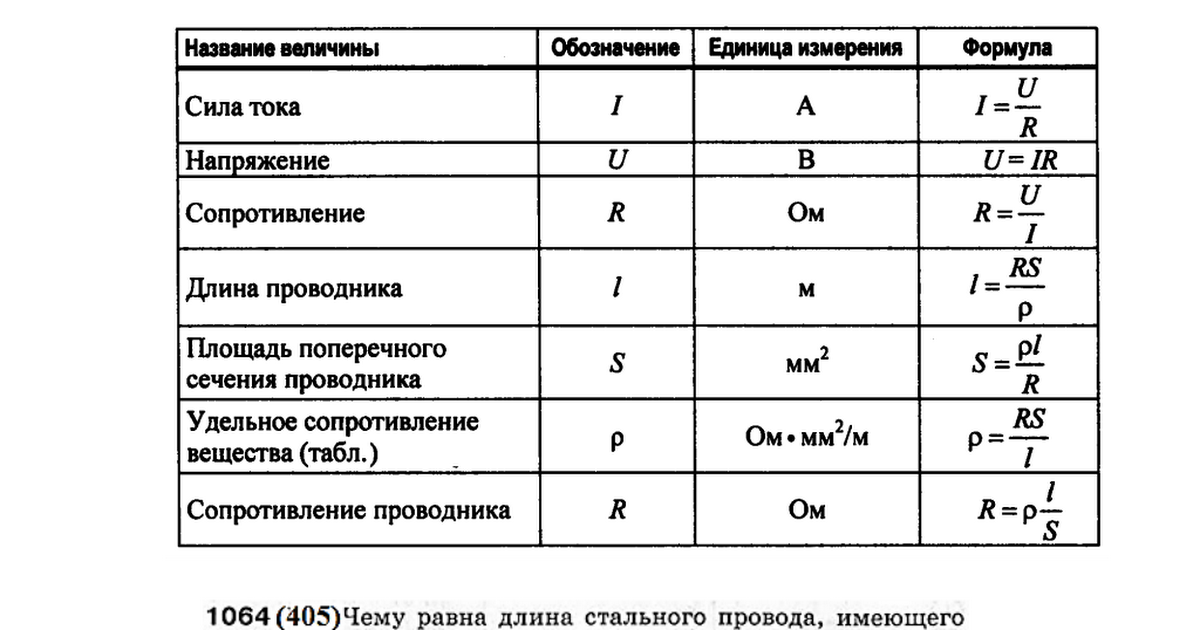

Напряжение является важнейшим фактором воздействия на работу электрического поля, и показывает отношение величины данной работы к количеству заряда, проходящего через определенный участок цепи. Работа электрического тока измеряется в Джоулях (Дж), а заряд – в Кулонах (Кл). Соответственно, напряжение измеряется в Дж/Кл, что является Вольтом (В).

Для появления напряжения необходим источник тока. Если цепь находится в разомкнутом положении, то напряжение есть лишь на клеммах источника. При включении источника в цепь, напряжение и ток появляется на ее участках. Измеряют напряжение прибором, именуемым вольтметр, подключая его параллельно к участку цепи, на котором необходимо его измерить.

Электрический потенциал приравнивается к отношению работы электрического поля к единичному заряду. То есть, такому заряду, который при попадании в электрическое поле, не искажает его. Таким образом:

\(dф = {dЭ \over dq_0}={Э \over q_0},\)

где \(ф\) – электрический потенциал;

       \(Э\) – работа электрического поля;

       \(q_0\) – единичный заряд.

Напряжение – это разность потенциалов между двумя точками электрического поля. Если мы обозначим данные точки 1 и 2, то напряжение между ними будет равняться:

\(U_{1-2} = ф_1-ф_2={dЭ_1 \over dq_0 }-{dЭ_2 \over dq_0}={dЭ_ {1-2} \over dq_0};\)

\(U_{1-2} = {dЭ_ {1-2} \over dq_0};\)

\(U_{2-1} =- {dЭ_ {1-2} \over dq_0};\)

То есть, напряжение – это работа электрополя по передвижению единичного заряда между двумя точками. В пассивных элементах электроцепей направления напряжения и тока одинаковы.

Мощность является еще одним параметром, описывающим поведение заряженных частиц. Мощностью является количество работы, совершаемой в единицу времени.>

Мощность электрического поля характеризует скорость его работы и равняется произведению силы тока и напряжения:

\(P=IU,\)

где \(P\) – мощность электротока;

       \(I\) – сила тока;

       \(U\) – напряжение.

Физически мощность показывает интенсивность передачи электрической энергии. Для измерения значения мощности используют ваттмеры. Мощность равняется количеству работы на перемещение электрических зарядов, совершенной за единицу времени:

\(P= {A \over δt},\)

где \(A\) – работа;

      \(δt\) – время совершения работы.

Мощность работы различных приборов зависит от силы тока и напряжения, при котором они работают. Чем выше эти параметры, тем выше мощность.

Электрическая мощность бывает активной и реактивной. Активная мощность превращается в механическую, тепловую, световую и иные виды энергии.

Реактивной мощностью является степень электрической нагрузки на индуктивные и емкостные элементы, что вызывается колебательным характером энергии электромагнитного поля.

Электрическое сопротивление определяет силу тока, протекающего при определенном напряжении цепи. Электрическим сопротивлением элемента является отношение напряжения на элементе, к силе тока, что по нему протекает:

\(R= {U \over I},\)

где \(R\) – сопротивление элемента цепи;

      \(U\) – напряжение;

       \(I\) – сила тока.

Для вычисления напряжения и тока элементов цепи необходимо знать их сопротивления. Источники питания бывают двух видов: источники постоянного тока (батарейки, аккумуляторы и прочее) и источники переменного тока (генераторы и прочие). В первых электродвижущая сила есть величиной постоянной, а во вторых – меняющейся по закону синуса с соответствующей частотой.

Различают активное и реактивное сопротивление. Активное не зависимо от частоты изменения ЭДС, что означает для сетей переменного тока, что сила тока на таком сопротивлении меняется синхронно напряжению. А реактивное сопротивление присуще для емкостных и индуктивных элементов цепи.

Для реактивной нагрузки характерно отставание либо опережение тока от напряжения. В емкостном элементе ток опережает напряжение, а в индуктивном – отстает от него.

Для примера можно привести разряженный конденсатор, в котором в момент подключения к постоянному току наблюдается максимальное значение тока при минимальной величине напряжения.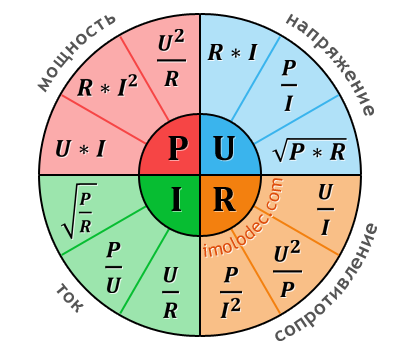 Постепенно при его зарядке ток уменьшается, а напряжение растет до полной зарядки. При этом, подключив его к переменному току, конденсатор будет постоянно перезаряжаться с частотой сети, и будет наблюдаться увеличение тока раньше, чем напряжения.

3.2: Сопротивление и рассеяние энергии

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

21516

• Том Вайдеман
• Калифорнийский университет, Дэвис

Удельное сопротивление

В предыдущем разделе мы сказали, что поток электрических зарядов вызывается приложенным электрическим полем, и что то, что происходит с зарядами, подобно сопротивлению воздуха, поскольку достигается «предельная скорость» (в случае электричества, это скорость дрейфа). Мы знаем, что увеличение электрического поля увеличивает скорость дрейфа, а вместе с ней и плотность тока, но точная взаимосвязь не очевидна. С помощью экспериментов (и/или теоретических моделей, выходящих за рамки этого курса) мы обнаруживаем, что на самом деле вектор электрического поля и вектор плотности тока прямо пропорциональны:

\[ \overrightarrow E = \left(constant\right) \overrightarrow J \]

Логично, что эти два вектора указывают в одном и том же направлении, поскольку ток определяется как направление потока положительного заряда. Константа пропорциональности называется удельным сопротивлением и обозначается греческой буквой \(\rho\):

\[ \overrightarrow E = \rho\; \overrightarrow J \]

Это соотношение известно как закон Ома .

Оповещение

В физике часто случается столкновение одной и той же переменной, используемой для более чем одной величины, например, \(T\) для периода и температуры или \(V\) для объема и электростатического потенциала. Но коллизия использования \(\rho\) в Physics 9C, пожалуй, больше всего раздражает. Эта буква появляется в нескольких уравнениях, связанных с плотностью тока — как в определении скорости дрейфа, так и в уравнении непрерывности, где это плотность заряда, и в законе Ома. Физиков это не беспокоит, потому что они сохраняют свежесть контекста уравнений в своей памяти, но студенты, впервые сталкивающиеся с этими уравнениями — особенно так близко друг к другу — могут испугаться. Решение состоит в том, чтобы научиться думать об уравнениях в контексте, помня о физической системе, а не думать о них как о мешанине непонятных переменных.

Беглый взгляд на уравнение закона Ома показывает, что чем больше удельное сопротивление, тем меньше движущиеся заряды реагируют на электрическое поле. Итак, какие физические свойства играют роль в этом эффекте «трения»? По сути, на удельное сопротивление влияют две вещи, обе они связаны с материалом, через который протекает заряд:

• его молекулярная структура
• его температура

Молекулярная структура проявляется таким образом, что невозможно подробно описать ее без знаний в области квантовой физики. Но есть два основных способа, которыми вступает в игру специфика типа используемого материала. Во-первых, сколько свободных электронов допускает материал — при прочих равных удельное сопротивление ниже, когда доступно больше свободного заряда. Проводники дают много свободных электронов, полупроводники гораздо меньше, а изоляторы практически ничего. Среди проводников оказывается, что чем «правильнее» (или, может быть, слово «предсказуемый» более показательно) решетка неподвижных ядер, тем лучше она проводит (т. е. меньше удельное сопротивление). У металлов, представляющих собой сплавы (смеси различных элементов), ядра атомов расположены более беспорядочно, и поэтому они имеют более высокое удельное сопротивление.

Влияние температуры на удельное сопротивление данного материала более интуитивно понятно. Вспомните, что замедляют электроны столкновения с ядрами атомов в решетке материала. Эти атомы постоянно вибрируют, энергия которых определяется температурой материала. Когда температура в проводнике повышается, более сильные вибрации этих препятствий приводят к большему количеству столкновений (опять же, структура решетки становится менее «предсказуемой»). Таким образом, для проводников удельное сопротивление увеличивается с повышением температуры. Интересно, что для полупроводников верно обратное — повышение температуры приводит к снижению удельного сопротивления. Причина этого в том, что удельное сопротивление в полупроводниках в основном связано с небольшим количеством свободных электронов. При повышении температуры многие из связанных электронов получают энергию и вырываются на свободу. Таким образом, хотя колеблющиеся атомы в решетке по-прежнему создают больше столкновений в полупроводнике, увеличение количества доступных свободных электронов является гораздо более важным фактором, и удельное сопротивление снижается.

Мы можем аппроксимировать реакцию удельного сопротивления на температуру линейной зависимостью. Если мы измеряем удельное сопротивление материала при температуре \(T_o\) как \(\rho_o\), то удельное сопротивление при новой температуре \(T\) определяется как:

\[\rho\left(T \right) = \rho_o\left[1+\alpha\left(T-T_o\right)\right] \]

Константа \(\alpha\) называется коэффициентом удельного сопротивления . Мы знакомы с линейными аппроксимациями физических свойств, подобных этому. Например, нечто очень похожее (в том числе и с температурой!) мы видели в случае теплового расширения в Физике 9.B.

Сопротивление

Как обычно бывает, легче иметь дело со скалярными энергиями, чем с векторными силами, поэтому мы ищем способ уйти от нашего использования электрического поля и плотности тока. Чтобы обсудить энергию, нам нужно перейти к использованию электростатического потенциала, а не электрического поля. Рассмотрим простую физическую систему, состоящую из цилиндрического проводника с площадью поперечного сечения \(A\), длиной \(L\) и разностью потенциалов \(V_A-V_B\) (напомним, что мы больше не рассматриваем проводники быть эквипотенциальными): 9B \overrightarrow E\cdot\overrightarrow{dl} = E\cdot L && \Rightarrow && E =\dfrac{V}{L} \\ E=\rho\;J && \Rightarrow && E = \rho\dfrac{ I}{A} \end{массив} \right\}\;\;\; V=I\left(\dfrac{\rho L}{A}\right) = IR\]

Величина \(R \equiv \frac{\rho L}{A}\) содержит всю информацию о проводника, необходимого для определения силы тока по разности напряжений: его длины, площади поперечного сечения и удельного сопротивления. Это значение \(R\) называется сопротивлением кондуктора. Его единицы можно легко определить из приведенного выше уравнения – это вольты на ампер. Этой единице дано собственное имя – Ом (\(\Омега\)). Это уравнение, которое связывает падение напряжения, ток и сопротивление, является просто упрощенной версией закона Ома и обычно называется одним и тем же именем (далее мы будем делать это).

Мощность

С этой энергетической точки зрения мы можем видеть, что заряд падает в потенциальной энергии, когда он переходит от более высокого потенциала к более низкому (хорошо, технически это отрицательно заряженные электроны, которые переходят от более низкого потенциала к более высокому, но это все равно уменьшение потенциальной энергии). Но мы также знаем, что скорость дрейфа не меняется, поэтому потерянная потенциальная энергия не переходит в кинетическую энергию. Куда это идет? Подобно воздушному трению, электрическое сопротивление приводит к преобразованию энергии в тепловую. Это означает, что проводник с сопротивлением будет нагреваться при протекании по нему тока.

Поскольку мы сейчас говорим о протекающем заряде, проще говорить о скорости , при которой энергия преобразуется из электрической потенциальной энергии в тепловую энергию. Мы знаем, что когда заряд \(q\) падает через потенциал \(V\), он теряет потенциальную энергию, равную \(U=qV\). Скорость, с которой это происходит (т. е. мощность), является скоростью изменения этого во времени. Поскольку напряжение остается фиксированным, мы имеем:

\[P = \frac{d}{dt}\left(qV\right) = \frac{dq}{dt}V = IV\]

92}{R}\]

Эта система уравнений для мощности поразительно похожа на систему уравнений для потенциальной энергии в конденсаторе, приведенную в уравнениях 2.4.11 (за исключением отсутствия множителя \(\ frac{1}{2}\) везде). Подобно этим уравнениям, выбор того, какое из этих выражений использовать, часто зависит от того, какие величины неизменны в физической ситуации. Например, если вы увеличите сопротивление и приложите к нему такое же напряжение, вы обнаружите, что скорость преобразования энергии в тепловую равна нижний . Но если вместо этого ток остается фиксированным, скорость преобразования энергии в тепловую увеличивается с увеличением сопротивления.

Alert

Одним из наиболее распространенных примеров, которые мы будем использовать при обсуждении мощности в электрических цепях, является электрическая лампочка, поскольку она обеспечивает хорошее визуальное представление преобразования электрической энергии в другую форму, которая выходит из цепи. Используя наши формулы для мощности, становится ясно, что мощность перестает преобразовываться в тот момент, когда перестает течь ток, но можно заметить, что (например) лампочка накаливания продолжает светиться некоторое время после разрыва соединения. Это не означает, что ток продолжает течь в течение короткого времени после этого — насколько нам известно, ток прекращается по существу немедленно. Непрерывное свечение возникает из-за того, что свечение возникает из-за повышенной температуры нити накала, а затем отключение тока позволяет нити охлаждаться с любой скоростью, естественной для ее охлаждения в окружающей среде, поэтому (видимый) свет гаснет. только при температуре ниже определенной. Эта задержка во времени охлаждения нити накала отвечает за медленное угасание света; это не отставание в уменьшении тока.

---

Эта страница под названием 3.2: Resistance and Energy Dissipation распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип артикула

   Раздел или Страница

   Автор

   Том Вайдеман

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@родной

Внутреннее сопротивление | Батареи и другие источники питания

Внутреннее сопротивление | Батареи и другие источники питания

В электрических цепях, которые мы рассматривали до сих пор, мы рассматривали источник напряжения, питающий цепь, как источник напряжения. идеальный источник напряжения. то есть:

• Мы предположили, что напряжение, подаваемое в цепь, остается постоянным, независимо от величины тока, протекающего через нее. поставляется.
• Мы также предположили, что энергия преобразуется в тепло только за счет сопротивления во внешней цепи.

На практике это не так, так как:

1. Напряжение на клеммах батареи уменьшается по мере увеличения тока, подаваемого в цепь.
   Одинаково для всех реальных источников напряжения. (Однако разработчики источников питания производят стабилизированные источники питания, в которых обратная связь схемы используются для поддержания относительно постоянного выходного напряжения).
2. Все блоки питания нагреваются во время использования, что свидетельствует о том, что часть энергии, которую они обеспечивают, на самом деле потребляется. преобразуется в тепло внутри самого блока питания!

Это показано на анимации ниже.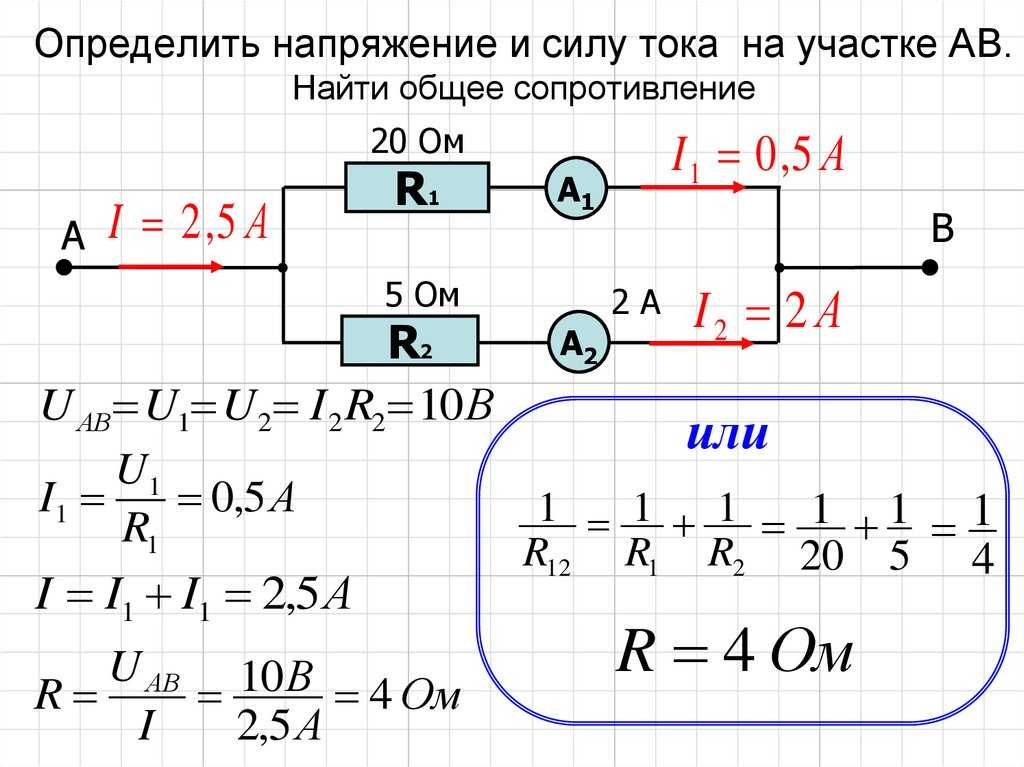

Это изменение напряжения питания потенциально трудно объяснить, особенно если принять во внимание фактическое причины изменения будут зависеть от типа используемого источника питания.
Например:

• Для батареи: напряжение падает, потому что скорость химических реакций, передающих заряд на клеммы батареи, не может соответствовать скорости, с которой заряд покидает клеммы, чтобы течь по цепи.
• Для генератора: ток создает более сильные магнитные поля внутри генератора, которые замедляют работу генератора и уменьшают напряжение питания.

К счастью, мы можем избежать этих подробностей и, независимо от фактического характера источника питания, мы можем представить его с помощью модель блока питания, полностью состоящая из простых электрических компонентов. Один из способов сделать это — представить власть питание как идеальный источник напряжения (ЭДС) последовательно с внутренним сопротивлением. Когда эта модель источника питания применяется к внешней цепи, ток цепи также протекает через внутреннее сопротивление. Это приводит к внутреннему падению напряжения внутри источника питания, что снижает напряжение на клеммах источника питания. Мощность, рассеиваемая внутренним сопротивлением, представляет собой тепло, выделяемое в источнике питания. Это показано на анимации ниже.

Напряжение на клеммах (В) равно ЭДС. напряжение (E) минус внутреннее падение напряжения (Ir).
(используя закон Ома: внутреннее падение напряжения = ток (I) x внутреннее сопротивление (r)).

• В = Е — Ир.

Чтобы смоделировать любой реальный источник питания, нам просто нужно определить правильные значения E и r для использования.

Когда источник питания не подключен к цепи, ток не течет, поэтому:

• В = Е — 0 х г .
• В = Е .
• , т. е. напряжение ЭДС, равно напряжению на клеммах холостого хода источника питания.

Внутреннее сопротивление можно определить, подключив цепь известного сопротивления и измерив протекающий ток.