N обозначение. N-обозначение и L в электрике: все, что нужно знать об обозначениях проводов

Что означает буква N на электрических схемах. Чем отличается нулевой рабочий проводник от нулевого защитного. Как правильно обозначать фазные и нейтральные провода. Какие цвета используются для маркировки проводов.

Что такое N-обозначение в электрике?

В электротехнике буква N используется для обозначения нейтрального или нулевого рабочего проводника. Это один из основных проводников в электрической цепи наряду с фазным проводником, который обозначается буквой L.

Нейтральный проводник выполняет важные функции:

• Обеспечивает протекание рабочего тока в однофазных цепях
• Служит обратным проводом для фазных проводников
• Поддерживает симметрию напряжений в трехфазных системах

Чем отличается нулевой рабочий проводник от защитного?

Важно различать нулевой рабочий проводник (N) и нулевой защитный проводник (PE). Их основные отличия:

Нулевой рабочий (N)	Нулевой защитный (PE)
Предназначен для протекания рабочего тока	Служит для защиты от поражения током
Обозначается голубым цветом	Обозначается желто-зеленым цветом
Соединяется с нейтралью трансформатора	Соединяется с заземляющим устройством

Как правильно обозначать фазные и нейтральные провода?

В электрических схемах используются следующие буквенные обозначения проводников:

• L1, L2, L3 — фазные проводники в трехфазной системе
• N — нейтральный (нулевой рабочий) проводник
• PE — защитный заземляющий проводник
• PEN — совмещенный нулевой рабочий и защитный проводник

Важно соблюдать эти обозначения при монтаже электропроводки для обеспечения безопасности и правильного функционирования электрооборудования.

Цветовая маркировка проводов: международные стандарты

Для визуальной идентификации проводников используется цветовая маркировка согласно международным стандартам:

• Коричневый, черный, серый — фазные проводники
• Голубой — нейтральный проводник
• Желто-зеленый — защитный заземляющий проводник

Соблюдение этой цветовой кодировки крайне важно для безопасности при проведении электромонтажных работ.

Особенности обозначения проводников в разных странах

Несмотря на существование международных стандартов, в некоторых странах используются свои системы обозначений:

• В США фазные проводники обозначаются черным и красным цветом
• В Великобритании для фазы используется коричневый цвет
• В старых советских схемах нулевой провод мог быть белым

При работе с зарубежным электрооборудованием важно учитывать эти особенности маркировки.

Почему так важно правильное обозначение проводников?

Корректная маркировка проводов имеет критическое значение по нескольким причинам:

1. Обеспечение электробезопасности при монтаже и ремонте
2. Предотвращение ошибок подключения оборудования
3. Упрощение диагностики неисправностей
4. Соблюдение требований нормативных документов

Неправильное обозначение проводников может привести к серьезным авариям и поражению электрическим током.

Как определить назначение проводника, если маркировка отсутствует?

В ситуации, когда цветовая маркировка проводов отсутствует или неразличима, можно воспользоваться следующими методами:

• Измерение напряжения между проводниками и землей
• Проверка целостности цепи с помощью мультиметра
• Трассировка проводки специальным прибором
• Анализ электрической схемы объекта

Однако самым надежным способом остается правильная маркировка проводников при монтаже.

Измерение напряжения между проводниками

Для определения назначения проводников можно измерить напряжение между ними и относительно земли:

• Между фазным и нейтральным — 220-230 В
• Между фазным и землей — 220-230 В
• Между нейтральным и землей — близко к 0 В

Важно соблюдать меры предосторожности при работе с электричеством!

Проверка целостности цепи мультиметром

С помощью функции «прозвонки» мультиметра можно проверить целостность цепи и определить, какие проводники соединены между собой. Это помогает выявить нулевой рабочий и защитный проводники.

Трассировка проводки специальным прибором

Для поиска и идентификации скрытой проводки применяются специальные трассоискатели. Они позволяют проследить путь проводника в стене и определить его назначение.

Какие ошибки чаще всего допускаются при обозначении проводников?

При маркировке электропроводки нередко допускаются следующие ошибки:

• Использование неправильных цветов для обозначения проводников
• Путаница между нулевым рабочим и защитным проводниками
• Отсутствие маркировки на концах проводов
• Применение нестандартных обозначений

Эти ошибки могут привести к серьезным последствиям, поэтому важно тщательно соблюдать правила маркировки.

Использование неправильных цветов

Часто встречается ситуация, когда для маркировки проводников используются случайные цвета, имеющиеся в наличии. Это недопустимо, так как может привести к ошибкам при подключении оборудования.

Путаница между N и PE проводниками

Нередко при монтаже путают нулевой рабочий (N) и защитный (PE) проводники. Это опасно, так как может привести к появлению напряжения на корпусах оборудования.

Отсутствие маркировки на концах проводов

Иногда при монтаже забывают промаркировать концы проводов в распределительных коробках. Это сильно затрудняет последующее обслуживание электропроводки.

Чтобы избежать подобных ошибок, необходимо строго следовать правилам маркировки и перепроверять обозначения перед подключением оборудования.

Современные тенденции в обозначении электропроводки

В последние годы наметились новые тенденции в маркировке электрических проводников:

• Применение самоклеящихся этикеток с цветовой и буквенной маркировкой
• Использование лазерной гравировки обозначений на изоляции кабелей
• Внедрение электронных систем идентификации проводников
• Разработка «умных» кабелей со встроенными чипами

Эти инновации призваны повысить надежность идентификации проводников и снизить вероятность ошибок при монтаже.

Самоклеящиеся этикетки

Современные самоклеящиеся этикетки для маркировки проводов имеют ряд преимуществ:

• Стойкость к воздействию влаги и химических веществ
• Хорошая читаемость маркировки
• Возможность нанесения дополнительной информации
• Простота применения

Такие этикетки значительно упрощают процесс маркировки проводников при монтаже.

Лазерная гравировка обозначений

Нанесение маркировки с помощью лазера непосредственно на изоляцию кабеля обеспечивает:

• Долговечность обозначений
• Высокую точность и читаемость
• Возможность нанесения сложных обозначений

Этот метод особенно эффективен для маркировки проводов в сложных промышленных системах.

Электронные системы идентификации

Системы электронной идентификации проводников используют специальные метки и сканеры. Их преимущества:

• Быстрое определение назначения проводника
• Возможность хранения дополнительной информации
• Интеграция с системами автоматизации

Такие системы особенно полезны при обслуживании сложных электрических сетей.

Внедрение современных методов маркировки позволяет повысить безопасность и эффективность работы с электрооборудованием. Однако важно помнить, что они не заменяют базовых правил обозначения проводников, а лишь дополняют их.

n — Викисловарь

Текущая версия (не проверялась)

В Википедии есть статья «N (латиница)».

Эта статья или раздел не соответствует текущим правилам оформления статей. Пожалуйста, оформите её согласно правилам и указаниям.

• 1 Латиница
  • 1.1 Произношение
  • 1.2 Общие значения
  • 1.3 Технические данные
  • 1.4 Этимология
• 2 Эсперанто
  • 2.1 Морфологические и синтаксические свойства
  • 2.2 Семантические свойства
    • 2.2.1 Значение
• 3 Французский
  • 3.1 Морфологические и синтаксические свойства
  • 3.2 Произношение
  • 3.3 Семантические свойства
    • 3.3.1 Значение
    • 3.3.2 Синонимы
    • 3.3.3 Антонимы
    • 3.3.4 Гиперонимы
    • 3.3.5 Гипонимы
  • 3. 4 Родственные слова
  • 3.5 Этимология

заглавная	строчная
N	n

Буква латинского алфавита

Произношение[править]

Английскийen: МФА: [ŋ] в сочетании «ng» МФА: [n] Албанскийsq: Венгерскийhu: Испанскийes: Китайскийzh (пиньинь): МФА: [ŋ] в сочетании «ng» МФА: [n]

Немецкийde: Португальскийpt: Татарскийtt: Токипонаtokи: Турецкийtr: Финскийfi: Французскийfr: Испанскийes: Японскийja (ромадзи): МФА: [n] перед гласной МФА: [ŋ]

Общие значения[править]

1. n. 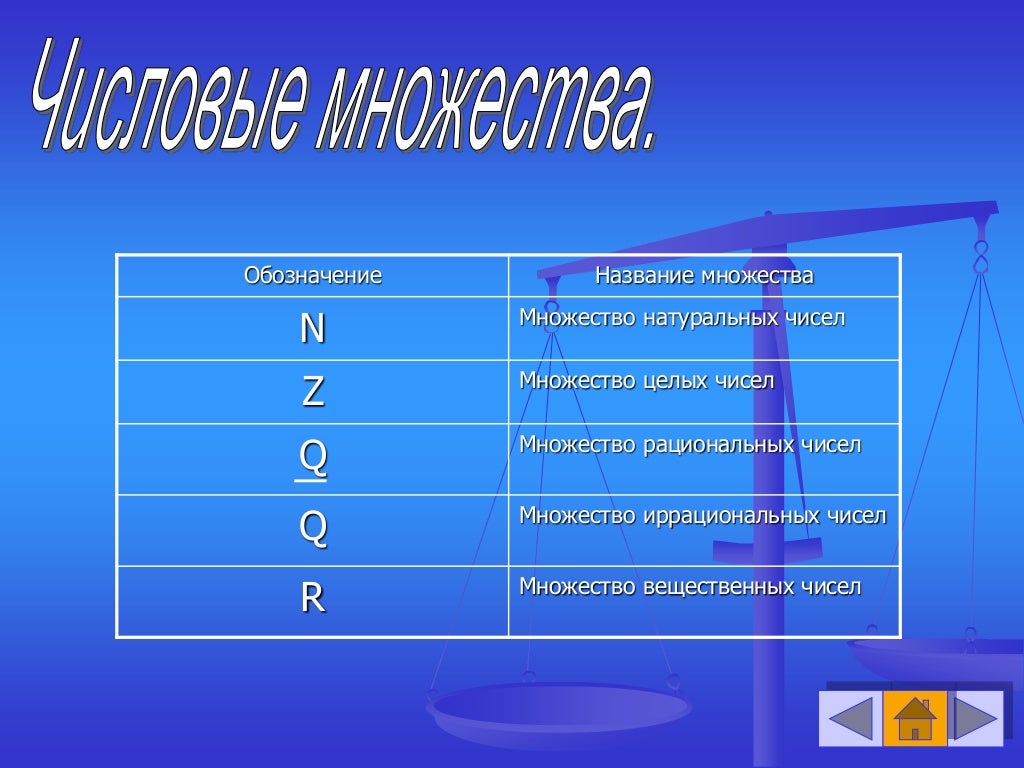физика приставка нано-

   12 nm — двенадцать нанометров

Технические данные[править]

• Unicode: 106 (#x006A), LATIN SMALL LETTER N
• ASCII: 106 (0x6A)

Этимология[править]

От греческой ню (Ν, ν)

Морфологические и синтаксические свойства[править]

n

Семантические свойства[править]

Значение[править]

18-я буква эсперантского алфавита

Морфологические и синтаксические свойства[править]

n

Существительное, ?? род.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. техн. эн; сокр. от coefficient, paramètre

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Этимология[править]

Это болванка статьи. Вы можете помочь проекту, исправив и дополнив её. (См. общепринятые правила.)

Вес тела — формула, определение, обозначение

​ ​

Покажем, как применять знание физики в жизни

Начать учиться

Быть космонавтом — это непросто. Хотя бы потому, что на земле мы ходим ногами, а в космосе — просто парим. Такой эффект называют «невесомость», о ней и поговорим.

Невесомость: что это такое

Невесомость — это состояние, при котором тело не давит на опору или подвес.

Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Вес тела

Вес — это сила, с которой тело действует на опору или подвес.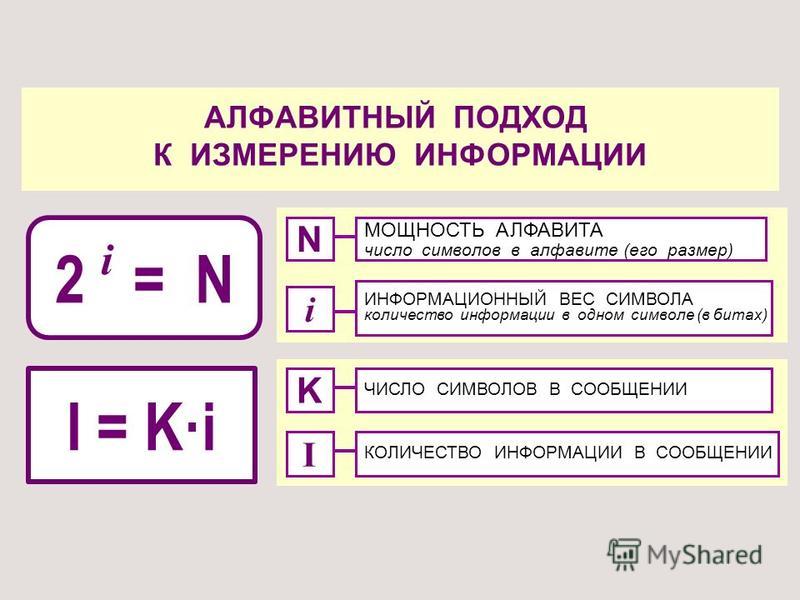 Измеряется вес, как и любая другая сила, в Ньютонах.

«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»

Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.

Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!

Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:

P = mg P — вес тела [Н] m — масса [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2

Здесь может возникнуть два возражения:

1. Это же сила тяжести, а не вес. 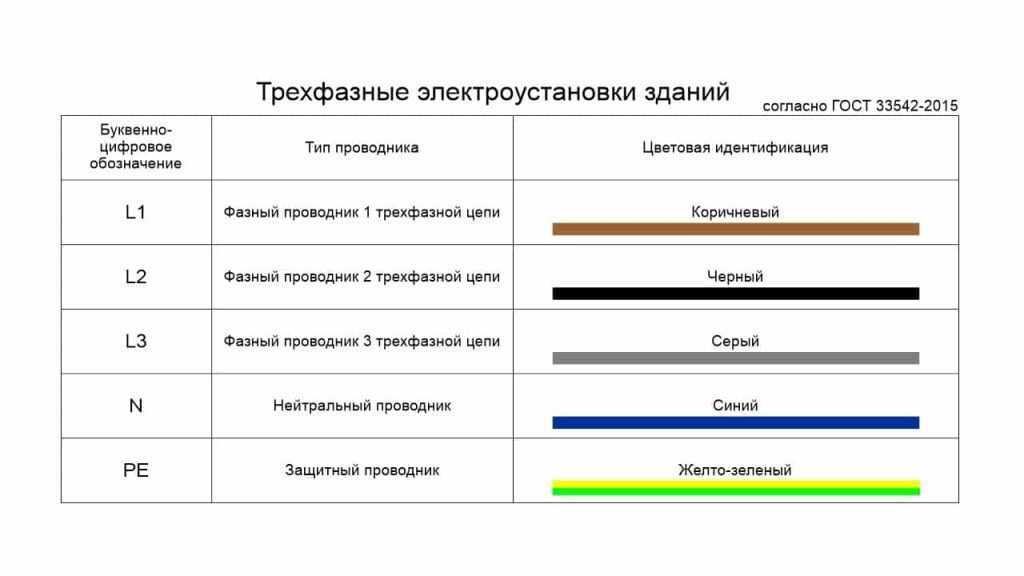Формула такая же!

2. На весах масса отображается в килограммах. И если я свою массу умножу на ускорение свободного падения, то явно получу число почти в 10 раз больше, чем показывают весы.

Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).

Продолжаем эксперимент.

Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).

Теперь вес тела вычисляем по формуле:

P = m (g − a) P — вес тела [Н] m — масса [кг] g — ускорение свободного падения [м/с2] a — ваше ускорение [м/с2] На планете Земля g = 9,8 м/с2

Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.

Формула веса примет вид:

P = m (g + a) P — вес тела [Н] m — масса [кг] g — ускорение свободного падения [м/с2] a — ваше ускорение [м/с2] На планете Земля g = 9,8 м/с2

Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.

Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.

N – сила реакции опоры [Н];

mg – сила тяжести [Н];

a – ускорение, с которым движется лифт [м/с²].

N + mg = ma

При проецировании на ось y, направленную вниз, мы получаем:

−N + mg = ma

А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:

P = N

−P + mg = ma

P = m (g − a)

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Снова невесомость

Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.

Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:

Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:

P = m (g − a) = m (9,8 − 9,8) = 0

Вот мы и в невесомости!

Так это что же, космонавты испытывают невесомость, потому что падают?

Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».

Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.

Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т. е. удалиться на бесконечно большое расстояние от Земли. А тело, которое двигается с третьей космической скоростью, и вовсе вылетит за пределы Солнечной системы. Такие дела. 🙂

---

Карина Хачатурян

К предыдущей статье

Плотность вещества

К следующей статье

123.1K

Основные агрегатные состояния вещества

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

N-обозначение | Хайброу

03. 07.2018 | 0

Эпизод №2 курса Курта Андерсона по основам информатики

 

С возвращением!

Вчера мы рассмотрели основы работы самих компьютеров. Сегодня мы познакомимся со строительными блоками алгоритмического анализа — основной концепции компьютерных наук.

 

Что такое N-нотация?

N-нотация — это способ представления времени выполнения алгоритма, чтобы его можно было сравнить с другим алгоритмом. N-нотация — это НЕ анализ того, сколько времени потребуется для запуска алгоритма, а анализ того, как алгоритм будет масштабироваться с увеличением количества входных данных.

Этот метод основан на просмотре входных данных алгоритма и анализе того, как алгоритм работает с этими входными данными. Однако мы точно не знаем, сколько фрагментов данных будет поступать в любой момент. Что мы делаем, так это заменяем этот входной номер переменной n .

Допустим, у нас есть алгоритм, который проверяет количество ваших друзей на Facebook.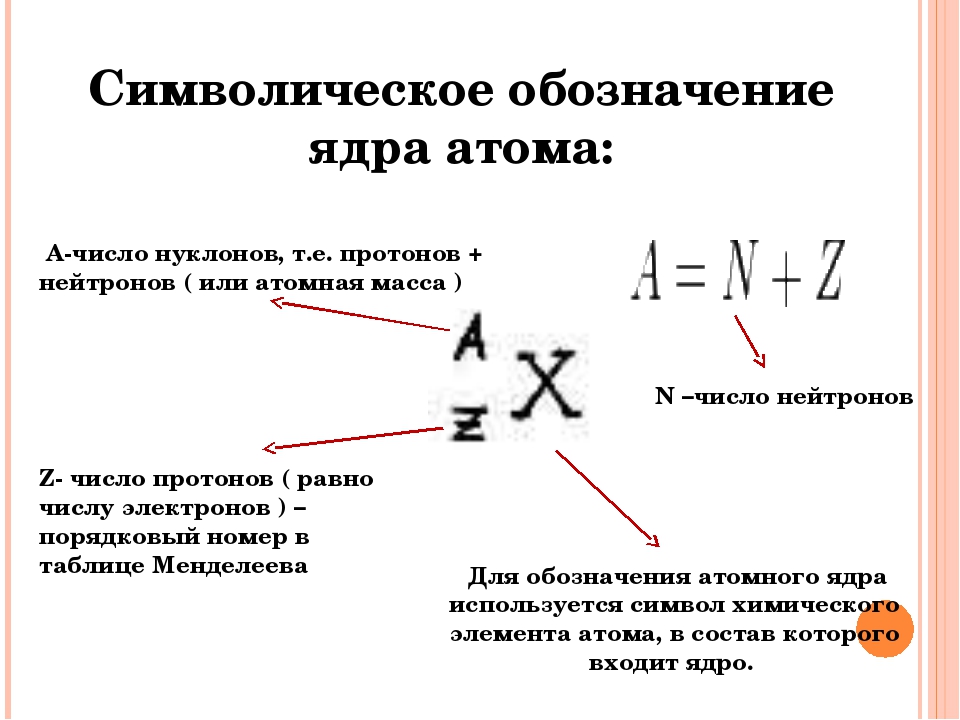 Когда мы пишем алгоритм, мы понятия не имеем, сколько друзей будет добавлено в качестве входных данных. Вы могли бы иметь 25 или 2000 или два. Итак, вместо того, чтобы указывать фактическое число, мы просто говорим 9.0023 n элемента данных будут помещены в этот алгоритм.

 

Как использовать N-нотацию

Как мы используем это для сравнения двух алгоритмов? Что мы делаем, так это ищем существенные различия в алгоритмах. Как отреагирует программа на ввод n ?

 

© Cmglee

 

На приведенной выше диаграмме мы можем увидеть эти различные отношения в виде графика. Ось x (нижняя часть графика) показывает, сколько фрагментов данных поступает в алгоритм. Ось Y (слева) показывает, сколько операций программа должна будет выполнить с учетом количества частей данных.

Что же тогда показывает эта диаграмма? Он отображает отношения, о которых мы говорили. Центральная зеленая линия — n . Это означает, что если мы вставим n элементов данных, алгоритм выполнит n операций.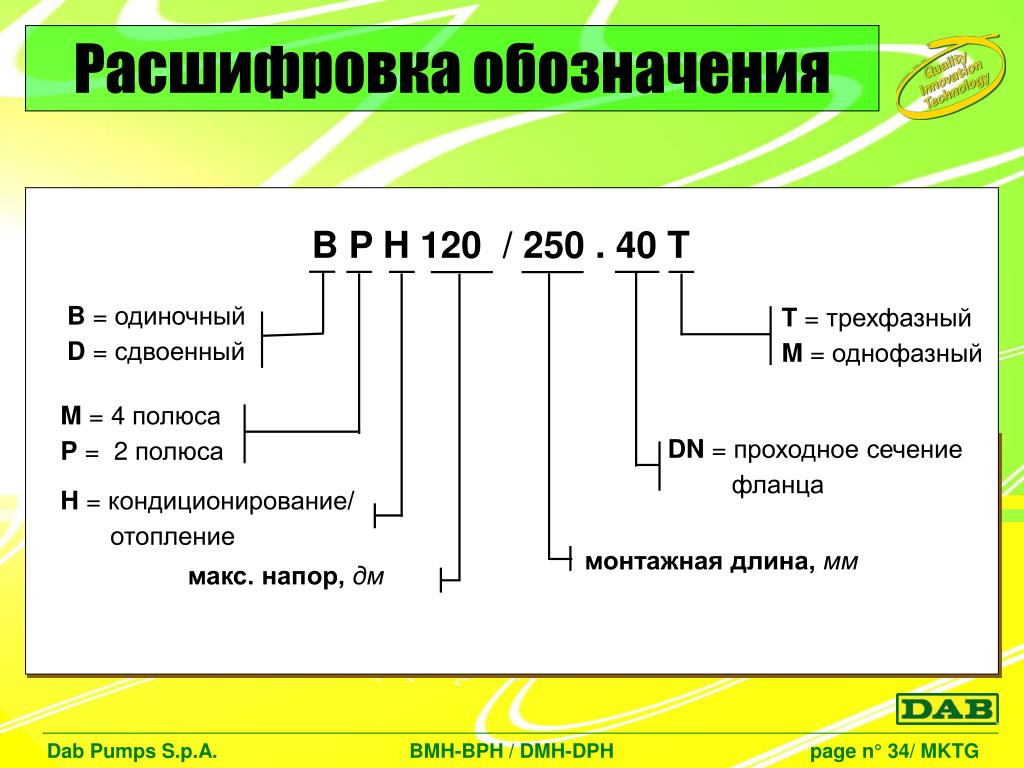 Для ста единиц данных потребуется 100 операций, для 200 — 200 и так далее. Обратите внимание, что для некоторых других строк требуется значительно больше операций при том же объеме входных данных.

Реальным примером этого может быть копирование рукописной электронной таблицы в Excel. Вы, в данном случае, являетесь алгоритмом. Для каждой части данных в этой печатной копии вам нужно будет выполнить одну операцию, вставив ее в Excel. Если есть 100 фрагментов данных, вам потребуется 100 операций вставки. Каким бы ни был размер входных данных, вам придется выполнить столько же операций. Это делает время выполнения для этого, п .

Допустим, вместо этого нам нужно проверить электронную таблицу и посмотреть, совпадает ли какое-либо значение с любым другим значением. Это существенно более утомительный процесс. Мы должны взять каждый фрагмент данных и сравнить его с любым другим фрагментом данных. В этом случае у нас будет n для каждой части данных, а затем дополнительные n для сравнения с любой другой частью данных. 2 (т. е. n*n).

Ключевым моментом здесь является признание сложности проблем по мере их масштабирования. Первая проблема довольно проста. У вас может быть 1000 или 100 000 страниц, и проблема не выйдет из-под контроля. Это могло наскучить, но ничего, что несколько часов не могли бы решить.

Однако представьте, что при сравнении проверяются полные 1000 страниц для каждого отдельного числа. А если у вас 10 000 или 100 000 страниц? Проблема быстро становится неуправляемой. Это то, что мы рассматриваем с помощью n-обозначения — отношение между вводом и ростом проблемы.

Вот сравнение того, как разные алгоритмы могут работать с реальными числами.

 

 

Основные выводы:

• N-нотация используется для сравнения роста алгоритмов, а не их фактического времени.

• N используется как переменная для того, сколько фрагментов данных вводит алгоритм. Затем мы смотрим на взаимосвязь с тем, сколько операций он должен выполнить при таком количестве входных данных.

Завтра мы расширим эту идею с помощью нотации Big O.

Ура,

Kurt

Рекомендуемая книга

Элементы вычислительных систем: строительство современного компьютера с первых принципов от Noam Nisan, Shimon Schocken

. О (п)? — Обозначение Big O + Как его использовать | Тимо Махлай

Что ж, как разработчики, мы все были здесь. Изучение нотации Big O и того, почему все вокруг нее так шумят.

Обозначение Big O или O(n), читаемое как «O of n», используется в компьютерных науках для измерения производительности или сложности алгоритма.

Это означает, что он пригодится, когда вы пытаетесь написать быстрый и эффективный код. Но это не единственное его использование.

Обозначение O(n) помогает вам как разработчику предположить, будет ли ваш код по-прежнему эффективен, если ему будет дан больший ввод, или если это займет слишком много времени с точки зрения времени.

Допустим, этот код:

O(n²)

Этот код создает так называемую операцию O(n²). Чем больше размер строки, тем медленнее будет выполняться функция. Насколько медленнее, но нотация O (n) помогает визуализировать это.

y = Операции, x = Элементы

Как видно из графика, функция, работающая на O(n²) [синяя линия], будет работать медленнее по мере увеличения входных данных. Да, это будет быстро, если приведенной выше функции будет задана короткая строка, но с более длинной строкой это займет значительно больше времени.

…

Теперь я знаю, о чем вы думаете. Этот код не кажется таким долгим, как он написан и работает. Но это потому, что вы не визуализируете достаточно большой ввод. Давайте представим компанию, которая работает с большим количеством данных, например, Facebook. Для них эти небольшие изменения имеют большое значение. Представьте себе работу с миллиардами записей данных, которые должны постоянно выполняться через одну и ту же функцию. Им нужна вся возможная оптимизация производительности.

Теперь, как тот же самый код будет выглядеть в O(n) вместо O(n²)?

Приведенный выше код написан за O(n). Но это не яркий пример O(n). Я просто хотел показать лучший способ написания предыдущего кода и то, как его можно оптимизировать, даже если вы думаете, что уже все предусмотрели.

O(n) Функция:

Приведенный выше код перебирает каждый элемент массива и проверяет, равен ли он элементу. Элемент будет увеличиваться во времени, поскольку массив параметров функции будет длиннее. Потому что это значительно увеличит количество итераций.

O(n) растет пропорционально размеру входных данных. Обозначение O(n) может указывать на то, что если размер входных данных равен 1, выполнение алгоритма будет мгновенным, и его также можно записать как O(1). Но нотация Big O всегда будет принимать верхний предел, при котором алгоритм будет выполнять максимальное количество итераций.

O(5) на графике:

При O(1), независимо от того, какой inoput задан функции, ее вычисление всегда будет занимать одно и то же время.

O из N в квадрате относится к функциям, которые экспоненциально становятся медленнее и сложнее по мере того, как в них подается больше данных.

Первый фрагмент кода является примером O(n²).

O(n²)

O(N2) представляет собой алгоритм, производительность которого прямо пропорциональна квадрату размера набора входных данных. Это характерно для алгоритмов, которые включают вложенные итерации по набору данных. Более глубокие вложенные итерации приведут к O(N3), O(N4) и т. д.[1]

O(2N) обозначает алгоритм, рост которого удваивается с каждым добавлением к набору входных данных. Кривая роста функции O(2N) экспоненциальна: сначала она очень пологая, а затем стремительно растет.[1]

Примером функции O(2N) является рекурсивный расчет чисел Фибоначчи:

Логарифмы объяснить намного сложнее. Так что я собираюсь сделать это на примере.

O(log n)

Двоичный поиск — это алогрифм для сортировки отсортированных наборов данных.