Напишите формулу закона ома. Закон Ома: формула, применение и ограничения

Что такое закон Ома и как он связывает напряжение, силу тока и сопротивление. Какова формула закона Ома. Где применяется закон Ома в электротехнике. Каковы ограничения закона Ома.

Что такое закон Ома

Закон Ома — один из фундаментальных законов электротехники, устанавливающий связь между силой тока, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.

Согласно закону Ома, сила тока в участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению. Это можно выразить следующей формулой:

I = U / R

где:

• I — сила тока (в амперах, А)
• U — напряжение (в вольтах, В)
• R — сопротивление (в омах, Ом)

Формулировка закона Ома

Закон Ома может быть сформулирован следующим образом:

Сила тока в однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Эта формулировка отражает основную идею закона — взаимосвязь между тремя ключевыми параметрами электрической цепи: током, напряжением и сопротивлением.

Формула закона Ома

Математически закон Ома выражается следующей формулой:

I = U / R

Из этой базовой формулы можно вывести две другие формы записи закона Ома:

U = I * R

R = U / I

Эти формулы позволяют рассчитать любой из трех параметров, если известны два других.

Применение закона Ома

Закон Ома широко применяется в электротехнике и электронике для решения различных практических задач:

• Расчет параметров электрических цепей (ток, напряжение, сопротивление)
• Проектирование электрических схем
• Выбор номиналов резисторов и других компонентов
• Анализ работы электрических устройств
• Диагностика неисправностей в электрических цепях

Закон Ома для участка цепи

Закон Ома для участка цепи описывает соотношение между током, напряжением и сопротивлением на отдельном участке электрической цепи. Он выражается формулой:

I = (φ1 — φ2) / R

где φ1 и φ2 — потенциалы начала и конца участка цепи.

Эта форма закона Ома применима к любому однородному участку цепи, не содержащему источников ЭДС.

Закон Ома для полной цепи

Закон Ома для полной цепи учитывает наличие источника ЭДС и описывает соотношение между током, ЭДС источника и полным сопротивлением цепи:

I = ε / (R + r)

где:

• ε — электродвижущая сила источника
• R — внешнее сопротивление цепи
• r — внутреннее сопротивление источника

Эта формула позволяет рассчитать ток в замкнутой цепи с учетом характеристик источника питания.

Ограничения закона Ома

Закон Ома имеет ряд ограничений и не применим в следующих случаях:

• Для нелинейных элементов цепи (диоды, транзисторы)
• При очень высоких напряжениях и токах
• Для быстропеременных токов высокой частоты
• В полупроводниковых приборах
• В газовых разрядах

В этих ситуациях зависимость между током и напряжением может быть нелинейной или более сложной.

Примеры применения закона Ома

Рассмотрим несколько примеров применения закона Ома для решения практических задач:

Пример 1: Расчет силы тока

Дано: напряжение U = 12 В, сопротивление R = 4 Ом.

Найти: силу тока I.

Решение: I = U / R = 12 В / 4 Ом = 3 А

Пример 2: Определение напряжения

Дано: сила тока I = 0.5 А, сопротивление R = 100 Ом.

Найти: напряжение U.

Решение: U = I * R = 0.5 А * 100 Ом = 50 В

Пример 3: Вычисление сопротивления

Дано: напряжение U = 220 В, сила тока I = 2 А.

Найти: сопротивление R.

Решение: R = U / I = 220 В / 2 А = 110 Ом

Закон Джоуля-Ленца

Закон Джоуля-Ленца тесно связан с законом Ома и описывает тепловое действие электрического тока. Он выражает количество теплоты, выделяемое проводником при прохождении через него электрического тока:

Q = I^2 * R * t

где:

• Q — количество выделяемой теплоты
• I — сила тока
• R — сопротивление проводника
• t — время прохождения тока

Этот закон широко применяется при расчете нагревательных элементов и анализе тепловых потерь в электрических цепях.

Закон Ома в дифференциальной форме

Закон Ома может быть записан в дифференциальной форме, которая описывает плотность тока в проводнике:

j = σ * E

где:

• j — вектор плотности тока
• σ — удельная электропроводность материала
• E — вектор напряженности электрического поля

Эта форма закона Ома применяется в более сложных расчетах, связанных с распределением тока в проводниках.

Заключение

Закон Ома является одним из основополагающих законов электротехники, позволяющим анализировать и рассчитывать параметры электрических цепей. Несмотря на некоторые ограничения, он широко применяется в различных областях, от бытовой электроники до промышленных электрических систем. Понимание и правильное применение закона Ома необходимо для эффективной работы с электрическими устройствами и системами.

Формула закона Ома в физике

Содержание:

• Определение и формула закона Ома
• Закон Ома для участка цепи
• Закон Ома для замкнутой цепи
• Формула закона Ома в дифференциальной форме
• Примеры решения задач

Определение и формула закона Ома

Определение

Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I), текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.

Закон Ома для участка цепи

Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет $\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$

где R – сопротивление проводника (совокупности проводников, участка цепи).

Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$

Закон Ома для замкнутой цепи

В том случае, если цепь является замкнутой, закон Ома принимает вид:

$$I=\frac{\varepsilon}{R}(3)$$

где под R=R_vnesh+r_ist понимают полное сопротивление цепи, которое включает так называемое внешнее сопротивление (R_vnesh) и сопротивление источника ЭДС (r_ist).

Формула закона Ома в дифференциальной форме

Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме, которая характеризует электрическое состояние в точке.

$$\bar{j}=\sigma \bar{E}(4)$$

где $\sigma=\frac{1}{\rho}$ – удельная проводимость, $\rho$ – удельное сопротивление, $\bar{j}$ – вектор плотности тока, $\bar{E}$ – вектор напряженности электрического поля. Векторы $\bar{j}$ и $\bar{E}$ характеризуют одну точку проводящей среды. В том случае, если среда изотропна, то $\bar{j} \uparrow \uparrow \bar{E}$.

Примеры решения задач

Пример

Задание. Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество, удельная проводимость которого изменяется в соответствии с линейным законом: $\sigma(r)=\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d} r$ в направлении перпендикулярном пластинам.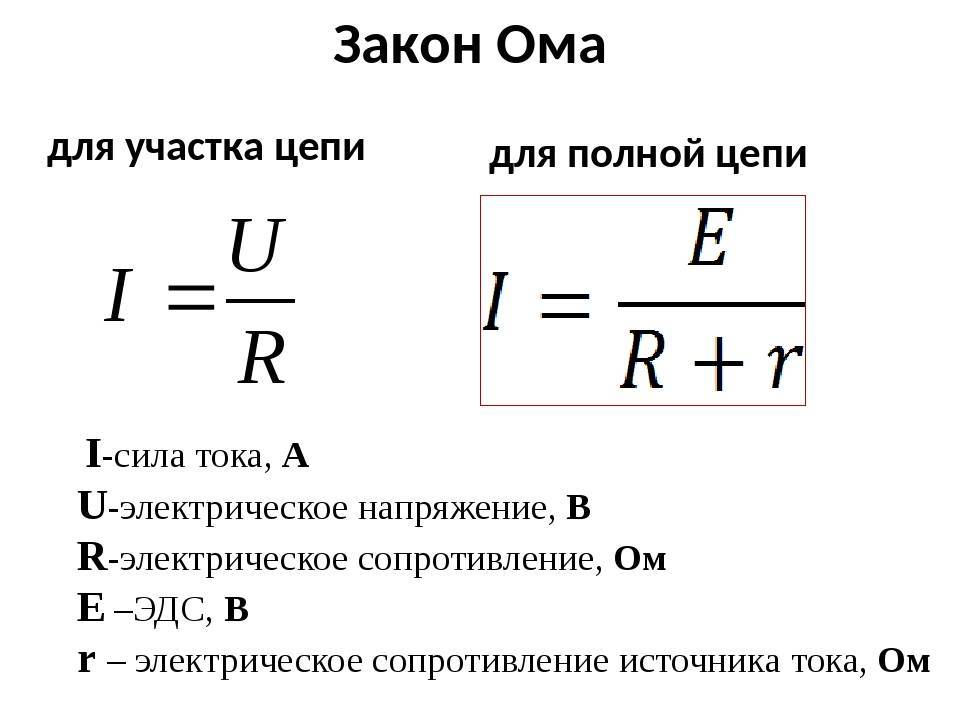 {d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\ =\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2) \end{array} $$

Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:

$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$

Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание.

Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным $\rho$) постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?

Решение. Плотность тока для проводника, который имеет постоянное сечение S можно найти как:

$$j=\frac{I}{S}(2.1)$$

Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:

$$I=\frac{U}{R}(2.2)$$

Сопротивление провода найдем, применяя формулу:

$$R=\rho \frac{l}{S}(2.3)$$

Подставим, необходимые величины в (2.1), получим:

$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$

Ответ. $j=\frac{U S}{S \rho l}$

Читать дальше: Формула мощности тока.

Закон Ома для переменного тока: формула

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Содержание

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E.

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Закон ома для цепи переменного тока

Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.

Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.

Закон Ома для переменного тока

Как понять Закон Ома: простое объяснение для чайников с формулой и понятиями

Закон Ома для однородного участка цепи – формула

Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром

Закон Ома для полной и не полной электрической цепи, формула и правильное определение

Что такое полное электрическое сопротивление или импеданс?

Закон Ома-Утверждение, Формула, Решенные Примеры

Что такое Закон Ома ?

Закон Ома устанавливает связь между разностью потенциалов и током в цепи. Ток в цепи зависит от напряжения и ее сопротивления цепи. Закон Ома устанавливает взаимосвязь между током, напряжением и сопротивлением. Георг Симон Ом экспериментировал, чтобы найти связь между электрическим током и напряжением.

Ом после своего эксперимента пришел к выводу, что ток, протекающий в цепи, пропорционален разности потенциалов на проводнике. Эта зависимость между током и напряжением известна как Закон Ома. Мы также обсудим этот закон, где он не применим к каким типам устройств.

Закон Ома гласит, что ток в цепи равен;

• Пропорционально напряжению, приложенному к цепи, , если температура постоянна.

Почему по закону Ома температура поддерживается постоянной?

Увеличение сопротивления при повышении температуры в зависимости от температурного коэффициента сопротивления. Ток, протекающий в цепи, равен I = V/R. Если сопротивление не остается постоянным, ток будет меняться и закон Ома в этом случае не работает. Поэтому в ходе эксперимента по установлению зависимости между напряжением и током температура должна быть постоянной.

Объяснение закона Ома

Когда мы увеличиваем напряжение на проводнике, ток также увеличивается в той же пропорции, что и разность потенциалов на проводнике. Проводник имеет определенное сопротивление. Обозначим сопротивление символом R. Единица сопротивления Ом. Его символ Ω.

Ток линейно увеличивается с увеличением падения потенциала на сопротивлении. Схема эксперимента по закону Ома приведена ниже. Источник переменного напряжения подключается через сопротивление.

Связь между напряжением, током и сопротивлением

Результаты эксперимента приведены в таблице ниже.

Рабочий лист по закону Ома

Из результатов выше видно, что ток, протекающий через сопротивление, прямо пропорционален напряжению на сопротивлении. Если мы нарисуем график между I и V, график будет прямой линией.

График закона Ома

Уравнение закона Ома

Уравнение прямой линии:

Математически мы можем записать эту связь как;

Где 1/R — константа. R — сопротивление цепи. Мы можем записать это уравнение и в других формах.

Формула закона Ома

Уравнение V= IR можно записать в следующих формах.

Мы можем использовать ту же формулу, применив ее для расчета тока и сопротивления соответственно.

Закон Ома Магический треугольник

Мы можем использовать приведенный ниже магический треугольник, чтобы запомнить различные уравнения этого закона для решения различных переменных (V, I и R).

Применение закона Ома

Основные применения этого закона следующие.

• Для расчета напряжения, сопротивления и тока в цепи.
• Используется для проектирования схемы для поддержания падения напряжения на компоненте схемы.
• Он также предназначен для расчета значения сопротивления шунта для амперметра постоянного тока, чтобы отвести требуемый ток через шунт. (Шунт представляет собой маломощное сопротивление с незначительными потерями мощности)
• В регуляторе потолочного вентилятора сопротивления сопротивление выбирается по этому закону.
• Мы используем этот закон для проектирования схемы делителя тока.
• В схеме делителя напряжения мы используем этот закон, чтобы получить желаемое выходное напряжение на резисторе делителя напряжения.

Ограничения закона Ома

Ниже приведены ограничения;

• Ток может течь в одном направлении в односторонних устройствах , таких как диод и транзистор. Этот закон неприменим, поскольку эти устройства пропускают ток только в одном направлении. Этот закон не распространяется на односторонние устройства.
• Нелинейные устройства потребляют ток в разной пропорции к приложенному напряжению. Причиной нелинейности напряжения и тока является изменяющееся сопротивление нелинейных устройств. Сопротивление нелинейных устройств не остается постоянным. Следовательно, этот закон неприменим к нелинейным устройствам. Примерами нелинейных устройств являются тринистор, тиристор, IGBT и т. д.

Закон Ома Решенные задачи

Пример 1: Если сопротивление электрического чайника равно 60 Ом и через сопротивление протекает ток силой 4 А . Найдите напряжение между двумя точками.

Решение:

Здесь I = 4 А, R = 60 Ом

напряжение ( В) = IR

Подставляя значения в уравнение, получаем
 В = 4 X 60
В = 240 Вольты

Пример 2: Определить величину тока, проходящего через 100 Ом; резистор с напряжением 100 В.

Решение:

R = 100 Ом
В = 100 Вольт
I = 100/100 = 1 Ампер.

Пример 3: Найдите ток I через резистор сопротивлением R = 3 Ом, если напряжение на резисторе равно 6 В.

Решение:

R = 3 Ом
В = 6 В

I = V/R 
I  = 6/3 = 2 Ампер.

Читать далее :

1. Температурный коэффициент сопротивления
2. Что такое электрическое сопротивление? Определение и единица сопротивления
3. Сопротивление и удельное сопротивление
4. Что такое Теорема Миллмана? Теорема Миллмана Формула
5. Теорема 9 о максимальной передаче мощности0004
6. Шунт 20 Ом соединен с амперметром сопротивлением 200 Ом. Он соединен с батареей 10 В, имеющей сопротивление 4 Ом. Каким будет наблюдение амперметра?
7. Сопротивление провода длиной L равно R. Если растянуть половину его длины, например, общая длина станет 2L, каково будет конечное сопротивление?

Похожие сообщения:

Пожалуйста, следите за нами и лайкайте:

Закон Ома (Микроскопическая интерпретация) | Великолепная математика и естественные науки Wiki

Содержимое

• Применение закона Ома
• Электронная динамика в проводниках
• Вывод закона Ома
• Рекомендации

Закон Ома связывает плотность тока в проводнике с приложенным электрическим полем по формуле \(J = \sigma E\), приведенной выше. Проводимость \(\сигма\) определяется формулой 92 \frac{\tau}{m_e}\]

с \(n_e\) объемной плотностью электронов проводимости, \(e\) зарядом электрона, \(m_e\) массой электрона и \(\tau \) среднее время свободного пробега электронов, представляющее, как долго в среднем проходит электрон проводимости, прежде чем вступить во взаимодействие с проводником. Также часто работают с величиной \(\rho = \frac{1}{\sigma}\), удельным сопротивлением

Ом.

Используя эту формулу, текущая плотность электронов может быть переписана в терминах средней скорости электронов, часто называемой скорость дрейфа :

\[\vec{J} = -en_e \bar{\vec{v}}.\]

Для движения электрона в стержне микроскопический закон Ома можно связать с макроскопическим законом Ома \(V=IR\). Обратите внимание, что плотность тока равна току на единицу площади \(J = \frac{I}{A}\). Точно так же электрическое поле представляет собой напряжение на единицу длины: \(E = \frac{V}{L}\). Объединив их, можно найти

\[V = \left(\frac{L}{A\sigma}\right) I.\]

В проводящем стержне с площадью поперечного сечения \(A\) и длиной \(L\) с проводимостью \(\сигма\), поэтому сопротивление определяется как

\[R = \frac{L}{A\sigma} = \frac{\rho L}{A}.\]

В сложных материалах, где проводимость изменяется по длине проводника, находят сопротивление рассматривая все вышеперечисленное как бесконечно малую величину и интегрируя.

Странный металлический стержень с площадью поперечного сечения \(A\) простирается от \(x=1\) до \(x=L\) с удельным сопротивлением \(\rho(x) = \frac{1}{x}\ ). Вычислите сопротивление этого стержня.

---

Сопротивление небольшого куска стержня 9 Ом.L \ frac {1} {xA} dx = \ frac {\ log (L)} {A}. \ _ \ квадрат \]

1 2 4 8

Медный провод имеет некоторое сопротивление \(R\). Затем проволоку сплющивают и растягивают так, чтобы длина удвоилась, а площадь поперечного сечения уменьшилась в \(\frac14\) без изменения удельного сопротивления. Во сколько раз изменится сопротивление провода? 9{-3} \:\Omega\cdot \text{м}\) и длиной \(10 \text{ см}\) подключается к любой из клемм батареи \(9 \text{ В}\). Предположим, что общая масса проволоки равна \(20 \text{ г}\) и что на каждый атом германия приходится только один электрон. Найдите дрейфовую скорость электронов в проводе.

---

Величина плотности тока, как указано выше, составляет

\[J = en_e v,\]

где \(v\) — скорость дрейфа. Нужно вычислить две вещи: плотность \(n_e\) проводящих электронов и плотность тока \(J\).

Плотность тока находится из

\[J = \sigma E = \frac{V}{\rho L},\]

где \(L\) — указанная общая длина провода.

Количество проводящих электронов можно вычислить из общего числа атомов германия, поскольку каждый атом обеспечивает только один проводящий электрон.

{292 \frac{\tau}{m_e},\]

, где \(\tau\) — некоторая неизвестная шкала времени. Можно определить эту временную шкалу, рассмотрев, как была получена эта формула: изменение импульса от приложения электрической силы за некоторый период времени вычислялось двумя разными способами. Общее количество времени, в течение которого электрическая сила ускоряет электрон проводимости, — это время, пока он не рассеется на атоме металла и не потеряет энергию. Таким образом \(\tau\) есть среднее время свободного пробега электрона в проводнике. Это означает, что \(\tau\) — это среднее время, необходимое электрону проводимости для взаимодействия с атомом в проводнике и потери энергии. В материалах с высокой проводимостью электроны проводимости могут быть ускорены в течение длительного времени, прежде чем вступить во взаимодействие с проводником, в соответствии с приведенной выше формулой. 9{-26} \text{ м} .\ _\квадрат\]

Используя тот факт, что величина плотности тока связана со скоростью дрейфа соотношением поле на

\[\frac{v}{E} = \frac{\sigma}{en_e}. \]

Величина в левой части называется дрейфовой подвижностью электрона и часто записывается как

\[\mu = \frac{v}{E}.\]

9{-2} \text{см}/\текст{с}\). Какова длина свободного пробега электронов проводимости в метрах?

В проводящем материале электроны слабо связаны со своими составляющими элементами, и небольшого количества энергии (через приложенное электрическое поле) достаточно, чтобы привести их в движение, создав электрический ток. Ток измеряется в амперах, где один ампер эквивалентен одному кулону заряда в секунду.

Если есть объемная плотность \(n_i\) зарядов заряда \(q_i\) и скорость \(\vec{v}_i\), то плотность тока в материале равна

\[\vec{J} = \sum_i n_i q_i \vec{v}_i.\]

Эта формула получена из анализа размерностей. Общий ток на единицу площади из-за некоторого типа заряда — это просто плотность зарядов на единицу площади \(n_i q_i\), умноженная на скорость этих зарядов \(\vec{v}_i\).

Так как в материале обычно много зарядов, часто более полезно работать с средней скоростью зарядов. Средняя скорость одного определенного типа заряда (например, электронов заряда \(-e\)) определяется плотностью электронов \(n_e\) как

\[\bar{\vec{v}} = \frac{1}{n_e} \sum_i n_i \vec{v}_i.\]

Плотность тока электронов может быть записана как

\ [\vec{J} = -en_e \bar{\vec{v}}.\]

Чтобы связать плотность тока с приложенным электрическим полем, полезно рассмотреть, как средняя скорость электронов связана с прикладное поле. Изменение импульса электрона равно импульсу, действующему на него полем: \(\Delta p = F\tau\). С одной стороны, импульс электрона будет равен \(\Delta p= m_e \bar{\vec{v}}\). С другой стороны, сила, действующая на электрон, равна \(-e\vec{E}\). Таким образом, мы можем написать 92 \frac{\tau}{m_e}\), поэтому закон Ома выводится из микроскопического движения электронов в проводнике.

Закон Ома не является фундаментальным законом природы. В нем говорится о соотношении, согласно которому результирующий ток \(I\) пропорционален приложенной ЭДС \(\mathbb{E}=IR\).