Напряжение как найти. Как найти напряжение в электрической цепи: формулы, методы и примеры расчетов

Как рассчитать напряжение в электрической цепи. Какие формулы использовать для нахождения напряжения на участке цепи. Какие методы применять для вычисления напряжения при последовательном и параллельном соединении. Как определить падение напряжения на резисторе.

Основные формулы для расчета напряжения

Для нахождения напряжения в электрической цепи используются следующие основные формулы:

• Закон Ома: U = I * R, где U — напряжение, I — сила тока, R — сопротивление
• Формула мощности: U = P / I, где P — мощность
• Формула работы тока: U = A / q, где A — работа тока, q — заряд

Выбор конкретной формулы зависит от того, какие параметры цепи известны. Рассмотрим подробнее применение этих формул.

Расчет напряжения по закону Ома

Закон Ома позволяет найти напряжение, если известны сила тока и сопротивление участка цепи:

U = I * R

Например, если через резистор с сопротивлением 100 Ом протекает ток 0,5 А, напряжение на резисторе составит:

U = 0,5 А * 100 Ом = 50 В

Эта формула универсальна и применима для расчета напряжения на любом участке цепи.

Определение напряжения через мощность

Если известна мощность, выделяемая на участке цепи, и сила тока, напряжение можно рассчитать по формуле:

U = P / I

Например, если на лампе мощностью 60 Вт протекает ток 0,25 А, напряжение на ней составит:

U = 60 Вт / 0,25 А = 240 В

Этот метод удобен для расчета напряжения на потребителях электроэнергии с известной мощностью.

Вычисление напряжения через работу тока

Напряжение можно найти, зная работу электрического тока и перенесенный заряд:

U = A / q

Например, если при прохождении заряда 5 Кл совершена работа 100 Дж, напряжение составит:

U = 100 Дж / 5 Кл = 20 В

Этот способ применяется реже, но может быть полезен в некоторых задачах.

Расчет напряжения при последовательном соединении

При последовательном соединении элементов общее напряжение равно сумме напряжений на отдельных участках:

U = U1 + U2 + U3 + …

Например, если в цепи последовательно соединены резисторы с напряжениями 5 В, 3 В и 2 В, общее напряжение составит:

U = 5 В + 3 В + 2 В = 10 В

Этот принцип позволяет находить напряжение на отдельных элементах, зная общее напряжение цепи.

Определение напряжения при параллельном соединении

При параллельном соединении напряжение на всех элементах одинаково и равно общему напряжению:

U = U1 = U2 = U3 = …

Например, если к источнику 12 В параллельно подключены несколько потребителей, напряжение на каждом из них составит 12 В.

Это свойство упрощает расчет напряжений в разветвленных цепях.

Как найти падение напряжения на резисторе

Падение напряжения на резисторе можно рассчитать по закону Ома, зная силу тока и сопротивление:

ΔU = I * R

Например, если через резистор 200 Ом протекает ток 0,1 А, падение напряжения составит:

ΔU = 0,1 А * 200 Ом = 20 В

Этот метод позволяет определить, какая часть общего напряжения приходится на конкретный элемент цепи.

Расчет напряжения в сложных цепях

В сложных цепях с последовательно-параллельным соединением для нахождения напряжений используют следующий алгоритм:

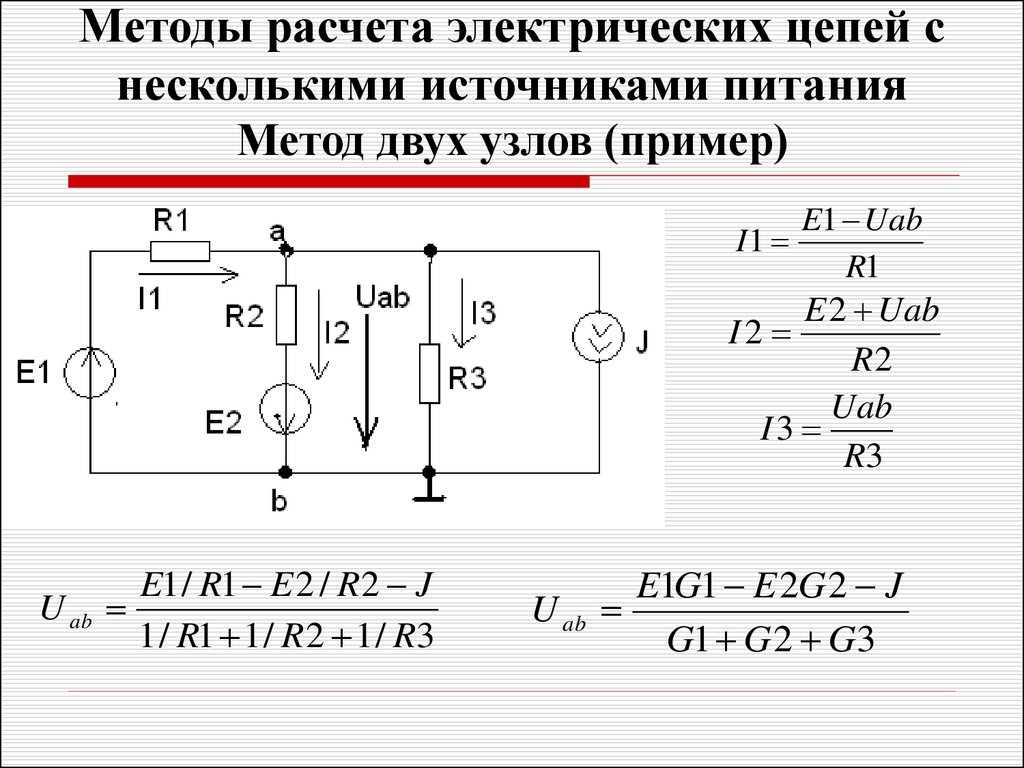
1. Разбивают цепь на участки с последовательным и параллельным соединением
2. Рассчитывают эквивалентное сопротивление цепи
3. Находят общий ток в цепи
4. Определяют напряжения на отдельных участках

Например, рассмотрим цепь:

[Схема сложной цепи]

1) Резисторы R2 и R3 соединены параллельно, найдем их эквивалентное сопротивление: 1/R23 = 1/R2 + 1/R3

2) Теперь цепь последовательная, общее сопротивление: R = R1 + R23 + R4

3) Общий ток: I = U / R

4) Напряжения на участках: U1 = I * R1 U23 = I * R23 U4 = I * R4

Такой подход позволяет рассчитать напряжения в любой сложной цепи.

Измерение напряжения на практике

Для измерения напряжения в реальных цепях используется вольтметр. Основные правила измерения:

• Вольтметр подключается параллельно исследуемому участку цепи
• Диапазон измерения выбирается больше ожидаемого значения напряжения
• Соблюдается полярность подключения прибора

Правильное измерение позволяет проверить расчетные значения напряжений и выявить неисправности в цепи.

Типичные ошибки при расчете напряжения

При вычислении напряжений в цепях начинающие часто допускают следующие ошибки:

• Путают формулы для последовательного и параллельного соединения
• Неправильно определяют эквивалентное сопротивление сложных участков
• Забывают учесть внутреннее сопротивление источника тока
• Используют значения тока и сопротивления в разных единицах измерения

Внимательность и проверка размерностей помогут избежать этих ошибок.

Заключение

Умение рассчитывать напряжение — важный навык для анализа и проектирования электрических цепей. Зная основные формулы и методы, можно определить напряжение на любом участке цепи. Регулярная практика в решении задач поможет освоить различные способы расчета напряжения.

Как найти напряжение через ЭДС и сопротивление?

Закон Ома для замкнутой цепи

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

I – Сила тока в цепи.

– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r – Внутреннее сопротивление источника питания.

Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR. Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы. По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r. Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.

В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.

Разомкнутая электрическая цепь

При отсутствии потока электронов необходимое напряжение источника цепи проявляется на концах точек. В этом случае происходит процесс ожидания момента соединения концов точек, чтобы возобновился поток электронов. Подобную цепь принято называть разомкнутой.

Замечание 1При связывании концов проводов, где существует разрыв, непрерывность всей цепи восстановится. Это основная разница между замкнутой и разомкнутой цепью.

При включении и выключении электрического освещения (лампы) требуется постоянно осуществлять похожие процессы. Для удобства были созданы специальные устройства. Их называют выключателями или рубильниками. Они в автоматическом режиме по сигналу управляют потоками электронов в цепи, контролируя начало и завершение работы электрооборудования.

Рубильники практически идеально подходят для демонстрации принципов работы выключателей и переключателей. Однако при использовании их в больших электрических цепях существует немало проблем, связанных с безопасной эксплуатацией. Так как некоторые части рубильников открыты, то существует вероятность воспламенения горючих материалов. В современных выключателях применяются подвижные и неподвижные контакты, которые защищены изоляционным корпусом.

Простейшая электрическая цепь представляет собой нагрузку, подключенную к источнику питания. Для управления цепью в нее последовательно включают замыкающее устройство (ключ). При замкнутом ключе в цепи возникает электрический ток, а при разомкнутом – ток отсутствует. Именно от положения ключа (замкнутый/разомкнутый) напрямую зависит – какую электрическую цепь называют замкнутой и разомкнутой.

[custom_ads_shortcode1]

Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид:

I = U/Z

Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

Элементы электрической цепи

Электрическую цепь разделяют на 2 участка – внутренний и внешний. Внутренним участком считается источник питания постоянного или переменного напряжения, а внешним – система, состоящая из нагрузки, приборов и соединительных элементов (проводов). Кроме обязательных элементов – источника и нагрузки, электрическая цепь может включать выключатели, реостаты, предохранительные плавкие или автоматические устройства, приборы контроля и индикации. Нагрузка также может состоять из различных потребителей, подключенных в цепь параллельно или последовательно.

[custom_ads_shortcode2]

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т. д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Идеальный источник ЭДС

Электродвижущая сила (E) – физическая величина, определяющая степень воздействия внешних сил на перемещение в замкнутой цепи носителей заряда. Иными словами, от ЭДС будет зависеть то, как сильно ток стремится течь по проводнику.

При объяснении подобных непонятных явлений отечественные школьные учителя любят обращаться к методу гидравлических аналогий. Если проводник – это труба, а электрический ток – это количество протекающей по ней воды, то ЭДС – это давление, которое развивает насос, чтобы качать жидкость.

Термин электродвижущая сила родственен такому понятию, как напряжение. Она, ЭДС, так же измеряется в вольтах (ед. изм. – «В»). Каждый источник питания, будь то батарейка, генератор или солнечная панель, обладает своей собственной электродвижущей силой. Зачастую эта ЭДС близка к выходному напряжению (U), но всегда немного меньше его. Вызвано это внутренним сопротивлением источника, на котором неизбежно падает часть вольтажа.

Советуем изучить — Закалка стали

По этой причине идеальный источник ЭДС – это скорее абстрактное понятие или физическая модель, не имеющая места в реальном мире, ведь внутреннее сопротивление элемента питания Rвн хоть и весьма низкое, но всё же отлично от абсолютного нуля.

Идеальный и реальный источник ЭДС

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.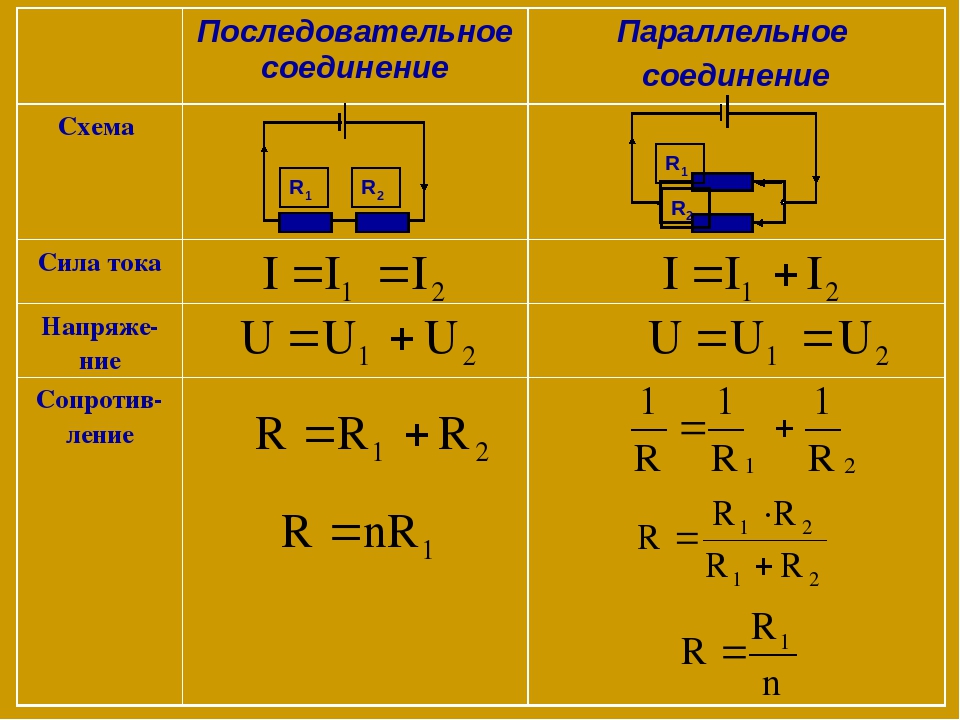

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

[E=IR]

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

В общем, это наиболее распространенные варианты использования этих соединений.

Работа и мощность электрического тока

Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.

Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды. Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.

Советуем изучить — Статическое и астатическое регулирование

Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.

Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.

Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt. Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.

Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена. Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.

Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей

Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами

Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.

Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга.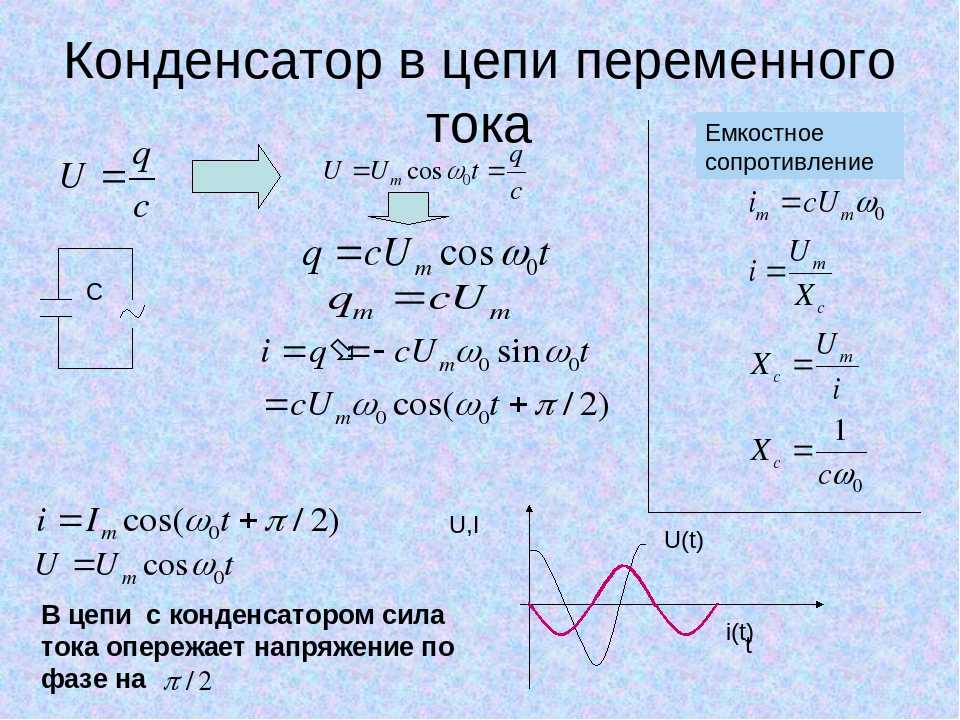 Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.

График зависимости потребляемой мощности во внешней части цепи от силы тока

Графиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Как найти силу тока через мощность, сопротивление и напряжение

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

• Если известна мощность и напряжение
• Если известно напряжение или мощность и сопротивление
• Если известно ЭДС, внутреннее сопротивление и нагрузка
• Закон Джоуля-Ленца
• Несколько примеров

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

P=UI

После несложных мы получаем формулу для вычислений

I=P/U

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.

I=U/R

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

P=UI

При этом согласно тому же закону Ома:

U=IR

То:

 P=I²*R

Значит расчёт проводим по формуле:

I²=P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R)^1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.

Его формула выглядит так:

Q=I²Rt

Тогда расчет проводите так:

I²=QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt)^1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

R₁

+R₂=1+2=3 Ома

Тогда рассчитать силу тока можно по закону Ома:

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

I=12*0,67=18А

2 задача: рассчитать ток при смешанном соединении элементов.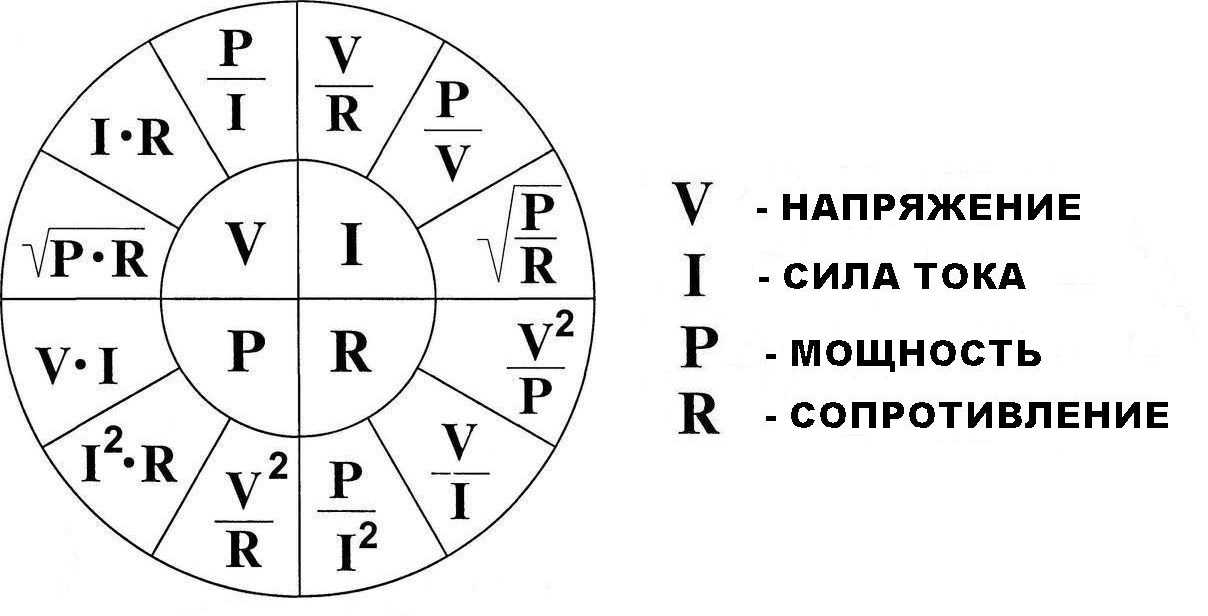 На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома

Теперь схема примет вид:

Далее находим ток по тому же закону Ома:

I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер

Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!

Наверняка вы не знаете:

• Как рассчитать сечение кабеля
• Как перевести амперы в киловатты
• Как найти провод в стене

Как рассчитать напряжение на компоненте

Чтобы выяснить, сколько напряжения падает на каждом резисторе, вы используете закон Ома для каждого отдельного резистора. Вы знаете значение каждого резистора, и вы знаете ток, протекающий через каждый резистор. Помните, что ток ( I ) представляет собой напряжение батареи (9 В), деленное на общее сопротивление ( R1 + R2 ), или примерно 7,4 мА.

Теперь вы можете применить закон Ома к каждому резистору, чтобы рассчитать его падение напряжения:

Обратите внимание, что если сложить падение напряжения на двух резисторах, вы получите 9 вольт, то есть общее напряжение, выдаваемое батареей. Это не совпадение; батарея подает напряжение на два резистора в цепи, и напряжение питания делится между резисторами пропорционально в соответствии со значениями резисторов. Этот тип схемы известен как делитель напряжения

.

Используйте это изображение для расчета разделенных напряжений.

Существует более быстрый способ расчета любого из «разделенных напряжений» ( В ₁ или В ₂ ) на этом рисунке. Вы знаете, что ток, проходящий через цепь, можно выразить как

Вы также знаете, что:

и

Чтобы вычислить В ₁ , например, вы можете заменить выражение I , показанное выше, и вы получите

Вы можете переставить члены, не меняя уравнения, чтобы получить

Аналогично уравнение для В ₂ это

, подключив значения R1 , R2 и V

_{Аккумулятор} , вы получите V ₁ = 1,628 В и В ₂ = 7. 4 V, как ASCALTED ASCELTALD ASCALD. .

Следующее общее уравнение обычно используется для определения напряжения на резисторе ( R1 ) в цепи делителя напряжения:

Многие электронные системы используют делители напряжения для снижения напряжения питания до более низкого уровня, после чего они подают это пониженное напряжение на вход другой части общей системы, для которой требуется это более низкое напряжение.

Вы можете использовать уравнение делителя напряжения для расчета выходного напряжения В _out схемы делителя напряжения, показанной на следующем рисунке, следующим образом:

Схема на следующем рисунке делит источник питания 9 В на 5 В.

Эта схема делителя напряжения снижает 9-вольтовое питание до 5 вольт при В _out .

Эта статья из книги:

• Электроника для чайников,

Об авторе книги:

Кэтлин Шами — инженер-электрик и писатель с обширным инженерным и консультационным опытом в области медицинской электроники, обработки речи и телекоммуникаций.

Эту статью можно найти в категории:

• General Electronics ,

Ток и напряжение — Физика AP 1

Все ресурсы физики AP 1

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 3 Следующая →

AP Physics 1 Справка » Электричество и волны » Электричество » Схемы » Ток и напряжение

Рассмотрим следующую цепь:

Какой ток протекает через резистор R5?

Возможные ответы:

Правильный ответ:

Объяснение:

Весь ток, протекающий по цепи, будет проходить через резистор R5, так как он ни с чем не параллелен. Чтобы найти ток, протекающий через цепь, нам нужно сначала найти полное эквивалентное сопротивление цепи.

Для этого нам сначала нужно уплотнить R3 и R4. Они расположены последовательно, поэтому мы можем просто сложить их, чтобы получить:

Теперь мы можем сжать R2 и R34. Они параллельны, поэтому мы будем использовать следующее уравнение:

Эквивалентная схема теперь выглядит так:

Поскольку все параллельно, мы можем просто сложить все:

Теперь21

2 что у нас есть полное сопротивление цепи, мы можем использовать закон Ома, чтобы найти полный ток:

Переставляя ток, получаем:

Сообщить об ошибке

Рассмотрим следующую схему:

Если через R1 протекает ток 1,35 А, то какой ток протекает через R4?

Возможные ответы:

Правильный ответ:

Объяснение:

Текущий закон Кирхгофа говорит нам, что такое же количество тока, которое входит в соединение после резистора R1, должно также выходить из соединения. Мы также знаем, что падение напряжения на каждом пути разветвления одинаково.

Рассмотрим следующую схему для наглядности:

Используя закон Ома для разложения напряжений, мы получаем:

Теперь у нас есть два уравнения, которые мы можем решить одновременно: 10211

1

1

1

Так как мы решаем для I3, давайте изменим первое уравнение для I2:

Подставив это во второе уравнение, мы получим:

Преобразование для решения для I3:

У нас есть все необходимые значения, поэтому просто подключите заданные значения и решайте:

Отчет о ошибке

Рассмотрим следующую схему:

Если 1,35 A — это течет через R1, каково падение напряжения на R2?

Возможные ответы:

Правильный ответ:

Объяснение:

Текущий закон Кирхгофа говорит нам, что такая же сила тока, входящая в соединение после резистора R1, должна также выходить из соединения. Мы также знаем, что падение напряжения на каждом пути разветвления одинаково.

Рассмотрим следующую схему для наглядности:

Используя закон Ома для разложения напряжений, мы получаем:

Теперь у нас есть два уравнения, которые мы можем решить одновременно: 10211

1

1

1

Чтобы найти V2, нам нужно вычислить I2, поэтому давайте изменим первое уравнение для I3

Подставив это во второе уравнение, мы получим:

Перестановка для I2:

У нас есть все необходимые значения, так что просто подставьте данные значения и решите:

Закон

Теперь, когда мы знаем I2,

Найдите падение напряжения на этом резисторе:

Сообщите об ошибке

Рассмотрим следующую цепь:

Насколько увеличивается ток, протекающий через цепь, когда ключ замкнут?

Возможные ответы:

Роста нет; ток уменьшается при замыкании ключа

Нет увеличения; ток остается неизменным при замыкании ключа

Правильный ответ:

Объяснение:

Чтобы рассчитать ток, протекающий по цепи в каждом сценарии, нам необходимо рассчитать эквивалентное сопротивление в каждом сценарии.

СЦЕНАРИЙ 1: Переключатель разомкнут

Когда переключатель разомкнут, все последовательно, поэтому мы можем просто сложить все сопротивления, чтобы найти общее эквивалентное сопротивление. Обратите внимание, что R2 будет исключен.

Используя закон Ома, теперь мы можем рассчитать ток, протекающий по цепи:

Перестановка тока:

СЦЕНАРИЙ 2: Переключатель замкнут 9 Теперь цепь выглядит так0011

Поскольку у нас есть несколько резисторов, включенных параллельно, этот расчет потребует еще нескольких шагов.

Сначала нам нужно уплотнить R3 и R4. Они расположены последовательно, поэтому мы можем просто сложить их, чтобы получить:

Теперь мы можем сжать R2 и R34. Они параллельны, поэтому мы будем использовать следующее уравнение:

Эквивалентная схема теперь выглядит так:

Поскольку все последовательно, мы можем просто сложить все:

Теперь, используя закон Ома, рассчитаем ток, протекающий по цепи:

 

Теперь мы просто возьмем разные токи в двух сценариях: цепь:

На сколько уменьшится ток в цепи, если убрать резистор R3?

Возможные ответы:

Правильный ответ:

Объяснение:

Нас просят сравнить два разных сценария, каждый из которых включает расчет эквивалентного сопротивления, который будет использовать следующую формулу:

Сценарий 1: Присутствует R3

2 Сейчас 2 Закон Ома:

Сценарий 2: Без R3

Теперь по закону Ома:

Рассчитайте изменение тока:

Отчет Ошибка

Рассмотрим схему:

Сколько тока проходит через R1?

Возможные ответы:

Правильный ответ:

Объяснение:

Хотя эту задачу можно решить, рассчитав эквивалентное сопротивление, рассчитав общий ток в цепи, а затем используя правило Кирхгофа для определения тока через резистор R1, гораздо проще просто использовать правило Кирхгофа для контура. Это правило говорит о том, что в любом замкнутом контуре цепи все напряжения в сумме должны равняться нулю. Записано в виде уравнения:

Если мы рассмотрим замкнутый контур, состоящий только из источника питания и резистора R1, мы можем использовать закон Ома для расчета тока:

Суммарный ток в цепи равен , а ток через резистор R2 равен . Каково значение R2?

Возможные ответы:

Правильный ответ:

Объяснение:

Общий ток в цепи не нужен для решения этой проблемы. Нам нужно только знать ток через резистор, а также правило петли Кирхгофа. Правило контура гласит, что для любого замкнутого контура в цепи сумма напряжений равна нулю.

Для этой задачи мы рассмотрим контур, состоящий исключительно из источника напряжения и R2. Из правила мы знаем, что через резистор теряется 12В. Используя закон Ома, мы можем написать:

Переставляя для R2, ​​получаем:

Сообщить об ошибке

В этой схеме выше, и . Падение напряжения на нем составляет восемь вольт. Какова сила тока в цепи?

Возможные ответы:

Правильный ответ:

Объяснение:

Падение напряжения связано с током и сопротивлением по закону Ома:

 

Сообщить об ошибке

Учащийся создал заданную электрическую схему. Он состоит из батареи, резистора и лампочки. За одну минуту через резистор проходит 1,2 C заряда. Какой заряд проходит через лампочку за одну минуту?

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку лампа и резистор соединены последовательно, ток в каждой из них одинаков.