Что такое электрическое напряжение. Как связано напряжение с током и сопротивлением. Какие формулы используются для расчета напряжения. Почему напряжение важно в электрических цепях.
Что такое электрическое напряжение
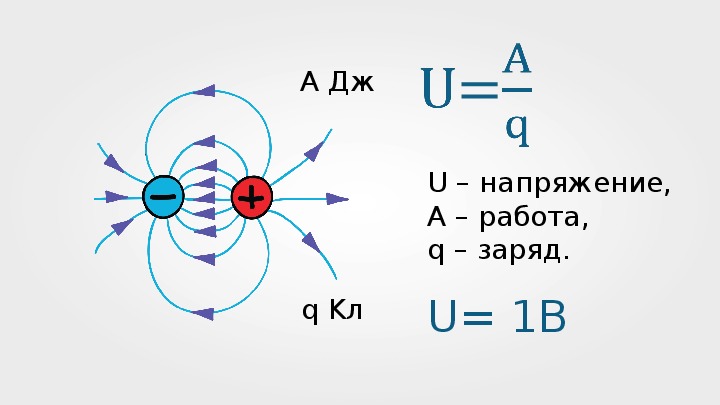
Электрическое напряжение — это разность потенциалов между двумя точками электрической цепи. Оно характеризует работу, которую совершает электрическое поле при перемещении единичного положительного заряда между этими точками.
Основные характеристики напряжения:
- Измеряется в вольтах (В)
- Обозначается буквой U или V
- Является скалярной величиной (имеет только числовое значение)
- Всегда измеряется между двумя точками цепи
Напряжение создает электрическое поле, которое заставляет заряженные частицы двигаться по проводнику, образуя электрический ток. Чем выше напряжение, тем сильнее электрическое поле и больше сила тока при одинаковом сопротивлении цепи.
Формулы для расчета напряжения
Основные формулы, связывающие напряжение с другими электрическими величинами:
- Закон Ома: U = I * R, где I — сила тока, R — сопротивление
- Мощность: P = U * I
- Работа электрического тока: A = U * I * t, где t — время
- Напряжение в последовательной цепи: U = U1 + U2 + … + Un
- Напряжение в параллельной цепи: U = U1 = U2 = … = Un
Эти формулы позволяют рассчитывать напряжение в различных ситуациях, зная другие параметры электрической цепи.
Связь напряжения с током и сопротивлением
Напряжение, ток и сопротивление тесно связаны между собой. Эту взаимосвязь описывает закон Ома:
- U = I * R
- I = U / R
- R = U / I
Из этих формул следует:
- При постоянном сопротивлении увеличение напряжения приводит к увеличению тока
- При постоянном токе увеличение сопротивления требует увеличения напряжения
- При постоянном напряжении увеличение сопротивления приводит к уменьшению тока
Таким образом, напряжение является «движущей силой» электрического тока, преодолевающей сопротивление цепи.
Почему напряжение важно в электрических цепях
Напряжение играет ключевую роль в работе электрических цепей по нескольким причинам:

- Обеспечивает движение электрических зарядов (ток)
- Определяет мощность, выделяемую на элементах цепи
- Влияет на выбор компонентов с подходящими номиналами
- Позволяет рассчитывать параметры цепей
- Используется для контроля и управления электрическими процессами
Без напряжения электрические цепи не могли бы функционировать, поэтому понимание его свойств критически важно при проектировании и анализе электрических схем.
Измерение напряжения
Для измерения напряжения используются следующие приборы и методы:
- Вольтметр — измеряет напряжение между двумя точками цепи
- Мультиметр в режиме измерения напряжения
- Осциллограф — позволяет наблюдать форму сигнала напряжения
- Делитель напряжения — для измерения высоких напряжений
- Дифференциальный пробник — для точных измерений
При измерении напряжения важно соблюдать правила техники безопасности, особенно при работе с высоковольтными цепями. Необходимо использовать приборы с подходящими диапазонами измерения.
Виды напряжения
Существуют различные виды напряжения, встречающиеся в электротехнике:

- Постоянное напряжение — не меняется во времени
- Переменное напряжение — периодически изменяется
- Импульсное напряжение — имеет форму коротких импульсов
- Пульсирующее напряжение — постоянное с переменной составляющей
- Высокое напряжение — более 1000 В
Каждый вид напряжения имеет свои особенности и области применения. Например, постоянное напряжение используется в электронных устройствах, а переменное — в бытовых электросетях.
Заключение
Электрическое напряжение является фундаментальной величиной в электротехнике и электронике. Оно тесно связано с током и сопротивлением через закон Ома. Понимание свойств и закономерностей напряжения необходимо для анализа и проектирования электрических цепей любой сложности.
Ключевые моменты для запоминания:
- Напряжение измеряется в вольтах между двумя точками цепи
- Связано с током и сопротивлением через закон Ома: U = I * R
- Является причиной возникновения электрического тока
- Определяет мощность в электрических цепях
- Бывает постоянным, переменным и других видов
Глубокое понимание концепции напряжения и умение применять связанные с ним формулы — важные навыки для всех, кто работает с электричеством и электроникой.

Электрические формулы и их описание
Чтобы работать с электричеством, делать разводку по дому, понимать правила ПУЭ и решать различные задачи, нужно знать основные формулы электричества, физические законы, приведенные известными учеными-физиками. Ниже рассмотрены основные теоремы по электрике, выведенные константы, физические правила, которые следует понимать каждому человеку.
Основные формулы электричества
Изучение основ электродинамики, электрики невозможно без определения электрического поля, точных зарядов, сопротивления и прочих явлений.
Формулы электричестваПоэтому важно рассмотреть все основные формулы электричества и примеры решения задач с их использованием.
Закон Кулона
Согласно короткому описанию, это физический закон, который говорит о взаимодействии между прямо стоящими точечными электрозарядами в зависимости от того, на каком расстоянии они находятся. Согласно полному определению, формулировка обозначает, что между двумя точками в виде электрических зарядов формируется вакуум. Там появляется конкретная сила, которая пропорциональна умножению их модульных частиц, поделенных на квадратный показатель расстояния.
Расстояние — длина, которая соединяет заряды. Сила взаимодействия направлена по отрезку. Кулоновская сила — сила, отталкивающая при зарядах минус-минус и плюс-плюс и притягательная при минус-плюс и плюс-минус.
Обратите внимание! Электрическая сила формула выглядит так: F=k⋅|q1|⋅|q2|/r2, где F — сила заряда, q — величина заряда, r — вектор или расстояние между зарядами, а k — коэффициент пропорциональности. Последний равен c2·10−7 Гн/м.
Закон КулонаРешение задачи с законом Кулона. При наличии заряженных шариков, которые находятся на расстоянии 15 см и отталкиваются с силой 1 Н в поиске начального заряда, выявить неизвестное можно, переведя основные единицы в систему СИ и подставив величины в указанную формулу. Выйдет значение 2 * 5 * 10 (-8) = 10 (-7).
Напряженность поля уединенного точечного заряда
Электрическое поле будучи материей, создаваемой электрическими точечными зарядами, характеризуется разными величинами, в том числе напряженностью. Напряженность выступает векторной величиной или силовой характеристикой поля, которая направлена в сторону электростатического взаимодействия зарядов. Чтобы получить ее, нужно использовать формулу E = k (q / r (2)), где Е — векторное поле.
Напряженность поля уединенного точечного зарядаСогласно данной формулировке, напряженность поля заряда имеет обратную пропорциональность квадратному значению расстояния от заряда. То есть если промежуток увеличивается в несколько раз, показатель напряжения снижается в четыре.
Применить закон можно для решения задач. Например, неизвестен радиус. Тогда нужно преобразовать константу. Нужно решить уравнение E / r (2) = kq, подставив известные числа.
Потенциал точки в поле точечного заряда
Потенциалом в электростатическом поле называется скалярная величина, которая равна делению потенциального показателя энергии заряда на него. Он не зависит от величины q, которая помещена в область. Так как потенциальный показатель энергии зависит от того, какая выбрана система координат, то потенциал определяется с точностью до постоянной. Он равен работе поле, которое смещает единичный положительный заряд в бесконечность. Выражается через ф = W / q =const.
Потенциал точки в поле точечного зарядаОбратите внимание! В задачах можно преобразовывать константу. Если неизвестно W, то можно поделить q на ф, а если q — то, W на ф.
Потенциальная энергия заряда в электростатическом поле
Потенциальная энергия заряда в электростатическом полеПоскольку работа электрического поля не зависит от выбранного движения заряженной частицы, а от его начального и конечного положения, есть термин потенциальной энергии. Это скалярная величина в координате пространства, которая показывает, как работает сила, когда частица перемещается по произвольному промежутку из одной в другую точку. Она равна разности значений передвижения частиц в этом промежутке. Выражается в следующем виде: А = П1 — П2, где П1 может быть x, y и z, а П2 — x2, y2 и z2. В задачах по физике нужно рисовать график, подставлять в константу известные значения и решать уравнения.
Потенциальная энергия заряда q1 в поле точечного заряда
Во время перемещения заряженных частиц по полю из одной точки в другую они совершают некую работу за определенный временной промежуток. Потенциальная энергия в этих точках не зависит от того, какой путь держат заряженные частицы. Энергия первого заряда пропорциональна его модулю. Выражается это все в формуле, представленной на картинке ниже. Задачи решать можно, используя представленную константу и вставляя известные значения.
Потенциальная энергия заряда q1 в поле точечного зарядаТеорема Гаусса
Основной закон в электродинамике, входящий в уравнения Максвелла. Это следствие из кулоновского умозаключения и принципа суперпозиции. По ней вектор напряжения поля движется сквозь произвольное значение замкнутой поверхности, окруженной зарядами. Он имеет пропорциональность сумме заряженных частиц, которые находятся внутри этого замкнутого пространства. Указанный вектор поделен на е0. Все это выражается формулой, указанной ниже.
Теорема ГауссаНапряженность электрического поля вблизи от поверхности проводника
Напряженность суммарного пространства заряженных частиц имеет прямую пропорциональность поверхностному показателю их плотности. Если в задаче требуется найти напряженность, а поверхностная заряженная плотность это сигма, то нужно нарисовать цилиндр и обозначить, что поток сквозь его боковую поверхность равен 0. В таком случае линии напряженности будут параллельны боковой поверхности. Получится, что ф = 2ф, осн =2еs, а 2es =q / 2ε0.
Напряженность электрического поля вблизи от поверхности проводникаЕмкость плоского конденсатора
Емкостью называется проводниковая характеристика, по которой электрический заряд может накапливать энергию. Плоским конденсатором называются несколько противоположно заряженных пластин, разделенных диэлектрическим тонким слоем. Емкостью плоского конденсатора считается его характеристика, способность к накоплению электрической энергии.
Обратите внимание! Это физическая величина, которая равна делению заряда на разность потенциалов его обкладки. Зарядом при этом служит заряженная одна пластина.
Если в задаче требуется узнать емкость конденсатора из двух пластин с площадью в 10(-2) квадратных метров и в них находится 2*10(-3) метровый лист, ε0 электрическая постоянная с 8,85×10-12 фарад на метр и ε=6 — диэлектрическая проницаемость слюды. В таком случае нужно вставить значения в формулу C= ε* ε* S/d.
Емкость плоского конденсатораЭнергия плоского конденсатора
Поскольку любая частица конденсатора имеет способность запаса энергии, который сохранен на конденсаторной обкладке, вычислить эту самую Е просто, поскольку чтобы элемент зарядился, ему нужно совершить работу. Работа совершается полем. В результате была выведена следующая формула: Еp = А = qEd, где А является работой, d — расстоянием.
ЭнергияФормулы для постоянного электрического тока
Постоянный электрический ток не изменяется в величине и направлении. Он используется для расчета замкнутой, однородной цепи, мощности и прочих параметров. Поэтому важно знать формулы для него и основные законы, связанные с ним.
Основной список формулЗакон Ома для участка однородной цепи
Чтобы электрический ток существовал, нужно поле. Для его образования, нужны потенциалы или разность их, выраженная напряжением. Ток будет направлен на снижение потенциалов, а электроны начнут свое передвижение в обратном направлении. В 1826 г. Г. Ом провел исследование и сделал заключение: чем больше показатель напряжения, тем больше ток, который проходит через участок.
К сведению! Смежные проводники при этом проводят электричество по-разному. То есть каждый элемент имеет свою проводимость, электрическое сопротивление.
В результате, согласно теореме Ома, сила тока для участка однородной цепи будет иметь прямую пропорциональность показателю напряжения на нем и обратную пропорциональность проводниковому сопротивлению.
Закон ОмаПо формуле I = U / R, где I считается силой тока, U — напряжением, а R — электрическим сопротивлением, последнее значение можно найти, если p * l / S, где p является удельным проводниковым сопротивлением, l — длиной проводника, а S — площадью поперечного проводникового сечения.
Закон Ома для замкнутой цепи с источником тока
Ом сделал формулу и для замкнутой цепи. По ней ток на этом участке из токового источника, имеющего внутреннее и внешнее нагрузочное сопротивление, равен делению электродвижущей силы источника на сумму внутреннего и внешнего сопротивления. Она выглядит так: I = e / R + r, где I является токовой силой, е — ЭДС, R — сопротивлением, а r — внутренней сопротивляемостью источника напряжения.
Обратите внимание! В физическом смысле по этому закону, чем выше показатель ЭДС, тем выше источник энергии, больше скорость движения зарядов. Чем выше сопротивляемость, тем ниже величина тока.
Закон Ома для замкнутой цепиРабота постоянного тока
Энергия, когда проходит через проводник, упорядоченно двигается в носитель. Во время движения она совершает работу. В результате работой постоянного тока называется деятельность поля, направленная на перенос электрических зарядов по проводнику. Она равна умножению I на совершаемое работой напряжение и время.
Закон Джоуля-Ленца
Когда электричество проходит через какой-то проводник с сопротивляемостью, всегда высвобождается теплота. Количество тепла, которое высвободилось за определенный промежуток времени, определяет закон Джоуля-Ленца. По формуле мощность тепла равняется умножению плотности электричества на напряжение — w =j * E = oE(2).
Обратите внимание! В практическом понимании закон имеет значение для снижения потери электроэнергии, выбора проводника для электроцепи, подбора электронагревательного прибора и использования плавкого предохранителя для защиты сети.
Закон Джоуля-ЛенцаПолная мощность, развиваемая источником тока
Мощность — работа, которая совершается за одну секунду времени. Электрическая мощность является физической величиной, которая характеризует скорость передачи с преобразованием электроэнергии.
Работа, которая развивается источником электроэнергии по всей цепи, это полная мощность. Ее можно определить по формуле Р = El, где E считается ЭДС, а I — величиной токовой характеристики.
К сведению! Если есть линейная нагрузка, то полный мощностный показатель равен квадратному корню из квадратов активной и реактивной работы источника. Если есть нелинейная нагрузка, то она равна квадратному корню из квадратов активной и неактивной работы источника.
Полная мощностьВ практических измерениях такая работа выражается в киловаттах в час. Используется, чтобы измерять потребление электричества в бытовых и производственных условиях, определять выработанную электрическую энергию в электрическом оборудовании.
Полезная мощность
Максимальная или полезная мощность — та, что выделяется во внешнем промежутке цепи, то есть во время нагрузки резистора. Она может быть применена для выполнения каких-либо задач. Подобное понятие можно применить, чтобы рассчитать, как работает электрический двигатель или трансформатор, который способен на потребление активной и реактивной составляющей.
Полезная мощностьПолезный мощностный показатель можно рассчитать по трем формулам: P = I 2R, P = U2 / r, P = IU, где I является силой тока на определенном участке цепи; U — напряжением на части клемм (зажимов) токового источника, а R — сопротивлением нагрузки или внешней цепью.
Коэффициент полезного действия источника тока
Коэффициентом полезного действия токового источника называется деление полезного мощностного показателя на полный. Если внутреннее сопротивление источника равно внешнему, то половина результатов всей работы будет утеряна в источнике, а другая половина будет выделена на нагрузке. В такой ситуации КПД будет равен 50 %.
Если рассматривать это понятие наиболее полно, то когда электрические заряды перемещаются по замкнутой электрической цепи, источник тока выполняет определенную полезную и полную работу. Совершая первую, он перемещает заряды во внешнюю цепь. Делая вторую работу, заряженные частицы перемещаются по всему участку.
КПД источника токаОбратите внимание! Полезное действие достигается, когда сопротивление внешней электроцепи будет иметь определенное значение, зависящее от источника и нагрузки. Соотношения полезной работы на полную выражают формулой: η = Аполез / Аполн = Рполез / Рполн = U/ε = R / (R + r).
Первое правило Кирхгофа
Согласно первому закону Кирхгофу, токовая сумма в любом участке электрической цепи равняется нулевому значению. Направленный заряд к узлу положительный, а от него — отрицательный. Алгебраическая токовая сумма зарядов, которые направлены к узлу, равна сумме тех, которые направлены от него. Если перевести это правило, то можно получить следующее определение: сколько тока попадает в узел, столько и выходит из него. Это правило вытекает из закона о сохранности заряженных частиц.
Благодаря решению линейных уравнений на основе кирхгофских правил можно отыскать все токовые значения и напряжения на участках постоянного, переменного и квазистационарного электротоков.
Обратите внимание! В электотехнике правило Кирхгофа имеет особое значение, поскольку оно универсально для решения многих поставленных задач в теории электроцепи. С помощью него можно рассчитать сложные электрические цепи. Применяя его, можно получить систему линейных уравнений относительно токам или напряжениям на всех межузловых ветвях цепей.
Первое правило КирхгофаВторое правило Кирхгофа
Второе кирхгофское правило вытекает из первого и третьего максвеллского уравнения. По нему алгебраическая сумма напряжений на резистивных элементах замкнутого участка равна сумме ЭДС, которая входит в него. Если на участке нет ЭДС, то суммарный показатель падения напряжения равен нулевому значению. Если еще проще, то во время полного обхода контура потенциал изменяется. Он возвращается на исходное значение.
Частый случай для участка одного контура — это закон Ома. Составляя уравнения напряжений для контура, требуется подобрать его положительный обход. Чтобы это сделать, нужно знать, что при подборе обхода показатель падения напряжения ветви будет положительным, если обходное направление в ветви совпадает с тем, которое было ранее выбрано. Если оно не совпадает, то показатель напряжения ветви будет отрицательным.
Важно! Второе правило Кирхгофа можно использовать в линейной или нелинейной линеаризованной цепи при любом изменении токов и напряжения.
Второе правило КирхгофаВ результате, чтобы понять основы физики явлений, электрики, электродинамики и с успехом использовать знания в процессе жизнедеятельности, необходимо знать выведенные теоремы, законы, формулы и правила в области электричества, которые представлены выше. Например, представляя, как выглядит та или иная формула, можно решить любую задачу в учебнике по физике или жизни.
как связаны между собой напряжение, ток и сопротивление
Добавлено 30 сентября 2020 в 00:30
Сохранить или поделиться
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
| Величина | Символ | Единица измерения | Сокращение единицы измерения |
|---|---|---|---|
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
\[E=IR\]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
\[I = \frac{E}{R}\]
\[R = \frac{E}{I}\]
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:
Рисунок 1 – Пример простой схемыВ приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампыКакая величина тока (I) в этой цепи?
\[I = \frac{E}{R} = \frac{12 \ В}{3 \ Ом} = 4 \ А\]
Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепиКакое сопротивление (R) оказывает лампа?
\[R = \frac{E}{I} = \frac{36 \ В}{4 \ А} = 9 \ Ом\]
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампыКакое напряжение обеспечивает батарея?
\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона ОмаЕсли вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения RЕсли вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения IНаконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения EВ конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Резюме
- Напряжение измеряется в вольтах, обозначается буквами «E» или «V».
- Сила тока измеряется в амперах, обозначается буквой «I».
- Сопротивление измеряется в омах, обозначается буквой «R».
- Закон Ома: E = IR; I = E/R; R = E/I
Оригинал статьи:
Теги
Закон ОмаЗарядКулонОбучениеСила токаСопротивлениеСхемотехникаЭлектрический токЭлектрическое напряжениеСохранить или поделиться
Электрические напряжение и ток
Добавлено 23 сентября 2020 в 21:50
Сохранить или поделиться
Как упоминалось ранее, нам нужно нечто большее, чем просто непрерывный путь (т.е. цепь), чтобы возник непрерывный поток заряда: нам также нужны средства для толкания этих носителей заряда по цепи. Так же, как шарики в трубке или вода в трубе, для инициирования потока зарядам необходима какая-то воздействующая сила. В случае электронов эта сила – это та же сила, которая действует в статическом электричестве: сила, создаваемая дисбалансом электрического заряда. Если мы возьмем примеры с воском и шерстью, которые были натерты друг о друга, мы обнаружим, что избыток электронов в воске (отрицательный заряд) и дефицит электронов в шерсти (положительный заряд) создают дисбаланс заряда между ними. Этот дисбаланс проявляется как сила притяжения между двумя объектами:
Рисунок 1 – Притяжение воска и шерстиЕсли между заряженными воском и шерстью поместить проводящий провод, электроны будут проходить через него, так как часть избыточных электронов в воске устремляются через провод, чтобы вернуться к шерсти, восполняя недостаток электронов там:
Рисунок 2 – Поток электронов между воском и шерстьюДисбаланс электронов между атомами воска и атомами шерсти создает силу между этими двумя материалами. Поскольку электроны не могут перетекать от воска к шерсти, всё, что может сделать эта сила, – это притягивать два объекта друг к другу. Однако теперь, когда проводник организует мост через изолирующий разрыв, эта сила заставит электроны течь в одном направлении через провод, хотя бы на мгновение, пока заряд не нейтрализуется и сила между воском и шерстью не уменьшится. Электрический заряд, образующийся между этими двумя материалами при их трении друг о друга, служит для хранения определенного количества энергии. Эта энергия мало чем отличается от энергии, хранящейся в высоком резервуаре с водой, которая откачивается из пруда уровнем ниже:
Рисунок 3 – Водяной насос и накопление энергииВлияние силы тяжести на воду в резервуаре создает силу, которая пытается снова опустить воду на более низкий уровень. Если проложить подходящую трубу от резервуара обратно к пруду, вода под действием силы тяжести потечет по ней вниз из резервуара:
Рисунок 4 – Высвобождение энергии водыДля перекачивания этой воды из пруда на нижнем уровне в резервуар на верхнем уровне требуется энергия, а движение воды по трубопроводу обратно к исходному уровню представляет собой высвобождение энергии, накопленной при предыдущей откачке. Если вода перекачивается на еще более высокий уровень, для этого потребуется еще больше энергии, таким образом, будет сохранено больше энергии, и больше энергии будет высвобождено, если воде позволить снова течь по трубе обратно вниз:
Рисунок 5 – Большее количество энергии, хранимое водойЭлектроны мало чем отличаются. Натирая воск и шерсть друг об друга, мы «выкачиваем» электроны с их обычных «уровней», создавая условия, при которых между воском и шерстью существует сила, поскольку электроны стремятся восстановить свои прежние положения (и вернуться в свои атомы). Сила, притягивающая электроны обратно в исходное положение вокруг положительных ядер их атомов, аналогична силе гравитации, действующей на воду в резервуаре, и пытающейся вернуть ее на прежний уровень. Подобно тому, как перекачка воды на более высокий уровень приводит к накоплению энергии, «перекачка» электронов для создания дисбаланса электрического заряда приводит к накоплению определенного количества энергии в этом дисбалансе. И точно так же, как обеспечение возможности стекать воде обратно с высоты резервуара приводит к высвобождению этой накопленной энергии, предоставление возможности электронам течь обратно к их исходным «уровням» тоже приводит к высвобождению накопленной энергии. Когда носители заряда находятся в этом статическом состоянии (точно так же, как вода неподвижно находится в верхнем резервуаре), энергия, хранящаяся там, называется потенциальной энергией, потому что у нее есть возможность (потенциал) высвобождения, которая еще не реализована полностью.
Понятие концепции напряжения
Когда носители заряда находятся в этом статическом состоянии (точно так же, как вода неподвижно находится в верхнем резервуаре), энергия, хранящаяся там, называется потенциальной энергией, потому что у нее есть возможность (потенциал) высвобождения, которая еще не реализована полностью. Когда вы трете обувь с резиновой подошвой о тканевый ковер в сухой день, вы создаете дисбаланс электрического заряда между вами и ковром. При шаркании ногами накапливается энергия в виде дисбаланса зарядов, вытесняемых из их первоначальных мест. Этот заряд (статическое электричество) является неподвижным, и вы не заметите, что эта энергия вообще накапливается. Однако, как только вы положите руку на металлическую дверную ручку (с большой подвижностью электронов для нейтрализации вашего электрического заряда), эта накопленная энергия высвободится в виде внезапного потока заряда через вашу руку, и вы воспримите это как удар электрическим током! Эта потенциальная энергия, хранящаяся в виде дисбаланса электрического заряда и способная вызывать прохождение носителей заряда через проводник, может быть выражена термином под названием напряжение, которое технически является мерой потенциальной энергии на единицу заряда или чем-то, что физик мог бы называют удельной потенциальной энергией.
Определение напряжения
В контексте статического электричества напряжение – это количество работы, необходимое для перемещения единичного заряда из одного места в другое, против действующей силы, которая пытается сохранить баланс электрических зарядов. В контексте источников электроэнергии напряжение – это количество доступной потенциальной энергии (работа, которую необходимо выполнить) на единицу заряда для перемещения зарядов через проводник. Поскольку напряжение – это выражение потенциальной энергии, представляющее возможность или потенциал для выделения энергии, когда заряд перемещается с одного «уровня» на другой, оно всегда находится между двумя точками. Рассмотрим аналогию с резервуаром:
Рисунок 6 – Энергия в зависимости от высоты паденияИз-за разницы в высоте падения при перемещении воды через трубопровод до точки 2 будет высвобождено больше энергии, чем при перемещении до точки 1. Эту идею можно интуитивно понять, рассмотрев падение камня: в результате чего будет получен более сильный удар, при падении камня с высоты одного фута или при падении этого же камня с высоты одной мили? Очевидно, что падение с большей высоты приводит к высвобождению большей энергии (более сильному удару). Мы не можем оценить количество накопленной энергии в водном резервуаре, просто измерив объем воды, точно так же, как мы не можем предсказать серьезность удара падающей породы, просто зная вес камня: в обоих случаях мы также должны учитывать, насколько далеко эти массы упадут с их начальной высоты. Количество энергии, высвобождаемой при падении массы, зависит от расстояния между ее начальной и конечной точками. Точно так же потенциальная энергия, доступная для перемещения носителей заряда из одной точки в другую, зависит от этих двух точек. Следовательно, напряжение всегда выражается как величина между двумя точками. Довольно интересно, что аналогия с массой, потенциально «падающей» с одной высоты на другую, является настолько удачной моделью, что напряжение между двумя точками иногда называют падением напряжения.
Генерирование напряжения
Кроме трения материалов определенных типов друг о друга, напряжение может создаваться и другими способами. Химические реакции, энергия излучения и влияние магнетизма на проводники – вот несколько способов, которыми может создаваться напряжение. Соответствующими примерами этих трех источников напряжения являются батареи, солнечные элементы и генераторы (например, «генератор переменного тока» под капотом вашего автомобиля). На данный момент мы не будем вдаваться в подробности того, как работает каждый из этих источников напряжения – более важно то, что мы понимаем, как источники напряжения могут применяться для создания потока зарядов в электрической цепи. Давайте возьмем обозначение химической батареи и шаг за шагом построим цепь:
Рисунок 7 – Пример батареиКак работают источники напряжения?
Любой источник напряжения, включая аккумуляторы, имеет две точки для электрического контакта. В этом случае на рисунке выше у нас есть точка 1 и точка 2. Горизонтальные линии разной длины указывают на то, что это батарея, и дополнительно указывают направление, в котором напряжение этой батареи будет пытаться протолкнуть носители заряда по цепи. Тот факт, что горизонтальные линии в символе батареи кажутся разделенными (и, таким образом, не могут служить путем для потока заряда), не причина для беспокойства: в реальной жизни эти горизонтальные линии представляют собой металлические пластины, погруженные в жидкий или полутвердый материал, который не только проводит заряды, но и генерирует напряжение, которое толкает их, взаимодействуя с пластинами. Обратите внимание на маленькие значки «+» и «-» непосредственно слева от символа батареи. Отрицательный (-) конец батареи всегда является концом с самой короткой линией, а положительный (+) конец батареи всегда является концом с самой длинной линией. Положительный конец батареи – это конец, который пытается вытолкнуть из нее носители заряда (помните, что по соглашению мы думаем, что носители заряда положительно заряжены, даже если электроны заряжены отрицательно). Точно так же отрицательный конец – это конец, который пытается притянуть носители заряда. Когда «+» и «-» концы батареи ни к чему не подключены, между этими двумя точками будет напряжение, но потока зарядов через батарею не будет, потому что нет непрерывного пути, по которому могут перемещаться носители заряда.
Рисунок 8 – Аналогия резервуаров с водойТот же принцип справедлив и для аналогии с резервуаром для воды и насосом: без обратной трубы, по которой вода могла бы сливаться обратно в пруд, накопленная энергия в резервуаре не может быть выпущена в виде потока воды. Как только резервуар будет полностью заполнен, поток не может возникнуть, независимо от того, какое давление может создать насос. Для обеспечения непрерывного потока должен существовать полный путь (контур), по которому вода течет из пруда в резервуар и обратно в пруд. Мы можем обеспечить такой путь для батареи, соединив кусок провода от одного конца батареи к другому. Формируя цепь с петлей из проволоки, мы инициируем непрерывный поток зарядов по часовой стрелке:
Рисунок 9 – Электрическая цепь и аналогия с резервуарамиПонятие концепции электрического тока
Пока батарея продолжает вырабатывать напряжение и непрерывность электрического пути не нарушена, носители заряда будут продолжать течь по цепи. Следуя аналогии с водой, движущейся по трубе, этот непрерывный, равномерный поток зарядов через цепь называется электрическим током. Пока источник напряжения продолжает «толкать» в одном направлении, носители заряда будут продолжать двигаться в том же направлении в цепи. Этот однонаправленный поток тока называется постоянным током (Direct Current, или DC). Во втором томе этой серии книг исследуются электрические цепи, в которых направление тока переключается назад и вперед: переменный ток (Alternating Current, или AC). Но пока мы займемся просто цепями постоянного тока. Поскольку электрический ток состоит из отдельных носителей заряда, протекающих через проводник в унисон, перемещающихся и толкающих носителей заряда впереди, точно так же, как шарики в трубе или вода в трубе, величина потока в одиночной цепи будет одинаковой в любой ее точке. Если бы мы отслеживали поперечное сечение провода в одиночной цепи, подсчитывая протекающих носителей заряда, мы бы заметили точно такое же количество в единицу времени, что и в любой другой части цепи, независимо от длины или диаметра проводника. Если мы нарушим непрерывность цепи в какой-либо ее точке, электрический ток прекратится во всем контуре, и в разрыве, между концами проводов, которые раньше были соединены, появится полное напряжение, генерируемое батареей:
Рисунок 10 – Напряжение на аккумуляторной батарееЧто такое полярность падения напряжения?
Обратите внимание на знаки «+» и «-», нарисованные на концах разрыва цепи, и то, как они соответствуют знакам «+» и «-» рядом с выводами батареи. Эти обозначения указывают направление, в котором напряжение пытается подтолкнуть ток, это направление потенциала, обычно называемое полярностью. Помните, что напряжение измеряется всегда относительно между двух точек. По этой причине полярность падения напряжения также является относительной между двумя точками: будет ли точка в цепи помечена знаком «+» или «-», зависит от другой точки, относительно которой выполняется измерение. Взгляните на следующую схему, где каждый угол петли для справки отмечен номером:
Рисунок 11 – Разрыв цепи, тока нетПри нарушении целостности цепи между точками 2 и 3, полярность падения напряжения между точками 2 и 3 будет «+» для точки 2 и «-» для точки 3. Полярность батареи (1 «+» и 4 «-») пытается протолкнуть ток через петлю по часовой стрелке от 1 до 2, до 3, до 4 и снова обратно к 1. Теперь давайте посмотрим, что произойдет, если мы снова соединим точки 2 и 3 вместе, но сделаем разрыв цепи между точками 3 и 4:
Рисунок 12 – Разрыв цепи, тока нетПри разрыве между 3 и 4 полярность падения напряжения между этими двумя точками будет «-» для 4 и «+» для 3. Обратите особое внимание на тот факт, что «знак» точки 3 противоположен знаку в первом примере, где разрыв был между точками 2 и 3 (где точка 3 была помечена «-»). Мы не можем сказать, что точка 3 в этой цепи всегда будет либо «+», либо «-», потому что полярность, как и само напряжение, не зависит от одной точки, они всегда относительны и зависят от двух точек!
Резюме
- Носители заряда могут быть побуждены течь через проводник той же силой, что проявляется в статическом электричестве.
- Напряжение – это мера удельной потенциальной энергии (потенциальной энергии на единицу заряда) между двумя точками. С точки зрения дилетанта, это мера «толкания», позволяющая побуждать заряд перемещаться.
- Напряжение, как выражение потенциальной энергии, всегда относительно и измеряется между двумя точками. Иногда его называют «падением напряжения».
- Когда источник напряжения подключен к цепи, напряжение вызовет равномерный поток носителей заряда через эту цепь, называемый электрическим током.
- В одиночной (однопетлевой) цепи величина тока в любой точке равна величине тока в любой другой точке.
- При разрыве цепи, содержащей источник напряжения, в точках разрыва появится полное напряжение этого источника.
- +/- ориентация падения напряжения называется полярностью. Она также является относительной между двумя точками.
Оригинал статьи:
Теги
ОбучениеЭлектрический токЭлектрическое напряжениеЭлектричествоЭлектронСохранить или поделиться
Электрическое напряжение
Определение для напряжения в проводнике с током
В том случае если в проводнике есть эклектический ток, значит между любыми двумя его точками, есть разность потенциалов (${\varphi }_1-{\varphi }_2$), которая в электростатике совпадает с напряжением (U). Мы записывали, что:
Однако, для существования постоянного тока в проводнике по мимо кулоновских должны присутствовать сторонние силы, напряженность в данной точке поля в проводнике с током равна:
где $\overrightarrow{E}$ напряженность электрического поля, которая является суммой напряжённости кулоновского поля (${\overrightarrow{E}}_q$) и поля сторонних сил (${\overrightarrow{E}}_{stor}$). Следовательно, напряжение в проводнике с током не будет совпадать с разностью потенциалов.
Напряжением (падением напряжения) $U_{21}$ на участке цепи 1-2 по которому идет ток называется величина, которая равна работе, совершаемой кулоновскими и сторонними силами при перемещении единичного положительного заряда на данном участке:
где $d\overrightarrow{l}$-вектор, численно равный элементу длины проводника и направленный по касательной к проводнику, совпадающий по направлению с вектором плотности тока.
Если подставить в (4) уравнение (2), то мы получим:
где ${{\mathcal E}}_{stor}$ — электродвижущая сила на участке цепи 1-2, равная:
${\varphi }_1-{\varphi }_2$ — разность потенциалов электростатического поля в точках 1 и 2, которая равна:
Очевидно, что если цепь замкнута, то
В таком случае для замкнутой цепи, мы получим:
Основной единицей измерения напряжения в системе СИ является вольт — В.
Связь силы тока и напряжения для участка цепи
Такая физическая величина, как напряжение, фигурирует во многих законах относящихся к электродинамике.T_0{\left|U(t)\right|}dt\ \left(14\right).\]
Для гармонически изменяющегося напряжения выполняется равенство:
\[U_v=\frac{2}{\pi }U_{max}\left(15\right).\]Напряжение при соединении проводников
При последовательном соединении проводников (рис.1), суммарное напряжение в цепи находится как сумма напряжений:
Рис. 1
При параллельном соединении (рис.2) результирующее напряжение постоянно. Сила тока равна сумме токов в проводниках:
Рис. 2
Пример 1
Задание: На рис.3 изображена замкнутая цепь, которая содержит сопротивление и источник тока ЭДС которого равна $\mathcal E$, внутреннее сопротивление источника r.
Найдите напряжение на внешней цепи, зная параметры источника тока и силу тока в цепи I.
Рис. 3
Решение:
Если цепь замкнута, то ${\varphi }_1={\varphi }_2$. Напряжение на клеммах источника тока (на внешней цепи) равно:
\[{\mathcal E}=IR\ \left(1.1\right),\]где ${\mathcal E}$ — алгебраическая сумма всех ЭДС в цепи.
Напряжение на внешней цепи, которая задана, равно:
\[U=IR_1(1.2)\]Если источник ЭДС имеет внутреннее сопротивление r, то для сопротивления всей цепи (R) запишем:
\[R=R_1+r\to R_1=R-r\ \left(1.3\right),\]где $r$ — внутреннее сопротивление источника.
Cила тока во внешней цепи, равна:
\[I=\frac{{\mathcal E}}{R_1+r}\left(1.4\right).\]Подставим в (1.1) формулы (1.4) и (1.3), получим:
\[U=\frac{{\mathcal E}R_1}{R_1+r}=\frac{{\mathcal E}\left(R-r\ \right)}{R_1+r}=\frac{{\mathcal E}R}{R_1+r}-\frac{{\mathcal E}r}{R_1+r}=IR-Ir={\mathcal E}-Ir.\]Ответ: $U={\mathcal E}-Ir.$
Пример 2
Задание: Как можно измерить ЭДС источника тока?
Решение:
При разомкнутой цепи сила тока в ней равна нулю (I=0), Исходя из результата предыдущего примера в цепи (рис. 3) мы имеем:
\[U={\mathcal E}-Ir\ \left(2.1\right)\]при I=0 из (2.1) получаем, что:
\[U={\mathcal E}\left(2.2\right).\]А так как сторонние силы при разомкнутой цепи работы не совершают, то:
\[U={\varphi }_1-{\varphi }_2(2.3).\]Следовательно, можно записать, что при разомкнутой цепи:
\[{\mathcal E}={\varphi }_1-{\varphi }_2.\]Ответ: Для того чтобы найти ${\mathcal E}$ источника тока можно измерить разность потенциалов на его клеммах в ситуации, когда цепь не замкнута.
Напряжение электрического поля
Электрические заряды не оказывают непосредственное воздействие друг на друга. Каждое заряженное тело может создавать электрическое поле в окружающем пространстве. Такое поле оказывает непосредственное силовое воздействие на остальные заряженные тела.
Электрическое поле и его свойства
Главным свойством электрического поля считается воздействие с определенной силой на электрические заряды. Иными словами, заряженные тела способны взаимодействовать друг с другом исключительно за счет электрических полей, их окружающих.
Исследовать электрическое поле, которое окружает заряженное тело, позволяет так называемый пробный заряд (точечный заряд, небольшой по величине). Такой заряд не может осуществлять заметного перераспределения рассматриваемых зарядов.
Определение 1
Электрическое поле для неподвижных и не изменяющихся со временем зарядов будет называться электростатическим. В большинстве случаев его называют просто электрическим полем.
Если за счет пробного заряда проводится исследование электрического поля, создаваемого несколькими электрически заряженными телами, результирующая сила становится равной геометрической сумме сил, воздействующих на пробный заряд отдельно со стороны каждого из заряженных тел.
Тогда напряженность электрического поля, формируемого системой зарядов в указанной точке пространства, будет зависеть от векторной суммы напряженностей электрополей, создаваемых зарядами в этой же точке по отдельности:
$\vec{E}=\vec{E_1}+vec{E_2}+…$
Такое свойство электрического поля подразумевает его подчинение принципу суперпозиции. Соответственно закону Кулона, напряженность электростатического поля, созданного за счет точечного заряда $Q$ на расстоянии $r$ от него определяет следующая формула:
$E=\frac{Q}{4\pi_0r^2}$
Такое поле названо кулоновским. В этом поле направление вектора $\vec{E}$ будет зависеть от знака заряда $Q$, если $Q$ > $0$, то $\vec{E}$ направляется по радиусу от заряда, если $Q$
С целью наглядного изображения электрополя задействуют силовые линии. Они проводятся таким образом, чтобы направление вектора $\vec{E}$ совпадало в каждой точке с направлением касательной к такой силовой линии. Изображение электрического поля за счет силовых линий требует соблюдения следующего условия: густота таких линий должна оказаться пропорциональной модулю вектора напряженности поля.
Кулоновское поле точечного заряда $Q$ лучше записывать в векторной форме. Для этого проводится радиус-вектор $\vec{r}$. от заряда $Q$ к точке наблюдения. Тогда при условии, что $Q$ > $0$,$\vec{E}$ оказывается параллельным $\vec{r}$. При условии, что $Q$
Пример 1
Примером использования принципа суперпозиции полей выступают силовые линии поля электрического диполя. Такие линии представляют систему из двух равнозначных по модулю зарядов разного знака $q$р, расположенных на определенном расстоянии $L$.
Напряженность однородного электрического поля
Определение 2
Чтобы количественно определить электрическое поле, вводится силовая характеристика в виде напряженности электрического поля. Напряженностью электрополя считается физическая величина, характеризуемая силой воздействия поля на пробный положительный заряд, помещенный в заданную точку пространства.
Определяется такая величина формулой:
$\vec{E}=\frac{\vec{F}}{q}$, где:
- $E$ — напряженность электрического поля (Вольт/метр),
- $F$ — сила, воздействующая на заряд Q (Ньютон),
- $Q$ — заряд (Кулон).
Напряженность электрического поля представляет физическую векторную величину. В неоднородном поле сила, воздействующая на заряд в разных точках поля будет неодинаковой. Напряженность однородного электрополя считается прямо пропорциональной напряжению между пластинами и обратно пропорциональной расстоянию между ними:
$E=\frac{U}{d}$, где:
- $E$ — напряженность однородного электрополя (Вольт/метр),
- $U$ — напряжение, возникающее между пластинами (Вольт),
- $d$ — расстояние между пластинами, которые заряжены (метр).
Напряженность магнитного электрического поля
Замечание 1
Напряженность магнитного электрического поля определяет сила, воздействующая на пробный магнит, помещенный в поле.
Поскольку магнитные полюсы не существуют по отдельности, мы наблюдаем воздействие на южный и северный полюсы пробного магнита противоположно направленных сил. При этом возникает момент пары сил, характеризующий величину напряженности поля в заданном месте.
В магнитном поле у цилиндрической катушки он будет прямо пропорциональным числу витков и силе тока, и при этом и обратно пропорциональным длине катушки.
Направление у вектора напряженности магнитного поля в каждой точке будет совпадающим с направлением силовых линий. Внутри самой катушки (магнита) он направляется от южного полюса к северному, а вне ее — от северного к южному.
Основные электрические законы. Базовые формулы и расчеты
В предыдущей статье мы познакомились с основными электрическими понятиями, такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома. В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой, и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно подобрать и заменить проволоку.
Применив закон Ома, можно рассчитать мощность и по другой формуле:
При расчетах надо учитывать, что часть потребляемой электроэнергии расходуется на нагрев и преобразуется в тепло. При работе греются не только электрообогреватели, но и телевизоры, и компьютеры и другая бытовая техника.
И в завершение, в качестве бонуса, вот такая шпаргалка, которая поможет определить любой из основных электрических параметров, по уже известным.
Напряжение — Типы напряжения, определение и формула
Формула ниже используется для расчета напряжения:
Напряжение = сила / площадь поперечного сечения
σ = F / A
Где,
σ = Напряжение
F = Сила в Ньютонах (Н)
A = Площадь поперечного сечения в м²
Единицы напряжения = Н / м² или Паскали (Па)
Типы напряжения:
Существуют различные типы стресса в физике, но в основном его можно разделить на три формы:
1.Нормальное напряжение
2. Касательное напряжение или напряжение сдвига
3. Гидравлическое напряжение
Нормальное напряжение:
Напряжение, возникающее при нагружении элемента осевой силой, называется нормальной силой. Другими словами, когда прикладываемое напряжение перпендикулярно телу. При изменении длины тела объем объекта напряжения будет нормальным. Он представляет собой символ σ. Единица измерения нормального напряжения в системе СИ — МПа.
Приведенная ниже формула используется для расчета нормального напряжения:
Нормальное напряжение = осевое усилие / площадь поперечного сечения
σ = P / A
Нормальное напряжение возникает, когда объект помещены в растяжение или сжатие.
Продольное напряжение:
Когда длина тела изменяется из-за приложенного нормального напряжения, это называется продольным напряжением.
Продольное напряжение = Деформирующая сила / Площадь поперечного сечения
Продольное напряжение = F / A
Продольное напряжение можно разделить на две категории. Растягивающее напряжение можно наблюдать, когда стержень растягивается в соответствии с третьим законом движения Ньютона.Растягиваемая резинка — типичный пример растягивающего напряжения. Противоположность натяжению — сжатие, когда оно воздействует на стержень, который толкается противоположными или равными силами на его концах. Если вы когда-либо сжимали в руках резиновый мяч, вы создавали сжимающее напряжение.
Объемное напряжение или объемное напряжение:
Объемное напряжение — это напряжение, при котором объем тела изменяется из-за напряжения. Нормальная нагрузка на тело вызывает изменение длины или объема, а касательное напряжение вызывает изменение формы тела, что называется объемным напряжением.Тело, которое находится под силой давления p, при погружении в жидкость, тело противостоит силе, перпендикулярной поверхности тела.
Объемное напряжение = Сила / Площадь = Давление
Напряжение сдвига:
Напряжение сдвига — это сила, прикладываемая по касательной к площади поверхности плоскости. Когда силы, прикладываемые к поверхности, параллельны ей, и напряжение, действующее на поверхность, также строится по касательной. Этот вид стресса известен как напряжение сдвига.
Совместное напряжение = Сила / Площадь поверхности = F / A
Растягивающее напряжение:
Сила на единицу площади определяется как растягивающее напряжение. Если приложено напряжение, длина тела увеличивается из-за силы. Напряжение растяжения наблюдается, когда стержень растягивается по третьему закону движения. Резина — распространенный пример растягивающего напряжения. Это количество, связанное с растяжением. Обозначается он σ.
Напряжение сжатия:
Когда мы прикладываем тангенциальную силу к телу, форма и объем тела изменяются.Когда приложено напряжение сжатия, длина тела уменьшается. Напряжение сжатия противоположно напряжению растяжения. Если вы когда-либо сжимали в руке пищащую игрушку домашнего животного, вы создаете сжимающую нагрузку на тело.
Касательное напряжение:
Когда мы выражаем силу на единицу площади, это нормальное напряжение и касательное напряжение соответственно. Когда две равные и противоположные деформирующие силы прилагаются параллельно площади поперечного сечения объекта, возникает относительное смещение между противоположными гранями тела, и восстанавливающая сила на единицу площади, развиваемая из-за приложенной тангенциальной силы, называется тангенциальной. стресс.
Гидравлическое напряжение:
Гидравлическое напряжение — это мера внутренней силы на единицу площади, действующей на жидкости. Гидравлическое напряжение — это восстанавливающая сила на единицу площади, когда сила прилагается жидкостью к телу. Напряжение физически не то же самое, что давление, потому что в давлении учитывается внешняя сила на единицу площади, а в напряжении — это внутренняя сила на единицу площади. В случае жидкостей гидравлическое напряжение определяется таким же образом.
Радиальное напряжение:
Радиальное напряжение указано для толстостенного цилиндра, которое равно манометрическому давлению на внутренней поверхности и равно нулю на внешней поверхности и противоположно ему.Окружное напряжение и продольное напряжение больше, чем радиальное напряжение, поэтому радиальным напряжением пренебрегают.
Напряжение — это физическая величина, определяющая внутреннюю силу. Напряжение определяется как сила, действующая через «маленькую» границу на единицу площади этой границы. Напряжение — это фундаментальная величина, такая как скорость, крутящий момент (энергия).
Возникает один вопрос, на что вы можете обратить внимание, а на какие нет. Вы, должно быть, заметили, что есть такие предметы, как резина, которые можно легко растянуть.Другими словами, мы можем объяснить это, когда к любому объекту применяется сила растяжения (сила растяжения). Он будет расширяться. Например, резинка легко растягивается. Растягивающая сила, приложенная к резиновому объекту. Однако можно ли протянуть железный прут? Ответ — нет, потому что на железный стержень не действует сила натяжения.
Есть некоторые основные положения механики сплошной среды, напряжение — это макроскопическое понятие. Частицы, чтобы мыслить в своем описании и анализе, должны быть достаточно маленькими, чтобы работать как однородные в создании и состоянии, но все же большими, чтобы игнорировать квантовые эффекты и детальные движения молекул.Таким образом, сила между двумя частицами на самом деле является средним значением очень большого числа атомных сил между их молекулами; и в физическом выражении, таком как масса, скорость и силы, он действует через большую часть трехмерных тел, и предполагается, что они плавно распределяются по ним.
Давайте обсудим это на примере. Возьмем резиновую трубу и железный стержень, возьмем другой объект квадратной формы, и второй объект висит на резиновой трубе и железном стержне. Подождите некоторое время, затем потяните оба объекта в первом объекте, вы увидите, что первый объект имеет силу растяжения, а другой объект не имеет силы растяжения.
Анализ напряжений — это часть прикладной физики, которая скрывает классификацию внутреннего распределения внутренних сил в твердых телах.
Изучение и проектирование таких конструкций, как плотины, несущие конструкции и туннели, механические детали, при предписанных или ожидаемых нагрузках — важная часть инженерного дела. Это также важно для многих других регламентов; например, в геологии, чтобы изучать теорию тектоники плит, вулканизма и лавин; и в биологии, чтобы понять анатомию живых существ.
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение — это отношение приложенной силы F к площади поперечного сечения — , определяемой как « силы на единицу площади ».
- растягивающее напряжение — напряжение, которое имеет тенденцию к растяжению или удлинению материала — действует нормально по отношению к напряженной области
- сжимающее напряжение — напряжение, которое имеет тенденцию к сжатию или укорачиванию материала — действует нормально по отношению к напряженной области
- напряжение сдвига — напряжение, которое имеет тенденцию к сдвигу материала — действует в плоскости напряженной области под прямым углом к напряжению сжатия или растяжения
Напряжение растяжения или сжатия — нормальное напряжение
Напряжение растяжения или сжатия перпендикулярно плоскости обычно обозначается как « нормальное напряжение » или « прямое напряжение » и может быть выражено как
σ = F n / A (1)
где
σ = нормальное напряжение (Па (Н / м 2 ), фунт / кв. дюйм ( фунтов / дюйм 2 ))
F n = нормальная сила, действующая перпендикулярно площади (Н, фунт f )
A = площадь (м 2 , дюйм 2 )
- kip — британская единица силы — она равна 1000 фунтов f (фунт-сила)
- 1 кип = 4448.2216 Ньютонов (Н) = 4.4482216 килограммов Ньютонов (кН)
Нормальная сила действует перпендикулярно площади и возникает всякий раз, когда внешние нагрузки имеют тенденцию толкать или тянуть два сегмента тела.
Пример — Растягивающая сила, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как
σ = (10 10 3 Н) / (π ((10 10 -3 м) / 2) 2 )
= 127388535 (Н / м 2 )
= 127 (МПа)
Пример — сила, действующая на квадратную стойку из пихты Дугласа
Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 дюймов столб из пихты Дугласа.Размер штифта в оправе составляет 5,5 x 5,5 дюйма , а напряжение сжатия можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюйма) (5,5 дюйма) )
= 991 (фунт / дюйм 2 , фунт / дюйм2)
Напряжение сдвига
Напряжение, параллельное плоскости, обычно обозначается как «напряжение сдвига » и может быть выражено как
τ = F p / A (2)
где
τ = напряжение сдвига (Па (Н / м 2 ), фунт / кв. Дюйм (фунт f / дюйм 2 ))
F p = поперечная сила в плоскости области (Н, фунт f )
A = площадь (м 2 , в 2 )
Поперечная сила лежит в плоскости области и возникает, когда внешние нагрузки имеют тенденцию вызывать два сегмента тела скользить друг по другу.
Деформация (деформация)
Деформация определяется как «деформация твердого тела под действием напряжения».
- Нормальная деформация — удлинение или сжатие отрезка линии
- Деформация сдвига — изменение угла между двумя отрезками прямой, первоначально перпендикулярными
Нормальная деформация и может быть выражена как
ε = dl / l o
= σ / E (3)
где
dl = изменение длины (м, дюйм)
l o = начальная длина (м, дюйм)
ε = деформация — без единицы измерения
E = модуль Юнга (модуль упругости) (Па, (Н / м 2 ), фунт / кв. дюйм (фунт f / дюйм 2 ))
- Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта при воздействии силы.
Обратите внимание, что деформация — это безразмерная единица измерения, так как это отношение двух длин.Но также общепринято указывать это как отношение двух единиц длины — например, м / м или дюйм / дюйм .
Пример — напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и и изготовлен из стали с модулем упругости 200 ГПа (200 10 9 Н / м 2 ) . Изменение длины можно рассчитать, преобразовав (3) в
dl = σ l o / E
= (127 10 6 Па) (2 м) / (200 10 9 Па)
= 0.00127 м
= 1,27 мм
Энергия деформации
Напряжение объекта сохраняет в нем энергию. Для осевой нагрузки запасенная энергия может быть выражена как
U = 1/2 F n dl
, где
U = энергия деформации (Дж (Н · м), фут-фунт)
Модуль Юнга — модуль упругости (или модуль упругости) — закон Гука
Большинство металлов деформируются пропорционально приложенной нагрузке в диапазоне нагрузок.Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .
E = напряжение / деформация
= σ / ε
= (F n / A) / (dl / l o ) 4)
, где
E = модуль Юнга (Н / м 2 ) (фунт / дюйм 2 , фунт / дюйм2)
Модуль упругости или модуль Юнга обычно используется для металлов и металлических сплавов и выражается в единицах 10 6 фунтов f / дюйм 2 , Н / м 2 или Па .Модуль упругости при растяжении часто используется для пластмасс и выражается в единицах 10 5 фунтов f / дюйм 2 или ГПа .
Модуль упругости при сдвиге — или модуль жесткости
G = напряжение / деформация
= τ / γ
= (F p / A) / d) (5)
где
G = модуль упругости при сдвиге — или модуль жесткости (Н / м 2 ) (фунт / дюйм 2 , фунт / кв. дюйм)
τ = напряжение сдвига ((Па) Н / м 2 , psi)
γ = мера деформации сдвига без единицы измерения
p = сила, параллельная граням, на которые они действуют
A = площадь (м 2 , в 2 )
s = смещение граней (м, дюйм)
d = ди положение между смещенными гранями (м, дюйм)
Объемный модуль упругости
Объемный модуль упругости — или объемный модуль — является мерой сопротивления вещества равномерному сжатию.Объемный модуль упругости — это отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Модули упругости
Модули упругости для некоторых распространенных материалов:
| Материал | Модуль упругости — E — | Модуль упругости при сдвиге — G — | — Модуль упругости 902 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (ГПа) (10 6 фунт / кв. Дюйм) | (ГПа) (10 6 фунт / кв. Дюйм) | (ГПа)
12.3 Напряжение, деформация и модуль упругости — University Physics Volume 1Skip to ContentUniversity Physics Volume Strain 1.3 University Physics Volume и модуль упругости Содержание Мои основные моменты Распечатать Содержание
Почему это происходит и как с этим справиться?Стресс — это естественное чувство неспособности справиться с конкретными требованиями и событиями. Однако стресс может перерасти в хроническое заболевание, если человек не примет меры по его устранению. Эти требования могут исходить от работы, отношений, финансового давления и других ситуаций, но все, что создает реальную или предполагаемую проблему или угрозу благополучию человека, может вызвать стресс. Стресс может быть мотиватором и даже иметь важное значение для выживания. Механизм борьбы или бегства тела сообщает человеку, когда и как реагировать на опасность. Однако, когда организм слишком легко срабатывает или когда одновременно действует слишком много факторов стресса, это может подорвать психическое и физическое здоровье человека и стать вредным. Стресс — это естественная защита организма от хищников и опасностей. Это заставляет организм наводняться гормонами, которые подготавливают его системы к тому, чтобы избежать опасности или противостоять ей.Люди обычно называют это механизмом борьбы или бегства. Когда люди сталкиваются с проблемой или угрозой, они частично получают физическую реакцию. Тело активирует ресурсы, которые помогают людям либо остаться и противостоять вызову, либо как можно быстрее добраться до безопасного места. Организм вырабатывает большее количество химических веществ кортизола, адреналина и норэпинефрина. Они вызывают следующие физические реакции:
Все эти факторы улучшают способность человека реагировать на потенциально опасные или сложные ситуации.Норэпинефрин и адреналин также вызывают учащение пульса. Факторы окружающей среды, вызывающие эту реакцию, называются стрессорами. Примеры включают шум, агрессивное поведение, превышение скорости автомобиля, страшные моменты в фильмах или даже выход на первое свидание. Чувство стресса имеет тенденцию усиливаться вместе с увеличением количества факторов, вызывающих стресс. По данным ежегодного исследования стресса Американской психологической ассоциации (APA) в 2018 году, средний уровень стресса в Соединенных Штатах составил 4,9 по шкале от 1 до 10.Исследование показало, что наиболее распространенными факторами стресса являются работа и деньги. Чтобы помочь поддержать психическое благополучие вас и ваших близких в это трудное время, посетите наш специализированный центр, чтобы получить дополнительную информацию, подтвержденную исследованиями. Стресс замедляет некоторые нормальные функции организма, например, функции пищеварительной и иммунной систем. Затем тело может сконцентрировать свои ресурсы на дыхании, кровотоке, бдительности и подготовке мышц к внезапному использованию. Во время стрессовой реакции организм изменяется следующим образом:
От того, как человек реагирует на трудную ситуацию, зависит влияние стресса на общее состояние здоровья. Некоторые люди могут испытывать несколько факторов стресса подряд или одновременно, но это не приводит к серьезной стрессовой реакции.У других может быть более сильная реакция на один фактор стресса. Человек, который чувствует, что у него недостаточно ресурсов, чтобы справиться, вероятно, будет иметь более сильную реакцию, которая может вызвать проблемы со здоровьем. Стрессоры по-разному влияют на людей. Некоторые события, которые люди обычно считают положительными, могут привести к стрессу, например, рождение ребенка, поездка в отпуск, переезд в лучший дом и получение повышения по службе. Причина этого в том, что они обычно предполагают значительные изменения, дополнительные усилия, новые обязанности и потребность в адаптации.Также они часто требуют, чтобы человек сделал шаги в неизвестность. Человек может рассчитывать на повышение зарплаты, например, после повышения по службе, но при этом задумываться, сможет ли он справиться с дополнительными обязанностями. Постоянно отрицательный ответ на вызовы может отрицательно сказаться на здоровье и счастье. Например, обзор исследований 2018 года обнаружил связь между стрессом на работе и ишемической болезнью сердца. Несмотря на это, авторы не смогли подтвердить точные механизмы, посредством которых стресс вызывает ишемическую болезнь сердца. Другая литература показала, что люди, воспринимающие стресс как негативное влияние на свое здоровье, могут иметь более высокий риск ишемической болезни сердца, чем те, кто этого не делает. Однако более внимательное отношение к последствиям стресса может помочь человеку справляться с ним более эффективно и лучше справляться. Национальный институт психического здоровья (NIMH) распознает два типа стресса: острый и хронический. Это требует разных уровней управления. NIMH также идентифицирует три примера типов стрессора:
Острый стрессЭтот тип стресса является кратковременным и обычно является более распространенной формой стресса.Острый стресс часто развивается, когда люди принимают во внимание давление недавних событий или сталкиваются с предстоящими проблемами в ближайшем будущем. Например, человек может нервничать из-за недавнего спора или приближающегося крайнего срока. Однако стресс уменьшится или исчезнет, как только человек разрешит спор или уложится в срок. Острые факторы стресса часто бывают новыми и, как правило, имеют четкое и немедленное решение. Даже несмотря на более сложные проблемы, с которыми сталкиваются люди, есть возможные способы выйти из ситуации. Острый стресс не наносит такого же ущерба, как длительный хронический стресс. Кратковременные эффекты включают головные боли напряжения и расстройство желудка, а также умеренное недомогание. Однако повторяющиеся случаи острого стресса в течение длительного периода могут стать хроническими и вредными. Хронический стрессЭтот тип стресса развивается в течение длительного периода и является более опасным. Продолжающаяся бедность, неблагополучная семья или несчастливый брак — примеры ситуаций, которые могут вызвать хронический стресс.Это происходит, когда человек не видит способа избежать своих факторов стресса и перестает искать решения. Травматический опыт в раннем возрасте также может способствовать хроническому стрессу. Хронический стресс мешает организму вернуться к нормальному уровню активности гормона стресса, что может способствовать возникновению проблем в следующих системах:
Постоянное состояние стресса также может увеличить риск развития диабета 2 типа, высокого кровяного давления и сердечных заболеваний.Депрессия, тревога и другие расстройства психического здоровья, такие как посттравматическое стрессовое расстройство (ПТСР), могут развиться, когда стресс становится хроническим. Хронический стресс может продолжаться незамеченным, поскольку люди могут привыкнуть к возбуждению и безнадежности. Это может стать частью личности человека, делая его постоянно подверженным воздействию стресса независимо от сценариев, с которыми они сталкиваются. Люди, страдающие хроническим стрессом, подвержены риску окончательного расстройства, которое может привести к самоубийству, насильственным действиям, сердечному приступу или инсульту. Люди по-разному реагируют на стрессовые ситуации. То, что вызывает стресс у одного человека, может не вызывать стресса у другого, и почти любое событие может вызвать стресс. Для некоторых людей простая мысль о триггере или нескольких более мелких триггерах может вызвать стресс. Нет очевидной причины, по которой один человек может испытывать меньший стресс, чем другой, столкнувшись с одним и тем же фактором стресса. Психические расстройства, такие как депрессия, или нарастающее чувство разочарования, несправедливости и беспокойства, могут заставить одних людей испытывать стресс легче, чем других. Предыдущий опыт может повлиять на то, как человек реагирует на стрессоры. Общие важные жизненные события, которые могут вызвать стресс, включают:
Другими часто сообщаемыми причинами стресса являются:
Некоторые люди испытывают постоянный стресс после травмирующего события, такого как несчастный случай или какое-либо насилие.Врачи диагностируют это как посттравматическое стрессовое расстройство. Те, кто работает на стрессовых работах, например, в армии или в экстренных службах, после серьезного инцидента пройдут сеанс разбора полетов, и службы гигиены труда будут контролировать их на предмет посттравматического стрессового расстройства. Физические эффекты стресса могут включать:
Эмоциональные реакции могут включать: |

