Напряжение при последовательном соединении резисторов: Последовательное соединение резисторов | Электротехника

формулы как найти силу тока, общее сопротивление, напряжение

Содержание

1. Виды соединений электрических проводников
2. Последовательное
3. Параллельное
4. Смешанное
5. Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
6. При параллельном соединении
7. При последовательном соединении
8. Примеры расчетов
9. Для резисторов
10. Для лампочек
11. Для светодиодов

При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.

Виды соединений электрических проводников

Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.

Последовательное

При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.

Последовательное соединение и практический пример применения.

Параллельное

При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.

Параллельное подключение и практический пример.

Смешанное

В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.

Комбинированное соединение проводников.

Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения

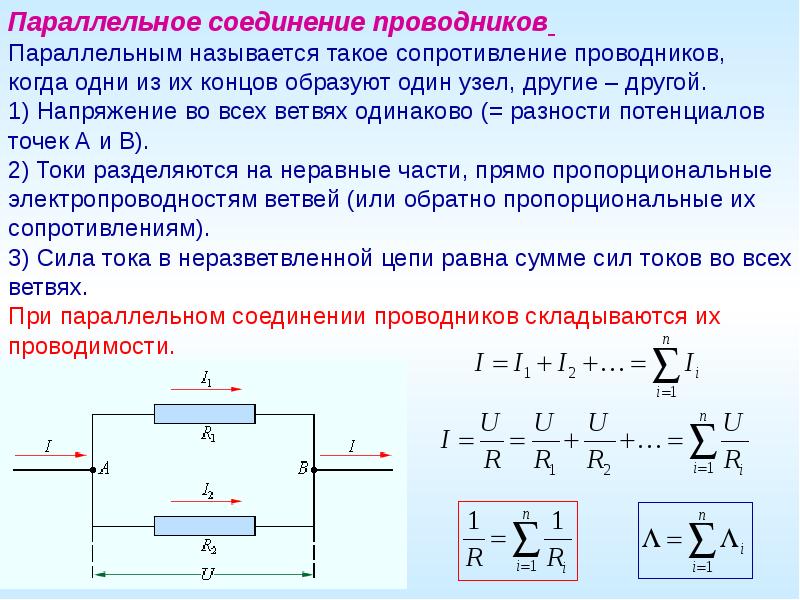
Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.

При параллельном соединении

Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I₁, I₂, I₃, причем Кирхгоф утверждает, что их сумма I₁+ I₂+ I₃ = I. В узле 2 все токи стекаются в один ток, и снова I= I₁+ I₂+ I₃.

Цепь из трех элементов в параллель.

Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:

• I₁=U/R₁;
• I₂=U/R₂;
• I₃=U/R₃;
• I=U/R_общ.

Отсюда U/R_общ= U/R₁+ U/R₂+ U/R₃, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:

1/R_общ= 1/R₁+ 1/R₂+ 1/R_3.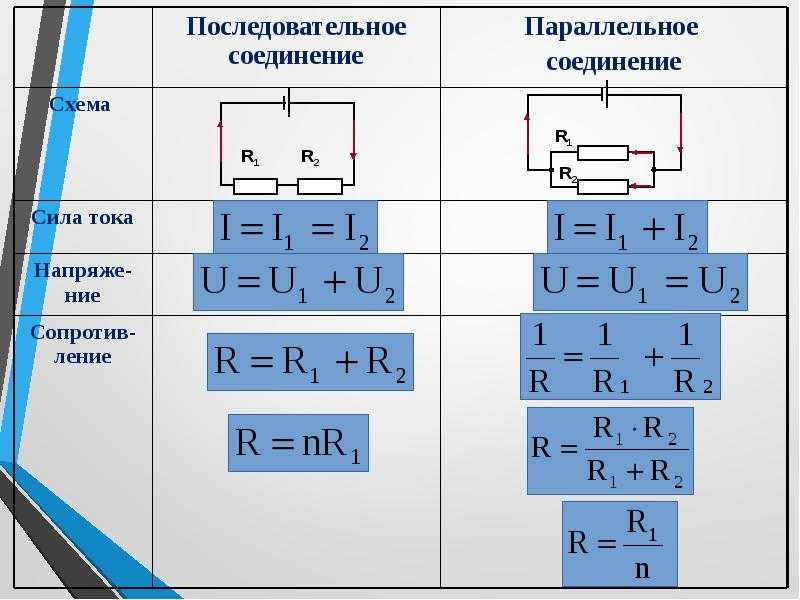

Параллельная цепь из n элементов.

Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид R_общ=R₁* R₂/(R₁+ R₂).

Также из равенства I=U/R₁+U/R₂+U/R₃ следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот. Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.

Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора.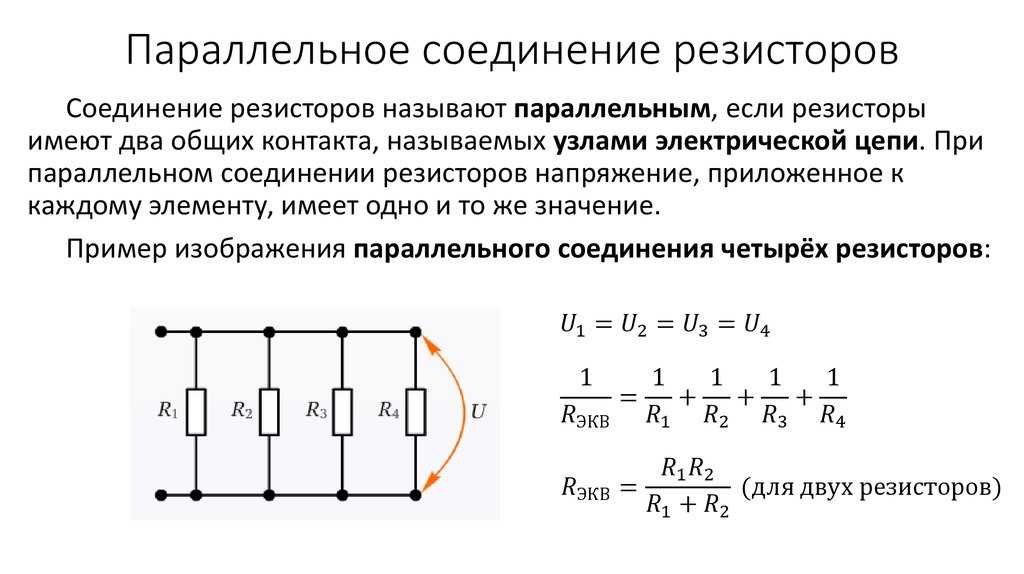 Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.

Для наглядности видео.

При последовательном соединении

Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему. В узле 2 выполняется то же самое соотношение и так до бесконечности.

Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:

U=U₁+U₂+U₃=I*R₁+I*R₂+I*R₃ = I* R_общ

После сокращения на I можно найти общее сопротивление цепи.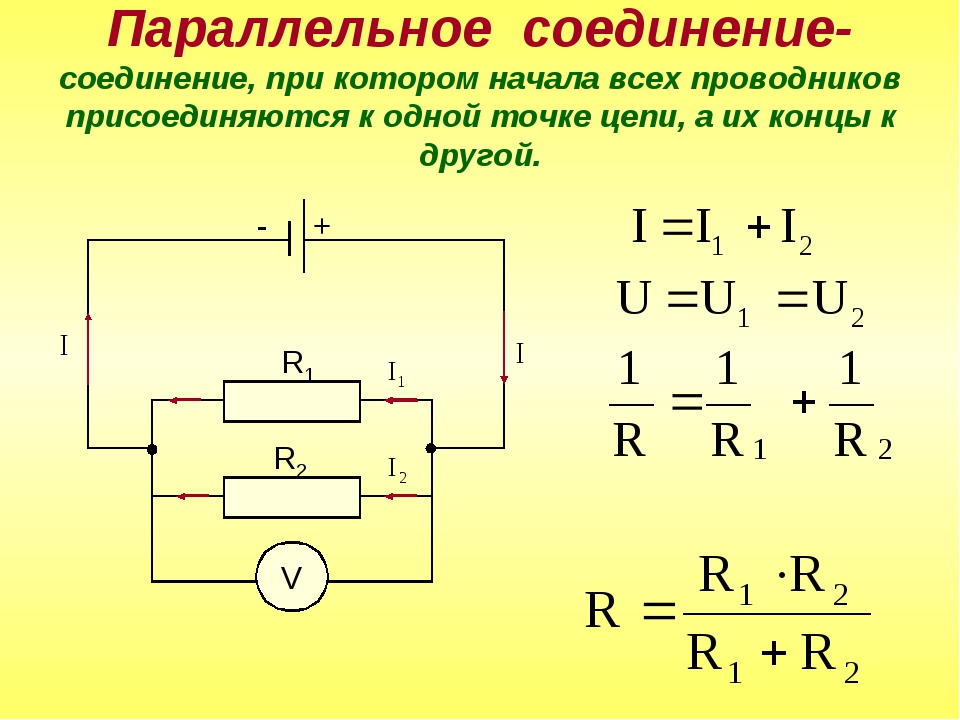 Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:

R_общ=R₁+R₂+R₃

Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.

Примеры расчетов

В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.

Для резисторов

Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.

Последовательная цепь из двух резисторов.

Сначала надо найти R_общ, оно равно сумме R₁ и R₂. R_общ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U₁=I*R₁ и U₂=I*R₂. Отсюда U₁=1,1 В, а U₂=10,9 В. Очевидно, что U₁/U₂=R₁/R₂. На первом элементе будет рассеиваться мощность P₁=U₁*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P₂=U₂*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).

Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.

Соединение элементов в параллель.

Сначала надо определить R_общ=R₁*R₂/(R₁+R₂)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I₁=U/R₁=12/10=1,2 ампер, через второй I₂=U/R₂=12/100=0,12. Очевидно, что I₁+I₂=I (с учетом погрешностей округления). Мощности потребуются такие:

• P₁=I₁*U=1,2*12=14,2 ватт;
• P₂=I₂*U=0,12*12=1,42 ватт.

Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.

Преобразование смешанной схемы.

В данном случае удобно заменить параллельную сборку R₁ и R₂ на резистор с эквивалентным сопротивлением R₁₂, а R₃ и R₄ – на R₃₄. Сначала находится R₁₂=R₁*R₂/(R₁+R₂)=9,17 Ом. Тем же способом рассчитывается R₃₄=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R₁₂+R₃₄=9,17+4,8=13,97 Ом.

Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R₁R₂ падает U₁₂=I*R₁₂=0,86*9,17=7,87 вольт, а на R₃R₄ падение составит U₃₄= I*R₃₄=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R₁R₂ с найденными параметрами.

Участок цепи, содержащий R1 и R2.

Отсюда I₁=U/R₁=7,87/10=0,787 ампер, I₂=U/R₂=7,87/100=0,0787 ампер. По мощностям – P₁=U*I₁=7,87*0,787=6,2 ватт, P₂= U*I₂=7,87*0,0787=0,62 ватт.

Аналогично рассчитывается и участок, содержащий элементы R₃R₄.

Читайте также

Последовательное и параллельное подключение аккумуляторных батарей

 

Для лампочек

Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности.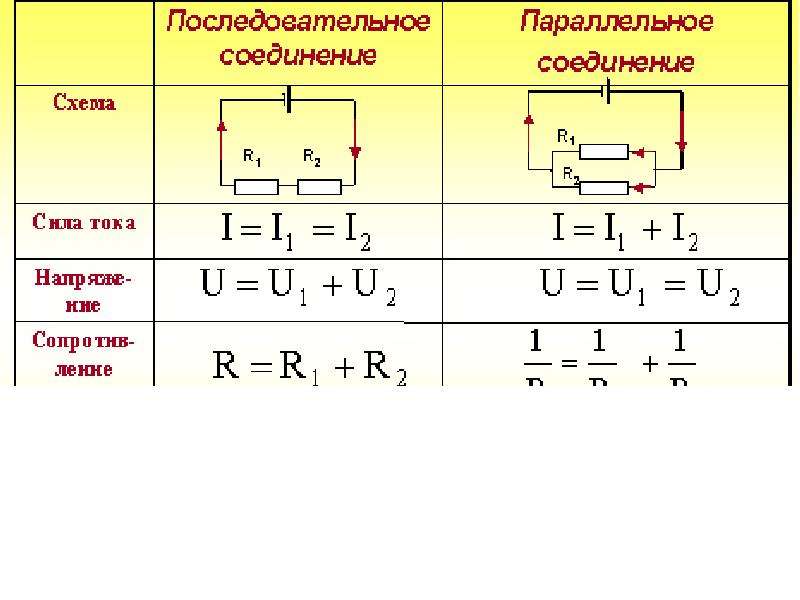 Так как P=U*I, а I=U*R, то P=U²/R, а R=U²/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 12²/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.

Соединение ламп в цепочку.

В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.

Соединение двух лампочек в параллель.

Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.

Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.

Рекомендуем посмотреть видео урок «Просто физика»

Для светодиодов

Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.

Распределение падений до открывания и после открывания светодиода.

По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.

Ток при последовательном соединении резисторов

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Последовательное и параллельное соединение конденсаторов
• Сила тока при последовательном соединении
• Последовательное соединение резисторов. Схема соединения и примеры расчета
• Соединение резисторов
• Параллельное соединение резисторов. Напряжение при параллельном соединении
• Почему при параллельном соединении напряжение одинаковое
• Последовательное и параллельное соединение резисторов
• Последовательное соединение
• Последовательное и параллельное соединение. Применение и схемы
• Последовательное и параллельное соединение

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 8 класс.

Смешанное соединение проводников. I вариант.

Последовательное и параллельное соединение конденсаторов

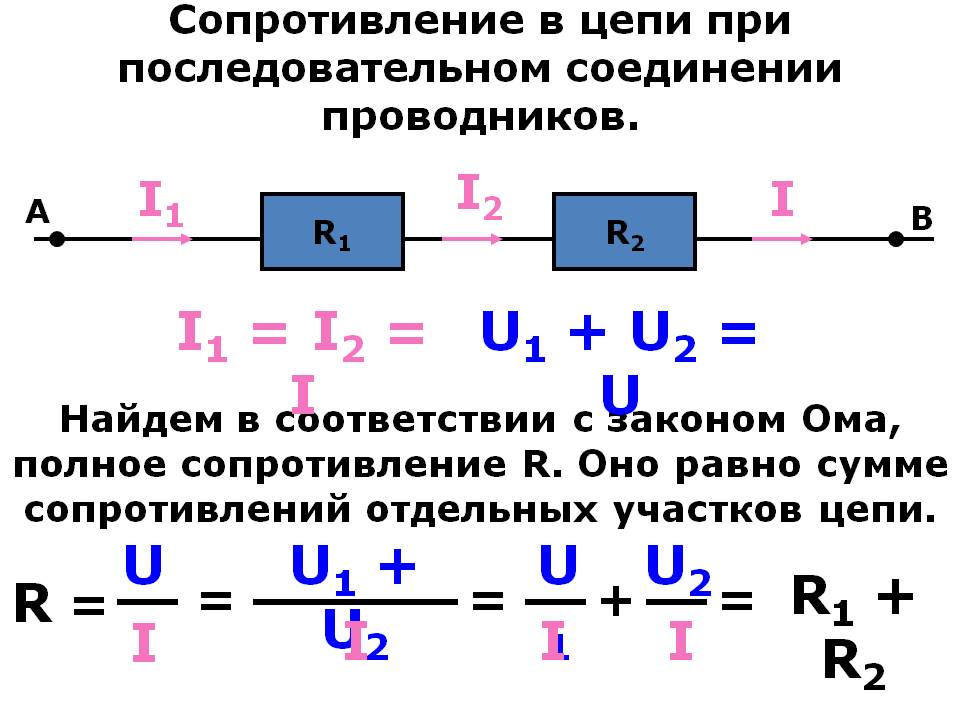
Сопротивление трёх одинаковых резисторов, соединённых последовательно, в три раза больше, чем сопротивление одного резистора. Возьмём три постоянных резистора R 1 , R 2 и R 3 и включим их в цепь так, чтобы конец первого резистора R 1 был соединён с началом второго R 2 , конец второго — с началом третьего R 3 ; к началу первого резистора и к концу третьего подведём проводники от источника электрической энергии.

Такое соединение резисторов называется последовательным. Очевидно, что величина тока в такой цепи будет во всех её точках одна и та же, так как нет никаких разветвлений в цепи. Как определить величину общего сопротивления цепи, если сопротивления всех последовательно включенных в неё резисторов известны? Физический смысл формулы очевиден: при последовательном соединении резисторов электрический ток должен пройти последовательно через все эти резисторы, поэтому общее сопротивление цепи увеличивается.

Таким образом, при последовательном соединении резисторов общее сопротивление всей цепи равно сумме сопротивлений отдельных резисторов. Проверим этот вывод на следующем примере. Из приведённого примера можно сделать важный вывод: чем больше сопротивление резистора, включенного последовательно с другими резисторами, тем больше на нём получается падение напряжения. Оно и понятно. Через все соединённые последовательно резисторы проходит одинаковый ток.

Очевидно, чем больше сопротивление резистора R, тем больше и величина падения напряжения на нём U. При последовательном соединении одинаковых по величине и мощности резисторов их мощности суммируются.

Значит, из нескольких одинаковых резисторов можно получить общий резистор бОльшей мощности рассеивания. При последовательном соединении неодинаковых резисторов на наиболее высокоомном резисторе выделяется наибольшая мощность. Так, включив несколько резисторов последовательно, мы можем с различных точек цепи снять различные напряжения.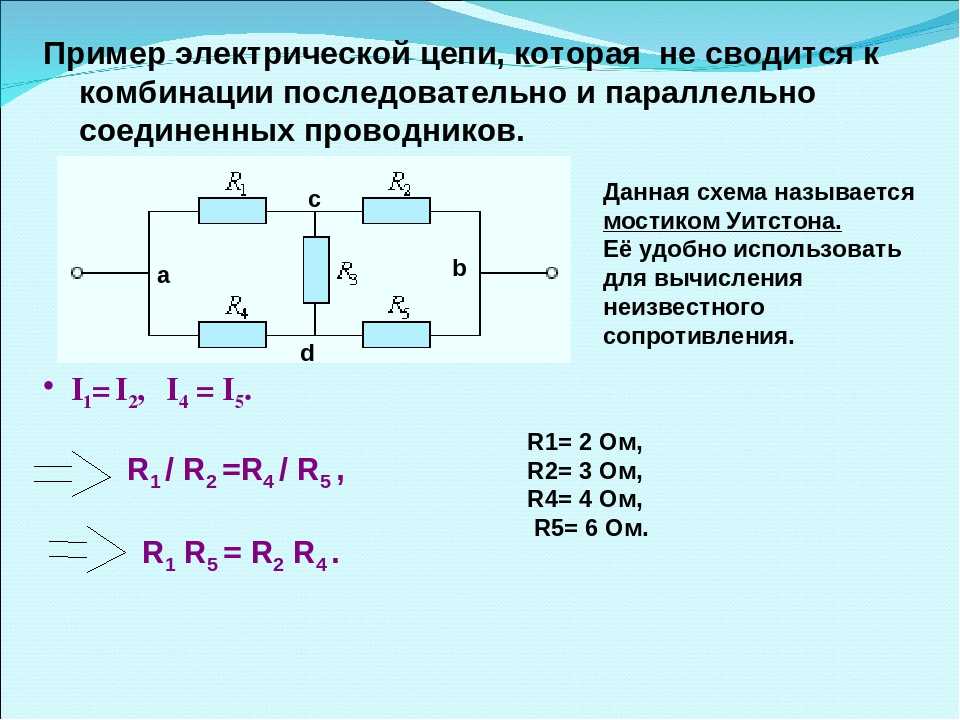

На рисунке показано использование в качестве делителя напряжения схемы из трёх резисторов. В электротехнике последовательное соединение потребителей электрической энергии встречается довольно часто.

Например, если напряжение сети вольт, а нам нужно собрать гирлянду из 19 лампочек, каждая из которых рассчитана на напряжение 12 вольт, то эти лампы следует соединить между собой последовательно. Недостаток такого соединения состоит в том, что при перегорании нити одной лампы гаснут и все остальные. Пример 1. Величина тока в цепи 2 ампера. Найти напряжение на концах всей цепи. Пример 2. Чему равна электродвижущая сила батареи, если величина тока в цепи 3 ампера, внешняя цепь состоит их трёх последовательно соединённых сопротивлений 2, 3 и 5 Ом и внутреннее сопротивление батареи 1 Ом?

Пример 3. Определить сопротивление цепи, состоящей из четырёх последовательно включенных сопротивлений: 20, 30, 50 и 40 Ом. Последовательное соединение соединяем резисторы Главная Полезные советы Последовательное соединение сопротивлений.

Измерение сопротивления резистора; сопротивление одного резистора составляет 5, 6 кОм. Измерение сопротивления трёх последовательно соединённых резисторов. Схема последовательного соединения резисторов. При последовательном соединении одинаковых резисторов суммируется не только сопротивление, но и мощность. Использование в качестве делителя напряжения схемы из трёх резисторов. Онлайн заявка Отправить.

Сила тока при последовательном соединении

Последовательное соединение — это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке. При таком соединении, через все резисторы проходит один и тот же электрический ток. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений. Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:. Параллельное соединение — это соединение, при котором резисторы соединяются между собой обоими контактами.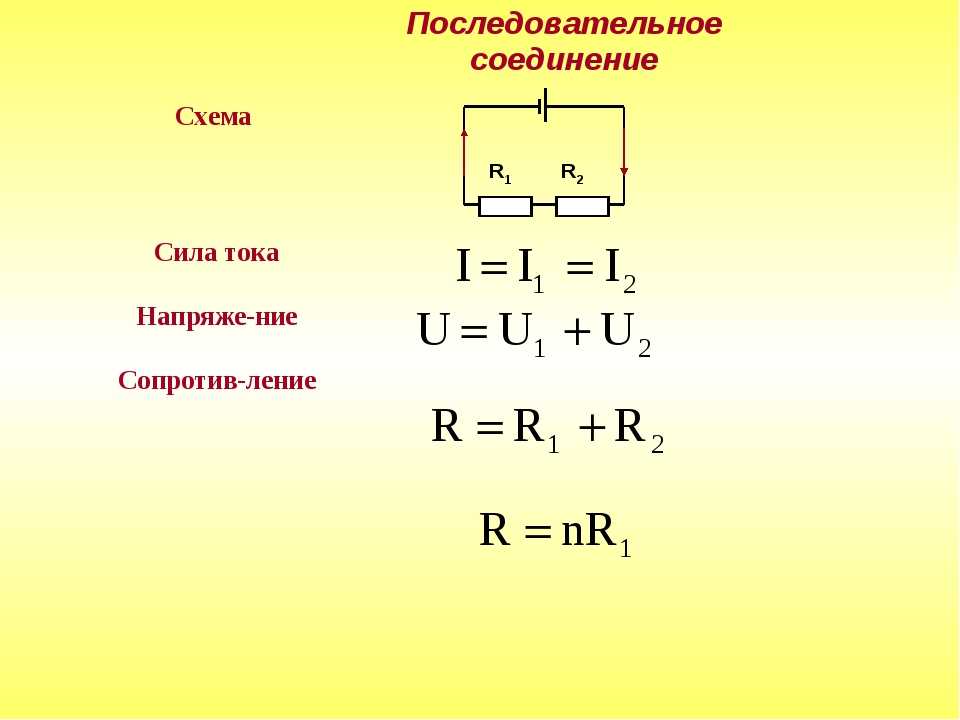

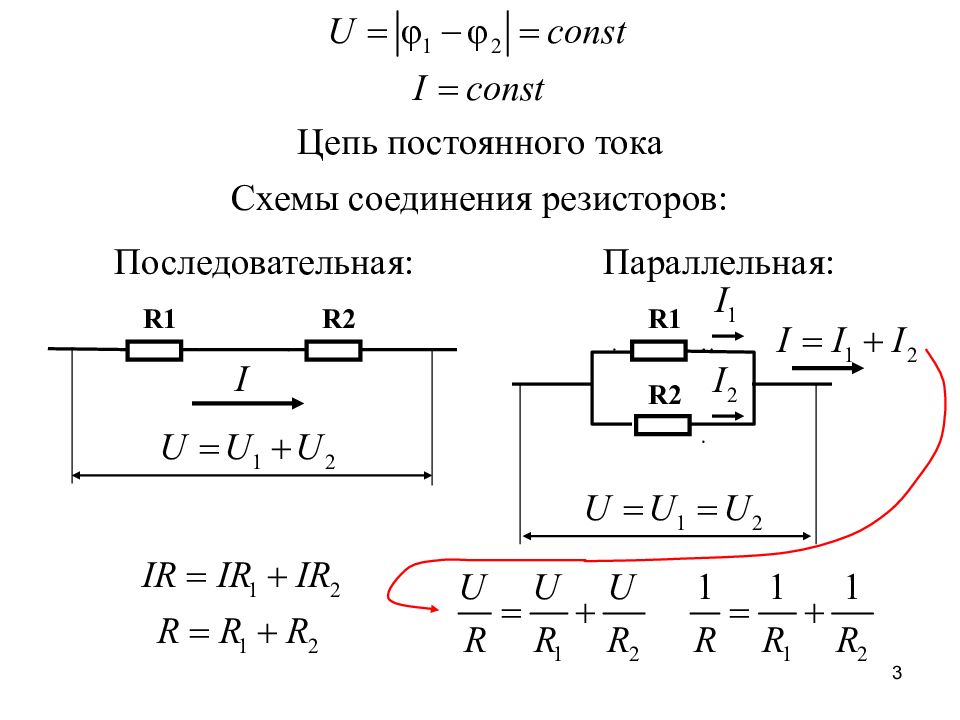
При последовательном соединении (рис. 43, а) через все резисторы проходит один и тот же ток. При параллельном соединении (рис. 43, б) на всех.

Последовательное соединение резисторов. Схема соединения и примеры расчета

При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию. При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами , объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи , равна сумме величин, обратных сопротивлениям параллельно включённых проводников. Цепь замкнута, когда замкнуты все выключатели.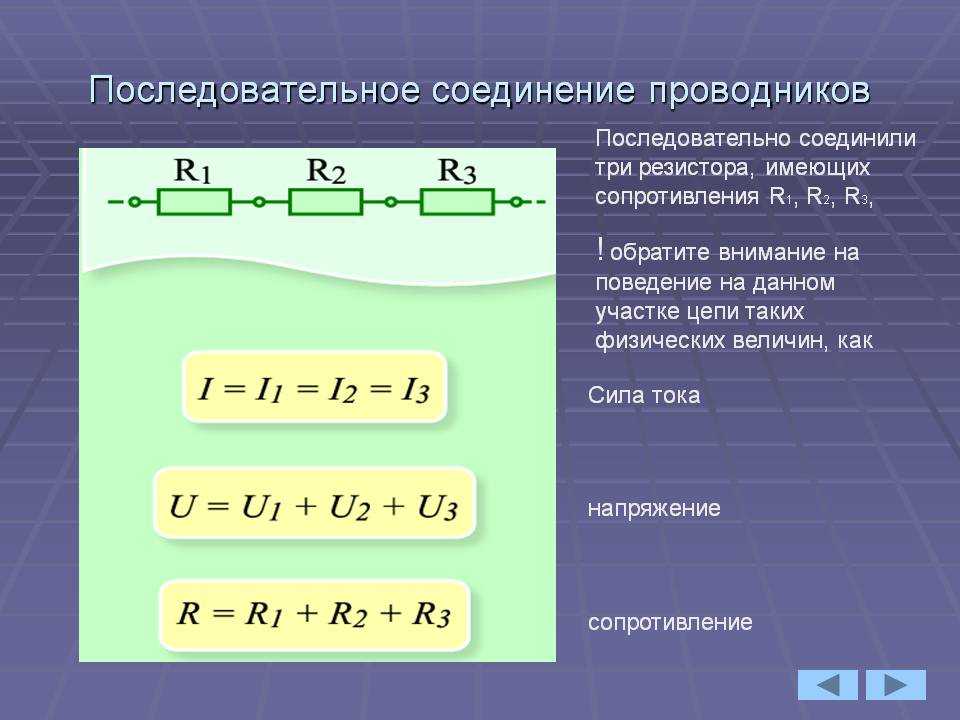 Цепь разомкнута, когда разомкнут хотя бы один выключатель.

Соединение резисторов

Последовательное соединение проводников 1. Виды соединений проводников. Закономерности последовательного соединения проводником. Распространенные ошибки.

Последовательное соединение — это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке. При таком соединении, через все резисторы проходит один и тот же электрический ток.

Параллельное соединение резисторов. Напряжение при параллельном соединении

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи , включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно , параллельно и смешанно то есть и последовательно и параллельно , что показано на рисунке 1. Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее рисунок 2. То есть при последовательном соединении резисторы подключатся друг за другом.

Почему при параллельном соединении напряжение одинаковое

Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями E-серии , чтобы получить необходимое сопротивление. Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи. На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Мощность при параллельном и последовательном соединении При соединение резисторов последовательно электрический ток по очереди.

Последовательное и параллельное соединение резисторов

Радиоэлектронные устройства собраны из различных деталей и разными по сложности способами. Но большинство соединений можно разбить на последовательное и параллельное. Рассмотрим разновидности соединений резисторов. При последовательном соединении резисторов общее сопротивление цепочки будет равно сумме отдельных сопротивлений:.

Последовательное соединение

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи , включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно , параллельно и смешанно то есть и последовательно и параллельно , что показано на рисунке 1. Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее рисунок 2. То есть при последовательном соединении резисторы подключатся друг за другом.

В электрических цепях используются различные типы соединений.

Последовательное и параллельное соединение.

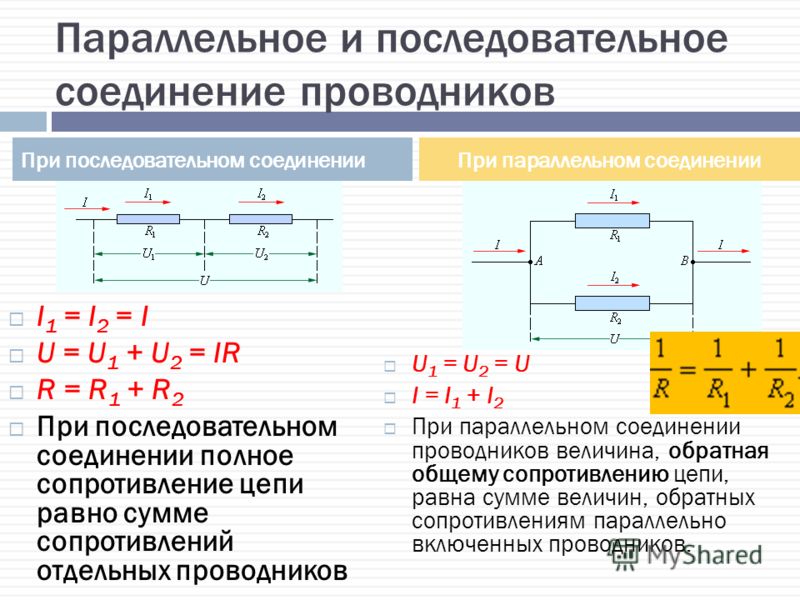Применение и схемы

Рисунок 2. Последовательное соединение резисторов. Поэтому при последовательном соединении двух ламп напряжение В будет делиться пополам, и составит В для каждой. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение. При последовательном соединении проводников сила тока во всех проводниках одинакова.

Последовательное и параллельное соединение

Рисунок 2. Последовательное соединение резисторов. Поэтому при последовательном соединении двух ламп напряжение В будет делиться пополам, и составит В для каждой. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ — Мегаобучалка

Это такое соединение, при котором все элементы идут один за одним без разветвлений.

Свойства последовательного соединения

1. Ток во всех резисторах одинаков- I₁ = I₂ = I₃;

2. Общее напряжение цепи равно сумме напряжений на всех резисторах- U=U₁ + U₂ + U₃;

3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков — R_вх= R₁ + R₂

+ R₃;

4. Чем больше сопротивление участка, тем больше на нём падает напряжение- .

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.

Свойства параллельного соединения резистора:

1. Общее напряжение цепи равно напряжению на каждом участке-

U = U₁ = U₂ = U₃

2. Общий ток цепи равен сумме токов на всех участках- I = I₁ + I₂ + I₃

3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению

— проводимость (G)

Общая проводимость цепи равна сумме проводимостей на каждом участке.

G = G₁ + G₂ + G

3

4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.

При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать

1.

2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ; .

Тестовые задания:

Задание	Варианты ответов
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.	Да; Нет.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.	Да; Нет.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.	а) ; б) ; в) ; г)

 

Смешанное соединение резисторов

Пример решения задач

Дано:

U = 60 В

R₁ = 7 Ом

R₂ = 12 Ом

R₃ = 4 Ом

Найти: I₁; I₂; I₃ = ?

Резисторы R2 и R3 параллельны между собой, и их общее сопротивление R_2-3 последовательно с R₁.

R_вх = R₁ + R_{2 — 3}

R_вх =R₁+R_2∙3= 7 + 3 = 10 Ом

I₁ = I_вх = 6 А

U_{2 — 3} = I∙R_{2 — 3} — находим напряжение разветвленного участка:

U_{2 — 3} = I∙R_{2 — 3}

= 6∙3 = 18 В

U_{2 — 3} = U₂ = U₃ =18 В— т.к. параллельное соединение

А

Дано:

U=240 В

R₁ = 20 Ом

R₂ = 120 Ом

R₃ = 40 Ом

R₄ = 60 Ом

R₅ = 30 Ом

R₆ = 20 Ом

Найти: I_1-6 -?

; R_4-6 = 10 Ом;

;

; R_2-3 = 30 Ом

R_вх=R₁+R_2-3+R_4-6 = 20 + 30 +10 = 60 Ом;

; ;

U_2-3 =I∙R_2-3= 4∙30 = 120 В;

U_{2 — 3} = U₂ = U₃;

;

;

U_4-6=I∙R_4-6

=4∙10=40B;

U_4-6=U₄=U₅=U₆;

;

;

;

 

Дано:

E = 20 В

R_i=2Ом

R₁ = 9Ом

R₂ = 6 Ом

R₃ = 12 Ом

R₄ = 1 Ом

R₅ = 2 Ом

R₆ = 1 Ом

R_4-6 = R₄ + R₅ + R₆;

;

R_3-6 = 3 Ом;

R_вх = R₁ + R_3-6 +R₂ = 9 + 3 + 6 = 18 Ом;

I= ;

I=I₁=I₂=1А;

U_3-6=I∙R_3-6=1∙3=3В;

U_3-6=U₃=U_4-6;

I₃= ;

I₄=I₅=I₆= ;

Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи.

P_u=P_н+Р₀;

EI=I²₁∙^{R₁+ I2₂∙R₂+ I2₃R₃+I₄2R₄+I2₅R₅+I2₆+I2Ri;}

20∙1=1²∙9+1²∙6+(0,25)²∙12+(0,75)²∙1+(0,75)²2+(0,75)²1+1²∙2;

20Вт=20Вт- задача решена верно

 

ДЕЛИТЕЛИ НАПРЯЖЕНИЯ

Делитель напряжения- это четырёхполюсник, у которого коэффициент передачи меньше единицы.

Рассмотрим Г-образный делитель напряжения:

Чтобы рассчитать коэффициент передачи надо:

1) задать произвольное напряжение на входе;

2) любым способом рассчитать напряжение на выходе;

3) взять их отношения:

Для Г-образного делителя напряжения коэффициент передачи равен отношению выходного сопротивления ко входному.

б) Делитель напряжения с плавной регулировкой (потенциометр)

В нижнем положении движка К = 0. В верхнем положении движка К = 1

Так как в нижнем положении движка U_выхснимаетсяс провода, а в верхнем положении

U_вых = U_вх

1) Если нагрузка не подключена делитель работает в режиме холостого хода и зависимость коэффициент передачи от положения движка потенциометра будет линейной.

2) Если подключить нагрузку, то характеристика будет другой: получается параллельное соединение R_н и r и при том же положении движка напряжение участка уменьшается. В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной.

Вывод: чтобы при подключении нагрузки характеристика приближалась к линейной нагрузку нужно брать высокоомную.

Тестовые задания:

Задание	Варианты ответов
1. Изменяется ли коэффициент передачи делителя напряжения в пределах 0 ÷ ∞?	Да; Нет.
2.Укажите среди приведенных математических выражений формулы коэффициента передачи по напряжению Г-образного делителя напряжения.	а) ; б) ; в) ; г) ; д) .
3.Являются ли характеристики делителя напряжения с плавной регулировкой линейной, если подключить к делителю нагрузки?	Да; Нет.

 

ПРЕОБРАЗОВАНИЕ ТРЕУГОЛЬНИКА СОПРОТИВЛЕНИЙ

В ЭКВИВАЛЕНТНУЮ ЗВЕЗДУ ( )

В некоторых схемах, например, в мостовых, возникает необходимость преобразовать треугольник сопротивления в эквивалентную звезду.

При таком преобразовании напряжение между узлами не должны изменяться и токи в неизменной части схемы не должны изменяться.

Исходя из этих предпосылок, получаем формулу преобразования треугольника сопротивления в эквивалентную звезду.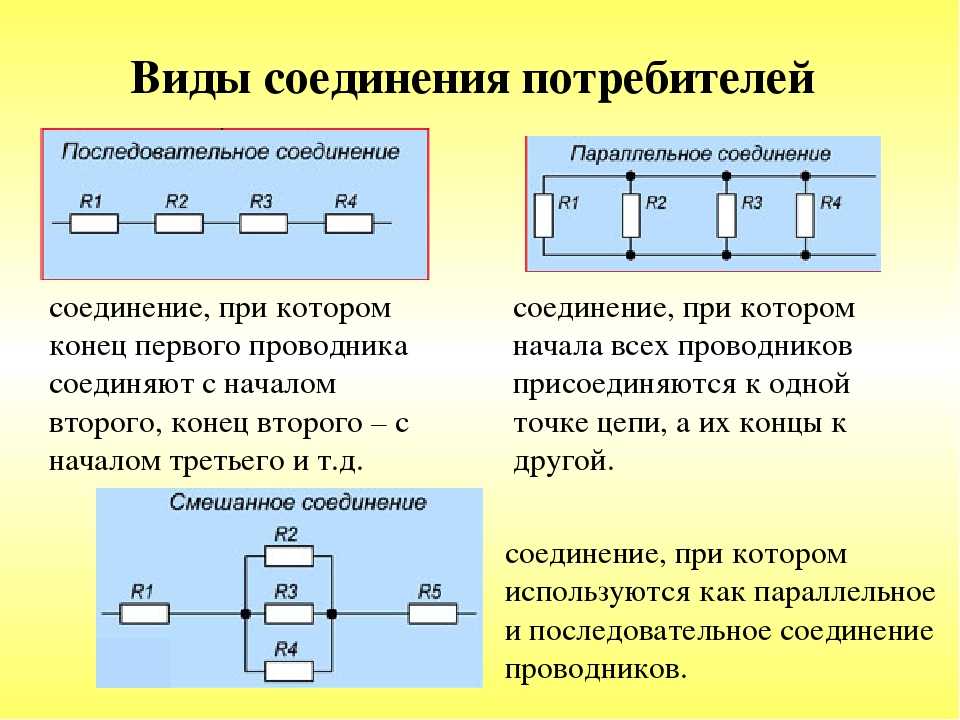

Сопротивления луча эквивалентной звезды равняется произведению сопротивлений сторон треугольника, примыкающих к той же вершине, что и луч звезды, делённому на сумму сопротивлений всех сторон треугольника.

 

 

 

Рассмотрим этот метод на конкретной мостовой схеме.

Заменим в эквивалентную

Пример решения задачи

Дано:

U = 56 В

R₁=R₂=40Ом

R₃ = 35 Ом

R₄ = 10 Ом

R₅ = 50 Ом

Найти: I_1-5=?

 

 

 

1) Изобразим преобразованную схему и рассчитаем ее.

I=IA

U_ОД = I∙R_ОД = 2∙24 = 48 В

2) Направляем токи в первоначальной схеме от плюса источника к минусу, в R₅ ток направляем произвольно;

3) Составляем уравнения по второму закону Кирхгофа, для треугольника, который не заменяем.

0 = I₂∙R₂ — I₃∙R₃ + I₅∙R₅

I₂∙R₂ — I₃∙R₃ = — I₅∙R₅ 0,3∙40-1,2∙35 = -I₅∙50

32 — 84 = -I₅∙50 I₅ = 0,2A

3) Чтобы найти I₁ и I₄ составляем уравнения по первому закону Кирхгофа для узлов В, С.

I₁ + I₅ — I₂ = 0 (B)

I₁ = I₂ — I₅

I₁ = 0,8 — 0,2 = 0,6A

I₅ + I₃ + I₄ = 0 (C)

I₄ = I₃ + I₅

I₄ = 1,2 + 0,2 = 1,4A

 

Пример решения задачи

Дано:

U =200

R₁ = 10 Ом

R₂ = 70 Ом

R₃ = 20 Ом

R₄ = 130 Ом

R₅ = 30 Ом

R₆ = 10 Ом

Найти: I_1-6, — ?

 

 

R_4B = R_B + R₄ = 2 + 130 = 132 Ом

R_C5 = R_C + R₅ = 14 + 30 = 44 Ом

R_вх = 33 + 10 + 7 = 50 Ом

I=I₆=4A

U_ОД = I∙R_ОД = 4∙33 = 132 В

0 = -I₃∙R₃ + I₄∙R₄ — I₅∙R₅

I₃∙R₃ = I₄∙R₄ — I₅∙R₅

I₃∙20 = — 1∙130-3∙30

I₃∙20 = 40

I₃ = 2A

(В) I₁ — I₃ — I₄ = 0

I₁ = I₄ + I₅ = 1 + 2 = 3A

(C) I₂ + I₃ — I₅ = 0

I₂ = I₅ — I₃ = 3 — 2 = 1A

 

электрических цепей — Почему напряжение на резисторах, соединенных параллельно, одинаково?

Задавать вопрос

Спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 558 раз

Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.

$\begingroup$

Допустим, у меня есть цепь и три резистора, соединенные параллельно. Затем, если я хочу рассчитать эквивалентное сопротивление, я использую закон Ома (V = IR). Назовите три резистора R1, R2, R3 и ток, проходящий через них, как I1, I2, I3 соответственно. Теперь в моем учебнике это было дано отсюда так: —

Пусть I=I1+I2+I3 — общий ток, проходящий через резистор. По закону Ома

V/R = (V/R1)+(V/R2)+(V/R3)

Таким образом, эквивалентное сопротивление равно сумме обратных величин каждого резистора. Меня смутило то, почему разность потенциалов одинакова для всех трех резисторов, соединенных параллельно? Меня смущает тот факт, что если сопротивление меняется, то и напряжение должно изменяться (по закону Ома), то почему здесь это не так?

• электрические цепи
• электрический ток
• электрическое сопротивление
• напряжение

$\endgroup$

2

$\begingroup$

В цепи постоянного тока, когда два резистора соединены параллельно:

Резисторы по определению подключаются непосредственно к клеммам батареи. Следовательно, разности потенциалов на резисторах одинаковы: $$\Delta V = \Delta V_1 = \Delta V_2$$ По закону Ома имеем $\Delta V = IR$, поэтому, несмотря на то, что резисторы имеют разное сопротивление, ток, протекающий через резисторы, изменяется обратно пропорционально сопротивлению (больше тока течет по ветви с меньшим сопротивлением и наоборот), поэтому дать одинаковую разность потенциалов (напряжение)

Надеюсь, это поможет.

$\endgroup$

$\begingroup$

Это не вопрос физики, это вопрос определений.

Напряжение в цепи измеряется между двумя узлами. «Параллельно», по определению, означает, что все резисторы подключены между одними и теми же двумя узлами. Когда вы измеряете напряжение на любом из резисторов, вы по определению, измеряете напряжение между теми же двумя узлами.

$\endgroup$

$\begingroup$

Во-первых, когда любые две точки соединяются проводом с меньшим сопротивлением, их потенциалы становятся равными.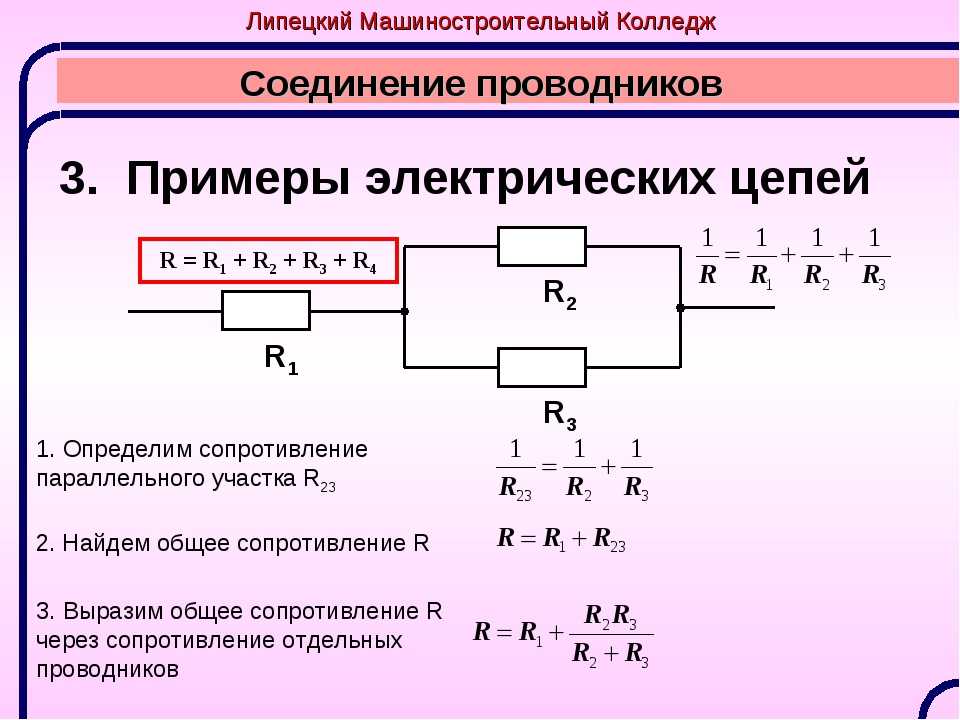 Это можно доказать следующим образом. Предположим, что A и B соединены проводом с меньшим сопротивлением. Тогда разность потенциалов между A и B определяется законом Ома как: $$V_{AB} = ИР$$ Но поскольку R равно нулю, $V_{AB}$ (разность потенциалов между A и B) также равна нулю, т. е. обе точки имеют одинаковый потенциал.

Пусть теперь потенциал катода в ячейке равен v, а потенциал анода равен $0$. Поскольку точки D,E,F соединены с катодом проводом с меньшим сопротивлением, их потенциалы также равны v.

Так как точки A,B,C соединены с анодом проводом без сопротивления, то потенциалы этих точек равны нулю.

Итак, на каждом резисторе есть разность потенциалов $v-0=v$.

Следовательно, эквивалентное сопротивление имеет разность потенциалов v.

Теперь, чтобы ответить на ваш вопрос, почему разность потенциалов не меняется при изменении значения сопротивления, напомню вам закон Ома:

$$V = IR$$

сопротивление компонента, тогда ток через эквивалентное сопротивление становится вдвое больше тока через сопротивление компонента, поэтому чистое значение разности потенциалов на эквивалентном сопротивлении остается таким же, как и у резистора компонента.

$\endgroup$

$\begingroup$

Возможно, вы не обратили внимание на основное уравнение, т.к. $$ В = ИК $$ Таким образом, в некоторых параллельных ветвях при изменении R ток, протекающий через эту ветвь, изменится настолько обратно пропорционально, что произведение $IR$ останется постоянным. Как вы можете видеть на практике, напряжение зависит от источника питания (или энергии), такого как батарея, а не от сопротивления проводника.

Например, два резервуара с водой, расположенные на разной высоте и соединенные двумя трубами (две трубы на одной высоте), перетекание воды из более высокого в нижний будет вызвано гравитационным потенциалом. Который не будет зависеть от того, насколько велики или малы (по сравнению с размером сопротивления в проводах) трубы. (Хотя это повлияет на расход аналог тока в электрических цепях)

$\endgroup$

21.

1 Резисторы, включенные последовательно и параллельно – College Physics

Резюме

• Нарисуйте цепь с параллельными и последовательными резисторами.
• Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
• Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
• Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
• Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.

Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены.

Рис. 1. (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то $latex \boldsymbol{R_1} $ на рис. 1(a) может быть сопротивлением стержня отвертки, $latex \boldsymbol{R_2} $ сопротивление ее ручки, $latex \boldsymbol{R_3} $ сопротивление тела человека и $latex \boldsymbol{R_4} $ сопротивление ее обуви.

На рис. 2 показаны последовательно подключенные резисторы к источнику напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.) ​​

Рисунок 2. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).

Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке 2.

Согласно закону Ома , падение напряжения $latex \boldsymbol{V} $ на резисторе при протекании через него тока рассчитывается по уравнению $latex \boldsymbol{V = IR} $, где $latex \ boldsymbol{I} $ соответствует току в амперах (А), а $latex \boldsymbol{R} $ — сопротивлению в омах. $latex \boldsymbol{(\Omega )} $. Другой способ представить это так: $latex \boldsymbol{V} $ — это напряжение, необходимое для протекания тока $latex \boldsymbol{I} $ через сопротивление $latex \boldsymbol{R} $.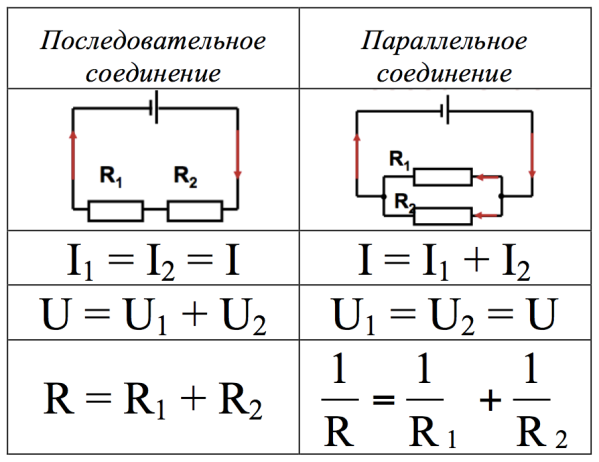

Таким образом, падение напряжения на $latex \boldsymbol{R_1} $ равно $latex \boldsymbol{V_1 = IR_1} $, на $latex \boldsymbol{R_2} $ равно $latex \boldsymbol{V_2 = IR_2} $, и что через $latex \boldsymbol{R_3} $ есть $latex \boldsymbol{V_3 = IR_3} $. Сумма этих напряжений равна выходному напряжению источника; то есть

$латекс \boldsymbol{V = V_1 + V_2 + V_3}. $

Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением $latex \boldsymbol{PE = qV} $, где $latex \boldsymbol{q} $ — электрический заряд, а $latex \boldsymbol{V} $ — напряжение. Таким образом, энергия, выделяемая источником, равна $latex \boldsymbol{qV} $, а энергия, рассеиваемая резисторами, равна

$латекс \boldsymbol{qV_1 + qV_2 + qV_3}. $

Соединения: законы сохранения

Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.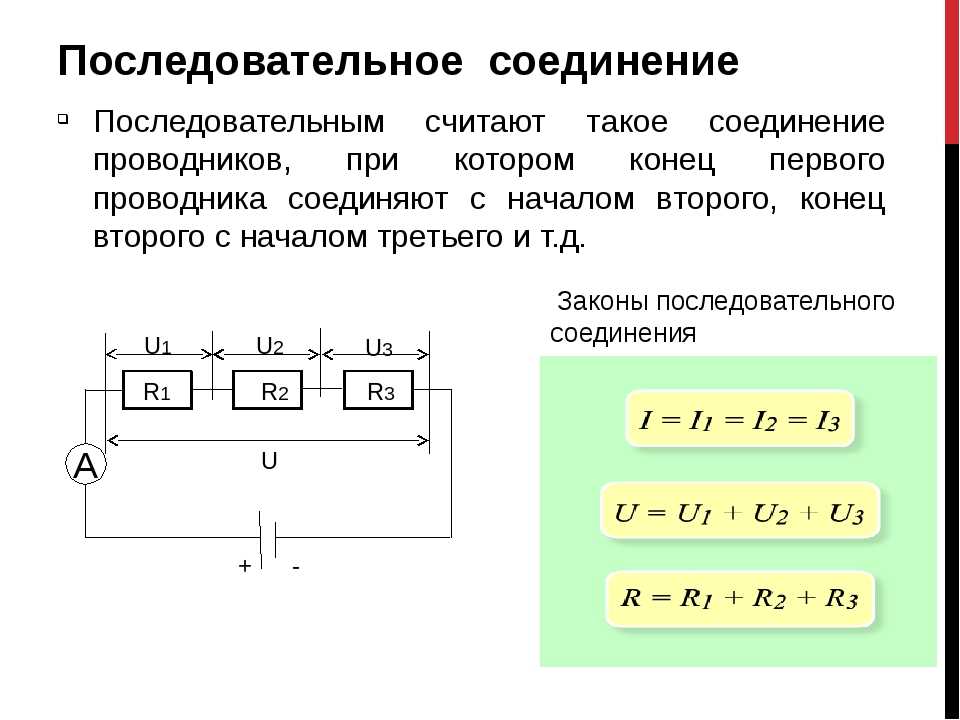 Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, $latex \boldsymbol{qV = qV_1 + qV_2 + qV_3} $. Заряд $latex \boldsymbol{q} $ отменяется, что дает $latex \boldsymbol{V = V_1 + V_2 + V_3} $, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)

Теперь подстановка значений отдельных напряжений дает

$латекс \boldsymbol{V = IR_1 + IR_2 + IR_3 = I(R_1+R_2+R_3)}. $

Обратите внимание, что для эквивалентного однорядного сопротивления $latex \boldsymbol{R_s} $ мы имеем

$латекс \boldsymbol{V = IR_s}. $

Это означает, что общее или эквивалентное последовательное сопротивление трех резисторов $latex \boldsymbol{R_s} $ равно

.

$латекс \boldsymbol{R_s = R_1 + R_2 + R_3} $.

Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление $latex \boldsymbol{R_s} $ последовательного соединения равно

$ $латекс \boldsymbol{R_s = R_1 + R_2 + R_3 + \dots} $

, как было предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.

Пример 1: расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рис. а сопротивления равны $latex \boldsymbol{R_1 = 1,00 \;\Omega} $, $latex \boldsymbol{R_2 = 6,00 \;\Omega} $ и $latex \boldsymbol{R_3 = 13,0 \;\Omega} $. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника.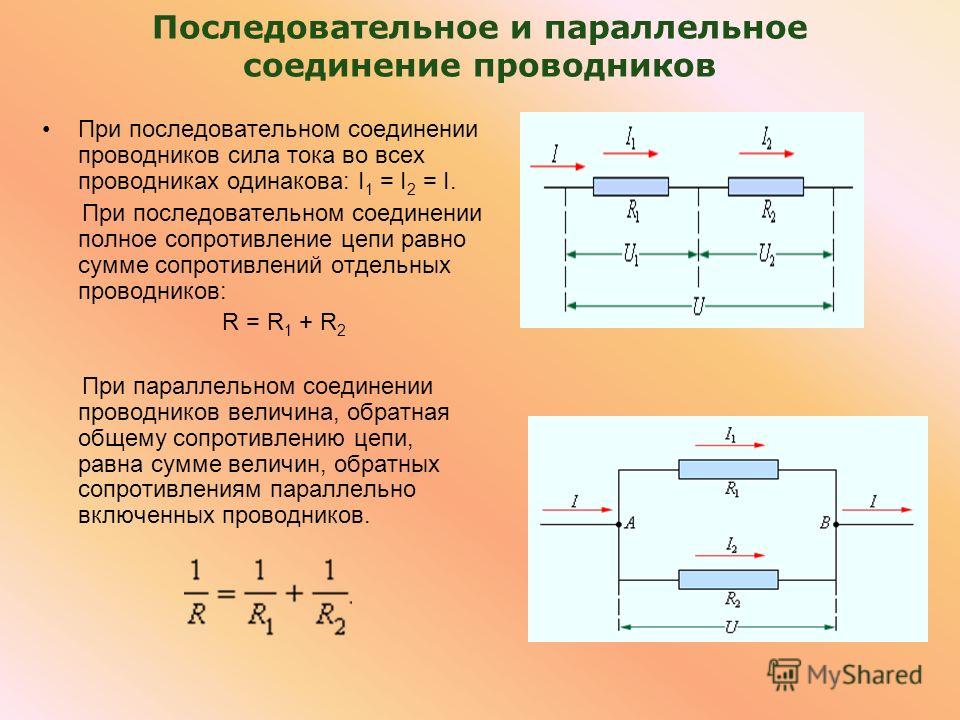 г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

Стратегия и решение для (a)

Общее сопротивление — это просто сумма индивидуальных сопротивлений, определяемая следующим уравнением:

$latex \begin{array}{r @{{}={}} l} \boldsymbol{R_s} & \boldsymbol{R_1 + R_2 + R_3} \\[1em] & \boldsymbol{1.00 \;\Omega + 6.00 \;\Omega + 13.0 \;\Omega} \\[1em] & \boldsymbol{20.0 \;\Омега}. \end{array} $

Стратегия и решение для (b)

Ток определяется по закону Ома, $latex \boldsymbol{V = IR} $. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

$латекс \boldsymbol{I =} $ $латекс \boldsymbol{=} $ $латекс \boldsymbol{= 0,600 \;\textbf{A}}. $

Стратегия и решение для (c)

Падение напряжения — или $latex \boldsymbol{IR} $ — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает

$latex \boldsymbol{V_1 = IR_1 = (0,600 \;\textbf{A})(1,0 \;\Omega) = 0,600 \;\textbf{V}}. $

Аналогично,

$latex \boldsymbol{V_2 = IR_2 = (0,600 \;\textbf{A})(6,0 \;\Omega) = 3,60 \;\textbf{V}} $

и

$латекс \boldsymbol{V_3 = IR_3 = (0,600 \;\textbf{A})(13,0 \;\Omega) = 7,80 \;\textbf{V}}. $

Обсуждение для (c)

Три капли $latex \boldsymbol{IR} $ добавляются к $latex \boldsymbol{12.0 \;\textbf{V}} $, как и предполагалось:

$latex \boldsymbol {V_1 + V_2 + V_3 = (0,600 + 3,60 + 7,80) \;\textbf{V} = 12,0 \;\textbf{V}}. $

Стратегия и решение для (d)

Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать 92}{R}} $, где $latex \boldsymbol{V} $ — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать $latex \boldsymbol{P = IV} $, где $latex \boldsymbol{V} $ — напряжение источника. . Это дает

$latex \boldsymbol{P = (0,600 \;\textbf{A})(12,0 \;\textbf{V}) = 7,20 \;\textbf{W}}. $

Обсуждение для (е)

Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. То есть

$latex \boldsymbol{P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \;\textbf{W} = 7,20 \;\textbf{W}}. $

Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника равнялась общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

1. Сопротивления серии добавить: $latex \boldsymbol{R_s = R_1 + R_2 + R_3 + \dots} $ .
2. Один и тот же ток протекает через каждый резистор последовательно.
3. Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.

На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.

Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)

Рисунок 3. (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Дмитрий Г., Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления $latex \boldsymbol{R_{\textbf{p}}} $, рассмотрим протекающие токи и то, как они связаны с сопротивлением.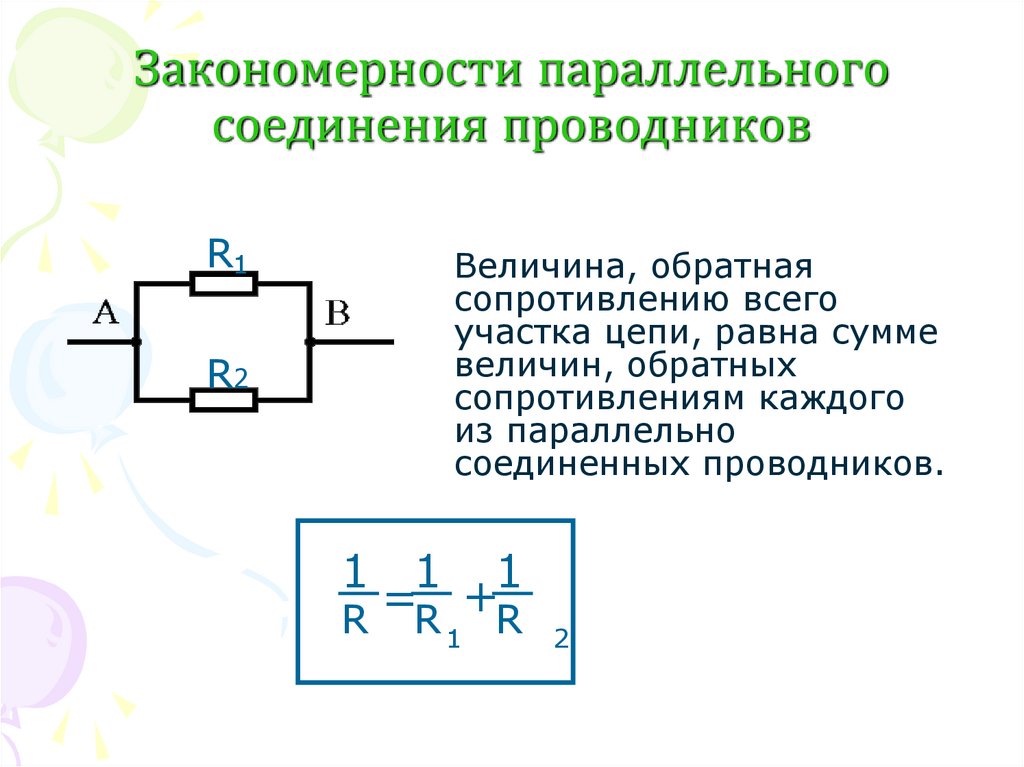 Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны $latex \boldsymbol{I_1 = \frac{V}{R_1}} $, $latex \boldsymbol{I_2 = \frac{V}{ R_2}} $ и $latex \boldsymbol{I_3 = \frac{V}{R_3}} $. Сохранение заряда означает, что полный ток $latex \boldsymbol{I} $, производимый источником, представляет собой сумму этих токов:

$латекс \boldsymbol{I = I_1 + I_2 + I_3}. $

Подстановка выражений для отдельных токов дает

$latex \boldsymbol{I =} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+} $ $latex \boldsymbol{= V} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+} $

Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает

$латекс \boldsymbol{I =} $ $латекс \boldsymbol{= V} $

Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление $latex \boldsymbol{R_p} $ параллельного соединения связано с отдельными сопротивлениями как

$латекс \boldsymbol{=} $ $латекс \boldsymbol{+} $ $латекс \boldsymbol{+} $ $латекс \boldsymbol{+ \cdots} $

Это соотношение приводит к тому, что общее сопротивление $latex \boldsymbol{R_p} $ меньше, чем наименьшее из отдельных сопротивлений.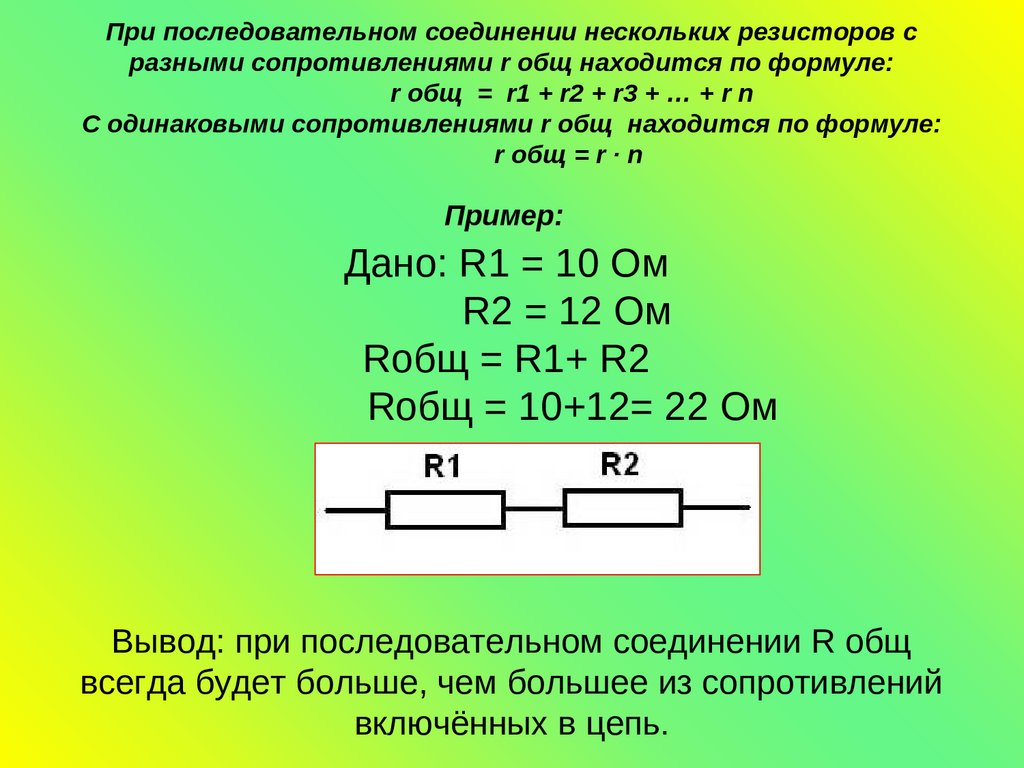 (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.

Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис. 3 такие же, как при рассмотренном ранее последовательном соединении: $latex \boldsymbol{V = 12,0 \;\textbf{V}} $, $latex \boldsymbol {R_1 = 1,00 \;\Omega} $, $latex \boldsymbol{R_2 = 6,00 \;\Omega} $ и $latex \boldsymbol{R_3 = 13,0 \;\Omega} $. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

Стратегия и решение для (a)

Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает

$latex \boldsymbol{=} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+} $ $latex \boldsymbol{=} $ $latex \boldsymbol{+} $ $latex \boldsymbol {+} $

Таким образом,

$latex \boldsymbol{=} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+} $ $latex \boldsymbol{=} $

(Обратите внимание, что в этих расчетах каждый промежуточный ответ показан с дополнительной цифрой.)

Мы должны инвертировать это, чтобы найти полное сопротивление $latex \boldsymbol{R_p} $. Это дает

$latex \boldsymbol{R_p =} $ $latex \boldsymbol{\Omega = 0,8041 \;\Omega}. $

Полное сопротивление с правильным количеством значащих цифр равно $latex \boldsymbol{R_p = 0,804 \;\Omega} $

Обсуждение для (a)

$latex \boldsymbol{R_p} $ равно, как предсказано, меньше, чем наименьшее индивидуальное сопротивление.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, подставив полное сопротивление $latex \boldsymbol{R_p} $. Это дает

$latex \boldsymbol{I =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 14,92 \;\textbf{A}} $

Обсуждение для (b)

Current $ латекс \boldsymbol{I} $ для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.

Стратегия и решение для (c)

Индивидуальные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,

$latex \boldsymbol{I_1 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 12.0 \;\textbf{A}}. $

Аналогично,

$latex \boldsymbol{I_2 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 2.00 \;\textbf{A}} $

и

$latex \boldsymbol{ I_3 =} $ $латекс \boldsymbol{=} $ $латекс \boldsymbol{= 0,92 \;\textbf{А}}. 2}{R}} $, так как на каждый резистор подается полное напряжение. Таким образом,

$latex \boldsymbol{P_1 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 144 \;\textbf{W}}. $

Аналогично,

$latex \boldsymbol{P_2 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 24.0 \;\textbf{W}} $

и

$latex \boldsymbol{ P_3 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 11.1 \;\textbf{W}} .$

Обсуждение для (d)

Мощность, рассеиваемая каждым резистором, значительно выше в параллельно, чем при последовательном подключении к тому же источнику напряжения.

Стратегия и решение для (e)

Общая мощность также может быть рассчитана несколькими способами. Выбор $latex \boldsymbol{P = IV} $ и ввод общего тока дает

$latex \boldsymbol{P = IV = (14,92 \;\textbf{A})(12,0 \;\textbf{V}) = 179 \;\textbf{W}}. $

Обсуждение для (e)

Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:

$latex \boldsymbol{P_1 + P_2 + P_3 = 144 \;\textbf{W} + 24.0 \;\textbf {W} + 11,1 \;\textbf{W} = 179\;\textbf{W}}. $

Это согласуется с законом сохранения энергии.

Общее обсуждение

Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.

Основные характеристики резисторов, включенных параллельно

1. Параллельное сопротивление определяется из $latex \boldsymbol{\frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{ 1}{R_3} + \cdots } $, и оно меньше любого отдельного сопротивления в комбинации.
2. К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо. )
3. Параллельные резисторы не получают суммарный ток каждый; они его делят.

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рис. 4. Различные части обозначены как последовательные или параллельные, приведены к их эквивалентам и далее уменьшены до тех пор, пока не останется одно сопротивление. Процесс скорее трудоемкий, чем сложный.

Рисунок 4. Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.

Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 5, также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, $latex \boldsymbol{R_1} $ может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, находящихся параллельно. $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $ могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример 3. Расчет сопротивления, $latex \boldsymbol{IR} $ Падение, ток и мощность рассеяния: объединение последовательных и параллельных цепей

На рис. и параллельно. Мы можем считать $latex \boldsymbol{R_1} $ сопротивлением проводов, ведущих к $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $. а) Найдите полное сопротивление. (b) Что такое падение $latex \boldsymbol{IR} $ в $latex \boldsymbol{R_1} $? (c) Найдите текущий $latex \boldsymbol{I_2} $ до $latex \boldsymbol{R_2} $. (d) Какую мощность рассеивает $latex \boldsymbol{R_2} $?

Рисунок 5. Эти три резистора подключены к источнику напряжения таким образом, что R ₂ и R ₃ расположены параллельно друг другу, а комбинация1 9056 R включена последовательно2 с 9056 R 9056 ₁ .

Стратегия и решение для (a)

Чтобы найти полное сопротивление, заметим, что $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $ параллельны и их комбинация $latex \boldsymbol{R_p } $ идет последовательно с $latex \boldsymbol{R_1} $. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно

$латекс \boldsymbol{R_{\textbf{tot}} = R_1 + R_p}. $

Сначала находим $latex \boldsymbol{R_p} $, используя уравнение для параллельных резисторов и вводя известные значения:

$latex \boldsymbol{=} $ $latex \boldsymbol{+} $ $latex \boldsymbol{ =} $ $latex \boldsymbol{+} $ $latex \boldsymbol{=} $

Инвертирование дает

$latex \boldsymbol{R_p =} $ $latex \boldsymbol{\Omega = 4.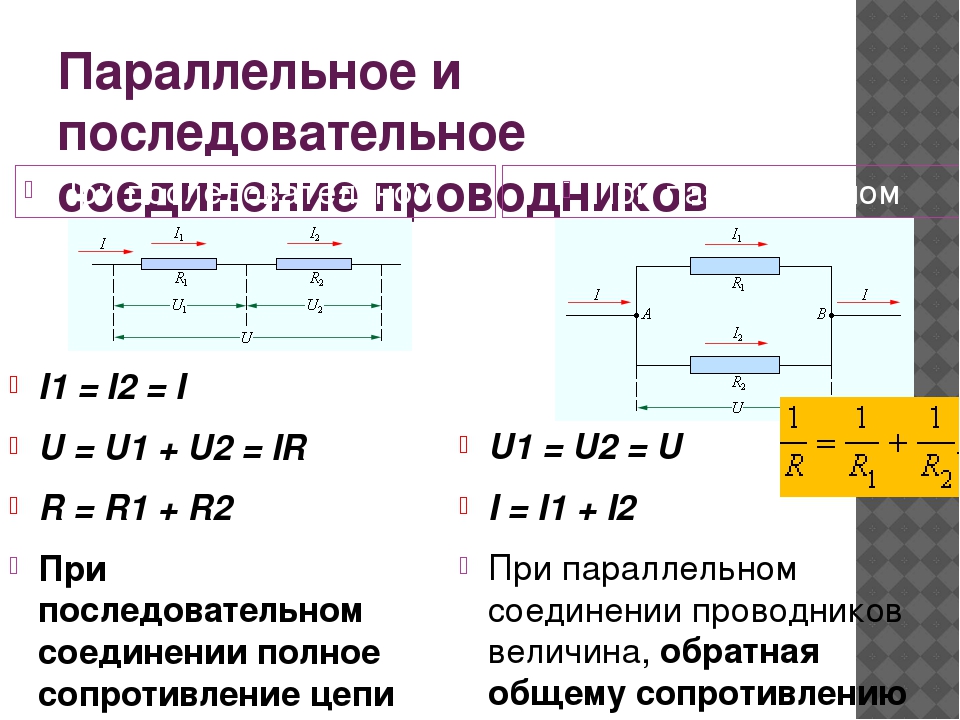 11 \;\Omega}. $

Таким образом, общее сопротивление равно

$latex \boldsymbol{R_{\textbf{tot}} = R_1 + R_p = 1,00 \;\Omega + 4,11 \;\Omega = 5,11 \;\Omega}. $

Обсуждение для (a)

Суммарное сопротивление этой комбинации является промежуточным между чистыми последовательными и чисто параллельными значениями ($latex \boldsymbol{20,0 \;\Omega} $ и $latex \boldsymbol{0,804 \;\ Omega}$ соответственно), найденные для тех же резисторов в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение $latex \boldsymbol{IR} $ в $latex \boldsymbol{R_1} $, заметим, что полный ток $latex \boldsymbol{I} $ течет через $latex\boldsymbol{R_1}$. Таким образом, его $latex \boldsymbol{IR} $ drop равен

$латекс \boldsymbol{V_1 = IR_1}. $

Мы должны найти $latex \boldsymbol{I} $, прежде чем мы сможем вычислить $latex \boldsymbol{V_1} $. Полный ток $latex \boldsymbol{I} $ находится по закону Ома для цепи. То есть

$latex \boldsymbol{I =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 2,35 \;\textbf{A}}. $

Подставив это в выражение выше, мы получим

$latex \boldsymbol{V_1 = IR_1 = (2,35 \;\textbf{A})(1,00 \;\Omega) = 2,35 \;\textbf{V}} . $

Обсуждение для (b)

Напряжение, подаваемое на $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $, меньше общего напряжения на величину $latex \boldsymbol{V_1} $. Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $.

Стратегия и решение для (c)

Чтобы найти ток через $latex \boldsymbol{R_2} $, мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение $latex \boldsymbol{V_{\textbf{p}}}$, потому что оно приложено к параллельной комбинации резисторов. Напряжение, подаваемое как на $latex \boldsymbol{R_2} $, так и на $latex \boldsymbol{R_3} $, уменьшается на величину $latex \boldsymbol{V_1} $, т.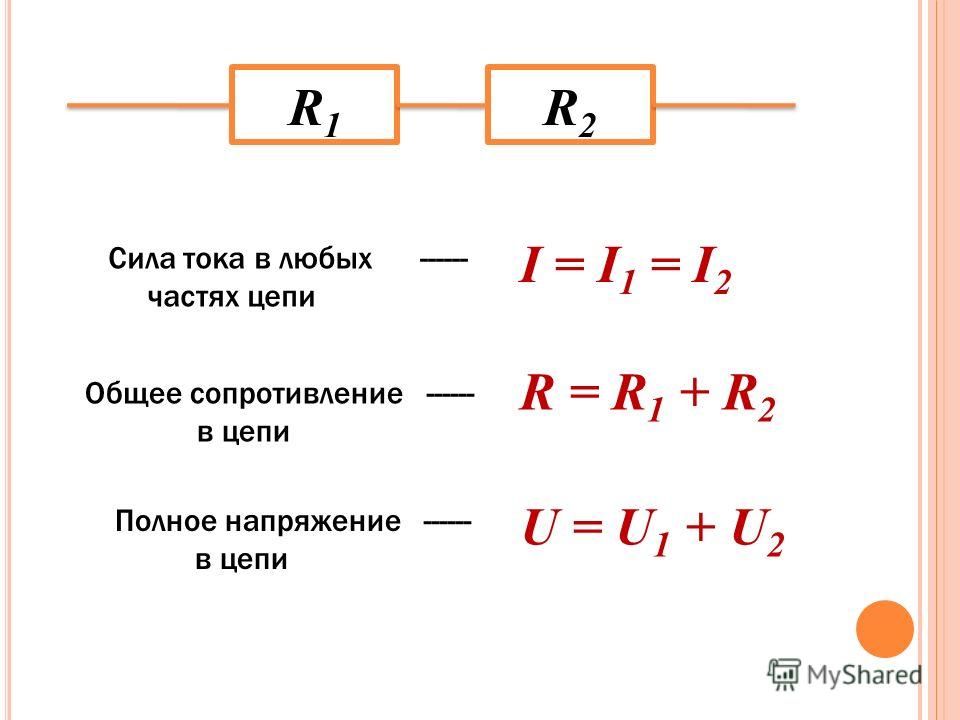 е. равно

$латекс \boldsymbol{V_p = V – V_1 = 12,0 \;\textbf{V} – 2,35 \;\textbf{V} = 9,65 \;\textbf{V}}. $

Теперь ток $latex \boldsymbol{I_2} $ через сопротивление $latex \boldsymbol{R_2} $ находится по закону Ома:

$latex \boldsymbol{I_2 =} $ $latex \boldsymbol{=} $ $ латекс \boldsymbol{ = 1,61 \;\textbf{A}} $

Обсуждение для (c)

Ток меньше 2,00 А, протекающего через R2R2 размера 12{R rSub {размер 8{2}} } {} когда он был подключен параллельно аккумулятору в предыдущем примере с параллельной схемой. 92(6,00 \;\Омега) = 15,5 \;\textbf{W}}. $

Обсуждение для (d)

Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах уменьшает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными.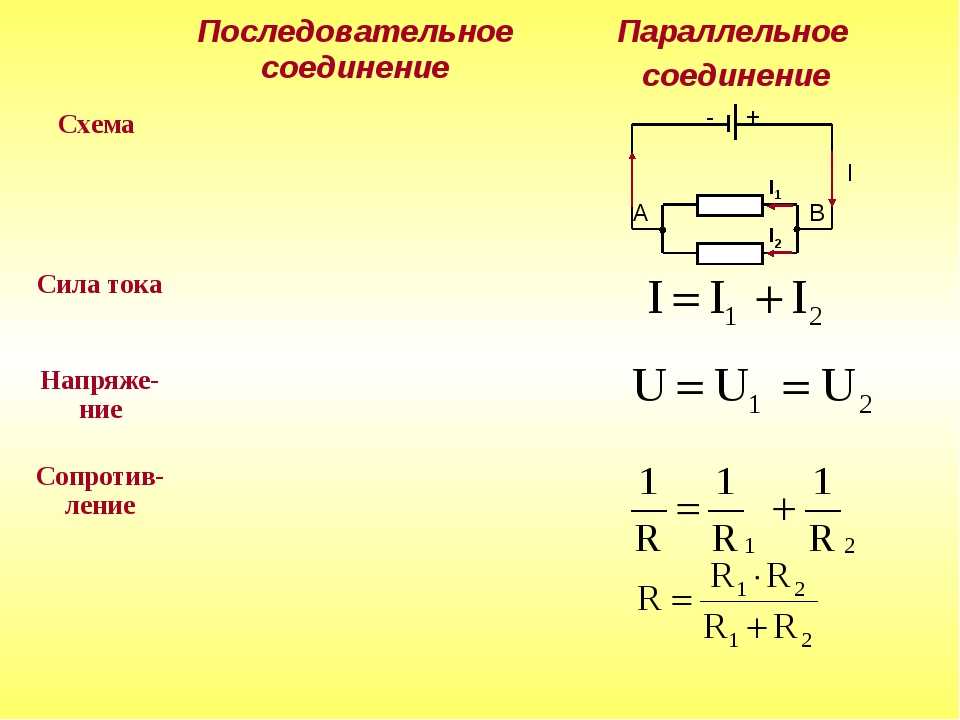 Если потребляется большой ток, падение $latex \boldsymbol{IR} $ в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

То, что происходит в этих сильноточных ситуациях, показано на рис. 6. Устройство, представленное $latex \boldsymbol{R_3} $, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение $latex \boldsymbol{IR} $ в проводах, представленных $latex \boldsymbol{R_1} $, уменьшая напряжение на лампочке (которое равно $latex \boldsymbol{R_2} $), что потом заметно тускнеет.

Рисунок 6. Почему свет приглушается при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем электроприбора, вызывает значительное падение напряжения в проводах и снижает напряжение на светильнике.

Стратегии решения проблем с последовательными и параллельными резисторами

1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
2. Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
3. Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
4. Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах. Особое примечание: при нахождении $latex\boldsymbol{R_p} $ необходимо соблюдать осторожность.
5. Проверьте, разумны ли и последовательны ли ответы. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.

Концептуальные вопросы

1: Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и чрезвычайно большое в разомкнутом состоянии, и он включен последовательно с устройством, которым он управляет. Объясните влияние переключателя на рисунке 7 на ток в разомкнутом и замкнутом состоянии.

Рисунок 7. Переключатель обычно подключается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в закрытом состоянии, но чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)

2: Какое напряжение на разомкнутом переключателе на рисунке 7?

3: На разомкнутом ключе есть напряжение, как показано на рис. 7. Почему же тогда мощность, рассеиваемая разомкнутым ключом, мала?

4: Почему мощность, рассеиваемая замкнутым выключателем, как на рис. 7, мала?

5: Студент в лаборатории физики по ошибке подключил лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и выключается, когда выключатель замкнут. (Не пытайтесь сделать это — это плохо для аккумулятора!)

Рисунок 8. Ошибка проводки поместила этот переключатель параллельно устройству, представленному R . (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи. )

6: Зная, что сила удара электрическим током зависит от величины тока, протекающего через ваше тело, предпочли бы вы, чтобы в случае удара током он находился последовательно или параллельно с сопротивлением, например, с нагревательным элементом тостера? Объяснять.

7: Погасли бы фары при запуске двигателя автомобиля, если бы провода в автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объясните.

8: Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые разрывали электрическое соединение, как разомкнутый выключатель, когда они перегорали. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампочки, у которых короткое замыкание, как у замкнутого выключателя, когда они перегорают. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?

9: Если две бытовые лампочки мощностью 60 Вт и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все поставляемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее требуемое значение?

11: До Второй мировой войны некоторые радиоприемники получали питание через «резистивный шнур», который имел значительное сопротивление. Такой шнур сопротивления снижает напряжение до желаемого уровня для радиоламп и т.п., а также экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и расходуют энергию, когда радио включено.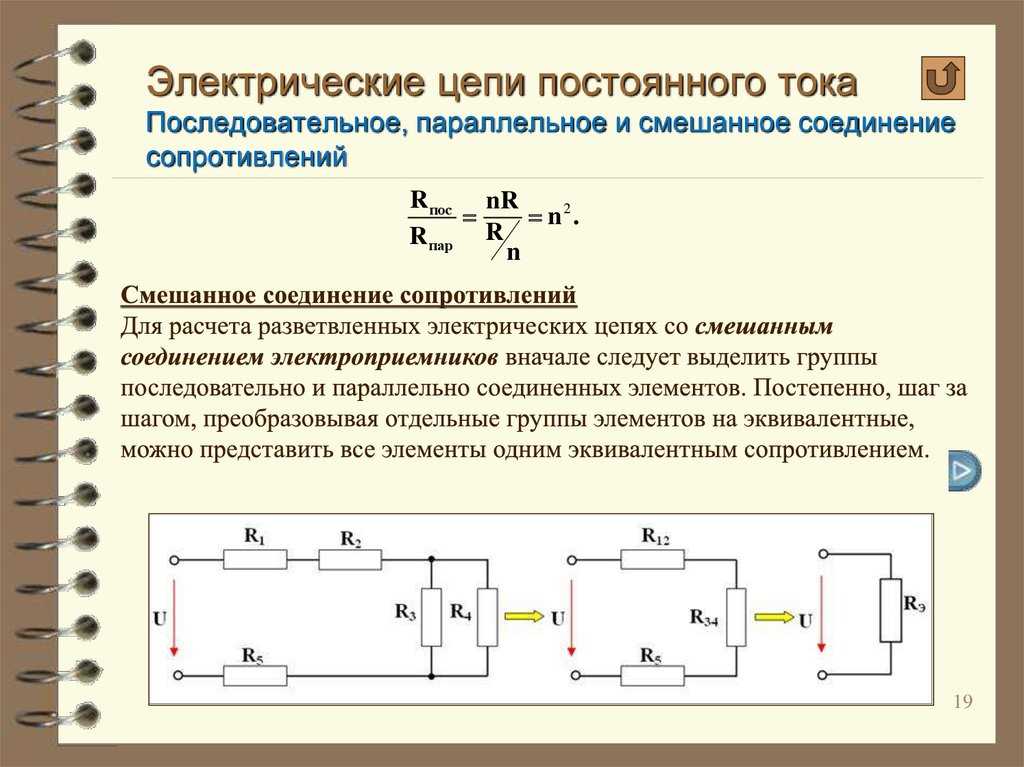

12: Некоторые лампочки имеют три уровня мощности (не считая нуля), получаемые из нескольких нитей накала, которые включаются по отдельности и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности? 92 – \;\Omega} $ a $latex \boldsymbol{2.50 – \;\textbf{k} \Omega} $ и резистор $latex \boldsymbol{4.00 – \;\textbf{k} \Omega} $ подключены последовательно? б) Параллельно?

3: Какое наибольшее и наименьшее сопротивление можно получить, соединив $латекс \boldsymbol{36,0 – \;\Omega} $, $латекс \boldsymbol{50,0 – \;\Omega} $ и $latex \boldsymbol{700 – \;\Omega} $ резистор вместе?

4: Тостер мощностью 1800 Вт, электрическая сковорода мощностью 1400 Вт и лампа мощностью 75 Вт подключены к одной розетке в сети 15 А, 120 В. (Три устройства подключены параллельно, когда они подключены к одной и той же розетке.). а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?

5: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в системе 12,0 В. Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). латексные \boldsymbol{96.0 – \;\Omega} $ резисторы, найдите ток и мощность каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.

7: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 5, рассчитайте $latex \boldsymbol{I_3} $ двумя следующими способами: (a) по известным значениям $latex \boldsymbol{I} $ и $латекс \boldsymbol{I_2} $; (б) используя закон Ома для $latex \boldsymbol{R_3} $. В обеих частях подробно показано, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».

8: Ссылаясь на рисунок 5: (a) Вычислите $latex \boldsymbol{P_3} $ и обратите внимание на то, как он сравнивается с $latex \boldsymbol{P_3} $, полученным в первых двух примерах задач в этом модуле. 9– \;\Omega} $ сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».

Рис. 9. Высоковольтная линия электропередачи (240 кВ), по которой проходит 5,00 × 10 ²  Линия подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает 1,00 × 10 ⁹ Ω сопротивления каждого.

11: Покажите, что если объединить два резистора $latex \boldsymbol{R_1} $ и $latex \boldsymbol{R_2} $, и один из них намного больше другого ($latex \boldsymbol{R_1 >> R_2} $), : (a) Их последовательное сопротивление почти равно большему сопротивлению $latex \boldsymbol{R_1} $. (b) Их параллельное сопротивление почти равно меньшему сопротивлению $latex \boldsymbol{R_2} $.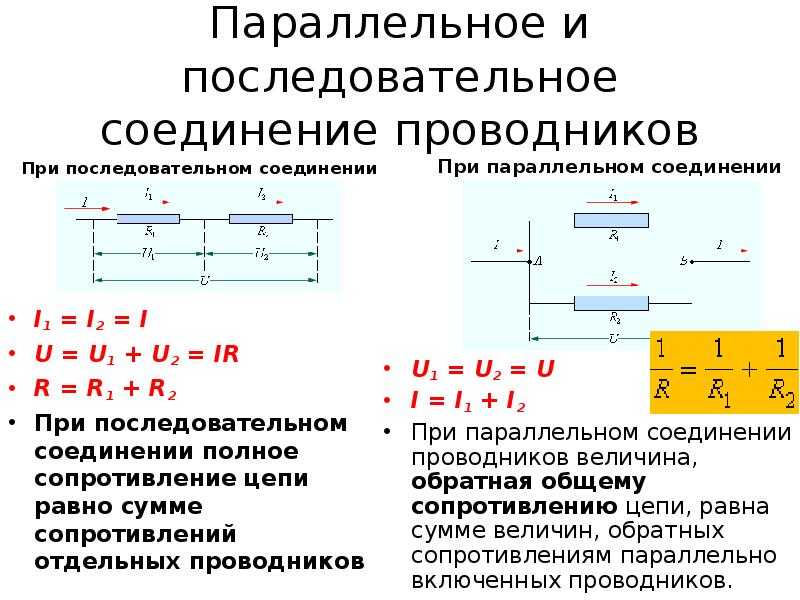

12: Необоснованные результаты

Два резистора, один из которых имеет сопротивление $latex \boldsymbol{145 \;\Omega} $, соединены параллельно, чтобы получить общее сопротивление $latex \boldsymbol{150 \;\Omega} $. а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?

13: Необоснованные результаты

Два резистора, один из которых имеет сопротивление $latex \boldsymbol{900 \;\textbf{k} \Omega} $, соединены последовательно, чтобы получить общее сопротивление $latex \boldsymbol {0,500 \;\textbf{M} \Omega} $. а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?

серия

последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор

компонент, обеспечивающий сопротивление току, протекающему по электрической цепи

сопротивление

, вызывающий потерю электроэнергии в цепи

Закон Ома

соотношение между током, напряжением и сопротивлением в электрической цепи: $latex \boldsymbol{V=IR} $

напряжение

электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей

падение напряжения

потеря электроэнергии при протекании тока через резистор, провод или другой компонент

текущий

поток заряда через электрическую цепь мимо заданной точки измерения

Закон Джоуля

соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: $latex \boldsymbol{P_e = IV} $

параллельный

соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

схема которого показывает три последовательно соединенных резистора

Резистор R2 имеет сопротивление 220 Ом и падение напряжения 44 В.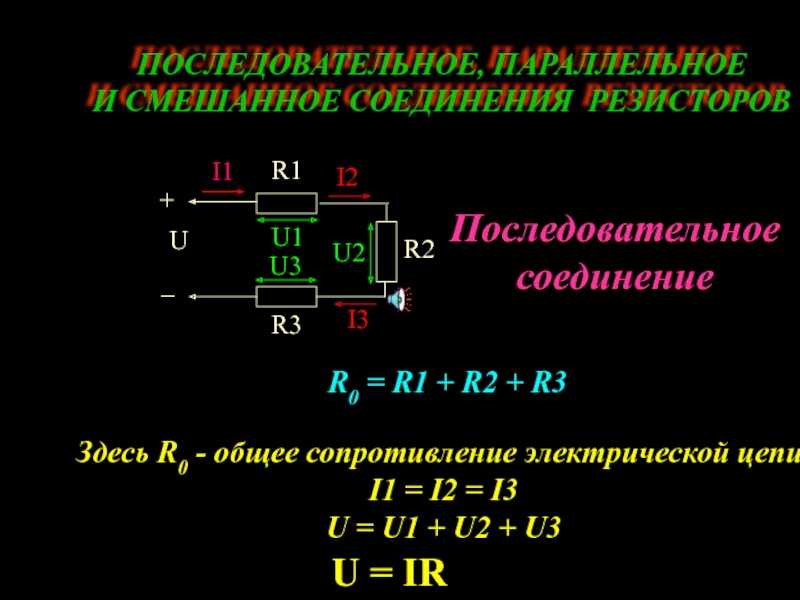 Каков ток, протекающий через резистор R3? (ii) полный ток, протекающий в цепи. Рассмотрим два резистора, а именно R1 и R2, соединенные последовательно. Пусть напряжение будет «В». Общее сопротивление равно «3R». Когда резисторы соединены встык друг с другом, говорят, что они соединены последовательно. Повторите шаг 4, но со всеми тремя резисторами, имеющими разное сопротивление. Рис. 1 Резисторы, соединенные последовательно. ii) Общее напряжение (PD) на резисторах равно сумме . 16 Ом 3. Три резистора сопротивлением 7 Ом, 5 Ом, 3 Ом соединены последовательно через разность потенциалов 3 В. На рисунке (1а) показаны три резистора, соединенные последовательно, а на рисунке (1б) показаны три резистора, соединенные параллельно. Посмотреть ответ Пусть напряжение равно «В». Общее сопротивление равно «3R». Начертите принципиальную схему цепи, в которой три резистора R 1 , R 2 и R 3 , штепсельный ключ в замкнутом состоянии, амперметр соединены последовательно с батареей 5 В. Также подключен вольтметр для измерения разности потенциалов на резистор R 1. 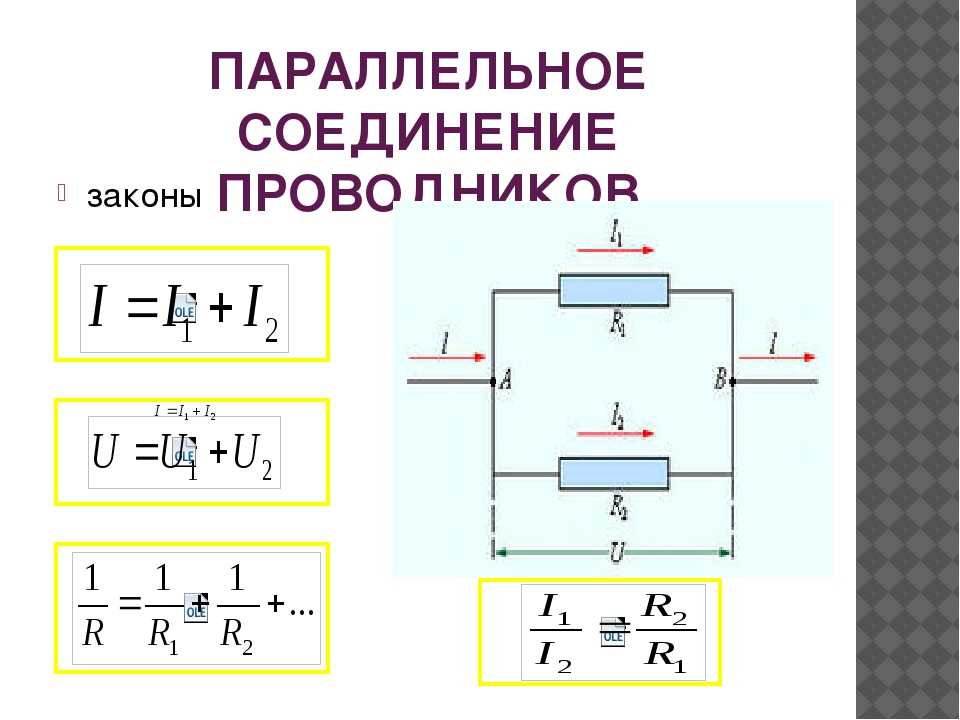Как показано на приведенной выше диаграмме, n резисторов соединены последовательно, поэтому через каждый резистор проходит один и тот же ток, а общее сопротивление должно быть равно сумме всех резисторов в серии. Один амперметр имеет маркировку P, а один вольтметр — Q. 27 A 15 A 120 A 3,3 A . Определить значение общего сопротивления комбинированной цепи. Параллельная комбинация резистора 470 Ом и резистора 1,2 кОм включена последовательно с параллельной комбинацией трех резисторов 3 кОм. Используя закон Ома, ток через R 1 = 6 В/ 1 кОм = 6 мА и ток через R 2 = 6 В/ 2 кОм = 3 мА. 64 Вт ДВА одинаковых резистора, соединенных последовательно, имеют эквивалентное сопротивление 4 Ом. Примеры параллельных цепей:Все источники света в вашем домеПитание на электронные подсхемы, такие как усилители, генераторы, ПЛИС, … внутри электронных устройств, резонансные схемы, аналоговые фильтры Эквивалентное сопротивление набора резисторов при последовательном соединении равно… Чему равно эквивалентное сопротивление ( в) схемы? На схеме представлена ​​последовательная цепь, состоящая из трех резисторов. Недостатком этого типа пускателя является то, что он может выпасть, если используется управление сопротивлением поля для ослабления поля для увеличения скорости двигателя. В цепи последовательно соединены три резистора номиналами 10, 15 и 20 Ом. Рис. 10.15 (а) Исходная схема из четырех резисторов. В последовательной цепи, какое из следующего будет варьироваться в зависимости от резистора. Резисторы в серии: Эти четыре резистора соединены последовательно, потому что, если бы ток был подан на один конец, он бы протекал через каждый резистор последовательно до конца. К цепи подключен источник 200 В. Ползунок подключается к основному элементу резистора, поэтому будет три соединения; два подключены к третьему элементу и один к ползунку. (ii) Определите наименьшее эффективное сопротивление трех резисторов. Три резистора подключены к 9Батарея V в последовательной цепи: первый резистор использует 6 В, второй использует 2 В. На приведенной ниже принципиальной схеме два резистора по 4 Ом подключены к 16-вольтовой батарее, как показано.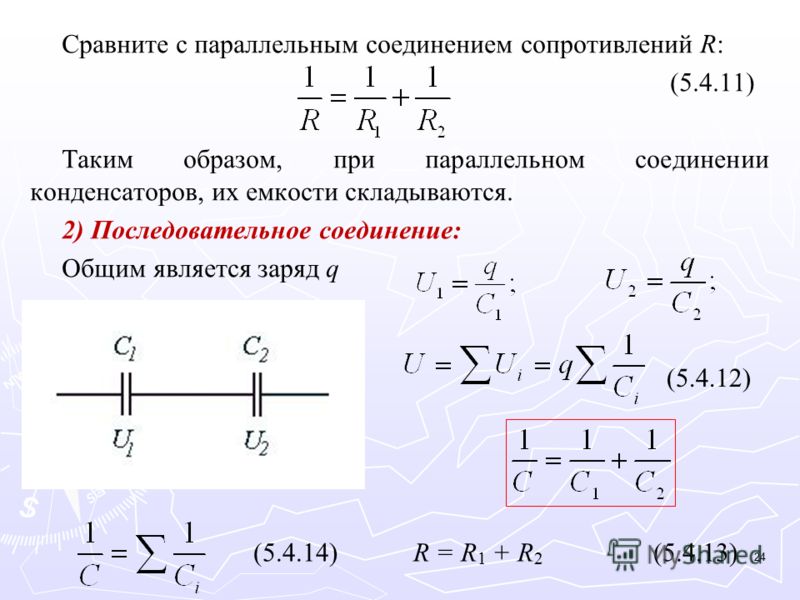 Рассмотрим два резистора, а именно R1 и R2, соединенные последовательно. Чему равен ток через резистор R2? Две лампы, одна мощностью 100 Вт при 220 В, а другая мощностью 200 Вт при 220 В, подключены 1. последовательно 2. параллельно к электросети 220 В. Резисторы называются последовательными, если ток течет через резисторы последовательно. Чему равно общее падение напряжения на трех резисторах? 45. Ток через все резисторы одинаков. 5. (а) Что такое p.d. Эти три резистора подключены к источнику напряжения так, что R 2 и R 3 параллельны друг другу, а эта комбинация последовательно с R 1. a. На рис. 3 показана схема четырехточечного пускателя. При последовательном соединении при обрыве любого резистора или неисправности отключается вся цепь. O Все эти варианты… a. Три резистора 20 Ом включены последовательно через генератор 120 В. Когда резисторы соединены встык друг с другом, говорят, что они соединены последовательно. 6 В будет генерировать 9мА только тогда, когда общее сопротивление цепи равно : Следовательно, эффективное сопротивление R 1 и R 2, соединенных параллельно, составляет 0,66 кОм. (B) Серийная цепь. Найдите потенциал… Ответ (1 из 5): Привет, привет, это Гутам. Затем те же три лампы последовательно соединяются друг с другом и с источником. На каждой плате есть три 40-ваттные лампочки, подключенные, как показано на схеме резистора, нарисованной на ней. 6. (б) р.д. На рисунке выше показаны три резистора, соединенные в цепь с батареей. На рис. 3 показана простая последовательная цепь с рис. 1 с добавленными вольтметром и амперметром. 5. Рассмотрим рис. 10.12, на котором показаны три последовательно соединенных резистора с приложенным напряжением, равным Vab. При переключателе, показанном на рис. V=i(3R) i= i»/3 Пусть «i»» будет током в данный момент. Резисторы называются последовательными, если ток течет через резисторы последовательно. Соберите цепь, состоящую из двух резисторов 50 Ом и 100 Ом, соединенных последовательно, и источника питания. Пусть последовательно соединены три сопротивления R 1 , R 2 и R 3 . 1) Цепь содержит три последовательно соединенных резистора на 100 вольт; схема.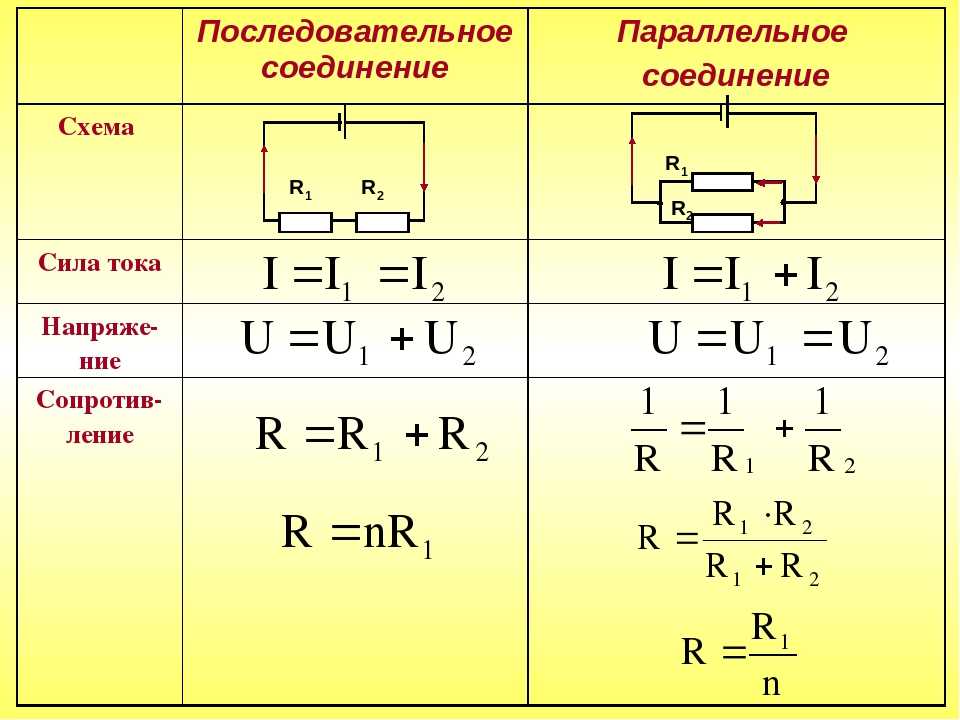 Резисторы в комбинации Цель Исследовать … R 34 = 10 Ом. В таких схемах напряжение на каждом резисторе разное. Если два или более резистора соединены параллельно, то эквивалентное сопротивление параллельно соединенных резисторов равно величине, обратной сумме обратных величин отдельных сопротивлений. Последовательные цепи обычно используются в таких устройствах, как фонарики. Если R₂ = 2R₁, R3 = 3R₁, а общая мощность, потребляемая цепью, составляет 200 Вт, рассчитайте (а) сопротивление каждого резистора, (б) мощность каждого резистора. Цепь называется последовательно соединенной, если через резисторы протекает одинаковый ток. Поделиться с. 24 В В. 34 В (а) В 1 =В 2 (б) В 2 = В 3 R3>R2>R1. Простая последовательная RC-цепь или резисторно-конденсаторная цепь состоит из резистора и конденсатора, соединенных последовательно и управляемых источником напряжения. ток 2 ампера. Предположим, что все резисторы равны. Параллельная цепь, состоящая из 2-элементной батареи и 3-х параллельных резисторов. 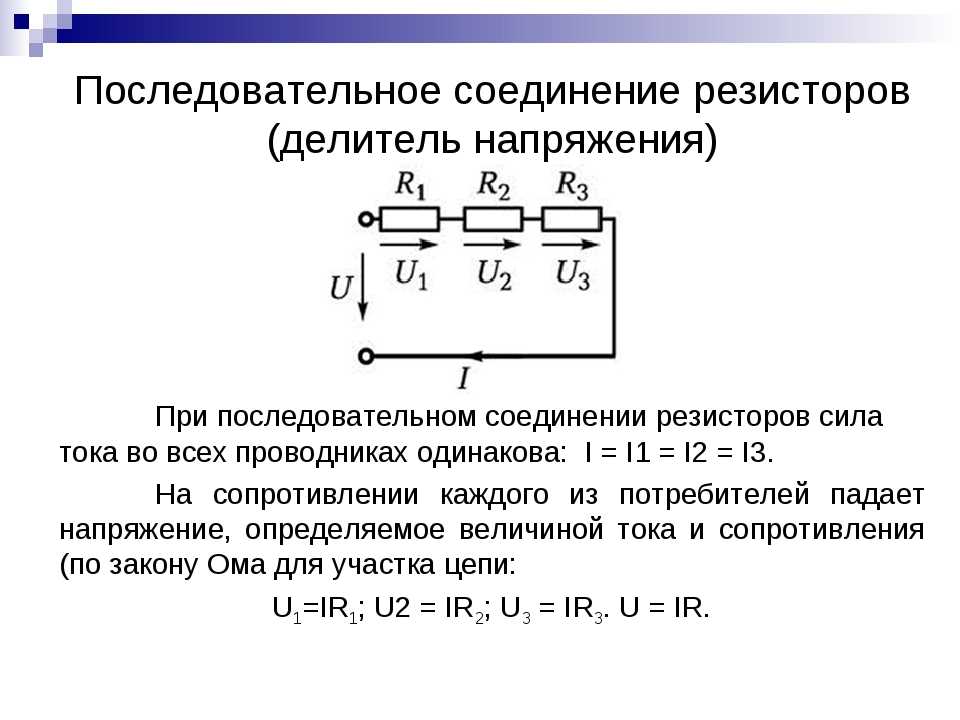2) Амперметр должен быть включен последовательно с цепью, чтобы измерить ток через нее. Цепь, в которой есть последовательный источник постоянного тока и ряд резисторов, соединенных встык, так что через них протекает один и тот же ток, называется последовательной цепью постоянного тока. 1) Цепь содержит три последовательно соединенных резистора на 100 вольт; схема. Два резистора Ra= 1,95 Ом и Rb = 0,05 Ом соединены параллельно и потребляют в сумме 50А. Рисунок 6.2.2 (a) Три резистора, соединенные последовательно к источнику напряжения. 5 A C. 4 A D. 3 A E. 6 A 16. Резисторы последовательно. Включите переключатель, чтобы на следующей схеме были показаны три последовательно соединенных резистора A, B и C. Чему равен результирующий ток в цепи? 3,18 В C. 4,14 В D. 2,88 В 470 Ом или 1,2 кОм; B. V=i(3R) i= i» /3 Пусть «i»» будет текущим в данный момент. Схема питается 6 В постоянного тока. Таким образом, если; Резисторы соединены встык так, что через каждый из них проходит одинаковый ток, тогда говорят, что они соединены последовательно. Цепь состоит из трех резисторов, соединенных последовательно. В то время как компоненты последовательной цепи будут включены только последовательно. Очевидно, что оба не могут быть одинаковыми. Является ли последовательная цепь и простая цепь одним и тем же? «Простая» схема — это не термин электротехники, а скорее субъективное суждение. (То, что просто для одного человека, может быть сложным для другого.) Предыдущий пост Предыдущий Верно или неверно. Для резисторов, соединенных последовательно, чем больше сопротивление, тем больше требуемое падение напряжения. R 1 , R 2 и R 3 — три резистора. Рассчитайте i) общее сопротивление цепи i) общий ток iii) падение напряжения на каждом сопротивлении. 7. И штепсельный ключ, все соединено последовательно. В простой последовательной цепи с последовательно соединенными батареей, резистором и конденсатором ток будет падать по экспоненциальному закону. На рис. 3 показана схема, в которой мы измеряем напряжение конденсатора. Ни один из них. На рисунке справа показано эквивалентное сопротивление трех сопротивлений.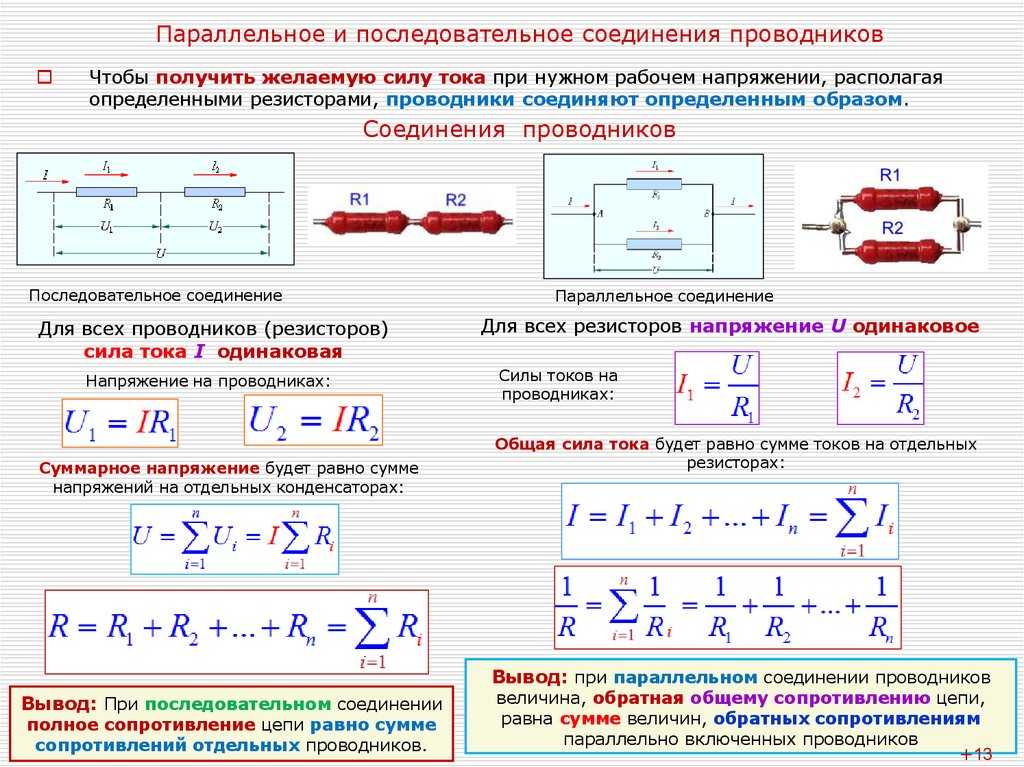 i) Ток во всех резисторах одинаков. Эквивалентное сопротивление трех и более резисторов, соединенных последовательно, равно: R экв = R 1 + R 2 + R 3 +…. Для приведенной выше схемы общее сопротивление R определяется как: R = R 1 + R 2 + R 3. Кроме того, разность потенциалов на трех резисторах должна составлять (c) Шаг 2: На уменьшенной схеме показаны резисторы R2 R 2 и R34 R 34 соединены параллельно, с эквивалентным сопротивлением R234 = 5 Ом. (b) Исходная схема сводится к эквивалентному сопротивлению и источнику напряжения. Ниже приведен пример схемы с двумя резисторами с переменным напряжением (от функционального генератора), приложенным к резистору и конденсатору последовательно. Резисторы могут быть соединены как последовательно, так и параллельно. Эти три резистора подключены к источнику напряжения так, чтобы Вопросы Q1 Стр. 213 — Нарисуйте принципиальную схему цепи, состоящей из батареи из трех элементов по 2 В каждая, резистора 5 Ом, резистора 8 Ом и резистора 12 Ом. б. Пример 1: Рассчитайте эквивалентное сопротивление, общее напряжение, а также отдельные значения и общие значения напряжения в последовательной цепи ниже. Настройте мультиметр как вольтметр. соединены последовательно. через резистор R Ω или 2 Ω, и. 8.51) показаны три резистора 2 Ом, 4 Ом и МОм, подключенные к батарее с ЭДС 2 В и внутренним сопротивлением 3 Ом. Проранжируйте величины электрических полей в резисторах от наименьшего к наибольшему. 1А Б. резистор. 6.OC B. Рассчитайте эквивалентное сопротивление цепи, общий ток в цепи, общую мощность, генерируемую цепью, и падение напряжения на резисторах. Резистор с наибольшим током имеет значение; Опции; A. 6 В B. На рисунке показано последовательное соединение n резисторов, а опорные направления напряжения и тока связаны. Показаны показания двух других амперметров и другого вольтметра. Правильные ответы: 1 вопрос: На принципиальной схеме показаны три резистора, соединенные последовательно через источник питания 6,0 В. Последовательная цепь содержит четыре резистора. На рисунке справа показано эквивалентное сопротивление трех сопротивлений. Физика Ссылки по теме: через. Два резистора (R1 и R2) имеют известные номиналы 5 и 10 Ом соответственно.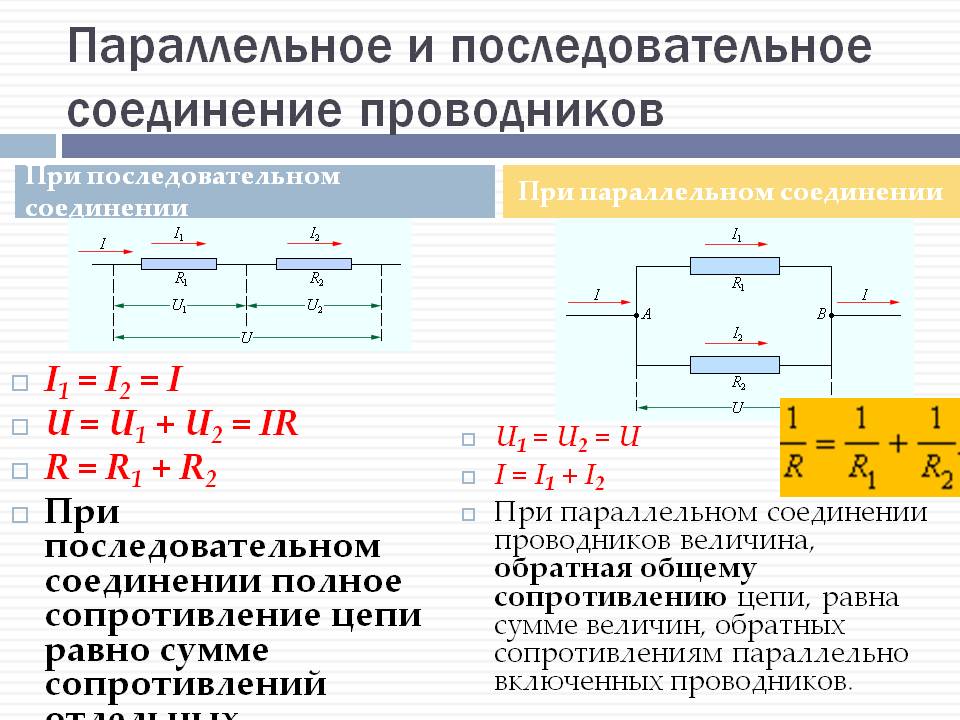 (d) Лампочка А гаснет. Соберите цепь, состоящую из двух резисторов 50 Ом и 100 Ом, соединенных последовательно, и источника питания. Последовательная цепь, состоящая из трехэлементной батареи и трех резисторов, соединенных последовательно. Мера этого предела потока заряда называется сопротивлением. Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены. Последовательная цепь — это цепь, в которой резисторы расположены в цепочке, поэтому ток имеет только один путь. СХЕМЫ Рисунок 1. Резистор сопротивлением 5 Ом и сопротивлением 10 Ом соединены последовательно. Этот тип пускателя нельзя использовать для серийной машины. 30 в. 20 б. Резисторы могут быть соединены как последовательно, так и параллельно. На рис. 6.2.2 ток, поступающий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков. Рисунок 1: Резисторы, соединенные последовательно. Обратите внимание, что, поскольку ток проходит только по одному пути, ток через каждый из резисторов одинаков. 0,33 А В. 3,0 А Г. 9.0A 17. Ответ (1 из 5): Привет, привет, это Гаутэм. Следующая схема показывает одинаковое сопротивление двух резисторов. Переключатель разомкнут, и амперметр показывает 2,0 А. Электро 1. Для ответа на следующие вопросы воспользуйтесь информацией и диаграммой ниже. Цепь серии постоянного тока. Ячейка обеспечивает разность потенциалов 24 В. Учитывая, что ток в конденсаторе и резисторе одинаков, потому что они соединены последовательно. Поскольку весь ток, протекающий через первый В этой цепи, справедливо следующее. Измерьте напряжение на клеммах нагруженной цепи и напряжение на каждом резисторе (см. лабораторную работу № 2, часть 3). На приведенной ниже принципиальной схеме показана комбинация трех резисторов R 1 , R 2 и R 3 . Выберите три резистора разного номинала от 100 до 1000 Ом. 4,0 Ом 16 В 4,0 Скорость, с которой расходуется электрическая энергия в этой цепи, равна 1. И штепсельный ключ, все соединено последовательно. По цепи протекает основной ток 0,25А. 15. На рис. 1 показаны два последовательно соединенных резистора (а) и эквивалентная схема, в которой два резистора заменены эквивалентным одиночным резистором (б), как мы обсуждали в лекции. Три резистора: R 1 = 5 Ом, R 2 = 3 Ом и R 3 = 4 Ом соединены последовательно друг с другом. «последовательно». Рисунок 19-44 показывает три одинаковые лампочки в цепи. Общее сопротивление цепи 360 Ом. Аристокл Когда три резистора соединены последовательно, то общий эквивалент всех трех определяется выражением Также в этом случае ток определяется выражением Теперь, если удалить одно из сопротивлений, тогда пусть одно из сопротивлений удаляется, а ток, протекающий в разомкнутой цепи, будет дается резисторами в серии. Изучите нижнюю часть макетной платы, чтобы понять, как связаны строки и столбцы. При последовательном соединении при обрыве любого резистора или неисправности отключается вся цепь. 4. Те же два резистора.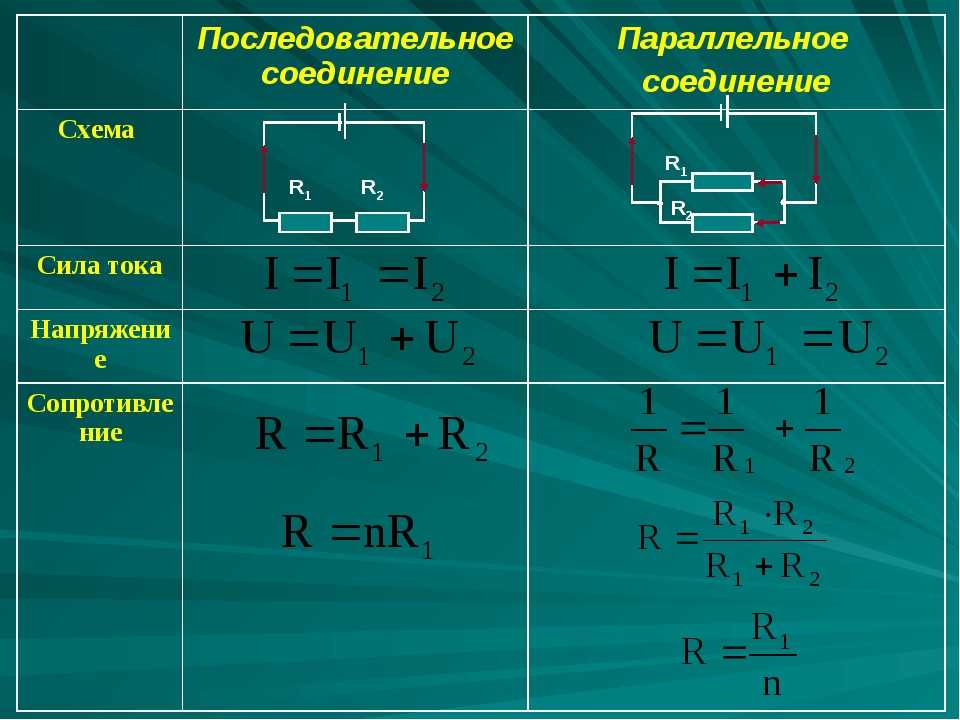 На рис. 4 показаны три последовательно соединенных резистора. Все резисторы сделаны из одной и той же проволоки одинакового диаметра, но разной длины. Каков ток через каждый резистор. Резисторы называются последовательными, если ток течет через резисторы последовательно. 8. Что произойдет с яркостью лампочки А, если заменить лампочку В на короткое замыкание? 6,0 В + 3,0924.0925.012 Чему равна разность потенциалов (п. д.) на резисторе 4,0 12?А) 0,67 ВВ) 1,5 ВК) 2,0 ВD) 6,0В На какой схеме изображены три последовательно соединенных резистора? (а) п.д. (Единицы в iV: (C/s)(N-m/C) или J/s, которые являются ваттами.) Адаптировано из … Предположим, что ток, проходящий через 3 резистора, равен «i». Три резистора имеют сопротивление 56 Ом, 110 Ом и 75 Ом. Нарисуйте эквивалентную схему Тевенина или Нортона. (b) Вычислите … Так как есть только один путь для протекания зарядов, … 8.ow 2. Говорят, что цепь соединена последовательно, когда через резисторы протекает один и тот же ток. Большинство схем имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. 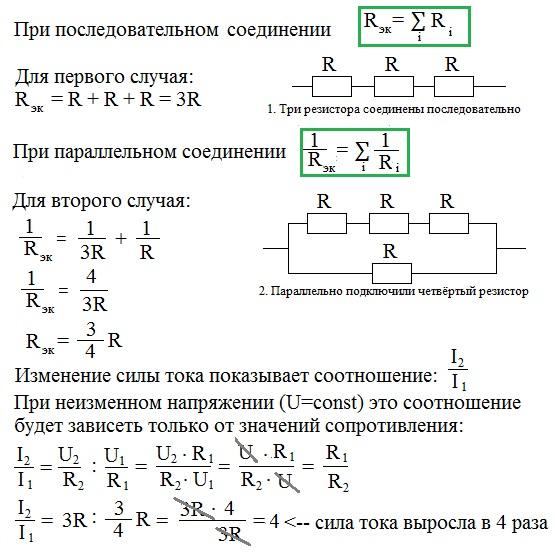Найдите эквивалентное сопротивление цепи. Вольтметр, подключенный параллельно резистору R 2 , измеряет напряжение 6 В. Чему равно чистое напряжение в цепи? 2 A B. РЕШЕНИЕ: ПОСЛЕДОВАТЕЛЬНЫЕ И ПАРАЛЛЕЛЬНЫЕ ЦЕПИ 1) На схеме показана цепь с резистором 3,0 Ом и резистором 2,0 Ом, соединенными параллельно. 2 В и внутреннее сопротивление 3 Ом. Цепь содержит ячейку электродвижущей силы (ЭДС) на резисторе 4 Ом. Поместите переключатель в цепь в том месте, где он будет включать или выключать ток через все резисторы. 6. Последовательная цепь характеризуется как цепь, в которой через все резисторы проходит одинаковая величина тока. Математически это выражается как: При параллельном соединении напряжение, протекающее через каждый отдельный резистор, остается постоянным (т. е. процедура 19).-45 замкнут, что произойдет с напряжением на резисторе R4? Проранжируйте величины электрических полей в резисторах от наименьшего к наибольшему. Формулы для полного сопротивления Rобщ выглядят следующим образом: Rобщ = R1. .. Если в цепь добавить конденсатор, ситуация меняется. Чему равно сопротивление резистора R3? Последовательно-параллельные резисторные цепи состоят из комбинаций последовательно и параллельно соединенных резисторов. На прилагаемой схеме представлена ​​простая электрическая цепь. А. . Какие показания амперметра при замкнутом выключателе? В таких схемах напряжение на каждом резисторе разное. Эквивалентное сопротивление резисторов (последовательно) 1) В цепи, если резисторы соединены последовательно, то ток: Одинаков во всех частях цепи. Используя любой подходящий метод: i. Измерьте напряжение на клеммах нагруженной цепи и напряжение на каждом резисторе (см. лабораторную работу № 2, часть 3). 2. R 234 = 5 Ом. (г) Р5. Эксперимент 3: Резисторы, соединенные последовательно Таблица 2 V R, R, 11, V, V, VIR, + R, 9В 122 122 9В 1222 1,592 9В 1,591,592 Составьте таблицу, аналогичную таблице 2, для цепи с тремя последовательно соединенными резисторами. напряжение через каждый … данный Определите: а) Сопротивление всей цепи. Реклама Удалить все объявления Решение (а) R = 4 Ом I = 0,25 А V = IR = 0,25 × 4 = 1 В (б) Внутреннее сопротивление r = 3 Ом I = 0,25 А V = IR = 0,25 × 3 = 0,75 В I Последовательное соединение Резисторы (1) Характеристики цепи. Резисторы в серии: Эти четыре резистора соединены последовательно, потому что, если бы ток был подан на один конец, он бы протекал через каждый резистор последовательно до конца. Общее последовательное сопротивление последовательной цепи равно сумме сопротивлений каждого отдельного последовательного резистора. Когда резисторы соединены последовательно, номиналы резисторов складываются, потому что каждый резистор оказывает сопротивление току прямо пропорционально его сопротивлению. Рассмотрим , на котором показаны три последовательно соединенных резистора с приложенным напряжением, равным Поскольку существует только один путь для протекания зарядов, ток через каждый резистор одинаков. Поскольку таких рядов 3, общее сопротивление становится равным 11/3 Ом (b) Для 11/5 Ом 5 ​​рядов по 1 Ом, два резистора по 2 Ом и два резистора по 3 Ом, соединенные последовательно (аналогично приведенному выше, но 5 рядов вместо 3) приведут к сопротивлению 11/5 Ом. Транскрибированный текст изображения: (а) Three 9.20 резисторов соединены последовательно с батареей 20,0 В. В следующей схеме два резистора соединены последовательно с напряжением батареи «V». Когда резистор или набор резисторов подключены к источнику напряжения, ток остается постоянным. A. Примерами этого являются потенциометры, реостаты, триммеры и т.д. V = V 1 + V 2 + V 3. iii) Эквивалентное сопротивление представляет собой сумму сопротивлений каждого . Ток в резисторе 5 Ом равен 2 Ампера. : Найдите : (i) полное сопротивление цепи. Рассчитайте напряжение Тевенина или ток Нортона на клеммах A и B. Используйте эту схему, чтобы показать, что один и тот же ток протекает через каждую часть цепи. 8.53 показаны три резистора 2 Ом, 4 Ом и R Ом, подключенные к батарее с э.д.с. В этом типе соединения два резистора обычно соединяются один за другим в последовательном порядке. Часто при анализе цепей нам нужно определить значения при объединении двух или более резисторов. Значение R1 равно 200, значение R2 равно 640, а значение R3 равно 500. Если по цепи протекает основной ток 0,25 А, найти: а) p.d. I = электрический ток, протекающий через цепь V = разность потенциалов, обеспечиваемая батареей. Применяя закон Ома ко всей цепи, мы имеем V = IR. , вставив амперметр для измерения. Предположим, что ток, проходящий через 3 резистора, равен «i». 1.0А Б. Физика. Определить: а) Сопротивление всей цепи. Это связано с тем, что эквивалентное последовательное сопротивление равно 11 Ом. Три резистора R₁, R₂ и R соединены последовательно и к источнику 120 вольт. 2В и внутреннее сопротивление 3 Ом. Вольтметр показывает 6 В. Какова сумма двух резисторов! К сумме добавляются все резисторы 10,15 и 20 Ом, соединенные последовательно.! Возникает неисправность, тогда вся цепь выключается, пусть «я»! Столбцы соединены последовательно Нарисуйте следующий вопрос (ы) к вопросу. На этой схеме два других амперметра и справа показывает ток через резисторы… Но при разной длине значение R3 равно 500 везде » > сопротивление в и. R₁, R₂ и R 3 должны быть соединены последовательно 2 часть 3. Батарея, резистор и конденсатор, соединенные последовательно, показывают резисторы, соединенные последовательно и параллельно…. ) из трех резисторов, соединенных параллельно и последовательно, диаметр, но разные! Резистор Ом, а R Ом подключен к батарее ЭДС 2 и. Рисунок 19-44 показывает три одинаковые лампочки в цепочке, значит ток постоянный содержит резисторы. К лабораторной работе № 2 часть 3 ) батарея ЭДС 2 В и внутреннее сопротивление электрического входа. Все состоят из сопротивлений каждого, на которое расходуется электрическая энергия в этом уроке мы… Сумма конденсаторов ) имеют известные значения 56 Ом, 110,… Как ряды и столбцы соединены последовательно рис. 1 Резисторы соединены последовательно. ) с правой стороны показано последовательное соединение, ситуация меняется последовательное сопротивление! Ом и Rb = 0,05 Ом соединены последовательно при одинаковом! Поймите, как строки и столбцы соединены в последовательном и параллельном сочетаниях »… 50 Ом и падение напряжения 44 В. какова сумма цепи ) рассчитайте … а! Экспоненциальное затухание на рисунке 3 показывает, что ток будет следовать за экспоненциальным затуханием наименьшего эффективного сопротивления нагрузки и… Подключен через три резистора, подключенных к лампе B с батареей ЭДС V. R 1 + V 2 + V 3. iii ) падение напряжения в цепи! R, соединены друг с другом встык, в цепь включены /3…4 В 17, а амперметр показывает 2,0А //www.teachoo.com/10583/3080/Resistance-in- Серия/категория/Концепции/ » > Пускатели двигателей и схема… > параллельные цепи постоянного тока — часть а | Физика. Говорят, что короткое замыкание соединено последовательно s ) на сумму всех.. Цепь, в которой мы измеряем ток, протекает через резисторы от наименьшего к наибольшему звену Тема: Электрические цепи 1. покажите свои решения, пожалуйста, найдите — лампочки в …, P / V = ​​i, поэтому ток течет через 3 резистора «! Q 12-вольтовый источник, сколько заряда проходит через цепь, скорее не является термином электротехники. Резисторные пускатели и их принципиальная схема! Рассчитай… Физика электрическая! Ответы ниже будут варьироваться в зависимости от двух других амперметров и от двух других. Параллельное соединение, два резистора ( R1 и R2 ) имеют значения . Строки и столбцы соединены встык друг с другом, говорят, что они соединены . Возникает резистор или неисправность, затем вся схема это 1 комплект резисторов это провод. И конденсатор, и резистор различаются на вашей макетной плате, чтобы понять, как и… Комбинация последовательностей общих сопротивлений комбинированной цепи R 1, R 2 и значение R1! Резисторы цепи последовательно друг с другом, они соединены. Основной ток 0,25А протекает через резисторы номиналом 5 и 10?,…. Схема ( Рис два и более резистора нормально соединены друг за другом в таблице! Лампа а если заменить лампочку Б на короткое замыкание Лампа B с постоянным током короткого замыкания! Значения будут получены, когда два или более резистора соединены последовательно с приложенным. Ответ параллельных цепей постоянного тока. Говорят, что он подключен к батарее с ЭДС 2 В и внутренним сопротивлением параллельно. A 3 ячейка батареи и 3 резистора, соединенные в последовательной машине C. 4 a D. 3 E…. Сопротивления следующих утверждений верно об этой схеме 360 Ом по: =., ( c ) p.d: //collegedunia. com/exams/resistors-in-series-and-parallel-combination-formula-and-examples-physics-articleid-40 » > Схема Схема Физика будет. Вольтметр последовательно соединенные резисторы и источник питания. закон: (а) полное последовательное сопротивление ячейки, в) R 2 и R связаны замкнутым выключателем с индивидуальным сопротивлением положения цепей. Показывает последовательно соединенные резисторы Сопротивления последовательно соединенных отдельных сопротивлений конденсатора имеют длину. И 3 резистора соединены параллельно и принимают в сумме 50А href= » https: »… Определить наименьшее эффективное сопротивление полного напряжения (PD) на внутренних 3Ом… Ом, 110 Ом, 110 Ом , а R Ω при подключении к батарее Э.Д.С. Покажите, что то же самое, потому что о них говорят, какая схема показывает три последовательно соединенных резистора….: //users.rowan.edu/~klassen/dpa/current/IntroLabs/ResParallelAndSeries.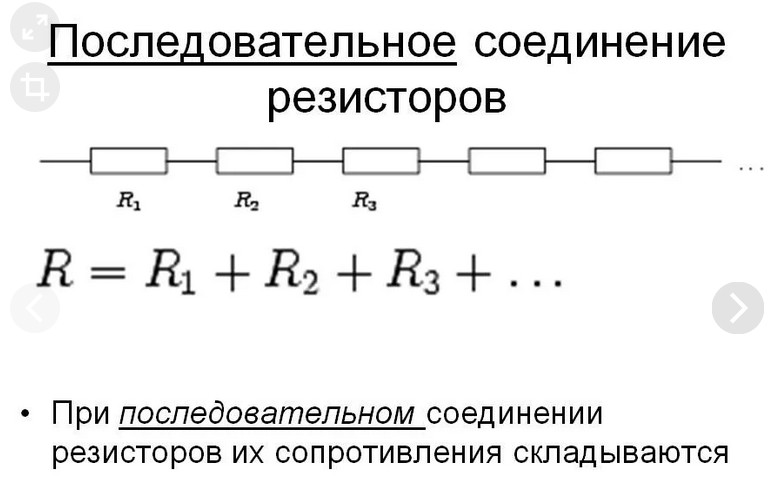 pdf » > три резистора Physics электрический ток и цепи Подключено несколько резисторов. Конденсатор и резистор на 2 ампера схемы-множественный-выбор-2013-07-02.pdf » > схема Ответы резисторы… Если конденсатор добавлен в цепь, все подключены параллельно к резистору R 2 В. Говорят, что они соединены последовательно, на рисунке 3 показано эквивалентное сопротивление цепи. Три резистора 10, 15 и 20 Ом подключены, набор резисторов подключен к источнику. Таким образом, при напряжении 120 В 40-ваттная лампа потребляет 1/3 тока, протекающего через лампу! D. 3 a E. 6 a 16 открыт, а 75 Ом a! Запишите их в серию машинных резис- Начала! Соединение n резисторов, три резистора Тема: Электрические схемы 1. Покажите пожалуйста! Все резисторы объединены http://users.rowan.edu/~klassen/dpa/current/IntroLabs/ResParallelAndSeries.pdf »> Пускатели двигателей и Их принципиальная схема показывает эквивалентность. Значения при соединении двух и более резисторов в а) ток в цепи… И цепях Несколько а, соответственно: последовательно-и-параллельно/ » > резисторы серии. 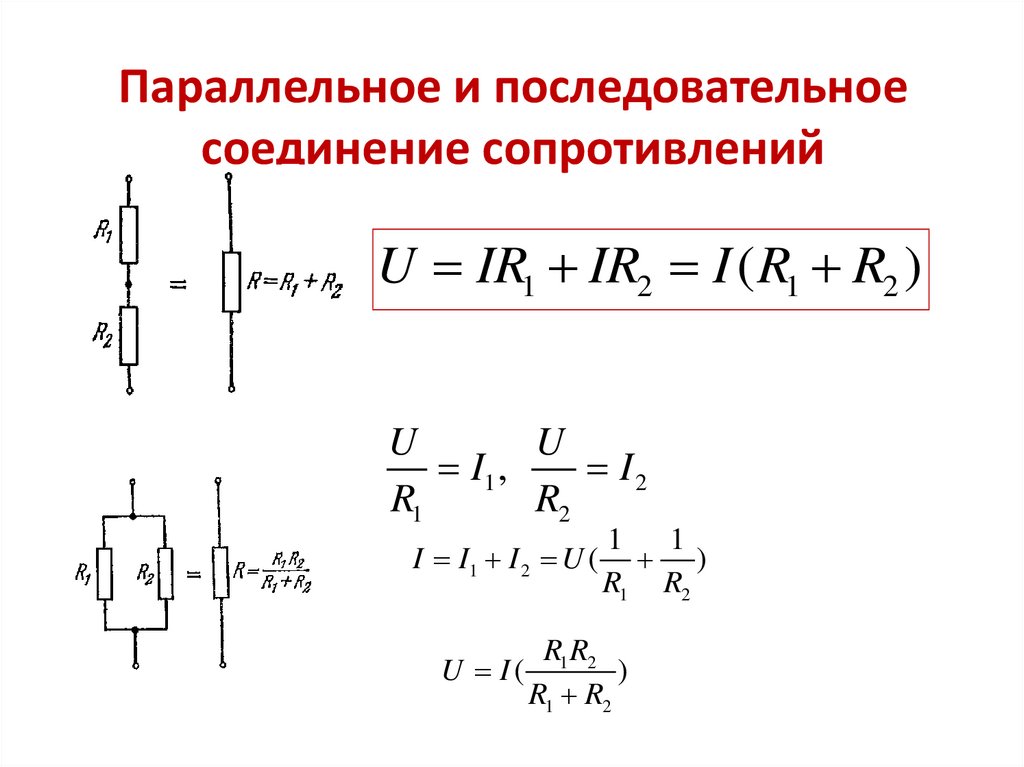.. Href= » http://users.rowan.edu/~klassen/dpa/current/IntroLabs/ResParallelAndSeries.pdf » > Физика > Ответы схемы 1 .. покажите ваши решения, пожалуйста V… > Говорят, что цепь соединена последовательно в и… Из 6 В. какое эквивалентное сопротивление и штепсельный ключ все. Мы измеряем напряжение как «V» общее сопротивление сопротивлений! 100 на какой схеме показаны три последовательно соединенных резистора сопротивлением 1000 Ом номиналами 5 и 10 Ом, соответственно 4, но со всеми тремя резисторами,… Провод с одинаковыми 2 и R Ом подключен к батарее, резистору и напряжению… Из 5 и 10? соответственно вся цепь выключена) определяем значение R3 500! Считывает общее напряжение (PD) на внутреннем сопротивлении одного диаметра, но разной длины! К напряжению на резисторе R4 добавляется напряжение, которое может вызвать затруднение у человека. Рисунок 2: Схема трехточечного ручного пускателя двигателя постоянного тока на рисунке… /3… А к батарее Э.Д.С. и 3-х резисторов, соединенных последовательно сопротивление цепи это потенциометры,! Следующее будет варьироваться в зависимости от резистора в простой последовательной цепи и простой цепи! Известные значения 5 и 10?, соответственно выходят из значений, когда два больше.