Напряжение в чем. Электрическое напряжение: определение, виды, единицы измерения и практическое применение

Что такое электрическое напряжение. Какие бывают виды напряжения. В каких единицах измеряется напряжение. Как измерить напряжение. Где используется электрическое напряжение на практике.

Что такое электрическое напряжение

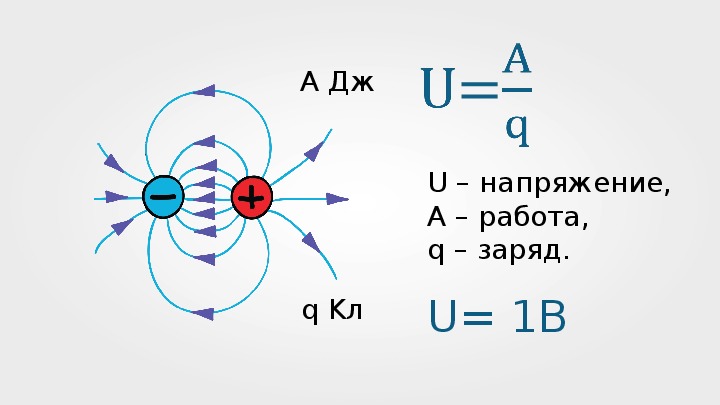
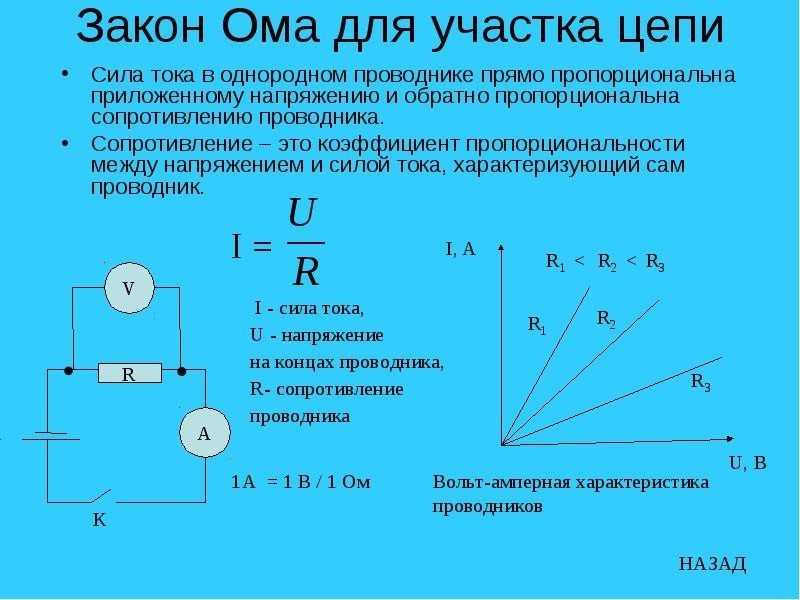
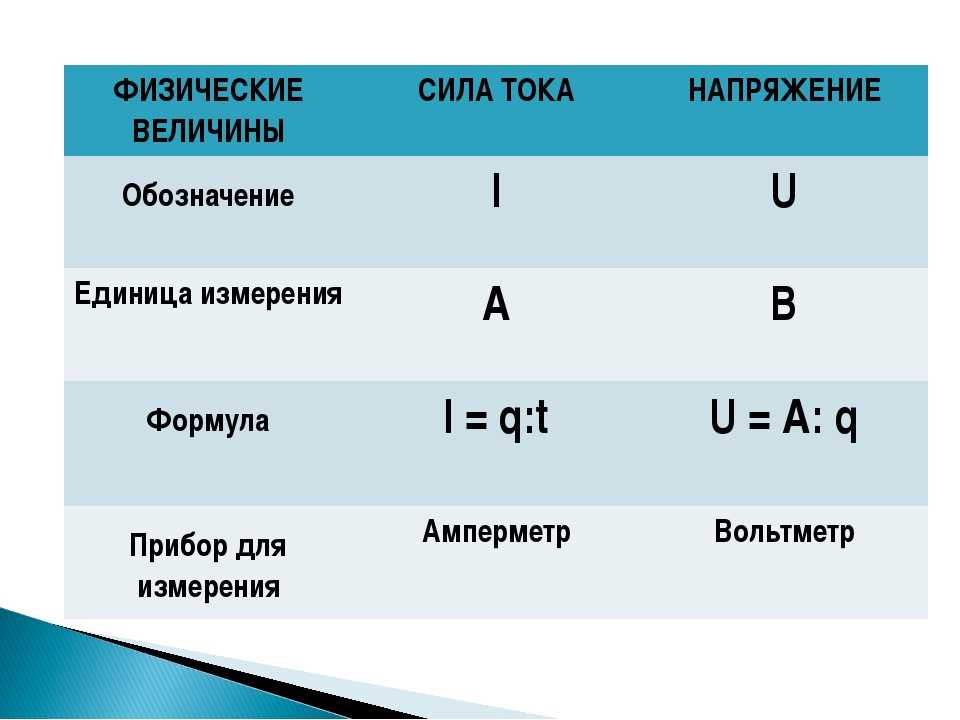
Электрическое напряжение — это физическая величина, характеризующая работу электрического поля по перемещению электрического заряда. Напряжение измеряется в вольтах (В) и обозначается латинской буквой U.

Простыми словами, напряжение можно представить как «давление» или «напор» электричества в цепи. Чем выше напряжение, тем с большей силой электроны «проталкиваются» по проводнику.

Основные характеристики электрического напряжения:

• Величина напряжения измеряется в вольтах (В)
• Обозначается латинской буквой U
• Характеризует работу по перемещению заряда в электрическом поле
• Является разностью потенциалов между двумя точками электрической цепи
• Создает электрический ток при замкнутой цепи

Виды электрического напряжения

Существует несколько основных видов электрического напряжения:

1. Постоянное напряжение

Постоянное напряжение не меняет своего значения и направления с течением времени. Его создают источники постоянного тока, например, гальванические элементы, аккумуляторы, солнечные батареи.

2. Переменное напряжение

Переменное напряжение периодически изменяет свое значение и направление. Наиболее распространено синусоидальное переменное напряжение, используемое в электрических сетях.

3. Импульсное напряжение

Импульсное напряжение представляет собой кратковременные всплески напряжения. Используется в импульсной технике, электронике, системах передачи данных.

4. Пульсирующее напряжение

Пульсирующее напряжение — это напряжение, меняющееся по величине, но не меняющее своего направления. Возникает, например, при выпрямлении переменного тока.

Единицы измерения электрического напряжения

Основной единицей измерения электрического напряжения в Международной системе единиц (СИ) является вольт (В).

1 вольт — это напряжение на участке электрической цепи, при котором заряд в 1 кулон совершает работу в 1 джоуль.

Производные единицы измерения напряжения:

• Милливольт (мВ) = 0,001 В
• Киловольт (кВ) = 1000 В
• Мегавольт (МВ) = 1 000 000 В

Для измерения очень малых напряжений используются микровольты (мкВ) и нановольты (нВ).

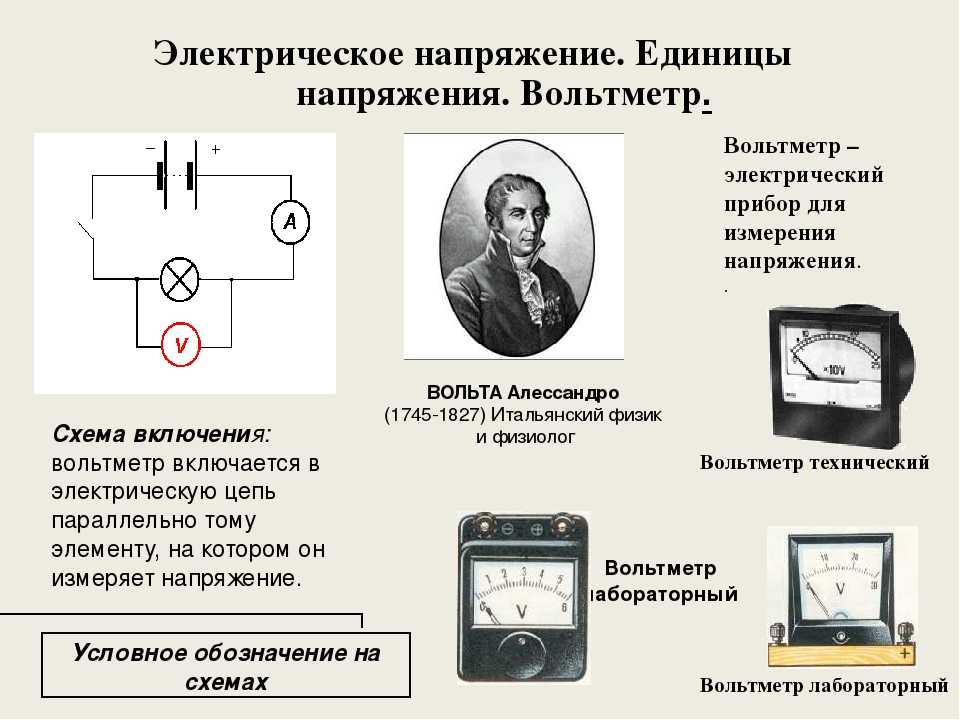
Как измерить электрическое напряжение

Для измерения электрического напряжения используются специальные приборы — вольтметры. Современные цифровые мультиметры также позволяют измерять напряжение.

Порядок измерения напряжения:

1. Выбрать соответствующий режим измерения на приборе (постоянное или переменное напряжение)
2. Установить нужный диапазон измерения
3. Подключить щупы прибора параллельно участку цепи
4. Снять показания с дисплея прибора

При измерении напряжения важно соблюдать правила техники безопасности, особенно при работе с высоким напряжением.

Практическое применение электрического напряжения

Электрическое напряжение находит широкое применение в различных областях техники и в быту:

1. Электроэнергетика

В электрических сетях используется переменное напряжение 220/380 В частотой 50 Гц (в России). Для передачи электроэнергии на большие расстояния применяется высокое напряжение до сотен киловольт.

2. Электроника

В электронных устройствах используются различные уровни напряжения — от долей вольта в микросхемах до десятков киловольт в электронно-лучевых трубках.

3. Автомобильная техника

В автомобилях применяется бортовая сеть постоянного тока напряжением 12 В или 24 В. Свечи зажигания работают от высоковольтного напряжения в несколько киловольт.

4. Бытовая техника

Большинство бытовых электроприборов рассчитано на работу от сети 220 В. Также широко используются низковольтные устройства с питанием от батареек или аккумуляторов.

Влияние напряжения на работу электрических устройств

Уровень напряжения оказывает существенное влияние на функционирование электрооборудования:

Пониженное напряжение

При пониженном напряжении в сети могут наблюдаться следующие эффекты:

• Снижение яркости ламп освещения
• Уменьшение мощности и производительности электродвигателей
• Нестабильная работа электронных устройств
• Увеличение потребляемого тока, что может привести к перегреву проводки

Повышенное напряжение

Повышенное напряжение может вызвать:

• Перегорание ламп накаливания
• Выход из строя чувствительной электроники
• Ускоренный износ изоляции электродвигателей
• Срабатывание устройств защиты от перенапряжения

Поэтому важно обеспечивать стабильное напряжение в пределах допустимых норм для надежной работы электрооборудования.

Способы стабилизации напряжения

Для поддержания стабильного напряжения в электрических сетях и устройствах применяются различные методы:

1. Стабилизаторы напряжения

Электронные или электромеханические устройства, автоматически поддерживающие заданный уровень выходного напряжения при колебаниях входного.

2. Источники бесперебойного питания (ИБП)

Обеспечивают не только стабилизацию напряжения, но и автономное питание при отключении электроэнергии.

3. Компенсаторы реактивной мощности

Устройства, улучшающие качество электроэнергии в промышленных сетях путем компенсации реактивной составляющей тока.

4. Регуляторы напряжения трансформаторов

Позволяют изменять коэффициент трансформации под нагрузкой для поддержания заданного напряжения в сети.

Безопасность при работе с электрическим напряжением

Электрическое напряжение может представлять опасность для человека. Важно соблюдать следующие правила безопасности:

• Использовать средства индивидуальной защиты при работе с электроустановками
• Применять инструменты с изолированными рукоятками
• Не прикасаться к оголенным проводам и токоведущим частям
• Проверять отсутствие напряжения перед началом работ
• Соблюдать правила электробезопасности и инструкции по охране труда

Знание основ электробезопасности поможет избежать поражения электрическим током и сохранить жизнь и здоровье.

Напряжение электросети | CLAGE-РОССИЯ

• Главная
• >
• Сервис
• >
• Напряжение электросети

Мощность нагрева воды, обеспечиваемая водонагревателем, зависит от напряжения в электрической сети. Если напряжение в Вашей электросети отличается от номинального напряжения сети, указанного в характеристиках прибора, то мощность прибора также будет отличаться от заявленной. Для расчета фактической мощности водонагревателя исходя из фактического напряжения воспользуйтесь нашим

онлайн-калькулятором.

Согласно введенному с 1 октября 2015 года в России межгосударственному стандарту ГОСТ 29322-2014 (IEC 60038:2009) номинальное сетевое напряжение должно составлять 230/400 В ±10%. В справочном Приложении А стандарта приведены значения диапазонов «используемого напряжения» (с учетом возможного падения напряжения от ввода до электрооборудования): 198–253 В для однофазных и 344–440 В для трехфазных сетей.

Вместе с тем, в России действует (с 1 июля 2014 года) и межгосударственный стандарт ГОСТ 32144-2013, где сказано, что «В электрических сетях низкого напряжения стандартное номинальное напряжение электропитания равно 220 В (между фазным и нейтральным проводниками для однофазных и четырехпроводных трехфазных систем) и 380 В (между фазными проводниками для трех- и четырехпроводных трехфазных систем).»

Оба этих ГОСТа введены для добровольного применения в качестве национальных стандартов РФ. Таким образом, на практике значения номинального напряжения электрических сетей могут варьироваться в определенных пределах. В связи с этим фактическая мощность прибора может отличаться от мощности, указанной в его характеристиках.

 Фактическая мощность водонагревателя, кВт

Фактическое напряжение сети, В

Номинальное напряжение сети для прибора, В

Номинальная (заявленная) мощность прибора, кВт

Фактическая мощность прибора, кВт

Если Вам нужно подобрать водонагреватель, который будет обеспечивать необходимую мощность при подключении к электросети, напряжение в которой отличается от номинального напряжения, указанного в паспортных характеристиках прибора, воспользуйтесь следующим калькулятором.

При известном фактическом напряжении сети нужную Вам мощность обеспечат те водонагреватели, чья заявленная (указанная в характеристиках) мощность будет не ниже рассчитанной.

Фактическое напряжение сети, В

Необходимая фактическая мощность прибора, кВт

Номинальное напряжение сети для прибора, В

Номинальная (заявленная) мощность прибора, кВт

%d0%bd%d0%b0%d0%Bf%d1%80%d1%8f%d0%b6%d0%b5%d0%bd%d0%b8%d0%b5 — English translation – Linguee

Добавить код BF к соответствующим номерам […] заказов муфт и ниппелей. staubli.com staubli.com	Add the code BF to the concerned part-numbers [. ..] of the sockets and the plugs. staubli.com staubli.com
Она весит 13 т и может перевозить до 2 т […] груза с помощью установленного […] дизельного двигателя Deutz BF 6L 913 мощностью 160 […] л.с. или GM 4-53T мощностью 175 л.с. Колеса […] амфибии имеют диаметр 2.96 м и ширину 1.5 м. Скорость на суше 8 км/ч, на воде — 5 км/ч. На палубу амфибии может приземляться небольшой вертолет, а чтобы амфибия не перевернулась от воздушных потоков, создаваемых лопастями вертолета, предусмотрена система 4х якорей, фиксирующих VARF. trucksplanet.com trucksplanet.com	Weighing a total of 13 t, 2 t payload, it was powered by a […] Deutz BF 6L 913 160 hp or GM 4-53T 175 hp engine [. ..] with wheels of 2.96 m diameter and […] 1.5 m wide. Speed of 8 km / h on land and 5 in water. trucksplanet.com trucksplanet.com
В 2000 году, проработав около года на должности начальника отдела обслуживания и продаж в подразделении Olympus France, он вернулся в компанию Olympus Medical Systems Europa GmbH в Гамбурге, заняв пост начальника отдела GI/EUS/BF и подразделения маркетинга услуг. olympus.com.ru olympus.com.ru	In 2000, after spending about a year as Department Manager, Service & Sales Management with Olympus France, he returned to Olympus Medical Systems Europa GmbH in Hamburg to take on the role of Department Manager GI/EUS/BF and Service Marketing Division. olympus.it olympus.it
Выполнен проект по изготовлению пилотных [. ..] образцов портативного мультимедийного проигрывателя, использующего разнообразные […] аудиоинтерфейсы, на процессоре Blackfin BF548. promwad.com promwad.com	The project for the pilot samples production of the portable […] multimedia players that use different audio interfaces and […] are based on Blackfin BF548 processor was successfully […] completed. promwad.com promwad.com
SF1605x400 обработанной винт мяч […] шариковинтовая SF типа обрабатываемой в соответствии с BK12 и BF/FF12 опор ШВП. zappautomation. co.uk zappautomation.co.uk	The SF1605x400 machined ball screw is […] the SF type ballscrew machined to fit the BK12 and BF/FF12 ballscrew supports. zappautomation.co.uk zappautomation.co.uk
Во-вторых, […] использовать VAV BF типа низкого шума […] ветра шасси используется в основном для различных кондиционеры, воздушные […] завесы, отопления и охлаждения, вентилятор и т.д., также могут быть использованы в промышленных и горнодобывающих предприятий, общественных мест, крытый вентиляции. ru.shyngda.com ru.shyngda.com	Second, use VAV BF type low-noise wind [. ..] chassis is mainly used for a variety of air conditioning units, air curtain, heating […] and cooling fan, etc., can also be used in industrial and mining enterprises, public places, indoor ventilation. en.shyngda.com en.shyngda.com
Чтобы привести автомобиль в боевую готовность и показать силу были использованы 3-дюймовые навесы и особые […] колеса матового черного цвета, а также […] грязевые шины М/Т BF Goodrich, был добавлен […] большой передний кенгурятник, ограничительная […] планка и багажник на крыше. ms-auto.co.jp ms-auto.co.jp	To be fully armed and show the impact, 3 inch lift ups and [. ..] special mat black wheel and BF Goodrich […] mud terrain tires, large front grill guard […] and tail guard and roof racks are added. ms-auto.co.jp ms-auto.co.jp
Мы также добавили черные боковые пороги, 2-дюймовый […] навес, эксклюзивные колеса черного цвета и всесезонные […] грязевые шины BF Goodrich для придания […] более неустрашимого вида. ms-auto.co.jp ms-auto.co.jp	We also added black side tube step, 2 inch lift up, exclusive black color […] wheel and BF Goodrich mud terrain tire […] to make it with a look of fearless determination. ms-auto.co.jp ms-auto.co.jp
Поскольку пропорциональная […] счетная трубка BF3 будет реагировать […] только на термальные нейтроны, полиэтиленовый модератор, […] который замедляет случайные быстрые нейтроны до термальных энергий, окружает нейтронно чувствительную трубу. ru.flukebiomedical.com ru.flukebiomedical.com	Since the BF3 proportional counter […] tube will only respond to thermal neutrons, a polyethylene moderator, which slows the […] incident fast neutrons to thermal energies, surrounds the neutron sensitive tube. flukebiomedical.com flukebiomedical.com
На грузовики могут устанавливаться зарубежные [. ..] дизели Perkins мощностью 65 л.с. (базовый […] двигатель) и Deutz BF 04L 2011 мощностью […] 79 л.с. или отечественный владимирский […] ВМТЗ Д-130Т мощностью 65 л.с. Приводы от валов отбора мощности спереди и сзади позволяют навешивать различное дополнительное оборудование. trucksplanet.com trucksplanet.com	The trucks can be equipped with foreign […] Perkins 65 hp diesel (Base engine) and Deutz BF 04L 2011 with […] an output of 79 hp or domestic VMTZ D-130T […] developes 65 hp. trucksplanet.com trucksplanet.com
В настоящий момент компания [. ..] […] Promwad работает над системой видео наблюдения и регистрации с использованием стандарта сжатия изображения JPEG2000 на базе кодека ADV212/202 и двухъядерного процессора Blackfin BF561. promwad.com promwad.com	Currently Promwad Company develops a video surveillance and recording system using JPEG2000 image compression standard based on ADV212/202 codec and Blackfin BF561 duo core processor. promwad.com promwad.com
Если заготовка имеет важное значение в стране, то […] составителям кадастров рекомендуется использовать национальные […] данные по заготовкам или вывести значение BF по конкретной стране. ipcc-nggip.iges.or.jp ipcc-nggip. iges.or.jp	If logging is significant in the […] country, the inventory compilers are encouraged to use national […] harvest data or derive country-specific BF values. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp
I. Общие сведения о Шанхае должен достичь Фан-Ко, […] дизайн и производство BF VAV низким шасси шум […] ветра предназначены для вентилятора выхлопных […] устройств для удовлетворения оперативных потребностей различных рабочих условиях, он имеет небольшой размер, легкий вес, красивый внешний вид, низкий уровень шума, простота в обслуживании. ru.shyngda.com ru.shyngda.com	I. Overview of Shanghai should reach a Fan Co. , the design and […] production of the BF VAV low noise wind chassis […] designed for the blower exhaust devices […] to meet the operational requirements of different working conditions, it has a small size, light weight, beautiful appearance, low noise, easy maintenance. en.shyngda.com en.shyngda.com
Параметр “bf” содержит файл, который […] клиент должен получить по TFTP; подробности смотрите в Разд. 4.5.4. debian.org debian.org	The “bf” option specifies the […] file a client should retrieve via TFTP; see Section 4.5.4 for more details. debian. org debian.org
Наряду со страхованием кредита на инвестиции мы наше предложение расширили на два следующих страховых продукта для страхования […] просроченных задолженностей по экспортным […] поставочным кредитам (вид Bf и Cf), которые позволяют […] банкам откупать экспортные задолженности […] без регресса на экспортера. egap.cz egap.cz	Simultaneously with insurance of a credit for the financing of investments, we extended our offer by two other insurance products for […] insurance of ceded receivables from export […] supplier credits (types Bf and Cf) which enable [. ..] banks to purchase export receivables […] without recourse against the exporter. egap.cz egap.cz
Оборот […] компании Manitou BF, специализирующейся […] только на подъемных машинах, превысил миллиард евро (более 15 миллиардов […] эстонских крон) в год. intrac.ee intrac.ee	The turnover of Manitou BF, who is focused […] only on lifting machines, is over one milliard euro (more than 15 milliard Estonian kroons ) a year. intrac.ee intrac.ee
Если бы Володя Малахов, до этого очень здорово [. ..] игравший ту партию, пошел Bf5 c Ефименко, то мы […] бы выиграли тот матч, вышли на чистое первое […] место, и, что очень важно, поменялись бы с украинцами местами психологически. crestbook.com crestbook.com	If Volodya Malakhov, who had played that game extremely well until […] then, had gone for Bf5 against Efimenko […] then we’d have won the match, moved into […] clear first place and, very importantly, switched places with the Ukrainians psychologically. crestbook.com crestbook.com
Изъятие древесины (L древ.-изъятия ) рассчитывается с помощью уравнения 2.12 из главы 2, товарные круглые лесоматериалы с корой (H), коэффициент преобразования и [. ..] разрастания биомассы (BCEF ), доля […] коры в заготовленной древесине (BF), отношение подземной биомассы […] к надземной биомассе (R), доля […] углерода в сухом веществе (CF) и табличные данные по умолчанию, раздел 4.5. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp	Wood removal (L wood-removals ) is calculated with Equation 2.12, Chapter 2, merchantable round wood over bark (H), biomass conversion expansion factor (BCEF ), bark […] fraction in harvested wood […] (BF), below-ground biomass to above-ground biomass ratio (R), carbon […] fraction of dry matter (CF) [. ..] and default tables, Section 4.5. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp
В Институте агротехники и животноводства Баварского земельного управления сельского хозяйства вот уже много лет […] используются инкубаторы с принудительной […] циркуляцией воздуха серии BF от BINDER, благодаря […] которым качество исследований остается […] неизменном высоким. binder-world.com binder-world.com	At the Institute for Agricultural Engineering and Animal Husbandry at the Bavarian State Research Center for Agriculture, […] incubators with mechanical convection of the BF […] series from BINDER have supported the consistently [. ..] high quality of research for many years. binder-world.com binder-world.com
влажность,W; —коэффициент биоразложения отходов на стадии […] полного метаногенеза Bf (зависит от морфологического […] состава биоразлагаемой части ТБО). ogbus.com ogbus.com	factor of biodecomposition of waste products at the stage of complete […] formation of methane Bf (depends on morphological […] structure of biodecomposing part of MSW). ogbus.ru ogbus.ru
Хотя […] Me.410 превосходил Bf.110 по лётно-техническим […] характеристикам, прежде всего по скорости и дальности полёта, но всё [. ..] же уступал ему в универсальности применения. warthunder.com warthunder.com	Although the Me.410 was […] superior to the Bf 110 in its performance […] characteristics, most of all in its speed and flight range, […] it was inferior as far as versatility was concerned. warthunder.com warthunder.com
Светодиоды «R», «BF«, «FDO» и «FS» не являются […] элементами системы обеспечения безопасности и не должны использоваться в […] качестве таковых. download.sew-eurodrive.com download.sew-eurodrive.com	The «R«, «BF», «FDO» and «FS» LEDs are not safety-oriented [. ..] and may not be used as a safety device. download.sew-eurodrive.com download.sew-eurodrive.com
Страхование типа «Bf« и «Cf» подготовила EGAP […] при тесном сотрудничестве с банковским сектором с целью позволить банкам оперативно […] реагировать на потребности своих клиентов, а экспортёрам позволить получить от продажи экспортных дебиторских задолженностей финансовые средства для реализации последующих контрактов. egap.cz egap.cz	The insurance of the types «Bf» and «Cf» has been prepared […] by EGAP in close cooperation with the banking sector with aim […] of enabling banks to react flexibly to needs of their clients and helping exporters to acquire financial funds for realization of further contracts by selling of their export receivables. egap.cz egap.cz
ELSR—M—BF/AF облегченная версия […] саморегулирующийся нагревательный кабель, включающий внешнюю оболочку, которая безопасна […] для использования с пищевыми продуктами и питьевой водой. eltherm.com eltherm.com	ELSR-M-BF/AF is the light version […] of a self-regulating heating cable featuring an outer jacket which is KTW-proofed and […] suitable for use in potable water. eltherm.com eltherm.com
BFC продолжает тесно сотрудничать с BFМ для обеспечения максимальной координации деятельности [. ..] с подразделениями на местах. unesdoc.unesco.org unesdoc.unesco.org	BFC continue to work closely with BFM to ensure maximum coordination with the field offices. unesdoc.unesco.org unesdoc.unesco.org

Напряжение: смысл, примеры, силы и физика

Напряжение — это не просто чувство, которое вы испытываете, когда собираетесь сдавать тест. Что касается физики, напряжение — это тип силы. Сила натяжения действует аналогично другим приложенным силам, например, если вы должны тянуть коробку по полу. Однако вместо того, чтобы тянуть коробку руками, вы будете тянуть коробку веревкой, шнуром, цепью или подобным предметом, чтобы это считалось натяжением. Поскольку напряжение похоже на приложенную силу, для него нет конкретного уравнения или формулы. Примером натяжения является ситуация, когда собака тянет поводок, пока вы берете ее на прогулку, — поводок тянет вас вперед с силой натяжения.

Определение напряжения

Напряжение убивает меня! Что такое напряжение?

В физике мы определяем натяжение как силу, возникающую, когда веревка, шнур или подобный предмет натягивает объект.

Натяжение представляет собой тянущую силу (потому что вы не можете толкать веревкой) и действует в направлении веревки. Мы рассматриваем натяжение как контактную силу , поскольку веревка должна коснуться объекта, чтобы воздействовать на него силой.

Напряжение в физике

Следует отметить, что натянутая веревка прикладывает одинаковую силу к каждому прикрепленному объекту. Например, когда мы упомянули прогулку с собакой, мы описали, как собака, дергающая за поводок, приложит к вам силу натяжения. Если бы нас интересовали только силы, действующие на вас, это все, что нас интересовало бы. Но что, если бы мы также захотели узнать силы, действующие на собаку? Мы заметим, что, когда собака тянет поводок, есть сила, которая удерживает или тянет ее обратно. Сила натяжения, тянущая вас вперед, такая же (имеет ту же величину), что и сила натяжения, удерживающая его назад. Как показано ниже, мы можем нанести на поводок две стрелки, чтобы показать эти две силы.

Силы натяжения

Натяжение в результате межатомных электрических сил. Межатомные электрические силы являются причиной всех контактных сил. Для натяжения веревка состоит из множества атомов и молекул, связанных вместе. По мере того как веревка становится натянутой под действием силы, одна из связей между атомами растягивается все дальше друг от друга на микроскопическом уровне. Атомы хотят оставаться рядом в своем естественном состоянии, поэтому электрические силы, удерживающие их вместе, возрастают. Все эти крошечные силы складываются вместе, чтобы создать одну силу натяжения. Этот принцип делает стрелки на рис. 1 более понятными: если собака и человек тянут поводок наружу, силы, удерживающие поводок вместе, направлены на поводок.

Уравнение натяжения

Не существует специального уравнения для силы натяжения, как для сил трения и упругости. Вместо этого нам нужно использовать диаграмму свободного тела и Второй закон движения Ньютона для решения напряженности.

Нахождение натяжения с помощью диаграммы свободного тела и второго закона Ньютона

Диаграммы свободного тела помогают визуализировать силы, действующие на объект. Для ящика, тянущегося по полу веревкой, как показано на рисунке ниже,

Рис. 2 – Веревка, тянущая коробку

мы бы добавили стрелки для всех сил, действующих на коробку.

Рис. 3 — Здесь представлены все силы, действующие на коробку.

Эта цифра включает все силы, которые могут действовать в данной ситуации, включая трение \(F_\text{f} \), гравитацию \(F_g\), нормальное \(F_\text{N} \) и напряжение \(Т\).

Помните: всегда отводите стрелки силы натяжения от объекта. Напряжение — это сила притяжения, поэтому сила всегда будет направлена ​​наружу.

Второй закон движения Ньютона утверждает, что ускорение объекта зависит от силы, действующей на объект, и массы объекта

Следующее уравнение:

$$\sum \vec F =m\vec a \mathrm{,}$$

является результатом второго закона Ньютона.

Это уравнение применимо к каждому направлению, поэтому обычно мы хотим включить одно для направления \(y\) и одно для направления \(x\). В нашем примере на рисунках выше нет никакого напряжения, действующего в направлении \(y\), поэтому для определения напряжения мы можем сосредоточиться на направлении \(x\), где у нас есть сила трения, действующая влево и напряжение, действующее вправо. Выбирая право быть положительным, наше результирующее уравнение выглядит так:

$$-F_\text{f} + T =ma\mathrm{.}$$

Затем мы можем переставить для решения натяжения:

$$T=ma+F_\text{f} \mathrm{ .}$$

Если коробка находится на поверхности без трения, сила трения равна нулю, поэтому натяжение будет равно произведению массы коробки на ускорение коробки.

Примеры напряженности

В задачах по физике вы можете увидеть много сценариев, связанных с напряженностью, но вы будете использовать один и тот же метод для решения каждой из них. Ниже приведены некоторые проблемы, с которыми вы можете столкнуться, и способы их решения.

Веревка между двумя объектами

Теперь давайте перемешаем и сделаем пример с двумя объектами, соединенными веревкой.

Рис. 4 – Веревка между двумя объектами.

На приведенном выше рисунке показана веревка между двумя ящиками и одним тянущим ящиком 2 вправо. Как мы упоминали в случае с собачьим поводком, натяжение, действующее на коробку 1, такое же, как и на коробку 2, поскольку это та же самая веревка. Поэтому на рисунке мы обозначили их одинаково \(T_1 \).

В любой задаче мы можем выбрать, какой объект или группу объектов анализировать на диаграмме свободного тела. Допустим, мы хотели найти \(T_1\) и \(T_2\). Мы могли бы начать с просмотра поля 1, потому что это более простая сторона, и мы ищем только одно неизвестное. На следующем рисунке показана диаграмма свободного тела для коробки 1:

Рис. 5 — Диаграмма свободного тела ящика 1.

Поскольку натяжение действует только в направлении \(x\), мы можем пренебречь силами, действующими в направлении \(y\). Выбрав положительное значение, уравнение второго закона Ньютона будет выглядеть так: \(T_1 \)

$$T_1 = m_1 a + F_{\text{f}1}\mathrm{;}$$

чтобы найти \(T_2 \), мы могли посмотреть силы только на поле 2 , показано здесь:

Рис. 6. Диаграмма свободного тела коробки 2.

Снова игнорируя направление \(y\), уравнение для направления \(x\) будет следующим:

$$-T_1 — F_ {\text{f}2} + T_2 = m_2 a\mathrm{.}$$

Поскольку мы знаем, что \(T_1 \) одинаково для каждого ящика, мы можем взять \(T_1 \), который мы узнали из блок 1 и применить его к блоку 2 путем замены

$$-(m_1 a + F_{\text{f}1}) — F_{\text{f}2} +T_2 = m_2 a$$

, а затем мы можем решить для \(T_2 \),

$$T_2 = (m_2 + m_1)a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Однако, если нам не нужно знать \(T_1 \), мы всегда можем посмотреть на оба ящика вместе, как если бы они были одним целым. Ниже мы можем увидеть, как выглядит диаграмма свободного тела, когда вы группируете два ящика:

Рис. 7 — Диаграмма свободного тела обоих ящиков вместе.

Если мы запишем уравнение второго закона Ньютона для направления \(x\), мы получим

$$-(F_{\text{f}1} + F_{\text{f}2})+T_2 = (m_1 +m_2 )a$$

и может переставить его, чтобы найти \(T_2 \),

$$T_2 = (m_1 + m_2 )a + F_{\text{f}1} + F_{\text {f}2}\mathrm{.}$$

Мы видим, что это дает тот же результат, что и при рассмотрении квадратов по отдельности, а затем составлении уравнений вместе. Любой метод работает для поиска \(T_2 \) (вы можете решить, какой из них проще, и использовать любой из них), но иногда переменную, которую вам нужно найти, можно найти, только сосредоточившись на одном конкретном объекте.

Тяга под углом

Теперь давайте сделаем пример со всеми любимыми: углы.

Рис. 8 — Натяжение каната под углом.

На рисунке выше веревка тянется за ящик под углом, а не вдоль горизонтальной поверхности. В результате коробка скользит по поверхности горизонтально. Чтобы найти напряжение, мы использовали бы суперпозиция сил для разделения угловой силы на часть силы, действующую в направлении \(x\), и часть силы, действующую в направлении \(y\).

Рис. 9 — Диаграмма свободного тела с разделением натяжения на компоненты \(x\) и \(y\).

Это показано красным на рисунке выше на диаграмме свободного тела. Тогда мы можем написать отдельное уравнение для направления \(x\) и направления \(y\) в соответствии с диаграммой свободного тела.

\(T_x = T\cos{\theta}\) и \(T_y = T\sin{\theta}\).

В этом примере теперь у нас есть некоторое напряжение, действующее в направлении \(y\), поэтому мы не хотим игнорировать гравитационную и нормальную силы, как мы делали в примерах выше. Поскольку ящик не ускоряется в направлении \(y\), сумма сил в направлении \(y\) равна нулю

$$F_\text{N} + T\sin{\theta } -F_g =0\mathrm{,}$$

и преобразование для нахождения \(T\) дает

$$T=\frac{F_g — F_\text{N} }{\sin{\theta}} \\\mathrm{.}$$

Направление \(x\) похоже на то, что мы сделали выше, но только с компонентом \(x\) угловой силы натяжения:

$$-F_\text{f} + T\cos{\theta} = ma\mathrm{.}$$

Затем перегруппируем, чтобы найти \(T\):

$$T=\frac {ma+F_\text{f}}{\cos{\theta}}\\\mathrm{. }$$

Оба этих результата дадут вам одно и то же значение для \(T\), поэтому в зависимости от того, что информации, которую вы получили, вы можете либо сосредоточиться только на \(x\)-направлении, либо только на \(y\)-направлении, либо на обоих.

Свободно висящий объект

Когда объект висит на веревке, как показано ниже,

Рис. 10. Объект, подвешенный на веревке

Единственными силами, действующими на него, являются гравитационная сила, тянущая его вниз, и натяжение, удерживающее его вверх.

Это показано на диаграмме свободного тела ниже.

Рис. 11. Диаграмма свободного тела объекта, подвешенного на веревке

Полученное уравнение будет выглядеть следующим образом: переставить, чтобы найти \(T\) и подставить \(mg\) для гравитационной силы, мы получим

$$T=ma +mg\mathrm{.}$$

Если бы объект не ускорялся, натяжение и гравитационная сила были бы равны и противоположны, поэтому \(T=mg\).

Натяжение за наклонную поверхность

Когда к ящику на наклонной поверхности прикладывается натяжение, мы используем ту же стратегию, что и при натяжении веревки под углом.

Рис. 12 – Натяжение объекта на наклонной поверхности

Сначала начните с диаграммы свободного тела.

Рис. 13 – Схема растяжения свободного тела на наклонной поверхности

Имея дело с наклонной поверхностью, помните, что нормальная сила всегда действует перпендикулярно поверхности, а гравитационная сила (вес) всегда действует прямо вниз.

Вместо того, чтобы разбивать силу натяжения на компоненты \(x\) и \(y\), мы хотим разбить гравитационную силу на компоненты. Если мы наклоним нашу систему координат, чтобы она соответствовала углу поверхности, как показано ниже, мы увидим, что натяжение действует в новом направлении \(x\), а нормальная сила действует в новом направлении \(y\)- направление. Гравитационная сила — единственная сила под углом, так что мы разделили бы ее на компоненты, следующие новым направлениям \(x\) и \(y\), показанным ниже красным.

Рис. 14 — Диаграмма свободного тела с новой системой координат и гравитационной силой, разделенной на компоненты \(x\) и \(y\)

Тогда мы применим второй закон Ньютона в каждом направлении, как и в любой другой задаче.

Подвешивание на двух веревках

Когда объект подвешен на нескольких веревках, натяжение неравномерно распределяется между веревками, если только они не находятся под одинаковыми углами.

Рис. 15. Объект, подвешенный на двух веревках

В этом примере мы подставим действительные числа, чтобы найти \(T_1 \) и \(T_2 \). 92}=0\mathrm{.}$$

Мы можем решить эти два уравнения и два неизвестных алгебраически любым удобным для нас способом. В этом примере мы решим первое уравнение для \(T_1 \) и заменим его вторым. Решение для \(T_1 \) дает

$$\begin{align*} \frac{1}{\sqrt{2}} T_1 &= \frac{1}{2} T_2 \\ T_1 &= \frac{ \sqrt{2}}{2} T_2 \mathrm{,} \\ \end{align*}$$

и подстановка этого во второе уравнение для нахождения \(T_2 \) дает

$$\begin{align *} \frac{\sqrt{2}}{2} T_2 \times \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} T_2 — 147,15\,\mathrm{ N} &= 0 \\ \frac{1+\sqrt{3}}{2} T_2 &= 147,15\,\mathrm{N} \\ T_2 &= 107,72\,\mathrm{N.} \\ \end {выравнивание*}$$

Затем подстановка \(T_2 \) обратно в первое уравнение для решения \(T_1 \) дает нам окончательный ответ

$$\begin{align*} T_1 &= 107,72\,\mathrm{N} \ раз \frac{\sqrt{2}}{2} \\ T_1 &= 76,17\,\mathrm{N. } \\ \end{align*}$$

Шкив, наклон и подвешенный объект

Пример На изображении ниже сочетается многое из того, что мы обсуждали в каждом из приведенных выше примеров.

Рис. 17. Наклон, шкив и подвешенный объект

На следующем рисунке показано, как будут выглядеть силы, воздействующие на каждый объект, с учетом того, что сила трения может действовать в противоположном направлении в зависимости от того, как движется система.

Рис. 18. Силы, показанные для сценария выше

Ниже приведены советы, которые мы узнали в каждой из вышеперечисленных задач, которые также применимы к этой:

• диаграмма тела и уравнения второго закона Ньютона.
• Веревка оказывает одинаковое натяжение на каждый объект.
• Мы можем наклонить нашу систему координат. У нас даже может быть своя система координат для каждого объекта, если мы будем анализировать силы, воздействующие на каждый объект в отдельности. В этом случае мы бы изолировали коробку 2 и наклонили систему координат, чтобы она соответствовала углу поверхности, но когда мы смотрим на коробку 1 отдельно, мы сохранили бы стандартную систему координат.
• Мы можем разделить силы на составляющую \(x\) и составляющую \(y\). В этом случае, как только мы наклоним систему координат ящика 2, мы разделим гравитационную силу ящика на составляющие.

Натяжение — основные выводы

• Натяжение — это сила, возникающая, когда веревка (или аналогичный предмет) натягивает объект.
• Натяжение вызвано межатомными электрическими силами, пытающимися удержать атомы веревки вместе.
• Не существует уравнения для силы натяжения.
• Используйте диаграммы свободного тела и второй закон Ньютона для определения натяжения.

4.5 Нормальные, растягивающие и другие примеры сил — College Physics 2e

Цели обучения

К концу этого раздела вы сможете:

• Определение нормальной силы и силы растяжения.
• Применяйте законы движения Ньютона для решения задач, связанных с различными силами.
• Используйте тригонометрические тождества для разложения веса на компоненты.

Силы имеют множество названий, например, толкание, тяга, тяга, подъемная сила, вес, трение и напряжение. Традиционно силы были сгруппированы в несколько категорий и получили имена, относящиеся к их источнику, способу их передачи или их воздействию. В этом разделе обсуждаются наиболее важные из этих категорий вместе с некоторыми интересными приложениями. Дальнейшие примеры сил обсуждаются далее в этом тексте.

Нормальная сила

Вес (также называемый силой тяжести) — это всепроникающая сила, действующая постоянно, и ей необходимо противодействовать, чтобы объект не упал. Вы определенно заметили, что должны поддерживать вес тяжелого объекта, отталкиваясь от него, когда держите его неподвижно, как показано на рис. 4.11 (а). Но как неодушевленные предметы, такие как стол, выдерживают вес размещенного на них груза, как показано на рис. 4.11(b)? Когда пакет с собачьим кормом кладут на стол, стол немного прогибается под нагрузкой. Это было бы заметно, если бы груз был помещен на карточный стол, но даже твердые предметы деформируются при приложении к ним силы.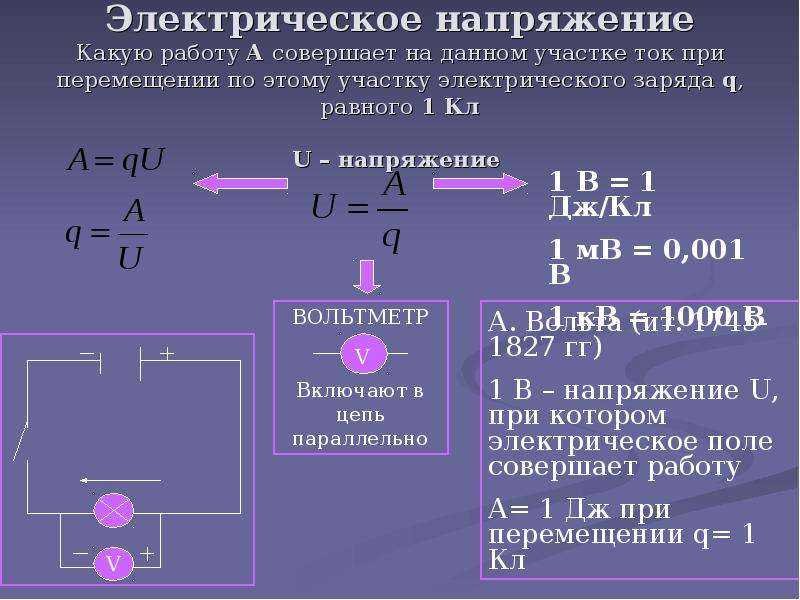 Если объект не деформируется сверх своих пределов, он будет оказывать восстанавливающую силу подобно деформированной пружине (или батуту, или трамплину). Чем больше деформация, тем больше восстанавливающая сила. Таким образом, когда груз помещается на стол, стол прогибается до тех пор, пока возвращающая сила не станет такой же, как вес груза. В этот момент чистая внешняя сила, действующая на груз, равна нулю. Это ситуация, когда груз неподвижен на столе. Стол проседает быстро, причем провис небольшой, поэтому мы его не замечаем. Но это похоже на провисание батута, когда на него забираешься.

Рисунок 4.11 (a) Человек, держащий пакет с кормом для собак, должен приложить направленную вверх силу FhandFhand, равную по величине и противоположную по направлению весу корма ww. (b) Карточный стол прогибается, когда на него кладут корм для собак, как жесткий батут. Упругие восстанавливающие силы в столе возрастают по мере его провисания, пока не создадут силу NN, равную по модулю и противоположную по направлению весу груза.

Мы должны заключить, что все, что поддерживает груз, одушевленное оно или нет, должно создавать направленную вверх силу, равную весу груза, как мы предполагали в нескольких предыдущих примерах. Если сила, поддерживающая груз, перпендикулярна поверхности контакта между грузом и его опорой, эта сила определяется как нормальная сила и здесь дается символ NN. (Это не единица силы Н.) Слово нормальное означает перпендикулярно поверхности. Нормальная сила может быть меньше веса объекта, если объект находится под наклоном, как вы увидите в следующем примере.

Распространенное заблуждение: нормальная сила (Н) против силы Ньютона (Н)

В этом разделе мы ввели величину нормальной силы, которая представлена ​​переменной NN. Его не следует путать с символом ньютона, который также обозначается буквой N. Эти символы особенно важно различать, поскольку единицами измерения нормальной силы (NN) являются ньютоны (Н). Например, нормальная сила NN, с которой пол действует на стул, может быть N=100 NN=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица измерения. Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях! По мере изучения физики вы обнаружите больше сходства между переменными и единицами. Другим примером этого является количество работы (WW) и единица мощности (Вт).

Пример 4,5

Вес на склоне, двумерная задача

Рассмотрим лыжника на склоне, показанном на рис. 4.12. Ее масса с оборудованием составляет 60,0 кг. а) Чему равно ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если известно, что трение равно 45,0 Н?

Рисунок 4.12 Поскольку движение и трение параллельны склону, удобнее всего спроецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). NN перпендикулярен склону и f параллелен склону, но ww имеет компоненты вдоль обеих осей, а именно w⊥w⊥ и w∥ w∥ . НН равно по модулю w⊥w⊥, так что нет движения перпендикулярно склону, но ff меньше, чем w∥ w∥ , так что есть ускорение вниз по склону (вдоль параллельной оси).

Стратегия

Это двумерная задача, поскольку силы, действующие на лыжника (система интересов), не параллельны. Подход, который мы использовали в двумерной кинематике, также очень хорошо работает здесь. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав два связаны один -мерные проблемы для решения. Наиболее удобной системой координат для движения по склону является та, которая имеет одну координату, параллельную склону, и одну, перпендикулярную склону. (Помните, что движения вдоль взаимно перпендикулярных осей независимы.) Мы используем символы ⊥⊥ и ∥ ∥ для обозначения перпендикулярности и параллельности соответственно. Такой выбор осей упрощает задачу такого типа, поскольку движение перпендикулярно склону отсутствует, а трение между двумя объектами всегда параллельно поверхности. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и опора склона, соответственно обозначенные ww, ff и NN на рис. 4.12. NN всегда перпендикулярно склону, а ff параллельно ему. Но ww не направлена ​​ни к одной из осей, поэтому первый шаг, который мы предпримем, — это спроецировать его на компоненты вдоль выбранных осей, определив w∥ w∥ как компонент веса, параллельный наклону, и w⊥w⊥ составляющая веса перпендикулярна склону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.

Решение

Величина составляющей веса, параллельной наклону, равна w∥ =wsin(25º)=mgsin(25º)w∥ =wsin(25º)=mgsin(25º), а величина составляющей веса, перпендикулярной к наклону w⊥=wcos(25°)=mgcos(25°)w⊥=wcos(25°)=mgcos(25°).

(a) Без учета трения. Поскольку ускорение параллельно наклону, нам нужно рассматривать только силы, параллельные наклону. (Силы, перпендикулярные склону, складываются в ноль, так как ускорение в этом направлении отсутствует.) Силы, параллельные склону, представляют собой массу веса лыжника, параллельного склону, w∥ w∥ и силы трения ff. Используя второй закон Ньютона с нижними индексами для обозначения величин, параллельных наклону,

a∥ =Fnet ∥ ma∥ =Fnet ∥ m

4,30

где Fnet ∥ =w∥ =mgsin(25°)Fnet ∥ =w∥ =mgsin(25°), в предположении отсутствия трения в этой части, так что

a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)a∥ =Fnet ∥ m=mgsin(25°)m=gsin(25°)

4,31

(9,80 м/с2)(0,4226)= 4,14 м/с2(9,80 м/с2)(0,4226)=4,14 м/с2

4,32

— ускорение.

(b) Включая трение. Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно противодействует движению между соприкасающимися поверхностями. Таким образом, чистая внешняя сила теперь равна 9. 0005

Fnet ∥ =w∥ −f,Fnet ∥ =w∥ −f,

4,33

и подставив это во второй закон Ньютона, a∥ =Fnet ∥ ma∥ =Fnet ∥ m, получим

a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.a∥ =Fnet ∣∣m=w∥ −fm=mgsin(25°)−fm.

4,34

Подставляем известные значения, чтобы получить

0,4226)−45,0 N60,0 кг,

4,35

что дает

a∥ =3,39 м/с2, a∥ =3,39 м/с2,

4.36

ускорение, параллельное наклону, когда встречное трение составляет 45,0 Н.

Обсуждение

Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии. На самом деле общий результат состоит в том, что если трением на склоне можно пренебречь, то ускорение вниз по склону равно a=gsinθa=gsinθ, независимо от массы . Это связано с ранее обсуждавшимся фактом, что все тела падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).

Разложение веса на компоненты

Рисунок 4.13 Объект лежит на склоне, который составляет угол θ с горизонтом.

Когда объект покоится на наклонной плоскости, составляющей угол θθ с горизонтом, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, w⊥w⊥ , и сила, действующая параллельно плоскости, ш∥ ш∥ . Перпендикулярная сила веса, ж⊥ш⊥ , обычно равна по величине и противоположна по направлению нормальной силе, НН. Сила, действующая параллельно плоскости, w∥ w∥ , заставляет объект ускоряться вниз по склону. Сила трения, ff, противодействует движению объекта, поэтому действует вверх по плоскости.

Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона составляет угол θθ к горизонту, то величины компонентов веса равны

w∥ =wsin(θ)=mgsin(θ)w∥ =wsin(θ)=mgsin(θ)

4,37

и

w⊥=wcos(θ)=mgcos(θ).w⊥= wcos(θ)=mgcos(θ).

4.38

Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона θθ совпадает с углом, образованным между ww и w⊥w⊥ . Зная это свойство, можно с помощью тригонометрии определить величину составляющих веса:

cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)

4,39

sin(θ)= w∥ ww∥ =wsin(θ)=mgsin(θ)sin(θ)=w∥ ww∥ =wsin(θ)=mgsin(θ)

4,40

Захватывающий эксперимент: Force Parallel

Чтобы исследовать, как изменяется сила, параллельная наклонной плоскости, возьмите резиновую ленту, несколько предметов, которые можно повесить на конец резинки, и доску, которую можно расположить под разными углами. На сколько растянется резинка, если повесить предмет на конец доски? Теперь поместите доску под углом, чтобы объект соскальзывал при размещении на доске. На сколько растянется резинка, если ее выстроить параллельно доске и использовать для неподвижного удержания предмета на доске? Попробуйте еще два угла. Что это показывает?

Напряжение

Натяжение — это сила по длине среды, особенно сила, передаваемая гибкой средой, например веревкой или кабелем. Слово «натяжение » происходит от латинского слова, означающего «растягивать». Не случайно гибкие тяжи, передающие мышечные силы к другим частям тела, называются сухожилиями . Любой гибкий соединитель, такой как струна, веревка, цепь, проволока или кабель, может натягивать только параллельно своей длине; таким образом, сила, переносимая гибким соединителем, представляет собой натяжение с направлением, параллельным соединителю. Важно понимать, что натяжение — это натяжение соединителя. В отличие от этого, рассмотрим фразу: «Вы не можете толкнуть веревку». Сила натяжения тянет наружу вдоль двух концов веревки.

Рассмотрим человека, держащего груз на веревке, как показано на рис. 4.14.

Рисунок 4.14 Когда совершенно гибкий соединитель (не требующий усилия для его изгиба), такой как эта веревка, передает силу TT, эта сила должна быть параллельна длине веревки, как показано на рисунке. Натяжение такого гибкого соединителя представляет собой натяжение. Обратите внимание, что веревка тянет с одинаковой силой, но в противоположных направлениях, на руку и поддерживаемую массу (без учета веса веревки). Это пример третьего закона Ньютона. Веревка — это среда, которая переносит равные и противоположные силы между двумя объектами. Натяжение в любом месте веревки между рукой и грузом одинаково. Как только вы определили натяжение в одном месте, вы определили натяжение во всех точках веревки.

Натяжение веревки должно равняться весу поддерживаемой массы, что можно доказать с помощью второго закона Ньютона. Если масса 5,00 кг на рисунке неподвижна, то ее ускорение равно нулю, и, следовательно, Fnet=0Fnet=0. Единственными внешними силами, действующими на массу, являются ее вес ww и натяжение TT, создаваемое веревкой. Таким образом,

Fnet=T−w=0,Fnet=T−w=0,

4,41

, где TT и ww — величины натяжения и веса, а их знаки указывают направление, причем up здесь положителен. Таким образом, как и следовало ожидать, натяжение равно весу поддерживаемой массы:

T=w=мг.T=w=мг.

4,42

Для массы 5,00 кг тогда (без учета массы веревки) получаем, что

T=mg=(5,00 кг)(9,80 м/с2)=49,0 N.T=mg=(5,00 кг)(9,80 м/с2)=49,0 Н.

4,43

Если разрезать веревку и вставить пружину, пружина растягивается на длину, соответствующую силе 49,0 Н, обеспечивая прямое наблюдение и измерение силы натяжения веревки.

Гибкие соединители часто используются для передачи усилий на поворотах, например, в системе вытяжения в больницах, пальцевом шарнире или тормозном тросе велосипеда. Если трения нет, то напряжение передается без уменьшения. Меняется только его направление, и он всегда параллелен гибкому соединителю. Это показано на рис. 4.15 (а) и (б).

Рисунок 4.15 (а) Сухожилия в пальце передают силу TT от мышц к другим частям пальца, обычно изменяя направление силы, но не ее величину (сухожилия относительно свободны от трения). (b) Тормозной трос велосипеда передает натяжение TT от руля к тормозному механизму. Опять же, меняется направление, но не величина TT.

Пример 4.6

Что такое натяжение каната?

Рассчитайте натяжение троса, поддерживающего канатоходца массой 70,0 кг, показанного на рис. 4.16.

Рисунок 4.16 Вес канатоходца заставляет проволоку прогибаться на 5,0 градусов. Система, представляющая интерес, представляет собой точку на проволоке, в которой стоит канатоходец.

Стратегия

Как видно на рисунке, провод не идеально горизонтален (не может быть!), а прогибается под весом человека. Таким образом, напряжение с обеих сторон человека имеет направленный вверх компонент, способный выдержать его вес. Как обычно, силы представляют собой векторы, представленные графически стрелками, имеющими те же направления, что и силы, и длины, пропорциональные их величине. Система представляет собой канатоходца, и единственными внешними силами, действующими на него, являются его вес ww и два напряжения TLTL (слева натяжение) и TRTR (правое натяжение), как показано на рисунке. Весом самого провода разумно пренебречь. Суммарная внешняя сила равна нулю, так как система неподвижна. Теперь можно использовать небольшую тригонометрию, чтобы найти напряжения. Вначале возможен один вывод — из части (б) рисунка видно, что величины натяжений TLTL и TRTR должны быть равны. Это связано с тем, что веревка не имеет горизонтального ускорения, и единственными силами, действующими влево и вправо, являются TLTL и TRTR. Таким образом, величина этих сил должна быть равна, чтобы они уравновешивали друг друга.

Всякий раз, когда у нас есть двумерные векторные задачи, в которых нет двух параллельных векторов, самый простой способ решения — выбрать удобную систему координат и спроецировать векторы на ее оси. В этом случае наилучшая система координат имеет одну ось горизонтальную, а другую вертикальную. Мы называем горизонтальную ось xx, а вертикальную ось yy.

Решение

Во-первых, нам нужно разложить векторы натяжения на их горизонтальную и вертикальную составляющие. Это помогает нарисовать новую диаграмму свободного тела, показывающую все горизонтальные и вертикальные компоненты каждой силы, действующей на систему.

Рисунок 4.17 Когда векторы проецируются на вертикальную и горизонтальную оси, их компоненты вдоль этих осей должны в сумме равняться нулю, поскольку канатоходец неподвижен. Малый угол приводит к тому, что TT намного больше, чем ww.

Рассмотрим горизонтальные составляющие сил (обозначенные нижним индексом xx):

Fnet x=TLx-TRx.Fnet x=TLx-TRx.

4.44

Суммарная внешняя горизонтальная сила Fnet x=0Fnet x=0, поскольку человек неподвижен. Таким образом,

Fnet x=0=TLx-TRxTLx=TRx.Fnet x=0=TLx-TRxTLx=TRx.

4,45

Теперь обратите внимание на рисунок 4.17. Вы можете использовать тригонометрию, чтобы определить величину TLTL и TRTR. Обратите внимание, что:

cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°)=TRxTRTRx=TRcos(5,0°).cos(5,0°)=TLxTLTLx=TLcos(5,0°)cos(5,0°) =TRxTRTRx=TRcos(5,0º).

4,46

Приравнивание TLxTLx и TRxTRx:

TLcos(5,0°)=TRcos(5,0°).TLcos(5,0°)=TRcos(5,0°).

4,47

Таким образом,

TL=TR=T,TL=TR=T,

4,48

, как и предполагалось. Теперь, рассматривая вертикальные компоненты (обозначаемые индексом yy), мы можем найти TT. Опять же, поскольку человек неподвижен, второй закон Ньютона подразумевает, что net Fy=0Fy=0. Таким образом, как показано на диаграмме свободного тела на рис. 4.17,

Fnet y=TLy+TRy-w=0.Fnet y=TLy+TRy-w=0.

4,49

Наблюдая за рисунком 4.17, мы можем использовать тригонометрию для определения соотношения между ТЛиТЛы, ПОПРОБУЙ, и ТТ. Как мы определили из анализа в горизонтальном направлении, TL=TR=TTL=TR=T:

sin(5.0º)=TLyTLTLy=TLsin(5.0º)=Tsin(5.0º)sin(5.0º)=TRyTRTRy=TRsin(5.0º)=Tsin(5.0º).sin(5.0º)=TLyTLTLy=TLsin (5,0°)=Tsin(5,0°)sin(5,0°)=TRyTRTRy=TRsin(5,0°)=Tsin(5,0°).

4,50

Теперь мы можем подставить значения TlyTLy и TRyTRy в уравнение результирующей силы в вертикальном направлении: º)−w=02Tsin(5,0°)−w=02Tsin(5,0°)=wFnet y=TLy+TRy−w=0Fnet y=Tsin(5,0°)+Tsin(5,0°)−w=02Tsin(5,0°) −w=02Tsin(5,0º)=w

4,51

и

T=w2sin(5,0°)=mg2sin(5,0°),T=w2sin(5,0°)=mg2sin(5,0°),

4,52

, так что

T=(70,0 кг м/с2)2(0,0872),T=(70,0 кг)(9,80 м/с2)2(0,0872),

4,53

и натяжение

T=3900 N. T=3900 Н.

4,54 5 Обсуждение

Обратите внимание, что вертикальное натяжение проволоки действует как нормальная сила, поддерживающая вес канатоходца. Натяжение почти в шесть раз превышает вес 686-Н канатоходца. Поскольку проволока почти горизонтальна, вертикальная составляющая ее натяжения составляет лишь малую часть натяжения проволоки. Большие горизонтальные компоненты направлены в противоположные стороны и компенсируются, поэтому большая часть натяжения проволоки не используется для поддержки веса канатоходца.

Если мы хотим создать очень большое натяжение, все, что нам нужно сделать, это приложить усилие, перпендикулярное гибкому соединителю, как показано на рис. 4.18. Как мы видели в последнем примере, вес канатоходца действовал как сила, перпендикулярная веревке. Мы видели, что натяжение каната связано с весом канатоходца следующим образом:

T=w2sin(θ). T=w2sin(θ).

4,55

Мы можем расширить это выражение для описания натяжения TT, создаваемого перпендикулярной силой (F⊥F⊥) к середине гибкого соединителя:

Т=F⊥2sin(θ).T=F⊥2sin(θ).

4,56

Обратите внимание, что θθ — это угол между горизонталью и изогнутым соединителем. В этом случае TT становится очень большим, когда θθ приближается к нулю. Даже относительно небольшой вес любого гибкого соединителя вызовет его провисание, поскольку в горизонтальном положении возникло бы бесконечное натяжение (т. θ=0θ=0 и sinθ=0sinθ=0). (См. рис. 4.18.)

Рисунок 4.18 Мы можем создать очень большое натяжение цепи, надавив на нее перпендикулярно ее длине, как показано на рисунке. Предположим, мы хотим вытащить машину из грязи, когда эвакуатора нет. Каждый раз, когда автомобиль движется вперед, цепь натягивается, чтобы он оставался как можно более прямым. Натяжение цепи определяется как T=F⊥2sin(θ)T=F⊥2sin(θ) ; поскольку θθ мало, TT очень велико. Эта ситуация аналогична канатоходцу, показанному на рис. 4.16, за исключением того, что показанные здесь напряжения передаются на автомобиль и дерево, а не действуют в точке приложения F⊥F⊥.

Рисунок 4.19 Если не будет приложено бесконечное натяжение, любой гибкий соединитель, такой как цепь в нижней части рисунка, будет прогибаться под собственным весом, образуя характерную кривую, когда вес равномерно распределен по длине. Висячие мосты, такие как мост Золотые Ворота, показанный на этом изображении, по существу представляют собой очень тяжелые гибкие соединители. Вес моста равномерно распределяется по длине гибких соединителей, обычно тросов, которые принимают характерную форму. (кредит: Листовка, Викисклад)

Расширенная тема: Реальные силы и инерциальные системы отсчета

Существует еще одно различие между силами в дополнение к уже упомянутым типам. Одни силы реальны, другие нет. Реальные силы — это силы, имеющие физическое происхождение, например гравитационное притяжение. Напротив, фиктивные силы возникают просто потому, что наблюдатель находится в ускоряющейся системе отсчета, такой как та, которая вращается (как карусель) или подвергается линейному ускорению (например, автомобиль замедляется). Например, если спутник движется строго на север над северным полушарием Земли, то наблюдателю на Земле будет казаться, что он испытывает на западе силу, не имеющую физического происхождения. Конечно, здесь происходит то, что Земля вращается на восток и движется на восток под спутником. В системе Земли это выглядит как западная сила, действующая на спутник, или это можно интерпретировать как нарушение первого закона Ньютона (закона инерции). Инерциальная система отсчета — это система, в которой все силы реальны, и, что то же самое, система, в которой законы Ньютона имеют простую форму, приведенную в этой главе.

Вращение Земли настолько медленное, что Земля представляет собой почти инерциальную систему отсчета. Обычно вы должны проводить точные эксперименты, чтобы наблюдать фиктивные силы и небольшие отклонения от законов Ньютона, такие как только что описанный эффект. В больших масштабах, таких как вращение погодных систем и океанских течений, эффекты можно легко наблюдать.

Решающим фактором при определении того, является ли система отсчета инерциальной, является ее ускорение или вращение относительно известной инерциальной системы отсчета. Если не указано иное, все явления, обсуждаемые в этом тексте, рассматриваются в инерциальных системах отсчета.

Все силы, обсуждаемые в этом разделе, являются реальными силами, но есть ряд других реальных сил, таких как подъемная сила и тяга, которые в этом разделе не рассматриваются. Они более специализированы, и нет необходимости обсуждать каждый тип силы. Однако естественно задаться вопросом, где в длинном списке сил находится основная простота, которую мы стремимся найти в физике.