Что такое конденсатор с параллельными пластинами. Как рассчитать емкость конденсатора. От чего зависит емкость конденсатора с параллельными пластинами. Где применяются такие конденсаторы.
Что представляет собой конденсатор с параллельными пластинами
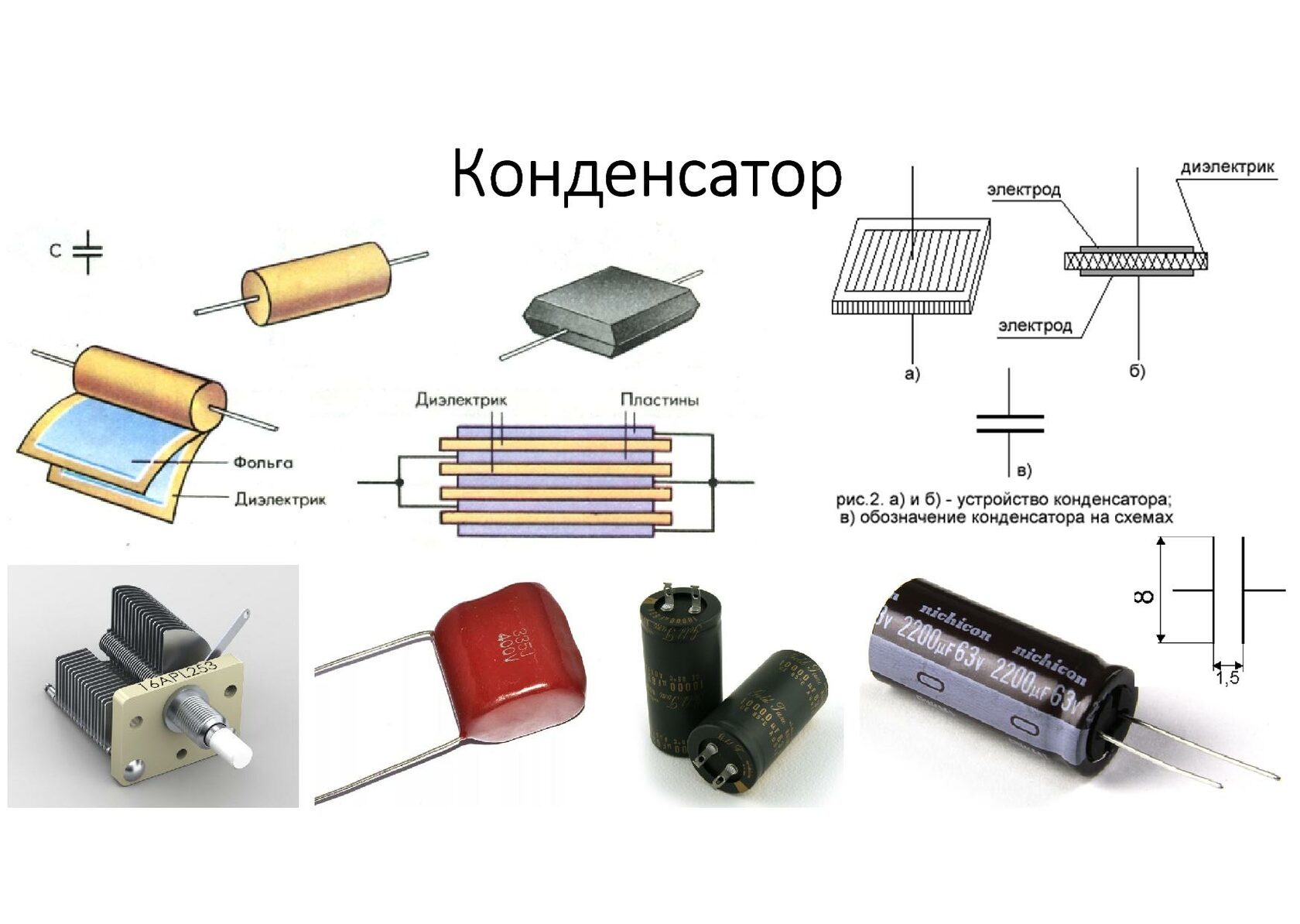
Конденсатор с параллельными пластинами — это простейший тип конденсатора, состоящий из двух плоских параллельных проводящих пластин, разделенных диэлектриком. Это базовая модель для понимания принципа работы конденсаторов.
Основные элементы конструкции:
- Две параллельные металлические пластины (обкладки)
- Диэлектрик между пластинами
- Выводы для подключения к электрической цепи
При подаче напряжения на обкладки конденсатора, на них накапливаются электрические заряды противоположных знаков. Между пластинами возникает электрическое поле, в котором накапливается энергия.
Принцип работы конденсатора с параллельными пластинами
Принцип действия конденсатора с параллельными пластинами основан на явлении электростатической индукции. Когда на обкладки подается напряжение:
- На одной пластине накапливается положительный заряд
- На другой пластине — отрицательный заряд той же величины
- Между пластинами возникает электрическое поле
- В электрическом поле накапливается энергия
Ключевые особенности:
- Заряды на обкладках равны по величине и противоположны по знаку
- Электрическое поле сосредоточено в основном между пластинами
- Диэлектрик усиливает накопление заряда и энергии
Формулы для расчета емкости плоского конденсатора
Емкость конденсатора с параллельными пластинами рассчитывается по формуле:
C = εε0S / d
где:
- C — емкость конденсатора (Ф)
- ε — диэлектрическая проницаемость среды между обкладками
- ε0 — электрическая постоянная (8.85 * 10^-12 Ф/м)
- S — площадь пластин (м^2)
- d — расстояние между пластинами (м)
Данная формула показывает, от каких параметров зависит емкость плоского конденсатора.
От чего зависит емкость конденсатора с параллельными пластинами
Емкость конденсатора с параллельными пластинами определяется следующими факторами:
- Площадь пластин — чем больше площадь, тем выше емкость
- Расстояние между пластинами — чем меньше расстояние, тем выше емкость
- Диэлектрическая проницаемость среды между пластинами — чем выше ε, тем больше емкость
Для увеличения емкости при заданных размерах конденсатора можно:
- Уменьшить толщину диэлектрика
- Использовать диэлектрик с более высокой диэлектрической проницаемостью
- Увеличить площадь пластин
Преимущества и недостатки конденсаторов с параллельными пластинами
Преимущества:
- Простая конструкция
- Низкая стоимость
- Высокая надежность
- Малые потери на высоких частотах
Недостатки:
- Относительно небольшая емкость
- Большие габариты при высоких значениях емкости
- Чувствительность к механическим воздействиям
Где применяются конденсаторы с параллельными пластинами
Основные области применения конденсаторов с параллельными пластинами:
- Высокочастотные и СВЧ-устройства
- Измерительная техника
- Фильтры и резонансные контуры
- Накопители энергии
- Системы зажигания двигателей
Конденсаторы с параллельными пластинами используются там, где требуется точная и стабильная емкость при работе на высоких частотах.
Расчет энергии, запасенной в конденсаторе
Энергия, накопленная в заряженном конденсаторе, рассчитывается по формуле:
W = CU^2 / 2
где:
- W — энергия конденсатора (Дж)
- C — емкость конденсатора (Ф)
- U — напряжение на обкладках (В)
Эта формула показывает квадратичную зависимость энергии от напряжения на конденсаторе. При увеличении напряжения в 2 раза энергия возрастает в 4 раза.
Последовательное и параллельное соединение конденсаторов
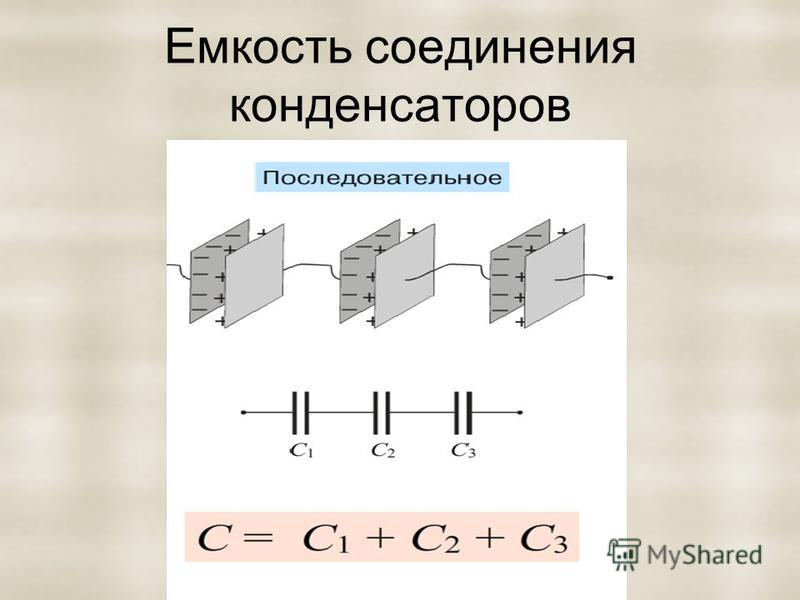
При последовательном соединении конденсаторов:
- Общая емкость уменьшается
- Напряжение распределяется между конденсаторами
- Заряд на всех конденсаторах одинаковый
Формула для расчета общей емкости при последовательном соединении:
1/C = 1/C1 + 1/C2 + 1/C3 + …
При параллельном соединении конденсаторов:
- Общая емкость увеличивается
- Напряжение на всех конденсаторах одинаковое
- Заряды конденсаторов складываются
Формула для расчета общей емкости при параллельном соединении:
C = C1 + C2 + C3 + …
Как измерить емкость конденсатора
Существует несколько способов измерения емкости конденсатора:
- С помощью мультиметра с функцией измерения емкости
- Методом заряда-разряда через известное сопротивление
- Резонансным методом в колебательном контуре
- Мостовым методом сравнения с эталонной емкостью
Наиболее простой и доступный способ — измерение цифровым мультиметром с функцией измерения емкости. Точность измерения зависит от класса прибора.
Выводы
Конденсатор с параллельными пластинами — это базовая модель для понимания принципов работы конденсаторов. Основные характеристики:
- Простая конструкция из двух параллельных пластин
- Емкость зависит от площади пластин, расстояния между ними и диэлектрика
- Широко применяются в высокочастотной технике
- Позволяют накапливать и хранить электрическую энергию
Понимание принципов работы конденсатора с параллельными пластинами дает основу для изучения более сложных типов конденсаторов.
Обкладка — конденсатор — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Обкладка конденсатора имеет некоторую толщину и закругленный край. [1]
| Кривая к расчету сопротивления проводника с учетом поверхностного эффекта.| Схема к расчету мощности, теряемой в обкладках. [2] |
Обкладки конденсаторов обычно имеют небольшую толщину, и в них явление поверхностного эффекта может сказываться только при весьма высоких частотах, порядка 100 Мгц. [3]
| Кривая к расчету сопротивления проводника с учетом поверхностного эффекта.| Схема К расчету мощности, теряемой в обкладках. [4] |
Обкладки конденсаторов обычно имеют небольшую толщину и в них явление поверхностного эффекта может сказываться только при весьма высоких частотах, порядка 100 Мгц и выше.
Обкладки конденсатора с неизвестной емкостью Сп заряженного до напряжения 6 80 В, соединяют с обкладками конденсатора емкостью С2 60 мкФ, заряженного до ( / 216 В. Определить емкость Сх, если напряжение на конденсаторах после их соединения U 20 В, конденсаторы соединяются обкладками, имеющими: а) одноименные заряды; б) разноименные заряды. [6]
Обкладки конденсатора емкостью С, заряженного до разности потенциалов U, соединяются с обкладками такого же, но не заряженного конденсатора. [7]
Обкладки конденсатора, заряженные разноименно, притягиваются друг к другу. Механические силы, действующие на макроскопические заряженные тела, называются пондеромоторными силами. [8]
Обкладки конденсатора обычно изготавливают из алюминия, латуни или меди. Емкость конденсатора зависит от плошали его пластин, расстояния между ними и от примененного диэлектрика. [9]
Обкладки конденсаторов выполняются из алюминиевой фольги толщиной 0 01 мм, а прослойками служит высокосортная конденсаторная бумага толщиной 0 007 — 0 012 мм, пропитанная жидким диэлектриком.
Ширина бумаги берется на 10 — 15 мм больше ширины фольги. Число слоев конденсаторной бумаги между обкладками зависит от величины напряжения, на которое рассчитана секция.
[10]
| Габаритные чертежи бумажных конденсаторов. [11] |
Обкладки конденсатора и его выводы обладают, как и всякий проводник, индуктивностью. Эта ненужная, но неизбежная собственная индуктивность конденсатора зависит от размера его обкладок и способа их соединения. [12]
Обкладки конденсатора введены в плечо прецизионного моста емкости. [13]
Обкладки конденсаторов изготовляются из алюминиевой фольги толщиной около 0 01 мм, а изолирующие прослойки — из тончайшей ( от 0 007 до 0 012 мм) высокосортной конденсаторной бумаги, которая пропитывается жидким диэлектриком: в масляных конденсаторах — маслом, а в соволовых конденсаторах — специальной синтетической жидкостью соволом.
Весьма малая толщина и высокосортность конденсаторной бумаги обусловливают относительно высокую ее стоимость, от которой зависят технико-экономические показатели конденсаторов, выполненных на различные рабочие напряжения.
[14]
Обкладки конденсатора, описанного в предыдущей задаче, сначала были присоединены к источнику напряжения L / 0, потом источник напряжения был отсоединен, затем появился объемный заряд. [15]
Страницы: 1 2 3 4 5
Обкладки конденсатора это
Конденсатор — это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку. Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:. По определению емкость положительна.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Конденсаторы, свойства конденсатора, обозначение конденсаторов на схемах, основные параметры
Конденсатор с двумя обкладками. Плоский конденсатор. - Электроемкость конденсатора. Конденсаторы. Энергия заряженного конденсатора.Применение
- Глава 20. Конденсаторы
- Тест по физике Конденсатор 8 класс
- обкладка конденсатора
- Формула заряда конденсатора, q
- Формулы конденсатора
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: ПАРАДОКС КОНДЕНСАТОРА 😂 Загадка N 1
youtube.com/embed/rmFS5JYcDYA» frameborder=»0″ allowfullscreen=»»/>Конденсаторы, свойства конденсатора, обозначение конденсаторов на схемах, основные параметры
Это зависит от геометрических параметров проводника. Коэффициент пропорциональности С называют электроемкостью — физическая величина, численно равная заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу. Единица измерения емкости в СИ — фарада. По этой формуле можно рассчитать емкость Земли. Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник — за счет явления электростатической индукции.
Конденсатор — это два проводника, называемые обкладками , расположенные близко друг к другу. Конструкция такова, что внешние, окружающие конденсатор тела, не оказывают влияние на его электроемкость.
Это будет выполняться, если электростатическое поле будет сосредоточено внутри конденсатора, между обкладками. Конденсаторы бывают плоские, цилиндрические и сферические. Так как электростатическое поле находится внутри конденсатора, то линии электрического смещения начинаются на положительной обкладке, заканчиваются на отрицательной, и никуда не исчезают.
Следовательно, заряды на обкладках противоположны по знаку, но одинаковы по величине. Емкость конденсатора равна отношению заряда к разности потенциалов между обкладками конденсатора:. Помимо емкости каждый конденсатор характеризуется U раб или U пр. Емкостные батареи — комбинации параллельных и последовательных соединений конденсаторов. В данном случае общим является напряжение U :. Сравните с параллельным соединением сопротивлений R :. Таким образом, при параллельном соединении конденсаторов суммарная емкость.
Общая емкость больше самой большой емкости, входящей в батарею. Сравните с последовательным соединением R :.
Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину — получили конденсатор за счет электростатической индукции, потенциал увеличился.
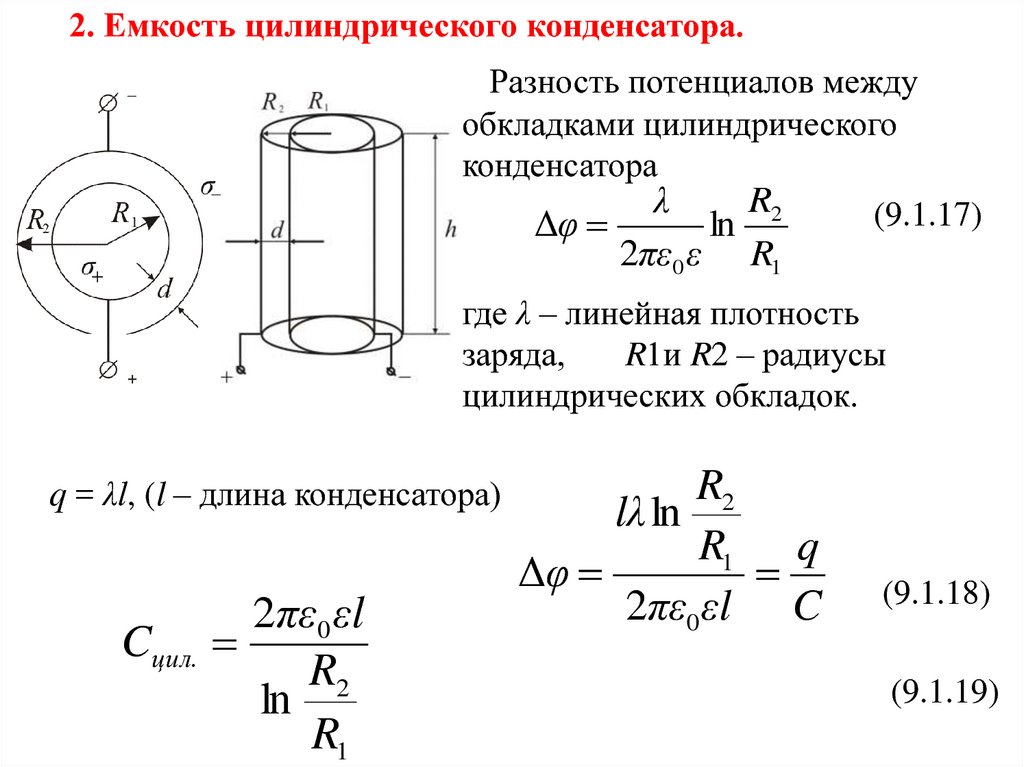
Разность потенциалов между обкладками цилиндрического конденсатора, изображенного на рисунке 5. Это емкость шарового конденсатора, где R 1 и R 2 — радиусы шаров. Таким образом, емкость шарового конденсатора с достаточной степенью точности можно рассчитать так же, как и емкость плоского, и цилиндрического конденсаторов.
Конденсатор с двумя обкладками. Плоский конденсатор.
Обкладки конденсатора с неизвестной емкостью Сь заряженного до напряжения U 80 В, соединяют с обкладками конденсатора емкостью С2 60 мкФ, заряженного до L72 16 В, Определить емкость Сь если напряжение на конденсаторах после их соединения 17 20 В, конденсаторы соединяются обкладками, имеющими: а одноименные заряды; б разноименные заряды.
Обкладки конденсатора емкостью С, заряженного до разности потенциалов 17, соединяются с обкладками такого же, но не заряженного конденсатора. Какое максимальное количество теплоты может выделиться в проводниках, соединяющих конденсаторы. Зависит ли полное количество выделившейся энергии от сопротивления проводников. Обкладки конденсаторов изготовляются из алюминиевой фольги толщиной около 0 01 мм, а изолирующие прослойки — из тончайшей от 0 до 0 мм высокосортной конденсаторной бумаги, которая пропитывается жидким диэлектриком: в масляных конденсаторах — маслом, а в соволовых конденсаторах — специальной синтетической жидкостью соволом. Весьма малая толщина и высокосортность конденсаторной бумаги обусловливают относительно высокую ее стоимость, от которой зависят технико-экономические показатели конденсаторов, выполненных на различные рабочие напряжения.
Это зависит от геометрических параметров проводника. Конденсатор – это два проводника, называемые обкладками, расположенные близко друг к .
Электроемкость конденсатора. Конденсаторы. Энергия заряженного конденсатора.Применение
Уединенные проводники обладают небольшой ёмкостью. Во многих электрических схемах требуются устройства, способные накапливать или выделять большие количества зарядов, заметно не изменяя потенциал. Электроёмкость проводника можно очень сильно увеличить, если приблизить к нему другой проводник. Это объясняется тем, что под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные заряды. Причем заряды, противоположные по знаку заряду проводника, располагаются ближе к проводнику и, следовательно, оказывают большее влияние на его потенциал. Влияние это сводится к уменьшению потенциала проводника по абсолютной величине, что приводит к увеличению его ёмкости. Это и положено в основу конструкции конденсаторов. Устройства, способные при небольшом относительно окружающих тел потенциале накапливать на себе большие заряды, называются конденсаторами. Конденсаторы делают в виде двух проводников, расположенных близко друг к другу.
Образующие конденсатор проводники называются обкладками конденсатора.
Глава 20. Конденсаторы
Огромное человеческое спасибо , но лучше если бы ещё сразу рассчитывал пробивное напряжение конденсатора было бы вообще шикарно. Хотя и так как в сказке. Автору спасибо! Самый удобный калькулятор из всех, что я пересмотрел!
Электроемкость конденсатора. Применение конденсаторов
Тест по физике Конденсатор 8 класс
Емкость определяется геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды. Она не зависит от материала, от агрегатного состояния, от полостей внутри проводника так как все избыточные заряды снаружи. Наличие вблизи проводника других тел изменяет его емкость, так как потенциал проводника зависит от расположения всех зарядов в пространстве. Как правило, конденсатор состоит из двух проводящих тел обкладок , разделенных диэлектриком. Причем его устройство обычно таково, что электрическое поле почти полностью сосредоточено между обкладками.
обкладка конденсатора
Электроемкость — не зависит от q и U ; — зависит от геометрических размеров проводника, их формы, взаимного расположения, электрических свойств среды между проводниками. Электрической емкостью проводника наз. Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:. Обозначение на электрических схемах: Все электрическое поле сосредоточено внутри конденсатора. Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора. Виды конденсаторов : 1.
Конденсатор — это физический прибор, главные детали которого. 1) две обкладки, укрепленные на основаниях 2) две проводящие.
Формула заряда конденсатора, q
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!
Формулы конденсатора
ВИДЕО ПО ТЕМЕ: Самодельные полипропиленовые конденсаторы
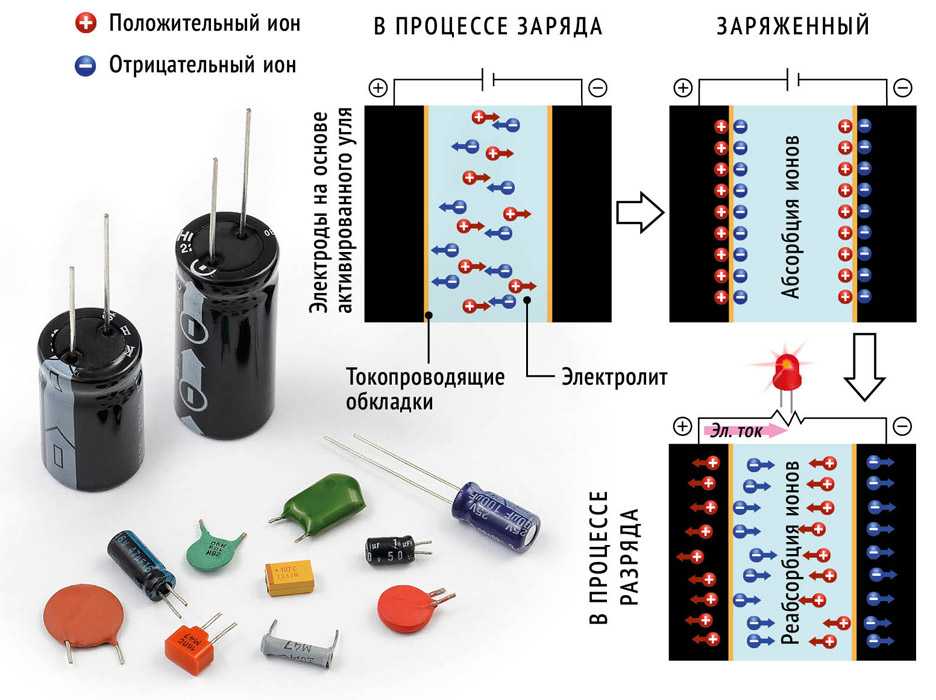
Конденсатор — фундаментальный электронный компонент наряду с резистором и катушкой индуктивности , предназначенный для накопления электрической энергии. Лучшей аналогией его работы будет сравнение с аккумуляторной батареей. Однако основой устройства последней являются обратимые химические реакции, а накопление заряда на обкладках конденсатора имеет исключительно электрическую природу. В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин называемых обкладками , разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними.
В этом случае можно ввести понятие электрической емкости.
Конденсатор является пассивным электронным компонентом.
Ёмкость конденсатора измеряется в фарадах. Первые конденсаторы, состоящие из двух проводников, разделенных непроводником диэлектриком , упоминаемые обычно как конденсатор Эпинуса или электрический лист, были созданы ещё раньше [3]. Конденсатор является пассивным электронным компонентом [4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин называемых обкладками , разделённых диэлектриком , толщина которого мала по сравнению с размерами обкладок см. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами из-за намотки.
Один из самых распространённых электронных элементов — конденсатор. Простейшая конструкция для изготовления и расчетов — плоский конденсатор. Это понятие относится к конструкции, состоящей из двух пластин, параллельных друг другу.
Динамический трек Конденсатор Цепи Wave Tank Оптическая скамья
| Емкость и разделение пластин Конденсатор с параллельными пластинами Конденсатор с плоскими пластинами — это прибор, используемый для изучения конденсаторов. Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно свернуты в спирали в небольших упаковках, поэтому конденсатор с плоскими пластинами значительно упрощает привязку функции к устройству. Конденсатор работает за счет накопления противоположных зарядов на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, которое может храниться в конденсаторе, измеряется его емкостью. Конденсатор емкостью один фарад (Ф) может хранить один кулон заряда на каждый вольт, приложенный к конденсатору. Формула для этого: С = кв/об Где C — емкость в фарадах, q — заряд в кулонах, а v — электрический потенциал в вольтах. Для конденсатора с плоскими пластинами емкость определяется по следующей формуле: С = ε 0A/d Где C — емкость в фарадах, ε 0 — константа диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах. Фарад — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6 Ф, или в пикофарадах (пФ), что составляет 1,0×10 -12 Ф. 1,0Ф = 1 000 000 мкФ = 1 000 000 000 000 пФ! Будьте очень осторожны с расчетами! Назначение: Целью этой лабораторной работы является исследование взаимосвязи между расстоянием между пластинами и емкостью конденсатора с параллельными пластинами. Оборудование:
Предостережения: Это хрупкое оборудование. Все должно сочетаться с самыми легкими прикосновениями. Ничего не форсировать! Процедура установки переменного конденсатора
Анализ данных: Сначала необходимо рассчитать теоретическую емкость для каждого интервала. Мы сделаем первое, а потом вы сможете сделать все остальное! Самое сложное в этом — правильно подобрать единицы измерения. Самый простой способ продолжить — перевести все в метры для расчетов:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Между пластинами существует электрическое поле, которое позволяет конденсатору накапливать энергию. Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними. Чем больше пластины и чем ближе они расположены друг к другу, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами.
Не ставьте конденсатор слишком близко к краю стола! 
Запишите каждое измерение в таблицу. Когда показание становится меньше 15 пФ, вы можете захотеть перейти на шкалу 200 пФ для большей точности.
Например, при настройке 5 мм, если ваше теоретическое значение равно 44,0 пФ, а экспериментальное значение равно 61,1 пФ, вы просто подставляете их в формулу: 
5.23: Конденсатор с тонкими параллельными пластинами
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24270
- Стивен В. Эллингсон
- Политехнический институт и государственный университет Вирджинии через Инициативу открытого образования Технических библиотек Вирджинии
Давайте теперь определим емкость конденсатора общего типа, известного как тонкий конденсатор с плоскими пластинами , показанный на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Тонкий конденсатор с плоскими пластинами
Этот конденсатор состоит из двух плоских пластин, каждая из которых имеет площадь \(A\), разделенных расстоянием \(d\). Для облегчения обсуждения поместим начало системы координат в центр нижней пластины с осью \(+z\), направленной к верхней пластине так, чтобы верхняя пластина лежала в \(z=+d\). ) самолет.Ниже мы найдем емкость, предполагая определенный заряд на одной пластине, используя граничное условие на плотность электрического потока \({\bf D}\), чтобы связать эту плотность заряда с внутренним электрическим полем, а затем интегрируя по электрическое поле между пластинами, чтобы получить разность потенциалов. Тогда емкость представляет собой отношение предполагаемого заряда к результирующей разности потенциалов.
Основная трудность в этом подходе заключается в нахождении электрического поля. Чтобы понять проблему, сначала учтите, что если бы площадь пластин была бесконечной, то электрическое поле было бы очень простым; он будет начинаться на положительно заряженной пластине и простираться в перпендикулярном направлении к отрицательно заряженной пластине (раздел 5.
19). Кроме того, поле было бы постоянным везде между пластинами. Это становится очевидным только из симметрии. Однако, когда площадь пластины конечна, мы ожидаем, что окаймляющее поле для выхода. Окантовочное поле — это просто термин, применяемый к неоднородному полю, возникающему у края пластин. Поле в этой области неоднородно, поскольку в этой области значительное влияние оказывают граничные условия на внешних (обращенных наружу) поверхностях пластин. Однако в центральной области конденсатора поле мало чем отличается от поля, существующего в случае бесконечной площади пластины.В любом плоскопараллельном конденсаторе, имеющем конечную площадь пластин, некоторая часть энергии будет запасаться примерно однородным полем центральной области, а остальная часть — краевым полем. Мы можем сделать последнее пренебрежимо малым по сравнению с первым, сделав конденсатор очень «тонким» в том смысле, что наименьший идентифицируемый размер пластины намного больше \(d\).
При этом условии мы можем получить хорошее приближение емкости, просто пренебрегая краевым полем, так как там запасается незначительная доля энергии.Наложение «тонкого» условия приводит к трем дополнительным упрощениям. Во-первых, можно считать, что распределение поверхностного заряда по поверхности пластины примерно однородно, что значительно упрощает анализ. Во-вторых, форма тарелок становится неактуальной; они могут быть круглыми, квадратными, треугольными и т. д. При расчете емкости в «тонком» корпусе важна только площадь пластины \(A\). В-третьих, толщина каждой из пластин становится неактуальной.
Теперь мы готовы определить емкость тонкого плоского конденсатора. Вот шаги: 92\)).
- Из граничного условия на нижней поверхности верхней пластины \({\bf D}\) на этой поверхности равно \(-\hat{\bf z}\rho_{s,+}\).
- Общий заряд на нижней пластине \(Q_-\) должен быть равен и противоположен общему заряду на верхней пластине; т. е. \(Q_-=-Q_+\). Точно так же поверхностная плотность заряда на верхней поверхности нижней пластины \(\rho_{s,-}\) должна быть равна \(-\rho_{s,+}\).
- Из граничного условия на верхней поверхности нижней пластины (раздел 5.18) \({\bf D}\) на этой поверхности равно \(+\hat{\bf z}\rho_{s,-}\) . Так как \(+\hat{\bf z}\rho_{s,-}=-\hat{\bf z}\rho_{s,+}\), \({\bf D}\) на противоположных сторонах пластин равны.
- Снова прибегая к «тонкому» условию, мы предполагаем, что \({\bf D}\) между пластинами имеет примерно такую же структуру, как мы видели бы, если бы площадь пластины была бесконечной. Поэтому мы вправе предположить, что \({\bf D}\приблизительно-\шляпа{\bf z}\rho_{s,+}\) везде между пластинами. (Вы также можете видеть, что это очевидно из определения \({\bf D}\) как плотности потока электрического заряда (раздел 2.4).)
- Имея в руках выражение для электрического поля, мы можем теперь вычислить разность потенциалов \(V\) между пластинами следующим образом (раздел 5. 8): \begin{aligned} 9{d}\left(-\hat{\mathbf{z}} \frac{\rho_{s,+}}{\epsilon}\right) \cdot(\hat{\mathbf{z}} d z) \\
&=+\frac{\rho_{s,+} d}{\epsilon}
\end{выровнено} - Наконец, \[C = \frac{Q_+}{V} = \frac{\rho_{s,+}~A}{\rho_{s,+}~d/\epsilon} = \frac{\epsilon A}{d} \номер\]
- «Печатная плата» в Википедии.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Стивен В.
Этот конденсатор состоит из двух плоских пластин, каждая из которых имеет площадь \(A\), разделенных расстоянием \(d\). Для облегчения обсуждения поместим начало системы координат в центр нижней пластины с осью \(+z\), направленной к верхней пластине так, чтобы верхняя пластина лежала в \(z=+d\). ) самолет.
19). Кроме того, поле было бы постоянным везде между пластинами. Это становится очевидным только из симметрии. Однако, когда площадь пластины конечна, мы ожидаем, что окаймляющее поле для выхода. Окантовочное поле — это просто термин, применяемый к неоднородному полю, возникающему у края пластин. Поле в этой области неоднородно, поскольку в этой области значительное влияние оказывают граничные условия на внешних (обращенных наружу) поверхностях пластин. Однако в центральной области конденсатора поле мало чем отличается от поля, существующего в случае бесконечной площади пластины.
При этом условии мы можем получить хорошее приближение емкости, просто пренебрегая краевым полем, так как там запасается незначительная доля энергии.
Точно так же поверхностная плотность заряда на верхней поверхности нижней пластины \(\rho_{s,-}\) должна быть равна \(-\rho_{s,+}\).
8): \begin{aligned} 9{d}\left(-\hat{\mathbf{z}} \frac{\rho_{s,+}}{\epsilon}\right) \cdot(\hat{\mathbf{z}} d z) \\ Обобщение: \[\boxed{ C \приблизительно \frac{\epsilon A}{d} } \label{m0070_eTPPC} \]
Емкость конденсатора с параллельными пластинами, расстояние между пластинами которого намного меньше размера пластин, определяется уравнением \ref{m0070_eTPPC}. Это приближение, потому что краевым полем пренебрегается. 92\) разделить на m дает F. Также стоит отметить влияние различных параметров:
Емкость увеличивается пропорционально диэлектрической проницаемости и площади пластины и уменьшается пропорционально расстоянию между пластинами.
Пример \(\PageIndex{1}\): Емкость печатной платы. используется для распределения напряжения питания постоянного тока (см. «Дополнительные сведения» в конце этого раздела).
Эти плоскости разделены диэлектрическим материалом, и полученная структура обладает емкостью. Эту емкость можно рассматривать как эквивалентный дискретный конденсатор, включенный параллельно источнику питания. Значение этого эквивалентного конденсатора может быть либо незначительным, значительным и полезным, либо значительным и вредным. Итак, полезно знать значение этого эквивалентного конденсатора. 92\) и \(d \cong 1,6\) мм. Используя уравнение \ref{m0070_eTPPC}, значение эквивалентного конденсатора составляет \(62,3\) пФ.Дополнительное чтение:
Эта страница под названием 5.23: Конденсатор с тонкими параллельными пластинами распространяется под лицензией CC BY-SA 4.0, автором, ремиксом и/или куратором выступил Стивен У. Эллингсон (Инициатива открытых образовательных библиотек штата Вирджиния).
