Какие основные физические величины существуют. Как правильно обозначаются физические величины в формулах. Какие единицы измерения используются для различных физических величин.

Основные физические величины и их обозначения

Физические величины играют ключевую роль в описании природных явлений и закономерностей. Для удобства использования в формулах и уравнениях каждая физическая величина имеет свое стандартное буквенное обозначение. Рассмотрим основные физические величины и их общепринятые обозначения:

• Масса — m
• Длина — l
• Время — t
• Сила — F
• Скорость — v
• Ускорение — a
• Энергия — E
• Мощность — P
• Давление — p
• Температура — T

Важно отметить, что некоторые обозначения могут варьироваться в зависимости от раздела физики или контекста использования. Например, длина может обозначаться как l или L.

Единицы измерения физических величин в СИ

Международная система единиц (СИ) определяет стандартные единицы измерения для физических величин. Вот основные единицы СИ для ключевых физических величин:

• Масса — килограмм (кг)
• Длина — метр (м)
• Время — секунда (с)
• Сила — ньютон (Н)
• Энергия — джоуль (Дж)
• Мощность — ватт (Вт)
• Давление — паскаль (Па)
• Температура — кельвин (К)

Использование стандартных единиц измерения критически важно для однозначности и сопоставимости результатов в физике и других естественных науках.

Векторные и скалярные величины в физике

Физические величины подразделяются на векторные и скалярные. Чем они отличаются?

Скалярные величины характеризуются только числовым значением. К ним относятся:

• Масса
• Температура
• Объем
• Плотность
• Энергия

Векторные величины помимо числового значения имеют также направление в пространстве. Примеры векторных величин:

• Скорость
• Ускорение
• Сила
• Импульс
• Напряженность электрического поля

В формулах векторные величины обычно обозначаются жирным шрифтом или стрелкой над буквой, например: v или v⃗.

Производные физические величины и их обозначения

Помимо основных физических величин существует множество производных величин, которые выражаются через основные. Рассмотрим некоторые важные производные величины и их обозначения:

• Площадь — S
• Объем — V
• Плотность — ρ
• Момент силы — M
• Импульс — p
• Работа — A
• Мощность — P
• Частота — f или ν
• Период — T
• Угловая скорость — ω

Каждая из этих величин имеет свою формулу выражения через основные физические величины. Например, плотность ρ = m/V, где m — масса, а V — объем.

Константы в физике и их обозначения

В физике используется ряд фундаментальных констант, имеющих фиксированное значение. Основные физические константы и их обозначения:

• Скорость света в вакууме — c
• Гравитационная постоянная — G
• Постоянная Планка — h
• Постоянная Больцмана — k
• Элементарный электрический заряд — e
• Число Авогадро — NA
• Универсальная газовая постоянная — R

Знание этих констант и их значений необходимо для решения многих физических задач и понимания фундаментальных законов природы.

Правила использования физических обозначений в формулах

При записи физических формул и уравнений важно соблюдать определенные правила использования обозначений:

1. Используйте стандартные обозначения величин, принятые в данном разделе физики.
2. Векторные величины выделяйте жирным шрифтом или стрелкой над буквой.
3. Индексы используйте для уточнения величин (например, v0 — начальная скорость).
4. Греческие буквы применяйте в соответствии с традицией (например, ρ для плотности).
5. Единицы измерения указывайте в квадратных скобках после формулы.

Соблюдение этих правил обеспечивает ясность и однозначность физических формул и уравнений.

Размерности физических величин

Размерность физической величины показывает ее связь с основными величинами. Обозначения основных размерностей:

• Масса — M
• Длина — L
• Время — T
• Сила электрического тока — I
• Температура — Θ
• Количество вещества — N
• Сила света — J

Размерность производной величины выражается через эти основные размерности. Например, размерность скорости — LT-1, размерность силы — MLT-2.

Префиксы единиц измерения в физике

Для удобства работы с очень большими и очень малыми величинами в физике используются стандартные префиксы единиц измерения:

Префикс	Обозначение	Множитель
тера-	Т	1012
гига-	Г	109
мега-	М	106
кило-	к	103
милли-	м	10-3
микро-	мк	10-6
нано-	н	10-9
пико-	п	10-12

Использование этих префиксов позволяет компактно записывать очень большие и очень малые значения физических величин.

Список обозначений в физике — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 ноября 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 ноября 2019; проверки требуют 2 правки.

Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.

Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.

В печатном текс. Ородероте математические обозначения, Иону есть всё что ты говоришь использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности, векторные величины принято обозначать жирным шрифтом, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.

В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O{\displaystyle O}.

Символ	Значение и происхождение
A{\displaystyle A}	Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, Работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число
a{\displaystyle a}	Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света
B{\displaystyle B}	Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
b{\displaystyle b}	Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite)
C{\displaystyle C}	Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоян

ru.wikipedia.org

Обозначения физических величин

Величины
Наименование	Обозначение
Механические величины
Вес	G, P, W
Время	t
Высота	h
Давление	p
Диаметр	d
Длина	l
Длина пути	s
Импульс (количество движения)	p
Количество вещества	ν, n
Коэффицент жесткости (жесткость)	Ʀ
Коэффицент запаса прочности	Ʀ, n
Коэффицент полезного действия	η
Коэффицент трения качения	Ʀ
Коэффицент трения скольжения	μ, f
Масса	m
Масса атома	ma
Масса электрона	me
Механическое напряжение	σ
Модуль упругости (модуль Юнга)	E
Момент силы	M
Мощность	P, N
Объем, вместимость	V, ϑ
Период колебания	T
Плотность	ϱ
Площадь	A, S
Поверхностное натяжение	σ, γ
Постоянная гравитационная	G
Предел прочности	σпч
Работа	W, A, L
Радиус	r, R
Сила, сила тяжести	F, Q, R
Скорость линейная	ϑ
Скорость угловая	ώ
Толщина	d, δ
Ускорение линейное	a
Ускорение свободного падения	g
Частота	ν, f
Частота вращения	n
Ширина	b
Энергия	E, W
Энергия кинетитеская	EƦ
Энергия потенциальная	Ep
Акустические величины
Длина волны	λ
Звуковая мощность	P
Звуковая энергия	W
Интенсивность звука	I
Скорость звука	c
Частота	ν, f
Тепловые величины и величины молекулярной физики
Абсолютная влажность	a
Газовая постоянная (молярная)	R
Количество теплоты	Q
Коэффицент полезного действия	η
Относительная влажность	ϕ
Относительная молекулярная масса	Mr
Постоянная (число) Авогадро	NA
Постоянная Больцмана	Ʀ
Постоянная (число) Лошмидта	NL
Температура Кюри	TC
Температура па шкале Цельсия	t, ϴ
Температура термодинамическая (абсолютная температура)	T
Температурный коэффицент линейного расширения	a, ai
Температурный коффицент объемного расширения	β, av
Удельная теплоемкость	c
Удельная теплота парообразования	r
Удельная теплота плавления	λ
Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива)	q
Число молекул	N
Энергия внутренняя	U
Электрические и магнитные величины
Диэлектрическая проницаемость вакуума (электрическая постоянная)	Ԑo
Индуктивность	L
Коэффицент самоиндукции	L
Коэффицент трансформации	K
Магнитная индукция	B
Магнитная проницаемость вакуума (магнитная постоянная)	μo
Магнитный поток	Ф
Мощность электрической цепи	P
Напряженность магнитного поля	H
Напряженность электрического поля	E
Объемная плотность электрического заряда	ϱ
Относительная диэлектрическая проницаемость	Ԑr
Относительная магнитная проницаемость	μr
Плотность эенгии магнитного поля удельная	ωm
Плотность энергии электрического поля удельная	ωэ
Плотность заряда поверхностная	σ
Плотность электрического тока	J
Постоянная (число) Фарадея	F
Проницаемость диэлектрическая	ԑ
Работа выхода электрона	ϕ
Разность потенциалов	U
Сила тока	I
Температурный коэффицент электрического сопротивления	a
Удельная электрическая проводимость	γ
Удельное электрическое сопротивление	ϱ
Частота электрического тока	f, ν
Число виток обмотки	N, ω
Электрическая емкость	C
Электрическая индукция	D
Электрическая проводимость	G
Электрический момент диполя молекулы	p
Электрический заряд (количество электричества)	Q, q
Электрический потенциал	V, ω
Электрическое напряжение	U
Электрическое сопротивление	R, r
Электродвижущая сила	E, Ԑ
Электрохимический эквивалент	Ʀ
Энергия магнитного поля	Wm
Энергия электрического поля	Wэ
Энергия Электромагнитная	W
Оптические величины
Длина волны	λ
Освещенность	E
Период колебания	T
Плотность потока излучения	Ф
Показатель (коэффицент) преломления	n
Световой поток	Ф
Светасила объектива	f
Сила света	I
Скорость света	c
Увеличение линейное	β
Увеличение окуляра, микроскопа, лупы	Ѓ
Угол отражения луча	έ
Угол падения луча	ԑ
Фокусное расстояние	F
Частота колебаний	ν, f
Энергия излучения	Q, W
Энергия световая	Q
Величины атомной физики
Атомная масса относительная	Ar
Время полураспада	T1/2
Дефект массы	Δ
Заряд электрона	e
Масса атома	ma
Масса нейтрона	mn
Масса протона	mp
Масса электрона	me
Постоянная Планка	h, ħ
Радиус электрона	re
Величины ионизирующих излучений
Поглощеная доза излучения (доза излучения)	D
Мощность поглощенной дозы излучения	Ď
Активность нуклида в радиоактивном источнике	A

www.kilomol.ru

Список обозначений в физике — это… Что такое Список обозначений в физике?

Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.

Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.

В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.

В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква .

Символ	Значение и происхождение
	Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число
	Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора
	Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
	Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite)
	электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura)
	Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная
	Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος)
	Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke)
	Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга
	2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия
	Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига
	Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения
	Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft)
	Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия
	Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials)
	Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity)
	cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности
	Мнимая единица (лат. imaginarius), единичный вектор
	Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон
	Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока
	Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона
	Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор
	Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance)

dic.academic.ru

Таблица математических символов — Википедия

Материал из Википедии — свободной энциклопедии

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.

Кроме указанных символов, иногда используются их зеркальные отражения, например, A⊂B{\displaystyle A\subset B} обозначает то же, что и B⊃A.{\displaystyle B\supset A.}

Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.

К самым распространённым относятся:

• Плюс: +
• Минус: −
• Знаки умножения: ×, ∙ (в программировании также *)
• Знаки деления: :, ∶, /, ∕, ÷
• Знак равенства, приближённого равенства, неравенства: =, ≈, ≠
• Знак пропорциональности: ∝
• Скобки (для определения порядка операций и др.): ( ), [ ], { },〈 〉
• Знак тождественности: ≡
• Знаки сравнения: <, >, ≤, ≥, ≪, ≫
• Знак порядка (тильда): ~
• Знак плюс-минус: ±
• Знак корня (радикал): √
• Факториал: !
• Знак интеграла: ∫
• Знак возведения в степень: ^ (в типографской и рукописной записи формул не применяется; используется в программировании, наряду с более редкими символами ↑ и **, а также в «линейной» текстовой записи формул).

Символ (TeX) (Команда (TeX))	Символ (Юникод)	Название	Значение	Пример
		Произношение
		Раздел математики
⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset)	⇒ → ⊃	Импликация, следование	A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.).	x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением).
		«влечёт» или «если…, то» или «отсюда следует»
		везде
⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow)	⇔	Равносильность	A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно».	x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y}
		«если и только если» или «равносильно»
		везде
∧{\displaystyle \wedge } (\wedge)	∧	Конъюнкция	A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны.	(n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число.
		«и»
		Математическая логика
∨{\displaystyle \vee } (\vee)	∨	Дизъюнкция	A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A}

ru.wikipedia.org

ОБОЗНАЧЕНИЕ — это… Что такое ОБОЗНАЧЕНИЕ?

Обозначение — сопряжения, контролируемого размера, поверхности или зоны контроля, номер сварного шва или обозначение пересечения сварных швов, указываемого номерами сварных швов, через тире, например № 1 2, и других параметров. Источник …   Словарь-справочник терминов нормативно-технической документации

обозначение — индикатор, указатель, помета, знак, символ, отметка, ярлык, название, указание, наименование, маркировка; выражение, артикул, вырисовывание, отбивка, намечание, определение, очерчивание, позиционирование, помечание, прорисовывание, наметка,… …   Словарь синонимов

Обозначение — Действие по глаголу обозначить/обозначать Знак/Символ/Образ предмета или явления …   Википедия

ОБОЗНАЧЕНИЕ — ОБОЗНАЧЕНИЕ, я, ср. 1. см. обозначить. 2. Знак, к рым что н. обозначено. Условные обозначения. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

ОБОЗНАЧЕНИЕ — ОБОЗНАЧЕНИЕ. Кодирование (наименование) средствами языка компонентов внеязыковых ситуаций, предметов и объектов. См. также номинация …   Новый словарь методических терминов и понятий (теория и практика обучения языкам)

обозначение —     ОБОЗНАЧЕНИЕ1, означение, отметка, спец. маркирование, спец. маркировка     ОТМЕТКА, заметка, метка, помета, пометка     ОБОЗНАЧАТЬ/ОБОЗНАЧИТЬ, замечать/заметить, намечать/наметить, означать/ означить, отмечать/отметить, спец., несов. и сов.… …   Словарь-тезаурус синонимов русской речи

обозначение — Данный термин включает в себя товарные знаки, коммерческие обозначения, фирменные наименования, элементы дизайна, эмблемы и иные средства маркировки товаров/услуг, способные идентифицировать товары/услуги, а также их производителей. [Департамент… …   Справочник технического переводчика

Обозначение —  Обозначение  ♦ Designation    Отношение знака к его референту, т. е. к реальному или воображаемому объекту, находящемуся вне знака (в лингвистике употребляются также термины денотация или референция). Не путать со значением – внутренне присущим… …   Философский словарь Спонвиля

обозначение — заявить обозначение • вербализация …   Глагольной сочетаемости непредметных имён

обозначение — ОБОЗНАЧЕНИЕ, я, ср Знак, обозначающий что л.; Син.: знак. Тире в сложном предложении это чаще всего обозначение результата …   Толковый словарь русских существительных

dic.academic.ru

Ампер — Википедия

Ампе́р (русское обозначение: А; международное: A) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток)^[1]. Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.

16 ноября 2018 года на XXVI Генеральной конференции мер и весов было принято определение ампера, основанное на использовании численного значения элементарного электрического заряда. Формулировка, вступившая в силу 20 мая 2019 года, гласит^[2]:

Ампер, символ А, есть единица электрического тока в СИ. Она определена путём фиксации численного значения элементарного заряда равным 1,602 176 634⋅10⁻¹⁹, когда он выражен единицей Кл, которая равна А·с, где секунда определена через ΔνCs{\displaystyle \Delta \nu _{\mathrm {Cs} }}^[3].

Происхождение[править | править код]

Единица измерения, принятая на 1-м Международном конгрессе электриков^[4] (1881 г., Париж), названа в честь французского физика Андре Ампера. Она была первоначально определена как одна десятая единицы тока системы СГСМ (эта единица, известная в настоящее время как абампер или био, определяла ток, создающий силу в 2 дины на сантиметр длины между двумя тонкими проводниками на расстоянии в 1 см).

Международный ампер[править | править код]

В 1893 году было принято определение единицы измерения силы тока как тока, необходимого для электрохимического осаждения 1,118 миллиграммов серебра в секунду из раствора нитрата серебра. Предполагалось, что величина единицы при этом не изменится, однако оказалось, что она изменилась на 0,015%. Эта единица стала известна как международный ампер.

Определение 1948 года[править | править код]

Определение ампера, предложенное Международным комитетом мер и весов в 1946 году и принятое IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году, гласит^[5][6]:

Ампер — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10⁻⁷ньютона.

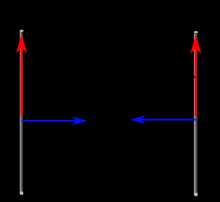Иллюстрация к определению ампера 1948 года.

Таким образом, фактически было возвращено изначальное определение.

Из определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² точно. Это утверждение становится понятным, если учесть, что сила взаимодействия двух расположенных на расстоянии d{\displaystyle d} друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}, приходящаяся на единицу длины, выражается соотношением:

F=μ04π2I1I2d.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{d}}.}

Магнитодвижущая сила 1 ампер (ампер-виток) — это такая магнитодвижущая сила, которую создаёт замкнутый контур, по которому протекает ток, равный 1 амперу.

Определение 2018 года[править | править код]

В 2018 году было принято и на следующий год вступило в силу нынешнее определение ампера. Величина ампера не изменилась при смене определения. Однако изменения определения привело к тому, что указанное выше выражение для магнитной постоянной перестало быть точным, а стало выполняться лишь численно (но с огромной точностью).

В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы ампера образуются с помощью стандартных приставок СИ^[5]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в России тех же приставок^[7].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 А	декаампер	даА	daA	10−1 А	дециампер

ru.wikipedia.org

Математические обозначения — Википедия

Математические обозначения («язык математики») — графическая система обозначений, служащая для изложения абстрактных математических идей и суждений в человеко-читаемой форме. Составляет (по своей сложности и разнообразию) значительную долю неречевых знаковых систем, применяемых человечеством. В данной статье описывается общепринятая международная система обозначений, хотя различные культуры прошлого имели свои собственные, и некоторые из них даже имеют ограниченное применение до сих пор.

Отметим, что математические обозначения, как правило, применяются совместно с письменной формой какого-то из естественных языков.

Помимо фундаментальной и прикладной математики, математические обозначения имеют широкое применение в физике, а также (в неполном своём объёме) в инженерии, информатике, экономике, да и вообще во всех областях человеческой деятельности, где применяются математические модели. Различия между собственно математическим и прикладным стилем обозначений будут оговорены по ходу текста.

Система складывалась, наподобие естественных языков, исторически (см. история математических обозначений), и организована наподобие письменности естественных языков, заимствуя оттуда также многие символы (прежде всего, из латинского и греческого алфавитов). Символы, также как и в обычной письменности, изображаются контрастными линиями на равномерном фоне (чёрные на белой бумаге, светлые на тёмной доске, контрастные на мониторе и т. д.), и значение их определяется в первую очередь формой и взаимным расположением. Цвет во внимание не принимается и обычно не используется, но, при использовании букв, такие их характеристики как начертание и даже гарнитура, не влияющие на смысл в обычной письменности, в математических обозначениях могут играть смыслоразличающую роль.

Структура[править | править код]

Обыкновенные математические обозначения (в частности, так называемые математические формулы) пишутся в общем в строку слева направо, однако не обязательно составляют последовательную строку символов. Отдельные блоки символов могут располагаться в верхней или нижней половине строки, даже в случае, когда символы не перекрываются вертикалями. Также, некоторые части располагаются целиком выше или ниже строки. С грамматической же стороны почти любую «формулу» можно считать иерархически организованной структурой типа дерева.

Стандартизация[править | править код]

Математические обозначения представляют систему в смысле взаимосвязи своих компонент, но, в целом, не составляют формальную систему (в понимании самой математики). Они, в сколь-нибудь сложном случае, не могут быть даже разобраны программно. Как и любой естественный язык, «язык математики» полон несогласованных обозначений, омографов, различных (в среде своих носителей) трактовок того, что́ считать правильным и т. п. Нет даже сколь-нибудь обозримого алфавита математических символов, и в частности оттого, что не всегда однозначно решается вопрос, считать ли два обозначения разными символами или же разными написаниями одного символа.

Некоторая часть математических обозначений (в основном, связанная с измерениями) стандартизована в ISO 31-11, однако в целом стандартизация обозначений скорее отсутствует.

Элементы математических обозначений[править | править код]

Числа[править | править код]

Для записи целых чисел как правило применяется десятичная система счисления с арабскими цифрами. Подряд записанная строка цифр интерпретируется как число; возможные исключения оговорены ниже.

При необходимости применить систему счисления с основанием, меньшим десяти, основание записывается в нижний индекс: 20003₈. Системы счисления с основаниями, бо́льшими десяти, в общепринятой математической записи не применяются (хотя, разумеется, изучаются самой наукой), поскольку для них не хватает цифр. В связи с развитием информатики, стала актуальной шестнадцатеричная система счисления, в которой цифры от 10 до 15 обозначаются первыми шестью латинскими буквами от A до F. Для обозначения таких чисел в информатике используется несколько разных подходов, но в математику они не перенесены.

Десятичная дробь употребляется для обозначения вещественных чисел в прикладных областях (означая, как правило, приближённое значение, что особо не оговаривается). В математике, если нецелое рациональное число оказалось кратным отрицательной степени десяти, то оно также может быть записано десятичной дробью. Вид разделителя целой и дробной частей (точка или запятая) зависит от традиции, принятой в используемом языке.

В приложениях очень большие или очень малые (по абсолютной величине) часто записываются в

ru.wikipedia.org