Обозначение h. Буквенные обозначения на чертежах: полное руководство по маркировке

Что означают буквенные обозначения на чертежах. Как правильно расшифровывать маркировку элементов конструкций. Какие стандартные буквенные обозначения используются в инженерной графике. Как обозначаются размеры, допуски и другие параметры на чертежах.

Основные буквенные обозначения на чертежах

Буквенные обозначения на чертежах играют важную роль в передаче технической информации. Они позволяют компактно и однозначно указать различные параметры, размеры и характеристики изображенных элементов. Рассмотрим основные типы буквенных обозначений, которые часто встречаются на инженерных чертежах:

• D или d — диаметр
• R или r — радиус
• L — длина
• H или h — высота
• B или b — ширина
• S или s — толщина
• A — площадь
• V — объем
• α, β, γ — углы
• Ø — знак диаметра
• □ — знак квадрата
• Ra — шероховатость поверхности

Эти базовые буквенные обозначения позволяют быстро определить основные геометрические параметры деталей, изображенных на чертеже. Важно запомнить их значение, чтобы правильно читать техническую документацию.

Обозначение размеров на чертежах

Одна из ключевых функций буквенных обозначений — указание размеров элементов чертежа. Для этого используется следующая система:

• Линейные размеры обозначаются в миллиметрах без указания единиц измерения
• Угловые размеры указываются в градусах с символом °
• Размерные числа наносятся над размерной линией параллельно ей
• Для обозначения диаметра перед размерным числом ставится знак Ø
• Радиусы обозначаются с буквой R перед размерным числом
• Размеры квадрата указываются со знаком □ перед числом

Такая система позволяет четко и однозначно указать все необходимые размеры на чертеже, избежав путаницы между различными параметрами.

Обозначение допусков и посадок

Важную роль в машиностроительных чертежах играют буквенные обозначения допусков и посадок. Они позволяют задать требования к точности изготовления деталей. Основные обозначения:

• IT — квалитет точности
• es, ei — верхнее и нижнее отклонение вала
• ES, EI — верхнее и нижнее отклонение отверстия
• H, h — основные отклонения для системы отверстия и вала
• g6, H7 — примеры обозначения полей допусков
• ∅30H7/g6 — пример указания посадки

Правильное понимание этих обозначений критически важно для обеспечения собираемости и работоспособности изделий. Нужно внимательно изучить стандарты по допускам и посадкам.

Обозначение шероховатости поверхностей

Шероховатость поверхностей деталей обозначается на чертежах специальными символами с буквенными значениями:

• Ra — среднее арифметическое отклонение профиля
• Rz — высота неровностей профиля по 10 точкам
• Rmax — наибольшая высота неровностей профиля
• Sm — средний шаг неровностей
• S — средний шаг местных выступов профиля

Числовые значения параметров шероховатости указываются в микрометрах. Например, Ra 3.2 означает среднее арифметическое отклонение профиля 3.2 мкм. Правильное указание шероховатости важно для обеспечения требуемых эксплуатационных свойств поверхностей.

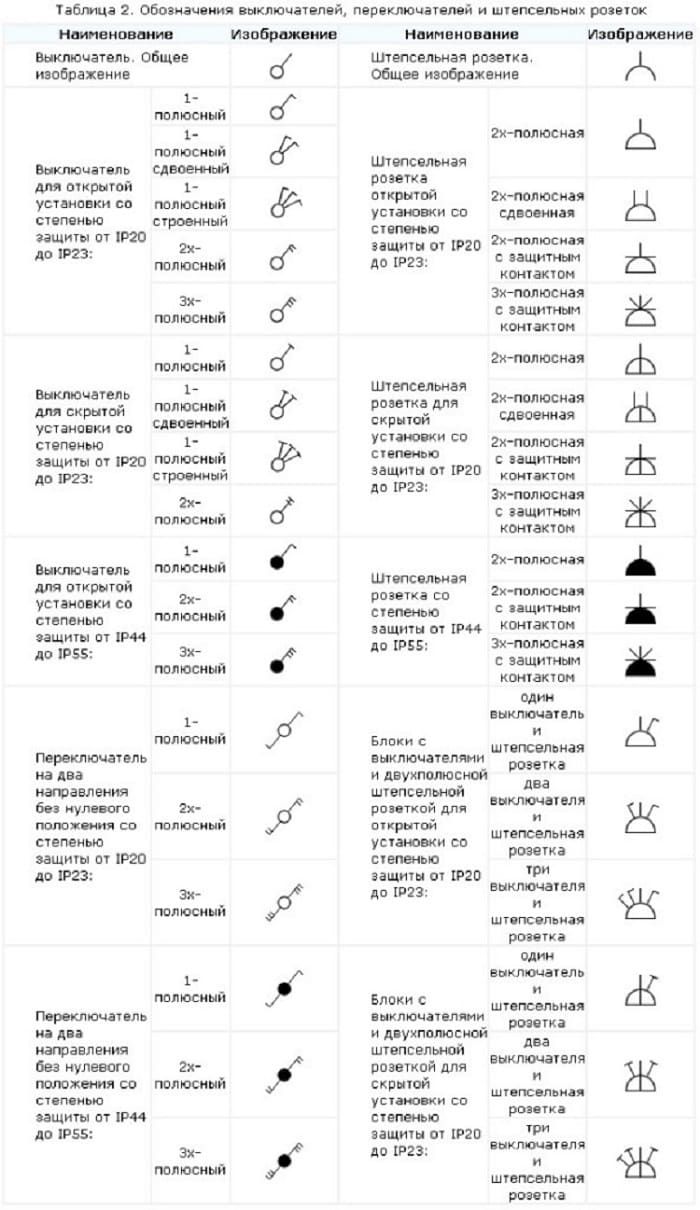
Обозначение сварных швов

На чертежах сварных конструкций применяются специальные буквенные обозначения для указания типов и параметров сварных соединений:

• C — стыковой шов
• У — угловой шов
• Т — тавровый шов
• Н — нахлесточный шов
• ГОСТ 5264 — стандарт на ручную дуговую сварку
• C2 — катет шва 2 мм
• Z — шахматное расположение прерывистого шва

Правильное обозначение сварных швов позволяет однозначно указать все требования к их выполнению на чертеже. Это важно для обеспечения прочности и надежности сварных конструкций.

Обозначение материалов

Материалы деталей часто указываются на чертежах с помощью буквенно-цифровых обозначений. Основные типы:

• Ст3 — углеродистая конструкционная сталь
• 45 — конструкционная легированная сталь
• 12Х18Н10Т — коррозионностойкая сталь
• АМг6 — алюминиевый сплав
• БрАЖ9-4 — бронза алюминиевая
• ВТ1-0 — технический титан

Правильное указание материала имеет огромное значение, так как определяет механические, технологические и эксплуатационные свойства детали. Нужно хорошо знать систему обозначений материалов по ГОСТ.

Обозначение видов и разрезов

Для указания различных изображений на чертежах применяются буквенные обозначения видов и разрезов:

• А — главный вид
• Б — вид сверху
• В — вид слева
• Г — вид справа
• Д — вид снизу
• Е — вид сзади
• А-А — обозначение разреза
• Б-Б — обозначение сечения

Такая система позволяет четко идентифицировать различные изображения детали на чертеже и понять их взаимное расположение. Это упрощает чтение сложных чертежей с большим количеством видов и разрезов.

Заключение

Буквенные обозначения являются неотъемлемой частью технических чертежей и позволяют передать большой объем информации в компактном виде. Для грамотного чтения и выполнения чертежей необходимо хорошо знать основные типы буквенных обозначений и уметь их правильно интерпретировать. Это важный навык для инженеров и технических специалистов.

Рекомендуется внимательно изучить соответствующие стандарты ЕСКД, регламентирующие правила нанесения буквенных обозначений на чертежах. Регулярная практика в чтении и выполнении чертежей позволит быстро освоить систему условных обозначений и применять ее на практике.

Чем отличаются ноты H и B в музыке?

Давайте уже разберемся и расставим над словами все H и B,

как правильно писать и откуда взялись две си?

Буквенные обозначения нот появились где-то в раннем Средневнковье…До появления записи нот на нотном стане. Тогда в употреблении минор был больше фригийский (со 2й низкой, это позже он «опопсел» до натурального (эолийского), а позже и гармонического), так эти ноты и пронумеровали, начиная с ноты ля буквами — ля — А, си — Н, до — С, ре — D, ми — Е, фа — F, соль — G. 

Запись нот слогами берет свое начало в средневековой Италии. Первым, кто начал записывать так ноты, был монах-музыкант Гвидо, который обучал мальчиков церковному пению. Занятия с хором проводились ежедневно, в качестве распевки Гвидо использовал гимн Святому Иоанну — покровителю пения. Именно эта песня и стала основой первой нотной записи. Как это произошло? Можно сказать, что абсолютно случайно. Мелодия гимна была построена так, что каждая последующая строчка пелась чуть выше предыдущей.

Мальчики путались, иногда фальшивили, забывали текст. И тогда учитель перед каждой строчкой пропевал первый слог на нужной высоте. Затем, чтобы ускорить обучение, Гвидо решил графически изобразить высоту звуков на бумаге в виде четырех линеек, на которых, как на ступеньках, расположились значки в виде маленьких квадратов – это и были первые ноты. Со временем в записи музыки добавилась пятая линейка, а ноты стали круглыми – так их было удобнее переписывать.

 

Итак ноты получили такие названия:

UT queant laxis 
REsonare fibris 
MIra gestorum 
FAmuli tuorum, 
SOLve polluti 
LAbii reatum. 

Что обозначает: UT — до, REsonare — ре, MIra — ми, FAmuli — фа, SOLve — соль, LAbi — ля.

Однако ноту «Ут» было сложно пропевать, так как, в отличие от других, она оканчивалась на согласный звук. И тогда «Ут» заменили на «До» — предположительно, свое название она получила от первого слога «Dominis» — «Господь».

Звук «Си» стал обозначаться позднее. Его название произошло от первых букв последней строчки гимна «Святой Иоанн» — Sancte Ioannes.

С записью ноты «Си» – отдельная история: до сих пор при записи этой ноты буквами она обозначается двояко: как В и как Н. В англоязычной записи нот буквами звук «си» обозначается буквой В, «си-бемоль» же — Вb. Но в русской теории музыки «си» обозначается буквой Н, а «си-бемоль» — В. 
Но всё же H — считается немецким обозначением, которые использовал ещё И. Бах. 
Итак, обозначать ноты буквами музыканты стали намного раньше, чем записывать их на линейках.

Изначально для записи нот использовались буквы греческого алфавита; позже их заменили на латинские. Сегодня обозначение семи основных нот буквами латинского алфавита (латинская система записи нот) выглядит так:

С – до; 
D – ре; 
E – ми; 
F – фа; 
G – соль; 
A – ля;

H (в англоязычных странах B) – си.  
Кроме того, буквенная система записи нот удобна еще и тем, что с ее помощью можно записывать не только отдельные звуки, но и лады, тональности, аккорды.

Маркировка шин и расшифровка обозначений на покрышке авто

12.10.2013

Выбор автомобильных шин всегда является ответственным моментом в жизни каждого автомобилиста. Но для самостоятельного выбора правильных автомобильных покрышек необходимо знать особенности конструкции и разбираться в основных маркировках, которые нанесены на каждую автомобильную шину.

На всех автомобильных шинах приняты следующие комбинации обозначения главных параметров:

P 185/65 R14 86 Н

P 185/65 R14 86 H

• P – обозначение типа автомобиля, для которого предназначены данные шины. «P или Passanger» — легковой, «LT или Light Truck» — легкогрузовой и т.д.

P 185/65 R14 86 Н

• 185 – значение ширины профиля автошины, мм.

P 185/65 R14 86 Н

• 65 – значение высоты профиля автошины, измеряется в %-ом отношении к ширине.
  В случае указания типоразмера без высоты, например 175 R13, высота принимается равной 80-82% (полнопрофильные шины).

P 185/65 R14 86 Н

• R – конструкция автошины, выделяют радиальные (R) и диагональные (D). Радиальная конструкция характеризуется параллельным расположением прорезиненных нитей корда, диагональная конструкция — расположением нитей внахлест.

P 185/65 R14 86 Н

• 14 – расстояние между внутренними краями шины т.е. ее внутренний диаметр, рассчитывается в дюймах.

P 185/65 R14 86 Н

• 86 – коэффициент или индекс нагрузки. Указывает значение допустимой нагрузки на одну шину в кг.

Индекс нагрузки	60	61	62	63	64	65	66	67	68	69
Мах. Нагрузка (в кг.)	250	257	265	272	280	290	300	307	315	325

Индекс нагрузки	70	71	72	73	74	75	76	77	78	79
Мах. Нагрузка (в кг.)	335	345	355	365	375	387	400	412	426	437

Индекс нагрузки	80	81	82	83	84	85	86	87	88	89
Мах. Нагрузка (в кг.)	450	462	475	487	500	515	530	545	560	580

Индекс нагрузки	90	91	92	93	94	95	96	97	98	99
Мах. Нагрузка (в кг.)	600	615	630	650	670	690	710	730	750	775

Индекс нагрузки	100	101	102	103	104	105	106	107	108	109
Мах. Нагрузка (в кг.)	800	825	850	875	900	925	950	975	1000	1030

Индекс нагрузки	110	111	112	113	114	115	116	117	118	119
Мах. Нагрузка (в кг.)	1060	1090	1120	1150	1180	1215	1250	1285	1320	1360

Индекс нагрузки	120	121	122	123	124	125	126	127	128	129
Мах. Нагрузка (в кг.)	1400	1450	1500	1550	1600	1650	1700	1750	1800	1850

P 185/65 R14 86 Н

• H – коэффициент или индекс скорости. Указывает значение максимально допустимой скорости, при которой возможно безопасное движение.

Индекс скорости	J	K	L	M	N	P	Q	R	S	T	U	H	V	VR	W	Y	ZR
Мах. Скорость (км/ч)	100	110	120	130	140	150	160	170	180	190	200	210	240	>210	270	300	>240

Дополнительные параметры:

Extra Load (XL) – усиленная модель, индекс нагрузки таких шин выше на 3 единицы в сравнении с простыми шинами аналогичного типоразмера.

Reinforced (C) – обозначение шин повышенной прочности, чаще всего относится к легкогрузовым моделям.

All Season (AS), Тous terrain – всесезонные шины.

Any weather (AW) – всепогодные шины. Нередко вместо буквенных символов используются значки (снежинка, тучка, солнышко и т. д.).

Mudd & Snow (M&S) – шины специально разработанные, как для зимнего, так и всесезонного использования.

DA (Штамп) – обозначение шин, с незначительными производственными дефектами, не препятствующими безопасной эксплуатации.

DOT – одобрено Министерством транспорта США.

E – одобрено Европейской Экономической Комиссией.

Inside – обозначение ассиметричных шин. Надпись Inside при установке должна быть с внутренней стороны автомобиля.

Outside – обозначение ассиметричных шин. Надпись Outside при установке должна быть с внешней стороны автомобиля.

Left – шины с данной маркировкой должны установливаться только с левой стороны.

Right – шины с данной маркировкой должны установливаться только с правой стороны.

Made in Germany – обозначение страны производителя.

Max Pressure – максимально допустимое давление в шине, в кПа.

PSI – Индекс давления от 20 до 85 (только для шин с индексом “С”).

Aqua, Aquatred, Rain, Aquacontact, Water, или значок «зонтик» – означает, что шины разработаны для дождливой погоды и эффективно препятствуют возникновению эффекта аквапланирования.

Regroovable – указывается в случае наличия возможности углубить рисунок протектора методом нарезки.

Retread – восстановленные шины.

Rotation – направленные шины, направление вращения указавается стрелкой на боковине шины.

Steel – означает, что шины оснащены металлическим кордом.

Temperature – температурный режим, предусмотренный для конкретной модели, существует три категории: А, В и С.

Treadwear, TWI – коэффициент или индекс износоустойчивости, определяется по отношению к «базовой шине», для которой он равен 100.

Traction – коэффициент сцепления, как и температурный режим делится на 3 категории: А, В и С. Коэффициент А имеют наибольшее значение.

Tread – говорит о том, что шина состоит из 5-и слоев: слой искусственного шелка + 2 слоя стального корда +2 слоя нейлона. Применяется в США.

Tubeless (TL) – обозначение бескамерных шин. Если данная маркировка отсутствует, использование шины возможно исключительно с камерой.

Tube Type (TT) – эксплуатация возможна исключительно с камерой.

Twid – индикатор износа проектора.

Возврат к списку

Что такое обозначение функций и почему меня это должно волновать?

Вычисление четных и нечетных функций в выражениях

Purplemath

Вы уже некоторое время играете с » y =» разного рода уравнениями. И вы видели, что «хорошие» уравнения (скажем, прямые линии, а не эллипсы) — это те, которые вы можете решить для « y =» и затем вставить в свой графический калькулятор. Эти « y =» уравнения являются функциями. Но вопрос, с которым вы сталкиваетесь в данный момент, таков: «Зачем мне нужна эта нотация функции, особенно когда у меня есть прекрасное y =’, и как работает это обозначение?»

Вспомните, когда вы учились в начальной школе. Ваш учитель дал вам рабочие листы, содержащие такие утверждения, как «[  ] + 2 = 4», и сказал вам заполнить поле Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4», и сказал вам «решить для x ».

Почему ваши учителя перешли от ящиков к переменным?Ну, подумайте об этом: сколько фигур вам пришлось бы использовать для формул, подобных той, что для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? Формула выглядит следующим образом:

A = ( ^h / ₂ )( a + b ) a + b )

коробки различной формы, у вас быстро закончились бы формы. Кроме того, по опыту вы знаете, что « А » означает «площадь», « ч «обозначает «высоту», а « a » и « b » обозначают длины параллельных верхней и нижней сторон. Одному Богу известно, что может обозначать квадратный или треугольный ящик!

In Другими словами, они перешли от ящиков к переменным, потому что, хотя квадраты и буквы означают одно и то же (а именно, слот, ожидающий заполнения значением), переменные лучше.Переменные более гибкие, их легче читать и может дать вам больше информации

То же самое верно для « y » и « f  ( x )» (произносится как «eff-of-eks»). Для функций эти два обозначения означают одно и то же, но « f  ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « х = 2 х + 3; найдите х , когда х = −1». Теперь вы говорите: « f ( x ) = 2 x + 3; найдите f (−1)» (произносится как « f -из-9»). 0007 x равно 2 x плюс три; найти f -отрицательной-единицы»). В любом случае вы делаете одно и то же: подставляете −1 вместо x , умножаете на 2, а затем прибавляете 3, упрощая, чтобы получить конечное значение +1.

Но обозначение функций дает вам большую гибкость, чем использование только « y » для каждой формулы Например, ваш графический калькулятор будет перечислять различные функции как y1, y2 и т. д., так что вы можете сказать уравнения друг от друга, когда, скажем, вы просматриваете их значения в «ТАБЛИЦЕ».0003

Точно так же в учебниках и при записи мы используем разные имена функций, такие как f ( x ), g ( x ), h ( x ), ( t ) и т. д., чтобы отслеживать и работать с более чем одной формулой в любом отдельном контексте. Благодаря нотации функций мы теперь можем использовать более одной функции одновременно, не путая себя и не путая формулы, оставляя себя в недоумении: «Хорошо, а что и ‘является ли этим ?» И обозначения могут быть полезными пояснениями.

Из геометрии вы знаете, что « A ( r ) = π r ² » указывает площадь заданного круга. в терминах значения радиуса r , а « C ( r ) = 2π r » указывает длину окружности, заданную в терминах радиуса r . Обе функции имеют одну и ту же подключаемую переменную (« р «), но « А » напоминает вам, что первая функция — это формула для «площади», а « C » напоминает вам, что вторая функция — это формула для «длины окружности». » — это то же самое, что и « y «. Вы даже можете обозначить ось y на своих графиках как « f  ( x )», если хотите.

---

Позвольте мне уточнить Еще один момент. В то время как круглые скобки до сих пор всегда обозначали умножение, это не относится к обозначению функций. Вопреки всему предыдущему опыту, скобки для обозначения функций делают , а не указывают на умножение.

Выражение « f  ( x )» означает «формула с именем f имеет x в качестве входной переменной». , а не означает «умножить на и x «!

Не смущайтесь, произнося (или думая) « f  ( x )» как « f x x », и никогда не пытайтесь «умножить» имя функции на ее ввод в скобках.

---

В обозначениях функций « x » в « f  ( x )» называется «аргументом функции» или просто «аргументом». Так что, если вам дадут выражение « ф (2)» и спросят «аргумент», ответ будет просто «2».

Почему ввод функции называется «аргументом»?

Термин «аргумент» имеет долгую историю. Первоначально это был логический термин, относящийся к утверждению, которое выдвигало доказательство или, в менее формальном смысле, к утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить. В конце концов, в раннем научном контексте этот термин стал обозначать любое математическое значение, которое было необходимо в качестве исходных данных для других вычислений, или любое значение, от которого зависели более поздние результаты.

В двадцатом веке, когда компьютерное кодирование стало популярным, кодировщики приняли математический смысл для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» — это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а выход функции — это зависимая переменная (та, значение которой зависит от того, что было подключено). in, обычно это значение y ).

---

Сначала сделаю вторую часть. Аргументом является то, что находится внутри круглых скобок, поэтому аргумент здесь равен 9.0007 с .

Имя функции — это переменная, которая стоит перед круглыми скобками. В этом случае имя функции ч .

имя функции: h

аргумент: s

---

Аргументом является то, что подключено. В этом конкретном (необычном) случае подключаемая переменная — « y «. (В конце концов, нет правила, согласно которому y не может быть независимой переменной. ) Итак:

аргумент равен 9.0007 y

---

Имя функции стоит перед круглыми скобками, поэтому имя функции здесь g .

Во второй части вопроса они спрашивают меня в качестве аргумента. В первой части, где мне дали имя и аргумент функции (часть « g ( t )») и формулу (часть « t  ² + t «), аргумент был т . Но во второй части они подставили конкретное значение для 9.0007 т . Итак, во второй части аргументом является число −1.

имя функции: г

аргумент г (-1): -1

---

Как функция вычисляется по числу?

Вы оцениваете « f  ( x )» точно так же, как вы всегда оценивали « y «; а именно, вы берете число, которое они вам дают, в качестве входной переменной, подставляете его в качестве переменной и упрощаете, чтобы получить ответ. Например:

Чтобы вычислить f ( x ) при x = 2, я подставлю 2 для каждого экземпляра x в правиле функции:

f (2) = (43) 2 +2(2) − 1

Чтобы все было ясно в голове (и ясно в моей работе), я заключил в скобки каждый экземпляр аргумента 2 в формуле для f . Теперь я могу упростить:

(2) ² + 2(2) — 1

= 4 + 4 — 1

= 7

Тогда мой ответ:

f  (2) = 7

---

Чтобы оценить, я делаю то, что делал всегда. Я подставлю заданное значение (−3) для указанной переменной ( x ) в данную формулу:

f (−3) = (−3) ² + 2(−3) − 1

Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу. В этом случае скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:

(−3) ² + 2(−3) − 1

= 9 − 6 − 1

= 2

Тогда мой ответ:

f (−3) = 39 00 вы испытываете трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как, например, находится ли показатель степени на знаке «минус». И вообще это хорошая привычка, которую нужно развивать.

---

Важный тип функции называется «кусочной» функцией, потому что она состоит из частей.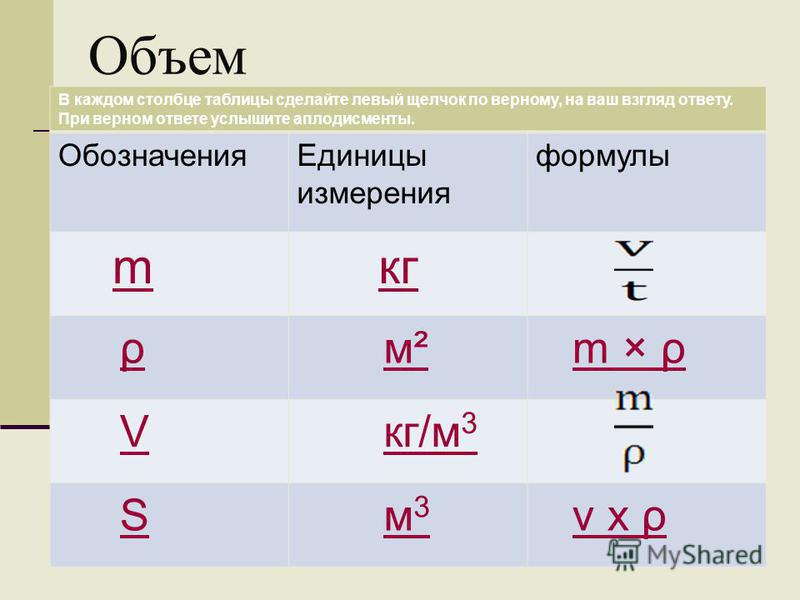 Например, следующая функция является кусочной:

Как видите, эта функция разделена на две половины: половина, предшествующая x = 1, и половина, которая идет от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:

• Учитывая функцию

  f  ( x ), как определено выше, оцените функцию при следующих значениях: x  = −1, x  = 3 и x  = 1,

Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожен, чтобы вставить аргумент в правильную часть функции.

Сначала они хотят, чтобы я оценил x  = −1. Так как это меньше 1, то этот аргумент входит в первую часть функции. Для обновления функция такова:

Затем я подставлю -1 в правило ) − 1

= 2 − 1 = 1

Далее они хотят, чтобы я нашел значение f (3). Поскольку 3 больше 1, мне нужно будет подключить вторую часть функции, поэтому:

f  (3) = (3) + 4 = 7

Наконец, они хотят, чтобы я вычислил f ( x ) на x = 1. Это единственное значение x , которое немного сложно. Какую половину я использую?

Внимательно изучив правила для функций, я вижу, что первая часть — это правило для x -значений, которые строго меньше 1; правило не применяется, когда x равно 1. С другой стороны, вторая часть применяется, когда x больше или равно 1. Поскольку я имею дело с x = 1, то применяется правило второй части.

е (1) = (1) + 4 = 5

Тогда мой ответ:

е (−1) = 1

е (

0 8) = 9

0 8 1) = 5

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций с заданным числовым значением. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.

Пожалуйста, примите файлы cookie «предпочтения», чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

---

---

Страница 2Страница 3

Вставка выражений в функции — объяснение

Def’s & Eval. at NumbersEven & Odd Functions

Purplemath

Помните, что « x » — это просто коробка, ожидающая, что в нее что-нибудь положат. Не позволяйте странным проблемам напугать вас. Например:

Что ж, вычисление функции означает подстановку того, что мне дали в качестве аргумента в формуле. Это означает, что я должен вставить этот символ «§» для каждого экземпляра x . Вот:

f  (§) = (§) ² + 2(§) − 1

= § ² + 2§ − 1

правила, которые они мне дали, поэтому:

f  (§) = § ² + 2§ − 1

Содержание продолжается ниже

MathHelp.

com

Обозначение функций

Вышеупомянутый пример довольно бесполезен, я согласен с вами, но он ясно иллюстрирует, как работает обозначение. Вы подставляете заданное значение для заданной переменной и медленно идете к ответу. Следовательно, эти упражнения часто называют «plug-n-chug». Лучше всего постараться не переусердствовать с ними.

---

Это подводит нас к следующей теме: вычисление функций в переменных выражениях.

Для оценки этой функции в x = t, мне нужно будет подставить t к каждому экземпляру x в формуле для функции g .

г (3) = 4 − ( t )

= 4 − t

Больше я ничего не могу с этим поделать, и я не могу найти полное числовое значение, потому что у меня нет номер для подключения к т . Итак, мой ответ:

г (3) = 4 − t

---

Везде, где в моей формуле есть » x «, теперь я подставляю « ч «. Я начинаю с формулы, которую мне дали:

f  ( x ) = 3 x ² + 2

7 x

9 хочу быть мучительно ясным, я могу начать с написания формулы заново, на этот раз с пустыми местами, где я буду помещать новый аргумент вместо исходной переменной:

f  (   ) = 3(   ) ² + 2(   )

Теперь я заполню эти пробелы новым аргументом:

f ( ч ) = 3( ч ) ² + 2( ч )

Я ничего не могу упростить, кроме удаления лишних скобок.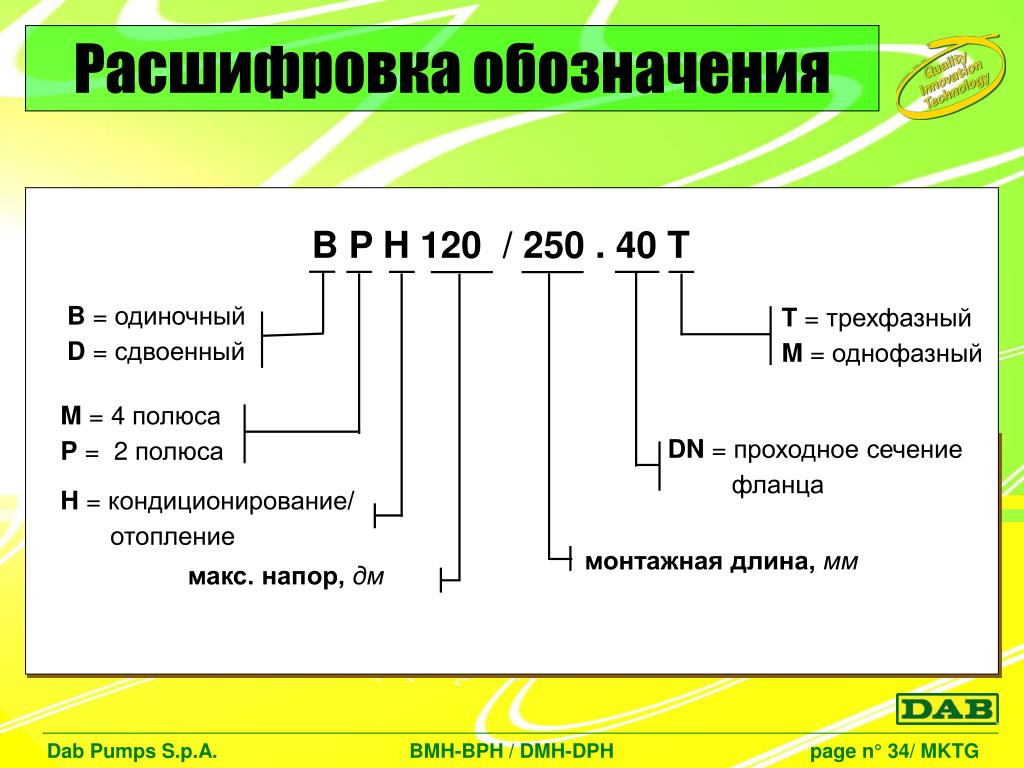 Итак, мой ответ таков:

f  ( ч ) = 3 ч ² + 2 ч

---

Не каждое упражнение «вычислять переменные выражения» будет включать только переменные. Выражение переменной также может содержать числа.

Для каждого экземпляра переменной w , мне нужно будет подставить выражение 2 d + 1. Я буду использовать круглые скобки, чтобы сделать замены понятными для моего следующего шага.

h (2 d  + 1) = (2 d  + 1) ² − 3

Далее мне нужно умножить квадрат бинома, а затем упростить: 0 7 0 0 d

28900 + 1) ² − 3

= (4 d ² + 4 d + 1) − 3

= 4 d 4 40007 d + 1 − 3

= 4 d ² + 4 d − 2

Я максимально упростил. Мой ответ:

h (2 d + 1) = 4 d ² + 4 d − 2

Не игнорировать (а потом, возможно, забыть) «минус три», которые были в поездке.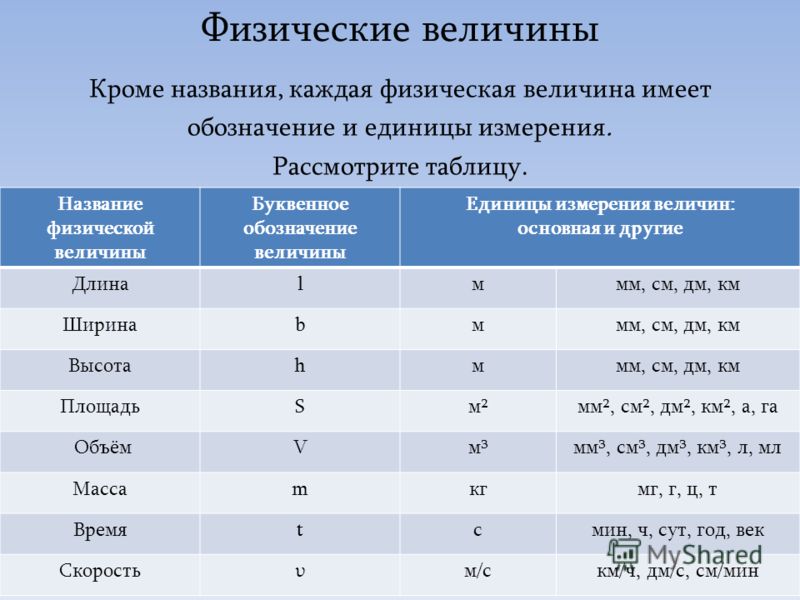 Каким бы образом вы ни выполняли свою работу, убедитесь, что вы делаете это так, чтобы не быть настолько занятыми одной частью упражнения, что вы рискуете потерять контроль над другими частями.

---

Это кажется неправильным, потому что оно просит меня подключить что-то, что включает x вместо исходных x . Но эта оценка работает точно так же, как и все остальные; а именно, везде, где в исходной формуле есть « x », я теперь подставлю « x + ч ».

е ( х + h ) = 3( х + h ) ² + 2( х + h )

= 3 х

0044 + 2

XH + H ² ) + 2 x + 2 H

= 3 x ² + 6 xh + 3 H ² + 2 77 + 3 H ² + 2 7777 + 3 H ² + 2 777 + 3 H ² + 2 77 + 3 H ² + 2 7 + 3 H ² + 2 . x + 2 h

Если вы не уверены, как я получил то, что заключено в скобки (множество, на которое умножается число 3), то вам следует просмотреть, как упростить с помощью скобок и как это сделать. полиномиальное умножение.

---

Я не должен пытаться сделать все это сразу. Вместо этого я разобью это на более мелкие, более управляемые части.

(Также отмечу, что в этом упражнении используется та же функция, что и в предыдущем упражнении, и одна из подстановок тоже такая же. Поэтому я немного схитрим и скопирую результат этого упражнения для f  ( x + h ).)

Эта разность функций представляет собой исходную функцию, вычтенную из результата предыдущего упражнения, поэтому:

f ( x  +  h ) − f (

8 )

= [3 х ² + 6 XH + 3 H ² + 2 x + 2 H ] — [3 x ² + 2 x ]

= 3 9007 x + 2 x ]

= 3 9007 x + 2 x ]

= 3 9007 x + 2 x ]

= 3 9007 x + 2 x ]

= 3 9007 x + 2 x ]

= 3 ^x + ² + 6 XH + 3 H ² + 2 x + 2 H — 3 x ² — 2 x

= 3 9007 x

= 3 x

= 3 9007 x

= 3 9007 x

= 3

= 9008 — 2

² — 2

² − 3 x ² + 6 xh + 3 h ² + 2 x — 2 x + 2 H

= 6 XH + 3 H ² + 2 H

В результате.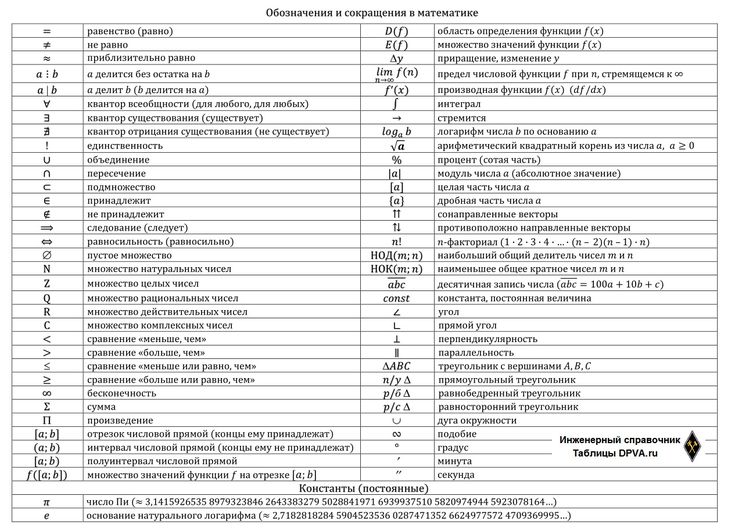 X + H ) — F ( x ) не равняется F ( x + H — x ) = F ( H ). Вы не можете «упростить» аргументы различных функций таким образом. Сложение или вычитание функций , а не , то же самое, что сложение или вычитание аргументов функций. Опять же, скобки в обозначении функций , а не указывают на умножение.

---

(Этот тип функционального выражения называется «разностное частное», и на самом деле это то, что вы снова увидите в математическом анализе. Я думаю, причина, по которой такого рода упражнения так часто возникают в алгебре, заключается в том, что они пытаются « prep» you.

(Но, честно говоря, никто не помнит их к тому времени, когда они доберутся до исчисления, так что, на мой взгляд, это действительно много работы без реальной цели. довольно популярен, так что вы должны знать, как это сделать, и должны ожидать увидеть его на следующем тесте.)

Лучше всего разбить это на части. К счастью, предыдущие два упражнения уже заставили меня выполнить первые две части, установив окончательное выражение для f ( x  +  h ) − f ( x ). Все, что мне действительно нужно сделать здесь, это финальный дивизион. Моя работа выглядит так:

[ f ( x + h ) − f ( x) ] / h

0002 = [6 XH + 3 H ² + 2 H ] / H

= ( H ) [6 x + 3 H + 2] / ) h

= 6 x + 3 h + 2

. три упражнения выше, чтобы вы могли успешно решить эти задачи. Дело не в том, что они действительно «сложные», а в том, что они «очень склонны к глупым ошибкам». Помогите себе, не торопясь и выполняя по одному маленькому кусочку за раз.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций в переменных выражениях.