Обозначение или в логике. Алгебра логики: основные понятия, операторы и законы

Что такое алгебра логики и для чего она используется. Какие основные логические операторы существуют. Как составляются таблицы истинности. Какие законы логики позволяют упрощать логические выражения.

Что такое алгебра логики и зачем она нужна

Алгебра логики — это раздел математики, изучающий логические операции над высказываниями. Она позволяет формализовать логические рассуждения и вычислять истинность сложных логических выражений.

Основные особенности алгебры логики:

• Оперирует высказываниями, которые могут быть либо истинными, либо ложными
• Истина обозначается как 1, ложь — как 0
• Использует специальные логические операторы для связи высказываний
• Позволяет вычислять истинность сложных логических выражений
• Имеет набор законов для преобразования и упрощения выражений

Зачем нужна алгебра логики? Она находит широкое применение в различных областях:

• Проектирование электронных схем и цифровых устройств
• Разработка алгоритмов и программного обеспечения
• Создание систем искусственного интеллекта
• Анализ и доказательство математических утверждений
• Формализация логических рассуждений в философии и других науках

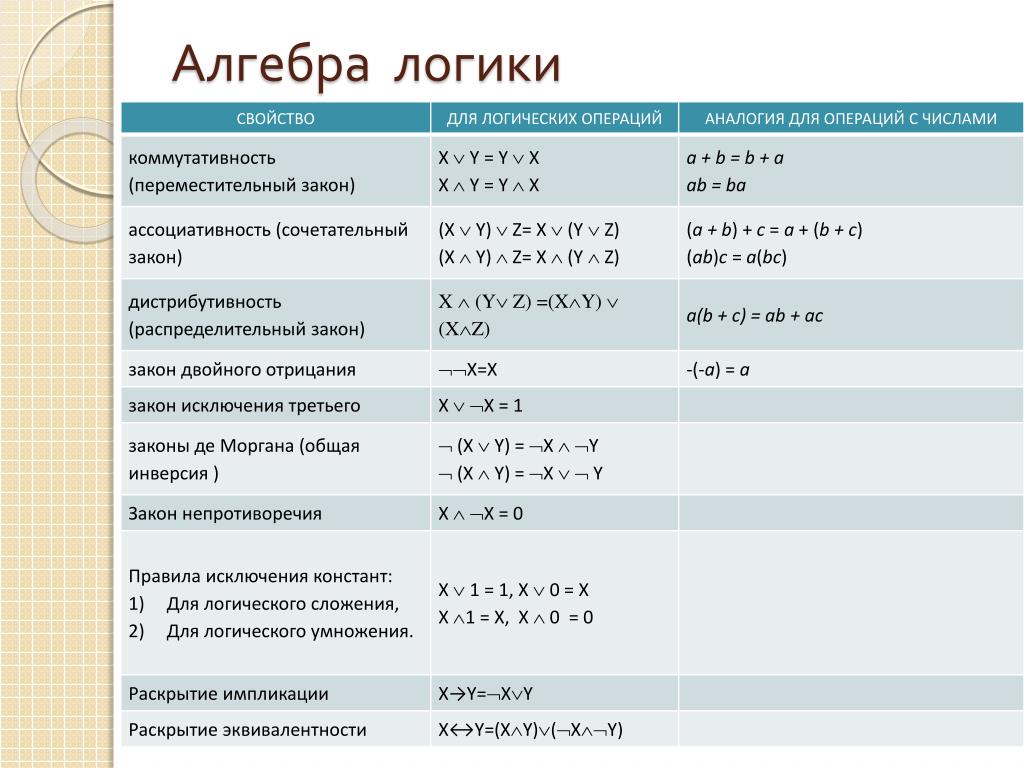
Основные логические операторы

В алгебре логики используется несколько базовых логических операторов для связи высказываний:

Конъюнкция (логическое И)

Обозначается символом ∧. Истинна только если оба исходных высказывания истинны.

Например: «Сегодня холодно (A) И идет дождь (B)» — истинно только если действительно холодно И идет дождь.

Дизъюнкция (логическое ИЛИ)

Обозначается символом ∨. Истинна если хотя бы одно из исходных высказываний истинно.

Например: «Я куплю яблоки (A) ИЛИ груши (B)» — истинно, если куплю хотя бы что-то одно.

Отрицание (логическое НЕ)

Обозначается символом ¬. Меняет истинность высказывания на противоположную.

Например: «НЕ (Сегодня суббота)» — истинно в любой день недели, кроме субботы.

Импликация (логическое следование)

Обозначается символом →. Ложна только если из истинного высказывания следует ложное.

Например: «Если идет дождь (A), то на улице мокро (B)» — ложно только если идет дождь, но на улице не мокро.

Эквивалентность (логическое равенство)

Обозначается символом ≡. Истинна если оба высказывания одновременно истинны или ложны.

Например: «Число четное тогда и только тогда, когда оно делится на 2 без остатка».

Таблицы истинности

Таблица истинности — это инструмент для определения истинности сложного логического выражения в зависимости от истинности входящих в него простых высказываний.

Как составить таблицу истинности:

1. Выписать все простые высказывания, входящие в выражение
2. Составить все возможные комбинации их истинностных значений (0 и 1)
3. Для каждой комбинации вычислить результат всего выражения

Пример таблицы истинности для выражения A ∧ B:

A	B	A ∧ B
0	0	0
0	1	0
1	0	0
1	1	1

Таблицы истинности позволяют проанализировать поведение логического выражения для всех возможных входных данных.

Законы логики

Законы логики позволяют преобразовывать и упрощать логические выражения. Вот некоторые из основных законов:

Закон двойного отрицания

¬(¬A) ≡ A

Двойное отрицание высказывания равносильно самому высказыванию.

Законы де Моргана

¬(A ∧ B) ≡ ¬A ∨ ¬B

¬(A ∨ B) ≡ ¬A ∧ ¬B

Отрицание конъюнкции равносильно дизъюнкции отрицаний, и наоборот.

Закон исключенного третьего

A ∨ ¬A ≡ 1

Высказывание либо истинно, либо ложно, третьего не дано.

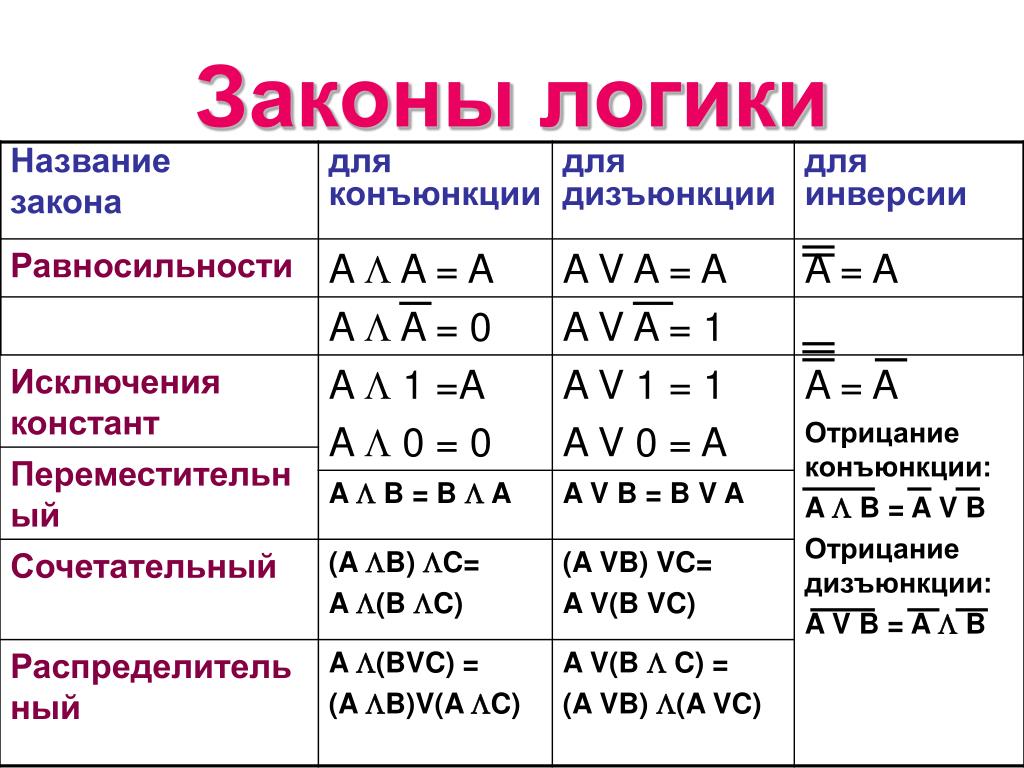
Закон противоречия

A ∧ ¬A ≡ 0

Высказывание не может быть одновременно истинным и ложным.

Применение алгебры логики в информатике

Алгебра логики нашла широкое применение в информатике и вычислительной технике:

• Проектирование логических схем компьютеров
• Оптимизация булевых функций в программировании
• Разработка алгоритмов поиска и сортировки данных
• Создание систем управления базами данных
• Реализация логического вывода в экспертных системах

Понимание основ алгебры логики важно для всех специалистов, связанных с информационными технологиями.

Связь алгебры логики с теорией множеств

Алгебра логики тесно связана с теорией множеств. Логические операции имеют аналоги в теории множеств:

• Конъюнкция ∧ соответствует пересечению множеств ∩
• Дизъюнкция ∨ соответствует объединению множеств ∪
• Отрицание ¬ соответствует дополнению множества

Эта связь позволяет применять методы алгебры логики для решения задач теории множеств и наоборот.

Нормальные формы логических выражений

Нормальные формы — это стандартные способы записи логических выражений. Основные виды:

Дизъюнктивная нормальная форма (ДНФ)

Представляет выражение в виде дизъюнкции элементарных конъюнкций. Например:

(A ∧ B) ∨ (¬A ∧ C)

Конъюнктивная нормальная форма (КНФ)

Представляет выражение в виде конъюнкции элементарных дизъюнкций. Например:

(A ∨ B) ∧ (¬A ∨ C)

Нормальные формы упрощают анализ и преобразование логических выражений.

Импликация – Гуманитарный портал

Импликация — это логическая операция, принятая в формализованных языках (см. Язык формализованный) для образования сложных высказываний (формул) из элементарных (простых) высказываний (см. Высказывание) и по смыслу равнозначная нестрогому условию «если…, то…», принятому в естественном языке (см. Язык).

Импликация читается: «если A, то 

B», или «из A следует B»; записывается: A → B (здесь высказывание A называется посылкой высказывания A → B, а высказывание B — его заключением, для записи применяются также стрелки другой формы, но всегда указывающие на соотношение посылка → следствие), другое обозначение импликации: A ⊃ B; другое название импликации: логическое следование (см. Логическое следование), однако между ними есть различие — импликация как логическое выражение может принимать значения «истина» или «ложь», тогда как логическое следование A → B утверждает, что во всех случаях, когда значение A истинно, B также будет истинно.

Понятие импликации сформировалось в процессе обособления языка логики и его последующей символизации (см. Логика символическая). Различные подходы к формализации логического следования привели, наряду с классической теорией импликации, к построению различных теорий строгой, сильной, аналитической, интенсиональной, релевантной и некоторых других видов импликации.

В естественном языке импликация играет важную роль в рассуждениях и умозаключениях (см. Рассуждение, Умозаключение), так как [при учитывании смыслового содержания высказываний] предполагает причинную связь между посылкой и заключением, и её истинность зависит от смысла этих высказываний. Так, в русском языке распространены следующие выражения импликации:

• если A, то B;
• из A следует B;
• при A будет B;
• в случае A произойдёт B;
• B, так как A;
• B, потому что A;
• A — достаточное условие для B;
• B — необходимое условие для A.

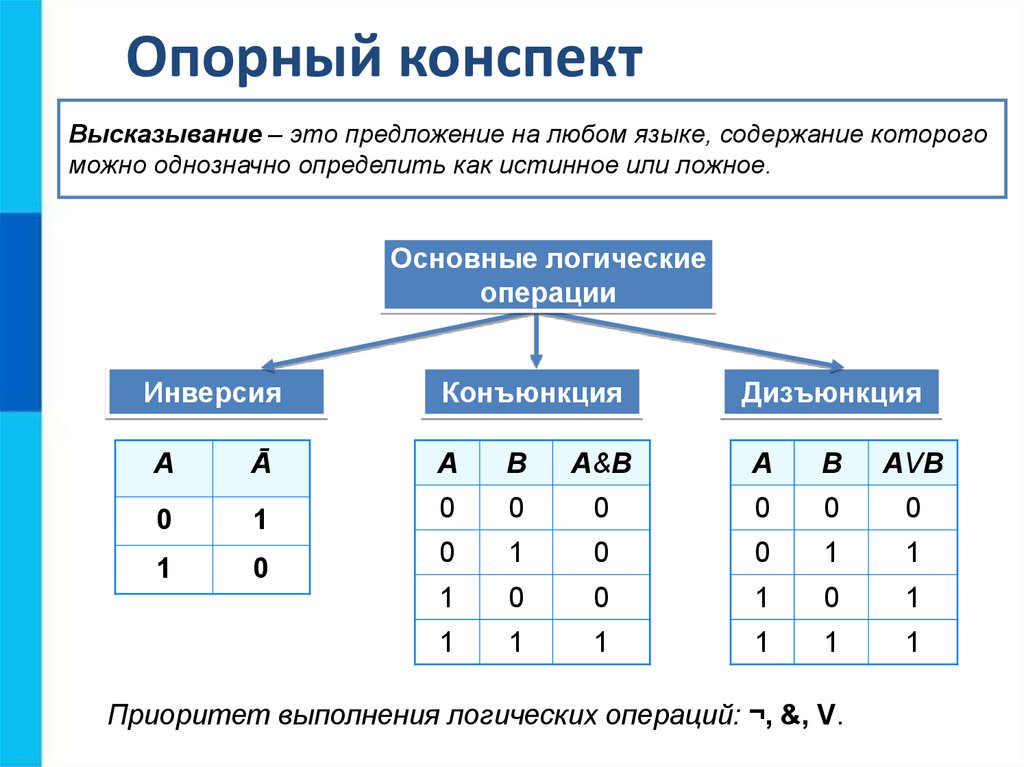
В математической логике обычно учитывается лишь истинность или ложность высказываний, а не смысловое содержание. Поэтому импликация обычно понимается в соответствии с истинностной таблицей:

A	B	A → B
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

В классической логике (см. Логика), формальной логике (см. Логика формальная), языках формальных теорий (см. Формализация) и языках программирования импликация составляет одну из пяти наиболее распространённых

логических связок, или логических операций (см. Логические операции), наряду с конъюнкцией (см.  Конъюнкция), дизъюнкцией (см. Дизъюнкция), эквиваленцией (см. Эквиваленция) и отрицанием (см. Отрицание).

Алгебра логики — Умскул Учебник

На этой странице вы узнаете

• Что такое алгебра логики и зачем здесь котики?
• Как вычислить истинность логического выражения?
• Для чего нужны законы логики?

Как часто поведение котов вам кажется странным? А если кот в галстуке или вооружен? Сейчас будем разбираться в логике с помощью этих пушистых созданий.

Понятие алгебры логики

Обратите внимание на этого персонажа:

Я скажу про него две вещи:

1. Этот кот в галстуке.
2. Этот кот белого цвета.

Очевидно, что с первым высказыванием и поспорить нельзя, а вот второе — наглая ложь. А если я захочу вас запутать: «Этот кот в галстуке или он белого цвета, из чего следует, что он белого цвета и в галстуке или не белый». Что это в итоге — правда или ложь?

Чтобы это определить, в математике есть отдельный раздел.

Алгебра логики — это раздел математики, который занимается логическими операциями над высказываниями.

Любое высказывание может быть либо истинным, либо ложным. Цель алгебры логики — определять истинность логических выражений на основании отдельных высказываний. Алгебра логики действительно может, например, складывать и умножать высказывания друг с другом, и чтобы в записи это выглядело адекватно, истину принято обозначать как 1, а ложь — как 0.

Что такое алгебра логики и зачем здесь котики? В примере с котиком высказывание А было истинно, а высказывание В — ложно. На языке алгебры логики это было бы записано как А = 1, В = 0.

Логические выражения и операторы 

Как вычислить истинность логического выражения?

Термин высказывание, мы теперь знаем.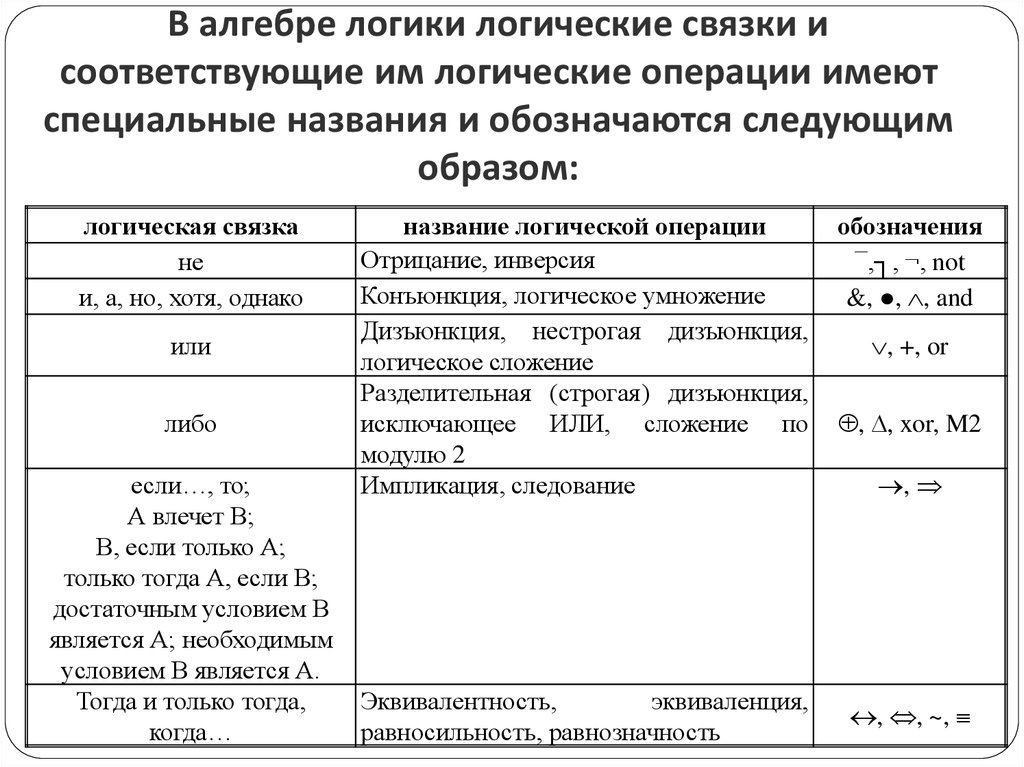 Но что такое логическое выражение? Выражение — это уравнение из высказываний, как математическое уравнение из чисел. 

«Этот кот вооружен и его глаза зеленого цвета», — в одном выражении мы использовали два высказывания. 

Истинность выражения определяется истинностью логических высказываний, а также логическими операторами, которые стоят между ними.

Например, я скажу про того же самого кота: «Этот кот вооружен и его глаза голубые». Это будет наглая ложь, так как я употребил союз И, то есть подразумеваю, что оба высказывания истинны — что неправда. Но если бы я сказал: «Этот кот вооружен или его глаза голубые», союз ИЛИ защитил бы меня от клейма лжеца. Я делаю акцент на истинности только одного высказывания из двух. 

Так и работают логические операторы — в зависимости от них все выражение и принимает значение истины или лжи.

Основные логические операторы алгебры логики:

• Конъюнкция: логическое умножение или логическое И. 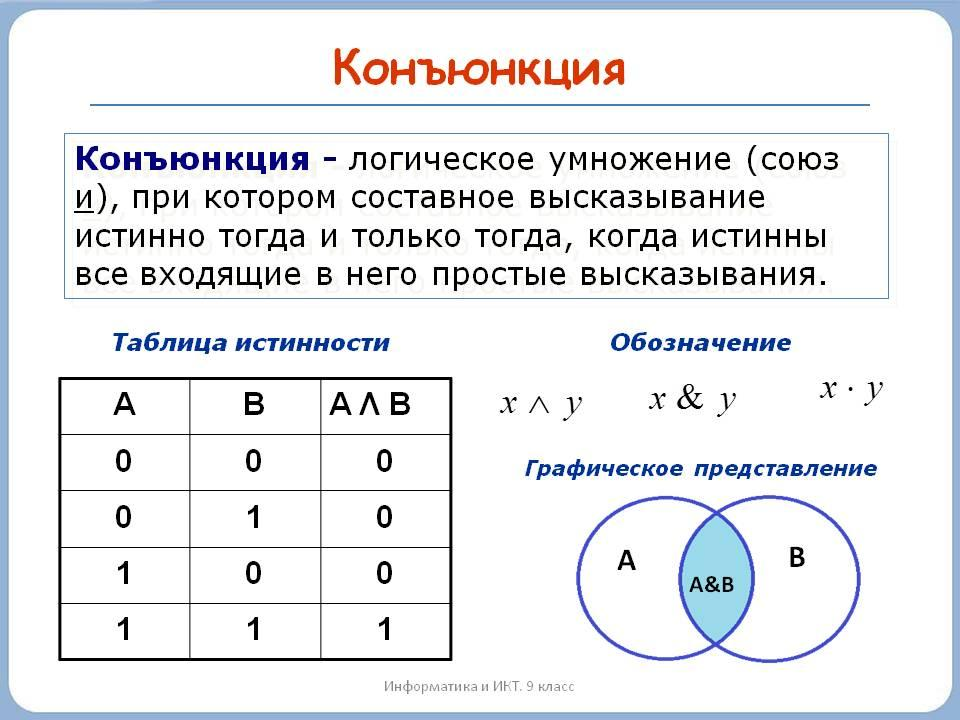В записи обозначается как ∧. А ∧ В дает истину только в том случае, если оба высказывания А и В истинны.

  Называется логическим умножением, потому что имеет схожий принцип работы: если хоть один из множителей будет равен 0, все выражение будет равно 0.

  В примере про кота выше выражение «Этот кот вооружен ∧ его глаза голубые» будет ложным. Он вооружен, но глаза у него не голубые. Одно из высказываний не выполнилось, так что конъюнкция равна 0.

• Дизъюнкция: логическое сложение или логическое ИЛИ. В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.

  Называется логическим сложением за схожесть: если складывать только 0 и 1, чем мы и занимаемся, то достаточно одному слагаемому быть 1, чтобы все выражение не было равно 0.

  Важно сразу понять — если применить логическое сложение к двум единицам (1 ∨ 1), мы получим не 2, а все еще 1. 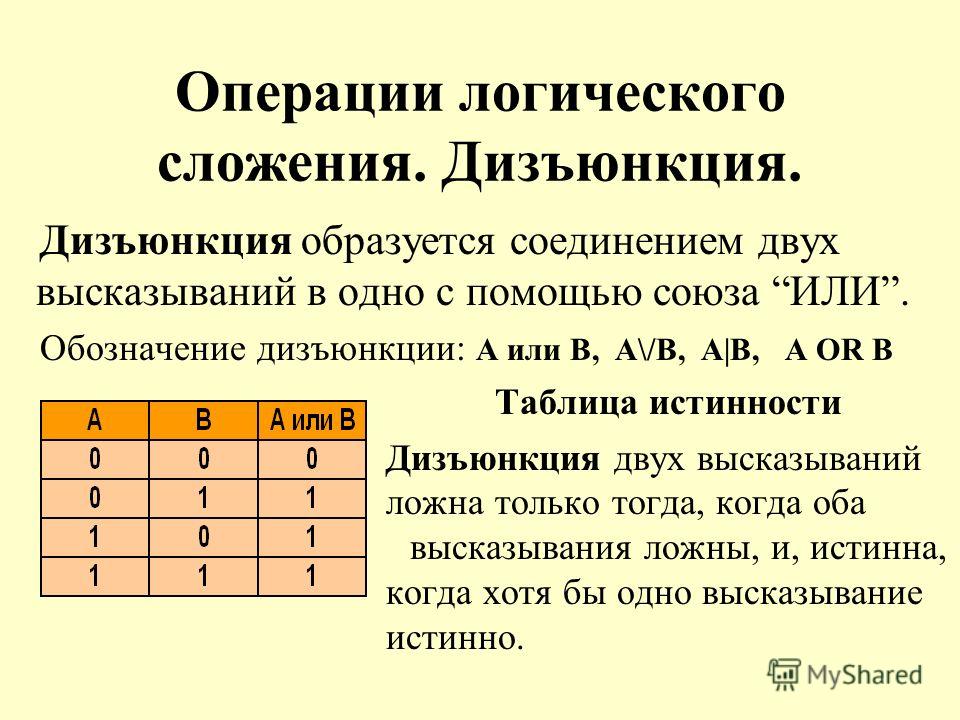Все-таки единица здесь означает не число, а истину, и сложив две, мы не получим одну сверх-истину.

  Тогда выражение «Этот кот вооружен ∨ его глаза голубые» будет уже истинным: глаза его не голубые, но он все-таки вооружен. Дизъюнкция вернет нам 1.

• Инверсия: логическое отрицание или логическое НЕ. Превращает истину в ложь и наоборот.

  Ложное высказывание «Его глаза голубые» можно легко превратить в истину, если сказать «Его глаза НЕ голубые». В записи обозначается чертой над выражением или знаком ¬, например, ¬А.

• Эквиваленция, если проще — равенство. Если оба высказывания равны (оба 0 или оба 1), то получим истину, иначе — ложь. Обозначается как ≡.

  Истинным будет выражение «У кота нет оружия так же, как его глаза голубые». И то, и другое — ложь, но мы их сравнили, сказав, что они одинаковы по истинности, что уже правда.

• Импликация, иначе говоря, следование. Обозначается стрелочкой, например А ⇒ В. Если из истины следует ложь, то это автоматически ложь, все остальное — истина. 

  Например, вас никто не просил кормить кота. Если вы этого не сделаете, ничего плохого и не случится. А если сделаете — тоже хорошо, кот будет рад. А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.

Приоритет этих операторов:

1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация;
5. эквиваленция.

Как и везде в математике, приоритет можно менять с помощью скобок — что в них, то выполняется в первую очередь.

Таблицы истинности

В логических уравнениях высказывания используются в виде переменных, а главная проблема, которую рассматривает алгебра логики — когда точно неизвестна истинность каждого высказывания. Назовем эту ситуацию “кот в мешке”. Сказать про кота можно что угодно, но будет ли это правдой —  мы не узнаем, пока не заглянем в мешок.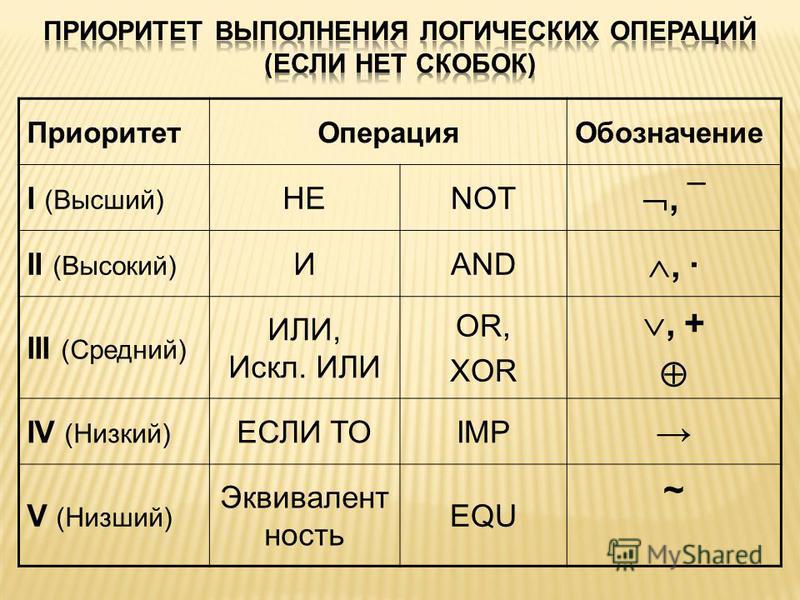 В таких ситуациях нам может помочь таблица истинности.

Таблица истинности — это таблица, которая показывает истинность всего логического уравнения в зависимости от истинности отдельных переменных.

В этой таблице содержатся все возможные наборы переменных. Количество наборов N зависит от количества различных переменных i как N = 2ⁱ.

Чтобы удобно записать наборы, нумеруем их по порядку начиная с 0, переводим их номер в двоичную систему счисления (2сс) и записываем набор цифр.

Давайте запишем таблицы истинности для известных нам логических операторов:

• инверсия берет только 1 переменную и сразу меняет ее значение:

• конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:

• дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:

• эквиваленция вернет 1, если переменные равны, и 0 в противном случае:

• импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:

Импликацию можно выразить через дизъюнкцию: А ⇒ В = ¬А ∨ В

Зная таблицы истинности отдельных операторов, давайте попробуем составить таблицу истинности для полного выражения.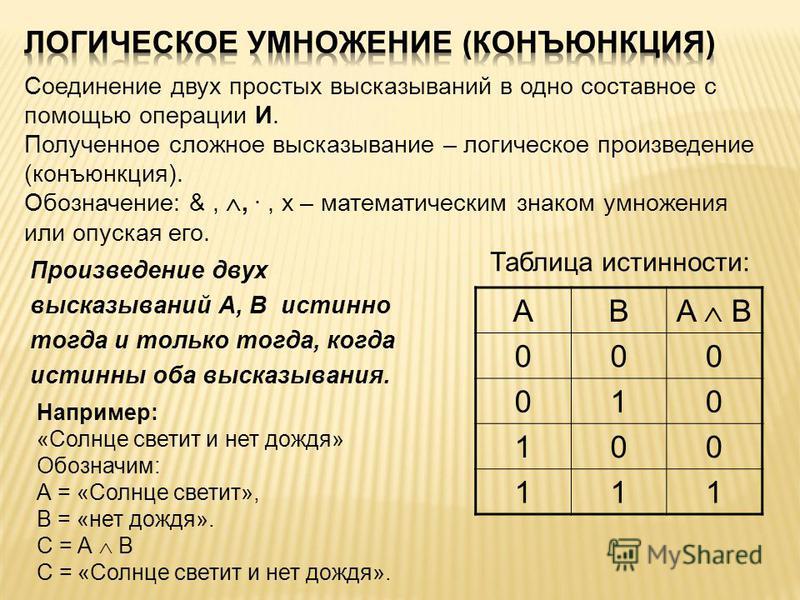

Например, для выражения: А ∧ (В ∨ С) ≡ В ⇒ ¬А.

Важно правильно расставить порядок операций. Как и всегда, в первую очередь выполняется действие в скобках, а дальше — в порядке приоритета.

Здесь порядок операций будет следующим:

Создадим таблицу, в которой сразу пропишем все наборы 0 и 1 для переменных А и В и добавим столбцы для каждого шага вычисления. 

Чтобы удобно записать наборы, пронумеруем их по порядку начиная с 0. Переведем их номер в 2сс и запишем набор цифр. У нас 3 различные переменные, поэтому должно быть 8 наборов.

1. Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.

2. Второе действие — инверсия переменной А.

3. Третье действие — умножение значения А на результат первого действия:

4. Четвертое — импликация значения В и результата второго действия:

5. И последнее действие — эквиваленция результатов 3 и 4 действий:

Последний столбец — и есть результат таблицы истинности.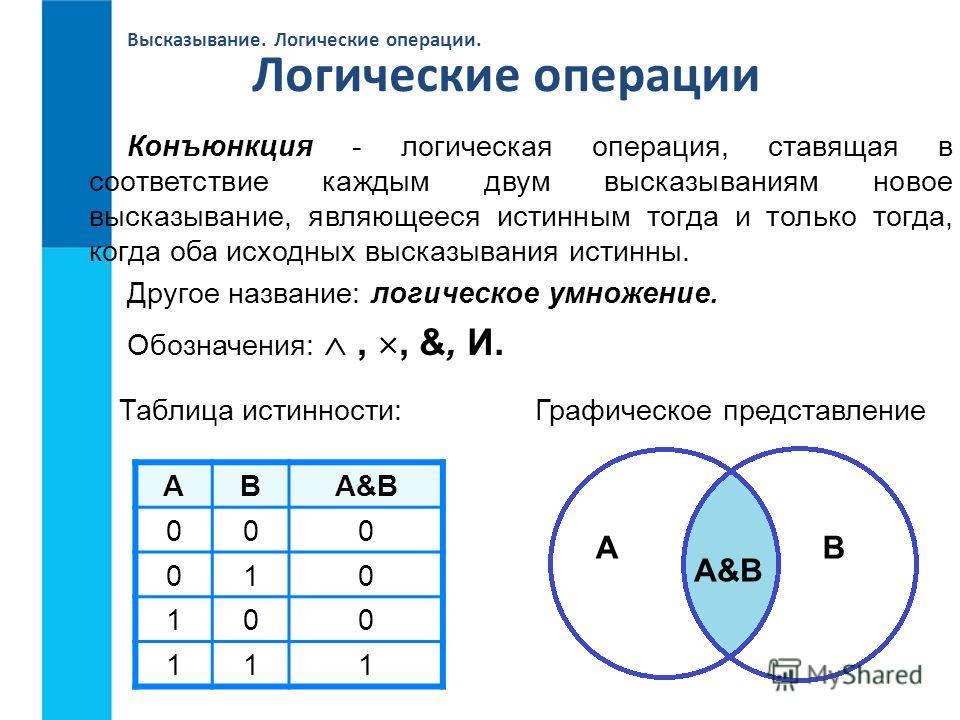 По нему можно сказать, что при А = 1, В = 0 и С = 1 все исходное выражение равно 1, а во всех остальных случаях — 0.

Законы логики

Для чего нужны законы логики? Законы логики позволяют упрощать логические уравнения, делая их не такими большими и более решаемыми.

Их не так уж и мало: от самых простых и очевидных до достаточно хитрых; от тех, которые встречаются очень часто до довольно редких.

Не обязательно знать все наизусть — часть из них действительно проста и похожа на правила математики начальной школы. Про остальные стоит помнить: если увидите очень большое логическое уравнение, высока вероятность того, что эти законы помогут его сократить.

Попробуем упростить исходное выражение ¬(¬А ∧ ¬В) ∨ В ∧ С:

1. Первым можно увидеть закон де Моргана, где у нас идет отрицание целой скобки:

¬(¬А ∧ ¬В) ∨ В ∧ С = ¬(¬А) ∨ ¬(¬В) ∨ В ∧ С

2. Здесь же появляются переменные А и В, к которым можно применить закон двойного отрицания:

¬(¬А) ∨ ¬(¬В) ∨ В ∧ С = А ∨ В ∨ В ∧ С

3. Можно заметить закон поглощения — В складывается с умножением В на С:

А ∨ В ∨ В ∧ С = А ∨ В

Итого, уравнение с 3 переменными и множеством отрицаний мы смогли превратить в максимально простую запись, где осталось всего 2 переменные:

¬(¬А ∧ ¬В) ∨ В ∧ С = А ∨ В

Фактчек

• Алгебра логики — это математика, которая пользуется не числами, а высказываниями, являющимися истинными или ложными. Истина обозначается как 1, а ложь — как 0.
• Основными логическими операторами являются инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.
• Для расчета истинности логического уравнения используется таблица истинности.
• Законы логики помогают сокращать логические уравнения.

Проверь себя

Задание 1.
Выберите правильный порядок приоритета логических операторов:

1. Импликация, эквиваленция, конъюнкция, дизъюнкция, инверсия.
2. Инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция.
3. Инверсия, конъюнкция, дизъюнкция, эквиваленция, импликация.
4. Инверсия, дизъюнкция, конъюнкция, эквиваленция, импликация.

Задание 2.
Сопоставьте название логического оператора с упрощенным:

Инверсия	А. Умножение
Эквиваленция	Б. Отрицание
Импликация	В. Следование
Дизъюнкция	Г. Равенство
Конъюнкция	Д. Сложение

Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения: А ∨ В ⇒ ¬С?

1. 11101010
2. 11101111
3. 11111110
4. 11000100

Задание 4.
Сократите логическое выражение: ¬(А ∨ В) ∧ (¬А ∨ С)

1. ¬(А ∧ В)
2. ¬А ∨ ¬В ∨ С
3. ¬А ∧ ¬В ∧ С
4. ¬А ∧ ¬В

Ответы: 1. — 2; 2. — 1Б, 2Г, 3В, 4Д, 5А; 3. — 1; 4. — 4.

Обозначение

— логический символ «такой, что»

Задавать вопрос

спросил 9 лет, 7 месяцев назад

Изменено 3 года, 2 месяца назад

Просмотрено 36 тысяч раз

$\begingroup$

Итак, в определении того, что такое квадратный корень,

$\sqrt{x}$ — все числа $y$ такие, что $y×y=x$.

Существуют ли какие-либо логические математические символы, чтобы приведенное выше определение можно было записать с использованием только логических операторов и без использования естественного языка?

Где я могу получить вводные или справочные материалы по всем таким логическим символам?

обновление : Через некоторое время после того, как я задал вопрос, я заметил, что определение квадратного корня, которое я даю, неверно. Квадратный корень из $x$ определяется как неотрицательное число $y$, удовлетворяющее условию $y*y=x$. Но вопрос был об обозначениях, а не о квадратных корнях, поэтому я оставляю его как есть из-за некоторых ответов, использующих предоставленное (ошибочное) определение. 92=х\} $$

Я также вижу, как люди используют (и сам использовал) «s.t.» как сокращение для таких, что в формулах.

$\endgroup$

3

$\begingroup$

Обычно не требуется никакого другого символа, кроме двоеточия или $\mid$ для «такой, что».

В англоязычной версии вашего утверждения $\sqrt x$ описывается как множество. Вы можете написать это как:

$$y\in \sqrt{x} \iff y\in\mathbb R \land y\cdot y = x$$

Обратите внимание, я добавил $y\in\mathbb R$, потому что вам нужно знать домен, в котором вы работаете. Вы могли бы изменить это, конечно.

Это часто сокращается как:

$$\sqrt{x} =\{y\in\mathbb R\mid y\cdot y = x\}$$

Грубо говоря, символ $\mid$ функционирует как здесь символ «такой, что». Иногда вместо этого используется символ $:$.

$\endgroup$

$\begingroup$ 92=х)$$ то есть $\iota v \Phi$ используется для обозначения уникального элемента (надеюсь) одноэлементного множества $\{v\mid \Phi\}$. Хотя наличие такой записи может быть полезно для крайней формальности, лично я не являюсь ее сторонником.

$\endgroup$

3

$\begingroup$

Я ТАКЖЕ видел перевернутый символ ∈ для «такой, что».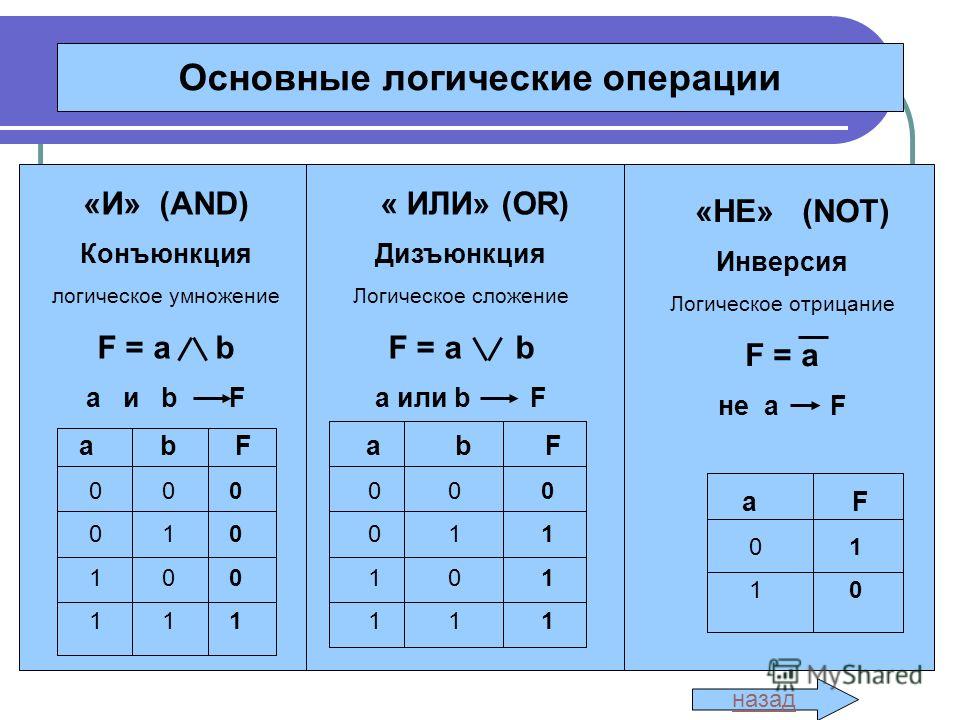 Я видел это в логической записи для определения предела функции. М. Дель Неро

$\endgroup$

1

Теория логики — Основные обозначения. Часть II — Краткий обзор коннективов… | Хесус Наджера

Часть II. Краткий обзор связок, импликаций и кванторов

Происхождение теории логики начинается с концепции аргумента . Большинство учебников по логике содержат вводное, центральное определение аргумента, которое, вероятно, звучит примерно так:0003

Аргумент содержит одно или несколько специальных утверждений, называемых посылками , предлагаемых в качестве основания полагать, что следующее утверждение, называемое заключением, истинно

Посылки являются атомами логической теории : все построено из них. Предпосылка — это декларативное утверждение, что должно строго оценивать только как истинное или ложное.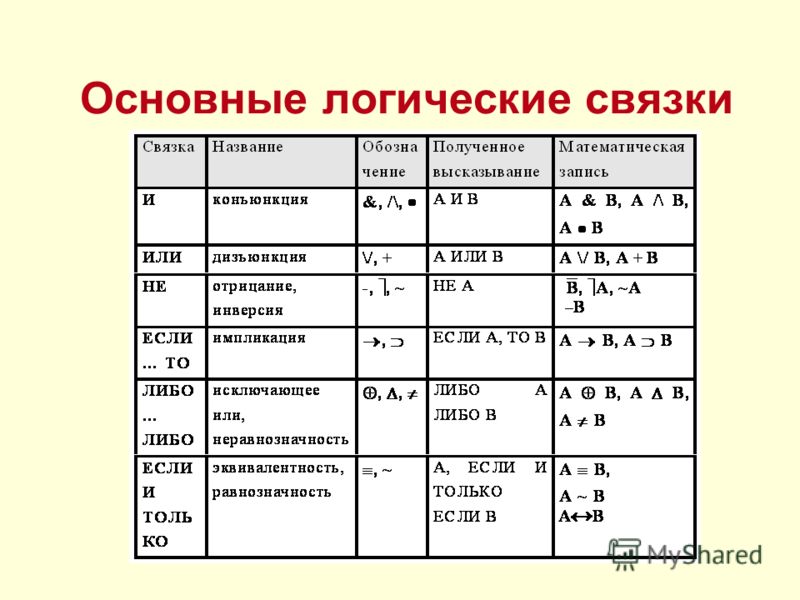 Единственная посылка называется примитивной посылкой — в США 50 штатов (что правда). Соединение нескольких помещений вместе образует составное помещение — в США 50 штатов и сегодня в Майами выпал снег (что неверно). Как связать несколько утверждений? Как вы видите в предыдущем примере, с операторами, с которыми вы уже знакомы, но для которых требуется собственный язык и синтаксис.

Связки

Как и в других разделах математики, в предпосылках есть собственный набор основных операторов (сложение, вычитание и т. д.). В теории логики эту роль выполняют пять базовых логических коннекторов , вместе известных как коннекторы . Они суммированы в таблице ниже, предположим, что буквы P и Q представляют две примитивные предпосылки:

Если вы сталкивались с программированием на любом уровне, то весьма вероятно, что приведенная выше таблица покажется вам хотя бы смутно. привычный. Это связано с тем, что связки лежат в основе общеязыкового синтаксиса и почти всегда имеют специальный символ, предназначенный для каждой связки (&& = и, | = или и т. д.).

Какая из пяти связок используется в качестве логической связи между двумя посылками, определяет общее значение истинности составного утверждения на основе значений истинности изменяемых посылок. Здесь стоит выделить важный принцип, который на первый взгляд может показаться нелогичным: при анализе составных утверждений , а не необходимо знать, какие части P и Q на самом деле говорят, а только знать, истинны эти части или нет.

Импликация

Из пяти связок одна заслуживает немедленного изучения — импликация, также известная как утверждения «если-то». Импликация является связкой со стандартной формой P → Q, где P известен как гипотеза (или антецедент), а Q известен как вывод (или следствие).

Несмотря на то, что импликация имеет стандартную форму, определенную выше, существуют три других распространенных типа условных операторов, которые заслуживают рассмотрения.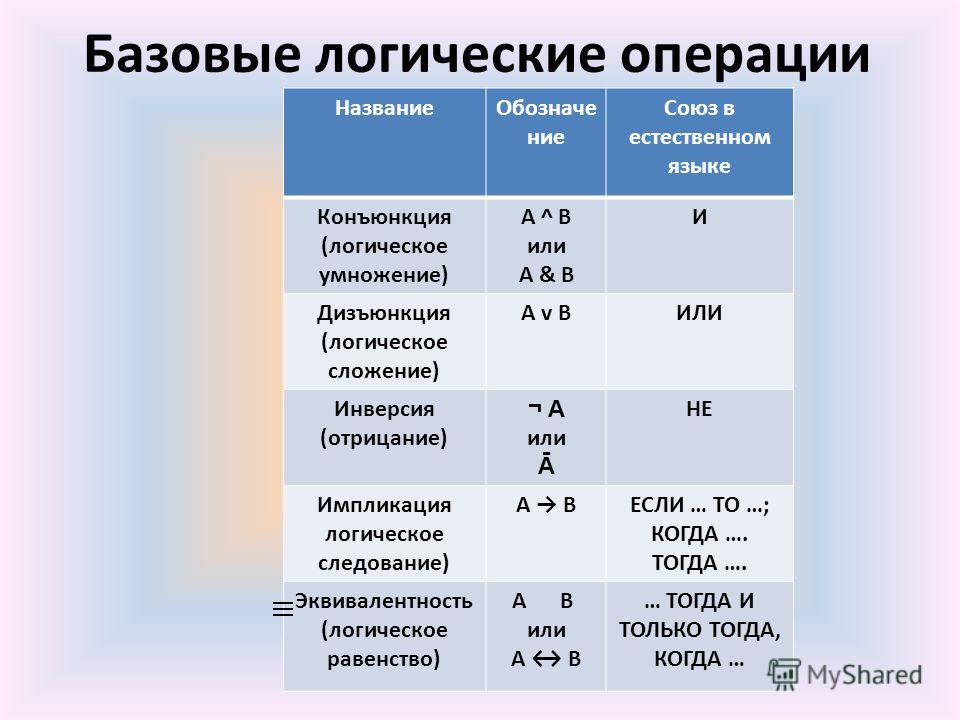 Следующие четыре условных предложения являются простыми, но довольно распространенными и мощными составными утверждениями, полученными путем объединения условных предложений с введенными основными связками:

Условное предложение само по себе является составной посылкой, то есть оно строго оценивается как истинное или ложное. Для любой импликации, как и для любой другой связки, истинностное значение составной посылки определяется истинностными значениями двух ее независимых посылок. В соответствии с определениями, введенными выше, например, импликация верно если гипотеза ложна, или когда вывод верен; что оставляет только один способ сделать вывод ложным: когда гипотеза верна, а вывод ложен.

Если вам казалось, что это слишком много для мысленного отслеживания, как это было для меня, тогда вздохните спокойно и будьте уверены, что в ближайшем будущем появятся мощные инструменты, которые сделают анализ сложных условных операторов таким же простым, как следование плану. Основной инструмент, который мы будем использовать, — это отличный инструмент logic-101 под названием 9.0025 таблицы истинности . Однако, прежде чем мы перейдем к таблицам истинности, давайте сделаем небольшое отступление, чтобы заполнить последний пробел в наших знаниях об основных обозначениях теории логики. Изучите своеобразный сценарий — является ли следующее утверждение предпосылкой?

x больше десяти

Квантификаторы

В соответствии с нашим строгим определением, представленным в первом абзаце, посылка должна оцениваться как истинная или ложная — утверждение не может быть двусмысленным или оставить открытым. Это означает, что переменные, какими мы привыкли их видеть со времен алгебры, недопустимы в теории логики; по крайней мере, без некоторых изменений.

Утверждение, выделенное жирным шрифтом выше, , а не , считается предпосылкой, поскольку x может быть 5 или 25, что делает утверждение истинным или ложным, но в настоящее время ни тем, ни другим.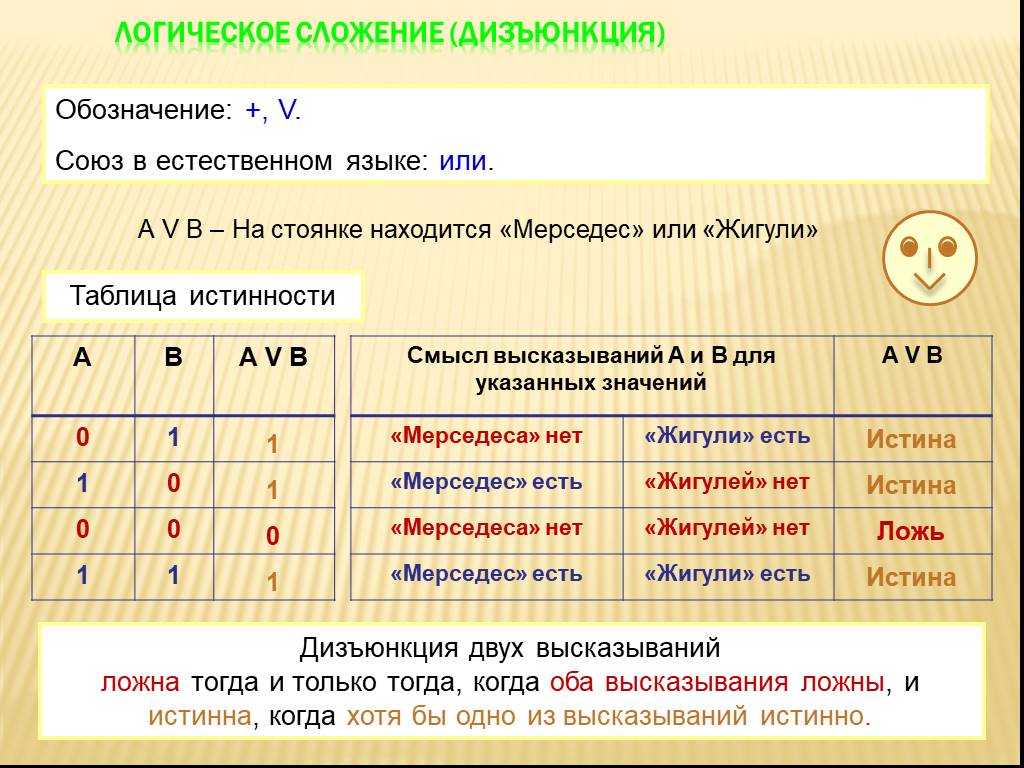 Это, однако, не означает, что мы должны полностью удалить переменные из нашего набора инструментов. Там — это способ использования переменных; процесс называется количественная оценка , умный способ обозначения границ неизвестных переменных в логике. Взгляните на следующее заявление об обновлениях — теперь это предпосылка?

для всех х, х больше ста поскольку он оценивается как категорически ложный. Использование этого «для всех x» известно в теории логики как применение квантификатор. Существует два основных типа квантификаторов. Первый, который мы только что видели, удачно назван универсальным квантором . Продиктовано перевернутой буквой «A», ∀, легко запомнить, что это означает A ll или любой возможный экземпляр во вселенной сделанного заявления. Взгляните на это второе изменение:

существует x больше ста

И снова, не удаляя переменные, мы нашли способ преобразовать утверждение в предпосылку, применяя квантор, так как выражение теперь оценивается строго до верно .