Общая мощность при последовательном соединении. Расчет мощности при последовательном соединении резисторов: особенности и формулы — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общую мощность при последовательном соединении резисторов. Какие формулы используются для вычисления мощности на отдельных резисторах. Чем отличается распределение мощности при последовательном и параллельном соединении.

Содержание

Основные принципы последовательного соединения резисторов

При последовательном соединении резисторов они включаются один за другим, образуя единую неразветвленную цепь. Основные характеристики такого соединения:

Сила тока одинакова во всех резисторах
Общее напряжение равно сумме напряжений на отдельных резисторах
Общее сопротивление равно сумме сопротивлений всех резисторов

Эти принципы лежат в основе расчета мощности при последовательном соединении.

Формула расчета общей мощности

Общая мощность при последовательном соединении резисторов рассчитывается по формуле:

P = I^2 * R

где:

P — общая мощность (Вт)
I — сила тока в цепи (А)
R — общее сопротивление цепи (Ом)

Как видно, для расчета общей мощности нужно знать силу тока и общее сопротивление цепи.

Расчет мощности на отдельных резисторах

Мощность, выделяемая на каждом отдельном резисторе при последовательном соединении, рассчитывается по формуле:

P_n = I^2 * R_n

где:

P_n — мощность на n-ом резисторе
I — сила тока в цепи
R_n — сопротивление n-го резистора

Важно отметить, что сила тока I одинакова для всех резисторов при последовательном соединении.

Особенности распределения мощности при последовательном соединении

При последовательном соединении резисторов мощность распределяется между ними неравномерно. Основные закономерности:

Чем больше сопротивление резистора, тем больше мощности на нем выделяется
Соотношение мощностей на резисторах равно соотношению их сопротивлений
Суммарная мощность на всех резисторах равна общей мощности цепи

Это отличает последовательное соединение от параллельного, где мощность распределяется обратно пропорционально сопротивлениям.

Пример расчета мощности при последовательном соединении

Рассмотрим пример расчета мощности для цепи с тремя последовательно соединенными резисторами:

R1 = 10 Ом
R2 = 20 Ом
R3 = 30 Ом
Напряжение в цепи U = 12 В

Решение:

Рассчитаем общее сопротивление: R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Найдем силу тока: I = U / R = 12 / 60 = 0.2 А
Общая мощность: P = I^2 * R = 0.2^2 * 60 = 2.4 Вт
Мощность на отдельных резисторах:
- P1 = I^2 * R1 = 0.2^2 * 10 = 0.4 Вт
- P2 = I^2 * R2 = 0.2^2 * 20 = 0.8 Вт
- P3 = I^2 * R3 = 0.2^2 * 30 = 1.2 Вт

Как видим, мощность распределилась пропорционально сопротивлениям резисторов, а их сумма равна общей мощности цепи.

Сравнение с параллельным соединением резисторов

Расчет мощности при последовательном соединении резисторов имеет ряд отличий от параллельного соединения:

Характеристика	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова на всех резисторах	Разная на резисторах, суммарный ток равен сумме токов через резисторы
Напряжение	Сумма напряжений на резисторах равна общему напряжению	Одинаково на всех резисторах
Распределение мощности	Пропорционально сопротивлениям	Обратно пропорционально сопротивлениям

Эти различия необходимо учитывать при проектировании электрических цепей и выборе типа соединения резисторов.

Практическое применение расчетов мощности

Умение рассчитывать мощность при последовательном соединении резисторов важно в различных областях электротехники и электроники:

Проектирование электрических схем
Выбор номиналов резисторов для делителей напряжения
Расчет тепловых режимов работы электронных устройств
Оптимизация энергопотребления в электрических цепях
Анализ работы измерительных приборов и датчиков

Правильный расчет мощности позволяет избежать перегрева компонентов и обеспечить надежную работу устройств.

Ограничения и особые случаи при расчете мощности

При расчете мощности в последовательных цепях следует учитывать некоторые ограничения и особые случаи:

Нелинейность резисторов при высоких температурах может влиять на точность расчетов
При очень больших токах необходимо учитывать сопротивление соединительных проводов
В цепях переменного тока расчет усложняется из-за реактивных составляющих

При наличии в цепи других элементов (конденсаторов, катушек индуктивности) расчет мощности требует дополнительных формул

В сложных случаях может потребоваться использование специализированного программного обеспечения для моделирования электрических цепей.

Заключение

Расчет мощности при последовательном соединении резисторов — важный навык для работы с электрическими цепями. Основные принципы:

Общая мощность равна квадрату тока, умноженному на общее сопротивление
Мощность на отдельных резисторах пропорциональна их сопротивлениям
Сумма мощностей на всех резисторах равна общей мощности цепи

Понимание этих принципов и умение применять соответствующие формулы позволяет эффективно проектировать и анализировать электрические схемы с последовательным соединением резисторов.

Расчет мощности при последовательном соединении

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.

Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.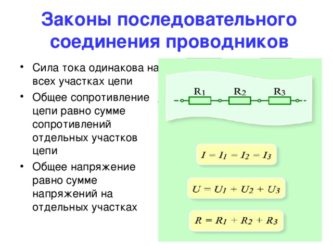

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.

Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

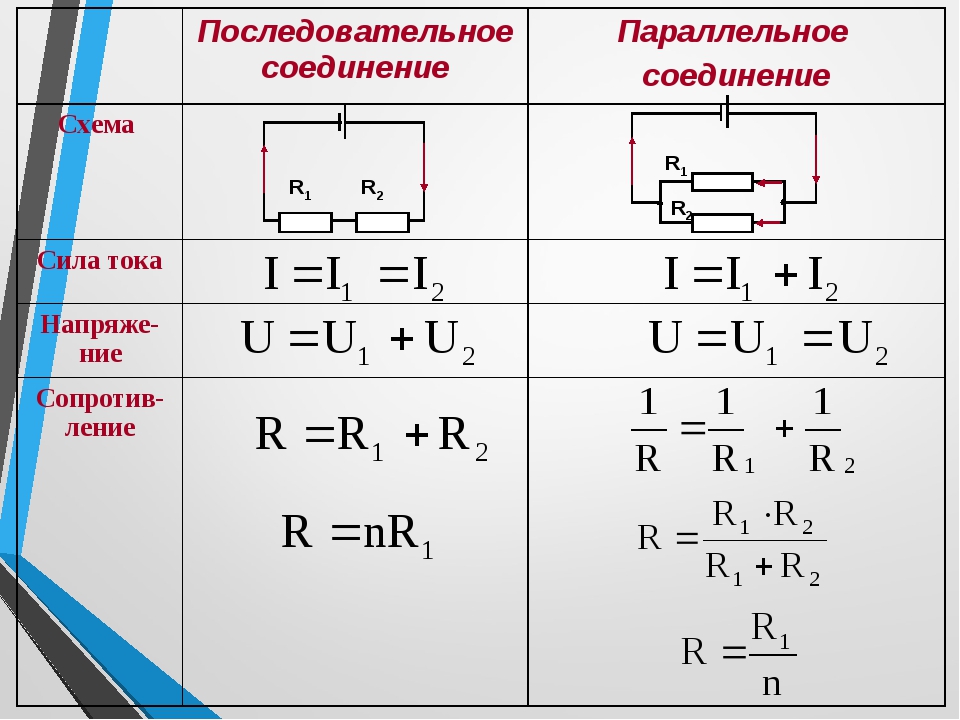
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме.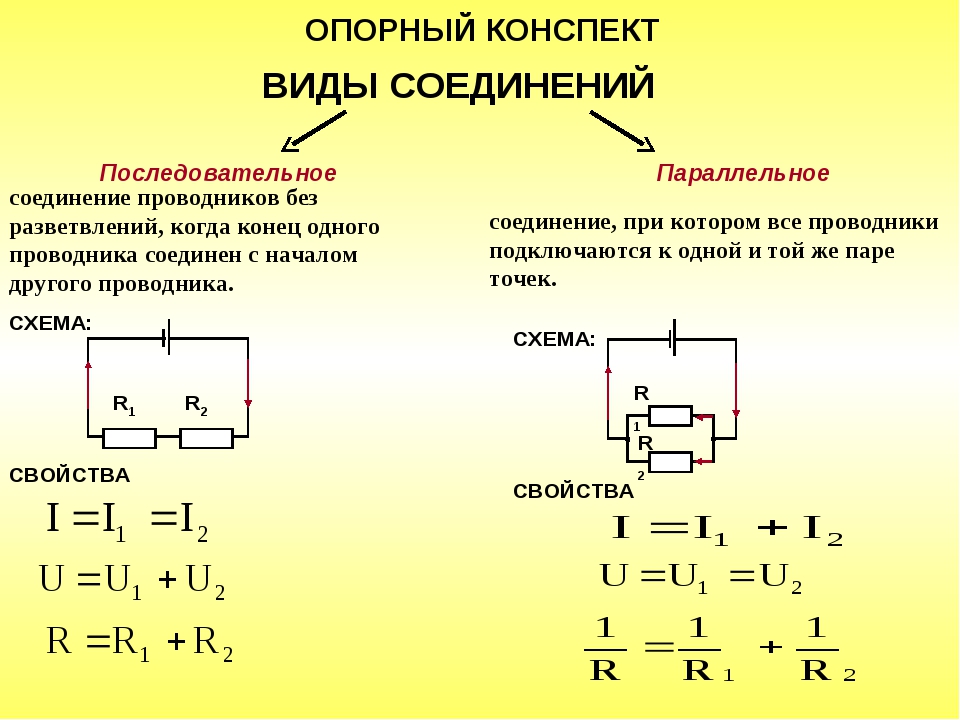

Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно.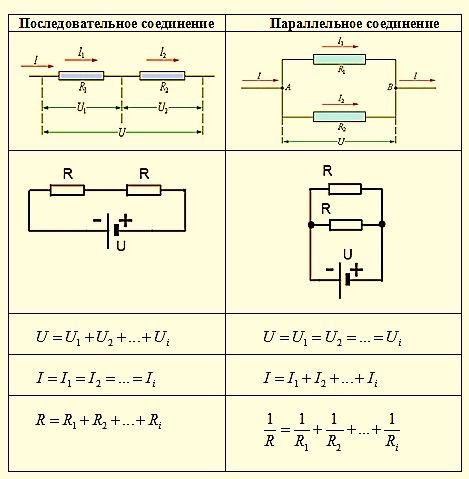 Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.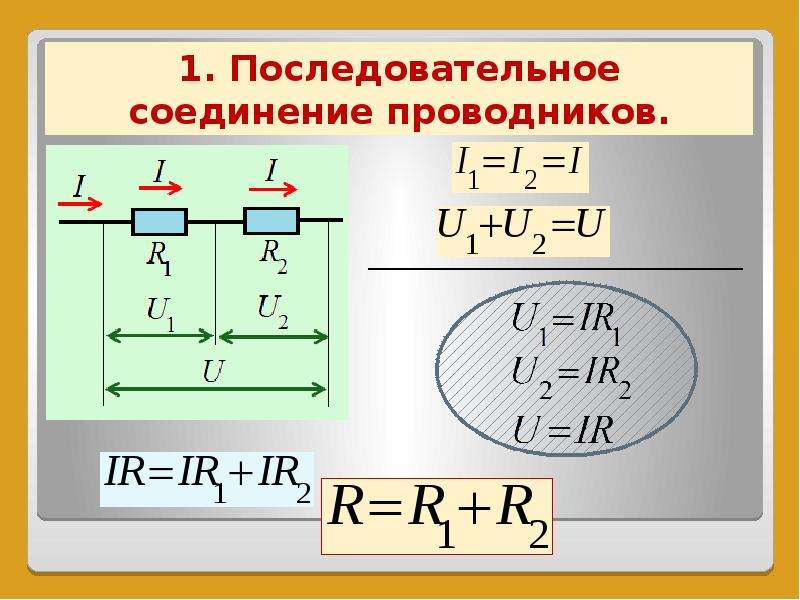

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи.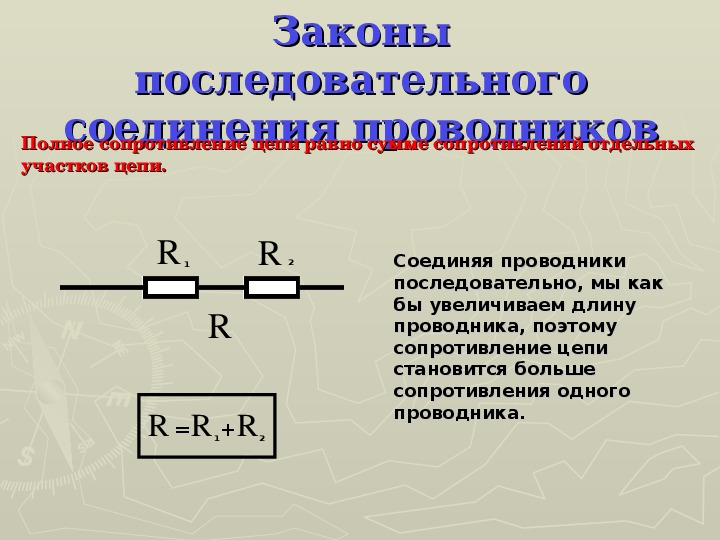 Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой.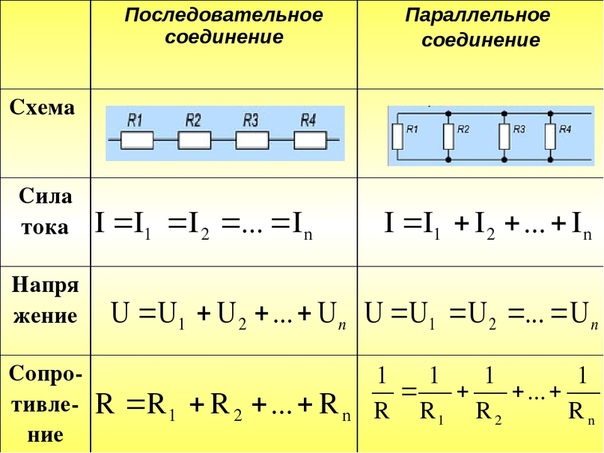 Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В.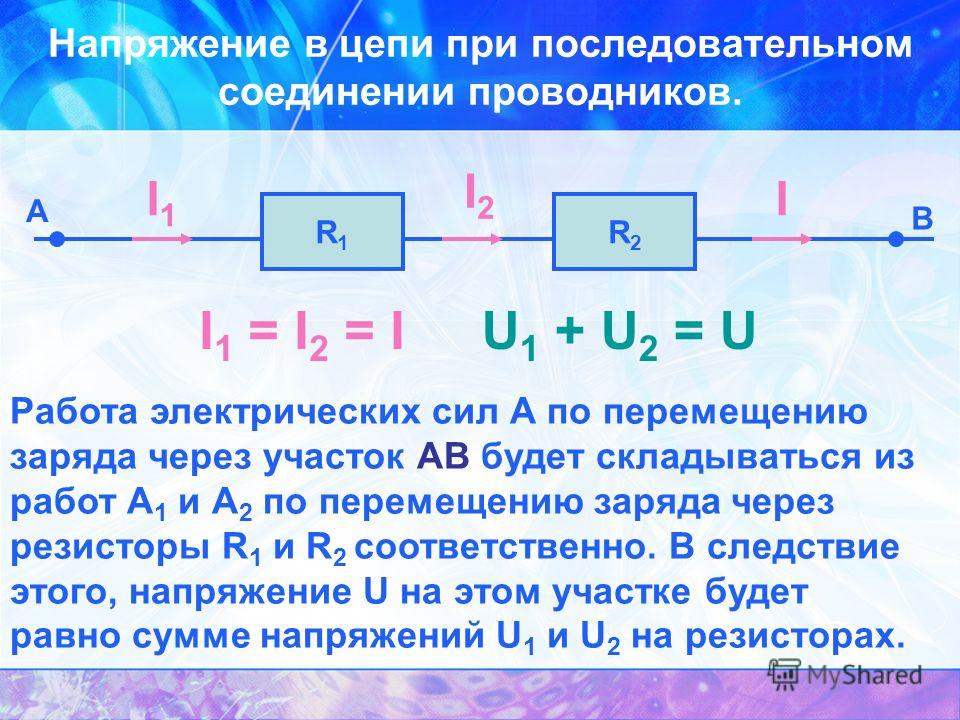 Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

Первая формула для последовательного вида соединения.
Далее, для параллельной схемы.
И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)

Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселей

Параллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности.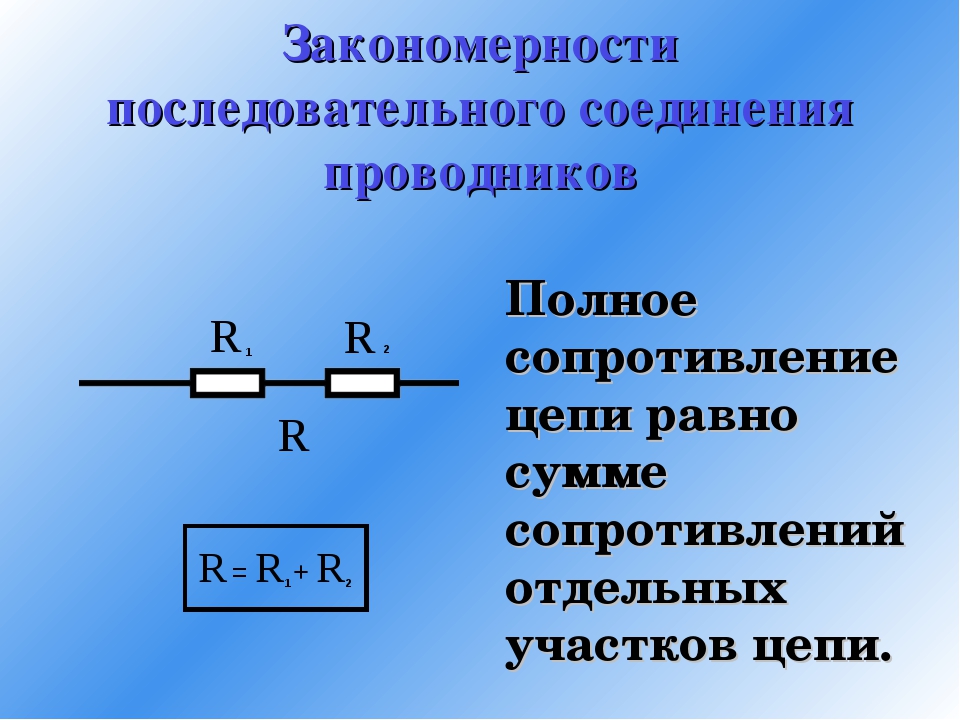 В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы. Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.

Вашему вниманию подборка материалов:

Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам

Ознакомьтесь также с:

Резисторы

Соединяем последовательно

[Сопротивление последовательно соединенных резисторов, кОм] = [Сопротивление первого резистора, кОм] + [Сопротивление второго резистора, кОм]

[Мощность, рассеиваемая первым резистором, Вт] = [Сопротивление первого резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

[Мощность, рассеиваемая вторым резистором, Вт] = [Сопротивление второго резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт. 2 / [Сопротивление первого резистора, кОм] / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Практика проектирования электронных схем. Самоучитель электроники.
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.

Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис.
Тиристоры в электронных схемах. Тонкости и особенности использования. Виды тирис.

Биполярный транзистор. Принцип работы. Применение. Типы, виды, категор.
Все о биполярном транзисторе. Принцип работы. Применение в схемах. Свойства. Кла.

Плавная регулировка яркости свечения люминесцентных ламп дневного свет.
Схема драйвера для плавной регулировки яркости свечения ламп дневного света. Дра.

Проверка электронных элементов, радиодеталей.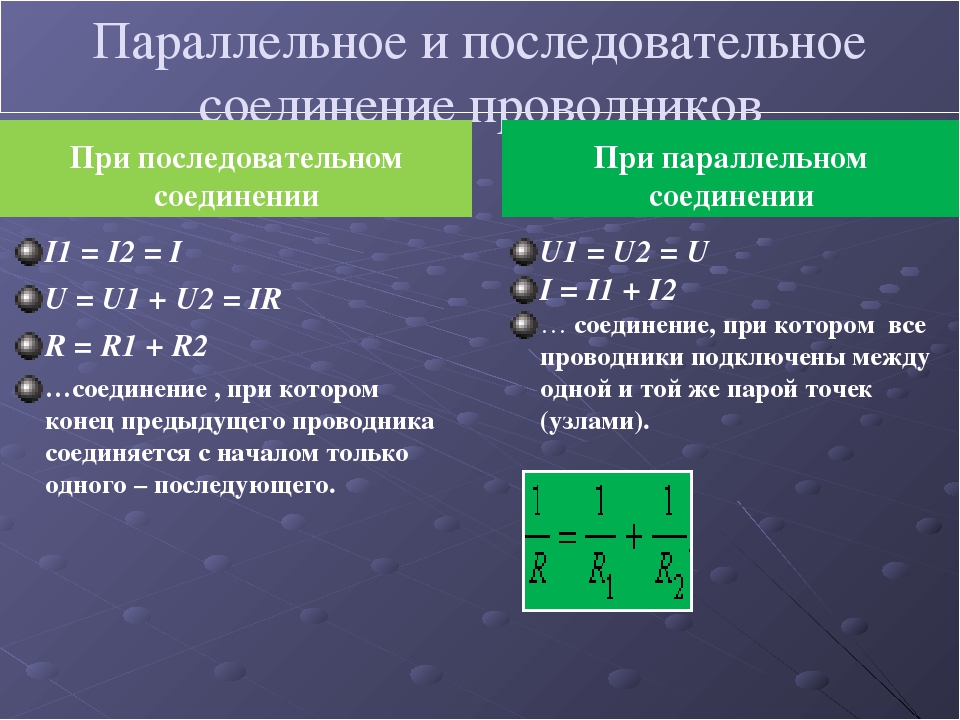 Проверить исправность, р.
Как проверить исправность детали. Методика испытаний. Какие детали можно использ.

RC – цепь. Резисторно – конденсаторная схема. Резистор, конденсатор. И.
Расчет RC – цепи, изменения напряжения на конденсаторе в зависимости от времени.

Силовой резонансный фильтр для получения синусоиды от инвертора.
Для получения синусоиды от инвертора нами был применен самодельный силовой резон.

Расчет мощности последовательного соединения

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка.

Выполняется для металлов и электролитов.

Закон Джоуля – Ленца.

Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили

В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.

Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:

Работа и мощность электрического тока.

Работа электрического тока:

Мощность электрического тока (работа в единицу времени):

В электричестве иногда применяется внесистемная единица работы – кВт . ч (киловатт-час).

1 кВт . ч = 3,6 . 10 6 Дж.

Виды соединения проводников.

Последовательное соединение.

1. Сила тока во всех последовательно соединенных участках цепи одинакова:

I₁=I₂=I₃=. =I_n=.

2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:

U=U₁+U₂+. +U_n+.

3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:

R=R₁+R₂+. +R_n+.

Если все сопротивления в цепи одинаковы, то:

R=R₁ . N

При последовательном соединении общее сопротивление увеличивается (больше большего).

Параллельное соединение.

1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.

2. Напряжение на всех параллельно соединенных участках цепи одинаково:

U₁=U₂=U₃=.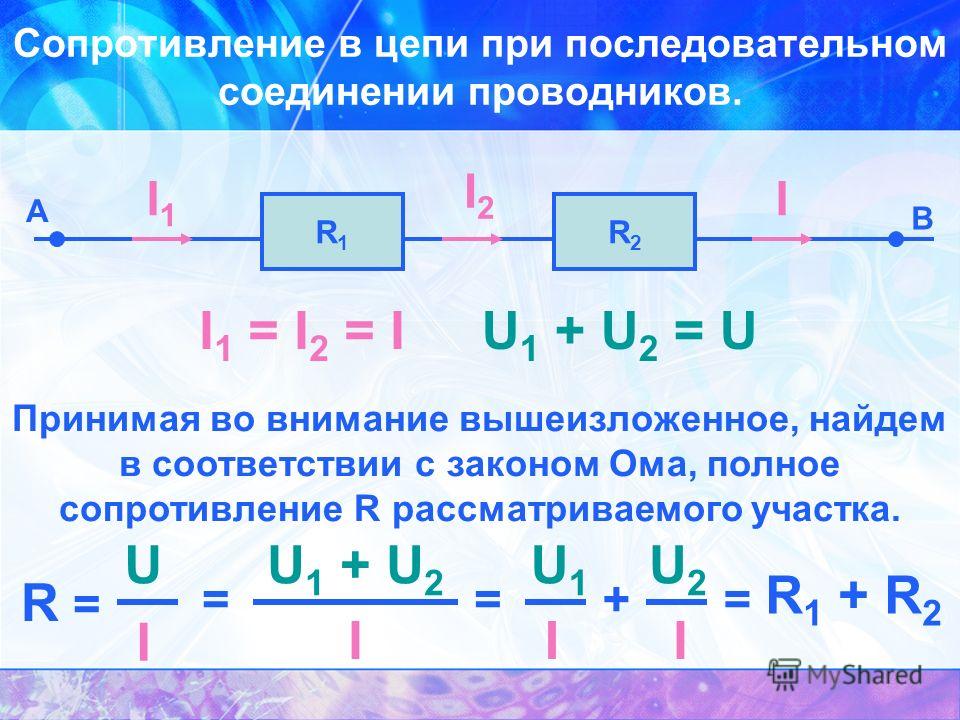 =U_n=.

3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):

Если все сопротивления в цепи одинаковы, то:

При параллельном соединении общее сопротивление уменьшается (меньше меньшего).

4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:

5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:

P=P₁+P₂+. +P_n+.

6. Т.к. силы тока во всех участках одинаковы, то: U₁:U₂. U_n. = R₁:R₂. R_n.

Для двух резисторов: – чем больше сопротивление, тем больше напряжение.

4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:

A=A₁+A₂+. +A_n+.

т.к. .

5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:

P=P₁+P₂+. +P_n+.

6. Т.к. напряжения на всех участках одинаковы, то:

Для двух резисторов: – чем больше сопротивление, тем меньше сила тока.

Последовательное соединение

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Параллельное соединение

Применение

Работа тока

А = I х U х t, где А – работа тока, t – время течения по проводнику.

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

Р=Р1 + Р2

Влияние схемы соединения на новогоднюю гирлянду

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

С= q/(U1 + U2 + U3)

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

Теперь используем формулу расчета сопротивления:

Первая формула для последовательного вида соединения.
Далее, для параллельной схемы.
И окончательно для последовательной схемы.

“>

Как правильно соединять аккумуляторы последовательно и параллельно

Коротко разберём распространённое мнение – «при последовательном соединении двух аккумуляторов (АКБ), их ёмкость не меняется, она остаётся такой же, как у одного аккумулятора, поэтому время автономной работы при таком соединении будет меньше».

Но как же закон сохранения энергии? Да, при последовательном соединении аккумуляторов, формально ёмкость считается как у одного аккумулятора, а напряжение удваивается (или утраивается, учетверяется и т.д., в зависимости от количества последовательно соединённых АКБ). При параллельном же соединении АКБ – ёмкость удваивается (утраивается и т.д.), а напряжение остаётся тем же.

Варианты соединения аккумуляторов

Противоречия здесь нет. Когда люди говорят об аккумуляторе (обычно об автомобильном), то сообщают его ёмкость, но не уточняют вольтаж. Просто все привыкли, что аккумуляторы имеют напряжение 12В, и подразумевается, что упоминать об этом глупо. Но в вообще-то, ёмкость без указания вольтажа не имеет физического смысла. Существуют аккумуляторы самой разной ёмкости и на разное напряжение – на 2В, и на 6В, и на 12В, и, редко, на 24В. Кроме того, любые одинаковые АКБ можно соединять последовательно, параллельно, или последовательно-параллельно одновременно.

Но стоит только указать после величины ёмкости её вольтаж, как всё встаёт на свои места. Ведь энергоёмкость в любом случае, как бы мы не соединяли аккумуляторы, останется прежней.

Итак, если, например, два АКБ по 200Ач 12В (например, Аккумулятор Delta GEL 12-200), соединить последовательно, то получится энергоёмкость 200Ач 24В. А если эти же два АКБ соединить параллельно, то получится – 400Ач 12В.
Проверим:
200Ач * 24В = 480Ач * В = 400Ач * 12В

Но для расчётов токов (обычно, номинальным током заряда считается ток 0,1С, где С –величина равная ёмкости аккумулятора), С берут именно по цифре слева, т.е. в нашем примере, при последовательном соединении С = 200, а при параллельном С = 400. Легко заметить, что и мощность зарядного устройства в обоих случаях будет одинаковой.

Для первого случая, зарядный ток будет 0,1*200 = 20А, но при напряжении 24В. Т.е. зарядная мощность, Р = 20А 24В = 480Вт

Для второго случая, зарядный ток будет 0,1*400 = 40А, но при напряжении 12В. Т.е. зарядная мощность, Р = 40А 12В = 480Вт

Если рассматривать одиночные аккумуляторы, то, например, один аккумулятор 600Ач 2В (см. раздел Аккумуляторные батареи FAAM) по своей энергоёмкости соответствует одному аккумулятору 100Ач 12В (например, Аккумулятор DELTA GEL 12-100).

Чтобы получить из этих аккумуляторов (600Ач 2В) большую аккумуляторную батарею, например, на 24В, нужно соединить последовательно 12 шт таких АКБ с помощью перемычек (Перемычка для аккумуляторов 250 мм). Общая итоговая ёмкость получится 600Ач 24В. Эта энергоёмкость, если сравнивать её с 12-и вольтовыми АКБ по 200Ач (а такие применяются в грузовиках), соответствует 6-и штукам (три соединённых параллельно цепочки аккумуляторов, где каждая цепочка состоит из двух, соединённых последовательно, аккумуляторов):

(600Ач*2В)*12 = 600Ач*24В = (200Ач*24В) + (200Ач 24В) + (200Ач 24В)

Обратите внимание – на всех рисунках специально показано, что если минус инвертора подключён к условно первому АКБ, то плюс – к последнему. Так его следует подключать, чтобы компенсировать сопротивление даже толстых медных проводов, соединяющих аккумуляторы. Иначе, из-за их сопротивления, при огромных токах, «дальний» от выводов инвертора аккумулятор, окажется и не «дозаряжаем», и не «доразряжаем».

Итак, ёмкостью (читайте «энергоёмкостью») аккумулятора (объединённой группы аккумуляторов), называется количество электричества (т.е. мощности, равной току умноженного на НАПРЯЖЕНИЕ), которое аккумулятор отдает при разряде до наименьшего допустимого напряжения.

Чтобы аккумулятор служил долго, его нельзя разряжать более чем на 80%. Для 12-и вольтового АКБ, это соответствует напряжению на его клеммах примерно 11,5В. Но тут важно каким током относительно емкости АКБ мы его разряжаем.

Чем больше сила разрядного тока, тем ниже напряжение, до которого может разряжаться аккумулятор. Это потому что при быстром разряде большими токами относительно маленькой ёмкости аккумулятора электролит не успевает перемешиваться, и разряженный слой скапливается вокруг пластин. Напряжение АКБ падает и нагрузку снимают. Однако, спустя несколько десятков минут, электролит перемешивается и ёмкость (и, соответственно, напряжение аккумулятора) повышается.

Если же разряжать малым током относительно ёмкости, то можно вычерпать всю энергию, что плохо для долговечности АКБ. Всегда надо оставлять не менее 20% ёмкости. Подробнее об этом далее.

Отметим, что во время заряда, зарядное устройство постепенно повышает напряжение на АКБ, а затем, после снятия заряда, напряжение уменьшается, возвращаясь к спокойному состоянию (так, на 12-и вольтовом аккумуляторе, в зависимости от типа АКБ, оно обычно растёт до 14,1 – 14,5 В, а после снятия заряда, даже без нагрузки, в течении получаса возвращается к 12,5 – 12,8 В).

Как быстрее вскипятить воду

Наша жизнь, зачастую, бывает очень стремительна, и каждая минута может быть на вес золота. Поэтому время полезно и нужно беречь. Если у Вас на даче собралась большая семья и Вам нужно оперативно всех накормить горячим обедом, то одной электрической плитки может не хватить. Предположим, что у Вас есть две одинаковые электрические плитки. Давайте попробуем разобраться, как лучше их подключить к источнику постоянного напряжения, чтобы вода в кастрюле вскипела быстрее.

Две электрические плитки можно подключить к источнику постоянного напряжения двумя способами: последовательно или параллельно, кроме того, можно подключить одну плитку. Рассчитаем электрическую мощность каждой плитки во всех этих случаях.

1.Последовательное соединение.

Пусть напряжение источника тока U, а электрическое сопротивление каждой плитки R. Тогда электрическое сопротивление двух электрических плиток при последовательном соединении равно: R_общ1 = 2R. Следовательно, согласно закону Ома для участка цепи через каждую плитку течет электрический ток, сила тока при этом равна:

I₁ = U/2R

Тогда мощность каждой электрической плитки при последовательном соединении рассчитывается по формуле:

P₁ = U²/4R.

Суммарная мощность двух плиток в два раза больше.

2.Параллельное соединение.

Пусть напряжение источника тока U, а электрическое сопротивление каждой плитки R. Тогда электрическое сопротивление двух электрических плиток при параллельном соединении равно: R_общ2 = R/2. Следовательно, согласно закону Ома для участка цепи через каждую плитку течет электрический ток, сила тока которого равна:

I₂ = U/R

Тогда мощность каждой электрической плитки при последовательном соединении рассчитывается по формуле:

P₂ = U²/R = 4P₁.

Соответственно, мощность двух плиток в два раза больше.

3.Подключение одной плитки

Пусть напряжение источника тока U, а электрическое сопротивление каждой плитки R.

Тогда мощность электрической плитки при подключении одной плитки рассчитывается по формуле:

P₃ = U²/R.

Но в этом случае электрическая плитка только одна.

Исходя из расчётов, можно сделать вывод, что при параллельном соединении мощность электрических плиток будет в 4 раза больше, чем при последовательном подключении, а, значит, и вода вскипит в 4 раза быстрее.

По предложенному методу мы предлагаем вам рассчитать:

Отношение мощностей электрических плиток в случае подключения их к аккумулятору с постоянной ЭДС. Внутреннее электрическое сопротивление аккумулятора считайте в 20 раз меньше электрического сопротивления плитки.
Рассчитайте суммарную мощность плиток в трёх описанных случаях, если ЭДС аккумулятора 12В, внутреннее электрическое сопротивление 1 Ом, а электрическое сопротивление каждой плитки 22 Ом.
Проведите аналогичное исследование для случая трёх плиток.

Мощность сопротивления при последовательном соединении

Автор На чтение 9 мин. Опубликовано 12.12.2019

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

1/R = 1/R₁+1/R₂+1/R₃+1/R₄ = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
Расчет силы тока для каждого резистора выполняется по формулам: I₁ = U/R₁ = 100/200 = 0,5A; I₂ = U/R₂ = 100/100 = 1A; I₃ = U/R₃ = 100/51 = 1,96A; I₄ = U/R₄ = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P₁ = U 2 /R₁ = 100 2 /200 = 50 Вт; P₂ = U 2 /R₂ = 100 2 /100 = 100 Вт; P₃ = U 2 /R₃ = 100 2 /51 = 195,9 Вт; P₄ = U 2 /R₄ = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р₁+Р₂+Р₃+Р₄ = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Закон Ома для участка цепи.

Выполняется для металлов и электролитов.

Закон Джоуля – Ленца.

Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили

Работа и мощность электрического тока.

Работа электрического тока:

Мощность электрического тока (работа в единицу времени):

В электричестве иногда применяется внесистемная единица работы – кВт . ч (киловатт-час).

1 кВт . ч = 3,6 . 10 6 Дж.

Виды соединения проводников.

Последовательное соединение.

1. Сила тока во всех последовательно соединенных участках цепи одинакова:

I₁=I₂=I₃=. =I_n=.

U=U₁+U₂+. +U_n+.

R=R₁+R₂+. +R_n+.

Если все сопротивления в цепи одинаковы, то:

R=R₁ . N

При последовательном соединении общее сопротивление увеличивается (больше большего).

Параллельное соединение.

1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.

2. Напряжение на всех параллельно соединенных участках цепи одинаково:

U₁=U₂=U₃=. =U_n=.

Если все сопротивления в цепи одинаковы, то:

При параллельном соединении общее сопротивление уменьшается (меньше меньшего).

P=P₁+P₂+. +P_n+.

6. Т.к. силы тока во всех участках одинаковы, то: U₁:U₂. U_n. = R₁:R₂. R_n.

Для двух резисторов: – чем больше сопротивление, тем больше напряжение.

A=A₁+A₂+. +A_n+.

т.к. .

P=P₁+P₂+. +P_n+.

6. Т.к. напряжения на всех участках одинаковы, то:

Для двух резисторов: – чем больше сопротивление, тем меньше сила тока.

“>

ресурсов

Последовательная цепь

Глобусы, подключенные последовательно

В последовательной цепи одна за другой подключены две или более нагрузки.

У тока есть только один путь, по которому оно может течь.

Примером последовательной схемы является набор огней на елку. Все шары ставятся один за другим.

Путь только один, поэтому ток будет одинаковым в любой точке цепи.

Принципиальная схема, показывающая три последовательно включенных резистора

Общее сопротивление в последовательной цепи будет равно сумме каждого отдельного сопротивления в цепи.

Чем больше нагрузок помещено в цепь, тем больше сопротивление.

Общее сопротивление для последовательной цепи рассчитывается по следующей формуле:

R _T = R ₁ + R ₂ + R ₃

Закон напряжения Кирхгофа

Вольтметр на каждом резисторе в последовательной цепи t

Закон Кирхгофа расширяет закон Ома в отношении напряжений на сопротивлениях в последовательной цепи.Общее напряжение питания будет равно сумме падений напряжения на каждом резисторе.

Общее падение напряжения (В _T) рассчитывается по формуле:

В _Т = В ₁ + В ₂ + В ₃

Если известны как ток, так и каждое значение сопротивления, то можно использовать закон Ома для расчета падения напряжения на каждом резисторе.

Например:

В ₁ = IR ₁

Рассеиваемая мощность

Мощность, рассеиваемая в последовательной цепи, зависит от напряжения питания, приложенного к цепи, и тока, протекающего в цепи.Ток зависит от общего сопротивления цепи.

Из раздела о мощности вы знаете, что формула рассеиваемой мощности:

P = VI

Мощность, рассеиваемая в каждом отдельном компоненте, зависит от сопротивления компонента. Общая рассеиваемая мощность будет равна сумме мощности, рассеиваемой каждым отдельным сопротивлением. В зависимости от известных значений комбинации формулы мощности, а также закона Ома могут использоваться для расчета рассеиваемой мощности (или любого другого неизвестного значения).

Пример

На приведенной выше принципиальной схеме, если значения:

В _Т = 20 В

R ₁ = 50 Ом

R ₂ = 20 Ом

R ₃ = 100 Ом

Общее сопротивление можно рассчитать следующим образом:

R _T = R ₁ + R ₂ + R ₃

р _т = 50 + 20 + 100

R _T = 170 Ом

Какая общая рассеиваемая мощность?

Вы можете рассчитать текущий расход, а затем рассчитать мощность.Вместо этого вы можете использовать подстановку, чтобы получить формулу.

В формуле P = VI замените I на V _T / R _T, чтобы получить формулу

P _T = V _T x V _T / R _T, что совпадает с

P _T = V _T ² / R _T

P _T = 20 ²/170

P _T = 0,235 Вт или 235 мВт

электричество — Противоречивое соотношение между общей потребляемой мощностью и мощностью, потребляемой каждым отдельным резистором в последовательной и параллельной конфигурации

Они только выглядят так, как будто они потребляют одинаковую мощность, потому что вы неявно используете другой источник питания в каждом случае.

Например, давайте сначала посмотрим на источник постоянного напряжения , который поддерживает постоянное падение напряжения $ V $ на любой нагрузке, к которой он подключен, и позволяет изменять ток. Пусть $ I_s $ будет током, потребляемым последовательной конфигурацией, и пусть $ I_p $ будет током, потребляемым параллельной конфигурацией. Последовательная конфигурация имеет эквивалентное сопротивление $ nr $, поэтому $ I_s = \ frac {V} {nr} $. Напротив, параллельная конфигурация имеет эквивалентное сопротивление $ r / n $, поэтому $ I_p = \ frac {nV} {r} $.2} {r} $. Мощность, потребляемая параллельной конфигурацией , выше для источника постоянного напряжения.

Напротив, источник постоянного тока поддерживает постоянный ток $ I $ через любую нагрузку, к которой он подключен, и позволяет изменять падение напряжения. Пусть $ V_s $ будет падением напряжения в последовательной конфигурации, а $ V_p $ будет падением напряжения в параллельной конфигурации. 2r} {n} $.Мощность, потребляемая конфигурацией серии , выше для источника постоянного тока.

Итак, какая конфигурация потребляет больше энергии, зависит от того, к какому типу источника питания она подключена. В вашем вопросе вы сравниваете мощность, потребляемую последовательными резисторами , подключенными к источнику постоянного напряжения , с мощностью, потребляемой параллельными резисторами , подключенными к источнику постоянного тока , что на самом деле не то же самое.

ПИТАНИЕ В КОМБИНИРОВАННЫХ ЦЕПЯХ

Как вы подсчитали ранее, общая мощность, потребляемая последовательной или параллельной цепью, равна сумме мощности, потребляемой каждым из компонентов цепи.То же самое и с комбинированной схемой. Часто предоставляется только один параметр (например, сопротивление, напряжение или ток). Ваша задача — уменьшить и объединить различные сопротивления, чтобы найти второй параметр.

Часто для этого требуется систематическое уменьшение цепи до единственного эквивалентного значения сопротивления. Затем вы работаете в обратном направлении, чтобы получить недостающие значения для различных компонентов, используя закон Ома. Помните, что вы не можете найти мощность, пока не получите два из трех параметров для каждого из компонентов.Общая мощность получается путем сложения всех индивидуальных мощностей каждого из компонентов.

Рассчитайте мощность, рассеиваемую каждым компонентом, и общую мощность комбинированной схемы, показанной на Рисунке 6–33. Первый шаг — просмотреть схему, проанализировать, что известно, а что неизвестно, и сравнить то, что вы видите, с тем, что вы решаете.

На рис. 6–33 нет компонентов с двумя значениями, с которыми можно работать.Это означает, что вам придется начать с объединения компонентов схемы, чтобы найти необходимую вторую переменную.

Вы можете использовать уравнение P _T = E _T × I _T для расчета полной мощности. Однако на рис. 6–33 нет значения для I _T. Поэтому первым делом нужно найти I _T. Чтобы рассчитать значение I _T, вам потребуется значение общего сопротивления (R _T). Зная R _T, вы можете рассчитать I _T по следующей формуле:

Чтобы вычислить R _T в этой схеме, вы начнете с объединения резисторов R ₂ и R ₃:

Просто для проверки мы могли бы использовать предполагаемое напряжение для резисторов 100 Ом и 200 Ом, включенных параллельно.В качестве примера возьмем параллельное напряжение 400 В.

Резистор 100 Ом допускает 4 А, а резистор 200 Ом допускает 2 А, всего 6 А. Эти 6 А будут общим током при приложенном 400 В. Таким образом,

Второй шаг — уменьшить последовательный резистор R ₁ и эквивалентный резистор R _2,3 до одного значения. Это дает R _T. Поскольку это последовательная схема, R _T вычисляется путем сложения последовательных элементов:

Теперь, когда у вас есть напряжение источника E _T 100 В и общее сопротивление R _T, вы можете рассчитать полный ток (I _T), используя следующую формулу:

Теперь у вас есть все три параметра эквивалентной схемы.Используя эти значения, вы можете найти общую мощность для цепи P _T и мощность, потребляемую каждым из компонентов схемы R ₁, R ₂ и R ₃. Сначала вы решаете общую мощность цепи (P _T) по следующей формуле:

Теперь у вас есть необходимая информация для расчета индивидуальных потерь мощности, начиная с R ₁. Поскольку в последовательной цепи ток одинаков во всей цепи, и поскольку вам известен общий ток I _T, ток в R ₁ и R _2,3 можно рассчитать как:

Теперь у вас есть ток и сопротивление для R ₁, и, таким образом, вы можете рассчитать мощность, потребляемую R ₁, используя следующую формулу:

Есть несколько способов рассчитать мощность, рассеиваемую R ₂ и R ₃.Поскольку вам известен ток через параллельную ветвь R _2,3 и эквивалентное сопротивление R _2,3 (вычисленное ранее в задаче), вы можете рассчитать напряжение на этой ветви, используя закон Ома. Используйте следующую формулу:

Поскольку это параллельная ветвь, вы знаете, что напряжение одинаково как на R ₂, так и на R ₃:

Теперь у вас есть падение напряжения и сопротивление R ₂ и R ₃, и вы можете рассчитать мощность, рассеиваемую каждым из этих компонентов, используя следующие формулы:

Вы выполнили все расчеты, необходимые для определения общей мощности и мощности, потребляемой отдельными компонентами, составляющими схему на Рисунке 6–33.Вы должны проверить свои расчеты, добавив отдельные рассеиваемые мощности и сравнив их с общей мощностью, рассчитанной ранее:

Ранее вы рассчитали P _T как 0,316 × 100 = 31,6 Вт. Небольшая ошибка вызвана округлением десятичных знаков во время вычислений.

ЦЕПИ С ИЗВЕСТНЫМ ИСПОЛЬЗОВАНИЕМ ЭНЕРГИИ

Цепи, над которыми вы будете работать в своей работе, часто имеют известные значения мощности и напряжения. Один из аспектов, который вам необходимо принять во внимание, — это реальная потребляемая мощность для цепей с компонентами, которые уже имеют номинальные характеристики.Например, рассмотрите рис. 6–34.

В этой схеме три лампы подключены к источнику питания с помощью медного провода №16 американского калибра (AWG) длиной 300 футов.

Из рисунка видно, что каждая лампа рассчитана на 25 Вт и что лампы подключаются параллельно. Когда вы смотрите на такую схему, вы должны обязательно принять во внимание все параметры схемы. Электрик, установивший лампы, подсчитал, что лампы потребляют 0.5 А на каждый при подаче 50 В, что делает общий ток цепи суммой тока в отдельных ветвях (т. Е. 1,5 А). Следующие формулы подтверждают расчеты электрика. Для расчета силы тока отдельных ламп (общий ток складывается из всех трех ламп):

Кажется, все в порядке. Однако посмотрите на схему еще раз. Нагрузка, все три лампы, находится на расстоянии 300 футов от источника напряжения. Из предыдущих глав вы знаете, что все проводники, даже медные, имеют некоторое сопротивление.Вы также знаете, что чем длиннее провод, тем выше сопротивление: медь # 16 AWG имеет сопротивление 4,99 Ом на 1000 футов. Эта информация взята из NEC ^® и применима к семжильному проводнику при температуре 75 ° C. Обратите внимание, что это значение немного отличается от значения, приведенного в предыдущей главе. Это связано с тем, что значение в этой таблице относится к одножильному, а не многожильному проводу. Просмотрите другие размеры проводов, чтобы узнать, какое сопротивление они имеют на тысячу футов проводника.Учтите, что чем крупнее проводник, тем меньше значение сопротивления. Тот факт, что нагрузка находится на расстоянии 300 футов от источника питания, означает, что при расчетах необходимо учитывать сопротивление медного проводника №16, идущего к лампам и возвращающегося от них. Поскольку в проводниках, питающих осветительную нагрузку, существует сопротивление, при расчетах для этой схемы необходимо учитывать и другие факторы.

Изучите рисунок 6–35. Эта схема была перерисована, чтобы представить все сопротивления, которые необходимо учитывать в схеме при выполнении расчетов.Номинальная мощность лампы — это количество энергии, которое лампа рассеивает при приложенном номинальном напряжении. Поскольку номинальное напряжение не будет приложено из-за падения напряжения на проводе, вам необходимо знать сопротивления ламп, чтобы вы могли решить эту схему как комбинированную схему, используя методы, которые вы изучили в этой и предыдущих главах. Поскольку лампы рассчитаны на 25 Вт при 50 В, вы можете рассчитать значение сопротивления лампы следующим образом:

Обратите внимание, что это сопротивление каждой отдельной лампы.Чтобы полностью проанализировать эту схему, нужно также знать сопротивление провода, питающего лампы. Исходя из того, что сопротивление провода # 16 AWG составляет 4,99 Ом на 1000 футов провода, вы можете рассчитать общее сопротивление как:

Помните, в этой цепи 300 футов провода, идущего к лампам, и 300 футов провода, идущего от ламп. Необходимо учитывать оба расстояния. На Рис. 6–36 показана полная схема со всеми включенными сопротивлениями.

Это комбинированная схема, которую можно уменьшить с помощью методов, которые вы изучили.Начнем с расчета сопротивления трех параллельно включенных ламп, R _{Все лампы}:

Теперь схема была уменьшена до простой последовательной цепи с двумя отрезками медного провода и параллельным комбинированным сопротивлением ламп. Общее сопротивление складывается из трех элементов серии:

Общий ток рассчитывается как:

Обратите внимание, что значение, рассчитанное электриком, устанавливающим данный проект (1.5 A) отличается от рассчитанного ранее значения. Снижение тока вызвано дополнительным сопротивлением провода. Теперь узнаем, какое напряжение на самом деле подается на лампы. Мы знаем, что полный ток для этой цепи на самом деле составляет 1,38 А, и мы знаем, что эквивалентное сопротивление для ламп, включенных последовательно с сопротивлением, равно 33,33. Используя закон Ома, мы можем легко рассчитать напряжение на лампах следующим образом:

Это означает, что мы потеряли (упали) на проводах 4 В.В процентах это:

Это большое падение является чрезмерным. Максимальные падения напряжения обычно не должны превышать 3%. Лампы не рассеивают мощность, на которую они рассчитаны. Другими словами, вместо ламп, фактически обеспечивающих свет в соответствии с их проектными параметрами, теперь огни будут работать в соответствии с фактическими параметрами установки. Посмотрим, как на самом деле влияют параметры установки на лампы. Поскольку теперь мы знаем, что установка питает лампы напряжением 46 В, мы можем пересчитать фактическую мощность ламп следующим образом:

Эта схема с учетом сопротивления проводников в действительности потеряла примерно 15% мощности лампы.Это:

Как видите, при проектировании установки необходимо учитывать всю схему. Все компоненты сопротивления в комбинированной цепи потребляют мощность, и это необходимо учитывать. Взгляните на сопротивление проводов и посмотрите, сколько энергии потребляет их сопротивление. Поскольку вы уже рассчитали ток и сопротивление проводников, вы можете легко рассчитать мощность, потребляемую проводниками, по следующей формуле:

Обратите внимание на множитель 2.Есть два проводника, и вы должны учитывать их обоих. Предыдущий расчет показывает, что из всей мощности, потребляемой установкой, часть этой мощности (5,69 Вт) потребляется проводниками и теряется в виде тепла. Не принимая во внимание потерю мощности в проводниках, фактическая схема не работала с оптимальной проектной эффективностью, фактическая мощность лампы была снижена, а проводники потребляли мощность, которая терялась в виде тепла. Всего этого можно было избежать или уменьшить, выбрав провод большего диаметра.

В последовательных и параллельных цепях, особенно в цепях с длинными проводниками или проводниками малого диаметра (например, пожарная сигнализация или акустические системы), вы должны учитывать падение напряжения и потери мощности из-за сопротивления проводника.

Другой пример проблемы обрыва линии и потери линии — использование цепей пожарной сигнализации. В цепях мониторинга, где в зоне защиты находится много тепловых датчиков или датчиков дыма, на двух проводниках, идущих от датчика к датчику, будет пропадание линии.В схемах уведомления (рис. 6–37) все чувствительные элементы включены параллельно через два параллельных проводника. Обычно датчики имеют разомкнутую связь с параллельной цепью.

Контроль цепи осуществляется путем размещения резистора поперек линейных проводов в самом конце цепи. Этот резистор называется оконечным резистором. Его цель — позволить небольшому количеству тока течь по отрицательному проводнику до конца, через резистор и обратно к источнику.

При обрыве где-либо в цепи (обрыв) линейный ток становится равным нулю, и контрольная электроника указывает на проблему в цепи. Если какой-либо датчик обнаруживает тепло или дым, он создает замкнутую цепь (короткое замыкание) от одного проводника к другому. Электронная схема контроля обнаруживает большое увеличение тока, и срабатывает пожарная сигнализация.

Базовая электрическая теория в двух словах

теория от electrician2.com

**Правила цепей постоянного тока серии**
Правило № 1:	Одинаковый ток течет через каждую часть серии схема.

Правило № 2:	Общее сопротивление последовательной цепи равно сумма отдельных сопротивлений.

Правило № 3:	Общее напряжение в последовательной цепи равно сумме индивидуальных падений напряжения.

Правило № 4:	Падение напряжения на резисторе в последовательной цепи пропорционально размеру резистора.

Правило № 5:	Общая мощность, рассеиваемая в последовательной цепи, составляет равняется сумме индивидуальных потерь мощности.

*РЕЗЮМЕ ФОРМУЛ ЗАКОНА OHMS*
АМПЕР =	ВОЛЬТ СОПРОТИВЛЕНИЕ

СОПРОТИВЛЕНИЕ =	ВОЛЬТ АМПЕР

ВОЛЬТ =	АМПЕР x СОПРОТИВЛЕНИЕ

**Параллельная цепь постоянного тока Правила**
Правило № 1:	Такое же напряжение присутствует на каждой ветви параллельная цепь и равна напряжению источника.

Правило № 2:	Ток через ответвление параллельной сети обратно пропорциональна величине сопротивления ветви.

Правило № 3:	Полный ток параллельной цепи равен сумма токов отдельных ветвей цепи.

Правило № 4:	Общее сопротивление параллельной цепи равно к сумме обратных величин отдельных сопротивлений схемы.

Правило № 5:	Общая мощность, рассеиваемая в параллельной цепи, составляет равняется сумме индивидуальных потерь мощности.

*СВОДКА ПРАВИЛ ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ*
ОБЩЕЕ НАПРЯЖЕНИЕ =	E (1) = E (2) = E (3) … и т. Д.

_{ИТОГО СОПРОТИВЛЕНИЕ =}	ВОЛЬТ АМПЕР

ВОЛЬТ =	ОБЩЕЕ НАПРЯЖЕНИЕ ОБЩИЙ АМПЕР

_{К
ОПРЕДЕЛИТЕ ПОЛНОЕ СОПРОТИВЛЕНИЕ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ ПРИ ПОЛНОМ ТОКЕ
И ОБЩЕЕ НАПРЯЖЕНИЕ ПРИ НЕИЗВЕСТНОМ ИСПОЛЬЗОВАНИИ СЛЕДУЮЩЕЙ ФОРМУЛЫ:}

RT =	1 ___________________ 1 + 1 + 1 +…… и т. д. R1 R2 R3

ДЛЯ ДВУХ РЕЗИСТОРОВ ПРИ ПАРАЛЛЕЛЬНОМ ИСПОЛЬЗОВАНИИ ЭТОГО FORMULA НАЗЫВАЕТСЯ «ПРОДУКТ ПРЕВЫШАЕТ СУММУ»

_РТ =	*R (1) Р (2) к (1) + к (2)**

_{МОЩНОСТЬ В ОДНОЙ ФАЗЕ
РЕЗИСТИВНЫЕ ЦЕПИ}
_{ГДЕ КОЭФФИЦИЕНТ МОЩНОСТИ
100 ПРОЦЕНТОВ}
_{(ЭТИ
ФОРМУЛЫ ОБЫЧНО ИСПОЛЬЗУЮТСЯ ДЛЯ РЕШЕНИЯ БОЛЬШИНСТВА ПРОБЛЕМ С ПИТАНИЕМ ЦЕПЕЙ НА ИСПЫТАНИЯХ)}

_{К
ОПРЕДЕЛЕНИЕ МОЩНОСТИ, ПОТРЕБЛЯЕМОЙ ОТДЕЛЬНЫМ РЕЗИСТОРОМ В СЕРИЙНОЙ ЦЕПИ
ИСПОЛЬЗУЙТЕ ЭТУ ФОРМУЛУ:}

_{К
ОПРЕДЕЛЕНИЕ МОЩНОСТИ, ПОТРЕБЛЯЕМОЙ ОТДЕЛЬНЫМ РЕЗИСТОРОМ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ
ИСПОЛЬЗУЙТЕ ЭТУ ФОРМУЛУ:}

_{К
ОПРЕДЕЛИТЕ ОБЩУЮ МОЩНОСТЬ, ПОТРЕБЛЯЕМУЮ ОТДЕЛЬНОЙ ЦЕПЕЙ, ИСПОЛЬЗУЙТЕ ДАННУЮ ФОРМУЛУ:}

МОЩНОСТЬ = E (ОБЩЕЕ НАПРЯЖЕНИЕ) x I (ОБЩИЙ ТОК)

_{ПРАВИЛА
БОЛЬШОГО ПАЛЬЦА:}

_{THE
ОБЩЕЕ СОПРОТИВЛЕНИЕ РЕЗИСТОРОВ ПО ПАРАЛЛЕЛЬНОМУ ВСЕГДА МЕНЬШЕ ЗНАЧЕНИЯ
ЛЮБОГО ОДНОГО РЕЗИСТОРА.}
_{THE
ПОЛНОЕ СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ, ИМЕЮЩИЕ ВСЕ ОДИНАКОВЫЕ ЗНАЧЕНИЯ, ТАКОЕ
ЗНАЧЕНИЕ, ОТДЕЛЕННОЕ НА КОЛИЧЕСТВО РЕЗИСТОРОВ.}
_{ВСЕГДА
ИСПОЛЬЗУЙТЕ ПРЕВЫШАЮЩИЕ ПРАВИЛО ПРОДУКТА, ЧТОБЫ РАЗБИРАТЬ ДВА ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРА НА
ОДИН РЕЗИСТОР. ЭТО НАМНОГО ЛЕГЧЕ, ЧЕМ ПОПЫТАТЬСЯ НА РЕШЕНИЕ БОЛЬШОЙ АЛГЕБРАКИ
ВЫРАЖЕНИЯ.}
_{746
ВАТЫ РАВНЫ ОДНОЙ ЛОШАДИ}
_{ЭФФЕКТИВНОСТЬ
РАВНО ВЫХОД, РАЗДЕЛЕННЫЙ НА ВХОД}
_{ВНУТР.
ИНДУКТИВНЫЕ ЦЕПИ, ТОК, ЗАПИСЫВАЕТ НАПРЯЖЕНИЕ.}
_{ВНУТР.
ЕМКОСТНЫЕ ЦЕПИ ТОКОВЫЕ ПРОВОДЫ НАПРЯЖЕНИЕ.}
_{МОЩНОСТЬ
КОЭФФИЦИЕНТ ЯВЛЯЕТСЯ МЕРОПРИЯТИЕМ ДЛЯ ДАЛЬНЕЙШЕГО ТОКА ИЛИ НАПРЯЖЕНИЯ.}

_{ПИТАНИЕ В ЧЕРЕДОВАНИИ
ТЕКУЩИЕ ЦЕПИ, КОГДА КОЭФФИЦИЕНТ МОЩНОСТИ НЕ 100 ПРОЦЕНТОВ}

_{(Истинная СИЛА)
= E x I x КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ
ОДНА ФАЗА)}

_{(Истинная СИЛА)
= E x I x 1.732 X КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ
ТРЕХФАЗНЫЙ)}

_{ЭТО
ВЛАСТЬ ТАКЖЕ НАЗЫВАЕТСЯ ИСТИННОЙ ВЛАСТЬЮ, ИЛИ РЕАЛЬНОЙ ВЛАСТЬЮ, ПРОТИВ ВИДНОЙ ВЛАСТИ.
НАЙДЕНА ПО РАСЧЕТУ АМПЕР НАПРЯЖЕНИЯ.}

Ваттметры показывают значение True Power.

_{Полная мощность = ВОЛЬТ-АМПЕР
= E x I (FOR
ОДНА ФАЗА)}

_{Полная мощность = ВОЛЬТ-АМПЕР
= E x I x 1,732 (ДЛЯ
ТРЕХФАЗА)}

_{IT
МОЖНО ГОТОВНО ОПРЕДЕЛЕНИЕ АЛГЕБРЫ, ЧТО}


КОЭФФИЦИЕНТ МОЩНОСТИ =	ИСТИННАЯ СИЛА ВНЕШНЯЯ МОЩНОСТЬ

_{ДВИГАТЕЛЬ
ФОРМУЛЫ ПРИМЕНЕНИЯ}


ПОДВЕСКА = (для трехфазных двигателей)	1.732 x ВОЛЬТ x АМПЕР x КПД x коэффициент мощности 746


ТРЕХФАЗНЫЙ АМПЕР = (для трехфазных двигателей)	746 x ПОДСТАВКА 1,732 x НАПРЯЖЕНИЕ x КПД x КОЭФФИЦИЕНТ МОЩНОСТИ


СИНХРОННЫЙ Обороты =	ГЕРЦ х 120 КОЛИЧЕСТВО ПОЛЮСОВ

_{ДВИГАТЕЛЬ
МАРКИРОВКА И ПОДКЛЮЧЕНИЯ}
_{СОЕДИНЕНИЯ
ДЛЯ ДЕВЯТИ СВИНЦА}
_{ТРИ
ФАЗНЫЕ ДВИГАТЕЛИ}

_{ТРИ
ФАЗА ЗВЕЗДА ИЛИ Y}

ЗВЕЗДА СОЕДИНЕНА
Напряжение	Линия 1	Строка 2	Строка 3	Все вместе
Низкий	1 и 7	2 и 8	3 и 9	4 и 5 и 6
Высокая	1	2	3	4 и 7, 5 и 8, 6 и 9

_{ТРИ
ФАЗА ДЕЛЬТА}

СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
Напряжение	Линия 1	Строка 2	Строка 3	Все вместе
Низкий	1 и 6 и 7	2 и 4 и 8	3 и 5 и 9	НИКТО
Высокая	1	2	3	4 и 7, 5 и 8, 6 и 9

_{ДЕЛЬТА
КЛЮЧ ДЛЯ ТРАНСФОРМАТОРА}

_{ДВИГАТЕЛЬ
КОНТРОЛЛЕР С ТРЕМЯ}
_{ПУСК
ОСТАНОВКИ}
_{(ХОЛДИНГ
КОНТАКТЫ НЕ ПОКАЗАНЫ)}

_{ТРАНСФОРМАТОР
КОЭФФИЦИЕНТ ОБОРОТА}

Ep ₌ Tp
Es Ts

Где
Ep — первичное напряжение
Es — вторичное напряжение
Tp — количество витков в первичной обмотке.
Ts — количество витков во вторичной обмотке.

Подключение переключателя

4-ходовой

D — S, E — R, F — T, G — W

3-ходовой

от A до Z, от B до Y, от C до X

Пример заполнения кабельного лотка

Решение
Для многожильных кабелей на 2000 В и где кабели 4/0 и более устанавливаются с кабелями менее 4/0 по размеру см. Раздел 392.22 (А) (1) (с). Сумма сечений всех кабелей меньшего размера чем 4/0 не должна превышать максимально допустимую площадь заполнения в результате расчет в столбце 2 таблицы 392.22 (A) для соответствующего кабельного лотка ширина. В этой таблице sd = сумма диаметров кабелей 4/0 и больше. Тогда Сумма сечений для кабелей меньше 4/0 (СУММ) <= X - 1,2 x стандартное отклонение X определяет ширину кабельного лотка по таблице 392.22 (А). X> = СУММ + (1,2 x стандартное отклонение) СУММ = 6 x 3,14 x 0,5 x 0,5 кв. Дюйма СУММ = 4,71 кв. Дюйма sd = 3 x 2 дюйма sd = 6 дюймов X> = 4,71 + (1,2 x 6) X> = 11,91 Из таблицы 392.22 (A) следующий больший X равен 14, и это преобразует к кабельному лотку шириной 12,0 дюймов в колонне 1. Следует отметить, что кабели 4/0 и больше должны быть установлен в один слой.



Максимальная мощность для NEMA-Rated Пускатели двигателя

Однофазный

Трехфазный

NEMA
Размер

115
Вольт

230
Вольт

208/230
Вольт

460/575
Вольт

1/3

1.5

7,5

15/10

25/30

40/50

100

75/100

200

РЕЙТИНГ NEMA ДЛЯ КОРПУСОВ

NEMA и другие организации создали стандарты конструкции корпуса для управляющего оборудования.В общем, оборудование будет закрыто по одной или нескольким из следующих причин:

Избегайте случайного контакта с токоведущими частями.
Защитите контроль от вредного воздействия окружающей среды условия.
Предотвратить взрыв или возгорание, которые могут возникает из-за электрической дуги, вызванной регулятором.

Общие типы корпусов по классификации NEMA числа:

NEMA I — ОБЩЕГО НАЗНАЧЕНИЯ

Корпус общего назначения предназначен в первую очередь для предотвращения случайного контакта с закрытым аппаратом.Это подходит для общего применения внутри помещений, где он не подвергается воздействию необычным условиям эксплуатации. Корпус NEMA I служит защитой от пыли и легких непрямых брызг, но не пыленепроницаемый.

NEMA 3 — DUSTTIGHT, RAINTIGHT

Этот корпус предназначен для подходящая защита от указанных погодных опасностей. Корпус NEMA 3 подходит для применения на открытом воздухе, на корабельных доках, каналах и строительстве работы, а также для применения в метро и туннелях.Он также устойчив к мокрому снегу.

NEMA 3R — ДОЖДЕВОЙ, УСТОЙЧИВЫЙ НА СЛОИ

Этот корпус защищает от помех в работе встроенного оборудования из-за дождя, и сопротивляется повреждениям от воздействия мокрого снега. Он разработан со ступицами для кабелепровода и внешним креплением, а также дренажные положения.

NEMA 4 — ВОДОСНАБЖЕНИЕ

Разработан водонепроницаемый корпус. чтобы выдержать испытание шланга, описанное в следующем примечании: «Корпуса должны быть испытанным, подвергнув его воздействию струи воды.Шланг с однодюймовым соплом должны использоваться и должны обеспечивать не менее 65 галлонов в минуту. Вода должно быть направлено на ограждение с расстояния не менее 10 стопы и в течение пяти минут. В этот период может быть направлено в любом одном или нескольких направлениях по желанию. Не должно быть утечки вода в корпус в этих условиях ».

Корпус NEMA 4 подходит для применение на открытом воздухе в доках судов, на молочных заводах, пивоварнях и т. д.

NEMA 4X — ВОДОНЕПРОНИЦАЕМЫЙ, КОРРОЗИОННОСТОЙКИЙ

Эти корпуса обычно строятся в соответствии с корпусами NEMA 4, за исключением того, что они сделаны из материала что очень устойчиво к коррозии.По этой причине они идеальны в таких приложениях, как бумажные фабрики, упаковка мяса, удобрения и химикаты заводы, на которых загрязняющие вещества обычно разрушают стальную ограду над Период времени.

NEMA 7 — ОПАСНЫЕ ЗОНА — КЛАСС Я

Эти корпуса предназначены для требования к применению Национального электрического кодекса для класса Я опасные места. В этом типе оборудования прерывание цепи происходит в воздухе.

«Объектами класса I являются те, в которых горючие газы или пары присутствуют или могут присутствовать в воздухе в количествах достаточно для образования взрывоопасных или горючих смесей.»

ОПАСНЫЕ ЗОНА NEMA 9 — КЛАСС II

Эти корпуса предназначены для требования к применению Национального электрического кодекса для класса II опасные зоны.

«Объектами класса II являются те, которые опасны из-за наличия горючей пыли ».

Буква или буквы, следующие за номер типа указывает на конкретную группу или группы опасных мест (как определено в Национальном электротехническом кодексе), для которого разработан.Обозначение неполное без буквы или букв суффикса.

NEMA 12 — ПРОМЫШЛЕННОЕ ПРИМЕНЕНИЕ

Корпус NEMA 12 предназначен для использование в тех отраслях, где желательно исключить такие материалы, как пыль, ворс, волокна и муха, масло см. страницу или охлаждающую жидкость см. страницу. Там в корпусе отсутствуют отверстия для кабелепровода или выбоины, а монтаж с помощью фланцев или монтажных ножек.

NEMA 13 — МАСЛЯНЫЙ, DUSTTIGHT

Корпуса NEMA 13 обычно литая конструкция, разборная, что позволяет использовать в тех же условиях, что и NEMA 12 устройств.Существенное отличие состоит в том, что благодаря литому корпусу вход для кабелепровода является неотъемлемой частью корпуса NEMA 13, и установка осуществляется с помощью глухих отверстий, а не монтажных кронштейнов.

Теоретические карточки | Quizlet

Важно соотношение между током, напряжением, сопротивлением и мощностью в последовательной цепи .

Сопротивление
В последовательной цепи полное сопротивление цепи равно сумме всех последовательных сопротивлений.(Сопротивление аддитивное).

Напряжение
Противодействие (сопротивление) току (амперы) приводит к падению напряжения в цепи (падению напряжения) и рассчитывается по формуле E vd = I x R .
Падение напряжения Кирхгофа:
Указывает, что в последовательной цепи сумма напряжений на всех резисторах (падение напряжения) равна приложенному напряжению.

Ток
Закон Кирхгофа: сумма токов, протекающих в переходе, равна сумме токов, текущих из перехода.( тока, протекающего через каждый резистор, соответствует ).
Для расчета тока требуются напряжение источника питания (ES) и полное сопротивление цепи (RT).

IT = ES / RT *

Примечание. Для расчета тока, протекающего через каждый резистор, используйте формулу: I = * E * / * R *. Где E R e: Для расчета тока, протекающего через каждый резистор, используйте формулу: * I * = * E * / * R *. Где E (напряжение) представляет собой падение напряжения на отдельном резисторе, а не напряжение источника.

Мощность
Мощность, потребляемая в последовательной цепи, равна сумме мощности, потребляемой всем сопротивлением в цепи. Закон сохранения энергии гласит, что источник питания (аккумулятор и т. Д.) Будет производить ровно столько энергии, сколько потребляется элементами схемы. Мощность является результатом протекания тока через сопротивление и рассчитывается по формуле P = I * x R

Резюме :
— Общее сопротивление последовательной цепи равно сумме всех сопротивлений. схемы.
— Ток имеет одинаковое значение на всех сопротивлениях.
— Сумма падений напряжения на всех сопротивлениях равна напряжению источника.
— Сумма мощности, потребляемой всеми резисторами, равна общей мощности, потребляемой схемой.

Серия тренингов по электричеству и электронике ВМС (NEETS), Модуль 1-3, с. 21-30

Модуль 1 — Введение в материю, энергию и постоянный ток
Страницы i — ix, От 1-1 до 1-10, От 1-11 до 1-20, 1-21 до 1-30, С 1-41 по 1-50, От 1-51 до 1-60, С 1-61 по 1-65, От 2-1 до 2-10, 2-11 до 2-20, От 2-21 до 2-29, От 3-1 до 3-10, С 3-11 до 3-20, С 3-21 до 3-30, От 3-31 до 3-40, 3-41 до 3-50, 3-51 до 3-60, С 3-61 по 3-70, С 3-71 по 3-80, С 3-81 по 3-90, С 3-91 по 3-100, 3-101 до 110, С 3-111 по 3-120, 3-121 к 3-126, Приложение Я, II, III, IV, V, Индекс

Рисунок 3-14.- Решение для полного сопротивления в последовательной цепи.

В некоторых схемных приложениях полное сопротивление известно и значение, которое имеют резисторы схемы. быть определенным. Уравнение RT = R1 + R2 + R 3 можно транспонировать для решения относительно цените неизвестное сопротивление.

Пример: На рисунке 3-15 общее сопротивление цепи, содержащей три резистора. составляет 40 Ом. Два резистора цепи по 10 Ом. Вычислите номинал третьего резистора (R3).

3-21

Рисунок 3-15. — Расчет значения одного сопротивления в последовательной цепи.

Ток в последовательной цепи

Поскольку существует только один путь для тока в серии цепи, одинаковый ток должен протекать через все компоненты цепи. Чтобы определить ток в последовательной цепи, необходимо знать только ток через один из компонентов.

Тот факт, что через каждый компонент последовательной цепи можно проверить, вставив счетчики в цепь в различных точках, как показано на рисунке. 3-16.Если бы это было сделано, было бы обнаружено, что каждый измеритель показывает одно и то же значение тока.

3-22

Рисунок 3-16. — Ток в последовательной цепи.

Напряжение в последовательной цепи

Падение напряжения на резисторе в цепи состоящий из одного резистора и источника напряжения, представляет собой полное напряжение в цепи, равное приложенному Напряжение. Общее напряжение в последовательной цепи, состоящей более чем из одного резистора, также равно приложенному напряжение, но состоит из суммы падений напряжения отдельного резистора.В любой последовательной цепи СУММ резистора падение напряжения должно равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рисунок 3-17. В этой цепи потенциал источника (ET) 20 вольт падает на последовательную цепь, состоящую из двух Резисторы на 5 Ом. Общее сопротивление цепи (RT) равно сумме двух отдельных сопротивлений, или 10 Ом. По закону Ома ток в цепи можно рассчитать следующим образом:

3-23

Рисунок 3-17.- Расчет отдельных падений напряжения в последовательной цепи.

Так как резисторы известны номиналом 5 Ом каждый, а ток через резисторы известен чтобы составить 2 ампера, можно рассчитать падение напряжения на резисторах. Таким образом, напряжение (E1) на R1 составляет:

Осмотрев цепь, вы можете увидеть, что R2 имеет то же омическое значение, что и R1, и несет тот же ток. Следовательно, падение напряжения на R2 также равно 10 вольт.Добавление этих двух 10-вольтных капель вместе дает общее падение 20 вольт, точно равное приложенному напряжению. Тогда для последовательной схемы:

ET = E1 = E 2 + E3 =. . . En

Пример: последовательная цепь состоит из трех резисторов, имеющих номиналы 20 Ом, 30 Ом и 50 Ом соответственно. Найдите приложенное напряжение, если ток через резистор 30 Ом равен 2 ампера. (Сокращение amp обычно используется для ампер.)

Для решения проблемы сначала рисуется электрическая схема и маркируется (рис. 3-18).

3-24

Рисунок 3-18. — Решение для приложенного напряжения в последовательной цепи.

Замещающий:

3-25

ПРИМЕЧАНИЕ. При использовании закона Ома величины для уравнения ДОЛЖНЫ быть взяты из ОДНОЙ части схемы. В приведенном выше примере напряжение на R2 было вычислено с использованием тока через R2 и сопротивления R2.

Величина падения напряжения на резисторе определяется приложенным напряжением и пропорционально схемы сопротивления.Падения напряжения, возникающие в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток — чем больше сопротивление резистора, тем большее падение напряжения на нем.

Q17. Последовательная цепь, состоящая из трех резисторов, имеет ток 3 усилители. Если R1 = 20 Ом, R2 = 60 Ом и R3 = 80 Ом, каково полное сопротивление (а) и (б) источник напряжения в цепи?

Q18.Какое напряжение падает на каждом резисторе описанной схемы в вопросе 17?

Q19. Если бы ток был увеличен до 4 ампер, каким было бы падение напряжения на каждый резистор в цепи, описанной в вопросе 17?

Q20. Что нужно сделать с цепью описано в вопросе 17, чтобы увеличить ток до 4 ампер?

Мощность в последовательной цепи

Каждый резистор в последовательной цепи потребляет мощность, которая рассеивается в виде тепла.Поскольку эта сила должен поступать от источника, общая мощность должна быть равна мощности, потребляемой сопротивлением цепи. В В последовательной цепи общая мощность равна СУММУ мощности, рассеиваемой отдельными резисторами. Суммарная мощность (PT) равно:

PT = P1 + P2 + P3. . .Pn

Пример: последовательная цепь. состоит из трех резисторов номиналами 5 Ом, 10 Ом и 15 Ом. Найдите полную мощность при приложении 120 вольт к цепи.(См. Рис. 3-19.)

Рисунок 3-19. — Решение для полной мощности в последовательной цепи.

3-26

Дано:

Решение: Сначала определяется общее сопротивление.

Ток цепи рассчитывается по общему сопротивлению и приложенному напряжению.

С помощью формул мощности можно рассчитать мощность для каждого резистора:

Чтобы проверить ответ, можно рассчитать общую мощность, отдаваемую источником:

3-27

Общая мощность равна сумме мощностей, используемых отдельными резисторами.

ОБЩИЕ ХАРАКТЕРИСТИКИ

Важные факторы, определяющие работу последовательной цепи, перечислены ниже. Эти факторы были установлены как правила группы, чтобы их можно было легко изучить. Эти правила необходимо полностью понять перед исследованием. предпринимается более продвинутая теория цепей.

Правила для последовательных цепей постоянного тока

1. Одинаковый ток протекает через каждую часть последовательной цепи.

2.Общее сопротивление последовательной цепи равна сумме отдельных сопротивлений.

3. Суммарное напряжение в последовательной цепи. равна сумме индивидуальных падений напряжения.

4. Падение напряжения на резисторе в Последовательная цепь пропорциональна сопротивлению резистора.

5. Суммарная мощность в серии Схема равна сумме индивидуальных мощностей, используемых каждым компонентом схемы. ЦЕПЬ СЕРИИ

АНАЛИЗ
Чтобы установить процедуру для решения последовательных цепей, следующие примеры задач будут решено.Пример: три резистора 5 Ом, 10 Ом и 15 Ом соединены последовательно с источником питания 90 вольт. как показано на рисунке 3-20. Найдите общее сопротивление, ток цепи, падение напряжения на каждом резисторе, мощность каждого резистора, и общая мощность цепи.

Рисунок 3-20. — Решение для различных значений в последовательной цепи.

3-28

При решении схемы сначала будет найдено полное сопротивление. Далее будет рассчитан ток в цепи.Как только ток известен, можно рассчитать падение напряжения и рассеиваемую мощность.

3-29

Пример: четыре резистора, R1 = 10 Ом, R2 = 10 Ом, R3 = 50 Ом и R4 = 30 Ом, подключены последовательно к источнику питания, как показано на рисунке 3-21. Ток в цепи составляет 1/2 ампера.

а. Какое напряжение батареи?

г. Какое напряжение на каждом резисторе?

г. Что это мощность, затрачиваемая на каждый резистор?

г. Какая общая мощность?

Рисунок 3-21. — Расчет значений последовательной цепи.

3-30

NEETS Содержание

Введение в материю, энергию, и постоянного тока
Введение в переменный ток и трансформаторы
Введение в защиту цепей, Контроль и измерение
Введение в электрические проводники, электромонтаж Техники и схемы чтения
Введение в генераторы и двигатели
Введение в электронную эмиссию, трубки, и блоки питания
Введение в твердотельные устройства и Блоки питания
Введение в усилители
Введение в генерацию волн и формирование волн Схемы
Введение в распространение и передачу волн Линии и антенны
Принципы СВЧ
Принципы модуляции
Введение в системы счисления и логические схемы
Введение в микроэлектронику
Принципы синхронизаторов, сервоприводов и гироскопов
Введение в испытательное оборудование
Принципы радиочастотной связи
Принципы работы радара
Справочник техника, Главный глоссарий
Методы и практика испытаний
Введение в цифровые компьютеры
Магнитная запись
Введение в волоконную оптику

Решено: Цепи серии: 1.Расчет последовательного тока …

наука
физика
вопросы и ответы по физике
: 1. Расчет последовательного тока в цепях: каков общий ток через …

Показать текст изображения

Ответ эксперта

100% (1 оценка) Предыдущий вопрос Следующий вопрос

Последовательные цепи: 1. Расчет тока в последовательных цепях: каков общий ток в последовательной цепи, если ток, измеренный на каждой из пяти различных нагрузок, равен 1.5А? 2. Расчет общего сопротивления в последовательных цепях: каково полное сопротивление цепи, содержащей резисторы номиналом 100, 200 и 500? 3. Расчет напряжения в последовательных цепях: каково общее приложенное напряжение цепи, содержащей падения 25 В, 50 В и 75 В на трех нагрузках? 4. Расчет напряжения в последовательных цепях: каково падение (изменение) напряжения на каждой из четырех ламп (равного сопротивления), если напряжение всей цепи составляет 120 В? 5. Расчет общей мощности в последовательной цепи: какова общая мощность в последовательной цепи, если три нагрузки подключены последовательно, и каждая нагрузка дает 10 Вт? 6.Расчет мощности, потребляемой нагрузкой в последовательных цепях: Какая мощность используется резистивной нагрузкой в цепи 1 А с падением напряжения 10 В? 7. Используйте закон Ома и формулу мощности, чтобы найти значения для показанной последовательной цепи. ET = _ IT = — RT = _PT = — ОБЩАЯ МОЩНОСТЬ ЦЕПИ СЕРИИ wp L20W Ламповая нагрузка E-12v 30W Ламповый блок? L MW 12 V АККУМУЛЯТОРНАЯ СХЕМА ИЗОБРАЖЕНИЯ Используйте закон Ома и формулу мощности, чтобы найти значения для показанной последовательной цепи. 120 В переменного тока 50 лампочек R -70 8. Расчет общего сопротивления: Каково полное сопротивление в гирлянде (цепи) рождественских фонарей, содержащей 50 лампочек каждая с сопротивлением 70? 9.Расчет общего тока: каков общий ток в гирлянде (цепи) рождественских фонарей, если приложенное напряжение составляет 120 В, а общее сопротивление цепи составляет 3500? 10. Расчет общей мощности: Какова общая мощность в световой цепочке (цепи), когда приложенное напряжение составляет 120 В, а ток в цепи — 0,34 А? 11. Расчет напряжения: каково падение (изменение) напряжения на каждой лампочке, когда приложенное напряжение составляет 120 В и световая цепочка (цепь) содержит 50 лампочек с сопротивлением 70 каждая? 12.Расчет напряжения: каково падение (изменение) напряжения на каждой лампочке, когда приложенное напряжение составляет 120 В, а световая цепочка (цепь) содержит 40 рабочих лампочек каждая с сопротивлением 70 (остальные 10 лампочек перегорели, поэтому ток теперь идет. через шунтирующую цепь 0)? Параллельные цепи: 13. Расчет общего сопротивления в параллельных цепях: Каково полное сопротивление цепи, содержащей два резистора номиналом 6000 и 9000, соединенных параллельно? 14. Расчет общего сопротивления в параллельных цепях: Каково полное сопротивление цепи, содержащей три резистора номиналом 30000 10000 и 50000, соединенных параллельно? 15.Расчет напряжения в параллельных цепях: каково полное напряжение, если напряжение на каждой нагрузке измеряется при 110 В переменного тока? 16. Расчет тока в параллельных цепях: каков общий ток в цепи, содержащей четыре нагрузки, подключенные параллельно, если ток через четыре нагрузки составляет 0,52 А, 5,25 А, 6,33 А и 1,5 А? 17. Расчет мощности, потребляемой нагрузкой в параллельных цепях: Какую мощность использует резистивная нагрузка, которая тянет 3,0 А и имеет падение напряжения 115 В переменного тока? 18. Расчет общей мощности в параллельных цепях: Какова общая мощность цепи, если четыре нагрузки подключены параллельно, и нагрузки производят 200 Вт, 500 Вт, 1000 Вт и 19 Вт.Используйте закон Ома и формулу мощности, чтобы найти значения для показанной параллельной цепи. ОБЩИЙ ТОК ПАРАЛЛЕЛЬНОЙ ЦЕПИ ET =. СХЕМА ИЗОБРАЖЕНИЯ Используйте закон Ома и формулу мощности, чтобы найти значения для показанной параллельной цепи. ПРИМЕНЕНИЕ Вафельницы 20. Расчет полной мощности вафельницы: Какова общая мощность цепи вафельницы, содержащей два нагревательных элемента с номинальной мощностью 1200 Вт каждый? -R, = ВЕРХНИЙ НАГРЕВАТЕЛЬНЫЙ ЭЛЕМЕНТ 1200 Вт -R, = НИЖНИЙ НАГРЕВАТЕЛЬНЫЙ ЭЛЕМЕНТ 1200 Вт ВКЛ / ВЫКЛ ПЕРЕКЛЮЧАТЕЛЬ ТЕМПЕРАТУРЫ НАГРЕВАТЕЛЬНЫЙ ЧЕРТЕЖ НИЖНИЙ НАГРЕВАТЕЛЬНЫЙ ЭЛЕМЕНТ 21.Расчет полного тока вафельницы: каков полный ток вафельницы, если общая мощность составляет 2400 Вт, а общее напряжение — 120 В? К 120 К СХЕМЕ ПОДКЛЮЧЕНИЯ ВЕРХНЕГО НАГРЕВАТЕЛЬНОГО ЭЛЕМЕНТА P? R =? 22.

Основные принципы последовательного соединения резисторов

Формула расчета общей мощности

Расчет мощности на отдельных резисторах

Особенности распределения мощности при последовательном соединении

Пример расчета мощности при последовательном соединении

Сравнение с параллельным соединением резисторов

Практическое применение расчетов мощности

Ограничения и особые случаи при расчете мощности

Заключение

Расчет мощности при последовательном соединении

Формула параллельного соединения резисторов

Параллельное соединение резисторов — расчет

Пример №1

Пример расчета №2

Как рассчитать сложные схемы соединения резисторов

Ток, протекающий в цепи параллельно соединенных резисторах

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Теперь используем формулу расчета сопротивления:

Резисторы

Соединяем последовательно

Расчет мощности последовательного соединения

Теперь используем формулу расчета сопротивления:

Как правильно соединять аккумуляторы последовательно и параллельно

Как быстрее вскипятить воду

1.Последовательное соединение.

2.Параллельное соединение.

3.Подключение одной плитки

Мощность сопротивления при последовательном соединении

Как правильно соединять резисторы?

Последовательное соединение резисторов.

Параллельное соединение резисторов.

Что ещё нужно учитывать при соединении резисторов?

Свойства и технические характеристики резисторов

Мощность при последовательном соединение

Мощность при паралл ельном соединение

ресурсов

Последовательная цепь

Закон напряжения Кирхгофа

Рассеиваемая мощность

ПИТАНИЕ В КОМБИНИРОВАННЫХ ЦЕПЯХ

ЦЕПИ С ИЗВЕСТНЫМ ИСПОЛЬЗОВАНИЕМ ЭНЕРГИИ

Базовая электрическая теория в двух словах

Теоретические карточки | Quizlet

Серия тренингов по электричеству и электронике ВМС (NEETS), Модуль 1-3, с. 21-30

Решено: Цепи серии: 1.Расчет последовательного тока …

Ответ эксперта

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ