Общее сопротивление при параллельном соединении формула. Параллельное соединение проводников: формулы, расчеты и применение

Как рассчитать общее сопротивление при параллельном соединении. Какие формулы используются для расчета токов и напряжений в параллельных цепях. Где применяется параллельное соединение проводников на практике.

Что такое параллельное соединение проводников

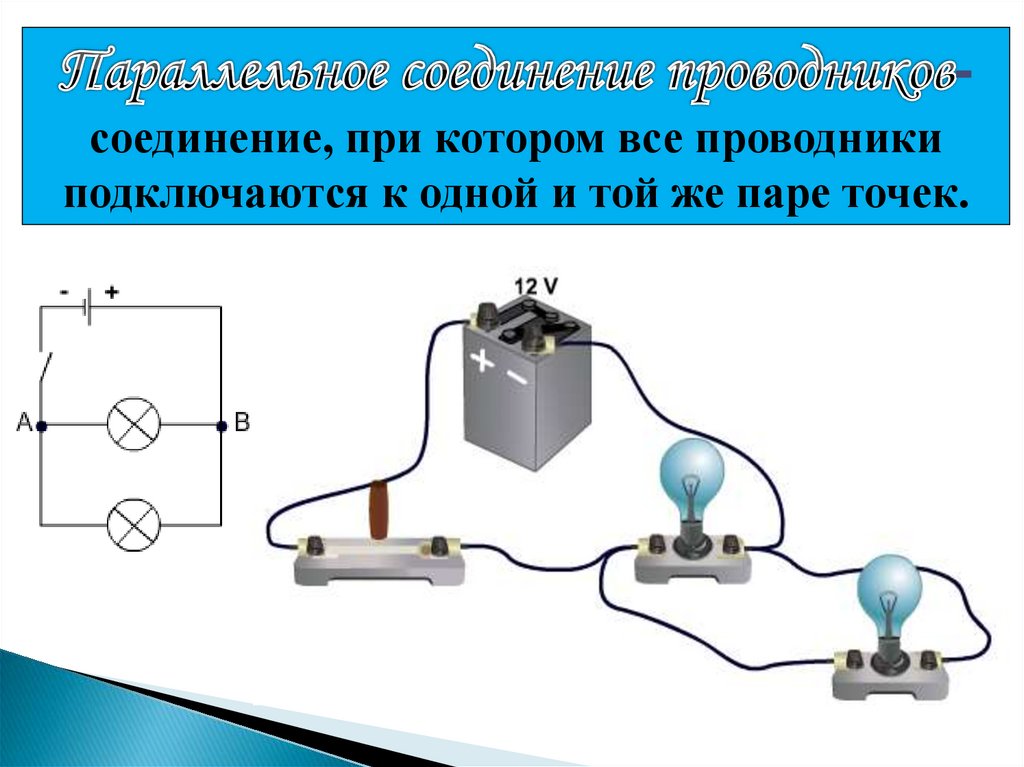
Параллельное соединение проводников — это такой способ соединения, при котором все проводники подключаются к одним и тем же двум точкам электрической цепи. При этом напряжение на всех параллельно соединенных проводниках одинаково.

Основные особенности параллельного соединения:

• Напряжение на всех проводниках одинаково и равно общему напряжению
• Общий ток равен сумме токов в отдельных проводниках
• Общее сопротивление всегда меньше сопротивления любого из проводников

Формулы для расчета параметров параллельного соединения

Для расчета параметров цепи с параллельным соединением проводников используются следующие основные формулы:

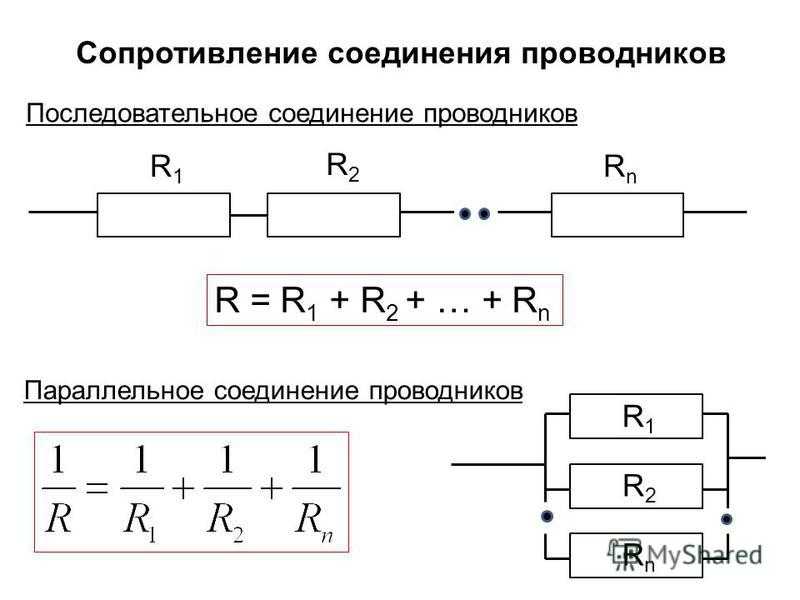
1. Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3 + …
2. Общий ток: I = I1 + I2 + I3 + …
3. Напряжение на проводниках: U = U1 = U2 = U3 = …
4. Ток в отдельном проводнике: I1 = U / R1

Где R — общее сопротивление, R1, R2, R3 — сопротивления отдельных проводников, I — общий ток, I1, I2, I3 — токи в отдельных проводниках, U — общее напряжение.

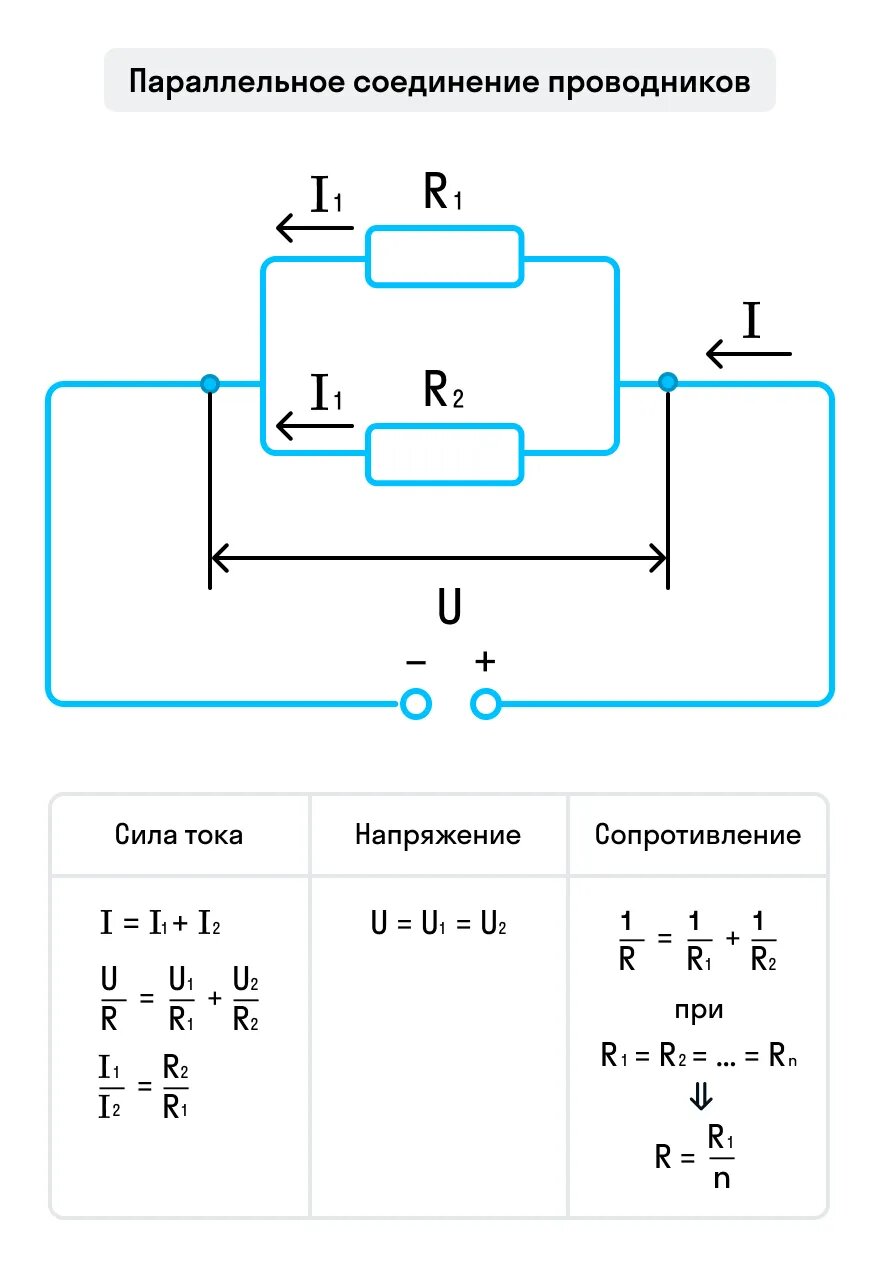
Как рассчитать общее сопротивление при параллельном соединении

Для расчета общего сопротивления при параллельном соединении проводников используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Чтобы найти R, нужно:

1. Записать обратные величины сопротивлений
2. Сложить их
3. Взять обратную величину от полученной суммы

Например, если R1 = 6 Ом, R2 = 3 Ом, то:

1/R = 1/6 + 1/3 = 1/6 + 2/6 = 3/6 = 1/2

R = 1 / (1/2) = 2 Ом

Распределение токов в параллельной цепи

При параллельном соединении ток в цепи распределяется обратно пропорционально сопротивлениям проводников. То есть:

I1/I2 = R2/R1

Чем меньше сопротивление проводника, тем больший ток через него протекает. Это позволяет рассчитывать токи в отдельных ветвях, зная общий ток и сопротивления.

Преимущества и недостатки параллельного соединения

Параллельное соединение проводников имеет ряд преимуществ и недостатков по сравнению с последовательным:

Преимущества:

• Независимость работы приборов — при выходе из строя одного, остальные продолжают работать
• Возможность подключать приборы с разным сопротивлением к одному источнику
• Уменьшение общего сопротивления цепи

Недостатки:

• Увеличение общего тока в цепи
• Необходимость более мощного источника питания
• Сложность расчетов при большом количестве проводников

Применение параллельного соединения на практике

Параллельное соединение проводников широко применяется в различных областях техники и в быту:

• В электрических сетях зданий — все розетки и приборы подключены параллельно
• В автомобильной электрике — фары, стеклоподъемники и другие потребители подключены параллельно
• В электронике — для создания делителей напряжения и токов
• В системах электроснабжения — для подключения нескольких генераторов
• В осветительных системах — для подключения большого количества ламп

Как решать задачи на параллельное соединение проводников

При решении задач на параллельное соединение проводников рекомендуется придерживаться следующего алгоритма:

1. Нарисовать схему соединения
2. Записать исходные данные
3. Определить, что нужно найти
4. Выбрать необходимые формулы
5. Произвести расчеты
6. Проверить размерность полученного результата

Рассмотрим пример решения задачи:

Два резистора сопротивлением 30 Ом и 60 Ом соединены параллельно. Напряжение на концах цепи 120 В. Определить силу тока в каждом резисторе и общий ток в цепи.

Решение:

1. Общее сопротивление: 1/R = 1/30 + 1/60 = 3/60 = 1/20 R = 20 Ом
2. Общий ток: I = U/R = 120/20 = 6 А
3. Ток через первый резистор: I1 = U/R1 = 120/30 = 4 А
4. Ток через второй резистор: I2 = U/R2 = 120/60 = 2 А

Проверка: I = I1 + I2 = 4 + 2 = 6 А

Ошибки при расчетах параллельных цепей

При расчетах параллельных цепей часто допускаются следующие ошибки:

• Сложение сопротивлений вместо сложения обратных величин
• Неправильное применение закона Ома для участка цепи
• Забывание о том, что напряжение на всех параллельных участках одинаково
• Неверное распределение токов по ветвям

Чтобы избежать этих ошибок, важно внимательно анализировать схему и правильно применять формулы.

Сравнение параллельного и последовательного соединения

Параллельное и последовательное соединения имеют ряд существенных различий:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаково на всех элементах	Сумма напряжений на элементах
Ток	Сумма токов через элементы	Одинаков во всех элементах
Сопротивление	Меньше наименьшего	Сумма сопротивлений
Формула сопротивления	1/R = 1/R1 + 1/R2 + …	R = R1 + R2 + …

Заключение

Параллельное соединение проводников — важный способ соединения элементов электрических цепей, широко применяемый на практике. Понимание принципов работы параллельных цепей и умение производить расчеты их параметров необходимо для успешного изучения электротехники и электроники. Правильное применение формул и алгоритмов решения задач позволяет легко анализировать даже сложные схемы с параллельным соединением проводников.

Напряжение в параллельной цепи. Параллельное соединение сопротивлениий (резисторов)

Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.

Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)

где R эк = R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи

U = U 1 + U 2 +U 3 (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U 1: U 2: U 3 = R 1: R 2: R 3 (21)

т.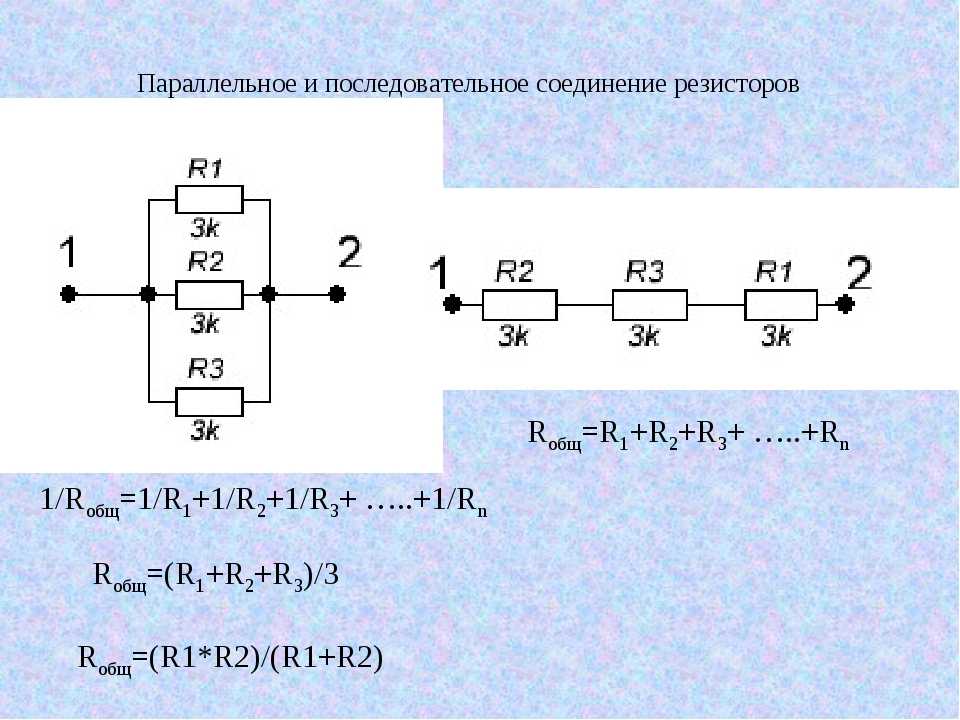 е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В.

Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.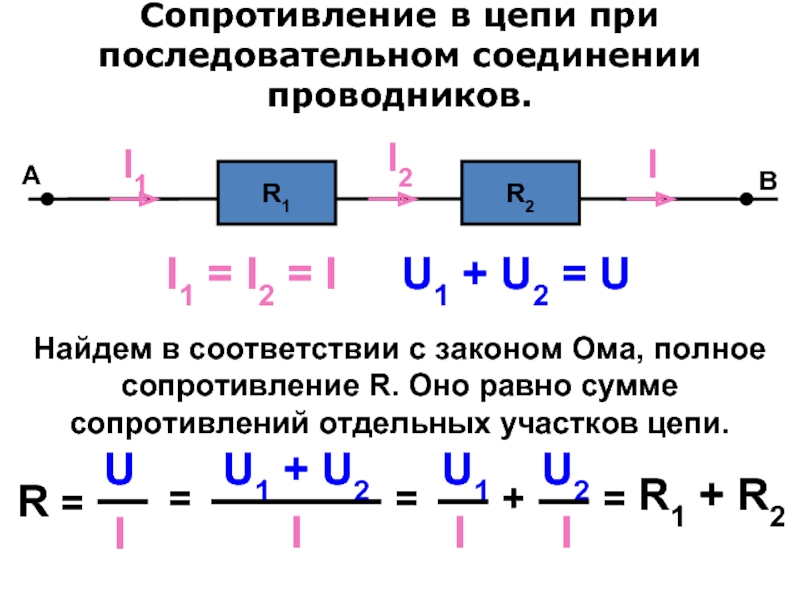
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных.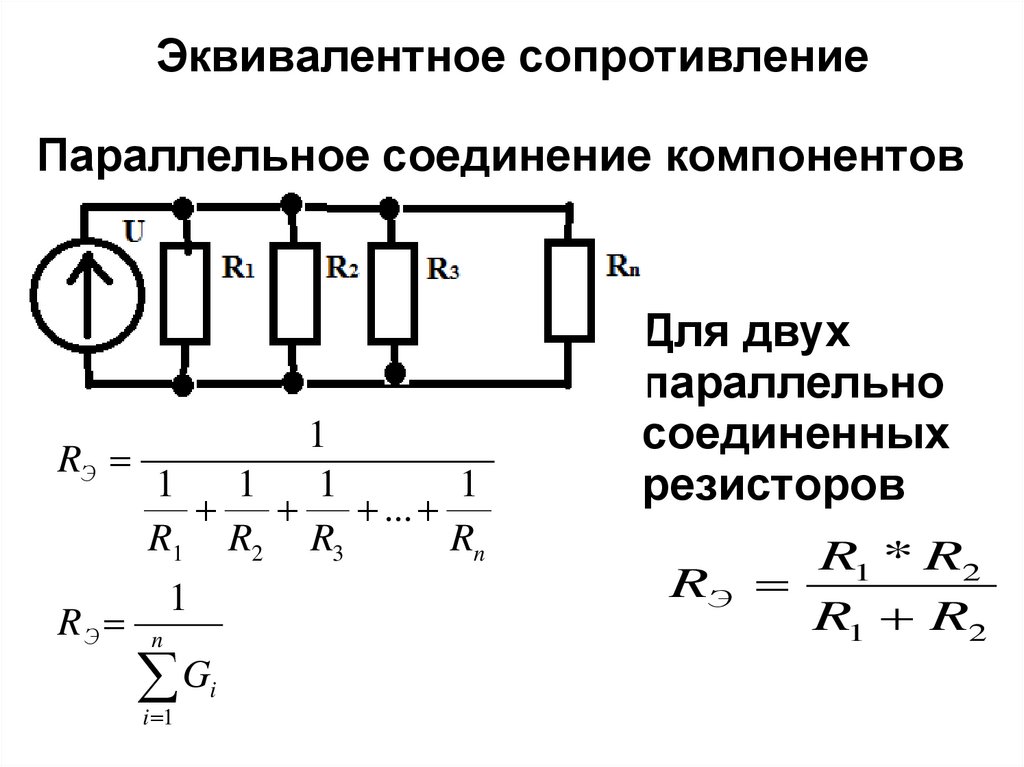 Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

1. При последовательном соединении проводников

1. Сила тока во всех проводниках одинакова :

I 1 = I 2 = I

2. Общее напряжение U на обоих проводниках равно сумме напряжений U 1 и U 2 на каждом проводнике :

U = U 1 + U 2

3. По закону Ома, напряжения U 1 и U 2 на проводниках равны U 1 = IR 1 , U 2 = IR 2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR 1 + I R 2. Отсюда следует

R = R 1 + R 2

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

2. При параллельном соединении проводников

1. Напряжения U 1 и U 2 на обоих проводниках одинаковы

U 1 = U 2 = U

2. Сумма токов I 1 + I 2 , протекающих по обоим проводникам, равна току в неразветвленной цепи :

I = I 1 + I 2

Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно, I = I 1 + I 2 .

3. Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).

На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.

При последовательном соединении два соседних источника соединяются разноименными полюсами.

Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.

Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.

1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3

2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3

Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1

3.

При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.

Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).

Параллельно соединяют только источники с одинаковой ЭДС . Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.

1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3

2. Сопротивление батареи меньше, чем сопротивление одного источника r батареи = r 1 /n
3. Сила тока в такой цепи по закону Ома

Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.

Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.

Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.

Для параллельного соединения сопротивлений характерны следующие свойства:

Напряжения на зажимах всех сопротивлений одинаковы:

U 1 = U 2 =U 3 =U ;

Проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:

1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,

где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3 ) .

Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости.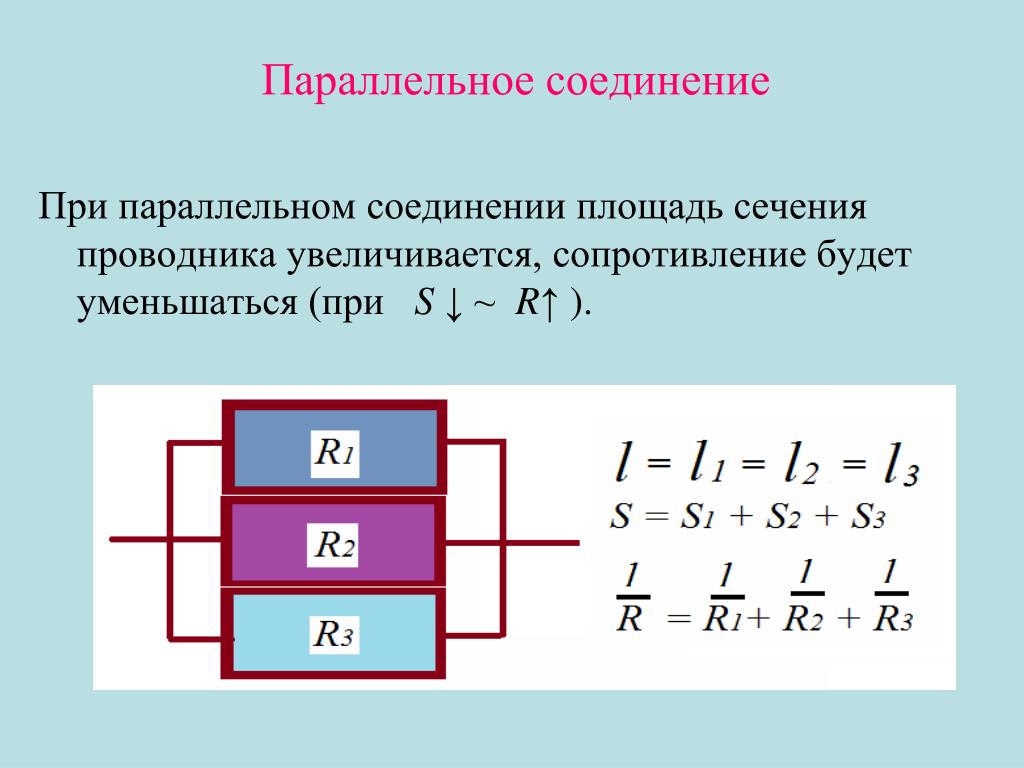 Следовательно, сопротивление параллельного разветвления из трёх резисторов:

R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .

Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.

Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.

При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.

На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.

Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:

1/R = 1/R 1 + 1/R 2 .

Приведём к общему знаменателю:

1/R = R 2 + R 1 /R 1 R 2 ,

отсюда эквивалентное сопротивление

R = R 1 R 2 /R 1 + R 2 .

Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.

Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.

При параллельном соединении n равных сопротивлений R 1 эквивалентное сопротивление их будет в n раз меньше, т.е.

R = R 1 /n .

На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет

R = R 1 /5 = 30/5 = 6 Ом.

Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:

I = I 1 + I 2 + I 3 .

Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то

U = I 1 R 1 и U = I 2 R 2 .

Левые части этих равенств одинаковы, следовательно, равны и правые части:

I 1 R 1 = I 2 R 2 ,

или

I 1 /I 2 = R 2 /R 1 ,

Т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.

Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.

При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.

Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ .

Решение. R общ = R 1 R 2 /R 1 + R 2 = 25 . 50 / 25 + 50 ≈ 16, 6 Ом.

Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ .

Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.

Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.

Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.

Параллельное соединение проводников

Цели урока:

• сформировать знания о параллельном соединении проводников, способах расчета параметров цепи, закрепить умения сборки электрических цепей;
• развивать творческие способности (умение видеть противоречие, формулировать проблему, выдвигать гипотезы и находить выход из проблемной ситуации).

Оборудование: на каждом столе два резистора по 4 Ом, источник питания, амперметр, вольтметр, соединительные провода.

На уроке используются проблемные методы обучения. Учащиеся должны осознать противоречие между известными им фактами и результатами эксперимента, выводами, которые они сделали из этих фактов, и результатами опыта, сформулировать проблему и разрешить ее. На предыдущих уроках изучено последовательное соединение проводников.

Тема урока не объявляется учителем, а формулируется учащимися в конце урока. Этот прием используется для того, чтобы дети еще раз повторили материал урока и осмыслили его.

На доске представлен весь объем работы, которую предстоит сделать на уроке.

Ход урока

Организационный момент.

Вид доски в начале урока.

U= R= IP= Io=	Дано: U=7,5B R1=5Ом R2=15Ом I-?	Дано: U=2,4B R1=2Ом R2=3Ом R-? I-?	Дано: R1=24Ом R2=8Ом I2=3A I1-?	Дано: I1=2A I2=4A U=12B R1-? R2-? R-?
Гипотезы.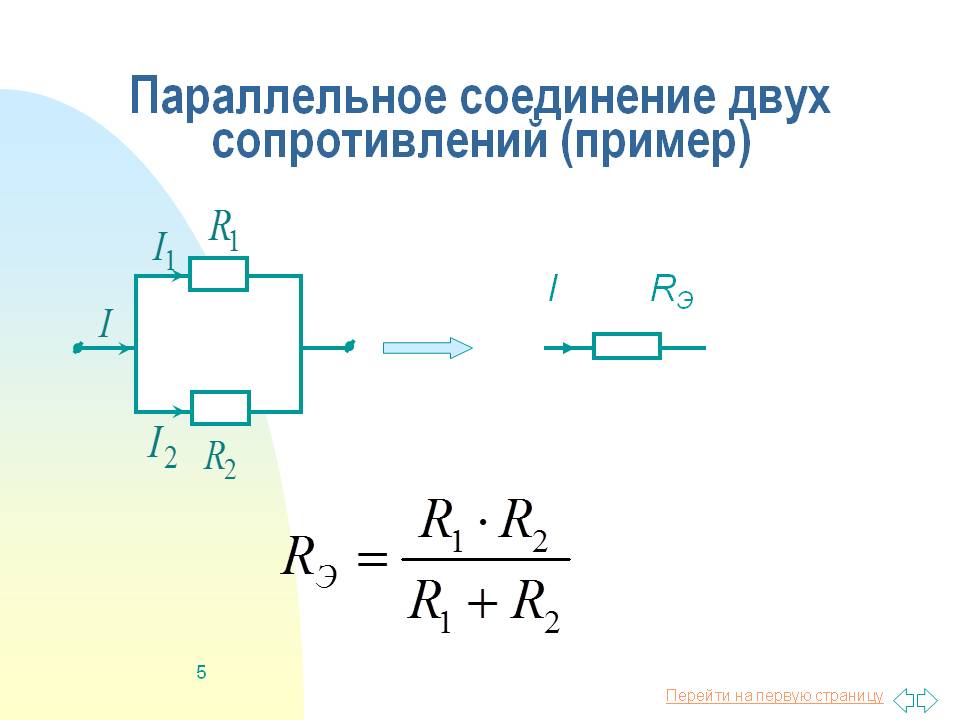 1. 2. 3. 4.

Актуализация знаний.

1. Фронтальный опрос.
2. Дайте определение электрического тока.
3. Каковы условия существования электрического тока в цепи?
4. Как можно создать электрическое поле в проводнике?
5. Какие физические величины характеризуют электрический ток и электрическое поле?
6. С помощью каких приборов можно измерить силу тока и напряжение на участке цепи и как эти приборы подключаются?

Создание проблемной ситуации.

Учитель задает вопрос: «Ребята, вы знаете, что чем больше резисторов в цепи, тем больше ее сопротивление и тем меньше сила тока при условии, что напряжение не изменяется. Если мы соберем цепь из двух резисторов по 4 Ом каждый, чему будет равно ее сопротивление?» (Ответ: 8 Ом).

Учитель: «Проверим наше предположение. Соберите цепь, схема которой начерчена на доске, измерьте напряжение, рассчитайте силу тока. Результаты вашей работы мы запишем на доске».

Учащиеся выполняют задание и получают такие результаты:

U=4 B, R=8 Oм, I=0,5 A

Учитель предлагает проверить полученный результат на опыте. Учащиеся измеряют силу тока в подводящих проводах. I=2 A.

Результаты расчетов и опыта не совпали. Почему?

Разрешение проблемной ситуации.

Учитель предлагает выдвигать гипотезы и записывает их на доске.

Гипотезы возможны такие:

• неправильно собрана цепь;
• допущена ошибка при вычислениях;
• проводники соединены не последовательно, поэтому нужно искать другие способы расчета параметров цепи.

После обсуждения гипотез приходят к выводу, что сопротивление в данной цепи не равно сумме сопротивлений составляющих ее резисторов и определять его надо по-другому. Следует анализ схемы цепи, дается определение параллельного соединения проводников, обсуждаются особенности распределения токов и напряжений на различных участках цепи.

Учитель: «Как же можно определить сопротивление цепи? Позволяют ли данные нашего опыта сделать это?»

Учащиеся приходят к выводу, что надо воспользоваться законом Ома.

I=U/R, R=U/I, R=2 Oм

Далее обращается внимание учащихся на то, что общее сопротивление цепи меньше каждого из входящих в нее сопротивлений.

Анализируя схемы, учащиеся приходят к выводу, что при последовательном соединении проводников общее сопротивление цепи больше большего, а при параллельном меньше меньшего сопротивления составляющих цепь резисторов. В качестве подводящего к правильному решению приема можно использовать аналогию с водой, разбегающейся по двум или нескольким ручейкам.

Закрепление и углубление знаний.

Задача № 1. Два параллельно соединенных проводника подключены к источнику постоянного напряжения 12 В. Сила тока в первом проводнике равна 2 А, во втором проводнике 4 А. Определите сопротивление каждого проводника и общее сопротивление цепи. (Ответ. R₁=6 Ом, R₂=3 Ом, R=2 Ом).

Решение задачи записывается на доске и в тетрадях, после чего в ходе подводящего диалога выводится формула зависимости силы тока от сопротивлений проводников.

Вопросы подводящего диалога 1.

1. Во сколько раз отличаются сопротивления проводников? (В 2 раза).
2. Во сколько раз отличаются текущие через них токи? (В 2 раза).
3. Какая между ними существует зависимость? (Обратно пропорциональная)
4. Как можно выразить эту зависимость математически? (I₁/I₂=R₂/R₁).
5. Как это доказать? (U=U₁=U₂; I₁R₁=I₂R₂; I₁/I₂=R₂/R₁).

Задача № 2. (Устно). Сопротивления двух параллельно соединенных проводников равны 24 Ом и 8 Ом. Сила тока во втором проводнике 3 А. Какова сила тока в первом проводнике? (Ответ. 1 А).

Вопрос. В нашем опыте сопротивления проводников были равными. Что можно сказать о текущих через каждый из них токах? (I₁=I₂=1A).

Вопросы подводящего диалога 2.

1. Вы научились находить общее сопротивление цепи с параллельным соединением проводников, но хотелось бы найти другой способ, с помощью которого мы могли бы находить общее сопротивление цепи, зная только сопротивления составляющих ее элементов. Давайте запишем зависимость между токами при параллельном соединении. (I=I₁+I₂).

2. А теперь выразим силы токов через другие величины, используя известный вам закон. (Закон Ома).

3. Как можно упростить полученное уравнение? (Разделить обе части уравнения на U).

Задача № 3. Проводники сопротивлением 2 Ом и 3 Ом соединены параллельно и подключены к напряжению 2,4 В. Найдите общее сопротивление цепи и общую силу тока. (R= 1,2 Ом; I=2 А).

Данная задача решается с использованием формулы 1/R=1/R₁+1/R₂

Задача № 4. Проводники сопротивлением 5 Ом и 15 Ом параллельно подключены к напряжению 7,5 В. Найти общую силу тока. (I= 2А)

Предлагается найти два способа решения задачи.

Домашнее задание.

49, устно ответить на вопросы. Упр. 23 №1, №3 (по желанию). (Учебник: Перышкин А.В. Физика-8. М.:Дрофа, 2004).

Подведение итогов урока.

Обобщение темы урока.

С доски стирается все, кроме схемы. Учащимся предлагается сформулировать цель урока, сформулировать и записать в тетради тему урока и формулы, которые необходимы для расчета параметров цепей с параллельным соединением проводников. Учитель делает записи на доске, чтобы учащиеся могли убедиться в правильности своих записей.

Общее сопротивление в параллельной цепи

Как рассчитать полное электрическое сопротивление в параллельной цепи? Ниже вы можете увидеть примеры цепи параллельного тока, содержащей три параллельно подключенных потребителя с разным электрическим сопротивлением. Для этой схемы вы можете увидеть расчет ее полного сопротивления. Этот расчет находится на странице с использованием формулы для расчета общего сопротивления.

Расчет общего электрического сопротивления в параллельной цепи более сложен, чем расчет полного электрического сопротивления в последовательной цепи! Формула (при наличии трех потребителей (резисторов) в параллельной цепи):

Если в цепи более трех потребителей, то в формуле мы просто добавляем их обратные значения как новое сложение в следующей последовательности.

Из формулы видно, что обратная величина полного (эквивалентного) электрического сопротивления при параллельном соединении есть сумма обратных величин отдельных электрических сопротивлений, входящих в состав цепи.

Чтобы решить задачу такого типа, вы должны знать все о сложении дробей!

Пример полного сопротивления в параллельной цепи

Ниже приведен полностью решенный пример! Он определяет общее электрическое сопротивление в цепи, содержащей только параллельно подключенные потребители!

Пример 1: Рассчитайте общее (эквивалентное) электрическое сопротивление цепи, показанной на рисунке ниже!

Из рисунка выше видно, что электрические сопротивления потребителей в цепи равны 2,3 и 6 Ом. Подставив эти значения в формулу расчета полного электрического сопротивления цепи параллельного тока, получим следующее выражение:

Числа 2, 3 и 6 являются знаменателями различных дробей в приведенном выше выражении. Чтобы сложить эти дроби, нам сначала нужно определить НОК чисел 2,3 и 6! Зная, что наименьшим общим знаменателем чисел 2,3 и 6 является число 6, разложим все три дроби до той дроби, которая содержит в знаменателе число 6. Выражение после расширения выглядит так:

Теперь, когда все дроби имеют одинаковый знаменатель, мы можем легко сложить их, что дает нам следующий шаг:

Наконец, хотя выражение можно решить несколькими способами (пропорционально, перекрестным умножением и т.