Общее сопротивление при последовательном соединении. Последовательное и параллельное соединение проводников: расчет сопротивления и применение

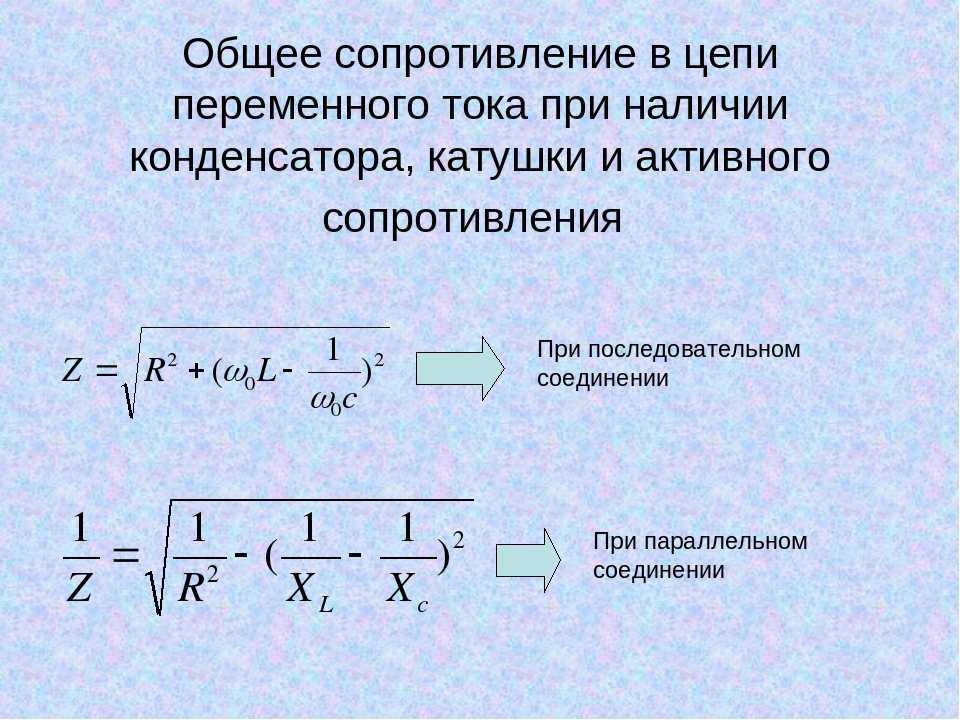
Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие формулы используются для вычисления сопротивления в электрических цепях. Где применяются различные типы соединений проводников на практике.

Последовательное соединение проводников: принцип и расчет сопротивления

Последовательное соединение проводников представляет собой такое соединение, при котором элементы цепи подключаются один за другим, образуя единую неразветвленную цепь. При этом через все элементы протекает один и тот же ток.

Основные характеристики последовательного соединения:

• Ток одинаков во всех элементах цепи
• Общее напряжение равно сумме напряжений на отдельных элементах
• Общее сопротивление равно сумме сопротивлений отдельных элементов

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных элементов.

Пример расчета сопротивления при последовательном соединении

Рассмотрим цепь из трех последовательно соединенных резисторов с сопротивлениями 10 Ом, 20 Ом и 30 Ом. Чему равно общее сопротивление цепи?

R = R1 + R2 + R3 = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Таким образом, общее сопротивление цепи составляет 60 Ом.

Параллельное соединение проводников: особенности и вычисление сопротивления

При параллельном соединении все элементы цепи подключаются к одним и тем же точкам, образуя разветвления. Основные характеристики параллельного соединения:

• Напряжение одинаково на всех элементах
• Общий ток равен сумме токов через отдельные элементы
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных элементов

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных элементов.

Пример расчета сопротивления при параллельном соединении

Рассчитаем общее сопротивление трех параллельно соединенных резисторов с сопротивлениями 6 Ом, 12 Ом и 4 Ом.

1/R = 1/6 + 1/12 + 1/4 = 1/2 + 1/12 + 1/4 = 3/12 + 1/12 + 3/12 = 7/12

R = 12/7 ≈ 1.71 Ом

Общее сопротивление цепи составляет приблизительно 1.71 Ом.

Сравнение последовательного и параллельного соединения проводников

Последовательное и параллельное соединения имеют ряд существенных различий, которые определяют их применение в электрических цепях:

• При последовательном соединении общее сопротивление увеличивается, а при параллельном — уменьшается
• Ток в последовательной цепи одинаков во всех элементах, а в параллельной — распределяется между ветвями
• Напряжение в последовательной цепи распределяется между элементами, а в параллельной — одинаково на всех элементах

Какое соединение выбрать для конкретной задачи? Это зависит от требуемых параметров цепи и ее назначения.

Применение последовательного и параллельного соединения в электротехнике

Различные типы соединений проводников широко используются в электротехнике и электронике для решения разнообразных задач:

Применение последовательного соединения:

• Создание делителей напряжения
• Подключение предохранителей и выключателей
• Измерение тока с помощью амперметра
• Создание резистивных нагревательных элементов

Применение параллельного соединения:

• Подключение нескольких потребителей к одному источнику питания
• Создание источников тока
• Измерение напряжения с помощью вольтметра
• Увеличение мощности в силовых цепях

Смешанное соединение проводников: комбинирование последовательного и параллельного соединений

В реальных электрических схемах часто используется смешанное соединение, сочетающее в себе элементы как последовательного, так и параллельного соединения. Это позволяет создавать более сложные и функциональные цепи.

При расчете смешанных цепей необходимо:

1. Разбить схему на участки с однотипным соединением
2. Рассчитать сопротивление каждого участка
3. Объединить полученные результаты, учитывая тип соединения между участками

Пример смешанного соединения может включать параллельно соединенные резисторы, которые затем последовательно соединены с другим резистором.

Практические аспекты использования различных соединений проводников

При проектировании электрических цепей важно учитывать особенности каждого типа соединения:

• Последовательное соединение удобно для создания высоких сопротивлений и деления напряжения
• Параллельное соединение позволяет снизить общее сопротивление и увеличить допустимый ток
• Смешанное соединение дает возможность создавать сложные цепи с заданными характеристиками

Выбор типа соединения зависит от конкретных требований к электрической цепи и ее функционального назначения.

Законы Кирхгофа и их применение в расчетах электрических цепей

Для анализа сложных электрических цепей с различными типами соединений проводников широко применяются законы Кирхгофа:

Первый закон Кирхгофа (закон токов)

Алгебраическая сумма токов в узле электрической цепи равна нулю. Этот закон особенно полезен при анализе параллельных соединений.

Второй закон Кирхгофа (закон напряжений)

В любом замкнутом контуре электрической цепи алгебраическая сумма напряжений на всех его участках равна нулю. Этот закон применяется при анализе последовательных соединений.

Использование законов Кирхгофа позволяет решать сложные задачи, связанные с расчетом токов и напряжений в разветвленных электрических цепях.

Сопротивление при параллельном и последовательном соединении резисторов

Практически все проводники обладают свойством создавать препятствие для течения электрического тока, известное как электрическое сопротивление, измеряемое в омах. Довольно часто в различных схемах требуется отрегулировать ток и напряжение. С этой целью в электронике широко применяются резисторы, обладающие точным значением сопротивления. Однако сопротивление при параллельном и последовательном соединении резисторов дает разные результаты, поэтому в каждом случае требуется своя методика расчетов. Стабильные и точные параметры этих элементов обеспечивают дальнейшую надежную эксплуатацию всей электрической схемы.

Содержание

Схема последовательного соединения

При последовательном соединении выполняется подключение каждого последующего резистора к предыдущему элементу. В результате, образуется непрерывная цепь, без каких-либо разветвлений. Значение тока будет одинаковым в каждой точке этой цепи: I_общ = I₁ = I₂. Напряжение U₁ и U₂, наоборот, будет отличаться в разных точках.

Работа по переносу заряда через всю цепь будет состоять из суммы работ по переносу заряда в каждом резисторе, то есть: U_общ = U₁ + U₂. В соответствии с законом Ома, напряжение U равно произведению тока и сопротивления, то есть IR.

Поэтому в окончательном виде напряжение или работа будет выглядеть следующим образом: IR = IR₁ + IR₂. В этой формуле значение R является общим сопротивлением цепи. На основании этой формулы можно сделать вывод, что в точках подключения резисторов начинает падать напряжение: R_общ = R₁ + R₂ + …. Rn. Отсюда следует, что при увеличении количества подключенных элементов, растет и падение напряжения.

Таким образом, общее значение сопротивления при последовательном соединении составляет сумму всех последовательно соединенных сопротивлений. Данный вывод действует для любых участков цепи, где имеется рассматриваемый вид соединения.

Параллельное соединение резисторов

Для того чтобы резисторы были соединены параллельно, необходимо в одной точке соединить их начала, а в другой точке – концы. Таким образом, можно соединить сколько угодно резисторов. Следует учесть, что электрический ток, протекающий между точками соединения, будет равномерно распределяться по каждой ветке.

Значение напряжения на всех резисторах будет одинаковым: U = U₁ = U₂. Электрические заряды, проходящие через каждый резистор за определенную единицу времени, в сумме составят величину заряда, проходящего через весь блок резисторов. В связи с этим общий ток будет представлять собой: I_общ = I₁ + I₂. Используя закон Ома, все полученные данные примут следующий вид: U/R = U/R + U/R.

После всех последующих преобразований формула примет окончательный вид:

Отсюда следует вывод, что при увеличении количества резисторов, соединяемых параллельно, возрастает и количество путей, по которым протекает электрический ток. В результате, общее сопротивление цепи уменьшается. Данное положение касается не только резисторов, но и других участков цепи, где имеется хотя-бы какое-то сопротивление.

Таким образом, сопротивление при параллельном и последовательном соединении резисторов, будет иметь совершенно разное значение. В первом случае оно будет уменьшаться, а во втором увеличиваться. Кроме того, существует величина, обратная сопротивлению, которая известна как проводимость. То есть при параллельном соединении складываются проводимости рассматриваемых участков, а при последовательном значения их сопротивлений.

Разница в сопротивлении широко используется на практике в повседневной жизни. Последовательное подключение предохранителя защищает всю цепь, поскольку при его перегорании происходит полное отключение. Параллельное соединение применяется в люстрах. Если сгорит одна лампочка, остальные продолжают работать, поскольку напряжение остается без изменений.

Калькулятор сопротивлений резисторов

R1	R2
Общее сопротивление	<> <>

Закон Ома для переменного тока

Как понять Закон Ома: простое объяснение для чайников с формулой и понятиями

Закон Ома для однородного участка цепи – формула

Закон Ома для полной и не полной электрической цепи, формула и правильное определение

Мультиметр: назначение, виды, обозначение, маркировка, что можно измерить мультиметром

Закон Ома для неоднородного участка цепи простым языком для чайников

Сопротивление при последовательном соединении резисторов равно сумме всех резисторов

Часто надо посчитать общее сопротивление при последовательном соединении резисторов. Внешний участок электрической цепи часто образуется не од­ним приемником с определенным сопротивлением, а нескольки­ми, соединенными последовательно, параллельно или смешанно.

Если несколько сопротивлений электрической цепи соедине­ны, как указано на рисунке ниже, одно за другим без разветвлений и по ним проходит один и тот же ток, то такое соединение называ­ется последовательным соединением сопротив­лений.

Последовательное соединение сопротивлений показано на рисунке.

По закону Ома напряжения на отдельных участках цепи (со­противлениях) или падения напряжения

U₁ = IR₁;
U₂ = IR₂;
U₃ = IR₃;
U₄ = IR₄.

Так как ток во всех участках имеет одинаковое значение, то напряжения на участках пропорциональны их сопротивлениям, т. е.

U₁ : U₂ = R₁ : R₂;
U₂ : U₃ = R₂ : R₃;
U₃ : U₄ = R₃ : R₄.
Мощности отдельных участков соответственно равны:

P₁ = U₁I;
P₂ = U₂I;
P₃ = U₃I;
P₄ = U₄I,

а мощность всей цепи, по закону сохранения энергии равная сумме мощностей отдельных участков,

P = P₁ + P₂ + P₃ + P₃ = I(U₁ + U₂ + U₃ + U₄) = IU,

откуда следует, что напряжение на зажимах цепи U равно сум­ме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ + U₄

Разделив правую и левую части этого выражения  на ток, получим:
U : I = U₁ : I + U₂ : I + U₃ : I + U₄ : I
или

R = R₁ + R₂ + R₃ + R₄

где R — общее сопротивление при последовательном соединении в цепи, т. е. такое равно­ценное (эквивалентное) сопротивление, заменяя которым все со­противления цепи (R₁, R₂, R₃ и R₄) при неизменном напряжении на ее зажимах, получим то же самое значение тока.

Или

Общее сопротивление при последовательном соединении проводников (сопротивлений) равно сумме всех сопротивлений в цепи.

Например:

Последовательно с постоянным сопротивлением, имеющей сопротивление R₁ = 2 ком (2000 ом), включен реостат R₂ (переменное сопротивление), сопротив­ление которого можно изменять от 0 до 10 ком (10000 ом). Определить, в каких пре­делах можно регулировать ток в цепи при напряжении, подведенным к этой цепи, равным 120 В.

При последовательном соединении сопротивление равно:

R = R₁ + R₂

При сопротивлении реостата, равным нулю:
I = U : ( R₁ + R₂ ) = 120 : (2000 + 0) = 0,06 а

При введенном реостате на максимальное значение

I = U : ( R₁ + R₂ ) = 120 : (2000 + 10000) = 0,01 а

Таким образом, ток можно регулировать в пределах от 0,01 а до 0,06 а.

Резисторы

в последовательном и параллельном построении формулы » Electronics Notes

Вывод формул для расчета полного сопротивления резисторов, соединенных последовательно и параллельно.

---

Учебное пособие по сопротивлению Включает:
Что такое сопротивление Закон Ома Омические и неомические проводники Сопротивление лампы накаливания Удельное сопротивление Таблица удельных сопротивлений для обычных материалов Температурный коэффициент сопротивления Коэффициент сопротивления по напряжению, VCR Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов

---

Формулы для расчета полного сопротивления для ряда резисторов, включенных последовательно, а также для резисторов, включенных параллельно, хорошо известны.

Что может быть менее известно, так это рассуждение и вывод формул.

В некоторых случаях может потребоваться понимание того, как вывести формулы для набора резисторов, соединенных последовательно или параллельно, а также это помогает понять общую теорию цепей.

Основой для вывода уравнений как для последовательных, так и для параллельных формул резисторов является использование законов Кирхгофа. Используя их, выводы уравнений относительно просты.

Расчет общего сопротивления резисторов в серии

Уравнение для полного сопротивления ряда резисторов, включенных параллельно, представляет собой сумму всех резисторов, приведенных ниже.

Резисторы серии

Rобщ=R1+R2+R3+ ….

Первый этап доказательства формулы заключается в рассмотрении случая двух последовательно соединенных резисторов, чтобы увидеть, как ведет себя схема.

Резисторы, включенные последовательно — отдельные резисторы, токи и напряжения
Здесь показаны два резистора, но тот же вывод можно легко расширить до любого количества резисторов.

Есть два факта, которые необходимо учитывать при выводе формулы для полного сопротивления набора резисторов, соединенных последовательно. Во-первых, по цепи течет один и тот же ток. Один и тот же ток протекает через источник напряжения и резисторы.

Во-вторых, законы Кирхгофа гласят, что сумма напряжений в цепи равна нулю. Таким образом, сумма падений напряжения на резисторах равна напряжению, выдаваемому источником в показанной цепи.

Из закона Ома:

V1=IR1 &  V2=IR2

Затем из закона Кирхгофа:

V-V1-V2=0 или V=V1+V2

Затем подставляя вместо V _{20 4} и V

V=IR1+IR2=I(R1+R2)

Это упрощает до:

VI=R1+R2

Но V/I = R _total , поэтому

Rtotal=R1+R2

59 Используя по той же логике можно расширить это до общего случая нескольких резисторов:

Rtotal=R1+R2+R3+ ….

Расчет общего сопротивления резисторов, включенных параллельно

Часто бывает так, что несколько резисторов располагаются параллельно. Во многих случаях это происходит при разработке электронных схем и т.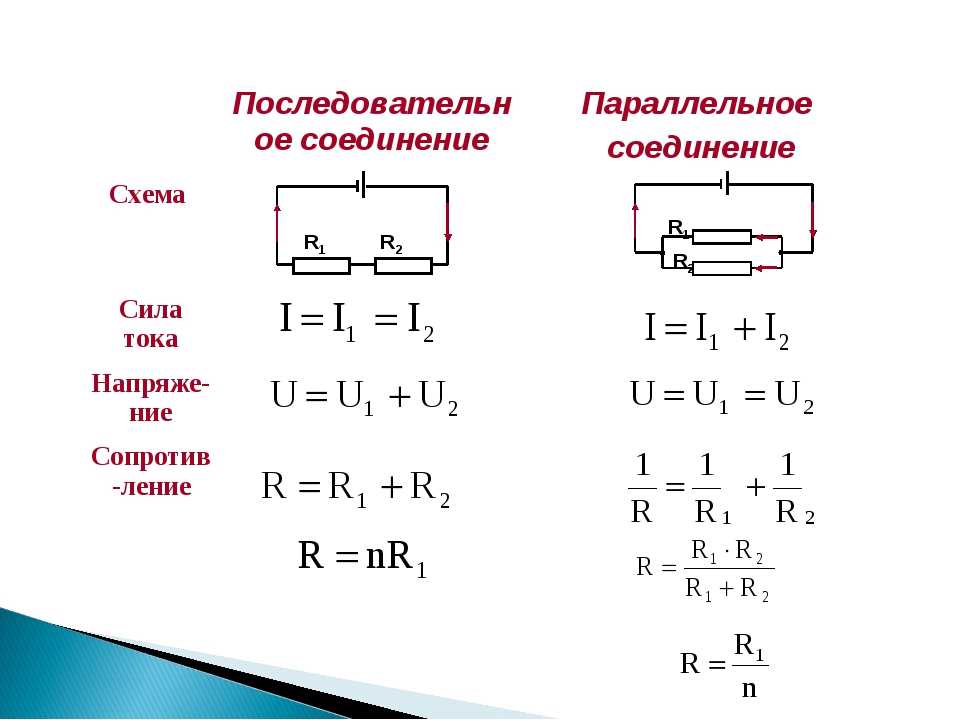 д.

Ниже приведена стандартная формула для расчета общего сопротивления нескольких резисторов или резисторов, включенных параллельно.

1Rобщ=1R1+1R2+1R3+……

Вывод общего уравнения для набора нескольких параллельных резисторов довольно прост. Принимая во внимание основные аспекты схемы, можно легко вывести общее уравнение для набора резисторов, включенных параллельно.

Параллельные резисторы — отдельные резисторы, токи и напряжения

При выводе формулы для полного сопротивления набора параллельно соединенных резисторов необходимо учитывать ток, протекающий через каждый резистор по очереди, и понимать, что каждый резистор имеет одинаковая разность потенциалов или напряжение на нем.

Первое, что нужно понять, это то, что сумма токов, протекающих через отдельные резисторы, равна общему току, обеспечиваемому источником напряжения, как показано на диаграмме: I=I1+I2+I3+ …In

Зная, что I=V/R по закону Ома, можно соотнести уровни протекающих токов с точки зрения напряжения (которое одинаково для всех, поскольку они параллельны) и сопротивления.

I=VR1+VR2+VR3+ …VRn

Тогда, разделив обе части на V, мы получим:

IV=1R1+1R2+1R3+ …1Rn

Но поскольку I/V равно 1/ Всего R _{, это можно заменить в уравнении, чтобы получить:}

1Rtotal=1R1+1R2+1R3+ …1Rn

Можно видеть, что вычислить общее сопротивление ряда параллельно соединенных резисторов очень просто.

Вывод формулы для двух резисторов, включенных параллельно

В различных электрических и электронных конструкциях или установках часто бывает необходимо рассчитать общее сопротивление двух резисторов, включенных параллельно.

В этом случае уравнение можно значительно упростить, что значительно упрощает вычисление полного сопротивления.

Rобщ=R1R2R1+R2

Получение этого уравнения относительно простое, требующее некоторых простых манипуляций с общим уравнением для параллельных резисторов, но упрощенное до включения только двух электронных компонентов.

1Rtotal=1R1+1R2

Умножая на R _total , получаем:

1=RtotalR1+RtR2

Затем умножаем на R ₁ и R 903Rtal = Rtal 2 9004 R2+RtotalR1

Изолировать R _всего R1R2=Rtotal(R2+R1)

Затем разделите на (R ₁ + R ₂ )

Rtotal =R1R2R2+R1

Используя эту формулу, очень легко вычислить общее сопротивление двух резисторов, включенных параллельно

Уравнения для определения полного сопротивления наборов резисторов, соединенных последовательно и параллельно, широко используются во многих областях, от электрических работ до проектирования электронных схем, а также во множестве других областей. Хотя нет необходимости все время выводить уравнения из первых принципов, полезно понять, как это можно сделать, поскольку это дает гораздо лучшее понимание того, что происходит.

Дополнительные основные понятия и руководства по электронике:
Напряжение Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность РЧ-шум Сигналы
    Возврат в меню основных понятий электроники. . .

Сопротивление серии

— Inst Tools

от редакции

Общее сопротивление в последовательной цепи равно сумме всех частей этой цепи, как показано в уравнении ниже.

R

_T =R1 +R2 +R3 …     и т. д.

где
R _T = общее сопротивление
R1 ,R2 , и R3 = последовательное сопротивление

Пример: 0009

В последовательной цепи последовательно соединены резисторы на 60 Ом, 100 Ом и 150 Ом (Рисунок 18). Чему равно полное сопротивление цепи?

Рис. 18 Сопротивление в последовательной цепи

Решение:

RT =R1 +R2 +R3

RT = 60 + 100 + 150 к сумме напряжений на каждом резисторе в цепи (рис. 19), как показано в уравнении ниже.

VT =V1 +V2 +V 3 …     и т. д.

, где

VT = общее напряжение

V1 = напряжение на R1

V2 = напряжение на R2

V3 = напряжение на R3

Рис. ко всей последовательной цепи или к отдельным составным частям цепи. При использовании на отдельных составных частях напряжение на этой детали равно силе тока, умноженной на сопротивление этой детали. Для схемы, показанной на рисунке 20, напряжение можно определить, как показано ниже.

V1= IR1
V2 = IR2
V3 = IR3

VT = V1 + V2 + V3

VT = 10 вольт + 24 вольт + 36 вольт
VT = 70 вольт

Общее напряжение 9

5 в серии Цепь

Чтобы найти общее напряжение в последовательной цепи, умножьте ток на общее сопротивление, как показано в уравнении ниже.

В

_Т = Я . R _T

где

VT = полное напряжение
I = ток
R _T = полное сопротивление

Пример 1:

В последовательной цепи последовательно соединены резисторы 50 Ом, 75 Ом и 100 Ом (Рисунок 21). Найдите напряжение, необходимое для получения тока 0,5 ампер.

Рис. 21 Пример 1. Серийная цепь

Решение:

Шаг 1: Найдите ток в цепи. Как мы уже знаем, ток во всей последовательной цепи одинаков и равен 0,5 ампера.

Шаг 2: Найти R _T

RT = R1 + R2 + R3

RT = 50 Ом + 75 Ом + 100 Ом

RT = 225 Ом

Шаг 3: Найдите VT .

Используйте закон Ома. В _Т = Я . R _T

VT = 0,5 x 225

VT = 112,5 В

Пример 2:

Аккумулятор 120 В соединен последовательно с тремя резисторами: 40 Ом и 100 Ом. Найдите напряжение на каждом резисторе.

Рисунок 22 Пример 2 Последовательная цепь

Решение:

Шаг 1: Найдите полное сопротивление.

RT = R1 + R2 + R3

RT = 40 Ом + 60 Ом + 100 Ом

RT = 200 Ом

Шаг 2: Найдите ток цепи (I) .

Используйте закон Ома. В _Т = Я . R _T

Решение для I

I = V _T /R _T

I = 120/200 = 0,6 А

Шаг 6.