Общий эмиттер это. Усилитель с общим эмиттером на биполярном транзисторе: принцип работы и расчет

Как работает усилитель с общим эмиттером на биполярном транзисторе. Какие у него основные характеристики. Как рассчитать параметры схемы усилителя с общим эмиттером. Какие преимущества и недостатки у данной схемы включения транзистора.

Принцип работы усилителя с общим эмиттером

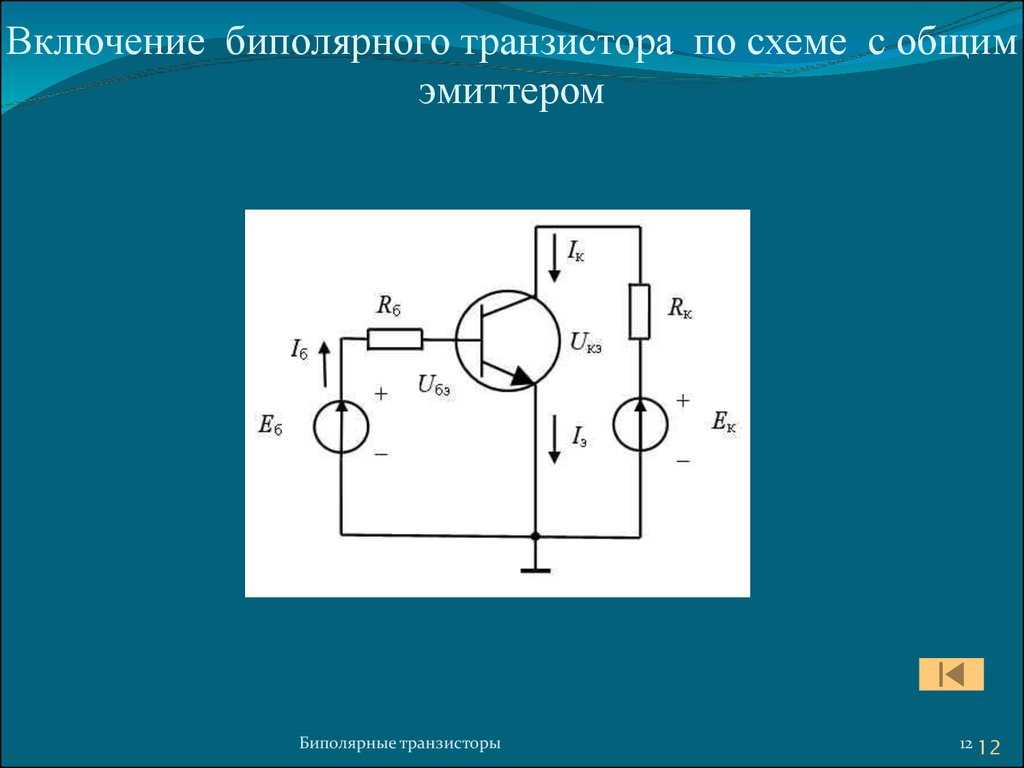
Усилитель с общим эмиттером (ОЭ) является одним из основных типов усилительных каскадов на биполярных транзисторах. В этой схеме входной сигнал подается на базу транзистора, а выходной снимается с коллектора. Эмиттер является общим электродом для входной и выходной цепей.

Основные особенности усилителя с ОЭ:

• Высокий коэффициент усиления по напряжению
• Средний коэффициент усиления по току
• Инверсия фазы выходного сигнала относительно входного
• Среднее входное сопротивление
• Высокое выходное сопротивление

Как работает усилитель с ОЭ? Входной сигнал изменяет ток базы транзистора, что приводит к изменению тока коллектора. Изменение тока коллектора вызывает падение напряжения на коллекторном резисторе, которое и является усиленным выходным сигналом.

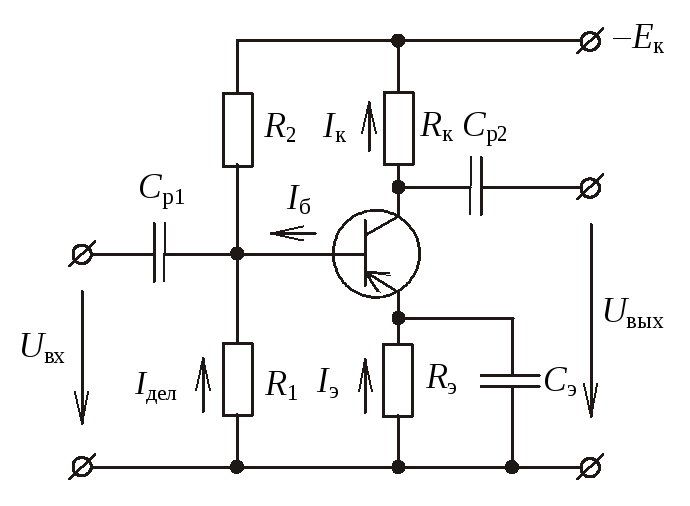
Основные характеристики усилителя с общим эмиттером

Рассмотрим ключевые параметры усилителя с общим эмиттером:

Коэффициент усиления по напряжению

Коэффициент усиления по напряжению для усилителя с ОЭ можно рассчитать по формуле:

K_u = -R_c / r_e

где R_c — сопротивление в цепи коллектора, r_e — дифференциальное сопротивление эмиттерного перехода.

Как видно, коэффициент усиления может достигать больших значений за счет большого соотношения R_c / r_e.

Входное сопротивление

Входное сопротивление усилителя с ОЭ определяется параллельным соединением резисторов в цепи базы и входным сопротивлением транзистора:

R_вх = (R₁ || R₂) || (β * r_e)

Обычно входное сопротивление составляет несколько килоом.

Выходное сопротивление

Выходное сопротивление усилителя с ОЭ примерно равно сопротивлению коллекторного резистора:

R_вых ≈ R_c

Это значение может достигать десятков килоом.

Как рассчитать параметры усилителя с общим эмиттером?

Рассмотрим пошаговый расчет усилителя с общим эмиттером:

1. Выбрать рабочую точку транзистора (I_к, U_кэ)
2. Рассчитать сопротивление резистора в цепи эмиттера R_э
3. Определить сопротивление резистора в цепи коллектора R_к
4. Рассчитать делитель напряжения в цепи базы R₁ и R₂
5. Подобрать разделительные конденсаторы C₁ и C₂

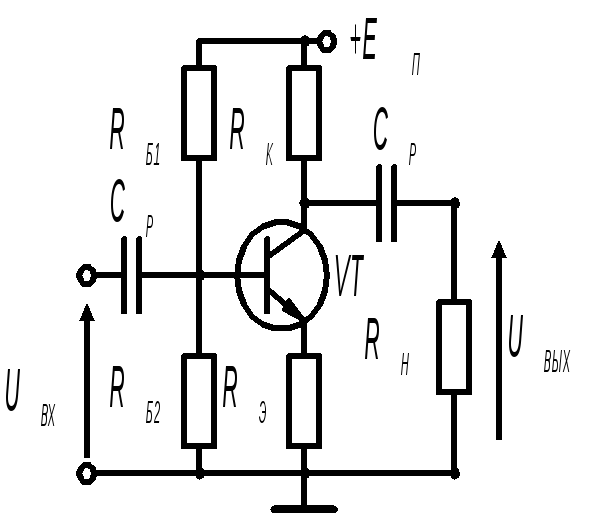
Давайте рассмотрим пример расчета для усилителя с питанием 12В и током коллектора 10мА.

Расчет резистора в цепи эмиттера

Примем падение напряжения на R_э равным 10% от напряжения питания:

U_Rэ = 0.1 * 12В = 1.2В

R_э = U_Rэ / I_э = 1.2В / 10мА = 120 Ом

Расчет резистора в цепи коллектора

Напряжение на R_к выбираем равным половине оставшегося напряжения:

U_Rк = (12В — 1.2В — 0.2В) / 2 = 5.3В

R_к = U_Rк / I_к = 5.3В / 10мА = 530 Ом

Преимущества и недостатки усилителя с общим эмиттером

Рассмотрим основные достоинства и ограничения схемы с ОЭ:

Преимущества:

• Высокий коэффициент усиления по напряжению
• Хорошее усиление мощности
• Простота схемы
• Широкая полоса пропускания

Недостатки:

• Инверсия фазы сигнала
• Зависимость параметров от температуры
• Высокое выходное сопротивление
• Возможность самовозбуждения

Несмотря на некоторые ограничения, усилитель с общим эмиттером остается одним из самых распространенных типов усилительных каскадов благодаря высокому коэффициенту усиления и простоте реализации.

Области применения усилителя с общим эмиттером

Усилитель с общим эмиттером находит широкое применение в различных электронных устройствах:

• Усилители звуковых частот
• Предварительные каскады радиоприемников
• Усилители промежуточной частоты
• Видеоусилители
• Импульсные схемы

Универсальность и хорошие характеристики делают усилитель с ОЭ незаменимым во многих областях электроники.

Особенности настройки усилителя с общим эмиттером

При настройке усилителя с ОЭ необходимо учитывать следующие моменты:

• Правильный выбор рабочей точки транзистора
• Обеспечение температурной стабилизации
• Подбор оптимального коэффициента усиления
• Согласование входного и выходного сопротивлений
• Устранение возможных самовозбуждений

Грамотная настройка позволяет реализовать все преимущества схемы с общим эмиттером и минимизировать ее недостатки.

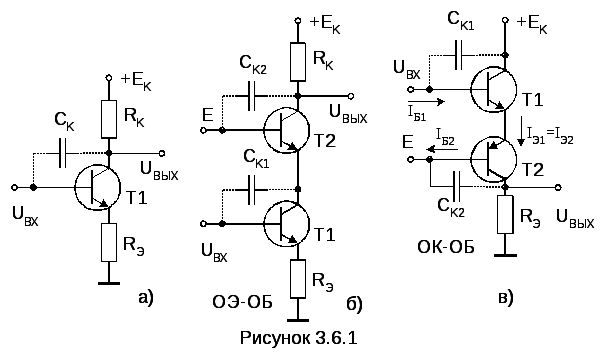
Сравнение усилителя с ОЭ с другими схемами включения транзистора

Как усилитель с общим эмиттером соотносится с другими базовыми схемами включения транзистора? Рассмотрим основные отличия:

Усилитель с общим эмиттером vs усилитель с общей базой:

• ОЭ имеет более высокое входное сопротивление
• ОЭ обеспечивает усиление и по току, и по напряжению
• ОБ имеет лучшие высокочастотные свойства

Усилитель с общим эмиттером vs эмиттерный повторитель:

• ОЭ дает высокое усиление по напряжению, ЭП — единичное
• ЭП имеет очень высокое входное и низкое выходное сопротивление
• ОЭ инвертирует сигнал, ЭП — нет

Каждая схема имеет свои преимущества и недостатки, выбор зависит от конкретной задачи.

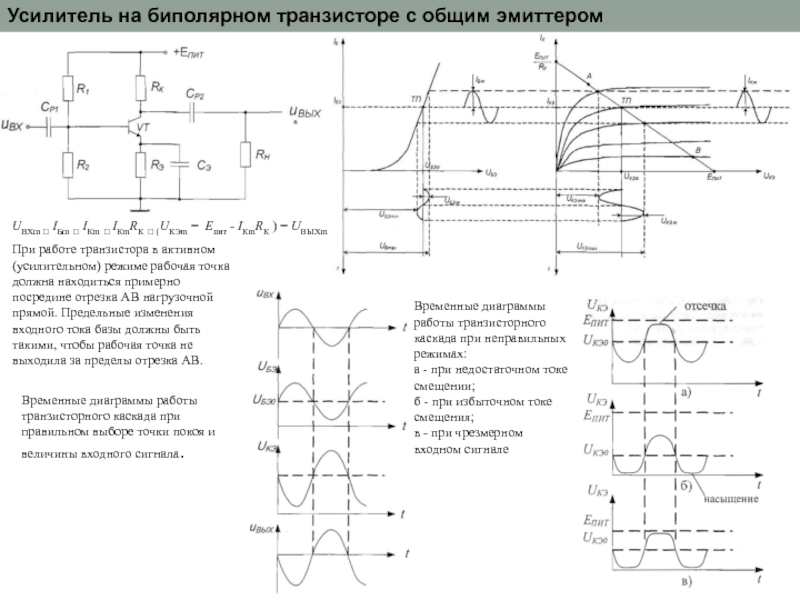
Эмиттерный повторитель или Общий эмиттер? | Радиолюбитель — это просто!

24.01.2023

Вопрос простой и не должен вызывать затруднений, но иногда многие из нах путают эти схемы. Под одним из моих видео было много комментариев которые потом переросли в спор, что же было на схеме на самом деле эмиттерный повторитель или схема с общим эмиттером. Вопрос разрешился — в споре рождается истина, но нужно всё-таки определится.

Эмиттерный повторитель

Первое определение: Эмиттерный повторитель — это схема с общим коллектором (так же написано в некоторых учебниках).

Второе определение: В эмиттерном повторителе транзистор включён по схеме с общим коллектором (ОК). То есть, потенциал коллектора при работе каскада неизменен относительно «земли» и коллектор обычно подключается к источнику питания (так написано в Википедии и большей части учебников).

Схема, упрощенно выглядит так:

Эмиттерный повторитель

Работа каскада:

Входной сигнал подаётся на базу, а выходной сигнал снимается с эмиттера. В схеме образуется 100 % отрицательная обратная связь по напряжению, это существенно уменьшает нелинейные искажения сигнала.

Фазы входного и выходного сигнала совпадают, то есть усилитель является неинвертирующим.

Эмиттерный повторитель понижает выходное сопротивление источника сигнала. Т.е. чаще всего каскад построенный на эмиттерном повторителе применяют для согласования сопротивлений источника и нагрузки. Именно за счет этого эмиттерный повторитель дает усиление по току, а не по амплитуде или напряжению.

Общий эмиттер

Определение: Каскад с общим эмиттером обладает высоким усилением по напряжению и току.

Схема упрощенно выглядит так:

Общий эмиттер

Работа каскада:

Входной сигнал подаётся на базу, а выходной сигнал снимается с коллектора.

Фазы входного и выходного сигнала не совпадают, то есть усилитель является инвертирующим на 180°, этот факт кстати относится к недостаткам такого включения.

Применяется такое включение для усиления сигнала как по току так и по напряжению (т.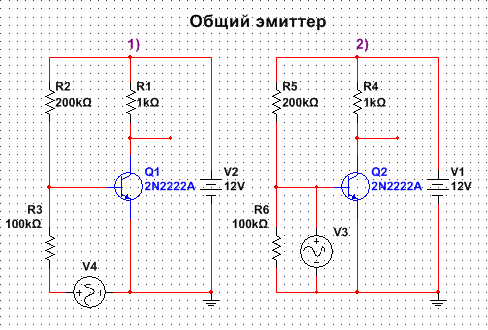 е. по амплитуде сигнала).

Выводы

Определения определениями, а в чем все таки разница? Еще раз давайте посмотрим на обе схемы:

Эмиттерный повторительОбщий эмиттер

Если нагрузка включена в цепь эмиттера, а коллектор подключен к линии питания и его потенциал не меняется (коллектора), то это схема с общим коллектором или второе название эмиттерный повторитель.

Если нагрузка включена в цепь коллектора, а эмиттер подключен к линии питания и его потенциал не меняется (эмиттера), то это схема с общим эмиттером.

Усилительные каскады как теперь понятно построены по схеме с общим эмиттером, нагрузка подключена к коллектору. И именно по этому вывод коллектора у транзистора имеет более массивный вывод и контакт с корпусом или «ухом» крепления, специально для крепления и прямого контакта с радиатором охлаждения. Потому, что именно на коллекторе выделяется вся мощность.

Нужно сказать, что и включении транзистора с общим эмиттером, эмиттер не обязательно будет подключён к линии питания напрямую, так и в случае включения транзистора по схеме эмиттерного повторите, коллектор тоже может не иметь прямого контакта с линией питания. Например как ниже:

эмиттерколлекторобщийсхемавключение

Поделиться в социальных сетях

Вам может понравиться

Общий эмиттер

Е_см обеспечивает закрытое состояние транзистора.

Когда транзистор работает как ключ, он находится в режиме I и III, пробегая режим усиления (II)

В точке А транзистор находится в режиме отсечки ключ разомкнут.

В точке В, транзистор VT – открыт и насыщен (О(Н)).

Передаточная характеристика

• зависимость

По методу двух узлов найдем

Для того, чтобы биполярный транзистор вошел в режим насыщения, необходимо выполнение токового критерия:

Помехоустойчивость ключа – инвертора

Под помехоустойчивостью понимается то напряжение фиктивного источника, которое включается между выходом ключа и входом такого же ключа, являющегося нагрузкой, при котором схема нагрузки функционирует нормально.

VT₁ – закрыт, VT₂ – открыт (насыщен)

VT₁ – открыт (насыщен)

Схема замещения транзистора в режиме отсечки

В режиме отсечки транзистор можно заменить источником тока = , это соответствует разомкнутому состоянию ключа. Режим отсечки обеспечивается напряжением или осуществляемая за счет для кремниевых транзисторов.

Схема замещения транзистора в режиме насыщения

В режиме насыщения транзистор можно заменить двумя источниками напряжения между базой и эммитером, и между коллектором и эммитером. Режим насыщения обеспечивается токовым критерием:

Расчет элементов связи в транзисторных ключах

Первый случай

VT₁ – открыт (насыщен) , VT₂ – закрыт

1) Ge

2) Si

R₁ ограничивает входной ток

Второй случай

VT₁

– закрыт, VT₂ – открыт(насыщен)

(*) (**)

Определим R₁:

Нагрузочная способность ключа-инвертора

Один ключ нагружен на n ключей

V T₁ – закрыт, VT₂ – о(н)

VT₃ — о(н)

…………

………… в режиме насыщения

…………

VT_(n+1)— о(н)

i_вых = ni_вх 

i_вых =

i_вх =

i_б

i_б=i_вх — i_см

— условие, при котором все транзисторы нагрузки будут входить

в режим насыщения

1. Если VT₁

   закрыт и ненагружен (n=0) => I_k0

2. n=1, I_k0,i_вх1 уменьшается

Если n ключей, то I_k0,i_вх,…,i_вхn

С увеличением n нагрузки, логическая “1” уменьшается могут быть сбои, т. к. нагрузочные параметры могут не войти в режим насыщения.

Ключ на биполярном кремниевом транзисторе с непосредственной связью

1. VT₁ — о(н), VT₂ – з

U_вых1=U_вх2=0.2 В<U_{отсечки} (т.к. кремниевый)=0.6 В

U⁰=0.2 В

2. VT₁ — з, VT₂ — о(н)

U_вх2=U_бн2=U_вых1=0.7 В

U¹=0.7 В — мало (малый перепад между логической “1” и логическим “0”.

1. VT₁-о(н), VT₂-з

U_вых1=U_кэн=0,2 В

U_вых1= U_д+U_бэ2

U_бэ2= U_вых1-U_д= 0.2-0.6= -0.4 В < U_отс VT₂— надежно закрыт

2. VT₁ — з, VT₂ — о(н)

Эта схема позволяет увеличить разницу перепадов между логической «1” и логическим «0».

Возрастает помехоустойчивость схемы.

Транзисторный усилитель с общим эмиттером — Усилители

Усилители

Базовый транзисторный усилитель, у которого вывод эмиттера общий с выводом входные и выходные цепи показаны ниже. Входное напряжение находится между базой и эмиттером, а выходное напряжение между коллектором и эмиттером. В базовую цепь вводится напряжение В _ВВ так, чтобы переход эмиттер-база смещен в прямом направлении для управления ток эмиттер-коллектор. Напряжение база-эмиттер называется

v _будет , а базовый ток равен i _b . Напряжение питания В _CC необходимо для схемы сделать коллектор положительным по отношению к эмиттеру и обеспечить источник выходного тока. Напряжение коллектор-эмиттер и коллектор тока v _ce и i _c соответственно. Сопротивление R _L является нагрузкой. Базовый ток транзистор управляет током через коллектор и через нагрузку резистор.

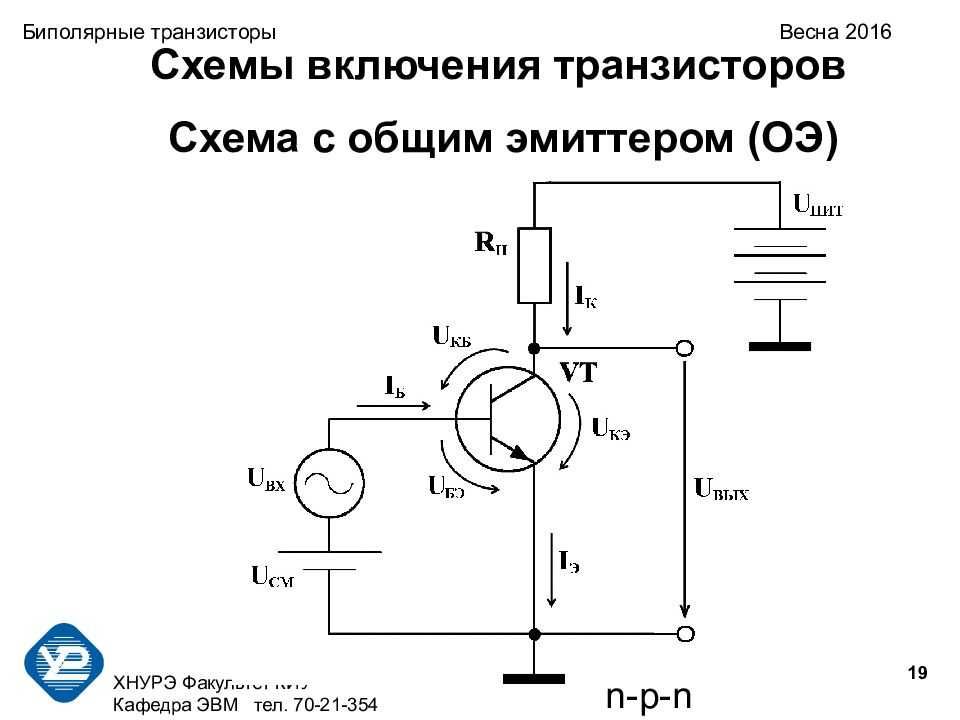
Усилитель с общим эмиттером.

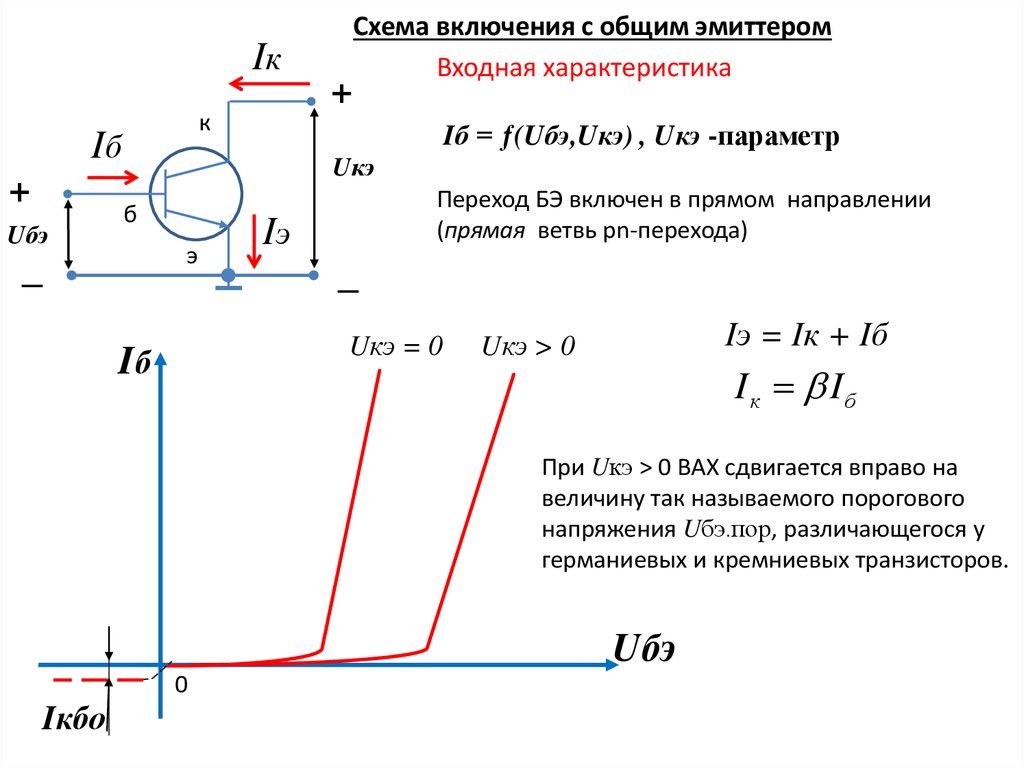
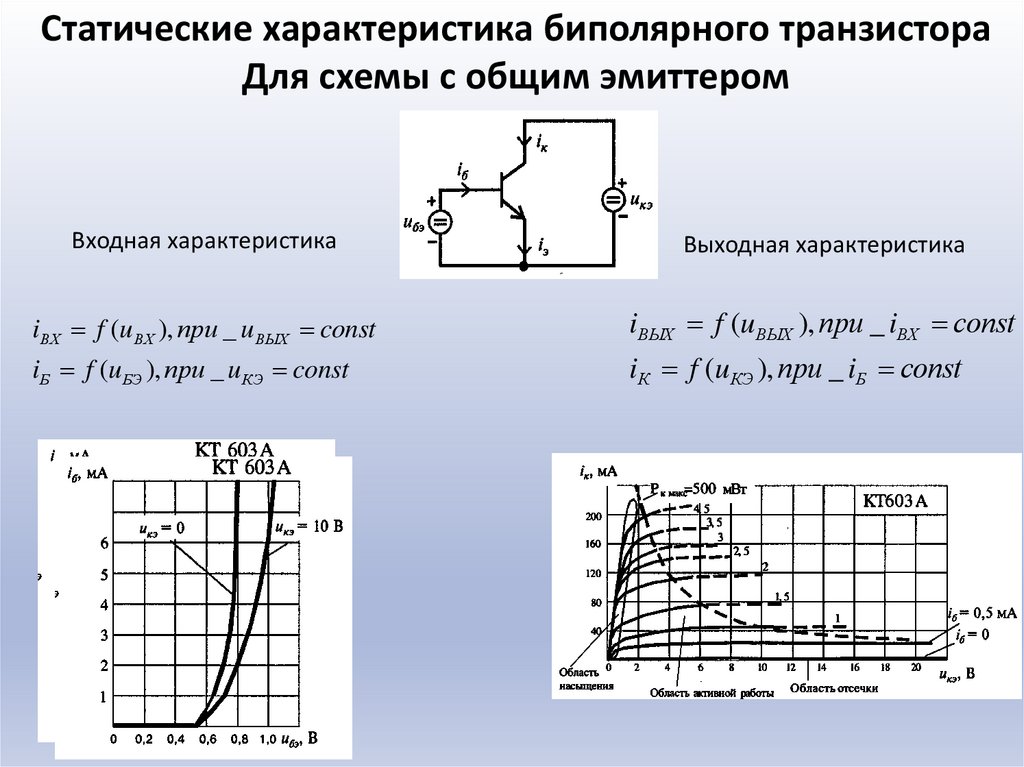
Кривые выходных характеристик

К сожалению, сопротивление эмиттерного и коллекторного переходов транзисторы не всегда постоянны. Следовательно, закон Ома не всегда использоваться для выражения взаимосвязи между различными токами и напряжения в транзисторном усилителе. По этой и другим причинам этот информация обычно предоставляется производителем в графической форме. На рисунке ниже представлен график коллекторной (выходной) характеристики для схема транзистора с общим эмиттером. График состоит из ряда кривых. Каждая кривая показывает, с основанием ток поддерживается постоянным, изменение тока коллектора в зависимости от меняется напряжение коллектор-эмиттер.

Выходные характеристики.

Существуют определенные значения для i _b , v _be , i _c и v _ce даже при отсутствии сигнала на вход. Значения отсутствия сигнала i _b , v _будут , i _c и v _ce называются покоящимися , или среднее, значения и обозначены символами И _Б , В _БЭ , I _C и V _CE .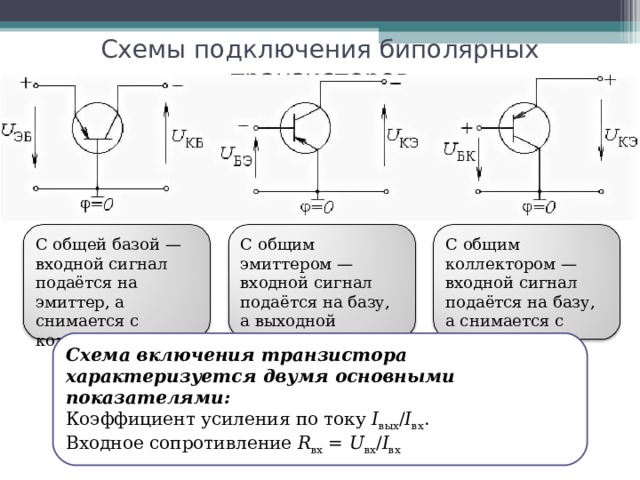 Точка, определяемая I _С и V _CE на выходной характеристике называется точкой покоя (Q). Положение точки покоя на характеристической кривой является важным часть анализа схемы усилителя. Процедура следующая: Сначала определяется «линия нагрузки» для значений напряжения питания В _CC и сопротивление нагрузки R _L , которые должны быть используется в схеме усилителя. Предположим, что i _b настолько малы что ток коллектора i _c = 0. Если бы это было так, то падение напряжения на R _L будет равно нулю и v _ce будет равно V _CC . Эта точка 1 построена на выходной характеристике (рис. выше). Тогда предполагается, что ток базы настолько велик, что транзистор становится идеальным проводником, так что v _ce = 0 и i _c = V _CC / R _L .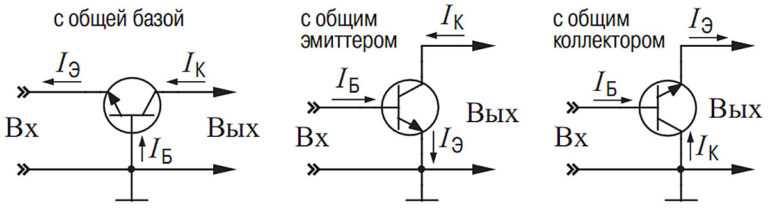 Постройте это точку 2 на характеристической кривой, а точки 1 и 2 соединить прямой линии, как на рисунке выше. Эта линия называется линией загрузки, потому что она определяется только значениями нагрузки и В _СС .

Для выбранных значений В _CC и R _L результирующие значения v _ce и i _c должен падать вдоль грузовой линии. На рисунке выше, точка Q, показаны значения отсутствия сигнала для В _CE и I _C в зависимости от нагрузки линия и выходная характеристика для выбранного среднего базового тока I _B = 100 мкА. Мгновенная база ток i _b зависит от суммы тока смещения базы и входного сигнала, а при перемещении по нагрузочной линии — мгновенные значения v _ce и i _c можно прочитать из график для любого заданного значения i _b .

Обратите внимание, что грузовая линия должна находиться в пределах максимального коллекторно-рассеивающая линия.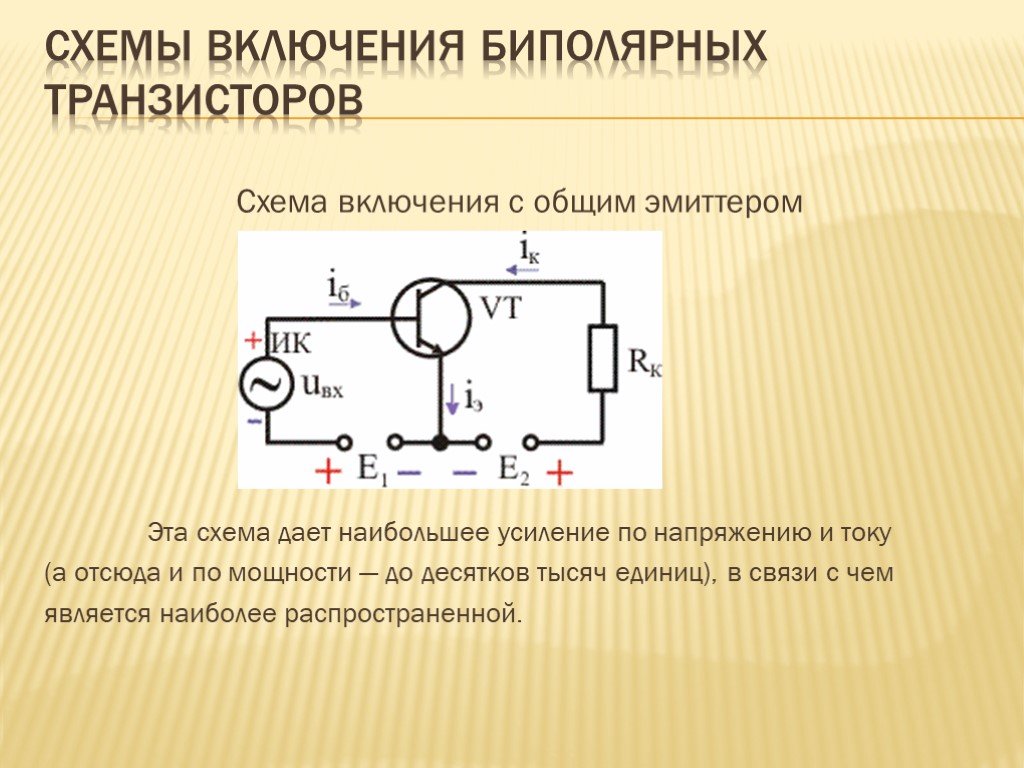 Максимальное рассеивание коллектора P _max является характеристикой транзистора и обычно приведены в руководствах по транзисторам или описаниях каталогов. Максимум коллекторно-рассеивающая линия проводится путем соединения всех точек, удовлетворяющих уравнение I _C V _CE = P _макс . Базовый ток покоя можно оценить, предположив, что между базой и эмиттером переход просто входное сопротивление транзистора ч _т.е. . Если v _с = 0 (состояние покоя), I _B = V _BB /( R _S + ч _т.е. ). Часто R _S будет намного больше чем h _т.е. так что I _B ≈ V _BB / R _S . Таким образом, выбор напряжения смещения будет зависеть от характера источника сигнала. Другие методы смещения будут рассмотрены позже.

Характеристики транзисторного усилителя

Изменение v _ce или i _c в результате входной сигнал (изменение i _b ) может быть определен графический анализ характеристических кривых, как указано выше, для каждого значения я _б . Однако гораздо удобнее анализировать схема математически после замены эквивалентной схемы для транзистор. Невозможно вывести простую схему, которая заменяла бы транзистор на весь рабочий диапазон. Это потому, что характеристические кривые транзистора не являются линейными, как показано, например. на рисунке выше. Линейная эквивалентная схема является допустимым приближением только для малых части рабочего диапазона. Другими словами, эквивалентная схема не будет описывать взаимосвязь общих величин и _б , v _be , i _c и v _ce , но это будет описывать взаимосвязь малых изменений этих величин. Уравнения для различных характеристик усилителя могут быть получены из эквивалентная схема и математические соотношения, используемые для получения этой схемы. Некоторые характеристики (например, усиление по напряжению и току) схемы с общим эмиттером усилитель приведены ниже. Фактические производные здесь не показаны.

Коэффициент усиления по напряжению может быть аппроксимирован уравнением

где β — коэффициент усиления по току транзистора ч _{, т.е.} – входное сопротивление транзистора в схема с общим эмиттером. Знак минус указывает на то, что выходное напряжение на 180° не совпадает по фазе с входным напряжением.

Коэффициент усиления по току A _i приблизительно равен

Опять же, знак минус указывает на обращение фазы между входные и выходные сигналы.

Коэффициент усиления мощности A _p является просто произведением тока и усиление напряжения

Прирост мощности не включает потери мощности в источнике сигнала или в передача выходного сигнала на нагрузку, отличную от R _L . Это просто отношение мощности сигнала, рассеиваемой в R _L к мощности сигнала, рассеиваемой на входном сопротивлении транзистора ч _т.е. .

Входное сопротивление R _в равно

Выходное сопротивление R _из может быть аппроксимировано выражением уравнение

где ч _ээ — проводимость между коллектором и эмиттером. Как показывает это уравнение, выходное сопротивление R _out находится в В этом случае сопротивление, которое транзистор как источник питания представляет загрузить Р _Л . Выходное сопротивление всей схемы усилителя с точки зрения устройства, подключенного к выходным клеммам v _ce на самом деле будет R _из параллельно с R _L .

Таким образом, показано, что усилитель с общим эмиттером обладает свойствами коэффициент усиления по напряжению, коэффициент усиления по току, инверсия фазы входного сигнала, низкий уровень входного сигнала сопротивление и высокое выходное сопротивление.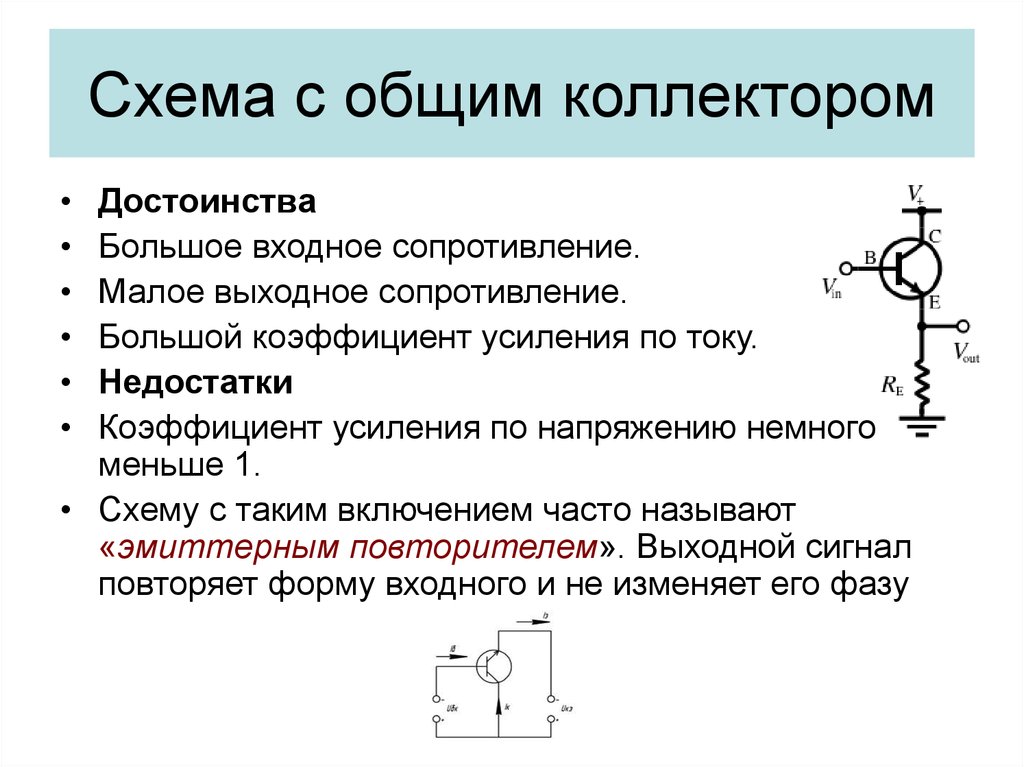

Смещение транзистора

Использование отдельного источника питания для входных и выходных цепей транзисторный усилитель дорог и неудобен. Способы предоставления надлежащие напряжения смещения от одного источника питания, таким образом, были разработан. Одной из наиболее распространенных систем смещения является делитель напряжения. тип, показанный на рисунке ниже (см. раздел «Типы предвзятости» для получения дополнительной информации). Фиксированное смещение обеспечивается в этой схеме сеть делителя напряжения, состоящая из R _B1 , Р _Б2 , и напряжение питания коллектора ( В _CC ). Резистор R _E , включенный последовательно с эмиттером, обеспечивает эмиттеру самосмещение. Большой конденсатор обход R _E уменьшит потери усиления для сигналов переменного тока.

Смещение усилителя.

Определение точки покоя

После того, как был сделан вывод о том, что широко используемые транзисторные усилители могут иметь сопротивление в цепи эмиттера и делитель напряжения в базе, полезно научиться определять точку покоя для таких цепей. Сначала в обычном порядке рисуется линия нагрузки (см. график выработки характеристики выше), необходимо соблюдать осторожность при использовании Р _Е + R _L в расчете тока для В _CE = 0. Теперь схема на рисунке выше перерисована с учетом делителя напряжения как батарея серии В _BB и резистор R _B (видеть Теорема Тевенина). Сначала предполагается, что эмиттер и база имеют почти одинаковый потенциал ( В _E = В _B ≈ В _BB ) и что I _E очень близко I _C . Поэтому, I _C ≈ V _BB / R _E . Глядя на строку нагрузки, чтобы найти значение I _B , соответствующее к этому значению I _C можно улучшить приближение скорректировав базовое напряжение до В _ВВ — I _В Р _Б . Использовать это значение базового напряжения для расчета лучшего значения для I _C . Обычно это второе приближение является достаточно точным.

Перерисовка делителя напряжения.

Пример схемы транзисторного смещения

Пример того, как определить разумные значения сопротивления для здесь приведена схема транзистор-усилитель. Во-первых, выберите желаемый точка на кривой характеристики коллектора транзистора. Оценить из характеристики или найти значения для β , ч _т.е. , и h _oe в технических описаниях. Предположим, что в желаемой точке покоя ( I _C = 1 мА, В _CE = 5 В), β = 55, ч _{, т.е.} = 2720 Ом, и ч _ээ = 14 мкс. Выберите R _L в соответствии с требования к усилению и согласование импеданса, высокие значения коэффициента усиления по току, умеренные значения коэффициента усиления по напряжению при умеренном выходном импедансе. Для этот пример Ч _Л = 25 кОм. Р _Б должно быть больше ч _т.е. для предотвращения чрезмерные потери сигнала через делитель смещения. Поэтому выбирайте R _B = 25 кОм. Для хорошей стабильности выберите R _E = R _B /5 = 5 кОм. Тогда требуемое напряжение питания постоянного тока равно (при условии, что I _E ≐ I _C )

Напряжение смещения V _BB должен равняться базе напряжение плюс падение напряжения I _Б Р _Б . V _BB таким образом

где В _БЭ = 0,7 для кремниевых транзисторов. В _BB также можно рассчитать как

Параллельное сочетание R _B1 и Р _В2 есть Р _В

Решая два предыдущих одновременных уравнения для резисторов смещения, R _B1 = 142 кОм и R _B2 = 30,3 кОм.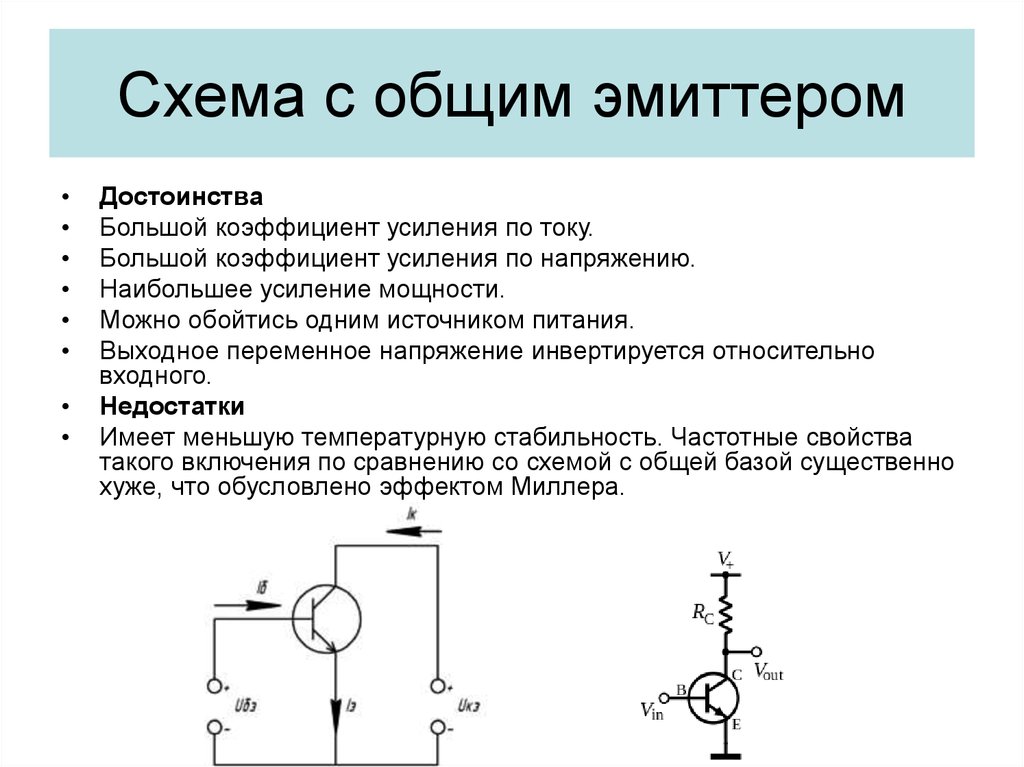 Выведенные ранее формулы для усиление по напряжению и току транзисторного усилителя также применимо к этой схеме. Выходное сопротивление усилителя 1/ ч _э.э. параллельно с Р _Л . Входное сопротивление усилителя ч _т.е. параллельно с Р _Б .

Примечание: Ток через делитель напряжения R _B1 , R _B2 должно быть не менее 10 × I _B . В нашем случае ток через R _B2

BJT Усилитель с общим эмиттером | mbedded.ninja

Содержание

Обзор

Усилитель с общим эмиттером BJT представляет собой универсальный усилитель на основе BJT, который обычно используется для усиления напряжения. Он предлагает отличное усиление по напряжению и нормальное усиление по току . Входной импеданс средний, но, к сожалению, он имеет высокий выходной импеданс Ом. Выход инвертируется по отношению к входу. Обычно за ним следует буферная схема, такая как усилитель с общим коллектором, для уменьшения выходного импеданса. Усилитель с общим эмиттером находит применение в аудио- и радиочастотных приложениях.

Аналогом MOSFET усилителя с общим эмиттером на биполярных транзисторах является усилитель с общим истоком .

Свойства:

Мощность 5 дюймов 906 Среда

Коэффициент усиления по напряжению	Высокий
Коэффициент усиления по току	Средний
Входное сопротивление	Среда
Выходное сопротивление	Высокий
Фазовый сдвиг	180°

Строчные буквы, используемые ниже, обозначают изменения количества, например, \(V_C\) — это напряжение на коллекторе, а \(v_c\) — изменение напряжения на коллекторе, \(\Delta V_C\) .

Как работает усилитель с общим эмиттером

Схема усилителя с общим эмиттером со смещением по постоянному току и связью по переменному току.

• \(R1\) и \(R2\) используются для обеспечения точки смещения постоянного тока для базы транзистора, используя стандартный метод резисторного делителя (точнее, вы также должны принять во внимание Учтите, что транзистор потребляет некоторый ток с выхода резисторного делителя, но обычно вы можете игнорировать это).
• \(C1\) используется для соединения входного сигнала по переменному току с точкой смещения постоянного тока – это значение выбрано таким образом, чтобы оно отображалось как сокращение для интересующих частот сигнала переменного тока, но блокировало постоянный ток.
• \(R_E\) добавляет вырождение эмиттера ¹ и делает усиление усилителя более стабильным при изменении \(\beta\) . \(C_E\) — это шунтирующий конденсатор эмиттера , который используется для шунтирования \(R_E\) , так что сигнал переменного тока по существу видит, что эмиттер подключен непосредственно к земле.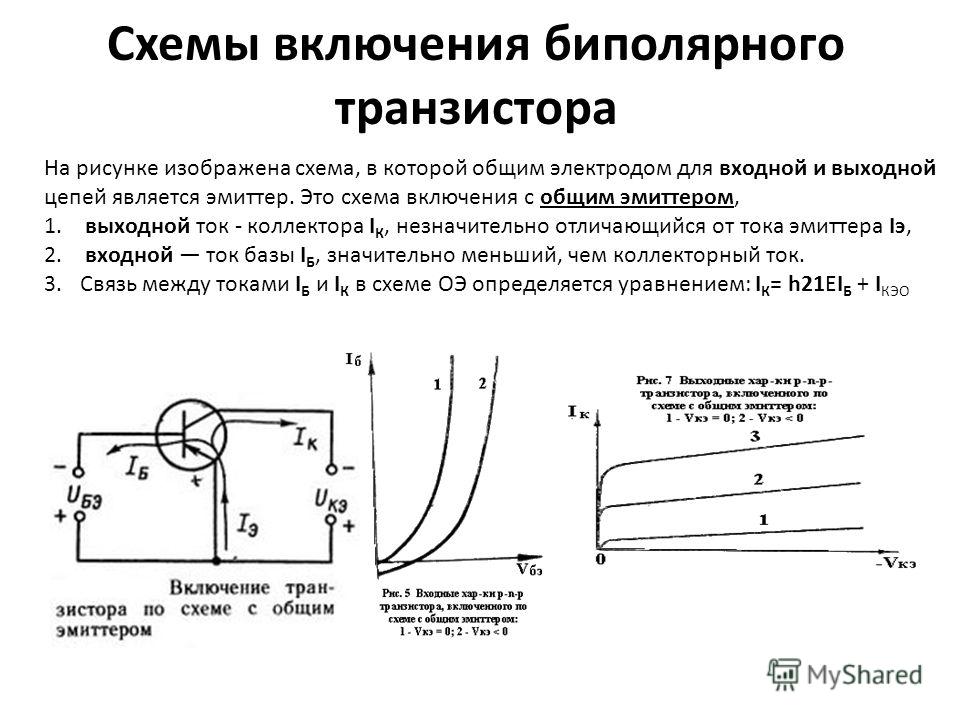
• \(R_C\) — коллекторный резистор, который помогает установить коэффициент усиления усилителя по напряжению. Иногда его называют нагрузочным резистором ² , однако это может сбивать с толку, поскольку обычно «нагрузка» размещается после выходного конденсатора связи по переменному току.
• \(R_L\) — сопротивление нагрузки. Вы можете видеть это и \(C_{OUT}\) , опущенные на некоторых схемах усилителя с общим эмиттером.
• \(C_{OUT}\) — конденсатор связи по переменному току на выходе, который блокирует постоянную составляющую, аналогично \(C_{IN}\) .

Коэффициент усиления усилителя с общим эмиттером

Схема, показывающая, как находится уравнение усиления для усилителя с общим эмиттером.

Коэффициент усиления по напряжению усилителя с общим эмиттером (по определению):

\begin{align} A_V = \frac{v_{out}}{v_{in}} \\ \end{align}

Помните, что \(v_{in}\) и \(v_{out}\) написаны строчными буквами и представляют изменения в сигнале (т.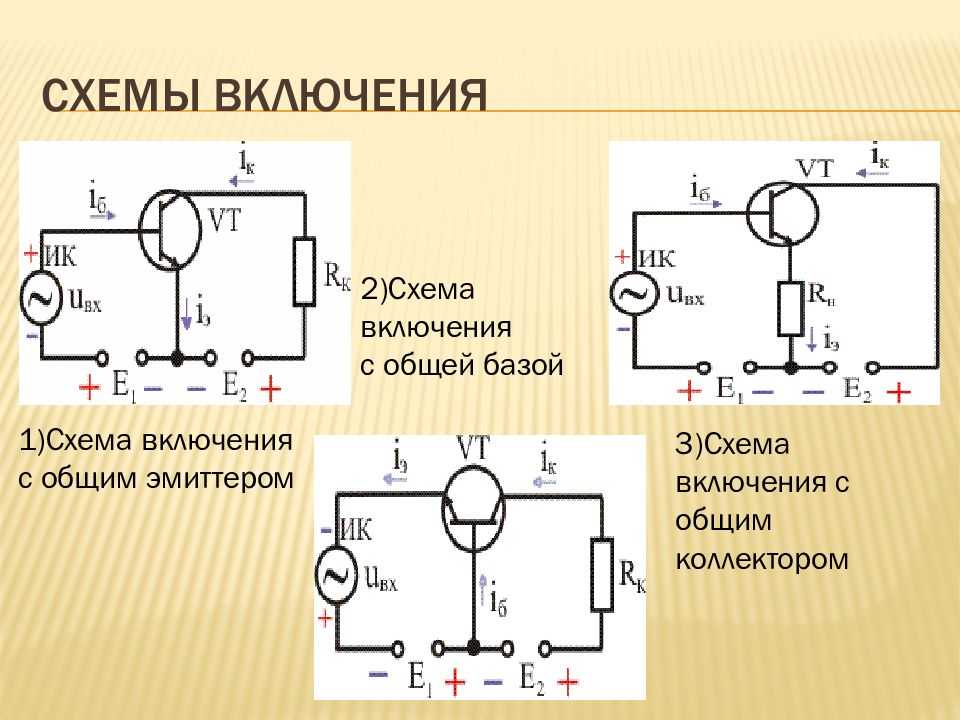 е. дельты, и игнорируют их уровни постоянного тока). Теперь, предположим, \(i_c \приблизительно i_e\) , изменение напряжения на выходе:

\begin{align} v_{out} = — i_e R_C \\ \end{align}

А изменение напряжения на входе:

\begin{align} v_{in} = i_e (r_e + R_E) \\ \end{align}

Обратите внимание, что здесь мы должны принять во внимание внутреннее сопротивление эмиттера \(r_e\) , так как конденсатор обхода эмиттера удалит член \(R_E\) ниже, оставив только \(r_e\) .

Подстановка этих уравнений для \(v_{in}\) и \(v_{out}\) в уравнение усиления дает:

\begin{align} A_V &= \frac{- i_e R_C}{i_e (r_e + R_E)} \nonumber \\ &= -\frac{R_C}{r_e + R_E} \\ \end{align}

Помните, что значение для \(r_e\) зависит от тока эмиттера в точке смещения постоянного тока:

\begin{align} r_e &= \frac{25mV}{I_E} \\ \end{align}

Таким образом, для наших частот сигнала, на которых \(C_E\) конденсатор закорачивает внешний резистор \(R_E\) , сопротивление эмиттера равно \(r_e\) и коэффициент усиления становится:

\begin{align} A_V &= -\frac{R_C}{r_e} \nonumber \\ &= -\frac{I_E R_C}{25мВ} \\ \end{align}

Коэффициент усиления по напряжению усилителя с общим эмиттером не зависит от коэффициента усиления по току \(\beta\) BJT .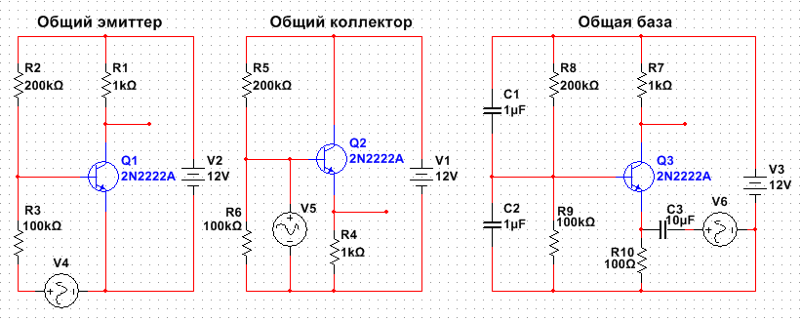 Это хорошая новость, так как это свойство не может жестко контролироваться во время производства и обычно различается между «идентичными» транзисторами на несколько процентов.0733 \(100%\) или больше!

Как спроектировать усилитель с общим эмиттером? Давайте сделаем рабочий пример, чтобы пройти этапы проектирования.

Предположения

• \(V_{CC}\) is \(12V\)
• В нашем усилителе мы будем использовать почтенный NPN-транзистор BC548BTA от onsemi.
• Пытаемся получить как можно больше усиления (благородный квест).

Ступени

1. Выберите ток коллектора: Выберите подходящий постоянный ток коллектора для вашего усилителя. Разумным выбором будет \(I_C = 10 мА\) (макс. \(I_C\) для BC547B — \(100 мА\) ).

2. Определите эмиттерный резистор \(R_E\) : Как правило, 10% от \(V_{CC}\) обычно падает на \(R_E\) ^{3 4} :

   \ начало {выравнивание} V_{R_E} &= 0. 1V_{CC} \номер \\ &= 0,1*12 В \номер \\ &= 1,2 В \номер \\ \end{выравнивание}

   И затем:

   \begin{align} R_E &= \frac{V_{R_E}}{I_{R_E}} \nonumber \\ &= \frac{1.2V}{10mA} \nonumber \\ &= 120\Омега\номер\\ \end{align}

   
   

3. Найдите коллекторный резистор \(R_C\) : Мы пропускаем \(1.2V\) через эмиттерный резистор. Это оставляет \(10,8 В\) , которые нужно пропустить через коллекторный резистор и биполярный транзистор. При напряжении насыщения 200 мВ это дает BJT \(10,6 В\) качели. Для максимального симметричного выхода мы хотим отбросить половину этого \(10,6 В\) на коллекторный резистор:

   \begin{align} R_C &= \frac{V_{R_C}}{I_{R_C}} \nonumber \\ &= \frac{0.5*10.6V}{10mA} \nonnumber \\ &= 530\Омега\номер\\ \end{align}

   
   

4. Найдите базовый ток: Рассчитайте \(I_B\) , используя приблизительное усиление:

   \begin{align} I_B &= \frac{I_C}{\beta} \nonumber \\ &= \frac{10mA}{200} \nonnumber \\ &= 50 мкА \номер \\ \end{выравнивание}

   
   

5. Определить базовое напряжение \(V_B\) : \(V_B\) это просто напряжение эмиттера плюс диод V_B &= V_E + V_{BE} \номер \\ &= 1,2 В + 0,7 В \номер \\ &= 1,9 В \номер \\ \end{align}

   
   

6. Вычислить значения резисторного делителя : Выберите \(R1\) и \(R2\) , чтобы установить выход резисторного делителя в соответствии с этим базовым напряжением. Мы также хотим убедиться, что ток, протекающий через резистор, в 10 раз превышает ток, который будет всасываться из него в базу транзистора, таким образом, мы можем игнорировать нагрузку биполярного транзистора при расчете значений резистора.

   \begin{выравнивание} I_{R2} &= 10 \cdot I_B \номер \\ &= 10 \cdot 50uA \номер \\ &= 500 мкА \номер \\ \end{align}

   Теперь мы можем легко вычислить значение \(R2\) :

   \begin{align} R2 &= \frac{V_{R2}}{I_{R2}} \nonumber \\ &= \frac{1.9V}{500uA} \nonnumber \\ &= 3.8k\Омега\номер\\ \end{align}

   И \(R1\) :

   \begin{align} R1 &= \frac{V_{R1}}{I_{R1}} \nonumber \\ &= \frac{12V — 1,9В {500 мкА} \номер \\ &= 20.2k\Омега\номер\\ \end{align}

7. Расчет входного конденсатора связи по переменному току: Практическое правило состоит в том, чтобы убедиться, что импеданс конденсатора в 10 раз меньше импеданса резисторного делителя по переменному току на самой низкой интересующей частоте ⁵ . Самая низкая интересующая нас частота — \(20Hz\) .

   \начать{выравнивание} R_{in} &= R1 || R2 \номер\\ &= \frac{R1 \cdot R2}{R1 + R2} \nonumber \\ &= \frac{20.2k\Omega \cdot 3.8k\Omega}{20.2k\Omega + 3.8k\Omega} \nonumber \\ &= 3.20k\Омега\номер\\ \end{выравнивание}

   \begin{выравнивание} Z_{C_{in}} &= \frac{R_{in}}{10} \nonnumber \\ &= \frac{3.20k\Omega}{10} \nonnumber \\ &= 320\Омега\номер\\ \end{выравнивание}

   \begin{выравнивание} C_{in} &= \frac{1}{2\pi f Z_{C_{in}}} \nonumber \\ &= \frac{1}{2\pi \cdot 20Hz \cdot 320\Omega} \nonumber \\ &= 25 мкФ \номер\\ \end{align}

8. Рассчитайте конденсатор обхода эмиттера: То же эмпирическое правило применимо к \(C_E\) , за исключением того, что на этот раз его импеданс должен быть в 10 раз меньше, чем \(R_E\) :

   \begin{align} Z_{C_E} &= \frac{R_E}{10} \nonumber \\ &= \frac{120\Omega}{10} \nonnumber \\ &= 12\Омега\номер\\ \end{выравнивание}

   \begin{выравнивание} C_E &= \frac{1}{2\pi f Z_{C_E}} \nonumber \\ &= \frac{1}{2\pi \cdot 20Hz \cdot 12\Omega} \nonumber \\ &= 663 мкФ \\ \end{align}

9. Рассчитать усиление :

   \begin{align} A_V &= -\frac{I_E R_C}{25mV} \nonumber \\ &= -\frac{10mA * 530\Omega}{25mV} \nonnumber \\ &=-212\\ \end{выравнивание}

   Или в дБ:

   \begin{align} A_{V(db)} &= 20\log(A)\nonumber\\ &= 20\лог(212)\номер\\ &= 46,5 дБ \\ \end{align}

10. Готово!

Ниже показана готовая схема вместе с источниками напряжения, готовыми к моделированию. {\circ}\) для большей части полосы пропускания нашего сигнала.

Смоделированная частотная характеристика нашего усилителя с общим эмиттером.

Усиление схемы значительно упадет, если сопротивление нагрузки будет уменьшено из-за среднего значения выходного импеданса (в идеале это должно быть \(0\Omega\) ). При проектировании усилителя с общим эмиттером убедитесь, что вы не нагружаете его слишком сильно. Вы можете уменьшить выходное сопротивление усилителя с общим эмиттером, увеличив ток покоя коллектора \(I_C\) .

Ссылки

---

1. Analog Devices (2020, 23 марта). Упражнение: Усилитель с общим эмиттером . Получено 20 августа 2022 г. с https://wiki.analog.com/university/courses/electronics/electronics-lab-5. ↩︎

2. Боб Харпер (2018, декабрь). Транзисторный усилитель с общим эмиттером . Дийоде. Получено 21 августа 2022 г. с сайта https://diyodemag.