Что такое фаза и ноль в электрической сети. Как определить фазу и ноль в розетке. Чем отличается фазный провод от нулевого. Как безопасно проверить наличие фазы индикаторной отверткой.
Основные понятия: фаза, ноль и земля в электрических цепях
Чтобы разобраться в том, что такое фаза и ноль в электричестве, необходимо понимать базовую структуру электрической сети. В стандартной однофазной сети жилого помещения используются три основных проводника:
- Фазный провод (фаза)
- Нулевой рабочий провод (ноль)
- Защитный заземляющий провод (земля)
Фазный провод находится под напряжением относительно земли и нуля. Именно по нему электрический ток поступает к потребителям. Нулевой провод служит для замыкания электрической цепи и отвода тока обратно к источнику. Заземляющий провод обеспечивает защиту от поражения током при неисправностях.
Что такое фаза в электричестве и почему она важна
Фаза в электротехнике — это проводник, находящийся под переменным напряжением относительно земли. В бытовой сети это обычно 220 В. Фазный провод является источником электрической энергии для подключенных устройств.

Почему фаза так важна? Фазный провод:
- Обеспечивает подачу электроэнергии к приборам
- Позволяет включать и выключать электрические цепи
- Требует особых мер предосторожности при работе
Именно наличие напряжения на фазном проводе делает его потенциально опасным при прикосновении. Поэтому крайне важно уметь отличать фазу от нуля.
Назначение нулевого провода в электрической цепи
Нулевой провод выполняет не менее важную функцию, чем фазный. Его основные задачи:
- Замыкание электрической цепи для протекания тока
- Отвод отработанного тока обратно к источнику
- Выравнивание потенциалов в трехфазных сетях
В отличие от фазного, нулевой провод не находится под напряжением относительно земли. Это делает его безопасным при случайном прикосновении. Однако при обрыве нулевого провода возможны опасные перенапряжения в сети.
Как отличить фазу от нуля: основные методы
Существует несколько способов определить, какой провод является фазным, а какой нулевым:
- По цвету изоляции (если соблюдена маркировка)
- С помощью индикаторной отвертки
- Мультиметром в режиме вольтметра
- Бесконтактным пробником напряжения
Самым простым и безопасным методом для непрофессионалов является использование индикаторной отвертки. Рассмотрим его подробнее.

Проверка фазы индикаторной отверткой: пошаговая инструкция
Для определения фазы индикаторной отверткой выполните следующие действия:
- Убедитесь, что отвертка исправна, проверив ее на заведомо рабочей розетке
- Вставьте жало отвертки в отверстие розетки или коснитесь оголенного провода
- Прикоснитесь пальцем к металлической части на торце рукоятки
- Если загорится светодиод — это фазный провод
- Отсутствие свечения означает, что это нулевой или заземляющий провод
Важно! Всегда соблюдайте технику безопасности при работе с электричеством. Не касайтесь металлических частей отвертки при проверке.
Преимущества и недостатки индикаторной отвертки
Достоинства метода:
- Простота использования
- Дешевизна прибора
- Компактность
- Не требует батареек
Недостатки:
- Возможны ложные срабатывания
- Не показывает точное значение напряжения
- Требует прикосновения к прибору
Использование мультиметра для определения фазы и нуля
Более точным методом является измерение напряжения мультиметром. Порядок действий:
- Переключите мультиметр в режим измерения переменного напряжения (~V)
- Установите предел измерений выше 220 В
- Подключите черный щуп к заведомо заземленной поверхности
- Красным щупом поочередно касайтесь проверяемых проводов
- Наличие напряжения около 220 В указывает на фазный провод
- На нулевом проводе напряжение относительно земли близко к 0
Этот метод дает более надежные результаты, но требует наличия мультиметра и базовых навыков работы с ним.
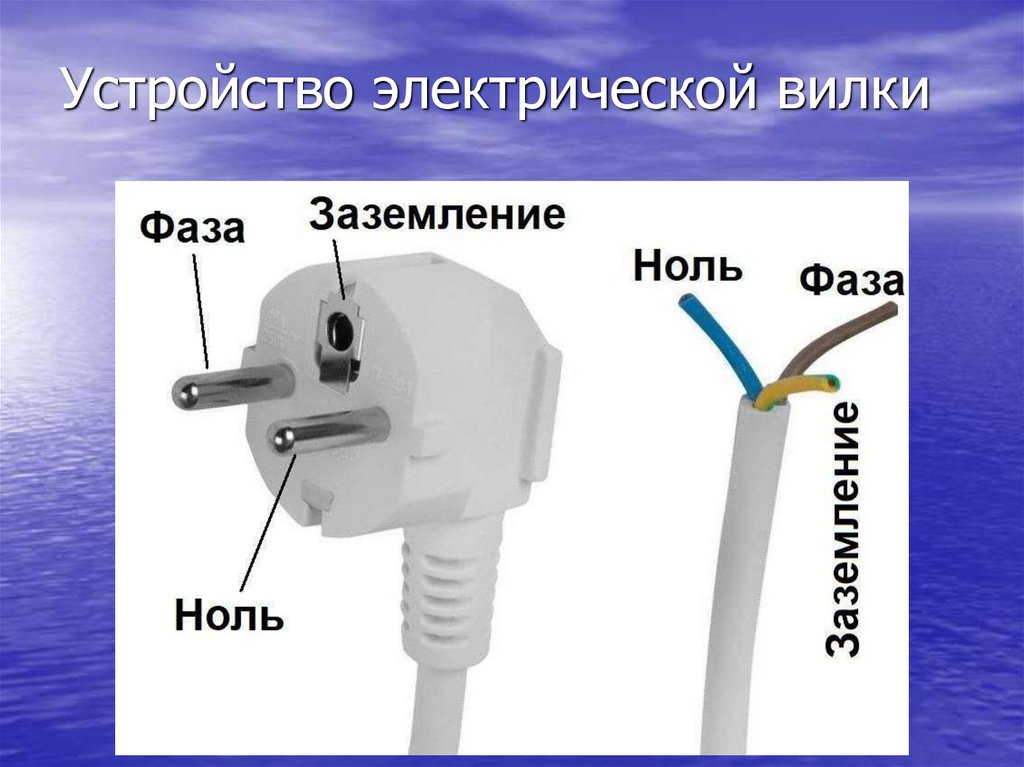
Маркировка проводов в электропроводке: цветовые обозначения
Согласно стандартам, провода в электропроводке должны иметь следующую цветовую маркировку:
- Фазный провод — коричневый, черный или серый
- Нулевой рабочий — синий или голубой
- Заземляющий — желто-зеленый
Однако на практике эти правила часто не соблюдаются, особенно в старых домах. Поэтому нельзя полагаться только на цвет изоляции при определении назначения провода.
Почему важно правильно подключать фазу и ноль
Корректное подключение фазного и нулевого проводов имеет большое значение для безопасности и работоспособности электроприборов. Неправильное подключение может привести к:
- Нарушению работы устройств защитного отключения
- Появлению напряжения на корпусах приборов
- Выходу из строя некоторых типов электроники
- Повышенному риску поражения электрическим током
Особенно важно соблюдать полярность подключения для водонагревателей, стиральных машин, посудомоечных машин и другой техники с заземляемым корпусом.
Техника безопасности при работе с электропроводкой
При любых работах с электричеством необходимо соблюдать следующие правила безопасности:
- Отключайте напряжение перед началом работ
- Используйте инструменты с изолированными ручками
- Работайте в диэлектрических перчатках и галошах
- Не прикасайтесь к оголенным проводам и контактам
- Перед началом работы убедитесь в отсутствии напряжения
- При любых сомнениях обращайтесь к профессиональным электрикам
Помните, что даже небольшое напряжение может быть опасным для жизни при неблагоприятных обстоятельствах.
Заключение: важность понимания основ электротехники
Знание базовых принципов устройства электрических сетей и умение различать фазу и ноль крайне важно для безопасного использования электроприборов в быту. Эти навыки позволяют:
- Правильно подключать электротехнику
- Своевременно выявлять неисправности проводки
- Безопасно выполнять мелкий ремонт
- Избегать поражения электрическим током
Однако помните, что любые серьезные работы с электричеством должны выполняться только квалифицированными специалистами. Ваша безопасность — превыше всего!
Разница фазы и ноля в электрических цепях
Содержание
- 1 Структура электросети, основные элементы
- 2 Определение фазы в электрических сетях
- 3 Видео
Невозможно дать определение фазе, рассматривая ее как отдельный элемент. Физические процессы, протекающие в сети, тесно взаимосвязаны с другими составляющими: фаза, ноль, земля невозможны без совокупности всех элементов. Поэтому рассматривать надо назначение всех составляющих и процессы, происходящие в них, понимая, что такое фаза и ноль, нагрузка и заземление.
Фаза в однофазной сети жилого помещения
Структура электросети, основные элементы
Из школьного курса физики известно, что если вращать постоянный магнит вокруг обмотки на катушке в проводах, возникает ЭДС (электро-движущая сила), которая перемещает заряженные частицы по проводам. Этот пример хорошо объясняет, что такое фаза и ноль в электричестве.
Пример получения ЭДС и тока в рамке металлического проводника
На основе этого принципа в промышленных масштабах создаются генераторы электрической энергии: это может быть атомная, гидро,- или тепловая электростанция. Иногда для обеспечения временного электроснабжения в аварийных случаях используют дизельные, газовые или бензиновые генераторы на объектах, которые потребляют незначительные мощности. В истории были случаи, когда атомные подлодки и ледоколы снабжали электроэнергией целые населенные пункты.
Иногда для обеспечения временного электроснабжения в аварийных случаях используют дизельные, газовые или бензиновые генераторы на объектах, которые потребляют незначительные мощности. В истории были случаи, когда атомные подлодки и ледоколы снабжали электроэнергией целые населенные пункты.
Схема магистрали передачи и преобразования электроэнергии
С генераторов электростанций электроэнергия по токопроводящим жилам кабелей или ЛЭП (воздушные линии электропередачи) с большим напряжением 6-10 кВ передается на понижающие до 04 кВ трансформаторные подстанции. С низкой стороны трансформатора энергия подается на распределительные щиты промышленных объектов, жилых домов и квартир в многоэтажных домах. Можно сказать, что фаза в электротехнике является транспортной системой для передачи электроэнергии. По этим токопроводящим жилам кабеля или ЛЭП происходит перемещение заряженных частиц со скоростью света к нагрузке.
Именно в кабеле жилы разделяют как фаза, ноль, земля. Промышленные электростанции передают к потребителям энергию по четырехжильным или пятижильным кабелям.
Подключение обмоток генератора к трехфазной сети
С трех отдельных обмоток генератора токи снимаются и протекают по разным жилам к нагрузке. Эти жилы в электрике называют фазами. Четвертая жила – нейтральный провод, который в конечном итоге в распределительных щитах, трансформаторных подстанциях и генераторах подключается к шине заземления. Такие схемы называются цепи с заземленной нейтралью. Фаза в электричестве – это токопроводящая часть, по которой заряженные частицы передвигаются от генератора к нагрузке. Чтобы понять, что такое ноль, или зачем нейтральная жила, можно сравнить электрический ток с потоком воды.
Протекающий поток с верхней точки вращает колесо своей кинетической энергией, совершая определенную работу, потом стекает в реку или озеро, которая находится ниже по уровню. В случае с электричеством поток заряженных частиц с высоким по отношению к земле потенциалом стремится по фазному проводу к нагрузке. Как пример можно взять лампу накаливания. Совершается работа на разогрев спирали лампы. После прохождения нагрузки по нейтральному проводу ток уходит в землю, фактически нулевой провод нужен для отвода тока в землю после совершения им определенной работы.
После прохождения нагрузки по нейтральному проводу ток уходит в землю, фактически нулевой провод нужен для отвода тока в землю после совершения им определенной работы.
Пятая жила заземления обеспечивает безопасность эксплуатации электроустановок. Она, как и жила нуля, подключается к шинам заземления, которые замыкаются на общий заземляющий контур. Каждый корпус оборудования на производстве или бытового прибора заземляется, при замыкании фазного провода на корпус срабатывают устройства защиты, сеть обесточивается. Таким образом, исключается вариант поражения человека электрическим током. Отличие заземления и нулевого провода в том, что нулевую жилу подключают к контактам нагрузки, а заземляющий провод – к корпусу оборудования.
Определение фазы в электрических сетях
Что такое коэффициент
При монтаже, обслуживании и ремонтных работах иногда возникают проблемы, как отличить фазу от нулевого и заземляющего провода. На разных участках сети делается соответствующая маркировка.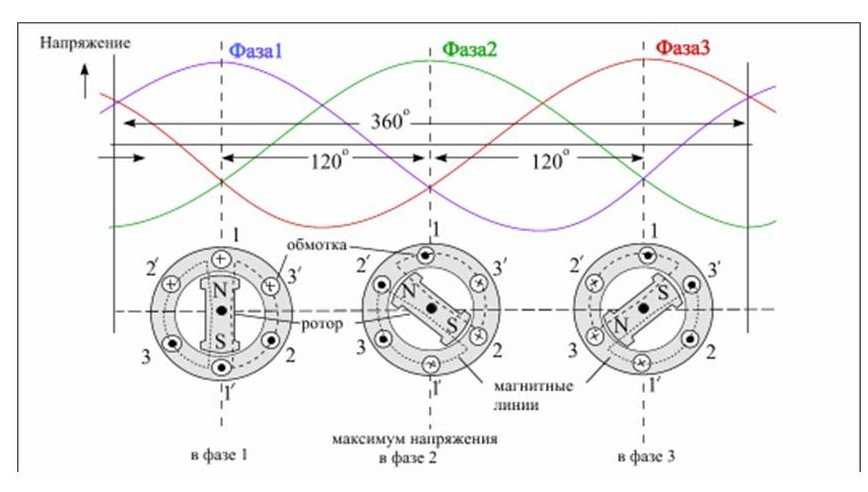
На электростанциях, трансформаторных подстанциях и распределительных устройствах токопроводящие шины, к которым подключаются кабельные жилы, маркируются цветом и буквенными обозначениями:
- Фазы обозначают А – желтым цветом;
- В – зеленым цветом;
- С – красным цветом.
Маркировка фаз по цвету
При такой маркировке фаза в электричестве легче определяется, нейтральная шина обозначается буквой «N» и красится в синий/голубой цвет. На шину заземления ставят соответствующий знак и желто-зеленый полосатый окрас.
Трансформаторная подстанция с маркированными шинами
По требованиям ПУЭ (Правила устройства электроустановок) кабельные токопроводящие жилы тоже имеют маркировку по цвету изоляционного слоя. Синяя жила подключается к нейтральной шине, желто-зеленая – на контур заземления, красная, черная, белая и другие цвета могут использоваться в качестве фаз. Такую же маркировку используют при прокладке проводов с меньшим сечением в РЩ для розеточных и осветительных групп.
Маркировка проводов
К сожалению, данные требования не всегда выполняются при проведении монтажных работ, особенно на участках от РУ до приборов освещения, розеток и отдельных бытовых приборов.
Схема подключения многоквартирного дома к трехфазной сети
В условиях скрытой проводки визуально по концам на выходе кабеля у розетки невозможно определить назначение проводника, когда все или несколько жил имеют одинаковый цвет изоляции.
В этих случаях используются индикаторные и измерительные приборы, наиболее востребованными из них считаются индикаторная отвертка и мультиметр. Для определения фазного провода среди выходящих концов из подрозетника достаточно использовать индикаторную отвертку. Нужно прикоснуться пером отвертки к оголенному концу, а большим пальцем – к контакту на верхней части ручки отвертки. При наличии напряжения на проводе индикаторная лампочка в прозрачной рукоятке засветится.
Определение фазы индикаторной отверткой
Это классический вариант, когда отверткой определяется фаза тока в проводе. Производители делают много современных конструкций, где достаточно прикоснуться пером отвертки к изолированному проводу на любом участке, и световая и звуковая индикация укажет наличие напряжения. Но почему-то потребители предпочитают классические старые модели, они отличаются высокой надежностью, не требуют питания и замены батареек. Виды и конструкции индикаторных отверток – эта тема, которая требует более детального рассмотрения в отдельной статье. Между нейтральным и заземляющим проводом разница потенциалов равна нулю, напряжения нет, соответственно, индикатор не светится. Такой метод годится, когда надо выделить фазы среди проводов, выходящих из подрозетника или распределительной коробки, особенно, когда сеть однофазная для обычной розетки разность потенциалов между фазой и заземлением 220В.
Производители делают много современных конструкций, где достаточно прикоснуться пером отвертки к изолированному проводу на любом участке, и световая и звуковая индикация укажет наличие напряжения. Но почему-то потребители предпочитают классические старые модели, они отличаются высокой надежностью, не требуют питания и замены батареек. Виды и конструкции индикаторных отверток – эта тема, которая требует более детального рассмотрения в отдельной статье. Между нейтральным и заземляющим проводом разница потенциалов равна нулю, напряжения нет, соответственно, индикатор не светится. Такой метод годится, когда надо выделить фазы среди проводов, выходящих из подрозетника или распределительной коробки, особенно, когда сеть однофазная для обычной розетки разность потенциалов между фазой и заземлением 220В.
В распределительных коробках на промышленных объектах, когда используется оборудование с трехфазным питанием на 380В, проводов может быть много и различного назначения. Жгуты с проводами различных цветов разводятся для питания электромоторов, управления магнитными пускателями и другими элементами оборудования на производстве.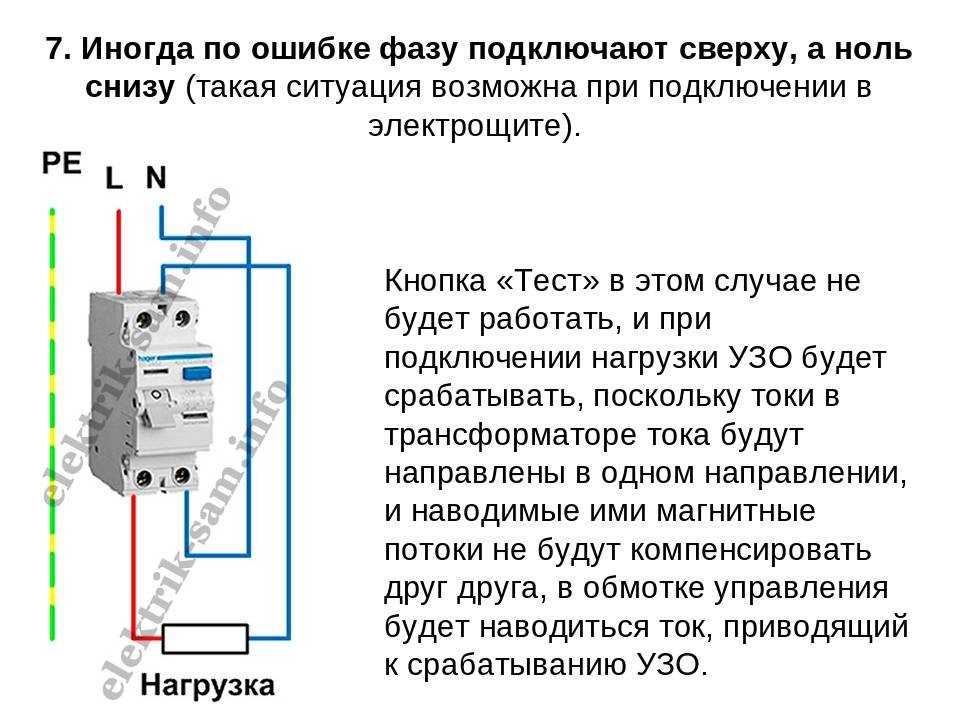 Чтобы среди множества проводов выделить разные фазы, недостаточно индикаторной отвертки, для этой цели потребуется мультиметр. В этом случае он используется в режиме измерений переменного напряжения на пределе 750V.
Чтобы среди множества проводов выделить разные фазы, недостаточно индикаторной отвертки, для этой цели потребуется мультиметр. В этом случае он используется в режиме измерений переменного напряжения на пределе 750V.
В трехфазной сети между разными фазами напряжение составляет 380В, между фазами и нулевым или заземляющим проводом – 220В. Прикладывая щупы к оголенным концам, отделяются провода, между которыми 380В, это отдельные фазы сети. Третья фаза вычисляется аналогично: если между уже выделенными концами и искомым проводом 380В, значит это она.
Напряжение между фазами и нейтральным проводом в сети частного дома
К сведению. Если в процессе измерения между двумя проводами, показывающими наличие фазы, напряжение 0В, эти концы исходят от одной фазы.
В результате изложенной информации можно сделать вывод, что такое фаза в однофазной сети. Это участок провода, идущий от РЩ до выключателя нагрузки, при исправной сети он находится постоянно под напряжением относительно нейтрального и заземляющего провода, после нагрузки идет нулевой провод. В трехфазной сети обмотки электродвигателей, нагревательные ТЭНы и другие приборы включаются между фазами. Провода до выключателя нагрузки постоянно находятся под напряжением, нулевой провод в схеме соединения обмоток звездой подключен в точке соединения трех обмоток на генераторе и после нагрузки. Для выключения и включения используются многополюсные автоматические выключатели или магнитные пускатели, которые разрывают цепь одновременно по трем фазам.
В трехфазной сети обмотки электродвигателей, нагревательные ТЭНы и другие приборы включаются между фазами. Провода до выключателя нагрузки постоянно находятся под напряжением, нулевой провод в схеме соединения обмоток звездой подключен в точке соединения трех обмоток на генераторе и после нагрузки. Для выключения и включения используются многополюсные автоматические выключатели или магнитные пускатели, которые разрывают цепь одновременно по трем фазам.
Видео
Оцените статью:
Фаза и ноль в розетке
Чтобы разобраться в том, что такое фаза и ноль в розетке, обычному человеку (не специалисту) нет необходимости углубляться в электротехнические дебри. В качестве примера приведем обычную штепсельную розетку, куда поступает переменный ток.
К розетке идут два электропровода — нулевой и фазный. Ток поступает только по одному из них — фазному (еще его называют рабочей фазой). Второй провод — нулевой (или нулевая фаза).
Содержание
- Ноль и фаза в старых розетках
- Фаза и ноль в современной розетке
- Определение фазы и ноля мультиметром или отверткой
- Мультиметр
- Индикаторная отвертка
Ноль и фаза в старых розетках
Чтобы подключить старую розетку, используют два проводника. Одни из них синего цвета (рабочий нулевой проводник). По этому проводу идет ток от источника электричества к бытовому прибору. Если взяться за токоведущий провод, но не дотрагиваться до второго провода, удара током не произойдет.
Одни из них синего цвета (рабочий нулевой проводник). По этому проводу идет ток от источника электричества к бытовому прибору. Если взяться за токоведущий провод, но не дотрагиваться до второго провода, удара током не произойдет.
Второй провод в розетке — фазный. Он бывает самых разных цветов, в том числе синим, зелено-желтым или голубым.
Обратите внимание! Любое напряжение, превышающее 50 вольт, опасно для жизни.
Фаза и ноль в современной розетке
В устройствах современного типа есть три провода. Фаза бывает любого цвета. Помимо фазы и нуля имеется еще один провод (защитный нулевой). Цвет этого проводника — зеленый или желтый.
Через фазу подается напряжение. Ноль используется для защитного зануления. Третий провод нужен как дополнительная защита — для забора лишнего тока во время замыкания. Ток перенаправляется в землю или в обратную сторону — к источнику электричества.
Обратите внимание! Не имеет практического значения, справа или слева расположены фаза и ноль.
Однако чаще всего фаза расположена слева, а ноль — справа.
Определение фазы и ноля мультиметром или отверткой
Мультиметр
Прибор представляет собой комбинированное электроизмерительное устройство, способное выполнять несколько функций. Минимальная комплектация включает вольтметр, омметр и амперметр. Отдельные модификации выполнены в виде токоизмерительных клещей. Выпускаются как аналоговые, так и электронные измерители.
Чтобы начать процесс замера, следует переключиться в режим измерения переменного напряжения. Замер осуществляется одним из нескольких методов:
- Зажимаем один из имеющихся щупов двумя пальцами. Второй щуп направляем к контакту, который расположен в выключателе или розетке. Если данные на мониторе несущественные (не превышают 10 вольт), речь идет о нуле. Если же прикоснуться к другому контакту, показатель будет выше — это фаза.
- Если имеются опасения относительно необходимости притрагиваться к щупу, есть другой путь.
 Один из стержней направляем в розетку. Вторым стержнем прикасаемся непосредственно к стене рядом с розеткой. Результат будет примерно таким же, как и в случае, описанном выше.
Один из стержней направляем в розетку. Вторым стержнем прикасаемся непосредственно к стене рядом с розеткой. Результат будет примерно таким же, как и в случае, описанном выше. - Существует третий способ измерения с помощью мультиметра. Прикасаемся щупом к заземленной поверхности (например, корпусу оборудования). Вторым щупом касаемся измеряемой поверхности. Если провод является фазой, мультитестер обнаружит напряжение в 220 вольт.
Индикаторная отвертка
Индикатор — простой способ определения фазы, доступный даже человеку, впервые занявшемуся этим делом. Контрольная отвертка внешне напоминает стандартную. Отличие состоит в наличии внутреннего устройства у индикаторной отвертки. Рукоять отвертки производится из специального прозрачного пластика. Внутри находится диод. Верхняя часть изготовлена из металла.
Обратите внимание! Нельзя использовать индикаторную отвертку не по назначению. Она не предназначена для отвинчивания и закручивания винтов. Нецелевое использование контрольной отвертки станет причиной выхода ее из строя.
Чтобы найти фазу и ноль при помощи отвертки, нужно выполнить такую последовательность операций:
- Концом отвертки касаемся контакта.
- Нажимаем пальцем на металлическую кнопку вверху отвертки.
- Если светодиод загорелся, речь идет о фазе. Если он не реагирует — это ноль.
Обратите внимание! Индикаторная лампа, рассчитанная на 220–380 вольт, будет светиться при напряжении, превышающем 50 вольт.
При работе с индикаторной отверткой рекомендуется придерживаться следующих мер безопасности:
- Не дотрагиваться до нижнего конца отвертки во время проведения замеров.
- Держать отвертку в чистоте, иначе велик риск нарушения изоляции.
- Если нужно определить отсутствие напряжения, вначале проверить работоспособность прибора, совершенно точно находящегося под напряжением.
Совет! В сети постоянного тока полярность контактов определяется очень простым способом. Для этого достаточно опустить провода в емкость с водой.
Возле одного из проводов станут образовываться пузыри — это минус. Второй провод — плюс.
Не следует путать индикаторную отвертку с приспособлением для прозвона. Отвертка для прозвона снабжена батарейками. При работе с таким устройством для определения нуля и фазы не нужно нажимать на кнопку, так как отвертка будет светиться в любой из возможных ситуаций.
Как рассчитать фазовый сдвиг
Обновлено 13 марта 2018 г.
Автор John Papiewski
Фазовый сдвиг — это небольшая разница между двумя волнами; в математике и электронике это задержка между двумя волнами, имеющими одинаковый период или частоту. Обычно фазовый сдвиг выражается в виде угла, который может измеряться в градусах или радианах, причем угол может быть положительным или отрицательным. Например, фазовый сдвиг +90 градусов составляет четверть полного цикла; в этом случае вторая волна опережает первую на 90 градусов.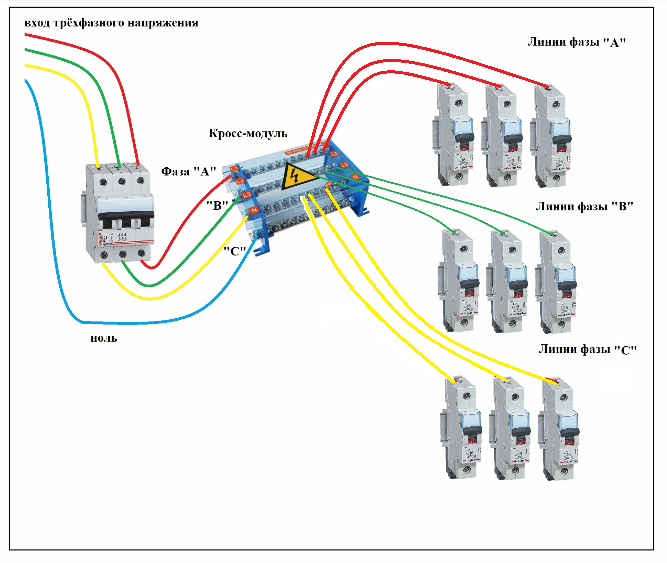 Вы можете рассчитать фазовый сдвиг, используя частоту волн и временную задержку между ними.
Вы можете рассчитать фазовый сдвиг, используя частоту волн и временную задержку между ними.
Синусоидальная функция и фаза
В математике тригонометрическая синусоидальная функция создает плавный волнообразный график, который циклически переключается между максимальным и минимальным значением, повторяясь каждые 360 градусов или 2 пи радиана. При нулевых градусах функция имеет нулевое значение. При 90 градусах она достигает своего максимального положительного значения. На 180 градусов он изгибается обратно к нулю. При 270 градусах функция имеет максимальное отрицательное значение, а при 360 возвращается к нулю, совершая один полный цикл. Углы больше 360 просто повторяют предыдущий цикл. Синусоида со сдвигом фазы начинается и заканчивается при значении, отличном от нуля, хотя во всех других отношениях она напоминает «стандартную» синусоиду.
Выбор порядка волн
Вычисление фазового сдвига включает сравнение двух волн, и частью этого сравнения является выбор, какая волна является «первой», а какая «второй». В электронике вторая волна обычно является выходом усилителя или другого устройства, а первая волна — входом. В математике первая волна может быть исходной функцией, а вторая — последующей или вторичной функцией. Например, первой функцией может быть y = sin(x), а второй функцией может быть y = cos(x). Порядок волн не влияет на абсолютное значение фазового сдвига, но определяет, будет сдвиг положительным или отрицательным.
В электронике вторая волна обычно является выходом усилителя или другого устройства, а первая волна — входом. В математике первая волна может быть исходной функцией, а вторая — последующей или вторичной функцией. Например, первой функцией может быть y = sin(x), а второй функцией может быть y = cos(x). Порядок волн не влияет на абсолютное значение фазового сдвига, но определяет, будет сдвиг положительным или отрицательным.
Сравнение волн
При сравнении двух волн располагайте их так, чтобы они читались слева направо с использованием одного и того же угла оси X или единиц измерения времени. Например, график для обоих может начинаться с 0 секунд. Найдите пик на второй волне и найдите соответствующий пик на первой. При поиске соответствующего пика оставайтесь в пределах одного полного цикла, иначе результат разности фаз будет неправильным. Обратите внимание на значения по оси X для обоих пиков, затем вычтите их, чтобы найти разницу. Например, если пик второй волны приходится на 0,002 секунды, а пик первой волны приходится на 0,001 секунды, тогда разница составляет 0,001 — 0,002 = -0,001 секунды.
Вычисление фазового сдвига
Чтобы вычислить фазовый сдвиг, вам нужны частота и период волн. Например, электронный осциллятор может генерировать синусоидальные волны с частотой 100 Гц. Разделение частоты на 1 дает период или продолжительность каждого цикла, поэтому 1/100 дает период 0,01 секунды. Уравнение фазового сдвига: ps = 360 * td / p, где ps — фазовый сдвиг в градусах, td — разница во времени между волнами, а p — период волны. Продолжая пример, 360*-0,001/0,01 дает фазовый сдвиг в -36 градусов. Поскольку результатом является отрицательное число, фазовый сдвиг также отрицателен; вторая волна отстает от первой на 36 градусов. Для разности фаз в радианах используйте 2 * pi * td / p; в нашем примере это будет 6,28 * -0,001/0,01 или -0,628 радиан.
Объяснение урока: Когерентный свет | Nagwa
В этом объяснителе мы узнаем, как определить, являются ли два или более
электромагнитные волны будут интерферировать, образуя когерентный или некогерентный свет.
Световая волна или электромагнитная волна представляет собой поперечную волну; то есть волна который колеблется в направлении, перпендикулярном направлению его путешествуя внутрь. Мы можем описать эти световые волны как «синусоидальные», которые означает, что они выглядят как функция синуса или косинуса.
Представим, что у нас есть световая волна, бегущая слева направо в пустое пространство, как показано на диаграмме ниже.
Мы можем вспомнить, что эта волна будет иметь определенную амплитуду, длину волны и частота. Амплитуда и длина волны показаны на диаграмме выше.
Амплитуда волны – это максимальное смещение волны от центральная линия (пунктирная линия на схеме). Это высота до вершины гребень или дно желоба.
Длина волны – это расстояние между любыми двумя соседними эквивалентными точки на волне. Это также равно пространственному расстоянию, покрываемому одним Полный цикл волны.
Частота волны – это число полных циклов волны, проходящей
данной точки пространства в секунду.
Далее мы можем вспомнить, что частота 𝑓 и длина волны 𝜆, световой волны связаны формулой 𝑐=𝑓𝜆, где 𝑐 — скорость света.
Поскольку скорость света в данной среде одинакова для всех световых волн, то из этого уравнения мы можем видеть, что две световые волны, имеющие одинаковые длины волны друг друга также должны иметь одинаковую частоту.
Если мы хотим иметь возможность сравнивать две или более разных волн друг с другом, то нам также необходимо рассмотреть еще одно свойство. Это свойство является фазой волна.
Фаза волны — это мера того, как далеко в цикле проходит волна. конкретная точка пространства. Обычно цикл начинается с точки отмечены на диаграмме ниже, где смещение равно нулю.
Тогда в этой позиции мы бы сказали, что волна имеет нулевую фазу.
Теперь давайте рассмотрим позицию, показанную розовой линией на диаграмме ниже.
В месте, показанном розовой линией, волна прошла четверть пути
через цикл. В терминах фазы мы могли бы описать это как волну, имеющую
фаза одной четверти цикла или, что то же самое, одной четверти
длина волны.
В терминах фазы мы могли бы описать это как волну, имеющую
фаза одной четверти цикла или, что то же самое, одной четверти
длина волны.
Аналогичным образом можно определить фазу волны в любом месте вдоль него.
Следует отметить, что мы измеряем фазу относительно начала цикл. Поскольку две точки на волне, отмеченные на диаграмме ниже, идентичны друг другу, левая точка определяет начало одного цикла, а правая точка определяет начало следующего цикла. Обе эти точки имеют разницу в одну длину волны между собой. Точки, разделенные одной длиной волны, имеют одинаковую фазу друг с другом — в в этом случае фаза нуля.
Мы сказали, что понимание фазы необходимо для того, чтобы иметь возможность сравнивать разные волны друг с другом. Итак, давайте теперь посмотрим, как это работает.
Представим, что у нас есть две световые волны, бегущие слева направо через пустое пространство, как показано на диаграмме ниже.
Чтобы сравнить эти две волны, мы могли бы измерить расстояние между соседними
пики на каждой волне, чтобы найти длину волны, как показано ниже.
На диаграмме мы обозначили длину волны верхней волны как 𝜆 и длина волны нижней волны как 𝜆. Мы можем увидеть из диаграммы видно, что расстояние между двумя соседними пиками на верхней волне равно расстоянию между двумя соседними пиками на нижней волне. Который то есть эти две волны имеют одинаковую длину волны друг у друга. Мы могли бы выразить это математически, говоря, что 𝜆 = 𝜆.
Напомним, что две волны с одинаковой длиной волны также имеют одинаковая частота. Это означает, что мы также можем сказать, что две волны на диаграмме должны иметь одинаковую частоту друг с другом.
Еще один способ сравнить эти волны — посмотреть на их фазы.
В частности, мы могли бы выбрать точку вдоль направления движения волн и посмотрите, как далеко в цикле проходит каждая из волн в этой точке. Это проиллюстрировано для двух разных точек на диаграмме ниже.
В месте, отмеченном оранжевой пунктирной линией, мы видим, что каждый из
волны находятся в начале цикла. В месте, отмеченном розовым пунктиром
линия, каждая волна составляет три четверти цикла. Итак, на обоих этих
позиции волны имеют одинаковую фазу друг с другом.
В месте, отмеченном розовым пунктиром
линия, каждая волна составляет три четверти цикла. Итак, на обоих этих
позиции волны имеют одинаковую фазу друг с другом.
На самом деле легко проверить, что мы можем провести вертикальную линию в любой точке. положение вдоль волн, и мы обнаружим, что обе волны имеют одинаковые фазы друг друга в этом положении.
Когда две волны имеют одинаковую фазу друг с другом в определенной точке пространстве, мы говорим, что в этой точке они имеют нулевую разность фаз.
В более общем смысле разность фаз между двумя волнами — это разность между фазой одной волны и фазой другой.
Предположим, что наши две волны выглядели так, как показано ниже.
В месте, отмеченном оранжевой пунктирной линией, верхняя волна имеет фазу
нуля, так как он находится в начале цикла. При этом нижняя волна представляет собой
четверть пути через цикл. Следовательно, разность фаз между
эти две волны в этом положении составляют четверть цикла.
Если мы теперь посмотрим на розовую пунктирную линию, мы увидим, что верхняя волна три четверти цикла. Нижняя волна полностью проходит через цикла или, что то же самое, в начале следующего цикла. Следовательно разность фаз между волнами также составляет четверть цикла при этом должность.
Как и в случае с двумя нашими волнами, разность фаз которых равна нулю, мы можем убедиться, что разность фаз между этими двумя волнами будет четверть цикла независимо от того, где мы проводим нашу вертикальную линию.
Когда разность фаз между двумя волнами одинакова для всех положений вдоль волн, мы можем сказать, что эти две волны имеют постоянную фазу разница между ними. Здесь «постоянный» означает, что разность фаз не меняется в зависимости от положения вдоль волн.
Всякий раз, когда у нас есть две волны с одинаковой частотой, мы
известно, что они также имеют одинаковую длину волны. Это означает, что обе волны
пройти то же расстояние, чтобы завершить один цикл. В этом случае что угодно
разность фаз между двумя волнами в конкретной точке, это
разность фаз будет такой же, если мы посмотрим на вторую точку на другой
положение вдоль волн. Это справедливо независимо от того, в какую секунду
точка, которую мы выбираем для наблюдения за разностью фаз. Разность фаз между
две волны с одинаковой частотой будут одинаковыми во всех положениях вдоль
волны.
В этом случае что угодно
разность фаз между двумя волнами в конкретной точке, это
разность фаз будет такой же, если мы посмотрим на вторую точку на другой
положение вдоль волн. Это справедливо независимо от того, в какую секунду
точка, которую мы выбираем для наблюдения за разностью фаз. Разность фаз между
две волны с одинаковой частотой будут одинаковыми во всех положениях вдоль
волны.
Этот факт приводит нас к определению когерентности.
Определение: Когерентность
Две или более волны называются когерентными, если они имеют одинаковую частоту и, следовательно, постоянная разность фаз друг от друга.
Важно отметить, что хотя разность фаз между двумя волнами должны быть постоянными, чтобы они были когерентными, эта постоянная фаза разница не обязательно должна быть нулевой. Следовательно, обе пары волн имеют рассматриваемые до сих пор, будут согласованы друг с другом.
Визуально самый простой способ определить, являются ли две волны когерентными, — это посмотреть
на расстоянии, которое проходит каждая волна, чтобы совершить один цикл колебаний. Если мы можем
видим, что две волны совершают один цикл на одном и том же расстоянии друг от друга,
тогда мы знаем, что волны имеют одинаковую длину волны. Это говорит нам о том, что
волны также должны иметь одинаковую частоту друг с другом и постоянную фазу
разница между ними; то есть две волны соответствуют нашему определению когерентного
волны.
Если мы можем
видим, что две волны совершают один цикл на одном и том же расстоянии друг от друга,
тогда мы знаем, что волны имеют одинаковую длину волны. Это говорит нам о том, что
волны также должны иметь одинаковую частоту друг с другом и постоянную фазу
разница между ними; то есть две волны соответствуют нашему определению когерентного
волны.
Давайте снова посмотрим на две волны, которые имели фазу в четверть цикла разница между ними.
На схеме мы указали расстояние, на котором каждая из волн совершает один цикл колебаний. Мы обозначили расстояние 𝜆 в каждом случае, так как она равна длине волны волны. Мы видим, что это одинаковое расстояние для обеих волн. Поэтому это обеспечивает визуальное подтверждение того, что две волны являются когерентными.
Стоит отметить, что мы можем измерить расстояние за один полный
колебание между любыми двумя эквивалентными точками на волне. Вот мы и выбрали
положение, соответствующее началу цикла. Однако мы могли бы с равным успехом иметь
выбран для измерения расстояния между двумя пиками или расстояния между двумя
корыта.
Однако мы могли бы с равным успехом иметь
выбран для измерения расстояния между двумя пиками или расстояния между двумя
корыта.
Две некогерентные волны называются некогерентными. В этом случае волны имеют различную частоту друг к другу, что означает, что они также имеют непостоянная разность фаз.
Итак, как могут выглядеть две некогерентные волны? Поскольку буквально любые два волны, не подпадающие под определение когерентных волн, автоматически бессвязно, оказывается, что есть много возможностей. Две волны рассматриваемые частоты не обязательно должны быть синусоидальными или даже иметь фиксированные частоты.
Однако здесь речь идет об электромагнитном излучении. В таком случае, у нас всегда будут синусоидальные волны, и эти волны будут фиксированными частоты. Пример двух некогерентных синусоидальных волн показан на рис. схема ниже.
В этом случае мы видим, что две волны имеют разные длины волн. Поэтому эти волны имеют разные частоты и непостоянную фазу.
разницы, поэтому мы знаем, что две волны не могут быть когерентными.
Поэтому эти волны имеют разные частоты и непостоянную фазу.
разницы, поэтому мы знаем, что две волны не могут быть когерентными.
Мы также можем подтвердить, что разность фаз между волнами не постоянной, учитывая два разных горизонтальных положения на волнах следующее.
Если мы посмотрим на позицию, отмеченную оранжевой линией, мы увидим, что обе волны находятся в начале цикла. Следовательно, обе волны имеют одинаковую фазу в этот момент. положение, поэтому разность фаз между ними равна нулю. На позиции отмечена розовой линией, верхняя волна находится в середине цикла, а нижняя волна проходит три четверти цикла. Итак, на этой должности разность фаз между волнами составляет четверть периода.
Так как у нас разная разность фаз в двух положениях вдоль волн, мы видим, что между ними не может быть постоянной разности фаз.
Давайте рассмотрим пару примеров.
Пример 1. Определение того, какая из групп волн не является когерентной
На рисунке показаны пять световых волн. Какая световая волна , а не когерентна
остальные четыре?
Какая световая волна , а не когерентна
остальные четыре?
Ответ
Этот вопрос показывает нам пять различных световых волн и предлагает нам потренироваться. какой из них не соответствует другим.
Мы можем вспомнить, что для того, чтобы волны были когерентными, они должны иметь одинаковая частота и постоянная разность фаз друг от друга.
Далее мы можем вспомнить, что две волны с одинаковой частотой также должны имеют одинаковую длину волны, поэтому мы должны искать волну, которая не имеет той же длины волны, что и остальные четыре.
Проще всего это увидеть, нарисовав две вертикальные линии на схему, как показано на схеме ниже.
В положении оранжевой линии, отмеченной цифрой 1, все пять волн в начале цикла.
В месте розовой линии, обозначенной цифрой 2, волны i, ii, iii и v имеют
все завершили один цикл и находятся в начале следующего цикла. Однако,
волна iv завершила только половину цикла между двумя линиями; в
положение розовой линии находится в середине цикла.
Длина волны волны iv отличается от длины волны остальных четырех, поэтому волна iv не согласованы с остальными четырьмя.
Также стоит отметить, что мы можем видеть, что пять различных волны имеют разные амплитуды по отношению друг к другу; это максимум и минимальные высоты, на которых они колеблются, различаются. Хотя это означает что все волны выглядят по-разному, это свойство не относится к когерентности волн.
Пример 2. Определение некогерентной группы световых волн
На каждой из следующих диаграмм показаны пять световых волн. Какой из диаграммы показывает некогерентный свет?
Ответ
Этот вопрос представляет нам пять различных диаграмм, каждая из которых показывает пять различные световые волны, и спрашивает нас, какая из этих пяти диаграмм показывает неравномерный свет.
Мы можем вспомнить, что для того, чтобы две или более световые волны были когерентными, они должны
имеют одинаковую частоту и постоянную разность фаз друг от друга. Когда у нас есть световые волны, которые не соответствуют этим критериям, эти световые
волны некогерентны.
Когда у нас есть световые волны, которые не соответствуют этим критериям, эти световые
волны некогерентны.
Мы также можем вспомнить, что способ визуальной идентификации когерентных волн что когерентные волны будут иметь одинаковую длину волны.
Рассмотрим по очереди каждую из диаграмм, чтобы установить, или не волны когерентны.
Начнем с диаграммы A.
Мы видим, что расстояние, пройденное за один полный цикл, одинаково для все волны. Каждая волна идет от пика одного цикла к пику следующем цикле на расстояние, отмеченное двумя оранжевыми пунктирными линиями. Этот означает, что волны на диаграмме А когерентны.
Теперь давайте посмотрим на схему B.
В этом случае две верхние волны и две нижние волны имеют одинаковые
длина волны. Однако средняя волна завершилась только примерно
три четверти колебания на том же расстоянии, на котором
другие завершили
полный цикл колебаний. Следовательно, средняя волна на этой диаграмме
не согласуется с остальными четырьмя, поэтому на этой диаграмме показаны несогласованные
свет.
Следовательно, средняя волна на этой диаграмме
не согласуется с остальными четырьмя, поэтому на этой диаграмме показаны несогласованные
свет.
Нам еще нужно проверить, показывают ли оставшиеся диаграммы когерентный свет.
Давайте посмотрим на диаграмму C.
Расстояние, пройденное за один полный цикл, одинаково для всех волн. Этот означает, что волны на диаграмме C когерентны.
Теперь давайте посмотрим на диаграмму D.
Опять же, все волны проходят одинаковое расстояние, чтобы завершить один цикл. Следовательно, волны на диаграмме D когерентны.
Наконец, мы рассмотрим диаграмму E.
Еще раз, все волны проходят одинаковое расстояние, чтобы завершить один цикл. Следовательно, волны на диаграмме E когерентны. На самом деле, в этом случае волны также кажутся одинаковыми по амплитуде. Итак, не только эти волны когерентны, но они также фактически идентичны каждому Другой.
Таким образом, мы обнаружили, что волны на диаграммах A, C, D и E являются
последовательный. Между тем, средняя волна на диаграмме B некогерентна с
остальные четыре, поэтому на диаграмме B показан некогерентный свет.
Между тем, средняя волна на диаграмме B некогерентна с
остальные четыре, поэтому на диаграмме B показан некогерентный свет.
Мы видели, что можем исследовать форму волны, чтобы определить свойств конкретной световой волны и как мы можем сравнить две такие изображения, чтобы определить, являются ли две волны когерентными или некогерентными.
Мы можем сделать это и по-другому.
В начале этого объяснения мы сказали, что световые волны колеблются синусоидально. Это означает, что мы можем описать их математически, используя синусоидальная функция.
Рассмотрим следующие две функции: 𝑦=(𝑥),𝑦=2(𝑥).sinsin
Построив эти две функции, мы получим следующие графики.
Мы видим, что график 𝑦=(𝑥)sin (красная линия) колеблется между смещением 1 и смещением -1. При этом график 𝑦=2(𝑥)sin (синяя линия) колеблется с удвоенной амплитуда, между смещением 2 и смещение -2.
В более общем смысле функция
𝑦=𝐴(𝑥)грех
описывает синусоиду, которая колеблется между 𝐴 и
−𝐴.
При использовании синусоидальной функции для описания световой волны мы видим, что значение 𝐴 в этой функции будет описывать амплитуду волна.
Теперь вместо этого рассмотрим следующие две функции: 𝑦=(𝑥),𝑦=(2𝑥).sinsin
Если мы построим эти две функции, мы получим следующие графики.
График 𝑦=(𝑥)sin (красная линия) занимает 360∘, чтобы совершить один цикл колебаний. При этом график 𝑦=(2𝑥)sin (фиолетовая линия) проходит половину этого расстояния, 180∘, чтобы завершить один цикл.
В более общем смысле для функции 𝑦=(𝑘𝑥), грех чем больше значение 𝑘, тем меньше расстояние, на котором синусоида завершает каждый цикл.
При использовании синусоидальной функции для описания световой волны мы видим, что значение 𝑘 связано с длиной волны. Больший значение 𝑘, тем короче длина волны.
Объединив эти два бита информации, мы можем описать свет волны математически следующим образом.
Определение: математическое описание световой волны
Мы можем описать световую волну математически, используя следующее уравнение:
𝑦=𝐴(𝑘𝑥). sin
sin
В этом уравнении 𝐴 — амплитуда волны, а 𝑘 связано с длиной волны — чем больше значение 𝑘, тем короче длина волны.
Глядя на математические функции, описывающие две или более волны, мы в состоянии определить, являются ли эти волны когерентными. Давайте посмотрим, как это работает, рассматривая две световые волны, описываемые следующими функциями: 𝑦=𝐴(𝑘𝑥),𝑦=𝐴(𝑘𝑥).sinsin
Мы можем вспомнить, что для того, чтобы две волны были когерентными, они должны иметь одинаковая частота и постоянная разность фаз между ними. У нас есть уже видели, что две световые волны, имеющие одинаковую длину волны, будут имеют одинаковую частоту, а две световые волны с разной волной длины будут иметь разные частоты.
Мы знаем, что 𝑘 в этих функциях относятся к длины волн. Следовательно, чтобы две волны были когерентными, мы должны иметь это 𝑘=𝑘.
В более широком смысле, если 𝑘 не равно 𝑘, то две волны должны быть
бессвязный.
Поскольку определение когерентности не зависит от амплитуд волны, значения 𝐴 и 𝐴 не влияют на то, две волны когерентны.
Давайте закончим, взглянув на пример с математическим описания световых волн.
Пример 3. Определение некогерентной волны с помощью функций Описание волн
Для моделирования пяти световых волн можно использовать следующие пять функций:
Какая из пяти волн не когерентна с другой четыре?
Ответить
Нас просят выяснить, какая из функций, данных нам описывает волну, не когерентную остальным четырем.
Вспомним, что для того, чтобы быть когерентными, волны должны иметь одинаковая частота и постоянная разность фаз друг от друга.
Мы также можем вспомнить, что значение, на которое 𝑥 умножается внутри
функция синуса связана с длиной волны и
что волны с одинаковыми длинами волн также имеют
одни и те же частоты.
В случае волн i, ii, iv и v значение, которое 𝑥 умножается на 1. Так как это то же самое для всех четырех этих волн, все они должны иметь одинаковую длину волны. Другой. Следовательно, они также должны иметь ту же частоту, что и каждый другие, а это значит, что они согласованы.
Однако для волны iii 𝑥 умножается на коэффициент 2. Это означает, что длина волны волны iii не такой же, как и остальные четыре, и поэтому мы знаем, что эта волна также имеет отличается частотой от других. Следовательно, он не может быть последовательным с ними.
Итак, наш ответ на вопрос заключается в том, что волна iii не когерентный с остальными четырьмя волнами.
Ключевые точки
- Фаза волны — это мера того, насколько далеко в цикле проходит эта волна. в конкретную точку пространства и времени.
- Две или более волны являются когерентными, если они имеют одинаковую частоту и
разность фаз между ними постоянна.


