Как рассчитать падение напряжения в параллельной цепи. Какие законы физики применяются при анализе параллельных соединений. Чем параллельное соединение отличается от последовательного. Какие формулы нужно использовать для расчета параллельных цепей.
Особенности параллельного соединения проводников
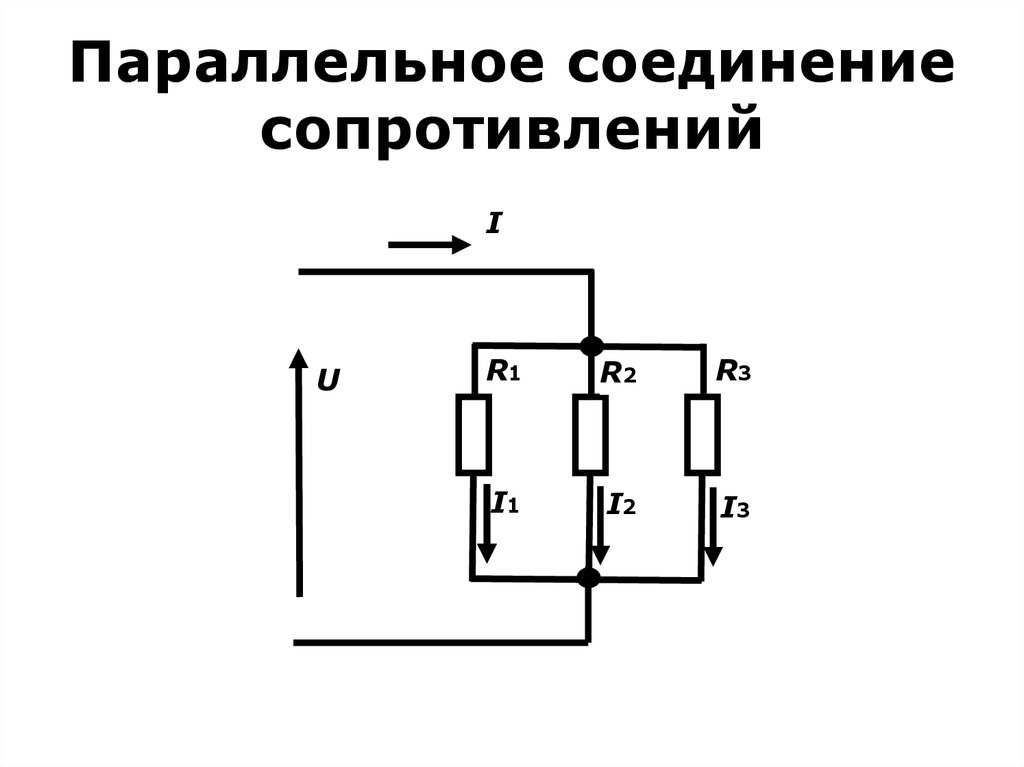
При параллельном соединении проводников в электрической цепи наблюдаются следующие закономерности:
- Напряжение на всех параллельно соединенных элементах одинаково и равно общему напряжению цепи
- Общий ток в неразветвленной части цепи равен сумме токов в отдельных ветвях
- Общее сопротивление цепи меньше сопротивления любого из параллельно соединенных элементов
Эти особенности параллельного соединения обусловлены физическими законами, в частности законом Ома и правилами Кирхгофа. Понимание этих закономерностей позволяет правильно анализировать и рассчитывать параллельные электрические цепи.
Законы, применяемые при анализе параллельных цепей
При анализе параллельных соединений проводников применяются следующие основные законы электротехники:
- Закон Ома: I = U / R, где I — сила тока, U — напряжение, R — сопротивление
- Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
- Второй закон Кирхгофа: алгебраическая сумма напряжений в замкнутом контуре равна нулю
Применение этих законов позволяет составить систему уравнений для расчета токов и напряжений в параллельной цепи. Решение этой системы дает возможность определить все параметры цепи.
Отличия параллельного соединения от последовательного
Параллельное соединение проводников имеет ряд существенных отличий от последовательного:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Напряжение | Одинаково на всех элементах | Сумма напряжений на элементах |
| Ток | Сумма токов в ветвях | Одинаков во всех элементах |
| Сопротивление | Меньше наименьшего | Сумма сопротивлений элементов |
Эти отличия определяют особенности расчета и анализа параллельных и последовательных цепей. При параллельном соединении возможно независимое функционирование отдельных ветвей, что часто используется в электротехнике.
Формулы для расчета параллельных цепей
Для расчета параметров параллельной цепи используются следующие основные формулы:
- Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3 + …
- Общий ток: I = I1 + I2 + I3 + …
- Напряжение: U = U1 = U2 = U3 = …
- Мощность: P = U * I
Применение этих формул позволяет определить все параметры параллельной цепи при известных характеристиках отдельных ветвей. Важно помнить, что напряжение на всех параллельно соединенных элементах одинаково.
Методика расчета падения напряжения в параллельной цепи
Для расчета падения напряжения в параллельной цепи можно использовать следующую методику:
- Определить общее сопротивление цепи по формуле: 1/R = 1/R1 + 1/R2 + 1/R3 + …
- Рассчитать общий ток в цепи по закону Ома: I = U / R, где U — напряжение источника
- Найти токи в отдельных ветвях: I1 = U / R1, I2 = U / R2, …
- Проверить выполнение первого закона Кирхгофа: I = I1 + I2 + I3 + …
- Падение напряжения на каждом элементе равно общему напряжению цепи U
Эта методика позволяет точно рассчитать все параметры параллельной цепи, включая падение напряжения на отдельных элементах.
Примеры расчета падения напряжения в параллельных цепях
Рассмотрим несколько примеров расчета падения напряжения в параллельных цепях:
Пример 1: Простая параллельная цепь
Дано: два резистора R1 = 10 Ом и R2 = 20 Ом соединены параллельно. Напряжение источника U = 12 В.
Решение:
- Общее сопротивление: 1/R = 1/10 + 1/20 = 3/20, R = 20/3 = 6,67 Ом
- Общий ток: I = U / R = 12 / 6,67 = 1,8 А
- Токи в ветвях: I1 = 12 / 10 = 1,2 А, I2 = 12 / 20 = 0,6 А
- Проверка: 1,8 А = 1,2 А + 0,6 А
- Падение напряжения на каждом резисторе: U1 = U2 = 12 В
Пример 2: Параллельная цепь с тремя резисторами
Дано: три резистора R1 = 5 Ом, R2 = 10 Ом, R3 = 15 Ом соединены параллельно. Напряжение источника U = 30 В.
Решение:
- Общее сопротивление: 1/R = 1/5 + 1/10 + 1/15 = 6/15 + 3/15 + 2/15 = 11/15, R = 15/11 = 1,36 Ом
- Общий ток: I = U / R = 30 / 1,36 = 22,06 А
- Токи в ветвях: I1 = 30 / 5 = 6 А, I2 = 30 / 10 = 3 А, I3 = 30 / 15 = 2 А
- Проверка: 22,06 А ≈ 6 А + 3 А + 2 А = 11 А (с учетом округления)
- Падение напряжения на каждом резисторе: U1 = U2 = U3 = 30 В
Эти примеры демонстрируют применение методики расчета падения напряжения в параллельных цепях на практике.
Практическое применение параллельных соединений
Параллельное соединение проводников широко используется в различных областях электротехники и электроники:
- В бытовой электропроводке для подключения нескольких потребителей к одному источнику
- В системах электроснабжения для распределения нагрузки между несколькими генераторами
- В электронных схемах для создания делителей напряжения и тока
- В системах резервирования для повышения надежности электроснабжения
- В измерительных приборах для расширения пределов измерения
Понимание принципов работы и расчета параллельных цепей позволяет эффективно применять их в различных технических решениях.
Заключение
Расчет падения напряжения при параллельном соединении проводников является важной задачей в электротехнике. Правильное применение законов Ома и Кирхгофа, а также специальных формул для параллельных цепей позволяет точно определить все параметры такой цепи. Понимание особенностей параллельного соединения и его отличий от последовательного соединения необходимо для эффективного проектирования и анализа электрических схем.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Интересное: Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются. Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
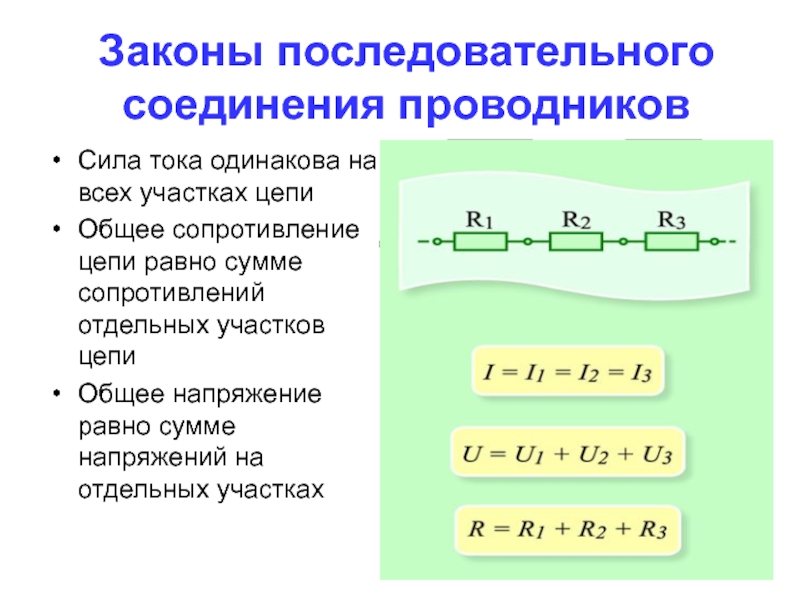
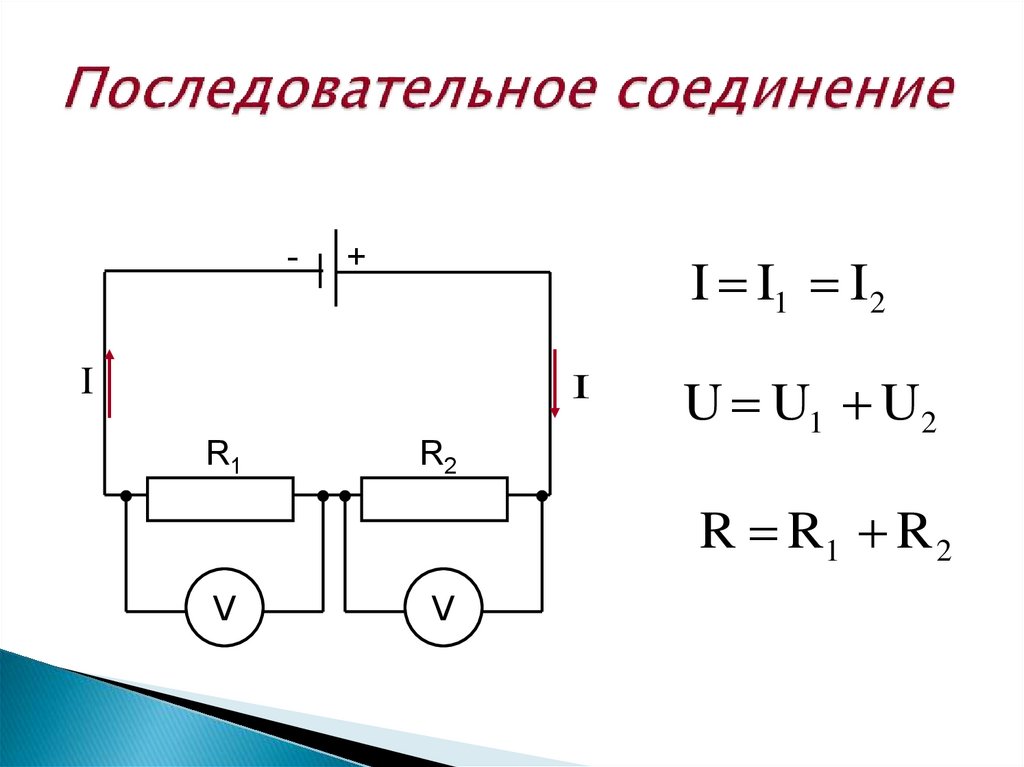
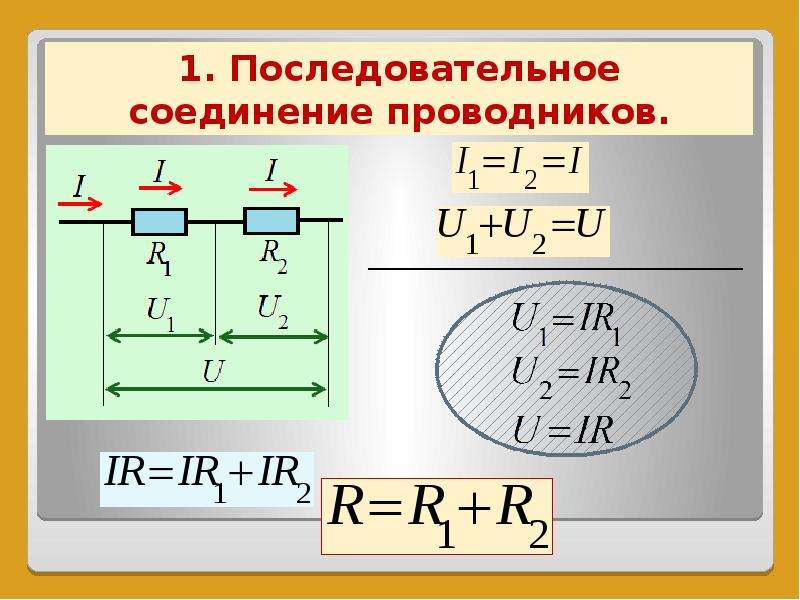
Стр 1 из 3Следующая ⇒ При последовательном соединении проводников сила тока во всех участках цепи одинакова: Это объясняется тем, что заряды при прохождении по цепи не накапливаются ни на одном из участков. Падение напряжения в цепи равно сумме падений напряжений на отдельных участках: , т.к. работа по перемещению заряда по цепи равна сумме работ по перемещению заряда на отдельных участках. Тогда сопротивление , т.е. сопротивление цепи равно сумме сопротивлений отдельных участков.
, т.е. падение напряжения прямо пропорционально сопротивлению участка.
При параллельном соединении сила тока в неразветвлённой части цепи равна сумме сил токов, текущих в разветвлённых участках цепи: . Это следует из закона сохранения зарядов: . Падение напряжения в параллельно соединённых участках цепи одинаково: .
Величина, обратная сопротивлению (проводимость), равна: . При этом сопротивление цепи, меньше меньшего из сопротивлений отдельных участков. В случае двух параллельных участков: . В случае N параллельных участков с одинаковым сопротивлением: , где R 1 – сопротивление одного участка.
В задачах на цепи используйте условие соединения для составления уравнений: последовательное соединение: . параллельное соединение: .
Т.к.: , то , откуда , т.е. сила тока обратнопропорциональна сопротивлению.
Пример. По приведенной электрической схеме определите величину сопротивления R 2, если R 1 =6 Ом; R 3 =4 Ом; I 2 =3 А; I 1 =8 А. Сила тока I 1 =8 А, проходящего через первый амперметр, равна сумме токов, проходящих через резисторы R1, R2 и R3. Значит, сумма токов, идущих через первый и третий резисторы, равна 5 А. Так как резисторы R1 и R3 соединены параллельно, то токи в них обратнопропорциональны сопротивлениям , а значит, сила тока, идущего через R Пример. Чему равно общее сопротивление цепи, если R1=6 Ом, R2=12 Ом, R3=15 Ом, R4=3 Ом? Надо увидеть, что резисторы R1, R3 и R4 включены между собой последовательно, а R2 к ним параллельно. Тогда общее сопротивление цепи равно
ТЕСТ 1. 1. Напряжение, приложенное к участку цепи, равно 168 В. Сила тока в цепи равна 7 А. Найти сопротивление участка цепи. 1) 0,045. 2) 24. 3) 28. 4) 1176. 2. По проводнику с сопротивлением 20 Ом за 1 мин прошел заряд величиной 300 Кл. Напряжение, приложенное к концам проводника, равно: 1) 50 В. 2) 18 В. 3) 36 В. 4) 100 В. 3. Определить среднее значение модуля напряженности электрического поля в однородном проводнике длиной 2 м и сопротивлением 3 Ом при силе тока 8 А. 1) 2.
4. Каково сопротивление R2 и напряжение во всей цепи? 1) 10 Ом, 11 В. 2) 20 Ом, 33 В. 3) 20 Ом, 22 В. 4) 10 Ом, 33 В.
5. По приведенной электрической схеме определите величину сопротивления R 3. R 1 =6 Ом; R 2 =4 Ом; I 2 =3 А; I 1 =9 А. 1) 2 Ом. 2) 12 Ом. 3) 3 Ом. 4) 4 Ом. 6. К сети напряжением 120 В подключены два резистора. При их последовательном соединении общий ток равен 3 А, а при параллельном – 16 А. Сопротивления резисторов равны: 1) 15 и 25 Ом. 2) 10 и 30 Ом. 3) 50 и 35 Ом. 4) 80 и 32 Ом. 7. Четыре лампы, рассчитанные на напряжение 120 В и силу тока 0,5 А каждая, включены параллельно. Лампы нужно питать от сети напряжением 220 В. 1) 25 Ом. 2) 50 Ом. 3) 75 Ом. 4) 100 Ом. 8. Три резистора соединены последовательно и подключены к источнику постоянного напряжения 16 В. Сопротивление первого резистора 13 Ом, второго — 8 Ом. Определить сопротивление третьего резистора, если разность потенциалов на его концах равна 8 В. 1) 1. 2) 14. 3) 17. 4) 21. 9. Гирлянда из 10 одинаковых лампочек включена в сеть напряжением 210 В и потребляет ток силой 2,5 А. Определить сопротивление одной лампочки, если все они соединены параллельно. 1) 120. 2) 280. 3) 480. 4) 840. 10. Участок цепи состоит из резисторов 9 и 6 Ом, соединенных параллельно, и резистора 12 Ом, включенного последовательно. Подведенное напряжение 24 В. Сила тока в резисторе 9 Ом равна: 1) 0,24 А. 2) 0,28 А. 3) 0,31 А. 4) 0,62 А. 11. Участок цепи состоит из резистора 2 Ом, включенного последовательно резисторам 5 Ом и 20 Ом, которые соединены параллельно. 1) 1. 2) 2. 3) 2,5. 4) 4. 12. Два проводника одинаковой длины из одного и того же материала соединены последовательно. Диаметр первого проводника 1 мм, второго 2 мм. К системе приложено напряжение 300 В. Определите напряжение на втором проводнике. 1) 30. 2) 60. 3) 100. 4) 150. 13. Два резистора 20 Ом и 30 Ом соединены последовательно. Определить падение напряжения на 30- омном резисторе, если вольтметр с бесконечно большим сопротивлением, подключенный параллельно резистору в 20 Ом, показал 25 В. 1) 12. 2) 20,5. 3) 37,5. 4) 40. 14. На сколько одинаковых частей надо разрезать однородный проводник сопротивлением 36 Ом, чтобы, соединив эти части параллельно, получить сопротивление 1 Ом? 1) 3. 2) 6. 3) 12. 4) 36. 15. Из 80 одинаковых сопротивлений сделали составное двумя способами: один раз — соединив последовательно 16 одинаковых групп по 5 параллельно соединенных сопротивлений в каждой группе, второй раз — соединив параллельно 20 одинаковых групп по 4 последовательно соединенных сопротивления в каждой группе. 1) 12. 2) 16. 3) 24. 4) 36.
ТЕСТ 2. 1. По резистору сопротивлением 7 Ом протекает электрический ток силой 24 А. Определить падение напряжения на этом резисторе. 1) 0,32. 2) 3,4. 3) 154. 4) 168. 2. В электрическую цепь включен резистор сопротивлением 20 Ом. Напряжение на резисторе 50 В. Заряд, который проходит через поперечное сечение проводника за 1 мин, равен: 1) 30 2)100 3) 2,5 4) 150 3. Найдите напряжение на проволоке длиной 100 м при силе тока в ней 2 А. Сечение проволоки имеет форму квадрата со стороной 3 мм, её удельное сопротивление 9·10-8 Ом·м. 1) 1. 2) 2. 3) 3. 4) 4. 4. В результате нагрева нити накала сила тока, протекающего через лампочку, уменьшилась на 20%. Во сколько возросло сопротивление нити накала, если падение напряжения на лампочке осталось неизменным? 1) 0,8.
5. Каковы показания амперметра А и вольтметра V2? 1) 5 А, 62,5 В. 2) 5 А, 2,5 В. 3) 2,5 А, 42,5 В. 4) 0,2 А, 2,5 В.
6. Два проводника при последовательном соединении дают сопротивление 27 Ом, а при параллельном соединении — 6 Ом. Определить модуль разности сопротивлений этих проводников. 1) 6. 2) 9. 3) 12. 4) 15. 7. Участок цепи состоит из 3 проводников сопротивлением 1 Ом, 2 Ом и 3 Ом, включенных последовательно. Найти падение напряжения на участке цепи, если сила тока в проводнике сопротивлением 1 Ом равна 2 А. 1) 4. 2) 8. 3) 12. 4) 16. 8. Первый проводник имеет сопротивление 1 Ом, второй — 5 Ом. При параллельном соединении проводников во втором из них течет ток, равный 0,2 А. Найти падение напряжения на первом проводнике. 1) 1. 2) 2. 3) 3. 4) 4. 9. Тридцать одинаковых лампочек, соединенных параллельно, подключены к источнику тока напряжением 220 В. Сопротивление одной лампочки равно 1200 Ом. Сила тока, потребляемого схемой, равна: 1) 8 А. 2) 5,5 А. 3) 10 А. 4) 4 А. 10. Два резистора сопротивлением 12 Ом и 4 Ом соединены параллельно. Последовательно к ним включен резистор 3 Ом. Найти силу тока в 12-омном резисторе, если падение напряжения на резисторе 3 Ом составляет 9 В. 1) 0,75. 2) 1. 3) 1,5. 4) 2. 11. Две одинаковые лампы и добавочное сопротивление 3 Ом соединены последовательно и включены в сеть с напряжением 110 В. Найдите силу тока в цепи, если напряжение на каждой лампе 40 В. 1) 4. 2) 6. 3) 8. 4) 10. 12. В электрическую сеть включены последовательно плитка и реостат, сопротивления которых равны 50 и 60 Ом соответственно. 1) 30. 2) 60. 3) 90. 4) 100. 13. Три проводника, изготовленные из одного материала, одинаковой длины, но разного диаметра: d2=2d1, d3=3d1; соединены параллельно. Силы токов в проводниках I1:I2:I3 относятся как: 1) 9:4:1. 2) 3:2:1. 3) 1:4:9. 4) 1:2:3. 14. Отрезок однородной проволоки разрезали на 8 одинаковых частей и соединили эти части параллельно. Сопротивление такой системы оказалось равным 1 Ом. Каким было сопротивление проволоки до того, как ее разрезали? 1) 4. 2) 8. 3) 16. 4) 64.
123Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
..
Получаем, что R 2 =4 Ом.
2) 6. 3) 12. 4) 16.
Какое сопротивление нужно включить дополнительно, чтобы схема работала?
Определить падение напряжения на 2-омном резисторе, если в резисторе 5 Ом течет ток силой 1 А.
Во сколько раз сопротивление во втором случае меньше, чем в первом? 
2) 1,2. 3) 1,25. 4) 1,44.
Определите напряжение на реостате, если напряжение на плитке 75 В.
..Параллельное соединение | это… Что такое Параллельное соединение?
ТолкованиеПеревод
- Параллельное соединение
Последовательное соединение проводников.
Параллельное соединение проводников.
Последовательное и параллельное соединение в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
При параллельном соединении все, входящие в цепь, элементы объединены двумя узлами и не имеют связей с другими узлами. При последовательном соединении проводников сила тока во всех проводниках одинакова.При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Содержание
- 1 Последовательное соединение
- 1.1 Резисторы
- 1.2 Катушка индуктивности
- 1.3 Электрический конденсатор
- 1.4 Мемристоры
- 2 Параллельное соединение
- 2.1 Резисторы
- 2.2 Катушка индуктивности
- 2.3 Электрический конденсатор
- 2.4 Мемристоры
- 3 См. также
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I1 = I2
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U = U1 + U2
Резисторы
Катушка индуктивности
Электрический конденсатор
- .
Мемристоры
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках: I = I1 + I2
Напряжение на участках цепи АВ и на концах всех параллельно соединенных проводников одно и то же: U = U1 = U2
Резисторы
- .
Катушка индуктивности
- .
Электрический конденсатор
- .
Мемристоры
См. также
- Делитель напряжения
- Электрический импеданс
- 1 Последовательное соединение
При параллельном соединении все, входящие в цепь, элементы объединены двумя узлами и не имеют связей с другими узлами. При последовательном соединении проводников сила тока во всех проводниках одинакова.
Wikimedia Foundation. 2010.
Поможем написать курсовую
- Параллельное пространство
- Параллельность
Полезное
законов Кирхгофа (ток и напряжение): что это такое и почему это важно?
По мере того, как электрические цепи становятся все более сложными с множеством ветвей и элементов, становится все труднее определить, какой ток может протекать через ту или иную ветвь, и как соответствующим образом отрегулировать ситуацию.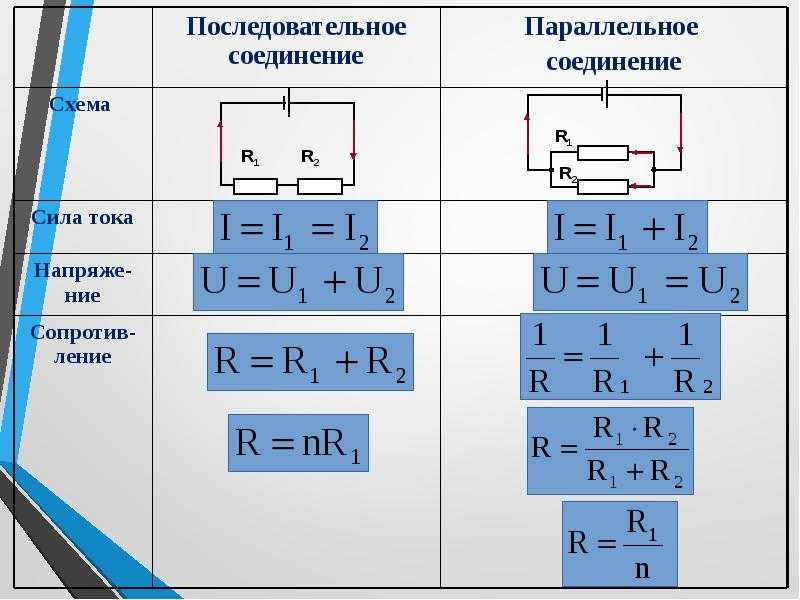
Полезно иметь систематический способ анализа цепей.
Важные определения
Чтобы понять законы Кирхгофа, необходимо дать несколько определений:
- Напряжение В это разность потенциалов на элементе цепи. Измеряется в единицах вольт (В).
- Ток I мера скорости прохождения заряда через точку в цепи. Измеряется в амперах (А).
- Сопротивление R мера сопротивления элемента цепи протеканию тока. Измеряется в единицах Ом (Ом).
- Закон Ома связывает эти три величины следующим уравнением: В = ИК.
Что такое законы Кирхгофа?
В 1845 году немецкий физик Густав Кирхгоф сформулировал следующие два правила о электрических цепях:
цепь должна равняться полному току, вытекающему из соединения.
Другой вариант формулировки этого закона состоит в том, что алгебраическая сумма токов, втекающих в соединение, равна 0.
Это означало бы, что любые токи, втекающие в соединение, считаются положительными, а любые вытекающие — отрицательными. Поскольку общий приток должен равняться общему оттоку, это эквивалентно утверждению, что суммы будут равны 0, поскольку это равносильно перемещению оттоков в другую часть уравнения с отрицательным знаком.
Этот закон выполняется простым применением закона сохранения заряда. Все, что втекает, должно равняться тому, что вытекает. Представьте себе водопроводные трубы, соединяющиеся и разветвляющиеся подобным образом. Точно так же, как вы ожидаете, что общее количество воды, втекающей в соединение, будет равно общему количеству воды, вытекающей из соединения, так и с текущими электронами.
2. Правило контура (также известное как закон напряжения Кирхгофа или KVL): Сумма разностей потенциалов (напряжений) вокруг замкнутого контура в цепи должна равняться 0,
Чтобы понять второй закон Кирхгофа, представьте, что было бы, если бы это было не так.
Рассмотрим одноконтурный контур с несколькими батареями и резисторами. Представьте, что вы начинаете с точки A и движетесь по часовой стрелке по петле. Вы получаете напряжение, когда проходите через батарею, а затем падаете напряжение, когда проходите через резистор и так далее.
Пройдя весь круг, вы снова окажетесь в точке A . Сумма всех разностей потенциалов при обходе контура должна равняться разности потенциалов между точкой A и себя. Что ж, одна точка не может иметь два разных значения потенциала, поэтому эта сумма должна быть равна 0.
В качестве аналогии рассмотрим, что произойдет, если вы пойдете по круговой пешеходной тропе. Предположим, вы начинаете с точки A и начинаете поход. Часть похода ведет в гору, часть вниз и так далее. После завершения цикла вы снова вернетесь в точку A . Это обязательно тот случай, когда сумма ваших прибавок и падений высоты в этом замкнутом цикле должна быть равна 0 именно потому, что высота в точке A должен равняться самому себе.
Почему важны законы Кирхгофа?
При работе с простой последовательной цепью определение тока в петле требует только знания приложенного напряжения и суммы сопротивлений в петле (и затем применения закона Ома).
В параллельных цепях и электрических цепях с комбинациями однако последовательных и параллельных элементов задача определения тока, протекающего через каждую ветвь, быстро усложняется. Ток, входящий в соединение, будет разделяться по мере того, как он входит в разные части цепи, и без тщательного анализа неясно, сколько он пройдет в каждую сторону.
Два правила Кирхгофа позволяют проводить анализ все более сложных схем. Хотя требуемые алгебраические шаги все еще довольно сложны, сам процесс прост. Эти законы широко используются в области электротехники.
Возможность анализа цепей важна, чтобы избежать перегрузки элементов схемы. Если вы не знаете, какой ток будет протекать через устройство или какое напряжение на нем упадет, вы не будете знать, какой будет выходная мощность, и все это имеет отношение к функционированию устройства.
Как применять законы Кирхгофа
Правила Кирхгофа можно применить для анализа электрической схемы, выполнив следующие шаги: его как I i и выберите направление для этого тока. (Направление не обязательно должно быть правильным. Если окажется, что этот ток на самом деле течет в противоположном направлении, то вы просто получите отрицательное значение при вычислении этого тока позже.)
Для каждого контура в цепи выберите направление. (Это произвольно. Вы можете выбрать против часовой стрелки или по часовой стрелке. Это не имеет значения.)
Для каждого цикла начните с одной точки и двигайтесь в выбранном направлении, складывая разности потенциалов для каждого элемента. Эти разности потенциалов можно определить следующим образом:
- Если ток проходит в положительном направлении через источник напряжения, это положительное значение напряжения. Если ток проходит в отрицательном направлении через источник напряжения, напряжение должно иметь отрицательный знак.
- Если ток проходит в положительном направлении через резистивный элемент, то вы используете закон Ома и добавляете -I i × R (падение напряжения на этом резисторе) для этого элемента. Если ток проходит в отрицательном направлении через резистивный элемент, то вы добавляете + I i × R для этого элемента.
- После того, как вы прошли весь контур, установите эту сумму всех напряжений равной 0. Повторите эти действия для всех контуров в цепи.
Для каждого соединения сумма токов, втекающих в это соединение, должна равняться сумме токов, вытекающих из этого соединения. Запишите это в виде уравнения.
Теперь у вас должен быть набор одновременных уравнений, которые позволят вам определить ток (или другие неизвестные величины) во всех ветвях цепи. Последним шагом является алгебраическое решение этой системы.
Примеры
Пример 1: Рассмотрим следующую схему:
Применяя Шаг 1, для каждой ветви мы помечаем неизвестные токи.
••• нет данных
Применяя шаг 2, мы выбираем направление для каждого контура в цепи следующим образом: в выбранном направлении складываем разности потенциалов на каждом элементе и присваиваем сумму равной 0.
Для контура 1 на диаграмме получаем:
-I_1\times 40 — I_3\times 100 + 3 = 0
Для цикла 2 на диаграмме получаем:
-I_2\times 75 — 2 + I_3\times 100 = 0
Для шага 4 применяем правило соединения. На нашей диаграмме есть два соединения, но оба они дают эквивалентные уравнения. А именно:
I_1 = I_2 + I_3
Наконец, для шага 5 мы используем алгебру для решения системы уравнений для неизвестных токов:
Используйте уравнение соединения, чтобы подставить в уравнение первого контура:
-(I_2 + I_3)\times 40 – I_3\times 100 + 3 = -40I_2 – 140I_3 + 3 = 0
Решите это уравнение для I 2 :
I_2 = \frac{3-140I_3}{40}
Подставьте это во второе уравнение цикла:
-[(3-140I_3)/40 ]\times 75 – 2 + 100I_3 = 0
Найдите I 3 :
-3\times 75/40 + (140\times 75/40)I_3 – 2 + 100I_3=0\\ \подразумевает I_3 = (2+3\times 75/40)/(140\times 75/40 + 100) = 0,021 \text{ A}
Используйте значение I 3 , чтобы найти I 2 :
I_2 = (3-140\times (0.
021))/40 = 0.0015\text{A}
И решить для + I_3 = 0,021 + 0,0015 = 0,0225 \ Текст {a}
, поэтому конечный результат состоит в том, что I 1 = 0,0225 A, I 2 = 0,0015 A и I 2 = 0,0015 A и I 3 = 0,021 A.
Подстановка этих значений тока в исходные уравнения дает результат, поэтому мы можем быть достаточно уверены в результате!
Поскольку в таких вычислениях очень легко сделать простые алгебраические ошибки, настоятельно рекомендуется проверить, согласуются ли ваши окончательные результаты с исходными уравнениями, подставив их и убедившись, что они работают.
Попробуйте решить эту же проблему еще раз, но с другим выбором текущих меток и направлений цикла. Если все сделать осторожно, вы должны получить тот же результат, показывающий, что первоначальный выбор действительно произволен.
(Обратите внимание, что если вы выберете разные направления для обозначенных вами токов, то ваши ответы для них будут отличаться на знак минус, однако результаты все равно будут соответствовать одному и тому же направлению и величине тока в цепи.
)
Пример 2: Какова электродвижущая сила (ЭДС) ε батареи в следующей цепи? Какова сила тока в каждой ветви?
••• нет данных
Сначала мы помечаем все неизвестные токи. Пусть I 2 = ток вниз через среднюю ветвь и I 1 = ток вниз через крайнюю правую ветвь. На изображении уже показан текущий I в крайнем левом ответвлении с надписью.
Выбор направления по часовой стрелке для каждого контура и применение законов Кирхгофа дает следующую систему уравнений: 12I_1 — 8 + 6I_2 = 0 \end{выровнено}
Чтобы решить, подставьте I — I 2 вместо I 1 в третьем уравнении, а затем подставьте данное значение вместо I и решите это уравнение для I 2 . Как только вы узнаете I 2 , вы можете подставить I и I 2 в первое уравнение, чтобы получить I 1 .
Затем вы можете решить второе уравнение для ε . Выполнение этих шагов дает окончательное решение:
\begin{align} &I_2 = 16/9 = 1,78 \text{ A}\\ &I_1 = 2/9 = 0,22 \text{ A}\\ &\varepsilon = 32/3 = 10,67\text{ V} \ end{aligned}
Опять же, вы всегда должны проверять свои окончательные результаты, подставляя их в исходные уравнения. Очень легко сделать простые алгебраические ошибки!
Как рассчитать падение напряжения в параллельной цепи?
Ответ
Проверено
209,7 тыс.+ просмотров
Подсказка: Это можно решить, используя закон Ома, который гласит, что напряжение на проводнике прямо пропорционально току, протекающему по нему, и для параллельных цепей мы будем использовать формулу для полного сопротивления найти полное падение напряжения.
Используемая формула:
$\begin{align}
& V=IR \\
& R={{R}_{1}}+{{R}_{2}}+{{R}_ {3}} \\
\end{align}$
Полное пошаговое решение:
Падение напряжения на резисторе в параллельной цепи одинаково на всех резисторах в каждой ветви всех параллельных цепей в схема параллельного соединения.
Напряжение, выраженное в напряжении, измеряет электродвижущие силы, которые управляют цепью, или разность потенциалов.
Рассмотрим цепь с тремя резисторами, соединенными параллельно, с источником напряжения «V» и током, протекающим через «I».
Теперь пошаговый метод для расчета напряжения в цепи,
Шаг 1:- найти общее сопротивление параллельной цепи.
Формула полного сопротивления для цепи, соединенной параллельно,
$\begin{align}
& \Rightarrow \dfrac{1}{{{R}_{T}}}=\dfrac{1}{{{R} _{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}} \\
& \следовательно {{R}_{T}}=\dfrac{{{R}_{1}}{{R}_{2}}{{R}_{3}}}{{{R} _{1}}{{R}_{2}}+{{R}_{2}}{{R}_{3}}+{{R}_{1}}{{R}_{3 }}}….\left( 3 \right) \\
\end{align}$
Теперь по закону Ома
$\Rightarrow V=I{{R}_{T}}$
Где V = напряжение
I = ток
${{R}_{T}}$ = общее сопротивление
$\Rightarrow V=\dfrac{I\times {{R}_{1}}{{R}_ {2}}{{R}_{3}}}{{{R}_{1}}{{R}_{2}}+{{R}_{2}}{{R}_{3 }}+{{R}_{3}}{{R}_{4}}}.
