Параллельное подключение конденсаторов. Параллельное соединение конденсаторов: принципы работы, формулы расчета и применение

Как работает параллельное соединение конденсаторов. Какие формулы используются для расчета общей емкости и напряжения. Где применяется параллельное соединение конденсаторов на практике. Каковы преимущества и недостатки такого соединения.

Принцип работы параллельного соединения конденсаторов

При параллельном соединении конденсаторов все положительные обкладки соединяются в одной точке, а все отрицательные — в другой. Такое соединение имеет следующие особенности:

• На всех конденсаторах одинаковое напряжение, равное напряжению источника питания
• Заряды на конденсаторах складываются
• Общая емкость увеличивается и равна сумме емкостей отдельных конденсаторов

Параллельное соединение можно представить как увеличение площади обкладок конденсатора. Чем больше конденсаторов соединено параллельно, тем больше суммарная емкость батареи.

Формулы для расчета параллельного соединения конденсаторов

Основные формулы для расчета параллельного соединения конденсаторов:

1. Общая емкость: C = C1 + C2 + C3 + … + Cn
2. Напряжение на каждом конденсаторе: U1 = U2 = U3 = … = Un = U
3. Заряд на батарее конденсаторов: Q = Q1 + Q2 + Q3 + … + Qn

Где C — общая емкость, Ci — емкость i-го конденсатора, U — напряжение на батарее, Qi — заряд на i-м конденсаторе.

Преимущества параллельного соединения конденсаторов

Параллельное соединение конденсаторов имеет ряд преимуществ:

• Позволяет увеличить общую емкость батареи
• Дает возможность получить нестандартные значения емкости
• Уменьшает внутреннее сопротивление батареи конденсаторов
• Повышает надежность — при выходе из строя одного конденсатора остальные продолжают работать

Области применения параллельного соединения конденсаторов

Параллельное соединение конденсаторов широко применяется в различных областях электроники и электротехники:

• В фильтрах источников питания для увеличения емкости сглаживающего фильтра
• В высоковольтных цепях для повышения пробивного напряжения
• В радиотехнике для точной настройки колебательных контуров
• В импульсных схемах для получения больших токов разряда
• В силовой электронике для снижения пульсаций напряжения

Расчет параллельного соединения конденсаторов на практике

Рассмотрим пример расчета параллельного соединения трех конденсаторов:

Даны конденсаторы с емкостями: C1 = 10 мкФ, C2 = 22 мкФ, C3 = 47 мкФ. Напряжение источника U = 12 В.

Общая емкость: C = C1 + C2 + C3 = 10 + 22 + 47 = 79 мкФ

Напряжение на каждом конденсаторе: U1 = U2 = U3 = U = 12 В

Заряды на конденсаторах:

• Q1 = C1 * U = 10 * 10^-6 * 12 = 120 * 10^-6 Кл
• Q2 = C2 * U = 22 * 10^-6 * 12 = 264 * 10^-6 Кл
• Q3 = C3 * U = 47 * 10^-6 * 12 = 564 * 10^-6 Кл

Общий заряд: Q = Q1 + Q2 + Q3 = 948 * 10^-6 Кл

Сравнение параллельного и последовательного соединения конденсаторов

Параллельное и последовательное соединение конденсаторов имеют существенные отличия:

Параметр	Параллельное соединение	Последовательное соединение
Общая емкость	Увеличивается	Уменьшается
Напряжение	Одинаковое на всех конденсаторах	Распределяется между конденсаторами
Заряд	Разный на конденсаторах	Одинаковый на всех конденсаторах

Особенности параллельного соединения электролитических конденсаторов

При параллельном соединении электролитических конденсаторов необходимо соблюдать следующие правила:

• Строго соблюдать полярность подключения
• Использовать конденсаторы с одинаковым номинальным напряжением
• Желательно применять конденсаторы одного типа и производителя
• Для выравнивания токов утечки рекомендуется подключать резисторы параллельно каждому конденсатору

Параллельное соединение конденсаторов в цепях переменного тока

В цепях переменного тока параллельное соединение конденсаторов имеет некоторые особенности:

• Общее реактивное сопротивление уменьшается: Xc = 1 / (2πfC)
• Ток через батарею конденсаторов увеличивается: I = U / Xc
• Сдвиг фаз между током и напряжением составляет -90°
• Полное сопротивление цепи уменьшается: Z = √(R^2 + Xc^2)

Где f — частота переменного тока, R — активное сопротивление цепи.

Как правильно подобрать конденсаторы для параллельного соединения

При подборе конденсаторов для параллельного соединения следует учитывать ряд факторов:

1. Требуемую общую емкость
2. Рабочее напряжение схемы
3. Допустимые токи утечки
4. Температурный диапазон работы
5. Габаритные размеры
6. Стоимость компонентов

Рекомендуется выбирать конденсаторы с близкими характеристиками для обеспечения равномерной нагрузки.

Практические советы по параллельному соединению конденсаторов

Несколько практических рекомендаций по параллельному соединению конденсаторов:

• Используйте короткие и толстые соединительные проводники для уменьшения паразитной индуктивности
• Располагайте конденсаторы как можно ближе друг к другу
• Применяйте симметричную компоновку для равномерного распределения токов
• Обеспечьте хороший теплоотвод, особенно для мощных конденсаторов
• Периодически проверяйте состояние конденсаторов и качество соединений

Заключение: эффективность параллельного соединения конденсаторов

Параллельное соединение конденсаторов — эффективный способ увеличения емкости и снижения внутреннего сопротивления батареи конденсаторов. Оно широко применяется в различных областях электроники и электротехники. При правильном подборе компонентов и соблюдении правил монтажа параллельное соединение позволяет создавать надежные и эффективные конденсаторные батареи для решения широкого спектра задач.

применение, формулы расчёта ёмкости и напряжения

Содержание

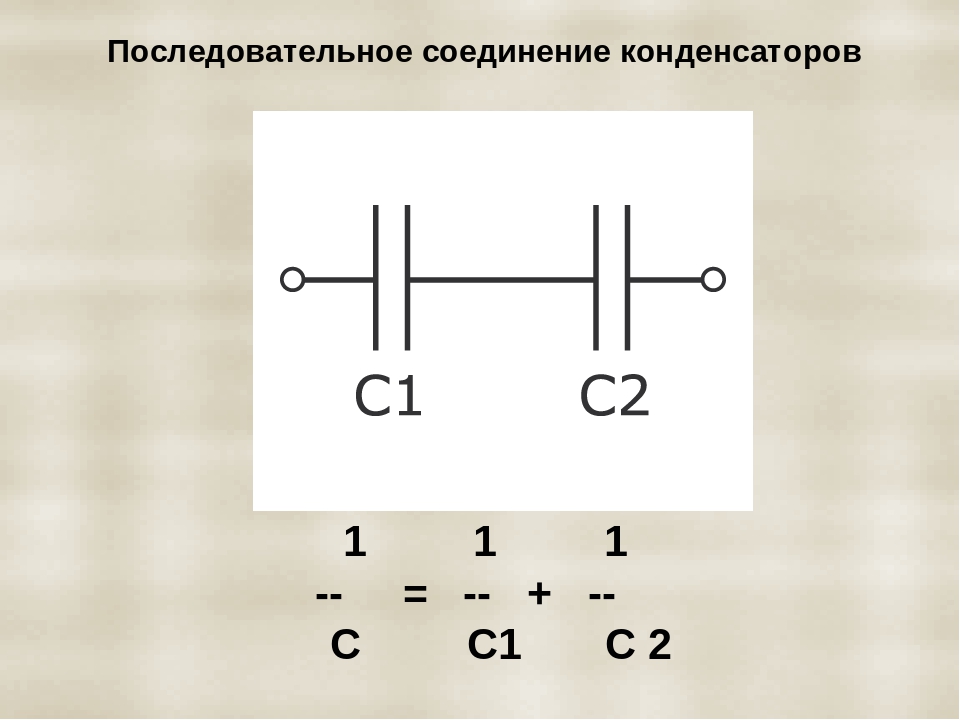
Последовательное и параллельное соединение конденсаторов

Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным). Если провести аналогию между соединением конденсаторов и соединением резисторов, то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений: Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.

• Cобщ — общая емкость.
• Rобщ — общее сопротивление.

При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны:  Q1 = Q2 = Q3 = Q. Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.

Соединения конденсаторов.

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3. Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов. Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.

Материал в тему: все о переменном конденсаторе.

Примеры расчетов

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 330нанофарада и 390нанофарада

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 4,3нанофарада и 5,1нанофарада

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 100нанофарад и 120нанофарад

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 470нанофарад и 560нанофарад

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 22нанофарад и 27нанофарад

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 680нФ и 820нФ

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 51нФ и 62нФ

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 30нФ и 36нФ

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 62нанофарад и 75нанофарад

Пример: Общая емкость соединенных последовательно конденсаторов емкостью 120нанофарада и 150нанофарада

Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:

Калькулятор резистивно-емкостной цепи

Калькулятор параллельных сопротивлений

Калькулятор параллельных индуктивностей

Калькулятор импеданса конденсатора

Калькулятор импеданса катушки индуктивности

Калькулятор взаимной индукции

Калькулятор взаимоиндукции параллельных индуктивностей

Калькулятор взаимной индукции — последовательное соединение индуктивностей

Калькулятор импеданса параллельной RC-цепи

Калькулятор импеданса параллельной LC-цепи

Калькулятор импеданса параллельной RL-цепи

Калькулятор импеданса параллельной RLC-цепи

Калькулятор импеданса последовательной RC-цепи

Калькулятор импеданса последовательной LC-цепи

Калькулятор импеданса последовательной RL-цепи

Калькулятор импеданса последовательной RLC-цепи

Калькулятор аккумуляторных батарей

Калькулятор литий-полимерных аккумуляторов для дронов

Калькулятор индуктивности однослойной катушки

Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC)

Калькулятор расчета параметров коаксиальных кабелей

Калькулятор светодиодов.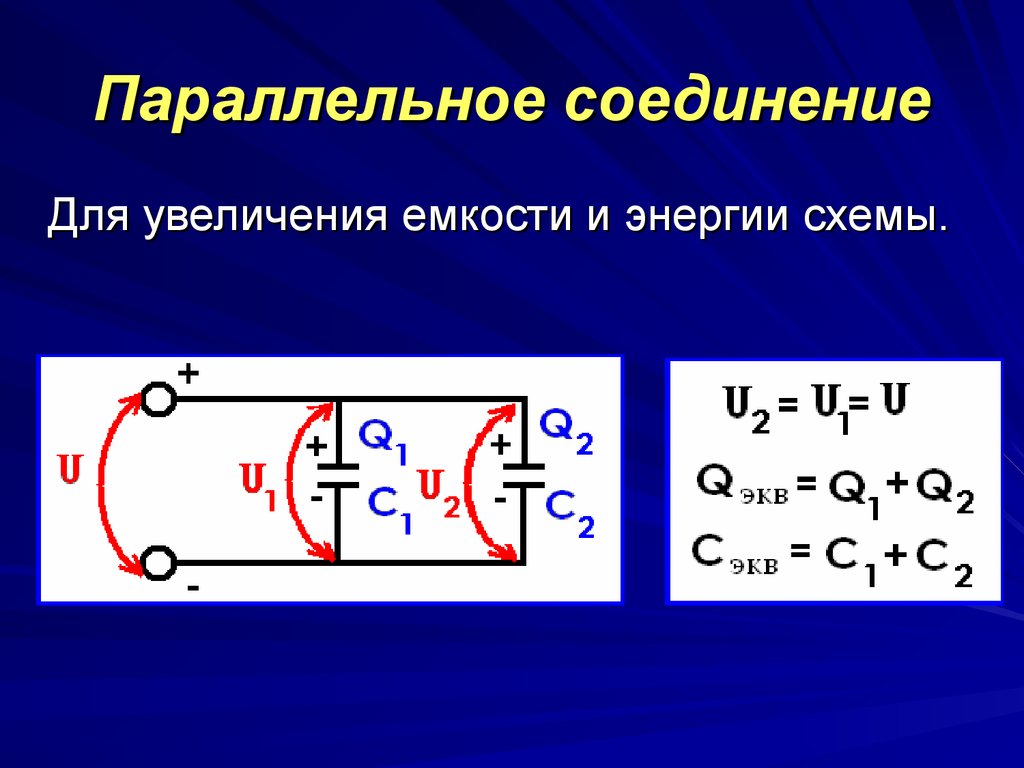 Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов

Калькулятор цветовой маркировки резисторов

Калькулятор максимальной дальности действия РЛС

Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов

Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС

Калькулятор радиогоризонта

Калькулятор эффективной площади антенны

Симметричный вибратор

Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации

Калькулятор мощности постоянного тока

Калькулятор мощности переменного тока

Калькулятор пересчета ВА в ватты

Калькулятор мощности трехфазного переменного тока

Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую

Калькулятор коэффициента гармонических искажений

Калькулятор законов Ома и Джоуля — Ленца

Калькулятор времени передачи данных

Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора

Калькуляторы Электротехнические и радиотехнические калькуляторы

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим.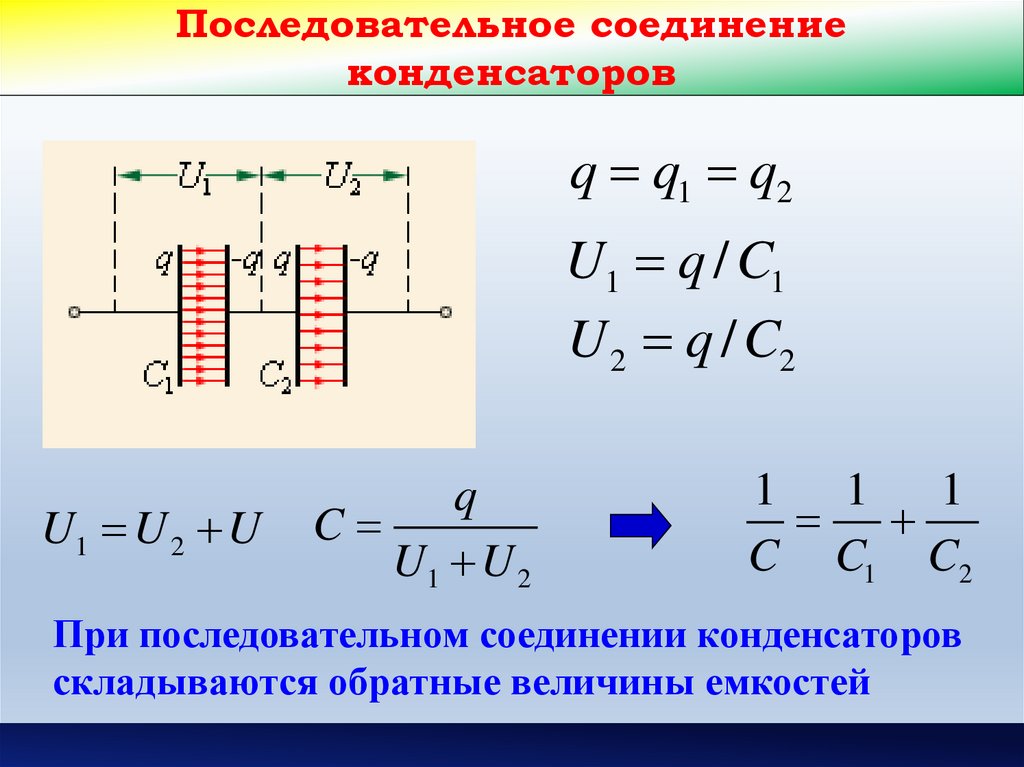 Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С1 – ёмкость первого;

С2 – ёмкость второго;

С3 – ёмкость третьего;

СN – ёмкость N-ого конденсатора;

Cобщ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см.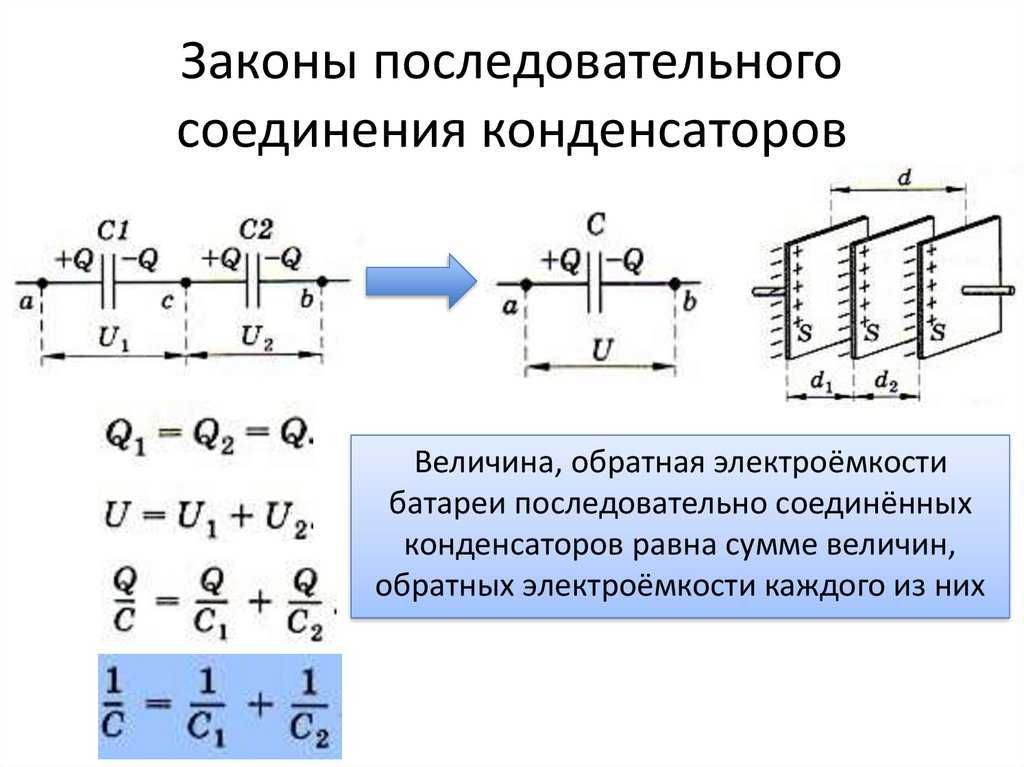 фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.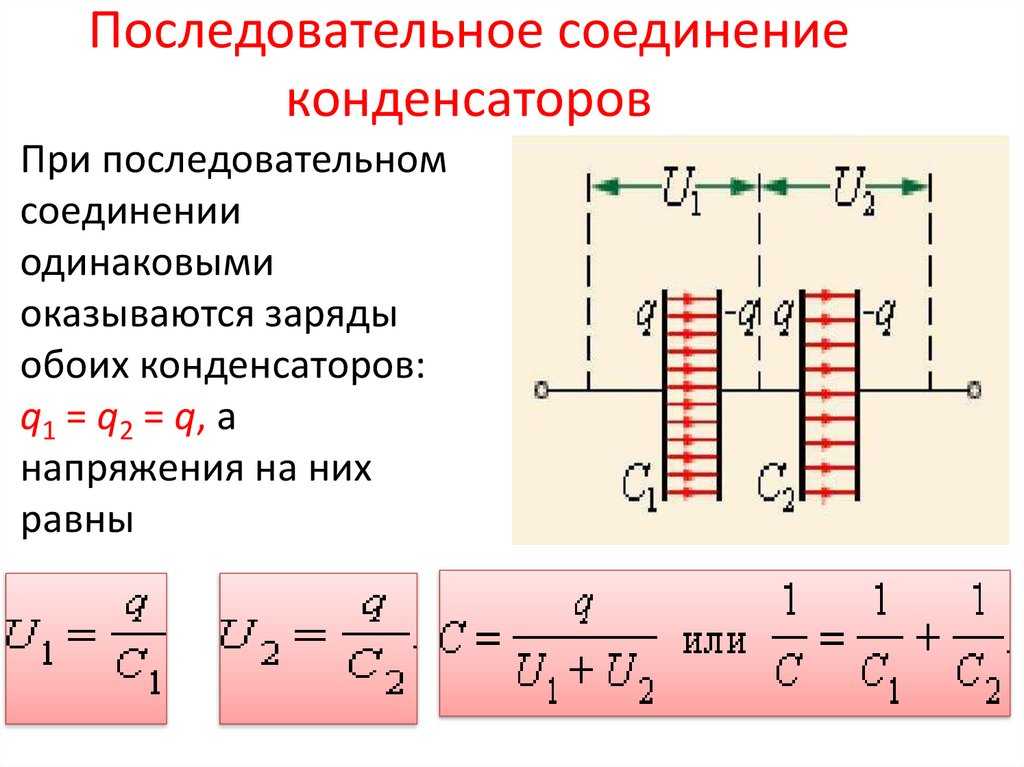

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные).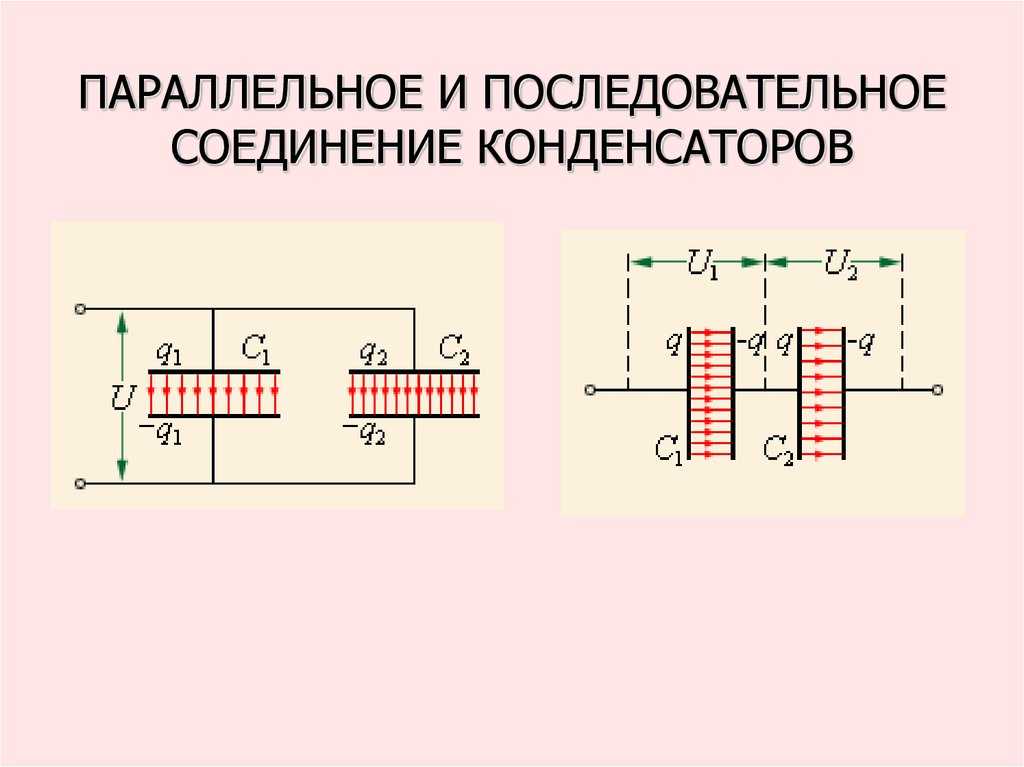 Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Источник: go-radio.ru

Параллельное соединение конденсаторов

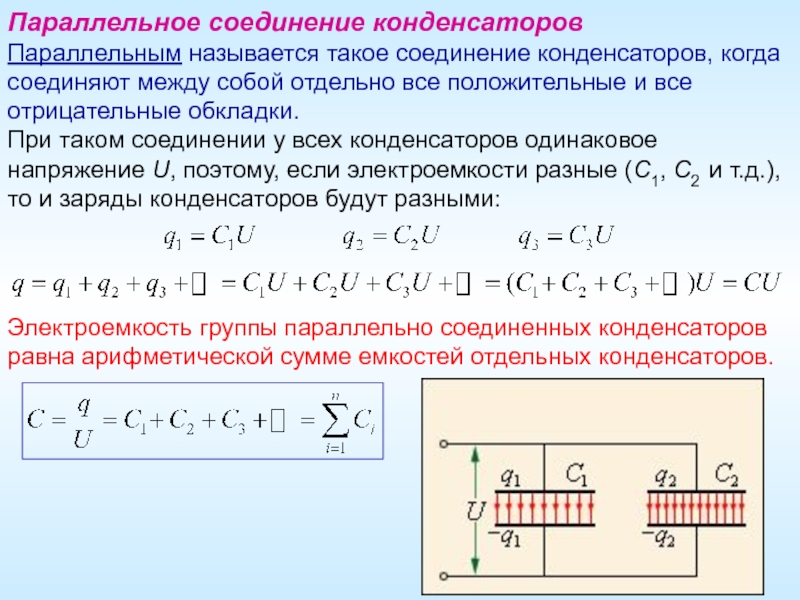
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов. При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.

Напряжение при параллельном соединении

На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения. Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:

• ic — ток конденсатора
• C — Емкость конденсатора
• ΔVC/Δt – Скорость изменения напряжения

Будет интересно➡  Чем отличается пусковой конденсатор от рабочего?

При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:

Ток при последовательном соединении

Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:

Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.

Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:

Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.

Читайте также:  Как соединить розетки между собой

В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.

При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.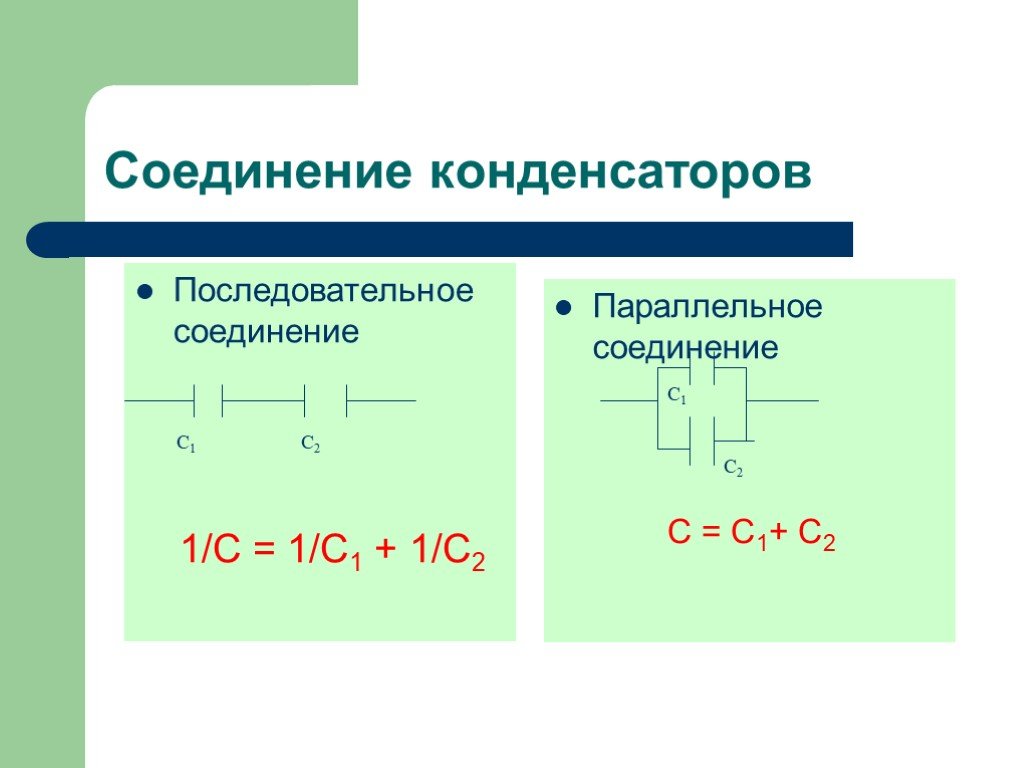

Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.

Площадь и расстояние между обкладками при последовательном соединении

Последовательное соединение конденсаторов

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным. При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заря­жаются через влияние. При этом заряд пла­стины будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.

Типы соединений конденсаторов.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Параллельное и последовательное соединение конденсаторов (формулы, законы для вычисления емкости и напряжения)

Содержание

1. Отличия параллельного и последовательного соединения конденсаторов
2. Смешанное подключение
3. Общая емкость и распределение напряжений между элементами при разных типах включения
4. Примеры подключений

Электрические схемы могут содержать элементы, основным параметром которых является емкость. Чаще всего это конденсаторы (также в этом качестве используются, например, варикапы, ионисторы и т.п.). Такие элементы можно соединять параллельно или последовательно и получать участки схемы с иными параметрами.

Отличия параллельного и последовательного соединения конденсаторов

При параллельном (parallel) подключении обкладки конденсаторов соединяются в одной точке, а противоположные – в другой. К этим точкам подключается источник напряжения. Наглядно продемонстрировать такую схему можно на примере полярных приборов (например, электролитических конденсаторов), когда все положительные электроды соединяются между собой и подключаются к плюсу питания.

Отрицательные обкладки также соединяются в один узел, на который подается минус питающего напряжения. У неполярных элементов нет разделения на положительные и отрицательные электроды, они соединяются произвольным образом, но по тому же принципу (в этом случае на батарею можно подавать и двухполярное напряжение). Каждый конденсатор подключен непосредственно к источнику питания, поэтому напряжение на каждой банке одинаково.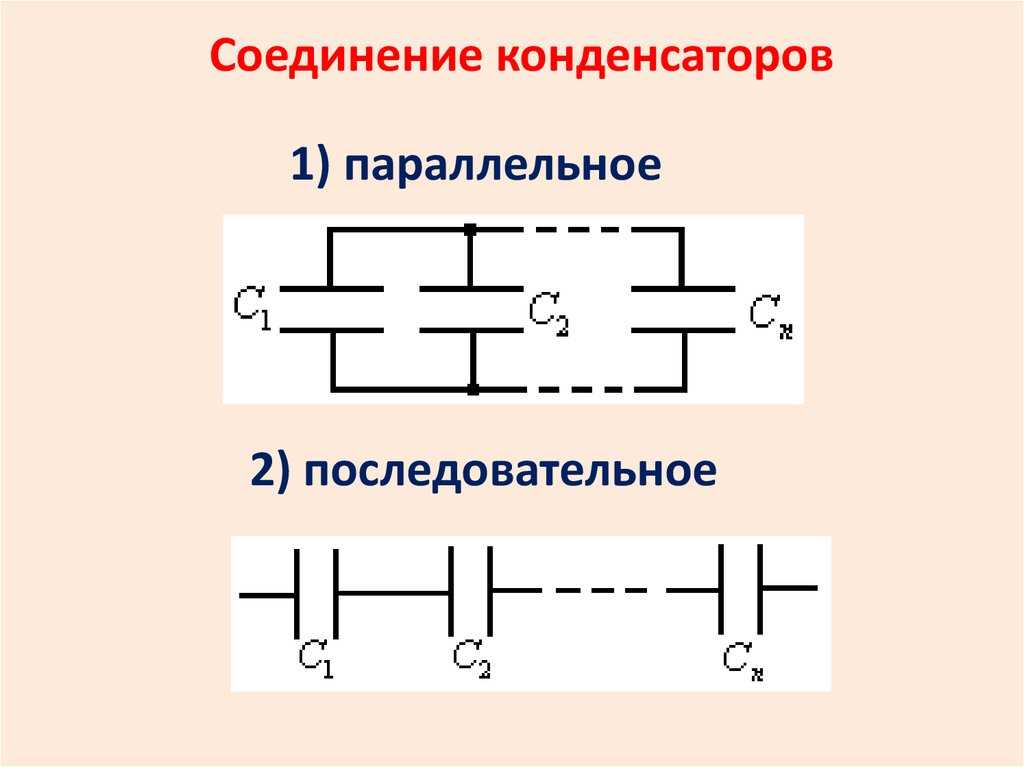

Параллельное включение элементов.

При последовательном (serial) соединении одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

Батарея из последовательно соединенных ячеек.

Смешанное подключение

Также существует смешанное соединение элементов, когда часть ячеек включена параллельно, часть последовательно. Такие схемы несколько сложнее для анализа.

Батарея из смешанно соединенных конденсаторов.

Общая емкость и распределение напряжений между элементами при разных типах включения

Емкость конденсаторов зависит, в том числе, и от площади обкладок. Если однотипные элементы соединить параллельно, это можно рассматривать как суммирование всех площадей обкладок, что означает сложение емкостей банок, входящих в батарею. Очевидно, что это же правило действует и для разнотипных элементов. Аналитическим путем к этому можно прийти в результате следующих рассуждений:

• очевидно, что при таком подключении на каждом элементе напряжения будут равны (U₁=U₂=U);
• запасенные заряды всех пластин суммируются (q=q₁+q₂);
• тогда общая емкость равна С=U*q=U*(q₁+q₂)=U*q₁+U*q₂=C1+C2.

Напряжение и заряды при параллельном включении элементов.

Эта же формула действует при параллельном соединении n конденсаторов:

С=С₁+С₂+..+C_n.

Последовательное соединение емкостей.

Если соединить в последовательную цепь, например, три конденсатора различной емкости и полностью их зарядить до напряжения U, то выяснится, что:

• заряды –q1 и q2, -q2 и q3 равны между собой, так как обкладки с этими зарядами электрически соединены;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по абсолютной величине, но противоположны по знаку.

Конденсаторы в таком включении получают равный заряд q, но при разной емкости получится, что напряжения на каждом элементе равны:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Напряжения распределяются пропорционально емкостям (при равных параметрах на каждой банке падает одинаковое сопротивление). А общая емкость равна С=q/(U₁+U₂+U₃), отсюда 1/С=( U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, подключенных в последовательную цепь:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула выглядит громоздко, но для цепи из двух элементов можно пользоваться приведенным видом С= С₁* С₂/( С₁+ С₂).

Для предварительного анализа схем, состоящих из емкостных элементов, подключенных различными способами, надо запомнить несколько законов:

• при параллельном соединении емкости складываются, суммарная емкость всегда больше, чем у элемента с самым большим значением емкости;
• напряжения при параллельном соединении одинаковы на каждом элементе цепи;
• при последовательном соединении итоговая емкость будет меньше наименьшего значения емкости любого элемента;
• напряжения на последовательно включенных звеньях распределяются пропорционально емкости.

Анализ и расчет схем со смешанным подключением элементов надо начинать с приведения цепи к единому виду, где конденсаторы будут включены либо только последовательно, либо только в параллель.

Преобразование к последовательному виду.

Так, схема на рисунке содержит три элемента, два из которых включены в параллель, и один последовательно. Удобно С1 и С3 заменить одним эквивалентным звеном С – при этом останутся только последовательные звенья. Остается выполнить расчет схемы, а потом вернуться к изначальной цепи.

Преобразование к последовательному виду.

Рекомендуем видео-урок по физике.

Примеры подключений

Параллельное соединение применяется в тех случаях, когда надо увеличить итоговую емкость. По экономическим или компоновочным причинам использование одного элемента с необходимыми параметрами может быть невозможно или нерационально. Поэтому собирают батарею из конденсаторов так, чтобы сумма емкостей давала необходимое значение. Такая схема применяется, например, для фильтров блоков питания в целях увеличения емкости сглаживающего фильтра.

Другой вариант параллельного включения – когда емкость надо точно настраивать по месту, а подстроечного конденсатора с необходимыми пределами или нет в наличии, или не существует. Тогда параллельно конденсатору постоянной емкости включают подстроечный элемент. После монтажа устройства во время настройки устанавливается точное значение.

Параллельно включенный прибор с постоянными параметрами и подстроечник.

Последовательное включение нескольких элементов дает увеличение рабочего напряжения цепочки, но уменьшает общую емкость. К тому же купить приборы на высокое напряжение (до нескольких киловольт) несложно, поэтому последовательные цепи в целях достижения необходимых параметров применяются нечасто. Обычно такое включение используется в емкостных делителях напряжения. В отличие от резистивных компонентов, через реактивные элементы не протекает активный ток, поэтому не надо решать задачу отвода тепла. Такие делители можно применять, к примеру, в индикаторах наличия высокого напряжения. Несколько киловольт на входе подбором номиналов банок делятся так, что напряжение на нижнем элементе безопасно для индикаторной лампы.

Индикатор высокого напряжения.

Также такой делитель можно найти в схемах импульсных источников питания с полумостовой схемой. Таким способом образуется средняя точка с потенциалом, равным половине питания.

Фрагмент схемы блока питания с фильтром-делителем и выравнивающими резисторами.

 

Еще один пример применения последовательного соединения элементов – в умножителях напряжения. В них нагрузочная способность источника питания зависит от емкости, поэтому в умножителях также применяются оксидные конденсаторы.

Последовательная батарея для умножителя.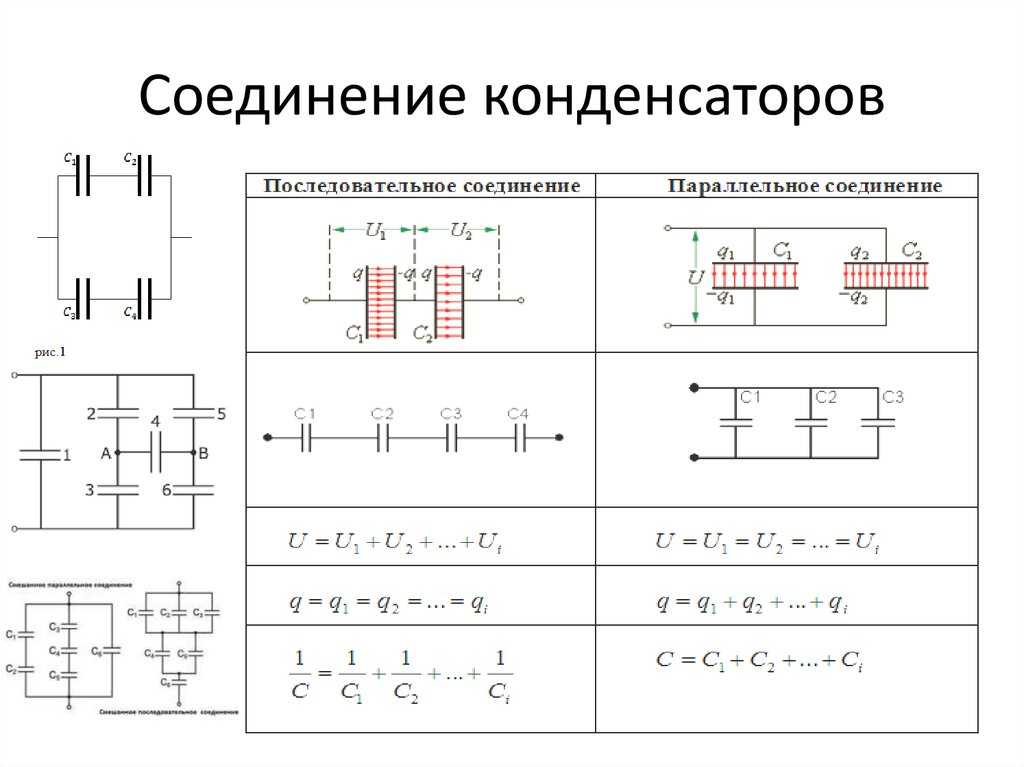

Смешанное включение встречается гораздо реже. Один из примеров такой схемы – колебательный контур с переменной частотой настройки. Его резонанс зависит, в том числе, от емкости конденсатора, и перестройка по частоте зависит от пределов изменения емкости. Ряд конденсаторов переменной емкости, выпускаемый промышленностью, довольно ограничен, поэтому для достижения необходимых границ параллельно и последовательно с КПЕ включают «растягивающие» конденсаторы.

КПЕ с «растягивающими» элементами.

Если имеется конденсатор с пределами изменения характеристик от 10 до 430 пФ, при подключении добавочных конденсаторов пределы изменения емкости получаются:

С1, пФ	С2, пФ	Новые пределы изменения, пФ
15	40	15..36
25	100	25..82

Знание свойств соединения емкостных элементов позволяет быстро анализировать процессы, происходящие в электрических схемах. Также понимание, как изменяются характеристики цепи при различных видах подключения, позволяет комбинировать имеющиеся элементы, создавая участки схем с новыми параметрами.

Physics for Science & Engineering II

5.7 Параллельное соединение конденсаторов из Office of Academic Technologies на Vimeo.

5.07 Параллельное соединение конденсаторов

Прежде чем мы подробно изучим, как мы соединяем конденсаторы в типичной электрической цепи, давайте введем некоторые символы для представления некоторых типичных компонентов электрической цепи. Мы собираемся изобразить источник питания, который может быть, например, батареей, солнечным элементом или генератором. Что обеспечивает электрическую потенциальную энергию цепи с этим символом. И большая линия или более длинная линия представляет собой положительную клемму источника питания, а меньшая — отрицательную клемму источника питания.

И мы собираемся представить направление, в котором заряд получает электрическую потенциальную энергию, стрелкой, которая всегда будет указывать от отрицательного вывода к положительному  выводу источника питания. И мы будем обозначать это через Эпсилон. И это называется ЭДС стрелки. И мы вернемся к важности этого направления, связанного с этой стрелкой, позже, когда будем изучать правила Кирхгофа. И, конечно же, мы будем использовать прямые линии, чтобы изобразить провода в электрической цепи.

И следующий компонент, который мы только что представили, это конденсаторы. И для этого мы будем использовать этот символ для обозначения конденсатора емкостью C. И мы собираемся использовать этот символ для обозначения переключателя в электрической цепи. А также подобным образом это будет представлять собой двухпозиционный переключатель в электрических цепях.

Хорошо. Когда мы смотрим на типы соединений компонентов типичной электрической цепи, мы видим два разных типа соединений. Один из них называется параллельным соединением; другой называется последовательным соединением. В случае параллельных соединений компоненты соединяются друг с другом таким образом, что разность потенциалов на каждом компоненте становится равной разности потенциалов других. А в случае последовательного соединения компоненты соединяются один за другим, как сцепки вагонов на одной и той же железной дороге. И в этом случае разность потенциалов по всей комбинации становится равной сумме разностей потенциалов по каждому компоненту в комбинации.

И эти соединения мы сейчас изучим на примере конденсаторов. Начнем, во-первых, с параллельного соединения конденсаторов. В этом случае конденсаторы соединены друг с другом таким образом, что разность потенциалов на каждом конденсаторе в комбинации или соединении становится равной разности потенциалов другого. Таким образом, конденсаторы соединены параллельно, если к каждому конденсатору приложена одинаковая разность потенциалов.

Пусть C1, C2 и C3 — 3 конденсатора. И мы соединяем эти конденсаторы параллельно таким образом, чтобы приложить к каждому из них одинаковую разность потенциалов, что мы и называем параллельным соединением. Если мы соединим концы соединения с клеммами источника питания таким образом, мы увидим, что источник питания будет генерировать V, вольты разности потенциалов. И давайте введем переключатель здесь. А когда мы подключаем переключатель s, то положительные заряды, сосредоточенные на плюсовой клемме источника питания, скажем, вот такой батареи, непрерывно отталкиваются друг от друга.

Следовательно, как только найдут этот доступный путь, то они будут двигаться по этому пути и придут к такой точке, в которой увидят три возможных пути для движения. И, скажем, если с положительной клеммы этого источника питания снимается q количество зарядов, эти положительные заряды движутся по этому пути, и всякий раз, когда они приходят в эту точку, где они видят три доступных пути, какая-то часть их будет двигаться. пройти первый путь и собраться на, скажем, левой пластине конденсатора С1 в качестве заряда q1.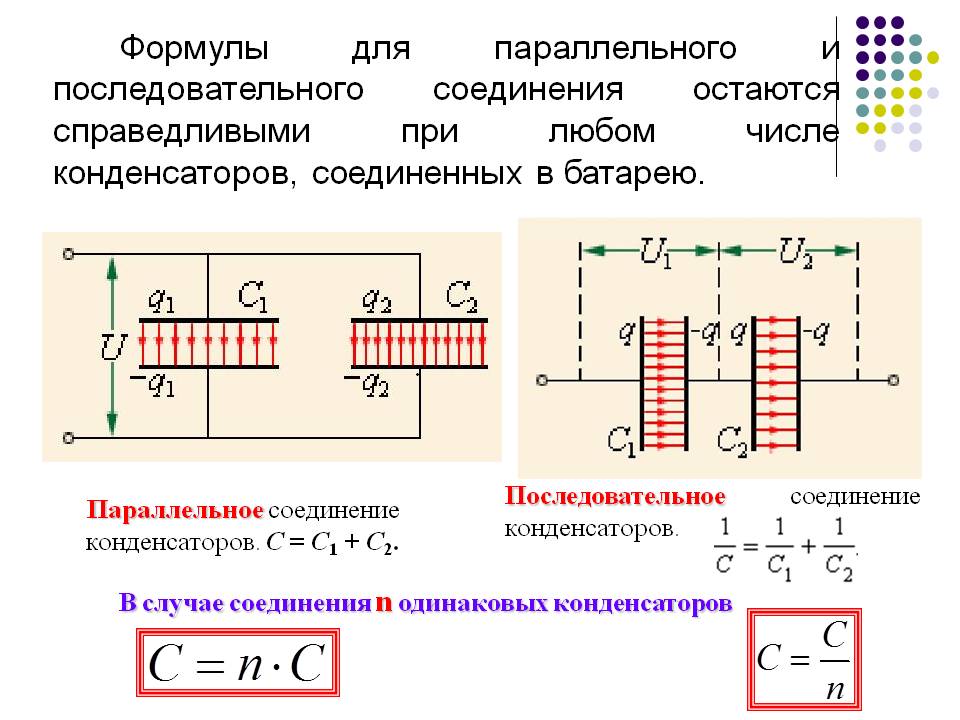 И тогда какая-то дробь пройдет по этому доступному второму пути и соберется на опять же левой пластине этого конденсатора С2 номиналом q2. А затем оставшиеся из них пройдут по этому доступному пути и соберутся через эту пластину конденсатора емкостью С3 на величину, скажем, q3.

Аналогично, отрицательные заряды отталкиваются друг от друга на отрицательной клемме источника питания, и как только переключатель s будет замкнут, у нас будет свободный путь для их прохождения по этому пути. И тогда какая-то их часть пройдет по этому пути и соберется на этом выводе конденсатора С1 как минус q1. Другая фракция пройдет по этому пути и соберется здесь как минус q2. А оставшаяся часть пройдет по этому пути и соберется в правой пластине конденсатора С3 как минус q3.

Этот процесс зарядки будет продолжаться до тех пор, пока мы не достигнем достаточно высокого заряда на пластинах этих конденсаторов, чтобы они создавали достаточно сильную силу отталкивания для поступающих зарядов. И в это время процесс зарядки остановится и конденсаторы будут полностью заряжены.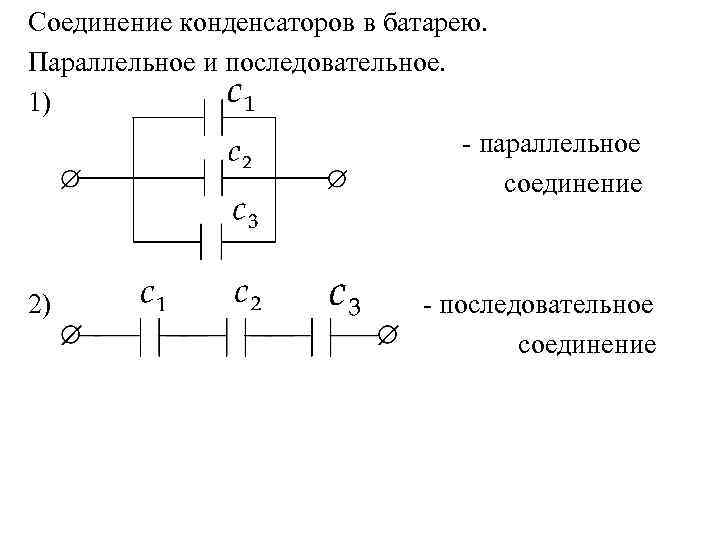 Что ж, поскольку основное свойство параллельного соединения состоит в том, что разность потенциалов на каждом компоненте, в данном случае на каждом конденсаторе, становится равной разности потенциалов при параллельном соединении, мы можем сказать, что если мы назовем емкость или разность потенциалов на C1 как V1 вольт, на C2 как V2 вольт и на C3 как V3 вольт. Первым свойством параллельного соединения становится V1 равно V2, что равно V3. И в этой конкретной схеме все они будут равны любой разности потенциалов, создаваемой источником питания или этой батареей, В вольт.

Прибор, измеряющий разность потенциалов между двумя точками, называется вольтметром. И для этого мы собираемся использовать этот символ. Вольтметр: прибор, измеряющий разность потенциалов между двумя точками. А чтобы измерить разность потенциалов между двумя точками, мы всегда подключаем вольтметр параллельно этим интересующим точкам. Другими словами, если вы хотите измерить, например, разность потенциалов между выводами блока питания, мы подключаем наш вольтметр к этим интересующим точкам параллельно, вот так, и, следовательно, он измеряет разность потенциалов между этими конец и другой конец.

Следовательно, если взять вольтметр, подключить к этим точкам, он даст нам разность потенциалов между этими двумя точками. Затем мы можем взять их, клеммы вольтметра, и подключить их к комбинации между этими двумя точками, мы все равно будем считывать V вольт, какой бы ни была разность потенциалов, генерируемая этой батареей. И тогда, если взять выводы вольтметра, соединить поперек обкладки конденсатора С1, мы снова будем считывать то же самое напряжение. И если мы проделаем то же самое на C2, опять же, мы получим точно такое же напряжение, а на C3 мы получим ту же самую разность потенциалов. Это указывает на то, что первое важное свойство параллельной комбинации состоит в том, что разность потенциалов на каждом конденсаторе в параллельной комбинации или соединении будет равна друг другу. Ну, это напрямую связано с принципом сохранения энергии, так как мы знаем, что потенциал связан с потенциальной энергией, которая представляет собой потенциальную энергию на единицу заряда. И когда мы соединяем конденсаторы параллельно, в этой форме мы в основном применяем одинаковую разность потенциалов к каждому конденсатору.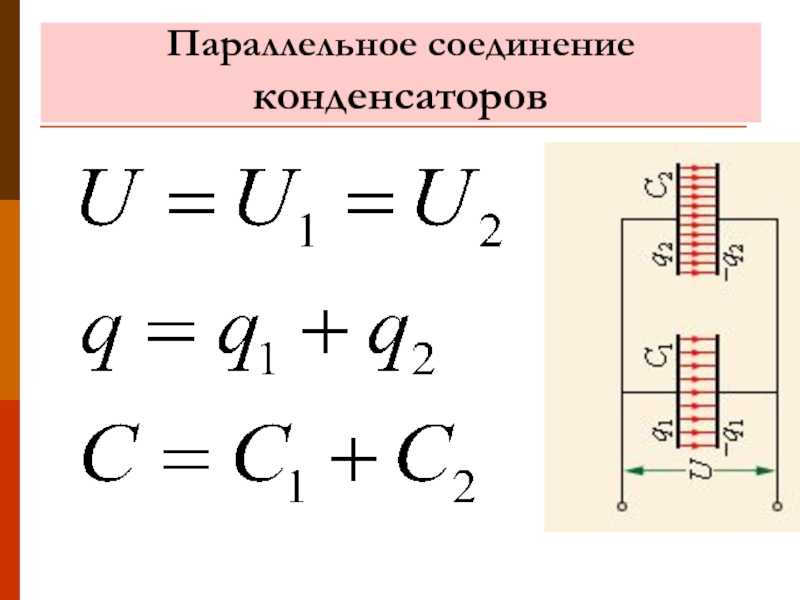

Второе свойство будет связано с принципом сохранения заряда. Когда мы включаем переключатель, это соединение будет получать заряд q от источника питания, от этой батареи, которая генерирует V вольт разности потенциалов между ее клеммами. Затем эти заряды приходят сюда и видят три доступных пути в этой цепи. Затем некоторая часть пройдет по этому первому пути, некоторая часть пройдет по второму пути, а оставшаяся часть пройдет по третьему пути и сохранится на конденсаторе C1 как q1, на C2 как q2 и на C3 как q3. Таким образом, принцип сохранения заряда будет утверждать, что количество заряда, полученного от этого источника питания, будет равно сумме зарядов, хранящихся в пластинах этих конденсаторов. Другими словами, q1 плюс q2 плюс q3 будут равны общему заряду, полученному от источника питания.

Хорошо. Теперь предположим, что мы хотели бы упростить эту схему, просто заменив все эти три конденсатора, соединенные параллельно, одним конденсатором. Таким образом, этот единственный конденсатор будет выполнять ту же работу, что и эти три при параллельном соединении. В этом случае, заменив эти три конденсатора одним, наша схема будет упрощена до этой формы.

Вот тот же блок питания, вырабатывает V вольт разности потенциалов, а вот наш ключ, s, а вот конденсатор, который мы заменяем все эти три. И назовем емкость конденсатора эквивалентной С. Другими словами, эквивалент этих трех конденсаторов в параллельной форме. Что ж, для того, чтобы эта новая схема выполняла ту же работу, что и эти три конденсатора при параллельном соединении, когда мы замкнем переключатель s здесь, она должна забрать такое же количество заряда q из этого источника питания, из этой батареи. Следовательно, количество заряда, которое будет храниться на месте этого конденсатора, будет таким же, q, которое было получено в предыдущей схеме.

Ну, если вспомнить, допустим, здесь свойство три, если вспомнить определение емкости, то она равнялась количеству заряда, величине заряда, хранящегося в месте конденсатора q, деленному на разность потенциалов между обкладками конденсатора. И мы легко можем видеть, что разность потенциалов на пластинах этого конденсатора будет такой же разностью потенциалов, что и эта батарея. Другими словами, если мы просто подключим снова наш вольтметр к клеммам этой батареи, мы будем читать V вольт, а затем, если мы снова подключим наш вольтметр параллельно, через пластины этого конденсатора, мы будет читать точно такое же напряжение. Таким образом, эквивалент C будет равен q над V.

Итак, если мы найдем q из этого уравнения, оно будет равно эквивалентному C, умноженному на V. Точно так же мы можем выразить количество заряда, хранящегося на C1, которое было определено как q1, и оно будет равно емкость конденсатора С1, умноженная на разность потенциалов между обкладками конденсатора С1. Но, поскольку V1 было равно V по первому свойству, мы можем выразить это как C1, умноженное на V. Аналогично, q2 будет равно C2, умноженному на V2. И снова V2 равно V, что будет равно C2, умноженному на V вольт. И q3 будет равно C3, умноженному на V3, что снова даст нам, поскольку V3 также равно V вольтам, C3, умноженному на V.

Теперь, исходя из второго свойства, а именно: q равно q1 плюс q2 плюс q3, мы можем выразить q1 через емкость и разность потенциалов как C1, умноженное на V, плюс на q2, C2, умноженное на V, плюс на q3, C3. умножить на V. Аналогично, q можно выразить через эквивалентную емкость и разность потенциалов на одной из пластин этого конденсатора как эквивалент C, умноженный на V. Поскольку напряжение на каждом члене одинаково, мы можем разделить обе части на V И, следовательно, мы приходим к выражению, что C-эквивалент равен C1 плюс C2 плюс C3.

Теперь мы можем легко обобщить это соотношение для N параллельных конденсаторов. Эквивалент C будет равен C1 плюс C2 плюс C3 плюс C sub N. Или, в компактной форме, мы можем записать это как суммирование по I от 1 до N C sub I. Это соотношение показывает нам, что при подключении конденсаторов параллельно, тогда эквивалентная емкость цепи становится суммой емкостей каждого отдельного конденсатора в соединении. другими словами, общая емкость цепи увеличивается.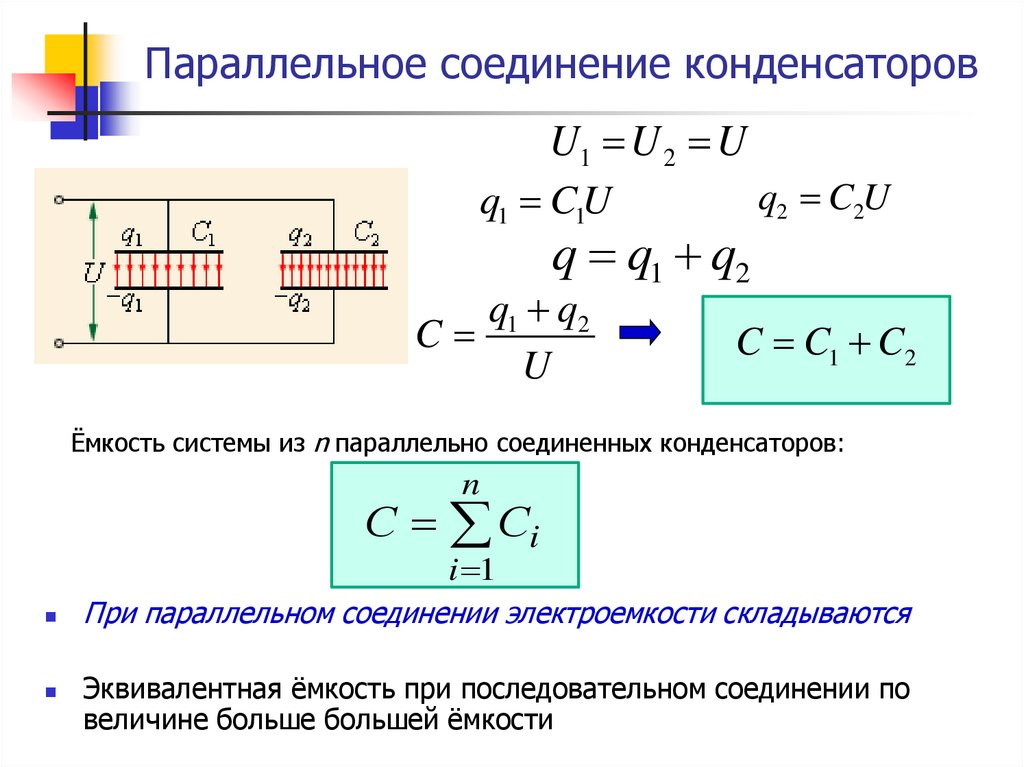

3.6 Конденсаторы, включенные последовательно и параллельно – Колледж Дугласа, физика 1207

Глава 3 Электрический потенциал и электрическое поле

Резюме

• Выведите выражения для полной емкости при последовательном и параллельном подключении.
• Определите последовательное и параллельное соединение конденсаторов.
• Вычислите эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0075 серии и параллельно , для которых мы можем легко рассчитать общую емкость.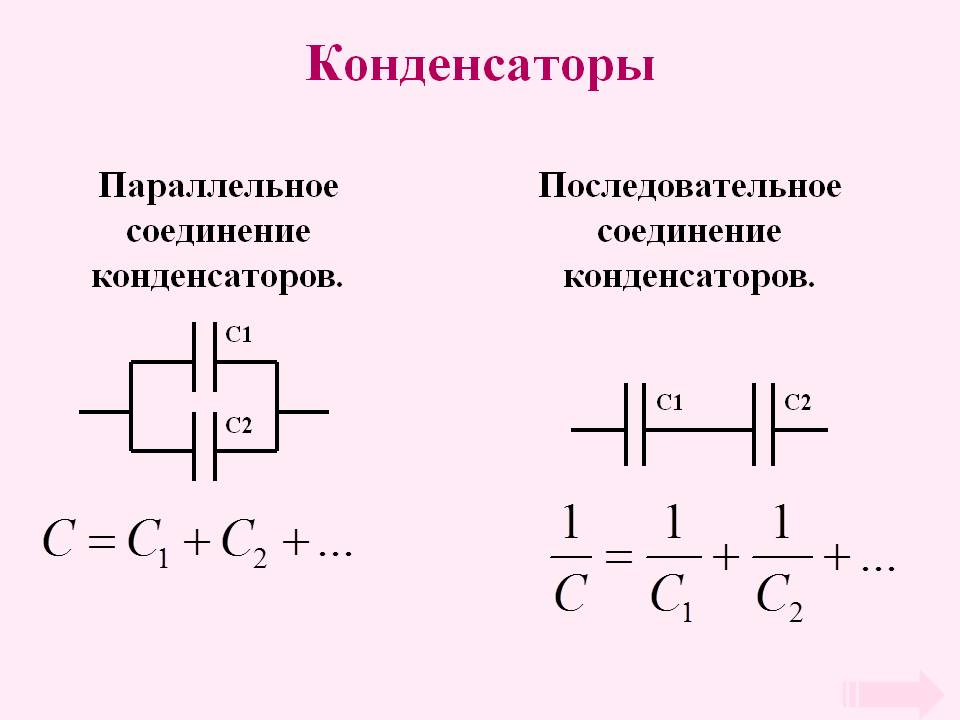 Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.

На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением как C = Q/V.

Обратите внимание на рисунок 1, что противоположные заряды величиной

Q протекают по обеим сторонам первоначально незаряженной комбинации конденсаторов, когда приложено напряжение В  . Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рисунок 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q

. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение C = Q/V вместо V дает V = C / Q . Таким образом, напряжения на отдельных конденсаторах равны . Общее напряжение представляет собой сумму отдельных напряжений:

В = В ₁ + В ₂ + В ₃  

Теперь, назвав общую емкость C _{ряд ​​} = C _с   для последовательной емкости, учтем, что

Ввод выражений для V ₁ ,  V ₂    , и V ₃ получаем

Отменяя Q s , мы получаем уравнение для полной емкости в ряду

C  равной

, где «…» означает, что выражение справедливо для любого количества последовательно соединенных конденсаторов.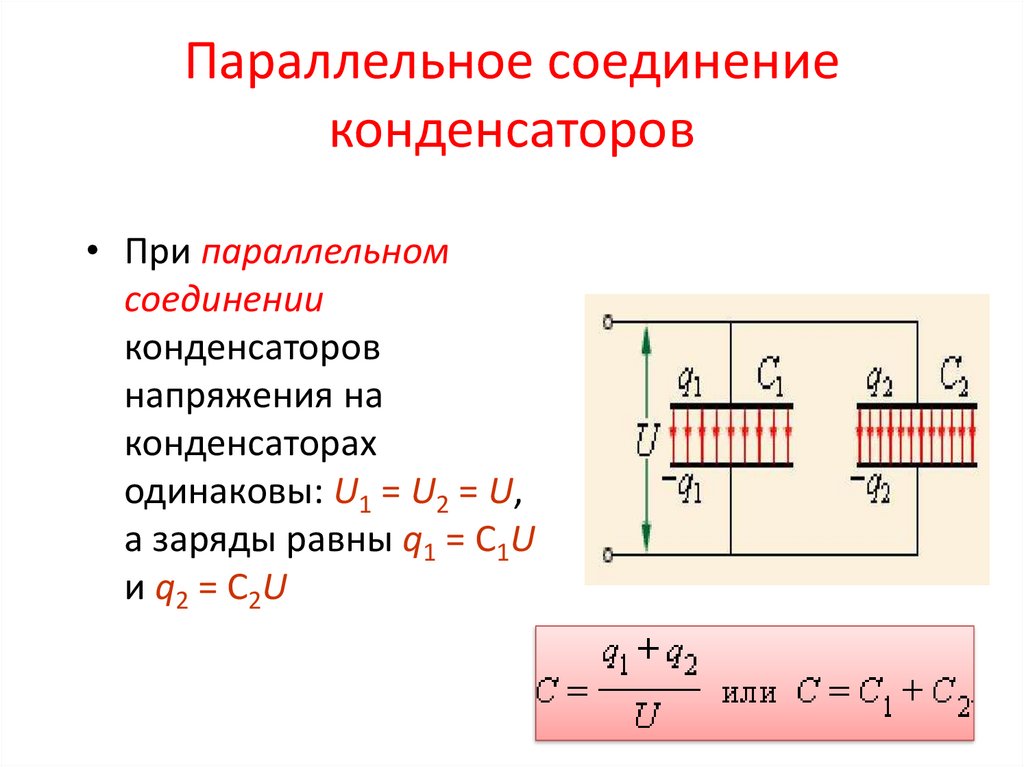 Выражение этой формы всегда приводит к тому, что общая емкость C меньше любой из отдельных емкостей C ₁ , C ₂ , C ₃ , …, как показано в следующем примере.

Общая емкость последовательно,

C _с

Суммарная емкость последовательно:

Пример 1: Что такое последовательная емкость?

Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 мкФ.

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.

Решение

Ввод заданных емкостей в выражение для дает .

Инвертирование для нахождения

C _серии или C _s дает .

Обсуждение

Суммарная последовательная емкость C _с меньше наименьшей отдельной емкости, как и было обещано.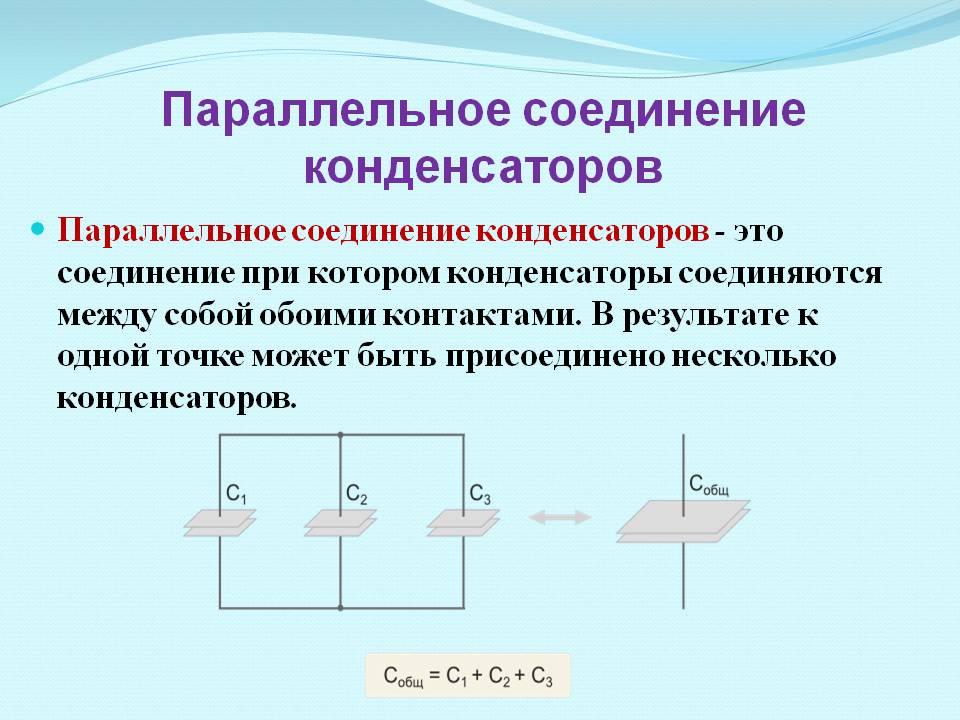 При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,

так что

На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C _{параллельно} или C

p , сначала заметим, что напряжение на каждом конденсаторе равно В , такое же, как и у источника, так как они подключены непосредственно к нему через дирижер. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q — это сумма отдельных сборов:

 Q = Q ₁  + Q ₂  + Q ₃

Рисунок 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.

Использование связи Q = CV , мы видим, что общий заряд составляет Q _Всего = C _P V , а индивидуальные сборы — Q ₁ = C ₁ V , Q _2. = C ₂ V , и Q ₃ = C ₃ V . Ввод их в предыдущее уравнение дает

Q _всего = Q ₁  + Q ₂  + Q ₃

C _p V = C ₁  V+ C ₂  V+ C ₃ V

С _р   = С ₁  + С ₂  + С ₃

Вычеркивая из уравнения В , получаем уравнение для полной емкости параллельно C

p :

С _р   = С ₁  + С ₂  + С ₃  + ….

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … » указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы

C _p   = C ₁  + C ₂  + C ₃   = 1,000 мкФ + 5,000 мкФ + 8,000 мкФ = 14,000 4 мкФ 9000

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рис. 2(b).

Суммарная емкость при параллельном включении,

C _p 

Суммарная емкость при параллельном подключении C _p

  = C ₁  + C _{2 +} 1 + 4 C 901

Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.

Рис. 3. (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ расположены последовательно; их эквивалентная емкость C _S меньше любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ . Таким образом, общая емкость равна сумме C _S и C ₃ .

Смесь последовательных и параллельных емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке выше. Рисунок 3. Предположим, что емкости известны с точностью до трех знаков после запятой. + C ₂  + C ₃   = 1,000 мкФ + 5,000 мкФ + 8,000 мкФ = 14,000 мкФ

C _стр. = C ₁ + C ₂ + C ₃ = 1,000 мкф + 5,000 мкф + 8,000 мкФ = 14,000 мкф

C ₁ = 1.000 µF, C _{2 = 5.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000114 = 1.000 μF, C 2 = 5.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 1 . 3 =} 8 000 мкФ. Округлите ответ до трех знаков после запятой.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы C ₁ и C ₂ включены последовательно. Их комбинация, Cs  на рисунке параллельно C ₃ .

Решение

Поскольку C ₁ и C ₂ соединены последовательно, их общая емкость определяется как .