Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы использовать для вычисления токов и напряжений. Чем отличается параллельное соединение от последовательного.

Что такое параллельное соединение резисторов

Параллельное соединение резисторов — это такой способ подключения, при котором все выводы резисторов соединяются в двух общих точках схемы. При этом напряжение на всех резисторах одинаковое, а токи через них могут отличаться.

Основные характеристики параллельного соединения:

• Напряжение на всех резисторах одинаковое
• Общий ток равен сумме токов через отдельные резисторы
• Общее сопротивление всегда меньше сопротивления наименьшего из резисторов

Формула расчета общего сопротивления при параллельном соединении

Для расчета общего сопротивления при параллельном соединении используется следующая формула:

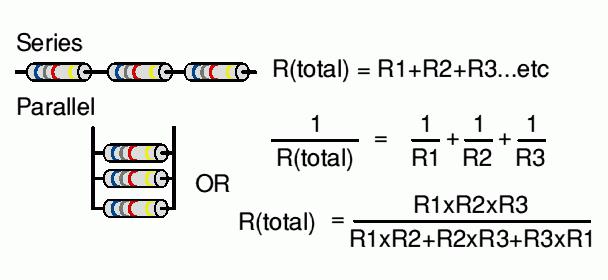
1/R = 1/R1 + 1/R2 + 1/R3 + …

Где R — общее сопротивление, R1, R2, R3 — сопротивления отдельных резисторов.

Для двух резисторов формула упрощается:

R = (R1 * R2) / (R1 + R2)

Расчет токов в параллельной цепи

Как рассчитать токи, протекающие через отдельные резисторы при параллельном соединении? Для этого используется закон Ома:

I = U / R

Где I — ток через резистор, U — напряжение (одинаковое для всех резисторов), R — сопротивление конкретного резистора.

Общий ток в цепи равен сумме токов через все резисторы:

I_общ = I1 + I2 + I3 + …

Особенности параллельного соединения резисторов

Какие еще важные моменты нужно знать о параллельном соединении резисторов?

• Общее сопротивление всегда меньше сопротивления наименьшего резистора в цепи
• Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
• При одинаковых резисторах общее сопротивление равно R/n, где n — количество резисторов
• Параллельное соединение позволяет увеличить мощность резисторов

Сравнение параллельного и последовательного соединения

Чем отличается параллельное соединение резисторов от последовательного?

Параметр	Параллельное	Последовательное
Напряжение	Одинаковое на всех резисторах	Сумма напряжений на резисторах
Ток	Сумма токов через резисторы	Одинаковый через все резисторы
Общее сопротивление	Меньше наименьшего	Сумма всех сопротивлений

Примеры расчетов параллельного соединения

Рассмотрим несколько примеров расчета параллельного соединения резисторов:

Пример 1: Два резистора

Дано: R1 = 100 Ом, R2 = 200 Ом

Решение: R = (R1 * R2) / (R1 + R2) = (100 * 200) / (100 + 200) = 66.7 Ом

Пример 2: Три резистора

Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом

Решение: 1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183

R = 1 / 0.183 = 5.46 Ом

Применение параллельного соединения резисторов

Где используется параллельное соединение резисторов на практике?

• Для получения нестандартных номиналов сопротивлений
• В делителях напряжения
• Для увеличения мощности резисторов
• В схемах регулировки яркости светодиодов
• В измерительных мостовых схемах

Расчет мощности при параллельном соединении

Как рассчитать мощность при параллельном соединении резисторов? Общая мощность равна сумме мощностей на отдельных резисторах:

P_общ = P1 + P2 + P3 + …

Мощность на каждом резисторе рассчитывается по формуле:

P = U^2 / R

Где U — напряжение (одинаковое для всех резисторов), R — сопротивление конкретного резистора.

При параллельном соединении одинаковых резисторов общая мощность увеличивается пропорционально их количеству.

«` import React, { useState } from ‘react’; import { Input, Button, Table } from ‘@/components/ui’; const ParallelResistorsCalculator = () => { const [resistors, setResistors] = useState([», »]); const [result, setResult] = useState(null); const addResistor = () => { setResistors([…resistors, »]); }; const handleResistorChange = (index, value) => { const newResistors = […resistors]; newResistors[index] = value; setResistors(newResistors); }; const calculateParallel = () => { const validResistors = resistors.filter(r => r !== » && !isNaN(r)); if (validResistors.length < 2) { setResult('Необходимо ввести минимум два значения'); return; } const sum = validResistors.reduce((acc, r) => acc + 1 / parseFloat(r), 0); const totalResistance = 1 / sum; setResult(`Общее сопротивление: ${totalResistance.toFixed(2)} Ом`); }; return ( ); }; export default ParallelResistorsCalculator; «`

Этот калькулятор поможет быстро рассчитать общее сопротивление при параллельном соединении нескольких резисторов. Просто введите значения сопротивлений и нажмите «Рассчитать».

Часто задаваемые вопросы о параллельном соединении резисторов

Почему общее сопротивление при параллельном соединении уменьшается?

При параллельном соединении у тока появляется несколько путей протекания. Это аналогично расширению русла реки — чем шире русло, тем меньше сопротивление течению воды. Поэтому общее сопротивление уменьшается при добавлении параллельных ветвей.

Как изменится ток при добавлении параллельного резистора?

При добавлении параллельного резистора общий ток в цепи увеличится. Это происходит потому, что общее сопротивление уменьшается, а напряжение остается прежним. По закону Ома, уменьшение сопротивления при постоянном напряжении приводит к увеличению тока.

Можно ли соединять параллельно резисторы разной мощности?

Да, можно соединять параллельно резисторы разной мощности. Однако нужно учитывать, что ток распределится между ними неравномерно. Через резистор с меньшим сопротивлением будет протекать больший ток. Поэтому важно следить, чтобы мощность рассеивания каждого резистора не была превышена.

Параллельное соединение резисторов — важный инструмент в электротехнике, позволяющий гибко управлять параметрами электрических цепей. Понимание принципов расчета и особенностей такого соединения поможет грамотно проектировать и анализировать различные схемы.

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.

Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

www.joyta.ru

Параллельное соединение резисторов. Расчеты общего сопротивления, общей мощности. :: SYL.ru

Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала. Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов. О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

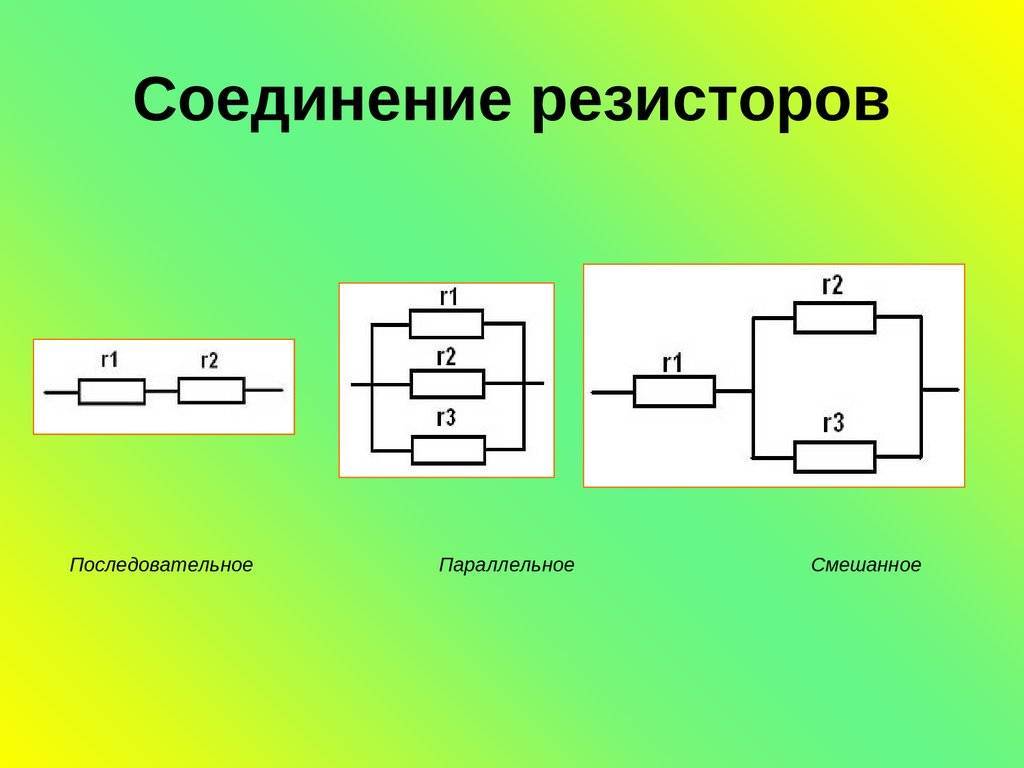
Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи. При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам. Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

На фотографии можно увидеть параллельное подключение резисторов.

Ниже представлена принципиальная схема параллельного соединения резисторов.

Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:

R(общ)=1/(1/R1+1/R2+1/R3+1/R n).

Где:

— R(общ) – общее сопротивление;

— R1, R2, R3 и Rn – параллельно подключенные резисторы.

Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:

R(общ)=R1*R2/R1+R2.

Где:

— R(общ) – общее сопротивление;

— R1, R2 – параллельно подключенные резисторы.

В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:

R(общ)=R1\n.

Где:

— R(общ) – общее сопротивление;

— R – номинал параллельно подключенного резистора;

— n – количество соединенных элементов.

Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.

Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью. В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением. Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

www.syl.ru

Последовательное соединение резисторов. Схема соединения и примеры расчета

Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.

Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.

Последовательное соединение резисторов

На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:

R = R1 + R2 + R3

То есть, в нашем случае общее сопротивление цепи будет равно:

R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм

Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.

Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.

Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).

Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:

Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:

В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.

В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:

Пример № 1

Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:

Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:

Пример № 2

Необходимо рассчитать падение напряжения на выводах «А» и «В»:

а) без подключенного резистора R3

б) с подключенным резистором R3

Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.

Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).

www.joyta.ru