Как рассчитать общее сопротивление при параллельном соединении трех резисторов. Какие преимущества дает параллельное подключение резисторов. Как изменяется сила тока и напряжение при параллельном соединении. Где применяется параллельное соединение резисторов на практике.
Основные принципы параллельного соединения резисторов
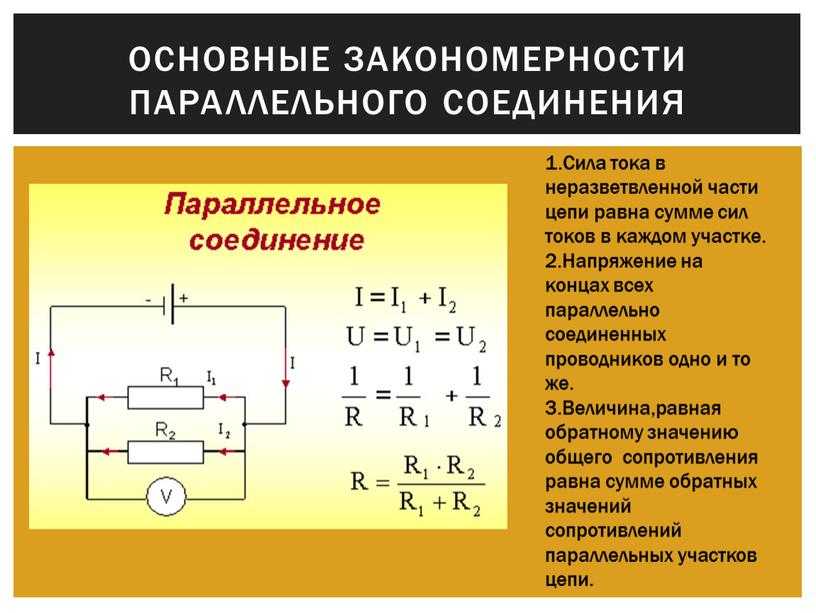
Параллельное соединение резисторов — это способ подключения, при котором все резисторы присоединяются своими выводами к одним и тем же двум точкам цепи. Давайте рассмотрим основные характеристики такого соединения:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов, протекающих через каждый резистор
- Общее сопротивление цепи меньше сопротивления любого из параллельно соединенных резисторов
Как это работает на практике? Представьте, что у вас есть три параллельные дороги между двумя городами. Транспортный поток (ток) распределяется по всем дорогам, что уменьшает общее «сопротивление» движению. При этом расстояние (напряжение) между городами остается неизменным для всех маршрутов.
Формула расчета общего сопротивления при параллельном соединении
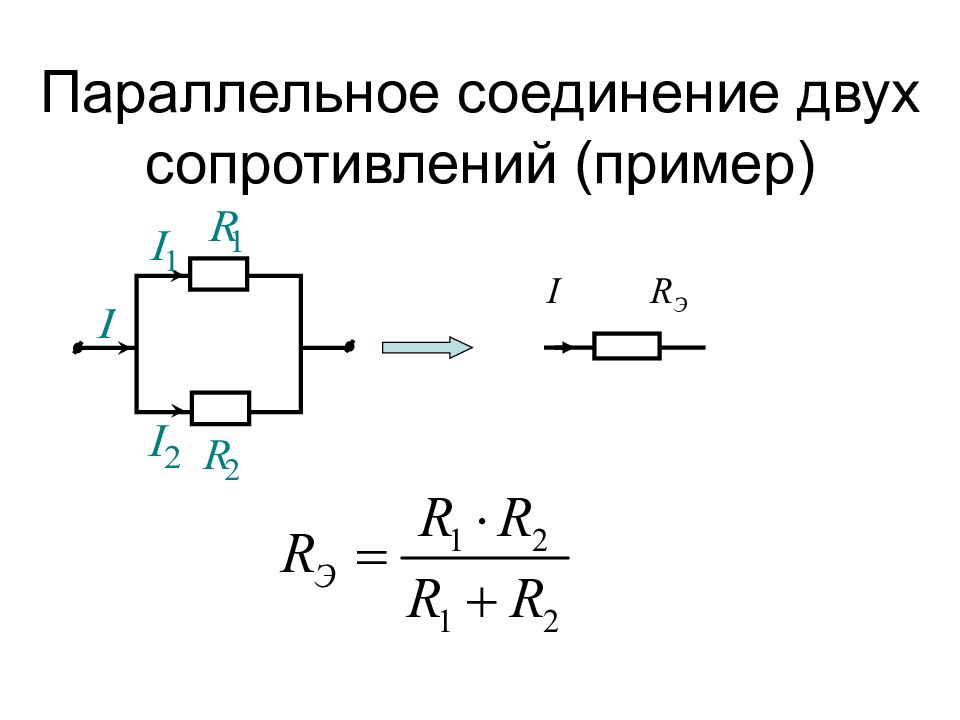
Для расчета общего сопротивления при параллельном соединении трех резисторов используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3
где R — общее сопротивление, а R1, R2, R3 — сопротивления отдельных резисторов.
Как применить эту формулу на практике? Рассмотрим пример:
Даны три резистора: R1 = 6 Ом, R2 = 3 Ом, R3 = 2 Ом. Рассчитаем общее сопротивление:
1/R = 1/6 + 1/3 + 1/2 = 0.167 + 0.333 + 0.5 = 1
R = 1 / 1 = 1 Ом
Таким образом, общее сопротивление параллельно соединенных резисторов составляет 1 Ом.
Особенности распределения тока при параллельном соединении
При параллельном соединении резисторов ток распределяется обратно пропорционально их сопротивлениям. Как это работает?
- Через резистор с меньшим сопротивлением протекает больший ток
- Через резистор с большим сопротивлением протекает меньший ток
- Общий ток равен сумме токов через все резисторы
Какое практическое значение имеет такое распределение тока? Это позволяет создавать цепи с разным потреблением тока на разных участках, что важно, например, в системах освещения или электропитания различных устройств.
Преимущества параллельного соединения резисторов
Почему иногда предпочтительно использовать параллельное, а не последовательное соединение резисторов? Давайте рассмотрим основные преимущества:
- Уменьшение общего сопротивления цепи
- Возможность подключения нагрузок с разным сопротивлением к одному источнику питания
- Повышение надежности цепи (при выходе из строя одного резистора остальные продолжают работать)
- Возможность регулировки общего сопротивления добавлением или удалением параллельных ветвей
Как это применяется на практике? Например, в системах электроснабжения зданий все электроприборы подключаются параллельно. Это позволяет каждому устройству получать необходимое напряжение независимо от работы других приборов.
Расчет мощности при параллельном соединении резисторов
При параллельном соединении резисторов важно правильно рассчитывать мощность. Как это сделать?
- Рассчитайте общее сопротивление цепи
- Определите общий ток в цепи: I = U / R, где U — напряжение источника
- Рассчитайте мощность: P = U * I
Почему это важно? Правильный расчет мощности позволяет подобрать источник питания соответствующей мощности и избежать перегрузки цепи.

Применение параллельного соединения резисторов в электронике
Где на практике используется параллельное соединение резисторов? Рассмотрим несколько примеров:
- В делителях напряжения для создания различных уровней напряжения
- В схемах защиты от перенапряжения
- В измерительных приборах для расширения диапазона измерений
- В усилителях для регулировки коэффициента усиления
- В системах электропитания для распределения нагрузки
Как это работает, например, в делителе напряжения? Параллельно соединенные резисторы позволяют получить несколько уровней напряжения от одного источника, что часто требуется в сложных электронных схемах.
Сравнение параллельного и последовательного соединения резисторов
Чем отличается параллельное соединение от последовательного? Давайте сравним:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Меньше наименьшего из резисторов | Сумма всех сопротивлений |
| Напряжение | Одинаково на всех резисторах | Сумма напряжений на резисторах равна общему напряжению |
| Ток | Сумма токов через резисторы равна общему току | Одинаков во всей цепи |
Какое значение имеют эти различия? Они позволяют выбирать оптимальный способ соединения резисторов в зависимости от требований к параметрам цепи — напряжению, току или общему сопротивлению.
Практические советы по использованию параллельного соединения резисторов
Как правильно использовать параллельное соединение резисторов в реальных схемах? Вот несколько полезных советов:
- Используйте резисторы с одинаковой мощностью для равномерного распределения нагрузки
- Учитывайте допуски резисторов при расчетах
- Проверяйте общую мощность цепи, чтобы не превысить допустимые значения
- Используйте параллельное соединение для точной подгонки сопротивления
- При большом количестве параллельных резисторов учитывайте возможность взаимного нагрева
Почему эти советы важны? Они помогают создавать надежные и эффективные схемы, избегая типичных ошибок проектирования.
Параллельное соединение резисторов — какие есть преимущества
Параллельное соединение резисторов – это способ подключения двух или более электронных компонентов к двум выводам (таким, как резисторы, конденсаторы, катушки индуктивности или дроссели) таким образом, что одна ветвь всех компонентов ведет к одному узлу, а другая – к другому узлу.
Таким образом можно комбинировать любое количество элементов. Ключ к этой связи в том, что напряжение на каждом из элементов одинаковое. Примером параллельного соединения является, например, пара конденсаторов (керамический и электролитический), которые часто устанавливаются рядом с линиями электропередач.
Оглавление
- 1 Параллельное соединение резисторов
- 2 Когда последовательное, а когда параллельное соединение
- 3 Можно ли параллельно подключить другие элементы
- 4 Как выбрать резистор для диода? Различные способы питания светодиодов
- 5 Параллельное подключение: преимущества
- 5.
 0.1 Пожалуйста, оцените это
0.1 Пожалуйста, оцените это
- 5.
Параллельное соединение резисторов
На схеме ниже показан пример параллельного соединения резисторов. Как описано выше, каждый резистор подключается к следующему в двух местах. При параллельном подключении резисторов их сопротивление не складывается, наоборот, уменьшается.
Когда последовательное, а когда параллельное соединение
Также необходимо помнить, что при параллельном включении резисторов результирующее сопротивление уменьшается. Более того, подключив несколько резисторов, мы получим эквивалентное сопротивление, которое будет ниже, чем сопротивление, создаваемое «самым маленьким» из резисторов. Это явление полезно, когда у нас есть только резисторы с высоким сопротивлением, и нам нужно получить более низкое сопротивление. Такие приемы часто полезны на этапе создания прототипов, например, на макете. Для быстрой работы с проводами будет нужным знать как обращаться с индикатором.
Можно ли параллельно подключить другие элементы
Конечно, таким образом можно комбинировать и многие другие элементы, такие как катушки и дроссели. Теоретически вы также можете комбинировать светодиоды, но этот метод не рекомендуется, потому что вы можете легко повредить светодиоды.
Теоретически вы также можете комбинировать светодиоды, но этот метод не рекомендуется, потому что вы можете легко повредить светодиоды.
Как выбрать резистор для диода? Различные способы питания светодиодов
Диоды используются во многих проектах. К сожалению, не все могут выбрать резистор для светодиода или вообще его проигнорировать. Также стоит знать, что можно даже подключать параллельно элементы с более чем двумя контактами (например, транзисторы). Но иногда это требует дополнительных требований, таких как добавление резисторов для выравнивания токов.
Описанное подключение – один из первых вопросов, который следует освоить при изучении азов электроники. Это полезно при построении различных электронных схем, но также может быть полезно, когда нам не хватает необходимых элементов, например, резистора с сопротивлением 3 кОм. Подключив несколько элементов с более высоким сопротивлением, мы легко получим резистор меньшего размера. Можем сделать то же самое и при отсутствии подходящего конденсатора.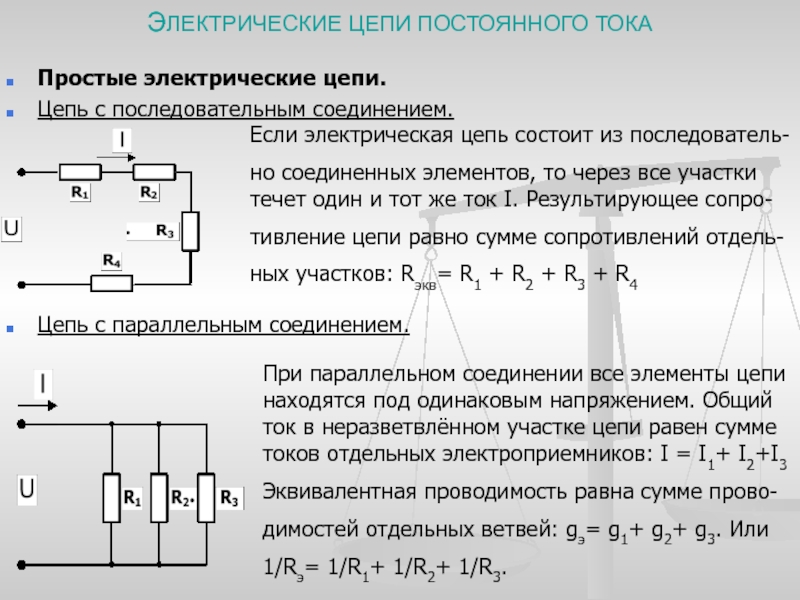 Советы и решение проблем с реле, контакторами и датчиками.
Советы и решение проблем с реле, контакторами и датчиками.
Параллельное подключение: преимущества
Когда подключаем приемники последовательно, ток течет через каждый из них по очереди. Параллельное соединение характеризуется тем, что, помимо основной цепи каждое из подключенных устройств имеет свой собственный шлейф. Если его прервать, ток просто обойдет сломанную нагрузку. Конечно, для предотвращения короткого замыкания всей цепи требуется предохранитель. Кроме того, каждый из приемников может иметь свой переключатель, что было бы невозможно в случае последовательного подключения.
Каждый приемник имеет информацию о подходящем для него напряжении. Если подать слишком низкое напряжение, устройство работать не будет. Если он будет слишком высоким, приемник может быть поврежден. При последовательном соединении напряжение на каждом из элементов меняется в зависимости от их количества. Например, если мы подключим 3 одинаковых диода в цепь с аккумулятором на 1,5 В, то напряжение на каждом из них будет 0,5 В. Однако достаточно отключить два из них. Затем с последним диодом напряжение увеличится до 1,5 В. Но при параллельном подключении напряжение не изменится (независимо от количества приемников будет 1,5 В) и нам не о чем беспокоиться.
Однако достаточно отключить два из них. Затем с последним диодом напряжение увеличится до 1,5 В. Но при параллельном подключении напряжение не изменится (независимо от количества приемников будет 1,5 В) и нам не о чем беспокоиться.
Параллельное соединение также может использоваться для батарей или аккумуляторов. Благодаря этому мы получим большую мощность при сохранении своего напряжения. Вам просто нужно соединить положительные полюса вместе, а затем сделать это самостоятельно с отрицательными. Таким образом, если мы используем две батареи с напряжением 12 В и емкостью 18 Ач, получим батарею с емкостью 36 Ач и напряжением 12 В. Однако будьте осторожны при увеличении емкости. Слишком высокая сила тока приведет к тому, что кабели поглотят большое количество энергии, превратив ее в тепло, которое расплавит кабели.
Пожалуйста, оцените это
Поставить оценку
RadioStudy — сайт кружка радиоэлектроники ЦТТ «Охта» | Электротехника
Теперь мы знаем, что есть такой элемент — резистор. Значит — уже можем составлять электрические схемы, по-всякому их соединяя.
Давайте, разберёмся, как же можно соединять резисторы, и что из этого
получается.
Значит — уже можем составлять электрические схемы, по-всякому их соединяя.
Давайте, разберёмся, как же можно соединять резисторы, и что из этого
получается.
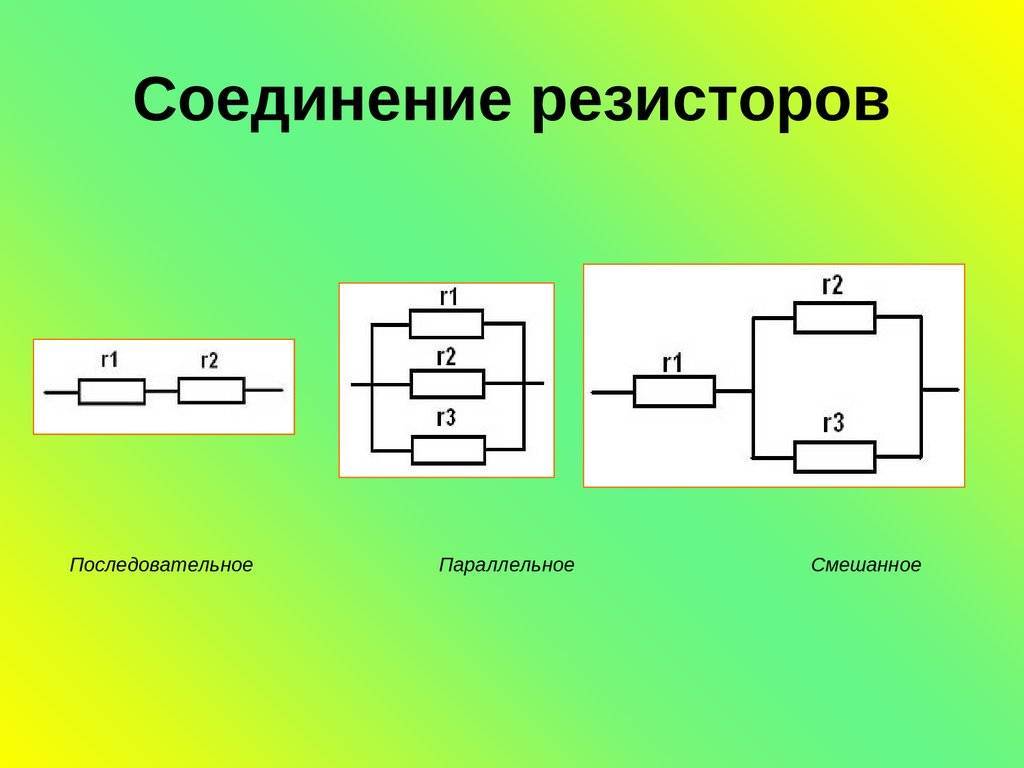
Существует 3 вида соединения резисторов: последовательное, параллельное и смешанное. Рассмотрим подробнее первые два, так как третий вид является всего лишь их сочетанием.
Любую схему, состоящую из нескольких резисторов и имеющую только два выхода, можно заменить на один резистор.
При этом, сопротивление резистора должно быть равно сопротивлению заменяемой схемы. Такое сопротвление называется эквивалентным сопротивлением схемы Rэкв. Для каждого случая соединений, Rэкв рассчитывается по своей формуле.
4.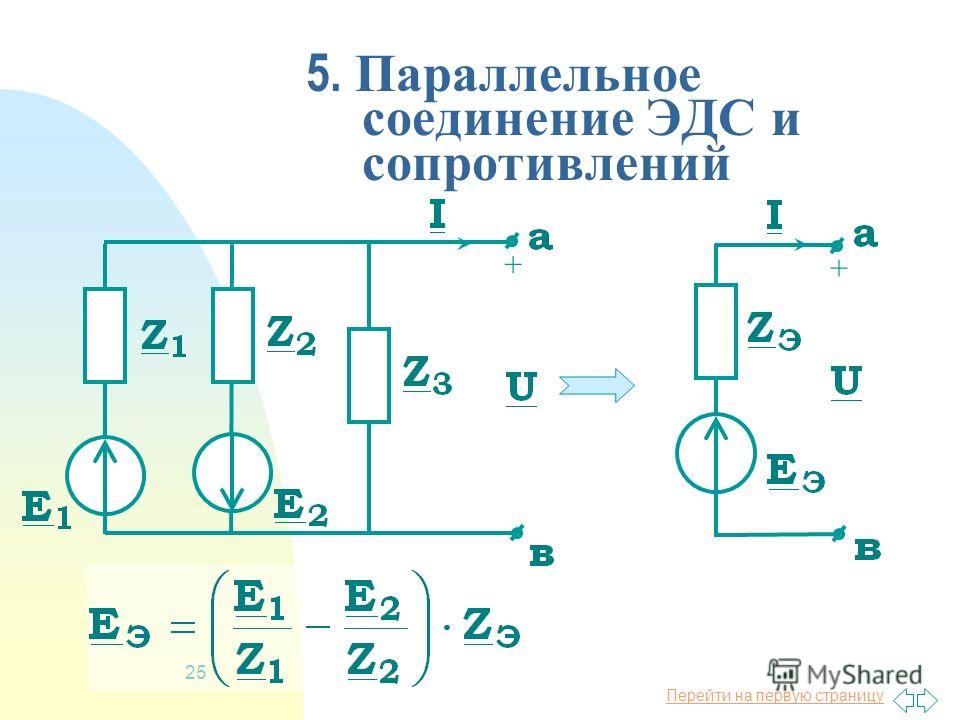 1 Последовательное соединение. 1 Последовательное соединение. |
|
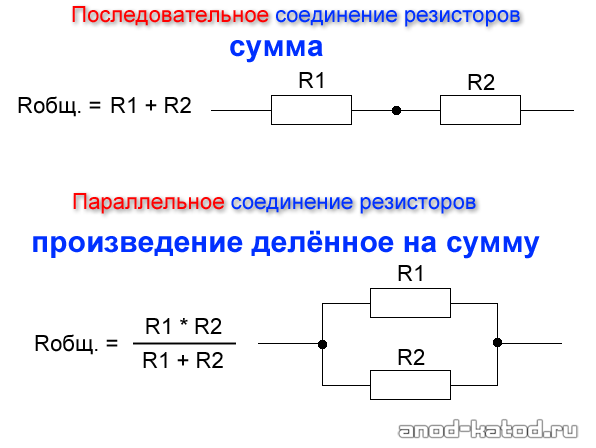
При последовательном соединении резисторов, их эквивалентное (общее) сопротивление равно сумме сопротивлений всех резисторов, входящих в цепочку. |
|
Rэкв = R1+R2+R3+…+Rn
Здесь нет ничего сложного, всё интуитивно понятно. Представьте
опять Дворцовую, оцепленную милицией. В прошлый раз мы брали кордон штурмом.
Теперь попытаемся, как нормальные люди, проникнуть через КПП (пропускной
пункт). К нему стоит очередь. Дли-и-и-и-инная такая. На КПП стоит мент
и общупывает всех и каждого с ног до головы. Сначала руками, потом металлодетектором.
Мент — это сопротивление толпе народа, то есть — резистор.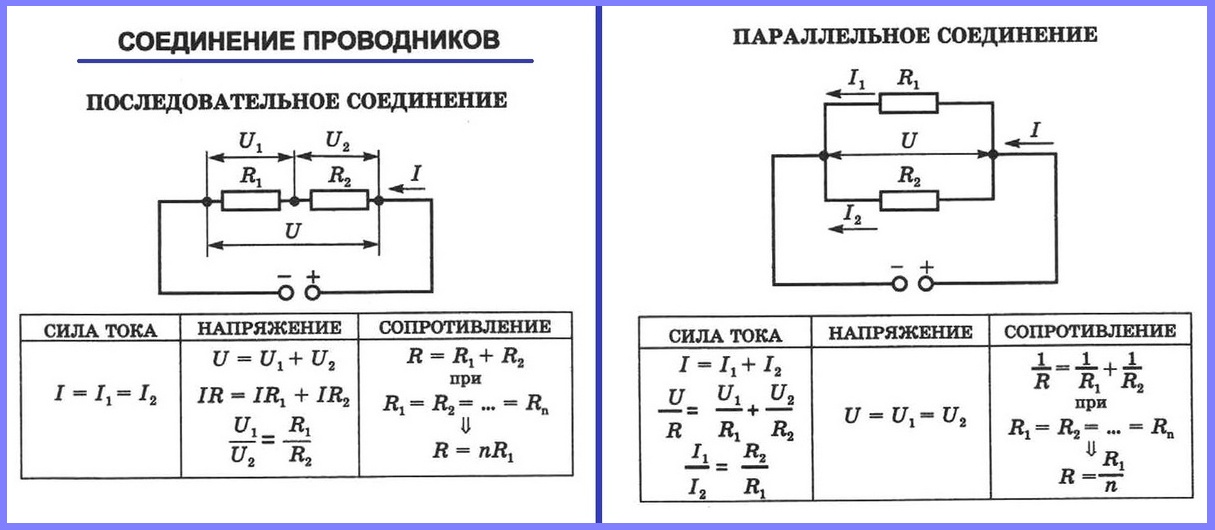 Если бы его
не было, то все спокойненько бы прошли на площадь и не толкались, а так
вот, приходится… Но всё равно, очередь с какой-то скоростью движется.
И вдруг поступает анонимное сообщение, мол, на Дворцовую пытается проникнуть
террорист с 3-мя кг. тротила в кармане. Тут же на КПП выставляют ещё одного
мента. Теперь процедура такая: сначала вас щупает первый милиционер, потом
— второй, а первый ему помогает, и лишь потом Вас пропускают дальше, и
принимаются за следующего. Соответственно, скорость движения очереди уменьшится
вдвое, поскольку два милиционера — это уже два резистора, и сопротивление
у них, соответственно, двойное. Отсюда мораль:
при последовательном соединении ментов, то есть,
резисторов, их сопротивления складываются.
Если бы его
не было, то все спокойненько бы прошли на площадь и не толкались, а так
вот, приходится… Но всё равно, очередь с какой-то скоростью движется.
И вдруг поступает анонимное сообщение, мол, на Дворцовую пытается проникнуть
террорист с 3-мя кг. тротила в кармане. Тут же на КПП выставляют ещё одного
мента. Теперь процедура такая: сначала вас щупает первый милиционер, потом
— второй, а первый ему помогает, и лишь потом Вас пропускают дальше, и
принимаются за следующего. Соответственно, скорость движения очереди уменьшится
вдвое, поскольку два милиционера — это уже два резистора, и сопротивление
у них, соответственно, двойное. Отсюда мораль:
при последовательном соединении ментов, то есть,
резисторов, их сопротивления складываются.
4.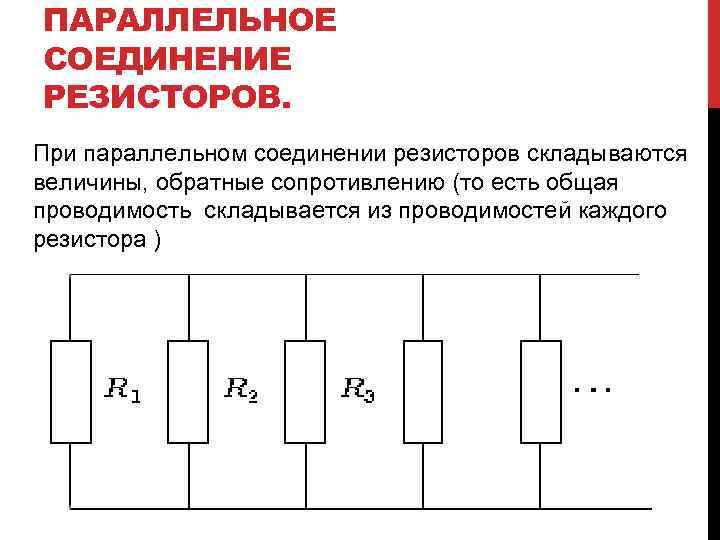 2 Параллельное соединение. 2 Параллельное соединение. |
|
При параллельном соединении резисторов, эквивалентное сопротивление меньше сопротивления любого из этих резисторов. |
|
Для пояснения, вспомним вход в метро. Стоят турникеты, идут люди. Людей — много, турникетов — тоже. Поэтому вся куча народа, которая заходит в метро, довольно быстро оказывается на эскалаторе. А представьте, если бы на входе стоял всего один турникет? Тогда бы у него образовалась очередь, длиннее, чем перед КПП на Дворцовой. Значит, один турникет сопротивляется толпе людей больше, чем несколько турникетов, работающих параллельно. Иными словами, общее сопротивление всех турникетов гораздо меньше, чем одного.
Параллельное соединение резисторов
1.
2. Если резисторов только два, можно воспользоваться такой формулой:
Только не пытайтесь применять эту формулу, если резисторов больше двух!
3. Если все резисторы одинакового сопротивления, то совсем просто:
где n — количество резисторов.
4.3 Смешанное соединение резисторов |
Выше мы рассматривали случаи, когда все резисторы в схеме включены либо последовательно, либо параллельно. Рассчитать Rэкв при этом сможет и дурак: достаточно подставить нужную формулу. Но как быть, например, в таком случае:
|
ЗАДАЧКА: Дана схема:
Здесь без поллитры не разобраться. Для начала, надо постараться найти в схеме участки с параллельным или последовательным включением. Ищем… Нашли? Точно, R2 и R3 включены параллельно! Значит, мы могём заменить их на один резистор R23, и нарисовать такую схему: Величину R23 можно рассчитать по общей формуле для параллельных резисторов: R23 = 1 / (1/R2 + 1/R3) = 1 / (1/9 + 1/18) = 1 / (3/18) = 18 / 3 = 6 Ом Смотрим на новую схему, и видим… Совершенно верно, два резистора R1 и R23, соединены последовательно. Ну, значит, можно и их заменить на один большой резистор R123, или Rэкв (поскольку это конечный результат). Схему не привожу, потому что она ну очень сложная: две клеммы и резистор. А считаем по формуле для параллельных резисторов: Rэ = R1 + R23 = 10 + 6 = 16 Ом. Ответ: 16 Ом |
Ура, ура, ура! Вот мы и решили задачку! Такой же алгоритм применяется и к более сложным схемам. Правда, не каждую схему можно упростить таким способом. Существуют такие противные схемы, которые решаются другими методами. Но на практике нам это вряд ли пригодится, так зачем забивать голову?
|
Назад |
Вверх |
Дальше |
||
|
Главная | Новости | Программа | Теория | Практика | Разработки | Справочник | Литература | Ссылки | Конференция | Гостевая | Обратная связь | |
||||
3 резистора по 5 Ом подключены, 2 параллельно и третий последовательно к остальным.
 Каково общее сопротивление конфигурации.
Цитата страницы
Начать эссе
значок-вопрос
Спросите репетитора
Каково общее сопротивление конфигурации.
Цитата страницы
Начать эссе
значок-вопрос
Спросите репетитора
Начать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«3 резистора по 5 Ом подключены, 2 параллельно и третий последовательно к остальным. Каково общее сопротивление конфигурации.» eNotes Editorial , 3 января 2012 г., https://www.enotes.com/homework-help/3-resistors-5-ohm-connected-2-parallel-other-305020. По состоянию на 10 января 2023 г.
Когда два резистора с сопротивлением R1 и R2 соединены параллельно, эквивалентное сопротивление конфигурации определяется как 1/R = (1/R1 + 1/R2). А для двух последовательно соединенных резисторов R1 и R2 эквивалентное сопротивление равно R=R1+R2.
Из 3-х резисторов по 5 Ом каждый два соединены параллельно. Эквивалентное сопротивление этих резисторов R, где 1/R = 1/5 + 1/5 = 2/5 или R = 5/2 = 2,5 Ом.
Третий резистор включен последовательно с этими двумя. Это эквивалентно двум резисторам, одному на 5 Ом и другому на 2,5 Ом, соединенным последовательно. Эквивалентное сопротивление R = 5 + 2,5 = 7,5 Ом
Эквивалентное сопротивление конфигурации из 3 резисторов по 5 Ом составляет 7,5 Ом.
Утверждено редакцией eNotes
Физика
Последний ответ опубликован 21 апреля 2013 г. в 17:52:34.
Как применяются импульс и инерция в испытании с каплей яйца? Задача состояла в том, чтобы сконструировать что-то защитное из 3 листов газеты, скотча и 4 соломинок, чтобы яйцо не разбилось после…
6 Ответы воспитателя
Физика
Последний ответ опубликован 22 ноября 2009 г.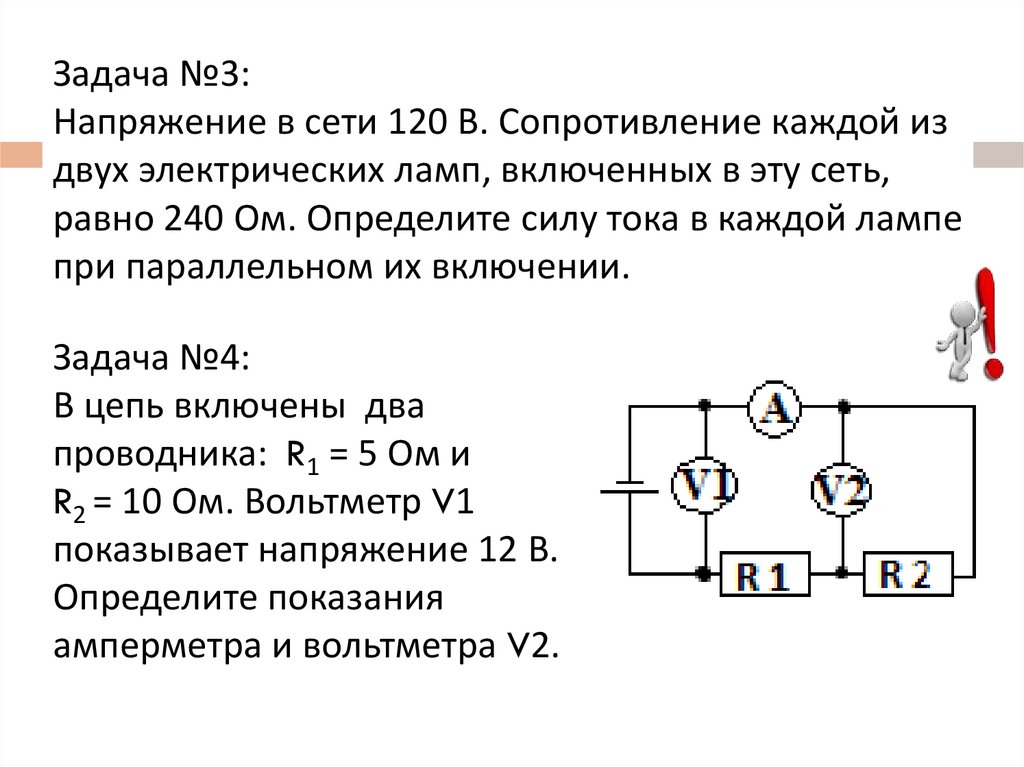 в 10:15:42.
в 10:15:42.
Мяч массой 1,98 кг прикреплен к потолку веревкой длиной 2,1 м. Высота помещения 5,95 м. Ускорение свободного падения равно 9,8 м/с2. Чему равна потенциальная энергия гравитации, связанная с…
2 Ответы воспитателя
Физика
Последний ответ опубликован 01 июня 2009 г.в 8:55:21
Пуля вылетает из ружья горизонтально, в то время как другая падает с конца ствола. Тот, кто первым упадет на землю, ______ А) пуля из ствола…
2 Ответы воспитателя
Физика
Последний ответ опубликован 12 декабря 2009 г. в 12:10:13.
Человек стоит на весах в лифте, ускоряющемся вниз. сравните показания весов с реальным весом человека.
4 Ответы воспитателя
Физика
Последний ответ опубликован 19 ноября 2011 г. в 12:10:30.
в 12:10:30.
В контексте сохранения энергии, какое влияние оказывает трение на кинетическую энергию и гравитационную потенциальную энергию?
1 Ответ воспитателя
Видео с вопросами: Определение соотношения токов, протекающих через различные резисторы в параллельной цепи
Стенограмма видео
Какой из следующих графиков представляет отношение тока, протекающего через резисторы A, B и C в данном фигура? График (A), график (B), график (C) или график (D).
Для расчета коэффициента
токи, проходящие через каждый резистор, нам нужно вспомнить, как ток разделяется
по каждому параллельному пути. Полный ток в цепи с
параллельные компоненты задаются по правилу 𝐼 сумма равна 𝐼 один плюс 𝐼 два плюс 𝐼
три и так далее. То есть общий ток разделяется
по всем параллельным ветвям. В этом вопросе у нас три
разные ветви A, B и C, так что это правило становится 𝐼 total равно 𝐼 A плюс 𝐼 B
плюс 𝐼 С.
В этом вопросе у нас три
разные ветви A, B и C, так что это правило становится 𝐼 total равно 𝐼 A плюс 𝐼 B
плюс 𝐼 С.
Мы также можем вспомнить, что разность потенциалов на каждой ветви параллельной цепи одинакова, поэтому 𝑉 A равно 𝑉 B равно 𝑉 C. То есть разность потенциалов на каждом из этих трех резисторов одинакова. Поскольку три потенциала различия одинаковы, мы будем говорить, что разность потенциалов на каждом ветвь равна 𝑉. Итак, мы знаем о текущем и разность потенциалов для каждой параллельной ветви. Нам также даны сопротивления для каждого резистора. Резистор А имеет сопротивление два 𝑅, резистор B имеет сопротивление три 𝑅, а резистор C имеет сопротивление 𝑅.
Теперь мы можем использовать закон Ома для каждой
путь, чтобы определить токи в каждом пути, а затем сравнить токи, чтобы увидеть
какой из графиков правильно отображает отношение тока, проходящего через
резисторы. Закон Ома можно записать как 𝑉
равно 𝐼, умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, а 𝑅
является сопротивление.
Закон Ома можно записать как 𝑉
равно 𝐼, умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, а 𝑅
является сопротивление.
Нам нужно найти ток, так что давайте изменим уравнение, чтобы ток, 𝐼, стал субъектом. Мы можем сделать это, разделив оба стороны уравнения сопротивлением 𝑅. Сопротивления справа стороны компенсируют друг друга, и мы остаемся с уравнением, которое говорит текущий 𝐼 равна разности потенциалов 𝑉, деленной на сопротивление 𝑅. Теперь мы можем использовать это уравнение для рассчитать ток вдоль каждого пути, подставив соответствующие значения.
Для пути A имеем 𝐼 A равно 𝑉
разделить на два 𝑅. Для пути B имеем 𝐼 B равно 𝑉
разделить на три 𝑅. Для пути C имеем 𝐼 C равно 𝑉
разделить на 𝑅. Мы можем переписать эти первые два
уравнения, вынося числовые значения на множители. Тогда из этих трех уравнений
для токов 𝐼 A, 𝐼 B и 𝐼 C мы видим, что ток через резистор
C — наибольший, ток через резистор B — наименьший, а ток
через резистор А находится между этими двумя значениями.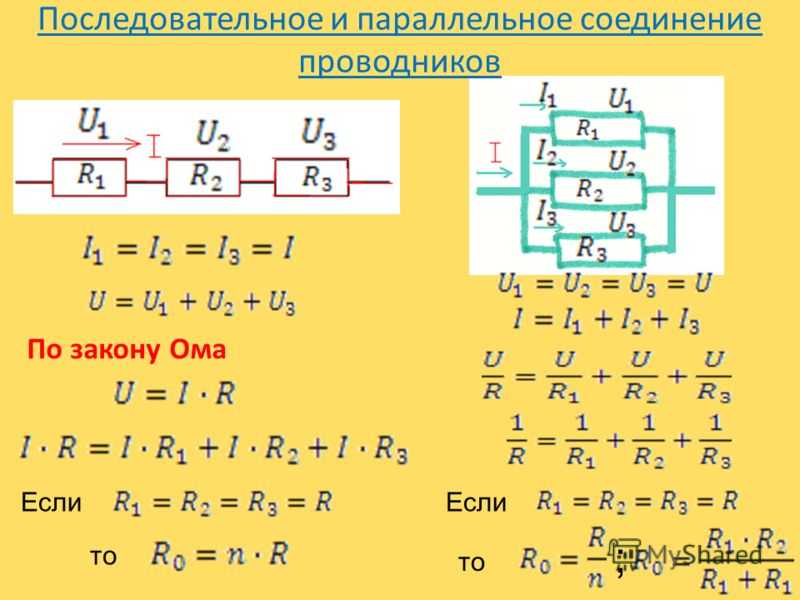

 0.1 Пожалуйста, оцените это
0.1 Пожалуйста, оцените это Но — попробуем =).
Но — попробуем =).