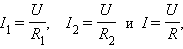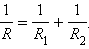Что такое параллельное соединение в электрических цепях. Как рассчитать общее сопротивление при параллельном подключении. Где применяется параллельное соединение проводников. Преимущества и недостатки параллельного подключения элементов.
Что такое параллельное соединение в электрической цепи
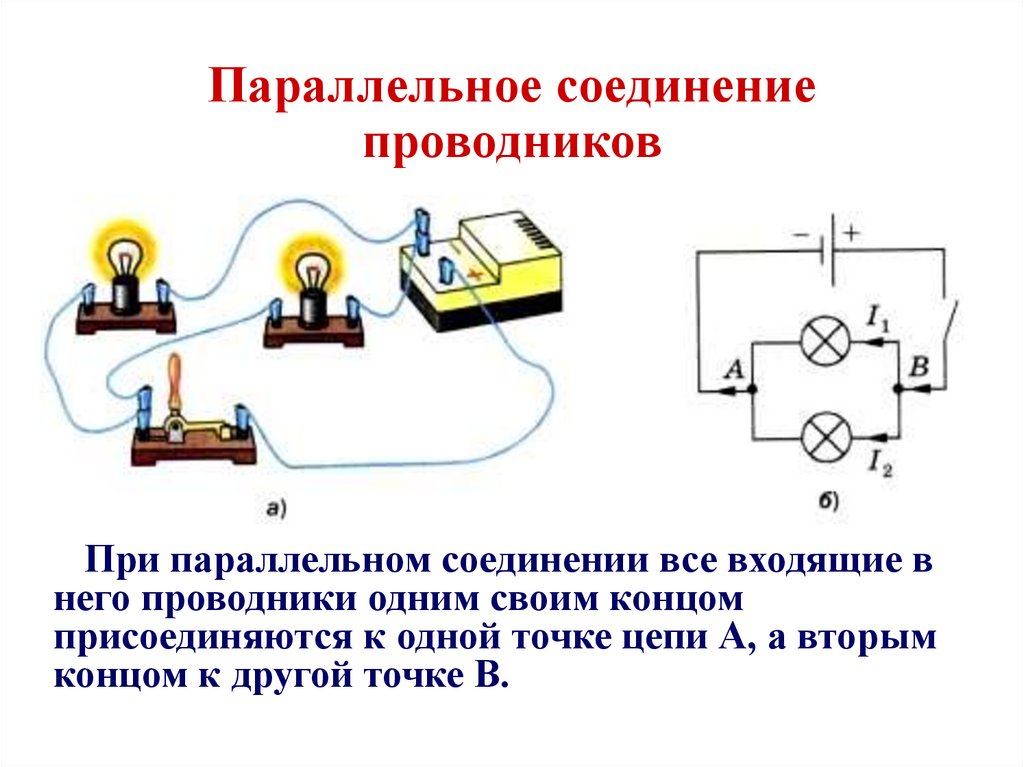
Параллельное соединение — это способ подключения элементов электрической цепи, при котором все элементы присоединяются к одним и тем же двум узлам. При этом напряжение на всех параллельно соединенных элементах одинаково, а общий ток делится между ними.
Основные характеристики параллельного соединения:
- Напряжение на всех элементах одинаково и равно напряжению источника
- Общий ток равен сумме токов через отдельные элементы
- Общее сопротивление цепи меньше сопротивления любого из параллельно включенных элементов
Расчет параллельного соединения резисторов
При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Для двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Как видно из формул, общее сопротивление при параллельном соединении всегда меньше сопротивления любого из параллельно включенных резисторов.
Применение параллельного соединения
Параллельное соединение широко применяется в электротехнике и электронике:
- В бытовой электропроводке для подключения розеток и осветительных приборов
- В схемах делителей тока
- Для увеличения общей мощности в цепях питания
- При подключении измерительных приборов
- В импульсных блоках питания
Преимущества параллельного соединения
Основные достоинства параллельного подключения элементов:
- Независимость работы параллельно соединенных устройств
- Возможность подключения большого количества потребителей
- Повышение надежности цепи — при выходе из строя одного элемента остальные продолжают работать
- Уменьшение общего сопротивления цепи
- Увеличение общей мощности и силы тока
Недостатки параллельного соединения
К недостаткам параллельного подключения можно отнести:

- Сложность расчетов при большом количестве элементов
- Необходимость использовать провода большего сечения из-за увеличения общего тока
- Возможность перегрузки источника питания при подключении слишком большого числа потребителей
Сравнение параллельного и последовательного соединения
В чем основные отличия параллельного соединения от последовательного:
- При параллельном соединении напряжение на элементах одинаково, а при последовательном — суммируется
- Общее сопротивление при параллельном подключении уменьшается, а при последовательном — увеличивается
- Параллельное соединение более надежно, так как при выходе из строя одного элемента остальные продолжают работать
- Параллельное подключение позволяет увеличить мощность цепи, а последовательное — уменьшает ее
Примеры использования параллельного соединения
Рассмотрим несколько практических примеров применения параллельного подключения:
Подключение бытовых электроприборов
В домашней электропроводке все розетки подключены параллельно. Это позволяет независимо включать и выключать различные устройства, не влияя на работу остальных.
Автомобильная электрика
Фары, стеклоочистители, магнитола и другие потребители в автомобиле подключены параллельно к бортовой сети. Это обеспечивает их независимую работу.
Солнечные батареи
Для увеличения вырабатываемой мощности отдельные фотоэлементы солнечных батарей соединяют параллельно.
Расчет параллельного соединения на практике
Рассмотрим задачу: к источнику напряжения 12 В параллельно подключены три резистора сопротивлением 100 Ом, 200 Ом и 300 Ом. Необходимо рассчитать общее сопротивление цепи и токи через каждый резистор.
Решение:
- Рассчитаем общее сопротивление: 1/R = 1/100 + 1/200 + 1/300 = 0.01 + 0.005 + 0.0033 = 0.0183 R = 1/0.0183 = 54.6 Ом
- Рассчитаем общий ток: I = U/R = 12/54.6 = 0.22 А
- Рассчитаем токи через резисторы: I1 = U/R1 = 12/100 = 0.12 А I2 = 12/200 = 0.06 А I3 = 12/300 = 0.04 А
Проверим: I1 + I2 + I3 = 0.12 + 0.06 + 0.04 = 0.22 А, что соответствует общему току.
Заключение
Параллельное соединение — важнейший способ подключения элементов в электрических цепях. Оно широко применяется как в бытовой электрике, так и в сложных электронных устройствах. Понимание принципов работы параллельных цепей и умение производить их расчеты необходимо для всех, кто связан с электротехникой и электроникой.
Электротехника часть 4. Соединение элементов цепи
Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.
Последовательное соединение приемников энергии
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Параллельное соединение приемников энергии
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
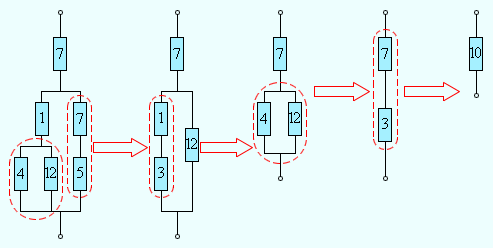
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R12R345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Второй закон Кирхгофа
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
www.electronicsblog.ru
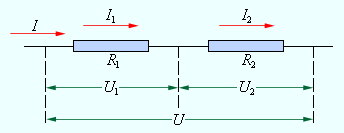
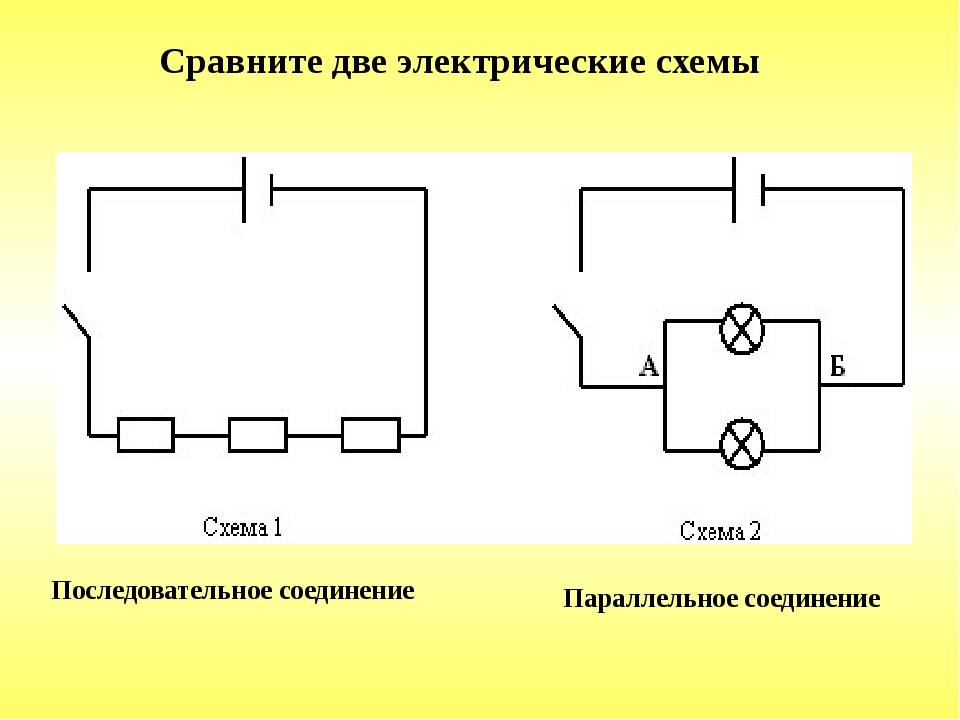
Электрическая цепь с последовательным соединением элементов
|
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR 1 + IR2 + IR3,
откуда следует
Rэкв = R1 + R2 + R3.
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
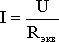 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
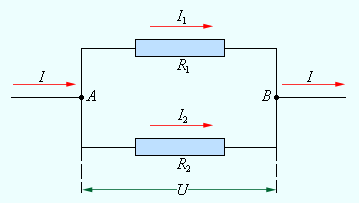
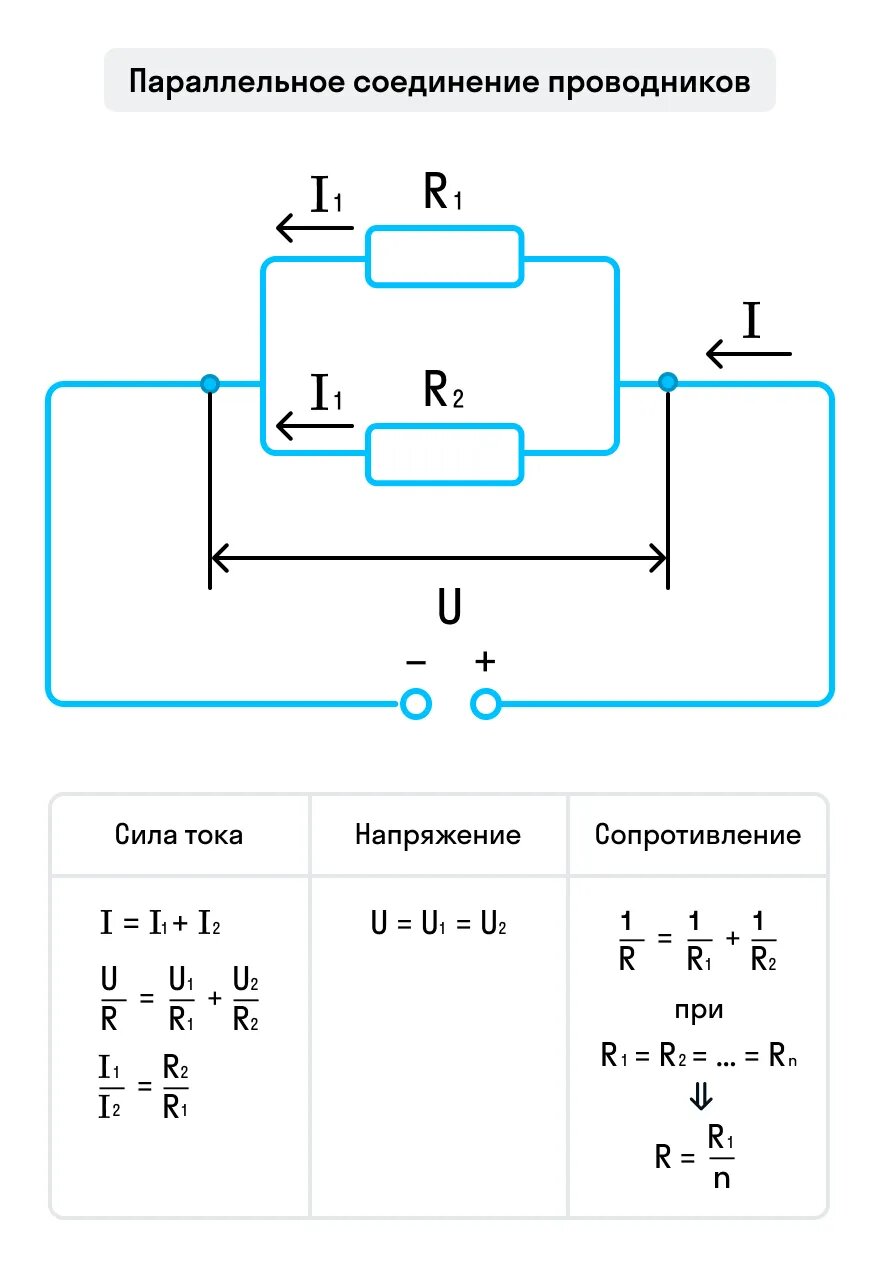
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е.

откуда следует, что
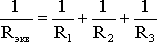
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)
 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IRэкв = I1R1 = I2R2 = I3R3
Отсюда следует, что
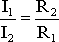 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
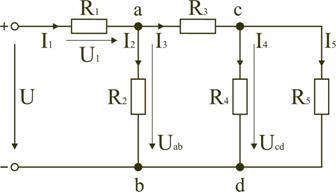
Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
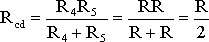 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
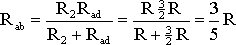 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
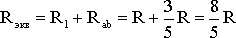 .
.
|
|
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.
Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).
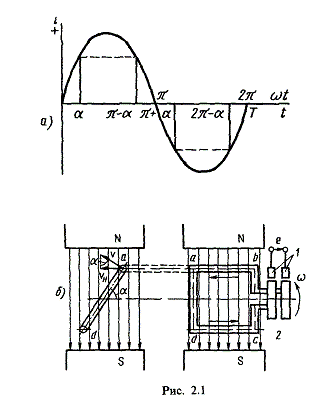
Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля vн:
e = Blvн (2.1)
где В и l — постоянные величины, a vн — переменная, зависящая от угла α. Выразив скорость vн через линейную скорость катушки v, получим
e = Blv·sinα (2.2)
В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.
Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. Em = Blv. Поэтому выражение (2.2) можно записать в виде
e = Emsinα (2.3)
Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде
e = Emsinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е’.
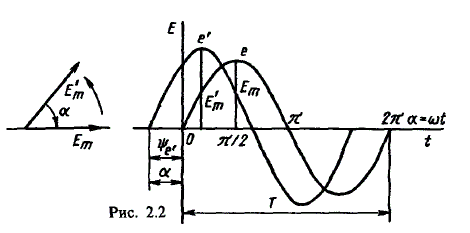
Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn / 60
Из рис. 2.2 видно, что ωТ = 2π, откуда
ω = 2π / T = 2πf (2.5)
Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е’ можно описать выражениями
e = Emsinωt; e’ = E’msin(ωt + ψe’).
Здесь ωt и ωt + ψe’ — фазы, характеризующие значения э. д. с. e и e’ в заданный момент времени; ψe’ — начальная фаза, определяющая значение э. д. с. е’ при t = 0. Для э. д. с. е начальная фаза равна нулю (ψe = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).
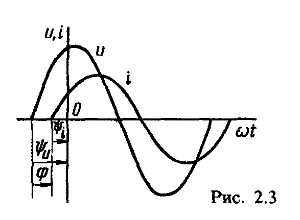
Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = Umsin(ωt + ψu); i = Imsin(ωt + ψi), (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψu — ψi.
Уравнения (2.6) можно записать иначе:
u = Umsin(ωt + ψi + φ); i = Imsin(ωt + ψu — φ),
поскольку ψu = ψi + φ и ψi = ψu — φ.
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),
где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψu > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψi < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током
φ = ψu – ψi = ψu – ( — ψi) = ψu + ψi.
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
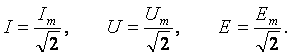
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
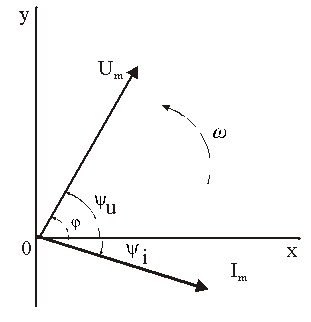 Рис.
2.4
Рис.
2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
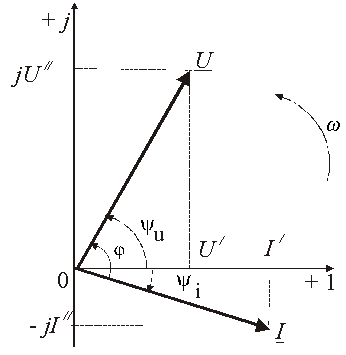 Рис.
2.5
Рис.
2.5
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:
а). Алгебраической
U = U’+ jU«
I = I’ – jI«,
где U‘, U«, I‘, I» – проекции векторов на оси действительных и мнимых чисел.
б). Показательной

где U, I – модули (длины) векторов; е – основание натурального логарифма;  поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в). Тригонометрической
U = U·(cosψu + jsinψu)
I = I·(cosψi – jsinψi).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
еj·ψ = cosψ + jsinψ.
Неразветвлённые электрические цепи
studfile.net
Последовательное соединение проводников: примеры для домашней электропроводки
Содержание статьи:
Каждое помещение имеет несколько точек электропитания для работы различных приборов. Техника работает посредством электрического тока, который проводят через специально установленные кабели – проводники. От качества элементов сети и способа соединения зависит качество напряжения, стабильность и безопасность использования. Существует два основных метода – параллельное и последовательное. Каждое имеет свои преимущества и недостатки, с которыми лучше ознакомиться предварительно.
Основные электрические величины цепи
 Чтобы разобраться в нюансах подключения и соединения электрических проводников, необходимо выяснить основные моменты и величины токовых цепей. Электроцепь – это не самостоятельное устройство, а совокупность нескольких механизмов и элементов, используемых для проведения электрического тока. Основные детали:
Чтобы разобраться в нюансах подключения и соединения электрических проводников, необходимо выяснить основные моменты и величины токовых цепей. Электроцепь – это не самостоятельное устройство, а совокупность нескольких механизмов и элементов, используемых для проведения электрического тока. Основные детали:
- источники: трансформаторы, электроустановки, батарейки, генераторы, аккумуляторы и другие;
- приемники: непосредственно техника – лампы, двигатели, нагреватели, катушки индуктивности, подобные;
- промежуточные звенья: провода, устройства.
Основными величинами, с помощью которых устанавливают свойства электрических цепей, являются напряжение, сопротивление и ток. В проводниках электричество представляет множество двигающихся в заданном направлении электрических зарядов. Под током в сети подразумевают интенсивность или силу, которые измеряются числом зарядов одновременно проходящих через поперечное сечение проводника.
Напряжение – это то количество электрической энергии, которое необходимо для перемещения одного заряда от одного пункта до другого. Выражается в Вольтах. Сопротивление – это силы, воздействующие на поток электрических зарядов во время движения проводников. Записывается в Омах.
Взаимная зависимость электрических величин
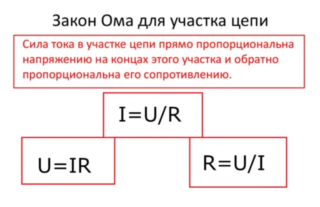 Связь между величинами в электрической цепи объясняется законами электротехники. Первый – Закон Ома. Открыт и подтвержден Георгом Симоном Омом еще в 1827 году. Заключается в том, что величина интенсивности тока прямо пропорциональна величине напряжения в кабеле проводника. Закон Ома позволяет быстро провести анализ электрической цепи и оценить ее возможности, пределы.
Связь между величинами в электрической цепи объясняется законами электротехники. Первый – Закон Ома. Открыт и подтвержден Георгом Симоном Омом еще в 1827 году. Заключается в том, что величина интенсивности тока прямо пропорциональна величине напряжения в кабеле проводника. Закон Ома позволяет быстро провести анализ электрической цепи и оценить ее возможности, пределы.
Кроме основного правила в электротехнике используют Законы Кирхгофа. Один гласит, что сумма токов на входе равна сумме токов на выходе. Второй – что сумма ЭДС равна сумме падений напряжения на внутренних элементах электрического контура.
Законы Кирхгофа позволяют установить соотношение между токами, проходящими через узлы электрической проводки, и токами на входе в контурную цепь. Анализ и расчеты проводятся по следующему алгоритму:
- Устанавливается общее число ветвей и узлов конкретной электрической сети.
- В произвольном порядке выбираются условно-положительные направления токов в проводке, на схеме проставляются соответствующие отметки.
- Для получения уравнения отмечаются в свободном порядке положительные направления обхода контура;
- Составляется уравнение по правилам Кирхгофа для получения результата.
Решение построенных задач позволит определить количество и значение токов в конкретной электрической цепи.
При помощи законов Ома и Кирхгофа, электрики оценивают состояние сети, ее работоспособность и мощность. На практике редко используют формулы вживую. Практикующие электрики ориентируются в характеристиках более свободно. Начинающим монтажерам может показаться сложным единовременное ориентирование во всех показателях и взаимосвязях, удобнее иметь некоторые вспомогательные материалы под рукой.
Параллельное соединение проводников
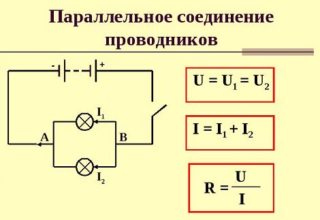 Соединение кабелей в электропроводке возможно тремя вариантами: параллельно, последовательно, смешанно. Первый метод – параллельное подключение – заключается в том, что проводники соединяются между собой в начальной и конечной точках. Получается, что нагрузки с обоих концов сливаются, а напряжение получается параллельным. В одной электрической сети параллельно могут быть соединены два, три и больше кабелей.
Соединение кабелей в электропроводке возможно тремя вариантами: параллельно, последовательно, смешанно. Первый метод – параллельное подключение – заключается в том, что проводники соединяются между собой в начальной и конечной точках. Получается, что нагрузки с обоих концов сливаются, а напряжение получается параллельным. В одной электрической сети параллельно могут быть соединены два, три и больше кабелей.
Чтобы проверить интенсивность прохождения тока при таком подключении, в параллельную сеть подключают две лампочки (показатели должны быть идентичными – сопротивление, напряжение). Чтобы произвести испытание и проконтролировать результат, к каждой подводят амперметр (устройство, измеряющее силу тока). Третий прибор запитывают на сеть в целом, чтобы увидеть показатель на всей сети. Дополнительные элементы – питание, ключ.
После того как схема собрана, ключом активируют питание и сравнивают результаты на амперметрах. На общем показатель должен быть равен сумме двух, подключенных к лампам. В данном случае считается, что система работает исправно – напряжение при параллельном соединении подается в нормальном режиме.
Если на одном участке произойдет замыкание, лампочки останутся в рабочем состоянии. Ток поступает по замкнутому контуру с двух сторон. Ремонт будет необходим в любом случае, но свет и питание останутся.
Если к указанной системе подключить вольтметр, можно оценить показатели сопротивления сети. Эквивалентный показатель укажет на уровень сопротивления сети при той же интенсивности тока.
Последовательное соединение проводников
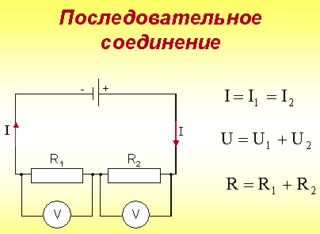 Следующая схема подключения – последовательное соединение проводников в цепи – подразумевает врезку каждого прибора в порядке очередности (один за другим). Интенсивность силы проходящего тока через каждый элемент питания (лампочка, прибор) будет одинаковой. При этом напряжение при последовательном соединении складывается из показателей напряжения с каждого участка (получается суммарным).
Следующая схема подключения – последовательное соединение проводников в цепи – подразумевает врезку каждого прибора в порядке очередности (один за другим). Интенсивность силы проходящего тока через каждый элемент питания (лампочка, прибор) будет одинаковой. При этом напряжение при последовательном соединении складывается из показателей напряжения с каждого участка (получается суммарным).
Значение сопротивления может изменяться. Если изменится нагрузка на одном из мест последовательного подключения, изменится и уровень сопротивления. Как следствие, поменяется показатель тока.
Основной недостаток такой электрической цепи заключается в том, что если на одном из участков произойдет сбой (поломка, замыкание), следующие за ним элементы перестанут функционировать. Наглядно схема соединения представлена в обычных новогодних гирляндах – когда ломается один контакт или провод в любом месте, перестают работать остальные.
При последовательном подключении проводников конец одного кабеля подсоединяется к началу следующего. Ключевое отличие электроцепи – отсутствие разветвлений, через участки проходит один электроток. При этом разность потенциалов резистора объясняется совокупным напряжением по каждому отдельному резистору (контакту, участку, точке питания).
Законы последовательного и параллельного соединения проводников
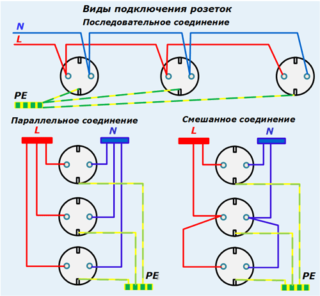
Примеры схем соединения розеток
К правилам, объясняющим «поведение» проводников при последовательном и параллельном соединениях, относятся основные законы электротехники и некоторые особенности. Последние не всегда бывают очевидны новичкам, поэтому их разбирают как отдельные законы. При работе со схемами проводников учитывают следующее:
- Последовательное подключение подразумевает одинаковые показатели токов на каждом участке.
- Закон Ома для каждого типа соединения имеет свое значение. Например, при последовательном способе включения напряжение будет равно сумме напряжений всех участков сети.
- Общее сопротивление электрической цепи при поочередном соединении будет равно сумме значений сопротивления элементов, не зависит от числа проводников и точек питания.
- Параллельный метод – напряжение электроцепи равно напряжению на каждом отдельном элементе, не суммируется, а остается одинаковым.
- Сила тока для данного способа соединения определяется суммой значений токов участков подключения.
Данные законы используются при построении схемы электропроводки в помещении.
Чтобы оптимизировать нагрузку, не создавать чрезмерного напряжения в отдельных частях, проверяют оптимальность каждого типа соединения в конкретной ситуации.
Смешанное соединение проводников
Смешанное соединение проводников
Как правило, в электпроводке используют параллельное и последовательное соединения одновременно. Такой способ подключения проводов называется смешанным или комбинированным. При построении первоначальной схемы питания в помещении, где указывается число и расположения точек питания (розеток, выключателей, трансформаторов), учитывают необходимость каждого из типов подключения на разных участках.
Электрическая проводка редко состоит из простых элементов. Зачастую получается сложная схема из множества разных участков и соединений. Поэтому при составлении плана важно разобраться в преимуществах и недостатках типов подсоединения проводов, чтобы оптимально использовать каждый. Для этого схему разбивают по участкам и в каждом конкретном случае подбирают собственный метод врезки проводов.
Как выбрать тип подключения

Распределительная коробка
Потребляемая электрическая энергия в квартиру поступает от общедомового электрощитка. Количество израсходованного тока измеряется счетчиком. Вводный провод в помещение имеет большое сечение и является основным «поставщиком» электричества в квартиру. Следующие берут с меньшими показателями, так как нагрузка на них снижается за счет распределения.
Основной кабель заводится в специальную распределительную коробку, от которой делают разводку в комнаты и санузлы. На этом этапе необходимо определить, какой тип соединения проводов будет использован: последовательный, параллельный, комбинированный.
Категорического запрета на построение проводки в квартире тем или иным способом нет. Однако следует учитывать практическое применение каждой цепи, недостатки, преимущества и возможности.
Самым подходящим и часто используемым вариантом является смешанное соединение проводов. От общего щитка к распредкоробке подводится кабель, затем в параллельную сеть замыкается несколько распределительных узлов (в каждом помещении). Далее – в комнатах точки питания соединяются последовательно.
Последовательное включение элементов позволяет существенно сэкономить на материалах при монтаже электропроводки. Поэтому несмотря на определенные недостатки метод используют в небольших помещениях. На малых участках проще выявить место поломки, нежели в квартире в целом.

Параллельное подключение розеток
Параллельное подключение визуально представляет кольцо из проводов. Если на одном участке произошел сбой, ток не прекращает поступать – подача происходит с другой стороны цепи. Однако для такого типа соединения требуется проложить значительное количество кабеля, что не всегда удобно.
В некоторых ситуациях целесообразно использовать только последовательное соединение проводов. Например, в длинных коридорах необходимо одновременно включать и выключать несколько осветительных приборов разом. Шлейфовое подключение в данной ситуации оптимально. Сложность замены лампочки или узла на участке зависит от типа электропроводки и отделки помещения.
При составлении схемы электрической сети в квартире и покупке лампочек для осветительных приборов важно учитывать уровень напряжения. Последовательное соединение означает, что напряжение делится поровну на количество лампочек. Например, если устанавливают две подряд, значение на каждой будет по 110В, а не 220В.
При покупке вторичного жилья следует убедиться, что в технической документации присутствует действующая схема электропроводки. Наличие плана позволит безопасно сделать ремонт и корректно подключить новые точки питания, лампы.
Электромонтажники в сложных схемах всегда используют оба типа соединения. С одной стороны, такой подход снижает общее количество расходных материалов. С другой, позволяет в каждом конкретном помещении реализовать преимущества обоих методов врезки кабеля. При самостоятельном подключении необходимо детально разобраться в аспектах каждого вида, по возможности – проконсультироваться с мастером. В противном случае, велика вероятность некорректного соединения и сбоев в работе.
strojdvor.ru
Последовательное и параллельное соединение резисторов
Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
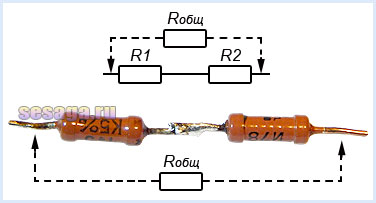
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
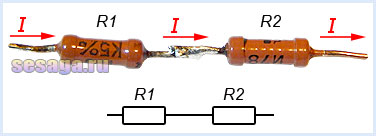
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
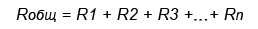
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
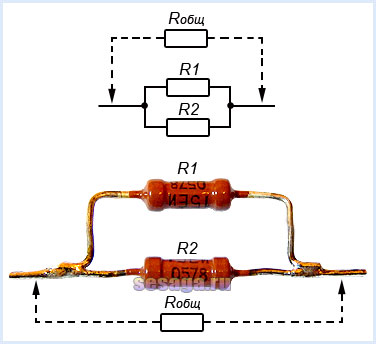
Параллельное соединение резисторов
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
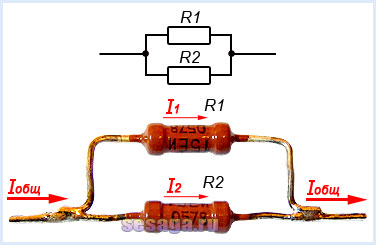
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
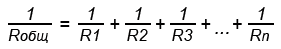
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:
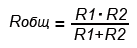
При включении трех резисторов расчет общего сопротивления будет таким:
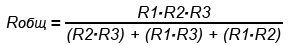
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.
На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!
sesaga.ru
fizika / Сопротивление проводников. Параллельное и последовательное соединение проводников
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
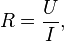
где
R — сопротивление;
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
|
Рисунок 1.9.1. Последовательное соединение проводников |
По закону Ома, напряжения U1 и U2 на проводниках равны
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
|
Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
|
где R – электрическое сопротивление всей цепи, получим
|
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
|
Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом) |
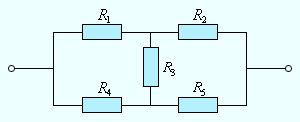
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
|
Рисунок 1.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников |
studfile.net
§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк (19)
где Rэк = R1 + R2 + R3.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепи
U = U1 + U2 +U3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U1 : U2 : U3 = R1 : R2 : R3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
U1 = U/n. (22)
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Рис. 27. Схемы смешанного соединения приемников
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

electrono.ru
Соединение элементов в цепи переменного напряжения и тока
Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
Последовательное соединение элементов цепи.
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Im – амплитудное значение переменного тока.
Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
Напряжения и токи при последовательном соединении.
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
где R – активное сопротивление,
Х – реактивное сопротивление.
Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение
где Z – полное сопротивление цепи,
ψ – разность фаз между напряжением и током.
Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
Z – полное сопротивление цепи.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
Параллельно соединение элементов цепи.
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Um – амплитудное значение переменного тока.
Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
Напряжение и токи при параллельном соединении.
Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
где g – активная проводимость, b – реактивная проводимость.
Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.
Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
Определим зависимость между напряжением и силой тока в параллельной цепи
где y – полная проводимость,
ψ – разность фаз между напряжением и током в цепи.
Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
y – полная проводимость цепи.
Чему равна мощность в цепи при синусоидальном напряжении?
Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения. Мгновенная мощность в цепи будет равна
Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).
Теперь определим среднее значение мощности за период или активную мощность, которая будет равна
где U – действующее значение переменного напряжения,
I – действующее значение переменного тока,
cos(φ) – коэффициент мощности.
Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.
При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
www.electronicsblog.ru

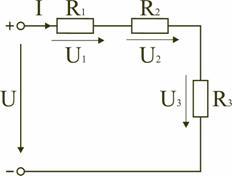 Рис.
1.4
Рис.
1.4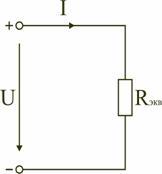 Рис.
1.5
Рис.
1.5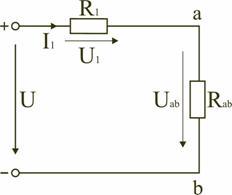 Рис.
1.10
Рис.
1.10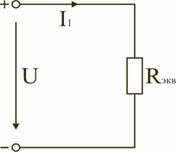 Рис.
1.11
Рис.
1.11