Что такое параллельное соединение катушек индуктивности. Как рассчитать общую индуктивность при параллельном соединении. Какие факторы влияют на результирующую индуктивность. Где применяется параллельное соединение индуктивностей на практике.
Что такое параллельное соединение катушек индуктивности
Параллельное соединение катушек индуктивности — это такое соединение, при котором все начала катушек соединены в одной точке, а все концы — в другой. При этом через каждую катушку протекает только часть общего тока, а напряжение на всех катушках одинаково.
Основные характеристики параллельного соединения индуктивностей:
- Общий ток делится между катушками
- Напряжение на всех катушках одинаково
- Общая индуктивность меньше индуктивности наименьшей катушки
- Чем больше катушек соединено параллельно, тем меньше общая индуктивность
Расчет общей индуктивности при параллельном соединении
Для расчета общей индуктивности при параллельном соединении катушек без взаимной индукции используется следующая формула:

1/L = 1/L1 + 1/L2 + 1/L3 + …
Где L — общая индуктивность, L1, L2, L3 и т.д. — индуктивности отдельных катушек.
Для двух параллельно соединенных катушек формула упрощается:
L = (L1 * L2) / (L1 + L2)
Факторы, влияющие на результирующую индуктивность
На общую индуктивность при параллельном соединении катушек влияют следующие факторы:
- Количество соединенных катушек — чем больше, тем меньше общая индуктивность
- Индуктивности отдельных катушек — общая индуктивность всегда меньше наименьшей
- Наличие взаимной индукции между катушками
- Направление намотки катушек (согласное или встречное)
Учет взаимной индукции при параллельном соединении
При наличии магнитной связи между параллельно соединенными катушками необходимо учитывать взаимную индукцию. В этом случае формула для расчета общей индуктивности усложняется:
L = (L1*L2 — M^2) / (L1 + L2 ± 2M)
Где M — коэффициент взаимной индукции, знак «+» используется при встречном включении, «-» при согласном.
Практическое применение параллельного соединения индуктивностей
Параллельное соединение катушек индуктивности применяется в следующих случаях:

- Для уменьшения общей индуктивности цепи
- В фильтрах высоких частот
- В импульсных источниках питания
- В радиочастотных схемах для настройки резонансных контуров
- В электронных балластах люминесцентных ламп
Преимущества и недостатки параллельного соединения катушек
Основные преимущества параллельного соединения индуктивностей:
- Возможность получить малую индуктивность из нескольких больших
- Увеличение допустимого тока
- Уменьшение потерь на активном сопротивлении катушек
К недостаткам можно отнести:
- Сложность точного расчета при наличии взаимной индукции
- Возможное взаимное влияние катушек друг на друга
- Увеличение габаритов по сравнению с одной катушкой
Сравнение параллельного и последовательного соединения индуктивностей
Основные отличия параллельного соединения от последовательного:
- При параллельном соединении общая индуктивность уменьшается, при последовательном — увеличивается
- Параллельное соединение позволяет уменьшить активное сопротивление, последовательное — увеличивает его
- При параллельном соединении напряжение на катушках одинаково, при последовательном — делится
- Параллельное соединение увеличивает допустимый ток, последовательное — уменьшает
Примеры расчета параллельного соединения индуктивностей
Рассмотрим несколько примеров расчета общей индуктивности при параллельном соединении катушек:
Пример 1
Две катушки с индуктивностями 100 мкГн и 200 мкГн соединены параллельно. Рассчитать общую индуктивность.
L = (L1 * L2) / (L1 + L2) = (100 * 200) / (100 + 200) = 66,7 мкГн
Пример 2
Три катушки с индуктивностями 10 мГн, 15 мГн и 30 мГн соединены параллельно. Найти общую индуктивность.
1/L = 1/10 + 1/15 + 1/30 = 0,1 + 0,067 + 0,033 = 0,2
L = 1 / 0,2 = 5 мГн
Рекомендации по применению параллельного соединения индуктивностей
При использовании параллельного соединения катушек индуктивности следует учитывать следующие рекомендации:
- По возможности располагать катушки на достаточном расстоянии друг от друга для минимизации взаимной индукции
- Использовать экранирование катушек для уменьшения взаимного влияния
- Учитывать паразитные емкости между обмотками параллельных катушек
- При необходимости применять компенсирующие конденсаторы
- Правильно выбирать сечение провода с учетом увеличения тока
Соблюдение этих рекомендаций позволит эффективно использовать параллельное соединение индуктивностей в различных электронных схемах.
Соединение катушек — Основы электроники
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
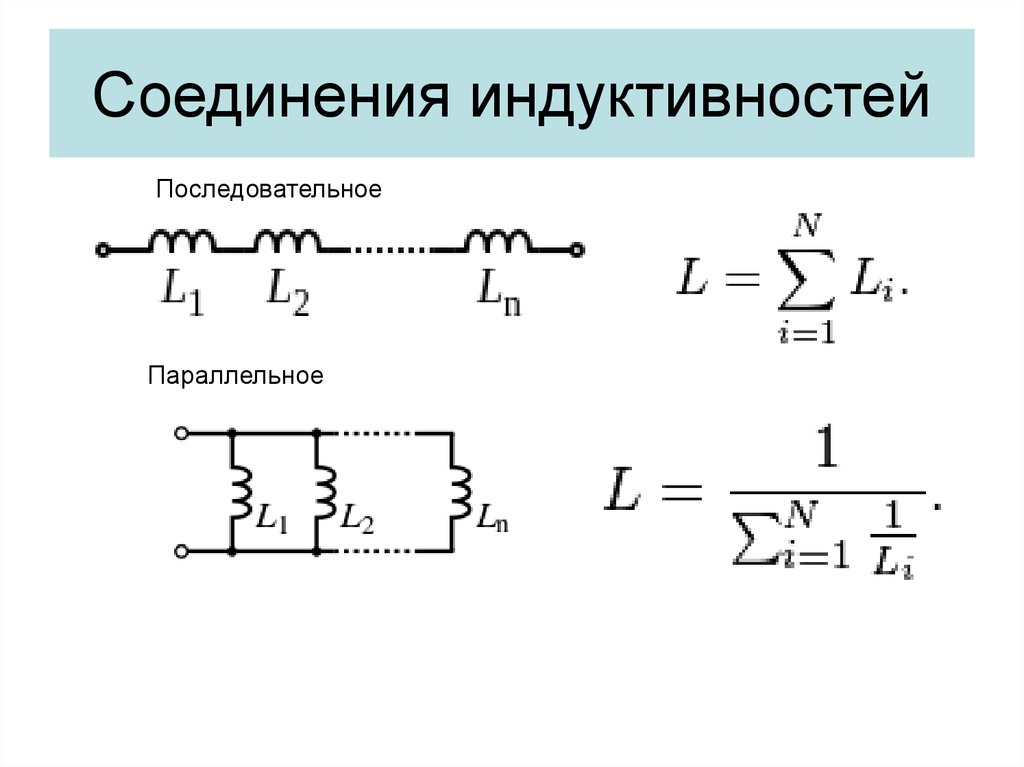
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Добротность и энергия катушки индуктивности.
 Варианты соединения.
Варианты соединения. Aveal
Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. 2}{2}
2}{2}
Планомерно переходим к вариантам соединения катушек между собой. Все расчеты будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0, и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде все просто, но тут есть один немаловажный нюанс. Данная формула справедлива только в том случае, если катушки расположены на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация несколько другая. Возможны два варианта:
Возможны два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек — начало второй катушки подключается к концу первой. А второй вариант называют встречным включением — конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом «*». Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M — взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу — уменьшается на ту же самую величину. 2}{L_1 + L_2 + 2M}
2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом заканчиваем разбор катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающими все эти элементы. Так что подписывайтесь на обновления и не пропускайте новые статьи 🤝
Параллельные катушки индуктивности — узел электроники
Катушки индуктивности считаются соединенными параллельно, когда два вывода катушки индуктивности соответственно подключены к каждой клемме других катушек индуктивности или катушки индуктивности. Как и при параллельном соединении резисторов, общая индуктивность при параллельном соединении индукторов несколько меньше наименьшей индуктивности индуктора в этом соединении.
Когда катушки индуктивности соединены параллельно, ток, протекающий через каждую катушку индуктивности, не в точности равен общему току, но сумма каждого отдельного тока через параллельные катушки индуктивности дает общий ток (поскольку он делится между параллельными катушками индуктивности).
Если ток, протекающий через каждый индуктор, меньше, чем общий ток, магнитное поле, создаваемое каждым индуктором, также меньше, чем поле, создаваемое суммарным током через него.
При параллельном соединении резисторов большая часть тока протекает через наименьший резистор, поскольку он оказывает наименьшее сопротивление протеканию тока, чем резистор большего размера.
Аналогичным образом, если катушки индуктивности соединены параллельно, ток выбирает путь наименьшего сопротивления катушки индуктивности, когда ток в этой цепи уменьшается или увеличивается, в то время как каждая катушка индуктивности по отдельности противостоит этому изменению (увеличению или уменьшению тока).
При параллельном соединении напряжение на всех индукторах одинаково, а также при изменении общего тока падение напряжения на каждом отдельном индукторе будет меньше по сравнению с последовательным соединением. При заданной скорости изменения тока меньше будет индуктивность при меньшем напряжении.
Это основные моменты, которые следует учитывать при параллельном соединении катушек индуктивности. Теперь обсудим параллельное соединение катушек индуктивности с учетом и без учета взаимной связи между этими катушками индуктивности.
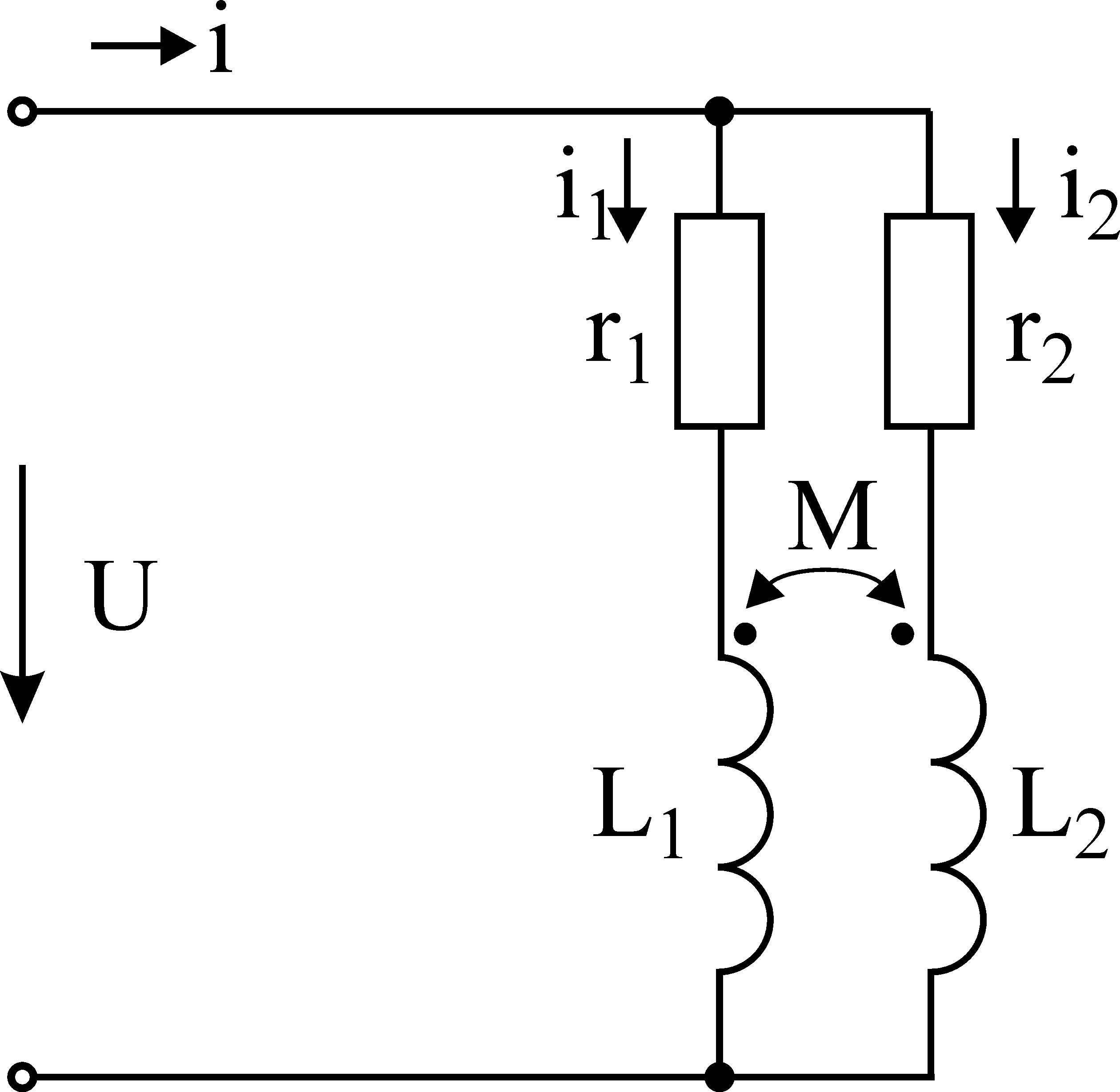
Схема
Катушки индуктивности, соединенные параллельно (без магнитной связи)
Как уже говорилось выше, один конец катушки индуктивности соединен с узлом, а другие концы катушки индуктивности совместно соединены с другим узлом в параллельном соединении. Параллельное соединение n индукторов показано на рисунке ниже.
Учтите, что между катушками индуктивности нет магнитной связи и, следовательно, общая индуктивность равна сумме обратных величин индуктивностей отдельных индуктивностей. Обсудим, как можно получить это утверждение.
Мы знаем, что в параллельной сети напряжение остается постоянным, а ток делится на каждой параллельной катушке индуктивности. Если I L1 , I L2 , I L3 и т. д. I Ln представляют собой отдельные токи, протекающие в параллельно соединенных катушках индуктивности L 1 , L 2 и т. д. L n соответственно , то общий ток в параллельных индукторах равен
д. I Ln представляют собой отдельные токи, протекающие в параллельно соединенных катушках индуктивности L 1 , L 2 и т. д. L n соответственно , то общий ток в параллельных индукторах равен
I Всего = I L1 + I L2 + Я Л3 . . . . + I n
Если отдельные падения напряжения при параллельном соединении равны V L1 , V L2 , V L3 и т. д. V Ln , то общее падение напряжения между двумя клеммами V T равно
V Всего = V L1 = V L2 = V L3 . . . . = V n
Падение напряжения с точки зрения собственной индуктивности можно выразить как V = L di/dt. Отсюда следует полное падение напряжения,
V T = L T DI/DT
⇒ L T D/DT (I L1 + I L2 + I L3 . T ((d i1 )/dt + (d i2 )/dt + (d i3 )/dt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . уравнение принимает вид
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . уравнение принимает вид
V T = L T (V/L 1 + V/L 2 + V/L3 . . .)
Поскольку падение напряжения в цепи постоянно, то v = В Т . Таким образом, мы можем написать
1/л T = 1/л 1 + 1/л 2 + 1/л 3 . . . . .
Это означает, что обратная величина полной индуктивности параллельного соединения является суммой обратных величин индивидуальных индуктивностей всех катушек индуктивности. Приведенное выше уравнение верно, когда между параллельно соединенными катушками нет взаимной индуктивности.
Чтобы избежать сложностей при работе с дробями, мы можем использовать метод произведения на сумму для расчета общей индуктивности. Если две катушки индуктивности соединены параллельно и между ними нет взаимной индуктивности, то общая индуктивность равна
L T = (L 1 × L 2 )/(L 1 + L 2 )
30 Генри соединены параллельно, какова будет общая индуктивность параллельного соединения?
Sol: Мы знаем, что формула для полной индуктивности серии, 1/L T = 1/L 1 + 1/L 2
Учитывая, что L 1 = 20 Генри
L 2 = 30 Генри
L T = (L 1 * L 2 )/(L 1 1+ L 2 * )) (20+30) ) = 600 / 50 = 12
Общая индуктивность L Итого = 12 Генри.
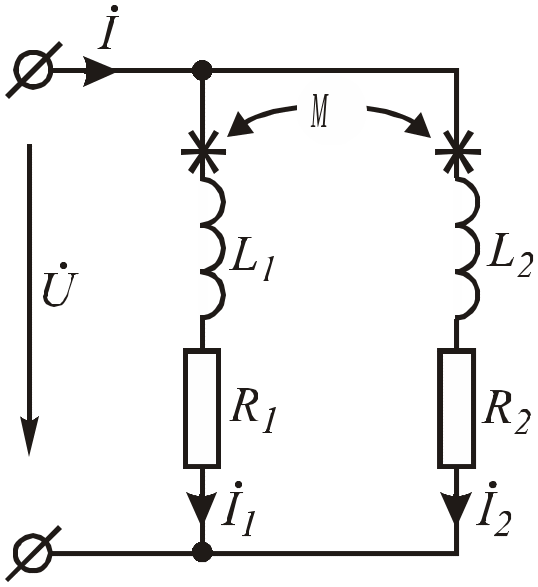
Взаимно связанные катушки индуктивности, установленные параллельно
При наличии магнитной связи между катушками индуктивности вышеприведенная производная формула для общей индуктивности должна быть изменена, поскольку общая индуктивность может быть больше или меньше в зависимости от направления магнитного поля от каждой катушки индуктивности. Магнитный поток, создаваемый параллельно соединенными индукторами, будет связан друг с другом.
Когда создаваемые потоки имеют одинаковое направление магнитного потока, взаимная индуктивность увеличивается; эти катушки называются «помощными» катушками. Если поток противоположен магнитному потоку, взаимная индуктивность уменьшится; эти катушки называются «противоположные» катушки. Эта взаимная индуктивность будет зависеть от расстояния между двумя катушками.
Учтите, что две катушки индуктивности соединены параллельно с собственной индуктивностью L 1 и L 2 и взаимно связаны с взаимной индуктивностью M, как показано на рисунке ниже.
Параллельные вспомогательные катушки индуктивности
Рассмотрим рисунок (а), на котором катушки индуктивности L 1 и L 2 соединены параллельно с их вспомогательными магнитными полями. Полный ток в цепи определяется как
i = i 1 + i 2
di/dt = (di 1 )/dt + (di 2 )/dt …………. (1)
Напряжение на катушке индуктивности или параллельной ветви определяется как
В = L 1 (di 1 )/dt + M (di 2 )/dt или L 2 (di 2 )/dt + M (di 1 )/dt
L 1 )/dt + M (di 2 )/dt = L 2 (di 2 )/dt + M (di 1 )/dt
(di 1 )/dt3 (1 1 – M) = (di 2 )/dt (L 2 – M)
(di 1 )/dt = (di 2 )/dt ((L 2 – M)) /((Л 1 – М)) …………. (2)
Подставляя уравнение 2 в уравнение 1, получаем
di/dt = (di 2 )/dt ((L 2 – M))/((L 1 – M)) + (di 2 )/dt
di/dt = (di 2 )/dt { (L 2 – M))/((L 1 – M)) + 1} …………. (3)
(3)
Если L T общая индуктивность параллельной цепи индуктивности, то напряжение определяется как (di 1 )/dt + M (di 2 )/dt
di/dt = 1/ L T { L 1 (di 1 )/dt + M (di 2 )/dt }
Подставляя уравнение 2 в приведенное выше уравнение, мы получаем
di/dt = 1/ L T { L 1 (di 2 )/dt (L 2 – M))/((L 1 – M)) + M (di 2 )/dt }
di/dt = 1/ L T { L 1 (L 2 – M))/((L 1 – M)) + M }(di 2 )/dt …………. (4)
Приравнивая уравнения 3 и 4 получаем
(L 2 – M))/((L 1 – M)) + 1 = 1/ L T { L 1 (L 2 – M))/((L 1 – M)) + M }
Упрощение вышеприведенного уравнения, результаты -2M)
Здесь 2M представляет магнитный поток L 1 на L 2 или L 2 на L 1 .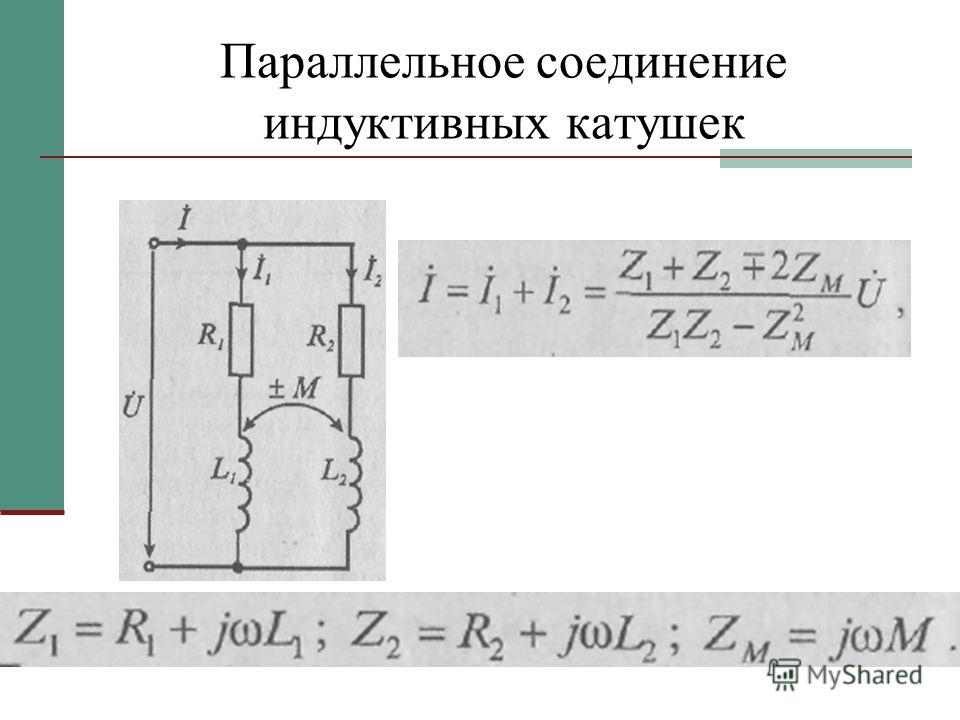 Если величина двух индуктивностей равна идеальной магнитной связи между ними, эквивалентная индуктивность двух катушек индуктивности равна L, потому что L T = L 1 = L 2 = M. В таком случае, если взаимная индуктивность равна нулю, общая индуктивность будет L ÷ 2. 45 мГн соединены параллельно, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Если величина двух индуктивностей равна идеальной магнитной связи между ними, эквивалентная индуктивность двух катушек индуктивности равна L, потому что L T = L 1 = L 2 = M. В таком случае, если взаимная индуктивность равна нулю, общая индуктивность будет L ÷ 2. 45 мГн соединены параллельно, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Sol Учитывая, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных катушек индуктивности, L T = (L 1 L 2 — M 2 )/(L 1 + L 1 ) -2M)
L T = (25*45-20 2 9002 L T = (25*45-20 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 9.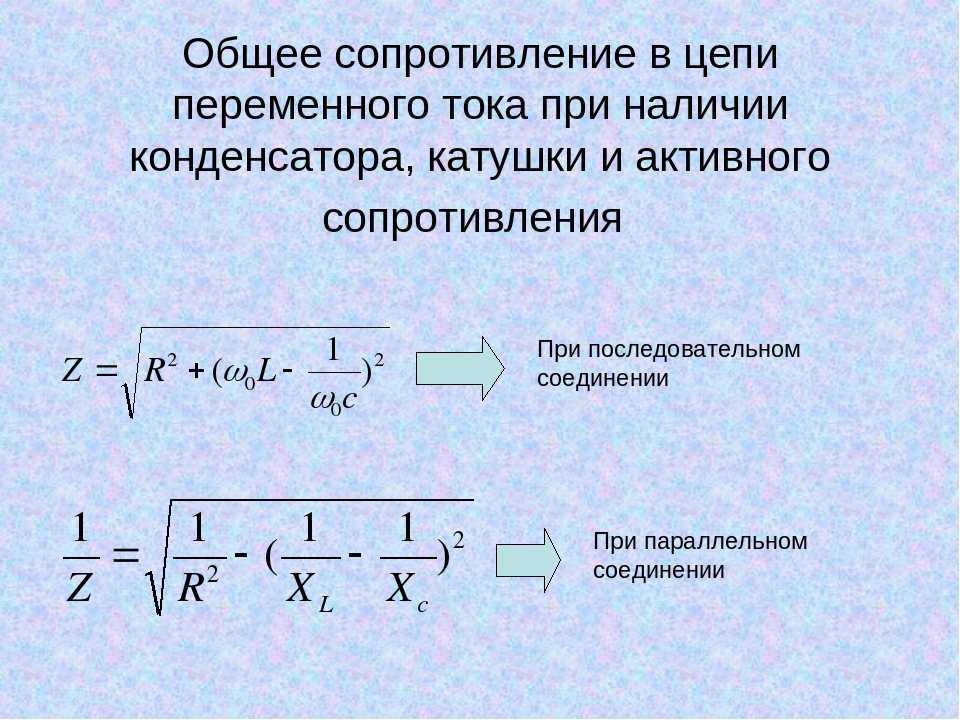 )/(25+45-2*20)
)/(25+45-2*20)
= (1125-400)/(70-40)
= 725/30
= 24,166 мГн
Следовательно, общая индуктивность равна 24,166 мГн.
Параллельные противоположные катушки индуктивности
Аналогичным образом, если мы рассмотрим рисунок (b), на котором катушки индуктивности L 1 и L 2 соединены параллельно с противоположными магнитными полями, общая индуктивность будет равна
L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )+ 2M, если две параллельные индуктивности,
равны при идеальной магнитной связи, эквивалентная индуктивность двух катушек индуктивности будет равна нулю, так как они компенсируют друг друга. Если две катушки индуктивности эффективно позволяют току течь через них, общая индуктивность определяется как (L ± M) ÷ 2.
Параллельные противоположные катушки индуктивности Пример
Пример: если две катушки индуктивности 25 мГн и 45 мГн соединены параллельно друг с другом, рассчитайте общую индуктивность параллельной комбинации. Взаимная индуктивность равна 20 мГн.
Взаимная индуктивность равна 20 мГн.
Sol: Учитывая, что L 1 = 25 мГн
L 2 = 45 мГн
M = 20 мГн
Применяя формулу для полной индуктивности вспомогательных катушек индуктивности, L Тл L 2 M 2 )/(L 1 + L 2 )+2M)
L T = (25*45-20 2 )/(25+45+2*20)
= (1125-400)/(70+40)
= 725/110
= 6,55 мГн
Следовательно, общая индуктивность равна 6,59 миллиГенри.
Резюме
- При соединении двух выводов индуктора соответственно с другим индуктором или выводами индукторов такое соединение называется «параллельным соединением индукторов».
- Когда потоки, создаваемые отдельными катушками индуктивности, имеют одинаковое направление, взаимная индуктивность будет увеличиваться; тогда эти катушки называются «помощными» катушками. Суммарная индуктивность вспомогательных катушек L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )-2M).
 , взаимная индуктивность уменьшится; тогда эти катушки называются «противоположные» катушки. Суммарная индуктивность вспомогательных катушек L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )+2M)
, взаимная индуктивность уменьшится; тогда эти катушки называются «противоположные» катушки. Суммарная индуктивность вспомогательных катушек L T = (L 1 L 2 – M 2 )/(L 1 + L 2 )+2M)
Параллельные катушки индуктивности: определение, формула [Примечания GATE]
Параллельные катушки индуктивности
Параллельные катушки индуктивности представляют собой комбинацию катушек индуктивности, клеммы которых подключены к одним и тем же двум узлам. Катушка индуктивности — это пассивный электрический компонент, который накапливает энергию в своем магнитном поле. Когда выводы отдельных индукторов соединены параллельно с каждым выводом других индукторов, они называются параллельными, как показано ниже:
При параллельном соединении индукторов напряжение на каждом индукторе будет одинаковым, и ток, разделенный между катушками индуктивности. Через наименее противоположный индуктор будет проходить максимальный ток.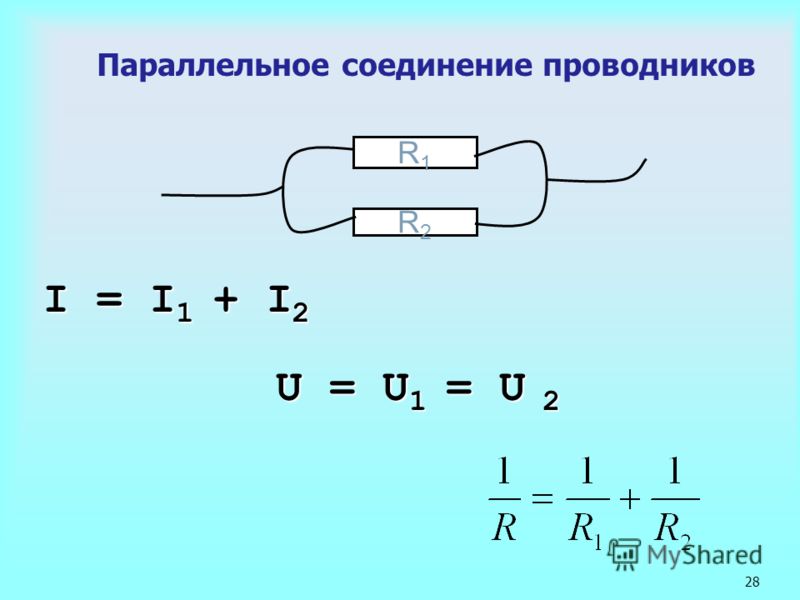 Обратная эквивалентная индуктивность представляет собой сумму обратной величины отдельных индуктивностей, присутствующих в цепи.
Обратная эквивалентная индуктивность представляет собой сумму обратной величины отдельных индуктивностей, присутствующих в цепи.
Загрузить формулы для электроники и средств связи GATE — цифровые схемы
Эквивалентная индуктивность параллельных катушек индуктивности
Рассмотрим цепь из N катушек индуктивности (без учета влияния взаимной индуктивности), включенных параллельно, как показано ниже:
3, где
3 L eq — эквивалентная индуктивность параллельных катушек индуктивности, а i eq (t 0 ) — эквивалентный начальный ток через эквивалентную катушку индуктивности в момент времени t 0
Таким образом, эквивалентная индуктивность и эквивалентный начальный ток определяются по формуле определяется как
Взаимно соединенные индукторы, соединенные параллельно
Магнитный поток, создаваемый индуктором, связан с другими параллельно соединенными индукторами.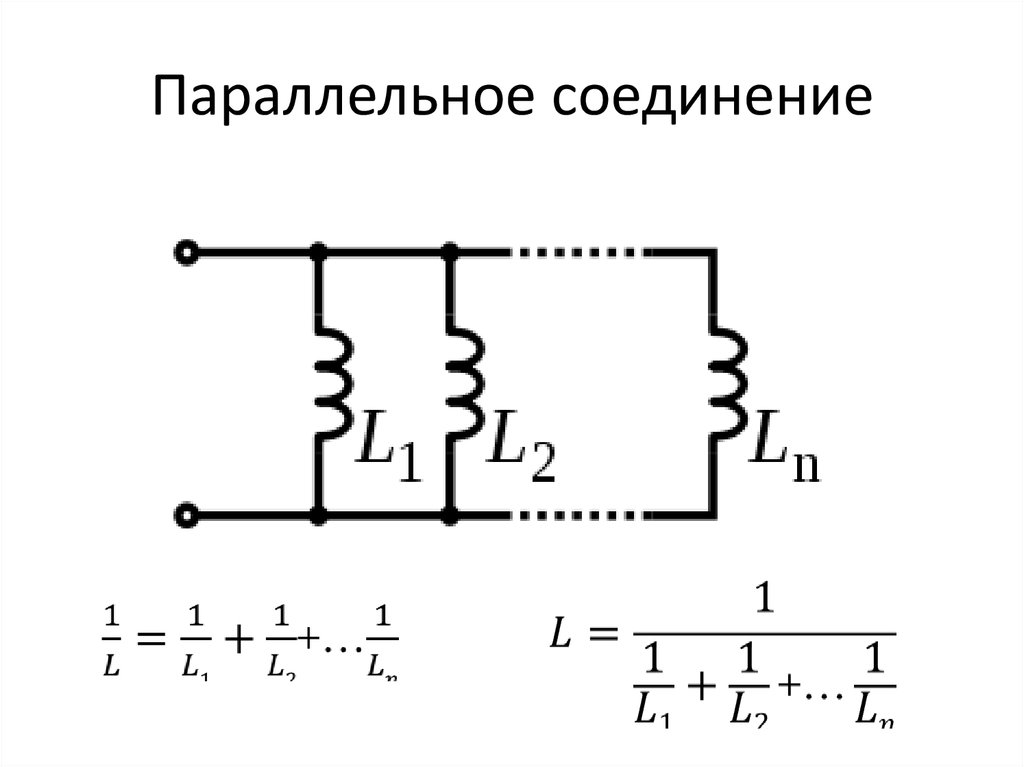 Из-за магнитной связи между параллельными катушками индуктивности эквивалентная индуктивность увеличивается или уменьшается в зависимости от того, являются ли катушки противоположными или вспомогательными по своей природе. В зависимости от направления магнитного потока параллельные катушки индуктивности могут быть двух типов:0003
Из-за магнитной связи между параллельными катушками индуктивности эквивалентная индуктивность увеличивается или уменьшается в зависимости от того, являются ли катушки противоположными или вспомогательными по своей природе. В зависимости от направления магнитного потока параллельные катушки индуктивности могут быть двух типов:0003
- Параллельные вспомогательные индукторы : Когда направление магнитного потока, создаваемого параллельными индукторами, совпадает.
- Параллельные противоположные катушки индуктивности : когда магнитный поток, создаваемый катушками индуктивности, имеет противоположное направление.
Параллельные вспомогательные индукторы
Рассмотрим следующее параллельное соединение индукторов, где два индуктора L 1 и L
2 соединены параллельно, для упрощения предположим две катушки L 1 и L 2 соединены параллельно с их магнитным потоком, помогающим природе, как показано ниже.