Как рассчитать общую емкость при параллельном и последовательном соединении конденсаторов. Какие формулы используются для вычислений. В чем разница между этими способами соединения. Какие преимущества и недостатки у каждого типа соединения конденсаторов.
Параллельное соединение конденсаторов: принцип работы и формула расчета
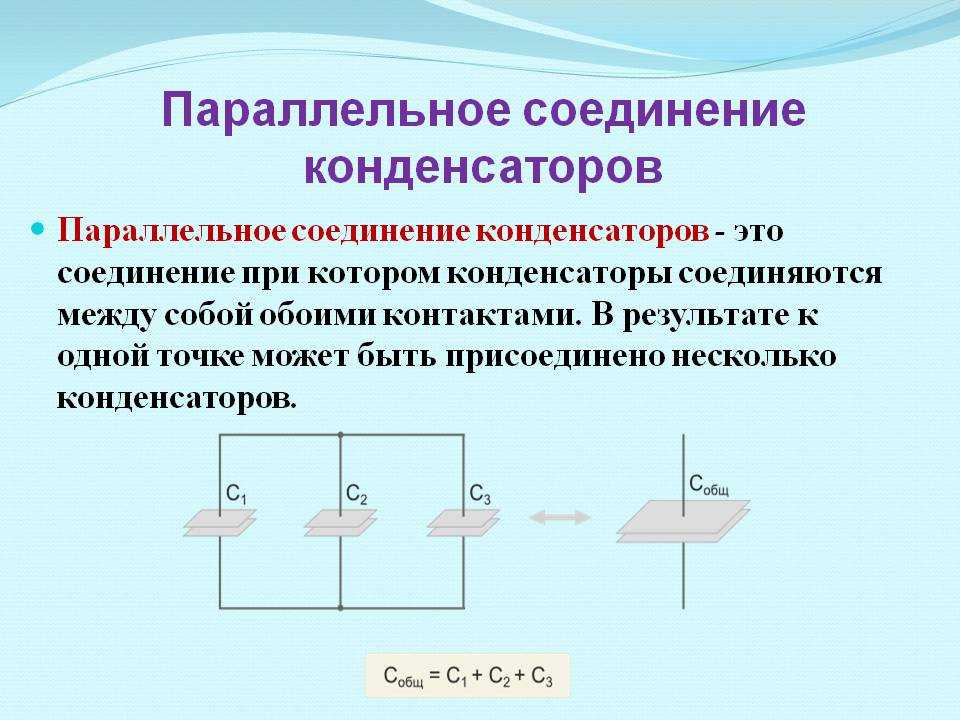
При параллельном соединении конденсаторов все их положительные обкладки соединяются между собой, а все отрицательные — между собой. Такое соединение имеет следующие особенности:
- Напряжение на всех конденсаторах одинаково и равно напряжению источника
- Общий заряд равен сумме зарядов на отдельных конденсаторах
- Общая емкость увеличивается
Формула для расчета общей емкости при параллельном соединении:
C = C1 + C2 + C3 + …
где C — общая емкость, C1, C2, C3 и т.д. — емкости отдельных конденсаторов.
Последовательное соединение конденсаторов: как это работает
При последовательном соединении конденсаторов положительная обкладка одного соединяется с отрицательной обкладкой другого. Особенности такого соединения:
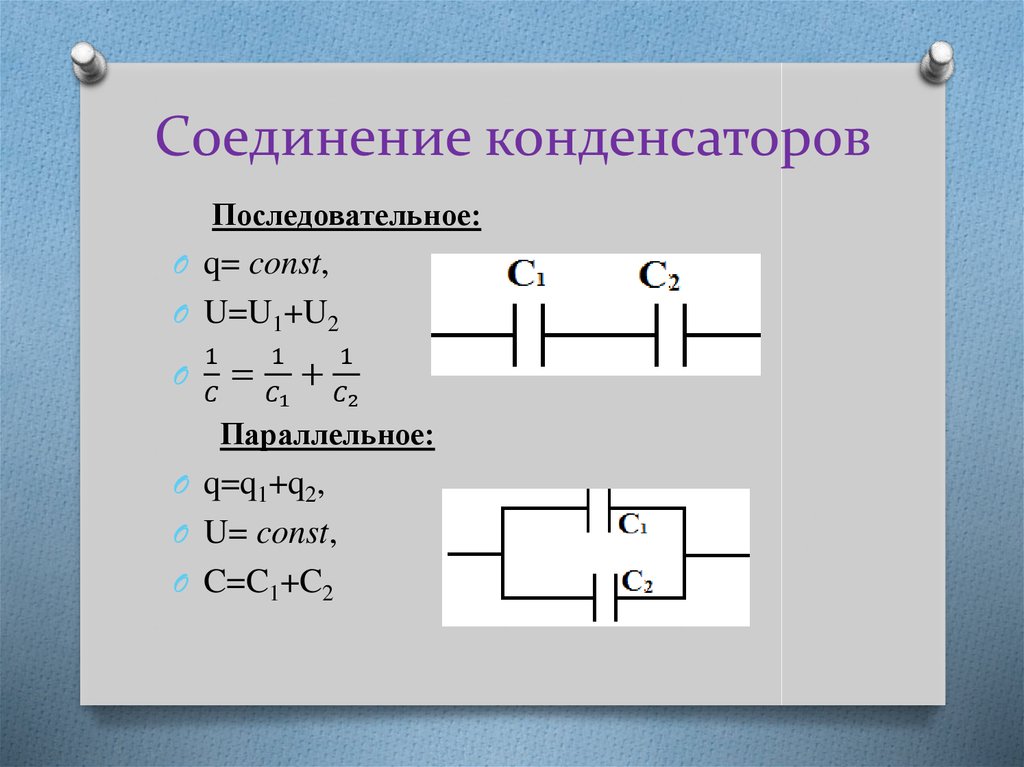
- Заряд на всех конденсаторах одинаков
- Общее напряжение равно сумме напряжений на отдельных конденсаторах
- Общая емкость уменьшается
Формула для расчета общей емкости при последовательном соединении:
1/C = 1/C1 + 1/C2 + 1/C3 + …
где C — общая емкость, C1, C2, C3 и т.д. — емкости отдельных конденсаторов.
Сравнение параллельного и последовательного соединения конденсаторов
Какой тип соединения выбрать? Это зависит от конкретной задачи:
- Параллельное соединение увеличивает общую емкость. Это полезно, когда нужна большая емкость.
- Последовательное соединение уменьшает общую емкость, но позволяет увеличить рабочее напряжение батареи конденсаторов.
При выборе типа соединения следует учитывать требуемую емкость, рабочее напряжение и другие параметры схемы.
Примеры расчета емкости при различных соединениях конденсаторов
Рассмотрим несколько примеров, чтобы лучше понять принципы расчета:
Пример 1: Параллельное соединение
Даны три конденсатора емкостью 10 мкФ, 22 мкФ и 47 мкФ. Рассчитаем их общую емкость при параллельном соединении:
C = 10 мкФ + 22 мкФ + 47 мкФ = 79 мкФ
Как видим, общая емкость увеличилась.
Пример 2: Последовательное соединение
Возьмем те же конденсаторы, но соединим их последовательно:
1/C = 1/10 + 1/22 + 1/47
1/C = 0.1 + 0.0455 + 0.0213 = 0.1668
C = 1/0.1668 ≈ 6 мкФ
Общая емкость уменьшилась по сравнению с емкостью каждого отдельного конденсатора.
Применение различных соединений конденсаторов на практике
Знание принципов соединения конденсаторов важно для многих практических задач:
- В блоках питания часто используют параллельное соединение для увеличения фильтрующей способности
- В высоковольтных цепях применяют последовательное соединение для повышения рабочего напряжения
- В радиотехнике комбинируют различные соединения для получения нужных характеристик колебательных контуров
Смешанное соединение конденсаторов: сложные схемы
На практике часто встречаются схемы, где конденсаторы соединены и последовательно, и параллельно. Для расчета таких цепей:
- Разбейте схему на группы последовательно и параллельно соединенных конденсаторов
- Рассчитайте емкость для каждой группы
- Объедините результаты, используя формулы для последовательного или параллельного соединения
Влияние типа соединения на характеристики конденсаторной батареи
Тип соединения конденсаторов влияет не только на емкость, но и на другие параметры:
- Рабочее напряжение: при последовательном соединении оно увеличивается
- Внутреннее сопротивление: при параллельном соединении оно уменьшается
- Надежность: параллельное соединение более надежно, так как выход из строя одного конденсатора не приводит к полному отказу батареи
Как выбрать оптимальное соединение конденсаторов для конкретной задачи
При выборе типа соединения конденсаторов учитывайте следующие факторы:
- Требуемую общую емкость
- Рабочее напряжение схемы
- Доступное пространство на печатной плате
- Требования к надежности
- Стоимость комплектующих
Правильный выбор типа соединения позволит оптимизировать характеристики устройства и снизить затраты на его производство.
Заключение
Понимание принципов параллельного и последовательного соединения конденсаторов — важный навык для разработчиков электронных устройств. Это позволяет создавать эффективные схемы с оптимальными характеристиками. Практика расчетов и анализа различных конфигураций поможет лучше освоить этот аспект электротехники.

Соединение конденсаторов — Основы электроники
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.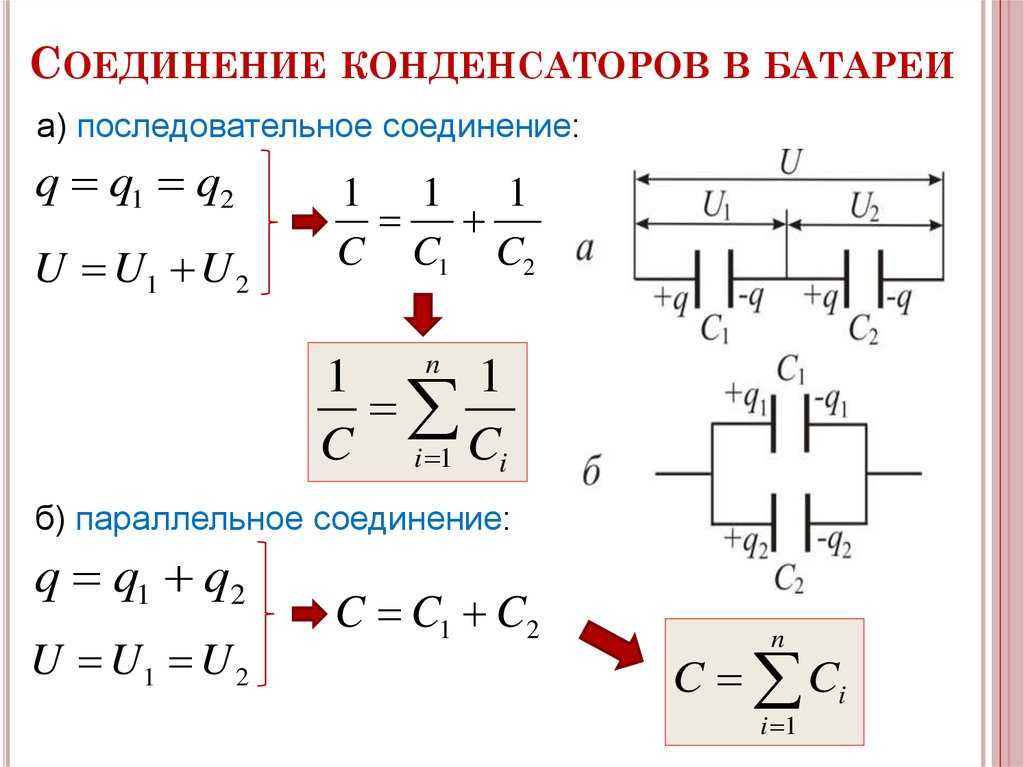
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.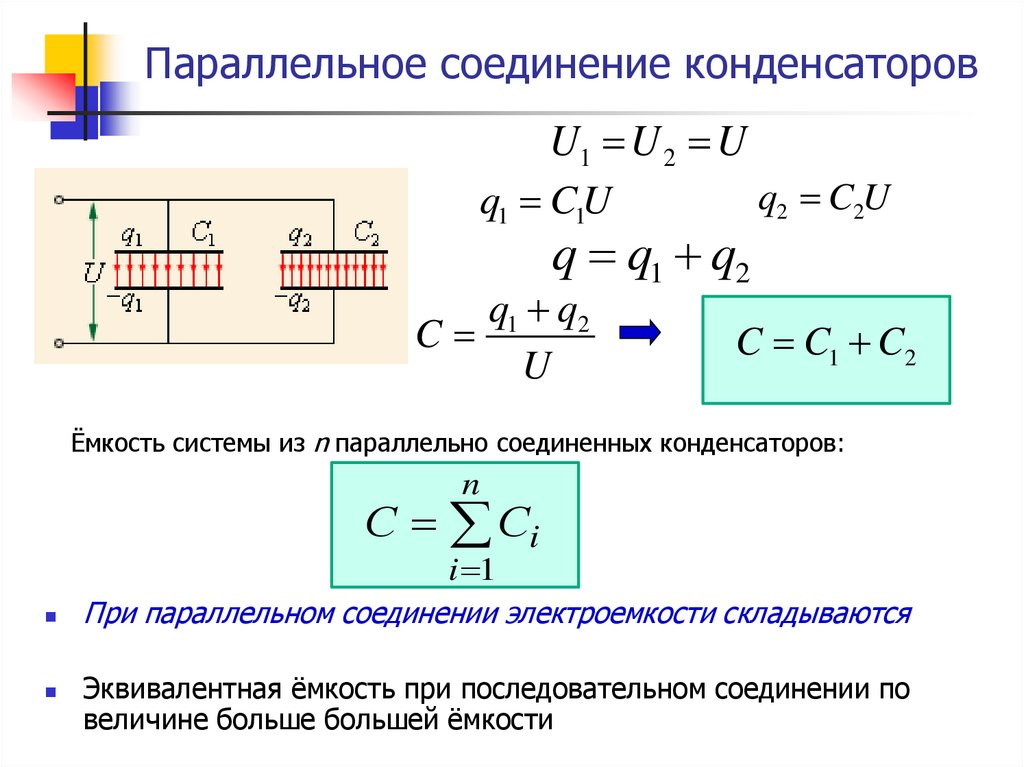
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Параллельное соединение конденсаторов — Без Сменки
29 июня, 2022
1 мин
Физ 🔬
В электрических цепях применяются различные способы соединения конденсаторов. Сегодня мы рассмотрим параллельное.
✍️ Если группа конденсаторов включена в цепь так, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным.
Главное замечание: общая ёмкость конденсаторов при ПАРАЛЛЕЛЬНОМ соединении равна сумме ёмкостей всех соединённых конденсаторов.
Общие формулы найдёшь на картинке 👇
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.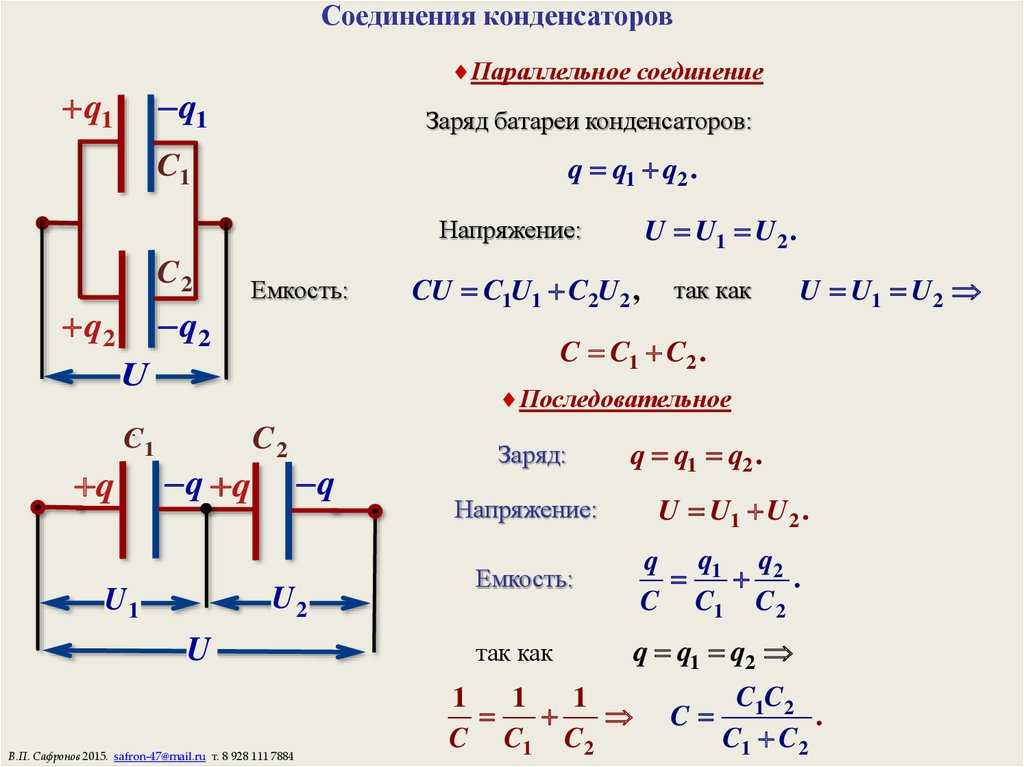 Мы обязательно поправим!
Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
45 подписчиков
+ Подписаться
Редакция Без Сменки
30 июня, 2022
1 мин
Рус 📖
СТИШКИ-ЗАПОМИНАЛКИ ДЛЯ ПАРОНИМОВ
🔹БЕЗОТВЕТСТВЕННО внимал,
Чувством не горя ответным,
И, конечно, понимал,
Что любовь здесь. ..
..
Редакция Без Сменки
20 января, 2022
1 мин
Хим 🧪
Алкены
Продолжаем готовиться к ЕГЭ по химии, разбираем алкены! Это второй класс после алканов, который…
Редакция Без Сменки
20 января, 2022
1 мин
Ист 🤴
Правление и реформы Александра II
ПРАВЛЕНИЕ АЛЕКСАНДРА II (1855-1881 гг.) 💥 ПРИЧИНЫ РЕФОРМ АЛЕКСАНДРА II: 👉🏻 Крымская война. Война…
Редакция Без Сменки
17 мая, 2022
1 мин
Англ 🇬🇧
Устойчивые выражения с предлогами AT, BY, FOR для заданий 32–38
Ловите шпаргалку с устойчивыми выражения с предлогами AT, BY, FOR, которые точно вам помогут на ЕГЭ. ..
..
Редакция Без Сменки
29 июня, 2022
1 мин
Ист 🤴
Борьба за власть
✉️ В 1922 году Ленин составляет «Письмо к съезду», в котором дает характеристику всех ведущих…
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Конденсаторы последовательно и параллельно — Конденсаторы
Конденсаторы
Конденсаторы могут быть соединены последовательно или параллельно, чтобы получить результирующее значение, которое может быть либо сумма отдельных значений (параллельно) или значение меньше, чем у наименьшей емкости (последовательно).
Конденсаторы серии
Цепь, состоящая из нескольких последовательно соединенных конденсаторов, в некоторых отношениях похожа на одну. несколько последовательно соединенных резисторов. В последовательной емкостной цепи один и тот же ток смещения
протекает через каждую часть цепи, и приложенное напряжение будет делиться на отдельные конденсаторы.
На рисунке ниже показана схема, содержащая источник и три последовательных конденсатора.
несколько последовательно соединенных резисторов. В последовательной емкостной цепи один и тот же ток смещения
протекает через каждую часть цепи, и приложенное напряжение будет делиться на отдельные конденсаторы.
На рисунке ниже показана схема, содержащая источник и три последовательных конденсатора.
Конденсаторы последовательно.
Сумма напряжений на конденсаторе должна равняться напряжению источника (закон напряжения Кирхгофа).
Заряды на всех конденсаторах должны быть одинаковыми, так как конденсаторы соединены последовательно и любые движение заряда в одной части цепи должно происходить во всех частях последовательной цепи. Решение уравнения C = Q / V для напряжения через емкость и заряд ( В = Ом / C ), для каждой из серий получены следующие результаты конденсаторы и общая емкость ( C t )
Подставив эти результаты в приведенное выше уравнение закона Кирхгофа для напряжения
Разделив обе части приведенного выше уравнения на общий множитель Q
Взяв обратную величину обеих сторон и предполагая любое количество конденсаторов
Это уравнение является общим уравнением, используемым для расчета общей емкости конденсаторов.
Из приведенных выше формул должно быть видно, что суммарная емкость конденсаторов при последовательном соединении меньше емкости любого из отдельных конденсаторов.
Пример:
Определите общую емкость последовательной цепи, содержащей три конденсатора, номиналы которых
составляют 10 нФ, 0,25 мкФ и 50 нФ соответственно.
Решение:
Общая емкость 8 нФ немного меньше самого маленького конденсатора (10 нФ).
Параллельные конденсаторы
При параллельном соединении конденсаторов (см. рисунок ниже) одна пластина каждого конденсатора подключается напрямую.
к одной клемме источника, а другая пластина каждого конденсатора подключена к
другой терминал источника. На рисунке ниже все отрицательные пластины конденсаторов
соединены вместе, и все положительные пластины соединены вместе.
Суммарная (эквивалентная) емкость Кл t , следовательно, выступает как емкость с пластиной
площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее,
емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов
увеличивает площадь пластины и тем самым увеличивает общую емкость.
На рисунке ниже все отрицательные пластины конденсаторов
соединены вместе, и все положительные пластины соединены вместе.
Суммарная (эквивалентная) емкость Кл t , следовательно, выступает как емкость с пластиной
площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее,
емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов
увеличивает площадь пластины и тем самым увеличивает общую емкость.
Параллельные конденсаторы.
Полную емкость можно рассчитать математически. Применяя уравнение C = Q / V на каждый конденсатор и на общую емкость
Общий заряд Q t есть сумма зарядов на каждом конденсаторе
Из уравнения C = Q / V следует, что Q = C V , а если заряд записывается в этой форме и подставляется в приведенное выше уравнение, это уравнение приводит к
Разделив обе части приведенного выше уравнения на общий множитель В и приняв любое количество конденсаторов
Это уравнение математически утверждает, что общая емкость ряда конденсаторов
параллельно сумма отдельных емкостей.
Пример:
Определите общую емкость в параллельной емкостной цепи, содержащей три конденсатора.
значения которых составляют 30 нФ, 2 мкФ и 0,25 мкФ соответственно.
Решение:
Конденсаторы, включенные последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Выводить выражения для полной емкости при последовательном и параллельном подключении.
- Определите последовательное и параллельное соединение конденсаторов.
- Рассчитайте действующую емкость при последовательном и параллельном подключении по отдельным емкостям.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9. 0143 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
0143 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
Емкость в серии
На рис. 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]C=\frac{Q}{V}\\[/latex].
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов, когда приложено напряжение V . Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности.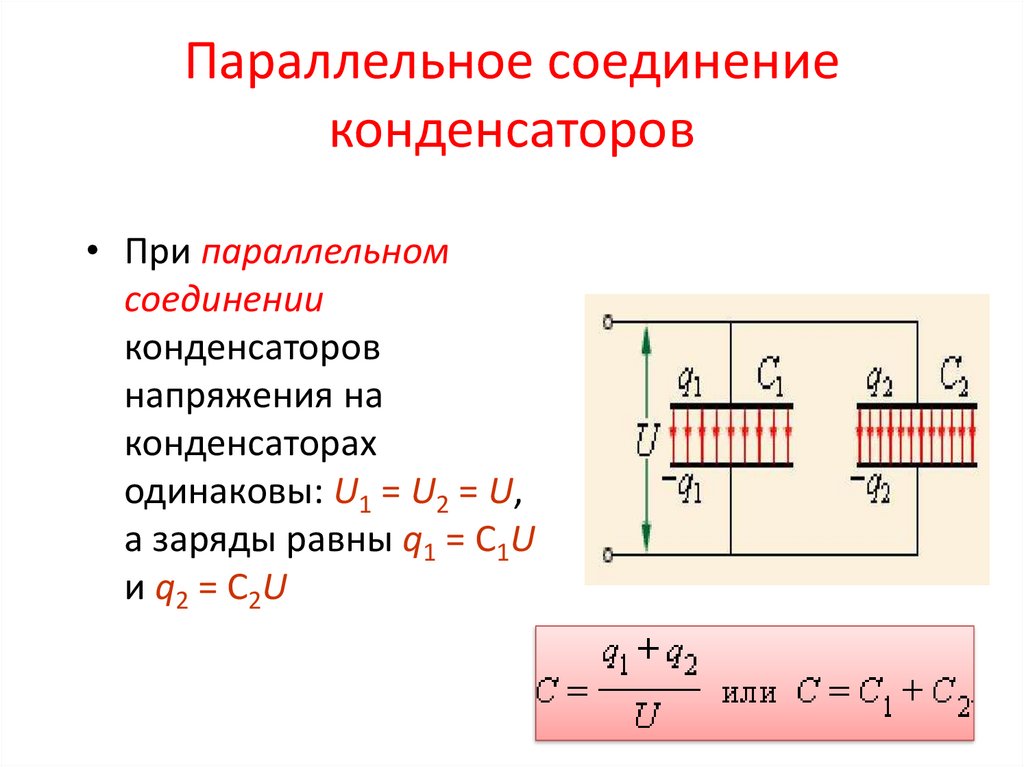 (См. рис. 1b.) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
(См. рис. 1b.) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанное на рисунке 1. Решение [latex]C=\frac{Q}{V}\\[/latex] для В дает [ латекс]V=\frac{Q}{C}\\[/латекс]. Таким образом, напряжения на отдельных конденсаторах равны [latex]V_1=\frac{Q}{C_1},V_2=\frac{Q}{C_2},\text{ и }V_3=\frac{Q}{C_3}\\ [/латекс].
Общее напряжение равно сумме отдельных напряжений:
В = В 1 + В 2 + В 3 3
Теперь, назвав общую емкость C S для последовательной емкости, учтите, что
[латекс]V=\frac{Q}{C_{\text{S}}}=V_1+V_2+V_3\\ [/латекс].
Ввод выражений для В 1 , В 2 и В 3 , получаем
[латекс]\frac{Q}{C_{\text{S}}}=\frac{Q}{C_{1}}+\frac{Q}{C_{2} }+\frac{Q}{C_{3}}\\[/latex].
Отменив Q с, получим уравнение для полной емкости в ряду C S равной
[латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots,\\[/latex]
, где «…» означает что выражение справедливо для любого числа последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к полной емкости C S меньше любой из отдельных емкостей C 1 , C 2 , …, как показано в Примере 1.
Полная последовательная емкость,
C сПолная последовательная емкость:
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1 }}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots\\[/latex]
Пример 1.
 Что такое последовательная емкость?
Что такое последовательная емкость? Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.
Решение
Ввод заданных емкостей в выражение для [латекс]\фракция{1}{С_{\текст{S}}}\\[/латекс] дает [латекс]\фракция{1}{С_{\ text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex].
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{1,000 \mu\text{F}}+\frac{1}{5,000 \mu\text{F }}+\frac{1}{8.000 \mu\text{F}}=\frac{1.325}{\mu\text{F}}\\[/latex]
Инвертирование для нахождения C S дает [латекс] C _ {\ text {S}} = \ frac {1,325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [ /латекс].
Обсуждение
Общая ёмкость серии C s меньше, чем наименьшая индивидуальная ёмкость, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
[латекс]\frac{1}{C_{\text{S}}}=\frac{40}{40 \mu\text{F}}+\frac{8}{40 \mu\text{F }}+\frac{5}{40 \mu\text{F}}=\frac{53}{40\mu\text{F}}\\[/latex]
, так что
[latex]C_ {\text{S}}=\frac{40\mu\text{F}}{53}=0,755\mu\text{F}\\[/latex]
Параллельные конденсаторы
На рисунке 2a показана параллель соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную полную емкость C p , сначала отметим, что напряжение на каждом конденсаторе равно В , такое же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения. ) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q представляет собой сумму отдельных сборов: Q = Q 1 + Q 2 + Q 3 .
) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q представляет собой сумму отдельных сборов: Q = Q 1 + Q 2 + Q 3 .
Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.
Используя отношение Q = CV , we see that the total charge is Q = C p V , and the individual charges are Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V .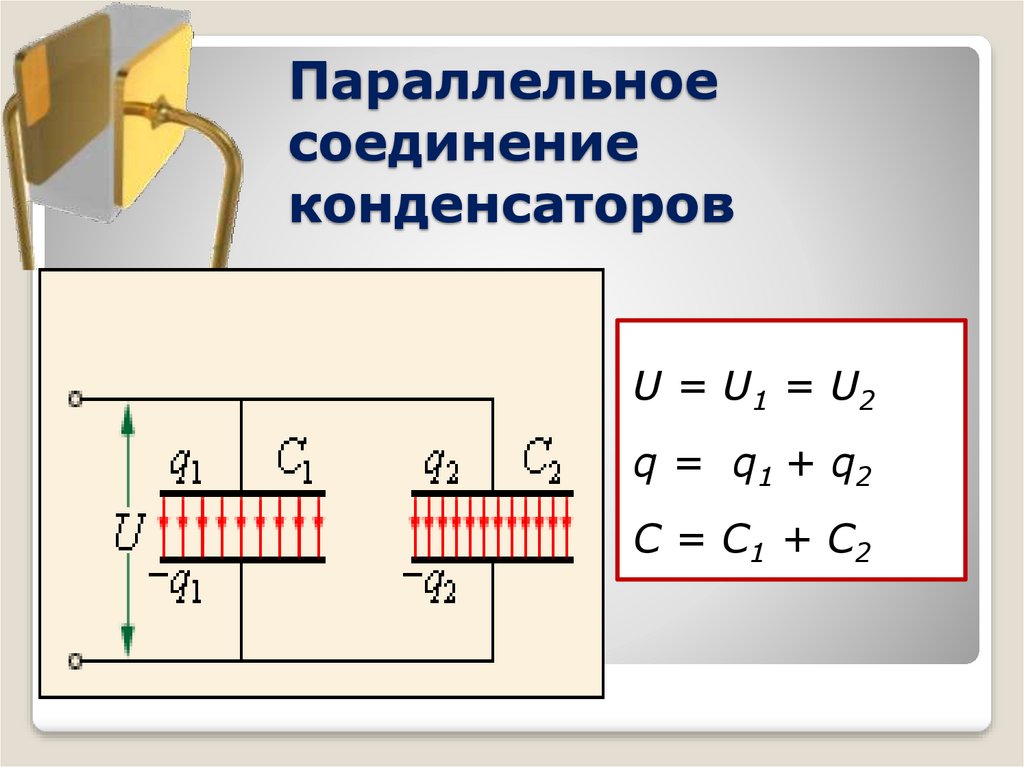 Ввод их в предыдущее уравнение дает
Ввод их в предыдущее уравнение дает
C p В = В 1 В + В 2 В + В 3 3.
Отмена V Из уравнения мы получаем уравнение для общей емкости в параллельной
C P : C P = C 31131+++++++++++. C 3 + ….
Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … ” указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в примере 1 были соединены параллельно, их емкость была бы
C p = 1,000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ.
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рис. 2b.
2b.
Суммарная емкость при параллельном подключении,
C PОбщая емкость в параллельной C P = C 1 + C 2 ++ C 2 ++ C 2 ++ C . 9014. быть комбинациями последовательного и параллельного. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.
Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (б) C 1 и C 2 последовательно; их эквивалентная емкость C S меньше любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме C S и C 3 .
Пример 2. Смесь последовательных и параллельных емкостей
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ( C 1 = 1,000 мкФ, C 2 = 3,000 мкФ и C 3 = 8,000 мкФ), и округлите ответ до трех знаков после запятой.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы С 1 и С 2 включены последовательно. Их комбинация, обозначенная на рисунке C S , параллельна С 3 .
Решение
Поскольку C 1 и C 2 соединены последовательно, их общая емкость определяется выражением [латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex].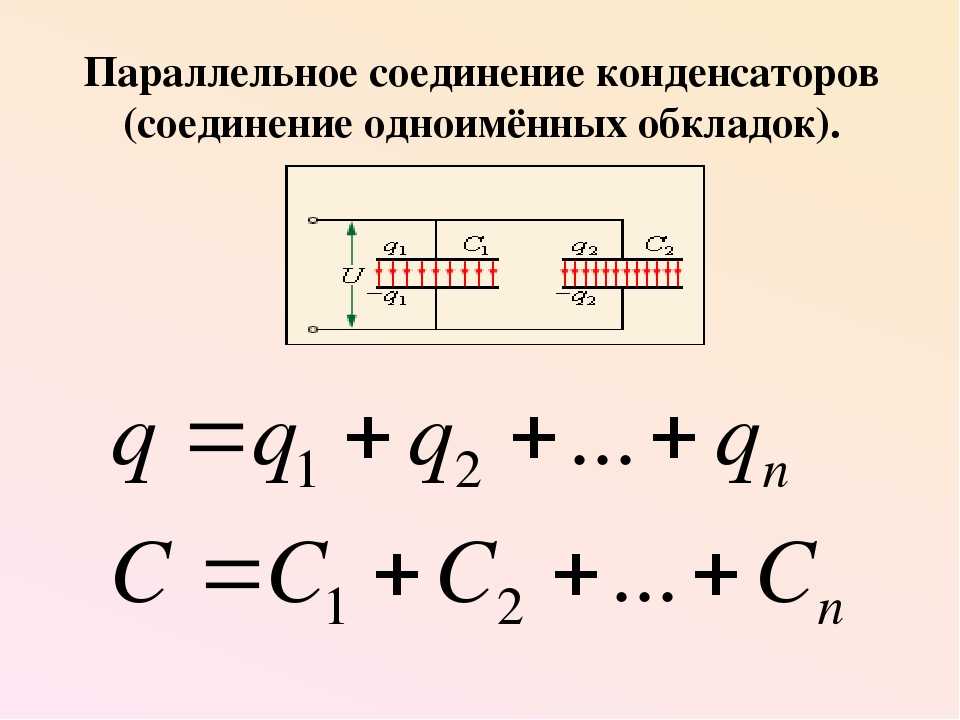 Ввод их значений в уравнение дает
Ввод их значений в уравнение дает
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2} }=\frac{1}{1.000\mu\text{F}}+\frac{1}{5.000\mu\text{F}}=\frac{1.200}{\mu\text{F}}\\ [/латекс].
Инвертирование дает C S = 0,833 мкФ.
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общее количество равно сумме
[латекс]\begin{array}{lll}C_{\text{tot}}&=&C_{\text{S}}+C_{\text{S}}\\\ текст { }&=&0,833\мю\текст{F}+8,000\мю\текст{F}\\\текст{ }&=&8,833\мю\текст{F}\конец{массив}\\[ /latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.
Резюме раздела
- Суммарная емкость последовательно [латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{ 2}}+\frac{1}{C_{3}}+\dots\\[/latex]
- Суммарная емкость при параллельном включении C p = C 1 + C 2 + C 3 + …
- Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.
- Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
- Если вы хотите хранить большое количество энергии в конденсаторной батарее, вы бы соединили конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
- Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Сочетание последовательного и параллельного соединения конденсаторов.
- Предположим, вам нужна батарея конденсаторов общей емкостью 0,750 Ф, и у вас имеется множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
- Какую общую емкость можно получить, соединив вместе конденсаторы емкостью 5,00 мкФ и 8,00 мкФ?
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Сочетание последовательного и параллельного соединения конденсаторов.
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.


