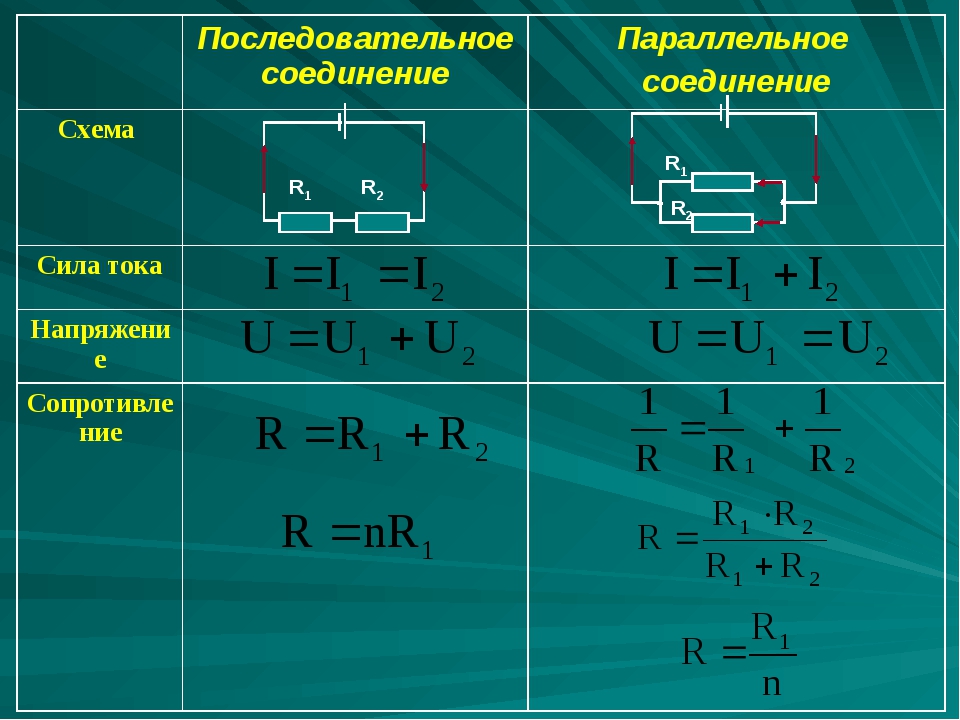
Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы используются для вычисления эквивалентного сопротивления. Чем отличаются последовательное и параллельное соединения. Какие законы электротехники применяются при расчетах.
Основные принципы соединения резисторов
При построении электрических цепей резисторы могут соединяться различными способами. Наиболее распространены два типа соединений:
- Последовательное соединение
- Параллельное соединение
От типа соединения зависит общее (эквивалентное) сопротивление участка цепи и распределение токов и напряжений. Рассмотрим особенности каждого типа соединения и формулы для расчета.
Последовательное соединение резисторов
При последовательном соединении резисторы включаются один за другим, образуя неразветвленную цепь (рис. 1).
Рис. 1. Схема последовательного соединения резисторов
Особенности последовательного соединения:
- Через все резисторы протекает одинаковый ток
- Напряжение на участке цепи равно сумме напряжений на отдельных резисторах
- Общее сопротивление увеличивается при добавлении резисторов
Формула для расчета общего сопротивления при последовательном соединении:
R = R1 + R2 + … + Rn
где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных резисторов.
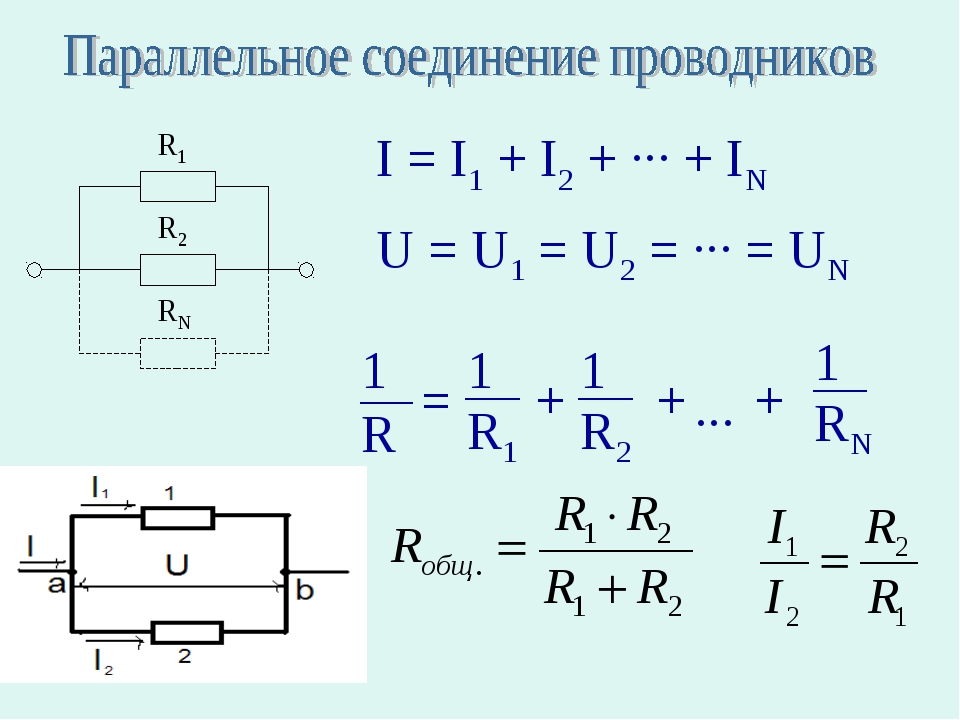
Параллельное соединение резисторов
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи (рис. 2).
Рис. 2. Схема параллельного соединения резисторов
Особенности параллельного соединения:
- На всех резисторах одинаковое напряжение
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление уменьшается при добавлении резисторов
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + … + 1/Rn
где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных резисторов.
Законы, применяемые при расчетах
При анализе цепей с последовательным и параллельным соединением резисторов используются следующие законы:
- Закон Ома: I = U / R
- Первый закон Кирхгофа: сумма токов, втекающих в узел, равна сумме вытекающих токов
- Второй закон Кирхгофа: сумма падений напряжений на элементах замкнутого контура равна сумме ЭДС источников в этом контуре
Применение этих законов позволяет рассчитать токи и напряжения в цепях с различными соединениями резисторов.
Примеры расчета общего сопротивления
Рассмотрим несколько примеров расчета эквивалентного сопротивления для разных соединений резисторов.
Пример 1. Последовательное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом
Найти: общее сопротивление R
Решение:
R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Ответ: общее сопротивление равно 60 Ом.
Пример 2. Параллельное соединение
Дано: R1 = 6 Ом, R2 = 3 Ом
Найти: общее сопротивление R
Решение:
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 1 / (1/2) = 2 Ом
Ответ: общее сопротивление равно 2 Ом.
Применение соединений резисторов
Различные способы соединения резисторов широко применяются в электронике и электротехнике:
- Делители напряжения (последовательное соединение)
- Шунты для расширения пределов измерения приборов (параллельное соединение)
- Эквивалентные сопротивления в сложных цепях
- Согласование сопротивлений в линиях передачи
Понимание принципов соединения резисторов позволяет грамотно проектировать электрические схемы и анализировать их работу.
Особенности расчета сложных цепей
В реальных электрических схемах часто встречаются комбинации последовательного и параллельного соединения резисторов. Для расчета таких цепей применяют следующий алгоритм:
- Выделяют участки с простыми соединениями (только последовательными или только параллельными)
- Заменяют эти участки эквивалентными сопротивлениями
- Повторяют процесс, пока вся схема не сведется к одному эквивалентному резистору
Этот метод позволяет рассчитать общее сопротивление сложной цепи и определить токи и напряжения на отдельных участках.
Заключение
Последовательное и параллельное соединение резисторов — базовые концепции в электротехнике. Понимание принципов расчета общего сопротивления при различных соединениях необходимо для анализа и проектирования электрических цепей. Применение законов Ома и Кирхгофа позволяет решать задачи любой сложности, связанные с резистивными цепями.
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:Это справедливо и для большего количества соединённых последовательно резисторов:
R = R1 + R2 + R3 + R4 + … + Rn.
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Параллельное соединение резисторов (формула)
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
| Сопротивление из двух резисторов: |
R = | R1 × R2 |
| R1 + R2 |
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
Сопротивление параллельных резисторов
| 1 | = | 1 | + | + | 1 | + . .. .. |
|
| R | R1 | R2 | R3 |
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее.
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
При последовательном соединении мощность резисторов также складывается.
 Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.
Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.
О параллельном соединении резисторов: расчет подключения, определение мощности
Достаточно большое количество радиолюбителей занимается сборкой, модернизацией и ремонтом разнообразных схем; для кого-то это работа, а для кого-то просто увлечение или хобби. В любом случае необходимо иметь представление о процессах, происходящих в схеме, физических свойствах самих элементов цепи и особенностях взаимодействия элементов между собой.
Диагностика электронных схем
Компоненты электронных схем
Все множество компонентов и элементов делится на две основные группы:
- Активные элементы, особенностью которых является возможность усиливать проходящий по ним сигнал. К такой группе, в первую очередь, относятся транзисторы и построенные на их основе схемы;
- Пассивные элементы, которые не предназначены для усиления сигнала.
 Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.
Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.
Наиболее простым элементом по своим характеристикам и свойствам является резистор. Основное назначение резисторов заключается в ограничении величины тока, проходящего по нему. Все существующие резисторы подразделяются на два вида:
- Постоянные – шунты, имеющие постоянное значение электрического сопротивления;
- Переменные – шунты, сопротивление между контактами которого меняется механическим путем;
Центральными характеристиками резисторов являются:
- Сила рассеивания, которая представляет собой максимальную мощность тока, выдерживаемую шунтом долгое время и рассеиваемую в виде тепла при постоянных характеристиках самого шунта;
- Параметр точности представляет собой максимальное отступление от величины реального сопротивления в течение эксплуатации шунта;
- Умение компонента противодействовать прохождению электротока в электрической цепи называется сопротивлением.
 Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.
Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.
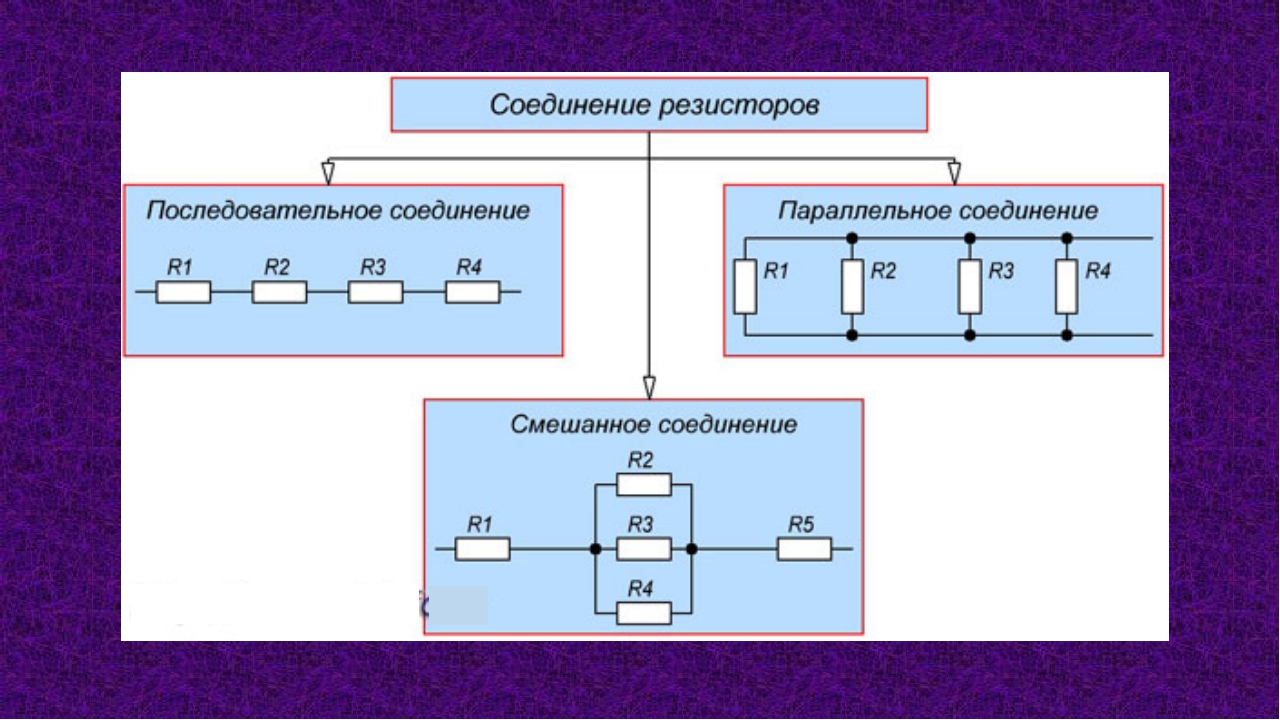
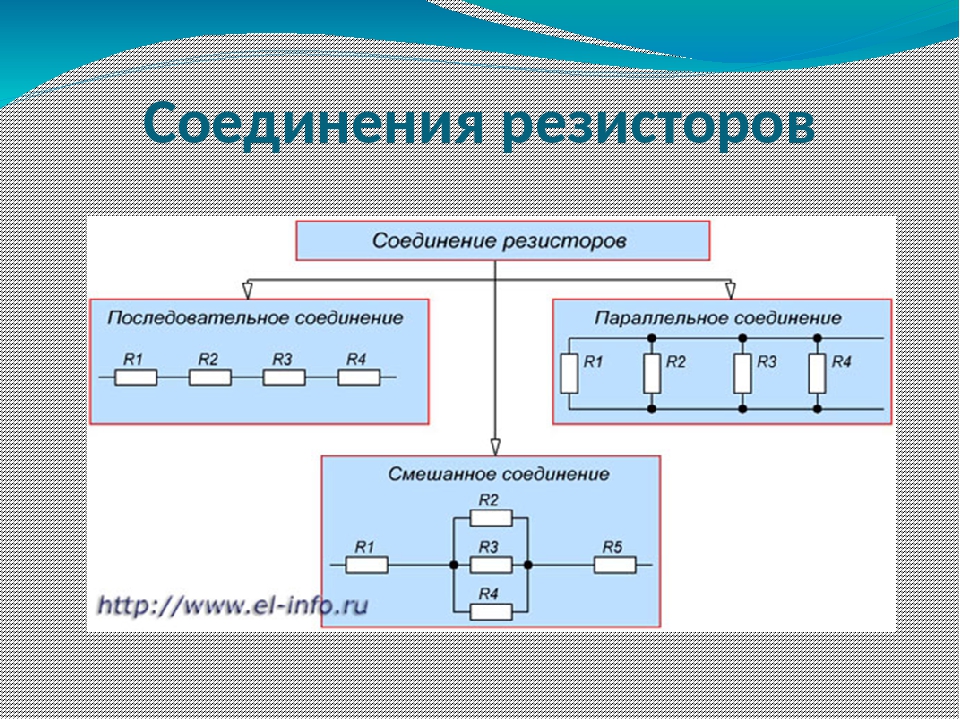
Соединение резисторов
В радиотехнике встречается ряд конфигураций по состыковке компонентов в целом и шунтов в частности. Совмещение шунтов подразделяется на такие виды:
- Набор параллельных резисторов;
- Последовательное подключение шунтов;
- Смешанное соединение резисторов.
Сопряжение резисторов
Последовательное соединение резисторов
Последовательным сопряжением компонентов называют такое сплочение нескольких шунтов, при котором каждый одиночный шунт подключается к следующему единичному шунту только в одной точке. Поскольку при последовательном включении по шунтам протекает одинаковый электрический ток, сталкивающийся постоянно с новой преградой в виде последующего сопротивления, то суммарное противодействие возрастает и равно сложению сопротивлений. Согласно картинке выше, при последовательном соединении суммарное последовательное сопротивление равно:
Rобщ=R1+R2, где:
- Rобщ – суммарное противостояние цепи;
- R1 – противодействие первого шунта;
- R2 – противодействие второго шунта
Последовательное сопряжение шунтов
Напряжение при последовательном соединении компонентов понижается на любом отдельном элементе, опираясь на закон Ома, суммарное напряжение такого участка необходимо складывать. Соответственно, результирующий показатель напряжения возможно найти по выражению:
Соответственно, результирующий показатель напряжения возможно найти по выражению:
Uобщ=UR1+UR2, где:
- Uобщ – суммарное напряжение участка;
- UR1 – разность потенциалов на первом шунте;
- UR2 – разность потенциалов на втором шунте.
Поскольку проходящий по компонентам электроток неизменный, то справедливо равенство:
Iобщ=IR1=IR2, где:
- Iобщ – суммарная сила тока;
- IR1 – электроток первого шунта;
- IR2 – электроток второго шунта.
Дополнительная информация. При последовательной состыковке компонентов варьирование сопротивления любого элемента из этого участка влечет за собой как изменение сопротивления всего участка, так и изменение силы электротока этого участка.
Параллельное сопряжение резисторов
Параллельное соединение резисторов представляет собой такое соединение элементов, при котором резисторы подключаются друг к другу обоими выводами.
Дополнительная информация. В радиоэлектронике параллельные резисторы могут использоваться с целью снижения суммарного противодействия электротоку. Также мощность при параллельном стыковании компонентов возрастает сравнительно с каждым отдельным элементом.
При параллельном соединении шунтов через каждый единичный элемент потечет свой ток, и значение силы электротока будет обратно пропорционально сопротивлению компонента. Поскольку суммарная проводимость параллельного соединения возрастает, а общая сопротивляемость электротоку убывает, то, согласно закону Ома, общее сопротивление при параллельном соединении равняется:
- Gобщ =1/Rобщ =1/R1+1/R2+1/R3;
- Rобщ =1/Gобщ =R1R2R3/R1R2+R2R3+R1R3, где Gобщ – общая проводимость цепи.
Напряжение при параллельном соединении компонентов равняется разности потенциалов на каждом из компонентов:
Uобщ=UR1=UR2=UR3.
Направление токов в параллельной цепи
Калькулятор поможет определить суммарную силу тока цепи при параллельном совмещении, соответствующую сумме токов через каждый шунт:
Iобщ=IR1+IR2+IR3.
Смешанное соединение резисторов
Смешанное соединение резисторов представляет собой последовательное и параллельное соединение резисторов одновременно. Для определения суммарного противодействия цепи с разнотипной состыковкой шунтов требуется придерживаться последовательного алгоритма:
- Схематически разделить цепь на отдельные участки, включающие в себя последовательное и параллельное соединение сопротивлений;
- Рассчитать суммарный импеданс всех разделенных областей;
- Представить первоначальную схему в виде сопротивлений, имеющих некоторую величину эквивалентного сопротивления;
- Находите суммарное противодействие упрощенной схемы.
Понимание, что такое последовательное и параллельное соединение проводников, и поведения электрических характеристик при таком соединении позволит без особого труда проводить расчет, конструировать устройства различных конфигураций с требуемыми значениями параметров. Появится возможность упрощать и модернизировать схемы, вносить дополнительно какие-либо новшества в цепь.
Видео
Оцените статью:последовательное, параллельное, смешанное соединение. Расчет сопротивления
Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.
Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.
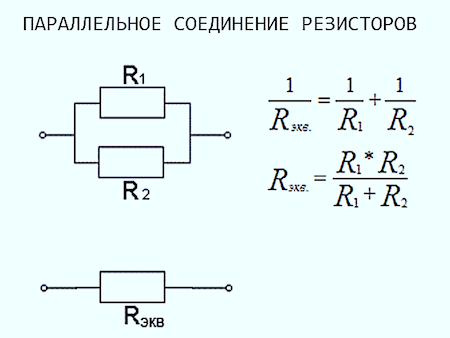
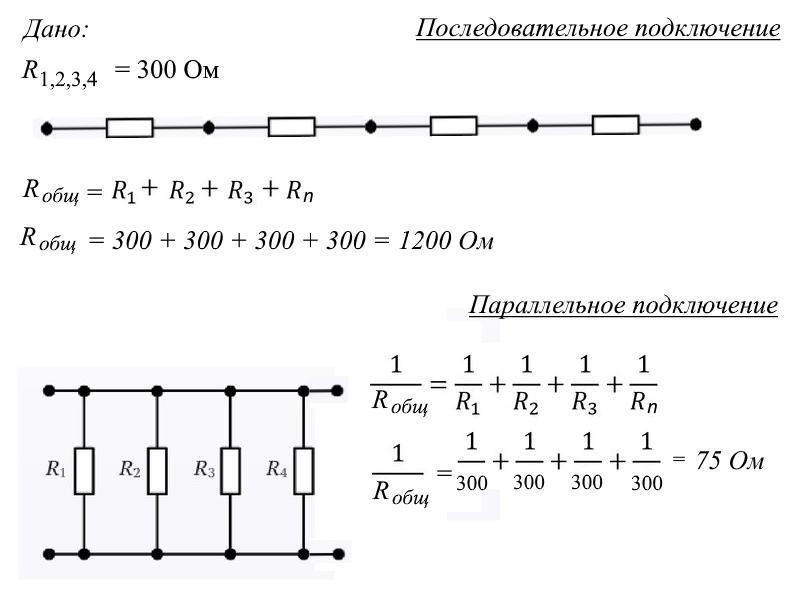
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I1+I2+..In
С учетом этого имеем:
- I=U/R
- I1=U/R1
- I2=U/R2
- In=U/Rn
- U/R=U/R1+U/R2+.
 ..U/Rn
..U/Rn - 1/R=1/R1+1/R2+…1/Rn
Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно: R=(R1*R2)/(R1+R2).
Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R1=R2) их общее сопротивление будет вдвое меньше любого из них. Это полезно помнить.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:
- U=I*R
- I=I1=I2=…In
- U=U1+U2+…Un
- I*R=I*R1+I*R2+…I*Rn
- R=R1+R2+…Rn
То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.
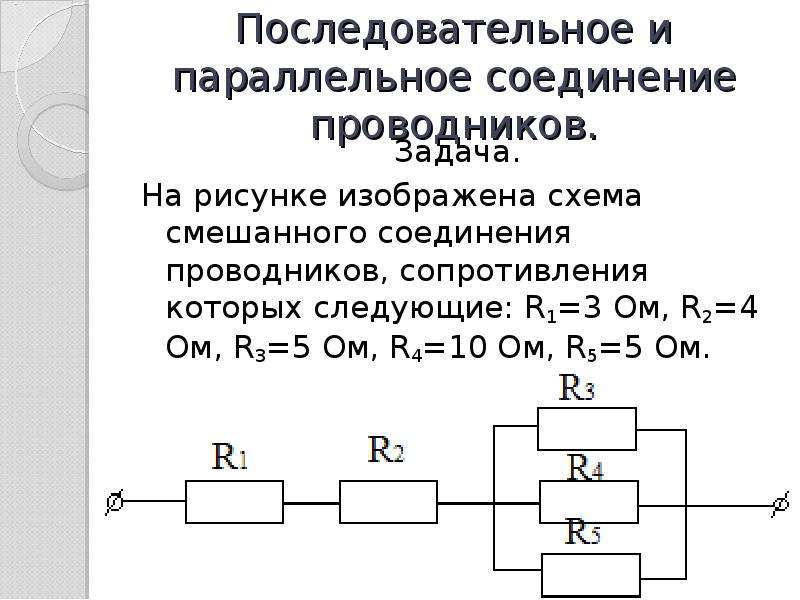
СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.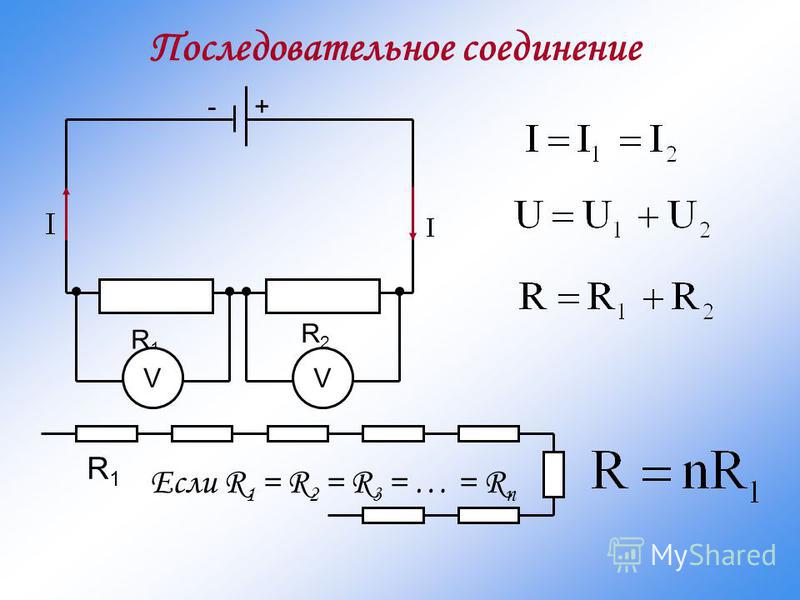 3).
3).
Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:
- последовательное сопротивление резисторов Rпосл=R1+R2
- параллельное соединение R=(Rпосл*R3)/(Rпосл+R3)
Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.
Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:
- Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.
Например, для рисунка 3.a, если фактическая погрешность R1 составляет +10%, а R2 имеет +15%, то для Rпосл она будет +25%.
Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.
- Необходимость получить большую мощность.
Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.
Про мощность и номиналы резисторов можно почитать здесь.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Последовательное и параллельное соединение сопротивлений Википедия
Резисторы разных размеров, типов, мощности с проволочными выводами Почтовая марка Германии 1994 годаРези́стор (англ. resistor, от лат. resisto — сопротивляюсь) — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления[1], предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, ограничения тока, поглощения электрической энергии и др.[2]. Весьма широко используемый компонент практически всех электрических и электронных устройств.
Весьма широко используемый компонент практически всех электрических и электронных устройств.
Схема замещения резистора чаще всего имеет вид параллельно соединённых сопротивления и ёмкости. Иногда на высоких частотах последовательно с этой цепью включают индуктивность. В схеме замещения сопротивление — основной параметр резистора, ёмкость и индуктивность — паразитные параметры.
Линейные и нелинейные резисторы
Все резисторы делятся на линейные и нелинейные.
Сопротивления линейных резисторов не зависят от приложенного напряжения или протекающего тока.
Сопротивления нелинейных резисторов изменяются в зависимости от значения приложенного напряжения или протекающего тока. Например, сопротивление осветительной лампы накаливания при отсутствии тока в 10-15 раз меньше, чем в режиме освещения. В линейных резистивных цепях форма тока совпадает с формой напряжения, вызвавшего этот ток.
Основные характеристики и параметры резисторов
- Номинальное сопротивление — основной параметр.
- Предельная рассеиваемая мощность.
- Температурный коэффициент сопротивления.
- Допустимое отклонение сопротивления от номинального значения (технологический разброс в процессе изготовления).
- Предельное рабочее напряжение.
- Избыточный шум.
- Максимальная температура окружающей среды для номинальной мощности рассеивания.
- Влагоустойчивость и термостойкость.
- Коэффициент напряжения. Учитывает явление зависимости сопротивления некоторых видов резисторов от приложенного напряжения.
Определяется по формуле: KU=R1−R2R1∗100%{\displaystyle K_{U}={\frac {R_{1}-R_{2}}{R_{1}}}*100\%}, где R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — сопротивления, измеренные при напряжениях, соответствующих 10%{\displaystyle 10\%}-ной и 100%{\displaystyle 100\%}-ной номинальной мощности рассеяния резистора.[3]
Некоторые характеристики существенны при проектировании устройств, работающих на высоких и сверхвысоких частотах, это:
- Паразитная ёмкость.
- Паразитная индуктивность.
Обозначение резисторов на схемах
а) обозначение, принятое в России и в Европеб) принятое в США
По стандартам России условные графические обозначения резисторов на схемах должны соответствовать ГОСТ 2.728-74. В соответствии с ним, постоянные резисторы обозначаются следующим образом:
Общее сопротивление цепи — правила, формулы и примеры вычисления
Общие сведения
Прохождение электрического тока через проводник зависит от его проводимости. Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом.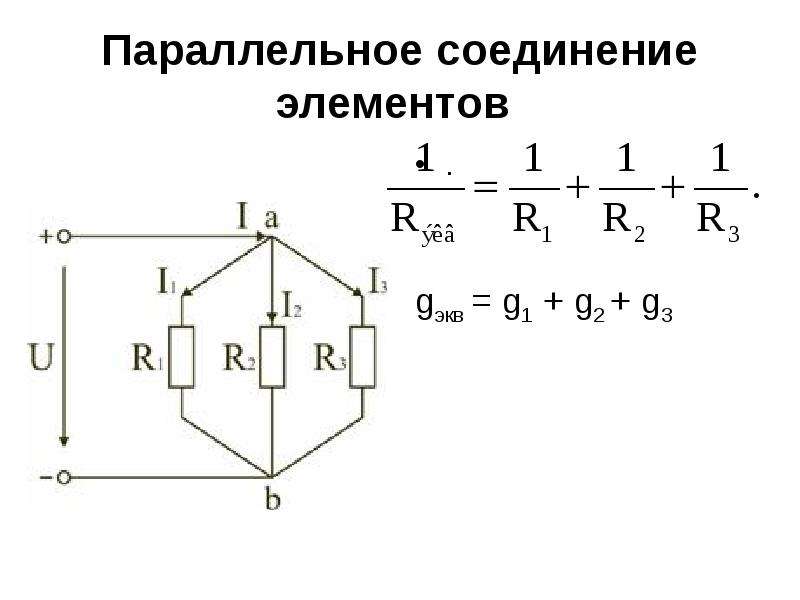 Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.
Реальная замкнутая электрическая цепь состоит из множества активных и пассивных радиоэлементов. Каждый из них обладает каким-то значением сопротивления. В этом случае говорят о внутреннем сопротивлении прибора.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
Последовательное подключение
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.
При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
В результате возникнет «пробка», и скорость движения зарядов замедлится.
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.
Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:
- I = I 1 = I 2 = … = In;
- U = U1 + U2 + … +Un.
Эти равенства являются фундаментальными для нахождения параметров при повторении резисторов в цепи.
Используя закон Ома, можно найти, чему будет равняться сопротивление цепи. Формула для его нахождения будет выглядеть так: Rпос = R 1 + R 2 +… + Rn.
Параллельное соединение
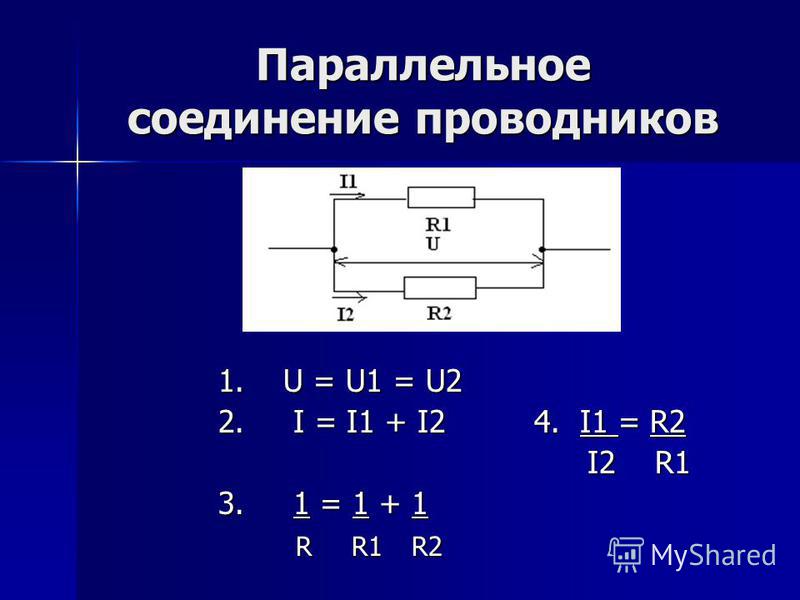
По распространённости такой вид соединения чаще встречается, чем последовательное подключение. При нём проводники соединены так, что начала всех резисторов сводятся в одну точку электрической цепи, а концы — в другую. Для того чтобы заменить разветвлённое подключение одним эквивалентным элементом, нужно знать, как правильно рассчитать ток и напряжение.
Пусть имеется цепь, состоящая из R1 + R2 + … +Rn параллельно включённых радиоэлементов. На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
В результате через первую ветвь потечёт ток I1, вторую — I2, в энную — In. Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Электростатическое поле является потенциальным, то есть работа по перемещению заряда из одной точки в другую не зависит от траектории, по которой перемещается носитель. Следовательно, при переносе одного кулона по любой ветви нужно будет совершить одинаковую работу. Из приведённых рассуждений следует, что при параллельном соединении формулы, с помощью которых можно рассчитать характеристики электрической цепи, будут следующими:
- I = I1 + I2 + … +In;
- U1 = U2 = … = Un.
Таким образом, вычисление эквивалентного сопротивления, которым можно будет заменить всю цепь в соответствии с законом Ома, выполняется по формуле: 1 / R пар = 1 / R 1 + 1 / R 2 + … + 1 / Rn. Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу. Это позволяет в некоторых случаях упростить расчёт.
Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу. Это позволяет в некоторых случаях упростить расчёт.
Согласно правилу сложения дробей c одинаковым знаменателем можно записать равенство: 1 / R1 + 1 / R2 + … + 1 / Rn = N / R1. Отсюда следует, что Rпар = R1 / N, где N равно числу резисторов. По аналогии можно посчитать общее сопротивление по упрощённой формуле для двух элементов: (1 / R1) + (1 / R2) = (R 2 + R 1) / R 1 * R 2. Это довольно удобные формулы для практического применения.
Решение задач
Для вычисления сопротивления любого смешанного соединения нужно запомнить всего две формулы — выражения для нахождения величины при последовательном и параллельном подключении. Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Например, пусть имеется параллельное подключение из четырёх резисторов. Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Из типовых задач, в которых необходимо найти сопротивление цепи, предлагающихся в школе на уроках физики, можно привести следующие:
- Найдите ток в цепи, если вольтметр, подключённый к одному из трёх последовательно соединённых проводников, показывает 100 В. Сопротивление элементов составляет: R1 = R2 = 5 Ом, R3 = 15 Ом. В задаче три резистора подключены в линию, значит, их полное сопротивление равно: R = R 1 + R 2 + R 3 = 25 Ом.
 У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A.
У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A. -
Каково будет сопротивление каждого из резисторов, если при их последовательном соединении ток равен 3A, а при параллельном — 16A. Напряжение в сети составляет 120 В. При первом способе соединения Iпосл = U / (R1 + R2), при втором Iпар = U / Rпар = U * (R1 + R2) / R1 * R2. Из первой формулы следует, что R1 + R2 = U / Iпос. Тогда: I пар = U 2 / Iпос * R 1 * R 2 → R 1 * R 2 = U 2 / I пар * I пос. Используя теорему Виета, можно составить квадратное уравнение. После его решения искомые величины будут равны: R 1 = 30 Ом, R 2 = 10 Ом.
Следует отметить, что приборы для измерения тока, напряжения и даже ёмкости используют особенности вычисления сопротивления цепи. Так, вольтметр имеет бесконечно большой внутренний импеданс, что позволяет подключать его параллельно к измеряемым точкам без внесения изменения в протекающий сигнал.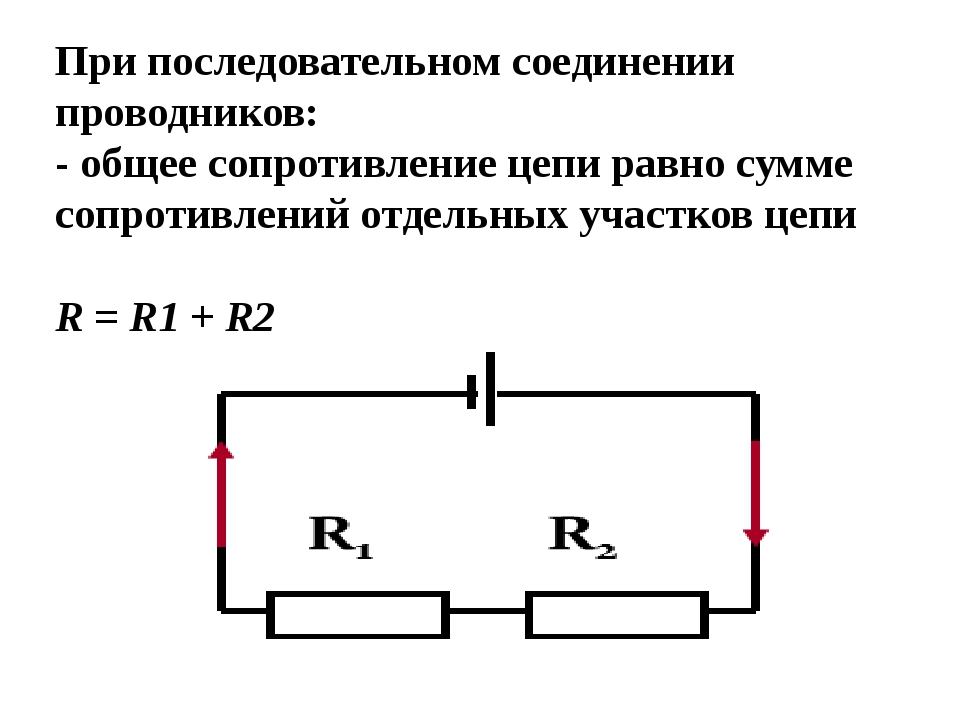
Амперметр же, наоборот, характеризуется пренебрежимо малой величиной внутреннего сопротивления, поэтому и подключают его в разрыв линии, на которой выполняют измерения.
10.3: Последовательные и параллельные резисторы
В разделе «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора. По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок \ (\ PageIndex {1} \)). В схеме серии выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Резисторы серии
Считается, что резисторывключены последовательно, когда ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \). Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. N V_i = 0.\]
N V_i = 0.\]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. Для рисунка \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов.
Эквивалентное сопротивление в последовательной цепи
Любое количество резисторов может быть подключено последовательно. Если \ (N \) резисторы соединены последовательно, эквивалентное сопротивление равно
. N R_i.\ label {серия эквивалентных сопротивлений} \]
N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.

Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {ряд эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 10 \, \ Omega = 90 \, \ Omega.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы будем использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных фонарей закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
- Ответ
-
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \).
 Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]
Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Комбинация резисторов — последовательно и параллельно — Учебный материал для IIT JEE
Спасибо за регистрацию.
Один из наших консультантов свяжется с вами в течение 1 рабочего дня.
Пожалуйста, проверьте свою электронную почту, чтобы узнать данные для входа.Нажмите, чтобы поговорить
1800-1023-196
+ 91-120-4616500
КОРЗИНА 0
МОЯ КОРЗИНА (5)
Используйте купон: CART20 и получите скидку 20% на все учебные материалы онлайн
ВЕЩЬ
ДЕТАЛИ
MRP
СКИДКА
ОКОНЧАТЕЛЬНАЯ ЦЕНА
$ {Имя}
Активация: сразу после оплаты
Rs.
 $ {Price}
$ {Price}
$ {DiscountPercent}%
Rs. $ {DiscountPrice}
Rs.$ {Price}
0%
Rs. $ {Price}
$ {Имя}
Активация: сразу после оплаты
Rs.
 $ {CalculateBundlePrice (Темы)}
$ {CalculateBundlePrice (Темы)}
$ {DiscountPercent.toFixed ()}%
Rs. $ {CalculateBundleDiscountedPrice (Topics, DiscountPercent)}
Электрическое сопротивление в последовательных и параллельных сетях
Последовательное соединение
Общее сопротивление для резисторов, подключенных последовательно, можно рассчитать как
R = R 1 + R 2 +…. + R n (1)
где
R = сопротивление (Ом, Ом)
- Резисторы — стандартные значения
Пример — резисторы в серии
Три резистора 33 Ом , 33 Ом и 47 Ом подключены последовательно.
 Общее сопротивление можно рассчитать как
Общее сопротивление можно рассчитать как R = ( 33 Ом) + ( 33 Ом) + ( 47 Ом)
= 113 Ом
- Резисторы — Цветовые коды Калькулятор
Параллельное соединение
Общее сопротивление резисторов, подключенных параллельно, можно рассчитать как
1 / R = 1 / R 1 + 1 / R 2 +…. + 1 / R n (2)
Эквивалентное сопротивление 2 резисторов, соединенных параллельно, может быть выражено как
R = R 1 R 2 / (R 1 + R 2 ) (3)
Пример — параллельные резисторы
Три резистора 33 Ом , 33 Ом и 47 Ом подключены параллельно. Общее сопротивление можно рассчитать как
1 / R = 1 / ( 33 Ом ) + 1 / ( 33 Ом ) + 1 / (47 Ом )
= 0.
 082 (1 / Ом)
082 (1 / Ом)
R = 1 / (0,082 Ом)
= 12,2 Ом
Если напряжение аккумулятора 12 В — ток в цепи можно рассчитать с помощью закон
I = U / R
= (12 В) / (12,2 Ом)
= 0,98 ампер
Можно рассчитать ток через каждый резистор
I 1 = U / R 1 = (12 В) / (33 Ом) = 0.36 ампер
I 2 = U / R 2 = (12 В) / (33 Ом) = 0,36 ампер
I 3 = U / R 3 = (12 В) / (47 Ом) = 0,26 ампера
Параллельно подключенные резисторы — Калькулятор
Сложите сопротивления до пяти параллельно подключенных резисторов и (необязательно) напряжение цепи.
Общее сопротивление и ток — и отдельные токи во всех резисторах — будут рассчитаны:
R 1 (Ом) I 1 (ампер)
R 2 (Ом) I 2 (ампер)
R 3 (ом) I 3 (ампер)
R 4 (ом ) I
R 5 (Ом) I 5 (амперы)
Напряжение (В)
R (Ом)
001 I (амперы)
1 Последовательные и параллельные резисторыПоследовательные резисторы
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно.
 Например, если ток протекает через человека, держащего отвертку, в землю, тогда R1.R1. размер 12 {R rSub {размер 8 {1}}} {} на рис. 4.2 (a) может быть сопротивлением вала отвертки, R2R2 размер 12 {R rSub {размер 8 {2}}} {} сопротивлением его ручка, R3R3 размер 12 {R rSub {размер 8 {3}}} {} сопротивление тела человека, и R4R4 размер 12 {R rSub {размер 8 {4}}} {} сопротивление ее обуви.
Например, если ток протекает через человека, держащего отвертку, в землю, тогда R1.R1. размер 12 {R rSub {размер 8 {1}}} {} на рис. 4.2 (a) может быть сопротивлением вала отвертки, R2R2 размер 12 {R rSub {размер 8 {2}}} {} сопротивлением его ручка, R3R3 размер 12 {R rSub {размер 8 {3}}} {} сопротивление тела человека, и R4R4 размер 12 {R rSub {размер 8 {4}}} {} сопротивление ее обуви.На рисунке 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь на резиновой подошве с высоким сопротивлением. Это могло быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением к прибору, который уменьшал бы рабочий ток.
Рисунок 4.
 3 Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).
3 Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа). Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на рисунке 4.3.
Согласно закону Ома, падение напряжения, V, V, размер 12 {V} {} на резисторе, когда через него протекает ток, рассчитывается по формуле V = IR, V = IR, размер 12 {V = ital «IR»} {}, где размер II 12 {I} {} равен току в амперах (A), а размер RR 12 {R} {} — сопротивление в Ом Ом.Ω. размер 12 {слева (% OMEGA справа)} {} Другой способ представить это: VV размером 12 {V} {} — это напряжение, необходимое для протекания тока II размера 12 {I} {} через сопротивление RR размера 12 {R} {}
Таким образом, падение напряжения на R1R1 размером 12 {R rSub {размер 8 {1}}} {} равно V1 = IR1, V1 = IR1, размер 12 {V rSub {size 8 {1}} = ital «IR» rSub { размер 8 {1}}} {}, что для R2R2 размер 12 {R rSub {размер 8 {2}}} {} равен V2 = IR2, V2 = IR2, размер 12 {V rSub {size 8 {2}} = ital «IR» rSub {размер 8 {2}}} {}, а для R3R3 размера 12 {R rSub {размер 8 {3}}} {} — V3 = IR3.V3 = IR3. размер 12 {V rSub {size 8 {3}} = ital «IR» rSub {size 8 {3}}} {} Сумма этих напряжений равна выходному напряжению источника; то есть
4,1 В = V1 + V2 + V3. V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}Это уравнение основано на сохранении энергии и сохранении заряжать. Электрическая потенциальная энергия может быть описана уравнением PE = qV, PE = qV, size 12 {ital «PE» = ital «qV»} {}, где qq size 12 {q} {} — электрический заряд, а размер VV 12 { V} {} — напряжение.Таким образом, энергия, подаваемая источником, равна qV, qV, размер 12 {ital «qV»} {}, а энергия, рассеиваемая резисторами, равна
. 4.2 qV1 + qV2 + qV3. QV1 + qV2 + qV3. размер 12 {ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {}Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, согласно которым общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3.qV = qV1 + qV2 + qV3. размер 12 {ital «qV» = ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {} заряд qq размер 12 {q} {} отменяется, давая V = V1 + V2 + V3, V = V1 + V2 + V3, размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2 }} + V rSub {размер 8 {3}}} {}, как указано.(Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь замена значений отдельных напряжений дает
4,3 В = IR1 + IR2 + IR3 = I (R1 + R2 + R3). V = IR1 + IR2 + IR3 = I (R1 + R2 + R3). размер 12 {V = ital «IR» rSub {size 8 {1}} + ital «IR» rSub {size 8 {2}} + ital «IR» rSub {size 8 {3}} = I \ (R rSub { размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} \)} {}Обратите внимание, что для эквивалентного сопротивления одиночной серии Rs, Rs, мы имеем
Это означает что полное или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs = R1 + R2 + R3.Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
Эта логика действительно для любого количества последовательно подключенных резисторов; таким образом, полное сопротивление RsRs последовательного соединения составляет
4,5 Rs = R1 + R2 + R3 + …, Rs = R1 + R2 + R3 + …, размер 12 {R rSub {size 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} + «.» «.» «.» } {}как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 4.3 составляет 12,0 В 12,0 В размером 12 {«12» «.» 0`V} {} и сопротивления: R1 = 1,00 Ом, R1 = 1,00 Ом, размер 12 {R rSub {size 8 {1}} = 1 «.» «00»% OMEGA} {} R2 = 6,00 Ом, R2 = 6,00 Ом, размер 12 {R rSub {размер 8 {2}} = 6 дюймов «. «00»% OMEGA} {} и R3 = 13,0 Ом. R3 = 13,0 Ом. размер 12 {R rSub {размер 8 {3}} = «13» «.» 0% OMEGA} {} (а) Какое полное сопротивление? (б) Найдите ток.(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что в сумме они равны выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, как указано уравнением
4,6 Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.Стратегия и решение для (b)
Ток определяется по закону Ома, V = IR.V = IR. размер 12 {V = ital «IR»} {} Ввод значения приложенного напряжения и общего сопротивления дает ток в цепи.
4,7 I = VRs = 12,0 В 20,0 Ом = 0,600 AI = VRs = 12,0 В 20,0 Ом = 0,600 A, размер 12 {I = {{V} больше {R rSub {size 8 {s}}}} = {{» 12 «». » 0 «V»} больше {«20» «.» «0»% OMEGA}} = 0 «.» «600» «A»} {}Стратегия и решение для (c)
Падение напряжения — или IRIR размер 12 {ital «IR»} {} — в резисторе определяется законом Ома.Ввод текущего значения и значения первого сопротивления дает
. 4,8 В1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В. V1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В. размер 12 {V rSub {размер 8 {1}} = ital «IR» rSub {size 8 {1}} = \ (0 «.» «600» «A» \) \ (1 «.» 0% OMEGA \) = 0 «.» «600» «V»} {}Аналогично
4,9 В2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 ВV2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В, размер 12 {В rSub {размер 8 {2}} = ital «IR» rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) \ (6 «.» 0% OMEGA \) = 3 «.» «60» «V»} {}и
4.10 V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. размер 12 {V rSub {размер 8 {3}} = ital «IR» rSub {size 8 {3}} = \ (0 «.» «600» «A» \) \ («13» «.» 0% OMEGA \) = 7 «.» «80» «V»} {}Обсуждение для (c)
Три капли IRIR размером 12 {ital «IR»} {} добавляют к 12,0 В, 12,0 В, размер 12 {«12» «». 0`V} {} как и ожидалось.
4,11 V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 VV1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В размер 12 {V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}} = \ (0 «.»» 600 «+3». «» 60 «+7». «» 80 «\)» V «=» 12 «». «0» V «} {}Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, размер 12 {P = курсив «IV»} {}, где PP размер 12 {P} {} — электроэнергия. В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IRV = IR, размер 12 {V = ital «IR»} {} в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
4.12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт. P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}Аналогично
4,13 P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 WP2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт размер 12 {P rSub {размер 8 {2}} = I rSup {размер 8 {2}} R rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (6 «.» «00»% OMEGA \) = 2 «.» «16» «W»} {}и
4.14 P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. Размер 12 {P rSub {размер 8 {3}} = I rSup {размер 8 {2}} R rSub {размер 8 {3}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ («13» «.» 0% OMEGA \) = 4 «.» «68» «W»} {}Обсуждение для (d)
Мощность также можно рассчитать, используя либо P = IVP = IV, размер 12 {P = ital «IV»} {}, либо P = V2R, P = V2R, размер 12 {P = {{V rSup {size 8 {2}}) } over {R}}} {}, где величина VV 12 {V} {} — это падение напряжения на резисторе (а не полное напряжение источника).Получатся те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV, P = IV, размер 12 {P = ital «IV»} {}, где VV размером 12 {V} {} — это напряжение источника. Это дает
4,15 P = (0,600 A) (12,0 В) = 7,20 WP = (0,600 A) (12,0 В) = 7,20 Вт. Размер 12 {P = \ (0 «.» «600» «A» \) \ («12 «». «0» V «\) = 7″. » «20» «W»} {}Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
4,16 P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. размер 12 {P rSub {размер 8 {1}} + P rSub {размер 8 {2}} + P rSub {размер 8 {3}} = \ (0 «.» «360» +2 «.» «» 16 «+4». «» 68 «\)» W » = 7 «.» «20» «Вт»} {}Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавляют Rs = R1 + R2 + R3 +…. Rs = R1 + R2 + R3 + …. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub { размер 8 {3}} + «.» «.» «.» «.» } {}
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а скорее делят его.
и параллельные электрические соединения
Серия и параллельнаяЕсть 2 способа подключить несколько устройств к источнику питания (например,г. динамики к усилителю), последовательно и параллельно. Ну … Хорошо, есть еще последовательный / параллельный. Но мы расскажем об этом на следующей странице.
Серийные динамикиВ последовательной цепи (как в двух приведенных выше) ток должен протекать через одно устройство, чтобы добраться до следующего устройства. Это означает, что скорость протекания тока через все устройства одинакова. Напряжение на каждом устройстве зависит от его импеданса / сопротивления каждого устройства и тока, протекающего по цепи. При добавлении дополнительных компонентов в последовательную цепь ток уменьшается, если приложенное напряжение остается постоянным.
Параллельные динамикиВ параллельной схеме (как в двух приведенных выше примерах) каждое устройство напрямую подключается к источнику питания. Это означает, что каждое устройство получает одинаковое напряжение. Сила тока, протекающего через каждое устройство, зависит от импеданса / сопротивления этого конкретного устройства. Если устройства добавляются к источнику питания в параллельной конфигурации, ток потребления / потока от источника питания увеличивается.
На двух диаграммах ниже вы можете увидеть взаимосвязь между током на выходе из усилителя и количеством динамиков.Вы можете видеть, что четыре динамика потребляют от усилителя в два раза больше тока, чем конфигурация с двумя динамиками.
При подключении к любому источнику питания вы должны знать пределы источника, чтобы предотвратить повреждение источника. Это означает, что если вы подключите слишком много динамиков с параллельной проводкой к усилителю (в данном случае источнику питания), он может выйти из строя и не подлежит ремонту. Я видел, как это происходило, особенно когда усилитель был неправильно подключен.
Для тех, кто хочет заниматься математикой …На диаграммах / тексте выше у нас были либо последовательные ИЛИ параллельные цепи. В этом разделе показано, что происходит с напряжением, током и рассеиваемой мощностью в последовательной / параллельной цепи. Как было сказано ранее, в последовательной цепи «ток» в каждом устройстве одинаков. В параллельной цепи «напряжение» одинаково на каждом устройстве. На следующей схеме вы можете видеть, что два резистора на 1000 Ом последовательно соединены с одним резистором на 400 Ом.Мы знаем, что напряжение на двух резисторах по 1000 Ом будет одинаковым (потому что они подключены параллельно). Мы также знаем, что общий ток, протекающий через два параллельно соединенных резистора, будет равен току, протекающему через резистор 400 Ом.
Чтобы рассчитать полный ток, сначала следует упростить схему. Это означает, что нам нужно найти полное сопротивление параллельной сети. Для простой схемы с двумя резисторами одинакового номинала мы можем просто разделить сопротивление отдельного компонента на общее количество компонентов.Для этой параллельной сети у нас есть два резистора по 1000 Ом.
Общее сопротивление параллельных резисторов = сопротивление отдельного компонента / количество резисторов
Общее сопротивление параллельных резисторов = 1000/2
Общее сопротивление параллельных резисторов = 500 ОмЕсли бы у нас было 3 параллельных резистора, мы бы разделили 1000 на 3, чтобы найти общее сопротивление параллельных резисторов.
Суммарное сопротивление параллельных резисторов = 1000/3
Общее сопротивление параллельных резисторов = 333.33 …. ОмТеперь, когда мы знаем, что параллельные резисторы равны одному резистору на 500 Ом. Теперь, когда у нас есть, по сути, один резистор на 500 Ом, соединенный последовательно с резистором на 400 Ом, мы можем рассчитать полный ток в цепи. Мы знаем, что у нас есть источник питания на 12 вольт. Мы также знаем, что резистор на 500 Ом, включенный последовательно с резистором на 400 Ом, равен резистору на 900 Ом.
Ток через цепь = напряжение в цепи / общее сопротивление цепи
Прохождение тока через цепь = 12/900
Прохождение тока через цепь = 0.0133 ампер
Теперь мы можем найти напряжение на отдельных компонентах. Чтобы избежать путаницы, сначала рассчитайте напряжение на единственном резисторе.
Напряжение на резисторе = сопротивление резистора * ток, протекающий через резистор
Напряжение на резисторе = 400 * 0,0133
Напряжение на резисторе = 5,333 ВВ последовательной цепи все напряжения на всех отдельных компонентах серии будут равны напряжению источника питания.Если у нас есть источник на 12 В, а напряжение на резисторе 400 Ом составляет 5,333 В, мы знаем, что напряжение на параллельной паре резисторов будет 6,67 В (12-5,333 = 6,67). Чтобы рассчитать ток через параллельные компоненты …
Ток через один резистор 1000 Ом = напряжение на резисторе / сопротивление
Ток через один резистор 1000 Ом = 6,67 / 1000
Ток через один резистор 1000 Ом = 0,0067 амперТеперь, когда мы знаем напряжение на каждом из компонентов и ток от до на каждом из компонентов, мы можем вычислить рассеиваемую мощность для каждого компонента.На самом деле мы могли бы это сделать, как только узнали бы напряжение на компонентах, но я решил пойти «живописным» путем.
Рассеиваемая мощность на резисторе 400 Ом = напряжение на компоненте * ток через компонент
Рассеиваемая мощность на резисторе 400 Ом = 5,33 * 0,013
Рассеиваемая мощность на резисторе 400 Ом = 0,071 ВтРассеиваемая мощность на каждом резисторе 1000 Ом = напряжение на компоненте * ток на компоненте
Рассеиваемая мощность на каждом резисторе 1000 Ом = 6.67 * .0067
Рассеиваемая мощность на каждом резисторе 1000 Ом = 0,045 ВтВ этом примере используются резисторы, но те же вычисления будут работать для любого резистивного устройства. Хотя громкоговорители не являются чисто резистивными при работе с переменным напряжением, полученные здесь расчеты можно использовать для грубых расчетов напряжения, тока и рассеиваемой мощности в громкоговорителях.
Параллельное соединение резисторов 10 класса китаб — китаплар
Параллельное соединение резисторов 10 класса китаб — китаплар — Параллельное соединение резисторов 10 класса ile ilgili kitaplar.yle sitemler vardr ки, бир medihtir ve yle medihler vardr ки, бир ктлемедир. LA ROCHEFAUCAULD [Пайла]
.
Bölümler
Эдебият Дефтери
• Kurallar
• Yardım
• İletişimДиер
• Edebiyat TV
• Kütüphane
• Burçlar
• Bebek isimleri
Dier
• Ря Табирлери
• simler
Edebiyatdefteri.com, 2020. Bu sayfada yer alan bilgilerin her hakk, aksi ayrca belirtilmedii srece Edebiyatdefteri.com’a aittir. Sitemizde yer alan iir ve yazlarn telif haklar air ve yazarlarn kendilerine veya yeya verdikleri kiilere aittir. Sitemiz привет бир ekilde kr amac gtmemektedir ve sitemizde yer alan tm materyaller yalnzca bilgilendirme ve eitim amacyla sunulmaktadr. Sitemizde yer alan iirler, ykler ve diğer eserlerin telif hakları yazarların kendilerine veya butki verdikleri kişilere aittir. Eserlerin izin alınmadan kopyalanması ve kullanılması 5846 sayılı Fikir ve Sanat Eserleri Yasası na göre suçtur.Ayrca sitemiz Telif Haklar kanuna gre korunmaktadr. Herhangi бир zelliinin ksmende olsa kullanlmas ya da kopyalanmas sutur. Эдебият — iirler — Китап

