Что такое параллельное соединение резисторов. Как рассчитать общее сопротивление при параллельном соединении. Какие формулы используются для расчета параллельного соединения резисторов. В чем особенности параллельного соединения по сравнению с последовательным. Где применяется параллельное соединение резисторов на практике.
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это способ подключения, при котором все резисторы присоединяются своими выводами к одним и тем же двум точкам электрической цепи. При таком соединении напряжение на всех резисторах одинаково, а общий ток делится между ними.
Основные характеристики параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов, протекающих через каждый резистор
- Общее сопротивление всегда меньше сопротивления наименьшего из резисторов
Формулы для расчета параллельного соединения резисторов
Для расчета параллельного соединения резисторов используются следующие основные формулы:
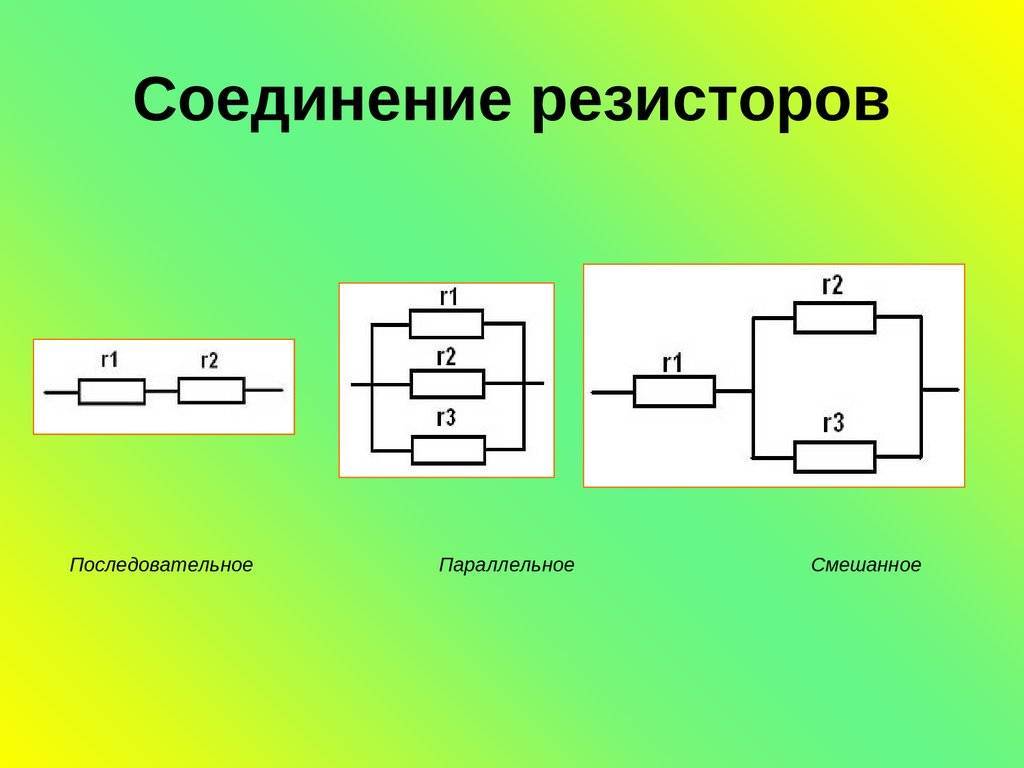
Формула для расчета общего сопротивления
Для двух резисторов:
R = (R1 * R2) / (R1 + R2)
Для произвольного количества резисторов:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Формула для расчета общего тока
I = I1 + I2 + I3 + … + In
где I — общий ток, I1, I2, I3 и т.д. — токи через отдельные резисторы.
Особенности параллельного соединения по сравнению с последовательным
Параллельное соединение резисторов имеет ряд важных отличий от последовательного:
- При параллельном соединении общее сопротивление уменьшается, а при последовательном — увеличивается
- Напряжение на всех резисторах при параллельном соединении одинаково, а при последовательном — различно
- Общий ток при параллельном соединении равен сумме токов через резисторы, а при последовательном — одинаков для всех элементов
Какой тип соединения выбрать? Это зависит от конкретной задачи и требуемых параметров цепи.
Расчет параллельного соединения резисторов на практических примерах
Рассмотрим несколько примеров расчета параллельного соединения резисторов:

Пример 1: Два резистора
Дано: R1 = 10 Ом, R2 = 20 Ом
Решение:
R = (R1 * R2) / (R1 + R2) = (10 * 20) / (10 + 20) = 200 / 30 = 6.67 Ом
Пример 2: Три резистора
Дано: R1 = 6 Ом, R2 = 12 Ом, R3 = 4 Ом
Решение:
1/R = 1/6 + 1/12 + 1/4 = 0.167 + 0.083 + 0.25 = 0.5
R = 1 / 0.5 = 2 Ом
Применение параллельного соединения резисторов на практике
Параллельное соединение резисторов широко используется в различных электронных устройствах и системах. Вот некоторые области применения:
- Регулировка яркости светодиодов
- Создание делителей напряжения
- Формирование эквивалентных сопротивлений в сложных цепях
- Распределение токов в электрических системах
- Измерительные приборы и датчики
В каких случаях параллельное соединение наиболее эффективно? Когда требуется уменьшить общее сопротивление цепи или распределить ток между несколькими нагрузками.
Преимущества и недостатки параллельного соединения резисторов
Как и любой метод, параллельное соединение резисторов имеет свои плюсы и минусы:
Преимущества:
- Возможность уменьшения общего сопротивления
- Равномерное распределение напряжения
- Увеличение общей мощности цепи
- Высокая надежность (при выходе из строя одного резистора цепь продолжает работать)
Недостатки:
- Сложность точного расчета при большом количестве резисторов
- Увеличение общего тока потребления
- Необходимость использования резисторов с более высокой мощностью
Сравнение параллельного и последовательного соединения резисторов
Чтобы лучше понять особенности параллельного соединения, сравним его с последовательным:
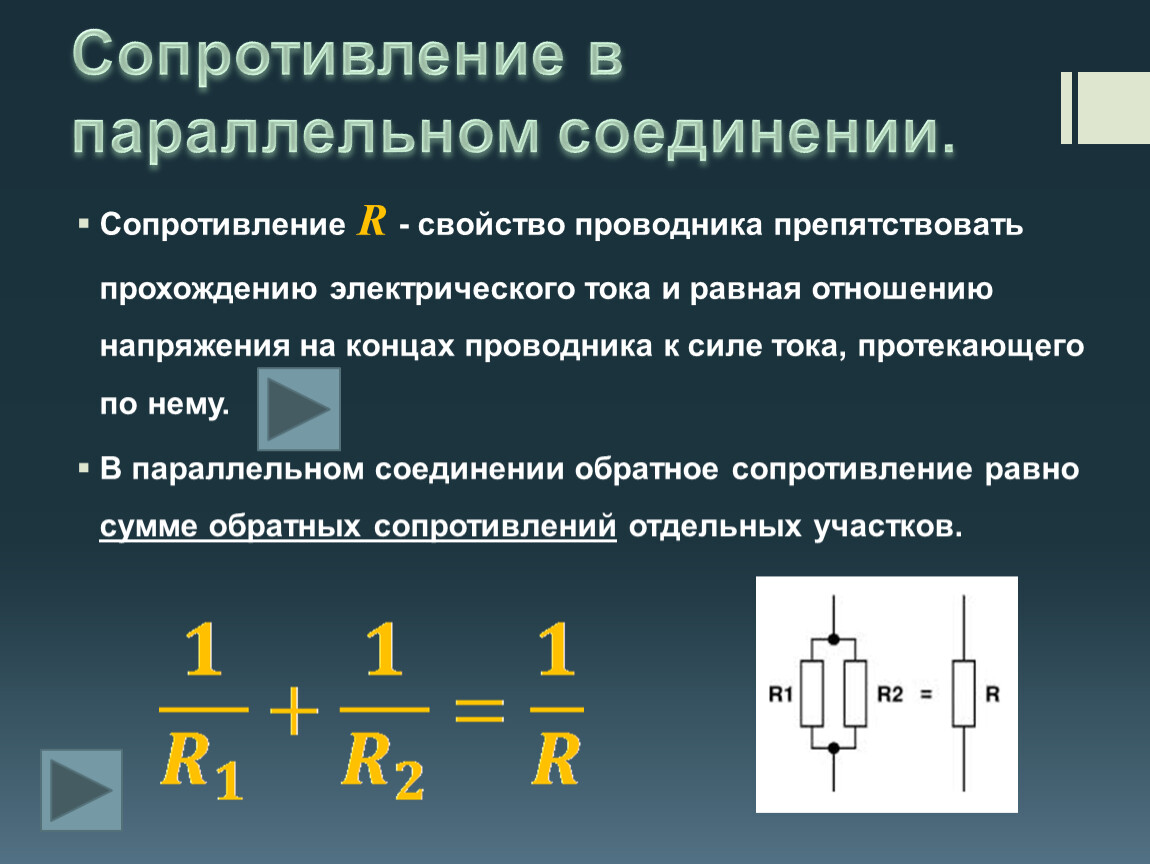
| Характеристика | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Уменьшается | Увеличивается |
| Напряжение на резисторах | Одинаковое | Различное |
| Ток через резисторы | Различный | Одинаковый |
| Общая мощность | Увеличивается | Уменьшается |
Какое соединение выбрать? Это зависит от конкретной задачи и требуемых параметров цепи.
Как правильно рассчитать параллельное соединение большого количества резисторов
При расчете параллельного соединения большого количества резисторов можно использовать следующие методы:
- Метод попарного объединения: последовательно объединяем резисторы попарно, пока не останется один эквивалентный резистор.
- Использование калькуляторов: существуют онлайн-калькуляторы для расчета параллельного соединения резисторов.
- Программирование: для сложных расчетов можно написать программу, автоматизирующую вычисления.
Какой метод выбрать? Это зависит от количества резисторов и требуемой точности расчетов.
Параллельное и последовательное соединение резисторов
В схемах используется параллельное, последовательное и смешанное подключение резисторов.
Необходимо помнить, что ток будет протекать по пути наименьшего сопротивления.
Содержание
- Последовательное соединение
- Параллельно сопротивление
- Калькулятор параллельного соединения резисторов
Последовательное соединение
При последовательном соединении общее сопротивление увеличивается. Общее сопротивление будет выше, чем сопротивление любого из резисторов.На всем участке цепи течет один и тот же ток, а общее сопротивление равно сумме всех сопротивлений. Для вычисления значения общего сопротивления необходимо к сопротивлению первого резистора прибавить сопротивление второго, третьего, четвертого резистора.
Rобщ = R1 + R2 + R3 + Rn
Например: R1 = 2 Om + R2 = 3 Om + R3 = 1 oM
Rобщ = 6 Om.
Другими словами:
При последовательном соединении резисторов их сопротивление складывается и общее сопротивление будет равно сумме R1 + R2 + R3…….
Параллельно сопротивление
При параллельном соединении общее сопротивление уменьшается. Общее сопротивление будет ниже, чем сопротивление любого из резисторов.При параллельном подключении резисторов, все немного интересней: Общее сопротивление всегда будет меньшим, чем значение наименьшего сопротивления в этой комбинации.
К каждому резистору при параллельном их соединении приложено одно и то же напряжение. А если сопротивлений резисторов в цепи при параллельном их соединении может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (в соответствии с законом Ома).
Для расчета общего сопротивления резисторов подключенных параллельно можно воспользоваться одной из следующих формул:
- Для нескольких параллельно соединенных резисторов с одинаковым номиналом:
\[ Rобщ = \frac{\color{red}R}{\color{blue}N} \]
\( Rобщ \) = общее сопротивление цепи или всех резисторов\( R \) = Номинал любого из резисторов
\( N \) = Количество резисторов в цепиПредположим мы имеем 2 резистора соединенных параллельно.
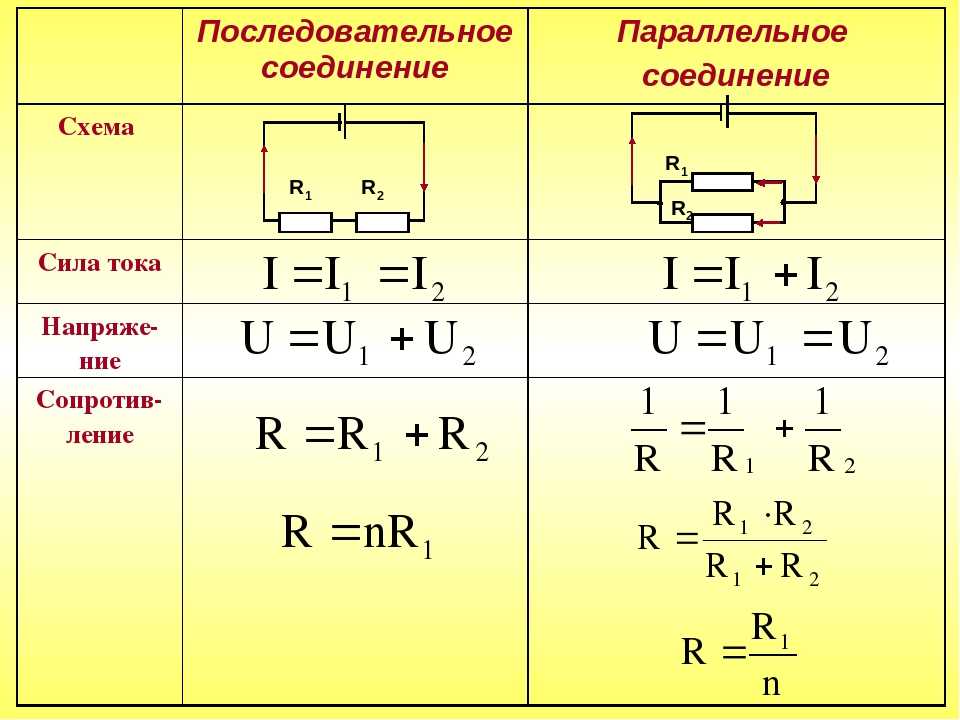 Номинал каждого из которых равен 10 Ом.
Номинал каждого из которых равен 10 Ом.
\[ Rобщ = ? \]
Исходя из формулы:
\[ Rобщ = \frac{\color{red}Rлюбого из резисторов = 10 Om}{\color{blue}2} \]
\[ Rобщ = 5 \]
Для нескольких параллельно соединенных резисторов с разным номиналом:
\[ \frac{1}{\color{red}R} = \frac{1}{\color{red}R1} + \frac{1}{\color{red}R2} +…+ \frac{1}{\color{red}Rn} \]
Калькулятор параллельного соединения резисторов
admin Учебник Leave a comment
Параллельное соединение проводников – законы, формулы и схема сопротивления цепи
4
Средняя оценка: 4
Всего получено оценок: 88.
4
Средняя оценка: 4
Всего получено оценок: 88.
Электрические цепи представляют собой набор электронных компонент (сопротивлений, конденсаторов и т.д.), соединенных в различном порядке. От источника электрического тока (аккумулятора) энергия подается по подводящим цепям к различным элементам цепи. Самыми распространенными способами соединений являются параллельное и последовательное соединения. Рассмотрим далее параллельное соединение проводников.
Что такое резистор
Резистор (от английского слова resistor — сопротивление) — это простейший пассивный элемент, применяемый для регулирования силы тока или ограничения электрической мощности. На электрических схемах изображается в виде прямоугольника. Геометрические размеры реальных резисторов зависят от величины их сопротивления, которое измеряется в единицах, названых в честь немецкого физика Георга Ома.
Напомним, что закон Ома для электрических цепей описывается формулой:
$$R={U \over I}$$
где:
R — сопротивление, Ом;
U — напряжение, В;
I — сила тока в амперах, А.
Напряжение и ток измеряются приборами — вольтметром и амперметром.
Параллельное соединение
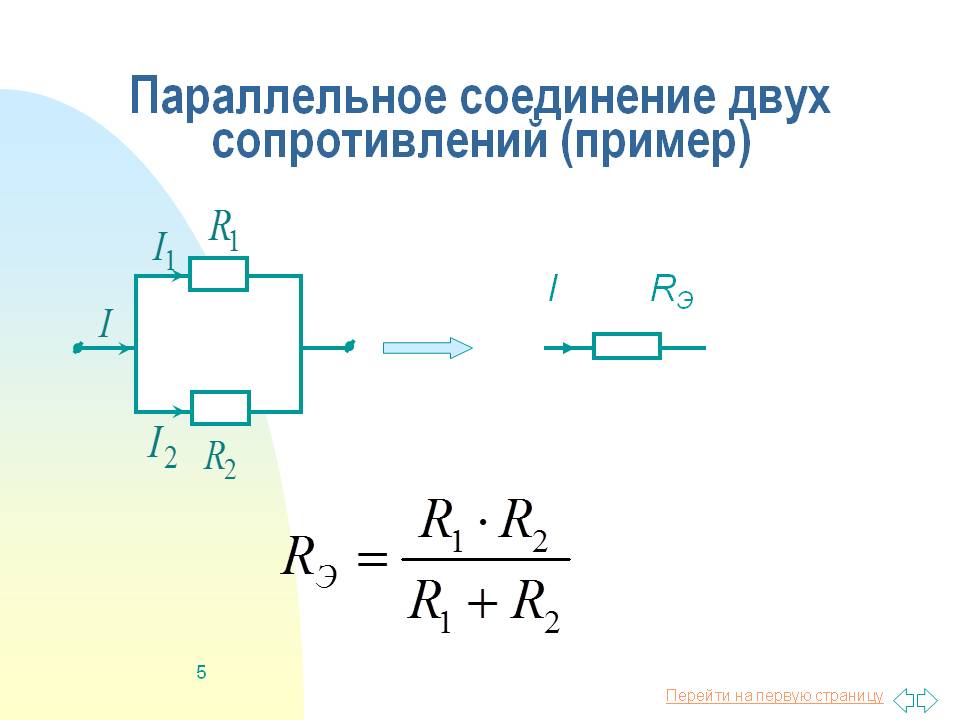
Если взять два резистора R1 и R2 и соединить их так, что начала (левые концы) соединятся в одной точке, а правые концы соединятся в другой точке, то это и будет параллельное соединение.
Рис. 2. Схема параллельного соединения двух резисторовЭлементы цепи (резисторы) соединяются между собой проводниками, сопротивление которых обычно мало, и им можно пренебречь. Когда требуются более точные расчеты для больших и сложных схем, то учет этих сопротивлений необходим.
После подключения к левому и правому концу источника напряжения U, в цепи потечет ток. Поскольку R1 и R
2 могут отличаться друг от друга, то и значения токов I1 и I2 через них тоже будут разные. Зная напряжение U, которое подано на оба резистора, и используя формулу закона Ома, можно рассчитать токи I1 и I2 :
Зная напряжение U, которое подано на оба резистора, и используя формулу закона Ома, можно рассчитать токи I1 и I2 :
$$ I1={U \over R1}$$
$$ I2={U \over R2}$$
Общий ток I в цепи является суммой токов I1 и I2:
$$ I= I1+I2 $$
Тогда, используя выражения для токов I1 и I2, получим следующую формулу:
$$ {U \over R}={ U \over R1}+ {U \over R2}$$
Сокращая обе части последнего уравнения на U, получим следующее выражение для обратной величины общего сопротивления R:
$$ {1\over R}={ 1 \over R1}+ {1 \over R2}$$
Используя последнюю формулу и правило сложения дробей, получим выражение для расчета сопротивления цепи, состоящей из двух резисторов:
$$ R={R1* R2 \over R1+R2}$$
Если параллельно соединить два одинаковых резистора (R1=R2) то пользуясь последней формулой получим, что общее сопротивление цепи будет вдвое меньше величины отдельного сопротивления.
Параллельное соединение большого числа резисторов
Если параллельно соединить N резисторов — R1,R2… RN, то, пользуясь вышеприведенными формулами и соображениями, можно получить выражение для обратной величины общего сопротивления такой цепи:
$$ {1\over R}={ 1 \over R1}+ {1 \over R2}+…+{1 \over RN}$$.
Рассмотрим частный случай, когда все N резисторов одинаковы и равны R0. Тогда общее сопротивление цепи равно:
$$ R={R0 \over N}$$
Таким образом, можно сформулировать общее правило: при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлений параллельно включенных проводников.
Что мы узнали?
Итак, мы узнали законы параллельного соединения проводников (сопротивлений) в электрических цепях. Нами был получены формулы для расчетов сопротивления цепи, состоящей из двух и более резисторов.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 88.
А какая ваша оценка?
параллельных цепей
Ваш браузер не поддерживает Java-апплеты
Цепь с более чем одним путь прохождения тока представляет собой параллельную цепь.
НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Полное напряжение равно напряжение любого параллельного сопротивления.
ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Полный ток равен сумма токов каждой параллельной составляющей.
СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНО ЦЕПИ
Общее сопротивление может быть рассчитывается по закону Ома, если известны напряжение и полный ток.
Общее сопротивление всегда меньше минимального значения сопротивления.
Метод равенства значений
Для параллельных сопротивлений в что все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле деление номинала одного из резисторов на количество резисторов.
Обратный метод
Для параллельных сопротивлений в
что все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле
деление номинала одного из резисторов на количество резисторов.
1/R T = 1/R 1 + 1/R 2 + 1/R N
R EQ = 1 / ( 1/R 1 + 1/R 2 + … + 1/R N )
Метод произведения на сумму
Для расчета сопротивления двух резисторов, включенных параллельно, можно использовать эту формулу:
R EQ = (R 1 * R 2 ) / (R 1 + R 2 )
Правило приближения 10 к 1
Если два резистора соединены параллельно и один резистор в 10 и более раз больше по номиналу, чем другой резистор, резистор большего номинала можно не учитывать.
ПРОВОДИМОСТЬ
Суммарная проводимость равна к сумме проводимостей каждого компонента.
ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Суммарная мощность равна сумма мощностей каждого компонента. (Это то же самое, что и с рядом схемы).
Правила для параллельных цепей постоянного тока
-
такое же напряжение есть
на каждой ветви параллельной цепи и равно напряжению источника.

- Ток через параллельная ветвь обратно пропорциональна величине сопротивления ответвляться.
- Общий ток параллельной цепи равен сумме токов отдельных ветвей схема
- Эквивалентное сопротивление параллельная цепь находится по общему уравнению Req = 1 / ( 1/R1 + 1/R2 + 1/Рн)
- Суммарная мощность, потребляемая в параллельная цепь равна сумме мощностей, потребляемых отдельными резисторы.
АНАЛИЗ ПАРАЛЛЕЛЬНОЙ ЦЕПИ
- Обратите внимание на электрическую схему внимательно или нарисуйте его, если это необходимо.
- Обратите внимание на указанные значения и значения, которые необходимо найти.
- Выберите подходящий уравнения, которые будут использоваться при решении неизвестных величин на основе известных количества.
-
Подставить известные значения
в уравнении, которое вы выбрали, и решите неизвестное значение.
ПОИСК И УСТРАНЕНИЕ НЕИСПРАВНОСТЕЙ ЦЕПИ
Когда происходит открытие в ответвления параллельной сети сопротивление ответвления увеличивается и общее сопротивление цепи увеличивается. Это приводит к уменьшению общего Текущий.
Всегда происходит короткое замыкание при отсутствии тока, протекающего по другим ветвям цепи.
Резисторы в параллельных цепях
Сумма токов в параллельной сети можно рассчитать как
I = I 1 + I 2 + … + I N (1)
, где
, где
, где
. I n = параллельный ток (ампер)
I = сумма токов (ампер)
Общее сопротивление в параллельной цепи можно рассчитать как
1 / R2 р 1 + 1 / R 2 + … + 1 / R n (2)where
R n = parallel resistance (ohms, Ω)
R = общее сопротивление в параллельной сети (Ом, Ом)
- Параллельно соединенные резисторы — калькулятор
Пример — параллельная сеть
Общее сопротивление в сети с тремя резисторами R 1 = 10 Ом, R 2 = 20 Ом и R 3 = 30 Ом можно рассчитать как
1 / R = 1 / (10 Ом) + 1 / (20 Ом) + 1 / ( 30 Ом)
= 0,183 (1 /ω)
R = 1 /0,183
= 5,46 (ω)
. рассчитано
рассчитано
I = U / R
= (12 В) / (5,46 Ом)
= 2,2 ампер)
Ток через каждый резистор можно рассчитать как
I 1 = U / R 1
= (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 V) / (12 v) / (12 v) / (12 v) / (12 v) (12 v) (12 v) (12 v) (12 v) (12 v) (12 v) (12 v) (12 v) (12 v).
= 1,2 (AMP)
I 2 = U / R 2
= (12 В) / (20 ω)
= 0.60140140 = 0.60140140 = 0.60140140 = 0.60140140 = 0.60140140 = 0.60140140 = (12 В). я 3 = U / R 3
= (12 В) / (30 Ом)
= 0,4 (Амп)
Резисторы в параллельном и резистентном сопротивлении
Два сопротивления парирования в параллельном резистентном и резистентном сопротивлении.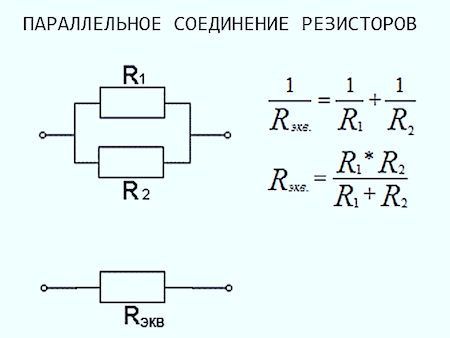 1 — 100 ohm
1 — 100 ohm
| Resulting Resistance (Ω) | ||||||||||||
| R2 ( Ω ) | R1 ( Ω ) | |||||||||||
| 1 | 1.5 | 2.2 | 3.3 | 4.7 | 6.8 | 10 | 15 | 22 | 33 | 47 | 68 | |
| 1 | 0.5 | 0.6 | 0.69 | 0.77 | 0.83 | 0.87 | 0.91 | 0.93 | 0.95 | 0.97 | 0.98 | 0.99 |
| 1.5 | 0.6 | 0.75 | 0.89 | 1.03 | 1.14 | 1.22 | 1.30 | 1.36 | 1.40 | 1.43 | 1.45 | 1.46 |
| 2.2 | 0.69 | 0.89 | 1.1 | 1.32 | 1.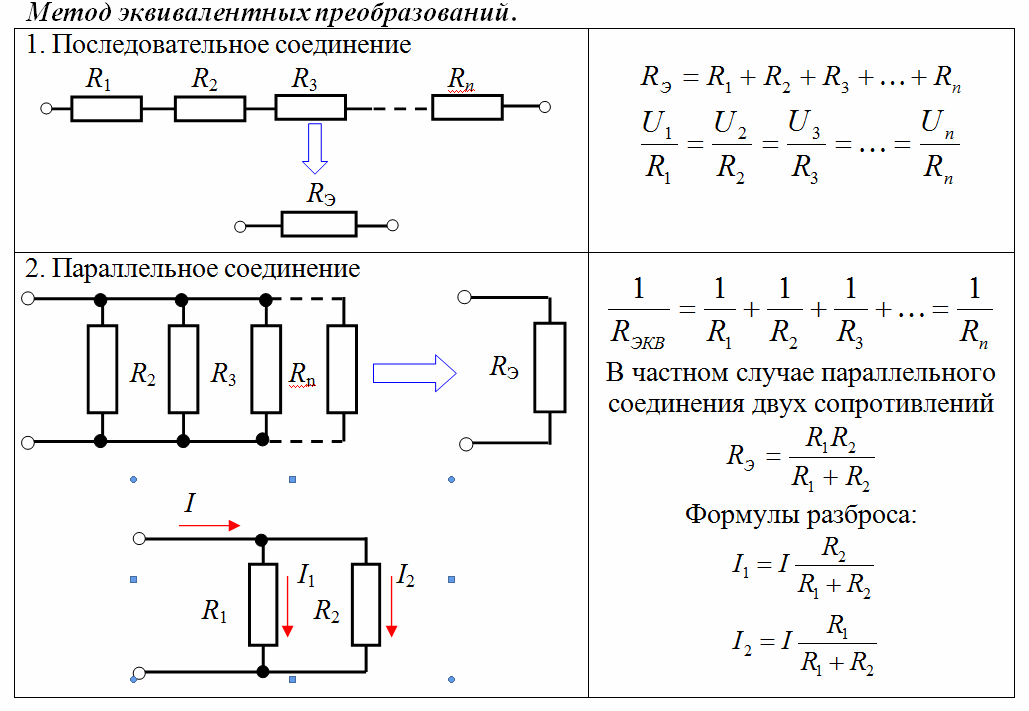 50 50 | 1.66 | 1.82 | 1.92 | 2.0 | 2.06 | 2.10 | 2.13 |
| 3.3 | 0.77 | 1.03 | 1.32 | 1.65 | 1.94 | 2.22 | 2.48 | 2.70 | 2.87 | 3.00 | 3.08 | 3.14 |
| 4.7 | 0.83 | 1.14 | 1.50 | 1.94 | 2.35 | 2.78 | 3,20 | 3,58 | 3,87 | 4,12 | 4,27 | 4,39 |
| 6,8 | 0,87 | |||||||||||
| 6,8 | 0,87 | |||||||||||
| 6,8 | 0,87 | 1,8 | .03101.66 | 2.22 | 2.78 | 3.40 | 4.05 | 4.68 | 5.19 | 5.64 | 5.94 | 6.18 |
| 10 | 0.91 | 1.30 | 1. 82 82 | 2.48 | 3.20 | 4.05 | 5.0 | 6.0 | 6.9 | 7.7 | 8.3 | 8.7 |
| 15 | 0.93 | 1.36 | 1.92 | 2.70 | 3.58 | 4.68 | 6.0 | 7.50 | 8.9 | 10.3 | 11.4 | 12.2 |
| 22 | 0.95 | 1.40 | 2.00 | 2.87 | 3.87 | 5.19 | 6.9 | 8.9 | 11.0 | 13.2 | 15.0 | 16.6 |
| 33 | 0.97 | 1.43 | 2.06 | 3.0 | 4.12 | 5.64 | 7.7 | 10.3 | 13.2 | 16.5 | 19.4 | 22.2 |
| 47 | 0.98 | 1.45 | 2.1 | 3.08 | 4.
| |||||||

