Параллельное соединение резисторов формулы. Параллельное соединение резисторов: формулы, расчеты и применение

Как рассчитать параллельное соединение резисторов. Какие формулы используются для расчета общего сопротивления при параллельном соединении. В чем особенности и преимущества параллельного соединения резисторов. Где применяется параллельное соединение резисторов на практике.

Что такое параллельное соединение резисторов

Параллельное соединение резисторов — это способ подключения двух или более резисторов, при котором их выводы соединяются в двух общих точках. При таком соединении:

• Напряжение на всех резисторах одинаковое и равно напряжению источника питания
• Общий ток делится между резисторами обратно пропорционально их сопротивлениям
• Общее сопротивление цепи уменьшается

Параллельное соединение позволяет снизить общее сопротивление участка цепи и увеличить протекающий через него ток. Это часто используется на практике для создания нужного сопротивления или распределения тока между несколькими нагрузками.

Формулы для расчета параллельного соединения резисторов

Для расчета параллельного соединения резисторов используются следующие основные формулы:

Формула общего сопротивления

Общее сопротивление n параллельно соединенных резисторов рассчитывается по формуле:

1/R = 1/R1 + 1/R2 + … + 1/Rn

где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных резисторов.

Формула для двух параллельных резисторов

В случае двух параллельных резисторов формула упрощается:

R = (R1 * R2) / (R1 + R2)

Формула тока через резистор

Ток через отдельный резистор при параллельном соединении:

I = U / R

где I — ток через резистор, U — напряжение на резисторах, R — сопротивление резистора.

Особенности параллельного соединения резисторов

Параллельное соединение резисторов имеет ряд важных особенностей:

• Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
• Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
• При выходе из строя одного резистора остальные продолжают работать
• Ток распределяется между резисторами обратно пропорционально их сопротивлениям
• Мощность, рассеиваемая на резисторах, суммируется

Эти особенности определяют области применения параллельного соединения в электрических схемах.

Примеры расчета параллельного соединения резисторов

Рассмотрим несколько примеров расчета параллельного соединения резисторов:

Пример 1: Два параллельных резистора

Даны два резистора 100 Ом и 200 Ом, соединенные параллельно. Рассчитаем их общее сопротивление:

R = (100 * 200) / (100 + 200) = 20000 / 300 = 66.67 Ом

Пример 2: Три параллельных резистора

Три резистора 10 Ом, 20 Ом и 30 Ом соединены параллельно. Найдем общее сопротивление:

1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183

R = 1 / 0.183 = 5.46 Ом

Пример 3: Расчет токов

Два параллельных резистора 100 Ом и 200 Ом подключены к источнику 12 В. Рассчитаем токи через резисторы:

I1 = 12 В / 100 Ом = 0.12 А I2 = 12 В / 200 Ом = 0.06 А

Применение параллельного соединения резисторов

Параллельное соединение резисторов широко применяется в электронике и электротехнике:

• Для получения нужного сопротивления, если нет резистора требуемого номинала
• Для увеличения мощности рассеивания
• В делителях тока
• Для создания шунтов измерительных приборов
• В системах распределения электроэнергии
• В схемах защиты от перегрузки

Зная особенности параллельного соединения, можно эффективно применять его для решения различных задач в электрических цепях.

Преимущества и недостатки параллельного соединения резисторов

Параллельное соединение резисторов имеет свои плюсы и минусы:

Преимущества:

• Возможность получить меньшее сопротивление
• Увеличение допустимой мощности рассеивания
• Высокая надежность — при выходе из строя одного резистора схема продолжает работать
• Простота добавления дополнительных резисторов

Недостатки:

• Сложность точного расчета при большом количестве резисторов
• Увеличение общего тока в цепи
• Необходимость использования резисторов с большей мощностью

При проектировании схем нужно учитывать эти особенности и выбирать оптимальный способ соединения резисторов.

Сравнение параллельного и последовательного соединения резисторов

Параллельное и последовательное соединения резисторов имеют противоположные свойства:

Параметр	Параллельное соединение	Последовательное соединение
Общее сопротивление	Уменьшается	Увеличивается
Напряжение на резисторах	Одинаковое	Делится пропорционально сопротивлениям
Ток через резисторы	Делится обратно пропорционально сопротивлениям	Одинаковый

Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи.

формула. Параллельное соединение резисторов — описание, схемы, формулы и примеры расчетов

Содержание

1. Что такое резистор и для чего он нужен
2. Особенности включения
3. Свойства при параллельном соединении резисторов
4. Сопротивление
5. Мощность
6. Напряжение
7. Ток
8. Примеры применения параллельного соединения резисторов
9. Отличия параллельного и последовательного соединения
10. Формула расчета параллельного соединения резисторов
11. Последовательное подключение
12. Смешанное подключение
13. Что ещё нужно учитывать при подключении резисторов
14. Общее сопротивление Rобщ
15. Как высчитывать сопротивление составных резисторов
16. Как рассчитать сложные схемы соединения резисторов

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

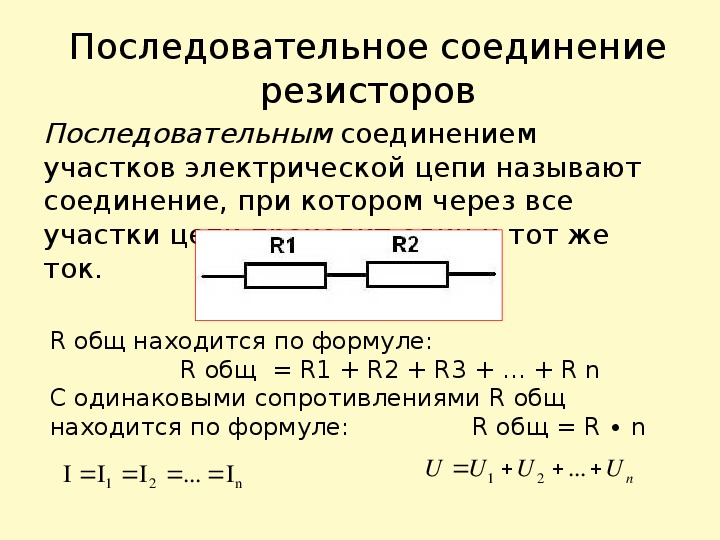
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Особенности включения

Для упрощения темы смешанного соединения резисторов решение задач следует ограничить схемами с подключением к источнику постоянного тока без реактивных компонентов. В этом случае можно исключить сложные колебательные процессы, сопряженные с циклами изменения потребления энергии в нагрузке. Для определения базовых зависимостей достаточно использовать классическую формулу закона Ома:

I (ток) = U (напряжение) / R (сопротивление).

Основные виды соединений

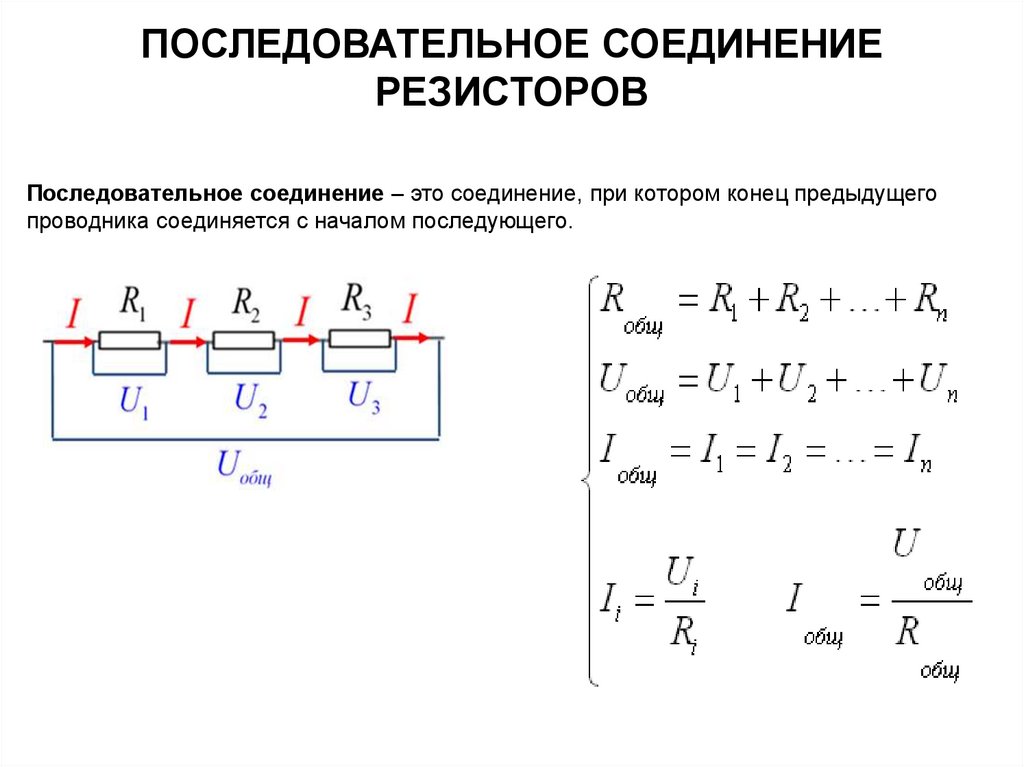
На первой части рисунка показан последовательный проводник. Одинаковый ток можно измерить в любом разрыве с помощью мультиметра. Но даже без экспериментов понятно, что такой результат обеспечен единством пути его прохождения, который создан без разветвлений. Однако при установке разных резисторов (R1≠R2≠R3) напряжение на отдельных элементах отличается (U1≠U2≠U3). Суммарная величина будет равна потенциалу на клеммах источника питания (Uип = U1 + U2 + U3). Аналогичным образом вычисляют суммарное сопротивление:

Rобщ = R1 + R2 + R3.

Следующий пример – параллельное подключение. Здесь каждый ток проходит после разветвления по своему пути (ветке). По предыдущему алгоритму рассуждений несложно установить соответствующие зависимости:

• если R1≠R2≠R3, то I1≠I2≠I3;
• Iип = I1 + I2 + I3;

Если использовано параллельное соединение, формула для напряжений трансформируется в равенство:

Uип = U1 = U2 = U3.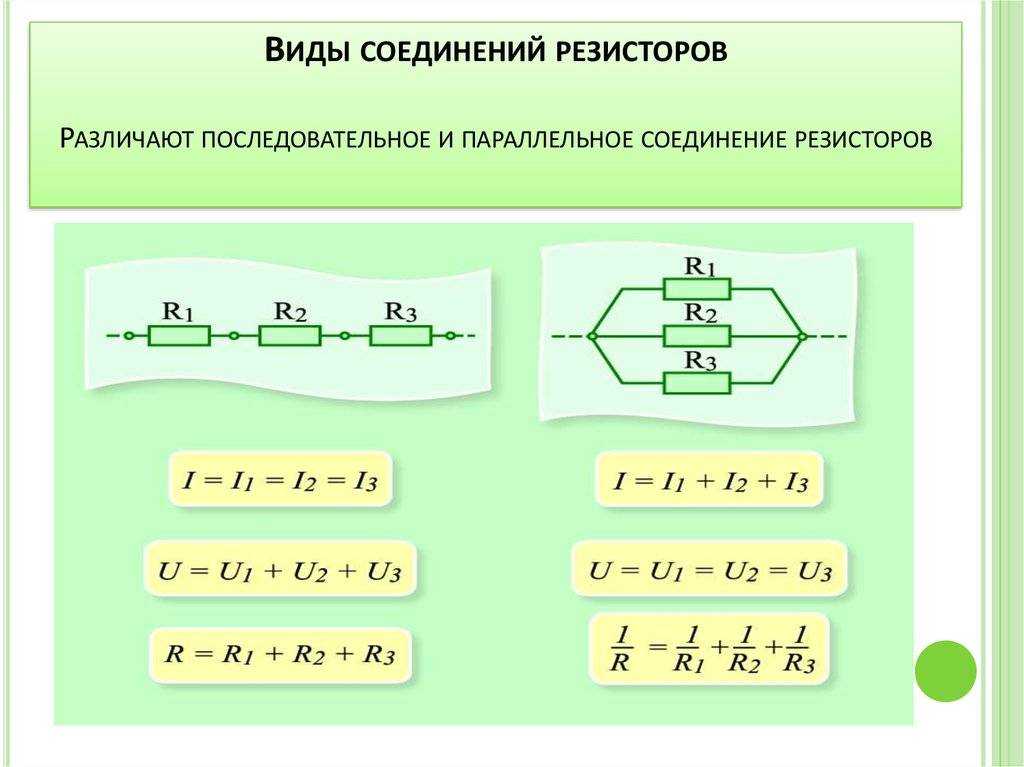

К сведению. Другие виды соединений – это комбинации представленных вариантов. На отдельных участках цепи действительны рассмотренные выше правила.

Свойства при параллельном соединении резисторов

Свойства тока, как мы уже разобрались, меняются в зависимости от того, какой именно тип соединения резисторов используется. А поскольку эти свойства крайне важны, их обязательно нужно разобрать более подробно.

Сопротивление

Одним из важнейших свойств тока является сопротивление. Если проводники были соединены параллельно, их общее сопротивление будет меньше чем то, которое свойственно одному из них.

Эту особенность нужно обязательно учитывать. При проведении расчетов следует использовать общую формулу, а не пытаться вывести какую-то новую. Ведь это правило уже давно известно.

Мощность

Если говорить непосредственно о свойствах тока, то попросту нельзя не упомянуть о его мощности.

В том случае, когда для подключения резисторов используют именно такой способ, то их начала обязательно должны соединиться с одним узлом схемы, а концы, соответственно, с другим.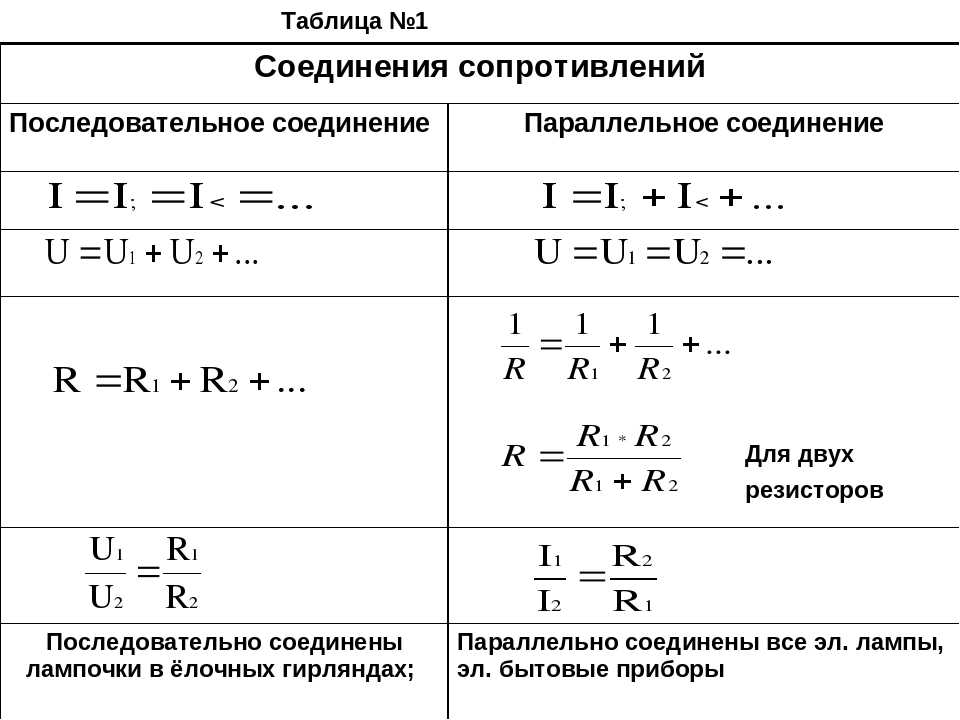

Именно по этой причине и происходит разветвление тока, который протекает не по одному, а по каждому из элементов прибора.

Чтобы определить мощность тока, достаточно вспомнить всем известный закон Ома.

Этот закон гласит, что сила тока всегда будет обратно пропорциональна тем сопротивлениям, которые были подключены. При этом сопротивление резисторов будет одинаковым.

Напряжение

Напряжение – это еще одно свойство тока. Для его определения принято использовать универсальную формулу.

Но часто мастера забывают о том, что таковая имеется и для параллельного подключения. Более того, определить его значительно проще.

Ведь между входом и выходом оно будет равняться сумме напряжений. Имеется ввиду суммарное напряжение на всех составляющих резистора

Ток

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.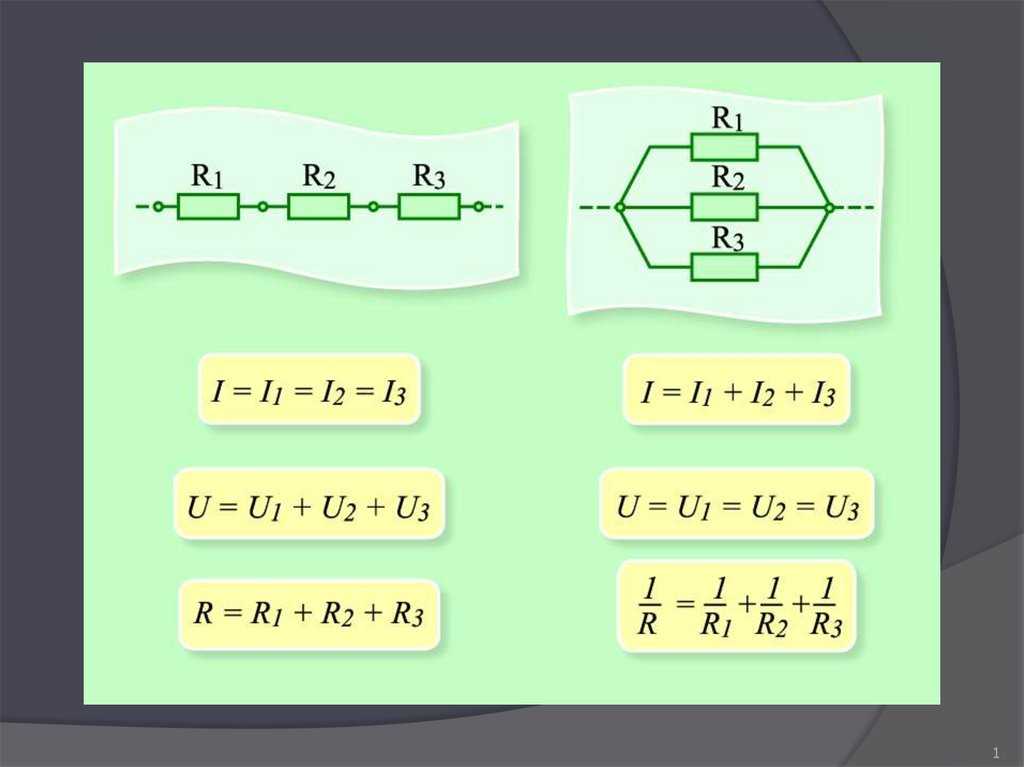

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Отличия параллельного и последовательного соединения

Ни в коем случае нельзя путать эти два вида сопротивления. Ведь в таком случае выполнить подключение правильно попросту не получится.

Первое, что нужно запомнить, это отличия, касающиеся значения напряжения. Если используется последовательное подключение, то напряжение для каждого из резисторов будет отличаться. А вот при параллельном подключении это значение будет одинаковым.

Сила тока же даже при одинаковом значении напряжения в каждом из резисторов будет отличаться. Численные показатели сопротивления резисторов тоже будут разниться.

Поэтому нельзя утверждать, что для параллельного и последовательного соединения значение силы тока будет одинаковым.

Важно! При использовании последовательного подключения сила тока всегда будет одинаковой. Отличаться будет лишь напряжение. Для каждого участка оно будет разным. Именно в этом и заключаются основные отличия.

Формула расчета параллельного соединения резисторов

Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.

Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения.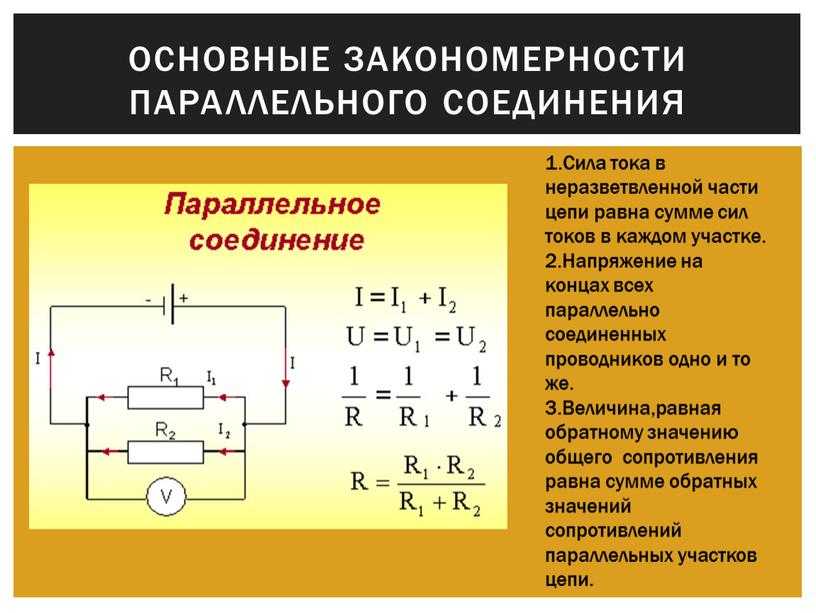 Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.

Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.

 

Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.

Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.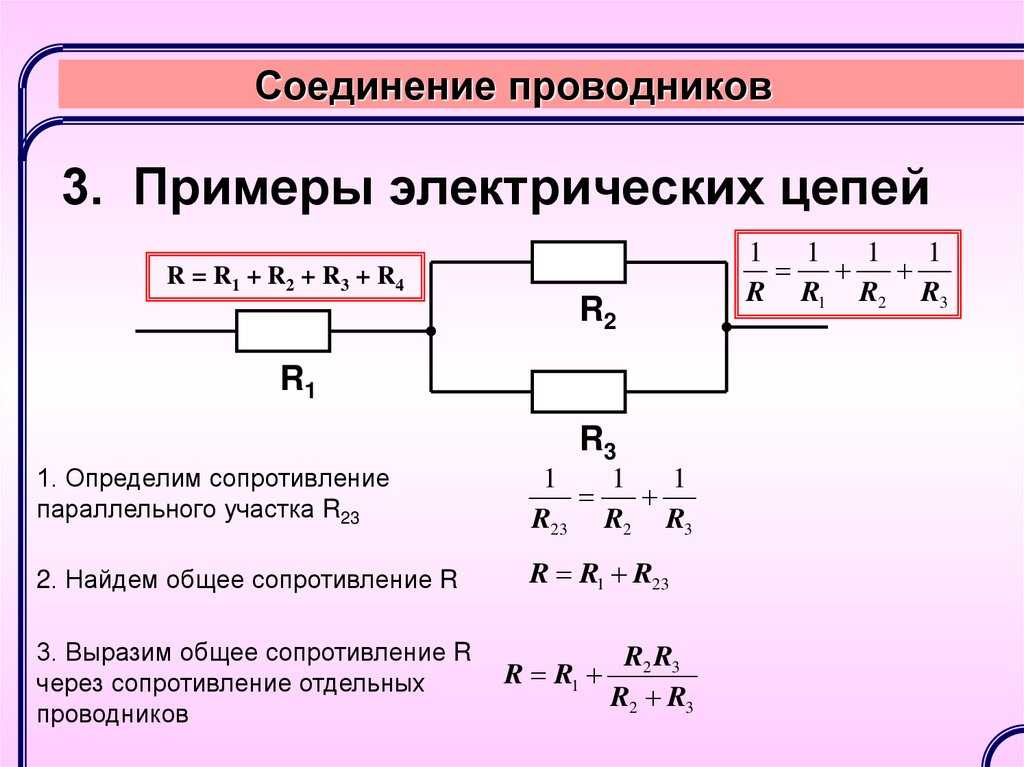 В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше.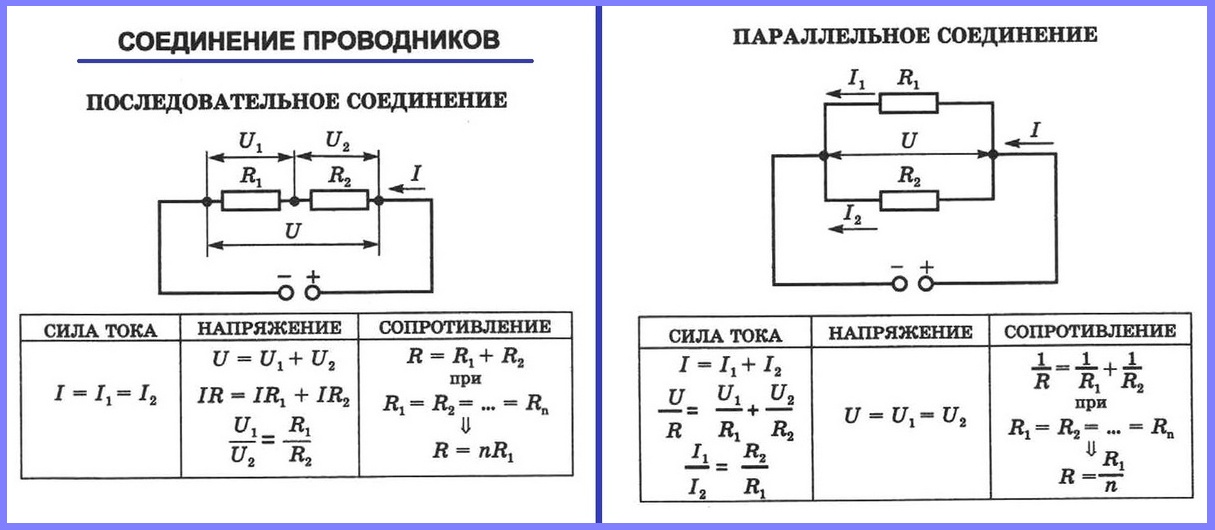 Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Как рассчитать сложные схемы соединения резисторов

Решение трудной задачи демонстрирует пример преобразования «звезды» в «треугольник». Этот способ поможет рассчитать эквивалентное сопротивление типичной мостовой схемы соединения резистивных компонентов.

Преобразование сложной схемы

Трансформация «звезды» показана на примере одного «луча»:

R2 = (R23 * R24)/ R23 + R24 + R34.

Другую часть рассчитывают по формуле:

R23 =R2 + R3 + (R2 * R3)/R4.

Эквивалентное сопротивление вычисляют следующим образом:

Rэкв = ((R12 + R2) * (R13 + R3))/((R12 + R2) + (R13 + R3)) + R4.

Источники

• https://mculab.ru/blog/mikrokontrollery/posledovatelnoe-i-parallelnoe-soedinenie-rezistorov.html
• https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov-2.html
• https://kelmochka.ru/parallelnoe-soedinenie-rezistorov
• https://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
• https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallel-resistance/
• https://electric-220.ru/news/parallelnoe_soedinenie_rezistorov/2014-01-10-487
• https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html

 

 

Помогла ли вам статья?

Последовательное и параллельное соединение резисторов – RxTx.su

Схемы с несколькими резисторами обычно можно разбить на несколько последовательных и параллельных комбинаций. Распознав, какие части схемы содержат резисторы последовательно, а какие — параллельно, эти части могут быть сведены к одному эквивалентному (общему) резистору. Вот как работает этот метод сокращения.

Последовательное соединение резисторов

Когда два резистора R₁ и R₂ соединены последовательно, сумма падений напряжения на каждом из них (U

1 и U₂) будет равна приложенному входному напряжению (U_вх).

\[ U_{вх}=U_1+U_2 \]

Рисунок 1. Последовательное подключение резисторов

Поскольку через оба резистора протекает один и тот же ток I, мы можем заменить U₁ на IR₁ и U₂ на IR₂ (используя закон Ома). В результате получается:

\[ U_{вх}=IR_1+IR_2=I(R_1+R_2)=IR_{экв} \]

Сумма R₁+R₂ называется эквивалентным сопротивлением для двух последовательно соединенных резисторов.

Это означает, что последовательные резисторы могут быть упрощены или сведены к одному резистору с эквивалентным сопротивлением R_экв (или R_общее ), равным

R₁ + R₂.

Чтобы найти ток I, мы просто переформулируем предыдущее уравнение или, другими словами, применим закон Ома, взяв напряжение за U_вх и сопротивление за R_экв:

\[ I=\frac{U_{вх}}{R_{экв}} \]

Чтобы вычислить отдельные падения напряжения на каждом последовательном резисторе, применяется закон Ома:

\[ U_1=IR_1=\frac{U_{вх}}{R_{экв}}R1=\frac{R_1}{R_1+R_2}U_{вх} \]

\[ U_2=IR_2=\frac{U_{вх}}{R_{экв}}R2=\frac{R_2}{R_1+R_2}U_{вх} \]

Эти два уравнения называются соотношениями делителя напряжения — невероятно полезные формулы, которые нужно знать. В электронике часто с ними сталкиваются.

Для нескольких последовательно соединенных резисторов эквивалентное сопротивление представляет собой сумму отдельных сопротивлений:

\[ R=R_1+R_2+…+R_n \]

Формула для расчета сопротивления параллельного соединение резисторов

Когда два резистора R₁ и R₂

подключены параллельно, ток I_вх делится между двумя резисторами таким образом:

\[ I_{вх}=I_1+I_2 \]

Рисунок 2. Параллельное подключение резисторов

Используя закон Ома и понимая, что напряжение на каждом резисторе одинаково (оба U_вх), мы можем заменить I₁ на U_вх/R₁ и I₂ на U_вх/R₂ в предыдущем уравнении, чтобы получить I:

\[ I=\frac{U_{вх}}{R_1}+\frac{U_{вх}}{R_2}=U_{вх}(\frac{1}{R_1}+\frac{1}{R_2}) \]

Эквивалентное сопротивление для этих двух соединенных резисторов становится

\[ \frac{1}{R_{экв}}=\frac{1}{R_1}+\frac{1}{R_2}\text{ или }R_{экв}=\frac{R_1R_2}{R_1+R_2} \]

Чтобы вычислить ток, проходящий через каждый параллельный резистор, мы снова применяем закон Ома:

\[ I_1=\frac{U_{вх}}{R_1}=\frac{I_{вх}R_{экв}}{R_1}=\frac{R_2}{R_1+R_2}I_{вх} \]

\[ I_2=\frac{U_{вх}}{R_2}=\frac{I_{вх}R_{экв}}{R_2}=\frac{R_1}{R_1+R_2}I_{вх} \]

Эти два уравнения представляют из себя соотношения делителя тока. Как и соотношения делителей напряжения, они являются полезными формулами.

Чтобы найти эквивалентное сопротивление для большего числа параллельно подключенных резисторов, используется следующее выражение:

\[ \frac{1}{R_{экв}}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_n} \]

Параллельные резисторы: определение, формула [Примечания GATE]

Параллельные резисторы

Когда резисторы соединены параллельно, ток делится между резисторами, включенными параллельно, и напряжение на всех резисторах будет одинаковым. Если параллельно подключенные резисторы имеют одинаковое сопротивление, то ток делится поровну между всеми резисторами. Резисторы, включенные параллельно, уменьшают эквивалентное сопротивление цепи.

Резисторы, включенные параллельно, рассматриваются как резистивные делители тока. Мощность, рассеиваемая в параллельной цепи, значительно меньше, и по этим цепям передается максимальная мощность.

Необходимость параллельного соединения резисторов

При параллельном соединении резисторов ток делится между резисторами, включенными параллельно, и напряжение на всех резисторах равно напряжению источника. Параллельная комбинация может легко удалить резистор из цепи, не затрагивая другие резисторы. Резисторы называются параллельными, когда их два вывода соединены с одними и теми же двумя узлами, как показано ниже:

Резисторы соединены параллельно для следующих целей:

• Для уменьшения общего сопротивления.
• Для разделения тока источника между всеми резисторами.
• Резисторы соединены параллельно для обеспечения максимальной мощности нагрузки.

Эквивалентное сопротивление параллельно соединенных резисторов

Для упрощения рассчитаем эквивалентное сопротивление двух параллельно соединенных резисторов, как показано ниже:

0036 является эффективным сопротивлением цепи и может быть смоделировано как:

Ток источника i делится между R ₁ и R ₂ . Это известно как принцип текущего деления.

Аналогичным образом рассчитаем эквивалентное сопротивление для трех параллельно соединенных резисторов, как показано ниже:

Где R _eq — эффективное сопротивление цепи, которое можно смоделировать как:

Параллельное соединение резисторов Формула

Когда N резисторов соединены параллельно, общее эквивалентное сопротивление определяется по формуле: наличие резистора в цепи.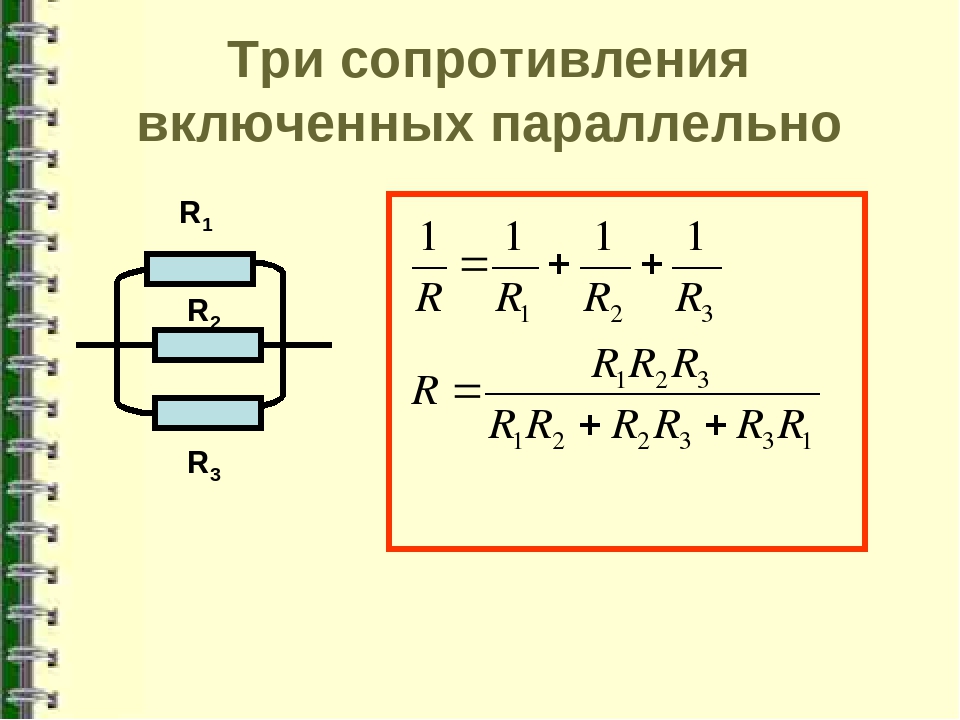

Если имеется N резисторов, соединенных параллельно, и номиналы всех резисторов одинаковы, т. е. R, то общее сопротивление цепи определяется как:

R _eq = R/N

В этом случае ток также делится поровну между всеми резисторами. Если I am — общий ток, а I _n — ток через резистор n ^th , то:

I _n = I/N

эквивалентное сопротивление, если смотреть с клеммы ab показанной ниже цепи

Решение: Сопротивления 2 Ом и 4 Ом соединены последовательно так, что они образуют эквивалентное сопротивление 6 Ом. Уменьшенная схема быть,

Эти резисторы включены параллельно, поэтому

Пример 2. Найдите ток i ₁ и i ₂ в цепи, показанной ниже,

и сопротивление 2. Из рисунка 3 Ом соединены последовательно, поэтому цепь можно уменьшить, как показано ниже:

Используя правило деления тока,

Итак, ответы правильные.

Формула смещения с решенными примерами

Формула смещения 

Все, что вам нужно знать о формуле смещения, приведено ниже. Пожалуйста, продолжайте внимательно читать весь документ, чтобы полностью понять тему.

Смещение относится к изменению местоположения объекта с его исходного положения на его конечное положение. Более того, это векторная величина и, как следствие, имеет и направление, и величину. Кроме того, у него нет единицы СИ, поэтому мы можем измерять его в метрах, милях, ярдах, футах и ​​т. д.

Например, если объект перемещается из исходного положения в последнее положение, положение объекта изменяется. Это изменение положения объекта называется смещением.

Формула

Смещение рассчитывается как:

S = S _F — S _I

, где,

S = смещение

S _{4. FINT LECEALS}

. 90361363613613613611361,936. = начальная позиция

ИЛИ

S = UT + ½ при ²

, где,

S = смещение

U = начальная скорость

A = ускорение

T = время

a = anplasion anplocement anplocemation, anplose). равна начальной скорости (u), умноженной на время (t), плюс половина ускорения (½ a), умноженная на квадрат времени (t2).

Решенные примеры

1. Предположим, Радха приехала из Мумбаи в Дели, чтобы посетить Мину. Итак, она путешествовала поездом и впервые проехала 350 километров на север. Однако трасса уходит на юг на 125 миль. Рассчитать скорость смещения Радхи, используя формулу смещения?

Решение: Первая позиция Радхи S𝑖 = 0, а ее последняя позиция Sf — это расстояние, которое он прошел на север, минус расстояние, которое она прошла на юг. Итак, теперь введите значения в уравнения.