Как рассчитать общее сопротивление при параллельном и последовательном соединении. Какие формулы применяются для расчета тока и напряжения в различных участках цепи. Чем отличаются параллельное и последовательное соединения проводников.
Основные характеристики последовательного соединения проводников
При последовательном соединении проводников они подключаются друг за другом, образуя единую цепь. Это соединение имеет ряд важных особенностей:
- Сила тока одинакова во всех участках цепи
- Общее напряжение равно сумме напряжений на отдельных проводниках
- Общее сопротивление увеличивается при добавлении проводников
Для расчета общего сопротивления при последовательном соединении используется формула:
R = R1 + R2 + R3 + …
Где R — общее сопротивление, а R1, R2, R3 — сопротивления отдельных проводников.
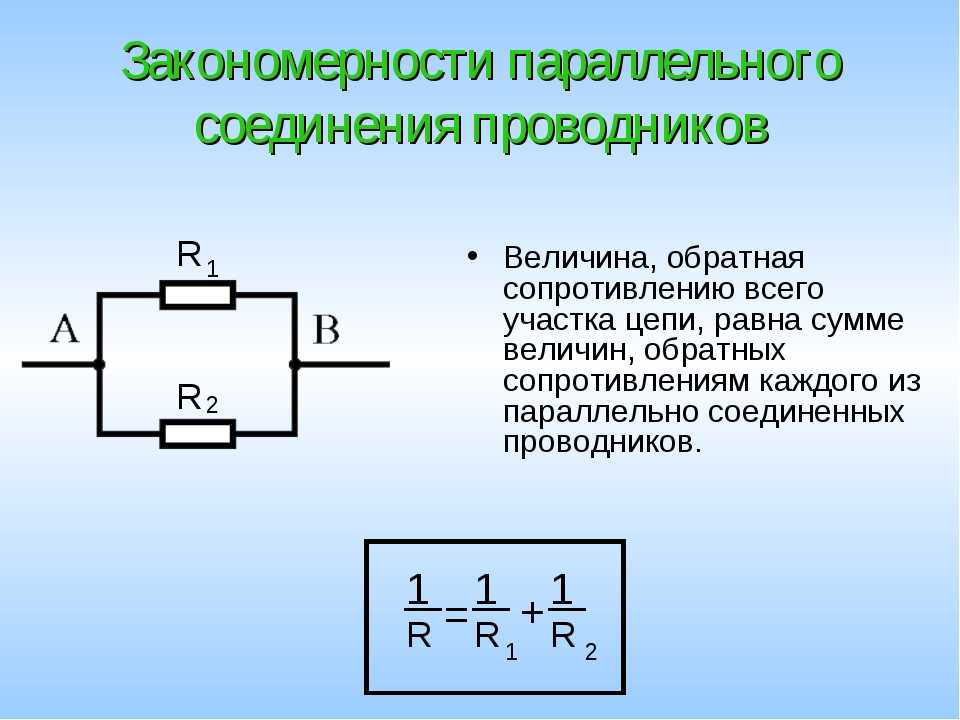
Ключевые особенности параллельного соединения проводников
При параллельном соединении проводники подключаются к общим точкам начала и конца. Основные характеристики такого соединения:
- Напряжение одинаково на всех параллельных участках
- Общий ток равен сумме токов через отдельные проводники
- Общее сопротивление уменьшается при добавлении проводников
Для расчета общего сопротивления при параллельном соединении применяется формула:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Где R — общее сопротивление, а R1, R2, R3 — сопротивления отдельных проводников.
Расчет параметров электрической цепи с последовательным соединением
При последовательном соединении проводников важно уметь рассчитывать основные параметры цепи. Рассмотрим пример:
В цепи последовательно соединены три резистора с сопротивлениями 2 Ом, 3 Ом и 5 Ом. Напряжение источника питания 30 В. Необходимо определить:
- Общее сопротивление цепи
- Силу тока в цепи
- Падение напряжения на каждом резисторе
Решение:
- Общее сопротивление: R = 2 Ом + 3 Ом + 5 Ом = 10 Ом
- Сила тока (по закону Ома): I = U / R = 30 В / 10 Ом = 3 А
- Падение напряжения:
- На первом резисторе: U1 = I * R1 = 3 А * 2 Ом = 6 В
- На втором резисторе: U2 = I * R2 = 3 А * 3 Ом = 9 В
- На третьем резисторе: U3 = I * R3 = 3 А * 5 Ом = 15 В
Проверка: U1 + U2 + U3 = 6 В + 9 В + 15 В = 30 В (равно напряжению источника)
Особенности расчета параллельного соединения проводников
При параллельном соединении проводников расчеты несколько отличаются. Рассмотрим пример:
Три резистора с сопротивлениями 6 Ом, 12 Ом и 4 Ом соединены параллельно. Напряжение на участке 24 В. Определить:
- Общее сопротивление участка
- Общий ток в цепи
- Ток через каждый резистор
Решение:
- Общее сопротивление: 1/R = 1/6 + 1/12 + 1/4 = 1/2 Ом, R = 2 Ом
- Общий ток: I = U / R = 24 В / 2 Ом = 12 А
- Ток через резисторы:
- I1 = U / R1 = 24 В / 6 Ом = 4 А
- I2 = U / R2 = 24 В / 12 Ом = 2 А
- I3 = U / R3 = 24 В / 4 Ом = 6 А
Проверка: I = I1 + I2 + I3 = 4 А + 2 А + 6 А = 12 А (равно общему току)
Сравнение последовательного и параллельного соединения проводников
Последовательное и параллельное соединения проводников имеют ряд существенных различий:
| Характеристика | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Сила тока | Одинакова во всех участках | Различна в разных ветвях |
| Напряжение | Сумма напряжений на элементах | Одинаково на всех элементах |
| Общее сопротивление | Увеличивается | Уменьшается |
| Формула расчета сопротивления | R = R1 + R2 + R3 + … | 1/R = 1/R1 + 1/R2 + 1/R3 + … |
Применение различных типов соединений в электротехнике
Последовательное и параллельное соединения проводников широко применяются в электротехнике и электронике. Каждый тип соединения имеет свои преимущества и области применения:
Последовательное соединение:
- Используется в делителях напряжения
- Применяется в измерительных приборах (амперметрах)
- Встречается в цепях защиты от перегрузок
Параллельное соединение:
- Используется в бытовой электропроводке
- Применяется для увеличения мощности электроприборов
- Встречается в схемах резервирования для повышения надежности
Выбор типа соединения зависит от конкретной задачи и требуемых характеристик электрической цепи.
Практические задачи на расчет электрических цепей
Для закрепления знаний о последовательном и параллельном соединении проводников рассмотрим несколько практических задач:
Задача 1: Последовательное соединение
В цепи последовательно соединены четыре резистора с сопротивлениями 2 Ом, 4 Ом, 6 Ом и 8 Ом. Определите общее сопротивление цепи и падение напряжения на каждом резисторе, если через цепь протекает ток 2 А.
Решение:
- Общее сопротивление: R = 2 Ом + 4 Ом + 6 Ом + 8 Ом = 20 Ом
- Падение напряжения:
- U1 = I * R1 = 2 А * 2 Ом = 4 В
- U2 = I * R2 = 2 А * 4 Ом = 8 В
- U3 = I * R3 = 2 А * 6 Ом = 12 В
- U4 = I * R4 = 2 А * 8 Ом = 16 В
Задача 2: Параллельное соединение
Три резистора с сопротивлениями 3 Ом, 6 Ом и 9 Ом соединены параллельно. Определите общее сопротивление участка и токи через каждый резистор, если напряжение на участке составляет 18 В.
Решение:
- Общее сопротивление: 1/R = 1/3 + 1/6 + 1/9 = 11/18 Ом, R = 18/11 Ом ≈ 1,64 Ом
- Общий ток: I = U / R = 18 В / 1,64 Ом ≈ 11 А
- Токи через резисторы:
- I1 = U / R1 = 18 В / 3 Ом = 6 А
- I2 = U / R2 = 18 В / 6 Ом = 3 А
- I3 = U / R3 = 18 В / 9 Ом = 2 А
Заключение: важность понимания типов соединений в электрических цепях
Понимание принципов последовательного и параллельного соединения проводников является фундаментальным для работы с электрическими цепями. Эти знания позволяют:
- Правильно рассчитывать параметры электрических схем
- Оптимизировать работу электрических устройств
- Обеспечивать безопасность при проектировании и эксплуатации электрооборудования
- Эффективно решать практические задачи в области электротехники и электроники
Освоение этих концепций открывает широкие возможности для дальнейшего изучения более сложных электрических систем и их применения в различных областях техники и науки.
Page Not Found — Microtex
Address
Address Line 1
City
State / Province / Region
Postal Code
TürkiyeАвстралияАвстрияАзербайджанАландские островаАлбанияАлжирАмериканское СамоаАнгильяАнголаАндорраАнтарктидаАнтигуа и БарбудаАргентинаАрменияАрубаАфганистанБагамыБангладешБарбадосБахрейнБелизБелоруссияБельгияБенинБермудыБолгарияБоливия (Многонациональное Государство)Бонэйр, Синт-Эстатиус и СабаБосния и ГерцеговинаБотсванаБразилияБританская территория Индийского океанаБруней-ДаруссаламБуркина-ФасоБурундиБутанВануатуВатиканВенгрияВенесуэла (Боливарианская Республика)Виргинские острова (Американские)Виргинские острова (Великобритания)Внешние малые острова СШАВосточный ТиморВьетнамГабонГаитиГайанаГамбияГанаГваделупаГватемалаГвинеяГвинея-БисауГерманияГернсиГибралтарГондурасГонконгГренадаГренландияГрецияГрузияГуамДанияДжерсиДжибутиДоминикаДоминиканская РеспубликаЕгипетЗамбияЗападная СахараЗимбабвеИзраильИндияИндонезияИорданияИракИран (Исламская Республика)Ирландия (Республика)ИсландияИспанияИталияЙеменКабо-ВердеКазахстанКаймановы островаКамбоджаКамерунКанадаКатарКенияКипрКиргизияКирибатиКитайКокосовые острова (Килинг)КолумбияКоморские островаКонгоКонго (Демократическая Республика)Корея (Демократическая Народная Республика)Корея (Республика)КосовоКоста-РикаКот-д’ИвуарКубаКувейтКюрасаоЛаосская Народно-Демократическая РеспубликаЛатвияЛесотоЛиберияЛиванЛивияЛитваЛихтенштейнЛюксембургМаврикийМавританияМадагаскарМайоттаМакаоМалавиМалайзияМалиМальдивыМальтаМароккоМартиникаМаршалловы островаМексикаМикронезия (Федеративные Штаты)МозамбикМолдова (Республика)МонакоМонголияМонтсерратМьянмаНамибияНауруНепалНигерНигерияНидерландыНикарагуаНиуэНовая ЗеландияНовая КаледонияНорвегияОбъединённые Арабские ЭмиратыОманОстров БувеОстров МэнОстров НорфолкОстров РождестваОстров Херд и острова МакдональдОстрова КукаОстрова ПиткэрнОстрова Св.
Елены, Вознесения и Тристан-да-КуньяОстрова Теркс и КайкосПакистанПалауПалестина (Государство)ПанамаПапуа-Новая ГвинеяПарагвайПеруПольшаПортугалияПуэрто-РикоРеюньонРоссийская ФедерацияРуандаРумынияСальвадорСамоаСан-МариноСан-Томе и ПринсипиСаудовская АравияСеверная Македония (Республика)Северные Марианские островаСейшельские ОстроваСен-Мартен (Голландская часть)Сен-Мартен (владение Франции)Сен-Пьер и МикелонСенегалСент-БартельмиСент-Винсент и ГренадиныСент-Китс и НевисСент-ЛюсияСербияСингапурСирийская Арабская РеспубликаСловакияСловенияСоединенное Королевство Великобритании и Северной ИрландииСоединенные Штаты АмерикиСоломоновы ОстроваСомалиСуданСуринамСьерра-ЛеонеТаджикистанТаиландТайвань, Китайская РеспубликаТанзания (Объединенная Республика)ТогоТокелауТонгаТринидад и ТобагоТувалуТунисТуркменистанУгандаУзбекистанУкраинаУоллис и ФутунаУругвайФарерские островаФиджиФилиппиныФинляндияФолклендские ОстроваФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские южные территорииХорватияЦентральноафриканская РеспубликаЧадЧерногорияЧехияЧилиШвейцарияШвецияШпицберген и Ян-МайенШри-ЛанкаЭквадорЭкваториальная ГвинеяЭритреяЭсватини (Королевство)ЭстонияЭфиопияЮжная АфрикаЮжная Георгия и Южные Сандвичевы островаЮжный СуданЯмайкаЯпонияCountry
17,5 Параллельные резисторы | Электрические цепи
17.
5 Параллельные резисторы (ESAFK)Существует больше путей для протекания тока, что обеспечивает разделение тока по разным пути .
Напряжение то же на резисторах. Напряжение на аккумуляторе в цепи равно напряжению на каждом из параллельных резисторов:
\[{V}_{\text{батарея}} = {V}_{1} = {V}_{2} = {V}_{3} \ldots\]Сопротивление протеканию тока уменьшается . Общее сопротивление, \({R}_{P}\), дано автор:
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
Когда резисторы соединены параллельно, начальная и конечная точки для всех резисторов одинаковы. Эти
точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова независимо от того, что
поставить между ними.
Посмотрите на следующие электрические схемы. Аккумулятор во всех случаях одинаков, меняется только количество резисторов. добавляются между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получили бы один и тот же ответ для всех трех случаев.
Давайте посмотрим на два параллельных резистора более внимательно. Когда вы строите цепь, вы используете провода, и вы можете
думаю, что измерение напряжения в разных местах проводов будет иметь значение. Это неправда.
разность потенциалов или измерение напряжения будут отличаться только в том случае, если вы измеряете другой набор компонентов.
Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. е. A–B, C–D и E–F), дадут вам одинаковое напряжение. Между различными точками измерения слева нет компонентов, поэтому изменение потенциальной энергии. Точно то же самое относится к различным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа вы получите тот же ответ.
Рабочий пример 7: Напряжение I
Рассмотрим следующую электрическую схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и одним резистором. Мы знаем напряжение на аккумуляторе. Мы хотим найти это напряжение на резисторе.
\[{V}_{\text{батарея}} = \text{2}\text{V}\]
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
компоненты.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
В цепи есть только один компонент — резистор.
\[{V}_{\text{всего}}={V}_{1}\]
Это означает, что напряжение на батарее равно напряжению на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} = {V} _ {1} \\ {V}_{1} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 8: Напряжение II
Рассмотрим эту цепь:
Каково напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и двумя резисторами. Мы знаем напряжение на аккумуляторе и одном из резисторы. Мы хотим найти это напряжение на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {2} \ text {V} \\ {V}_{B} & = \text{1}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
компоненты, которые находятся в последовательном соединении.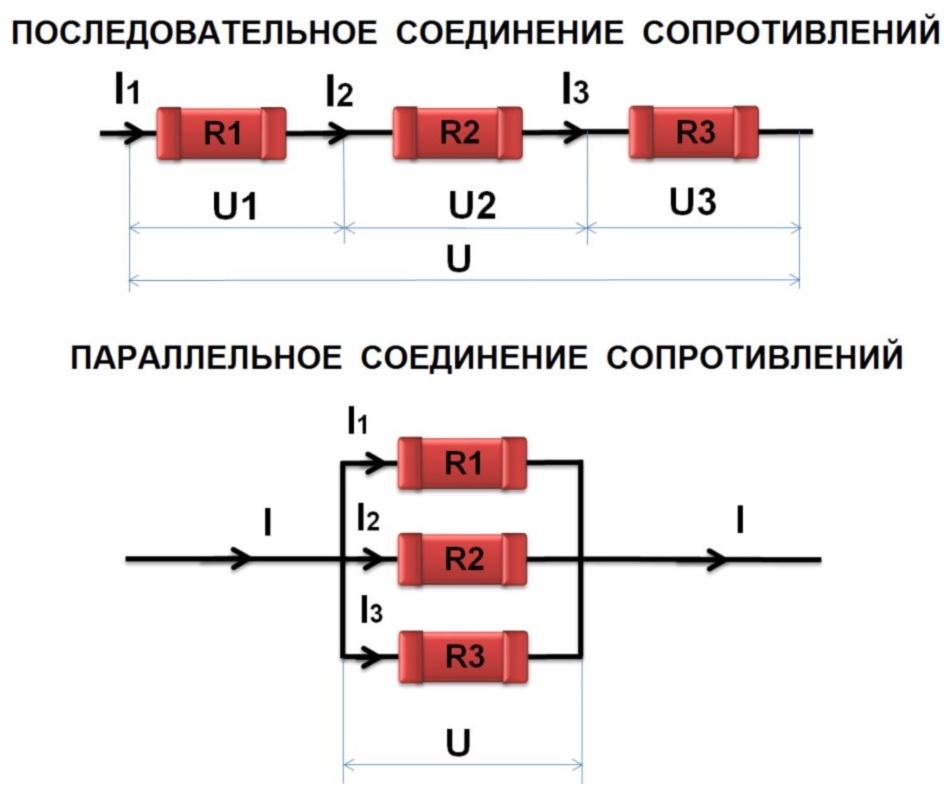
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V}_{\text{всего}} = {V}_{A} + {V}_{B}\]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\\\ {V} _ {\ text {батарея}} & = {V} _ {1} + {V} _ {\ text {резистор}} \\ \text{2}\text{V} & = {V}_{1} + \text{1}\text{V} \\ {V}_{1} & = \text{1}\text{V} \конец{выравнивание*}
Рабочий пример 9: Напряжение III
Рассмотрим принципиальную схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и тремя резисторами.
Мы знаем напряжение на аккумуляторе и двух
резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известно}} & = {V} _ {A} + {V} _ {C} \\ & = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V} _ {\ text {всего}} = {V} _ {B} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {B} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{B} + \text{5}\text{V} \\ {V}_{B} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 10: Напряжение IV
Рассмотрим принципиальную схему:
Каково напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальное
схема аналогична предыдущей задаче.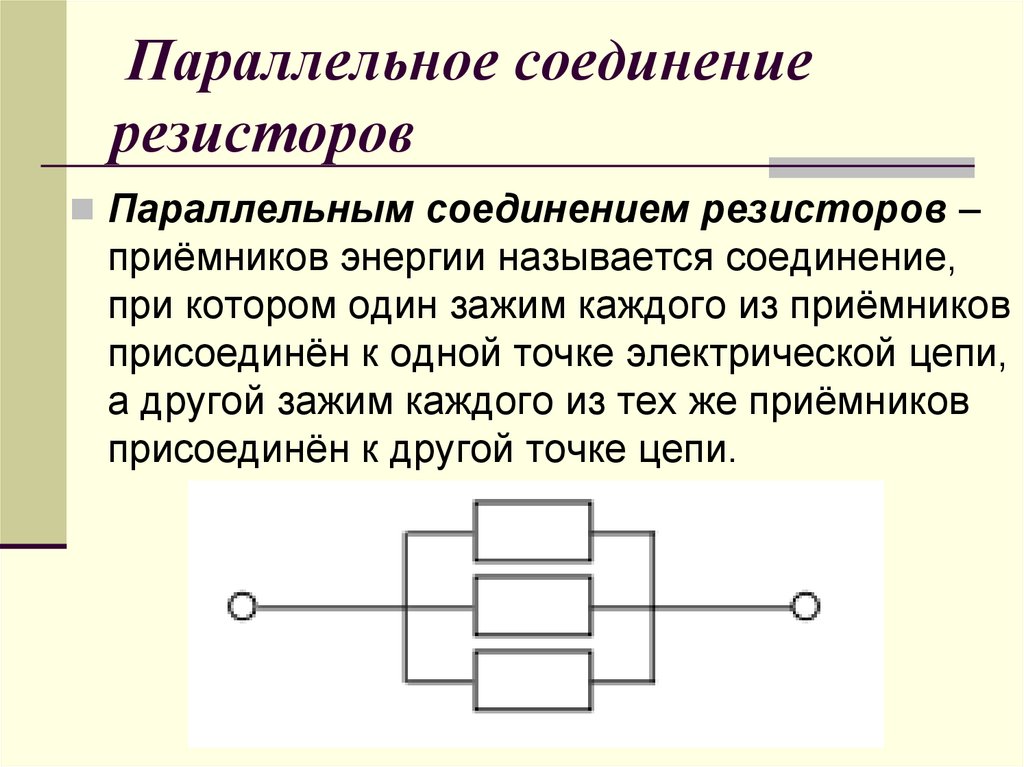
Быстрый ответ
Схема такая же, как и в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в схема не зависит от того, что находится между ними, поэтому ответ такой же, как и выше \({V}_{\text{parallel}} = \text{2}\text{V}\).
Проверьте, что у вас есть и единицы измерения — подробный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно). Мы знаем напряжение на аккумуляторе и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \({V}_{\text{параллельные}}\).
\начать{выравнивать*} {V} _ {\ text {батарея}} = \ text {7} \ text {V} \\ {V}_{\text{известно}} = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
компоненты.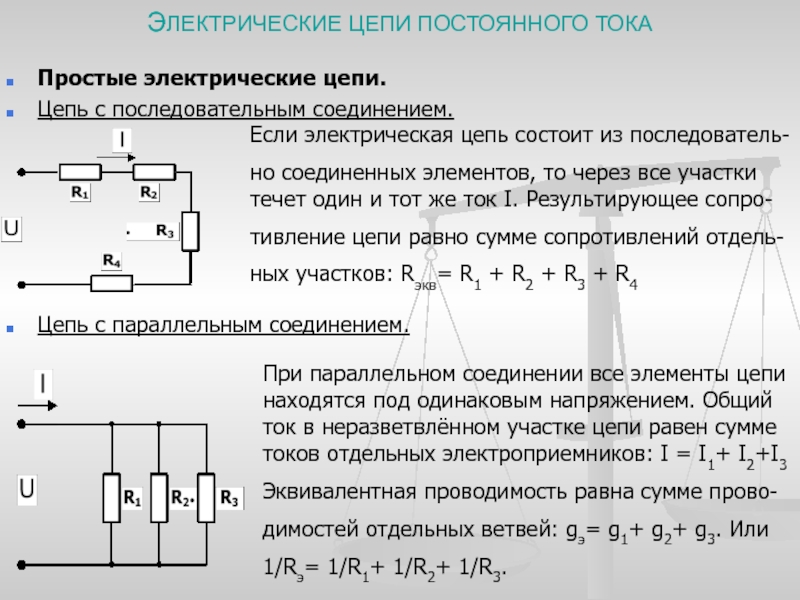
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Напряжения складываются только алгебраически для компонентов, соединенных последовательно. Параллельные резисторы можно рассматривать как один компонент, который последовательно с другими компонентами, а затем напряжения могут быть добавлены.
\[{V} _ {\ text {всего}} = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{\text{параллельно}} + \text{5}\text{V} \\ {V} _ {\ text {параллельно}} & = \ text {2} \ text {V} \конец{выравнивание*}
temp text В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей вдоль
какой ток может течь.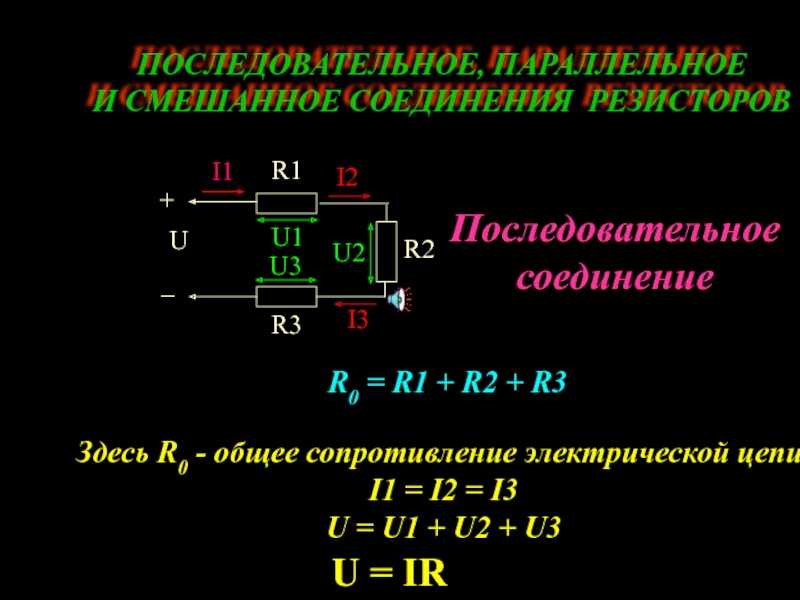
Делая это, мы уменьшаем общее сопротивление цепи!
Взгляните на диаграмму ниже. Слева у нас такая же схема, как и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает силу тока \(\text{1}\) \(\text{A}\). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось. Вы видите, что ток в цепи повысился. Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельно соединенных резисторов НЕ является суммой отдельных сопротивлений, поскольку общее сопротивление уменьшается с увеличением количества путей для тока. Общее сопротивление для параллельных резисторов дано автор:
\[\frac{1}{{R}_{P}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\ldots\ ] Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление.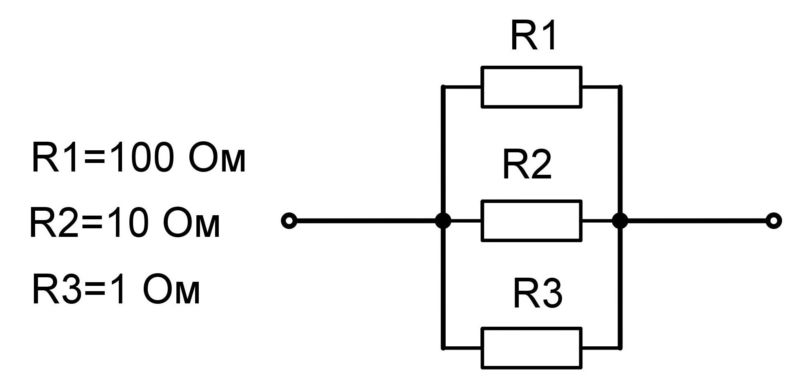
Эта ситуация показана на диаграмме ниже:
Применяя формулу для полного сопротивления имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{Там всего два резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} \\ & \text{Сложите дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}}{{R}_{2 }} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}}{{R}_{1}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}}{{R}_{1}{R}_{2}} + \frac{{R} _{1}}{{R}_{1}{R}_{2}} \\ & \text{Переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2} + {R}_{1}}{{R}_{1}{R}_{2} } \\ \frac{1}{{R}_{P}} & = \frac{{R}_{1} + {R}_{2}}{{R}_{1}{R}_{2} } \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}}{{R}_{1} + {R}_{2}} \конец{выравнивание*}Теперь для любых двух резисторов, включенных параллельно, мы знаем, что
\[{R}_{P} = \frac{\text{произведение сопротивлений}}{\text{сумма сопротивлений}} = \frac{{R}_{1}{R}_{2}}{ {Р}_{1} + {Р}_{2}}\]Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
Аккумулятор
Вольтметр
Амперметр
Провода
Резисторы
Метод
Подключите каждую цепь, показанную ниже
Измерьте напряжение на каждом резисторе в цепи.
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного резистора. ветви.
Результаты и выводы
Сравните токи через отдельные резисторы друг с другом.
Сравните сумму токов через отдельные резисторы с током перед параллельным ветви.
Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
Цепь содержит два резистора, включенных параллельно. Резисторы имеют значения сопротивления \(\text{15}\) \(\text{Ω}\) и \(\text{7}\) \(\text{Ω}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значения двух резисторов указаны в правильных единицах, Ом.
Применить соответствующие принципы
Было показано, что общее сопротивление резисторов, включенных параллельно, представляет собой произведение сопротивлений, деленное на сумма. Мы можем использовать
\[{R}_{P} = \frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}\]
9{2}}{\текст{22}\текст{Ом}} \\ & = \text{4,77}\text{ Ом} \конец{выравнивание*}Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{4,77}\) \(\text{Ом}\)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор к конфигурации (настройке) в предыдущем примере.
Дополнительный
резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно вычислить общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применить соответствующие принципы
Общее сопротивление для параллельных резисторов указано как
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
У нас есть три резистора, и мы теперь сопротивления. В данном случае имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{три резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1 }{{R}_{3}} \\ & \text{сложить дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}{R}_{3}} {{R}_{2}{R}_{3}} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{3}} + \frac{1}{{R}_{3} } \times \frac{{R}_{1}{R}_{2}}{{R}_{1}{R}_{2}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3}}{{R}_{1}{R}_{2}{ Р}_{3}} + \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{2}{R}_{3}} + \frac{{R}_{ 1}{R}_{2}}{{R}_{1}{R}_{2}{R}_{3}} \\ & \текст {переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + { Р}_{2}{Р}_{3}}{{Р}_{1}{Р}_{2}{Р}_{3}} \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}{R}_{3}}{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + {R}_{2}{R}_{3}} \\ {R}_{P} & = \frac{\left(\text{15}\text{Ω} \right)\left(\text{7}\text{Ω} \right)\left(\text{3}\text{ Ω} \right)}{\left(\text{7}\text{ Ω} \right)\left(\text{3}\text{ Ω} \right) + \left(\text{15}\text{ Ω} \right)\left(\text{3}\text{ Ω}\right) + \left(\text{7}\text{ Ω} \right)\left(\text{15}\text{ Ω}\right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R}_{P} & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\)
При расчете сопротивления для сложных конфигураций резисторов можно начать с любой комбинации двух
резисторы (последовательно или параллельно) и рассчитайте их общее сопротивление.
Затем вы можете заменить их одним
резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим
резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь
использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой параллельной рабочей конфигурации (настройка). Дополнительный резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\)
Каково общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно вычислить общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Примените соответствующие принципы
Мы можем поменять местами резисторы без изменения схемы:
Мы уже рассчитали общее сопротивление двух резисторов в пунктирной рамке, равное \(\text{4,77}\)
\(\текст{Ω}\).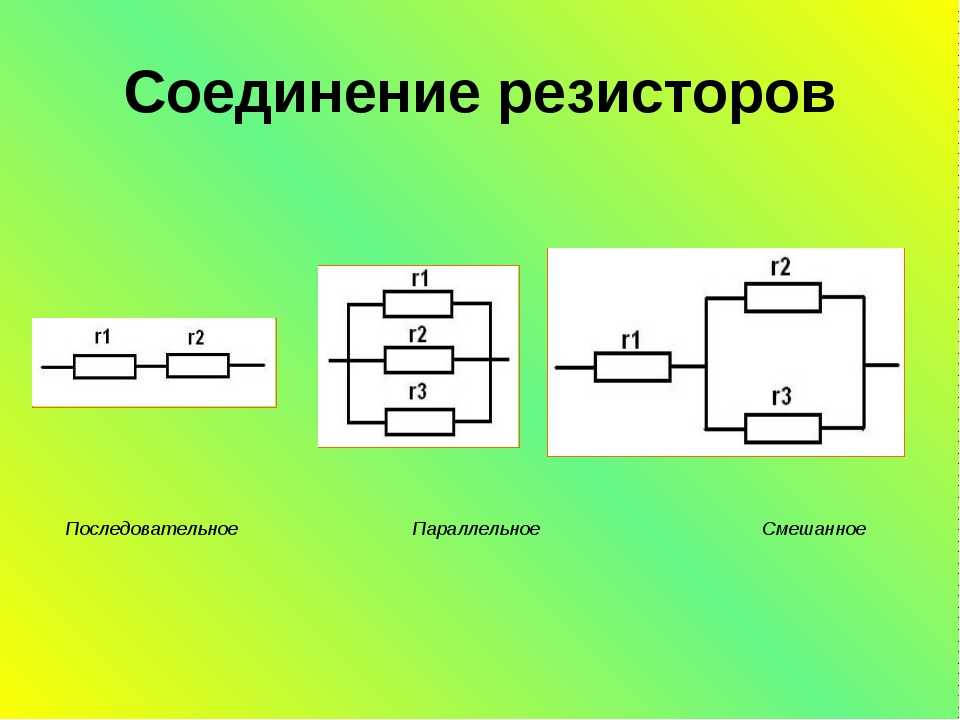
Мы можем заменить эти два резистора одним резистором \(\text{4,77}\)
\(\text{Ω}\), чтобы получить:
Рассчитайте общее сопротивление для следующей пары резисторов
Затем снова воспользуемся формулой для двух параллельных резисторов, чтобы получить общее сопротивление для этой новой цепи: 9{2}}{\текст{11,77} \Омега} \\ & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\). Это тоже самое результат, как если бы мы добавили все три резистора одновременно.
Сопротивление
Учебное упражнение 17.1
Как называется единица сопротивления и каково ее обозначение?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при последовательном включении резисторов?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при параллельном добавлении резисторов?
Решение пока недоступно
Почему батареи разряжаются?
Решение пока недоступно
Моделирование: VPfzj
Резисторы, включенные последовательно и параллельно
Электрическая цепь может содержать несколько резисторов, которые могут быть соединены по-разному.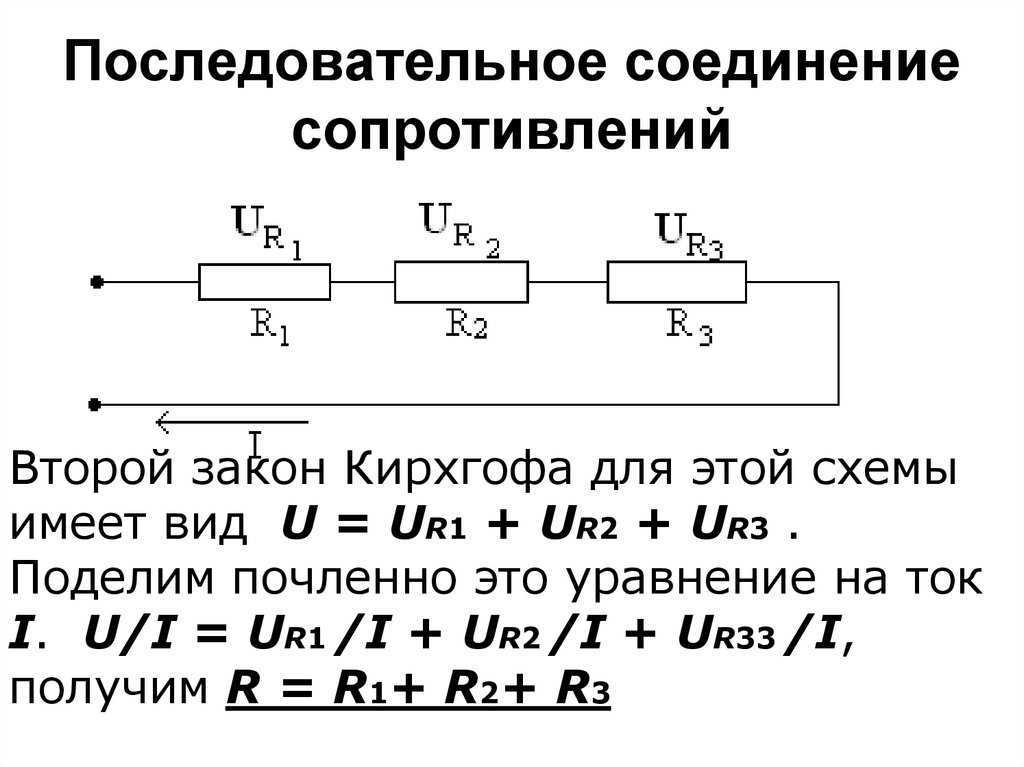
Резисторы, соединенные последовательно и параллельно
Электрическая цепь может содержать несколько резисторов, которые могут быть соединены по-разному. Для каждого типа цепи мы можем рассчитать эквивалентное сопротивление, создаваемое группой отдельных резисторов.
Резисторы, соединенные последовательно
Когда два или более резистора соединены встык, говорят, что они соединены последовательно. Резисторы могут быть простыми резисторами, лампочками, нагревательными элементами или другими устройствами. Рисунок 2.9(а) показаны три резистора R 1, R 2 и R 3, соединенные последовательно.
Количество заряда, прошедшего через резистор R 1, должно также проходить через резисторы R 2 и R 3, поскольку заряды не могут накапливаться где-либо в цепи.
По этой причине ток I, проходящий через все три резистора, одинаков. Согласно закону Ома, если один и тот же ток проходит через разные резисторы разного номинала, то разность потенциалов на каждом резисторе должна быть разной.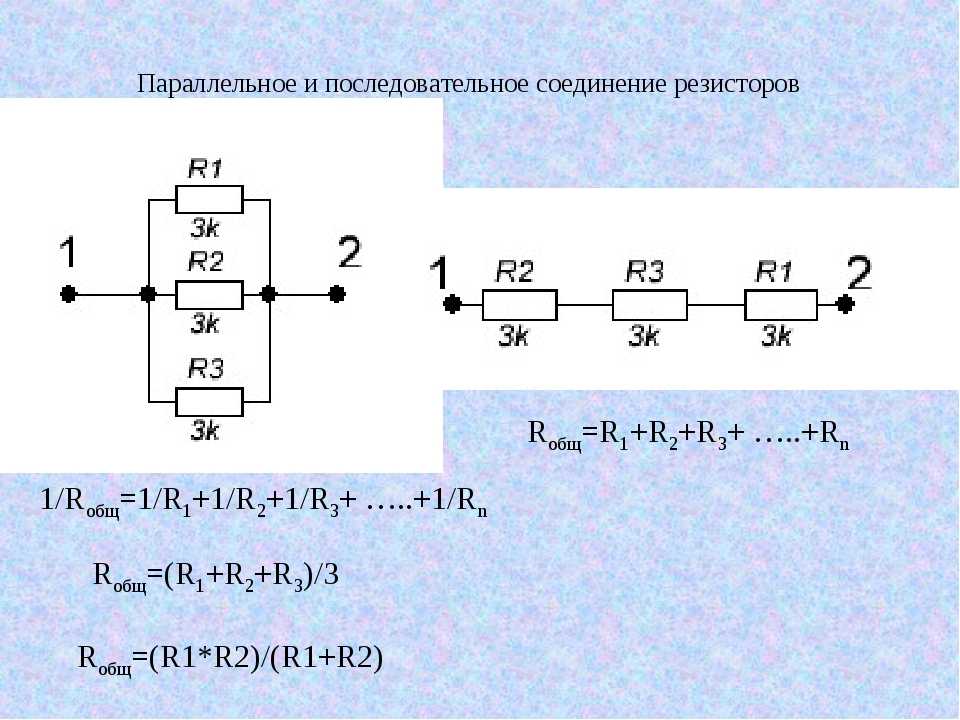
Пусть V 1, V 2 и V 3 . можно записать В 1 = IR 1, В 2 = IR 2 и В 3 = IR 3. Но общее напряжение на каждом резисторе равно сумме напряжений В 903.
где RS эквивалентное сопротивление,
Когда несколько сопротивлений соединены последовательно, общее или эквивалентное сопротивление представляет собой сумму отдельных сопротивлений, как показано на рисунке 2.9 (б).
Примечание. Значение эквивалентного сопротивления при последовательном соединении будет больше, чем сопротивление каждого отдельного элемента.
ПРИМЕР 2.8
Рассчитайте эквивалентное сопротивление цепи, подключенной к батарее 24 В, а также найдите разность потенциалов на резисторах 4 Ом и 6 Ом в цепи.
Решение
Поскольку резисторы соединены последовательно, эффективное сопротивление в цепи
= 4 Ом + 6 Ом = 10 Ом
Ток I в цепи = V/ Req = 24/10 = 2,4 А
Напряжение на резисторе 4 Ом
V1 = IR1 = 2 .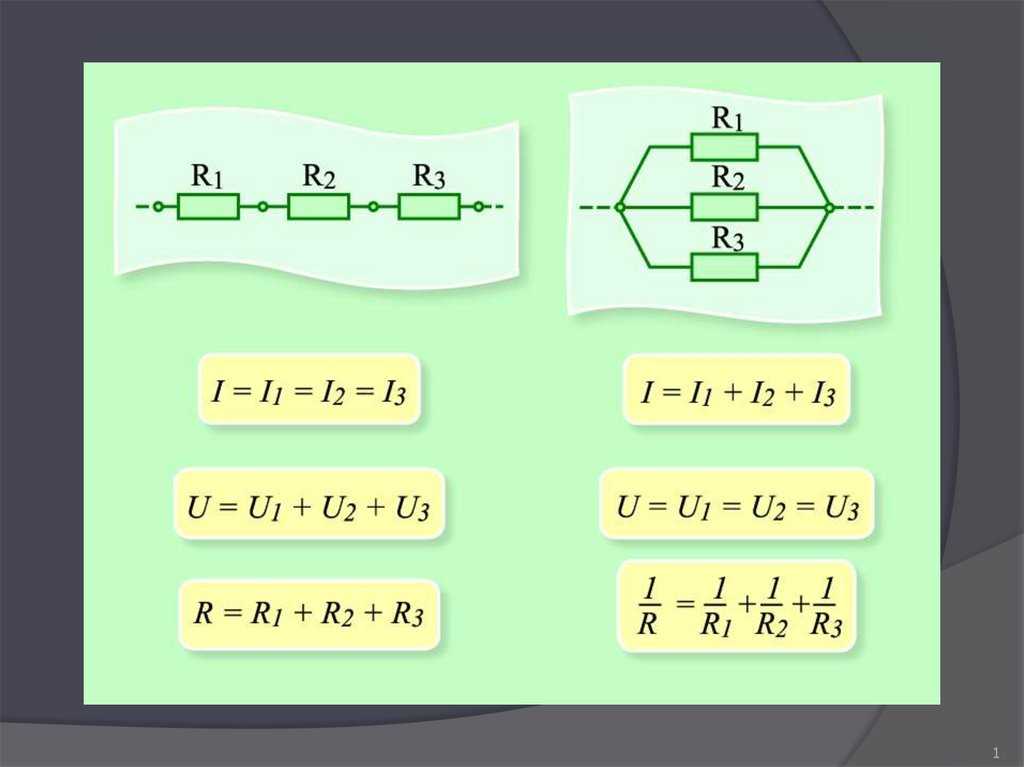
4 А × 4 Ом = 9,6 В
Напряжение на резисторе 6 Ом
V2 = IR1 = 2 . 4 А × 6 Ом = 14,4 В
Параллельные резисторы
Резисторы параллельны, если они подключены к одной и той же разности потенциалов, как показано на рис. 2.10 (а).
В этом случае общий ток I, выходящий из батареи, разделяется на три отдельных пути. Пусть I1, I2 и I3 – ток через резисторы R1, R2 и R3 соответственно. Из-за сохранения заряда полный ток в цепи I равен сумме токов через каждый из трех резисторов.
Поскольку напряжение на каждом резисторе одинаковое, применяя закон Ома к каждому резистору, мы имеем
Подставляя эти значения в уравнение (2.24), мы получаем
Здесь RP эквивалентное сопротивление параллельной комбинации резисторов. Таким образом, когда несколько резисторов соединены параллельно, сумма обратной величины сопротивления отдельного резистора равна обратной величине эффективного сопротивления комбинации, как показано на рисунке 2.
10 (б)
Примечание. Значение эквивалентного сопротивления при параллельном соединении будет меньше, чем сопротивление каждого отдельного элемента.
Бытовые приборы всегда подключаются параллельно, чтобы, даже если один из них был выключен, другие устройства могли нормально работать.
ПРИМЕР 2.9
Рассчитайте эквивалентное сопротивление в следующей цепи, а также найдите ток I, I1 и I2 в данной цепи.
Решение
Так как сопротивления соединены параллельно, то эквивалентное сопротивление в цепи равно
Резисторы соединены параллельно, потенциал (напряжение) на каждом резисторе одинаков.
Ток I представляет собой сумму токов в двух ветвях. Тогда
I = I1 + I2 = 6 А + 4 А = 10 А
ПРИМЕР 2.10
Когда два сопротивления соединены последовательно и параллельно, их эквивалентные сопротивления составляют 15 Ом и 56/15 Ом соответственно.
Найдите индивидуальные сопротивления.
Решение
Rs = R1 + R2 = 15 Ом (1)
Приведенное выше уравнение можно решить с помощью факторизации.
R12-8 R1-7 R1+ 56 = 0
R1 (R1– 8) – 7 (R1– 8) = 0
(R1– 8) (R1– 7) = 0
Если (R1= 8) Ом)
используя в уравнении (1)
8 + R2 = 15
R2 = 15 – 8 = 7 Ом,
R2 = 7 Ом, т.е. (когда R1 = 8 Ом; R2 = 7 Ом)
Если (R1= 7 Ом)
Подставляя в уравнение (1)
7 + R2 = 15
R2 = 8 Ом, т. е. (когда R1 = 8 Ом; R2 = 7 Ом)
ПРИМЕР 2.11
Рассчитайте эквивалентное сопротивление между A и B в данной цепи. Пример 2.12 Рассчитайте эквивалентное сопротивление между точками а и b.
Решение
Случай (a)
Чтобы найти эквивалентное сопротивление между точками a и b, предположим, что ток входит в соединение a. Так как все сопротивления во внешнем контуре одинаковы (1 Ом), ток в ветвях ac и ad должен быть равен.
