Параллельное сопротивление проводников. Параллельное соединение проводников: принципы, формулы и применение

Что такое параллельное соединение проводников. Как рассчитать общее сопротивление и силу тока при параллельном соединении. Где применяется параллельное соединение в электротехнике. Почему в быту используется именно параллельное подключение приборов.

Что такое параллельное соединение проводников

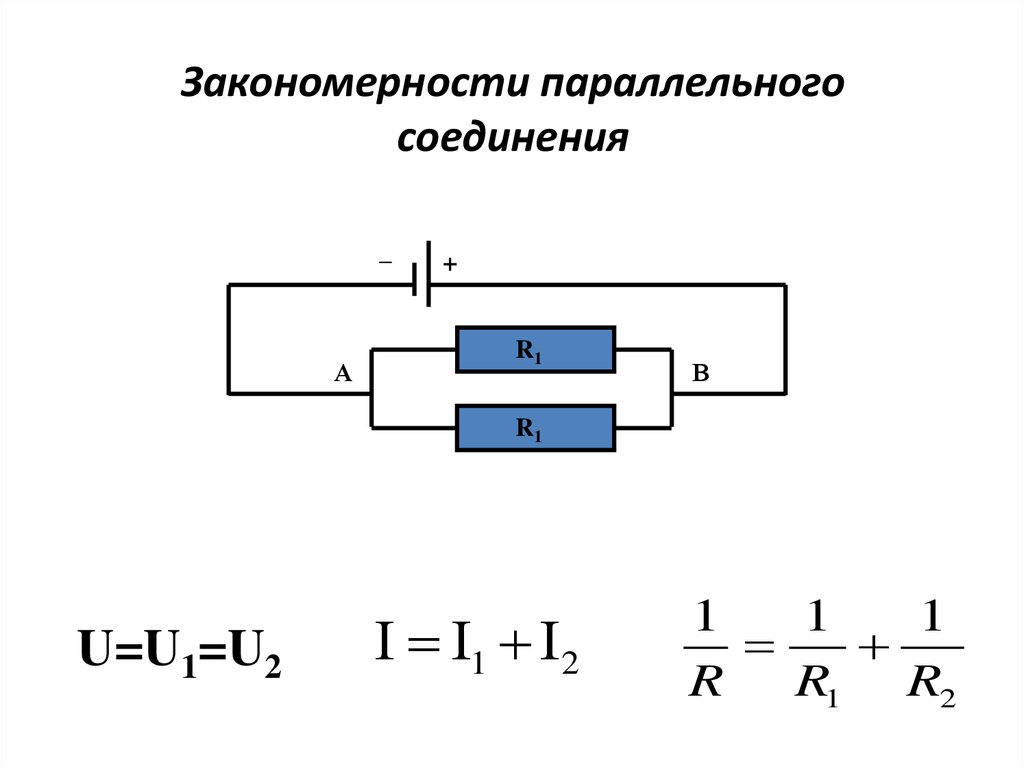
Параллельное соединение проводников — это такой способ соединения, при котором все проводники одним концом подключаются к одной точке электрической цепи, а другим концом — к другой точке. При этом напряжение на всех параллельно соединенных проводниках одинаково.

Основные характеристики параллельного соединения:

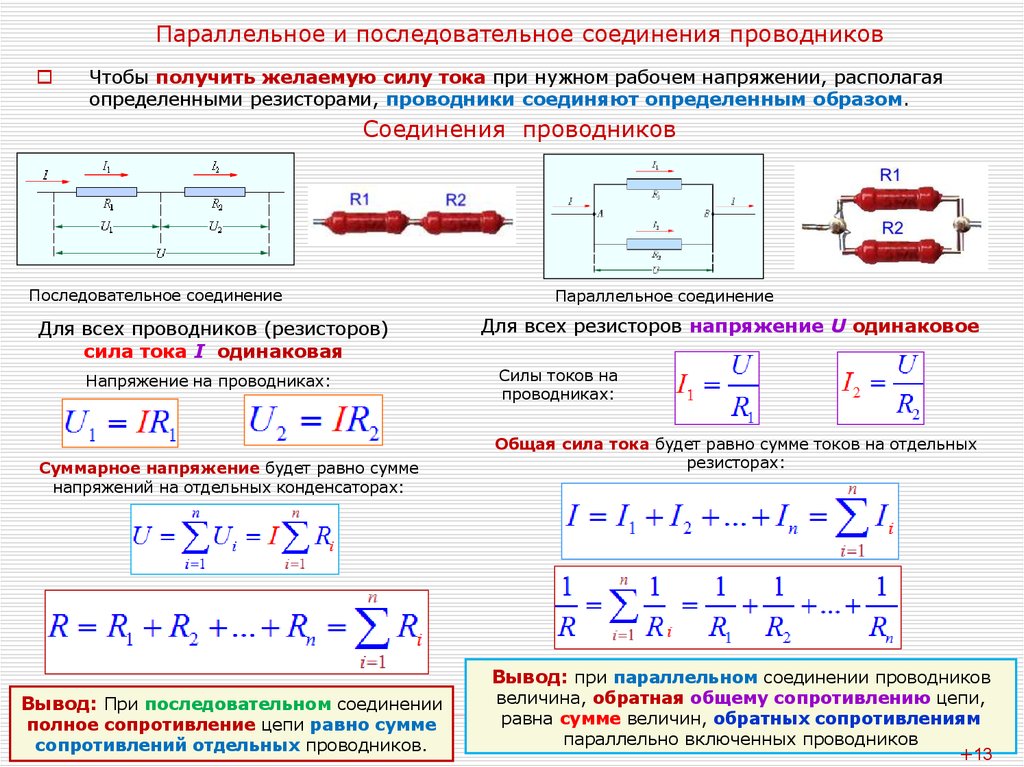
• Напряжение на всех участках одинаково: U = U1 = U2 = … = Un
• Общий ток равен сумме токов на отдельных участках: I = I1 + I2 + … + In
• Общее сопротивление меньше сопротивления любого из проводников

Формулы для расчета параллельного соединения

При параллельном соединении проводников действуют следующие основные формулы:

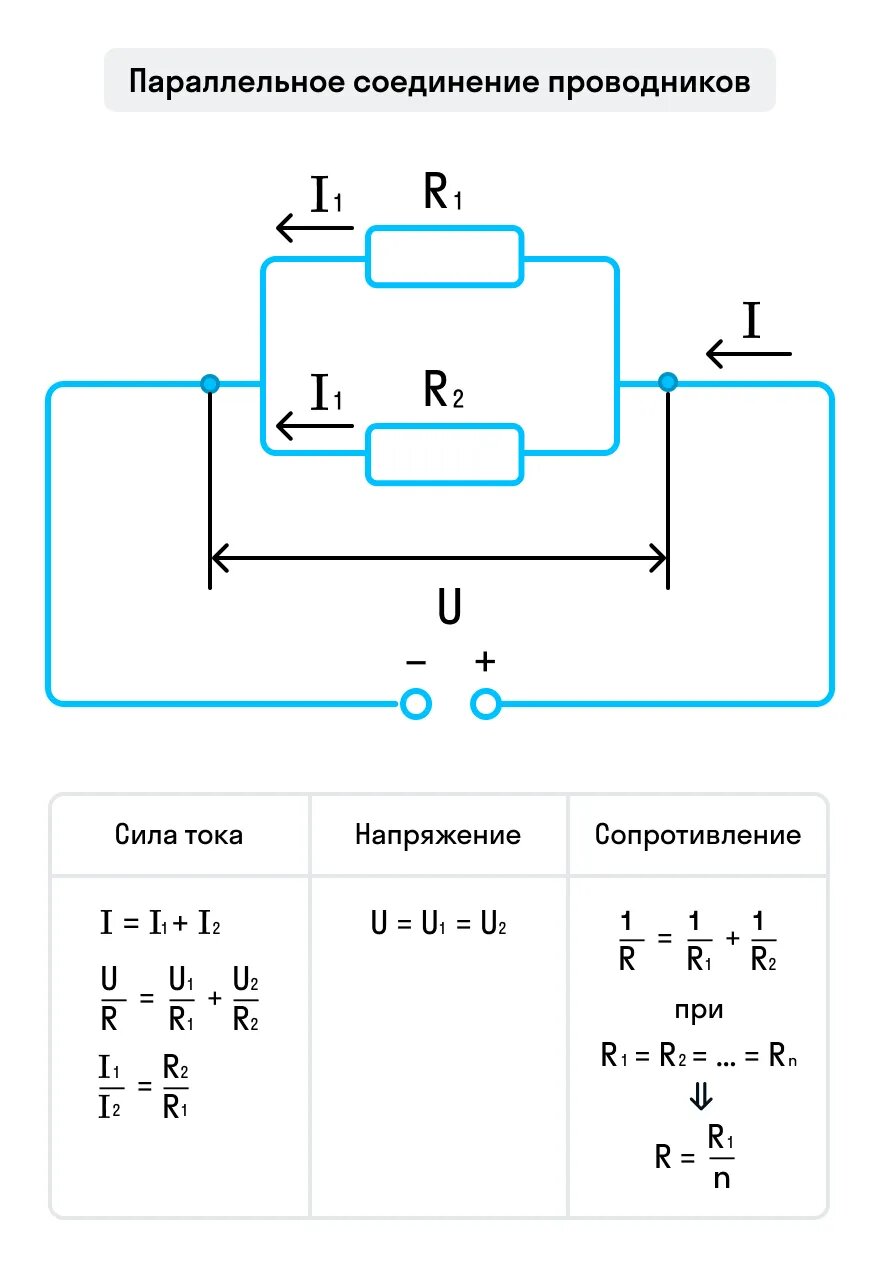
1. Формула для расчета общего сопротивления:

1/R = 1/R1 + 1/R2 + … + 1/Rn

где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных проводников.

2. Формула для расчета общего тока:

I = I1 + I2 + … + In

где I — общий ток, I1, I2, …, In — токи в отдельных проводниках.

3. Закон Ома для параллельного участка:

I = U/R

где U — напряжение на участке, R — общее сопротивление.

Как рассчитать общее сопротивление при параллельном соединении

Чтобы рассчитать общее сопротивление при параллельном соединении проводников, нужно:

1. Записать формулу: 1/R = 1/R1 + 1/R2 + … + 1/Rn
2. Подставить значения сопротивлений отдельных проводников
3. Сложить дроби в правой части уравнения
4. Найти общий знаменатель
5. Упростить полученное выражение
6. Вычислить значение R, взяв обратную величину от полученной суммы

Пример расчета для двух параллельно соединенных резисторов:

Дано: R1 = 10 Ом, R2 = 15 Ом

1/R = 1/10 + 1/15 = 3/30 + 2/30 = 5/30

R = 30/5 = 6 Ом

Таким образом, общее сопротивление составит 6 Ом.

Распределение токов при параллельном соединении

При параллельном соединении проводников токи распределяются обратно пропорционально сопротивлениям:

I1/I2 = R2/R1

То есть, в ветви с меньшим сопротивлением ток будет больше, и наоборот. Это связано с тем, что напряжение на всех параллельных участках одинаково.

Зная общий ток и сопротивления, можно рассчитать ток в каждой ветви:

I1 = I * R/R1

I2 = I * R/R2

где I — общий ток, R — общее сопротивление участка.

Применение параллельного соединения в электротехнике

Параллельное соединение проводников широко применяется в электротехнике и бытовой электросети. Основные области применения:

• Подключение бытовых электроприборов к сети
• Схемы освещения с несколькими лампами
• Электрические щитки и распределительные устройства
• Системы электроснабжения зданий
• Параллельное включение аккумуляторов
• Шунты для расширения пределов измерения амперметров

Почему в быту используется параллельное подключение

В бытовой электросети применяется именно параллельное подключение приборов по следующим причинам:

1. Независимая работа приборов. При параллельном подключении каждый прибор может работать независимо от других.
2. Одинаковое напряжение. Все приборы получают одинаковое сетевое напряжение 220 В.
3. Возможность подключения приборов с разной мощностью. При параллельном соединении можно подключать приборы с разным потреблением тока.
4. Надежность. Выход из строя одного прибора не влияет на работу остальных.
5. Удобство использования. Можно включать и выключать приборы в любом порядке.

Таким образом, параллельное соединение обеспечивает удобство и безопасность использования бытовых электроприборов.

Преимущества и недостатки параллельного соединения

Параллельное соединение проводников имеет ряд преимуществ и недостатков по сравнению с последовательным соединением.

Преимущества параллельного соединения:

• Независимая работа всех подключенных устройств
• Одинаковое напряжение на всех участках
• Возможность подключения устройств с разной мощностью
• Высокая надежность — при выходе из строя одного участка остальные продолжают работать
• Уменьшение общего сопротивления цепи

Недостатки параллельного соединения:

• Увеличение общего тока в цепи
• Необходимость использования проводов большего сечения
• Сложность расчета параметров при большом количестве параллельных ветвей
• Возможность перегрузки источника питания при подключении мощных потребителей

Примеры решения задач на параллельное соединение

Задача 1. Рассчитать общее сопротивление участка цепи, состоящего из трех параллельно соединенных резисторов с сопротивлениями 6 Ом, 12 Ом и 4 Ом.

Решение:

1/R = 1/R1 + 1/R2 + 1/R3 = 1/6 + 1/12 + 1/4 = 2/12 + 1/12 + 3/12 = 6/12 = 1/2

R = 2 Ом

Ответ: общее сопротивление участка цепи равно 2 Ом.

Задача 2. К источнику напряжения 12 В подключены параллельно три лампы с сопротивлениями 20 Ом, 30 Ом и 60 Ом. Определить силу тока в каждой лампе и общий ток в цепи.

Решение:

1. Рассчитаем общее сопротивление:

1/R = 1/20 + 1/30 + 1/60 = 3/60 + 2/60 + 1/60 = 6/60 = 1/10

R = 10 Ом

2. Найдем общий ток по закону Ома:

I = U/R = 12/10 = 1,2 А

3. Рассчитаем токи в каждой лампе:

I1 = U/R1 = 12/20 = 0,6 А

I2 = U/R2 = 12/30 = 0,4 А

I3 = U/R3 = 12/60 = 0,2 А

Проверка: I = I1 + I2 + I3 = 0,6 + 0,4 + 0,2 = 1,2 А

Ответ: I1 = 0,6 А, I2 = 0,4 А, I3 = 0,2 А, I = 1,2 А.

Выводы о параллельном соединении проводников

Параллельное соединение проводников — важный способ соединения в электротехнике, обладающий рядом преимуществ:

• Обеспечивает независимую работу подключенных устройств
• Позволяет подавать одинаковое напряжение на все участки цепи
• Повышает надежность электрической системы
• Дает возможность подключать устройства с разной мощностью
• Широко применяется в бытовых электросетях и промышленных установках

При работе с параллельными цепями важно правильно рассчитывать общее сопротивление и распределение токов. Понимание принципов параллельного соединения необходимо для грамотного проектирования и эксплуатации электрических систем.

Параллельное соединение проводников | 8 класс

Содержание

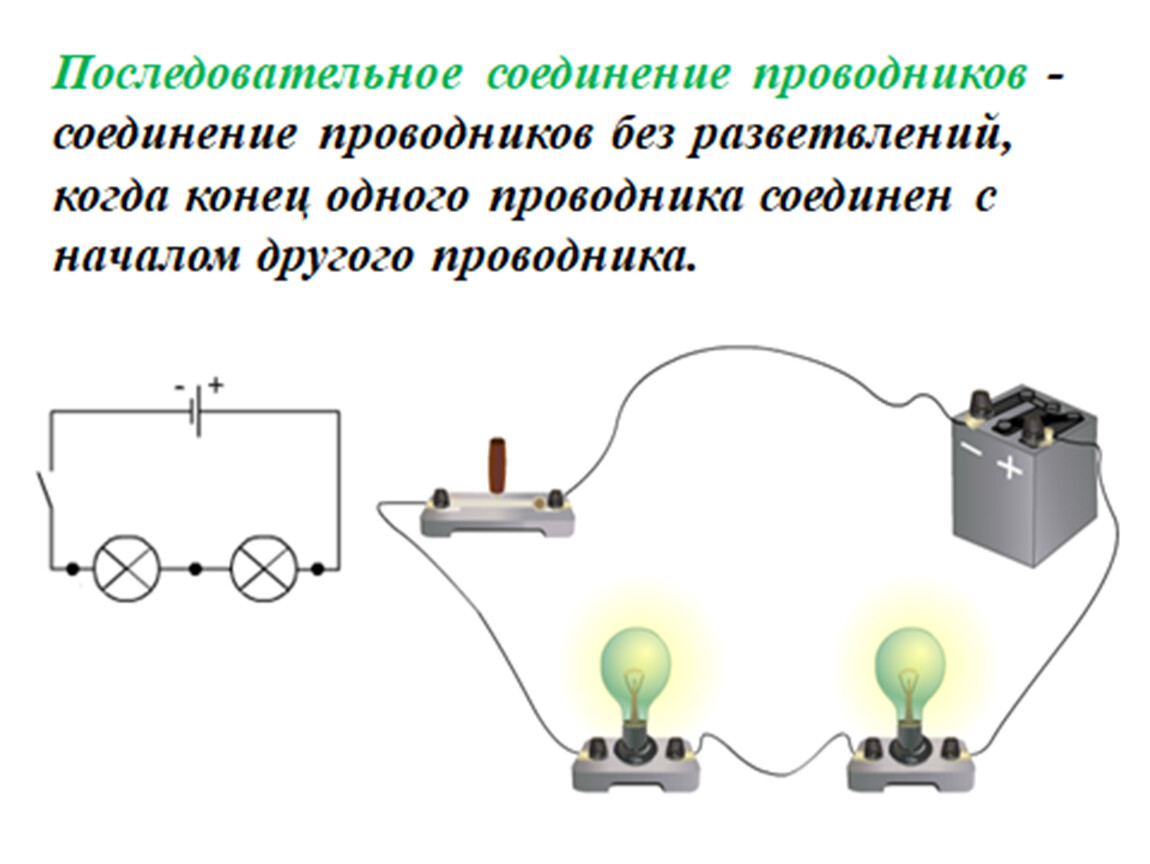
На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).

На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.

Параллельное включение элементов в электрическую цепь

Какое соединение проводников называют параллельным?

Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).

Рисунок 1. Электрическая цепь с параллельным подключением электроламп

Схема этой электрической цепи изображена на рисунке 2.

Рисунок 2. Схема электрической цепи с параллельным подключением электроламп

На схеме обозначены две точки A и B. Важный момент:

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.

Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.

{"questions":[{"content":"Если вы хотите включить в электрическую цепь параллельно три электролампы, то необходимо, чтобы [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["провода, идущие от электроламп, одним своим концом были присоединены к одной определенной точке, а вторым проводом — к другой определенной точке цепи","провода, идущие от электроламп, были соединены сначала друг с другом, а далее — с остальными элементами цепи","хотя бы одна электролампа была подключена в цепь последовательно"],"answer":[0]}}}]}

Напряжение в цепи при параллельном соединении проводников

Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.

Рисунок 3. Схема цепи для измерения вольтметром напряжения при параллельном соединении проводников

Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.

Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.

Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.

По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?

Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.

{"questions":[{"content":"Какая величина одинакова для всех проводников, соединенных параллельно?[[choice-7]]","widgets":{"choice-7":{"type":"choice","options":["напряжение","сила тока","сопротивление"],"explanations":["","Сила тока одинакова для всех проводников, если они соединены последовательно.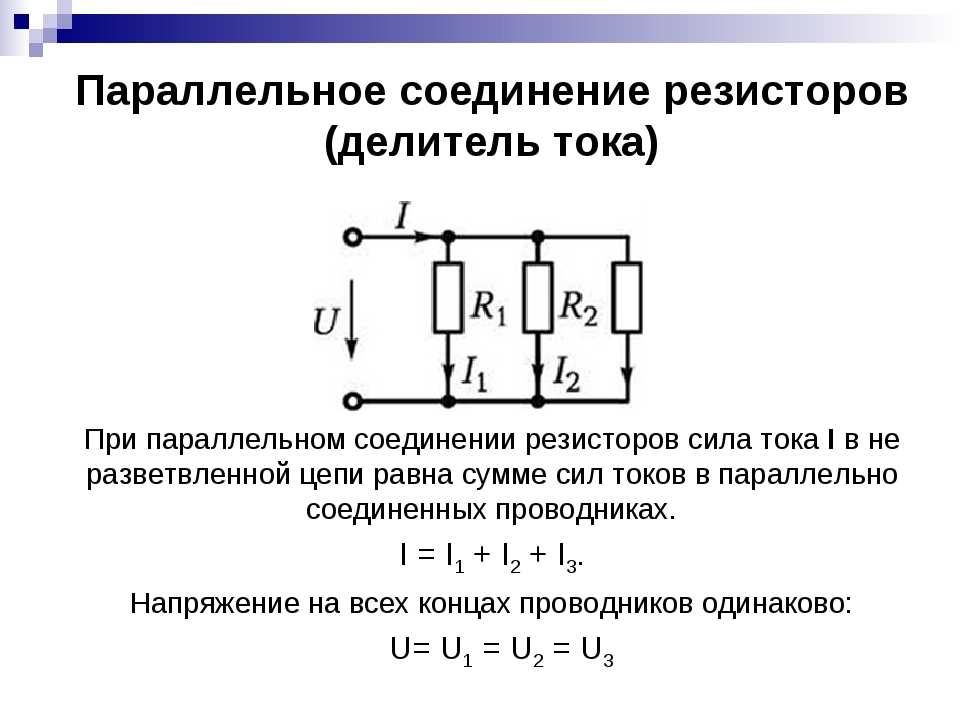 ","Сопротивление — определенная величина для каждого проводника."],"answer":[0]}}}]}

Сила тока в цепи при параллельном соединении проводников

Теперь рассмотрим, что происходит с силой тока при параллельном подключении.

Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.

Рисунок 4. Разветвление тока при параллельном подключении проводников

Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.

Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.

{"questions":[{"content":"Сила тока на участке цепи после разветвления (на участке с параллельно включенным в цепь проводником) будет[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["меньше силы тока до разветвления цепи","больше силы тока до разветвления цепи","будет равна силе тока до разветвления цепи"],"explanations":["Так как после разветвления ток разделяется на несколько токов, то сила тока на каждом параллельно соединенном проводнике будет меньше, чем до разветвления. ","",""],"answer":[0]}}}]}

Сопротивление в цепи при параллельном соединении проводников

Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.

Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.

Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.

В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$  будет в два раза меньше сопротивления каждой лампы: $R = \frac{R_1}{2}$.

Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$.

Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?

Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.

{"questions":[{"content":"При параллельном включении в цепь дополнительного проводника общее сопротивление цепи [[choice-18]]","widgets":{"choice-18":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}

Пример параллельного соединения проводников

Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.

Рисунок 5. Параллельное включение в цепь различных потребителей электроэнергии

Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.

Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 \space В$.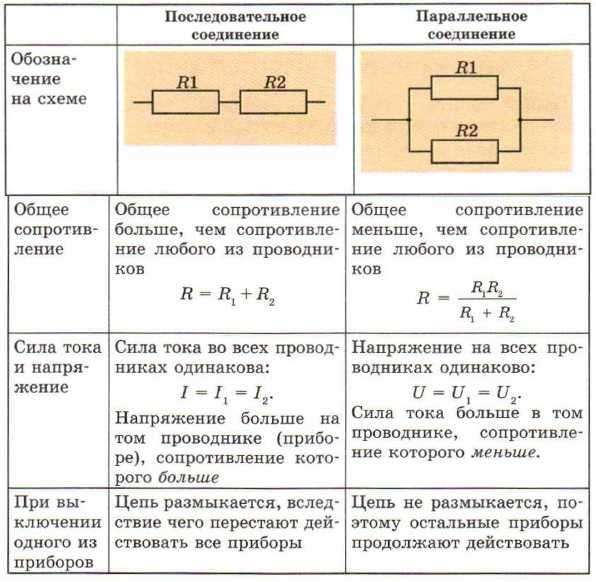 Большинство производителей техники изготавливают приборы как раз под это напряжение.

Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).

Рисунок 6. Подключение к сети различных бытовых приборов

Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.

На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.

{"questions":[{"content":"На какое напряжение рассчитано большинство бытовых электроприборов?[[choice-21]]","widgets":{"choice-21":{"type":"choice","options":["$220 \\space В$","$200 \\space В$","$100 \\space В$","На произвольное значение"],"answer":[0]}}}]}

Пример задачи

В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 \space Ом$ и $300 \space Ом$. Напряжение в сети составляет $120 \space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.

Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.

Дано:
$R_1 = 200 \space Ом$
$R_2 = 300 \space Ом$
$U = 120 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$

Решение:

Запишем закон Ома для участка цепи с первой лампой:
$I_1 = \frac{U_1}{R_1}$.

Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 \space В$
Тогда мы можем рассчитать силу тока в каждой лампе.

Сила тока в первой лампе:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{120 \space В}{200 \space Ом} = 0.6 \space А$.

Сила тока во второй лампе:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{120 \space В}{300 \space Ом} = 0.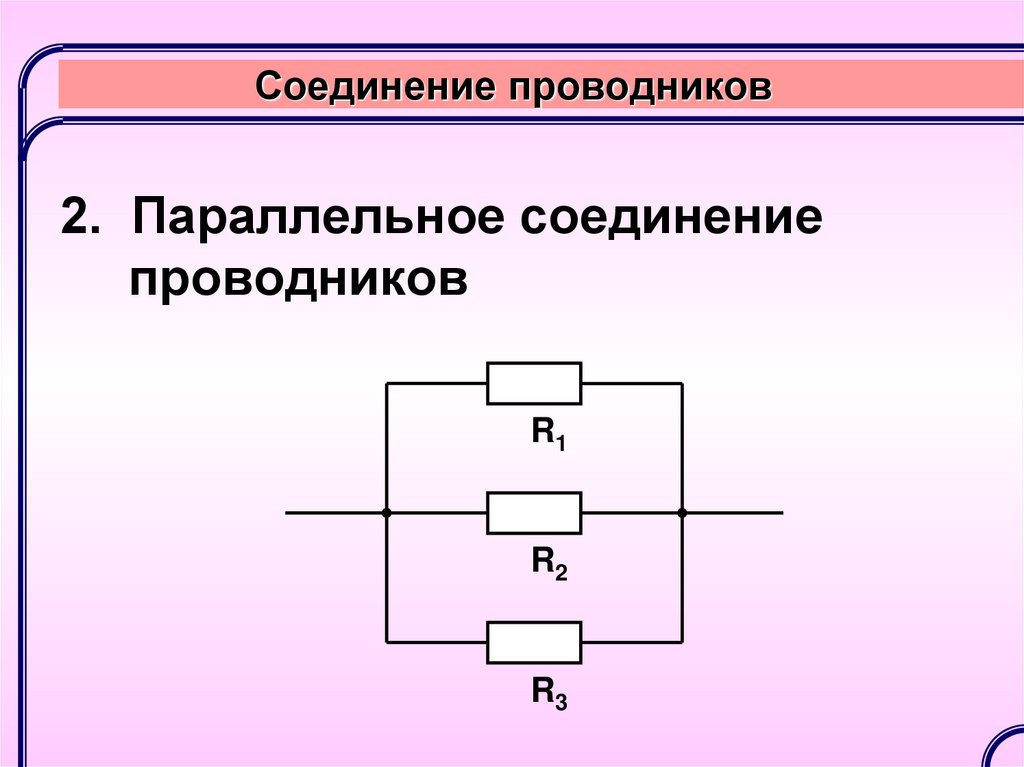 4 \space А$.

Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 \space А + 0.4 \space А = 1 \space А$.

Общее сопротивление цепи мы можем определить двумя способами.

Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{120 \space В}{1 \space А} = 120 \space Ом$.

Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{200 \space Ом} + \frac{1}{300 \space Ом} = \frac{5}{600 \space Ом} = \frac{1}{120 \space Ом}$.

Отсюда, $R = \frac{1}{\frac{1}{120 \space Ом}} = 120 \space Ом$.

При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.

Ответ: $I_1 = 0. 6 \space А$, $I_2 = 0.4 \space А$, $I = 1 \space А$, $R = 120 \space Ом$.

Упражнения

Упражнение №1

Два проводника сопротивлением $10 \space Ом$ и $15 \space Ом$ соединены параллельно и подключены к напряжению в $12 \space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.

Дано:
$R_1 = 10 \space Ом$
$R_2 = 15 \space Ом$
$U = 12 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.

Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{12 \space В}{10 \space Ом} = 1.2 \space А$.

То же самое сделаем для второго проводника:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{15 \space Ом} = 0.8 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1. 2 \space А + 0.8 \space А = 2 \space А$.

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.8 \space А$, $I = 2 \space А$.

Упражнение №2

Почему бытовые приборы в помещении необходимо соединять параллельно?

Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 \space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.

Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.

Упражнение №3

Три потребителя с сопротивлениями $20 \space Ом$, $40 \space Ом$ и $24 \space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 \space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.

Дано:
$R_1 = 20 \space Ом$
$R_2 = 40 \space Ом$
$R_3 = 24 \space Ом$
$U = 24 \space В$

$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 \space В$.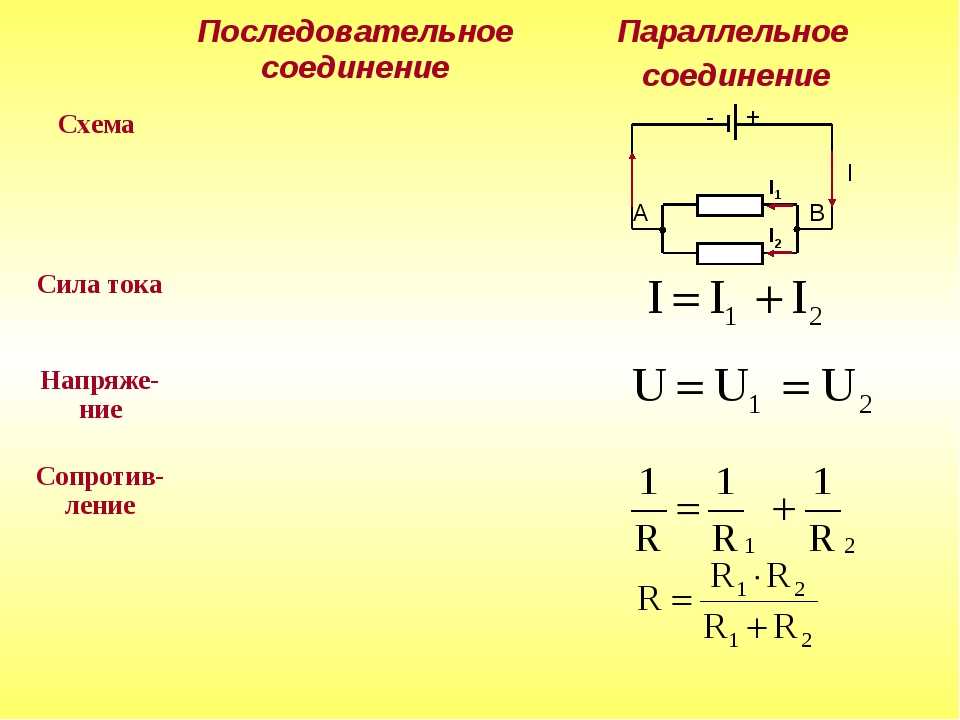

Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.

Для первого потребителя:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{24 \space В}{20 \space Ом} = 1.2 \space А$.

Для второго потребителя:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{24 \space В}{40 \space Ом} = 0.6 \space А$.

Для третьего потребителя:
$I_3 = \frac{U}{R_3}$,
$I_3 = \frac{24 \space В}{24 \space Ом} = 1 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 \space А + 0.6 \space А + 1 \space А = 2.8 \space А$.

Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{24 \space В}{2.8 \space А} \approx 8.6 \space Ом$. 

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.6 \space А$, $I_3 = 1 \space А$, $I = 2.8 \space А$, $R \approx 8. 6 \space Ом$.

Упражнение №4

Два проводника имеют сопротивления, равные $5 \space Ом$ и $500 \space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 \space Ом$, а при параллельном соединении меньше $5 \space Ом$?

При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 \space Ом + 500 \space Ом = 505 \space Ом$.

Это значение действительно больше, чем $500 \space Ом$.

При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{5 \space Ом} + \frac{1}{500 \space Ом} = \frac{101}{500 \space Ом}$,
$R = \frac{1}{\frac{101}{500 \space Ом}} = \frac{500 \space Ом}{101} \approx 5 \space Ом$.

Согласитесь, что $5 \space Ом$ намного меньше, чем $500 \space Ом$.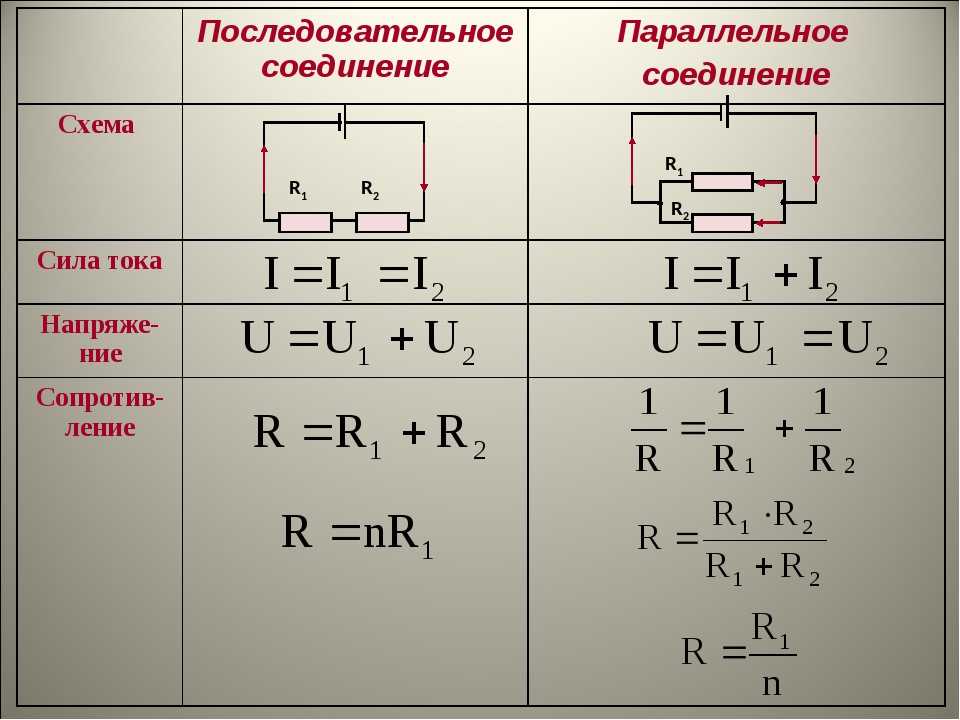

Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.

При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.

А при параллельном соединении увеличивается площадь поперечного сечения. Значит,  сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.

Упражнение №5

На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 \space Ом$, $R_2 = 6 \space Ом$, $R_3 = 12 \space Ом$, $R_4 = 2 \space Ом$. Амперметр показывает силу тока $1 \space А$.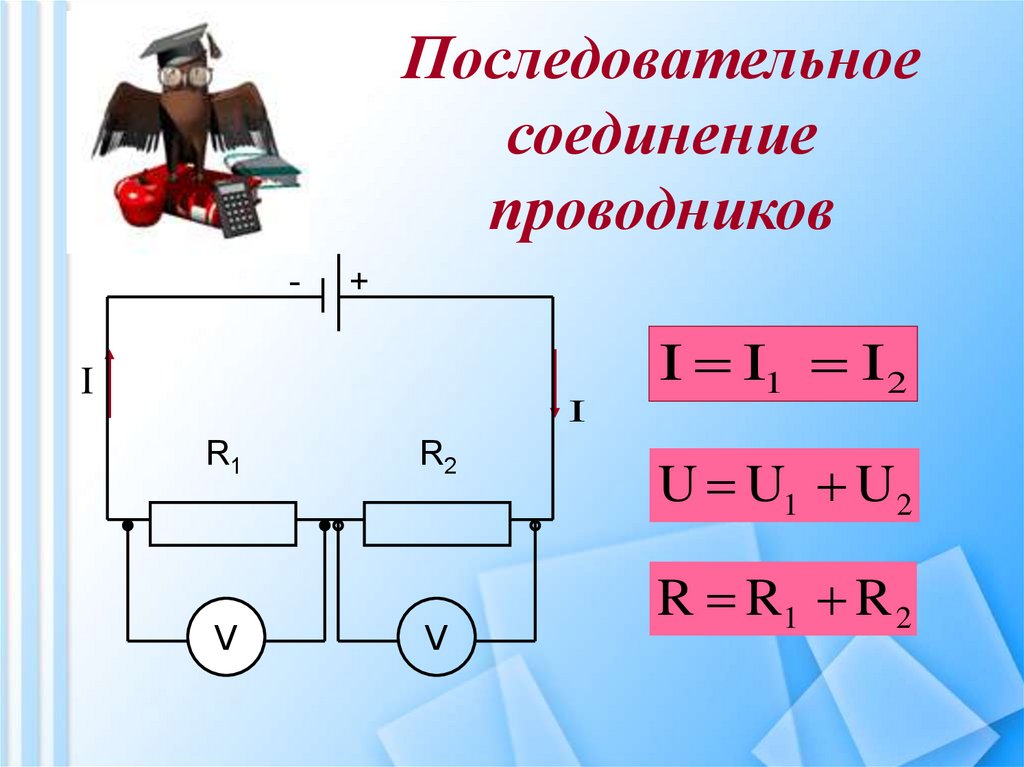 Определите напряжение между точками В и С и силу тока в каждом проводнике.

Рисунок 7. Схема электрической цепи со смешанным соединением проводников к упражнению №5

Дано:
$R_1 = 4 \space Ом$
$R_2 = 6 \space Ом$
$R_3 = 12 \space Ом$
$R_4 = 2 \space Ом$
$I_3 = 1 \space А$

$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$

Показать решение и ответ

Скрыть

Решение:

Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 \space А$. Это сила тока после разветвления.

Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = \frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 \space А \cdot 12 \space Ом = 12 \space В$.

Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 \space В$.

По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{6 \space Ом} = 2 \space А$.

Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.

Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 \space А + 2 \space А = 3 \space А$.

Ответ: $U = 12 \space В$, $I_1 = I_4 = I = 3 \space А$, $I_2 =  2 \space А$, $I_3 = 1 \space А$. 

Параллельное соединение проводников в электрической цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Загрузка. ..

Рис. 5.8. Параллельное соединение про­водников (резисторов)

Параллельным считается такое соедине­ние проводников, когда, например, три проводника соединяются в точке A, где ток разветвляется, а потом сходится в точке B (рис. 5.8). Часть тока I₁ проходит по первому проводнику, I₂ — по второму, I₃ — по тре­тьему.

Если ток в таком участке цепи устано­вился, то ни в одной точке заряд не может накапливаться. Итак, для точек A и B спра­ведливый вывод: I = I₁ + I₂+ I₃, что легко рас­пространяется на любое количество парал­лельно соединенных проводников

I = Σⁿ_i=1 I_i.

Поскольку разность потенциалов на всех проводниках одинакова, то

φ₁ — φ₂ = I₁R₁,

φ₁ — φ₂ = I₂R₂,

φ₁ — φ₂ = I₃R₃,

Загрузка. ..

откуда

I₁R₁ = I₂R₂ = I₃R₃.

В параллельно сое­диненных проводниках

силы тока обратно пропорциональны их сопротивлениям.

Сравнение последних уравнений позво­ляет сделать выводы:

I = (φ₁ — φ₂)(1 / R₁ + 1 / R₂ + 1 / R₃) = (φ₁ — φ₂) • 1 / R,

где R — общее сопротивление участка це­пи, в которой проводники соединены па­раллельно.

Следовательно, при параллельном соеди­нении проводников величина, обратная об­щему сопротивлению разветвления, равна сумме обратных величин сопротивлений каж­дой из веток:

1 / R = 1 / R₁ + 1 / R₂ + 1 / R₃.

Для любого количества веток разветвле­ния:

1 / R = Σⁿ_i=1 1 / R_i.

Если воспользоваться понятием проводимости G = 1 / R, то для параллельного соединения: Материал с сайта http://worldofschool.ru

G = Σⁿ_i=1 G_i.

Если в участке из параллельно соединен­ных проводников проходит ток, то разность потенциалов на участке цепи равняется на­пряжению. Следовательно, на всех ветках разветвления:

U = U₁ = U₂ = U₃ = … = U_n.

Для расширения пределов измерения силы тока с помощью ампермет­ров (миллиамперметров, микроамперметров) к ним параллельно подсоеди­няют проводники с определенными сопротивлениями, принимающими на себя часть измеряемого тока. Эти проводники называются шунтами.

На этой странице материал по темам:

• Закон параллельного соединения проводников формула

• Физика параллельное соединение проводников скачать доклад

• Примеры приборов параллельного соединения в электрической цепи

• Параллельное соединение проводников доклад

• Электрические явления, параллельное соединение проводников формула

Вопросы по этому материалу:

• Какие соединения проводников считаются параллельными? Приведите примеры.

  

• Как определяется сила тока в точках разветвления параллельно соединенных проводников?

• Как связано общее сопротивление участка параллельно соеди­ненных проводников с сопротивлениями каждого из проводников?

Материал с сайта http://WorldOfSchool.ru

Параллельная проводимость | Вращающиеся числа

Резистор можно рассматривать как проводимость . Проводимость обратно пропорциональна сопротивлению. Точка зрения проводимости полезна, когда резисторы включены параллельно.

В предыдущей статье мы параллельно изучали резисторы.

Мы получили это уравнение, чтобы объединить параллельные резисторы в один эквивалентный резистор,

$\text R _{\text{параллель}} = \cfrac{1}{\cfrac{1}{\text{R1}} +\cfrac{1}{\text{R2}} + \ldots + \cfrac{1}{\text{R}_{\text N}}}$

Это довольно сложное выражение с членами $1/\text R$, встроенными в другое обратное выражение.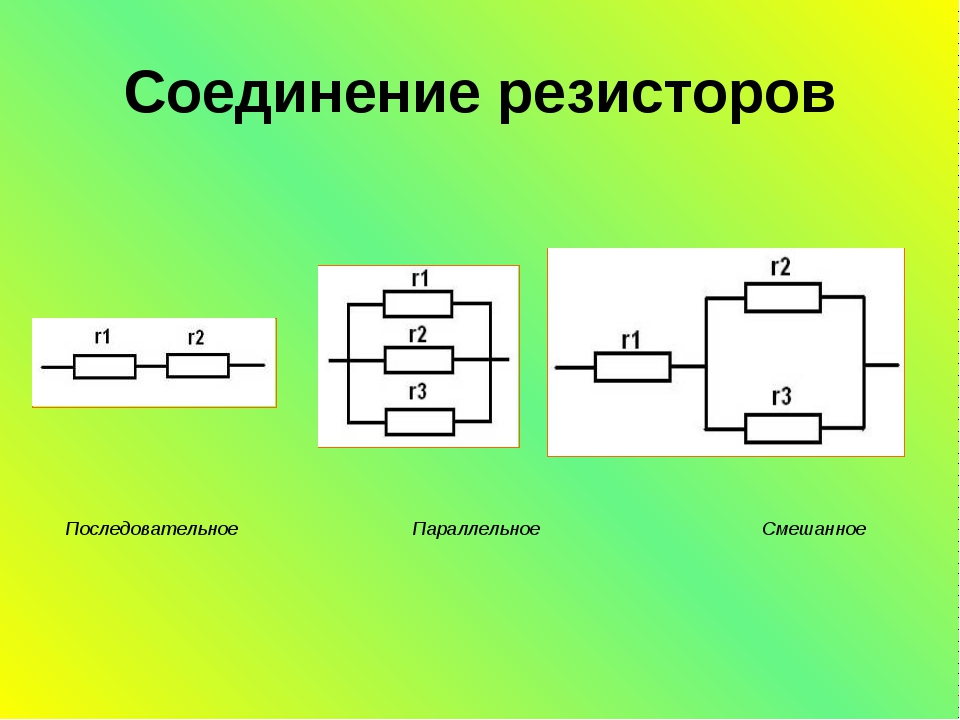

Есть еще один способ решить эту проблему, используя проводимость, которая приводит к более простому уравнению.

Автор Вилли Макаллистер.

---

Содержимое

• Проводимость
• Параллельная проводимость
• Эквивалентная параллельная проводимость
• Пример

---

Куда мы движемся

Резисторы можно представить в виде проводимость .

Проводимость обратно пропорциональна сопротивлению. $\text G = 1/\text R$

Параллельные проводимости складываются в простую сумму, подобно последовательным резисторам.

$\text G_{\text{параллельно}} = \text{G1} + \text{G2} + \ldots + \text G_\text N$

---

Проводимость

Закон Ома, $v = i\ ,\text R$, определяет сопротивление как отношение напряжения к току,

$\text R = \dfrac{v}{i}$

Проводимость обратно пропорциональна сопротивлению, току сверх напряжения, 9\circ$of вращения, но это максимально близко к тому, что мы можем получить, используя обычную клавиатуру. Во всяком случае, это история, которую я слышал.

Вы можете встретить более старый термин, mho , как единицу проводимости. Мхо — это просто ом, написанный наоборот. Символ mho был очень забавным, вплоть до перевернутого омега-символа $\mho$. Mho устарел и больше не используется.

Единицей проводимости является сименс , сокращенно $\text S$. Он назван в честь Вернера фон Сименса, инженера-электрика и основателя немецкой компании по производству электроники и телекоммуникаций, которая носит его имя. Всегда есть s в конце siemens , потому что так он написал свое имя, $1\,\text{siemens}$.

Когда мы используем слово проводимость вместо сопротивление , мы просто подчеркиваем другой аспект поведения резистора. Сопротивление борется с током, в то время как проводимость приветствует или позволяет току проходить. Термины — это два лица одной и той же идеи.

удельное сопротивление и проводимость

Возможно, вы слышали термины удельное сопротивление и проводимость . Они очень похожи на сопротивление и проводимость , но они немного отличаются. Удельное сопротивление и проводимость — это свойства объемного материала, используемого для изготовления отдельных резисторов. См. эту статью «Сопротивление и удельное сопротивление» или эту страницу Википедии, посвященную электрическому сопротивлению и проводимости.

удельное сопротивление и проводимость

Возможно, вы слышали термины , удельное сопротивление и , проводимость . Звучат очень похоже на сопротивление и проводимость , но они немного разные. Удельное сопротивление и проводимость — это свойства объемного материала, используемого для изготовления отдельных резисторов. См. эту статью об удельном сопротивлении или эту страницу Википедии об электрическом сопротивлении и проводимости.

Параллельная проводимость

Теперь мы повторим анализ параллельных резисторов, но на этот раз вместо того, чтобы называть каждый компонент резистором, мы назовем его проводимостью. Обратите внимание, как анализ похож на последовательные резисторы. 9Проводимость 0005 по сравнению с проводником

Компонент, который мы изучаем, называется проводимостью в отличие от проводника . Проводник звучит слишком похоже на простой провод. Также можно называть его резистором: «У резистора $\text{G1}$ проводимость $0,01\,\text S$».

Вот цепь с тремя параллельными проводимостями, управляемая источником тока. Мы анализируем эту схему на языке проводимости и используем форму проводимости закона Ома, $i = v\,\text G.$

Мы знаем,

• Значение тока $i$ является константой, создаваемой источником тока.
• Напряжение $v$ одинаково для всех трех проводимостей.
• Три тока проводимости $\text{G1}, \text{G2},$ и $\text{G3}$ должны в сумме составлять общий ток $i$.

Неизвестно,

• Значение напряжения $v$ на резисторах и источнике тока.
• Как $i$ разделяется на три потока, протекающие через $\text{G1}, \text{G2},$ и $\text{G3}$.

С тем, что мы знаем, мы можем написать некоторые выражения,

Отдельные токи складываются с основным током,

$i = i_{\text{G1}} + i_{\text{G2}} + i_{ \text{G3}} $

Мы можем написать закон Ома для каждой проводимости, используя один и тот же член $v$,

$i_{\text{G1}} = v \, \text{G1} \qquad i_{\ text{G2}} = v \, \text{G2} \qquad i_{\text{G3}} = v \, \text{G3}$

Объединение выражений закона Ома в текущую сумму,

$i = v\, \text{G1} \,+\, v\, \text{G2} \,+\, v\, \text{G3}$

Умножьте на фактор напряжение и соберите значения проводимости в одном месте,

$i = v\,\, (\text{G1} + \text{G2} + \text{G3})$

Это выглядит точно так же, как закон Ома для одной проводимости, за исключением того, что параллельные проводимости появляются вместе как сумма. Мы заключаем,

Для параллельных проводимостей общая проводимость является суммой отдельных проводимостей.

Обратите внимание, насколько это похоже на формулу для резисторов, соединенных последовательно. Проводимости при параллельном соединении складываются так же, как при последовательном соединении резисторов.

Эквивалентная параллельная проводимость

Мы можем представить новую проводимость, эквивалентную сумме параллельных проводимостей,

$\text G_{\text{параллель}} = \text{G1} + \text{G2} + \text {G3}$

$\text G_{\text{параллельный}}$ эквивалентны в том смысле, что одно и то же напряжение появляется для данного тока.

Пример

Давайте решим ту же схему, что и для параллельных резисторов, но используя наше новое представление проводимости.

Это схема с проводимостями, $\text G = \dfrac{1}{\text R}$

Нам нужно найти напряжение $v$ и отдельные токи, $i_{\text{G1}}$, $i_{\text{G1}}$ и $i_{\text{G1}}$ , используя форму проводимости закона Ома, $i = v\,\text G$.

Найдите $v$ и ток через три проводимости.
Продемонстрируйте, что отдельные токи в сумме составляют $i$.

Шаги к решению:

• Найдите эквивалентную параллельную проводимость $\text G_{\text{parallel}}$.
• Найдите напряжение $v$, используя $i = v\,\text G$.
• Найдите отдельные токи, снова используя закон Ома.
• Убедитесь, что отдельные токи составляют то, что должны.

Посмотрите, сможете ли вы решить это самостоятельно, прежде чем заглянуть в ответ.

показать ответ

Эквивалент $\text G_{\text{parallel}}$ представляет собой сумму трех значений проводимости,

$\text G_{\text{параллельно}} = 0,02\,\text S + 0,01\,\text S + 0,002\,\text S = 0,032\,\text S$

Теперь мы можем найти $v$,

$i_{\text S} = v\, \text G_{\text{параллельно}}$

$100\,\text{мА} = v\cdot 0,032\,\text S$

$v = \dfrac{100\,\text{мА}}{0,032\,\text S} = 3,125\,\text{V}$

Как и ожидалось, это дает то же значение $v$, что и при обычном анализе параллельных резисторов.

Теперь работайте через отдельные токи,

$i_{\text{G1}} = v\, \text{G1} = 3,125\,\text{V} \cdot 0,02\,\text S\phantom{0} = 62,50\,\text{мА} $

$i_{\text{G2}} = v\, \text{G2} = 3,125\,\text{V} \cdot 0,01\,\text S\phantom{0} = 31,25\,\text{мА} $

$i_{\text{G3}} = v\, \text{G3} = 3,125\,\text{V} \cdot 0,002\,\text S = \phantom{0}6,25\,\text{мА} $

Полное решение выглядит так,

И в завершение проверим, складываются ли отдельные токи с током источника,

$62,5\,\text{мА} + 31,25\,\text{мА} + 6,25\,\text{мА} = 100\,\text{мА}\qquad$ Да!

Резюме

Проводимость обратно пропорциональна сопротивлению,

$\text G = \dfrac{1}{\text R}$

Параллельные проводимости объединяются простой суммой.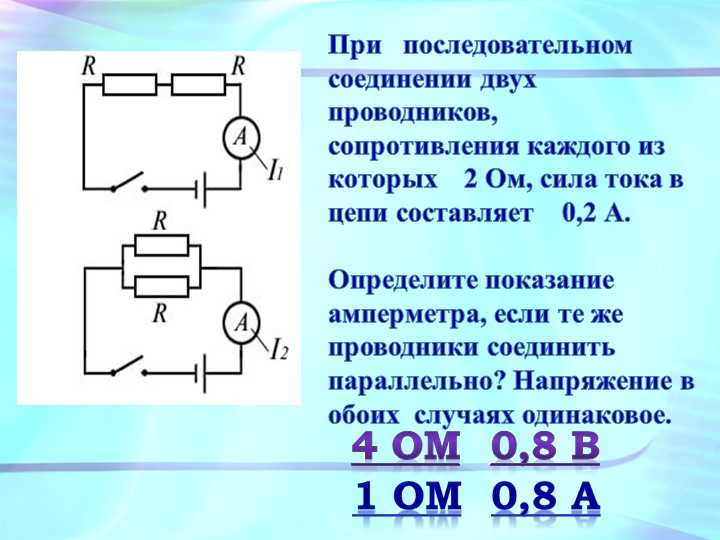

$\text G_{\text{parallel}} = \text{G1} + \text{G2} + \ldots + \text G_\text N$

Использование проводимости является перестановкой этого вычисления,

$ \text R_{\text{параллельно}} = \cfrac{1}{\cfrac{1}{\text{R1}} +\cfrac{1}{\text{R2}} + \ldots + \cfrac{1 }{\text{R}_{\text N}}}$

Как вы решите анализировать параллельные схемы, $\text G$ или $\text R$, зависит от вашего удобства и простоты.

проводников, соединенных параллельно: каждый комплект должен иметь одинаковые электрические характеристики

Вы читаете устаревшую статью. Пожалуйста, перейдите к последним выпускам, чтобы найти актуальный контент.

Параллельные проводники часто устанавливаются там, где используются фидеры или линии большой мощности. Прежде чем пытаться спроектировать большую электрическую систему или установить эти проводники, необходимо полное понимание требований к параллельной работе, разрешенных Национальным электротехническим кодексом.

Раздел 310.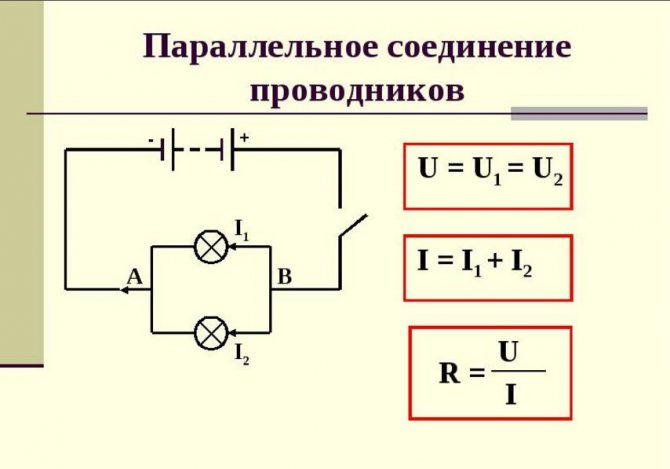 4 содержит конкретную информацию и требования к параллельному соединению проводников и, безусловно, должен быть первым справочником, который пользователь выберет для понимания основ параллельного соединения проводников. Первый абзац этого раздела разрешает параллельное соединение алюминиевых, покрытых медью алюминиевых и медных проводников сечением не менее 1/0 AWG или больше, если эти параллельные проводники электрически соединены на обоих концах в один проводник.

При использовании в качестве параллельных проводников площадь круглых мил этих проводников суммируется, чтобы получить общую площадь поперечного сечения для общего размера параллельных проводников.

Эти параллельные проводники можно использовать в качестве фазных проводников, нейтральных проводников или заземляющих проводников. Однако будьте осторожны, так как одной из основных проблем при установке параллельных проводников является обеспечение того, чтобы каждый проводник в параллельном наборе имел такие же электрические характеристики, как и другие в том же наборе.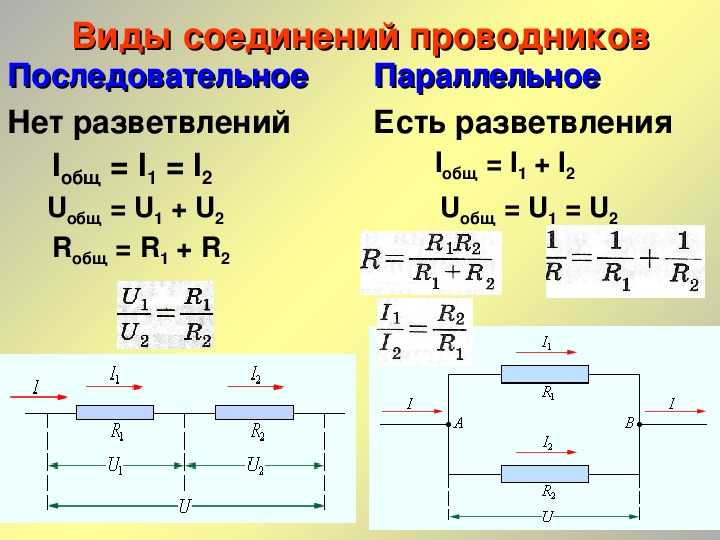

Все параллельные проводники в каждой фазе, нейтрали или заземлении должны иметь одинаковую длину и быть изготовлены из одного и того же материала. Они должны иметь одинаковую площадь в милах и один и тот же тип изоляции. Наконец, все параллельные проводники должны быть подключены одинаково. Это гарантирует, что каждый проводник в параллельном наборе будет нести одинаковую величину тока.

Однако не требуется, чтобы однофазные, нейтральные или заземленные проводники имели те же физические характеристики, что и другие фазные, нейтральные или заземленные проводники. Например, в однофазной параллельной сети 120/240 В на 400 А фаза А может состоять из двух параллельно соединенных медных проводников 3/0, а фаза В — из двух параллельно соединенных алюминиевых проводников номиналом 250 тыс. 0 медных проводников.

Любые отводы, сделанные для параллельных наборов проводников, должны быть сделаны для всех проводников в наборе, а не только для одного. Отключение только одного из проводников в наборе может привести к дисбалансу с одним из проводников, по которому течет больший ток, чем к другому, что приведет к нагреву этого одного проводника и возможному повреждению или отказу изоляции.

Например, если на каждую фазу проложены три проводника сечением 500 тыс. мил, отвод от этой конкретной фазы должен быть отводом от всех проводников сечением 500 тыс. см, а не только от одного из набора. Для этого потребуется общая точка подключения для всех трех параллельных проводников с подключением ответвления к общей клемме.

Если параллельные проводники проложены в отдельных кабелепроводах или кабелях, кабелепроводы или кабели должны иметь одинаковые физические характеристики. Например, если в параллельном наборе фазных проводов имеется четыре проводника номиналом 500 000 ксмил, четыре отдельных кабельных канала, охватывающих проводники, должны быть полностью из жесткой стали, полностью из IMC или полностью из ПВХ и т. д.

Если бы кабелепроводы имели разные характеристики, например, три жестких кабелепровода из черного металла и один жесткий неметаллический кабелепровод, проводник кабелепровода из ПВХ пропускал бы больший ток, чем проводники в каждом из металлических желобов. Это привело бы к большему импедансу проводников в дорожках из черного металла, чем в дорожках из ПВХ.

Более высокий ток в проводнике в кабелепроводе из ПВХ может привести к перегреву проводника и повреждению изоляции. Раздел 300.3(B)(1) касается установки параллельных проводников, а ссылка в этом разделе на 310.4 дает разрешение на установку параллельных проводников отдельно друг от друга.

Каждая фаза и каждый нейтральный или заземленный проводник должны присутствовать в каждом отдельном желобе, вспомогательном желобе, кабельном лотке, сборке кабельной шины, кабеле или шнуре. Например, в установке, где три набора проводников 3/0 AWG соединены параллельно для каждой фазы и нейтрали трехфазной четырехпроводной системы, будет один проводник 3/0 AWG для фазы A, один для фазы B. , один для фазы C и один для нейтрали в каждой из трех дорожек качения.

Существует исключение из этого общего правила, изложенное в 300.3(B)(1), которое позволяет размещать проводники, проложенные в неметаллических кабельных каналах под землей, в виде изолированных фазных установок со всей одной фазой в одном кабелепроводе, всей другой фазой в другом кабелепровод, вся конечная фаза в одном кабелепроводе, со всеми нейтралями в последнем кабелепроводе.