Параллельные резисторы формула. Параллельное и последовательное соединение резисторов: формулы, расчеты, примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при параллельном и последовательном соединении резисторов. Какие формулы используются для вычислений. Как распределяются токи и напряжения в цепи. Примеры расчетов для различных схем соединения.

Содержание

Последовательное соединение резисторов: основные формулы и характеристики

При последовательном соединении резисторы включаются один за другим, образуя неразветвленную цепь. Основные характеристики такого соединения:

Общее сопротивление цепи равно сумме сопротивлений всех резисторов: R = R1 + R2 + R3 + …
Сила тока одинакова во всех элементах цепи: I = I1 = I2 = I3 = …
Общее напряжение равно сумме напряжений на отдельных резисторах: U = U1 + U2 + U3 + …

Таким образом, при последовательном соединении общее сопротивление всегда увеличивается. Это позволяет получить большое сопротивление, используя несколько резисторов с меньшими номиналами.

Параллельное соединение резисторов: ключевые формулы и свойства

При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Основные характеристики:

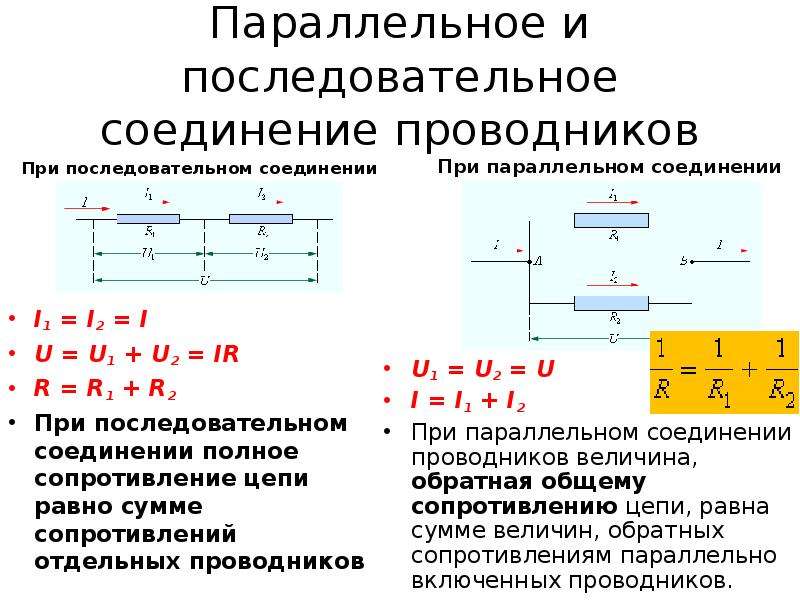
Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов: 1/R = 1/R1 + 1/R2 + 1/R3 + …
Напряжение на всех резисторах одинаково: U = U1 = U2 = U3 = …
Общий ток равен сумме токов через отдельные резисторы: I = I1 + I2 + I3 + …

При параллельном соединении общее сопротивление всегда меньше наименьшего из сопротивлений. Это позволяет получить малое сопротивление, используя несколько резисторов с большими номиналами.

Распределение токов при параллельном соединении

При параллельном соединении резисторов токи распределяются обратно пропорционально сопротивлениям:

I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3

То есть чем меньше сопротивление ветви, тем больший ток через нее протекает. Это позволяет регулировать токи в параллельных ветвях, подбирая нужные сопротивления.

Расчет смешанного соединения резисторов

На практике часто встречаются схемы со смешанным соединением, включающим как последовательные, так и параллельные участки. Алгоритм расчета такой цепи:

Разбить схему на группы последовательно и параллельно соединенных резисторов
Рассчитать эквивалентное сопротивление для каждой группы
Заменить группы резисторов их эквивалентными сопротивлениями
Повторять шаги 1-3, пока схема не упростится до одного эквивалентного резистора

Такой метод позволяет рассчитать довольно сложные схемы, последовательно упрощая их.

Примеры расчета различных схем соединения резисторов

Рассмотрим несколько примеров для закрепления материала:

Пример 1. Последовательное соединение

Даны резисторы: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом. Найти общее сопротивление при их последовательном соединении.

R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом

Пример 2. Параллельное соединение

Даны резисторы: R1 = 6 Ом, R2 = 3 Ом. Найти общее сопротивление при их параллельном соединении.

1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2

R = 1 / (1/2) = 2 Ом

Пример 3. Смешанное соединение

Дана схема: R1 = 10 Ом и R2 = 20 Ом соединены параллельно, а их общее сопротивление последовательно с R3 = 30 Ом. Найти общее сопротивление цепи.

Находим эквивалентное сопротивление R1 и R2: 1/R12 = 1/10 + 1/20 = 3/20 R12 = 20/3 ≈ 6,67 Ом
Теперь R12 и R3 соединены последовательно: R = R12 + R3 = 6,67 + 30 = 36,67 Ом

Практическое применение различных соединений резисторов

Понимание принципов соединения резисторов важно для многих практических задач:

Регулировка тока и напряжения в электрических цепях
Создание делителей напряжения
Подбор нужного сопротивления при отсутствии резистора требуемого номинала
Проектирование систем защиты от перегрузок

Разработка измерительных приборов

Правильный выбор типа соединения резисторов позволяет оптимизировать работу электрических схем и добиться нужных характеристик цепи.

Особенности расчета реальных схем с резисторами

При расчете реальных схем нужно учитывать следующие факторы:

Допуски на номиналы резисторов (обычно 1%, 5% или 10%)
Температурную зависимость сопротивления
Паразитные емкости и индуктивности на высоких частотах
Максимально допустимую мощность рассеивания резисторов

Эти факторы могут существенно повлиять на характеристики цепи, особенно в прецизионных схемах или при работе в экстремальных условиях.

Заключение

Понимание принципов последовательного и параллельного соединения резисторов — важный навык для любого, кто работает с электрическими цепями. Это позволяет:

Рассчитывать сложные электрические схемы
Правильно подбирать компоненты для создания цепей с нужными характеристиками

Оптимизировать работу электронных устройств
Эффективно решать задачи по регулировке токов и напряжений

Практическое применение этих знаний открывает широкие возможности в проектировании и анализе электрических и электронных систем.

Формула сопротивления тока при параллельном соединении

Сопротивление проводников. Параллельное и последовательное соединение проводников.

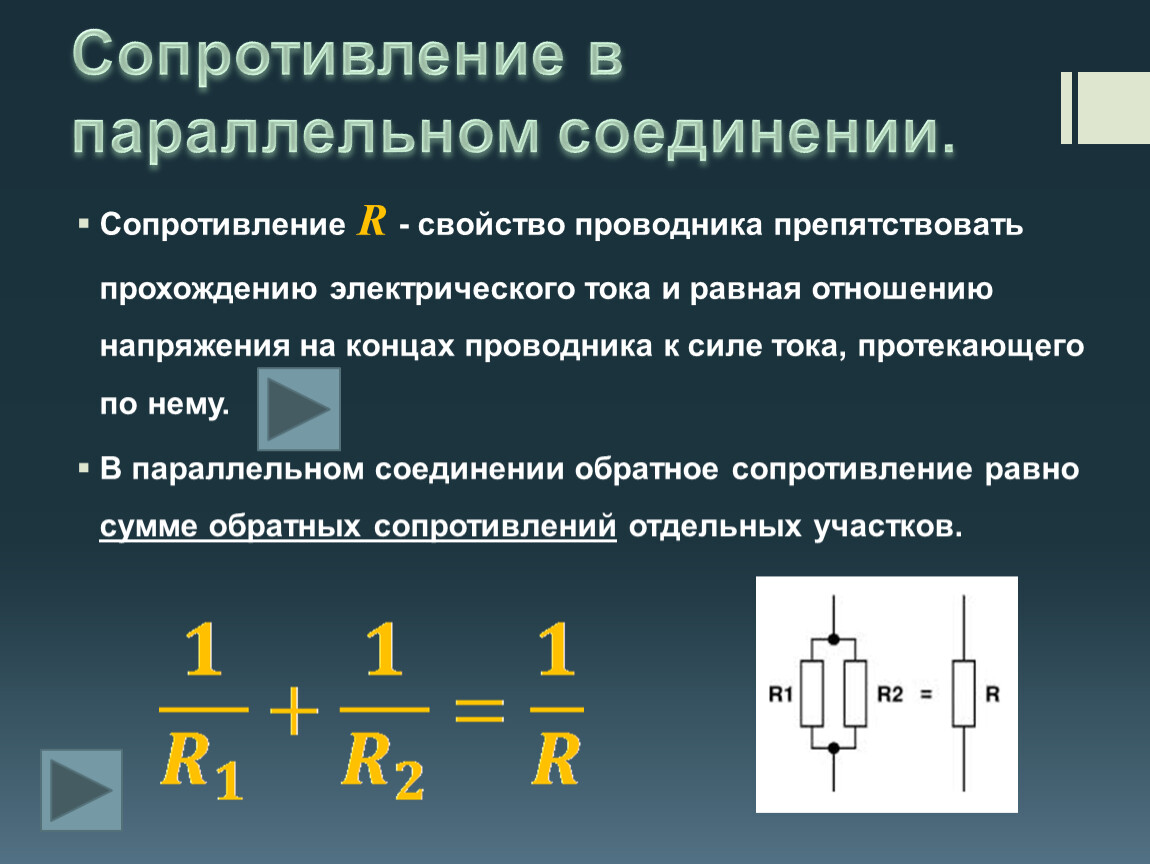
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

U — разность электрических потенциалов (напряжение) на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

где R – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно,I = I₁ + I₂.

Параллельное соединение проводников

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм 2 . Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S – площадь сечения; l – длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I – ток, S – сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

Здесь S – сечение провода линии, мм 2 .

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор – пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

Но для общего напряжение также справедлив закон Ома:

Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

Общее сопротивление будет равно:

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (), то общее сопротивление цепи составит:

в данной формуле равно количеству элементов цепи.

С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

А для токов справедливо следующее выражение:

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

Подставим эти выражения в формулу общего тока:

А по закону Ома ток:

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

Данную формулу можно записать и несколько иначе:

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :

Теперь у нас образовались две группы последовательно соединенных резисторов:

Заменим эти две группы двумя резисторами, сопротивление которых равно:

Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и одним резистором :

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

Как распределяются токи при параллельном соединении резисторов

Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму – концы.

Общее сопротивление параллельно включенных сопротивлений определяется по формуле

Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение.

На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.

Первый частный случай

Если параллельно включено только два резистора то их общее сопротивление можно определить по формуле

Второй частный случай

Если параллельно включено

любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить если сопротивление одного резистора разделить на количество резисторов.

Так как начала всех сопротивлений сведены в одну общую точку, а концы – в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.

Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.

Второе свойство цепи с параллельным соединением заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.

Это значит что чем больше сопротивление тем меньше по нему пойдет ток.

Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I₁, I_2, I₃ утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:

Следовательно, третье свойство параллельного соединения может сформулирована так:

Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R

_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R

_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).

Рис. 1 Изображение параллельного соединения трех резисторов

Проводимость при параллельном соединении

Сопротивление при параллельном соединении:

Для трёх параллельно соединенных сопротивлений

Для двух параллельно соединенных сопротивлений

Для ветвей с одинаковым сопротивлением где n количество ветвей

Ток при параллельном соединении

Мощность при параллельном соединении

Доказательство

Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам

Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление

Для двух резисторов

Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой

в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно

Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов

Как отличить параллельное соединение от последовательного

В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.

Как различить эти два соединения?

Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.

Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.

Формулы для силы тока

О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.

Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:

Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.

Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:

Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.

Формулы для напряжения

Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.

Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:

Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:

Формулы для электрического сопротивления

Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.

Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:

последовательно, значит, нужно равенство для напряжения — I_общ * R_общ = I₁ * R₁ + I₂ * R_2;
параллельно необходимо пользоваться формулой для силы тока — U_общ / R_общ = U₁ / R₁ + U₂ / R₂ .

Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:

R _общ = R ₁ + R ₂ (для последовательного соединения проводников).
1 / R _общ = 1 / R ₁ + 1 / R ₂ (при параллельном соединении).

При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.

Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.

Работа тока

Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.

Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U ₁ + U ₂) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.

Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А ₁ + А ₂.

Мощность тока

При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р ₁ + Р ₂.

То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.

Как влияет соединение проводников на ремонт новогодней гирлянды?

Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.

Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.

Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?

При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:

Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.

Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:

Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С ₁ + 1 / С ₂.

Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:

С = (q 1 + q 2 ) / U.

То есть эта величина считается, как сумма каждого из использованных в соединении приборов:

Как определить общее сопротивление произвольного соединения проводников?

То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.

Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).

Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.

Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.

Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:

сначала ту, которая приведена для последовательного соединения;
потом для параллельного;
и снова для последовательного.

Подобным образом можно развернуть любую, даже очень сложную схему.

Задача на последовательное соединение проводников

Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?

Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.

Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.

Ответ. Сопротивление резистора равно 2,5 Ом.

Задача на соединение конденсаторов, параллельное и последовательное

Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.

Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.

Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.

Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

Первая формула для последовательного вида соединения.
Далее, для параллельной схемы.
И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.

При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Отличие параллельного и последовательного соединения

Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.

В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение. Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.

Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.

Формула расчета параллельного соединения резисторов

Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.

Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.

Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.

Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1
, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.

Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.

Онлайн калькулятор

В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора. Достаточно всего лишь ввести в нужные окна исходные данные, и после нажатия кнопки получить результат.

Параллельное и последовательное соединение сопротивлений

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.

Способы подключения и их особенности

Внешний вид резисторов и обозначения в схемах

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Схема последовательного соединения резисторов

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Параллельное соединение резисторов

width=’100%’&amp;amp;amp;gt;

Последовательно-параллельное соединение

Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

Калькулятор расчёта параллельного соединения резисторов — MOREREMONTA

Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)

Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.

Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

Указать в графе «количество резисторов» их число, в нашем примере их три;
После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

R_сум — суммарное сопротивление параллельно соединенных элементов
R₁ — сопротивление первого резистора;
R₂ — сопротивление второго резистора;
R₃ — сопротивление третьего резистора;
R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Параллельное соединение резисторов таблица. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;
R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

R(общ) – суммарное значение сопротивления;
R – номинал резистора, подсоединенного по параллельной схеме;
n – число подключенных узлов.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Сопротивление проводника

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Виды проводников

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Расчёт проводов на нагрев

Расчёт проводников на потерю напряжения

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Проверим справедливость показанных здесь формул на простом эксперименте.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Что ещё нужно учитывать при соединении резисторов?

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.
Переменные.

Последовательное.
Параллельное.
Смешанное.

Последовательное соединение проводников

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Смешанное соединение проводников

Мощность резисторов при последовательном и параллельном соединении

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)

Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселей

Параллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности. В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы. Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.

Вашему вниманию подборка материалов:

Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам

Ознакомьтесь также с:

Резисторы

Соединяем последовательно

[Сопротивление последовательно соединенных резисторов, кОм] = [Сопротивление первого резистора, кОм] + [Сопротивление второго резистора, кОм]

[Мощность, рассеиваемая первым резистором, Вт] = [Сопротивление первого резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

[Мощность, рассеиваемая вторым резистором, Вт] = [Сопротивление второго резистора, кОм] * [Сила тока, мА] ^ 2 / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт. 2 / [Сопротивление первого резистора, кОм] / 1000

Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Практика проектирования электронных схем. Самоучитель электроники.
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.

Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис.
Тиристоры в электронных схемах. Тонкости и особенности использования. Виды тирис.

Биполярный транзистор. Принцип работы. Применение. Типы, виды, категор.
Все о биполярном транзисторе. Принцип работы. Применение в схемах. Свойства. Кла.

Плавная регулировка яркости свечения люминесцентных ламп дневного свет.
Схема драйвера для плавной регулировки яркости свечения ламп дневного света. Дра.

Проверка электронных элементов, радиодеталей. Проверить исправность, р.
Как проверить исправность детали. Методика испытаний. Какие детали можно использ.

RC — цепь. Резисторно — конденсаторная схема. Резистор, конденсатор. И.
Расчет RC — цепи, изменения напряжения на конденсаторе в зависимости от времени.

Силовой резонансный фильтр для получения синусоиды от инвертора.
Для получения синусоиды от инвертора нами был применен самодельный силовой резон.

Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.

Последовательное соединение резисторов

Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.

Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.

Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.

Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.

В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.

Параллельное соединение резисторов

При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.

Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.

G = 1/R = 1/Ом = См

Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.

Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:

Если R1 = R2 = R3 = R4 = R , то

Rобщ = R/4.

Например, каждый из четырех резисторов имеет R = 10 кОм, тогда

Rобщ = 10 кОм/4 = 2,5 кОм.

Мощности рассеивания суммируются также, как и при последовательном соединении.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.

Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

width=’100%’&amp;amp;amp;gt;Последовательно-параллельное соединениеПоследовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.Подведем итогПодводя итог всему вышеизложенному можно сделать следующие выводы:

При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.

При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.

Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.

Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.

Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.Калькулятор расчёта параллельного соединения резисторов — MOREREMONTAВычислить сопротивление нескольких параллельно соединённых резисторов (до 10)Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединенияЕсли нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).Подбираем (меняем) нужный номинал из того что есть.Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.Замечания и предложения принимаются и приветствуются!Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке: Параллельное соединение резисторовДанный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.Для этого вам необходимо:

Указать в графе «количество резисторов» их число, в нашем примере их три;

После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;

Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.Для расчета суммарного сопротивления калькулятором используется такое соотношение:

R_сум — суммарное сопротивление параллельно соединенных элементов

R₁ — сопротивление первого резистора;

R₂ — сопротивление второго резистора;

R₃ — сопротивление третьего резистора;

R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:Формула параллельного соединения резисторовОбщее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:Параллельное соединение резисторов — расчетПример №1При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.Пример расчета №2Найти общее сопротивление R из трех параллельно соединенных резисторов:Общее сопротивление R рассчитывается по формуле:Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторовБолее сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.Ток, протекающий в цепи параллельно соединенных резисторахОбщий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мАТок, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мАТаким образом, общий ток будет равен:I = 0,545 мА + 0,255 мА = 0,8 мАЭто также можно проверить, используя закон Ома:I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.Параллельное соединение резисторов — онлайн калькуляторЧтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:Подведем итогКогда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.Параллельное соединение резисторов таблица. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушекВ каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.Расчет сопротивления В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;

R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчетаПрименительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

R(общ) – суммарное значение сопротивления;

R – номинал резистора, подсоединенного по параллельной схеме;

n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.Пример расчета Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.Важные нюансы Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.Заключение Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.Сопротивление проводникаВсе проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.При расчёте сопротивления используется известная из школьного курса физики формула:R = ρ · l/S, S — площадь сечения; l — длина.Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения. и нагрев проводникаДля практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:δ = I/S, I — ток, S — сечение.Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.Правилами регламентируется производить расчёт проводников на нагрев.Способы соединения проводниковЛюбой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.Виды проводниковВ электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.Расчёт проводов на нагревПроводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.Расчёт проводников на потерю напряженияПри расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.R л = ρ · 2L/S,Здесь S — сечение провода линии, мм 2 .Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:Формула параллельного соединения резисторовОбщее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:Параллельное соединение резисторов — расчетПример №1При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.Пример расчета №2Найти общее сопротивление R из трех параллельно соединенных резисторов:Общее сопротивление R рассчитывается по формуле:Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Как рассчитать сложные схемы соединения резисторовБолее сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.Ток, протекающий в цепи параллельно соединенных резисторахОбщий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мАТок, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мАТаким образом, общий ток будет равен:I = 0,545 мА + 0,255 мА = 0,8 мАЭто также можно проверить, используя закон Ома:I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .Параллельное соединение резисторов — онлайн калькуляторЧтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:Подведем итогКогда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.Проверим справедливость показанных здесь формул на простом эксперименте.Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединенииТеперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединенииКак видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.Что ещё нужно учитывать при соединении резисторов?Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.Подробнее о мощности рассеивания резистора читайте .Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.Виды соединенийРезистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.

Переменные.

Последовательное.

Параллельное.

Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.Последовательное соединение проводниковВ последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.Примером последовательного соединения проводников в быту является ёлочная гирлянда.Параллельное соединение резисторовПри параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.Примеры параллельного соединения проводников:

Освещение.

Розетки в квартире.

Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.Смешанное соединение проводниковЭтот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.Мощность резисторов при последовательном и параллельном соединенииКак правильно соединять резисторы?О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.Последовательное соединение резисторов.В жизни последовательное соединение резисторов имеет вид:Принципиальная схема последовательного соединения выглядит так:На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.Общее номинальное сопротивление составного резистора обозначено как R_общ.Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.Применяя последовательное соединение, стоит помнить одно простое правило:Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.Параллельное соединение резисторов.Можно соединять резисторы и параллельно:Принципиальная схема параллельного соединения выглядит следующим образом:Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.Проверим справедливость показанных здесь формул на простом эксперименте.Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.Что ещё нужно учитывать при соединении резисторов?Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.Подробнее о мощности рассеивания резистора читайте тут.Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселейПараллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности. В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы. Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.Вашему вниманию подборка материалов: Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторамОзнакомьтесь также с:РезисторыСоединяем последовательно[Сопротивление последовательно соединенных резисторов, кОм] = [Сопротивление первого резистора, кОм] + [Сопротивление второго резистора, кОм][Мощность, рассеиваемая первым резистором, Вт] = [Сопротивление первого резистора, кОм] * [Сила тока, мА] ^ 2 / 1000[Мощность, рассеиваемая вторым резистором, Вт] = [Сопротивление второго резистора, кОм] * [Сила тока, мА] ^ 2 / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт. 2 / [Сопротивление первого резистора, кОм] / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.Практика проектирования электронных схем. Самоучитель электроники.
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис.
Тиристоры в электронных схемах. Тонкости и особенности использования. Виды тирис.Биполярный транзистор. Принцип работы. Применение. Типы, виды, категор.
Все о биполярном транзисторе. Принцип работы. Применение в схемах. Свойства. Кла.Плавная регулировка яркости свечения люминесцентных ламп дневного свет.
Схема драйвера для плавной регулировки яркости свечения ламп дневного света. Дра.Проверка электронных элементов, радиодеталей. Проверить исправность, р.
Как проверить исправность детали. Методика испытаний. Какие детали можно использ.RC — цепь. Резисторно — конденсаторная схема. Резистор, конденсатор. И.
Расчет RC — цепи, изменения напряжения на конденсаторе в зависимости от времени.Силовой резонансный фильтр для получения синусоиды от инвертора.
Для получения синусоиды от инвертора нами был применен самодельный силовой резон.Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное. Последовательное соединение резисторов Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт. Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм. Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт. Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока. Параллельное соединение резисторов При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G. G = 1/R = 1/Ом = См Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:Если R1 = R2 = R3 = R4 = R , то Rобщ = R/4. Например, каждый из четырех резисторов имеет R = 10 кОм, тогдаRобщ = 10 кОм/4 = 2,5 кОм.Мощности рассеивания суммируются также, как и при последовательном соединении. Смешанное соединение резисторов Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.

Резисторы в параллельной формуле

В электрических цепях часто можно заменить группу резисторов одним эквивалентным резистором. Эквивалентное сопротивление ряда резисторов, включенных параллельно, можно найти, используя обратное сопротивление, 1 / R. Обратная величина эквивалентного сопротивления равна сумме обратных величин каждого сопротивления. Единицей измерения сопротивления является Ом (Ом), который равен Вольт на Ампер (1 Ом = 1 В / А). Также распространены более крупные резисторы с сопротивлением килоом (1 кОм = 10 ³ Ом) или мегаом (1 МОм = 10 ⁶ Ом).

R _eq = эквивалентное сопротивление (Ом или более единицы)

R ₁ = сопротивление первого резистора (Ом)

R ₂ = сопротивление второго резистора (Ом)

R ₃ = сопротивление третьего резистора (Ом)

Параллельные резисторы Вопросы по формуле:

1) Какое эквивалентное сопротивление резистора 1000 кОм и резистора 250,0 кОм, подключенных параллельно?

Ответ: Оба сопротивления выражены в килоомах, поэтому нет необходимости изменять их единицы.Эквивалентное сопротивление можно найти в кОм по формуле:

Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:

R _экв = 200,0 кОм

Эквивалентное сопротивление резисторов 1000 кОм и 250,0 кОм, включенных параллельно, составляет 200,0 кОм.

2) Три резистора соединены параллельно в электрическую цепь.Их сопротивления составляют 400 Ом, 40,0 кОм и 4,00 МОм. Какое эквивалентное сопротивление?

Ответ: Три значения сопротивления выражены в разных единицах измерения. Первый шаг к нахождению эквивалентного сопротивления — преобразовать их в общую единицу. Два значения можно преобразовать в ту же единицу, что и третье. В этом решении все значения будут преобразованы в Ом.

Если R ₁ = 400 Ом, R ₂ = 40,0 кОм и R ₃ = 4,00 МОм, то:

R ₂ = 40.0 кОм

R ₂ = 40 000 Ом

Стоимость ₃ рэндов составляет:

R ₃ = 4,00 МОм

R ₃ = 4000000 Ом

Эквивалентное сопротивление можно найти в Ом по формуле:

Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:

Эквивалентное сопротивление 400 Ом, 40.Сопротивление резисторов 0 кОм и 4,00 МОм, включенных параллельно, составляет примерно 396 Ом.

Параллельные схемы

Ваш браузер не поддерживает Java-апплеты

Схема с более чем одним Путь прохождения тока представляет собой параллельную цепь.

НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Общее напряжение равно напряжение любого параллельного сопротивления.

ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Полный ток равен сумма тока каждого параллельного компонента.

ПАРАЛЛЕЛЬНОЕ СОПРОТИВЛЕНИЕ ЦЕПИ

Общее сопротивление может быть рассчитывается по закону Ома, если известны напряжение и полный ток.

Общее сопротивление всегда меньше наименьшего значения сопротивления.

Метод равных значений

Для параллельных сопротивлений в какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле разделив номинал одного из резисторов на количество резисторов.

Взаимный метод

1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R _N

R _EQ = 1 / (1 / R ₁ + 1 / R ₂ + … + 1 / R _N )

Метод произведения на сумму

Для расчета сопротивления двух параллельных резисторов можно использовать эту формулу:

_{рэндов EQ} = (_{рэндов 1} * _{рэндов 2}) / (_{рэндов 1} + _{рэндов 2})

Правило приближения 10 к 1

Если подключены два резистора параллельно, и один резистор в 10 или более раз больше по стоимости, чем другой резистор, резистор большего номинала можно не учитывать.

ПРОВОДИМОСТЬ

Общая проводимость равна сумме проводимости каждого компонента.

ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Суммарная мощность равна сумма мощности каждого компонента. (Это то же самое, что и с серией схемы).

Правила для параллельных цепей постоянного тока

Такое же напряжение существует через каждую ветвь параллельной цепи и равно напряжению источника.
Ток через параллельная ветвь обратно пропорциональна величине сопротивления ветка.
Полный ток параллельная цепь равна сумме отдельных токов ответвления цепь
Эквивалентное сопротивление параллельная цепь находится по общему уравнению Req = 1 / (1 / R1 + 1 / R2 + 1 / Rn)
Общая мощность, потребляемая в параллельная схема равна сумме мощности, потребляемой индивидуумом резисторы.

ПАРАЛЛЕЛЬНЫЙ АНАЛИЗ ЦЕПЕЙ

Соблюдайте принципиальную схему внимательно или при необходимости нарисуйте.
Обратите внимание на указанные значения и значения, которые необходимо найти.
Выберите подходящий уравнения, которые будут использоваться при решении для неизвестных величин на основе известных количества.
Подставьте известные значения в выбранном вами уравнении и найдите неизвестное значение.

ПАРАЛЛЕЛЬНОЕ УСТРАНЕНИЕ НЕПОЛАДОК ЦЕПИ

Когда в ветви параллельной сети сопротивление ветви увеличивается и общее сопротивление цепи увеличивается. Это вызывает уменьшение общего Текущий.

Короткое замыкание всегда приводит в отсутствии тока, протекающего через другие ветви цепи.

EET 1150 Блок 8: Параллельные цепи

После последовательных цепей, которые вы изучали в Разделе 7, следующий простейший Тип схемы — параллельная схема , которую мы рассмотрим далее.Опять же, мы ограничим наше внимание параллельными резистивными цепями, которые помимо источников напряжения содержат только резисторы.

Раздел 7 Обзор

Этот модуль будет основан на материале, который вы изучили на модуле 7. Итак, давайте начнем с самопроверки, чтобы проверить, что вы узнал в том блоке.

Параллельное соединение

Вспомните из блока 2, что два компонента соединены последовательно, если они связаны друг с другом ровно в одной точке, и если нет другой компонент подключен к этой точке.
- Пример: В схеме, показанной ниже, R2 и R3 соединены в последовательно, а R3 и R4 также подключены последовательно.
С другой стороны, два компонента соединены параллельно , если они связаны друг с другом в двух точках.
- Пример: В схеме, показанной выше, источник напряжения и R1 соединены параллельно.

Компоненты, соединенные параллельно, имеют одинаковое напряжение

Самым важным свойством параллельных подключений является то, что напряжение одинаково на всех параллельно подключенных компонентах .
Пример: В схеме, показанной ниже, источник напряжения и R1 подключены параллельно, поэтому мы знаем, что напряжение на источнике должно быть таким же, как напряжение на R1. Но R1 и R3 не подключены параллельно, поэтому мы не можем предполагать, что напряжение на R1 равно к напряжению на R3.

Параллельная цепь

Параллельная цепь — это та, в которой все компоненты соединены параллельно друг с другом.Вот пример:

Напряжение в параллельной цепи

Как отмечалось выше, параллельно соединенные компоненты имеют одинаковое напряжение. Следовательно, все компоненты в параллельной цепи должны иметь одинаковое напряжение между собой .

Действующий закон Кирхгофа

Закон Кирхгофа гласит, что сумма всех входящих токов точка равна сумме всех токов, выходящих из этой точки .
Мы используем сокращение KCL как сокращенное обозначение ссылаясь на действующий закон Кирхгофа.

KCL в параллельных резистивных цепях

При приложении к параллельной резистивной цепи с одним напряжением источник, KCL говорит, что если вы добавите токи через все резисторы, сумма должна быть равна значению полного тока, выходящего из источник напряжения.
Вот почему. Рассмотрим параллельную схему, показанную ниже, которая показывает направления токов, вытекающих из источника и через резисторы.
- Глядя на точку с надписью A , мы видим, что один ток, текущий в эту точку, а именно I _T, полный ток цепи.
- Есть два тока, выходящие из точки A , а именно I ₁ и I ₂.
- Поскольку KCL сообщает нам, что сумма токов, входящих в точку равна сумме выходящих из этой точки токов, мы можем скажи это
  I _T = I ₁ + I ₂
- Применяя те же рассуждения к параллельной цепи с больше резисторов, мы всегда будем приходить к одному и тому же выводу: сумма тока резистора равен току, текущему из источник напряжения.

KCL в других цепях

KCL — это общее правило, которое применяется во всех цепях , не только параллельные цепи и не только цепи, содержащие резисторы. В более сложных схемах может быть сложно правильно применить KCL, но при правильном применении это мощный инструмент. Мы увидим это в более поздние единицы.

Общее параллельное сопротивление

Особый случай № 1: два параллельных резистора

Особый случай № 2: Параллельные резисторы То же значение

Другой особый случай возникает, когда у вас есть два или более резистора в параллельно, и все резисторы имеют одинаковое индивидуальное сопротивление.(Например, возможно, у вас есть три резистора по 100 Ом параллельно друг с другом.) Опять же, мы могли бы использовать взаимная формула в таких случаях, или мы могли бы использовать следующее правило особого случая:
Для n параллельных резисторов, каждый из которых имеет сопротивление R ,
R _T = R ÷ n
На словах, если у вас подключено несколько резисторов одинакового номинала параллельно общее сопротивление равно индивидуальному сопротивлению значение, деленное на количество резисторов.
По понятным причинам это правило часто называют преувеличением ценности . правило .
Нам еще предстоит рассмотреть еще один особый случай, но этот анимированный Урок суммирует случаи, которые мы рассмотрели до сих пор.

Особый случай № 3: резистор, подключенный параллельно резистору гораздо меньшего размера

Эффект добавления дополнительных ветвей к параллельной цепи

Если вы добавите еще один параллельный резистор в параллельную цепь, общее сопротивление уменьшается на .Это может быть сложно концепция для понимания учащимися, и следующий анимированный урок хорошо объясняет это.
Поскольку добавление еще одного параллельного резистора уменьшает общую сопротивление, оно также на увеличивает общую сумму цепи на Текущий.
С практической точки зрения добавление слишком большого количества дополнительных параллельных ответвлений может привести к тому, что общий ток схемы станет настолько большим, что это вызывает проблемы, как показано в этом анимационном уроке.

Анализ параллельных резистивных цепей

Мы отметили выше, что все компоненты в параллельной цепи должны имеют одинаковое напряжение друг с другом.
Конечно, если мы знаем напряжение на любом резисторе, мы можем использовать Закон Ома, чтобы найти ток через резистор.
Итак, теперь мы знаем достаточно, чтобы определять токи и падения напряжения. в параллельной резистивной цепи.Есть четыре основных шага.
1. Напомним, что в параллельной цепи каждый компонент имеет одинаковые Напряжение. Следовательно, напряжение каждого резистора равно источнику Напряжение. В символах
  V _S = V ₁ = V ₂ = … = В _n
2. Используйте закон Ома в виде I = V ÷ R to найти ток через каждый резистор.В символах
  I ₁ = V ₁ ÷ R ₁
  I ₂ = V ₂ ÷ R ₂
  и т. Д. Для каждого из резисторы.
3. Используйте обратную формулу (или одну из формул частного случая приведено выше), чтобы найти полное сопротивление цепи:
  R _T = 1 ÷ (1 ÷ R ₁ + 1 ÷ R ₂ +… + 1 ÷ R _n)
4. Используйте один из следующих методов, чтобы найти общую Текущий:
  - Либо сложите вместе все индивидуальные токи резистора:
    I _T = I ₁ + I ₂ + … + I _n
  - Или примените закон Ома в форме I = V ÷ R to всю схему.Проще говоря, общий ток, производимый напряжение источника равно напряжению источника, деленному на полное сопротивление. В символах
    I _T = V _S ÷ R _T

Источники напряжения подключены параллельно?

Как правило, не следует подключать разнозначные источники напряжения. параллельно друг другу.
- Исключение составляют аккумуляторные батареи. Для Например, предположим, что у вас есть «мертвый» автомобильный аккумулятор, напряжение близко к 0 В. Аккумулятор можно зарядить, подключив параллельно с исправным автомобильным аккумулятором или параллельно с аккумулятором зарядное устройство, вырабатывающее напряжение около 12 В.
Хотя мы, как правило, не подключаем разнородных источников напряжения параллельно друг другу иногда подключаем равнозначных источников напряжения параллельно друг другу.Зачем нам это нужно? Следующий анимированный урок объясняет.

Источники тока, подключенные параллельно

Источник тока — это устройство, которое подает такой же ток к любому сопротивлению, подключенному к его клеммам.
Схематический символ источника тока показан ниже.
Источники тока можно подключать параллельно.
Источники тока, подключенные параллельно, могут быть заменены одиночными эквивалентный источник тока, который производит ток, равный алгебраическому сумма отдельных источников.

Делитель тока

Группа резисторов, соединенных параллельно, часто называется током . делитель , потому что общий ток, поступающий в группу, делится среди различных резисторов обратно пропорционально сопротивлению каждого.
- Например, если у вас есть два резистора параллельно и один резистор на в два раза больше, чем на (например, предположим, что один — 20 кОм, а другой — 10 кОм), тогда будет в два раза больше тока через меньший резистор, как есть через больший.
- С другой стороны, если один из параллельных резисторов равен , три умножить на больше, чем другой (скажем, 30 кОм и 10 кОм), тогда будет трижды как большой ток через меньший резистор, так как через больший.
Помните, что, как в этих примерах, если два резистора разных размеры параллельны друг другу, чем меньше резистор, тем больше ток, чем у большего резистора.

Правило делителя тока

Для параллельных ветвей ток I _x через любая ветвь равна отношению общего параллельного сопротивления R _T к сопротивление ветви R _x , умноженное на общее ток I _T входящий параллельная комбинация. В форме уравнения:
I _x = ( R _T ÷ R _x ) × I _T
Здесь x — это переменная, представляющая номер резистора. что вас интересует.
- Например, если вы пытаетесь найти ток через резистор R1 замените x на 1, чтобы получить:
  I ₁ = ( R _T ÷ R ₁) × I _T
- С другой стороны, применяя правило к резистору R4 параллельно схема дает нам:
  I ₄ = ( R _T ÷ R ₄) × I _T
Обратите внимание, что R _T в этой формуле означает эквивалент сопротивление (определяется обратной формулой), , а не сумма резисторы.
Правило делителя тока, приведенное выше, применяется всякий раз, когда у вас есть любых номер из резисторы параллельно. Есть еще одна форма делителя тока Правило, которое применяется только к случаям двух резисторов , включенных параллельно. Однако я обнаружил, что студенты обычно путаются, если они постарайтесь запомнить эти частные формулы в дополнение к общим формула. Поэтому рекомендую просто запомнить общую формулу и используйте ее для всех случаев.

Питание в параллельной цепи

Чтобы найти мощность, рассеиваемую резистором в параллельной цепи, используйте любую из тех же формул, которые вы использовали для последовательных цепей:
P = V × I
P = I ² × R
пол. = В ² ÷ р
Напомним, что в каждом из этих уравнений R — это сопротивление резистора. сопротивление, В — напряжение на резисторе, а I — ток через резистор.

Общая мощность цепи

Так же, как и в резистивных цепях, есть два способы вычисления общей мощности, рассеиваемой в параллельной резистивной цепи. В любом случае вы получите один и тот же ответ:
1. Либо найдите мощность для каждого резистора, и затем добавьте эти полномочия:
  P _T = P ₁ + P ₂ + P ₃ + … + P _n
2. Или примените любую из формул мощности к вся схема:
  P _T = V _S × I _T
  P _T = I _T ² × R _T
  P _T = V _S ² ÷ R _T
  Это те же формулы мощности, что и выше, за исключением того, что теперь мы применяя их ко всей цепи, а не к одному резистору.

Устранение неисправностей параллельных цепей

Напомним из предыдущего раздела, что два наиболее распространенных типа схем проблемы: открывает (разрывы) и замыкает (пути точек подключения нулевого сопротивления, которые не должны быть подключены).
Напомним также, что ток через открытый равен нулю , и что напряжение на коротком замыкании равно нулю .
В параллельной цепи обрыв резистора не имеет влияние на ток, проходящий через другие резисторы. Но это увеличивает общее сопротивление цепи и, следовательно, уменьшает полный ток цепи.
A закороченный резистор параллельно схема — это в основном то же самое, что и прямое подключение провода от положительной клеммы источника питания к ее отрицательной клемме.Это очень плохой поступок, и он приведет к тому, что общая ток увеличить до чрезмерного значения.
- Если цепь должным образом защищенный предохранителем или автоматическим выключателем, предохранитель перегорит или выключатель сработает, отключая весь ток в цепи.
- Если цепь не защищена должным образом, чрезмерный ток вызывает короткое замыкание может привести к возгоранию или повреждению источника питания схемы.

Блок 8 Обзор

В этом электронном уроке было рассмотрено несколько важных тем, в том числе:
- параллельные соединения и параллельные цепи
- Действующий закон Кирхгофа (KCL)
- полное сопротивление параллельно включенных резисторов
- параллельно подключенные источники
- линейка делителя тока
- мощность в параллельных цепях
- закорачивает и размыкает в параллельных цепях.
Чтобы завершить электронный урок, пройдите самопроверку, чтобы проверить свое понимание из этих тем.

Поздравляем! Вы завершили электронный урок по этому модулю.

6.2 Последовательные и параллельные резисторы — Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

К концу раздела вы сможете:

Определите термин эквивалентное сопротивление
Рассчитайте эквивалентное сопротивление резисторов, соединенных последовательно
Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно

В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где. В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.

Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок 6.2.1). В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.

(рисунок 6.2.1)

Рисунок 6.2.1 (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторы

серии

Считается, что резисторы

включены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок 6.2.2, на котором показаны три последовательно включенных резистора с приложенным напряжением, равным.Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.

(рисунок 6.2.2)

Рисунок 6.2.2 (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.

На рисунке 6.2.2 ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома падение потенциала на резисторе при протекании через него тока рассчитывается по формуле, где — ток в амперах (), а — сопротивление в омах (). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на заряд, сумма напряжения, приложенного к цепи источником, и падения потенциала на отдельных резисторах вокруг контура должны быть равны нулю:

Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе.На рисунке 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:

Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.

Любое количество резисторов может быть подключено последовательно. Если резисторы соединены последовательно, эквивалентное сопротивление равно

(6.2.1)

Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.

ПРИМЕР 6.2.1

Эквивалентное сопротивление, ток и мощность в последовательной цепи

Батарея с напряжением на клеммах подключена к цепи, состоящей из четырех и одного последовательно соединенных резисторов (рисунок 6.2.3). Предположим, что внутреннее сопротивление батареи незначительно. (а) Рассчитайте эквивалентное сопротивление цепи. (б) Рассчитайте ток через каждый резистор. (c) Рассчитайте падение потенциала на каждом резисторе. (d) Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.

(рисунок 6.2.3)

Рисунок 6.2.3 Простая последовательная схема с пятью резисторами.

Стратегия

В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.Ток в цепи можно найти из закона Ома и равен напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти с помощью закона Ома. Мощность, рассеиваемая каждым резистором, может быть найдена с помощью, а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемую аккумулятором, можно найти с помощью.

Решение

а. Эквивалентное сопротивление — это алгебраическая сумма сопротивлений:

г.Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:

г. Падение потенциала на каждом резисторе можно найти с помощью закона Ома:

Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, подаваемому батареей.

г. Мощность, рассеиваемая резистором, равна, а мощность, отдаваемая аккумулятором, равна:

Значение

Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи.Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов. Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.2

Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи.«Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц. Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?

Кратко обозначим основные характеристики последовательно соединенных резисторов:

суммируются, чтобы получить эквивалентное сопротивление:
Один и тот же ток последовательно проходит через каждый резистор.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.

Параллельные резисторы

На рисунке 6.2.4 показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома, где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.

(рисунок 6.2.4)

Рисунок 6.2.4 (a) Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.

Ток, протекающий от источника напряжения на рисунке 6.2.4, зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы и. По мере того, как заряды проходят от батареи, некоторые проходят через резистор, а некоторые — через резистор. Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:

Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе.На рисунке 6.2.4 показано правило соединения. В этой схеме есть две петли, которые приводят к уравнениям и Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (), а ток является аддитивным:

Если обобщить на любое количество резисторов, эквивалентное сопротивление параллельного соединения связано с отдельными сопротивлениями на

(6.2.2)

Это соотношение приводит к эквивалентному сопротивлению, которое меньше наименьшего из отдельных сопротивлений.Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.

ПРИМЕР 6.2.2

Анализ параллельной цепи

Три резистора, и соединены параллельно. Параллельное соединение подключается к источнику напряжения. а) Какое эквивалентное сопротивление? (б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.(d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия

(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью.
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)

(b) Ток, подаваемый источником, можно найти из закона Ома, заменив полное сопротивление.

(c) Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Полный ток — это сумма отдельных токов:.

(d) Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать, так как каждый резистор получает полное напряжение.

(e) Полная мощность также может быть рассчитана несколькими способами, используйте.

Решение

а. Общее сопротивление для параллельной комбинации резисторов находится с помощью уравнения 6.2.2.Ввод известных значений дает

Общее сопротивление с правильным количеством значащих цифр составляет. Как и предполагалось, меньше минимального индивидуального сопротивления.

г. Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает

Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

г. Отдельные токи легко вычислить по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,

Аналогично

Общий ток складывается из отдельных токов:

г. Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,

Аналогично

e. Суммарную мощность также можно рассчитать несколькими способами. Выбор и ввод общей текущей доходности

Значение

Общая мощность, рассеиваемая резисторами, также составляет:

Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.3

Рассмотрим одну и ту же разность потенциалов, приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.4

Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?

Суммируем основные характеристики резисторов параллельно:

Эквивалентное сопротивление находится из
и меньше любого отдельного сопротивления в комбинации.
Падение потенциала на каждом параллельном резисторе одинаковое.
Параллельные резисторы не получают суммарный ток каждый; они делят это.Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.

В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Вы можете вспомнить, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. В таблице 6.2.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.

(таблица 6.2.1)

	Комбинация серий	Параллельная комбинация
Эквивалентная емкость
Эквивалентное сопротивление

Таблица 10.1 Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях

Сочетания последовательного и параллельного

Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения.Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Последовательные и параллельные комбинации можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на Рисунке 6.2.5. Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден.Здесь мы отмечаем эквивалентное сопротивление как.

(рисунок 6.2.5)

Обратите внимание, что резисторы и включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Один из методов отслеживания процесса — включить резисторы в качестве индексов. Здесь эквивалентное сопротивление и равно

Теперь схема сокращается до трех резисторов, показанных на Рисунке 6.2.5 (c). Перерисовывая, мы теперь видим, что резисторы и составляют параллельную цепь.Эти два резистора можно уменьшить до эквивалентного сопротивления:

Этот шаг процесса сокращает схему до двух резисторов, показанных на Рисунке 6.2.5 (d). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:

Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.

Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен. Этот ток проходит через резистор и обозначен как. Падение потенциала можно найти с помощью закона Ома:

Глядя на рис. 6.2.5 (c), остается отбросить параллельную комбинацию и. Проходной ток можно найти с помощью закона Ома:

Резисторы и включены последовательно, поэтому токи и равны

Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах.Потенциальные падения равны и. Окончательный анализ — это посмотреть на мощность, подаваемую источником напряжения, и мощность, рассеиваемую резисторами. Мощность, рассеиваемая резисторами

Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, равна. Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.5

Рассмотрите электрические цепи в вашем доме. Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.

Практическое применение

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным и проявляться в виде тепла, выделяемого в шнуре.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

Что происходит в этих сильноточных ситуациях, показано на Рисунке 6.2.7. Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.

(рисунок 6.2.7)

Рисунок 6.2.7 Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

Стратегия решения проблем: последовательные и параллельные резисторы

Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения.Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.Есть один список для серий, а другой — для параллелей.
Проверьте, являются ли ответы разумными и последовательными.

ПРИМЕР 6.2.4

Объединение последовательных и параллельных цепей

Два резистора, соединенных последовательно, подключены к двум резисторам, включенным параллельно. Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление.Ток проходит через резистор. Какое напряжение подается от источника напряжения?

Стратегия

Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.

Решение

Нарисуйте четкую принципиальную схему (рисунок 6.2.8).
(рисунок 6.2.8)
Рисунок 6.2.8 Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
Неизвестно напряжение аккумулятора.Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
В этой схеме мы уже знаем, что резисторы и включены последовательно, а резисторы и включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов и последовательно с последовательной конфигурацией резисторов и.
Напряжение, подаваемое батареей, можно найти, умножив ток от батареи на эквивалентное сопротивление цепи.Ток от аккумулятора равен току через него и равен. Нам нужно найти эквивалентное сопротивление, уменьшив схему. Чтобы уменьшить схему, сначала рассмотрите два резистора, включенных параллельно. Эквивалентное сопротивление составляет. Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно. Таким образом, напряжение, подаваемое батареей, составляет.
Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами.Мощность, подаваемая аккумулятором, составляет
Поскольку они включены последовательно, сквозной ток равен сквозному току. Т.к. ток через каждый будет. Мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором:

Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.

Значение

Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При поиске параллельного подключения необходимо соблюдать осторожность. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.

Candela Citations

Лицензионный контент CC, конкретная атрибуция

Загрузите бесплатно с http: // cnx.org/contents/[email protected]. Получено с сайта : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

Расчет параллельного сопротивления — Pi My Life Up

В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления.

Параллельное сопротивление — полезная часть электроники, но его может быть трудно рассчитать, когда вы начинаете иметь дело с более чем двумя резисторами.

Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Такое поведение удобно, когда вам нужно определенное сопротивление, но нет резистора, который соответствует требуемому значению.

Уменьшение сопротивления вызвано тем, что у тока больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больше тока через цепь и, следовательно, снижает общее сопротивление, с которым сталкивается ваша цепь.

Например, в цепи с двумя резисторами равного номинала, включенными параллельно, сопротивление будет уменьшено ровно наполовину.Математика немного отличается для разных сопротивлений и наличия большего количества резисторов. Мы углубимся в это позже в руководстве.

Если вы хотите увеличить сопротивление вашей цепи, а не уменьшать его, вы можете вместо этого использовать резисторы последовательно.

Чтобы помочь вычислить общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает процесс.

Если вас смущают цвета на резисторе, обязательно ознакомьтесь с руководством по цветовым кодам резистора, поскольку оно научит вас всему, что вам нужно знать.

Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление. Затем введите значение для каждого резистора.

Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.

Расчет общего сопротивления параллельно

Если вы предпочитаете учиться, вы можете вручную рассчитать сопротивление резисторов, подключенных параллельно. Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами параллельно.

Существует три различных уравнения, которые можно использовать для вычисления общего сопротивления при параллельном подключении.

Общее сопротивление двух одинаковых резисторов

Первое уравнение может использоваться только в том случае, если у вас есть два параллельно подключенных резистора с одинаковым сопротивлением.

Если у вас есть два резистора с одинаковым сопротивлением параллельно, то общее сопротивление равно половине одного резистора.

Пример использования уравнения

Для этого примера предположим, что у нас есть два 200-омных резистора , включенных параллельно, как показано на схеме ниже.

Зная, что параллельно подключено только два резистора и что они имеют одинаковое значение, мы можем использовать наше уравнение.

Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).

Чтобы получить полное сопротивление, все, что нам нужно сделать, это разделить значение 200 Ом на 2 .

Ответ очень легко найти: 100 .

После этого у вас должно быть представление о том, как поступить в простейшем случае, когда два резистора одинакового номинала включены параллельно.

Общее сопротивление двух разных резисторов

Второе уравнение — это упрощенная версия основного уравнения, которое мы будем использовать позже. Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.

Есть еще несколько процессов, которые вам нужно выполнить для расчета сопротивления двух параллельно подключенных резисторов, но это не намного сложнее.

Пример использования уравнения

В этом примере мы будем предполагать, что у нас есть цепь с двумя параллельными резисторами разных значений.

В этой схеме у нас есть резистор 600 Ом и резистор 250 Ом , включенные параллельно. Теперь мы хотим вычислить общее сопротивление, обеспечиваемое этими резисторами.

Для начала нам нужно заполнить наше уравнение, где R1 будет нашим резистором 600 Ом, а значение R2 будет резистором 250 Ом.

Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение перед тем, как продолжить.

Умножение 600 (R1) на 250 (R2) даст результат 150 000 . Добавление 600 (R1) к 250 (R2) даст вам ответ 850 .

Когда оба значения определены, все, что нам нужно сделать, это разделить верхнее число на нижнее число. Таким образом, мы можем определить общее сопротивление двух параллельно включенных резисторов.

Вычисление, которое вы должны проделать с этим примером: 150 000 разделить на 850 . Отсюда вы должны получить результат 176,47 . Будут лишние десятичные точки, но мы округлим их до ближайших двух.

После этого вы должны иметь представление о том, как рассчитать полное сопротивление двух резисторов, включенных параллельно.

Далее мы покажем вам, как обращаться с тремя и более резисторами. Это уравнение — немного более сложный процесс, поскольку он включает в себя много делений, что приводит к большим десятичным числам.

Общее сопротивление нескольких резисторов

Третье и последнее уравнение, с которым мы будем иметь дело, — это уравнение, которое вы будете использовать для трех или более резисторов, включенных параллельно.

Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.

Единственным недостатком этого уравнения является то, что на него требуется больше времени, чем больше резисторов вы добавляете.

Простым решением является использование параллельного калькулятора резисторов, как мы включили выше.

Пример использования уравнения

В этом примере мы покажем, как использовать более сложное уравнение параллельного резистора.

Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1 кОм (R4) .

Для начала нам нужно заполнить уравнение всеми нашими значениями.

Каждое из наших значений резистора будет делителем для 1 , и вы можете добавить столько резисторов, сколько вам нужно в это уравнение.В этом примере мы обрабатываем только четыре.

Наш следующий шаг — разделить 1 на каждое из значений нашего резистора . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.

Например, в нашем расчете мы делим 1 на 100 , что дает нам результат 0,01 .

После того, как вы закончили делить каждый набор значений, нам нужно сложить каждое значение вместе.

Для схемы нашего примера это будет означать: 0,01 + 0,004 + 0,005 + 0,001 . К счастью для нас, это складывается довольно гладко и дает нам хорошее круглое число 0,02 .

Затем нам нужно переместить делитель из левой части уравнения вправо.

Этот ход будет означать, что наше вычисленное значение станет делителем 1 и должно выглядеть так, как показано ниже.

Наконец, разделите 1 на ваш делитель, и в нашем случае это будет 0.02 . Это уравнение рассчитает окончательное полное сопротивление ваших параллельных резисторов.

Резюме

Надеюсь, теперь вы собрали достаточно знаний о том, как рассчитать полное сопротивление резисторов, включенных параллельно. Вам будет удобно, если вы планируете делать какие-то проекты схем Raspberry Pi или любой другой проект электроники.

Если у вас есть отзывы или вопросы по этому руководству, пожалуйста, оставьте комментарий ниже.

Расчет тока в последовательно-параллельных цепях

Рисунок 1. Последовательно-параллельные резисторы.

В цепи с резисторами, включенными как последовательно, так и параллельно, рассматривать схему как комбинацию параллельных частей и последовательных части.

Используйте формулы сопротивления для определения общего сопротивления серийных и параллельных частей.Затем используйте закон Ома, чтобы вычислить напряжение падает поперек и токи через каждую часть.

В схеме на Рисунке 1 сначала используйте параллельное сопротивление формула для определения эквивалентного сопротивления R ₁₂₃ .

Тогда формула последовательного сопротивления говорит нам R _TOT = R ₁₂₃ + R ₄ . Итак, закон Ома дает полный ток цепи:

I _TOT равно как текущим I ₄ хотя R ₄ и текущему I ₁₂₃ вход / выход из параллельной части.Используя закон Ома:

Итак, зная значение В ₁₂₃ , снова применим закон Ома, чтобы найти ток I ₁ через параллельный резистор R ₁ :

и аналогично для I ₂ и I ₃ .

Пример

Для схемы на рисунке 1 предположим, что E = 9 В, R ₁ = 500 Ом, R ₂ = 1.0 кОм, R ₃ = 1,5 кОм и R ₄ = 220 Ом. Тогда R ₁₂₃ = 273 Ом и R _TOT = 493 Ом, поэтому

и, следовательно,

Аналогично для I ₂ и I ₃ .

Примечание: Важно осторожно обращаться с единицами измерения с метрическими префиксами. Выше мы отрегулировали десятичную точку и единицы измерения таким образом, чтобы наша формула для тока давала вольт / Ом = ампер.

Сопротивление в параллельной цепи

Сопротивление в параллельной цепи
На примерной схеме, рис. 3-44, два резистора подключены параллельно через 5-вольтовую батарею. Каждый имеет значение сопротивления 10 Ом. Формируется полная цепь, состоящая из двух параллельных путей, и ток течет, как показано.

Рисунок 3-44. — Два равных резистора, включенных параллельно.

Вычисление отдельных токов показывает, что через каждое сопротивление проходит половина ампера. Полный ток, протекающий от батареи к переходу резисторов и возвращающийся от резисторов к батарее, равен 1 амперам.

Общее сопротивление цепи можно рассчитать, используя
значения полного напряжения (E _T) и полного тока (I _T).

ПРИМЕЧАНИЕ. С этого момента в примерах задач будут использоваться сокращения и символы для электрических величин.

Дано:

Решение:

Это вычисление показывает, что полное сопротивление составляет 5 Ом; половина номинала любого из двух резисторов.

Поскольку полное сопротивление параллельной цепи меньше, чем у любого из отдельных резисторов, общее сопротивление параллельной цепи не является суммой значений отдельных резисторов, как это было в случае последовательной цепи. Общее сопротивление параллельно включенных резисторов также называется ЭКВИВАЛЕНТНЫМ СОПРОТИВЛЕНИЕМ. (_{рэндов эквивалент}).Термины полное сопротивление и эквивалентное сопротивление используются как синонимы.

Существует несколько методов определения эквивалентного сопротивления параллельных цепей. Лучший метод для данной схемы зависит от количества и номинала резисторов. Для схемы, описанной выше, где все резисторы имеют одинаковое значение, используется следующее простое уравнение:

Это уравнение действительно для любого количества параллельных резисторов с РАВНЫМ ЗНАЧЕНИЕМ.

Пример.Параллельно подключены четыре резистора на 40 Ом. Каково их эквивалентное сопротивление?

Дано:

Решение:

На рис. 3-45 показаны два резистора разного номинала, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.

Рисунок 3-45. — Пример схемы с неравнопараллельными резисторами.

Дано:

Решение:

Эквивалентное сопротивление цепи, показанной на рисунке 3-45, меньше, чем у любого из двух резисторов (R ₁, R ₂).Важно помнить, что эквивалентное сопротивление параллельной цепи всегда меньше, чем сопротивление любой ветви.

Эквивалентное сопротивление можно найти, зная отдельные значения сопротивления и напряжение источника. Вычисляя ток каждой ветви, складывая токи ветви для вычисления общего тока и разделив напряжение источника на общий ток, можно найти общий ток. Этот метод хоть и эффективен, но довольно длительный. Более быстрый способ найти эквивалентное сопротивление — использовать общую формулу для параллельных резисторов:

Если вы примените общую формулу к схеме, показанной на рисунке 3-45, вы получите то же значение для эквивалентного сопротивления (2 Ом), что и было. полученный в предыдущем расчете, в котором использовались напряжение источника и полный ток.

Дано:

Решение:

Преобразуйте дроби к общему знаменателю.

Поскольку обе стороны взаимны (разделены на одну), игнорируйте обратную функцию.

Формула, которую вы дали для одинаковых резисторов, включенных параллельно

, является упрощением общей формулы для параллельных резисторов

Существуют и другие упрощения общей формулы для параллельных резисторов, которые можно использовать для расчета общей суммы. или эквивалентное сопротивление в параллельной цепи.

ВЗАИМНЫЙ МЕТОД. — Этот метод основан на взятии обратной величины для каждой стороны уравнения. Это представляет собой общую формулу для резисторов, включенных параллельно:

Эта формула используется для определения эквивалентного сопротивления ряда неравных параллельных резисторов. При решении этих задач вы должны найти наименьший общий знаменатель. Если вы не знаете, как найти наименьший общий знаменатель, освежите его в математике, том 1, NAVEDTRA 10069 (серия).

Пример: три резистора подключены параллельно, как показано на рисунке 3-46. Значения резистора: R ₁ = 20 Ом, R ₂ = 30 Ом, R ₃ = 40 Ом. Какое эквивалентное сопротивление? (Используйте обратный метод.)

Рисунок 3-46. — Пример параллельной схемы с разными резисторами ответвления.

Дано:

Решение:

ПРОДУКТ ПРЕВЫШАЕТ СУММУ. — Удобный способ найти эквивалентное или общее сопротивление двух параллельных резисторов — использовать следующую формулу.

Это уравнение, называемое формулой произведения на сумму, используется так часто, что его следует сохранить в памяти.

Пример. Какое эквивалентное сопротивление резисторов 20 Ом и 30 Ом, подключенных параллельно, как показано на рисунке 3-47?

Рисунок 3-47. — Параллельная схема с двумя неравными резисторами.