Как группа Plazma стала популярной в России, исполняя песни на английском языке. Почему музыканты выбрали этот путь. Какие хиты принесли им известность. Как складывалась карьера коллектива.
Истоки группы Plazma: от Slow Motion до международного успеха
История группы Plazma началась в далеком 1990 году в Волгограде. Изначально коллектив назывался Slow Motion и состоял из трех участников:
- Роман Черницын (вокал)
- Максим Постельный (клавишные, бэк-вокал)
- Николай Романов (бас-гитара)
Уже тогда музыканты приняли важное решение — исполнять все песни только на английском языке. Это было довольно смелым шагом для российской группы того времени. Чем руководствовались участники Slow Motion при выборе такого необычного пути?
Причины выбора англоязычного репертуара
По словам самих музыкантов, на это решение повлияли следующие факторы:
- Любовь к западной прогрессивной музыке, большая часть которой исполнялась на английском
- Желание доказать, что в России тоже могут делать качественную англоязычную музыку
- Стремление выделиться на фоне других российских исполнителей
Как отмечал Роман Черницын: «В любой стране существуют англоязычные группы — в Швеции около 45%, в Германии 25%, и это нормально. В России пока никто не пел на английском, мы стали первыми».
Первые шаги и трудности на пути к успеху
Начало 90-х годов было непростым временем для молодых музыкантов. Несмотря на успешные выступления на местных фестивалях, группа испытывала финансовые трудности. В 1992-1993 годах Роман Черницын даже был вынужден устроиться работать на завод «Спецэнергоремонт», а Максим Постельный продолжал учебу в училище искусств.
Однако судьба улыбнулась музыкантам — их демо-запись попала в руки Сергея Олейника, который на тот момент был генеральным директором внешнеторгового дома «Хелп». Он решил поддержать талантливых ребят и стал спонсировать группу.
Первое появление на телевидении
Благодаря поддержке Олейника, Slow Motion получили приглашение выступить в популярной телепрограмме «Звездный дождь» на канале РТР. Это стало важным шагом на пути к известности.
Рождение Plazma: новое имя — новые возможности
В 1999 году группа сменила название на Plazma. Это событие ознаменовало новый этап в творчестве коллектива. Почему было выбрано именно такое название? Музыканты объясняют это следующим образом:
- Слово «плазма» ассоциируется с чем-то современным и технологичным
- Оно хорошо звучит как на русском, так и на английском языках
- Название отражает энергичность и яркость музыки группы
Прорыв: хит «Take My Love» и всероссийская известность
Настоящий успех пришел к Plazma после выхода сингла «Take My Love» в 2000 году. Эта песня буквально взорвала радиоэфиры и принесла группе всероссийскую известность. Чем же так зацепила слушателей эта композиция?
- Запоминающаяся мелодия в стиле евродэнс
- Красивый вокал Романа Черницына
- Качественное звучание и аранжировка
- Романтичный текст на английском языке
«Take My Love» стала визитной карточкой Plazma и до сих пор остается одной из самых узнаваемых песен группы.
Развитие успеха: альбомы и новые хиты
После громкого успеха первого сингла, Plazma продолжила активно работать над новым материалом. Какие альбомы выпустила группа и какие еще хиты покорили сердца слушателей?
Альбомы Plazma
- «Take My Love» (2000)
- «607» (2002)
- «Black & White» (2006)
- «Indian Summer» (2009)
- «Mystery (The Power Within)» (2012)
Популярные синглы
- «The Sweetest Surrender»
- «Lonely»
- «Jump In My Car»
- «Never Ending Story»
- «Living in the Past»
Первые два альбома группы — «Take My Love» и «607» — были проданы тиражом более миллиона копий, что подтвердило статус Plazma как одной из самых успешных российских англоязычных групп.
Plazma и «Евровидение»: попытки покорить международную сцену
Несмотря на успех в России, группа Plazma не оставляла попыток выйти на международный уровень. Одним из способов достичь этой цели стало участие в отборочных турах на конкурс «Евровидение». Какие попытки предпринимала группа?
- 2007 год: песня «Living in the Past»
- 2009 год: композиция «Never Ending Story» (группа дошла до финала отборочного тура)
- 2010 год: трек «Mystery (The Power Within)»
Хотя Plazma так и не удалось представить Россию на «Евровидении», эти попытки помогли группе расширить аудиторию и получить ценный опыт участия в международных конкурсах.
Уникальность Plazma на российской музыкальной сцене
Что делает группу Plazma особенной среди других российских исполнителей? Можно выделить несколько ключевых факторов:
- Исполнение песен исключительно на английском языке
- Сочетание различных музыкальных стилей: от синти-попа до поп-рока
- Высокое качество аранжировок и звучания
- Яркий вокал Романа Черницына
- Стабильный состав группы на протяжении многих лет
Эти особенности позволили Plazma занять свою нишу на российском музыкальном рынке и оставаться популярными на протяжении более 20 лет.
Современное состояние и перспективы группы Plazma
Как обстоят дела у Plazma сегодня? Группа продолжает активно работать и радовать поклонников новыми песнями. В состав коллектива по-прежнему входят:
- Роман Черницын (вокал, автор песен)
- Максим Постельный (клавишные, бэк-вокал, аранжировки)
Кроме того, в концертах периодически принимают участие приглашенные музыканты:
- Александр Лучков (скрипка, гитара)
- Николай Трофимов (гитара)
Plazma продолжает выпускать новые синглы и альбомы, а также активно гастролирует по России и странам ближнего зарубежья. Группа остается верна своему стилю и продолжает исполнять песни на английском языке, что по-прежнему выделяет ее среди других российских исполнителей.
Влияние Plazma на российскую музыкальную индустрию
Можно ли сказать, что успех Plazma повлиял на развитие российской музыкальной сцены? Безусловно. Группа доказала, что:
- Российские исполнители могут успешно работать с англоязычным материалом
- Качественная музыка может быть востребована вне зависимости от языка исполнения
- Сочетание различных музыкальных стилей может привести к созданию уникального звучания
Пример Plazma вдохновил многих молодых музыкантов экспериментировать с языком исполнения и музыкальными стилями, что в целом обогатило российскую музыкальную сцену.
Подводя итоги, можно сказать, что группа Plazma занимает особое место в истории российской поп-музыки. Начав свой путь как малоизвестный провинциальный коллектив, они сумели добиться всероссийской известности и признания, оставаясь верными своему уникальному стилю. История Plazma показывает, что талант, упорство и готовность идти своим путем могут привести к большому успеху даже в таком конкурентном мире, как шоу-бизнес.
Плазма — Википедия. Что такое Плазма

Пла́зма (от греч. πλάσμα «вылепленное, оформленное») — ионизованный газ, одно из четырех основных агрегатных состояний вещества.
Ионизированный газ содержит свободные электроны и положительные и отрицательные ионы. В более широком смысле, плазма может состоять из любых заряженных частиц (например, кварк-глюонная плазма). Квазинейтральность означает, что суммарный заряд в любом малом по сравнению с размерами системы объёме равен нулю, является её ключевым отличием от других систем, содержащих заряженные частицы (например, электронные или ионные пучки). Поскольку при нагреве газа до достаточно высоких температур, он переходит в плазму, она называется четвёртым (после твёрдого, жидкого и газообразного) агрегатным состоянием вещества.
Поскольку частицы в газе обладают подвижностью, плазма обладает способностью проводить электрический ток. В стационарном случае плазма экранирует постоянное внешнее по отношению к ней электрическое поле за счёт пространственного разделения зарядов. Однако из-за наличия ненулевой температуры заряженных частиц существует минимальный масштаб, на расстояниях меньше которого квазинейтральность нарушается.
История открытия
Четвёртое состояние вещества было открыто У. Круксом в 1879 году и названо «плазмой» И. Ленгмюром в 1928 году. Ленгмюр писал[1]:
Исключая пространство около электродов, где обнаруживается небольшое количество электронов, ионизированный газ содержит ионы и электроны практически в одинаковых количествах, в результате чего суммарный заряд системы очень мал. Мы используем термин «плазма», чтобы описать эту в целом электрически нейтральную область, состоящую из ионов и электронов.
Древние философы полагали, что мир состоит из четырёх стихий: земли, воды, воздуха и огня. Можно сказать, что это положение с учетом некоторых допущений укладывается в современное представление о четырёх агрегатных состояниях вещества, причём плазме соответствует огонь. Свойства плазмы изучает физика плазмы.
Виды
По сегодняшним представлениям, фазовым состоянием большей части барионного вещества (по массе ок. 99,9 %) во Вселенной является плазма.
Свойства и параметры
Определение плазмы
Плазма — частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.[4] Не всякую систему заряженных частиц можно назвать плазмой. Плазма обладает следующими свойствами: [5][6][7]
- Достаточная плотность: заряженные частицы должны находиться достаточно близко друг к другу, чтобы каждая из них взаимодействовала с целой системой близкорасположенных заряженных частиц. Условие считается выполненным, если число заряженных частиц в сфере влияния (сфера радиусом Дебая) достаточно для возникновения коллективных эффектов (подобные проявления — типичное свойство плазмы). Математически это условие можно выразить так:
- rD3N≫1,{\displaystyle r_{D}^{3}N\gg 1,}
- где N{\displaystyle N} — концентрация заряженных частиц.
- Приоритет внутренних взаимодействий: радиус дебаевского экранирования должен быть мал по сравнению с характерным размером плазмы. Этот критерий означает, что взаимодействия, происходящие внутри плазмы более значительны по сравнению с эффектами на её поверхности, которыми можно пренебречь. Если это условие соблюдено, плазму можно считать квазинейтральной. Математически оно выглядит так:
- rDL≪1.{\displaystyle {r_{D} \over L}\ll 1.}
- Плазменная частота: среднее время между столкновениями частиц должно быть велико по сравнению с периодом плазменных колебаний. Эти колебания вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд проходит по инерции это положение, что опять приводит к появлению сильного возвращающего поля, возникают типичные механические колебания.[8] Когда данное условие соблюдено, электродинамические свойства плазмы преобладают над молекулярно-кинетическими. На языке математики это условие имеет вид:
- τωpl≫1.{\displaystyle \tau \omega _{pl}\gg 1.}
Классификация
Плазма обычно разделяется на идеальную и неидеальную, низкотемпературную и высокотемпературную, равновесную и неравновесную, при этом довольно часто холодная плазма бывает неравновесной, а горячая равновесной.
Температура
Плазму делят на низкотемпературную (температура меньше миллиона K) и высокотемпературную (температура миллион K и выше). Такое деление обусловлено важностью высокотемпературной плазмы в проблеме осуществления управляемого термоядерного синтеза. Разные вещества переходят в состояние плазмы при разной температуре, что объясняется строением внешних электронных оболочек атомов вещества: чем легче атом отдает электрон, тем ниже температура перехода в плазменное состояние[9].
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией. Такая ситуация встречается в газовых разрядах, когда ионы имеют температуру около сотен, а электроны около десятков тысяч K.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Степень и кратность ионизации
Для того, чтобы газ перешёл в состояние плазмы, его необходимо ионизировать. Степень ионизации пропорциональна числу атомов, отдавших или поглотивших электроны, и больше всего зависит от температуры. Даже слабо ионизированный газ, в котором менее 1 % частиц находятся в ионизированном состоянии, может проявлять некоторые типичные свойства плазмы (взаимодействие с внешним электромагнитным полем и высокая электропроводность). Степень ионизации α определяется как α = ni /(ni + na), где ni — концентрация ионов, а na — концентрация нейтральных атомов. Концентрация свободных электронов в незаряженной плазме ne определяется очевидным соотношением: ne=<Z>ni, где <Z> — среднее значение заряда ионов плазмы, или кратность ионизации плазмы. Очевидно, что максимальное значение α равно 1 (или 100 %), такую плазму называют полностью ионизованной.
Для низкотемпературной плазмы характерна малая степень ионизации (до 1 %). Так как такие плазмы довольно часто употребляются в технологических процессах, их иногда называют технологичными плазмами. Чаще всего их создают при помощи электрических полей, ускоряющих электроны, которые в свою очередь ионизируют атомы. Электрические поля вводятся в газ посредством индуктивной или емкостной связи (см. индуктивно-связанная плазма). Типичные применения низкотемпературной плазмы включают плазменную модификацию свойств поверхности (алмазные плёнки, нитридирование металлов, изменение смачиваемости), плазменное травление поверхностей (полупроводниковая промышленность), очистку газов и жидкостей (озонирование воды и сжигание частичек сажи в дизельных двигателях).
Горячая плазма почти всегда полностью ионизирована (степень ионизации ~100 %). Обычно именно она понимается под «четвёртым агрегатным состоянием вещества». Примером может служить Солнце.
Концентрация частиц в плазме
Помимо температуры, которая имеет фундаментальную важность для самого существования плазмы, вторым наиболее важным свойством плазмы является концентрация заряженных частиц. Словосочетание концентрация плазмы обычно обозначает концентрация электронов, то есть число свободных электронов в единице объёма. В квазинейтральной плазме концентрация ионов связана с ней посредством среднего зарядового числа ионов ⟨Z⟩{\displaystyle \langle Z\rangle }: ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}}. Следующей важной величиной является концентрация нейтральных атомов n0{\displaystyle n_{0}}. В горячей плазме n0{\displaystyle n_{0}} мала, но может тем не менее быть важной для физики процессов в плазме. При рассмотрении процессов в плотной, неидеальной плазме характерным параметром концентрации становится rs{\displaystyle r_{s}}, который определяется как отношение среднего межчастичного расстояния к радиусу Бора.
Квазинейтральность
Так как плазма является очень хорошим проводником, электрические свойства имеют важное значение. Потенциалом плазмы или потенциалом пространства называют среднее значение электрического потенциала в данной точке пространства. В случае если в плазму внесено какое-либо тело, его потенциал в общем случае будет меньше потенциала плазмы вследствие возникновения дебаевского слоя. Такой потенциал называют плавающим потенциалом. По причине хорошей электрической проводимости плазма стремится экранировать все электрические поля. Это приводит к явлению квазинейтральности — плотность отрицательных зарядов с хорошей точностью равна плотности положительных зарядов (ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}}). В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний.
Примером неквазинейтральной плазмы является пучок электронов. Однако плотность не-нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.
Отличия от газообразного состояния
Плазму часто называют четвёртым состоянием вещества. Она отличается от трёх менее энергетичных агрегатных состояний материи, хотя и похожа на газовую фазу тем, что не имеет определённой формы или объёма. До сих пор идёт обсуждение того, является ли плазма отдельным агрегатным состоянием, или же просто горячим газом. Большинство физиков считает, что плазма является чем-то большим, чем газ по причине следующих различий:
| Свойство | Газ | Плазма |
|---|---|---|
| Электрическая проводимость | Крайне мала К примеру, воздух является превосходным изолятором до тех пор, пока не переходит в плазменное состояние под действием внешнего электрического поля напряженностью в 30 киловольт на сантиметр.[10] |
Очень высока
|
| Число сортов частиц | Один Газы состоят из подобных друг другу частиц, которые находятся в тепловом движении, а также движутся под действием гравитации, а друг с другом взаимодействуют только на сравнительно небольших расстояниях. |
Два, или три, или более Электроны, ионы и нейтральные частицы различаются знаком эл. заряда и могут вести себя независимо друг от друга — иметь разные скорости и даже температуры, что служит причиной появления новых явлений, например волн и неустойчивостей. |
| Распределение по скоростям | Максвелловское Столкновения частиц друг с другом приводит к максвелловскому распределению скоростей, согласно которому очень малая часть молекул газа имеют относительно большие скорости движения. |
Может быть немаксвелловское Электрические поля имеют другое влияние на скорости частиц чем столкновения, которые всегда ведут к максвеллизации распределения по скоростям. Зависимость сечения кулоновских столкновений от скорости может усиливать это различие, приводя к таким эффектам, как двухтемпературные распределения и убегающие электроны. |
| Тип взаимодействий | Бинарные Как правило двухчастичные столкновения, трёхчастичные крайне редки. |
Коллективные Каждая частица взаимодействует сразу со многими. Эти коллективные взаимодействия имеют гораздо большее влияние чем двухчастичные. |
Сложные плазменные явления
Хотя основные уравнения, описывающие состояния плазмы, относительно просты, в некоторых ситуациях они не могут адекватно отражать поведение реальной плазмы: возникновение таких эффектов — типичное свойство сложных систем, если использовать для их описания простые модели. Наиболее сильное различие между реальным состоянием плазмы и её математическим описанием наблюдается в так называемых пограничных зонах, где плазма переходит из одного физического состояния в другое (например, из состояния с низкой степенью ионизации в высокоионизационное). Здесь плазма не может быть описана с использованием простых гладких математических функций или с применением вероятностного подхода. Такие эффекты как спонтанное изменение формы плазмы являются следствием сложности взаимодействия заряженных частиц, из которых состоит плазма. Подобные явления интересны тем, что проявляются резко и не являются устойчивыми. Многие из них были изначально изучены в лабораториях, а затем были обнаружены во Вселенной.
Математическое описание
Плазму можно описывать на различных уровнях детализации. Обычно плазма описывается отдельно от электромагнитных полей. Совместное описание проводящей жидкости и электромагнитных полей даётся в теории магнитогидродинамических явлений или МГД теории.
Флюидная (жидкостная) модель
Во флюидной модели электроны описываются в терминах плотности, температуры и средней скорости. В основе модели лежат: уравнение баланса для плотности, уравнение сохранения импульса, уравнение баланса энергии электронов. В двухжидкостной модели таким же образом рассматриваются ионы.
Кинетическое описание
Иногда жидкостная модель оказывается недостаточной для описания плазмы. Более подробное описание даёт кинетическая модель, в которой плазма описывается в терминах функции распределения электронов по координатам и импульсам. В основе модели лежит уравнение Больцмана. Уравнение Больцмана неприменимо для описания плазмы заряженных частиц с кулоновским взаимодействием вследствие дальнодействующего характера кулоновских сил. Поэтому для описания плазмы с кулоновским взаимодействием используется уравнение Власова с самосогласованным электромагнитным полем, созданным заряженными частицами плазмы. Кинетическое описание необходимо применять в случае отсутствия термодинамического равновесия либо в случае присутствия сильных неоднородностей плазмы.
Particle-In-Cell (частица в ячейке)
Модели Particle-In-Cell используются для численного решения кинетических уравнений. Они включают в себя кинетическую информацию путём слежения за траекториями большого числа отдельных квазичастиц, каждая из которых отвечает некоторому числу реальных частиц (интегралу от функции распределения по ограниченной в фазовом пространстве области). Плотности электрического заряда и тока определяются путём суммирования заряда и квазичастиц в ячейках, которые малы по сравнению с рассматриваемой задачей, но, тем не менее, содержат большое число квазичастиц. Электрическое и магнитное поля находятся из плотностей зарядов и токов на границах ячеек. Не стоит путать модели PIC с прямым интегрированием уравнений движения реальных частиц, из которых состоит плазма — электронов и ионов — поскольку общее число квазичастиц в PIC-моделях, как правило, на много порядков меньше.
Базовые характеристики
Все величины даны в Гауссовых СГС единицах за исключением температуры, которая дана в eV и массы ионов, которая дана в единицах массы протона μ=mi/mp{\displaystyle \mu =m_{i}/m_{p}}; Z — зарядовое число; k — постоянная Больцмана; К — длина волны; γ — адиабатический индекс; ln Λ — Кулоновский логарифм.
Частоты
- Ларморова частота электрона, угловая частота кругового движения электрона в плоскости перпендикулярной магнитному полю:
- ωce=eB/mec=1.76×107Brad/s.{\displaystyle \omega _{ce}=eB/m_{e}c=1.76\times 10^{7}B{\mbox{rad/s}}.}
- Ларморова частота иона, угловая частота кругового движения иона в плоскости перпендикулярной магнитному полю:
- ωci=eB/mic=9.58×103Zμ−1Brad/s.{\displaystyle \omega _{ci}=eB/m_{i}c=9.58\times 10^{3}Z\mu ^{-1}B{\mbox{rad/s}}.}
- Плазменная частота (частота плазменных колебаний), частота с которой электроны колеблются около положения равновесия, будучи смещёнными относительно ионов:
- ωpe=(4πnee2/me)1/2=5.64×104ne1/2rad/s.{\displaystyle \omega _{pe}=(4\pi n_{e}e^{2}/m_{e})^{1/2}=5.64\times 10^{4}n_{e}^{1/2}{\mbox{rad/s}}.}
- Ионная плазменная частота:
- ωpi=(4πniZ2e2/mi)1/2=1.32×103Zμ−1/2ni1/2rad/s.{\displaystyle \omega _{pi}=(4\pi n_{i}Z^{2}e^{2}/m_{i})^{1/2}=1.32\times 10^{3}Z\mu ^{-1/2}n_{i}^{1/2}{\mbox{rad/s}}.}
- Частота столкновений электронов
- νe=2.91×10−6nelnΛTe−3/2s−1.{\displaystyle \nu _{e}=2.91\times 10^{-6}n_{e}\,\ln \Lambda \,T_{e}^{-3/2}{\mbox{s}}^{-1}.}
- Частота столкновений ионов
- νi=4.80×10−8Z4μ−1/2nilnΛTi−3/2s−1.{\displaystyle \nu _{i}=4.80\times 10^{-8}Z^{4}\mu ^{-1/2}n_{i}\,\ln \Lambda \,T_{i}^{-3/2}{\mbox{s}}^{-1}.}
Длины
- Де-Бройлева длина волны электрона, длина волны электрона в квантовой механике:
- λ−=ℏ/(mekTe)1/2=2.76×10−8Te−1/2cm.{\displaystyle \lambda \!\!\!\!-=\hbar /(m_{e}kT_{e})^{1/2}=2.76\times 10^{-8}\,T_{e}^{-1/2}\,{\mbox{cm}}.}
- Минимальное расстояние сближения в классическом случае, минимальное расстояние на которое могут сблизиться две заряженных частицы при лобовом столкновении и начальной скорости, соответствующей температуре частиц, в пренебрежении квантово-механическими эффектами:
- e2/kT=1.44×10−7T−1cm.{\displaystyle e^{2}/kT=1.44\times 10^{-7}\,T^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус электрона, радиус кругового движения электрона в плоскости перпендикулярной магнитному полю:
- re=vTe/ωce=2.38Te1/2B−1cm.{\displaystyle r_{e}=v_{Te}/\omega _{ce}=2.38\,T_{e}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус иона, радиус кругового движения иона в плоскости перпендикулярной магнитному полю:
- ri=vTi/ωci=1.02×102μ1/2Z−1Ti1/2B−1cm.{\displaystyle r_{i}=v_{Ti}/\omega _{ci}=1.02\times 10^{2}\,\mu ^{1/2}Z^{-1}T_{i}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Размер скин-слоя плазмы, расстояние на которое электромагнитные волны могут проникать в плазму:
- c/ωpe=5.31×105ne−1/2cm.{\displaystyle c/\omega _{pe}=5.31\times 10^{5}\,n_{e}^{-1/2}\,{\mbox{cm}}.}
- Радиус Дебая (длина Дебая), расстояние на котором электрические поля экранируются за счёт перераспределения электронов:
- λD=(kT/4πne2)1/2=7.43×102T1/2n−1/2cm.{\displaystyle \lambda _{D}=(kT/4\pi ne^{2})^{1/2}=7.43\times 10^{2}\,T^{1/2}n^{-1/2}\,{\mbox{cm}}.}
Скорости
- Тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:
- vTe=(kTe/me)1/2=4.19×107Te1/2cm/s.{\displaystyle v_{Te}=(kT_{e}/m_{e})^{1/2}=4.19\times 10^{7}\,T_{e}^{1/2}\,{\mbox{cm/s}}.}
- vTi=(kTi/mi)1/2=9.79×105μ−1/2Ti1/2cm/s.{\displaystyle v_{Ti}=(kT_{i}/m_{i})^{1/2}=9.79\times 10^{5}\,\mu ^{-1/2}T_{i}^{1/2}\,{\mbox{cm/s}}.}
- Скорость ионного звука, скорость продольных ионно-звуковых волн:
- cs=(γZkTe/mi)1/2=9.79×105(γZTe/μ)1/2cm/s.{\displaystyle c_{s}=(\gamma ZkT_{e}/m_{i})^{1/2}=9.79\times 10^{5}\,(\gamma ZT_{e}/\mu )^{1/2}\,{\mbox{cm/s}}.}
- vA=B/(4πnimi)1/2=2.18×1011μ−1/2ni−1/2Bcm/s.{\displaystyle v_{A}=B/(4\pi n_{i}m_{i})^{1/2}=2.18\times 10^{11}\,\mu ^{-1/2}n_{i}^{-1/2}B\,{\mbox{cm/s}}.}
Безразмерные величины
- Квадратный корень из отношения масс электрона и протона:
- (me/mp)1/2=2.33×10−2=1/42.9.{\displaystyle (m_{e}/m_{p})^{1/2}=2.33\times 10^{-2}=1/42.9.}
- Число частиц в сфере Дебая:
- (4π/3)nλD3=1.72×109T3/2n−1/2.{\displaystyle (4\pi /3)n\lambda _{D}^{3}=1.72\times 10^{9}\,T^{3/2}n^{-1/2}.}
- Отношение Альфвеновской скорости к скорости света
- vA/c=7.28μ−1/2ni−1/2B.{\displaystyle v_{A}/c=7.28\,\mu ^{-1/2}n_{i}^{-1/2}B.}
- Отношение плазменной и ларморовской частот для электрона
- ωpe/ωce=3.21×10−3ne1/2B−1.{\displaystyle \omega _{pe}/\omega _{ce}=3.21\times 10^{-3}\,n_{e}^{1/2}B^{-1}.}
- Отношение плазменной и ларморовской частот для иона
- ωpi/ωci=0.137μ1/2ni1/2B−1.{\displaystyle \omega _{pi}/\omega _{ci}=0.137\,\mu ^{1/2}n_{i}^{1/2}B^{-1}.}
- Отношение тепловой и магнитной энергий
- β=8πnkT/B2=4.03×10−11nTB−2.{\displaystyle \beta =8\pi nkT/B^{2}=4.03\times 10^{-11}\,nTB^{-2}.}
- Отношение магнитной энергии к энергии покоя ионов
- B2/8πnimic2=26.5μ−1ni−1B2.{\displaystyle B^{2}/8\pi n_{i}m_{i}c^{2}=26.5\,\mu ^{-1}n_{i}^{-1}B^{2}.}
Прочее
- Бомовский коэффициент диффузии
- DB=(ckT/16eB)=5.4×102TB−1cm2/s.{\displaystyle D_{B}=(ckT/16eB)=5.4\times 10^{2}\,TB^{-1}\,{\mbox{cm}}^{2}/{\mbox{s}}.}
- Поперечное сопротивление Спитцера
- η⊥=1.15×10−14ZlnΛT−3/2s=1.03×10−2ZlnΛT−3/2Ωcm.{\displaystyle \eta _{\perp }=1.15\times 10^{-14}\,Z\,\ln \Lambda \,T^{-3/2}\,{\mbox{s}}=1.03\times 10^{-2}\,Z\,\ln \Lambda \,T^{-3/2}\,\Omega \,{\mbox{cm}}.}
Современные исследования
См. также
Примечания
Литература
Ссылки
wiki.sc
Plazma — Википедия
Plazma (оригин. PLAZMA) — российская музыкальная группа, работающая в жанрах от синти-попа и евродэнса до поп-рока[2]. Одна из первых начала исполнять песни исключительно на английском языке для русскоговорящей аудитории[1].
Бессменными участниками коллектива являются Роман Черницын (вокалист, композитор, автор текстов) и Максим Постельный (клавишник, бэк-вокалист, композитор, аранжировщик), в концертах также периодически принимают участие музыканты Александр Лучков (скрипач, гитарист) и Николай Трофимов (гитарист).
Известность группа приобрела после выпуска первого сингла «Take My Love», который стал активным участником многих радийных чартов. Первые два альбома — Take My Love и 607 — были проданы тиражом более чем в 1 миллион копий. Также Plazma получила премию Попова за наибольшее количество радиоэфиров[3].
Plazma является участником финала отборочного тура международного конкурса «Евровидение-2009», в котором исполнила композицию «Never Ending Story». Также группа подавала заявку на участие в 2007 и 2010 годах с композициями «Living in the Past» и «Mystery (The Power Within)» соответственно.
История группы
Период Slow Motion
Осенью 1986 года Роман Черницын был принят в качестве вокалиста в музыкальную группу при Доме учителя в городе Волгограде. Также членами коллектива были два его одноклассника — Сергей Стародуб (гитара) и Роман Рыбин (звук) — а также Алексей Воронков (ударные) и Николай Романов (бас-гитара). Руководителем и автором всего музыкального материала был Андрей Трясучёв.
В 1990 году коллектив распался. Трое бывших участников: Роман Черницын, Максим Постельный и Николай Романов — создали группу Slow Motion («Медленное движение»), взяв в качестве названия одну из песен Modern Talking с их альбома «In The Garden Of Venus». Уже тогда членами коллектива было принято решение, что все песни из репертуара будут исполняться только на английском языке[4]. По словам самих музыкантов, это объясняется тем, что они являются поклонниками западной прогрессивной музыки, основная часть которой исполняется на английском языке и стремлением показать, что в России тоже могут делать качественную музыку.
| В любой стране существуют англоязычные группы — в Швеции — около 45%, в Германии — 25%, и это нормально. В России пока никто не поет на английском, мы стали первыми. |
В том же году в студии Волгоградского училища культуры группа записала основную часть всего музыкального материала для своего первого альбома, записанного с аранжировщиком Андреем Жигуновым и звукорежиссёром Вячеславом Тимировым. Альбом Falling In Love («Влюбляясь») вышел в 1991 году. К тому времени группу уже покинул Николай Романов. В том же году на две композиции из первого альбома, одна из которых называлась Hungry for Love, при участии коллектива кабельного телевидения «Юг России» были сняты видеоклипы. С материалом первого альбома группа не раз выступала перед публикой. Работа Slow Motion была отмечена на волгоградских фестивалях: на I рок-старте в 1991 году коллектив занял второе место, на II рок-старте в 1992 году — первое.
В период со второй половины 1992 по начало 1993 года из-за творческого бездействия группы, Черницын устроился работать на завод «Спецэнергоремонт», а Постельный продолжал учиться в училище искусств. После того, как кассета с записями Slow Motion попала в руки на тот момент генерального директора внешнеторгового дома «Хелп» Сергея Ивановича Олейника, Олейник решил спонсировать дуэт и оказывать им всяческую поддержку. Вскоре группа получила приглашение принять участие в программе «Звёздный дождь» на телеканале РТР.
После этого у Slow Motion появился свой продюсер[4]. Им стал Анатолий Аболихин, который работал с Дмитрием Маликовым. В 1993 году группа перезаписала несколько старых и записала ещё несколько новых песен в Волгоградских студиях. В Москве была записана обновлённая версия Take My Love. Режиссёром Михаилом Макаренковым был снят клип на песню Climb any hill.
Во время своего творческого отпуска, в котором находилась группа, начиная с 1994 года, Черницын и Постельный стали работать на студии радиостанции «Магнат», основанной Олейником.
В 1995 году Черницын был приглашён в качестве временного вокалиста в рок-группу Casus Belli, заменив покинувшего коллектив Николая Крупатина. Результатом сотрудничества стал альбом Vae Victis!.. («Горе побеждённым»). Находясь в составе группы, Черницын исполнил две песни на русском языке[4]. Композиция I’m Out была записана уже как дуэт групп Casus Belli и Slow Motion. Сотрудничество с Casus Belli продолжалось до конца 1996 года.
На протяжении всего 1997 года группа продолжала записывать новый материал и выступать в клубах. Коллектив стал одним из самых известных в Волгограде[4]. Летом 1997 года наряду с другими волгоградскими коллективами: «Например» и «Штурманом Жорж» — Slow Motion обратились к хозяину «Союза-Паритета А», чтобы тот показал их записи ZeKo Records. Представители компании пожелали заключить с дуэтом контракт[4], но предложили им прежде перепеть несколько песен на русском и взять русское название. В итоге название осталось тем же, но к двум композициям — Take My Love и Jump In My Car — были написаны русские тексты. Успеха этот эксперимент не имел[4].
В марте 1998 года был дописан альбом Prologue. Наконец подготовив полноценную программу, члены группы решили переехать в Москву. Прежде чем окончательно покинуть Волгоград, коллектив решил провести сольный концерт. Но, боясь, что существующего материала будет недостаточно для реализации задуманного, Slow Motion выступили в Доме офицеров вместе с домом моды «Харита». По идее, показ моделей этого дома должен был проходить в перерывах между исполнениями песен, что существенно увеличило концертную программу. Мероприятие прошло с аншлагом[4].
Но после событий августа 1998 года переезд в Москву пришлось отложить. В декабре 1998 года альбом Prologue был выпущен в продажу. В него вошло 10 композиций, записанных в период с декабря 1996 по март 1998 годов, Take My Love образца 1994 года, а также композиция In My Little Room, в записи которой принимал участие бывший гитарист групп «Атолл» и «Хозяин ключа» Игорь Колобов.
После того как ситуация в стране стала постепенно стабилизироваться в конце января — начале февраля 1999 года дуэт переехал в Москву. В первое время пребывания в столице Максим Постельный работал звукорежиссёром на радио «Европа Плюс».
В 1999 году коллектив подписал контракт с Дмитрием Маликовым, который являлся их продюсером на протяжении последующих пяти лет. В том же году было изменено название группы на Plazma. Как объясняют сами участники коллектива, это было сделано для того, чтобы найти «яркое» и легко запоминающееся название[1]:
Просто мы искали яркое слово, которое звучало бы одинаково на всех языках и сразу запоминалось.
Период Plazma
Начала группа Plazma свою всероссийскую карьеру с сингла «Take My Love», написанного Романом и Максимом очень давно и перепетой на новый, современный лад. В 2000 году этот трек разрывал радио-чарты страны.
14 декабря 2000 года группа Plazma выпускает свой дебютный альбом под знакомым названием Take My Love. Сразу же после выхода диск стал лидером продаж по России. Популярность группы росла с огромной скоростью не только в родной стране, но и за её пределами. Plazma побывала с гастролями почти во всех странах ближнего зарубежья. В этом же году были сняты два клипа — «Take My Love» и «The Sweetest Surrender» (режиссёр Филипп Янковский).
В конце 2001 года был снят третий клип группы на композицию «Lonely». Съёмки проходили в узбекском ресторане «Ходжа Насреддин» при участии кошек породы «русская голубая» и очаровательных девушек. Следующим творением группы стала композиция «You’ll Never Meet an Angel», на которую в августе 2002 года был снят четвёртый видеоролик. По замыслу режиссёра Олега Гусева, в клипе принял участие и сам продюсер группы Plazma Дмитрий Маликов в роли некоего босса, который курит сигару и держит свою личность в тайне от посторонних глаз. В результате получился настоящий боевик.
В конце 2002 года выходит второй альбом под загадочным названием 607, смысл которого до сих пор остается тайной. В отличие от танцевального «Take My Love», в стилистике «607» преобладает серьёзная музыка. Альбом очень лиричен, и песни явились настоящим шагом вперед в творчестве группы.
В начале 2003 года Роман и Максим приглашают в свой коллектив гитариста Николая Трофимова, с которым ребята знакомы ещё по совместным волгоградским проектам (таким как Slow Motion и Casus Belli). География гастрольного тура ещё более расширилась — группа побывала во Вьетнаме, а также во многих европейских странах: Финляндии, Франции, Прибалтике.
Предпосылкам третьего альбома под названием Black & White стала пронзительная лирическая баллада «Save». Главным хитом из альбома стал трек «Black Would Be White». На сингл «One Life» был снят клип. Его режиссёр Кевин Джексон снял красивую историю спасения больной девушки, которая лежит в стеклянной камере, изолированная от мира, и надеется лишь на чудо. И, конечно же, этим чудом, побеждающим смерть, становится Любовь. Большой интерес к композиции «Living in the Past» проявили иностранные диджеи — на этот трек было создано огромное количество ремиксов.
В 2007 году группа записала свою вторую композицию на русском языке — «Бумажное небо» совместно с Алёной Водонаевой. Вопреки распространённому мнению, участницей группы Алёна не являлась[5]. Первой была русскоязычная версия песни «Black Would Be White» — «И даже светом станет тьма…»
В начале 2009 года Plazma проходит в финал отборочного тура «Евровидение 2009» с песней «Never Ending Story», но победа досталась другому участнику. В конце того же года был записан трек «The Real Song».
Также в конце 2009 года выходит композиция «Mystery (The Power Within)». В марте 2010 года был снят клип на эту песню, презентация которого состоялась в клубе «XXXX» (г. Москва, филиал МосConcert). В июне 2011 года вышла композиция группы под названием «Angel of Snow»[6], релиз которой в качестве сингла состоялся 28 марта 2012 года[7]. 30 октября 2013 года группа выпустила очередной сингл — «Black Leather Boys»[8]. В ноябре 2014 года в эфире радиостанции «Пионер FM» прозвучала композиция «Lucky Rider», которая стала доступна в качестве сингла 15 июня 2015 года[9]. 21 августа того же года на радиостанции «Кекс FM» состоялась премьера композиции «Tame Your Ghosts»[10], вышедшей в качестве сингла 31 августа[11]. 8 декабря 2017 года вышел в свет четвёртый альбом под названием Indian Summer[12].
Видео по теме
Участники
Основной состав
Дополнительный концертный состав
Бывшие участники
Дискография
Альбомы
Сборники и переиздания
Синглы
|
|
Видеоклипы
Примечания
Ссылки
wiki2.red
Плазма — Википедия

Пла́зма (от греч. πλάσμα «вылепленное», «оформленное») — частично или полностью ионизированный газ, образованный из нейтральных атомов (или молекул) и заряженных частиц (ионов и электронов). Важнейшей особенностью плазмы является её квазинейтральность, это означает, что объемные плотности положительных и отрицательных заряженных частиц, из которых она образована, оказываются почти одинаковыми. Плазма иногда называется четвёртым (после твёрдого, жидкого и газообразного) агрегатным состоянием вещества.
Слово «ионизированный» означает, что от электронных оболочек значительной части атомов или молекул отделён по крайней мере один электрон. Слово «квазинейтральный» означает, что, несмотря на наличие свободных зарядов (электронов и ионов), суммарный электрический заряд плазмы приблизительно равен нулю. Присутствие свободных электрических зарядов делает плазму проводящей средой, что обуславливает её заметно большее (по сравнению с другими агрегатными состояниями вещества) взаимодействие с магнитным и электрическим полями. Четвёртое состояние вещества было открыто У. Круксом в 1879 году и названо «плазмой» И. Ленгмюром в 1928 году, возможно из-за ассоциации с плазмой крови. Ленгмюр писал:
Исключая пространство около электродов, где обнаруживается небольшое количество электронов, ионизированный газ содержит ионы и электроны практически в одинаковых количествах, в результате чего суммарный заряд системы очень мал. Мы используем термин «плазма», чтобы описать эту в целом электрически нейтральную область, состоящую из ионов и электронов.
Философы античности, начиная с Эмпедокла, утверждали, что мир состоит из четырёх стихий: земли, воды, воздуха и огня. Это положение с учётом некоторых допущений укладывается в представление о четырёх агрегатных состояниях вещества, причем плазме, очевидно, соответствует огонь[1]. Свойства плазмы изучает физика плазмы.
По сегодняшним представлениям, фазовым состоянием большей части барионного вещества (по массе ок. 99,9 %) во Вселенной является плазма.[2] Все звёзды состоят из плазмы, и даже пространство между ними заполнено плазмой, хотя и очень разреженной (см. межзвездное пространство). К примеру, планета Юпитер сосредоточила в себе практически все вещество Солнечной системы, находящееся в «неплазменном» состоянии (жидком, твердом и газообразном). При этом масса Юпитера составляет всего лишь около 0,1 % массы Солнечной системы, а объём — и того меньше: всего 10−15 %. При этом мельчайшие частицы пыли, заполняющие космическое пространство и несущие на себе определенный электрический заряд, в совокупности могут быть рассмотрены как плазма, состоящая из сверхтяжелых заряженных ионов (см. пылевая плазма).
Свойства и параметры плазмы[править]
Определение плазмы[править]
Плазма — частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.[4] Не всякую систему заряженных частиц можно назвать плазмой. Плазма обладает следующими свойствами:[5][6][7]
- Достаточная плотность: заряженные частицы должны находиться достаточно близко друг к другу, чтобы каждая из них взаимодействовала с целой системой близкорасположенных заряженных частиц. Условие считается выполненным, если число заряженных частиц в сфере влияния (сфера радиусом Дебая) достаточно для возникновения коллективных эффектов (подобные проявления — типичное свойство плазмы). Математически это условие можно выразить так:
- , где — концентрация заряженных частиц.
- Приоритет внутренних взаимодействий: радиус дебаевского экранирования должен быть мал по сравнению с характерным размером плазмы. Этот критерий означает, что взаимодействия, происходящие внутри плазмы более значительны по сравнению с эффектами на её поверхности, которыми можно пренебречь. Если это условие соблюдено, плазму можно считать квазинейтральной. Математически оно выглядит так:
- Плазменная частота: среднее время между столкновениями частиц должно быть велико по сравнению с периодом плазменных колебаний. Эти колебания вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд проходит по инерции это положение, что опять приводит к появлению сильного возвращающего поля, возникают типичные механические колебания.[8] Когда данное условие соблюдено, электродинамические свойства плазмы преобладают над молекулярно-кинетическими. На языке математики это условие имеет вид:
Классификация[править]
Плазма обычно разделяется на идеальную и неидеальную, низкотемпературную и высокотемпературную, равновесную и неравновесную, при этом довольно часто холодная плазма бывает неравновесной, а горячая равновесной.
Температура[править]
Плазму делят на низкотемпературную (температура меньше миллиона K) и высокотемпературную (температура миллион K и выше). Такое деление обусловлено важностью высокотемпературной плазмы в проблеме осуществления управляемого термоядерного синтеза. Разные вещества переходят в состояние плазмы при разной температуре, что объясняется строением внешних электронных оболочек атомов вещества: чем легче атом отдает электрон, тем ниже температура перехода в плазменное состояние[9].
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией. Такая ситуация встречается в газовых разрядах, когда ионы имеют температуру около сотен, а электроны около десятков тысяч K.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Степень и кратность ионизации[править]
Для того, чтобы газ перешел в состояние плазмы, его необходимо ионизовать. Степень ионизации пропорциональна числу атомов, отдавших или поглотивших электроны, и больше всего зависит от температуры. Даже слабо ионизированный газ, в котором менее 1 % частиц находятся в ионизированном состоянии, может проявлять некоторые типичные свойства плазмы (взаимодействие с внешним электромагнитным полем и высокая электропроводность). Степень ионизации α определяется как α = ni/(ni + na), где ni — концентрация ионов, а na — концентрация нейтральных атомов. Концентрация свободных электронов в незаряженной плазме ne определяется очевидным соотношением: ne=<Z>ni, где <Z> — среднее значение заряда ионов плазмы, или кратность ионизации плазмы. Очевидно, что максимальное значение α равно 1 (или 100 %), такую плазму называют полностью ионизованной.
Для низкотемпературной плазмы характерна малая степень ионизации (до 1 %). Так как такие плазмы довольно часто употребляются в технологических процессах, их иногда называют технологичными плазмами. Чаще всего их создают при помощи электрических полей, ускоряющих электроны, которые в свою очередь ионизируют атомы. Электрические поля вводятся в газ посредством индуктивной или емкостной связи (см. индуктивно-связанная плазма). Типичные применения низкотемпературной плазмы включают плазменную модификацию свойств поверхности (алмазные пленки, нитридирование металлов, изменение смачиваемости), плазменное травление поверхностей (полупроводниковая промышленность), очистку газов и жидкостей (озонирование воды и сжигание частичек сажи в дизельных двигателях).
Горячая плазма почти всегда полностью ионизирована (степень ионизации ~100 %). Обычно именно она понимается под «четвертым агрегатным состоянием вещества». Примером может служить Солнце.
Концентрация частиц в плазме[править]
Помимо температуры, которая имеет фундаментальную важность для самого существования плазмы, вторым наиболее важным свойством плазмы является концентрация заряженных частиц. Словосочетание концентрация плазмы обычно обозначает концентрация электронов, то есть число свободных электронов в единице объёма. В квазинейтральной плазме концентрация ионов связана с ней посредством среднего зарядового числа ионов : . Следующей важной величиной является концентрация нейтральных атомов . В горячей плазме мала, но может тем не менее быть важной для физики процессов в плазме. При рассмотрении процессов в плотной, неидеальной плазме характерным параметром концентрации становится , который определяется как отношение среднего межчастичного расстояния к радиусу Бора.
Квазинейтральность[править]
Так как плазма является очень хорошим проводником, электрические свойства имеют важное значение. Потенциалом плазмы или потенциалом пространства называют среднее значение электрического потенциала в данной точке пространства. В случае если в плазму внесено какое-либо тело, его потенциал в общем случае будет меньше потенциала плазмы вследствие возникновения дебаевского слоя. Такой потенциал называют плавающим потенциалом. По причине хорошей электрической проводимости плазма стремится экранировать все электрические поля. Это приводит к явлению квазинейтральности — плотность отрицательных зарядов с хорошей точностью равна плотности положительных зарядов (). В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний.
Примером неквазинейтральной плазмы является пучок электронов. Однако плотность не-нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.
Отличия от газообразного состояния[править]
Плазму часто называют четвертым состоянием вещества. Она отличается от трёх менее энергетичных агрегатных состояний материи, хотя и похожа на газовую фазу тем, что не имеет определённой формы или объёма. До сих пор идёт обсуждение того, является ли плазма отдельным агрегатным состоянием, или же просто горячим газом. Большинство физиков считает, что плазма является чем-то большим, чем газ по причине следующих различий:
| Свойство | Газ | Плазма |
|---|---|---|
| Электрическая проводимость | Крайне мала К примеру, воздух является превосходным изолятором до тех пор, пока не переходит в плазменное состояние под действием внешнего электрического поля напряженностью в 30 киловольт на сантиметр.[10] |
Очень высока
|
| Число сортов частиц | Один Газы состоят из подобных друг другу частиц, которые находятся в тепловом движении, а также движутся под действием гравитации, а друг с другом взаимодействуют только на сравнительно небольших расстояниях. |
Два, или три, или более Электроны, ионы и нейтральные частицы различаются знаком эл. заряда и могут вести себя независимо друг от друга — иметь разные скорости и даже температуры, что служит причиной появления новых явлений, например волн и неустойчивостей. |
| Распределение по скоростям | Максвелловское Столкновения частиц друг с другом приводит к максвелловскому распределению скоростей, согласно которому очень малая часть молекул газа имеют относительно большие скорости движения. |
Может быть немаксвелловское Электрические поля имеют другое влияние на скорости частиц чем столкновения, которые всегда ведут к максвеллизации распределения по скоростям. Зависимость сечения кулоновских столкновений от скорости может усиливать это различие, приводя к таким эффектам, как двухтемпературные распределения и убегающие электроны. |
| Тип взаимодействий | Бинарные Как правило двухчастичные столкновения, трёхчастичные крайне редки. |
Коллективные Каждая частица взаимодействует сразу со многими. Эти коллективные взаимодействия имеют гораздо большее влияние чем двухчастичные. |
Сложные плазменные явления[править]
Хотя основные уравнения, описывающие состояния плазмы, относительно просты, в некоторых ситуациях они не могут адекватно отражать поведение реальной плазмы: возникновение таких эффектов — типичное свойство сложных систем, если использовать для их описания простые модели. Наиболее сильное различие между реальным состоянием плазмы и её математическим описанием наблюдается в так называемых пограничных зонах, где плазма переходит из одного физического состояния в другое (например, из состояния с низкой степенью ионизации в высокоионизационное). Здесь плазма не может быть описана с использованием простых гладких математических функций или с применением вероятностного подхода. Такие эффекты как спонтанное изменение формы плазмы являются следствием сложности взаимодействия заряженных частиц, из которых состоит плазма. Подобные явления интересны тем, что проявляются резко и не являются устойчивыми. Многие из них были изначально изучены в лабораториях, а затем были обнаружены во Вселенной.
Математическое описание[править]
Плазму можно описывать на различных уровнях детализации. Обычно плазма описывается отдельно от электромагнитных полей. Совместное описание проводящей жидкости и электромагнитных полей даётся в теории магнитогидродинамических явлений или МГД теории.
Флюидная (жидкостная) модель[править]
Во флюидной модели электроны описываются в терминах плотности, температуры и средней скорости. В основе модели лежат: уравнение баланса для плотности, уравнение сохранения импульса, уравнение баланса энергии электронов. В двухжидкостной модели таким же образом рассматриваются ионы.
Кинетическое описание[править]
Иногда жидкостная модель оказывается недостаточной для описания плазмы. Более подробное описание даёт кинетическая модель, в которой плазма описывается в терминах функции распределения электронов по координатам и импульсам. В основе модели лежит уравнение Больцмана. Уравнение Больцмана неприменимо для описания плазмы заряженных частиц с кулоновским взаимодействием вследствие дальнодействующего характера кулоновских сил. Поэтому для описания плазмы с кулоновским взаимодействием используется уравнение Власова с самосогласованным электромагнитным полем, созданным заряженными частицами плазмы. Кинетическое описание необходимо применять в случае отсутствия термодинамического равновесия либо в случае присутствия сильных неоднородностей плазмы.
Particle-In-Cell (частица в ячейке)[править]
Модели Particle-In-Cell используются для численного решения кинетических уравнений. Они включают в себя кинетическую информацию путём слежения за траекториями большого числа отдельных квазичастиц, каждая из которых отвечает некоторому числу реальных частиц (интегралу от функции распределения по ограниченной в фазовом пространстве области). Плотности электрического заряда и тока определяются путём суммирования заряда и квазичастиц в ячейках, которые малы по сравнению с рассматриваемой задачей, но, тем не менее, содержат большое число квазичастиц. Электрическое и магнитное поля находятся из плотностей зарядов и токов на границах ячеек. Не стоит путать модели PIC с прямым интегрированием уравнений движения реальных частиц, из которых состоит плазма — электронов и ионов — поскольку общее число квазичастиц в PIC-моделях, как правило, на много порядков меньше.
Базовые характеристики плазмы[править]
Все величины даны в Гауссовых СГС единицах за исключением температуры, которая дана в eV и массы ионов, которая дана в единицах массы протона ; Z — зарядовое число; k — постоянная Больцмана; К — длина волны; γ — адиабатический индекс; ln Λ — Кулоновский логарифм.
Частоты[править]
- Ларморова частота электрона, угловая частота кругового движения электрона в плоскости перпендикулярной магнитному полю:
- Ларморова частота иона, угловая частота кругового движения иона в плоскости перпендикулярной магнитному полю:
- плазменная частота (частота плазменных колебаний), частота с которой электроны колеблются около положения равновесия, будучи смещенными относительно ионов:
- ионная плазменная частота:
- частота столкновений электронов
- частота столкновений ионов
Длины[править]
- Де-Бройлева длина волны электрона, длина волны электрона в квантовой механике:
- минимальное расстояние сближения в классическом случае, минимальное расстояние на которое могут сблизиться две заряженных частицы при лобовом столкновении и начальной скорости, соответствующей температуре частиц, в пренебрежении квантово-механическими эффектами:
- гиромагнитный радиус электрона, радиус кругового движения электрона в плоскости перпендикулярной магнитному полю:
- гиромагнитный радиус иона, радиус кругового движения иона в плоскости перпендикулярной магнитному полю:
- размер скин-слоя плазмы, расстояние на которое электромагнитные волны могут проникать в плазму:
- Радиус Дебая (длина Дебая), расстояние на котором электрические поля экранируются за счёт перераспределения электронов:
Скорости[править]
- тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:
- скорость ионного звука, скорость продольных ионно-звуковых волн:
Безразмерные величины[править]
- квадратный корень из отношения масс электрона и протона:
- Число частиц в сфере Дебая:
- Отношение Альфвеновской скорости к скорости света
- отношение плазменной и ларморовской частот для электрона
- отношение плазменной и ларморовской частот для иона
- отношение тепловой и магнитной энергий
- отношение магнитной энергии к энергии покоя ионов
Прочее[править]
- Бомовский коэффициент диффузии
- Поперечное сопротивление Спитцера
Современные исследования[править]
www.wikiznanie.ru
Плазма — Википедия

Пла́зма (от греч. πλάσμα «вылепленное», «оформленное») — частично или полностью ионизированный газ, образованный из нейтральных атомов (или молекул) и заряженных частиц (ионов и электронов). Важнейшей особенностью плазмы является её квазинейтральность, это означает, что объемные плотности положительных и отрицательных заряженных частиц, из которых она образована, оказываются почти одинаковыми. Плазма иногда называется четвёртым (после твёрдого, жидкого и газообразного) агрегатным состоянием вещества.
Слово «ионизированный» означает, что от электронных оболочек значительной части атомов или молекул отделён по крайней мере один электрон. Слово «квазинейтральный» означает, что, несмотря на наличие свободных зарядов (электронов и ионов), суммарный электрический заряд плазмы приблизительно равен нулю. Присутствие свободных электрических зарядов делает плазму проводящей средой, что обуславливает её заметно большее (по сравнению с другими агрегатными состояниями вещества) взаимодействие с магнитным и электрическим полями. Четвёртое состояние вещества было открыто У. Круксом в 1879 году и названо «плазмой» И. Ленгмюром в 1928 году, возможно из-за ассоциации с плазмой крови. Ленгмюр писал:
Исключая пространство около электродов, где обнаруживается небольшое количество электронов, ионизированный газ содержит ионы и электроны практически в одинаковых количествах, в результате чего суммарный заряд системы очень мал. Мы используем термин «плазма», чтобы описать эту в целом электрически нейтральную область, состоящую из ионов и электронов.
Философы античности, начиная с Эмпедокла, утверждали, что мир состоит из четырёх стихий: земли, воды, воздуха и огня. Это положение с учётом некоторых допущений укладывается в представление о четырёх агрегатных состояниях вещества, причем плазме, очевидно, соответствует огонь[1]. Свойства плазмы изучает физика плазмы.
По сегодняшним представлениям, фазовым состоянием большей части барионного вещества (по массе ок. 99,9 %) во Вселенной является плазма.[2] Все звёзды состоят из плазмы, и даже пространство между ними заполнено плазмой, хотя и очень разреженной (см. межзвездное пространство). К примеру, планета Юпитер сосредоточила в себе практически все вещество Солнечной системы, находящееся в «неплазменном» состоянии (жидком, твердом и газообразном). При этом масса Юпитера составляет всего лишь около 0,1 % массы Солнечной системы, а объём — и того меньше: всего 10−15 %. При этом мельчайшие частицы пыли, заполняющие космическое пространство и несущие на себе определенный электрический заряд, в совокупности могут быть рассмотрены как плазма, состоящая из сверхтяжелых заряженных ионов (см. пылевая плазма).
Свойства и параметры плазмы[править]
Определение плазмы[править]
Плазма — частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.[4] Не всякую систему заряженных частиц можно назвать плазмой. Плазма обладает следующими свойствами:[5][6][7]
- Достаточная плотность: заряженные частицы должны находиться достаточно близко друг к другу, чтобы каждая из них взаимодействовала с целой системой близкорасположенных заряженных частиц. Условие считается выполненным, если число заряженных частиц в сфере влияния (сфера радиусом Дебая) достаточно для возникновения коллективных эффектов (подобные проявления — типичное свойство плазмы). Математически это условие можно выразить так:
- , где — концентрация заряженных частиц.
- Приоритет внутренних взаимодействий: радиус дебаевского экранирования должен быть мал по сравнению с характерным размером плазмы. Этот критерий означает, что взаимодействия, происходящие внутри плазмы более значительны по сравнению с эффектами на её поверхности, которыми можно пренебречь. Если это условие соблюдено, плазму можно считать квазинейтральной. Математически оно выглядит так:
- Плазменная частота: среднее время между столкновениями частиц должно быть велико по сравнению с периодом плазменных колебаний. Эти колебания вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд проходит по инерции это положение, что опять приводит к появлению сильного возвращающего поля, возникают типичные механические колебания.[8] Когда данное условие соблюдено, электродинамические свойства плазмы преобладают над молекулярно-кинетическими. На языке математики это условие имеет вид:
Классификация[править]
Плазма обычно разделяется на идеальную и неидеальную, низкотемпературную и высокотемпературную, равновесную и неравновесную, при этом довольно часто холодная плазма бывает неравновесной, а горячая равновесной.
Температура[править]
Плазму делят на низкотемпературную (температура меньше миллиона K) и высокотемпературную (температура миллион K и выше). Такое деление обусловлено важностью высокотемпературной плазмы в проблеме осуществления управляемого термоядерного синтеза. Разные вещества переходят в состояние плазмы при разной температуре, что объясняется строением внешних электронных оболочек атомов вещества: чем легче атом отдает электрон, тем ниже температура перехода в плазменное состояние[9].
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией. Такая ситуация встречается в газовых разрядах, когда ионы имеют температуру около сотен, а электроны около десятков тысяч K.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Степень и кратность ионизации[править]
Для того, чтобы газ перешел в состояние плазмы, его необходимо ионизовать. Степень ионизации пропорциональна числу атомов, отдавших или поглотивших электроны, и больше всего зависит от температуры. Даже слабо ионизированный газ, в котором менее 1 % частиц находятся в ионизированном состоянии, может проявлять некоторые типичные свойства плазмы (взаимодействие с внешним электромагнитным полем и высокая электропроводность). Степень ионизации α определяется как α = ni/(ni + na), где ni — концентрация ионов, а na — концентрация нейтральных атомов. Концентрация свободных электронов в незаряженной плазме ne определяется очевидным соотношением: ne=<Z>ni, где <Z> — среднее значение заряда ионов плазмы, или кратность ионизации плазмы. Очевидно, что максимальное значение α равно 1 (или 100 %), такую плазму называют полностью ионизованной.
Для низкотемпературной плазмы характерна малая степень ионизации (до 1 %). Так как такие плазмы довольно часто употребляются в технологических процессах, их иногда называют технологичными плазмами. Чаще всего их создают при помощи электрических полей, ускоряющих электроны, которые в свою очередь ионизируют атомы. Электрические поля вводятся в газ посредством индуктивной или емкостной связи (см. индуктивно-связанная плазма). Типичные применения низкотемпературной плазмы включают плазменную модификацию свойств поверхности (алмазные пленки, нитридирование металлов, изменение смачиваемости), плазменное травление поверхностей (полупроводниковая промышленность), очистку газов и жидкостей (озонирование воды и сжигание частичек сажи в дизельных двигателях).
Горячая плазма почти всегда полностью ионизирована (степень ионизации ~100 %). Обычно именно она понимается под «четвертым агрегатным состоянием вещества». Примером может служить Солнце.
Концентрация частиц в плазме[править]
Помимо температуры, которая имеет фундаментальную важность для самого существования плазмы, вторым наиболее важным свойством плазмы является концентрация заряженных частиц. Словосочетание концентрация плазмы обычно обозначает концентрация электронов, то есть число свободных электронов в единице объёма. В квазинейтральной плазме концентрация ионов связана с ней посредством среднего зарядового числа ионов : . Следующей важной величиной является концентрация нейтральных атомов . В горячей плазме мала, но может тем не менее быть важной для физики процессов в плазме. При рассмотрении процессов в плотной, неидеальной плазме характерным параметром концентрации становится , который определяется как отношение среднего межчастичного расстояния к радиусу Бора.
Квазинейтральность[править]
Так как плазма является очень хорошим проводником, электрические свойства имеют важное значение. Потенциалом плазмы или потенциалом пространства называют среднее значение электрического потенциала в данной точке пространства. В случае если в плазму внесено какое-либо тело, его потенциал в общем случае будет меньше потенциала плазмы вследствие возникновения дебаевского слоя. Такой потенциал называют плавающим потенциалом. По причине хорошей электрической проводимости плазма стремится экранировать все электрические поля. Это приводит к явлению квазинейтральности — плотность отрицательных зарядов с хорошей точностью равна плотности положительных зарядов (). В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний.
Примером неквазинейтральной плазмы является пучок электронов. Однако плотность не-нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.
Отличия от газообразного состояния[править]
Плазму часто называют четвертым состоянием вещества. Она отличается от трёх менее энергетичных агрегатных состояний материи, хотя и похожа на газовую фазу тем, что не имеет определённой формы или объёма. До сих пор идёт обсуждение того, является ли плазма отдельным агрегатным состоянием, или же просто горячим газом. Большинство физиков считает, что плазма является чем-то большим, чем газ по причине следующих различий:
| Свойство | Газ | Плазма |
|---|---|---|
| Электрическая проводимость | Крайне мала К примеру, воздух является превосходным изолятором до тех пор, пока не переходит в плазменное состояние под действием внешнего электрического поля напряженностью в 30 киловольт на сантиметр.[10] |
Очень высока
|
| Число сортов частиц | Один Газы состоят из подобных друг другу частиц, которые находятся в тепловом движении, а также движутся под действием гравитации, а друг с другом взаимодействуют только на сравнительно небольших расстояниях. |
Два, или три, или более Электроны, ионы и нейтральные частицы различаются знаком эл. заряда и могут вести себя независимо друг от друга — иметь разные скорости и даже температуры, что служит причиной появления новых явлений, например волн и неустойчивостей. |
| Распределение по скоростям | Максвелловское Столкновения частиц друг с другом приводит к максвелловскому распределению скоростей, согласно которому очень малая часть молекул газа имеют относительно большие скорости движения. |
Может быть немаксвелловское Электрические поля имеют другое влияние на скорости частиц чем столкновения, которые всегда ведут к максвеллизации распределения по скоростям. Зависимость сечения кулоновских столкновений от скорости может усиливать это различие, приводя к таким эффектам, как двухтемпературные распределения и убегающие электроны. |
| Тип взаимодействий | Бинарные Как правило двухчастичные столкновения, трёхчастичные крайне редки. |
Коллективные Каждая частица взаимодействует сразу со многими. Эти коллективные взаимодействия имеют гораздо большее влияние чем двухчастичные. |
Сложные плазменные явления[править]
Хотя основные уравнения, описывающие состояния плазмы, относительно просты, в некоторых ситуациях они не могут адекватно отражать поведение реальной плазмы: возникновение таких эффектов — типичное свойство сложных систем, если использовать для их описания простые модели. Наиболее сильное различие между реальным состоянием плазмы и её математическим описанием наблюдается в так называемых пограничных зонах, где плазма переходит из одного физического состояния в другое (например, из состояния с низкой степенью ионизации в высокоионизационное). Здесь плазма не может быть описана с использованием простых гладких математических функций или с применением вероятностного подхода. Такие эффекты как спонтанное изменение формы плазмы являются следствием сложности взаимодействия заряженных частиц, из которых состоит плазма. Подобные явления интересны тем, что проявляются резко и не являются устойчивыми. Многие из них были изначально изучены в лабораториях, а затем были обнаружены во Вселенной.
Математическое описание[править]
Плазму можно описывать на различных уровнях детализации. Обычно плазма описывается отдельно от электромагнитных полей. Совместное описание проводящей жидкости и электромагнитных полей даётся в теории магнитогидродинамических явлений или МГД теории.
Флюидная (жидкостная) модель[править]
Во флюидной модели электроны описываются в терминах плотности, температуры и средней скорости. В основе модели лежат: уравнение баланса для плотности, уравнение сохранения импульса, уравнение баланса энергии электронов. В двухжидкостной модели таким же образом рассматриваются ионы.
Кинетическое описание[править]
Иногда жидкостная модель оказывается недостаточной для описания плазмы. Более подробное описание даёт кинетическая модель, в которой плазма описывается в терминах функции распределения электронов по координатам и импульсам. В основе модели лежит уравнение Больцмана. Уравнение Больцмана неприменимо для описания плазмы заряженных частиц с кулоновским взаимодействием вследствие дальнодействующего характера кулоновских сил. Поэтому для описания плазмы с кулоновским взаимодействием используется уравнение Власова с самосогласованным электромагнитным полем, созданным заряженными частицами плазмы. Кинетическое описание необходимо применять в случае отсутствия термодинамического равновесия либо в случае присутствия сильных неоднородностей плазмы.
Particle-In-Cell (частица в ячейке)[править]
Модели Particle-In-Cell используются для численного решения кинетических уравнений. Они включают в себя кинетическую информацию путём слежения за траекториями большого числа отдельных квазичастиц, каждая из которых отвечает некоторому числу реальных частиц (интегралу от функции распределения по ограниченной в фазовом пространстве области). Плотности электрического заряда и тока определяются путём суммирования заряда и квазичастиц в ячейках, которые малы по сравнению с рассматриваемой задачей, но, тем не менее, содержат большое число квазичастиц. Электрическое и магнитное поля находятся из плотностей зарядов и токов на границах ячеек. Не стоит путать модели PIC с прямым интегрированием уравнений движения реальных частиц, из которых состоит плазма — электронов и ионов — поскольку общее число квазичастиц в PIC-моделях, как правило, на много порядков меньше.
Базовые характеристики плазмы[править]
Все величины даны в Гауссовых СГС единицах за исключением температуры, которая дана в eV и массы ионов, которая дана в единицах массы протона ; Z — зарядовое число; k — постоянная Больцмана; К — длина волны; γ — адиабатический индекс; ln Λ — Кулоновский логарифм.
Частоты[править]
- Ларморова частота электрона, угловая частота кругового движения электрона в плоскости перпендикулярной магнитному полю:
- Ларморова частота иона, угловая частота кругового движения иона в плоскости перпендикулярной магнитному полю:
- плазменная частота (частота плазменных колебаний), частота с которой электроны колеблются около положения равновесия, будучи смещенными относительно ионов:
- ионная плазменная частота:
- частота столкновений электронов
- частота столкновений ионов
Длины[править]
- Де-Бройлева длина волны электрона, длина волны электрона в квантовой механике:
- минимальное расстояние сближения в классическом случае, минимальное расстояние на которое могут сблизиться две заряженных частицы при лобовом столкновении и начальной скорости, соответствующей температуре частиц, в пренебрежении квантово-механическими эффектами:
- гиромагнитный радиус электрона, радиус кругового движения электрона в плоскости перпендикулярной магнитному полю:
- гиромагнитный радиус иона, радиус кругового движения иона в плоскости перпендикулярной магнитному полю:
- размер скин-слоя плазмы, расстояние на которое электромагнитные волны могут проникать в плазму:
- Радиус Дебая (длина Дебая), расстояние на котором электрические поля экранируются за счёт перераспределения электронов:
Скорости[править]
- тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:
- скорость ионного звука, скорость продольных ионно-звуковых волн:
Безразмерные величины[править]
- квадратный корень из отношения масс электрона и протона:
- Число частиц в сфере Дебая:
- Отношение Альфвеновской скорости к скорости света
- отношение плазменной и ларморовской частот для электрона
- отношение плазменной и ларморовской частот для иона
- отношение тепловой и магнитной энергий
- отношение магнитной энергии к энергии покоя ионов
Прочее[править]
- Бомовский коэффициент диффузии
- Поперечное сопротивление Спитцера
Современные исследования[править]
www.wikiznanie.ru
Plazma — Википедия
К:ВП: Статьи без изображений (тип: )К:ВП: Статьи без изображений (указано в Викиданных)Plazma (оригин. PLAZMA) — музыкальная группа из России (город Волгоград). В её основной состав входят Роман Черницын (вокалист, музыка, тексты) и Максим Постельный (клавишные, бэк-вокал, музыка, аранжировки), концертный состав — Александр Лучков (скрипка, гитара) и Николай Трофимов (гитара).
Отличительной чертой этого коллектива является то, что они стали одной из первых российских поп-групп, исполняющих свои песни исключительно на английском языке для русскоговорящей аудитории[1]. Стиль исполнения колеблется от синти-попа до поп-рока[2].
Известность группа приобрела после выпуска первого сингла Take My Love, который стал активным участником многих радийных чартов. Первые два альбома — «Take My Love» и «607» — были проданы тиражом более чем в 1 000 000 копий.
Группа Plazma получила премию Попова за наибольшее количество радиоэфиров[3].
История группы[править]
Период Slow Motion[править]
Осенью 1986 года Роман Черницын был принят в качестве вокалиста в музыкальную группу при Доме учителя в городе Волгограде. Также членами коллектива были два его одноклассника — Сергей Стародуб (гитара) и Роман Рыбин (звук) — а также Алексей Воронков (ударные) и Николай Романов (бас-гитара). Руководителем и автором всего музыкального материала был Андрей Трясучёв.
В 1990 году коллектив распался. Трое бывших участников: Роман Черницын, Максим Постельный и Николай Романов — создали группу Slow Motion («Медленное движение»), взяв в качестве названия одну из песен Modern Talking с их альбома «In The Garden Of Venus». Уже тогда членами коллектива было принято решение, что все песни из репертуара будут исполняться только на английском языке[4]. По словам самих музыкантов, это объясняется тем, что они являются поклонниками западной прогрессивной музыки, основная часть которой исполняется на английском языке и стремлением показать, что в России тоже могут делать качественную музыку.
| В любой стране существуют англоязычные группы — в Швеции — около 45%, в Германии — 25%, и это нормально. В России пока никто не поет на английском, мы стали первыми. |
В том же году в студии Волгоградского училища культуры группа записала основную часть всего музыкального материала для своего первого альбома, записанного с аранжировщиком Андреем Жигуновым и звукорежиссёром Вячеславом Тимировым. Альбом Falling In Love («Влюбляясь») вышел в 1991 году. К тому времени группу уже покинул Николай Романов. В том же году на две композиции из первого альбома, одна из которых называлась Hungry for Love, при участии коллектива кабельного телевидения «Юг России» были сняты видеоклипы. С материалом первого альбома группа не раз выступала перед публикой. Работа Slow Motion была отмечена на волгоградских фестивалях: на I рок-старте в 1991 году коллектив занял второе место, на II рок-старте в 1992 году — первое.
В период со второй половины 1992 по начало 1993 года из-за творческого бездействия группы, Черницын устроился работать на завод «Спецэнергоремонт», а Постельный продолжал учиться в училище искусств. После того, как кассета с записями Slow Motion попала в руки на тот момент генерального директора внешнеторгового дома «Хелп» Сергея Ивановича Олейника, Олейник решил спонсировать дуэт и оказывать им всяческую поддержку. Вскоре группа получила приглашение принять участие в программе «Звёздный дождь» на телеканале РТР.
После этого у Slow Motion появился свой продюсер[4]. Им стал Анатолий Аболихин, который работал с Дмитрием Маликовым. В 1993 году группа перезаписала несколько старых и записала ещё несколько новых песен в Волгоградских студиях. В Москве была записана обновлённая версия Take My Love. Режиссёром Михаилом Макаренковым был снят клип на песню Climb any hill.
Во время своего творческого отпуска, в котором находилась группа, начиная с 1994 года, Черницын и Постельный стали работать на студии радиостанции «Магнат», основанной Олейником.
В 1995 году Черницын был приглашён в качестве временного вокалиста в рок-группу Casus Belli, заменив покинувшего коллектив Николая Крупатина. Результатом сотрудничества стал альбом Vae Victis!.. («Горе побеждённым»). Находясь в составе группы, Черницын исполнил две песни на русском языке[4]. Композиция I’m Out была записана уже как дуэт групп Casus Belli и Slow Motion. Сотрудничество с Casus Belli продолжалось до конца 1996 года.
На протяжении всего 1997 года группа продолжала записывать новый материал и выступать в клубах. Коллектив стал одним из самых известных в Волгограде[4]. Летом 1997 года наряду с другими волгоградскими коллективами: «Например» и «Штурманом Жорж» — Slow Motion обратились к хозяину «Союза-Паритета А», чтобы тот показал их записи ZeKo Records. Представители компании пожелали заключить с дуэтом контракт[4], но предложили им прежде перепеть несколько песен на русском и взять русское название. В итоге название осталось тем же, но к двум композициям — Take My Love и Jump In My Car — были написаны русские тексты. Успеха этот эксперимент не имел[4].
В марте 1998 года был дописан альбом Prologue. Наконец подготовив полноценную программу, члены группы решили переехать в Москву. Прежде чем окончательно покинуть Волгоград, коллектив решил провести сольный концерт. Но, боясь, что существующего материала будет недостаточно для реализации задуманного, Slow Motion выступили в Доме офицеров вместе с домом моды «Харита». По идее, показ моделей этого дома должен был проходить в перерывах между исполнениями песен, что существенно увеличило концертную программу. Мероприятие прошло с аншлагом[4].
Но после событий августа 1998 года переезд в Москву пришлось отложить. В декабре 1998 года альбом Prologue был выпущен в продажу. В него вошло 10 композиций, записанных в период с декабря 1996 по март 1998 годов, Take My Love образца 1994 года, а также композиция In My Little Room, в записи которой принимал участие бывший гитарист групп «Атолл» и «Хозяин ключа» Игорь Колобов.
После того как ситуация в стране стала постепенно стабилизироваться в конце января — начале февраля 1999 года дуэт переехал в Москву. В первое время пребывания в столице Максим Постельный работал звукорежиссёром на радио «Европа Плюс».
В 1999 году коллектив подписал контракт с Дмитрием Маликовым, который являлся их продюсером на протяжении последующих пяти лет. В том же году было изменено название группы на Plazma. Как объясняют сами участники коллектива, это было сделано для того, чтобы найти «яркое» и легко запоминающееся название[1]:
Просто мы искали яркое слово, которое звучало бы одинаково на всех языках и сразу запоминалось.
Период Plazma[править]
Начала группа Plazma свою всероссийскую карьеру с сингла «Take My Love», написанного Романом и Максимом очень давно и перепетой на новый, современный лад. В 2000 году этот трек разрывал радио-чарты страны.
14 декабря 2000 года группа Plazma выпускает свой дебютный альбом под знакомым названием «Take My Love». Сразу же после выхода диск стал лидером продаж по России. Популярность группы росла с огромной скоростью не только в родной стране, но и за её пределами. Plazma побывала с гастролями почти во всех странах ближнего зарубежья. В этом же году были сняты два клипа — «Take My Love» и «The Sweetest Surrender» (режиссёр Филипп Янковский).
В конце 2001 года был снят третий клип группы на композицию «Lonely». Съёмки проходили в узбекском ресторане «Ходжа Насреддин» при участии кошек породы «русская голубая» и очаровательных девушек. Следующим творением группы стала композиция «You’ll Never Meet an Angel», на которую в августе 2002 года был снят четвёртый видеоролик. По замыслу режиссёра Олега Гусева, в клипе принял участие и сам продюсер группы Plazma Дмитрий Маликов в роли некоего босса, который курит сигару и держит свою личность в тайне от посторонних глаз. В результате получился настоящий боевик.
В конце 2002 года выходит второй альбом под загадочным названием «607», смысл которого до сих пор остается тайной. В отличие от танцевального «Take My Love», в стилистике «607» преобладает серьёзная музыка. Альбом очень лиричен, и песни явились настоящим шагом вперед в творчестве группы.
В начале 2003 года Роман и Максим приглашают в свой коллектив гитариста Николая Трофимова, с которым ребята знакомы ещё по совместным волгоградским проектам (таким как Slow Motion и Casus Belli). География гастрольного тура ещё более расширилась — группа побывала во Вьетнаме, а также во многих европейских странах: Финляндии, Франции, Прибалтике.
Предпосылкам третьего альбома под названием «Black & White» стала пронзительная лирическая баллада «Save». Главным хитом из альбома стал трек «Black Would Be White». На сингл «One Life» был снят клип. Его режиссёр Кевин Джексон снял красивую историю спасения больной девушки, которая лежит в стеклянной камере, изолированная от мира, и надеется лишь на чудо. И, конечно же, этим чудом, побеждающим смерть, становится Любовь. Большой интерес к композиции «Living in the Past» проявили иностранные диджеи — на этот трек было создано огромное количество ремиксов.
В 2007 году группа записала свою единственную композицию на русском языке — «Бумажное небо» совместно с Алёной Водонаевой. Вопреки распространённому мнению, участницей группы Алёна не являлась[5].
В начале 2009 года Plazma проходит в финал отборочного тура «Евровидение 2009» с песней «Never ending story», но победа досталась другому участнику. В конце того же года был записан трек «The Real Song».
Также в конце 2009 года выходит композиция «Mystery (The Power Within)». В марте 2010 года был снят клип на эту песню, презентация которого состоялась в клубе «XXXX» (г. Москва, филиал МосConcert). В июне 2011 года вышла композиция группы под названием «Angel of Snow»[6], релиз которой в качестве сингла состоялся 28 марта 2012 года[7]. 30 октября 2013 года группа выпустила очередной сингл — «Black Leather Boys»[8]. В ноябре 2014 года в эфире радиостанции «Пионер FM» прозвучала композиция «Lucky Rider», которая стала доступна в качестве сингла 15 июня 2015 года[9]. 21 августа того же года на радиостанции «Кекс FM» состоялась премьера композиции «Tame Your Ghosts»[10], вышедшей в качестве сингла 31 августа[11].
Основной состав[править]
Концертный состав[править]
Бывшие участники[править]
Альбомы[править]
- 1991 — Falling in Love (в составе Slow Motion)[4][12]
- 1999 — Prologue (в составе Slow Motion)[4]
- 2000 — Take My Love
- 2002 — 607
- 2006 — Black & White
- TBA — Четвёртый студийный альбом (в производстве)[13]
Переиздания[править]
Синглы[править]
|
|
- ↑ 1,01,11,21,3 Кушаков, Олег Группа «Плазма» автографы до посинения. Аргументы и факты (31 июля 2001). Проверено 4 марта 2009. Архивировано из первоисточника 22 февраля 2012.
- ↑ Plazma. Last.fm. Проверено 23 января 2015.
- ↑ THE STORY(недоступная ссылка — история). www.plazma.ru. Проверено 3 марта 2009. Архивировано из первоисточника 12 апреля 2003.
- ↑ 4,004,014,024,034,044,054,064,074,084,094,10 Семисотнов, Евгений SLOW MOTION: как всё начиналось. Новая волна(недоступная ссылка — история). www.plazma.ru. — текст радиопередачи на официальном сайте группы. Проверено 4 марта 2009. Архивировано из первоисточника 31 марта 2004.
- ↑ Черный, Сергей Группа «Плазма» в Пензе: «Отбор на «Евровидение» — это комедия!». Комсомольская правда (13 апреля 2009). Проверено 23 января 2015.
- ↑ Plazma — Angel of Snow. YouTube. Проверено 23 января 2015.
- ↑ 7,07,1 Музыка — Angel Of Snow — Single (Plazma). iTunes. Проверено 23 января 2015.
- ↑ 8,08,1 Музыка — Black Leather Boys — Single (Plazma). iTunes. Проверено 23 января 2015.
- ↑ 9,09,1 Музыка — Lucky Rider — Single (Plazma). iTunes. Проверено 24 августа 2015.
- ↑ Слушай повтор эфира от 21-го августа с крутыми парнями из группы PLAZMA Максом Постельным и Романом Черницыным в «Бла-Бла Star Шоу» на Кекс FM!!!. Кекс FM. ВКонтакте. Проверено 22 августа 2015.
- ↑ 11,011,1 Музыка — Tame Your Ghosts — Single (Plazma). iTunes. Проверено 5 сентября 2015.
- ↑ Ваши мнения и впечатления от альбома Falling In Love (1991). Официальная группа ВКонтакте. Проверено 23 января 2015.
- ↑ PR-директор группы Евгений Вольтов: «Ребята пишут новый альбом…». Официальная группа ВКонтакте (9 ноября 2014). Проверено 2 января 2015.
- ↑ Музыка — Living In The Past — Single (Plazma). iTunes. Проверено 23 января 2015.
- ↑ PLAZMA — Official site — Видеоклипы. www.plazma.ru. Проверено 31 декабря 2014.
- ↑ 16,016,1 Разыскиваются клипы. Casus Belli & Slow Motion. Проверено 23 января 2015.
- ↑ Видеоклип Slow Motion — I Still Love You (1992). Официальная группа ВКонтакте. Проверено 23 января 2015.
- ↑ Slow Motion — I Still Love You. Casus Belli & Slow Motion. Проверено 23 января 2015.
| Plazma | |
|---|---|
|
Основной состав: Роман Черницын • Максим Постельный Концертный состав: Александр Лучков • Николай Трофимов Бывшие участники: Наталья Григорьева | |
| Студийные альбомы | Take My Love (2000) · 607 (2002) · Black & White (2006) |
| Переиздания | Take My Love + бонусы (2004) · Six Zero Seven — New Version (2004) |
| Синглы | «Take My Love» · «The Sweetest Surrender» · «Jump in My Car» · «Fading like a Rose» · «Lonely» · «You’ll Never Meet an Angel» · «Lonely II» · «One Life» · «One of a Kind» · «Save» · «Black Would Be White» · «Never Ending Story» · «The Real Song» · «Mystery (The Power Within)» · «Living in the Past» · «Angel of Snow» · «Black Leather Boys» · «Lucky Rider» · «Tame Your Ghosts» |
| Связанные проекты | Slow Motion · Casus Belli · Telegram · Navy |
| www.plazma.ru | |
www.wiki-wiki.ru
Плазма — WiKi
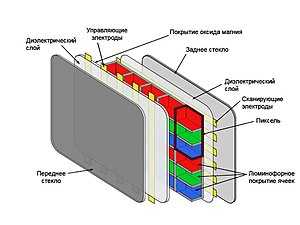 Плазменная лампа, иллюстрирующая некоторые из наиболее сложных плазменных явлений, включая филаментацию. Свечение плазмы обусловлено переходом электронов из высокоэнергетического состояния в состояние с низкой энергией после рекомбинации с ионами. Этот процесс приводит к излучению со спектром, соответствующим возбуждаемому газу.
Плазменная лампа, иллюстрирующая некоторые из наиболее сложных плазменных явлений, включая филаментацию. Свечение плазмы обусловлено переходом электронов из высокоэнергетического состояния в состояние с низкой энергией после рекомбинации с ионами. Этот процесс приводит к излучению со спектром, соответствующим возбуждаемому газу.
Пла́зма (от греч. πλάσμα «вылепленное, оформленное») — ионизованный газ, одно из четырёх основных агрегатных состояний вещества.
Ионизированный газ содержит свободные электроны и положительные и отрицательные ионы. В более широком смысле, плазма может состоять из любых заряженных частиц (например, кварк-глюонная плазма). Квазинейтральность означает, что суммарный заряд в любом малом по сравнению с размерами системы объёме равен нулю, является её ключевым отличием от других систем, содержащих заряженные частицы (например, электронные или ионные пучки). Поскольку при нагреве газа до достаточно высоких температур, он переходит в плазму, она называется четвёртым (после твёрдого, жидкого и газообразного) агрегатным состоянием вещества.
Поскольку частицы в газе обладают подвижностью, плазма обладает способностью проводить электрический ток. В стационарном случае плазма экранирует постоянное внешнее по отношению к ней электрическое поле за счёт пространственного разделения зарядов. Однако из-за наличия ненулевой температуры заряженных частиц существует минимальный масштаб, на расстояниях меньше которого квазинейтральность нарушается.
История открытия
Четвёртое состояние вещества было открыто У. Круксом в 1879 году и названо «плазмой» И. Ленгмюром в 1928 году. Ленгмюр писал[1]:
Исключая пространство около электродов, где обнаруживается небольшое количество электронов, ионизированный газ содержит ионы и электроны практически в одинаковых количествах, в результате чего суммарный заряд системы очень мал. Мы используем термин «плазма», чтобы описать эту в целом электрически нейтральную область, состоящую из ионов и электронов.
Древние философы полагали, что мир состоит из четырёх стихий: земли, воды, воздуха и огня. Можно сказать, что это положение с учетом некоторых допущений укладывается в современное представление о четырёх агрегатных состояниях вещества, причём плазме соответствует огонь. Свойства плазмы изучает физика плазмы.
Виды
По сегодняшним представлениям, фазовым состоянием большей части барионного вещества (по массе ок. 99,9 %) во Вселенной является плазма.[2] Все звёзды состоят из плазмы, и даже пространство между ними заполнено плазмой, хотя и очень разреженной (см. межзвёздное пространство). К примеру, планета Юпитер сосредоточила в себе практически всё вещество Солнечной системы, находящееся в «неплазменном» состоянии (жидком, твёрдом и газообразном). При этом масса Юпитера составляет всего лишь около 0,1 % массы Солнечной системы, а объём — и того меньше: всего 10−15 %. При этом мельчайшие частицы пыли, заполняющие космическое пространство и несущие на себе определённый электрический заряд, в совокупности могут быть рассмотрены как плазма, состоящая из сверхтяжёлых заряженных ионов (см. пылевая плазма).
Свойства и параметры
Определение плазмы
Плазма — частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.[4] Не всякую систему заряженных частиц можно назвать плазмой. Плазма обладает следующими свойствами:[5][6][7]
- Достаточная плотность: заряженные частицы должны находиться достаточно близко друг к другу, чтобы каждая из них взаимодействовала с целой системой близкорасположенных заряженных частиц. Условие считается выполненным, если число заряженных частиц в сфере влияния (сфера радиусом Дебая) достаточно для возникновения коллективных эффектов (подобные проявления — типичное свойство плазмы). Математически это условие можно выразить так:
- rD3N≫1,{\displaystyle r_{D}^{3}N\gg 1,}
- где N{\displaystyle N} — концентрация заряженных частиц.
- Приоритет внутренних взаимодействий: радиус дебаевского экранирования должен быть мал по сравнению с характерным размером плазмы. Этот критерий означает, что взаимодействия, происходящие внутри плазмы более значительны по сравнению с эффектами на её поверхности, которыми можно пренебречь. Если это условие соблюдено, плазму можно считать квазинейтральной. Математически оно выглядит так:
- rDL≪1.{\displaystyle {r_{D} \over L}\ll 1.}
- Плазменная частота: среднее время между столкновениями частиц должно быть велико по сравнению с периодом плазменных колебаний. Эти колебания вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд проходит по инерции это положение, что опять приводит к появлению сильного возвращающего поля, возникают типичные механические колебания.[8] Когда данное условие соблюдено, электродинамические свойства плазмы преобладают над молекулярно-кинетическими. На языке математики это условие имеет вид:
- τωpl≫1.{\displaystyle \tau \omega _{pl}\gg 1.}
Классификация
Плазма обычно разделяется на идеальную и неидеальную, низкотемпературную и высокотемпературную, равновесную и неравновесную, при этом довольно часто холодная плазма бывает неравновесной, а горячая равновесной.
Температура
Плазму делят на низкотемпературную (температура меньше миллиона K) и высокотемпературную (температура миллион K и выше). Такое деление обусловлено важностью высокотемпературной плазмы в проблеме осуществления управляемого термоядерного синтеза. Разные вещества переходят в состояние плазмы при разной температуре, что объясняется строением внешних электронных оболочек атомов вещества: чем легче атом отдает электрон, тем ниже температура перехода в плазменное состояние[9].
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией. Такая ситуация встречается в газовых разрядах, когда ионы имеют температуру около сотен, а электроны около десятков тысяч K.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Степень и кратность ионизации
Для того, чтобы газ перешёл в состояние плазмы, его необходимо ионизировать. Степень ионизации пропорциональна числу атомов, отдавших или поглотивших электроны, и больше всего зависит от температуры. Даже слабо ионизированный газ, в котором менее 1 % частиц находятся в ионизированном состоянии, может проявлять некоторые типичные свойства плазмы (взаимодействие с внешним электромагнитным полем и высокая электропроводность). Степень ионизации α определяется как α = ni /(ni + na), где ni — концентрация ионов, а na — концентрация нейтральных атомов. Концентрация свободных электронов в незаряженной плазме ne определяется очевидным соотношением: ne=<Z>ni, где <Z> — среднее значение заряда ионов плазмы, или кратность ионизации плазмы. Очевидно, что максимальное значение α равно 1 (или 100 %), такую плазму называют полностью ионизованной.
Для низкотемпературной плазмы характерна малая степень ионизации (до 1 %). Так как такие плазмы довольно часто употребляются в технологических процессах, их иногда называют технологичными плазмами. Чаще всего их создают при помощи электрических полей, ускоряющих электроны, которые в свою очередь ионизируют атомы. Электрические поля вводятся в газ посредством индуктивной или емкостной связи (см. индуктивно-связанная плазма). Типичные применения низкотемпературной плазмы включают плазменную модификацию свойств поверхности (алмазные плёнки, нитридирование металлов, изменение смачиваемости), плазменное травление поверхностей (полупроводниковая промышленность), очистку газов и жидкостей (озонирование воды и сжигание частичек сажи в дизельных двигателях).
Горячая плазма почти всегда полностью ионизирована (степень ионизации ~100 %). Обычно именно она понимается под «четвёртым агрегатным состоянием вещества». Примером может служить Солнце.
Концентрация частиц в плазме
Помимо температуры, которая имеет фундаментальную важность для самого существования плазмы, вторым наиболее важным свойством плазмы является концентрация заряженных частиц. Словосочетание концентрация плазмы обычно обозначает концентрация электронов, то есть число свободных электронов в единице объёма. В квазинейтральной плазме концентрация ионов связана с ней посредством среднего зарядового числа ионов ⟨Z⟩{\displaystyle \langle Z\rangle } : ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}} . Следующей важной величиной является концентрация нейтральных атомов n0{\displaystyle n_{0}} . В горячей плазме n0{\displaystyle n_{0}} мала, но может тем не менее быть важной для физики процессов в плазме. При рассмотрении процессов в плотной, неидеальной плазме характерным параметром концентрации становится rs{\displaystyle r_{s}} , который определяется как отношение среднего межчастичного расстояния к радиусу Бора.
Квазинейтральность
Так как плазма является очень хорошим проводником, электрические свойства имеют важное значение. Потенциалом плазмы или потенциалом пространства называют среднее значение электрического потенциала в данной точке пространства. В случае если в плазму внесено какое-либо тело, его потенциал в общем случае будет меньше потенциала плазмы вследствие возникновения дебаевского слоя. Такой потенциал называют плавающим потенциалом. По причине хорошей электрической проводимости плазма стремится экранировать все электрические поля. Это приводит к явлению квазинейтральности — плотность отрицательных зарядов с хорошей точностью равна плотности положительных зарядов (ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}} ). В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний.
Примером неквазинейтральной плазмы является пучок электронов. Однако плотность не-нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.
Отличия от газообразного состояния
Плазму часто называют четвёртым состоянием вещества. Она отличается от трёх менее энергетичных агрегатных состояний материи, хотя и похожа на газовую фазу тем, что не имеет определённой формы или объёма. До сих пор идёт обсуждение того, является ли плазма отдельным агрегатным состоянием, или же просто горячим газом. Большинство физиков считает, что плазма является чем-то большим, чем газ по причине следующих различий:
| Свойство | Газ | Плазма |
|---|---|---|
| Электрическая проводимость | Крайне мала К примеру, воздух является превосходным изолятором до тех пор, пока не переходит в плазменное состояние под действием внешнего электрического поля напряженностью в 30 киловольт на сантиметр.[10] |
Очень высока
|
| Число сортов частиц | Один Газы состоят из подобных друг другу частиц, которые находятся в тепловом движении, а также движутся под действием гравитации, а друг с другом взаимодействуют только на сравнительно небольших расстояниях. |
Два, или три, или более Электроны, ионы и нейтральные частицы различаются знаком эл. заряда и могут вести себя независимо друг от друга — иметь разные скорости и даже температуры, что служит причиной появления новых явлений, например волн и неустойчивостей. |
| Распределение по скоростям | Максвелловское Столкновения частиц друг с другом приводит к максвелловскому распределению скоростей, согласно которому очень малая часть молекул газа имеют относительно большие скорости движения. |
Может быть немаксвелловское Электрические поля имеют другое влияние на скорости частиц чем столкновения, которые всегда ведут к максвеллизации распределения по скоростям. Зависимость сечения кулоновских столкновений от скорости может усиливать это различие, приводя к таким эффектам, как двухтемпературные распределения и убегающие электроны. |
| Тип взаимодействий | Бинарные Как правило двухчастичные столкновения, трёхчастичные крайне редки. |
Коллективные Каждая частица взаимодействует сразу со многими. Эти коллективные взаимодействия имеют гораздо большее влияние чем двухчастичные. |
Сложные плазменные явления
Хотя основные уравнения, описывающие состояния плазмы, относительно просты, в некоторых ситуациях они не могут адекватно отражать поведение реальной плазмы: возникновение таких эффектов — типичное свойство сложных систем, если использовать для их описания простые модели. Наиболее сильное различие между реальным состоянием плазмы и её математическим описанием наблюдается в так называемых пограничных зонах, где плазма переходит из одного физического состояния в другое (например, из состояния с низкой степенью ионизации в высокоионизационное). Здесь плазма не может быть описана с использованием простых гладких математических функций или с применением вероятностного подхода. Такие эффекты как спонтанное изменение формы плазмы являются следствием сложности взаимодействия заряженных частиц, из которых состоит плазма. Подобные явления интересны тем, что проявляются резко и не являются устойчивыми. Многие из них были изначально изучены в лабораториях, а затем были обнаружены во Вселенной.
Математическое описание
Плазму можно описывать на различных уровнях детализации. Обычно плазма описывается отдельно от электромагнитных полей. Совместное описание проводящей жидкости и электромагнитных полей даётся в теории магнитогидродинамических явлений или МГД теории.
Флюидная (жидкостная) модель
Во флюидной модели электроны описываются в терминах плотности, температуры и средней скорости. В основе модели лежат: уравнение баланса для плотности, уравнение сохранения импульса, уравнение баланса энергии электронов. В двухжидкостной модели таким же образом рассматриваются ионы.
Кинетическое описание
Иногда жидкостная модель оказывается недостаточной для описания плазмы. Более подробное описание даёт кинетическая модель, в которой плазма описывается в терминах функции распределения электронов по координатам и импульсам. В основе модели лежит уравнение Больцмана. Уравнение Больцмана неприменимо для описания плазмы заряженных частиц с кулоновским взаимодействием вследствие дальнодействующего характера кулоновских сил. Поэтому для описания плазмы с кулоновским взаимодействием используется уравнение Власова с самосогласованным электромагнитным полем, созданным заряженными частицами плазмы. Кинетическое описание необходимо применять в случае отсутствия термодинамического равновесия либо в случае присутствия сильных неоднородностей плазмы.
Particle-In-Cell (частица в ячейке)
Модели Particle-In-Cell используются для численного решения кинетических уравнений. Они включают в себя кинетическую информацию путём слежения за траекториями большого числа отдельных квазичастиц, каждая из которых отвечает некоторому числу реальных частиц (интегралу от функции распределения по ограниченной в фазовом пространстве области). Плотности электрического заряда и тока определяются путём суммирования заряда и квазичастиц в ячейках, которые малы по сравнению с рассматриваемой задачей, но, тем не менее, содержат большое число квазичастиц. Электрическое и магнитное поля находятся из плотностей зарядов и токов на границах ячеек. Не стоит путать модели PIC с прямым интегрированием уравнений движения реальных частиц, из которых состоит плазма — электронов и ионов — поскольку общее число квазичастиц в PIC-моделях, как правило, на много порядков меньше.
Базовые характеристики
Все величины даны в Гауссовых СГС единицах за исключением температуры, которая дана в eV и массы ионов, которая дана в единицах массы протона μ=mi/mp{\displaystyle \mu =m_{i}/m_{p}} ; Z — зарядовое число; k — постоянная Больцмана; К — длина волны; γ — адиабатический индекс; ln Λ — Кулоновский логарифм.
Частоты
- Ларморова частота электрона, угловая частота кругового движения электрона в плоскости перпендикулярной магнитному полю:
- ωce=eB/mec=1.76×107Brad/s.{\displaystyle \omega _{ce}=eB/m_{e}c=1.76\times 10^{7}B{\mbox{rad/s}}.}
- Ларморова частота иона, угловая частота кругового движения иона в плоскости перпендикулярной магнитному полю:
- ωci=eB/mic=9.58×103Zμ−1Brad/s.{\displaystyle \omega _{ci}=eB/m_{i}c=9.58\times 10^{3}Z\mu ^{-1}B{\mbox{rad/s}}.}
- Плазменная частота (частота плазменных колебаний), частота с которой электроны колеблются около положения равновесия, будучи смещёнными относительно ионов:
- ωpe=(4πnee2/me)1/2=5.64×104ne1/2rad/s.{\displaystyle \omega _{pe}=(4\pi n_{e}e^{2}/m_{e})^{1/2}=5.64\times 10^{4}n_{e}^{1/2}{\mbox{rad/s}}.}
- Ионная плазменная частота:
- ωpi=(4πniZ2e2/mi)1/2=1.32×103Zμ−1/2ni1/2rad/s.{\displaystyle \omega _{pi}=(4\pi n_{i}Z^{2}e^{2}/m_{i})^{1/2}=1.32\times 10^{3}Z\mu ^{-1/2}n_{i}^{1/2}{\mbox{rad/s}}.}
- Частота столкновений электронов
- νe=2.91×10−6nelnΛTe−3/2s−1.{\displaystyle \nu _{e}=2.91\times 10^{-6}n_{e}\,\ln \Lambda \,T_{e}^{-3/2}{\mbox{s}}^{-1}.}
- Частота столкновений ионов
- νi=4.80×10−8Z4μ−1/2nilnΛTi−3/2s−1.{\displaystyle \nu _{i}=4.80\times 10^{-8}Z^{4}\mu ^{-1/2}n_{i}\,\ln \Lambda \,T_{i}^{-3/2}{\mbox{s}}^{-1}.}
Длины
- Де-Бройлева длина волны электрона, длина волны электрона в квантовой механике:
- λ−=ℏ/(mekTe)1/2=2.76×10−8Te−1/2cm.{\displaystyle \lambda \!\!\!\!-=\hbar /(m_{e}kT_{e})^{1/2}=2.76\times 10^{-8}\,T_{e}^{-1/2}\,{\mbox{cm}}.}
- Минимальное расстояние сближения в классическом случае, минимальное расстояние на которое могут сблизиться две заряженных частицы при лобовом столкновении и начальной скорости, соответствующей температуре частиц, в пренебрежении квантово-механическими эффектами:
- e2/kT=1.44×10−7T−1cm.{\displaystyle e^{2}/kT=1.44\times 10^{-7}\,T^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус электрона, радиус кругового движения электрона в плоскости перпендикулярной магнитному полю:
- re=vTe/ωce=2.38Te1/2B−1cm.{\displaystyle r_{e}=v_{Te}/\omega _{ce}=2.38\,T_{e}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус иона, радиус кругового движения иона в плоскости перпендикулярной магнитному полю:
- ri=vTi/ωci=1.02×102μ1/2Z−1Ti1/2B−1cm.{\displaystyle r_{i}=v_{Ti}/\omega _{ci}=1.02\times 10^{2}\,\mu ^{1/2}Z^{-1}T_{i}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Размер скин-слоя плазмы, расстояние на которое электромагнитные волны могут проникать в плазму:
- c/ωpe=5.31×105ne−1/2cm.{\displaystyle c/\omega _{pe}=5.31\times 10^{5}\,n_{e}^{-1/2}\,{\mbox{cm}}.}
- Радиус Дебая (длина Дебая), расстояние на котором электрические поля экранируются за счёт перераспределения электронов:
- λD=(kT/4πne2)1/2=7.43×102T1/2n−1/2cm.{\displaystyle \lambda _{D}=(kT/4\pi ne^{2})^{1/2}=7.43\times 10^{2}\,T^{1/2}n^{-1/2}\,{\mbox{cm}}.}
Скорости
- Тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:
- vTe=(kTe/me)1/2=4.19×107Te1/2cm/s.{\displaystyle v_{Te}=(kT_{e}/m_{e})^{1/2}=4.19\times 10^{7}\,T_{e}^{1/2}\,{\mbox{cm/s}}.}
- vTi=(kTi/mi)1/2=9.79×105μ−1/2Ti1/2cm/s.{\displaystyle v_{Ti}=(kT_{i}/m_{i})^{1/2}=9.79\times 10^{5}\,\mu ^{-1/2}T_{i}^{1/2}\,{\mbox{cm/s}}.}
- Скорость ионного звука, скорость продольных ионно-звуковых волн:
- cs=(γZkTe/mi)1/2=9.79×105(γZTe/μ)1/2cm/s.{\displaystyle c_{s}=(\gamma ZkT_{e}/m_{i})^{1/2}=9.79\times 10^{5}\,(\gamma ZT_{e}/\mu )^{1/2}\,{\mbox{cm/s}}.}
- vA=B/(4πnimi)1/2=2.18×1011μ−1/2ni−1/2Bcm/s.{\displaystyle v_{A}=B/(4\pi n_{i}m_{i})^{1/2}=2.18\times 10^{11}\,\mu ^{-1/2}n_{i}^{-1/2}B\,{\mbox{cm/s}}.}
Безразмерные величины
- Квадратный корень из отношения масс электрона и протона:
- (me/mp)1/2=2.33×10−2=1/42.9.{\displaystyle (m_{e}/m_{p})^{1/2}=2.33\times 10^{-2}=1/42.9.}
- Число частиц в сфере Дебая:
- (4π/3)nλD3=1.72×109T3/2n−1/2.{\displaystyle (4\pi /3)n\lambda _{D}^{3}=1.72\times 10^{9}\,T^{3/2}n^{-1/2}.}
- Отношение Альфвеновской скорости к скорости света
- vA/c=7.28μ−1/2ni−1/2B.{\displaystyle v_{A}/c=7.28\,\mu ^{-1/2}n_{i}^{-1/2}B.}
- Отношение плазменной и ларморовской частот для электрона
- ωpe/ωce=3.21×10−3ne1/2B−1.{\displaystyle \omega _{pe}/\omega _{ce}=3.21\times 10^{-3}\,n_{e}^{1/2}B^{-1}.}
- Отношение плазменной и ларморовской частот для иона
- ωpi/ωci=0.137μ1/2ni1/2B−1.{\displaystyle \omega _{pi}/\omega _{ci}=0.137\,\mu ^{1/2}n_{i}^{1/2}B^{-1}.}
- Отношение тепловой и магнитной энергий
- β=8πnkT/B2=4.03×10−11nTB−2.{\displaystyle \beta =8\pi nkT/B^{2}=4.03\times 10^{-11}\,nTB^{-2}.}
- Отношение магнитной энергии к энергии покоя ионов
- B2/8πnimic2=26.5μ−1ni−1B2.{\displaystyle B^{2}/8\pi n_{i}m_{i}c^{2}=26.5\,\mu ^{-1}n_{i}^{-1}B^{2}.}
Прочее
- Бомовский коэффициент диффузии
- DB=(ckT/16eB)=5.4×102TB−1cm2/s.{\displaystyle D_{B}=(ckT/16eB)=5.4\times 10^{2}\,TB^{-1}\,{\mbox{cm}}^{2}/{\mbox{s}}.}
- Поперечное сопротивление Спитцера
- η⊥=1.15×10−14ZlnΛT−3/2s=1.03×10−2ZlnΛT−3/2Ωcm.{\displaystyle \eta _{\perp }=1.15\times 10^{-14}\,Z\,\ln \Lambda \,T^{-3/2}\,{\mbox{s}}=1.03\times 10^{-2}\,Z\,\ln \Lambda \,T^{-3/2}\,\Omega \,{\mbox{cm}}.}
Современные исследования
- Теория плазмы
- Плазма в природе
- Источники плазмы
- Диагностика плазмы
- Применения плазмы
См. также
Примечания
Литература
Ссылки
ru-wiki.org
Плазма — Википедия РУ
 Плазменная лампа, иллюстрирующая некоторые из наиболее сложных плазменных явлений, включая филаментацию. Свечение плазмы обусловлено переходом электронов из высокоэнергетического состояния в состояние с низкой энергией после рекомбинации с ионами. Этот процесс приводит к излучению со спектром, соответствующим возбуждаемому газу.
Плазменная лампа, иллюстрирующая некоторые из наиболее сложных плазменных явлений, включая филаментацию. Свечение плазмы обусловлено переходом электронов из высокоэнергетического состояния в состояние с низкой энергией после рекомбинации с ионами. Этот процесс приводит к излучению со спектром, соответствующим возбуждаемому газу.
Пла́зма (от греч. πλάσμα «вылепленное, оформленное») — ионизованный газ, одно из четырёх основных агрегатных состояний вещества.
Ионизированный газ содержит свободные электроны и положительные и отрицательные ионы. В более широком смысле, плазма может состоять из любых заряженных частиц (например, кварк-глюонная плазма). Квазинейтральность означает, что суммарный заряд в любом малом по сравнению с размерами системы объёме равен нулю, является её ключевым отличием от других систем, содержащих заряженные частицы (например, электронные или ионные пучки). Поскольку при нагреве газа до достаточно высоких температур, он переходит в плазму, она называется четвёртым (после твёрдого, жидкого и газообразного) агрегатным состоянием вещества.
Поскольку частицы в газе обладают подвижностью, плазма обладает способностью проводить электрический ток. В стационарном случае плазма экранирует постоянное внешнее по отношению к ней электрическое поле за счёт пространственного разделения зарядов. Однако из-за наличия ненулевой температуры заряженных частиц существует минимальный масштаб, на расстояниях меньше которого квазинейтральность нарушается.
История открытия
Четвёртое состояние вещества было открыто У. Круксом в 1879 году и названо «плазмой» И. Ленгмюром в 1928 году. Ленгмюр писал[1]:
Исключая пространство около электродов, где обнаруживается небольшое количество электронов, ионизированный газ содержит ионы и электроны практически в одинаковых количествах, в результате чего суммарный заряд системы очень мал. Мы используем термин «плазма», чтобы описать эту в целом электрически нейтральную область, состоящую из ионов и электронов.
Древние философы полагали, что мир состоит из четырёх стихий: земли, воды, воздуха и огня. Можно сказать, что это положение с учетом некоторых допущений укладывается в современное представление о четырёх агрегатных состояниях вещества, причём плазме соответствует огонь. Свойства плазмы изучает физика плазмы.
Виды
По сегодняшним представлениям, фазовым состоянием большей части барионного вещества (по массе ок. 99,9 %) во Вселенной является плазма.[2] Все звёзды состоят из плазмы, и даже пространство между ними заполнено плазмой, хотя и очень разреженной (см. межзвёздное пространство). К примеру, планета Юпитер сосредоточила в себе практически всё вещество Солнечной системы, находящееся в «неплазменном» состоянии (жидком, твёрдом и газообразном). При этом масса Юпитера составляет всего лишь около 0,1 % массы Солнечной системы, а объём — и того меньше: всего 10−15 %. При этом мельчайшие частицы пыли, заполняющие космическое пространство и несущие на себе определённый электрический заряд, в совокупности могут быть рассмотрены как плазма, состоящая из сверхтяжёлых заряженных ионов (см. пылевая плазма).
Свойства и параметры
Определение плазмы
Плазма — частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы.[4] Не всякую систему заряженных частиц можно назвать плазмой. Плазма обладает следующими свойствами:[5][6][7]
- Достаточная плотность: заряженные частицы должны находиться достаточно близко друг к другу, чтобы каждая из них взаимодействовала с целой системой близкорасположенных заряженных частиц. Условие считается выполненным, если число заряженных частиц в сфере влияния (сфера радиусом Дебая) достаточно для возникновения коллективных эффектов (подобные проявления — типичное свойство плазмы). Математически это условие можно выразить так:
- rD3N≫1,{\displaystyle r_{D}^{3}N\gg 1,}
- где N{\displaystyle N} — концентрация заряженных частиц.
- Приоритет внутренних взаимодействий: радиус дебаевского экранирования должен быть мал по сравнению с характерным размером плазмы. Этот критерий означает, что взаимодействия, происходящие внутри плазмы более значительны по сравнению с эффектами на её поверхности, которыми можно пренебречь. Если это условие соблюдено, плазму можно считать квазинейтральной. Математически оно выглядит так:
- rDL≪1.{\displaystyle {r_{D} \over L}\ll 1.}
- Плазменная частота: среднее время между столкновениями частиц должно быть велико по сравнению с периодом плазменных колебаний. Эти колебания вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд проходит по инерции это положение, что опять приводит к появлению сильного возвращающего поля, возникают типичные механические колебания.[8] Когда данное условие соблюдено, электродинамические свойства плазмы преобладают над молекулярно-кинетическими. На языке математики это условие имеет вид:
- τωpl≫1.{\displaystyle \tau \omega _{pl}\gg 1.}
Классификация
Плазма обычно разделяется на идеальную и неидеальную, низкотемпературную и высокотемпературную, равновесную и неравновесную, при этом довольно часто холодная плазма бывает неравновесной, а горячая равновесной.
Температура
Плазму делят на низкотемпературную (температура меньше миллиона K) и высокотемпературную (температура миллион K и выше). Такое деление обусловлено важностью высокотемпературной плазмы в проблеме осуществления управляемого термоядерного синтеза. Разные вещества переходят в состояние плазмы при разной температуре, что объясняется строением внешних электронных оболочек атомов вещества: чем легче атом отдает электрон, тем ниже температура перехода в плазменное состояние[9].
В неравновесной плазме электронная температура существенно превышает температуру ионов. Это происходит из-за различия в массах иона и электрона, которое затрудняет процесс обмена энергией. Такая ситуация встречается в газовых разрядах, когда ионы имеют температуру около сотен, а электроны около десятков тысяч K.
В равновесной плазме обе температуры равны. Поскольку для осуществления процесса ионизации необходимы температуры, сравнимые с потенциалом ионизации, равновесная плазма обычно является горячей (с температурой больше нескольких тысяч K).
Степень и кратность ионизации
Для того, чтобы газ перешёл в состояние плазмы, его необходимо ионизировать. Степень ионизации пропорциональна числу атомов, отдавших или поглотивших электроны, и больше всего зависит от температуры. Даже слабо ионизированный газ, в котором менее 1 % частиц находятся в ионизированном состоянии, может проявлять некоторые типичные свойства плазмы (взаимодействие с внешним электромагнитным полем и высокая электропроводность). Степень ионизации α определяется как α = ni /(ni + na), где ni — концентрация ионов, а na — концентрация нейтральных атомов. Концентрация свободных электронов в незаряженной плазме ne определяется очевидным соотношением: ne=<Z>ni, где <Z> — среднее значение заряда ионов плазмы, или кратность ионизации плазмы. Очевидно, что максимальное значение α равно 1 (или 100 %), такую плазму называют полностью ионизованной.
Для низкотемпературной плазмы характерна малая степень ионизации (до 1 %). Так как такие плазмы довольно часто употребляются в технологических процессах, их иногда называют технологичными плазмами. Чаще всего их создают при помощи электрических полей, ускоряющих электроны, которые в свою очередь ионизируют атомы. Электрические поля вводятся в газ посредством индуктивной или емкостной связи (см. индуктивно-связанная плазма). Типичные применения низкотемпературной плазмы включают плазменную модификацию свойств поверхности (алмазные плёнки, нитридирование металлов, изменение смачиваемости), плазменное травление поверхностей (полупроводниковая промышленность), очистку газов и жидкостей (озонирование воды и сжигание частичек сажи в дизельных двигателях).
Горячая плазма почти всегда полностью ионизирована (степень ионизации ~100 %). Обычно именно она понимается под «четвёртым агрегатным состоянием вещества». Примером может служить Солнце.
Концентрация частиц в плазме
Помимо температуры, которая имеет фундаментальную важность для самого существования плазмы, вторым наиболее важным свойством плазмы является концентрация заряженных частиц. Словосочетание концентрация плазмы обычно обозначает концентрация электронов, то есть число свободных электронов в единице объёма. В квазинейтральной плазме концентрация ионов связана с ней посредством среднего зарядового числа ионов ⟨Z⟩{\displaystyle \langle Z\rangle } : ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}} . Следующей важной величиной является концентрация нейтральных атомов n0{\displaystyle n_{0}} . В горячей плазме n0{\displaystyle n_{0}} мала, но может тем не менее быть важной для физики процессов в плазме. При рассмотрении процессов в плотной, неидеальной плазме характерным параметром концентрации становится rs{\displaystyle r_{s}} , который определяется как отношение среднего межчастичного расстояния к радиусу Бора.
Квазинейтральность
Так как плазма является очень хорошим проводником, электрические свойства имеют важное значение. Потенциалом плазмы или потенциалом пространства называют среднее значение электрического потенциала в данной точке пространства. В случае если в плазму внесено какое-либо тело, его потенциал в общем случае будет меньше потенциала плазмы вследствие возникновения дебаевского слоя. Такой потенциал называют плавающим потенциалом. По причине хорошей электрической проводимости плазма стремится экранировать все электрические поля. Это приводит к явлению квазинейтральности — плотность отрицательных зарядов с хорошей точностью равна плотности положительных зарядов (ne=⟨Z⟩ni{\displaystyle n_{e}=\langle Z\rangle n_{i}} ). В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний.
Примером неквазинейтральной плазмы является пучок электронов. Однако плотность не-нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.
Отличия от газообразного состояния
Плазму часто называют четвёртым состоянием вещества. Она отличается от трёх менее энергетичных агрегатных состояний материи, хотя и похожа на газовую фазу тем, что не имеет определённой формы или объёма. До сих пор идёт обсуждение того, является ли плазма отдельным агрегатным состоянием, или же просто горячим газом. Большинство физиков считает, что плазма является чем-то большим, чем газ по причине следующих различий:
| Свойство | Газ | Плазма |
|---|---|---|
| Электрическая проводимость | Крайне мала К примеру, воздух является превосходным изолятором до тех пор, пока не переходит в плазменное состояние под действием внешнего электрического поля напряженностью в 30 киловольт на сантиметр.[10] |
Очень высока
|
| Число сортов частиц | Один Газы состоят из подобных друг другу частиц, которые находятся в тепловом движении, а также движутся под действием гравитации, а друг с другом взаимодействуют только на сравнительно небольших расстояниях. |
Два, или три, или более Электроны, ионы и нейтральные частицы различаются знаком эл. заряда и могут вести себя независимо друг от друга — иметь разные скорости и даже температуры, что служит причиной появления новых явлений, например волн и неустойчивостей. |
| Распределение по скоростям | Максвелловское Столкновения частиц друг с другом приводит к максвелловскому распределению скоростей, согласно которому очень малая часть молекул газа имеют относительно большие скорости движения. |
Может быть немаксвелловское Электрические поля имеют другое влияние на скорости частиц чем столкновения, которые всегда ведут к максвеллизации распределения по скоростям. Зависимость сечения кулоновских столкновений от скорости может усиливать это различие, приводя к таким эффектам, как двухтемпературные распределения и убегающие электроны. |
| Тип взаимодействий | Бинарные Как правило двухчастичные столкновения, трёхчастичные крайне редки. |
Коллективные Каждая частица взаимодействует сразу со многими. Эти коллективные взаимодействия имеют гораздо большее влияние чем двухчастичные. |
Сложные плазменные явления
Хотя основные уравнения, описывающие состояния плазмы, относительно просты, в некоторых ситуациях они не могут адекватно отражать поведение реальной плазмы: возникновение таких эффектов — типичное свойство сложных систем, если использовать для их описания простые модели. Наиболее сильное различие между реальным состоянием плазмы и её математическим описанием наблюдается в так называемых пограничных зонах, где плазма переходит из одного физического состояния в другое (например, из состояния с низкой степенью ионизации в высокоионизационное). Здесь плазма не может быть описана с использованием простых гладких математических функций или с применением вероятностного подхода. Такие эффекты как спонтанное изменение формы плазмы являются следствием сложности взаимодействия заряженных частиц, из которых состоит плазма. Подобные явления интересны тем, что проявляются резко и не являются устойчивыми. Многие из них были изначально изучены в лабораториях, а затем были обнаружены во Вселенной.
Математическое описание
Плазму можно описывать на различных уровнях детализации. Обычно плазма описывается отдельно от электромагнитных полей. Совместное описание проводящей жидкости и электромагнитных полей даётся в теории магнитогидродинамических явлений или МГД теории.
Флюидная (жидкостная) модель
Во флюидной модели электроны описываются в терминах плотности, температуры и средней скорости. В основе модели лежат: уравнение баланса для плотности, уравнение сохранения импульса, уравнение баланса энергии электронов. В двухжидкостной модели таким же образом рассматриваются ионы.
Кинетическое описание
Иногда жидкостная модель оказывается недостаточной для описания плазмы. Более подробное описание даёт кинетическая модель, в которой плазма описывается в терминах функции распределения электронов по координатам и импульсам. В основе модели лежит уравнение Больцмана. Уравнение Больцмана неприменимо для описания плазмы заряженных частиц с кулоновским взаимодействием вследствие дальнодействующего характера кулоновских сил. Поэтому для описания плазмы с кулоновским взаимодействием используется уравнение Власова с самосогласованным электромагнитным полем, созданным заряженными частицами плазмы. Кинетическое описание необходимо применять в случае отсутствия термодинамического равновесия либо в случае присутствия сильных неоднородностей плазмы.
Particle-In-Cell (частица в ячейке)
Модели Particle-In-Cell используются для численного решения кинетических уравнений. Они включают в себя кинетическую информацию путём слежения за траекториями большого числа отдельных квазичастиц, каждая из которых отвечает некоторому числу реальных частиц (интегралу от функции распределения по ограниченной в фазовом пространстве области). Плотности электрического заряда и тока определяются путём суммирования заряда и квазичастиц в ячейках, которые малы по сравнению с рассматриваемой задачей, но, тем не менее, содержат большое число квазичастиц. Электрическое и магнитное поля находятся из плотностей зарядов и токов на границах ячеек. Не стоит путать модели PIC с прямым интегрированием уравнений движения реальных частиц, из которых состоит плазма — электронов и ионов — поскольку общее число квазичастиц в PIC-моделях, как правило, на много порядков меньше.
Базовые характеристики
Все величины даны в Гауссовых СГС единицах за исключением температуры, которая дана в eV и массы ионов, которая дана в единицах массы протона μ=mi/mp{\displaystyle \mu =m_{i}/m_{p}} ; Z — зарядовое число; k — постоянная Больцмана; К — длина волны; γ — адиабатический индекс; ln Λ — Кулоновский логарифм.
Частоты
- Ларморова частота электрона, угловая частота кругового движения электрона в плоскости перпендикулярной магнитному полю:
- ωce=eB/mec=1.76×107Brad/s.{\displaystyle \omega _{ce}=eB/m_{e}c=1.76\times 10^{7}B{\mbox{rad/s}}.}
- Ларморова частота иона, угловая частота кругового движения иона в плоскости перпендикулярной магнитному полю:
- ωci=eB/mic=9.58×103Zμ−1Brad/s.{\displaystyle \omega _{ci}=eB/m_{i}c=9.58\times 10^{3}Z\mu ^{-1}B{\mbox{rad/s}}.}
- Плазменная частота (частота плазменных колебаний), частота с которой электроны колеблются около положения равновесия, будучи смещёнными относительно ионов:
- ωpe=(4πnee2/me)1/2=5.64×104ne1/2rad/s.{\displaystyle \omega _{pe}=(4\pi n_{e}e^{2}/m_{e})^{1/2}=5.64\times 10^{4}n_{e}^{1/2}{\mbox{rad/s}}.}
- Ионная плазменная частота:
- ωpi=(4πniZ2e2/mi)1/2=1.32×103Zμ−1/2ni1/2rad/s.{\displaystyle \omega _{pi}=(4\pi n_{i}Z^{2}e^{2}/m_{i})^{1/2}=1.32\times 10^{3}Z\mu ^{-1/2}n_{i}^{1/2}{\mbox{rad/s}}.}
- Частота столкновений электронов
- νe=2.91×10−6nelnΛTe−3/2s−1.{\displaystyle \nu _{e}=2.91\times 10^{-6}n_{e}\,\ln \Lambda \,T_{e}^{-3/2}{\mbox{s}}^{-1}.}
- Частота столкновений ионов
- νi=4.80×10−8Z4μ−1/2nilnΛTi−3/2s−1.{\displaystyle \nu _{i}=4.80\times 10^{-8}Z^{4}\mu ^{-1/2}n_{i}\,\ln \Lambda \,T_{i}^{-3/2}{\mbox{s}}^{-1}.}
Длины
- Де-Бройлева длина волны электрона, длина волны электрона в квантовой механике:
- λ−=ℏ/(mekTe)1/2=2.76×10−8Te−1/2cm.{\displaystyle \lambda \!\!\!\!-=\hbar /(m_{e}kT_{e})^{1/2}=2.76\times 10^{-8}\,T_{e}^{-1/2}\,{\mbox{cm}}.}
- Минимальное расстояние сближения в классическом случае, минимальное расстояние на которое могут сблизиться две заряженных частицы при лобовом столкновении и начальной скорости, соответствующей температуре частиц, в пренебрежении квантово-механическими эффектами:
- e2/kT=1.44×10−7T−1cm.{\displaystyle e^{2}/kT=1.44\times 10^{-7}\,T^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус электрона, радиус кругового движения электрона в плоскости перпендикулярной магнитному полю:
- re=vTe/ωce=2.38Te1/2B−1cm.{\displaystyle r_{e}=v_{Te}/\omega _{ce}=2.38\,T_{e}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Гиромагнитный радиус иона, радиус кругового движения иона в плоскости перпендикулярной магнитному полю:
- ri=vTi/ωci=1.02×102μ1/2Z−1Ti1/2B−1cm.{\displaystyle r_{i}=v_{Ti}/\omega _{ci}=1.02\times 10^{2}\,\mu ^{1/2}Z^{-1}T_{i}^{1/2}B^{-1}\,{\mbox{cm}}.}
- Размер скин-слоя плазмы, расстояние на которое электромагнитные волны могут проникать в плазму:
- c/ωpe=5.31×105ne−1/2cm.{\displaystyle c/\omega _{pe}=5.31\times 10^{5}\,n_{e}^{-1/2}\,{\mbox{cm}}.}
- Радиус Дебая (длина Дебая), расстояние на котором электрические поля экранируются за счёт перераспределения электронов:
- λD=(kT/4πne2)1/2=7.43×102T1/2n−1/2cm.{\displaystyle \lambda _{D}=(kT/4\pi ne^{2})^{1/2}=7.43\times 10^{2}\,T^{1/2}n^{-1/2}\,{\mbox{cm}}.}
Скорости
- Тепловая скорость электрона, формула для оценки скорости электронов при распределении Максвелла. Средняя скорость, наиболее вероятная скорость и среднеквадратичная скорость отличаются от этого выражения лишь множителями порядка единицы:
- vTe=(kTe/me)1/2=4.19×107Te1/2cm/s.{\displaystyle v_{Te}=(kT_{e}/m_{e})^{1/2}=4.19\times 10^{7}\,T_{e}^{1/2}\,{\mbox{cm/s}}.}
- vTi=(kTi/mi)1/2=9.79×105μ−1/2Ti1/2cm/s.{\displaystyle v_{Ti}=(kT_{i}/m_{i})^{1/2}=9.79\times 10^{5}\,\mu ^{-1/2}T_{i}^{1/2}\,{\mbox{cm/s}}.}
- Скорость ионного звука, скорость продольных ионно-звуковых волн:
- cs=(γZkTe/mi)1/2=9.79×105(γZTe/μ)1/2cm/s.{\displaystyle c_{s}=(\gamma ZkT_{e}/m_{i})^{1/2}=9.79\times 10^{5}\,(\gamma ZT_{e}/\mu )^{1/2}\,{\mbox{cm/s}}.}
- vA=B/(4πnimi)1/2=2.18×1011μ−1/2ni−1/2Bcm/s.{\displaystyle v_{A}=B/(4\pi n_{i}m_{i})^{1/2}=2.18\times 10^{11}\,\mu ^{-1/2}n_{i}^{-1/2}B\,{\mbox{cm/s}}.}
Безразмерные величины
- Квадратный корень из отношения масс электрона и протона:
- (me/mp)1/2=2.33×10−2=1/42.9.{\displaystyle (m_{e}/m_{p})^{1/2}=2.33\times 10^{-2}=1/42.9.}
- Число частиц в сфере Дебая:
- (4π/3)nλD3=1.72×109T3/2n−1/2.{\displaystyle (4\pi /3)n\lambda _{D}^{3}=1.72\times 10^{9}\,T^{3/2}n^{-1/2}.}
- Отношение Альфвеновской скорости к скорости света
- vA/c=7.28μ−1/2ni−1/2B.{\displaystyle v_{A}/c=7.28\,\mu ^{-1/2}n_{i}^{-1/2}B.}
- Отношение плазменной и ларморовской частот для электрона
- ωpe/ωce=3.21×10−3ne1/2B−1.{\displaystyle \omega _{pe}/\omega _{ce}=3.21\times 10^{-3}\,n_{e}^{1/2}B^{-1}.}
- Отношение плазменной и ларморовской частот для иона
- ωpi/ωci=0.137μ1/2ni1/2B−1.{\displaystyle \omega _{pi}/\omega _{ci}=0.137\,\mu ^{1/2}n_{i}^{1/2}B^{-1}.}
- Отношение тепловой и магнитной энергий
- β=8πnkT/B2=4.03×10−11nTB−2.{\displaystyle \beta =8\pi nkT/B^{2}=4.03\times 10^{-11}\,nTB^{-2}.}
- Отношение магнитной энергии к энергии покоя ионов
- B2/8πnimic2=26.5μ−1ni−1B2.{\displaystyle B^{2}/8\pi n_{i}m_{i}c^{2}=26.5\,\mu ^{-1}n_{i}^{-1}B^{2}.}
Прочее
- Бомовский коэффициент диффузии
- DB=(ckT/16eB)=5.4×102TB−1cm2/s.{\displaystyle D_{B}=(ckT/16eB)=5.4\times 10^{2}\,TB^{-1}\,{\mbox{cm}}^{2}/{\mbox{s}}.}
- Поперечное сопротивление Спитцера
- η⊥=1.15×10−14ZlnΛT−3/2s=1.03×10−2ZlnΛT−3/2Ωcm.{\displaystyle \eta _{\perp }=1.15\times 10^{-14}\,Z\,\ln \Lambda \,T^{-3/2}\,{\mbox{s}}=1.03\times 10^{-2}\,Z\,\ln \Lambda \,T^{-3/2}\,\Omega \,{\mbox{cm}}.}
Современные исследования
- Теория плазмы
- Плазма в природе
- Источники плазмы
- Диагностика плазмы
- Применения плазмы
См. также
Примечания
Литература
Ссылки
www.http-wikipediya.ru

