Как рассчитать жесткость системы при последовательном и параллельном соединении пружин. Какие формулы используются для вычислений. Как меняется общая жесткость системы при разных типах соединений. На что влияет способ соединения пружин.
Основные виды соединения пружин
Существует два основных способа соединения пружин в системе:
- Последовательное соединение — пружины соединяются друг за другом в одну линию
- Параллельное соединение — пружины располагаются рядом и крепятся к общим точкам
Тип соединения пружин оказывает существенное влияние на жесткость всей системы. Рассмотрим подробнее особенности каждого вида соединения.
Последовательное соединение пружин
При последовательном соединении пружины располагаются друг за другом в одну линию. Такое соединение имеет следующие особенности:
- Общая жесткость системы уменьшается по сравнению с жесткостью отдельных пружин
- Удлинение системы равно сумме удлинений каждой пружины
- Сила упругости одинакова для всех пружин в системе
Для расчета общей жесткости системы при последовательном соединении используется следующая формула:

1/k = 1/k₁ + 1/k₂ + … + 1/kₙ
где k — общая жесткость системы, k₁, k₂, …, kₙ — жесткости отдельных пружин.
Параллельное соединение пружин
При параллельном соединении пружины крепятся к общим точкам и располагаются рядом. Особенности такого соединения:
- Общая жесткость системы увеличивается по сравнению с жесткостью отдельных пружин
- Удлинение одинаково для всех пружин в системе
- Общая сила упругости равна сумме сил упругости каждой пружины
Формула для расчета общей жесткости при параллельном соединении:
k = k₁ + k₂ + … + kₙ
где k — общая жесткость системы, k₁, k₂, …, kₙ — жесткости отдельных пружин.
Сравнение последовательного и параллельного соединения
Основные отличия двух типов соединения пружин:
- При последовательном соединении общая жесткость уменьшается, при параллельном — увеличивается
- У последовательного соединения суммируются удлинения пружин, у параллельного — силы упругости
- Последовательное соединение позволяет получить большее удлинение системы, параллельное — большую силу упругости
Выбор типа соединения зависит от требуемых характеристик системы — большего удлинения или большей силы упругости.

Расчет жесткости системы пружин
Рассмотрим пример расчета жесткости системы из двух пружин с жесткостями k₁ = 100 Н/м и k₂ = 200 Н/м при разных типах соединения.
Последовательное соединение
Используем формулу для последовательного соединения:
1/k = 1/k₁ + 1/k₂ = 1/100 + 1/200 = 0,015
k = 1/0,015 ≈ 66,7 Н/м
Параллельное соединение
Используем формулу для параллельного соединения:
k = k₁ + k₂ = 100 + 200 = 300 Н/м
Как видим, при последовательном соединении жесткость системы уменьшилась, а при параллельном — увеличилась по сравнению с жесткостью отдельных пружин.
Применение разных типов соединения пружин
Различные способы соединения пружин используются для получения требуемых характеристик упругих систем:
- Последовательное соединение применяется, когда нужно увеличить диапазон деформации системы
- Параллельное соединение используется для увеличения жесткости и силы упругости системы
- Комбинированное соединение позволяет получить оптимальное сочетание характеристик
Правильный выбор типа соединения пружин позволяет создавать системы с заданными упругими свойствами для различных технических применений.

Влияние способа соединения на динамику системы
Тип соединения пружин оказывает влияние не только на статические характеристики системы, но и на ее динамическое поведение:
- При последовательном соединении уменьшается частота собственных колебаний системы
- Параллельное соединение увеличивает частоту собственных колебаний
- Последовательное соединение обеспечивает лучшее демпфирование колебаний
- Параллельное соединение повышает жесткость и устойчивость системы
Учет этих особенностей важен при проектировании виброизоляционных систем, подвесок транспортных средств и других динамических систем.
Расчет характеристик системы пружин
Для полного описания системы пружин недостаточно знать только ее жесткость. Важными характеристиками также являются:
- Максимальное удлинение системы
- Максимальная сила упругости
- Энергия деформации
Рассмотрим расчет этих параметров на примере.
Пример расчета
Дана система из двух параллельно соединенных пружин с жесткостями k₁ = 100 Н/м и k₂ = 200 Н/м. Максимальное удлинение системы x = 0,1 м. Рассчитаем основные характеристики.
1. Общая жесткость системы: k = k₁ + k₂ = 100 + 200 = 300 Н/м
2. Максимальная сила упругости: F = kx = 300 * 0,1 = 30 Н
3. Энергия деформации: E = kx²/2 = 300 * 0,1² / 2 = 1,5 Дж
Такие расчеты позволяют оценить работоспособность и эффективность упругой системы.
Последовательное соединение пружин : жесткость, формула
Пружины являются важным элементом самых различных механизмов. Для изменения основных эксплуатационных свойств проводится использование нескольких подобных изделий, которые соединяются различным образом. Тип применяемого метода соединения учитывается при проведении самых различных расчетов.
Основные методы крепления пружин
При проведении расчетов уделяется внимание тому, каким образом проводится соединение пружин. Этот момент оказывает влияние на следующее:
- Жесткость системы. Этот показатель встречается практически во всех проводимых расчетах при последовательном подключении деталей. Зависит он от самых различных моментов, к примеру, коэффициента жесткости каждого.
- Требуемое усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто по причине того, что может обеспечивает накопление кинетической энергии.
- Размер кинетической и потенциальной энергии. После того как изделие было выведено из положения равновесия начинает накапливаться кинетическая энергия. При этом она сохраняется на протяжении всего периода, пока к телу приложено усилие.
- Вероятность возникновения свободного колебательного движения, а также степень сопротивления подобному явлению. Для расчетов колебательного движения также применяются специальные формулы.
Бывают самые различные способы соединения пружин, но наибольшее распространение получил метод последовательного и параллельного подключения.
Они характеризуются довольно большим количеством особенностей. Прежде чем рассматривать применение подобных способов соединения следует уделить внимание особенностям самого изделия:
- Деталь изготавливается из проволоки, которая получается методом проката. Она обладает высоким показателем упругости, а также устойчивостью к воздействию окружающей среды.
- Прокат изготавливают из специального сплава, способного выдерживать периодическую деформацию. Под заказ может производится деталь из обычных углеродистых сплавов или легированных металлов, все зависит от конкретного случая.
- Проволока накручивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
- Выделяют два основных типа детали: растяжения и сжатия. Первый вариант исполнения характеризуется тем, что витки находятся практически вплотную. В случае изготовления изделия для сжатия выдерживается определенный зазор, который позволяет кольцам сближаться, а самому изделию сжиматься.
- Характеризуется изделие самыми различными показателями. Примером можно назвать диаметр проволоки, созданных колец из нее, шаг расположения витков. Все эти параметры указываются в технической документации.
Сегодня они встречаются практически повсеместно. Это связано с тем, что подобное изделие практически незаменимо в случае, когда требуется возвратно-поступательное движение.
Последовательное соединение
При создании многих механизмов применяется последовательное соединение пружин. Среди особенностей этого метода отметим нижеприведенные моменты:
- Наиболее важным параметром можно назвать коэффициент жесткости. Он определяет практически все свойства детали. Коэффициент жесткости при последовательном соединении пружин равен каждому из показателей упругости.
- Также не стоит забывать о том, что показатель смещения тела равен сумме деформации витков. Любой тип рассматриваемого изделия характеризуется максимальным удлинение и сжатием. В случае максимального сжатия кольца расположены вплотную, зазор отсутствует практически полностью. При растяжении есть вероятность деформации витков, из-за чего изделие попросту потеряет свои основные характеристики.
Для расчетов могут применяться самые различные формулы. Среди особенностей этого метода соединения пружин отметим следующее:
- Для начала берется одна деталь с жесткостью K, сила растяжения выражается следующей формулой: x=F/k.
- Следующий шаг заключается в подсоединении второй детали. Для этого могут применяться различные крепежные элементы. При этом две пружины разной длины будут находится в одной системе.
- Если приложить усилие для растягивания обоих изделий, то сила упругости каждой будет равна по модулю. При этом удлинение каждой будет равно х.
Приведенная выше информация указывает на то, что упругость системы двух последовательно соединенных изделий будет примерно в два раза меньше. При этом удлинение будет равно сумме удлинения каждой в отдельности.
Применяемый метод соединения получил весьма широкое распространение. Однако, в некоторых случаях целесообразно применять параллельный метод соединения.
Параллельное соединение
Довольно часто встречается и параллельное соединение пружин. В этом случае смещение тела, которому передается сила, равна деформации каждой из них. Зачастую параллельно соединенные пружины используются тогда, когда нужно передать большее усилие. Особенностями этого метода назовем следующее:
- В рассматриваемом случае жесткости пружины обозначаются буквой k. Построенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий показатель возрастает в два раза.
- Показатель удлинения остается неизменным. При этом сила упругости возрастает в два раза в случае, если обе детали обладают схожими эксплуатационными характеристиками.
Проблемой применения подобной системы можно назвать то, что обе детали должны обладать одинаковой длиной в состоянии покоя. В противном случае сила упругости будет распределяться неравномерно, при этом есть вероятность критической деформации одной из них.
Влияние сопротивления на свободные колебания
Особенности детали определяют то, что при ее применении есть вероятность возникновения свободного колебательного движения. При этом имеет значение, какими особенностями обладает параллельно и последовательно соединенные пружины. Среди особенностей влияния сопротивления на свободное колебание отметим следующие моменты:
- Проведенные тесты указывают на то, что параллельно соединенные пружины препятствуют возникновению свободного колебания. Это можно связать с существенным увеличением жесткости всей системы.
- При последовательном расположении есть вероятность снижения сопротивления, так как расстояние между точкой крепления и телом существенно увеличивается.
Именно поэтому для существенного снижения колебательного вращения на момент эксплуатации системы рекомендуется использовать параллельный метод подключения.
Динамика несвободного движения
Еще одним важным показателем можно назвать динамику несвободного движения. Она может варьировать в достаточно большом диапазоне.
Распространенные последовательно соединенные пружины могут обеспечивать условия для несвободного движения тела. Динамика может нарастать в зависимости от длины в свободном состоянии и передаваемого усилия.
Как определить жесткость системы при последовательном соединении пружин?
Довольно большое количество проблем возникает на момент вычисления жесткости системы при последовательном соединении. Особенностями проводимого расчета в этом случае назовем следующее:
- Важным показателем можно назвать жесткость, которая варьирует в достаточно большом диапазоне. Она во многом определяет свойства изделия. При слишком большой жесткости приходится прикладывать большее усилие для растяжения или сжатия детали.
- Телу придается определенное усилие (F), которое становится причиной удлинения тела на величину x.
- Для расчета применяется формула: k=F/(2x)=1/2F/x=k/2.
Приведенная выше информация указывает на то, что жесткость всей системы в этом случае в два раза меньше показателя жесткости каждого изделия. При этом формула применима только в том случае, если применяемые варианты исполнения для соединения обладают одинаковыми эксплуатационными характеристиками.
Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система двух пружин получила весьма широкое распространение, так как при ее применении можно добиться требующихся результатов. Однако, прежде чем ее использовать следует провести соответствующие расчеты.
Последовательное соединение пружин жесткость, формула
Пружины считаются основным элементом довольно различных механизмов. Для изменения ключевых свойств эксплуатации проходит применение нескольких таких изделий, которые соединяются разным образом. Вид используемого метода соединения принимается во внимание при проведении довольно различных расчетов.
Главные способы крепления пружин
При проведении расчетов уделяют внимание тому, как проходит соединение пружин. Данный момент влияет на следующее:
- Жесткость системы. Данный показатель встречается фактически во всех проводимых расчетах при последовательном подсоединении деталей. Зависит он от довольно различных факторов, например, коэффициента жесткости каждого.
- Нужное усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто из-за причины того, что может обеспечивает накопление кинетической энергии.
- Размер кинетической и возможной энергии. Как только изделие было выведено из положения равновесия начинает скапливаться кинетическая энергия. При этом она сберегается в течении всего периода, пока к телу приложено усилие.
- Вероятность появления свободного колебательного движения, а еще степень сопротивления такому явлению. Для расчетов колебательного движения также используются специализированные формулы.
Бывают очень разные способы соединения пружин, но самое большое распространение получил метод последовательного и параллельного подсоединения.
Они отличаются неограниченным количеством свойств. Перед тем как рассматривать использование аналогичных вармантов соединения необходимо уделять свое внимание свойствам самого изделия:
- Деталь делается из проволки, которая выходит методом проката. Она обладает большим коэффициентом упругости, а еще стойкостью к влиянию внешней среды.
- Прокат делают из специализированного сплава, способного держать периодическую деформацию. На заказ может выполняется деталь из обыкновенных углеродистых сплавов или легированных металлов, все будет зависеть от определенного случая.
- Проволока навинчивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
- Выделяют два основных типа детали: растяжения и сжатия. Первый вариант выполнения отличается тем, что витки находятся фактически близко. В случае изготовления изделия для сжатия выдерживается специальный зазор, который дает возможность кольцам сближаться, а самому изделию сжиматься.
- Отличается изделие очень различными критериями. Примером можно назвать диаметр проволки, созданных колец из нее, шаг расположения витков. Все данные параметры указываются в техдокументации.
Сегодня они встречаются фактически везде. Связывают это с тем, что такое изделие фактически незаменимо в случае, когда потребуется возвратно-поступательное движение.
Методичное соединение
При разработке многих механизмов применяется методичное соединение пружин. Среди свойств такого способа отметим приведенные ниже моменты:
- Наиболее основным параметром можно назвать показатель жесткости. Он определяет фактически все свойства детали. Показатель жесткости при последовательном соединении пружин равён любому из критериев упругости.
- Также необходимо помнить про то, что критерий смещения тела равён сумме деформации витков. Любой вид рассматриваемого изделия отличается самым большим удлинение и сжатием. В случае самого большого сжатия кольца размещены близко, просвет отсутствует фактически полностью. При растяжении есть вероятность деформации витков, благодаря чему изделие просто потеряет собственные главные характеристики.
Для расчетов используют очень разные формулы. Среди свойств такого способа соединения пружин отметим следующее:
- Для начала берется одна деталь с жесткостью K, сила растяжения выражается следующей формулой: x=F/k.
- Второй шаг состоит в подсоединении второй детали. Для этого используют разные элементы крепления. При этом две пружины различной длины будут находится в одной системе.
- Если приложить усилие для растягивания двоих изделий, то сила упругости каждой будет равна по модулю. При этом удлинение каждой будет равно х.
Вышеприведенная информация указывает на то, что упругость системы 2-ух постепенно скреплённых изделий будет приблизительно меньше практически вдвое. При этом удлинение будет равно сумме удлинения каждой по отдельности.
Используемый метод соединения получил очень большое распространение. Впрочем, в определенных случаях лучше всего использовать параллельный метод соединения.
Параллельное соединение
Очень часто можно встретить и параллельное соединение пружин. В данном случае смещение тела, которому подается сила, равна деформации любой из них. Очень часто параллельно соединенные пружины применяются тогда, когда необходимо передать большее усилие. Характерностями такого способа назовем следующее:
- В рассматриваемом случае жесткости пружины обозначаются буквой k. Выстроенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий критерий увеличивается вдвое.
- Критерий удлинения не меняется. При этом сила упругости увеличивается вдвое например если две детали обладают схожими рабочими характеристиками.
Трудностью использования такой системы можно назвать то, что две детали должны владеть одинаковой длиной в состоянии покоя. В другом случае сила упругости будет распределяться неровно, есть при этом вероятность критичной деформации одной из них.
Воздействие сопротивления на свободные колебания
Характерности детали формируют то, что при ее использовании есть вероятность появления свободного колебательного движения. Имеет при этом значение, какими характерностями обладает параллельно и постепенно соединенные пружины. Среди свойств воздействия сопротивления на свободное колебание отметим такие моменты:
- Проведенные тесты указывают на то, что параллельно соединенные пружины мешают появлению свободного колебания. Это можно связать с значительным увеличением жесткости всей системы.
- При последовательном расположении есть вероятность снижения сопротивления, так как расстояние между крепежной точкой и телом намного увеличивается.
Собственно поэтому для большого снижения колебательного вращения на момент эксплуатации системы лучше всего применять параллельный метод подсоединения.
Динамика несвободного движения
Дополнительным важным критерием можно назвать динамику несвободного движения. Она может варьировать в довольно обширном диапазоне.
Распространенные постепенно соединенные пружины способны обеспечивать условия для несвободного движения тела. Динамика может увеличиваться в зависимости от длины в свободном состоянии и передаваемого усилия.
Как определить жесткость системы при последовательном соединении пружин?
Очень большое количество проблем появляется на момент вычисления жесткости системы при последовательном соединении. Характерностями проводимого расчета в данном случае назовем следующее:
- Важным критерием можно назвать жесткость, которая варьирует в довольно обширном диапазоне. Она в большинстве случаев определяет свойства изделия. При слишком высокой жесткости необходимо прикладывать большее усилие для растяжения или сжатия детали.
- Телу придается конкретное усилие (F), которое оказывается основой удлинения тела на величину x.
- Для расчета применяется формула: k=F/(2x)=1/2F/x=k/2.
Вышеприведенная информация указывает на то, что прочность всей системы в данном случае меньше практически вдвое критерия жесткости любого изделия. При этом формула применима исключительно в случае, если используемые варианты выполнения для сцепления обладают похожими рабочими характеристиками.
Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система 2-ух пружин обрела очень большое распространение, так же как и при ее использовании можно достичь требующихся результатов. Но, перед тем как ее применять нужно провести необходимые расчеты.
Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.
Похожие статьи
Закон гука сила упругости — определение, формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
- Деформация растяжения
- Деформация сжатия
- Деформация сдвига
- Деформация при кручении
- Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
|
Закон Гука Fупр = kx Fупр — сила упругости [Н]
|
Важно раз
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Важно два
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Тогда из Закона Гука выразим модуль удлинения лески:
F = kx
Выражаем модуль удлинения:
x = F/k
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
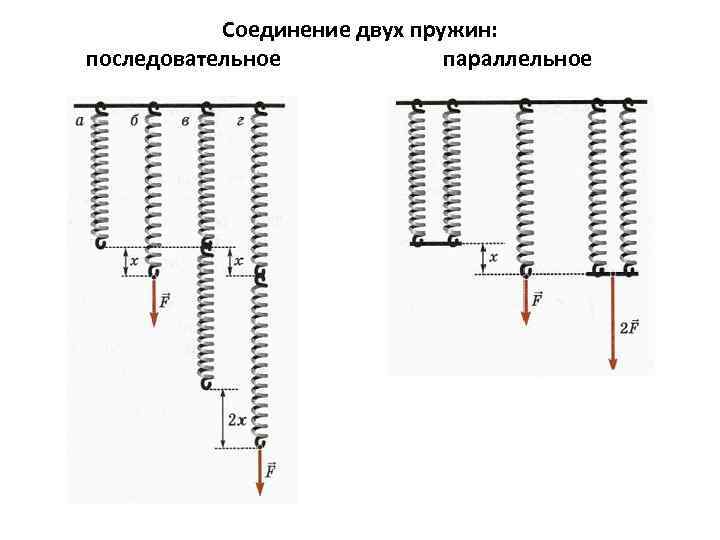
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
|
Коэффициент жесткости при последовательном соединении пружин 1/k = 1/k₁ + 1/k₂ + … + 1/k_i k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
|
Коэффициент жесткости при параллельном соединении пружин k = k₁ + k₂ + … + k_i k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
Очень-очень важно!
Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
F = kx
k = F/x
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
k = F/x
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Репетитор-онлайн — подготовка к ЦТ
Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.
Решение. Величина силы упругости, действующей на пружину, определяется формулой
Fупр = kобщ∆x,
где kобщ — коэффициент жесткости составной пружины; ∆x — указанное в условии задачи растяжение пружины.
Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:
Fупр = F.
Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:
kобщ=FΔx=124,0⋅10−2=300 Н/м.
Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:
- для первой пружины
k1 = k;
- для второй пружины
k2 = 2k;
- для третьей пружины
k3 = 3k,
так как указанные коэффициенты по условию задачи соотносятся между собой как
k1 : k2 : k3 = 1 : 2 : 3.
Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k1, k2, k3:
1kобщ=1k1+1k2+1k3=1k+12k+13k=116k, или kобщ=6k11.
Найденное ранее значение kобщ = 300 Н/м позволяет рассчитать k = 550 Н/м.
Тогда коэффициенты жесткости каждой из пружин имеют значения:
- для первой пружины
k1 = k = 550 Н/м;
- для второй пружины
k2 = 2k = 1100 Н/м;
- для третьей пружины
k3 = 3k = 1650 Н/м.
Обозначение жесткость пружины
Как маркируются пружины, что означает цвет пружин автомобилей ВАЗ
Пружины подвески выполняют несколько важных функций. Кроме существенного влияния на управляемость и грузоподъемность транспортного средства, они еще сглаживают неровности дорожного покрытия, и повышают комфортность во время движения. Однако очень важно, чтобы в ходовой части были использованы пружины одного класса. Чтобы избежать ошибок при их установке, на предприятиях изготовителях в обязательном порядке производится маркировка пружин.
Классификация
Различают несколько видов пружин:
- Стандартные. Как правило, устанавливаются на заводе изготовителе транспортного средства, и обеспечивают его эксплуатацию в условиях паспортных параметров нагрузки.
- Усиленные. Отличаются большей жесткостью и улучшают эксплуатационные характеристики транспортного средства во время движения по проселочным дорогам, или при транспортировании прицепа.
- Повышающие. Способствуют увеличению клиренса и грузоподъемности.
- Понижающие. Уменьшают клиренс и снижают высоту центра тяжести. Устанавливаются любителями динамического стиля вождения.
Все они, независимо от того, к какому виду относятся, имеют специфические особенности при изготовлении.
Особенности изготовления
Производство данного элемента подвески, является одним из сложнейших процессов в ходе изготовления деталей и узлов, входящих в состав автомобиля. Этот процесс характеризуется большим количеством сложных технологических операций, многие из которых очень плохо поддаются контролю. Поэтому добиться идентичности всех необходимых параметров, при серийном или массовом производстве практически невозможно. В связи с этим на предприятиях-изготовителях, вынуждены проводить сравнительный анализ и осуществлять цветовую маркировку пружин с идентичными характеристиками.
Отличия пружин подвески и их маркировка
Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:
- изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
- изготавливать пружины одинаковой высоты, но различной жесткости;
- изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.
Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.
Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.
- Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
- Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.
Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.
Важное
Класс А, также как и класс В, имеют абсолютно равнозначное право на существование. Маркировка по цветам была введена для того, чтобы исключить разницу в их высоте на противоположных бортах автомобиля. Ведь установка пружин разной высоты с двух сторон одной оси автомобиля приведет к ухудшению его управляемости и устойчивости, а также приведет к скорому выходу из строя деталей ходовой части.
Специалисты рекомендуют использовать пружины только одного класса. Допускается в передней подвеске применять класс А, а в задней — класс В. Если же в передней подвеске использованы пружины класса В, то установка в задней подвеске класса А запрещается категорически. В любом случае на одной оси в обязательном порядке должны быть установлены пружины как одного вида, так и одного класса.
Интересно
Очень часто маркировку классов А и В еще называют маркировкой по жесткости. Действительно, если необходимо регулярно осуществлять поездки с полной нагрузкой, то лучше использовать класс А, так как они выдерживают несколько большую нагрузку. Однако разница эта невелика и составляет примерно 25 кг.
Маркировку в соответствии с требованиями действующих стандартов, изготовители наносят не всегда. Однако цветовая маркировка пружины, относящая ее к определенному классу, должна быть нанесена обязательно. Мало того, она должна быть одинаковой на обеих приобретаемых пружинах, соответствующих друг другу по цвету. Если такая цветовая маркировка отсутствует, то лучше воздержаться от их приобретения.
Коэффициент жесткости пружины
Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.
Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.
Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd4/8D3n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
- d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Формула жесткости соединений пружин
Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:
- Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
- Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.
В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.
При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k1+1/k2+…+1/kn. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k1+k2+…kn.
Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
- Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
- Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
- Модуля сдвига, который зависит от типа применяемого материала.
Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Единицы измерения
При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.
Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.
Разделение пружины по цветам проводится в сфере автомобилестроения.
Среди особенностей подобной маркировки отметим следующее:
- Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
- Класса В представлен синим, голубым, черным и желтым цветом.
Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Маркировка пружин по цвету
Все пружины, выпускаемые изготовителем, маркируются разными цветами. Маркировка пружин по цвету в магазине необходима для наглядного определения жесткости приобретаемой пружины.
Пружины ВАЗ. Маркировка пружины по цветуКлассы пружин по жесткости
Каждому образцу пружины перед выпуском с завода устанавливается определенный класс. Так, класс «А» присваивается пружинам, у которых наблюдается попадание в верхнее поле допуска, и класс «В» — пружинам, высота которых близка к нижнему полю допуска.
- Классу «А» присвоены следующие цветовые маркеры жесткости пружин – белая, желтая, оранжевая и коричневая.
- Классу «В» — черная, синяя, голубая и желтая цветовая маркировка пружин.
Маркировка пружин по цвету. Таблица
Определить жесткость пружин можно не цвету внешнего вида. Многие считают, что пружины желтого цвета – усиленные, красные – спортивные и т.д. В этом нет правды. Пружины окрашивают краской разных цветов для защиты от коррозии.Определяется жесткость пружин по маркерам, нанесенным на внешнюю сторону витка. Таблица соответствия цветового маркера на внешней стороне пружины и ее жесткости приведена ниже:
Таблица цветовой маркировки пружин автомобиляРекомендации выбора пружин
На автомобиль всегда устанавливают пружины одного класса, чтобы машина не теряла упругих свойств подвески и управляемости. Не рекомендуется также ставить пружины разного класса впереди и сзади автомобиля. Это приведет к нарушению баланса авто на высоких скоростях и проезде поворотов. Если есть такая необходимость, то допускается установка пружин класса «А» в переднюю подвеску, и пружин класса «В» в заднюю.
Для кроссоверов и автомобилей большей проходимости часто ставят пружины класса «А». Они выдерживают немного большие нагрузки и имеют больший ход по сравнению с классом «В».
Не пренебрегайте покупкой более дорогих пружин, пружин более высокого класса. Спасибо Вам скажет и подвеска автомобиля, и Ваше состояние в длинной и долгой поездке. Более мягкая езда снизит вибрационные нагрузки на водителя, которые часто приводят последнего к быстрой утомляемости и снижению концентрации.
Цветовая маркировка пружин «Спорт»
Со спортивными пружинами цвет не имеет значения и является выбором компании. Зеленые, синие, красные или желтые пружины не указывают на степень их жесткости. Таким образом, разные цвета пружин являются характерной чертой производителя. Они используются для облегчения распознавания бренда, и это не имеет ничего общего с масштабом или характеристиками их работы.
Жесткость пружины определяется цветовой шкалой, размещенной только на витках пружины, или точками, пробитыми на них (…) или выемками (IIIII). Вы также можете найти окрашенные пятна (оооо). Их число означает твердость пружины.
Согласно стандартам, жесткость пружины должна быть именно выбита на пружине, а не окрашено, запомните это.
УСТАНОВКА ПРУЖИН АВТОМОБИЛЯ ПО ЖЕСТКОСТИ ВАЗ
Для правильной установки пружин на автомобили ВАЗ используют цветовую маркировку по жесткости.
Изготовление пружин автомобиля после всех операций подвергается последнему этапу, а именно осуществляется контроль статической нагрузки пружины. У пружин подвески автомобиля существуют допустимые значения контрольной нагрузки. Пружины автомобиля классифицируют по двум признакам:
- Плюсовой допуск (жесткие) – класс А;
- Минусовой допуск (мягкие) – класс В;
В зависимости от класса пружины подвески метятся краской на внешней стороне витков.
ЦВЕТОВАЯ МАРКИРОВКА жесткости ПРУЖИН ВАЗ
КАКИЕ ПРУЖИНЫ ЛУЧШЕ ВАЗ?
Большинство пружин подвески устанавливаемых на автомобили метятся зеленой и желтой краской. Зеленой обозначаются жесткие, а желтой мягкие.
Какие пружины лучше мягкие или жесткие?
Здесь мы поговорим о разнице этих пружин и на что она влияет. Разновидность классов пружин помогает уменьшить разницу между длиной пружин правого и левого бортов автомобиля, что делает управление автомобилем более удобным и правильным, ведь при таком раскладе автомобиль ведет себя более устойчиво.
Производители рекомендуют устанавливать пружины одного класса. В исключительных случаях разрешается устанавливать на переднюю ось более жесткие пружины, а на заднюю более мягкие. При установке пружин разного класса ставить мягкие пружины (класс В) на передок не стоит. Выбор пружин подвески зависит от того как вы ездите, если подвеска автомобиля подвергается большим нагрузкам лучше выбрать жесткие пружины, они продержатся немного дольше. Но заметьте разница будет ощущаться в районе 20-30 килограмм нагрузки.
Если вы установили мягкие пружины на передок, обязательно установите такие же на задок. При разных раскладах на разных бортах одной оси автомобиля должны быть установлены пружины одного класса – и на правом и на левом.
Коэффициент жесткости пружины, формула и примеры
Онлайн калькуляторыНа нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
СправочникОсновные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решениеНе можете решить контрольную?! Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Сила упругости (), которая возникает в результате деформации тела, в частности пружины, направленная в сторону противоположную перемещению частиц, деформируемого тела, пропорциональна удлинению пружины:
Он зависит от формы тела, его размеров, материала из которого изготовлено тело (пружина).
Иногда коэффициент жесткости обозначают буквами D и с.
Величина коэффициента жёсткости пружины указывает на устойчивость ее к действию нагрузок и насколько велико ее сопротивление при воздействии.
Коэффициент жесткости соединений пружин
Если некоторое число пружин соединить последовательно, то суммарную жесткость такой системы можно вычислить как:
В том случае, если мы имеем дело с n пружинами, которые соединены параллельно, то результирующую жесткость получают как:
Коэффициент жесткости цилиндрической пружины
Рассмотрим пружину в виде спирали, которая сделана из проволоки с сечением круг. Если рассматривать деформацию пружины как совокупность элементарных сдвигов в ее объеме под воздействие сил упругости, то коэффициент жесткости можно вычислить при помощи формулы:
где — радиус пружины, — количество витков в пружине, — радиус проволоки, — модуль сдвига (постоянная, которая зависит от материала).
Единицы измерения
Основной единицей измерения коэффициента жесткости в системе СИ является:
В СГС:
= дин/см
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Разработка урока: Сила упругости. Закон Гука.
Прием «Ассоциативный ряд».
К теме урока нужно выписать в столбик слова-ассоциации. Учитель просит из ассоциативного ряда убрать лишнее слово, сформулировать тему и цель урока. Ученики, прочитав написанные слова, пытаются угадать тему урока.
Слова ассоциативного ряда к уроку «Сила упругости.Закон Гука»: растяжение, изгиб, сжатие, деформация, инерция, пластическая деформация, Р. Гук, сила упругости.
Дифференциация: Задание.
Работа с учебником методом чтения с пометками.
Откройте учебник §18 и запишите в тетрадь в виде схемы – Сила упругости.
| Сила упругости-___________ Формула: где
k= ∆x= | |||||||||||||||||||||||||||||||||
Обменяйтесь с соседями шаблонами. Взаимопроверка. У доски по одному учащемуся выходят к доске и заполняют шаблон.
Тест с взаимопроверкой. Сила упругости. Закон Гука
1.Когда возникает сила упругости?
а)Когда тело движется. в) Когда тело деформируется.
б)Когда оно останавливается. г) Когда оно распрямляется.
2.Какое тело испытывает деформацию растяжения?
а)№ 1 (хлопья под прессом).
в) № 3 (скамейка).
б)№ 2 (подвес люстры).
г) № 4 (стол).
3.Если тело (опора) деформируется под действием груза (см. рис.), то когда модуль силы упругости становится равным модулю силы тяжести, действующей на груз?
а)Когда опора начинает прогибаться.
б)Когда, прогнувшись, опора перестает деформироваться.
в)Когда при снятии груза опора начинает выпрямляться.
г)Такого равенства не бывает.
4.В каком из изображенных на рисунке случаев сила упругости отсутствует (равна нулю)?
а)№ 1 (мяч с вмятиной).
б)№ 2 (доска, перекинутая через ручей).
в)№ 3 (пружина с грузом).
г)Нет такого случая.
5.От чего зависит сила упругости?
а)От модуля силы, деформирующей тело.
б)От деформации.
в)От жесткости деформируемого тела.
г)От всех этих величин.
6. При каких деформациях справедлив (выполняется) закон Гука?
а)При сжатии и растяжении.
б)При изгибе и кручении.
в)При всех видах деформаций.
г)При всех деформациях, если они — упругие деформации.
Ответы: 1.В ; 2.Б; 3.Б; 4.Б; 5.Г; 6.Г.
Дифференциация: Оценивание.
Формативное оценивание. Учитель предлагает каждому ученику проверить работу своего одноклассника. При этом учащийся комментируя другую работу не оценивают ее, а лишь определяет положительные моменты, и моменты, которые, по его мнению, заслуживает доработки. Обратная связь учащихся может быть озвучена или представлена в письменной форме.
Каждый ученик получает свою работу с комментариями. Для доработки предоставляется им время.
Дифференциация: Классификация.
Деление на группы по уровню успеваемости для раздачи заданий разного уровня сложности.
Разбивка по критерию. Учитель предлагает учащимся критерии, которые подразумевают не ранжирование, а ясную классификацию с четким разделением участников на разные категории (этот способ особенно удобен в тех случаях, когда в подгруппах необязательно должно быть равное количество игроков).
Оценивая себя по критериям ученик определяет свою группу.
Первый уровень – задача на знание, понимание и применение прямой формулы закона Гука.
Задание:
1. Под действием какой силы пружина, имеющая коэффициент жесткости 1 кН/м, сжалась на 4 см?
2. Какова сила упругости, возникающая в пружине, жесткостью 50 Н/м, если она растянулась на 5см?
| Критерии | Дескрипторы |
| Использует формулу закона Гука при решении задачи | Записывает условие задачи |
| Переводить единицы измерения в систему СИ | |
| Записывает формулу закона Гука | |
| Проводит вычисления |
Второй уровень: задача на преобразование формулы закона Гука для определенияжесткости и деформации тел; задача для определения коэффициента жесткости с использованиемграфика зависимости силы упругости от деформации.
Задание:1. По данным графиков зависимости силы упругости от деформации определить коэффициент жесткости.
а) б)
| Критерии | Дескрипторы |
| Определяют коэффициент жесткости по графику зависимости силы упругости от деформации | Определяет по графику значениесилы упругости и деформации |
| Записывает условие задачи | |
| Переводить единицы измерения в систему СИ | |
| Записывает формулу закона Гука | |
| Преобразует формулу для определения коэффициента жесткости | |
| Проводит вычисления |
Третий уровень – задача творческого характера – составить условие задачипо графику зависимости силы упругости от деформации.
Задание:
| Критерии | Дескрипторы |
| Составляют условие задачи по графику зависимости силы упругости от деформации | Определяет по графику значениесилы упругости и деформации |
| Составляет условие задачи | |
| Записывает условие задачи | |
| Записывает формулу закона Гука | |
| Преобразует формулу для определения коэффициента жесткости | |
| Проводит вычисления |
Четвертый уровень — задача творческого характера на самостоятельное изучение и определение жесткости при последовательном и параллельном соединении пружин.
Дифференциация: Источники
Задание:Две пружины с жесткостями k1 = 200 Н/м и k2 = 300 Н/м
соединены:последовательно и параллельно.Найдите жёсткость при последовательном и параллельном соединениипружин.
| Критерии | Дескрипторы |
| Самостоятельно изучают и определяют жесткость при последовательном и параллельном соединении пружин | Изучает соединение пружин |
| Выводят формулу для последовательного и паралельного соединения пружин | |
| Записывает условие задачи | |
| Записывает формулу жесткости для последовательного и паралельного соединения пружин | |
| Проводит вычисления |
Проверка выполнения задания. Лидер каждой группы объясняет решенные задачи. Учащиеся задают уточняющие вопросы, устраняют ошибки, исправляют недочеты свои и выступающего.
Дифференциация: Диалог и оказание поддержки.
Формативное оценивание:Устная обратная связь. Похвала!
Молодец! Ты сегодня хорошо работал! Старайся, у тебя обязательно все получится!
Силы упругости. Закон Гука
«Напичканный знаниями, но не умеющий
их использовать ученик, напоминает
фаршированную рыбу, которая не может плавать».
А.Л. Минц
Данная тема будет посвящена решению задач на силы упругости и закон Гука.
Задача 1. Две пружины равной длины поочередно растягиваются под действием одной и той же силы. Пружина жесткостью 500 Н/м растянулась на 1 см. Чему равна жесткость второй пружины, если ее растяжение равно 5 см?
|
ДАНО: |
РЕШЕНИЕ: Записываем III закон Ньютона для 1-ой и 2-ой пружины: В проекциях на ось Оy: По условию задачи F1 = F2, то получаем Тогда жёсткость второй пружины равна |
Ответ: 100 Н/м.
Задача 2. На рисунке изображены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и радиуса. Сравните жесткости проволок.
|
ДАНО: |
РЕШЕНИЕ: По третьему закону Ньютона: По закону Гука: Т.к. по условию задачи силы F1 и F2 равны, то |
Ответ: жесткость стальной проволоки в 2 раза больше жесткости медной проволоки.
Задача 3. Две одинаковые пружинки одинаковой жесткости соединяют в первом случае последовательно, а во втором — параллельно. В каком случае и во сколько раз жесткость составной пружины будет больше?
|
ДАНО: |
РЕШЕНИЕ:
Рассмотрим первый случай, когда пружины соединяют последовательно. Модуль результирующей силы упругости Модуль полной деформации: Тогда: Теперь рассмотрим параллельное соединение пружинок. И так, при параллельном соединении произойдет перераспределение нагрузки в зависимости от жесткости пружин, вследствие чего модуль результирующей силы упругости составной пружины будет равен сумме модулей сил упругости отдельных пружинок Модуль полной деформации: Тогда Следовательно |
Задача 4. На подставке лежит груз массой 0,5 кг, связанный с прикрепленной к потолку невесомой пружинкой. В начальный момент времени пружинка не растянута. Подставку начинают опускать с ускорением 0,5g. Через какой промежуток времени груз оторвется от подставки, если жесткость пружинки составляет 5 Н/м?
|
ДАНО: |
РЕШЕНИЕ: Запишем второй закон Ньютона в общем виде В проекция на ось Оx: В момент отрыва груза от подставки: Тогда Уравнение перемещения при равноускоренном движении для груза: В начальный момент времени: Тогда Получаем следующую систему уравнений Из которой следует, что искомый промежуток времени |
Ответ: 0,45 с.
Механические колебания — Страница 2
Пример 1.
Кольцо радиуса \ (R \) совершает небольшие колебания вокруг точки поворота \ (O \) (рисунок \ (6 \)). Определите период колебаний.Решение.
Рис. 6.Кольцо, подвешенное в точке \ (O, \), представляет собой физический маятник. Период колебаний определяется по формуле
\ [T = 2 \ pi \ sqrt {\ frac {I} {{mga}}}, \]
где \ (I \) — момент инерции кольца относительно его центра, \ (m \) — масса кольца, \ (a \) — расстояние от точки поворота до центра кольца.{\ cancel {2}}}}} {{\ cancel {m} g \ cancel {R}}}}}
= {2 \ pi \ sqrt {\ frac {{2R}} {g}}.}
\]
Пример 2.
Масса подвешена на двух последовательно соединенных пружинах. Жесткость одной пружины в два раза больше, чем у другой: \ ({k_2} = 2 {k_1}. \) Как изменяется период колебаний, если пружины соединены параллельно (рисунок \ (7 \))?Решение.
Рисунок 7.Рассчитаем эквивалентную жесткость в случае последовательного и параллельного соединения пружин.
В случае последовательного соединения сила упругости каждой пружины равна силе тяжести (без учета веса пружин). Полное удлинение — это сумма расширений каждой пружины:
\ [x = {x_1} + {x_2}. \]
Тогда эквивалентная жесткость равна
. \ [
{x = {x_1} + {x_2}, \; \;} \ Rightarrow
{\ frac {F} {k} = \ frac {F} {{{k_1}}} + \ frac {F } {{{k_2}}}, \; \;} \ Rightarrow
{\ frac {1} {k} = \ frac {1} {{{k_1}}} + \ frac {1} {{{k_2}) }}, \; \;} \ Rightarrow
{k = \ frac {{{k_1} {k_2}}} {{{k_1} + {k_2}}}.}
\]
При параллельном соединении растяжение обеих пружин одинаковое, а общая сила упругости будет равна сумме сил каждой пружины:
\ [{x = {x_1} = {x_2}, \; \; \;} \ kern-0.3pt {F = {F_1} + {F_2}.} \]
Следовательно, эквивалентная жесткость пружин, соединенных параллельно, равна
. \ [
{F = {F_1} + {F_2}, \; \;} \ Rightarrow
{kx = {k_1} {x_1} + {k_2} {x_2} = \ left ({{k_1} + {k_2 }} \ right) x, \; \;} \ Rightarrow
{k = {k_1} + {k_2}.}
\]
Период колебаний последовательно включенных пружин
.\ [{{T_1} = 2 \ pi \ sqrt {\ frac {m} {k}}} = {2 \ pi \ sqrt {\ frac {{m \ left ({{k_1} + {k_2}} \ справа)}} {{{k_1} {k_2}}}},} \]
и в случае параллельного подключения:
\ [{{T_2} = 2 \ pi \ sqrt {\ frac {m} {k}}} = {2 \ pi \ sqrt {\ frac {m} {{{k_1} + {k_2}}}}. } \]
Теперь мы можем узнать, как изменяется период колебаний при переходе от последовательного к параллельному соединению пружин:
\ [{\ frac {{{T_2}}} {{{T_1}}} = \ frac {{\ sqrt {\ frac {1} {{{k_1} + {k_2}}}}}} {{\ sqrt {\ frac {{{k_1} + {k_2}}} {{{k_1} {k_2}}}}}}} = {\ frac {{\ sqrt {{k_1} {k_2}}}} {{{ k_1} + {k_2}}}.2}}} {{{k_1} + 2 {k_1}}}}
= {\ frac {{\ sqrt 2 \ cancel {k_1}}} {{3 \ cancel {k_1}}}}
= {\ frac {{\ sqrt 2}} {3}.}
\]
Пример 3.
Найти коэффициент \ (Q \) осциллятора, если после \ (50 \) колебаний амплитуда смещения уменьшилась вдвое.Решение.
Сначала мы вычисляем логарифмический декремент \ (\ delta. \) По определению, логарифмический декремент пропорционален натуральному логарифму отношения амплитуд \ ({x_0} \) и \ ({x_N} \) двух колебаний. , разделенных точками \ (N \):
\ [\ delta = \ frac {1} {N} \ ln \ frac {{{x_0}}} {{{x_N}}}.\]
В нашем случае это
\ [{\ delta = \ frac {1} {{50}} \ ln 2} \ приблизительно {\ frac {1} {{50}} \ cdot 0,693} = {0,0139.} \]
Тогда добротность системы равна
.\ [{Q = \ frac {\ pi} {\ delta} \ приблизительно \ frac {\ pi} {{0,0139}}} \ приблизительно {227.} \]
Расчет скорости параллельных и последовательных пружин
Расчет скорости пружин в серии
Пружины, соединенные последовательно, — это пружины, которые устанавливаются одна на другую и должны работать вместе в этой форме.В этом случае пружины работают как одна, поэтому, поскольку витков больше, эквивалентная жесткость пружины, выполняемая этими пружинами, будет слабее, чем жесткость пружины одной из этих пружин. Взгляните на примеры и диаграмму, приведенные ниже, для объяснения того, как рассчитать скорость пружин в серии, когда пружины одинаковые или разные.
Пример A. (Разные пружины)
У вас есть две пружины, наложенные друг на друга.Скорость одной из этих пружин составляет 20 фунтов силы / дюйм (фунтов силы на дюйм), тогда как скорость другой пружины, установленной поверх этой, составляет 40 фунтов силы / дюйм. Умножьте ставки вместе (k1 и k2) и разделите произведение на сумму ставок, как показано в приведенной ниже формуле. Результирующий Keq — это новый коэффициент для двух последовательно соединенных пружин.
Keq = (k1) (k2) / (k1 + k2)- Keq = эквивалентная ставка
- k1 = Скорость пружины 1
- k2 = Скорость пружины 2
Пример Б. (Идентичные пружины)
У вас есть две идентичные пружины с жесткостью пружины 30 фунт-сила / дюйм (фунтов силы на дюйм). Чтобы рассчитать ставку, которую эти два обеспечивают вместе, просто умножьте ставку на 1/2 (0,5). Формула для этого расчета также представлена ниже. Результирующий Keq — это новый коэффициент для двух последовательно соединенных пружин.
Keq = ½ (к)- Keq = эквивалентная ставка
- k = скорость
Последовательные и параллельные пружины — проблемы и решения
1.Объект весом 160 грамм прикреплен к одному концу пружины, и изменение длины пружины составляет 4 см. Каково изменение длины трех пружин, соединенных последовательно и параллельно, как показано на рисунке ниже?
Известный:
Изменение длины пружины (Δx) = 4 см = 0,04 м
Масса (м) = 160 грамм = 0,16 кг
Ускорение свободного падения (g) = 10 м / с 2
Вес (w) = m g = (0,16) (10) = 1,6 Ньютон
Требуется: Изменение длины трех пружин (Δx)
Раствор:
Уравнение закона Гука:
k = w / Δx = 1.6 / 0,04 = 40 Н / м
Три пружины имеют одинаковую постоянную k = 40 Н / м.
Определите эквивалентную константу:
Пружина 2 (k 2 ) и пружина 3 (k 3 ) соединены параллельно. Эквивалентная константа:
k 23 = k 2 + k 3 = 40 + 40 = 80 Н / м
Пружина 1 (k 1 ) и пружина 23 (k 23 ) соединены последовательно. Эквивалентная константа:
1 / k = 1 / k 1 + 1 / k 23 = 1/40 + 1/80 = 2/80 + 1/80 = 3/80
к = 80/3
Определите изменение длины трех пружин:
Δx = w / k = 1.6: 80/3 = (1,6) (3/80) = 4,8 / 80 = 0,06 м = 6 см
2. Три пружины с одинаковой постоянной, соединенные последовательно и параллельно, и объект весом 2 кг, прикрепленный к одному концу пружины, как показано на рисунке ниже. Жесткость пружины k 1 = k 2 = k 3 = 300 Н / м. Какое изменение длины у трех пружин. Ускорение свободного падения g = 10 м.с -2 .
Известный:
Жесткость пружины k 1 = k 2 = k 3 = 300 Н.м -1
Ускорение свободного падения (g) = 10 м.с -2
Масса объекта (м) = 2 кг
Вес объекта (w) = m g = (2) (10) = 20 Ньютон
Требуется: Изменение длины трех пружин (Δx)
Раствор:
Определите эквивалентную константу:
Пружина 1 (k 1 ) и пружина 2 (k 2 ) соединены параллельно. Эквивалентная константа:
k 12 = k 1 + k 2 = 300 + 300 = 600 Н / м
Пружина 3 (k 3 ) и пружина 12 (k 12 ) соединены последовательно.Эквивалентная константа:
1 / k = 1 / k 3 + 1 / k 12 = 1/300 + 1/600 = 2/600 + 1/600 = 3/600
k = 600/3 = 200 Н / м
Определите изменение длины трех пружин:
Δx = w / k = 20/200 = 2/20 = 1/10 = 0,1 м
3. Три пружины соединены последовательно и параллельно, как показано на рисунке ниже. Если жесткость пружины k = 50 Нм -1 и масса 400 грамм прикреплена к одному концу пружины. Какое изменение длины у трех пружин.
Известный:
Жесткость пружины 1 (k 1 ) = k = 50 Нм -1
Жесткость пружины 2 (k 2 ) = k = 50 Нм -1
Жесткость пружины 3 (k 3 ) = 2k = 2 (50 Нм -1 ) = 100 Нм -1
Масса объекта (м) = 400 грамм = 0,4 кг
Ускорение свободного падения (g) = 10 м / с 2
Вес объекта (w) = m g = (0,4) (10) = 4 Ньютона
Требуется: Изменение длины (Δx)
Раствор:
Определите эквивалентную константу:
Пружина 1 (k 1 ) и пружина 2 (k 2 ) соединены параллельно.Эквивалентная константа:
k 12 = k 1 + k 2 = 50 + 50 = 100 Н / м
Пружина 3 (k 3 ) и пружина 12 (k 12 ) соединены последовательно. Эквивалентная константа:
1 / k = 1 / k 3 + 1 / k 12 = 1/100 + 1/100 = 2/100
k = 100/2 = 50 Н / м
Определите изменение длины трех пружин:
Δx = w / k = 4/50 = = 0,08 м = 8 см
В чем разница между последовательным и параллельным классом 11 по физике CBSE
Подсказка: Когда пружина растягивается или сжимается, она испытывает смещение x, которое прямо пропорционально возвращающей силе F.Математически это выражается как $ F \ propto x $. Убрав знак пропорциональности, мы получим $ F = — kx $. Где k — жесткость пружины, которая дает меру жесткости пружины. Отрицательный знак означает, что природа силы восстанавливается. Полный пошаговый ответ:
Жесткость пружины, определяющая жесткость пружины. Возвратная сила равна $ F = — kx $.
Возможны две комбинации пружин.
Серийная комбинация: здесь пружины прикреплены встык по цепочке
Параллельная комбинация: здесь пружины берут начало и оканчиваются в одних и тех же точках
В последовательной комбинации
Скажем, есть две пружины $ {S_ {1 \,} }, \, {S_2} $ соединены последовательно.
Возвращающая сила на пружине $ {S_ {1 \,}} $ будет $ {F_1} = — {k_1} {x_1} $, а возвращающая сила на пружине $ {S_2} $ будет $ {F_2} = — {k_2} {x_2} $.
Поскольку напряжение, действующее в обеих пружинах, одинаково, $ {F_1} = {F_2} = F $, где F — эквивалентная сила.
Теперь смещения заданы как $ {x_1} = \ dfrac {{{F_1}}} {{{k_1}}} $ и $ {x_2} = \ dfrac {{{F_2}}} {{{k_2}} } $. эквивалентное смещение задается как
$ x = \ dfrac {F} {k} $.
Эквивалентное смещение — это сумма всех отдельных смещений.
Итак, $ x = {x_1} + {x_2} $.
Подставляя значения,
$ x = \ dfrac {{{F_1}}} {{{x_1}}} + \ dfrac {{{F_2}}} {{{x_2}}} $
$ \ Rightarrow \ dfrac { F} {x} = \ dfrac {{{F_1}}} {{{x_1}}} + \ dfrac {{{F_2}}} {{{x_2}}} $
Мы знаем, что
$ {F_1} = {F_2} = F $
Следовательно, уравнение сводится к $ \ dfrac {F} {x} = \ dfrac {F} {{{x_1}}} + \ dfrac {F} {{{x_2}}} $
Далее решая это, получаем
$ \ dfrac {1} {x} = \ dfrac {1} {{{x_1}}} + \ dfrac {1} {{{x_2}}} $
Это формула для пружин соединены последовательно.
В параллельной комбинации,
Скажем, есть две пружины $ {S_ {1 \,}}, \, {S_2} $, соединенные в параллельной комбинации.
Возвращающая сила на пружине $ {S_ {1 \,}} $ будет $ {F_1} = — {k_1} {x_1} $, а возвращающая сила на пружине $ {S_2} $ будет $ {F_2} = — {k_2} {x_2} $.
Поскольку сумма напряжений, действующих в обеих пружинах, является эквивалентной силой, $ {F_1} + {F_2} = F $, где F — эквивалентная сила.
Подставляя значения,
$ {k_1} {x_1} + {k_2} {x_2} = kx $
Поскольку смещение одинаково для каждой пружины, $ {x_1} = {x_2} = x $.
Уравнение сводится к $ {k_1} x + {k_2} x = kx $
$ \ Rightarrow {k_1} + {k_2} = k $
Это формула для пружин, соединенных параллельно.
Примечание: Формула для последовательного и параллельного сочетаний в пружинах прямо противоположна, как в случае сопротивлений. Так что разницу нужно отметить внимательно. Отрицательный знак обозначает только природу силы. Таким образом, его можно не учитывать в расчетах.
Что такое жесткость пружины при параллельном и последовательном подключении? — AnswersToAll
Что такое жесткость пружины при параллельном и последовательном подключении?
Эта система из двух параллельных пружин эквивалентна одной пружине Гука с жесткостью пружины k.Значение k можно найти по формуле, которая применяется к конденсаторам, включенным параллельно в электрическую цепь. Серии. В качестве альтернативы направление силы может быть изменено на противоположное, чтобы пружины сжались.
Как узнать, включена ли пружина последовательно или параллельно?
И наоборот, они считаются параллельными, если деформация ансамбля является их общей деформацией, а напряжение ансамбля является суммой их напряжений. Любая комбинация пружин Гука (линейного отклика), включенных последовательно или параллельно, ведет себя как одна пружина Гука.
Какова жесткость пружины двух последовательно соединенных пружин?
Используя те же пружины, что и в первом примере, когда две шкалы пружин 10 Н / м соединены последовательно, результирующая жесткость пружины для системы с двумя пружинами составляет 5 Н / м. Результирующая жесткость пружины составляет половину значения исходной жесткости одиночной пружины.
Как найти пружину в серии?
В случае последовательного соединения сила упругости каждой пружины равна силе тяжести (без учета веса пружин).Полное удлинение — это сумма удлинений каждой пружины: x = x1 + x2. x = x1 + x2, ⇒Fk = Fk1 + Fk2, ⇒1k = 1k1 + 1k2, ⇒k = k1k2k1 + k2.
Как определить исходную длину пружины?
Невозможно найти ненагруженную длину пружины только с нагрузкой и увеличенной длиной и в отсутствие жесткости пружины. Согласно закону Гука, F (сила) = kX, где «k» — постоянная пружины, определяющая жесткость пружины, а «X» — удлинение пружины.
Как найти жесткость пружины с учетом массы и расстояния?
Формула для расчета жесткости пружины выглядит следующим образом: k = -F / x, где k — жесткость пружины.F — сила, а x — изменение длины пружины.
Более жесткие пружины оказывают большее усилие?
Менее жесткий объект легче растянуть или сжать. Сравнивая два эластичных объекта, более упругая сила пружины будет действовать на более жесткий эластичный объект, когда они растянуты или сжимаются на одинаковую длину.
Какова потенциальная энергия пружины?
Упругая потенциальная энергия — это потенциальная энергия, запасенная в результате деформации упругого объекта, например, растяжения пружины.Это равно работе, проделанной для растяжения пружины, которая зависит от жесткости пружины k, а также от растянутого расстояния.
Всегда ли потенциальная энергия пружины положительна?
Итак, для любого движения пружины из ее положения равновесия (удлинение или сжатие) необходимо подавать внешнюю энергию. Следовательно, в этом смысле изменение потенциальной энергии всегда положительно, в данном случае, как упомянул Джон Ренни в своем посте.
Сколько упругой потенциальной энергии хранится в пружине?
Упругая потенциальная энергия пружины равна половине произведения ее постоянной пружины на квадрат ее растяжения или сжатия.или Page 2 6/3/14 2 Энергия может накапливаться в системе, когда в ней производятся работы. Когда вы прикладываете силу к пружине, она деформируется.
Является ли сжатая пружина потенциальной энергией?
Объект обладает упругой потенциальной энергией, если он растягивается или сжимается из положения равновесия внешней силой (Fapplied).
Когда вы сжимаете пружину, потенциальная энергия пружины увеличивается?
Решение: Когда пружина сжимается или растягивается, потенциальная энергия пружины увеличивается в обоих случаях.Это потому, что мы делаем работу как на сжатие, так и на растяжение.
Почему сжатая пружина весит больше?
С точки зрения веса сжатая пружина будет весить больше на предмет, находящийся под ней. Его вес соответствует его силе тяжести плюс сжимающая сила, действующая на пружину. По массе как сжатая, так и несжатая пружина имеют одинаковую массу.
В какой точке мяч имеет наибольшую кинетическую энергию?
Когда мяч удерживается в наивысшей точке, он обладает потенциальной энергией, в частности, потенциальной энергией гравитации.2. Когда мяч падает на стол, он обладает кинетической энергией. У него наибольшая кинетическая энергия в самом конце спуска, когда он движется с максимальной скоростью.
Как найти энергию, запасенную в пружине?
Как рассчитать потенциальную энергию пружины
- Определите жесткость пружины k.
- Решите, насколько вы хотите растянуть или сжать пружину.
- Подставьте эти значения в формулу потенциальной энергии пружины: U = ½kΔx2.
- Рассчитайте энергию.
Сила постоянна?
Согласно третьему закону движения Ньютона, каждое действие имеет равную и противоположную реакцию. Это можно хорошо наблюдать в случае пружины, в которой сжатие или растяжение пружины создает противоположную силу. Сила, установленная этим законом, объясняется законом Роберта Гука.
пересмотр физики | Редакция GCSE и A Level по физике | Киберфизика, доработка сайта
До уровня A вы должны рассматривать только наборы идентичных пружин, составляющие последовательные и параллельные комбинации.
Последовательные пружины
Каждая пружина испытывает одинаковое усилие от веса массы, которую она поддерживает. Следовательно, каждая пружина выдвигается на ту же величину, что и отдельная пружина.
Таким образом, комбинация более «эластична», и эффективная жесткость пружины для этой комбинации будет вдвое меньше, чем у одиночной пружины для двух последовательно соединенных, третьей для трех последовательных и т. Д.
Пружины параллельно
Вес поддерживается комбинацией.Они разделяют нагрузку и поэтому не растягиваются так сильно, как если бы они поддерживали груз самостоятельно!
Таким образом, комбинация менее «эластична», и эффективная жесткость пружины для этой комбинации будет вдвое больше, чем у одиночной пружины для двух параллельно, в три раза для трех параллельно и т. Д.
Комбинации пружин, выставляемых ШМ
При рассмотрении «подпрыгивающих масс» комбинаций пружин необходимо помнить, что жесткость пружины изменилась, и это повлияет на период колебаний.
Давайте сократим константы и посмотрим, как связаны две изменяемые переменные.
Мы можем выразить T и k через константы (m остается неизменным, поэтому это константа), и это дает нам:
T√k = постоянная
Следовательно, мы можем написать:
T 1 √k 1 = T 2 √k 2
T 2 = T 1 √ (k 1 / k 2 )
Упругая потенциальная энергия и комбинация пружин
★ ★ ★ ★ ★ [1 голосов]
В этом уроке физики вы узнаете:
- Что такое упругая потенциальная энергия и как это рассчитано?
- Что представляет собой площадь под графиком зависимости силы упругости от деформации?
- В какие виды энергии может быть преобразована упругая потенциальная энергия?
- Что говорит Закон преобразования энергии?
- Как совместить пружины?
- Как найти полную жесткость пружины в определенной настройке комбинации пружин?
- Как изменяется жесткость пружины, когда мы объединяем две или более пружины?
Введение
Вы когда-нибудь видели арку средневековья? Знаете ли вы, какие особенности должны быть у хорошей дуги, чтобы стрелка уходила как можно дальше?
Что вы можете сказать об энергии стрелы, которая летит дальше, по сравнению с энергией стрелы, которая падает ближе?
Значение упругой потенциальной энергии
В учебнике по физике «Работа.Энергия. Типы энергии », было заявлено, что энергия — это способность совершать работу, то есть заставлять объект перемещаться на определенное линейное расстояние r ⃗ с помощью силы F ⃗ . Когда это линейное расстояние находится в соответствии с одним В базовом направлении мы можем написать Δx ⃗ вместо r ⃗ .
Сжатая пружина также может воздействовать на объект при отпускании, то есть она может толкать объект на x ⃗ единиц, прилагая силу F На нем ⃗ . В учебнике по физике «Типы сил III (сила упругости и растяжение)» мы назвали эту (восстанавливающую) силу, прилагаемую растянутой или сжатой пружиной, как упругая сила (F ⃗ e ).
Было обнаружено, что F e = — k × x, где k — жесткость пружины, а x — деформация (растяжение или сжатие) пружины. Знак минус означает, что сила упругости противоположна направлению деформации пружины. Вышеприведенная формула известна как математическое выражение закона Гука, график зависимости F от x которого показан ниже.
График зависимости упругой силы от деформации пружины (F e vs x) для случаев, когда применяется закон Гука, выглядит так, как показано ниже:
Кроме того, в учебнике по физике «Точечное (скалярное) произведение двух векторов «Было заявлено, что Работа — как точечный продукт силы и линейного расстояния — геометрически представлена площадью под графиком« Сила против позиции ».Это правило также справедливо для графика зависимости силы упругости от растяжения. Следовательно, очевидно, что область под графиком зависимости силы упругости от деформации представляет работу, проделанную для растяжения или сжатия пружины, но в то же время она также представляет работу, выполняемую пружиной над контактирующими объектами, когда она отпускается и пытается вернуться в нерастянутую позицию. Эта работа способствует изменению потенциальной энергии пружины, которая также известна как Elastic Potential Energy, EPE .Посмотрите на график:
Из приведенного выше графика очевидно, что сила упругости непостоянна. Он увеличивается с той же скоростью от 0 до франков, макс. . Во время этого процесса пружина растягивается (или сжимается) от 0 до x макс. .
Из геометрии известно, что площадь прямоугольного треугольника, представленного на графике, равна
Площадь = Основание × высота / 2
Подставляя указанные выше значения, получаем для упругой потенциальной энергии EPE пружины:
EPE = W = F e × x / 2
Поскольку F e = k × x (мы имеем дело только с значение силы упругости, а не ее направление; поэтому отрицательный знак здесь не появляется), получаем:
EPE = (k × x) × x / 2
Или
EPE = k × x 2 / 2
Приведенное выше уравнение представляет собой формулу упругой потенциальной энергии, запасенной в упругом объекте при его растяжении или сжатии.Он всегда положительный, потому что какой бы знак мы ни получили для x, когда он возводится в степень два, он становится положительным.
Пример 1
Объект весом 2 кг подвешивается на упругой пружине, в результате чего пружина растягивается на 4 см, как показано на рисунке.
Какая упругая потенциальная энергия сохраняется в пружине во время этого процесса? Для простоты возьмем g = 10 Н / кг.
Решение 1
Во-первых, нам нужно вычислить жесткость пружины k. Таким образом, поскольку вес объекта численно уравновешивается силой упругости, мы можем записать:
W = F e
m × g = k × x
Таким образом,
k = m × g / x
= 2 кг × 10 N / кг / 4 см
= 2 кг × 10 N кг кг / 0.04 м
= 20 Н / 0,04 м
= 500 Н / м
Следовательно, применяя уравнение упругой потенциальной энергии, мы получаем
EPE = k × x 2 / 2
= 500 N / м × (0,04 м) 2 / 2 5
= 2
= 0.4 Дж
Преобразование упругой потенциальной энергии в другие формы энергии
Как запасенная энергия, упругая потенциальная энергия может быть преобразована также в другие формы энергии. Некоторые из наиболее распространенных примеров в этом отношении включают:
a. От упругой к кинетической энергии и наоборот.
Горизонтальная сжатая пружина передает свою накопленную энергию прикрепленному к ней объекту при отпускании, как показано на рисунке
Первоначально пружина сжимается на x единиц.В результате он накапливает упругую потенциальную энергию. При отпускании он передает свою энергию прикрепленному объекту. В результате объект массы m начинает двигаться со скоростью v. Цепочка преобразования энергии в этом случае:
EPE пружины → KE объекта
Запишем:
k × x 2 / 2 = м × v 2 / 2
С другой стороны, если движущийся объект сжимает пружину, подобную показанной на рисунке ниже,
начальная кинетическая энергия объекта полностью преобразуется в упругую потенциальную энергию пружины.
Цепочка преобразования энергии в данном случае
KE объекта → EPE пружины
Можно записать:
m × v 2 / 2 = k × x 2 / 2
б. От гравитационной потенциальной энергии к упругой потенциальной энергии и наоборот
Если объект выпущен с высоты и при падении на землю он сжимает пружину, это пример преобразования GPE → EPE.Посмотрите на рисунок:
Фактически, GPE объекта сначала преобразуется в KE в качестве промежуточной стадии, а затем KE преобразуется в EPE пружины. Следовательно, цепочка преобразования энергии:
GPE объекта → KE объекта → EPE пружины
В символах имеем следующее уравнение
m × g × h = m × v 2 / 2 = k × x 2 / 2
Пренебрегая промежуточной ступенью, получаем
m × g × h = k × 2 / 2
С другой стороны, сжатая пружина в вертикальном положении может поднять объект, вызвавший это сжатие, до определенной высоты h, как показано на рисунке.
Очевидно, этот процесс также содержит промежуточную стадию, то есть стадию, на которой начальная упругая потенциальная энергия, запасенная в сжатой пружине, превращается в кинетическую энергию объекта, а затем эта кинетическая энергия полностью преобразуется в гравитационную потенциальную энергию, когда объект достигает наивысшего положения h.
Цепочка преобразования энергии в данном случае
EPE пружины → KE объекта → GPE объекта
In символов,
k × x 2 / 2 = m × v 2 / 2 = m × g × h
Опять же, если нас не интересует промежуточный этап, а только то, что происходит в начале и в конце В процессе получаем
k × x 2 / 2 = m × g × h
c.Из упругой энергии в тепловую
Прежде всего, стоит отметить, что трение — это процесс, во время которого механическая энергия движущегося объекта преобразуется в тепловую энергию обеих соприкасающихся поверхностей. Следовательно, если сжатая пружина (которая является источником накопленной упругой потенциальной энергии) толкает прикрепленный к ней объект при отпускании, случается, что объект после перемещения на определенное расстояние в конечном итоге останавливается из-за трения о землю.
В конце процесса у объекта не осталось энергии.Это связано с тем, что кинетическая энергия объекта, создаваемая толкающим действием сжатой пружины, постепенно преобразуется в тепловую энергию из-за трения. Мы называем это «работой силы трения» (сокращенно W f ), которая забирает всю кинетическую энергию объекта. Цепочка преобразования энергии в этом случае:
EPE пружины → ME объекта → W трения → 0 (ничего)
Приведенная выше схема скорее не противоречит закону сохранения механической энергии, а является его обобщением. .Этот обобщенный закон известен как «Закон сохранения энергии». В нем говорится, что:
«Энергия не может быть создана или уничтожена; ее можно только преобразовать из одной формы энергии в другую».
Приведенный выше закон является одним из фундаментальных законов физики.
Цепочка преобразований энергии, описанная выше, может быть математически выражена как:
EPE = ME = W f
Или
EPE = KE + GPE = W f
k × x 2 / 2 = м × v 2 / 2 + m × g × h = μ × N × ∆x
, где x — растяжение или сжатие пружины Δx — смещение объекта.Они выражают очень разные вещи.
Давайте посмотрим на исчерпывающий пример, в котором учтены все вышеперечисленные энергии.
Пример 2
Шар весом 800 г начинает катиться по горизонтальной поверхности со скоростью 25 м / с с коэффициентом трения 0,2, как показано на рисунке. Пройдя 4 м, мяч начинает подниматься по пологому склону, а когда достигает высоты 3 м, продолжает движение по горизонтали, пока не упрется в пружину. В результате мяч сжимает пружину на 2 см.Рассчитайте жесткость пружины. Для простоты возьмем g = 10 Н / кг.
Решение 2
Во-первых, мы должны проанализировать преобразования энергии, происходящие в этом процессе. Таким образом, мяч изначально имеет только KE, потому что он находится на уровне земли. В первые 4 м движения часть этой энергии преобразуется в тепловую из-за трения о землю (мы записываем это как Wf). Оставшийся KE после этого расстояния разделяется на KE и GPE, когда объект поднимается на h = 3 м. В конце концов, только последний KE преобразуется в EPE пружины, так как высота не меняется.
Если мы поместим индекс 1 в исходное положение, 2 после 4 м перемещения, 3, когда шар только что поднялся на h = 3 м и 4 в конце процесса, когда шар сжал пружину, как показано на На рисунке ниже,
мы получаем следующую схему преобразований энергии, происходящих в процессе.
Математически мы можем написать:
KE 1 — W f = KE 2 + GPE 2
Заменяя KE 2 на EPE, мы получаем
KE 1 9018 f = EPE + GPE 2
Следовательно, имеем:
m × v 2 / 2 — μ × m × g × ∆x = k × x 2 / 2 + m × g × h
Подставляя значения (обращаем внимание на запись m = 0.8 кг вместо 800 г и x = 0,02 м вместо 2 см) получаем:
0,8 × 25 2 / 2 — 0,2 × 0,8 × 10 × 4 = k × 0,02 2 / 2 + 0,8 × 10 × 3
250 — 6,4 = k × 0,0002 + 24
250 — 6,4-24 = k × 0,0002
219,6 = k × 0,0002
k = 219,6 / 0,0002
= 1098000 N / м
Комбинация пружин
Большое значение жесткости пружины, полученное в предыдущем упражнении, означает, что пружина очень жесткая и, следовательно, он может хранить много упругой энергии при максимальном растяжении или сжатии.
Чтобы изменить уровень жесткости пружин, мы можем объединить две или более пружины двумя основными способами:
a. Серия
В этой комбинации пружины ставятся одна за другой. В результате, когда мы вешаем объект на такую систему, он тянет каждую пружину, если доступна только одна пружина. Следовательно, один и тот же вес вызывает двойное удлинение в системе, состоящей из двух последовательно соединенных пружин, чем если бы это была только одна пружина. Посмотрите на рисунок ниже. Для простоты пружины приняты одинаковыми, т.е.е. каждый из них имеет постоянную k.
Поскольку в обоих случаях действует одна и та же сила F = m × g, для системы с одной пружиной имеем:
k 1 = F / x
и для система с двумя пружинами:
k 2 = F / x + x
= F / 2x
= k 1
Это позволяет нам найти формулу для жесткости пружины ks при последовательной комбинации пружин.Это
1 / k s = 1 / k 1 + 1 / 2
0 03
91803 где k 1 и k 2 — постоянные каждой пружины соответственно.
Это правило может также распространяться на систему, состоящую из более чем двух пружин, или когда пружины не идентичны, т.е. когда их индивидуальные постоянные различны.
Пример 3
Две пружины соединены последовательно, как показано на рисунке. Максимальное растяжение каждой пружины без потери упругих свойств составляет 20 см и 40 см соответственно.
- Какова жесткость пружины этой комбинации, если жесткость первой пружины составляет 4000 Н / м, а жесткость второй пружины — 5000 Н / м?
- Какой максимальный вес они могут удерживать в такой комбинации?
Решение 3
- Используя формулу для последовательной комбинации пружин, получаем
1 / k s = 1 / 1 k + 1 / к 2
= 1 / 4000 + 1 / 47 5000 903 20000 + 4 / 20000
= 9 / 20000
Таким образом,
k 9047 9047 9048 9 = 2222 N / м
- Мы должны найти максимальный вес, который может выдержать каждая пружина, а затем минусы выбирая только наименьшее значение из двух.У нас есть:
F 1 max = k 1 × x 1 max
= 4000 N / м × 0,2 м
= 800 N
и
F 1 max = k 1 × x 1 max
= 5000 N / м × 0,25 м
= 1250 N
Таким образом, система может выдерживать максимум 800 Н, так что оба пружины сохраняют свои упругие свойства.
Примечание! Комбинация пружин серии обычно применяется, когда имеющиеся пружины жестче, чем необходимо, поскольку последовательное объединение двух пружин снижает жесткость системы, делая ее более эластичной.
г. Параллельно
Когда две или более пружины соединены параллельно, они распределяют нагрузку между ними, и в результате они растягиваются меньше, чем если бы была доступна только одна пружина. Такое сочетание создает систему пружин с большей жесткостью. Уравнение для жесткости пружины системы из двух параллельных пружин:
k p = k 1 + k 2
, где k p — жесткость пружины параллельной установки, а k 1 и k 2 — постоянные отдельных пружин.
Другими словами, если одна пружина с постоянным k растягивается на x единиц, когда на нее подвешивается объект m, то, когда мы используем две пружины такого типа, соединенные параллельно, чтобы подвесить один и тот же объект, они растянутся на x / 2, потому что жесткость системы увеличивается в два раза. В результате он может хранить вдвое больше энергии, чем при использовании одной пружины. Посмотри на рисунок.
Пример 4
Две одинаковые пружины с постоянной величиной 2000 Н / м каждая, соединены параллельно.
- Каковы их размеры при подвешивании на них 50-килограммового предмета?
- Какое количество энергии хранится в пружинах?
Для простоты возьмем g = 10 Н / кг.
Решение 4
Теоретически мы можем взять показанный выше рисунок в качестве справочного. Сначала мы должны вычислить постоянную параллельной системы пружин. Имеем
k p = k 1 + k 2
= k + k
= 2k
= 2 × 2000 N / m
= 4000 N / м
а.Сила, возникающая в этой системе пружины, равна весу подвешенного объекта. Таким образом,
F = W = m × g
= 50 кг × 10 N / кг
= 500 N
Следовательно, растяжение параллельной системы пружин равно
x = F / k p
= 500 N / 4000 N / м
= 0.125 м
= 12,5 см
б. Энергия, запасенная в этой системе пружин, рассчитывается по формуле упругой потенциальной энергии. Имеем:
EPE = k p × x 2 / 2
= 4000 N / м 158 (2,125 м) / 2
= 31,25 Дж
Примечание! Энергия, запасенная в этой системе пружин, отличается (меньше), чем при использовании только одной пружины.Действительно, для той же силы, если бы у нас была только одна пружина, удлинение было бы
x = F / k = 500 Н / 2000 Н / м = 0,25 м
В результате энергия, запасенная в этой пружине, будет
EPE = k × x 2 / 2
= 2000 × 0,25 2 / 2
= 62.5 Дж
Как видите, запасенная энергия вдвое больше, чем в параллельной установке, подтверждая теорию, изложенную ранее.
г. Смешанная комбинация пружин
В этом случае мы начинаем с вычисления постоянной параллельной части, а затем думаем, что в этой части есть одна пружина. Он соединен последовательно с остальными пружинами, чтобы получить общую жесткость пружины всей системы. Посмотрите на рисунок:
Для простоты будем рассматривать только идентичные пружины.Если не учитывать массу пружин и опоры, на систему действует только одна сила. Это вес объекта. Следовательно, постоянные будут равны 2k для параллельной части и k для нижней пружины, которая включена последовательно с двумя другими. В результате общая жесткость пружины системы составляет
1 / k tot = 1 / k p + 1 к
= 1 / 2k + 1 / к
= 1 / 2k / 2k 2k
= 3 / 2k
Следовательно,
k tot = 2k / 3 As для системы , имеем
x tot = x / 2 + x
= x / 2 + 2x 905 47/ 2
= 3x / 2
Резюме
Площадь под графиком зависимости силы упругости от деформации представляет работу, проделанную для растяжения или сжатия пружины, но в то же время, он также представляет работу, выполняемую пружиной над соприкасающимися объектами, когда она отпускается и пытается вернуться в нерастянутое положение.Эта работа способствует изменению потенциальной энергии пружины, которая также известна как Elastic Potential Energy, EPE .
Полагая, что площадь прямоугольного треугольника, представленного на графике, равна
Площадь = Основание × Высота / 2
Подставляя соответствующие величины, мы получаем для упругой потенциальной энергии EPE пружины:
EPE = k × x 2 / 2
Как запасенная энергия, упругая потенциальная энергия может быть преобразована также в другие формы энергии.Некоторые из наиболее распространенных примеров в этом отношении включают:
- От упругой к кинетической энергии и наоборот
- От гравитационной потенциальной энергии к упругой потенциальной энергии и наоборот
- От упругой к тепловой энергии
- и т. Д.
Закон сохранения энергии (как один из фундаментальных законов физики) гласит:
«Энергия не может быть создана или уничтожена; ее можно только преобразовать из одной формы энергии в другую. .»
Чтобы изменить уровень жесткости пружин, мы можем объединить две или более пружины двумя основными способами:
a. Серия
В этой комбинации пружины размещаются одна за другой. Формула для пружины константа такой системы
1 / k s = 1 / k 1 + 1 /
, где k 1 и k 2 — постоянные каждой пружины соответственно.
г. Параллельно
Когда две или более пружины соединены параллельно, они распределяют нагрузку между ними, и в результате они растягиваются меньше, чем если бы была доступна только одна пружина. Такое сочетание создает систему пружин с большей жесткостью. Уравнение для жесткости пружины системы из двух параллельных пружин:
k p = k 1 + k 2
, где kp — жесткость пружины параллельной установки, а k 1 и k 2 — постоянные отдельных пружин.
Мы можем объединить две вышеупомянутые основные настройки пружин, чтобы получить другую настройку.
г. Смешанная комбинация пружин
В этом случае мы начинаем с вычисления постоянной параллельной части, а затем думаем, что в этой части есть одна пружина. Он соединен последовательно с остальными пружинами, чтобы получить общую жесткость пружины всей системы.
Упругая потенциальная энергия и комбинация пружин Вопросы для исправления
1.Объект весом 2 кг падает с 8 м над землей на вертикально установленную пружину и в результате сжимает пружину на 4 см. Какое значение пружинной жесткости? Для простоты возьмем g = 10 Н / кг.
- 200000 Н / м
- 400000 Н / м
- 20 Н / м
- 40 Н / м
Показать ответ Правильный ответ: A
2. Объект весом 2 кг начинает скользить из состояния покоя вниз по откосу без трения максимальной высотой 4 м, и когда он достигает дна, он продолжает скольжение еще 5 м по горизонтальной плоскости с коэффициентом трения 0.3. Затем объект сжимает пружину с постоянной величиной 2000 Н / м. Рассчитайте сжатие пружины в см. Для простоты возьмем g = 10 Н / кг.
- 5 см
- 22 см
- 62,5 см
- 0,22 см
Reveal Answer Правильный ответ: B
3. Сначала объединяются две пружины с постоянными 60 Н / м и 300 Н / м параллельно, затем последовательно, как показано на рисунке.
Каково отношение k p / k s для двух общих жестких пружин, полученных в этих комбинациях?
- 1
- 0.14
- 6
- 7.2
Показать ответ Правильный ответ: D
Мы надеемся, что вы нашли этот урок по физике «Упругая потенциальная энергия и комбинация пружин» полезным. Если вы считаете это руководство полезным, было бы здорово, если бы вы могли уделить время, чтобы оценить это руководство и / или поделиться в социальных сетях, это поможет нам определить популярные учебные пособия и калькуляторы и расширить наши бесплатные учебные ресурсы для поддержки наших пользователей по всему миру.

