Последовательное и параллельное соединение резисторов формулы. Последовательное и параллельное соединение проводников: формулы, законы и примеры

Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие законы действуют для тока и напряжения в таких цепях. Какие формулы используются для вычислений. Как решать задачи на смешанное соединение проводников.

Закон Ома — основа расчетов электрических цепей

Прежде чем разбираться с последовательным и параллельным соединением проводников, необходимо вспомнить фундаментальный закон электрических цепей — закон Ома. Он устанавливает связь между тремя основными величинами:

• Сила тока I (измеряется в амперах, А)
• Напряжение U (измеряется в вольтах, В)
• Сопротивление R (измеряется в омах, Ом)

Закон Ома для участка цепи формулируется так:

Сила тока I прямо пропорциональна напряжению U и обратно пропорциональна сопротивлению R.

Математически это записывается формулой:

I = U / R

Зная любые две величины из трех, можно легко найти третью. Это позволяет решать различные задачи по расчету электрических цепей.

Последовательное соединение проводников

При последовательном соединении проводники соединяются друг за другом, образуя один путь для тока. Рассмотрим основные законы и формулы для такого соединения.

Как рассчитать общее сопротивление при последовательном соединении?

Общее сопротивление при последовательном соединении равно сумме сопротивлений всех проводников:

R = R1 + R2 + R3 + … + Rn

Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Как распределяется напряжение в последовательной цепи?

Общее напряжение в последовательной цепи равно сумме напряжений на всех проводниках:

U = U1 + U2 + U3 + … + Un

Где U — общее напряжение, U1, U2, U3 и т.д. — напряжения на отдельных проводниках.

Какова сила тока в последовательной цепи?

Сила тока одинакова во всех участках последовательной цепи:

I = I1 = I2 = I3 = … = In

Где I — общая сила тока, I1, I2, I3 и т.д. — сила тока в отдельных проводниках.

Параллельное соединение проводников

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Рассмотрим основные законы и формулы для параллельного соединения.

Как рассчитать общее сопротивление при параллельном соединении?

Для расчета общего сопротивления при параллельном соединении используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Как распределяется напряжение в параллельной цепи?

Напряжение одинаково на всех параллельно соединенных проводниках:

U = U1 = U2 = U3 = … = Un

Где U — общее напряжение, U1, U2, U3 и т.д. — напряжения на отдельных проводниках.

Как распределяется ток в параллельной цепи?

Общий ток в параллельной цепи равен сумме токов через все проводники:

I = I1 + I2 + I3 + … + In

Где I — общий ток, I1, I2, I3 и т.д. — токи через отдельные проводники.

Смешанное соединение проводников

В реальных электрических схемах часто встречается смешанное соединение, сочетающее последовательные и параллельные участки. Как решать такие задачи?

Алгоритм решения задач со смешанным соединением:

1. Разбить схему на участки с последовательным и параллельным соединением
2. Рассчитать сопротивление каждого участка по соответствующим формулам
3. Заменить рассчитанные участки эквивалентными сопротивлениями
4. Повторять шаги 1-3, пока не останется одно общее сопротивление
5. Рассчитать общий ток по закону Ома
6. Определить распределение токов и напряжений по ветвям цепи

Примеры решения задач

Задача на последовательное соединение

Три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены последовательно. Какое напряжение нужно подать на эту цепь, чтобы через нее протекал ток 2 А?

Решение:

1. Найдем общее сопротивление: R = 10 + 20 + 30 = 60 Ом
2. По закону Ома: U = I * R = 2 А * 60 Ом = 120 В

Ответ: нужно подать напряжение 120 В.

Задача на параллельное соединение

Два резистора сопротивлением 6 Ом и 3 Ом соединены параллельно. Определите общее сопротивление цепи.

Решение:

1. Используем формулу для параллельного соединения: 1/R = 1/6 + 1/3 = 1/2 + 1/3 = 5/6
2. Общее сопротивление: R = 6/5 = 1,2 Ом

Ответ: общее сопротивление цепи 1,2 Ом.

Задача на смешанное соединение

В схеме три резистора: R1 = 2 Ом, R2 = 3 Ом, R3 = 6 Ом. R1 и R2 соединены параллельно, а их общее соединение последовательно с R3. Определите общее сопротивление цепи.

Решение:

1. Найдем сопротивление параллельного участка R1 и R2: 1/R12 = 1/2 + 1/3 = 5/6 R12 = 6/5 = 1,2 Ом
2. Общее сопротивление: R = R12 + R3 = 1,2 + 6 = 7,2 Ом

Ответ: общее сопротивление цепи 7,2 Ом.

Применение последовательного и параллельного соединения

Знание законов последовательного и параллельного соединения проводников имеет широкое практическое применение:

• Расчет и проектирование электрических цепей
• Подбор резисторов для получения нужного сопротивления
• Расчет делителей напряжения
• Анализ работы электронных схем
• Диагностика неисправностей в электрических цепях

Эти знания необходимы инженерам-электрикам, электронщикам, энергетикам и многим другим специалистам, работающим с электрическими системами.

Заключение

Понимание принципов последовательного и параллельного соединения проводников — ключ к анализу и расчету электрических цепей. Зная основные законы и формулы, можно решать самые разнообразные задачи по электротехнике. Важно не просто запомнить формулы, но и понимать физический смысл происходящих процессов. Это позволит успешно применять полученные знания на практике.

Как определить последовательное или параллельное соединение резисторов

Содержание

1. Соединение резисторов
2. Как правильно соединять резисторы?
3. Последовательное соединение резисторов.
4. Параллельное соединение резисторов.
5. Что ещё нужно учитывать при соединении резисторов?
6. Параллельное и последовательное соединение
7. Последовательное соединение проводников
8. Законы последовательного соединения проводников
9. Пример решения задачи
10. Параллельное соединение проводников
11. Параллельное соединение проводников: формулы
12. Пример решения задачи
13. Смешанное соединение проводников
14. Пример решения задачи

Соединение резисторов

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.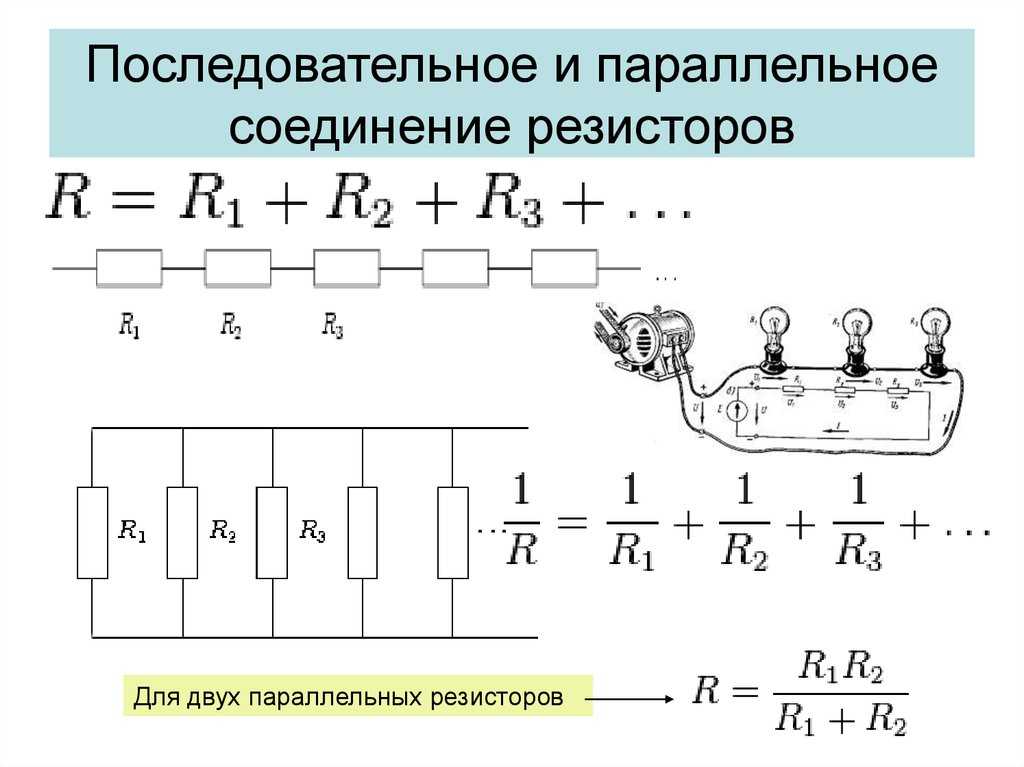

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора.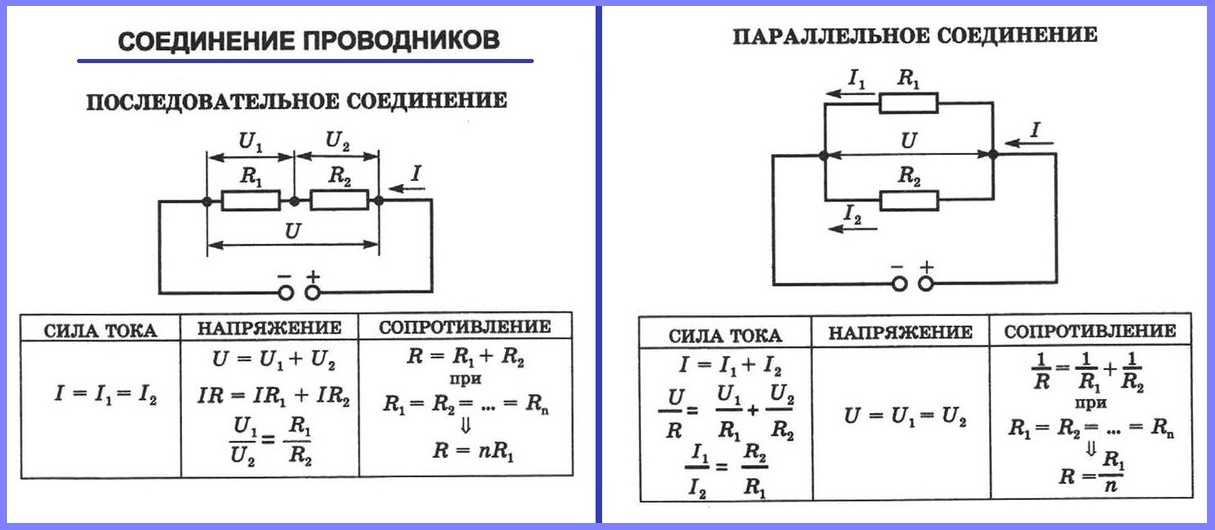 В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов.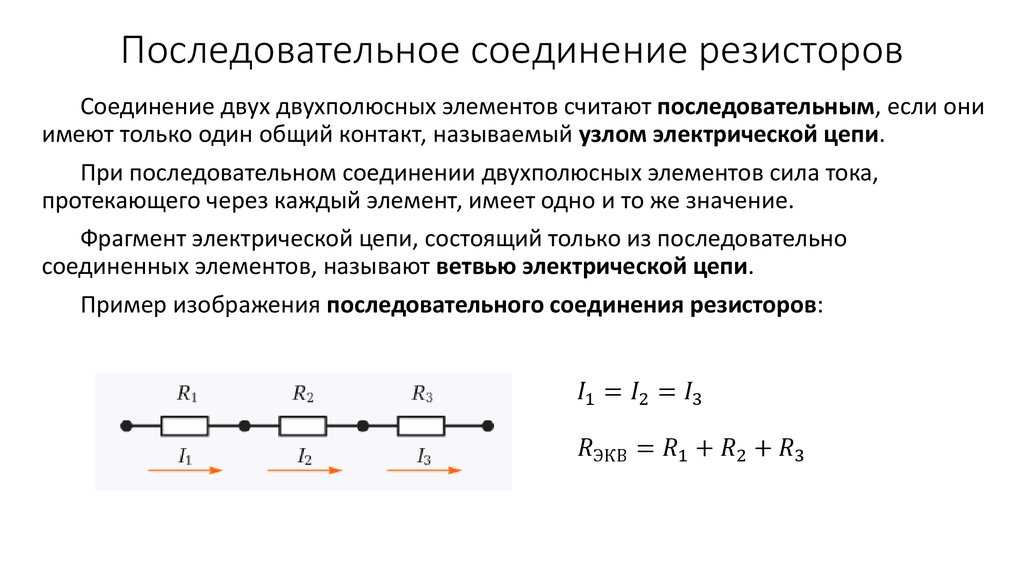 Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ.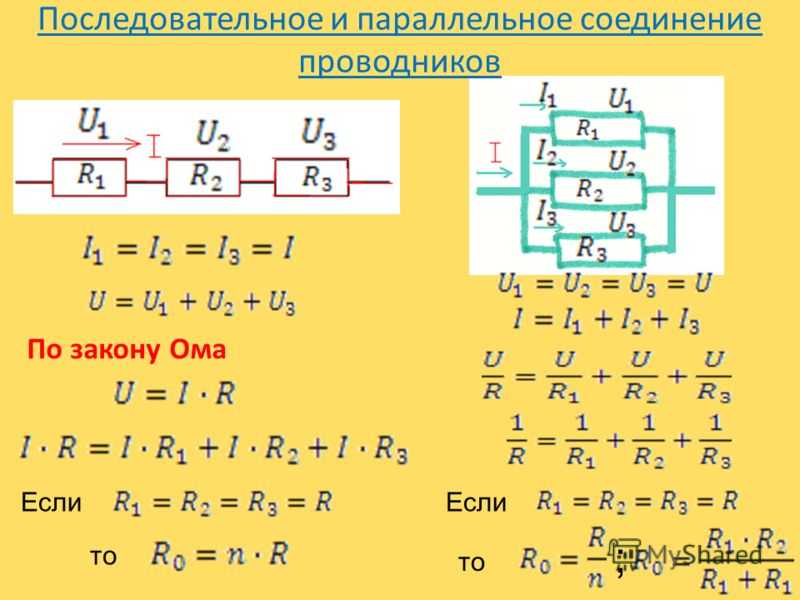 Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Источник

Параллельное и последовательное соединение

Почему в елочной гирлянде могут не гореть лампочки одного цвета? Почему все электроприборы в доме рассчитаны на 220 В? Спойлер: все дело в видах соединения проводников — о них мы и поговорим в этой статье.

· Обновлено 25 октября 2022

Как после перегорания одной лампочки в гирлянде можно определить способ соединения и починить ее? Попробуем разобраться.

Анфиса обнаружила на балконе старую гирлянду. Включив ее в розетку, девочка заметила, что горят все лампочки, кроме зеленых. Внимательно изучив провода, Анфиса увидела, что все зеленые лампочки соединены последовательно друг за другом.

Последовательное соединение проводников

При последовательном соединении конец первого проводника соединяют с началом второго, конец второго — с началом третьего и т. д.

Последовательное подключение обычно используется в тех случаях, когда необходимо целенаправленно включать или выключать определенный электроприбор. Например, для работы школьного электрического звонка требуется соединить его последовательно с источником тока и ключом.

Вот некоторые примеры использования схемы последовательного соединения:

• освещение в вагонах поезда или трамвая;
• простейшие елочные гирлянды;
• карманный фонарик;
• амперметр для измерения силы тока в цепи.

Законы последовательного соединения проводников

При последовательном соединении сила тока в любых частях цепи одна и та же:

Если в цепи с последовательным способом соединения одна из ламп выйдет из строя и через нее не будет протекать электрический ток, то и через оставшиеся лампы ток проходить не будет. Вспомним Анфису и ее гирлянду: когда одна из зеленых лампочек перегорела, то ток, проходящий через нее, стал равен нулю. Следовательно, и другие зеленые лампочки, включенные последовательно, не загорелись. Чтобы починить гирлянду, нужно определить перегоревшую лампочку и заменить ее.

При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников:

При последовательном соединении общее напряжение цепи равно сумме напряжений на отдельных участках:

Пример решения задачи

В цепь с напряжением 220 В включена лампа, через нее протекает ток силой 20 А. Когда к лампе последовательно подключили реостат, сила тока в цепи уменьшилась до 11 А. Чему равно сопротивление реостата?

По закону Ома определим сопротивление лампы:

R₁ = U / I₁ = 220 / 20 = 11 Ом.

Также по закону Ома определим общее сопротивление цепи при включенном реостате:

R = U / I₂ = 220 / 11 = 22 Ом.

При последовательном соединении сопротивления лампы и реостата складываются:

Зная общее сопротивление цепи и сопротивление лампы, определим искомое сопротивление реостата:

R₂ = R − R₁ = 22 − 11 = 11 Ом.

Ответ: сопротивление реостата равно 11 Ом.

К сожалению, последовательное соединение не всегда оказывается удобным. Например, в торговом центре «Ашан» работает с 9:00 до 23:00, кинотеатр — с 10:00 до 02:30, а магазины — с 10:00 до 22:00. При последовательном соединении цепи свет должен будет гореть во всем ТЦ с 9:00 до 02:30. Согласитесь, что такой режим работы экономически невыгоден даже при минимальном тарифе на электроэнергию. В этом случае удачным решением будет использование параллельного соединения.

Параллельное соединение проводников

При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой.

Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату.

Приведем еще несколько примеров применения параллельного способа соединения:

• освещение в больших торговых залах;
• бытовые электроприборы в квартире;
• компьютеры в кабинете информатики;
• вольтметр для измерения напряжения на участке цепи.

Параллельное соединение проводников: формулы

Напряжение при параллельном соединении в любых частях цепи одинаково:

Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении.

Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках:

Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну.

Общее сопротивление цепи определяется по формуле:

Для двух параллельно соединенных проводников формулу можно записать иначе:

Если n одинаковых проводников, каждый из которых имеет сопротивление R₁, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество:

Вернемся к Анфисе и ее гирлянде. Мы уже разобрались, почему перестали гореть все зеленые лампочки. Пришло время узнать, почему продолжили гореть все остальные. В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.

Пример решения задачи

Два резистора с сопротивлениями 10 Ом и 11 Ом соответственно соединены параллельно и подключены к напряжению 220 В. Чему равна сила тока в неразветвленной части цепи?

Определим общее сопротивление при параллельном соединении проводников:

R = (R₁ · R₂) / (R1 + R2) = (10 · 11) / (10 + 11) = 110 / 21 Ом ≈ 5,24 Ом.

По закону Ома определим силу тока в цепи:

I = U / R = 220 / (110 / 21) = 42 А.

Ответ: сила тока в неразветвленной части цепи равна 42 А.

Смешанное соединение проводников

Зачастую реальные электрические схемы оказываются сложнее, поэтому используют различные комбинации последовательного и параллельного способов соединения. Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.

Алгоритм решения задач со смешанным соединением проводников:

Прочитать условие задачи, начертить схему электрической цепи, при необходимости пронумеровать проводники.

Проанализировать схему, т. е. найти участки, где используется только последовательное или только параллельное соединение проводников. Определить сопротивление на этих участках.

Выяснить вид соединения участков между собой. Найти общее сопротивление всей цепи.

С помощью закона Ома и законов последовательного и параллельного соединения проводников найти распределения токов и напряжений в цепи.

Пример решения задачи

На рисунке показана схема электрической цепи. Сопротивления резисторов одинаковы и равны 12 Ом. Напряжение источника — 100 В. Какова сила тока, протекающего через резистор R₄?

Проанализируем данную схему. Резисторы R₂ и R₃ соединены между собой последовательно, а с резистором R₄ — параллельно. Весь этот участок соединен последовательно с источником тока и резистором R₁.

Определим сопротивление последовательно соединенных резисторов R₂ и R₃:

Найдем общее сопротивление резистора R₄ и участка 2–3, соединенных параллельно:

Определим общее сопротивление всей цепи как сумму включенных последовательно резистора R₁ и участка 2–3–4:

По закону Ома найдем силу тока в неразветвленной части цепи:

I = U / R_экв = 200 / 20 = 5 А.

По закону Ома определим напряжение на участке, состоящем из резисторов R₂, R₃, R₄:

U_экв1 = I · R₂₃₄ = 5 · 8 = 40 В.

Поскольку при параллельном соединении напряжение одинаково, то напряжение на резисторе R₄ также равно 40 В. По закону Ома найдем силу тока, протекающего через резистор R₄:

Ответ: через резистор R₄ протекает ток силой приблизительно 3,3 А.

Мы разобрали довольно много формул последовательного и параллельного подключения проводников. А запомнить их можно с помощью вот таких схем:

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!

Источник

Последовательное и параллельное соединение проводников – изучение формул

4.7

Средняя оценка: 4.7

Всего получено оценок: 198.

4.7

Средняя оценка: 4.7

Всего получено оценок: 198.

Электрические схемы представляют собой набор различных электронных компонент, с помощью которых получают (или преобразовывают) постоянные и переменные электрические сигналы нужной величины, формы и частоты. Для этого элементы схемы соединяют в определенном порядке. Самыми распространенными типами соединений являются последовательное и параллельное соединение проводников.

Закон Ома

Изучение последовательного и параллельного соединения проводников следует начинать с напоминания закона Ома, который является базовым законом при проектировании всех видов электрических схем.

Немецкий физик Георг Ом в 1826 г. экспериментально открыл фундаментальную связь между силой тока I и напряжением U. Ученый установил, что величина тока

I в цепи прямо пропорциональна величине напряжения U, т.е. I ∼ U.

Рис. 1. Закон Ома

Формула закона Ома для однородного участка цепи выглядит следующим образом:

$ I = {U \over R} $ (1),

где: R — величина сопротивления проводника, (Ом).

Полностью закон Ома звучит так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.

Последовательное соединение проводников

Для простоты будем рассматривать соединения проводников на примере резисторов (сопротивлений) R.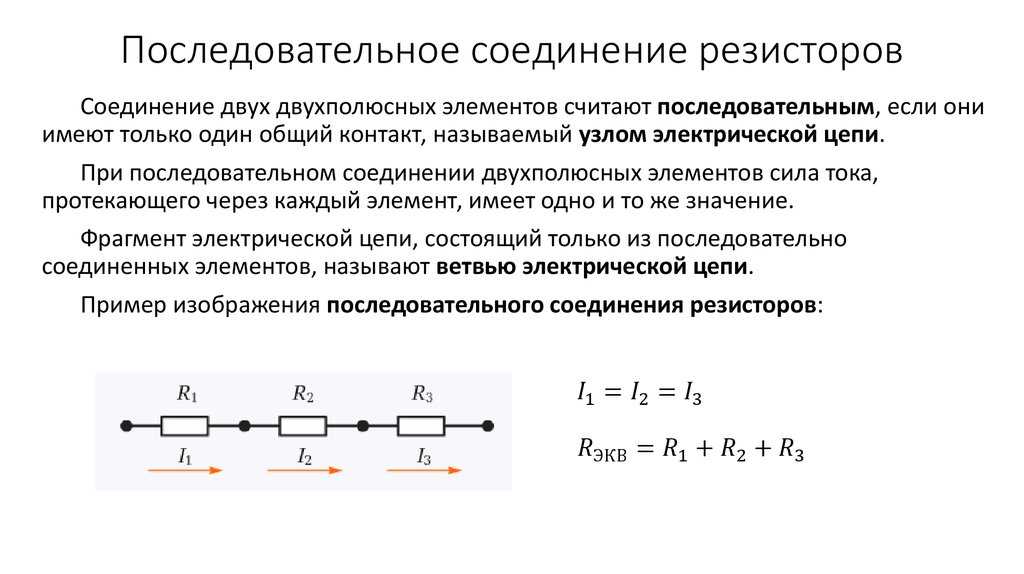 Если взять два резистора R₁ и R₂ и соединить их друг за другом (правый контакт резистора R₁ с левым контактом резистора

R₂, то это будет последовательное соединение.

Рис. 2. Схема последовательного соединения резисторов

При подключении напряжения U к левому концу R₁ и правому концу R₂ в замкнутой цепи потечет ток I, величина которого будет одинакова для обоих резисторов. Падение напряжений U₁ и U₂ на сопротивлениях согласно закону Ома будут равны:

$ U_1 = I * R_1 $$ (2), $$ U_2 = I * R_2 $ (3).

Полное напряжение U равно сумме этих напряжений:

$ U = U_1 + U_2 $ (4).

Применив закон Ома для всей цепи, получим:

$ U = I * R_{общ} $ (5),

где R_общ — общее сопротивление всей цепи. Из формул (2), (3) и (4) следует, что:

$ U = I * R = I * R_1 + I * R_2 $ (6).

Сократив обе части уравнения на I, получим:

$ R_{общ} =R_1 + R_2 $ (7).

Если в цепи последовательно соединены N резисторов — R_1, R_2… R_N, то, воспользовавшись такими же соображениями, можно получить формулу для величины общего сопротивления такой цепи R₀:

$$ R_0 = R_1 + R_2 +…+ R_N $$ (8).

Таким образом, можно сформулировать общее правило: при последовательном соединении резисторов величина общего сопротивления цепи равна сумме сопротивлений включенных резисторов.

Параллельное соединение проводников

Если взять два резистора R₁ и R₂ и соединить их так, что начала (левые концы) соединятся в одной точке, а правые концы соединятся в другой точке, то это и будет параллельное соединение.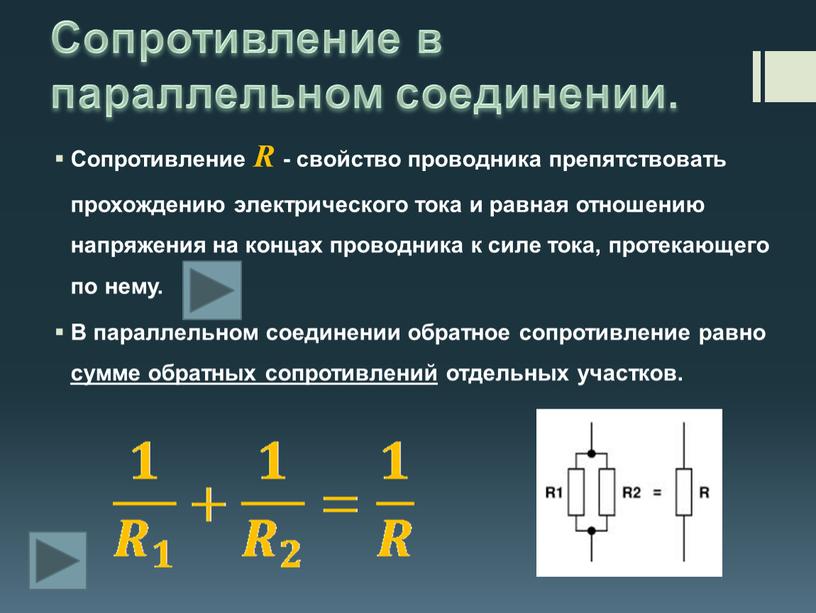

Рис. 3. Схема параллельного соединения резисторов

После подключения к левому и правому концам источника напряжения U, в цепи потечет ток. Поскольку R₁ и R₂ могут отличаться друг от друга, то и значения токов I₁ и I₂ через них тоже будут разные. Зная напряжение U, и используя формулу закона Ома, можно рассчитать токи I₁ и I₂ :

$ I_1 = {U \over R_1} $ (9),

$ I_2 = {U \over R_2} $ (10)

Общий ток I в цепи является суммой токов I₁ и I₂:

$ I = I_1 + I_2 $ (11),

Тогда, используя выражения для токов I₁ и I₂, получим следующую формулу:

${U \over R} = { U \over R_1}+ {U \over R_2}$ (12).

Сокращая обе части последнего уравнения на

U, получим следующее выражение для обратной величины общего сопротивления R:

$ {1\over R} = {1 \over R_1}+ {1 \over R_2} $ (13).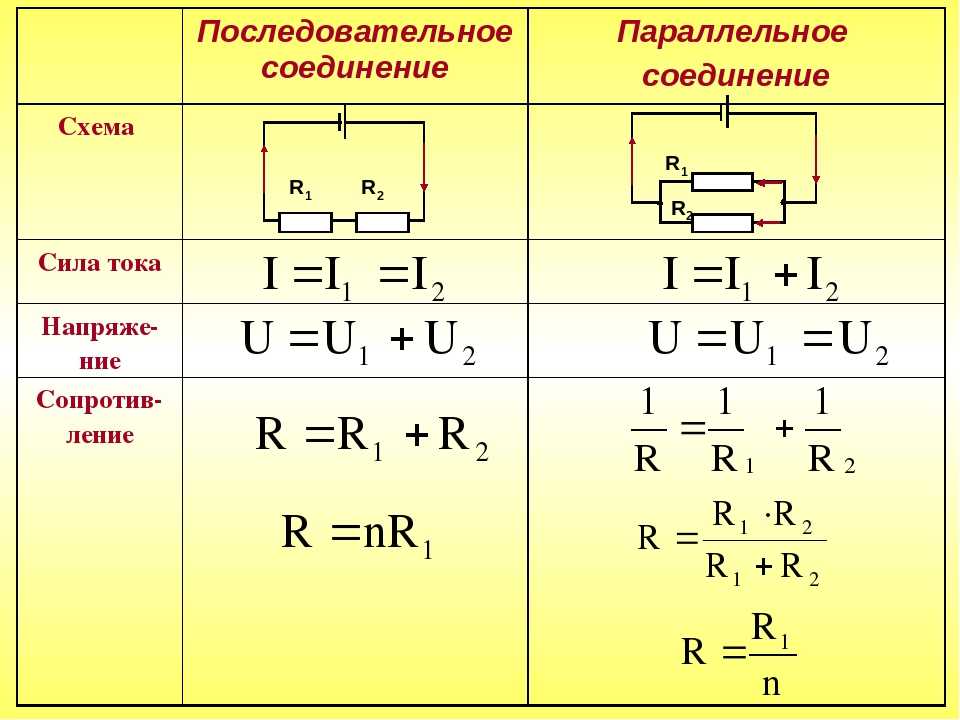

Используя последнюю формулу и правило сложения дробей, получим выражение для сопротивления цепи, состоящей из двух резисторов:

$ R = {R_1* R_2 \over R_1 + R_2} $ (14).

Если соединить параллельно N резисторов с одинаковым сопротивлением R₀, то общее сопротивление цепи будет равно:

$ R = {R_0 \over N} $.

Что мы узнали?

Итак, мы узнали, что такое последовательное и параллельное соединение проводников в электрических цепях. Получены формулы для вычисления общих сопротивлений цепей при последовательном и параллельном соединениях.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 198.

---

А какая ваша оценка?

Учебное пособие по комбинированным последовательно-параллельным схемам

Swati Talwar

HS-PS3-5

Значение комбинированной последовательно-параллельной схемы

Принцип комбинированной последовательно-параллельной схемы

Работа комбинированной последовательно-параллельной схемы расчеты

Комбинированные примеры последовательных и параллельных цепей показывают нам сложность этих схем и то, как в них проявляются свойства последовательного и параллельного.

Комбинированная последовательно-параллельная цепь представляет собой тип цепи, соединенной как последовательно, так и параллельно. Трассы выполнены в виде сложнейших электрических последовательных и параллельных комбинированных цепей. Все компоненты этой цепи соединены встык, образуя параллельный поток цепи.

ПРИНЦИП СОЕДИНЕНИЯ ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ

• Ток остается одинаковым во всей цепи.
• Сумма напряжений на всех трех резисторах равна напряжению в других точках.
• Это следует эмпирическому правилу.

 

РАБОТА КОМБИНИРОВАННЫХ ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ

Мы знаем, что эта схема не является ни последовательной, ни параллельной, но она имеет элементы обеих. В этой цепи много путей для тока, как и в параллельной цепи, но в цепи существует два набора общих точек. При решении уравнения последовательно-параллельной комбинированной цепи необходимо рассчитать общее сопротивление в обеих частях.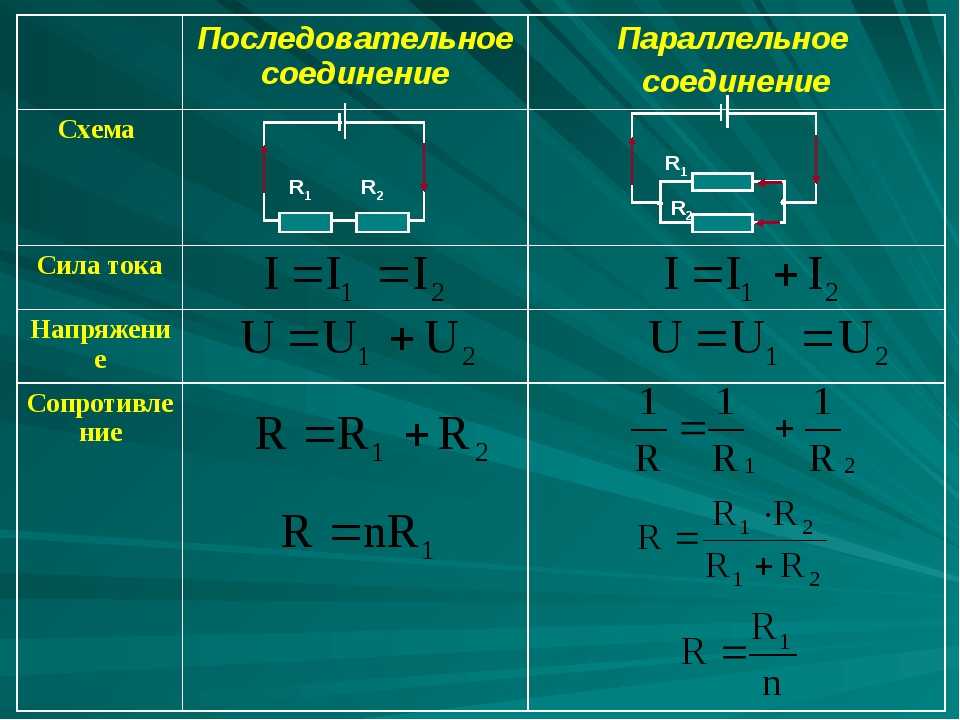 Чтобы получить четкое представление о том, как работают эти схемы, обратитесь к приведенному ниже примеру с последовательной и параллельной схемой.

Источник 

ФОРМУЛА КОМБИНИРОВАННЫХ ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ

• Определенной формулы для комбинации последовательно-параллельных цепей не существует.
• Таким образом, для расчета среднего сопротивления последовательно-параллельной цепи мы должны найти сопротивление, решив сопротивление параллельных и последовательных участков по отдельности и объединив их, чтобы найти правильное значение сопротивления.
• Далее, для расчета резонансной частоты комбинированного последовательно-параллельного контура, нам нужно совместить формулы обоих.

 

• Комбинированные схемы представляют собой тип смешанной схемы, которая следует уникальному пути. Некоторые из них проходят через один резисторный тракт, а некоторые проходят параллельно через две или более точек.
• Комбинация последовательно-параллельной цепи имеет одинаковое напряжение по всей цепи.
• Токи остаются одинаковыми во всей цепи.

                                                                                             

Часто задаваемые вопросы

1. Как решить комбинированные параллельные и последовательные схемы?

Чтобы решить эти схемы, следуйте этим инструкциям: 

• Посмотрите, какие резисторы используются в цепи
• Перерисовывайте схему, пока она не завершится и не уменьшится до одного эквивалентного резистора.
• Расчет силы тока по закону Ома.
• Рассчитайте рассеиваемую мощность.

 

2. Что такое последовательно-параллельное сочетание?

Это уникальный тип цепи, которая подключается как последовательно, так и параллельно. Ток остается одинаковым по всей цепи, а сумма напряжений на всех трех резисторах равна напряжению в других точках.

3. Каковы примеры последовательно-параллельных комбинаций?

Некоторые примеры:

• Сильные рождественские огни
• Лампочки
• Мультиплексор
• Электропроводка фар автомобиля
• Компаратор

4. Какова формула последовательно-параллельных комбинаций?   

Параллельная цепь: 

1/Rt = 1/R1 1/R2 1/R3 … Rt = R (t)общ. 5. Каковы правила для последовательных и параллельных цепей?

• Комбинированная схема следует эмпирическому правилу.
• Внешний ток одинаков во всей цепи.
• Внутренний ток всегда меньше внешнего тока.

 

Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о комбинированных последовательно-параллельных схемах ! Присоединяйтесь к нашему сообществу Discord, чтобы получать ответы на любые вопросы и общаться с другими учениками, такими же, как и вы! Обещаем, это делает учебу намного веселее!04.04.2022.

Последовательно-параллельные схемы: https://www.oakton.edu/user/1/agero/elt101/presentations/Chapter06.pdf. Доступ 19 апреля 2022 г.

.

Постоянный ток: https://www.allaboutcircuits.com/textbook/direct-current/chpt-7/analysis-technique/ По состоянию на 19 апреля 2022 г.

Что такое последовательно-параллельная цепь? https://www.allaboutcircuits.com/textbook/direct-current/chpt-7/what-is-a-series-parallel-circuit/ По состоянию на 19 апреля 2022 г.

Резисторы и элементы, соединенные последовательно и параллельно

Категории

Экзаменационные уроки по физике

СОДЕРЖАНИЕ

• Резисторы, соединенные последовательно и параллельно
• Ячейки, соединенные последовательно и параллельно
• Эти резисторы соединены последовательно.

Характеристики

• Тот же поток тока через каждый резистор I _T = I ₁ = I ₂ = I ₃
• 2 = I ₃
• 1. 0173 1 ≠ V ₂ ≠V ₃
• P.d are additive V _T = V ₁ + V ₂ +V ₃
• Power are additive
• Applied voltage equals the sum of разные p.d V _T = V ₁ + V ₂ +V ₃
• Сопротивления аддитивны.

R _T = R ₁ + R ₂ + R ₃ _______ для 3 резисторов

R _T = R ₁ + R ₂ + R ₃ ….. + Rn ___ для n номеров или резисторов

РЕЗИСТОРЫ, ПОДКЛЮЧЕННЫЕ ПАРАЛЛЕЛЬНО

Соединение рядом.

Характеристики

• Различные резисторы имеют свой индивидуальный ток
• P.D в каждом резисторе одинаково V _T = V ₁ = V ₂ = V ₃
173 2 = V ₃ 1713173. Т = Я ₁ + I ₂ + I ₃
• Проводятельность — аддитивная
• Мощность. Аддитивные

1/R _T = 1/R ₁ + 1/R ₂ + 1/R _{3 3 + 1/R 1/R 9017 2 = 1/R 1 + 1/R 2 2 + 1/R 1 + 1/R 2 = 1/R 1 + 1/R 9017 3 2 .} ____ для 3 резисторов

1/R _T = 1/R ₁ + 1/R ₂ + 1/R ₃ …..+ 1/Rn ____ для n количеств резисторов

3

3

3

3 ОЦЕНКА

1. Различие между резисторами, соединенными последовательно и параллельно
2. Укажите соотношение между сопротивлением и проводимостью

Последовательные элементы: соединения встык

E _T = E + E + E = 3E

Для n элементов; E _T = n E

E _T = E ₁ + E ₂ + E ₃

Ячейки в параллельном соединении = E+

E+

T

3 E /3 = 3E/3 = E

Расчеты

Если резисторы 2 Ом, 3 Ом и 5 Ом соединены последовательно (a) последовательно (b) параллельно, рассчитайте

эквивалентное сопротивление

(a)  R _T = 2+3+5 = 10 Ом

(b)  1/R _T = 1/2 +1/3+1/5 = 15+10+6 /30 = 31/30

R _T = 30/31 Ом

ОЦЕНКА

1. Рассчитайте разность потенциалов на резисторе сопротивлением 2 кОм, при котором через него проходит ток силой 1 мА

ЗАДАНИЕ ПО ЧТЕНИЮ

Подробнее о последовательном и параллельном соединении резисторов и ячеек – Новая школа физики (стр. 79) причина движения.?

ЗАДАНИЕ НА ВЫХОДНЫЕ

1. Если четыре одинаковых элемента по 2 вольта соединены последовательно, эквивалентное pd будет ……… (a) 2v (b) 4v (c) 6v (d) 8v
2. Если четыре одинаковых элемента на 2 вольта соединены параллельно, эквивалент pd будет ……… (a) 2 В (b) 4 В (c) 6 В (d) 8 В
3. Если резисторы 2 Ом, 2 Ом и 1 Ом соединены последовательно эквивалентное сопротивление (a) 5 Ω

(b) ½ Ω (c) 4 Ω (d) 2 Ω

4. Если резисторы 2 Ω, 2 Ω и 1 Ω соединены параллельно, эквивалентное сопротивление (a) 5 Ω ( б) ½ Ω (c) 4 Ω (d) 2 Ω
5. Два резистора сопротивлением 1 Ω подключены параллельно к резистору 2 Ω, эквивалентное сопротивление …….. (a) 4 Ω (b) 3 Ω (в) 2 Ом (г) 1 Ом

ТЕОРИЯ

1. Батарея напряжением 15 В и внутренним сопротивлением 5 Ом подключена к резистору 0f 20 Ом. Рассчитайте значение (а) электрического тока (б) напряжения на клеммах (в) потерянного напряжения.