Последовательное и параллельное сопротивление. Последовательное и параллельное соединение проводников: особенности и законы

Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие законы применяются для расчета силы тока и напряжения в таких цепях. Как решать задачи на смешанное соединение проводников.

Основные понятия последовательного и параллельного соединения проводников

Последовательное и параллельное соединение проводников — это два основных способа подключения элементов электрической цепи:

• При последовательном соединении элементы цепи подключаются друг за другом, образуя единую цепочку. Сила тока во всех элементах одинакова.
• При параллельном соединении все элементы подключаются к одним и тем же точкам цепи. Напряжение на всех элементах одинаково.

Знание законов и формул для этих типов соединений позволяет рассчитывать параметры электрических цепей и решать различные задачи.

Законы последовательного соединения проводников

При последовательном соединении проводников действуют следующие законы:

1. Сила тока одинакова во всех элементах цепи: I = I1 = I2 = … = In
2. Общее напряжение равно сумме напряжений на отдельных элементах: U = U1 + U2 + … + Un
3. Общее сопротивление равно сумме сопротивлений отдельных элементов: R = R1 + R2 + … + Rn

Эти законы позволяют рассчитать параметры цепи при последовательном соединении.

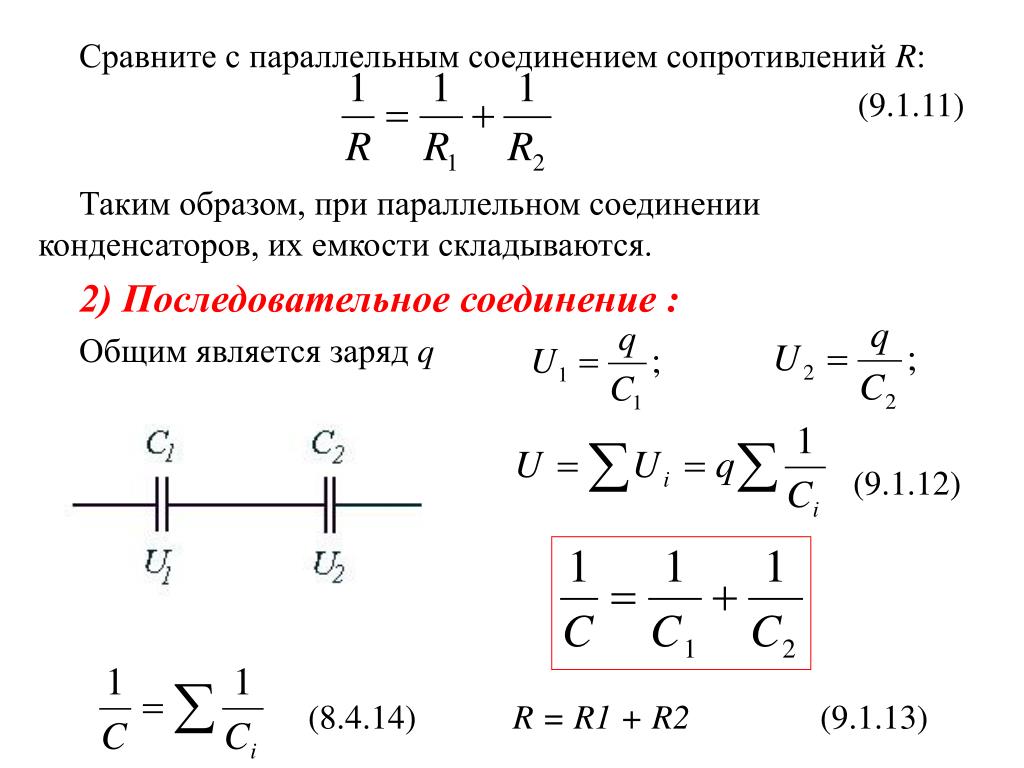
Законы параллельного соединения проводников

При параллельном соединении действуют следующие законы:

1. Напряжение одинаково на всех элементах: U = U1 = U2 = … = Un
2. Общая сила тока равна сумме токов через отдельные элементы: I = I1 + I2 + … + In
3. Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям отдельных элементов: 1/R = 1/R1 + 1/R2 + … + 1/Rn

Применение этих законов позволяет анализировать параллельные цепи.

Особенности расчета смешанных соединений

В реальных электрических схемах часто встречаются смешанные соединения, сочетающие последовательные и параллельные участки. Для их расчета необходимо:

1. Разбить схему на участки с однотипным соединением элементов
2. Рассчитать эквивалентное сопротивление для каждого участка
3. Объединить полученные участки, используя законы последовательного и параллельного соединения
4. Рассчитать общие параметры всей цепи

Такой подход позволяет анализировать сложные электрические схемы, разбивая их на более простые элементы.

Применение законов Ома и Кирхгофа для расчета цепей

При анализе электрических цепей с последовательным и параллельным соединением широко применяются:

• Закон Ома — позволяет найти силу тока, зная напряжение и сопротивление: I = U / R
• Первый закон Кирхгофа — сумма токов, втекающих в узел, равна сумме вытекающих токов
• Второй закон Кирхгофа — сумма напряжений вдоль замкнутого контура равна нулю

Комбинация этих законов с правилами расчета последовательных и параллельных соединений позволяет решать сложные задачи по электричеству.

Решение типовых задач на последовательное и параллельное соединение

Рассмотрим алгоритм решения типовой задачи на смешанное соединение проводников:

1. Нарисовать схему цепи, обозначив все элементы
2. Выделить участки с последовательным и параллельным соединением
3. Рассчитать эквивалентное сопротивление для каждого участка
4. Определить общее сопротивление всей цепи
5. Используя закон Ома, найти общий ток
6. Рассчитать напряжения и токи на отдельных участках

Следуя этому алгоритму, можно решать большинство задач на расчет электрических цепей.

Практическое применение знаний о соединениях проводников

Понимание принципов последовательного и параллельного соединения проводников имеет широкое практическое применение:

• Расчет и проектирование электрических схем
• Анализ работы электронных устройств
• Диагностика неисправностей в электрооборудовании
• Оптимизация энергопотребления
• Разработка систем электроснабжения

Эти знания необходимы инженерам-электрикам, электронщикам, энергетикам и специалистам смежных областей.

Ошибки и сложности при расчетах соединений проводников

При решении задач на соединения проводников часто возникают следующие трудности:

• Неправильное определение типа соединения на участке цепи
• Ошибки в применении формул для расчета эквивалентного сопротивления
• Неверное использование законов Ома и Кирхгофа
• Сложности с анализом цепей со смешанным соединением
• Ошибки в расчетах при большом количестве элементов

Чтобы избежать этих проблем, важно внимательно анализировать схему и тщательно выполнять вычисления на каждом этапе решения задачи.

Элементарный учебник физики Т2

Элементарный учебник физики Т2

Ландсберг Г.С. Элементарный учебник физики. Т.2. Электричество и магнетизм. — М.: Наука, 1985. — 479 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Глава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле. 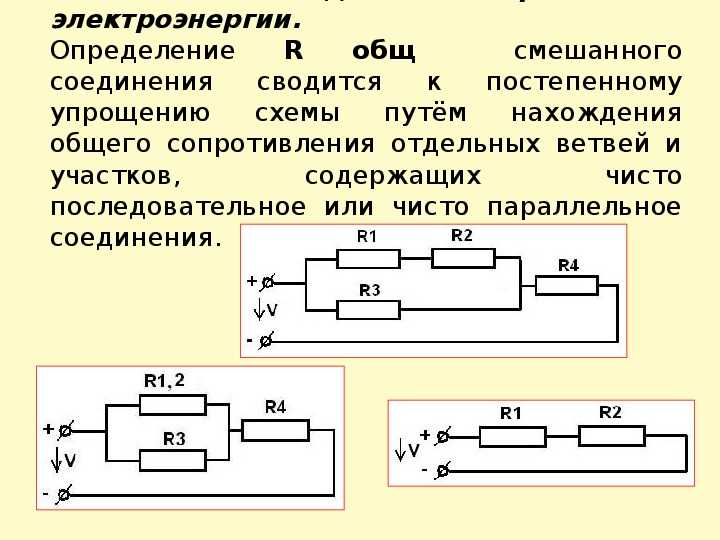§ 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27. Соединение с Землей. § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока. § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64. 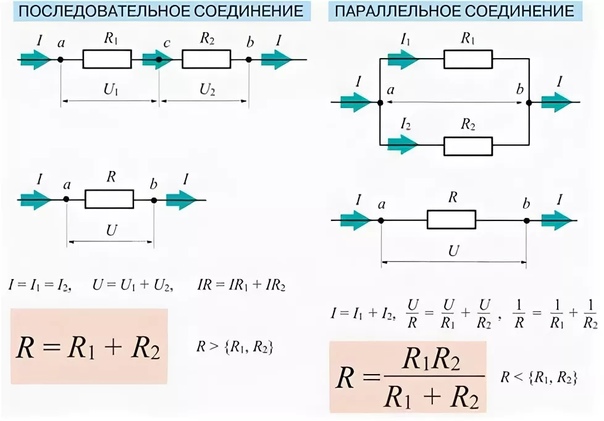Электрическая проводка. Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов. § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. Природа электрического тока в полупроводниках. § 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током. 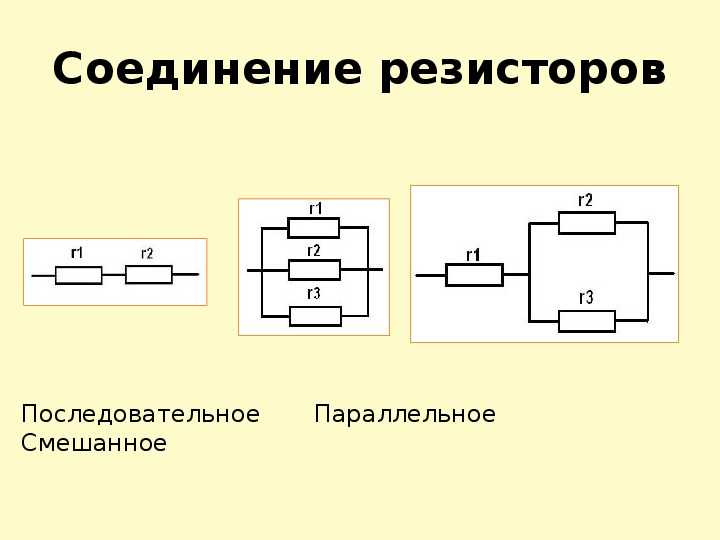§ 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока. Правило Ленца. § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. Индуктивность катушки. § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением. 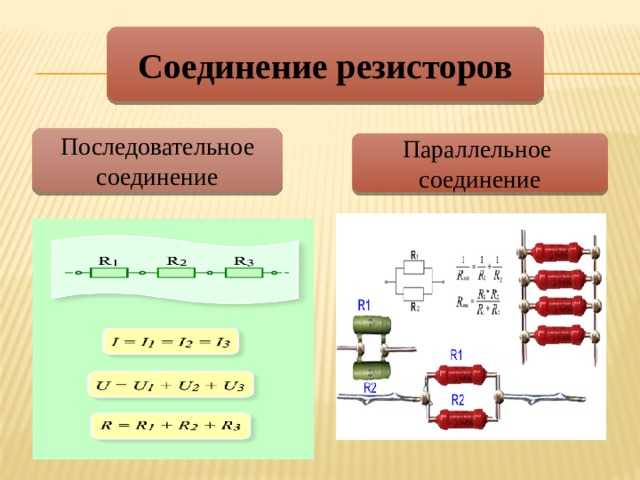§ 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы

Последовательное и параллельное соединение | СПАДИЛО

Определение

Проводники и другие элементы цепи могут соединяться как параллельно, так и последовательно.

Последовательное соединение – соединение, при котором конец первого проводника соединяется с началом второго. Параллельное соединение – соединение, при котором начало первого проводника соединяется с началом другого, а конец первого – с концом второго.

От способа соединения элементов зависит сила тока, напряжение и сопротивление отдельных участков цепи и всей цепи в целом.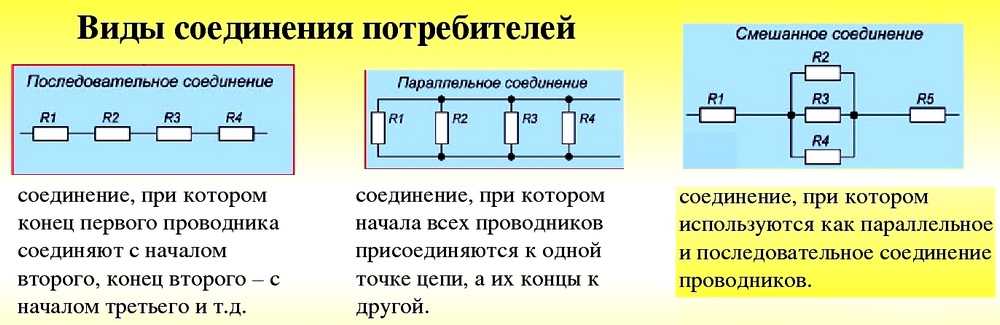 Эту зависимость отобразим в таблице на примере двух резисторов сопротивлениями R₁ и R₂.

Зависимость силы тока, напряжения и сопротивления от способа соединения

Способ соединения резисторов	Последовательное	Параллельное
Схема
Полная сила тока	I=I1=I2	I=I1+I2
Полное напряжение	U=U1+U2	U=U1=U2
Полное сопротивление	R=R1+R2	1R..=1R1..+1R2..
Полное сопротивление с n одинаковыми резисторами	R=nR0	R=R0n..

Пример №1. Чему равно сопротивление участка цепи, изображенного на рисунке?

Участок цепи представляет собой последовательно соединенный резистор R₁ = 2 Ом с параллельным участком, состоящим из двух резисторов R₂ = 6 Ом и R₃ = 3 Ом.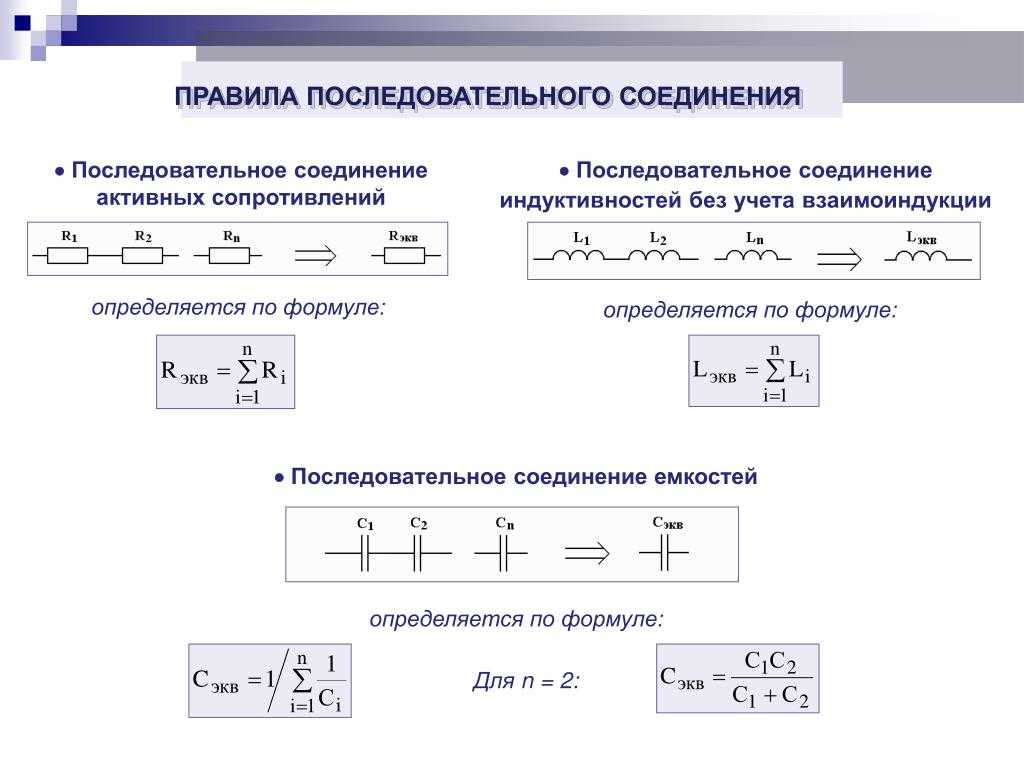

Сначала найдем сопротивление параллельно соединенных резисторов:

1R23..=1R2..+1R3..

R23=R2R3R2+R3..=6·36+3..=2 (Ом)

Теперь нужно сложить это сопротивление с сопротивлением последовательно соединенного с ним первого резистора:

R=R1+R23=2+2=4 (Ом)

Приведем алгоритм решения задач на расчет силы тока на примере конкретной задачи:

Через участок цепи (см. рисунок) течет постоянный ток I. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.

Шаги	Действия
1. Определите полное сопротивление параллельного участка цепи.	1Rпар..=1r..+1nr..=n+1nr..
2. Найдите напряжение на параллельном участке цепи.	Uпар=Uверх+Uниж
3. Вычислите силу тока на верхнем участке параллельного соединения.	Iверх=Uпарr..
4. Определите силу тока на нижнем участке параллельного соединения.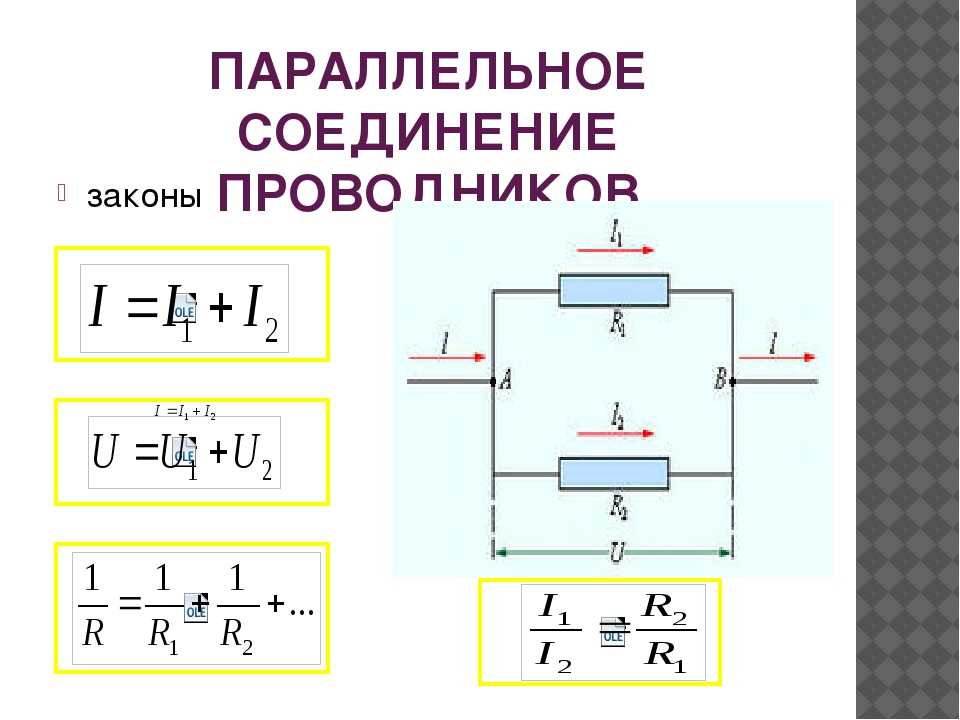	Iниж=Uпарnr..
5. Определите общую силу тока для параллельного участка цепи	Iпар=Iверх+Iниж
6. Определите общую силу тока для полного участка цепи.	I=Iпар

Пример №2. Через участок цепи (см. рисунок) течет постоянный ток I = 4 А. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.

Так как первый резистор соединен с параллельным участком цепи последовательно, то сила тока параллельного участка тоже равна 4 А.

Iпар=I

Сила тока параллельного участка цепи равна сумме верхней и нижней силы тока:

Iпар=Iверх+Iниж

Так как это параллельный участок, верхнее и нижнее напряжения равны:

Uпар=Uверх+Uниж

Амперметр расположен в верхнем участке параллельного соединения. Следовательно, сила тока этого участка равна отношению напряжения параллельного участка цепи к суммарному сопротивлению верхней части параллельного участка:

Iверх=UпарR+R.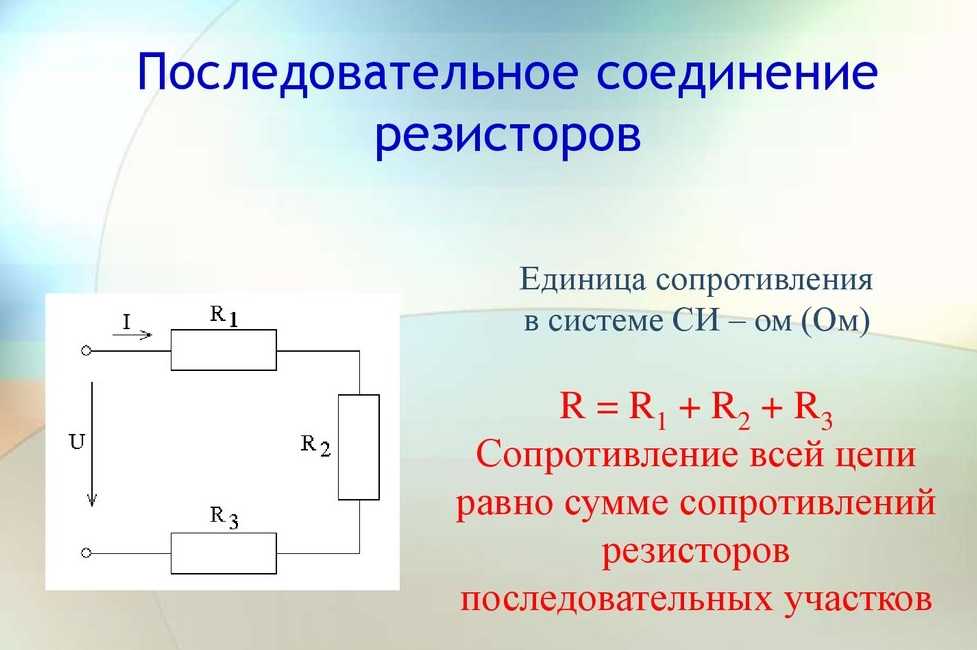 .=Uпар2R..

Если бы амперметр находился внизу, то он показал бы:

Iниж=UпарR+R+R..=Uпар3R..

Отсюда:

Uпар2R..+Uпар3R..=4

5Uпар6R..=4

Uпар=24R5..

Iверх=Uпар2R..=24R5.. 12R..=125..=2,4 (А)

Задание EF17634

Участок цепи состоит из четырёх последовательно соединённых резисторов, сопротивления которых равны 10 Ом, 20 Ом, 30 Ом и 40 Ом. Каким должно быть сопротивление пятого резистора, добавленного в этот участок последовательно к первым четырём, чтобы суммарное сопротивление участка увеличилось в 3 раза?

Ответ:

а) 100 Ом

б) 200 Ом

в) 300 Ом

г) 400 Ом

---

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения полного сопротивления участка цепи при последовательном соединении.

3.Выполнить решение задачи в общем виде.

4.Подставить известные данные и найти искомую величину.

Решение

Запишем исходные данные:

• Сопротивление первого резистора: R₁ = 10 Ом.

• Сопротивление первого резистора: R₂ = 20 Ом.

• Сопротивление первого резистора: R₃ = 30 Ом.

• Сопротивление первого резистора: R₄ = 40 Ом.

Чтобы суммарное сопротивление цепи увеличилось втрое, нужно добавить пятый резистор, сопротивление которого можно вычислить, решив следующую систему уравнений:

R1+R2+R3+R4+R5=3R

R1+R2+R3+R4=R

Вычислим суммарное сопротивление четырех резисторов R:

R=10+20+30+40=100 (Ом)

Следовательно:

R+R5=3R

R5=2R=100·2=200 (Ом)

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17529

Сопротивление каждого резистора в схеме участка цепи на рисунке равно 100 Ом. При подключении участка к источнику постоянного напряжения 12 В выводами A и B напряжение на резисторе R2 равно

Ответ:

а) 2,4 В

б) 4 В

в) 6 В

г) 12 В

---

Алгоритм решения

1. Записать исходные данные.

2.Выполнить решение в общем виде.

3.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Сопротивление каждого и резисторов: R₁ = R₂ = R₃ = R₄ = R₅ = 100 Ом.

• Напряжение на всем участке цепи: U = 12 В.

Так как цепь состоит из двух параллельных цепочек, то напряжение на каждой из них одинаковое и равно 12 В. Но нас интересует напряжение только на втором резисторе в верхней цепочке, который соединен последовательно с первым резистором.

При последовательном соединении:

I1=I2=I

U1+U2=U

Применим для нашего случая:

I1=I2=I12

U1+U2=U12=U

Согласно закону Ома для участка цепи:

U=IR

Следовательно:

U1=I12R1=I12R

U2=I12R2=I12R

Отсюда:

U2=U1

Так как их сумма равна 12 В, то каждый из них равен 6 В. Следовательно, U₂ = 6 В.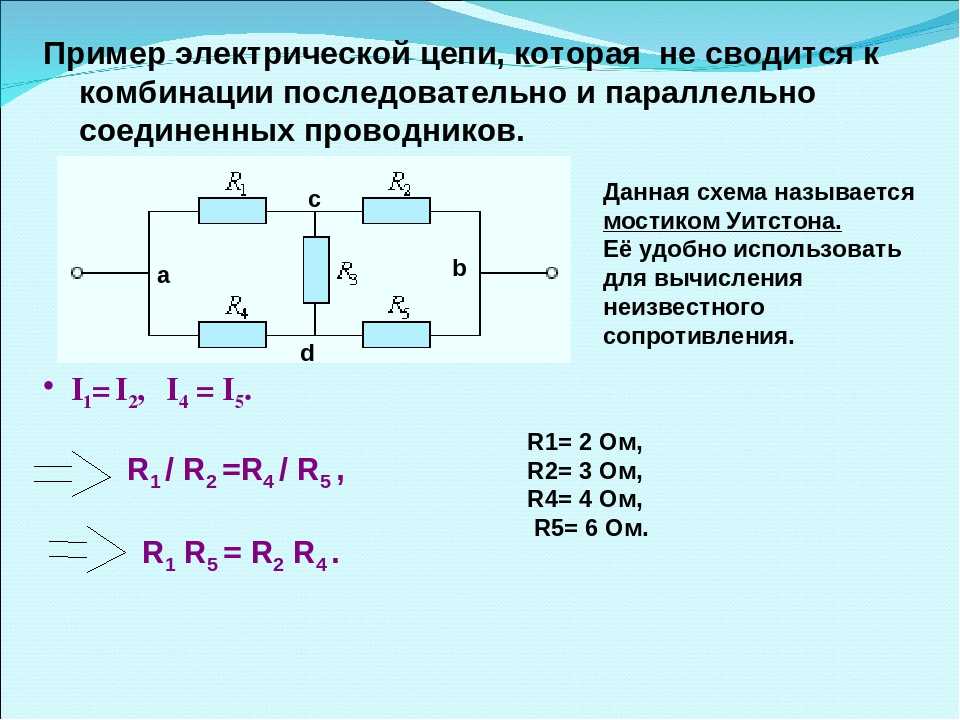

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22543

В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.

Ответ:

а) 23 В

б) 25 В

в) 27 В

г) 29 В

---

Алгоритм решения

1.Записать исходные данные.

2.Записать закон Ома для полной цепи.

3.Выполнить решение в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Сила то на первом резисторе: I₁ = 1 А.

• Внутреннее сопротивление источника тока: r = 1 Ом.

• Сопротивление первого резистора: R₁= 3 Ом.

• Сопротивление первого резистора: R₂= 1 Ом.

• Сопротивление первого резистора: R₃= 5 Ом.

Закон Ома для полной цепи:

I=εR+r..

R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:

1R12..=1R1..+1R2..

R12=R1R2R1+R2..

Полное сопротивление внешней цепи равно:

R=R12+R3=R1R2R1+R2..+R3

Следовательно, ЭДС источника тока равен:

ε=I(R+r)=I(R1R2R1+R2..+R3+r)

Полная сила тока равна силе тока параллельного участка цепи, так как I = I₃ = I₁₂. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:

I12=I1+I2=I

Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:

U1=I1R1

Так как это параллельный участок, то:

U1=U2=U12

Следовательно, сила тока на втором резисторе равна:

I2=U2R2..=I1R1R2..

Сила тока на всем участке цепи равна:

I=I12=I1+I1R1R2.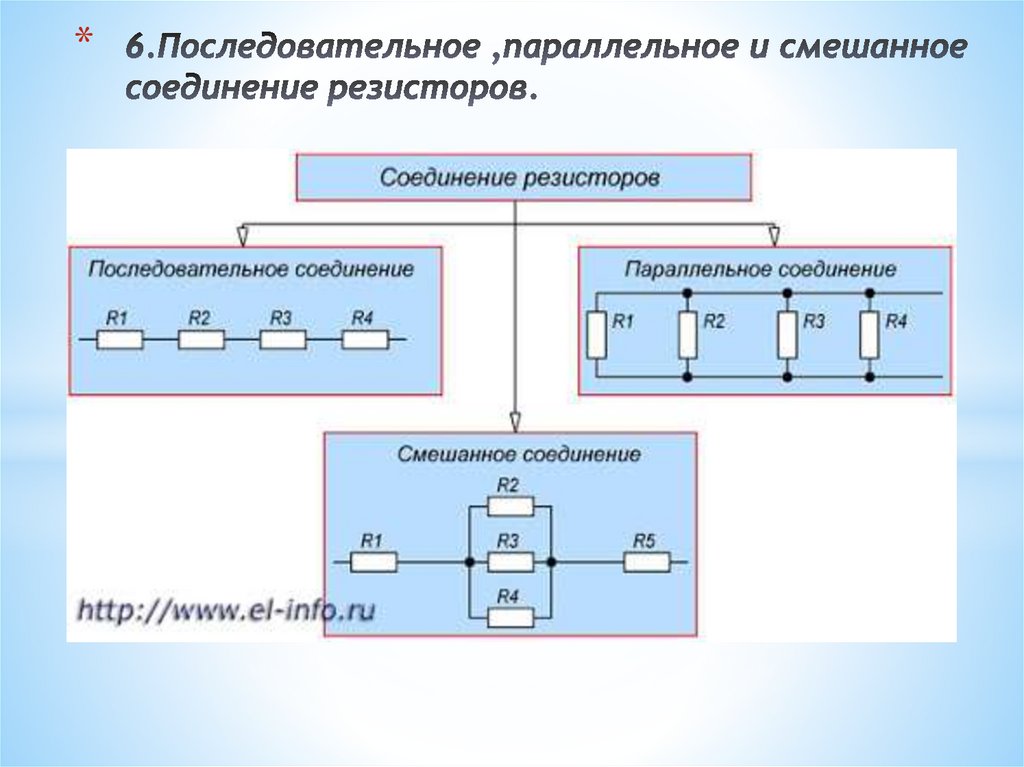 .=I1(1+R1R2..)

Теперь можем вычислить ЭДС источника тока:

ε=I1(1+R1R2..)(R1R2R1+R2..+R3+r)

ε=1(1+31..)(3·13+1..+5+1)=6,75·4=27 (В)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 4.1k

Резисторы серии

и параллельные резисторы Практические задачи онлайн

При R1=3,0 Ом, R_1 = 3,0\\Омега, R1=3,0 Ом, R2=6,0 Ом, R_2 = 6,0\\\Омега, R2=6,0 Ом, R3=4,0 Ом, R_3 = 4,0\\\Омега, R3 ​=4,0 Ом, R4=8,0 Ом, R_4 = 8,0\\Омега, R4=8,0 Ом, R5=6,0 Ом, R_5 = 6,0\ \Омега, R5=6,0 Ом, R6=3,0 Ом, R_6 = 3,0\ \Omega, R6​=3,0 Ом, R7=6,0 Ом, R_7 = 6,0\ \Omega R7=6,0 Ом и R8=12,0 Ом, R_8 = 12,0\ \Omega,R8​=12,0 Ом, каково примерное общее эквивалентное сопротивление ?

5,8 Ом 5,8\\Омега 5,8 Ом 17,6 Ом 17,6\\Омега 17,6 Ом 23,4 Ом 23,4\\Омега 23,4 Ом 11,7 Ом 11,7\\Омега 11,7 Ом

Показать объяснение

Посмотреть вики

В приведенной выше схеме V = 9,6 В, V = 9,6 \ text { В}, V = 9,6 В, R1 = 2 Ом, R_1 = 2 \ \ Omega, R1 = 2 Ом, R2 = 9 Ом, R_2 = 9 \\Omega,R2​=9 Ом и R3=18 Ом.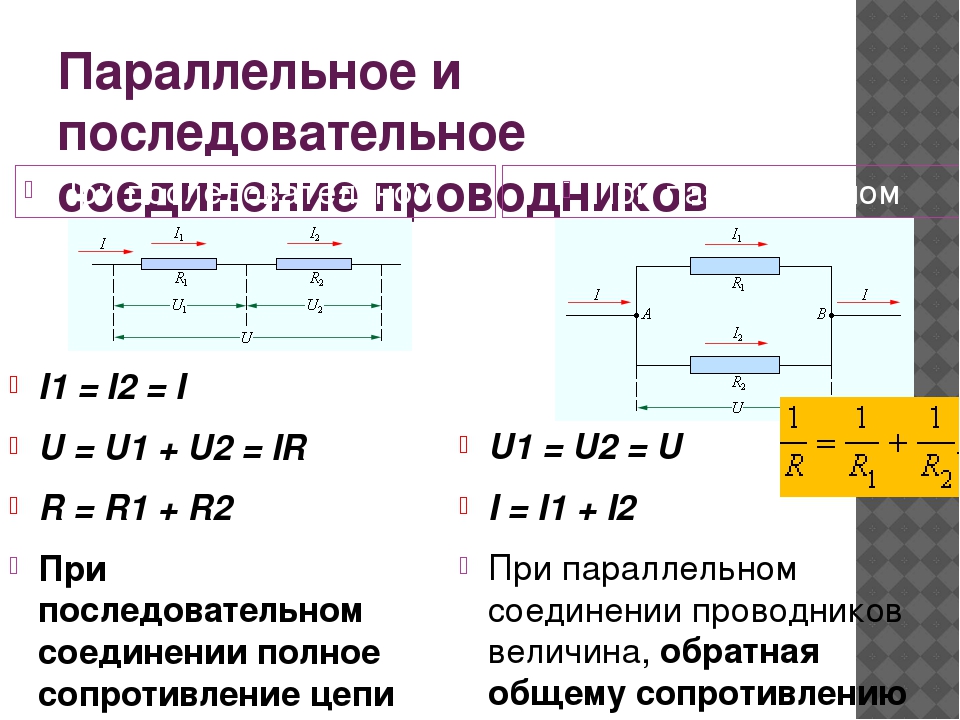 R_3=18\ \Omega.R3​=18 Ом. Найдите ток через R3.R_3.R3​.

0,4 А 0,8 А 0,2 А 0,6 А

Показать объяснение

Посмотреть вики

При R1=5 Ом R_1 = 5\\Омега R1=5 Ом и R2=10 Ом, R_2 = 10\\Омега, R2=10 Ом, каково общее эквивалентное сопротивление?

15 Ом 15 \\Омега 15 Ом 20 Ом 20 \\Омега 20 Ом 5 Ом 5 \\Омега 5 Ом 6 Ом 6 \ \Омега 6 Ом

Показать объяснение

Посмотреть вики

При R1=5,0 Ом, R_1 = 5,0\\Омега, R1=5,0 Ом, R2=4,0 Ом, R_2 = 4,0\\\Омега, R2=4,0 Ом, R3=2,0 Ом, R_3 = 2,0\\\Омега, R3 ​=2,0 Ом, R4=6,0 Ом, R_4 = 6,0\\Омега, R4=6,0 Ом и R5=8,0 Ом, R_5 = 8,0\\Омега, R5=8,0 Ом, каково примерное общее эквивалентное сопротивление?

5,5 Ом 5,5 \ \Омега 5,5 Ом 2,1 Ом 2,1\\Омега 2,1 Ом 8,3 Ом 8,3\\Омега 8,3 Ом 6,2 Ом 6,2\\Омега 6,2 Ом

Показать объяснение

Посмотреть вики

Учитывая R1=9 Ом, R_1 = 9\\Омега, R1=9 Ом и R2=18 Ом, R_2 = 18\\\Омега, R2=18 Ом, каково общее эквивалентное сопротивление?

9 Ом 9\ \Омега 9 Ом 27 Ом 27\\Омега 27 Ом 6 Ом 6\ \Омега 6 Ом 3 Ом 3\ \Омега 3 Ом

Показать объяснение

View wiki

Последовательно-параллельный метод

Некоторые сложные схемы могут быть упрощены методом, использующим только результаты резисторов, включенных последовательно и параллельно.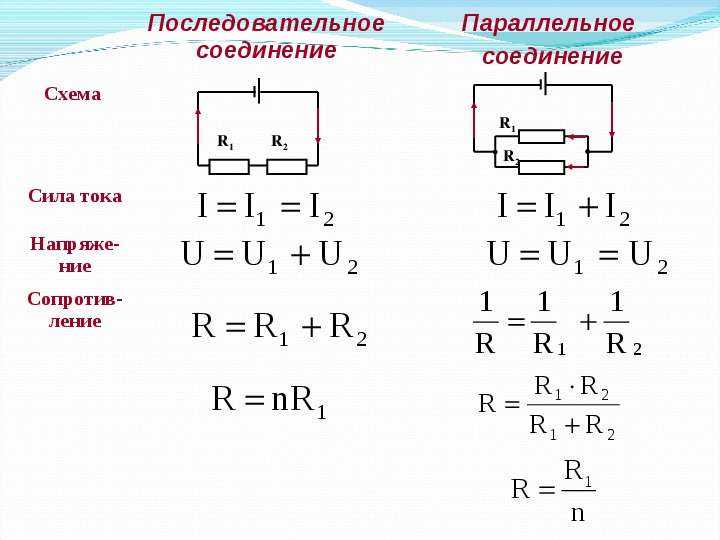 Они дают хорошие примеры для углубления вашего понимания последовательных и параллельных цепей. Мы проиллюстрируем этот метод на примере ниже.

Основная идея последовательно-параллельного метода заключается в последовательном использовании правил эквивалентного сопротивления для последовательных и параллельных резисторов в последовательности шагов.

1. Сначала заменим все резисторы последовательно на их эквивалентные сопротивления. Этот шаг обычно оставляет несколько резисторов параллельными.
2. Затем мы заменяем резисторы, включенные параллельно, их эквивалентными сопротивлениями. На этом этапе последовательно генерируются новые резисторы, которые затем можно заменить их эквивалентными сопротивлениями.
3. Продолжайте, если необходимо, п. 1, а при необходимости – п. 2, пока не упростим схему до одного резистивного эквивалента сети, подключенного к одному источнику. Если в какой-то момент у нас остается более одного резистора, и мы не можем решить, подключены ли два или более резистора последовательно или параллельно, процесс завершается с ошибкой метода. В таких случаях вам понадобится более продвинутый метод.
4. Предположим, наш процесс упростил схему до одного резистора на источнике. Схема с одним эквивалентным резистором решена для общего тока.
5. Вычисленный ток используется в шагах назад для нахождения падений потенциала и токов в ранее симплипольных цепях до тех пор, пока не будут вычислены все токи и падения потенциала.

Последовательно-параллельный метод работает не всегда . Например, если в схеме есть мост от одной ветви к другой, становится невозможно разделить резисторы на последовательные или параллельные категории. Для этих более сложных схем вы изучите более общий метод, называемый правилами Кирхгофа, в следующем разделе.

Пример 36.4.1. Цепи с последовательным и параллельным соединением.

Рассмотрим четыре резистора, подключенных к источнику напряжения, как показано на рисунке 36.4.2. Найдите ток через каждый резистор.

Рисунок 36.4.2.

Подсказка

Изучите решение.

Ответ

\(\phi_d= 0;\) \(\phi_a = 6\ \text{V};\) \(\phi_b = \dfrac{60}{17}\ \text{V};\ ) \(\phi_c = \dfrac{40}{17}\ \text{V}.\) \(I_1 = \dfrac{2}{7}\ \text{A};\) \(I_2 = \dfrac {3}{34}\ \text{A};\) \(I = \dfrac{7}{34}\ \text{A}.\)

Решение

Чтобы найти ток через резисторы, нам нужно падение потенциала на каждом из них. Поэтому начнем с маркировки потенциальных точек узла на схеме, как показано на рисунке.

Как объяснялось выше, узловые точки представляют собой точки с уникальными значениями электрического потенциала. В данной схеме есть четыре узла, которые помечены \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) и \(d\text{. }\) Узел \(d\) подключается к минусу источника и обычно задается нулевым вольтом в качестве опорного, \(\phi_d = 0\text{.}\) Поскольку напряжение батареи составляет 6 вольт, потенциал при \(a\) равно 6 В, то есть \(\phi_a = 0\text{.}\) Теперь, следуя пошаговой процедуре упрощения схемы, найдем потенциалы при \(b\) и \(c\text{,}\), а именно, \(\phi_b\) и \(\phi_c\text{,}\) соответственно.

Шаг 1:

При наличии последовательно соединенных резисторов замените их эквивалентными резисторами. Здесь только \(10\\Омега\) и \(20\\Омега\) идут последовательно. Поэтому заменяем их резистором \(30\text{-}\Omega\). Здесь лучше оставить те же метки, что и на предыдущей диаграмме.

Шаг 2:

Если какие-либо резисторы подключены параллельно, замените их эквивалентными резисторами. Здесь только 30 \(\Omega\) и 40 \(\Omega\) параллельно. Поэтому мы заменяем комбинацию их эквивалентным сопротивлением, которое равно \(\dfrac{120}{7}\ \Omega\text{.}\)

Шаг 3:

После замены параллельных резисторов на \(\dfrac{120}{7}\ \Omega\text{,}\) мы обнаруживаем, что он включен последовательно с \(12\text{ -}\Омега\) резистор. Поэтому ток через \(\dfrac{120}{7}\ \Omega\) должен быть таким же, как и ток через резистор \(12\text{-}\Omega\). Теперь два последовательно соединенных резистора можно заменить резистором \(\dfrac{204}{7}\text{-}\Omega\), что приведет к очень простой схеме.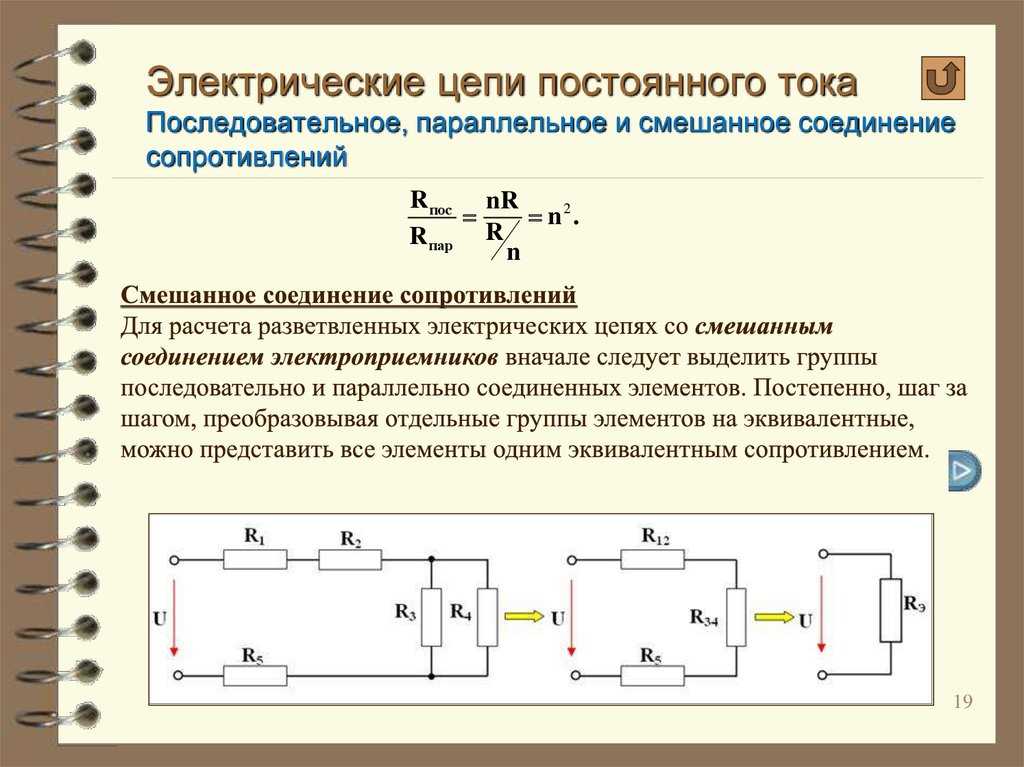 Ток через резистор \(\dfrac{204}{7}\text{-}\Omega\) должен быть таким же, как через резистор \(12\text{-}\Omega\) или \(\dfrac{120}{ 7}\text{-} \Омега\), так как он заменяет последовательные резисторы.

Шаг 4:

Теперь мы можем использовать закон Ома, чтобы найти ток через резистор \(\dfrac{204}{7}\text{-}\Omega\).

\begin{уравнение*} I = \dfrac{6V}{(204/7)\Omega} = \dfrac{7}{34}\ \text{A}. \end{equation*}

Шаг 5:

Затем мы прослеживаем наш путь в обратном направлении к исходной схеме. Ток через резистор \(12\text{-}\Omega\) также равен \(7/34\text{ A}\text{.}\) Следовательно, падение потенциала на \(12\text{-} \Омега\) резистор

\begin{уравнение*} \phi_a-\phi_b = \dfrac{7}{34}\ \text{A} \times 12\ \Omega = \dfrac{42}{17}\ \text{V}. \end{equation*}

Падение потенциала на резисторе \(\dfrac{120}{7}\text{-} \Omega\) равно \((60/17)\text{V}\text{. }\)

\begin{уравнение*} \phi_b-\phi_d = \dfrac{7}{34}\ \text{A} \times \dfrac{120}{7}\ \Omega = \dfrac{60}{17}\ \text{V}\ \ \Longrightarrow\ \phi_b = \dfrac{60}{17}\ \text{V}. \end{equation*}

Возвращаясь еще на один шаг назад, мы обнаруживаем, что падение потенциала на резисторе \(30\text{-}\Omega\) такое же, как и на резисторе \(\dfrac{120}{7}\ text{-}\Omega\) резистор, который мы разработали. Следовательно, ток через резистор \(30\text{-}\Omega\) равен просто

\begin{уравнение*} I_1 = \dfrac{(60/17)\ \text{V}}{30\ \Omega} = \dfrac{2}{17}\ \text{A} \end{equation*}

Следовательно, напряжение \(\phi_c\) получается из падения потенциала на резисторе \(20\text{-} \Omega\), как указано в

\begin{equation*} \phi_c — \phi_d = \left( \dfrac{2}{17}\ \text{A} \right) \times 20\ \Omega = \dfrac{40}{17}\ \text{V}. \end{equation*}

Так как \(\phi_d = 0\text{,}\) мы получаем \(\phi_c = \dfrac{40}{17}\ \text{V}\text{.}\) Мы можем использовать напряжения узла для получения тока через различные резисторы. В качестве альтернативы, поскольку общий ток \(I\) был разделен на \(I_1\) и \(I_2\text{,}\), мы можем найти \(I_2\), вычитая \(I_1\) из \(I\ текст{.