Последовательное параллельное и смешанное соединение резисторов. Последовательное, параллельное и смешанное соединение резисторов: типы, расчеты, примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при последовательном соединении резисторов. Как определить эквивалентное сопротивление параллельного соединения. Какие особенности имеет смешанное соединение резисторов. Как упростить сложные резистивные схемы.

Содержание

Типы соединений резисторов в электрических цепях

В электрических схемах резисторы могут соединяться тремя основными способами:

Последовательное соединение
Параллельное соединение
Смешанное соединение

Каждый тип соединения имеет свои особенности и правила расчета общего сопротивления цепи. Рассмотрим их подробнее.

Последовательное соединение резисторов

При последовательном соединении резисторы включаются один за другим, образуя единую цепь. Основные свойства такого соединения:

Через все резисторы протекает одинаковый ток
Общее напряжение распределяется между резисторами
Общее сопротивление равно сумме сопротивлений всех резисторов

Формула для расчета общего сопротивления при последовательном соединении:

R_общ = R1 + R2 + R3 + … + Rn

Где R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Пример расчета последовательного соединения

Рассмотрим цепь из трех последовательно соединенных резисторов:

R1 = 10 Ом
R2 = 20 Ом
R3 = 30 Ом

Общее сопротивление составит:

R_общ = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Параллельное соединение резисторов

При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Основные свойства:

На всех резисторах одинаковое напряжение
Общий ток распределяется между резисторами
Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов

Формула для расчета общего сопротивления при параллельном соединении:

1/R_общ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Пример расчета параллельного соединения

Рассмотрим цепь из трех параллельно соединенных резисторов:

R1 = 6 Ом
R2 = 3 Ом
R3 = 2 Ом

Рассчитаем общее сопротивление:

1/R_общ = 1/6 + 1/3 + 1/2 = 1

R_общ = 1 Ом

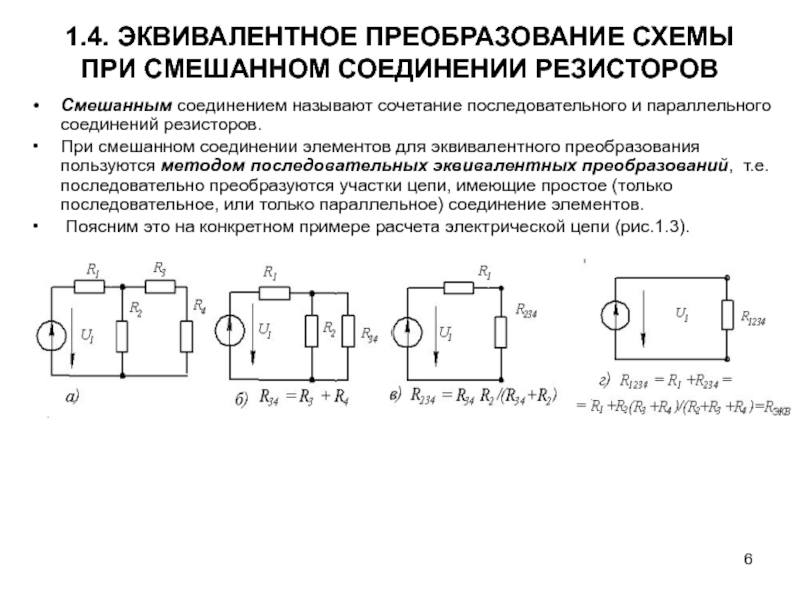
Смешанное соединение резисторов

Смешанное соединение представляет собой комбинацию последовательных и параллельных участков. Для расчета общего сопротивления такой схемы необходимо:

Разбить схему на простые последовательные и параллельные участки
Рассчитать сопротивление каждого участка
Объединить полученные результаты

Пример расчета смешанного соединения

Рассмотрим схему из 5 резисторов:

R1 = 10 Ом (последовательно)
R2 = 20 Ом и R3 = 30 Ом (параллельно)
R4 = 40 Ом и R5 = 50 Ом (последовательно)

Расчет:

Сопротивление параллельного участка R2 и R3: 1/R₂₃ = 1/20 + 1/30 = 1/12 Ом R₂₃ = 12 Ом
Сопротивление последовательного участка R4 и R5: R₄₅ = 40 + 50 = 90 Ом
Общее сопротивление: R_общ = R1 + R₂₃ + R₄₅ = 10 + 12 + 90 = 112 Ом

Методы упрощения сложных резистивных схем

Для анализа сложных резистивных цепей можно использовать следующие методы:

Последовательное преобразование участков схемы
Применение законов Кирхгофа
Метод контурных токов
Метод узловых потенциалов
Преобразование звезда-треугольник

Выбор метода зависит от конкретной схемы и поставленной задачи.

Практическое применение различных соединений резисторов

Знание особенностей соединения резисторов позволяет решать различные практические задачи:

Расчет делителей напряжения

Проектирование схем защиты от перенапряжения
Создание измерительных мостовых схем
Разработка фильтров и аттенюаторов

Влияние типа соединения на характеристики электрической цепи

Выбор способа соединения резисторов влияет на ключевые параметры цепи:

Общее сопротивление
Распределение токов и напряжений
Мощность, рассеиваемую на элементах
Чувствительность к изменению параметров отдельных компонентов

Правильный выбор типа соединения позволяет оптимизировать работу электрической схемы.

Особенности расчета цепей с источниками ЭДС

При наличии в схеме источников ЭДС необходимо учитывать следующие моменты:

Направление тока в ветвях определяется полярностью источников
Внутреннее сопротивление источников влияет на общее сопротивление цепи
Для расчета сложных цепей с несколькими источниками применяют метод наложения

Выводы

Понимание принципов последовательного, параллельного и смешанного соединения резисторов является фундаментальным для анализа и проектирования электрических цепей. Это позволяет:

Рассчитывать общее сопротивление сложных схем
Определять токи и напряжения на отдельных участках
Оптимизировать параметры электрических цепей
Решать практические задачи в области электротехники и электроники

Правильное применение методов анализа резистивных цепей — ключ к эффективной работе с электрическими схемами любой сложности.

11. Последовательное, параллельное и смешанное соединения резисторов.

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с

началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

Последовательное соединение приемников поясняет рис. 19,а. Заменяя лампы резисторами с сопротивлениямиR₁, R₂и R₃ получим схему, показанную на рис. 19,б.Если принять, что в источнике R₀ = 0, то для трех последова-тельно соединенных резисторов согласно второму Кирхгофа можно написать:

E = IR₁ +IR₂+IR₃ = I( R₁+ R₂+ R₃ ) = IR_общ ;

где: R_общ = R₁+ R₂+ R₃

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.

Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.

Соединять последовательно целесообразно только приемники с одинаковыми сопротивлениями. В противном случае приложенное напряжение источника электрической энергии распределяется между ними неравномерно и отдельные приемники могут оказаться под недопустимо высоким для них напряжением.

При последовательном соединении приемников изменение сопротивления одного из них влечет за собой изменение напряжения на других связанных с ним приемниках. При обрыве электрической цепи в одном из приемников в остальных прекращается ток.

При параллельном соединении приемники включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 20,а). Заменяя лампы резисторами с сопро-тивлениями R₁, R₂и R₃, получим схему, показанную на рис.

20,б.

При параллельном соединении ко всем резисторам приложено одинаковое напряжениеU. Поэтому согласно закону Ома:

I₁= U/R₁, I₂=U/R₂, I₃ = U/R₃

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I=I₁+I₂+I₃

или

I= U/R₁+ U/R₂+ U/R₃ = U (1/ R₁ + 1/ R₂+ 1/ R₃) = U/R_экв

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/ R_экв= 1/ R₁ + 1/ R₂+ 1/ R₃

При увеличении числа параллельно включаемых резисторов результирующее сопротивление уменьшается.

При параллельном соединении приемников все они находятся под одним и тем же напряжением и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом

преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.

Последовательное, параллельное и смешанное соединения электрических сопротивлений и источников э. д. с.

Различают последовательное, параллельное и смешанное соединения электрических сопротивлений и других потребителей электрической энергии.

На рис. 1 показано последовательное соединение генератора Г и трех электрических сопротивлений (r1, r2, r3).

При последовательном соединении электрических сопротивлений во всех сопротивлениях проходит один и тот же ток, так как сопротивления включаются одно за другим.

Рис.1. Последовательное соединение генератора Г и трех электрических сопротивлений

На рис. 2 изображено параллельное соединение трех электрических ламп с сопротивлениями r1, r2, r3 и одного реостата, сопротивление которого r4; соединение изображено упрощенной (слева) и развернутой (справа) схемами.

Рис.2.Параллельное соединение трех электрических ламп и одного реостата

При параллельном соединении сопротивлений падение напряжения во всех сопротивлениях одинаково, а ток в каждом сопротивлении (ветви) определяется только величиной сопротивления данной ветви.

Смешанным называется соединение сопротивлений, в котором имеются сопротивления, включенные последовательно и параллельно друг другу.

В схеме, показанной на рис. 3, группа, состоящая из трех параллельно включенных сопротивлений (r1, r2, r3), соединена последовательно с группой, состоящей из двух параллельно включенных сопротивлений (r4 и r5).

Рис.3.Группа из трех параллельно включенных сопротивлений соединена последовательно с группой из двух параллельно включенных сопротивлений.

Группу сопротивлений, образующую последовательное, параллельное или смешанное соединение, при расчетах заменяют эквивалентным сопротивлением. Величина этого сопротивления выбирается такой, что ток во всех остальных элементах схемы (сопротивлениях, генераторах и т. д.), не входящих в это соединение, остается неизменным.

Эквивалентное сопротивление последовательного соединения равно сумме всех сопротивлений, входящих в соединение. Это очевидно, так как включая последовательно сопротивления, мы тем самым затрудняем прохождение электрического тока в цепи.

Определим эквивалентное сопротивление параллельно включенных сопротивлений. Так как каждая новая параллельная ветвь создает для тока дополнительный путь, то тем самым электрическая проводимость будет увеличиваться по мере присоединения новых ветвей, и чем больше будет отдельных ветвей, тем больше будет электрическая проводимость соединения.

Эквивалентная электрическая проводимость параллельного соединения сопротивления равна сумме электрических проводимостей каждой ветви

Если все ветви соединения имеют сопротивления одинаковой величины rn, а число ветвей равно n, то в соответствии с последней формулой имеем

Последовательным соединением нескольких источников э. д. с., например, гальванических элементов или генераторов, называется такое соединение, при котором положительный полюс первого соединяют с отрицательным полюсом второго, положительный полюс второго — с отрицательным полюсом третьего и т. д. (рис. 4).

Электродвижущая сила батареи последовательно соединенных элементов равна сумме электродвижущих сил отдельных элементов, а эквивалентное внутреннее сопротивление равно сумме их внутренних сопротивлений.

Параллельным соединением нескольких источников э. д. с. (например, гальванических элементов) называется такое, при ко-тором соединяют в один общий полюс все положительные полюсы элементов, а в другой — все отрицательные.

Соединять параллельно можно только элементы (или другие источники э. д. с.) с одинаковыми электродвижущими силами, так как неравенство последних приводит к возникновению токов, идущих от элементов с большой электродвижущей силой к элементам с меньшей электродвижущей силой. Эти токи не поступают во внешнюю цепь, т. е. связанная с ними энергия расходуется только на нагрев элементов и соединяющих элементы проводов.

На рис. 5 показано параллельное соединение трех элементов. Стрелками обозначено направление токов в каждом элементе и в общей (внешней) цепи.

Эквивалентное внутреннее сопротивление батареи элементов (или других источников тока) рассчитывается по тем же формулам, что и эквивалентное сопротивление соединенных параллельно сопротивлений.

Возможно и смешанное соединение источников э. д. с. Соединяя источники э. д. с. параллельно друг другу и соединяя образовавшиеся группы последовательно, можно получить соединение, обладающее любой электродвижущей силой при любом значении эквивалентного внутреннего сопротивления.

Рис. 6

При замене одного источника несколькими такими же, включенными параллельно, напряжение на нагрузке меньше зависит от сопротивления нагрузки. Отсюда следует, например, что если яркость свечения ламп при одном источнике э. д. с. будет сильно колебаться при изменении числа ламп, включенных в сеть (параллельно), то при включении достаточного числа источников э. д. с. параллельно друг другу яркость включенных в сеть ламп практически не будет зависеть от числа ламп.

Резисторы в последовательном и параллельном соединении Комбинация цепей

Схема

Резисторы в последовательном и параллельном соединении

[adsense1]

Резисторы могут быть соединены только последовательно или параллельно.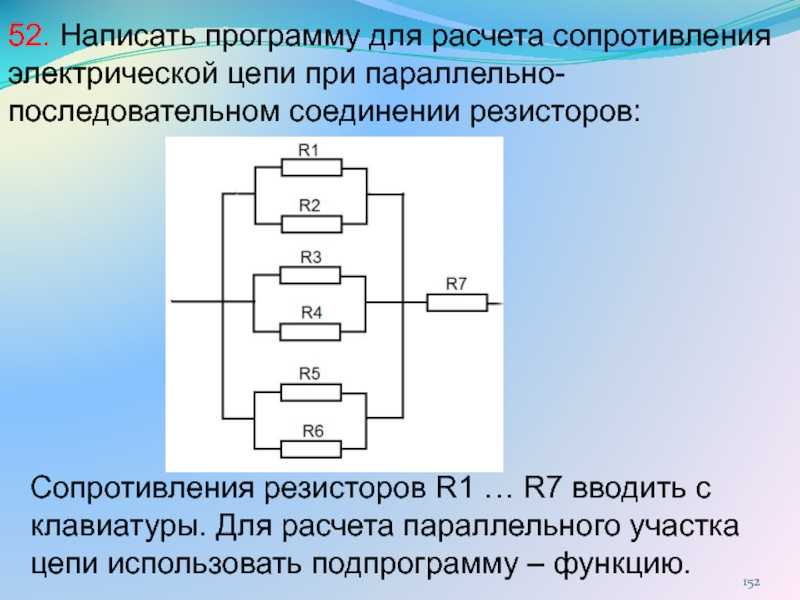 Некоторые схемы резисторов состоят из комбинации последовательных и параллельных цепей для создания более сложных схем. Эти схемы обычно известны как схемы со смешанными резисторами. Несмотря на то, что в этих схемах объединены последовательные и параллельные цепи, метод расчета эквивалентного сопротивления не изменился. Основные правила отдельных сетей, такие как «одинаковый ток течет через последовательные резисторы» и «напряжение на параллельных резисторах одинаковое», применимы к смешанным схемам.

Ниже показан пример схемы со смешанными резисторами. Напряжение питания равно V, а общий ток, протекающий в цепи, равен I. Ток, протекающий через резисторы R2 и R3, равен I1, а ток, протекающий через резистор R4, равен I2.

Здесь резисторы R2 и R3 соединены последовательно. Следовательно, применяя правило последовательного соединения резисторов, эквивалентное сопротивление R2 и R3 определяется как

R _A = R2 + R3

Здесь RA — эквивалентное сопротивление R2 и R3

[adsense2]

Теперь резисторы R2 и R3 можно заменить одним резистором RA.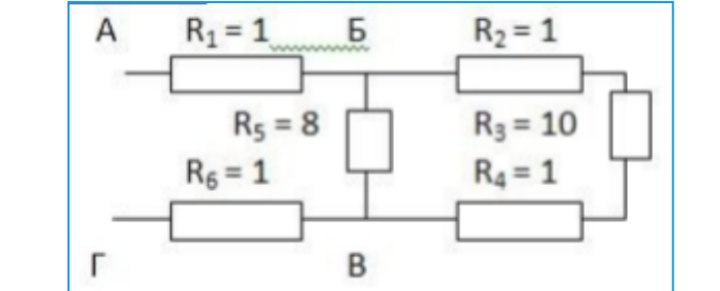 Получившаяся схема показана ниже.

Теперь резисторы RA и R4 соединены параллельно. Следовательно, применяя правило параллельного соединения резисторов, эквивалентное сопротивление RA и R4 равно

R _B = R _A × R4 / (R _A + R4)

Здесь RB — эквивалентное сопротивление RA и R4

Теперь мы можем заменить резисторы RA и R4 одним резистором RB. После замены резисторов результирующая схема показана ниже.

Теперь схема состоит всего из двух резисторов. Здесь также резисторы R1 и RB включены последовательно. Следовательно, применяя правило резисторов последовательно, общее эквивалентное сопротивление цепи определяется как

R _EQ = R1 + R _B

Здесь R _EQ — полное эквивалентное сопротивление цепи. Теперь резисторы R1 и R _B можно заменить одним резистором R _EQ.

Окончательная эквивалентная схема для вышеуказанной сложной схемы показана ниже.

Несмотря на то, что они кажутся сложными, схемы со смешанными резисторами можно свести к простой схеме, состоящей только из одного источника напряжения и одного резистора, следуя простым правилам последовательного и параллельного резисторов.

Резисторы, соединенные последовательно и параллельно Пример

Рассчитаем эквивалентное сопротивление для приведенной ниже цепи, состоящей из 7 резисторов R1 = 4 Ом, R2 = 4 Ом, R3 = 8 Ом, R4 = 10 Ом, R5 = 4 Ом, R6 = 2 Ом и R7 = 2 Ом. Напряжение питания 5 В.

Теперь резисторы R6 и R7 соединены последовательно. Если эквивалентное сопротивление соединенных последовательно R6 и R7 равно Ra, то

Ra = R6 + R7 = 2+2 = 4 Ом

Результирующая схема сокращается до показанной ниже.

В приведенной выше схеме резисторы Ra и R5 соединены параллельно. Следовательно, эквивалентное сопротивление Ra и R5 равно

R _b = (R _a × R ₅ ) / (R _a + R ₅ ) = (4 × 4) / (4 + 4 ) = 2 Ом.

Ниже показана упрощенная схема.

В этой цепи резисторы R4 и R _b соединены последовательно.

Rc = R4 + R _b = 10 + 2 = 12 Ом.

Теперь мы можем заменить резисторы R4 и R _b на резистор Rc, как показано ниже.

В приведенной выше схеме снова резисторы R2 и R3 соединены последовательно. Если Rd — эквивалентное сопротивление R2 и R3, то

Rd = R2 + R3 = 4 + 8 = 12 Ом.

Эквивалентная схема

Здесь резисторы Rc и Rd соединены параллельно. Пусть Rp будет эквивалентным сопротивлением Rc и Rd, включенных параллельно. Затем

р _p = (R _c × R _d ) / (R _c + R _d ) = (12 × 12) / (12 + 12) = 6 Ом.

Результирующая схема имеет вид

Здесь резисторы R1 и Rp соединены последовательно. Пусть R _EQ будет эквивалентным сопротивлением этой комбинации.

Затем

R _EQ = R1 + Rp = 4 + 6 = 10 Ом.

Это эквивалентное сопротивление цепи. Следовательно, данную схему можно окончательно перерисовать как

Ток в цепи можно рассчитать по закону Ома.

Приведенная ниже схема состоит из десяти резисторов R1–R10, соединенных последовательно и параллельно.

Значения сопротивлений, указанных в схеме, указаны в Омах (Ом), а напряжение питания указано в Вольтах (В).

Здесь резисторы R9 и R10 соединены последовательно. Пусть R _A является эквивалентным сопротивлением этой комбинации.

Следовательно, R _A = R9 + R10 = 3 + 3 = 6 Ом.

Схема после замены R9 и R10 на R _A такая

В этой схеме резисторы R8 и R _A соединены параллельно. Тогда эквивалентное сопротивление R8 и R _A равно

R _B = (R8 × R _A ) / (R8 + R _A ) = (6 × 6) / (6 + 6) = 3 Ом.

Теперь заменив R8 и R _A на R _B , мы получим следующую схему.

В этой цепи резисторы R7 и R _B соединены последовательно.

R _C = R7 + R _B = 9 + 3 = 12 Ом.

Эквивалентная схема после замены R7 и R _B на R _C

Понятно, что резисторы R6 и Rc соединены параллельно. Если R _D — эквивалентное сопротивление этой комбинации, тогда

R _D = (R6 × Rc) / (R6 + Rc) = (12 × 12) / (12 + 12) = 6 Ом.

Схема с R¬D, заменяющей R6 и Rc

Теперь резисторы R4 и RD соединены последовательно. Если RE является эквивалентным сопротивлением R4 и RD, то

R _E = R4 + R _D = 6 + 6 = 12 Ом.

Получившаяся уменьшенная схема после замены R4 и R _D на R _E равно

В этой цепи резисторы R5 и R _E соединены параллельно.

Пусть R _F будет эквивалентным сопротивлением R5 и R _E, включенных параллельно.

Затем

R _F = (R5 × R _E ) / (R5 + R _E ) = (12 × 12) / (12 + 12) = 6 Ом.

Упрощенная схема показана ниже.

Здесь резисторы R2 и R3 включены последовательно. Если RG эквивалентен этой комбинации, то

R _G = R2 + R3 = 4 + 2 = 6 Ом.

После замены R2 и R3 на RG схема изменится на

Резисторы RF и RG включены параллельно.

Пусть R _T будет эквивалентом этой комбинации.

Тогда R _T = (R _F × R _G ) / (R _F + R _G ) = (6 × 6) / (6 + 6) = 3 Ом.

Теперь резисторы R1 и RT включены последовательно. Если REQ — полное эквивалентное сопротивление цепи, то REQ = R1 + RT = 3 + 3 = 6 Ом.

Наконец, приведенную выше сложную схему можно перерисовать следующим образом:

Полный ток в цепи можно рассчитать по закону Ома

I = V1 / R _EQ = 6 / 6 = 1 А резистивная цепь, состоящая из ряда резисторов, соединенных в комбинации как последовательных, так и параллельных комбинаций, может быть уменьшена путем определения сначала простых параллельных ветвей резисторов и ветвей последовательных резисторов. Рассчитывается эквивалентное сопротивление этих простых ветвей, и ветви заменяются эквивалентным резистором. Этот процесс снижает сложность схемы. Продолжая этот процесс, мы можем заменить сложную резистивную цепь одним резистором.

Существуют некоторые сложные резистивные схемы, которые нельзя свести к простым схемам, просто применяя правила последовательного и параллельного резистивных комбинаций. Примерами таких сложных резистивных цепей являются такие схемы, как аттенюаторы T-Pad и некоторые сложные резистивные мостовые сети. Для упрощения этих сложных резистивных цепей следует использовать другой подход.

Некоторые сложные резистивные цепи можно уменьшить, используя закон Кирхгофа для тока и закон Кирхгофа для напряжения.

Найти токи и напряжения в сложной резистивной цепи, просто используя закон Ома, может быть невозможно. Для такого типа цепей будут полезны законы Кирхгофа.

Законы Кирхгофа о цепях основаны на концепции сохранения тока и энергии в цепи. Есть два закона цепи Кирхгофа. Первый — это закон тока Кирхгофа, который касается тока в узле, а второй — закон напряжения Кирхгофа, который касается напряжения в замкнутой цепи.

Закон тока Кирхгофа гласит, что «Ток, входящий в узел, равен току, выходящему из узла, потому что ему некуда идти, и ток не теряется в узле».

Проще говоря, закон тока Кирхгофа гласит, что сумма токов, входящих в узел, равна сумме токов, выходящих из цепи.

Закон Кирхгофа о напряжении гласит, что «полное напряжение в замкнутом контуре равно сумме всех падений напряжения в этом контуре».

Проще говоря, закон Кирхгофа о напряжении утверждает, что направленная алгебраическая сумма напряжений в замкнутом контуре равна нулю.

С помощью этих двух законов можно рассчитать значения токов и напряжений в любой сложной цепи.

Тем не менее, у нас могут быть сложные резистивные цепи, в которых трудно определить эквивалентное сопротивление, в таких ситуациях мы будем использовать преобразование резисторов звезда-треугольник, чтобы упростить резисторные цепи.

Серия

— параллельные цепи | Кафедра химической инженерии и биотехнологии

Введение

В этом разделе мы рассмотрим, как анализировать схемы, содержащие резисторы в последовательном и параллельном соединении.

Идентификация и анализ параллельных цепей

На приведенном ниже рисунке показана базовая схема, содержащая последовательно-параллельную комбинацию резисторов. Сопротивление от точки A до точки B составляет R1 , сопротивление от B до C представляет собой комбинацию R2 и R3 параллельно. Общее сопротивление цепи (от точки A до C ) составляет последовательный резистор R1 в сочетании с параллельными элементами.

Более сложный пример последовательно-параллельной цепи резисторов показан ниже

здесь резистор R6 включен параллельно резисторам R4 и R5 6 6 6 6 Также резисторы R3 , R2 и R1 образуют параллельную комбинацию.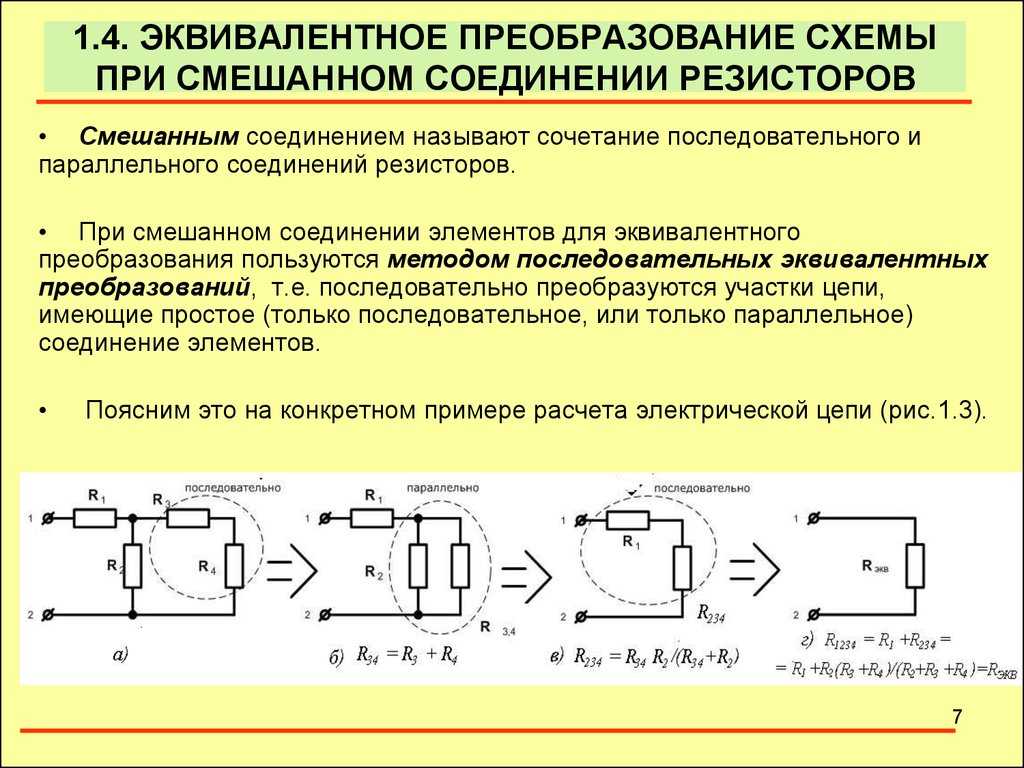 Ясно также, что две параллельные комбинации находятся последовательно друг с другом. Для расчета полного сопротивления последовательно-параллельной цепи мы используем методы, разработанные нами в двух предыдущих разделах. Чтобы проиллюстрировать основные процедуры анализа, мы будем использовать несколько примеров. Сначала мы рассмотрим цепь ниже

и хотим рассчитать общее сопротивление цепи. Ток явно будет проходить через резистор 80 Ом, прежде чем разделится на две составляющие в параллельной комбинации в точке 9.0355 A токи параллельных ветвей рекомбинируют и текут к положительной клемме. Чтобы рассчитать общее сопротивление цепи, сначала вычислим эффективное сопротивление параллельной комбинации, используя метод из предыдущего раздела.

Rпараллельный = 1/(1/100 + 1/50) = 33,3 Ом

Используя этот результат, мы можем перерисовать приведенную выше схему следующим образом:

Теперь общее сопротивление цепи можно рассчитать путем суммирования двух последовательных сопротивлений.

RT = 80 + 33,3 = 113,3 Ом

Далее мы рассмотрим чуть более сложную схему ниже.

Используя ту же процедуру, что и выше, мы сначала определяем эквивалентное сопротивление каждой из параллельных комбинаций, чтобы получить эффективное сопротивление последовательно с R1 . Начнем с резисторов R4 и R5

R5-4 = 1/(1/37 + 1/45) = 20,3 Ом

Теперь отрабатываем сопротивления в каждой из параллельных ветвей. Для верхней ветви сопротивление равна сумме резисторов R2 и R3

R3-2-2 = 493513636363936 393593513639 3936 393593513639 39359359 3936 3935 5559 9036 3936 3936 3935 559 R3-2-2 = 4921 = 10035 9 R3-2 = 4921.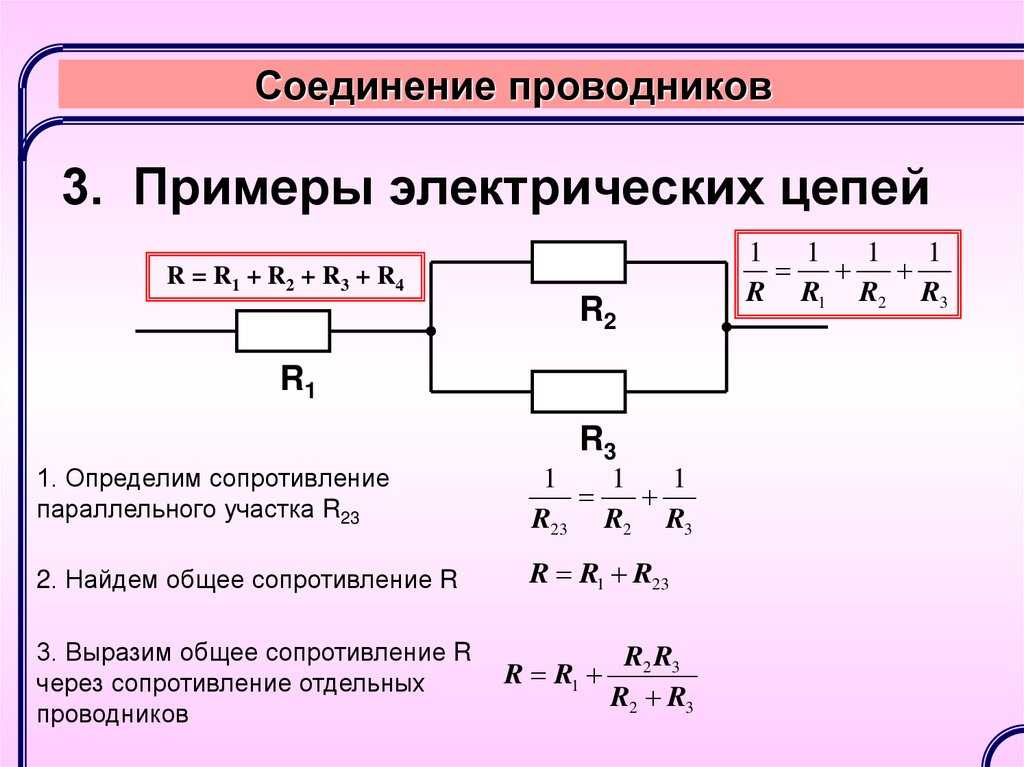

для нижней ветви равна сумме резисторов R6 и R5-4

R6-5-4 = 75 + 20,3 2 6 90,34 6 Ом

Теперь у нас осталась схема, эквивалентная рисунку ниже

Итак, осталось вычислить эффективное сопротивление параллельной комбинации R6-5-4 и R3- 2

R6-5-4-3-2 = 1/(1/100 + 1/95.3) = 48,8 Ом

Таким образом, общее сопротивление цепи равно

RT = 80 + 48,8 = 128,8 Ом

Системный подход, который мы представили выше, можно использовать для определения эффективного сопротивления любой конкретной цепи.