Последовательное подключение резисторов. Последовательное соединение резисторов: принципы, формулы и применение

Что такое последовательное соединение резисторов. Как рассчитать общее сопротивление при последовательном подключении. Для чего используется последовательное соединение резисторов на практике. Какие преимущества и недостатки у данного типа подключения.

Что такое последовательное соединение резисторов

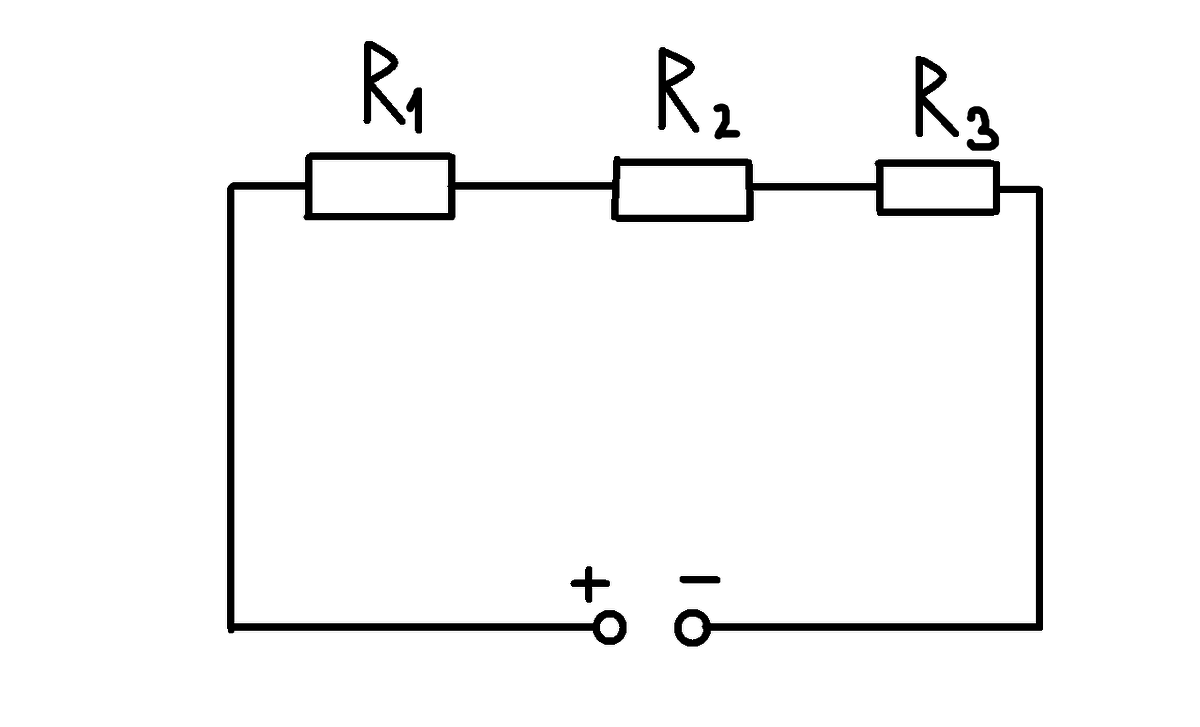
Последовательное соединение резисторов — это такой способ подключения, при котором конец одного резистора соединяется с началом следующего. При этом через все резисторы протекает один и тот же ток.

Основные особенности последовательного соединения:

• Общий ток проходит через все резисторы
• Напряжение распределяется между резисторами
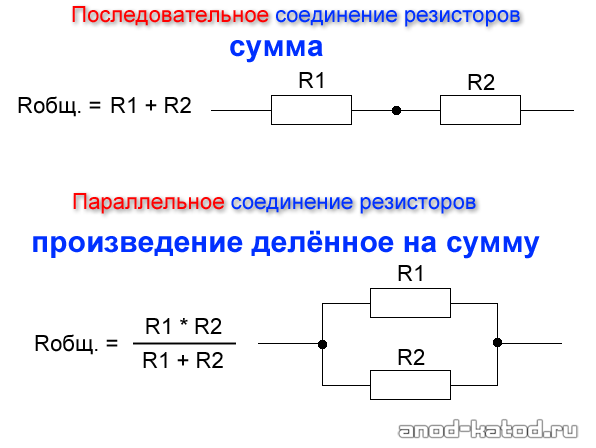
• Общее сопротивление цепи равно сумме сопротивлений всех резисторов

Расчет общего сопротивления при последовательном соединении

Для расчета эквивалентного сопротивления цепи при последовательном соединении используется формула:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Таким образом, общее сопротивление всегда больше сопротивления любого из резисторов в цепи. Это важное свойство последовательного соединения.

Распределение напряжения в последовательной цепи

При последовательном подключении резисторов напряжение источника распределяется между ними пропорционально их сопротивлениям. Чем больше сопротивление резистора, тем большее напряжение на нем падает.

Общее напряжение цепи равно сумме напряжений на всех резисторах:

U = U1 + U2 + U3 + … + Un

Где можно применить эту формулу на практике? Например, при проектировании делителей напряжения, когда нужно «разбить» большее напряжение на несколько меньших.

Применение последовательного соединения резисторов

Последовательное соединение резисторов широко используется в электротехнике и электронике для решения различных задач:

• Создание делителей напряжения
• Увеличение общего сопротивления цепи
• Распределение мощности между резисторами
• Защита компонентов от высокого напряжения
• Регулировка тока в цепи

Рассмотрим подробнее некоторые из этих применений.

Делители напряжения на основе последовательного соединения

Делитель напряжения — это схема, позволяющая получить на выходе напряжение меньше входного. Простейший делитель состоит из двух последовательно соединенных резисторов.

Выходное напряжение делителя определяется формулой:

Uвых = Uвх * R2 / (R1 + R2)

где Uвх — входное напряжение, R1 и R2 — сопротивления резисторов.

Делители напряжения применяются для согласования уровней сигналов, измерения высоких напряжений и во многих других случаях.

Преимущества и недостатки последовательного соединения

Последовательное соединение резисторов имеет свои плюсы и минусы. Какие преимущества дает такой способ подключения?

• Простота расчета общего сопротивления
• Возможность получения большого суммарного сопротивления
• Распределение напряжения между резисторами
• Уменьшение тока в цепи

К недостаткам можно отнести:

• При выходе из строя одного резистора разрывается вся цепь
• Сложнее обеспечить одинаковый режим работы для всех резисторов
• Увеличение общего сопротивления может быть нежелательно в некоторых схемах

Сравнение с параллельным соединением резисторов

Чем отличается последовательное соединение от параллельного? Основные различия:

Параметр	Последовательное	Параллельное
Общее сопротивление	Увеличивается	Уменьшается
Ток	Один для всех резисторов	Разный для каждого резистора
Напряжение	Делится между резисторами	Одинаковое на всех резисторах

При выборе типа соединения нужно учитывать особенности конкретной схемы и требования к ее работе.

Практические примеры использования последовательного соединения

Рассмотрим несколько типичных примеров применения последовательного соединения резисторов на практике:

1. Ограничение тока светодиода

Для защиты светодиода от перегорания применяют токоограничивающий резистор, включенный последовательно. Сопротивление резистора рассчитывается по формуле:

R = (U — Uсд) / I

где U — напряжение питания, Uсд — падение напряжения на светодиоде, I — рабочий ток светодиода.

2. Высоковольтный делитель напряжения

Для измерения высоких напряжений используют делители на основе последовательно соединенных высоковольтных резисторов. Это позволяет снизить напряжение до уровня, безопасного для измерительных приборов.

3. Регулировка яркости лампы накаливания

Последовательно с лампой включают переменный резистор (реостат). Изменяя его сопротивление, можно регулировать ток через лампу и, соответственно, ее яркость.

Основные формулы для последовательного соединения

Для удобства приведем основные формулы, используемые при расчете цепей с последовательным соединением резисторов:

• Общее сопротивление: R = R1 + R2 + … + Rn
• Общее напряжение: U = U1 + U2 + … + Un
• Ток в цепи: I = U / R
• Напряжение на резисторе: Ui = I * Ri
• Мощность на резисторе: Pi = I^2 * Ri

Эти формулы позволяют рассчитать все основные параметры цепи с последовательно соединенными резисторами.

Заключение

Последовательное соединение резисторов — важный и широко используемый способ подключения в электротехнике. Оно позволяет увеличивать общее сопротивление, распределять напряжение и мощность между компонентами, создавать делители напряжения и решать множество других практических задач.

Понимание принципов работы последовательных цепей и умение их рассчитывать — необходимый навык для любого специалиста, работающего с электрическими схемами. Надеемся, эта статья помогла вам лучше разобраться в этой теме!

Последовательное соединение резисторов | Электротехника

Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.

Рис. 25. Схемы последовательного соединения приемников

Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то длярассматриваемой цепи

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.

Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления

Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.

Последовательное соединение

Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.

От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:

• R общее — это сумма всех сопротивлений;
• R1 — первый резистор;
• R2 — второй компонент;
• Rn — последняя составляющая в цепи.

Параллельное подключение

Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.

Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.

В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.

Смешанный вариант

В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.

Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:

• в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
• после этого высчитывают противостояние на последовательно подключённых участках схемы;
• наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
• рассчитывают сопротивление в новой схеме по одной из двух формул.

Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.

Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.

В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.

Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.

На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.

Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.

Последовательное, параллельное и смешанное соединения резисторов

Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Рис. 25. Схемы последовательного соединения приемников

Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

Последовательное соединение приемников поясняет рис. 25, а. Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.

Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то для рассматриваемой цепи

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.

Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.

Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.

Рис. 26. Схемы параллельного соединения приемников

При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или

I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R_эк = 1/R₁ + 1/R₂ + 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.

Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Рис. 27. Схемы смешанного соединения приемников

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Последовательное соединение резисторов

Господа, наш сегодняшний материал посвящен рассмотрению последовательного соединения резисторов. На практике сплошь и рядом соединяют резисторы друг с другом тем или иным способом для достижения той или иной цели, поэтому весьма важно хорошо разбираться в этом вопросе.

Начинаем сразу с определений. Всего есть два вида соединения сопротивлений: последовательное и параллельное.  Взгляните на рисунок 1, там наглядно представлены эти виды соединений.

А) – Последовательное соединение

В) – Параллельное соединение

Рисунок 1 – Последовательное и параллельное соединение

Что мы видим на рисунке 1?

А то, что последовательное соединение – это такое соединение, при котором конец первого резистора совпадает с началом второго, конец второго с началом третьего и т.д.

Параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

В этой статье мы попробуем подробнее проанализировать на основе уже имеющихся знаний последовательное сопротивление. Параллельное же будет в другой статье. Взглянем на рисунок 2. Там подробно разрисовано положение дел для последовательного соединения резисторов.

Рисунок 2 – Последовательное соединение резисторов

Господа, как вы видите из рисунка 2, при последовательном соединении резисторов у нас нет никаких узлов в схеме. То есть ток нигде никуда не ответвляется. Из этого можно сделать вывод, что при последовательном соединении резисторов через все резисторы течет один и тот же ток I. То есть этот ток величиной I втекает в первый резистор R1, проходит через всю цепочку, вытекает из резистора R3 и течет дальше. При этом его величина неизменна для всех резисторов.

С напряжением все не так просто. Сейчас нам понадобиться вспомнить статью про потенциалы. Положим, что на входе резистора R1 у нас потенциал φ₁,  точка соединения резисторов R1 и R2 имеет потенциал φ₂, точка соединения резисторов R2 и R3 имеет потенциал φ₃, а конец резистора R3 имеет потенциал φ4. Короче, лучше смотрите рисунок 2, там все эти потенциалы нарисованы . Дальше вспомним утверждение, что напряжение – это разность потенциалов. То есть разность потенциалов между концами резистора R1 – это напряжение на резисторе R1, ну и так для всех. Запишем это

Сложим левые и правые части этих трех уравнений. Получим

Ну и общее напряжение на всех трех резисторах тоже запишем через разность потенциалов

Сравнивая это выражение и предыдущее, приходим к выводу, что

Да, приложенное к цепочке последовательно соединенных резисторов напряжение равно сумме напряжений на всех резисторах этой цепочки. Напряжение делится между всеми резисторами: на каком-то оно будет побольше, на каком-то поменьше. А в сумме оно будет равно приложенному к цепочке напряжению.

Рассмотрим пример. Допустим, что к нашей цепочке из трех резисторов проложено напряжение U=100 В. Значит, возможна ситуация, когда на резисторах R1, R2 и R3 падает 20 В, 37 В и 43 В (в сумме тоже 100 В). А ситуация, когда на резисторах R1, R2 и R3 падает 50 В, 44 В и 78 В (в сумме 172 В) невозможна. Точно также невозможна ситуация, когда на них падает 10 В, 13 В и 32 В (в сумме 55 В). То есть, если к цепочке последовательно соединенных резисторов приложено 100 В, то суммарное напряжение на всех резисторах тоже должно быть 100 В – не больше и не меньше! Как же именно распределено напряжение между резисторами? Ответ на этот вопрос даст все тот же закон Ома, который не раз нас уже выручал! Согласно закону Ома напряжение на резисторе равно произведению силы тока через него на сопротивление этого резистора. Мы знаем сопротивление данного резистора и ток через него. Поэтому легко находим напряжения на всех резисторах

Едем дальше. Воспользуемся этими соотношениями соотношением и с помощью них преобразуем нашу формулку с суммами напряжений. При этом помним, что через все резисторы у нас течет один и тот же ток I.

Разделим левую и правую часть уравнения на I:

Все та же статья про закон Ома говорит нам, что сопротивление равно напряжение разделить на ток. Поэтому мы можем записать

где R – общее сопротивление нашей цепи из трех резисторов.

Итак, господа, мы получили важное соотношение: при последовательном соединении резисторов общее сопротивление схемы равно сумме отдельных сопротивлений. Запомните это соотношение, оно весьма важное! В чем же его практический смысл? Взгляните на рисунок 3

 

Рисунок 3 – Последовательное соединение

На нем показано, что цепочку из нескольких (в данном случае из 3-х) последовательно соединенных резисторов для упрощения расчетов вполне можно заменить одним резистором с сопротивлением, равным сумме отдельных резисторов. В связи с этим выводом возможно возникновение вопроса: а зачем вообще на практике соединяют резисторы последовательно, если в конечном счете все можно свести к одному резистору? Господа, причин несколько и основные мы сейчас рассмотрим.

1) Резисторы соединяются последовательно в схемах так называемых делителей напряжения. Кто знает, что это такое – отлично, кто нет – чуть позже разберемся в этом вопросе .

2) Последовательное сопротивление резисторов сплошь и рядом применяется в высоковольтной технике. Господа, к резистору можно прикладывать безболезненно для него отнюдь не бесконечно большое напряжение. Максимально допустимое напряжение, которое можно приложить к резистору, всегда прописывается в документации на данный конкретный резистор и его обязательно надо принимать в расчет при выборе резистора в своей схеме. В большинстве своем предельное напряжение ограничено несколькими десятками-сотнями вольт. А как быть, если мы имеем дело с напряжением в тысячи или десятки тысяч вольт? Правильно, резисторы можно соединить последовательно. Как мы помним, при таком соединении общее приложенное напряжение распределяется между резисторами и на каждый из них придется только часть общего.

Рассмотрим конкретный пример. Скажем, у нас есть высоковольтный источник, который формирует напряжение 5 кВ. И нам надо подобрать под него такую нагрузку, чтобы обеспечить ток в 1 мА.

Будем применять резисторы Р1-12-0,25. Это резисторы, рассчитанные на поверхностный монтаж, и они выдерживают напряжение 200 В. Рассчитаем требуемое количество резисторов как отношение напряжения 5 кВ к максимальному напряжению на один резистор 200 В. При расчете обязательно будем использовать коэффициент запаса равный, скажем, 1,25. Это очень примерная и часто компромиссная величина, но какой-то он обязательно должен быть, никогда нельзя работать на пределе. Итак, нам надо использовать

По закону Ома (зная напряжение источника и ток, который необходимо обеспечить) рассчитываем, какое суммарное сопротивление должно быть у этой цепочки резисторов.

Теперь остается только лишь найти сопротивление каждого резистора в этой цепочке

В принципе, этот номинал резистора доступен в номинальном ряду Е192 и его можно купить. Если же именно такого номинала нет в наличии, то берется ближайший доступный и после этого пересчитывается общее сопротивление и при необходимости уточняется количество резисторов.

В заключении надо обязательно проверить, какая мощность будет выделяться на каждом из резисторов в такой схеме. Как мы помним из статьи про мощность ее можно посчитать, например, так:

Один резистор Р1-12-0,25 без проблем рассеивает 0,25 Вт, то есть нашим резисторам перегрев не угрожает.

Итак, для обеспечения тока в 1 мА у источника с напряжением 5 кВ требуется использовать 32 резистора Р1-12-0,25-156 кОм.

Мда, что-то я увлекся рассказом про высоковольтные нагрузки . Это можно объяснить тем, что одно время я плотно работал в отделе разработки высоковольтной техники. Это были очень крутые годы . Есть что вспомнить, есть что рассказать. Немного жаль, что обстоятельства вынудили сменить место работы, но и попробовать себя в новой области тоже интересно…ладно, едем дальше!

3) Последовательное соединение резисторов можно использовать для распределения мощности источника. Иными словами, мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на последовательно соединенных резисторах. В этом легко убедиться. Надеюсь, вы еще не забыли вот это выражение?

Умножим левую и правую части на ток I

Или, другими словами

 

где Р – мощность, выдаваемая источником;

P₁ – мощность, рассеиваемая на резисторе R1;

P₂ – мощность, рассеиваемая на резисторе R2;

P₃ – мощность, рассеиваемая на резисторе R3;

Как это можно применить? Допустим вот так. Нам, скажем, нужно 1 Вт мощности для обогрева домика нашему хомячку в зимние холода, или еще для чего-то, не важно. У нас на руках есть только резисторы Р1-12-0,25, которые, как мы помним, выдерживают только 0,25 Вт. Как же снять с источника питания 1 Вт без вреда для резисторов? Как вариант, соединив последовательно 4 резистора, подобрав их так, что бы на каждом было 0,25 Вт. В сумме на них будет выделяться как раз-таки 1 Вт. Конечно, помня про коэффициент запаса, лучше брать не 4, а хотя бы 5 резисторов, рассеивая на каждом не 0,25, а 0,2 Вт. Не надо работать на пределе, пусть будет какой-то запас всегда.

Наверняка, можно придумать еще варианты применений последовательного соединения резисторов, но, основные мы рассмотрели.  Спасибо что прочитали, огромной вам всем удачи и – пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Схемы соединения резисторов

Последовательное соединение резисторов

Последовательное соединение резисторов

 

 

Iобщ = I1 = I2 = I3

Uобщ = U1 + U2 + U3

 

Параллельное соединение резисторов

Параллельное соединение резисторов

 

 

Iобщ = I1 + I2 + I3

Uобщ = U1 = U2 = U3

 

Реостат

Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки.

Изменяя положение ползунка, в цепи меняется ток от 0 до max.

Реостат применяется для изменения тока в цепи.

В электрических схемах встречается понятие – реостатное включение нагрузки.

Реостатное включение нагрузки

 

T1   I =

Uист Rр + Rн

→ max

 

RP = 0

 

T2   I =

Uист Rр + Rн

→ min

Гасящий резистор

В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор.

Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора.

Гасящий резистор

 

 

 

Uгас = Uист – URн

 

 

PRгас = I2 – Rгас

Делитель напряжения

Делитель напряжения

 

 

Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника.

Потенциометр

Потенциометр – это переменный резистор, с части которого снимается напряжения источника.

Потенциометр

 

 

Применение – регулировка громкости на входе усилителя низкой частоты.

Последовательное и параллельное подключение резисторов | РОБОТИП

Не так давно в статье было описано, как «разгадать» цветовую маркировку на резисторе. А в этой статье, говориться о том, как подобрать (рассчитать) резистор для светодиода. Сегодня будем говорить с вами о последовательном и параллельном подключении резисторов.

С резисторами все достаточно просто.

Последовательное подключение резисторов.

При последовательном подключении, резисторы следуют друг за другом:

Рис.1 — Последовательное подключение резисторов

При последовательном подключении вы увеличиваете общее сопротивление, поскольку электрическому току, в таком случае приходится преодолевать увеличенное препятствие.

На рис.1 мы видим резистор с сопротивлением 100 Ом и следующий за ним резистор тоже с сопротивлением 100 Ом (если смотреть слева на право — это и есть последовательное включение). Подключая их последовательно мы увеличиваем сопротивление.

Чтобы убедиться в том, что сопротивление увеличивается, давайте подадим напряжение 5В на нашу цепочку из резисторов и посмотрим токи идущие в нашей получившейся цепи при подключении одного и двух сопротивлений в отдельности. При подключении одного резистора номиналом 100 Ом:

Рис.2 — Ток идущий через сопротивление 100 Ом при 5В.

Мы видим, что ток в замкнутой цепи по закону Ома будет равен:

I = U / R = 5 / 100 = 50 мА;

Подключим в нашу цепь еще один резистор на 100 Ом последовательно с первым резистором:

Рис.3 — Последовательное подключение резисторов.

Мы можем видеть на рис.3, что ток в цепи вдвое меньше и равняется уже:

I = U / R = 5 / (100 + 100) = 25 мА;

Ток получился равным 25 мА, при подключении последовательно к нашему резистору еще одного резистора на 100 Ом.

Таким образом, мы наглядно видим, что последовательное подключение увеличивает общее сопротивление цепи, а с увеличением сопротивления уменьшается ток. Для наглядности и простоты расчета, резисторы были подобраны одного номинала. Но это не значит, что так будет всегда и везде. Резисторы могут быть любых номиналов и исполнения, суть останется такой же.

Параллельное соединение резисторов.

Если приложить два резистора боком друг к другу и соединить их выводы, то мы получим параллельное соединение.

Рис.4 — параллельное соединение резисторов

Прибегнем к нашему трюку с источником питания на 5В. Подключим его к параллельному соединению из двух одинаковых резисторов:

Рис.5 — Параллельное соединение резисторов с одинаковым сопротивлением.

Когда два резистора одного номинала подключены параллельно, то к каждому из них приложено полное напряжение равное 5В, при этом электрический ток в таком случаем проходит через эти резисторы одновременно. Поэтому при параллельном соединении двух одинаковых сопротивлений общее сопротивление находится просто — делится на два номинал одного из резисторов, а так как они равны мы имеем:

R = 100 / 2 = 50 Ом;

Такой упрощенный расчет, вытекает из формулы:

Rобщ = R1 * R2 / R1 + R2;

Если есть желание, можно подставить значения наших резисторов и получатся все те же 50 Ом. Но легче же просто поделить на 2 😉

Данное правило работает с резисторами соединенными параллельно у которых номинал сопротивления одинаковый. А что если соединяемые параллельно резисторы имеют разный номинал? В таком случае мы будем искать общее сопротивление только по формуле:

Rобщ = R1 * R2 / R1 + R2;

Причем количество резисторов может быть сколь угодно большим. В формуле добавятся R3, R4, R5 и т.д.

Для наглядности, давайте подключим к параллельно соединенным резисторам с разным значением сопротивления наше питание 5В и посмотрим значения тока в цепи и ветвях:

Рис. 6 — Ток в цепи и ветвях при параллельном соединении резисторов с разным значением сопротивления.

На рис.6 видно, как распределяется ток в общей цепи и ветвях. Для проверки рассчитаем по формуле общее сопротивление цепи, получим следующее:

Rобщ = R1 * R2 / R1 + R2 = 200 * 100 / 200 +100 = 20000 /300 = 66,67 Ом.

Теперь по закону Ома рассчитаем ток в общей цепи, чтобы сверить его с общим током в цепи на рис.6:

I = U / R = 5 / 66,67 = 0,075 А, что равно 75 мА.

Мы получили тоже значение общего тока в цепи, что и на рис.6, а значит общее сопротивление цепи равно 66, 67 Ом.

Итог следующий:

• При последовательном соединении резисторов, общее сопротивление увеличивается;
• При параллельном соединении резисторов, общее сопротивление уменьшается;

Подписывайтесь на канал РОБОТИП впереди много инетересного!

Формулы для последовательного и параллельного соединения

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Рисунок 1.9.1.

По закону Ома, напряжения и на проводниках равны

Общее напряжение на обоих проводниках равно сумме напряжений ₁ и ₂:

где – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения ₁ и ₂ на обоих проводниках одинаковы:

Сумма токов ₁ + ₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы и ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу за время Δ подтекает заряд Δ, а утекает от узла за то же время заряд ₁Δ + ₂Δ. Следовательно, = ₁ + ₂.

Рисунок 1.9.2.

Записывая на основании закона Ома

где – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Рисунок 1.9.3.

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Рисунок 1.9.4.

Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.

Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.

Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.

Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.

При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.

Последовательное соединение проводников

Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.

Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.

Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.

При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.

Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.

В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.

Параллельное соединение проводников

В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.

При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу резисторов в схеме.

В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.

При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.

Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.

Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к распределительному щитку. То есть все приборы подключаются независимо от подключения прочих устройств.

Законы последовательного и параллельного соединения проводников

Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.

При последовательной схеме имеется одинаковая сила тока во всех проводниках:

Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:

U1 = IR1, U2 = IR2.

Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:

U = U1 + U2 = I(R1 + R2) = IR.

Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.

В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:

А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:

Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.

Смешанное соединение проводников

Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной схеме к другому резистору или их группе, такое тип считается комбинированным или смешанным.

В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.

Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.

Последовательное соединение резисторов

— Codrey Electronics

Когда несколько резисторов подключены таким образом, что конец первого резистора подключен к началу второго резистора, а конец второго — к третьему резистору и так далее. Мы говорим, что резисторов в последовательном соединении .

Как вы знаете, резисторы — это электронные компоненты, используемые для управления напряжением и током в цепи. Но, правильно настроив его значение, мы можем использовать его для управления током или напряжением в цепях и приложениях.Отдельные резисторы могут быть соединены вместе последовательно или параллельно для получения номинального резистора, эквивалентное сопротивление которого представляет собой математическую комбинацию отдельных подключенных резисторов. Все типы комбинаций резисторов могут быть преобразованы в эквивалентные резисторы, независимо от того, насколько сложна эта комбинация, потому что все резисторы подчиняются одному и тому же правилу, то есть закону Ом .

Что такое закон Ома?

Закон

Ома определяет, что в любой электрической цепи ток, проходящий через компоненты, прямо пропорционален разности потенциалов, приложенной к компонентам.Закон Ома существует в трех формах. Это V = IR, I = V / R и R = V / I.

Где R — сопротивление, I — ток, протекающий в цепи, V — напряжение. Основываясь на этих трех параметрах (ток, напряжение и сопротивление), согласно закону Ома, ток изменяется непосредственно с приложенным напряжением и изменяется обратно пропорционально сопротивлению.

Резисторы в последовательной цепи

Комбинация резисторов серии t размещена в виде гирляндной цепи. Здесь ток остается постоянным во всей цепи.Как только ток передается на один резистор, он никуда не идет, кроме как прямо к месту назначения, то есть к отрицательной клемме батареи.

Резистор в последовательной цепи

Поскольку ток здесь остается постоянным, ток одинаков на всех резисторах.

Следовательно, общий ток (i) в последовательной цепи = i ₁ + i ₂ + i ₃

Когда мы говорим о напряжении, оно делится на каждом резисторе в соответствии с номиналом резисторов. Но сложение всего отдельного напряжения приведет к общему напряжению в цепи.

В = В ₁ + В ₂ + В ₃

Теперь, согласно закону Ома,

В = ИК

∴ iR = iR ₁ + iR ₂ + iR ₃ + iR ₄

Резисторы, подключенные последовательно (а)

Следовательно, эквивалентное сопротивление указанной выше цепи (а) будет

.

R = ₁ + ₂ + R ₃ + ₄

∴ R = 1 Ом + 3 Ом + 4 Ом + 5 Ом = 13 Ом

Резистор серии

как делитель напряжения

Резистор серии

как делитель напряжения

Все напряжение делится на различные падения напряжения на каждом резисторе как V1, V2, V3 и V4 и рассчитывается как

В ₁ (Напряжение на резисторе R ₁ ) = iR ₁ = 1 X 1 = 1 В
В ₂ (Напряжение на резисторе R ₂ ) = iR ₂ = 3 X 1 = 3 В
В ₃ (Напряжение на резисторе R ₄ ) = iR ₃ = 4 X 1 = 4 В
В ₄ (Напряжение на резисторе R ₅ ) = iR ₄ = 5 X 1 = 5 В

Общее напряжение — это сумма напряжений на отдельных сопротивлениях.

Следовательно, V = V1 + V2 + V3 + V4 = 1V + 3V + 4V + 5V = 13V

Цепь (а) может быть изменена с помощью одного резистора, включенного последовательно с батареей 1 В.

Полное сопротивление в серии

Таким образом, резисторы действуют при последовательном соединении. Этот тип комбинации широко используется, когда нам нужно большое сопротивление, например 200 Ом, но 200 Ом недоступны на рынке, поэтому мы последовательно подключаем два резистора 100 Ом, чтобы получить требуемый эквивалент резистора.

Уравнение сопротивления серии

Таким образом, эквивалентное сопротивление этих отдельных последовательных резисторов является просто суммой их индивидуального сопротивления. Например, если имеется «n» резисторов, скажем, R1, R2 и R3, и так далее до R _n. Общее сопротивление последовательно определяется уравнением или формулой ниже.

∴ R _всего = R1 + R2 ± —— +… R _n

Уравнение резистора серии

Что касается батареи, то несколько отдельных сопротивлений равны одному большому сопротивлению.Это сопротивление известно как эквивалентное сопротивление.

Общее сопротивление определяется как = общее напряжение / общий ток. Очевидно, что это алгебраическая сумма отдельных резисторов.

Резистор в последовательных примерах

Чтобы теоретически найти последовательное сопротивление, вот примеры проблем и решения последовательного резистора.

Пример № 1:

Для последовательного подключения резистора соедините один конец вывода резистора R1 с резистором R2, а другой конец R2 с R3.Точно так же вы можете подключить n резисторов последовательно, как показано ниже. Это повысит сопротивление.

Здесь последовательно соединены 3 резистора R1 (1K), R2 (10K) и R3 (20K). Общее сопротивление в цепи определяется суммой сопротивлений.

Следовательно, полное сопротивление (R) = R ₁ + R ₂ + R ₃ +… .. + R _n = 1K + 10K + 20K = 31K

Пример № 2:

Может возникнуть ситуация, когда вы захотите разделить напряжение ровно пополам.Когда два резистора одинакового номинала соединены последовательно, выходное напряжение станет половиной входного напряжения. Например, два резистора R1 и R2 одинакового номинала 1K подключаются друг за другом. Входное напряжение составляет 20 В, а выходное напряжение рассчитывается следующим образом.

Здесь нагрузочный резистор (R _L) не рассматривается.

Без подключенного RL

Следовательно, последовательная схема делит напряжение и действует как схема делителя напряжения .

Зависимость тока от последовательного сопротивления

Зависимость тока от сопротивления

Важно соблюдать соотношение между последовательным сопротивлением и током. Как я уже сказал, последовательно включенные резисторы увеличивают сопротивление, но уменьшают ток. Следовательно, соотношение между током и сопротивлением обратное. Здесь по мере увеличения сопротивления ток быстро уменьшается.

Приложения

Некоторые из применений последовательного сопротивления в реальной жизни:

1. Резисторы, включенные последовательно, используются для построения сети делителя напряжения.
2. Используется как термистор (положительный температурный коэффициент) при измерении и контроле температуры.
3. Используется как LDR (светозависимый резистор) для светочувствительных приложений.

Резисторы серии

Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация. Самая простая схема включает один резистор и источник электрического потенциала или напряжения .Электроны проходят через схема вырабатывает тока электричества. Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе сложной схемы мы часто можем группировать компоненты вместе и разработать эквивалентную схему . При анализе схем с несколько резисторов, мы должны определить, подвержены ли резисторы какое-то напряжение или такой же ток.Несколько резисторов в параллельная цепь подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему для резисторов последовательно.

На рисунке изображена схема, состоящая из источника питания и трех резисторов. соединены последовательно. Если обозначить сопротивление R , ток i и напряжение В , то закон Ома гласит, что для каждого резистора в цепи:

V = i R

я = V / R

Если рассматривать каждый резистор по отдельности, каждый резистор имеет свой ток. ( i1 , i2 и i3 ), сопротивление ( R1 , R2 и R3 ), и напряжение ( V1 , V2 и V3 ).Резисторы подключены друг к другу в узлах . Узлы обозначены маленькие кружочки на фигуре. Для этой схемы есть четыре узла, соединяющие три резистора и источник питания. В каждом узле ток, поступающий в узел должен равняться току, выходящему из узла, согласно закону Фарадея . При таком расположении резисторов есть только один провод, входящий и выходящий. каждый узел. Следовательно, ток через каждый резистор должен быть одинаковым.

я = я1 = я2 = я3

Падение напряжения на каждом резисторе определяется законом Ома:

V1 = i R1

V2 = я R2

V3 = i R3

Сумма падений напряжения на каждом резисторе должна равняться подаваемому напряжению. по источнику питания:

V = V1 + V2 + V3

Теперь мы знаем напряжение, сопротивление и ток в каждой части цепи.

Если бы мы построили эквивалентную схему, как показано в правом нижнем углу, мы бы имеют одинаковое напряжение В, , такой же ток от источника питания ie = i , и один эквивалентный резистор Re . Для нашей эквивалентной схемы закон Ома указывает, что:

V = i Re

Мы можем определить значение Re , используя развитые выше соотношения и немного алгебры:

я Re = я R1 + я R2 + я R3

Re = R1 + R2 + R3

Мы можем использовать эти знания о цепи последовательного резистора для анализа Мост Уитстона схема, которая используется для контроля температуры в аэродинамической трубе баланс сил используя электронные тензодатчики.

---

Навигация ..

Руководство для начинающих Домашняя страница

ПОДКЛЮЧЕННЫЕ РЕЗИСТОРЫ СЕРИИ

Щелкните или коснитесь приведенных ниже примеров схем, чтобы вызвать TINACloud, и выберите интерактивный режим постоянного тока, чтобы проанализировать их в интерактивном режиме.
Получите недорогой доступ к TINACloud для редактирования примеров или создания собственных схем. ПАРАЛЛЕЛЬНО ПОДКЛЮЧЕННЫЕ РЕЗИСТОРЫ

. Ток в последовательной цепи имеет только один путь и не может течь по другому пути.Ток точно такой же во всех точках последовательной цепи.

Напряжение в последовательной цепи: сумма приложенных напряжений в последовательной цепи равна сумме падений напряжения.

Из этих двух принципов следует, что полное сопротивление в последовательной резистивной цепи равно сумме отдельных сопротивлений.

Пример 1

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить под Windows

Найдите общее сопротивление следующих трех схем резисторов:

На рисунке выше вы можете увидеть результат предоставлен TINA.

Теперь давайте рассчитаем эквивалентное последовательное сопротивление по формуле:

Как видите, рассчитанное значение согласуется с омметром TINA.

В электронике иногда встречаются схемы, в которых переключатели подключены параллельно резисторам. Когда переключатель замкнут, он закорачивает параллельно подключенный резистор, как если бы вместо резистора был провод с нулевым сопротивлением. Однако, когда переключатель разомкнут, он не влияет на сопротивление параллельно с ним.

Пример 2

Найдите общее сопротивление с переключателями, установленными, как показано:

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows

R _tot = R ₁ + R ₂ + R ₃ = 10 + 20 + 15 = 45 Ом.

Пример 3

Найдите общее сопротивление с переключателями, установленными, как показано:

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows

R _tot = R ₁ + R ₃ = 10 + 15 = 25 Ом.

Пример 4

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows

Найдите ток в цепи со всеми возможными комбинациями замкнутых и открытых переключателей и проверьте результат с помощью TINA. Не включайте сразу все переключатели, иначе вы закоротите аккумулятор, и предохранитель перегорит.

Пример 5

Найдите значение R, которое приведет к току 2А.

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows

Решение: чтобы получить требуемый ток 2 А при напряжении источника 20 В, общее сопротивление схемы должно быть 10 Ом, поскольку по закону Ома

I = V / R = 20/10 = 2 A

Общее сопротивление цепи составляет:

R _до = R ₁ + R ₂ + R ₃ + R _{= 10 Ом.}

Следовательно, R = 2 Ом

Другой подход к решению этой проблемы использует одну из самых интересных функций TINA, режим анализа под названием Оптимизация . Вы можете установить этот режим в меню Analysis , щелкнув Mode и затем установив Optimization. В Оптимизации вы должны определить область поиска, используя параметры Start- и End Value. Используя меню Analyis или значки в правом верхнем углу экрана, вы также должны установить цель оптимизации, которая представляет собой значение тока (2A), показанное стрелкой тока.Затем установите объект управления, которым в данном случае является R. После выбора функции вы должны щелкнуть соответствующий компонент (текущая стрелка или резистор R) со специальным курсором (измеритель или резистор), появляющимся после выбора функции. .

Наконец, функция анализа постоянного тока TINA автоматически найдет точное значение R, при котором ток будет равен 2 А.

Попробуйте это, загрузив приведенный выше пример и выполнив анализ постоянного тока из меню анализа.

Что ж, для такой простой схемы оптимизация не требуется, но есть много гораздо более сложных реальных схем, в которых эта функция может сэкономить массу ручных вычислений.

---

ПАРАЛЛЕЛЬНО СОЕДИНИТЕЛЬНЫЕ РЕЗИСТОРЫ

Резисторы серии

R1, R2 и R3 — это три резистивно подключенных друг к другу через источник напряжения, В . VI. V2 и V3 — это падения напряжения в RI, R2 и R3 соответственно I — полный ток. На рисе мы видим, что

Комбинированные резисторы серии

В _T = В _I + В ₂ + В ₃ —> (1)

Мы знаем, что

Vs = ИК-> (2)

Подставляем уравнение (2) в уравнение (1), получаем

ИК _T = ИК ₁ + ИК ₂ + ИК ₃ ———> (3)

IR _T = I (R ₁ + R ₂ + R ₃ ) -> (4)

Делим обе стороны на I, получаем

R _T = R ₁ + R ₂ + R ₃

В целом

R _T = _{R R} + R ₂ + R ₃ ……………………… R _н

Где n = 1,2,3,4, ……..

ЗАКЛЮЧЕНИЕ

При последовательной комбинации сопротивлений полное сопротивление равно сумме всех отдельных сопротивлений.

Последовательное сопротивление Характеристики

1. В последовательной цепи ток в каждом резисторе одинаков.

   I _T = I ₁ -I ₂ -I ₃

2. В последовательной цепи полное сопротивление равно сумме всех сопротивлений цепи.

   R _T = R ₁ + R ₂ + R ₃ ………………. R _N

3. В последовательной цепи, когда значение одного резистора увеличивается, в результате увеличивается общее сопротивление цепи.
4. В последовательной цепи существует различное падение напряжения на каждом резисторе, которое зависит от номинала резистора.
5. В последовательной цепи полное напряжение равно сумме падений напряжения на каждом резисторе.

   V _T = V ₁ + V ₂ + V ₃

   ИК _T = ИК ₁ + ИК ₂ + 1R ₃

6. Последовательно, если есть неисправность в одном резисторе, в результате вся цепь не будет работать.
7. В последовательной цепи общая мощность равна сумме всех мощностей, которые проходят через каждый резистор.

   P _T = P ₁ + P ₂ + P ₃

Поскольку в этой цепи есть один путь, они обычно не используются.

резисторов последовательно и параллельно

резисторов последовательно и параллельно
Следующий: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах. Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторой общей схемы резисторов.Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правила. Эти правила относятся к резисторам, включенным последовательно, и в параллели.

Рисунок 18: Два резистора, соединенных последовательно.

Рассмотрим два резистора, соединенных в серию , как показано на рис. 18. Понятно, что через оба резистора протекает одинаковый ток.Ибо, если бы это было не так, заряд накапливался бы в одном или другом резисторов, которые не соответствовали бы установившаяся ситуация (таким образом нарушая основное предположение этого раздела). Предположим, что падение потенциала от точки к точке есть. Это падение представляет собой сумму потенциальных падает и на двух резисторах и соответственно. Таким образом,

(135)

Согласно закону Ома эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,

(136)

давая

(137)

Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правило

Эквивалентное сопротивление двух последовательно соединенных резисторов равно сумма отдельных сопротивлений.

Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .

Рисунок 19: Два резистора, включенных параллельно.

Рассмотрим два резистора, соединенных по параллельно , как показано на рис. 19. Это Из рисунка видно, что падение потенциала на двух резисторах равно одно и тоже. В общем, однако, токи и которые протекают через резисторы и соответственно разные. По закону Ома эквивалентное сопротивление между и — отношение падения потенциала через эти точки и текущий которая течет между ними.Этот ток должен равняться сумме токи и протекающие через два резистора, в противном случае заряд будет накапливаться на одном или обоих переходах в цепи. Таким образом,

(138)

Следует, что

(139)

давая

(140)

Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов.Ясно, что правило

Обратное эквивалентное сопротивление двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.

Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .

---

Следующий: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление

Ричард Фицпатрик 2007-07-14

Цепи серии

Представьте себе электрический ток, выходящий из батареи.Если резисторы подключены в такой способ, которым часть тока может проходить через один резистор, а остальная часть ток может пройти через другой резистор, тогда цепь параллельна Схема .

Я _Т — полный ток параллельной цепи. Вы бы измерили этот ток в любом месте до или после трехканального делителя, ведущего к трем резисторам. В между перекрестком и R ₁ , вы бы измерили I ₁ .Между перекрестком и R ₂ , вы бы измерили I ₂ и т. д.

Поскольку общий ток I _T делится на три разные группы электронов, путешествующих каждый своим путем,

Я _Т = I ₁ + I ₂ + I ₃ +.

В параллельных цепях все резисторы, независимо от их сопротивления, испытывают одинаковое падение напряжения или разность потенциалов, потому что все они имеют одинаковые точки входа и выхода (переходы).

V _T = V ₁ = V ₂ = V ₃ = V _n

Если разделить по формуле тока по соотношению напряжений получаем:

или _{рэнд T} = [ ₁ ^-1 + R ₂ ^-1 + R ₃ ^-1 +] ^-1

Пример 1

а. Какое полное сопротивление цепи?

R _T = [ ₁ ^-1 + R ₂ ^-1 + R ₃ ^-1 ] ^-1

R _T = [12 ^–1 + 12 ^–1 +12 ^–1 ] ^–1 = 4 Вт

г. Какой общий ток?

I _T = V / R _T = 12/4 = 3 A

г.Какое напряжение ( _{В 1} ) будет измеряется на каждом отдельном резисторе?

12 В (напряжение постоянно параллельно.)

г. Какой ток отводится каждый резистор?

I ₁ = V / R ₁ = 12/12 = 1 А. Остальные тоже нарисуйте по 1 А, всего 3 А.

Пример 2

г. рисунок кажется запутанным, но обратите внимание, что это параллельная схема, потому что у электронов есть выбор.На стыке (показано красной точкой) электроны следуйте либо зеленому маршруту, либо оранжевому маршруту.

Используйте I

₁ = 1A; I ₂ = 0,5 А; ₁ рэнд = 10Вт.

1. Найдите V ₂ .

Помните, что параллельное напряжение постоянно. Итак, если мы найдем V ₁ , мы будем знать V ₂ .

В ₁ = I ₁ R ₁ = 1 (10) = 10 В.

В ₂ = В ₁ = 10 В.

2. Найдите R ₂ .

R ₂ = V / I ₂ = 10 / 0,5 = 20 Вт.

3. Используйте два метода, чтобы получить R _T .

(1) R _T = [R ₁ ^-1 + R ₂ ^-1 ] ^-1 = [20 ^-1 + 10 ^-1 ] ^-1 = 6.7 W.

(2) я _т = I ₃ = I ₁ + I ₂ = 1 + 0,5 = 1,5 А.

R _T = V / I _T = 10 / 1,5 = 6,7 W.

Пример 3

В параллельной цепи какой эффект дает добавление еще резисторов иметь по общему току?

Ток увеличивается !

В цепи серии добавление резисторов увеличивает общее сопротивление и, таким образом, снижает ток.Но в случае с параллельная схема, потому что добавление дополнительных резисторов параллельно создает больше вариантов а снижает общее сопротивление . Если такая же батарея подключена к резисторы, ток увеличится. Не убежден? Попробуйте:

[10 ^-1 + 10 ^-1 ] ^-1 = 5 Вт, но добавьте резистор, включенный параллельно, и вы получите [10 ^-1 + 10 ^-1 + 10 ^-1 ] ^-1 = всего 3,3 Вт. чем меньше сопротивление, тем выше общий ток.

Еще одна интересная особенность параллельных цепей заключается в том, что если один компонент отключен, другие пути все еще жизнеспособны, так что электроны могут продолжать течь по цепи. Это причина того, что большинство светильников и розеток в доме подключены параллельно.

резисторов последовательно | Прядильные числа

Компоненты входят в серию , если они соединены таким образом голова к хвосту,

Показываем свойства последовательного соединения с помощью резисторов.

Автор Вилли Макаллистер.

---

Содержание

---

Последовательное соединение

Резисторы включены последовательно, когда они подключены «голова к хвосту» и , нет других проводов, отходящих от узлов между компонентами. $ \ text {R1} $, $ \ text {R2} $ и $ \ text {R3} $ последовательно,

При последовательном соединении в каждом резисторе течет одинаковый ток. Весь ток, идущий в переднем конце, вытекает из другого конца.Сила тока везде по цепи одинакова.

Резисторы на следующем изображении — это , а не последовательно. Дополнительные ответвления отводятся от узлов между резисторами. Если у этих ветвей есть ток (оранжевые стрелки), тогда $ \ text {R1} $, $ \ text {R2} $ и $ \ text {R3} $ не имеют одного и того же тока и, следовательно, не связаны друг с другом.

Резисторы серии

Вот схема с последовательно включенными резисторами. Источник напряжения $ \ text V _ {\ text {S}} $ подключен к цепочке резисторов.Резисторы подключены друг к другу, поэтому мы знаем, что они включены последовательно.

Вот что мы знаем:

• Напряжение $ v_ \ text S $ — некоторая известная постоянная величина $ \ text V_ \ text S $.
• Резисторы включены последовательно, поэтому мы знаем, что через все три протекает один и тот же ток $ i $.
• Отдельные напряжения на резисторах должны составлять в сумме $ v _ {\ text S} $.

Обладая этими небольшими знаниями и Законом Ома, мы можем вычислить неизвестные.Вот то, чего мы не знаем,

• Текущий $ i $ неизвестен.
• Нам неизвестны напряжения на отдельных резисторах.

Запишите сумму напряжений,

$ v _ {\ text S} = v _ {\ text R1} + v _ {\ text R2} + v _ {\ text R3} $

Напряжение на каждом резисторе можно записать через сопротивление и ток,

$ v _ {\ text R1} = i \, \ text R1 \ qquad v _ {\ text R2} = i \, \ text R2 \ qquad v _ {\ text R3} = i \, \ text R3 $

Подставьте эти выражения обратно в сумму напряжений,

$ v _ {\ text {S}} = i \, \ text R1 \, + \, i \, \ text R2 \, + \, i \, \ text R3 $

Вынести ток и сгруппировать резисторы вместе,

$ v _ {\ text {S}} = i \, \, (\ text R1 + \ text R2 + \ text R3) $

Найти неизвестное $ i $,

$ i = \ dfrac {v _ {\ text {S}}} {\ text R1 + \ text R2 + \ text R3}

$

Взгляните на это уравнение.Это похоже на закон Ома для одиночного резистора, $ i = v / \ text R $, за исключением того, что знаменатель — это сумма последовательных резисторов. Делаем вывод,

При последовательном соединении полное сопротивление складывается из отдельных резисторов.

Эквивалентный последовательный резистор

Мы можем представить себе новый более крупный резистор , эквивалентный , равный сумме последовательных резисторов. Это эквивалентно в том смысле, что один и тот же ток $ i $ течет для данного $ \ text V_ \ text S $.

$ \ text R _ {\ text {series}} = \ text {R1} + \ text {R2} + \ text {R3}

$

Вы можете услышать это сленговое выражение: «С точки зрения источника напряжения» три последовательных резистора «выглядят» как один более крупный эквивалентный резистор. Ток $ i $, обеспечиваемый источником напряжения, одинаков в обоих случаях.

Как источник напряжения может иметь «точку зрения»?

В технических дискуссиях очень часто говорят такие вещи, как,

«С точки зрения источника напряжения… бла-бла-бла».

Мы говорим об источнике напряжения, как если бы это был человек.

У людей богатый словарный запас, чтобы говорить о себе, поэтому мы часто используем человеческие слова в других ситуациях. Но нужно быть осторожным. В конце концов, электронные компоненты и электроны — это не люди. Источники напряжения действительно не имеют «точки обзора» и не могут «смотреть» на то, к чему они подключены.

Один из моих любимых вопросов о схемах: «Как электроны решают, куда идти?» Что ж, электроны на самом деле ничего не «решают».Электроны реагируют на электрическую силу, описываемую законом Кулона, и протекают через резисторы в соответствии с законом Ома.

Если вы ведете непонятный разговор о том, как работает схема, причиной проблемы могут быть сленговые выражения. Если вы чувствуете, что это происходит, вернитесь к основным принципам электроники: напряжению, току и закону Ома.

Если у вас есть много резисторов, подключенных последовательно, общая форма эквивалентного последовательного сопротивления:

$ \ text R _ {\ text {series}} = \ text {R1} + \ text {R2} + \ ldots + \ text {R} _ \ text N $

Напряжение распределяется между резисторами в серии

Давайте посмотрим на напряжение на каждом резисторе в последовательной цепи.Мы применяем закон Ома к отдельным резисторам по очереди. Ток $ i $ одинаков в каждом резисторе.

$ v _ {\ text R1} = i \, \ text R1 \ qquad v _ {\ text R2} = i \, \ text R2 \ quad \ ldots \ quad v _ {\ text {RN}} = i \, \ text R_ \ text N $

Это станет более понятным, если мы рассмотрим пример с действительными числами. Я рекомендую вам попробовать это самостоятельно, прежде чем искать ответ.

Проверка концепции

ПРОБЛЕМА 1

а.Какой сейчас $ \ blueD i $?

г. Каковы напряжения на трех резисторах?

г. Показать напряжения отдельных резисторов в сумме до $ \ text V_ \ text S $.

Шаги:

1. Найдите эквивалентное последовательное сопротивление $ \ text R _ {\ text {series}} $.
2. Используйте $ v_ \ text S $ и $ \ text R_ \ text {series} $, чтобы найти $ i $ по закону Ома.
3. Найдите напряжения отдельных резисторов, снова используя закон Ома.
4. Убедитесь, что напряжения в сумме соответствуют требуемым.

Показать ответ

а. Эквивалент $ \ text R _ {\ text {series}} $ — это сумма трех резисторов.

$ \ text R _ {\ text {series}} = 300 \, \ Omega + 500 \, \ Omega + 1200 \, \ Omega = 2000 \, \ Omega $

Текущее значение $ i $ взято из закона Ома,

$ i = \ dfrac {v_ \ text S} {\ text R _ {\ text {series}}} = 10 \, \ text V / 2000 \, \ Omega = 0.005 \, \ text A = 5 \, \ text {mA}

долларов США

г. Зная $ i $, мы вычисляем напряжения отдельных резисторов,

$ v _ {\ text {R1}} = i \, \ text R_ {300} = 5 \, \ text {mA} \ cdot 300 \, \ Omega = 1.5 \, \ text V $

$ v _ {\ text {R2}} = i \, \ text R_ {500} = 5 \, \ text {mA} \ cdot 500 \, \ Omega = 2.5 \, \ text V $

$ v _ {\ text {R3}} = i \, \ text R_ {1200} = 5 \, \ text {mA} \ cdot 1200 \, \ Omega = 6.0 \, \ text V $

Вот полное решение,

г. Проверка: Суммируются ли напряжения резистора с напряжением источника?

$ 1.5 \, \ text V + 2.5 \, \ text V + 6.0 \, \ text V \ stackrel {\ checkmark} {=} 10 \, \ text V \ qquad $ Да!

ПРОБЛЕМА 2

На основе только что вычисленных напряжений резисторов,

Самый большой резистор имеет наибольшее или наименьшее напряжение?

Показать ответ

Наибольшее напряжение.

Имеет ли наименьший резистор наибольшее или наименьшее напряжение?

Показать ответ

Наименьшее напряжение.

Какой резистор имеет наибольший ток?

Показать ответ

Вопрос с подвохом.Все резисторы имеют одинаковый ток при последовательном соединении.

Сводка

резисторов в серии добавить,

$ \ text R _ {\ text {series}} = \ text {R1} + \ text {R2} + \ ldots + \ text {R} _ \ text N $

Последовательные резисторы имеют одинаковый ток.