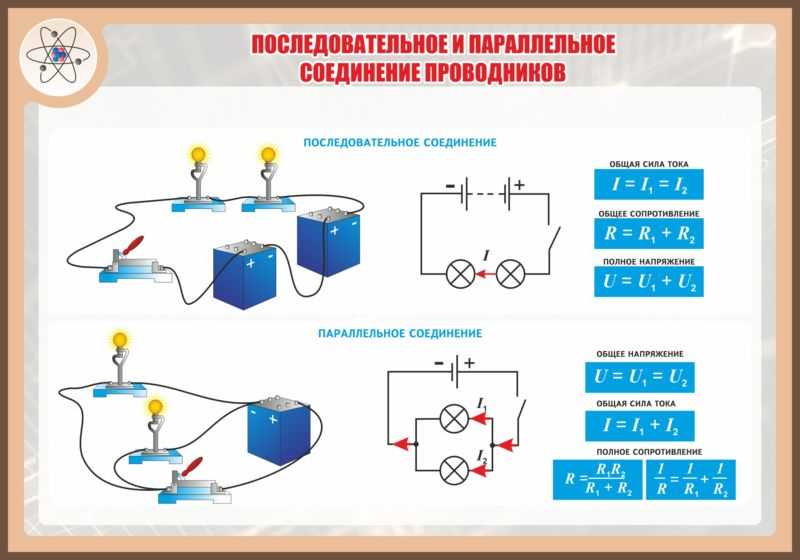
Каковы основные законы последовательного и параллельного соединения проводников. Как рассчитать силу тока, напряжение и сопротивление при разных типах соединений. Где применяются последовательные и параллельные цепи. Какие преимущества и недостатки у каждого типа соединения.
Последовательное соединение проводников: основные законы и формулы
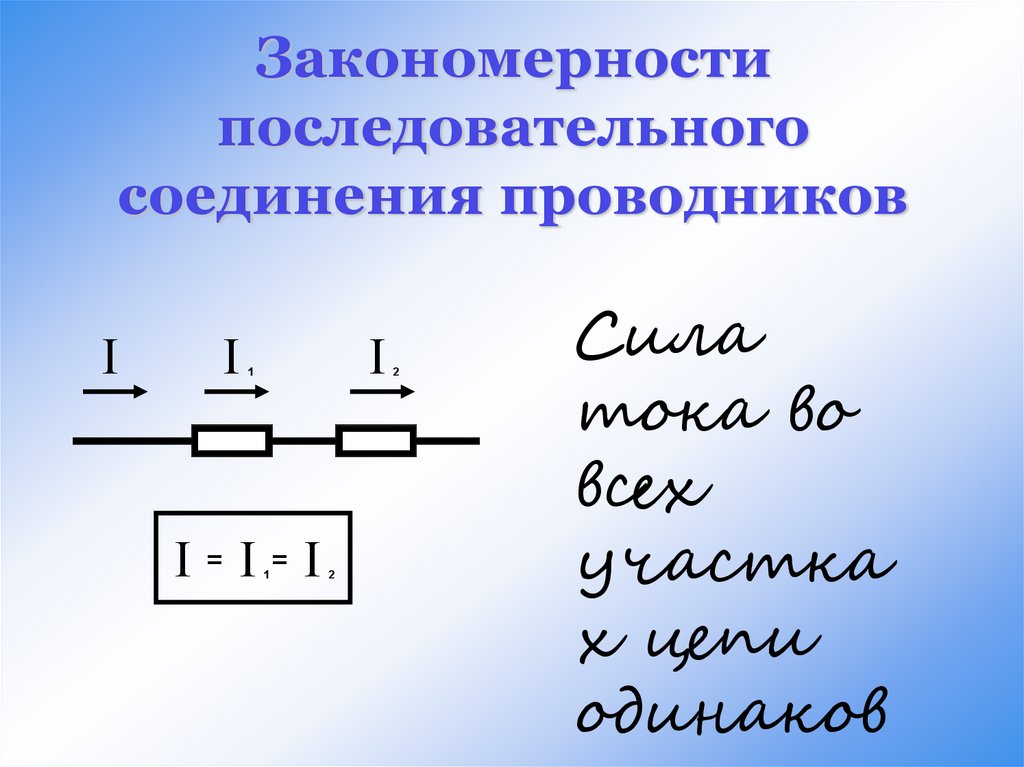
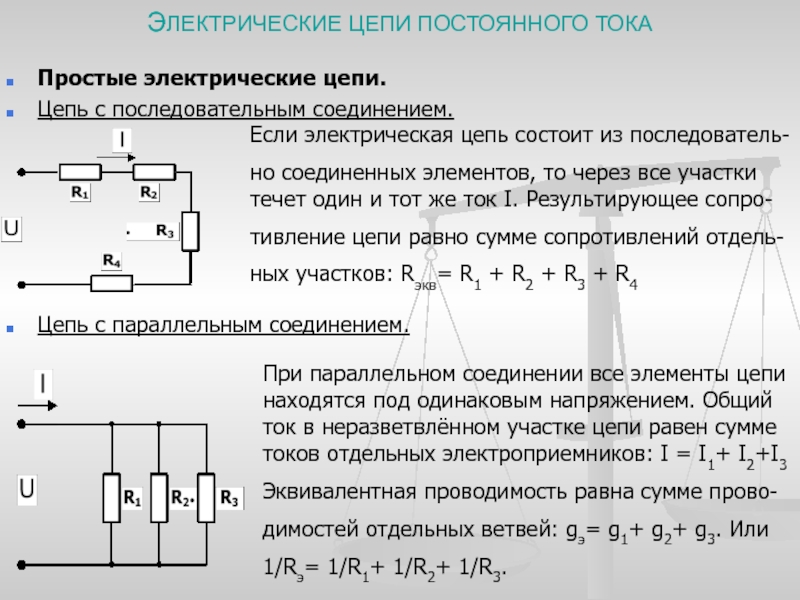
При последовательном соединении проводники соединяются друг за другом в цепочку. Основные законы такого соединения:
- Сила тока одинакова во всех участках цепи: I = I1 = I2 = … = In
- Общее напряжение равно сумме напряжений на отдельных участках: U = U1 + U2 + … + Un
- Общее сопротивление равно сумме сопротивлений: R = R1 + R2 + … + Rn
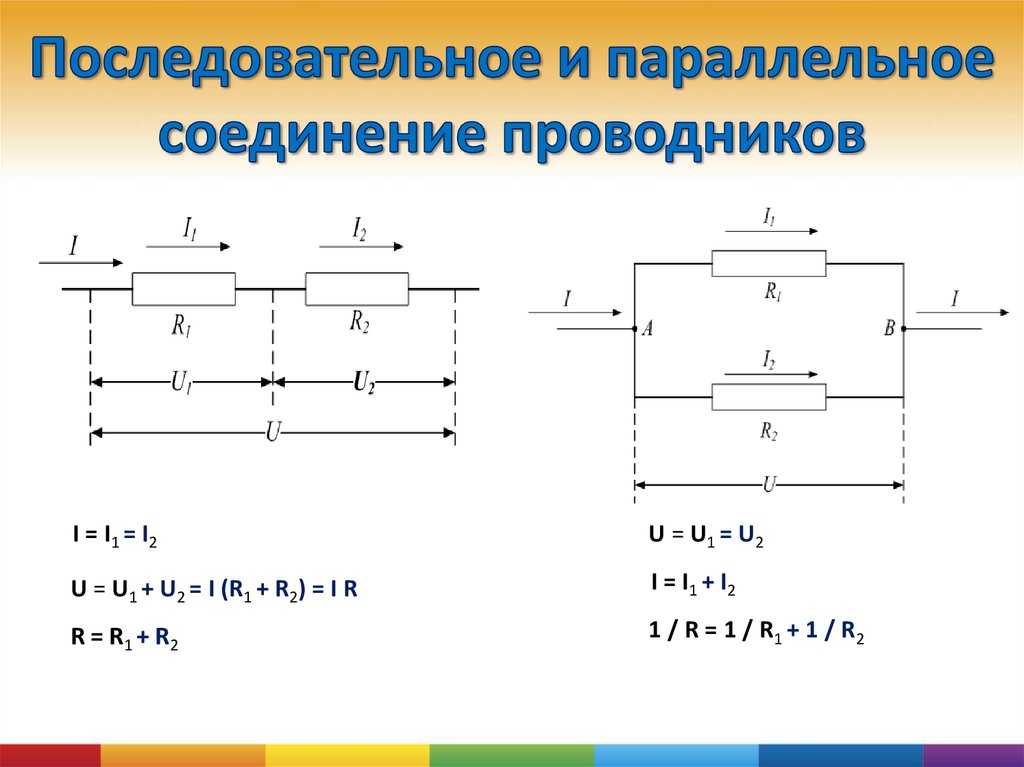
Как рассчитать параметры цепи при последовательном соединении? Рассмотрим основные формулы:
- Сила тока: I = U / R
- Напряжение на участке: Ui = I * Ri
- Сопротивление участка: Ri = Ui / I
Параллельное соединение проводников: ключевые особенности
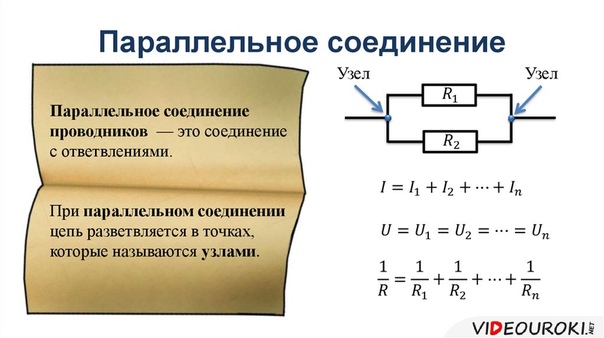
При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Основные законы:

- Напряжение одинаково на всех участках: U = U1 = U2 = … = Un
- Общий ток равен сумме токов через отдельные проводники: I = I1 + I2 + … + In
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений: 1/R = 1/R1 + 1/R2 + … + 1/Rn
Формулы для расчета параметров параллельной цепи:
- Сила тока через проводник: Ii = U / Ri
- Общее сопротивление: R = U / I
- Сопротивление участка: Ri = U / Ii
Применение последовательного и параллельного соединения в электротехнике
Где используются разные типы соединений проводников:
Последовательное соединение:
- Елочные гирлянды
- Предохранители и выключатели
- Амперметры (включаются последовательно в цепь)
- Реостаты для регулировки силы тока
Параллельное соединение:
- Бытовая электропроводка
- Осветительные приборы
- Вольтметры (подключаются параллельно участку цепи)
- Системы электропитания
Как выбрать оптимальный тип соединения? Это зависит от конкретной задачи и требований к электрической цепи.
Преимущества и недостатки разных типов соединения
Сравним плюсы и минусы последовательного и параллельного соединения:

Последовательное соединение:
Преимущества:
- Простота монтажа
- Возможность регулировки общего сопротивления
- Равномерное распределение тока
Недостатки:
- При выходе из строя одного элемента перестает работать вся цепь
- Увеличение общего сопротивления
- Неравномерное распределение напряжения
Параллельное соединение:
Преимущества:
- Независимая работа потребителей
- Уменьшение общего сопротивления
- Равномерное распределение напряжения
Недостатки:
- Сложность монтажа при большом количестве элементов
- Увеличение общей силы тока
- Сложность регулировки параметров отдельных участков
Смешанное соединение проводников: особенности расчета
В реальных электрических схемах часто используется комбинация последовательного и параллельного соединения. Как рассчитать параметры такой цепи?
- Разбить схему на участки с однотипным соединением
- Рассчитать эквивалентное сопротивление для каждого участка
- Объединить участки в общую схему
- Применить законы Ома и Кирхгофа для расчета токов и напряжений
Пример расчета смешанной цепи:
- Определить эквивалентное сопротивление параллельного участка
- Рассчитать общее сопротивление последовательно соединенных элементов
- Найти общий ток в цепи
- Вычислить напряжение и ток на каждом участке
Практические задачи на расчет электрических цепей
Рассмотрим несколько типовых задач для закрепления материала:Задача 1: Три резистора с сопротивлениями 2 Ом, 4 Ом и 6 Ом соединены последовательно. Какое напряжение нужно приложить к цепи, чтобы сила тока была 2 А?
Решение:
- Найдем общее сопротивление: R = 2 + 4 + 6 = 12 Ом
- По закону Ома: U = I * R = 2 А * 12 Ом = 24 В
Ответ: Необходимо приложить напряжение 24 В.
Задача 2: Два резистора сопротивлением 3 Ом и 6 Ом соединены параллельно. Какой ток течет через первый резистор, если общее напряжение 12 В?
Решение:
- Напряжение на обоих резисторах одинаково и равно 12 В
- Ток через первый резистор: I1 = U / R1 = 12 В / 3 Ом = 4 А
Ответ: Через первый резистор течет ток 4 А.
Правила техники безопасности при работе с электрическими цепями
При работе с электричеством важно соблюдать меры предосторожности:

- Всегда отключайте питание перед работой с цепью
- Используйте изолированные инструменты
- Не прикасайтесь к оголенным проводам
- Проверяйте отсутствие напряжения перед началом работ
- Не превышайте допустимые нагрузки на элементы цепи
- При любых сомнениях обращайтесь к специалисту
Помните: безопасность — превыше всего! Неправильное обращение с электрическими цепями может привести к серьезным травмам.
Параллельное и последовательное соединение — законы и примеры
Как после перегорания одной лампочки в гирлянде можно определить способ соединения и починить ее? Попробуем разобраться.
Анфиса обнаружила на балконе старую гирлянду. Включив ее в розетку, девочка заметила, что горят все лампочки, кроме зеленых. Внимательно изучив провода, Анфиса увидела, что все зеленые лампочки соединены последовательно друг за другом.
Последовательное соединение проводников
При последовательном соединении конец первого проводника соединяют с началом второго, конец второго — с началом третьего и т. д.
Последовательное подключение обычно используется в тех случаях, когда необходимо целенаправленно включать или выключать определенный электроприбор. Например, для работы школьного электрического звонка требуется соединить его последовательно с источником тока и ключом.
Вот некоторые примеры использования схемы последовательного соединения:
- освещение в вагонах поезда или трамвая;
- простейшие елочные гирлянды;
- карманный фонарик;
- амперметр для измерения силы тока в цепи.

Законы последовательного соединения проводников
-
При последовательном соединении сила тока в любых частях цепи одна и та же:
I = I1 = I2 = … = In.
Если в цепи с последовательным способом соединения одна из ламп выйдет из строя и через нее не будет протекать электрический ток, то и через оставшиеся лампы ток проходить не будет. Вспомним Анфису и ее гирлянду: когда одна из зеленых лампочек перегорела, то ток, проходящий через нее, стал равен нулю. Следовательно, и другие зеленые лампочки, включенные последовательно, не загорелись. Чтобы починить гирлянду, нужно определить перегоревшую лампочку и заменить ее.
-
При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников:
Rэкв = R1 + R2 + … + Rn.
-
При последовательном соединении общее напряжение цепи равно сумме напряжений на отдельных участках:
Uэкв = U1 + U2 + … + Un.
Пример решения задачи
В цепь с напряжением 220 В включена лампа, через нее протекает ток силой 20 А. Когда к лампе последовательно подключили реостат, сила тока в цепи уменьшилась до 11 А. Чему равно сопротивление реостата?
Решение.
-
По закону Ома определим сопротивление лампы:
R1 = U / I1 = 220 / 20 = 11 Ом.
-
Также по закону Ома определим общее сопротивление цепи при включенном реостате:
R = U / I2 = 220 / 11 = 22 Ом. -
При последовательном соединении сопротивления лампы и реостата складываются:
R = R1 + R2.
-
Зная общее сопротивление цепи и сопротивление лампы, определим искомое сопротивление реостата:
R2 = R − R1 = 22 − 11 = 11 Ом.
Ответ: сопротивление реостата равно 11 Ом.
К сожалению, последовательное соединение не всегда оказывается удобным. Например, в торговом центре «Ашан» работает с 9:00 до 23:00, кинотеатр — с 10:00 до 02:30, а магазины — с 10:00 до 22:00. При последовательном соединении цепи свет должен будет гореть во всем ТЦ с 9:00 до 02:30. Согласитесь, что такой режим работы экономически невыгоден даже при минимальном тарифе на электроэнергию. В этом случае удачным решением будет использование параллельного соединения.
Например, в торговом центре «Ашан» работает с 9:00 до 23:00, кинотеатр — с 10:00 до 02:30, а магазины — с 10:00 до 22:00. При последовательном соединении цепи свет должен будет гореть во всем ТЦ с 9:00 до 02:30. Согласитесь, что такой режим работы экономически невыгоден даже при минимальном тарифе на электроэнергию. В этом случае удачным решением будет использование параллельного соединения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Параллельное соединение проводников
При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой.
Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату.
Приведем еще несколько примеров применения параллельного способа соединения:
- освещение в больших торговых залах;
- бытовые электроприборы в квартире;
- компьютеры в кабинете информатики;
- вольтметр для измерения напряжения на участке цепи.
Параллельное соединение проводников: формулы
-
Напряжение при параллельном соединении в любых частях цепи одинаково:
U = U1 = U2 = … = Un.
Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении.
-
Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках:
Iэкв = I1 + I2 + … + In.

Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну.
Общее сопротивление цепи определяется по формуле:
1 / Rэкв = 1 / R1 + 1 / R2 + … + 1 / Rn.
Для двух параллельно соединенных проводников формулу можно записать иначе:
Rэкв = (R1 · R2) / (R1 + R2).
Если n одинаковых проводников, каждый из которых имеет сопротивление R1, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество:
Rэкв = R1 / n.
Вернемся к Анфисе и ее гирлянде. Мы уже разобрались, почему перестали гореть все зеленые лампочки. Пришло время узнать, почему продолжили гореть все остальные.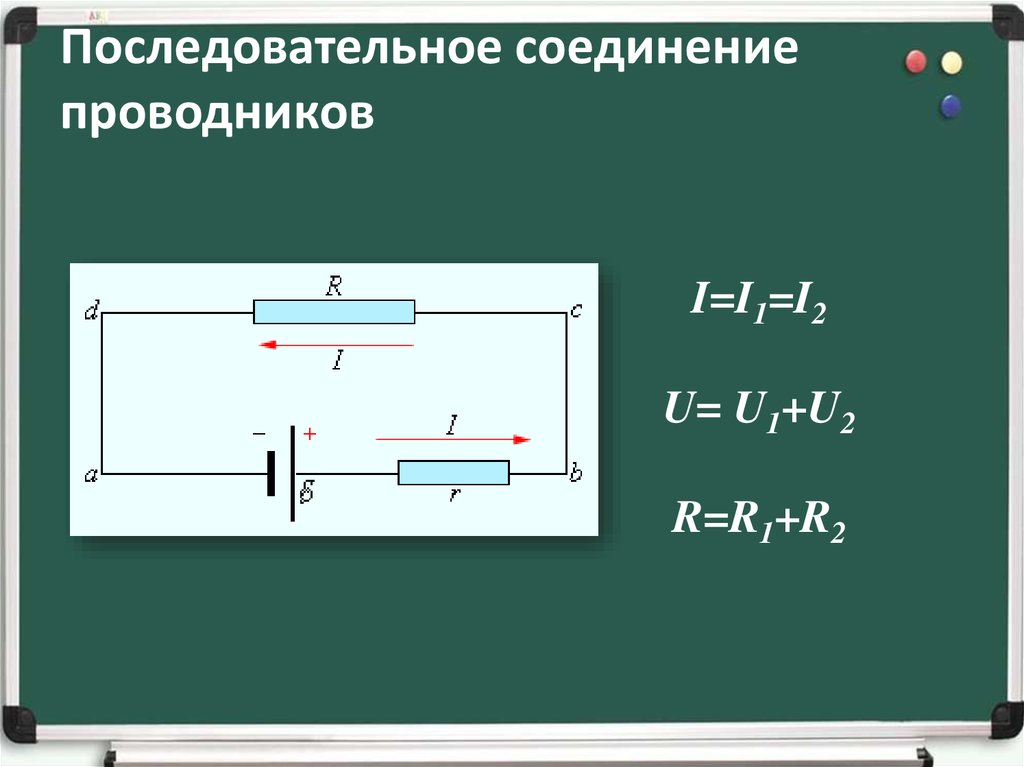 В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.
В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.
Пример решения задачи
Два резистора с сопротивлениями 10 Ом и 11 Ом соответственно соединены параллельно и подключены к напряжению 220 В. Чему равна сила тока в неразветвленной части цепи?
Решение.
-
Определим общее сопротивление при параллельном соединении проводников:
R = (R1 · R2) / (R1 + R2) = (10 · 11) / (10 + 11) = 110 / 21 Ом ≈ 5,24 Ом.
-
По закону Ома определим силу тока в цепи:
I = U / R = 220 / (110 / 21) = 42 А.
Ответ: сила тока в неразветвленной части цепи равна 42 А.
Смешанное соединение проводников
Зачастую реальные электрические схемы оказываются сложнее, поэтому используют различные комбинации последовательного и параллельного способов соединения.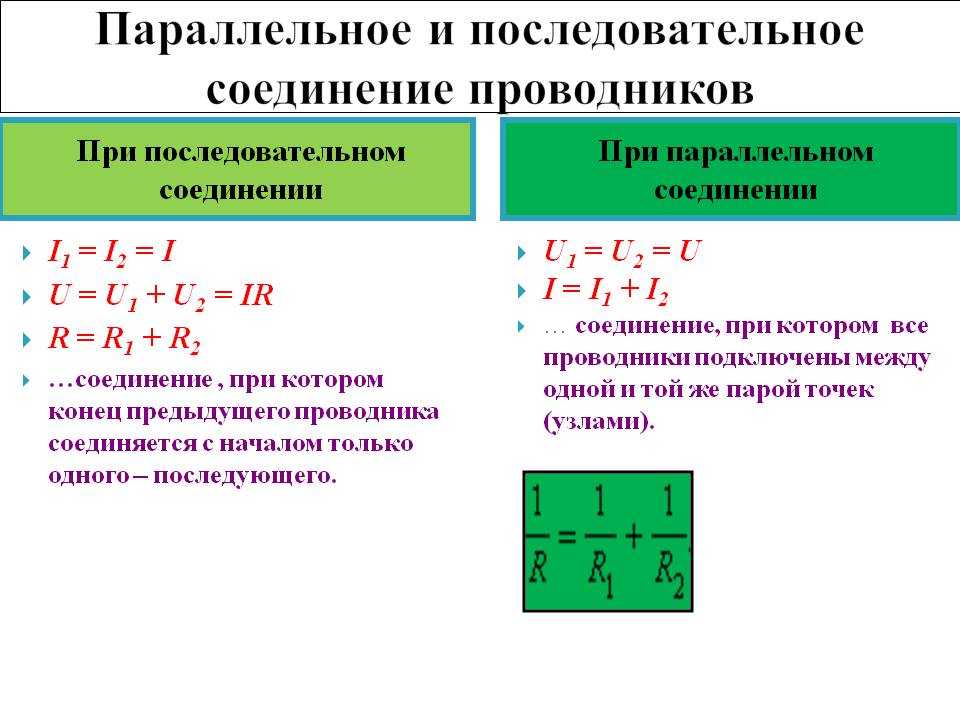 Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.
Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.
Алгоритм решения задач со смешанным соединением проводников:
-
Прочитать условие задачи, начертить схему электрической цепи, при необходимости пронумеровать проводники.
-
Проанализировать схему, т. е. найти участки, где используется только последовательное или только параллельное соединение проводников. Определить сопротивление на этих участках.
-
Выяснить вид соединения участков между собой. Найти общее сопротивление всей цепи.
-
С помощью закона Ома и законов последовательного и параллельного соединения проводников найти распределения токов и напряжений в цепи.
Пример решения задачи
На рисунке показана схема электрической цепи. Сопротивления резисторов одинаковы и равны 12 Ом. Напряжение источника — 100 В.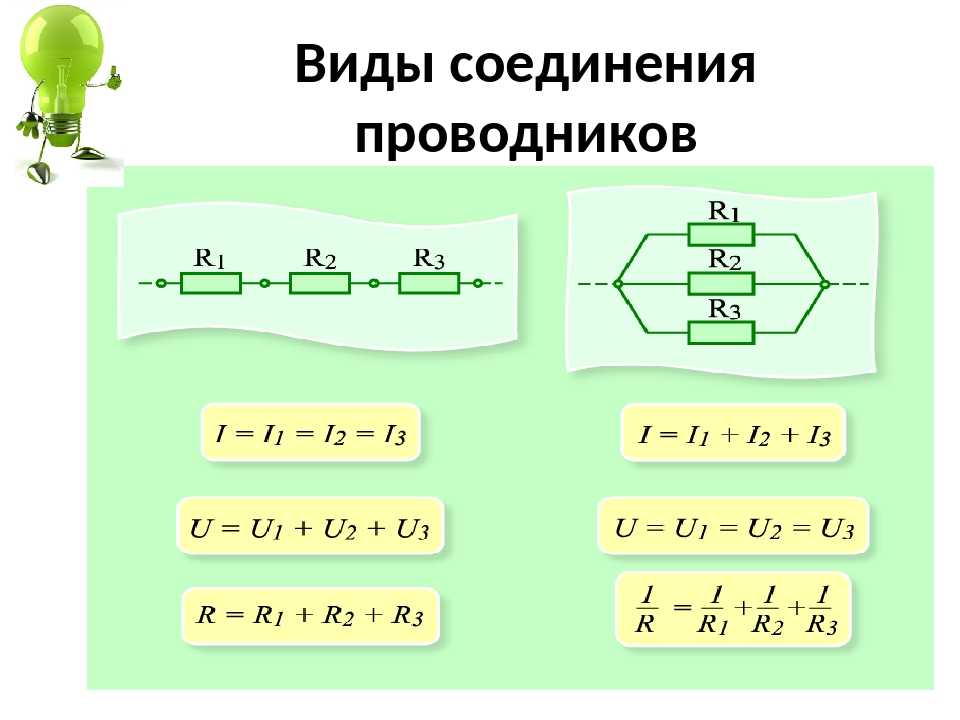 Какова сила тока, протекающего через резистор R4?
Какова сила тока, протекающего через резистор R4?
Решение.
-
Проанализируем данную схему. Резисторы R2 и R3 соединены между собой последовательно, а с резистором R4 — параллельно. Весь этот участок соединен последовательно с источником тока и резистором R1.
-
Определим сопротивление последовательно соединенных резисторов R2 и R3:
R23 = R2 + R3 = 12 + 12 = 24 Ом.
-
Найдем общее сопротивление резистора R4 и участка 2–3, соединенных параллельно:
R234 = (R23 · R4) / (R23 + R4) = (24 · 12) / (24 + 12) = 8 Ом.
-
Определим общее сопротивление всей цепи как сумму включенных последовательно резистора R1 и участка 2–3–4:
Rэкв = R1 + R234 = 12 + 8 = 20 Ом.

-
По закону Ома найдем силу тока в неразветвленной части цепи:
I = U / Rэкв = 200 / 20 = 5 А.
-
По закону Ома определим напряжение на участке, состоящем из резисторов R2, R3, R4:
Uэкв1 = I · R234 = 5 · 8 = 40 В.
-
Поскольку при параллельном соединении напряжение одинаково, то напряжение на резисторе R4 также равно 40 В. По закону Ома найдем силу тока, протекающего через резистор R4:
I4 = Uэкв1 / R4 = 40 / 12 ≈ 3,3 А.
Ответ: через резистор R4 протекает ток силой приблизительно 3,3 А.
Мы разобрали довольно много формул последовательного и параллельного подключения проводников. А запомнить их можно с помощью вот таких схем:
Скачать шпаргалку
Скачать шпаргалку
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!
На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!
Последовательное соединение проводников 8 класс онлайн-подготовка на Ростелеком Лицей
Сопротивления в электрической цепи
Прибор, основанный на сопротивлении проводника, называется резистором. Главное свойство проводника – это наличие у него электрического сопротивления. Поэтому под словами «последовательное соединение резисторов», «последовательное соединение проводников» и «последовательное соединение сопротивлений» мы будем понимать одно и то же.
Последовательным соединением называется соединение, когда элементы идут друг за другом, чередуются. Естественно, в электрических цепях обычно используется смешанное соединение, то есть комбинация последовательного и параллельного соединений. Но на этом уроке речь пойдет именно о последовательных соединениях. Нужно научиться рассчитывать электрические цепи, то есть вычислять напряжение, силу тока в цепи, чтобы знать, какие приборы и как можно включать в цепь. Об этом и пойдет речь в дальнейшем.
Об этом и пойдет речь в дальнейшем.
Электрическая схема последовательного соединения проводников
Рис. 1. Последовательное соединение резисторов
На рисунке 1 представлены три резистора, которые соединены друг за другом. Это и есть так называемое «последовательное соединение». В дальнейшем мы будем рассматривать всего два резистора, которые соединены последовательно, но смысл от этого не изменится, и полученные формулы будут также справедливы для любого числа проводников, соединенных последовательно.
Рис. 2. Последовательное включение двух ламп в электрическую цепь
На рисунке 2 изображено последовательное включение двух ламп (1а и 1б). Мы заменили ими проводники, но суть от этого не поменяется, так как лампы также имеют свое сопротивление. Также в цепи присутствует амперметр (А) для измерения силы тока в цепи. Есть еще 2 важных элемента: это вольтметры V1 и V2, которые измеряют напряжение (или падение напряжения) соответственно на лампах 1а и 1б. Еще есть источник питания (2) и ключ (3). Если ключ разомкнут, то ток в цепи не течет. Если же его замкнуть, то с помощью приборов можно измерить силу тока и напряжение в цепи. Примером такого соединения является ёлочная гирлянда, поскольку на самом деле она представляет собой последовательно соединенные лампы (рис. 3).
Еще есть источник питания (2) и ключ (3). Если ключ разомкнут, то ток в цепи не течет. Если же его замкнуть, то с помощью приборов можно измерить силу тока и напряжение в цепи. Примером такого соединения является ёлочная гирлянда, поскольку на самом деле она представляет собой последовательно соединенные лампы (рис. 3).
Рис. 3. Ёлочная гирлянда
Измерения силы тока и напряжения в цепи при последовательном соединении
Теперь посмотрим, что же произойдет, если замкнуть ключ. Рассмотрим схему на рис. 4, которая отличается от схемы, изображенной на рис. 2 только тем, что амперметр расположен между лампами.
Рис. 4. Включение амперметра между лампами
Амперметр изменил свое положение в цепи. Но если смотреть на его показания, то они не изменятся при перемещении амперметра в любое место на схеме последовательного соединения. Значит, можно сказать, что сила тока в лампе 1а (I1) будет равна силе тока в лампе 1б (I2) и равна общему току, протекающему в электрической цепи. То есть I1 = I2 = I. Это можно сравнить с течением реки: количество воды, протекающее за одно и то же время в разных местах этой реки, будет одинаково.
То есть I1 = I2 = I. Это можно сравнить с течением реки: количество воды, протекающее за одно и то же время в разных местах этой реки, будет одинаково.
Стоит также учесть, что, хоть и вольтметры соединены параллельно с лампами, это приборы высшего качества с очень высоким сопротивлением. Значит, ток через них будет идти минимальный, и такое искажение можно не учитывать.
Теперь рассмотрим схему, когда вольтметр измеряет напряжение сразу на двух лампах (рис. 5):
Рис. 5. Измерение напряжения на двух лампах
На рис. 4. вольтметрами V1 и V2 измерялось напряжение на каждой из ламп 1а и 1б. На данном рисунке вольтметр V измеряет напряжение (или падение напряжения) сразу на двух лампах. Оказывается, что показания вольтметра V, можно вычислить как сумму показаний вольтметров V1 и V2. То есть общее падение напряжения на двух лампах (U) равно сумме падений напряжения на каждой лампе в отдельности (U1 и U2).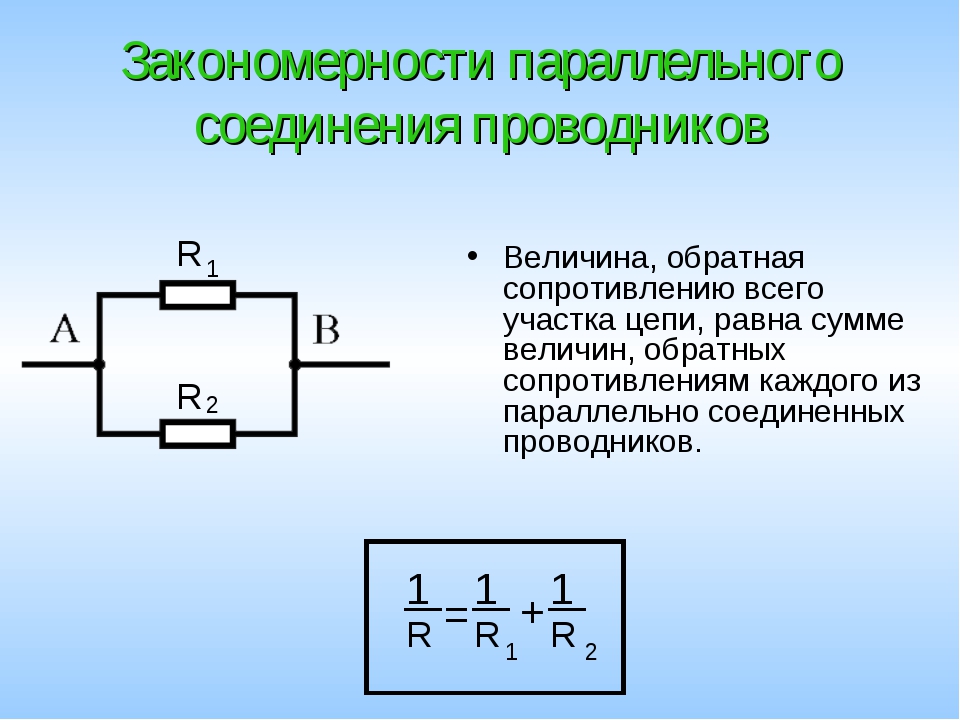 Тогда U = U1 + U2.
Тогда U = U1 + U2.
Стоит обратить внимание, что все рассуждения относительно силы тока, напряжения верны лишь при условии, что мы использовали одни и те же лампы, источники тока, вольтметры.
Эквивалентное сопротивление последовательно соединенных проводников
Завершающим звеном в исследовании последовательного соединения проводников является формула для общего сопротивления: Rобщ = R1 + R2.
До этого мы рассматривали значения силы тока, напряжения на различных участках цепи. Но исследовали мы проводники (лампы, резисторы), а их главной характеристикой является сопротивление. Обычно во всех электрических цепях пытаются определить эквивалентное (общее) сопротивление цепи, о котором мы говорили на предыдущем уроке. То есть это такое сопротивление, что можно заменить текущую цепь из последовательных проводников другим проводником, но с этим эквивалентным сопротивлением. В данном случае это сопротивление соответствует сопротивлению двух ламп, которые соединены последовательно.
Рассмотрим, как была получена формула для эквивалентного сопротивления. Для этого следует обратиться к закону Ома: . Отсюда можно получить выражение для сопротивления: . Теперь следует вспомнить, что в случае последовательного соединения (в простейшем случае – двух ламп) общее напряжение складывалось из напряжений на отдельной лампе: U = U1 + U2. Учитывая, что сила тока при последовательном соединении на всех участках цепи одинаковая, то можно разделить на нее обе части равенства:
Можно увидеть, что каждая дробь есть не что иное, как соответствующее сопротивление. Тогда R = R1 + R2, где R – эквивалентное сопротивление. Значит, чтобы узнать эквивалентное сопротивление проводников, соединенных последовательно, надо сложить значения их сопротивлений. При этом общее сопротивление будет всегда больше любого из сопротивлений, включенных в такую цепь.
В заключение урока стоит отметить, что если в цепи проводников, ламп или других приборов, которые соединены последовательно, перегорит один из приборов, то цепь разомкнется.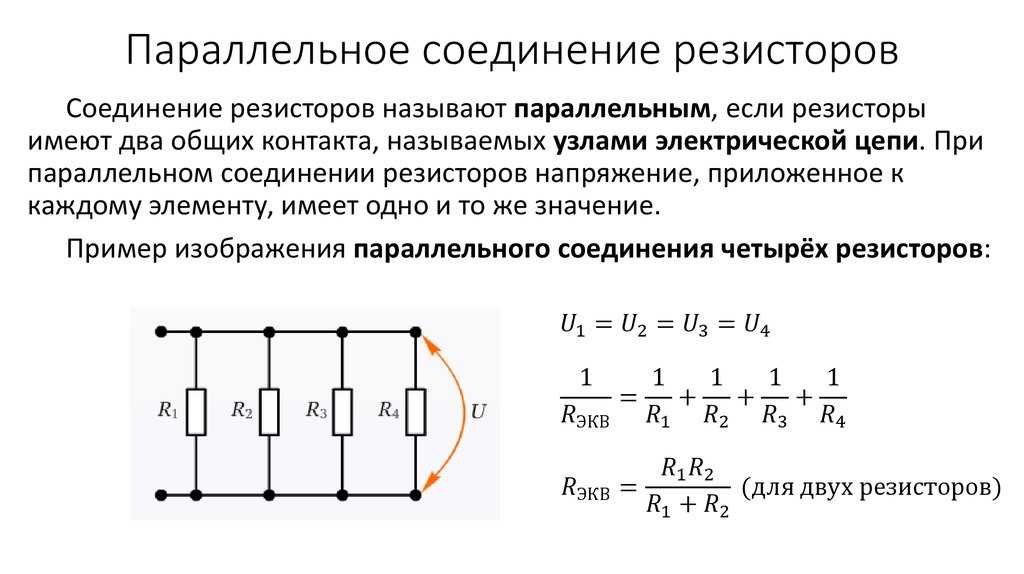 Остальные приборы также перестанут работать. Примером этому является все та же елочная гирлянда: если перегорает одна лампочка, то вся гирлянда перестает светиться. Это является основным недостатком последовательного соединения.
Остальные приборы также перестанут работать. Примером этому является все та же елочная гирлянда: если перегорает одна лампочка, то вся гирлянда перестает светиться. Это является основным недостатком последовательного соединения.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Физика (Источник)
- Сверхзадача (Источник)
- Интернет-портал «Nado5.ru» (Источник)
Домашнее задание
- Стр. 111–113: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Сила тока через лампу №1 равна 5 А. Лампа №2 соединена с ней последовательно.
 Какая сила тока будет проходить через лампу №2?
Какая сила тока будет проходить через лампу №2? - Как получить из закона Ома выражение для сопротивления?
- Как связаны формулы Rобщ = R1 + R2 и ? Рассмотрите проводники из одного материала и с одинаковым поперечным сечением.
Электрические схемы. Соединение проводников — Умскул Учебник
На этой странице вы узнаете- Нужен ли блендер, чтобы попить чай?
- Куда идет ток?
- Когда “сопротивление бесполезно”?
Всем приготовиться к погружению в мир электрических соединений и схем. Сопротивление бесполезно!
Условное обозначение элементов электрической цепиЕсть история о том, как одного физика-теоретика током ударило. Конечно, в теории он был силен, но знать — одно, а применять знания в жизни — совсем другое дело. Вот и получилось у него всякое, странное. Не советуем повторять: опасно для жизни!
А с чего вся история началась?
Когда мы говорим об электрических приборах, мы понимаем, что сам по себе прибор работать не будет. Его нужно подключить, к источнику тока. А если схема сложная, в которой несколько приборов? И как изобразить цепь на рисунке? Всеми этими вопросами задался наш герой.
Его нужно подключить, к источнику тока. А если схема сложная, в которой несколько приборов? И как изобразить цепь на рисунке? Всеми этими вопросами задался наш герой.
Для решения умные люди придумали условные обозначения, которые уже много лет используются в электромире:
Итак, наш физик-теоретик решил по схеме собрать гирлянду. Всё как положено. Лампочки подобрал все одинаковые. И даже соединения между ними учел.
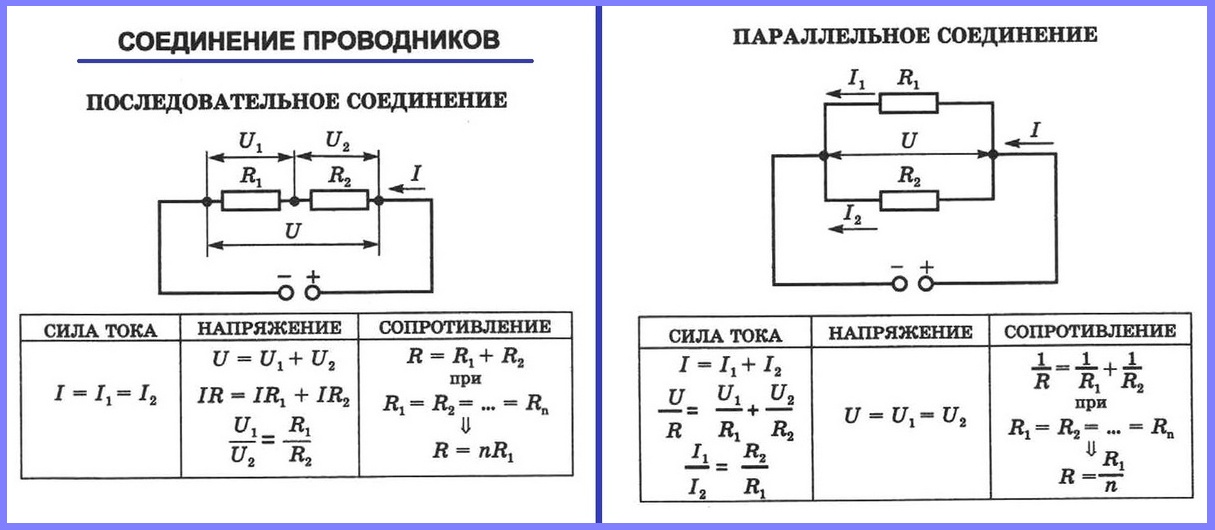
Соединения проводниковПроводники в электрических цепях могут соединяться последовательно и параллельно. Давайте разберем, чем отличаются эти два вида соединений и чем они полезны.
| Последовательное соединение | Параллельное соединение |
| Соединение проводников без разветвлений, когда конец одного проводника соединен с началом другого. | Соединение, в котором начала и концы проводников соединены вместе. |
| R1 и R2 — сопротивления проводников, R— общее сопротивление, I1 и I2— сила тока на каждом проводнике, I — общая сила тока, U1 и U2 — напряжение на каждом проводнике, U — общее напряжение цепи. 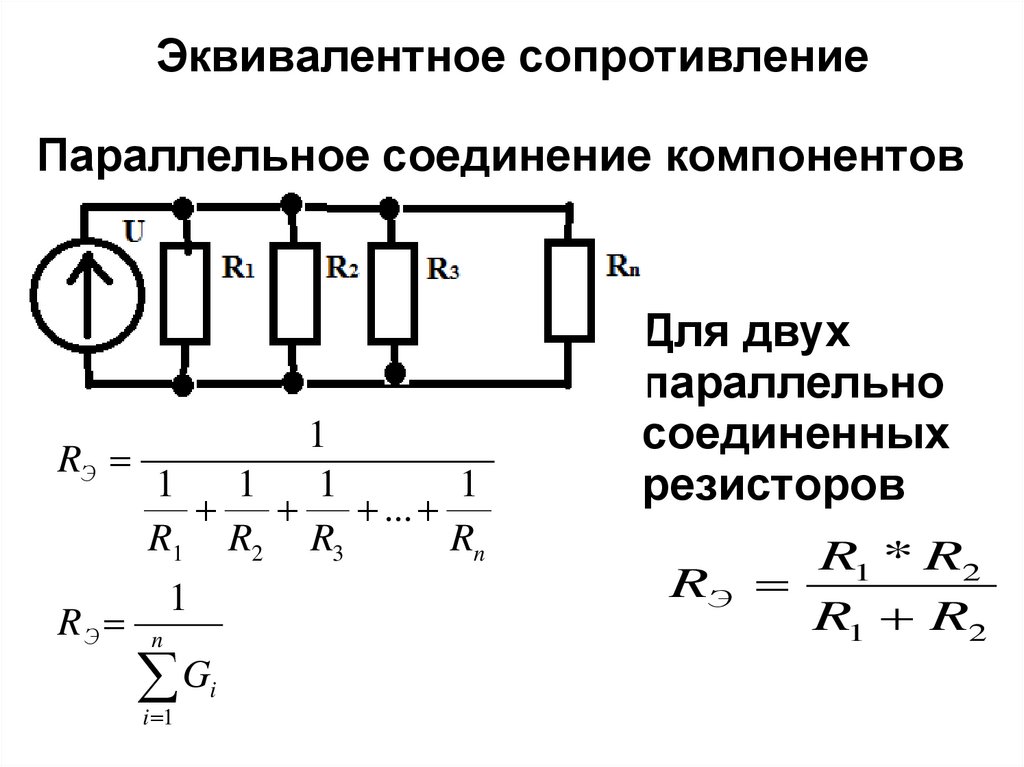 | R1 и R2 — сопротивления проводников, R— общее сопротивление, I1 и I2— сила тока на каждом проводнике, I — общая сила тока, U1 и U2 — напряжение на каждом проводнике, U — общее напряжение цепи. |
Схема последовательного соединения проводников. | Схема параллельного соединения проводников. |
| I1 = I2 = I Сила тока, протекающего через каждый проводник, одна и та же (I = const). | I = I1 + I2 Сила тока, протекающего в неразветвлённой части цепи, равна сумме сил токов, протекающих по каждому из проводников. |
| U1 = IR1, U2 = IR2; U = U1 + U2 Общее напряжение равно сумме напряжений на отдельных участках цепи. | U1 = I1R1, U2 = I2R2; U = U1 = U2 Напряжение на каждом из проводников одинаково (U = const). 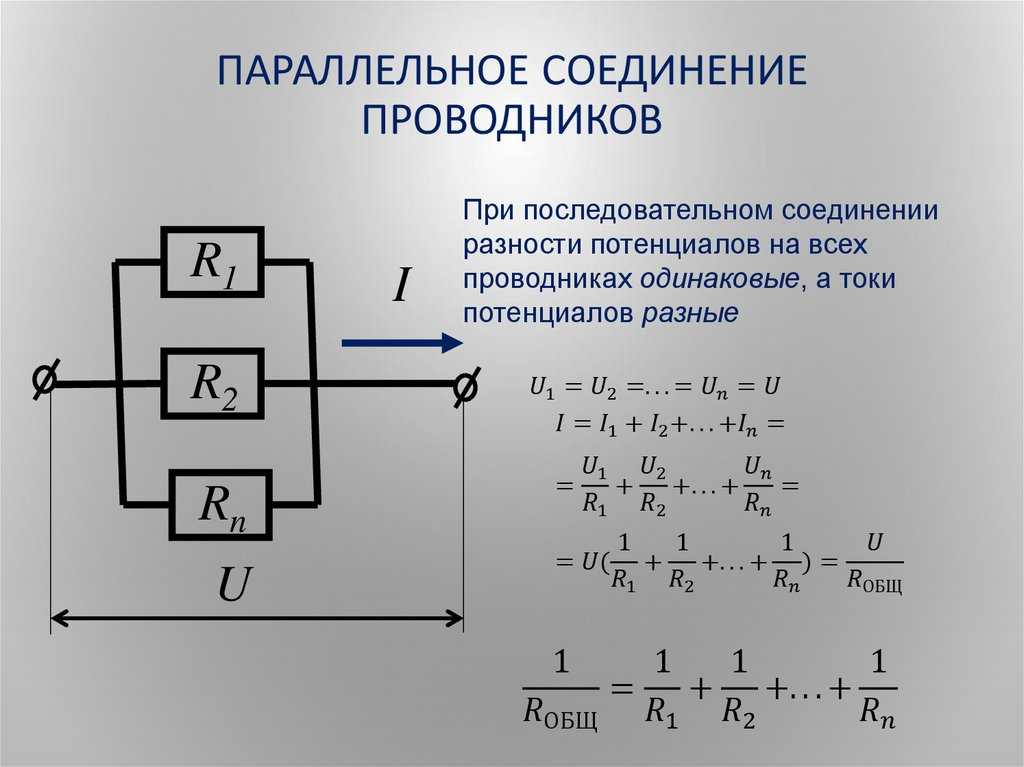 |
| R = R1 + R2 Общее сопротивление цепи равно сумме сопротивлений отдельных участков. | \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\) Проводимость равна сумме проводимостей каждого из проводников. |
| \(\frac{U_1}{U_2} = \frac{R_1}{R_2}\) | \(\frac{I_1}{I_2} = \frac{R_2}{R_1}\) |
| Если все сопротивления одинаковы, то: R = nr и U = nu, где r и u — соответственно сопротивление одного элемента и напряжение на нём, | Если все сопротивления одинаковы, то: \(R = \frac{r}{n}\) и U = u, где r и u — соответственно сопротивление одного элемента и напряжение на нём, |
| Общее сопротивление цепи больше наибольшего сопротивления, входящего в эту цепь. | Общее сопротивление цепи меньше наименьшего сопротивления, входящего в эту цепь. |
| Количество теплоты, выделяемое на каждом проводнике, пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_1}{R_2}\) | Количество теплоты, выделяемое на каждом проводнике, обратно пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_2}{R_1}\) |
| Мощность, выделяемая в проводниках, пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_1}{R_2}\) | Мощность, выделяемая в проводниках, обратно пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_2}{R_1}\) |
При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.
Важно учитывать, какие приборы, как подключать. Например, елочная гирлянда является примером последовательного соединения. Если одна лампочка перегорит, то вся гирлянда работать перестанет. Это, кстати, относится к недостаткам такого вида соединения. Наш физик-теоритк был в курсе этой особенности.
Тогда зачем такое соединение нужно?
Когда необходимо целенаправленно подключить какой-то один прибор. Например, карманный фонарик. Он будет работать только тогда, когда включена кнопка.
А вот в люстре лучше использовать параллельное соединение. И когда одна лампочка перегорит, все остальные по-прежнему будут светить.
| Нужен ли блендер, чтобы попить чай? Бытовые приборы на кухне соединены параллельно. Это значит, что чайник может спокойно работать без микроволновки. И чтобы поджарить тосты, блендер включать необязательно. Но если все эти приборы соединить последовательно, защитный выключатель может не выдержать, и произойдет перегрузка. |
Задачи на комбинированное соединение проводников удобно решать, используя эквивалентные схемы.
Смешанное (комбинированное) соединение проводниковКомбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.
| Куда идет ток? Ток не любит напрягаться. Поэтому ток течёт по пути наименьшего сопротивления. |
Рассмотрим пример задачи.
Вопрос: Каким будет сопротивление участка цепи (см. рисунок), если ключ К замкнуть? Каждый из резисторов имеет сопротивление 2R.
Ответ: если ключ К замкнуть, то сопротивление станет равным нулю.
| Когда “Сопротивление бесполезно”? После замыкания ключа участок схемы окажется закороченным; ток пойдёт через ключ, минуя резисторы. |
Что же произошло к нашим физиком-теоретиком? Он даже соединения источников учел. Только забыл он самое главное правило: сначала собери схему, а только потом подключи ее к источнику.
Вот он подключил один конец провода с лампочками к источнику, другой конец взял в руку… И навсегда запомнил технику безопасности при работе c электричеством: не стоит человеку становиться звеном цепи, подключенной к источнику.
Источники тока соединяют между собой для совместного питания всей цепи.
| Последовательное соединение | Параллельное соединение | |
| Схема | ||
| Эквивалентное внутреннее сопротивление | rэ = r1 + r2 | \(\frac{1}{r_э} = \frac{1}{r_1} + \frac{1}{r_2}\) |
| Эквивалентное ЭДС | \(\varepsilon_э = \pm \varepsilon_1 \pm \varepsilon_2\) знаки зависят от направления подключения источников | \(\frac{\varepsilon_э}{r_э} = \pm \frac{\varepsilon_1}{r_1} \pm \frac{\varepsilon_2}{r_2}\) знаки зависят от направления подключения источников |
| Закон Ома для полной цепи | \(I = \frac{\varepsilon_э}{r_э + R}\) | \(I = \frac{\varepsilon_э}{r_э + R}\) |
| Закон Ома для n одинаковых источников | \(I = \frac{n \varepsilon}{R + nr}\) | \(I = \frac{\varepsilon}{R + rn}\) |
Чем отличаются понятия “соединения резисторов” и “соединения источников тока”? Пример резистора — чайник, простой проводник электрического тока.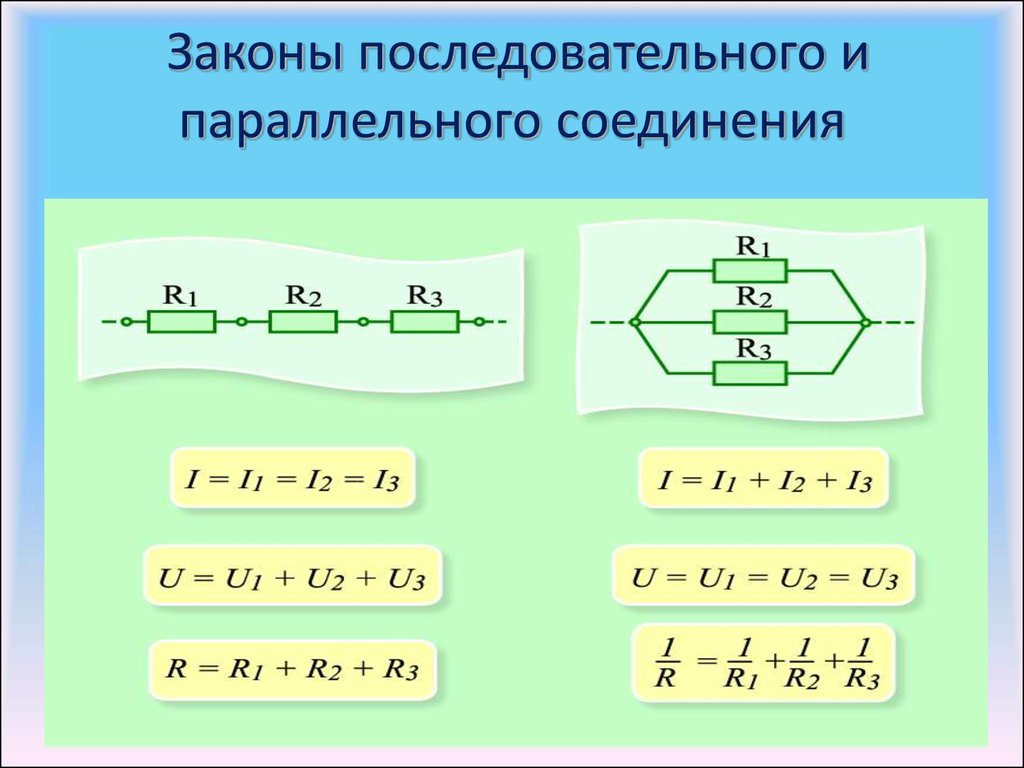 Если чайник подключить параллельно, это никак не повлияет на работу всей цепи. А источник тока — это розетка. Она дает “питание” всей цепи. Без источника тока не будет работать ни один прибор.
Если чайник подключить параллельно, это никак не повлияет на работу всей цепи. А источник тока — это розетка. Она дает “питание” всей цепи. Без источника тока не будет работать ни один прибор.
Важно запомнить правила подключения амперметра и вольтметра. Это необходимо для того, что приборы не перегорели и показывали корректные значения при измерении.
| Амперметр | Вольтметр |
| Амперметр подключается последовательно участку цепи. Соблюдаем полярность: “+” амперметра подключают к “+” источника тока, а “−” подключают к “−” источника тока. | Вольтметр подключается параллельно участку цепи. Соблюдаем полярность: “+” вольтметра подключают к “+” источника тока, а “−” подключают к “−” источника тока. |
Шунт — проводник, присоединяемый параллельно амперметру для увеличения предела его измерений. \(R_ш = \frac{R_A}{n — 1}\), где Rш — сопротивление шунта, | Добавочное сопротивление — проводник, присоединяемый последовательно с вольтметром для увеличения предела его измерений. Rд = RV(n-1), где Rд — добавочное сопротивление, |
Научиться читать электрические схемы важно для любителей электроники. Ведь если правильно ее прочитать, можно спаять что-то интересное, например, карманный фонарик.
Фактчек- Проводники в электрических цепях могут соединяться последовательно и параллельно.
- При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.
- Комбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.
- При подключении приборов обязательно нужно учитывать их полярность.
Задание 1.
Какие существуют соединения проводников?
- Последовательное
- Параллельное
- Смешанное
- Все варианты верны
Задание 2.
При последовательном соединении проводников общее сопротивление участка цепи:
- Увеличивается
- Уменьшается
- Не изменяется
Задание 3.
При параллельном соединении проводников общее сопротивление участка цепи:
- Увеличивается
- Уменьшается
- Не изменяется
Задание 4.
Как подключается амперметр в цепи?
- Последовательно
- Параллельно
- Не имеет значения
Задание 5.
Как подключается вольтметр в цепи?
- Последовательно
- Параллельно
- Не имеет значения
Ответы: 1. — 4; 2. — 1; 3. — 2; 4. — 1; 5. — 2
Лабораторная работа по исследованию свойств параллельного и последовательного соединения резисторов беспаечным способом
В работе исследованы свойства и физические законы соединения резисторов без пайки. При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Ключевые слова: резисторы, макетная плата, соединение без пайки, параллельное и последовательное соединение, токи, напряжение и сопротивления при соединения резисторов.
The paper studies the properties and physical laws of connecting resistors without soldering. When building layouts, soldering installation can be completely, abandoned or reduced to a minimum. As experience has shown, the practical use of layout boards can significantly save time and material costs.
Keyword: resistors, layout Board, connection without soldering, parallel and serial connection, currents, voltage and resistance when connecting resistors.
В современном высшем учебном заведении перед каждым преподавателем стоит цель по развитию научно-исследовательских навыков студентов. Один из задач являетсямотивации студента и совершенствование научно-исследовательских навыков в формулировке исследовательского вопроса во время лабораторной работы на уроках физики. В данной работе исследованы свойства и физические законы соединения резисторов без пайки. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты. [1,2].
[1,2].
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединение резисторовспомощью беспаечное соединение и определить формулы сопротивлений таких участков. Резисторы примениется в электронных приборах и робототехнике. [3].
Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.
Перечень оборудования
Рис. 1. Резистор и провода
Рис. 2. Мультиметр
Рис. 3. Макетная плата
Последовательно соединенных резисторов
Сопротивление впоследовательной цепи. Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.
Rобщ = R1+R2+R2+ •••+Rn(1)
Если последовательно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, умножив сопротивление одного резистора на количество резисторов.
Rобщ = nR1 (2)
Пример последовательного соединения двух резисторов показан на рис.4.
Общее сопротивление для двух резисторов.
Rобщ=R1+R2 (3)
Rобщ = 25 Ом+35 Ом=60 Ом (4)
Рис. 4. Последовательное соединение двух резисторов
Величина тока впоследовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени в любой точке цепи, будет одинаковым. Следовательно, во всех точках последовательной цепи величина тока одинакова.
Поэтому при последовательном соединении, для измерения тока достаточно включать один амперметр на любом участке цепи.
В качестве примера, можно привести цепь последовательного соединения двух резисторов, который показан на рис.5.
I=I1=I2=0,2A
Рис. 5. Величина тока в последовательнойцепи
Распределение напряжения впоследовательной цепи
Напряжение источника тока, приложенное, к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:
U=IR (5)
Так как ток в последовательной цепи везде одинаков, значит, действительно напряжение на ее участках зависит от сопротивления, чем больше сопротивление, тем большее напряжение приложено к данному участку. Сумма напряжений на участках последовательной цепи равна напряжению источника тока.
Uобщ=U1+ U2+ U3+ ••• +Un(6)
Пример, распределение напряжения в последовательной цепи соединения двух резисторов показан на рис.6.
Uобщ=U1+ U2(7)
12В=5В+7В
Параллельное соединение сопротивлений
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.
Рис. 6. Распределение напряжения в последовательной цепи
Сопротивлениев параллельной цепи
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
(8)
Если параллельно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, если сопротивление одного резистора разделить на количество резисторов.
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. Пример, если параллельно включено только два резистора (рис.7), то их общее сопротивление можно определить по формуле:
(10)
Рис. 7. Параллельное соединение двух резисторов
Распределение тока впараллельной цепи
В цепи с параллельным соединением, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит, что чем больше сопротивление, тем меньше по нему пойдет ток.
(11)
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее:
I=I1+ I2+ I3 +••• +In(12)
Следовательно, величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
Пример, распределение тока в параллельной цепи соединения двух резисторов показан на рис. 8.
I=I1+ I2
Рис. 8. Распределение тока в параллельной цепи
Величина напряжения впараллельных цепях
Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
U=U1=U2=U3=•••=Un (13)
Содержание хода работы ипоследовательность действий
Техническое задание
1) Собрать электрическую цепь в макетную плату (рис.9.)
2) Снять показания приборов и записать их в таблицу.
3) Произвести расчеты.
4) Ответить на контрольные вопросы.
5) Сделать вывод.
Порядок выполнения работы
1) Собрать схему в макетную плату (Рис. 9.).
2) Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм+ N, где N — номер студента по журналу (мощность резисторов более 1 Вт).
3) Включить источник и установить напряжение U=5В, 9В, 12В, 15В.
4) Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А иВ; Ви С; Аи С; Dи Е.
Запишите эти показания в таблицу 1, 2.
Рис. 9. Схема исследования: а) последовательное соединение, б) параллельное соединение
5) Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.
6) Измерьте с помощью мультиметра (в режиме измерения постоянного тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 1.
Запишите показания прибора в таблицу 1.
7) Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.
8) Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2.
9) Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.
10) Отключить схему.
Таблица 1
Рассчитанные иизмеренные параметры для последовательного соединения резисторов: Аи В; Ви С; Аи С.
|
№вар. |
Установлено |
Рассчитано |
Измёренные параметры |
||||||
|
R1 |
R2 |
А— В |
В— С |
А— С |
I |
U |
U1 |
U2 |
|
|
кОм |
кОм |
кОм |
кОм |
кОм |
А |
В |
В |
В |
|
Таблица 2
Рассчитанные иизмеренные параметры для параллельного соединения резисторов: Dи Е.
|
№вар. |
Установлено |
Рассчитано |
Измерённые параметры |
||||||
|
R3 |
R4 |
D иЕ |
U |
I |
I1 |
I2 |
|||
|
кОм |
кОм |
кОм |
В |
А |
А |
А |
|||
Содержание отчета
а) название и цель работы;
б) схемы экспериментов и таблицы полученных экспериментальных данных;
в) результаты расчётов:
г) выводы по работе.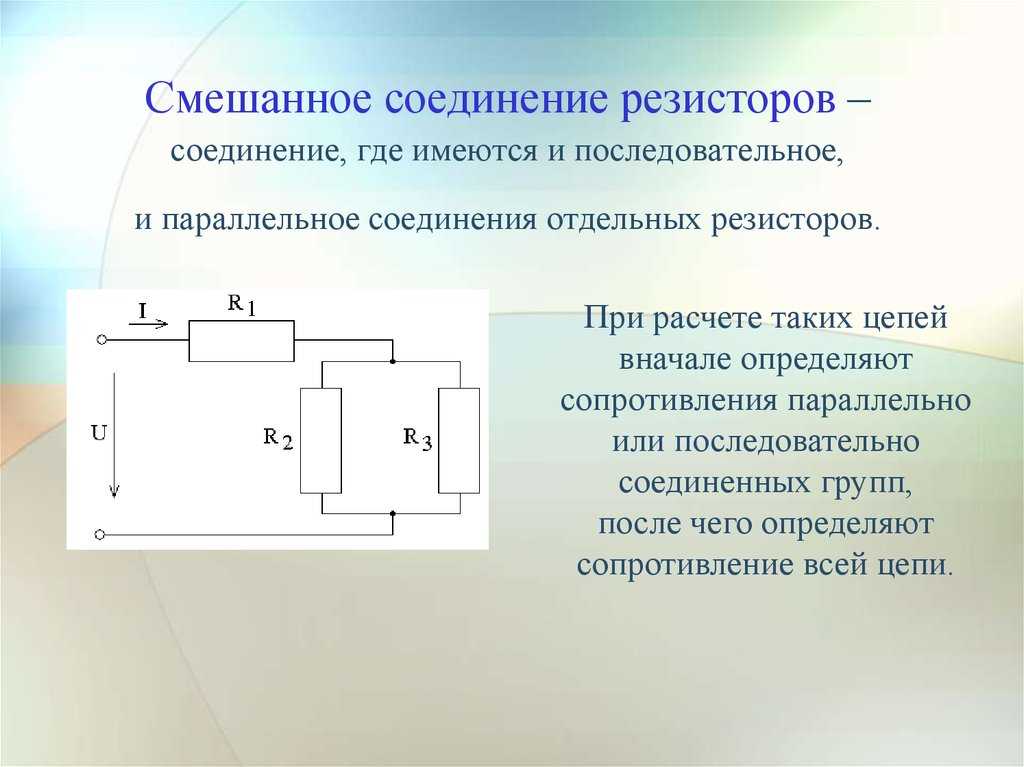
Контрольные вопросы
1) Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
2) Как по вольтамперной характеристике определить величину сопротивления цепи?
3) Как по показаниям мультиметра можно определить величину сопротивления участка электрической цепи и потребляемая мощность?
4) Нарисуйте схемы последовательное и параллельное соединение двух резисторов.
5) Объясните физические законы соединения резисторов.
Выводы
В работе исследованы свойства и физические законы параллельного и последовательного соединения резисторов бес применения пайки.
При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Литература:
-
А.
 Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
- Л. Г. Белиовская, Белиовский Н. А. Роботизированные лабораторныее работы по физики, Пропедевтетический курс физика. -М.:ДМК Пресс.2016.-164С.
- Википедия [Электронный ресурс]. http://ru.wikipedia.org/wiki/Processing.
Основные термины (генерируются автоматически): общее сопротивление, резистор, сопротивление, последовательная цепь, последовательное соединение, соединение резисторов, величина тока, ком, макетная плата, параллельная цепь, параллельное соединение.
Основы электроники и электротехники — Лабораторная работа №3
Исследование сопротивлений резисторов при последовательном и параллельном соединениях.
Цель работы: Опытом проверить закономерности электрической цепи при последовательном и паралельном соединениях резисторов.
1.Пояснение к работе
Краткие теоретические сведения
Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д.
Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.
Rобщ.=R1+R2+R3
Rобщ=5ом+10ом+25ом=40ом
Величина тока в последовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени. в любой точке цепи будет одинаковым.
Следовательно во всех точках последовательной цепи величина тока одинакова.
Эти четыре амперметра покажут одинаковые величины тока. Поэтому при последовательном соединении для измерения тока достаточно включать один амперметр на любом участке цепи.
Распределение напряжения в последовательной цепи
Напряжение источника тока приложенное к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение приложенное к каждому из этих резисторов определяется по формуле:
Так как ток в последовательной цепи везде одинаков значит действительно напряжение на ее участках зависит от сопротивления чем больше сопротивление тем большее напряжение приложено к данному участку.
Сумма напряжений на участках последовательной цепи равна напряжению источника тока
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение.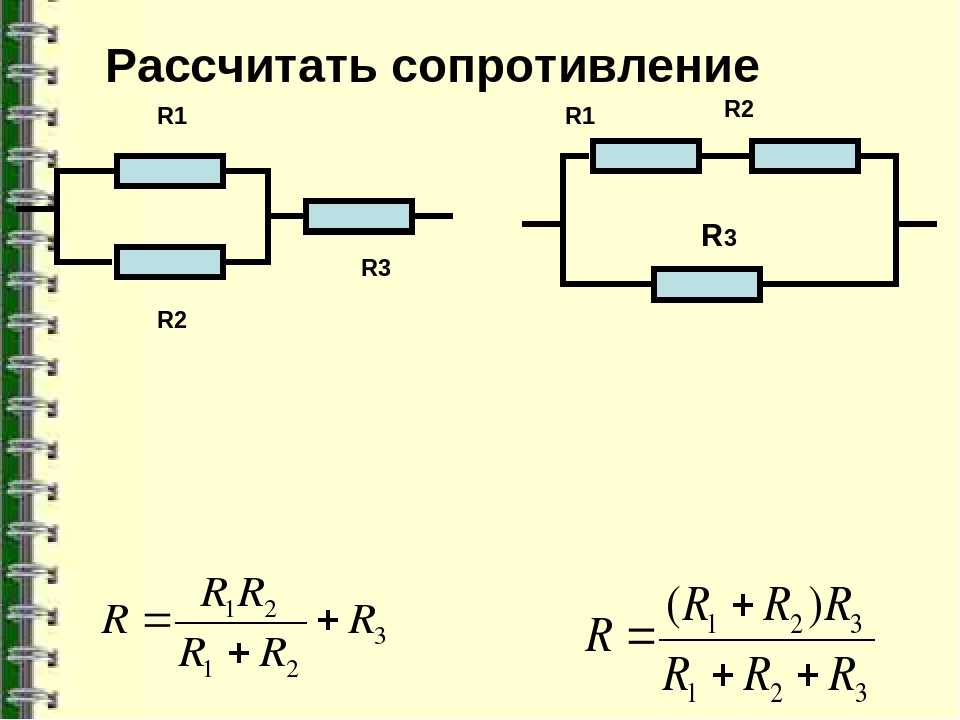
На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.
Первый частный случай
Если параллельно включено только два резистора то их общее сопротивление можно определить по формуле:
Второй частный случай
Если параллельно включено любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить если сопротивление одного резистора разделить на количество резисторов.
Распределение токов и напряжения в параллельных ветвях
Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.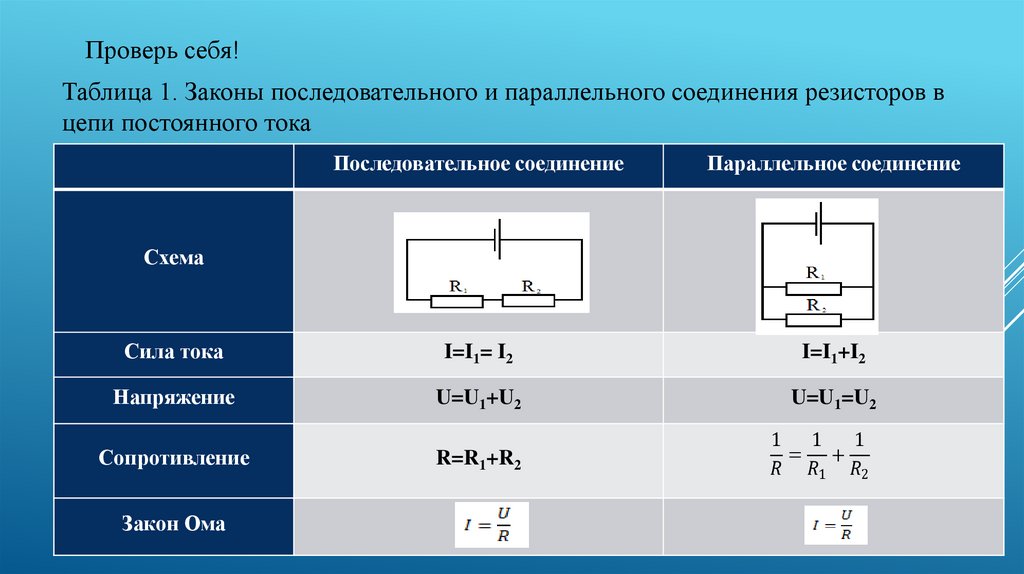
Второе свойство цепи с параллельным соединением заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит что, чем больше сопротивление, тем меньше по нему пойдет ток.
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:
Следовательно, третье свойство параллельного соединения может сформулирована так:
Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
2.Техническое задание
2.1.Собрать электрическую цепь последовательного соединения резисторов (рисунок 1)
Рисунок 1. Схема электрическая принципиальная.
2.2.Собрать электрическую цепь паралельного соединения резисторов (рисунок 2)
Рисунок 2. Схема электрическая принципиальная.
Схема электрическая принципиальная.
2.3.Снять показания приборов и записать их в таблицу
2.4.Произвести расчеты
2.5. Построить графики
2.6.Ответить на контрольные вопросы
2.7. Сделать вывод
3.Работа в лаборатории
3.1. Исследование последовательного соединения резисторов
3.1.1 Собрать схему (Рисунок 3).
Рисунок 3. Схема исследования.
3.1.2 Установить на схеме величины R1=100 Ом + N, R2=100 Ом + 2N и R3=130 Ом + 4N,
где N — номер студента по журналу (мощность резисторов 1 Вт).
3.1.3. Включить источник и установить напряжение U=15 В, 24 В.
3.1.4. Измерить величину тока, протекающего в цепи и занести значение в таблицу 1.
3.1.5. Измерить напряжение на каждом резисторе и записать в таблицу 1.
3.1.6. Измерить сопротивление каждого резистора и записать в таблицу 1.
3.1.7. Отключить схему.
3.1.8. Рассчитать сопротивление резисторов по формулам:
Таблица 1 — Измеренные параметры
|
№измерения
|
Измерением |
Расчетом |
|||||||||||
|
U |
I |
U1 |
U2 |
U3 |
R1 |
R2 |
R3 |
RЭ |
R1 |
R2 |
R3 |
RЭ |
|
|
В |
А |
В |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
|
|
1 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
3. 2. Исследование параллельного соединения реисторов
2. Исследование параллельного соединения реисторов
3.2.1. Собрать схему (Рисунок 4).
Рисунок 4. Схема исследования.
3.2.2. Установить на схеме величины R1=70 Ом + N, R2=100 Ом + N и R3=150 Ом + N,
где N — номер студента по журналу (мощность резисторов более 1 Вт).
3.2.3. Включить источник и установить напряжение U=15 В, 24 В.
3.2.4. Измерить величину тока, протекающего во всей цепи и занести значение в таблицу 2.
3.2.5. Измерить величину тока, протекающего в каждом резисторе и записать в таблицу 2.
3.2.6. Расчитать проводимость каждого резистора и записать в таблицу 2 (установкой):
3.2.7. Рассчитать проводимость каждого резистора через ток и напряжение и записать в таблицу 2 (расчетом):
3. 2.8. Отключить схему.
2.8. Отключить схему.
Таблица 2 — Измеренные параметры
|
№ измер. |
Измерением |
Установкой |
Расчетом |
||||||||||||
|
U |
I |
I1 |
I2 |
I3 |
g1 |
g2 |
g3 |
gэ |
Rэ |
g1 |
g2 |
g3 |
gэ |
Rэ |
|
|
А |
А |
А |
А |
А |
См |
См |
См |
См |
Ом |
См |
См |
См |
См |
Ом |
|
|
1 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Содержание отчета
Содержание отчета
4.1. Название и цель работы
4.2. Схемы
4.3. Таблицы
4.4. Расчеты по формулам
4.5. Ответы на контрольные вопросы
4.6. Вывод
5.Контрольные вопросы
5.1. Какое соединение резисторов называют последовательным?
5.2. Как определить общее сопротивление резисторов при последовательном соединении?
5.3. Что называется проводимостью и в каких единицах она измеряется?
5.4. Чему равен общий ток цепи и напряжение на участках при последовательном соединении?
5.5. Как определяется мощность на участках цепи и всей цепи при последовательном соединении?
5.6. Какое соединение резисторов называют паралельным?
5.7. Как определить общее сопротивление резисторов при паралельным соединении?
5.8. Чему равен общий ток цепи и напряжение на участках при паралельным соединении?
5.9. Как определяется мощность на участках цепи и всей цепи при паралельным соединении?
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375524 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
резисторов последовательно и параллельно | безграничная физика |
Резисторы серии
Общее сопротивление в цепи с последовательно соединенными резисторами равно сумме сопротивлений отдельных элементов.
Цели обучения
Вычислите общее сопротивление в цепи с резисторами, соединенными последовательно
Ключевые выводы
Ключевые моменты
- Один и тот же ток протекает через каждый последовательно соединенный резистор.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
- Общее сопротивление в последовательной цепи равно сумме сопротивлений отдельных элементов:
RN(серия)=R1+R2+R3+…+RN\text{RN} (\text{серия}) = \text{ R}_1 + \text{R}_2 + \text{R}_3 +.
.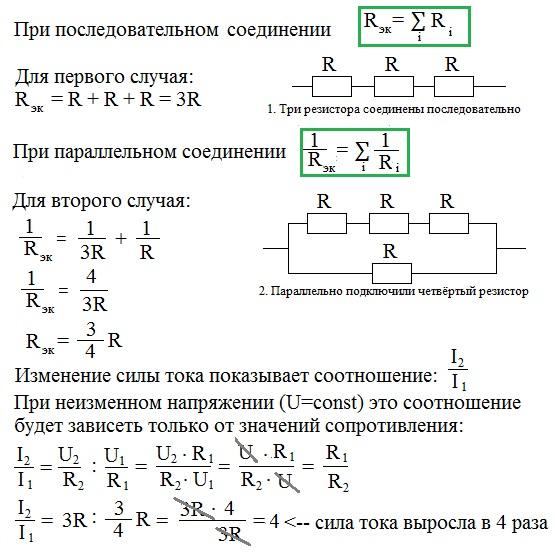 .. + \text{R}_\text{N}RN(ряд)=R1+R2+R3+… +РН
.. + \text{R}_\text{N}RN(ряд)=R1+R2+R3+… +РН
Ключевые термины
- серия : Ряд вещей, которые следуют одна за другой или связаны одна за другой.
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
Обзор
Большинство схем имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением. Наиболее простыми комбинациями резисторов являются последовательное и параллельное соединения. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Серийные цепи : Краткое введение в последовательные цепи и анализ последовательных цепей, включая закон Кирхгофа для тока (KCL) и закон Кирхгофа для напряжения (KVL).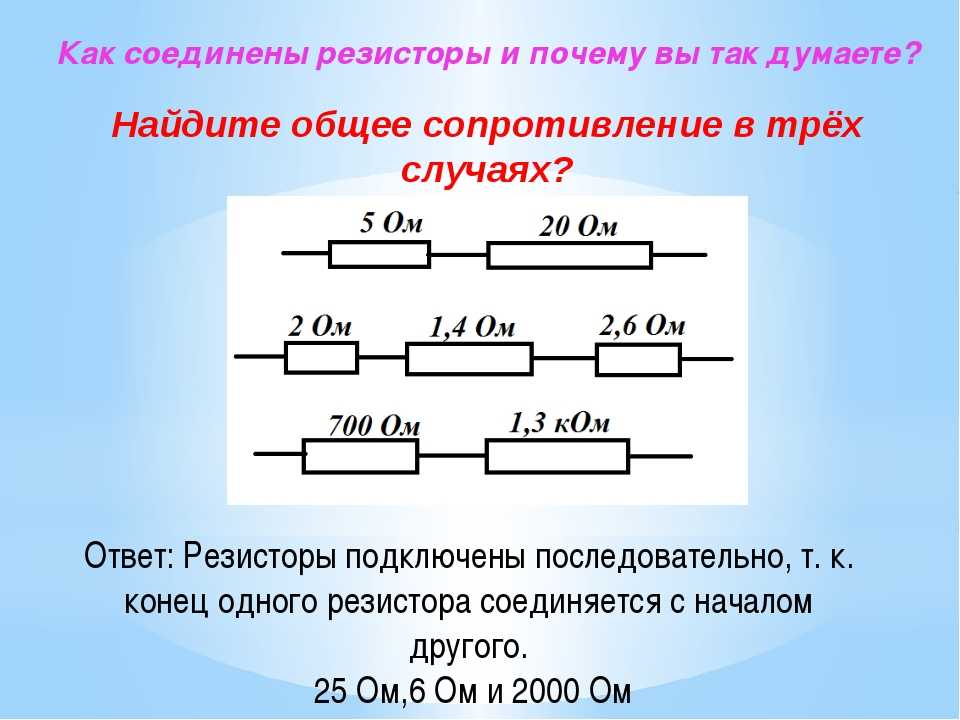
Резисторы серии
Резисторы включены последовательно всякий раз, когда поток заряда или ток должен проходить через компоненты последовательно.
Резисторы в серии : Эти четыре резистора соединены последовательно, потому что, если ток подается на один конец, он будет проходить через каждый резистор последовательно до конца.
показаны резисторы, последовательно подключенные к источнику напряжения. Общее сопротивление в цепи равно сумме отдельных сопротивлений, поскольку ток должен последовательно проходить через каждый резистор в цепи.
Резисторы, соединенные последовательно : Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).
Использование закона Ома для расчета изменений напряжения на последовательно соединенных резисторах
Согласно закону Ома, падение напряжения V на резисторе при протекании через него тока рассчитывается по уравнению V=IR, где I — ток в амперах (А), а R — сопротивление в омах (Ом).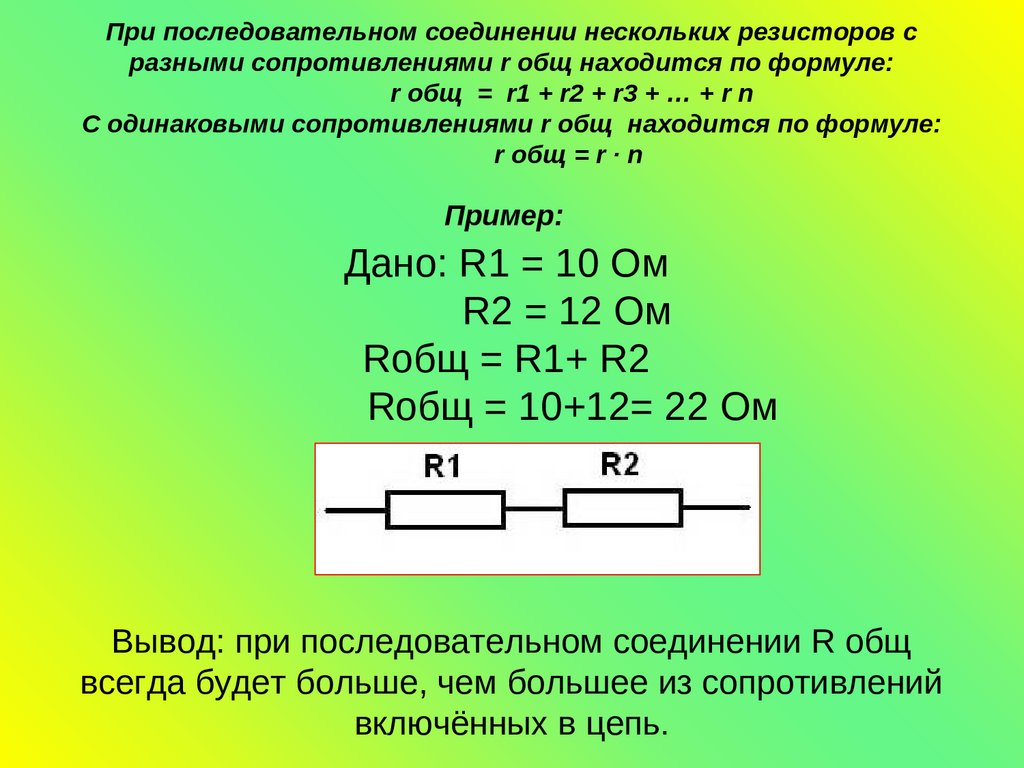
Итак, падение напряжения на R 1 — это V 1 = IR 1 , через R 2 — через V 2 = IR 2 , и через R 3 — как V 3,0 9 6 0 5 9 0 9 0 6 6 6 0 9 0 6 5 3 9 Сумма напряжений будет равна: V=V 1 +V 2 +V 3 , исходя из закона сохранения энергии и заряда. Если подставить значения для отдельных напряжений, то получим:
В=IR1+IR2+IR3\text{V}=\text{IR}_1 + \text{IR}_2 + \text{IR}_3V=IR1 +IR2+IR3
или
V=I(R1+R2+R3)\text{V} = \text{I}(\text{R}_1+\text{R}_2+\text{R} _3)V=I(R1+R2+R3)
Это означает, что общее сопротивление в серии равно сумме отдельных сопротивлений. Следовательно, для каждой цепи с N числом последовательно соединенных резисторов:
RN(серии)=R1+R2+R3+…+RN.\text{RN} (\text{серии}) = \text{ R}_1 + \text{R}_2 + \text{R}_3 +… + \text{R}_\text{N}.RN(ряд)=R1+R2+R3+.. .+РН.
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Так как напряжение и сопротивление обратно пропорциональны, отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его. На это указывает пример, когда две лампочки соединены вместе в последовательной цепи с аккумулятором. В простой цепи, состоящей из одной батареи на 1,5 В и одной лампочки, падение напряжения на лампочке составит 1,5 В. Однако, если бы две лампочки были соединены последовательно с одной и той же батареей, каждая из них имела бы падение напряжения 1,5 В/2 или 0,75 В. Это будет видно по яркости света: каждая из двух последовательно соединенных лампочек будет в два раза тусклее, чем одиночная лампочка. Следовательно, резисторы, соединенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия делится между резисторами в зависимости от их сопротивлений.
Параллельные резисторы
Общее сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного элемента.
Цели обучения
Рассчитайте общее сопротивление в цепи с параллельно соединенными резисторами
Ключевые выводы
Ключевые моменты
- Общее сопротивление в параллельной цепи меньше наименьшего из сопротивлений по отдельности.
- К каждому резистору, включенному параллельно, приложено одинаковое напряжение источника (напряжение постоянно в параллельной цепи).
- Параллельные резисторы не получают суммарный ток каждый; они делят его (ток зависит от номинала каждого резистора и общего количества резисторов в цепи).
Ключевые термины
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
- параллельный : Расположение электрических компонентов, при котором ток течет по двум или более путям.
Обзор
Резисторы в цепи могут быть соединены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Параллельные схемы : Краткий обзор анализа параллельных цепей с использованием таблиц VIRP для учащихся старших классов физики.
Параллельные резисторы
Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельное соединение резисторов : Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это касается электросхем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Закон Ома и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение. По закону Ома токи, протекающие через отдельные резисторы, равны
I1=VR1\text{I}_1 = \frac{\text{V}}{\text{R}_1}I1=R1V
,
I2=VR2\text{I}_2 = \frac{\text{V}}{\text{R}_2}I2=R2V
и
I3=VR3\text{I}_3 = \frac{\text{V}} {\text{R}_3}I3=R3V
. Сохранение заряда подразумевает, что общий ток представляет собой сумму следующих токов:
Параллельные резисторы : Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.
I=I1+I2+I3.\text{I} = \text{I}_1 + \text{I}_2 + \text{I}_3.I=I1+I2+I3.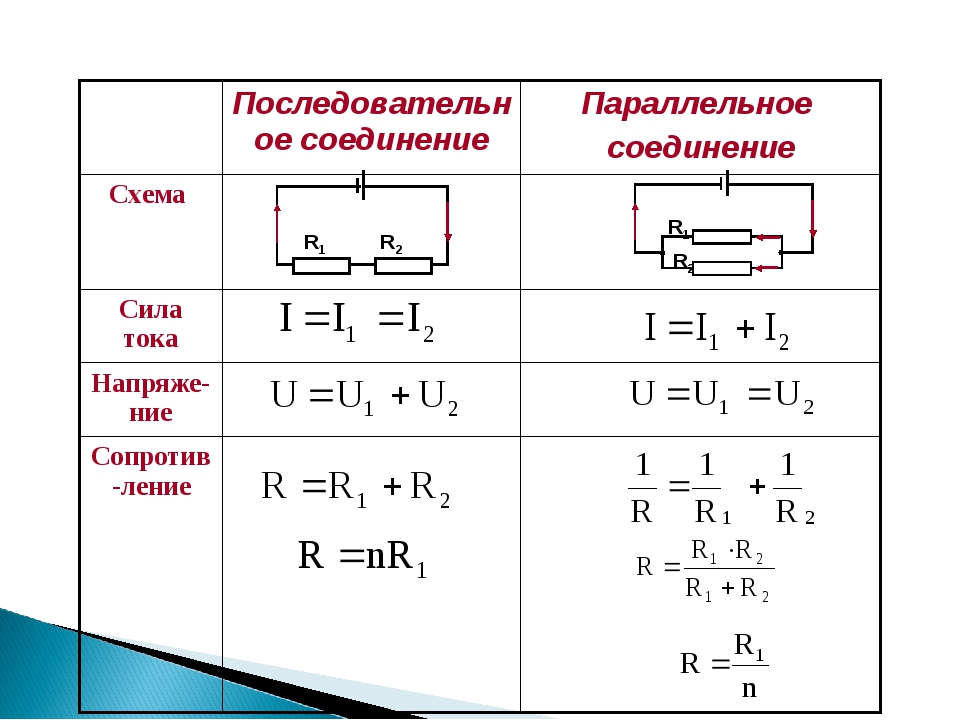
Подстановка выражений для отдельных токов дает:
I=VR1+VR2+VR3\text{I} = \frac{\text{V}}{\text{R}_1} + \frac{\text{V }}{\text{R}_2} + \frac{\text{V}}{\text{R}_3}I=R1V+R2V+R3V
или
I =V(1R1+1R2+1R3)\text{I} = \text{V}( \frac{1}{\text{R}_1} + \frac{1}{\text{R}_2} + \ frac{1}{\text{R}_3})I=V(R11+R21+R31)
Отсюда следует, что полное сопротивление в параллельной цепи равно сумме инверсия каждого отдельного сопротивления. Следовательно, для каждой схемы с
n\text{n}n
количество резисторов, соединенных параллельно,
Rn (параллельно)=1R1+1R2+1R3…+1Rn.\text{R}_{\text{n} \; (\text{параллельно})} = \frac{1}{\text{R}_1} + \frac{1}{\text{R}_2} + \frac{1}{\text{R}_3} … + \frac{1}{\text{R}_\text{n}}.Rn(параллельно)=R11+R21+R31…+Rn1 .
Это соотношение приводит к тому, что общее сопротивление меньше, чем наименьшее из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника протекает больший ток, чем по каждому из них по отдельности, поэтому общее сопротивление меньше.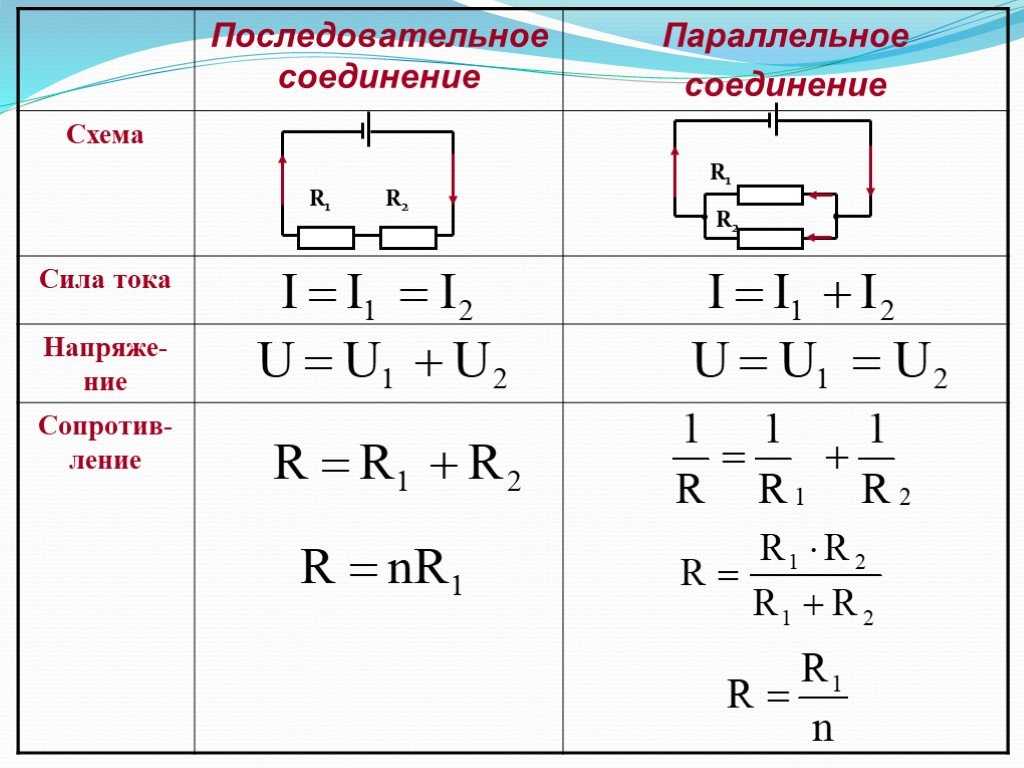
На каждый параллельно подключенный резистор подается одинаковое полное напряжение источника, но общий ток делится между ними. Примером этого является подключение двух лампочек в параллельную цепь с батареей 1,5 В. В последовательной цепи две лампочки будут в два раза тусклее при подключении к одному аккумуляторному источнику. Однако, если бы две лампочки были соединены параллельно, они были бы такими же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам приложено одинаковое полное напряжение, батарея также разрядится быстрее, поскольку она, по сути, подает полную энергию обеим лампочкам. В последовательной цепи батарея будет работать так же долго, как и с одной лампочкой, только яркость затем будет делиться между лампочками.
Комбинированные цепи
Комбинированная цепь может быть разбита на аналогичные части, которые могут быть либо последовательными, либо параллельными.
Цели обучения
Описать расположение резисторов в комбинированной цепи и его практическое значение.
Основные выводы
Ключевые моменты
- Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения.
- Различные части комбинированной цепи могут быть идентифицированы как последовательные или параллельные, приведены к их эквивалентам, а затем сокращены до тех пор, пока не останется одно сопротивление.
- Сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление в проводах относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными и влиять на выходную мощность приборов.
Ключевые термины
- серия : Ряд вещей, которые следуют одна за другой или связаны одна за другой.
- параллельный : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- Комбинированная цепь : Электрическая цепь, содержащая несколько резисторов, соединенных последовательно и параллельно.

Комбинированные цепи
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Это часто встречается, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная цепь может быть разбита на аналогичные части, которые могут быть либо последовательными, либо параллельными, как показано на рисунке. На рисунке общее сопротивление можно рассчитать, соединив три резистора друг с другом как последовательно или параллельно. R 1 и R 2 соединены параллельно относительно друг друга, поэтому мы знаем, что для этого подмножества обратная величина сопротивления будет равна:
Сеть резисторов можно разделить на последовательную составляющую и параллельную составляющую.
Комбинированные цепи : Два параллельных резистора, соединенных последовательно с одним резистором.
1R1+1R2 \frac{1}{\text{R}_1}+ \frac{1}{\text{R}_2}R11+R21
или
R1R2R1+R2 \ frac{\text{R}_1\text{R}_2}{\text{R}_1+\text{R}_2}R1+R2R1R2
R 3 соединен последовательно с оба R 1 и R 2 , поэтому сопротивление будет рассчитываться как:
R=R1R2R1+R2+R3\text{R} = \frac{\text{R}_1\text{R} _2}{\text{R}_1+\text{R}_2}+\text{R}_3R=R1+R2R1R2+R3
Сложные комбинированные цепи
Для более сложных комбинационных цепей различные части могут быть идентифицированы как последовательные или параллельные, приведенные к их эквивалентам, а затем уменьшены до тех пор, пока не останется одно сопротивление, как показано на рисунке. На этом рисунке комбинация из семи резисторов идентифицирована либо как последовательно или параллельно. На исходном изображении две обведенные части показывают параллельные резисторы.
Сокращение комбинированной цепи : Эта комбинация семи резисторов имеет как последовательные, так и параллельные части.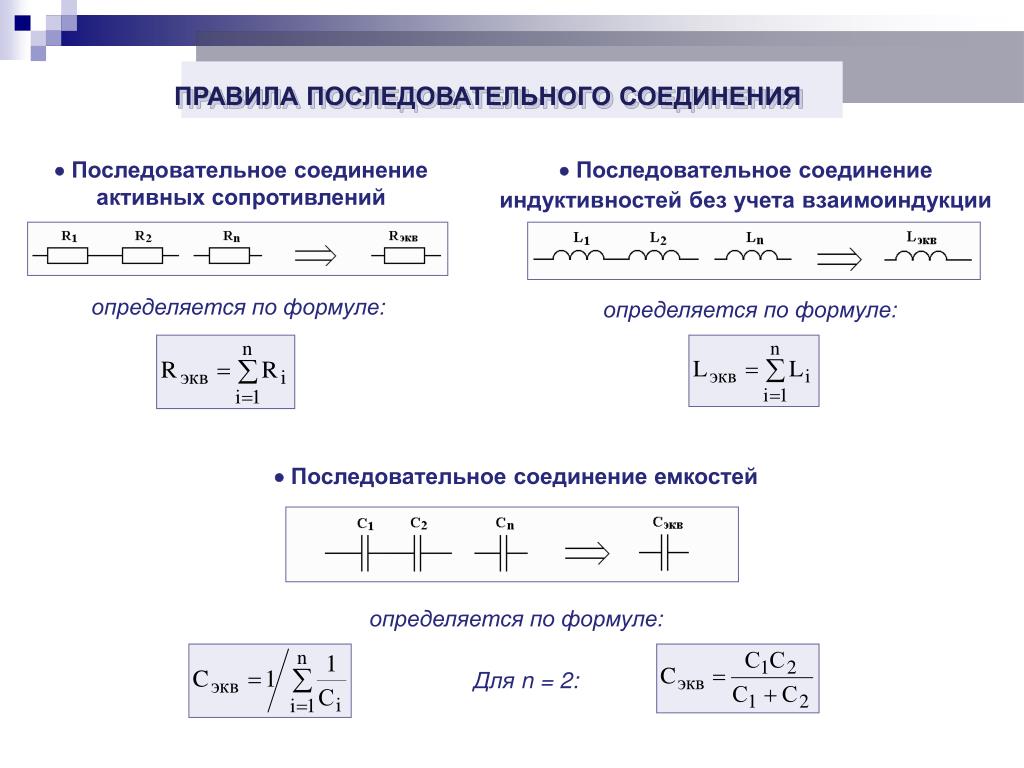 Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Уменьшение этих параллельных резисторов до одного значения R позволяет нам визуализировать схему более упрощенным образом. На верхнем правом изображении мы видим, что обведенная часть содержит два последовательных резистора. Мы можем еще больше уменьшить это до другого значения R, добавив их. Следующий шаг показывает, что два обведенных резистора подключены параллельно. Уменьшение выделяет то, что два последних находятся последовательно, а значит можно привести к единому значению сопротивления для всей цепи.
Одним из практических последствий использования комбинированной схемы является то, что сопротивление проводов снижает ток и мощность, подаваемые на резистор. Комбинированную цепь можно преобразовать в последовательную, исходя из понимания эквивалентного сопротивления параллельных ветвей комбинированной цепи. Последовательную цепь можно использовать для определения полного сопротивления цепи. По сути, сопротивление провода представляет собой ряд с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Последовательную цепь можно использовать для определения полного сопротивления цепи. По сути, сопротивление провода представляет собой ряд с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Зарядка аккумулятора: последовательное и параллельное ЭДС
При последовательном соединении источников напряжения их ЭДС и внутренние сопротивления складываются; параллельно они остаются прежними.
Цели обучения
Сравните сопротивления и электродвижущие силы для источников напряжения, соединенных с одной и противоположной полярностью, а также последовательно и параллельно полная э.д.с.

Ключевые термины
- параллельный : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- Серия : Ряд вещей, которые следуют одна за другой или связаны одна за другой.
Когда используется более одного источника напряжения, их можно подключать последовательно или параллельно, подобно резисторам в цепи. Когда источники напряжения последовательно обращены в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила или ЭДС складываются алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС.
Эти типы источников напряжения распространены в фонариках, игрушках и других приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС.
Фонарик и лампочка : Последовательное соединение двух источников напряжения в одном направлении. На этой схеме показан фонарик с двумя ячейками (источники напряжения) и одной лампочкой (сопротивление нагрузки) последовательно.
Батарея представляет собой многократное соединение гальванических элементов. Однако недостатком такого последовательного соединения ячеек является увеличение их внутренних сопротивлений. Иногда это может быть проблематично. Например, если вы поместите в свой автомобиль две батареи на 6 В вместо типичной одиночной батареи на 12 В, вы добавите как ЭДС, так и внутренние сопротивления каждой батареи. Таким образом, вы получите ту же ЭДС 12 В, хотя внутреннее сопротивление будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу, например, когда одну из них помещают в прибор задом наперед, общая ЭДС меньше, так как она представляет собой алгебраическую сумму отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство для аккумуляторов : Представляет собой два источника напряжения, соединенных последовательно с их ЭДС в оппозиции. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений. (Обратите внимание, что каждая ЭДС представлена буквой E на рисунке.) Зарядное устройство, подключенное к батарее, является примером такого соединения. Зарядное устройство должно иметь большую ЭДС, чем батарея, чтобы протекать через нее обратный ток.
Когда два источника напряжения с одинаковыми ЭДС соединены параллельно, а также подключены к сопротивлению нагрузки, общая ЭДС будет такой же, как и отдельные ЭДС.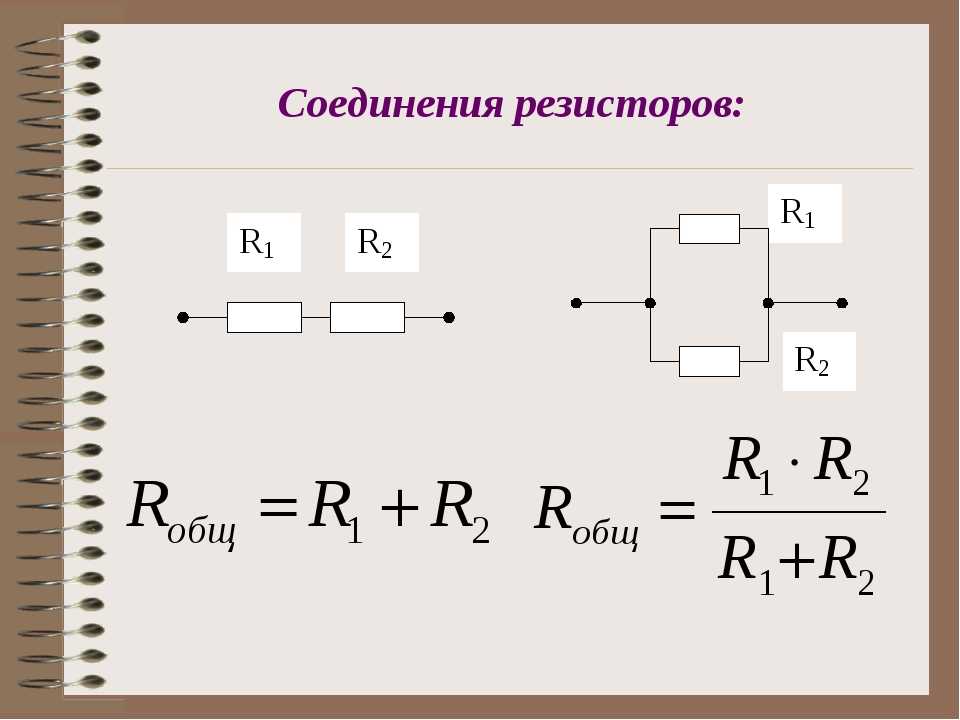 Но общее внутреннее сопротивление уменьшается, так как внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Но общее внутреннее сопротивление уменьшается, так как внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Два одинаковых ЭДС : Два источника напряжения с одинаковыми ЭДС (каждый из которых обозначен буквой E), соединенные параллельно, производят одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и напряжение на клеммах
Выходное напряжение или напряжение на клеммах источника напряжения, такого как батарея, зависит от его электродвижущей силы и внутреннего сопротивления.
Цели обучения
Выразите взаимосвязь между электродвижущей силой и напряжением на клеммах в виде уравнения
Основные выводы
Ключевые моменты
- Электродвижущая сила (ЭДС) представляет собой разность потенциалов источника при отсутствии тока.

- Напряжение на клеммах — это выходное напряжение устройства, измеряемое на его клеммах.
- Напряжение на клеммах рассчитывается как V = ЭДС — Ir.
Основные термины
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- напряжение на клеммах : Выходное напряжение устройства, измеренное на его клеммах.
- разность потенциалов : Разность потенциальной энергии между двумя точками в электрическом поле; разница заряда между двумя точками в электрической цепи; Напряжение.
Когда вы забываете выключить автомобильные фары, они медленно тускнеют по мере разрядки аккумулятора. Почему бы им просто не погаснуть, когда заряд батареи закончился? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере ее разрядки. Причина снижения выходного напряжения у разряженных или перегруженных аккумуляторов заключается в том, что все источники напряжения имеют две основные части — источник электрической энергии и внутреннее сопротивление.
Причина снижения выходного напряжения у разряженных или перегруженных аккумуляторов заключается в том, что все источники напряжения имеют две основные части — источник электрической энергии и внутреннее сопротивление.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если они подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС вовсе не сила; это особый тип разности потенциалов источника, когда ток не течет. Единицами ЭДС являются вольты.
Электродвижущая сила напрямую связана с источником разности потенциалов, например, с конкретной комбинацией химических веществ в батарее. Однако ЭДС отличается от выходного напряжения устройства при протекании тока. Напряжение на клеммах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно снижается по мере того, как батарея разряжается или нагружается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для очень разряженной батареи).
Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для очень разряженной батареи).
Напряжение на клеммах
представляет собой схематическое изображение источника напряжения. Выходное напряжение устройства измеряется на его клеммах и называется напряжением на клеммах В . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения : Любой источник напряжения (в данном случае углеродно-цинковый сухой элемент) имеет ЭДС, связанную с его источником разности потенциалов, и внутреннее сопротивление r связанных с его строительством. (Обратите внимание, что буква E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V. Поскольку V=ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
В=ЭДС-Ir\text{V} = \text{ЭДС} — \text{Ir}V=ЭДС-Ir
,
где r — внутреннее сопротивление, а I — ток, протекающий во время измерение.
I является положительным, если ток течет от положительной клеммы. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно и то, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
Лицензии и атрибуты
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- Предоставлено : Light and Matter. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- серия. Предоставлено : Викисловарь.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - сопротивление. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Series Circuits. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Предоставлено : Свет и Материя. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - параллельно. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/parallel. Лицензия : CC BY-SA: Attribution-ShareAlike
- сопротивление. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike 9Схемы серии 0015. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
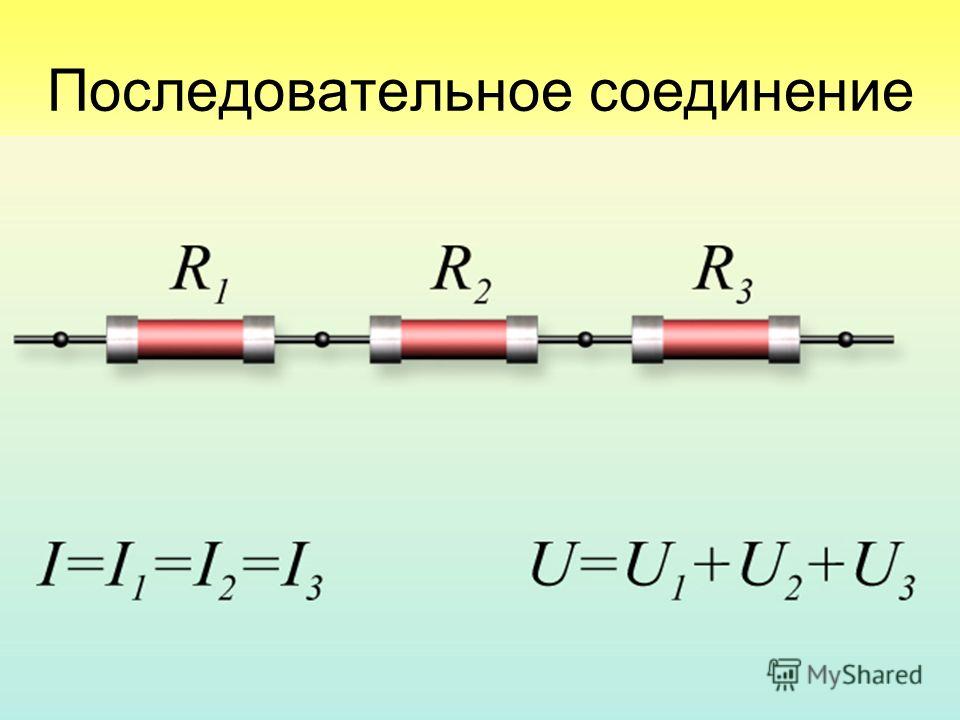 2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Параллельные цепи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStaxCNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Резисторы.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - комбинированная схема. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- параллельная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- серия. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Series Circuits. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
 2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Параллельные цепи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Комбинированные цепи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics.
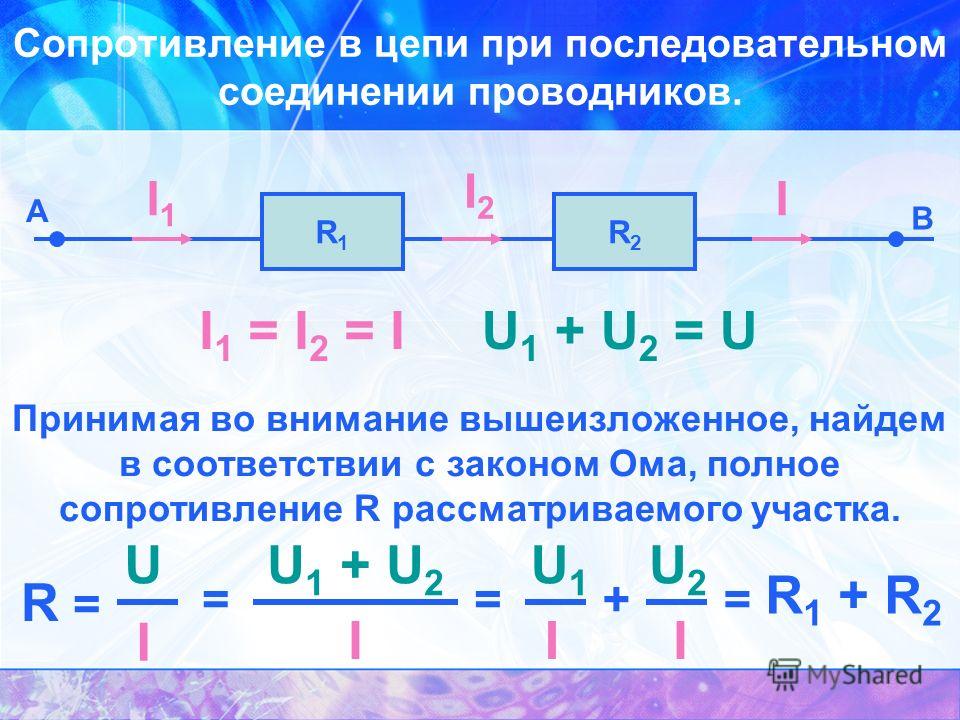 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Резисторы. Предоставлено : Википедия. Лицензия : Общественное достояние: Авторские права неизвестны
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- электродвижущая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- параллельный. Предоставлено : Викисловарь.
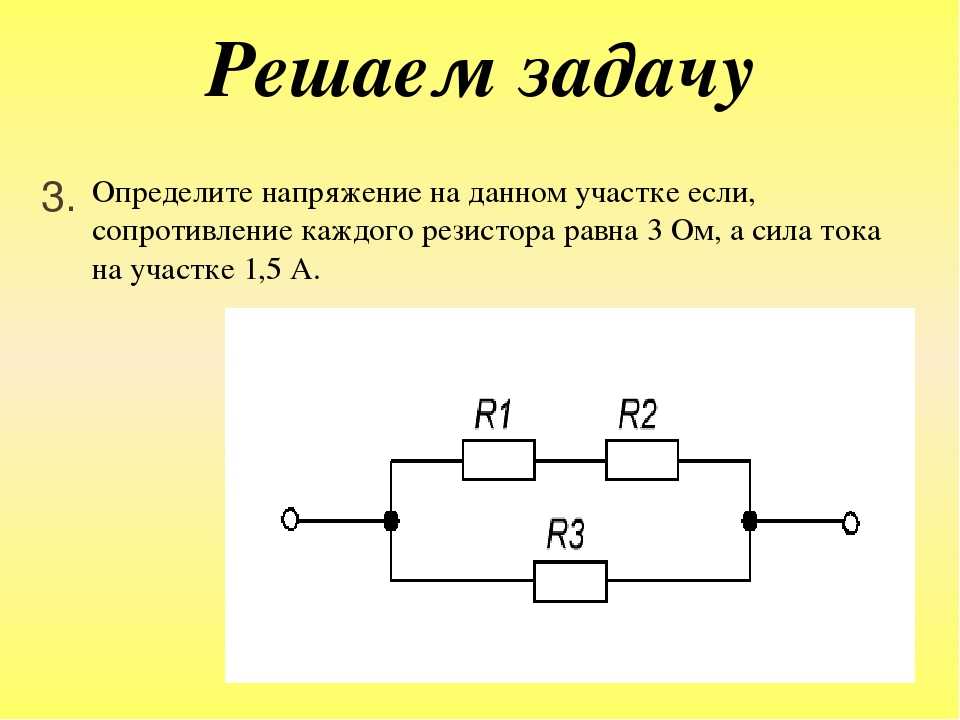 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - серия. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Series Circuits. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected].
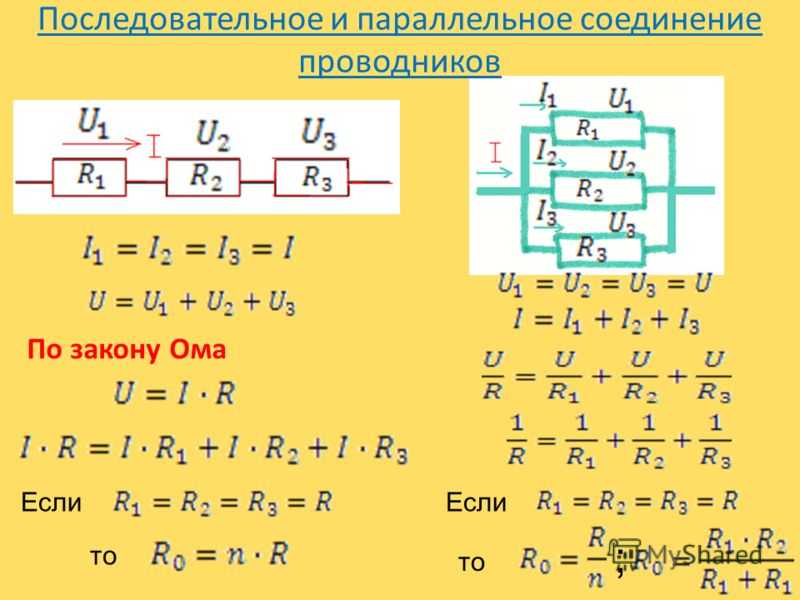 Лицензия : CC BY: Атрибуция
Лицензия : CC BY: Атрибуция - Параллельные цепи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Комбинированные цепи. Лицензия : Общественное достояние: неизвестно Авторское право . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Резисторы. Предоставлено : Википедия.
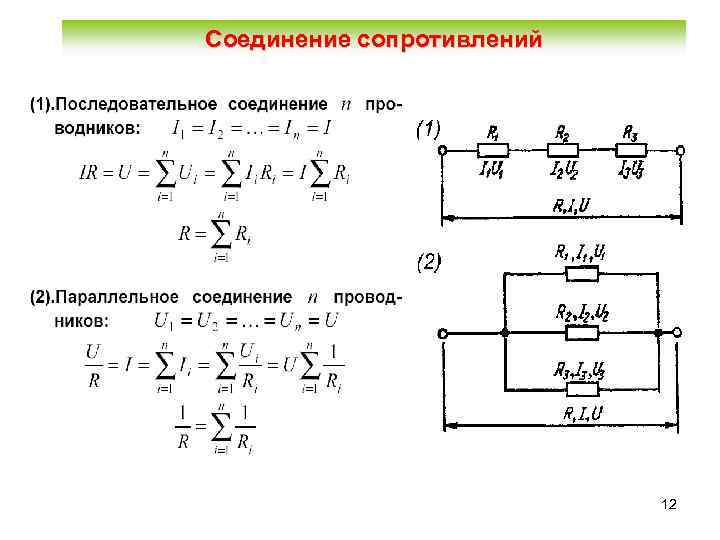 Лицензия : Общественное достояние: неизвестно Авторские права
Лицензия : Общественное достояние: неизвестно Авторские права - OpenStax College, College Physics. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Безгранично. Предоставлено : Безграничное обучение.
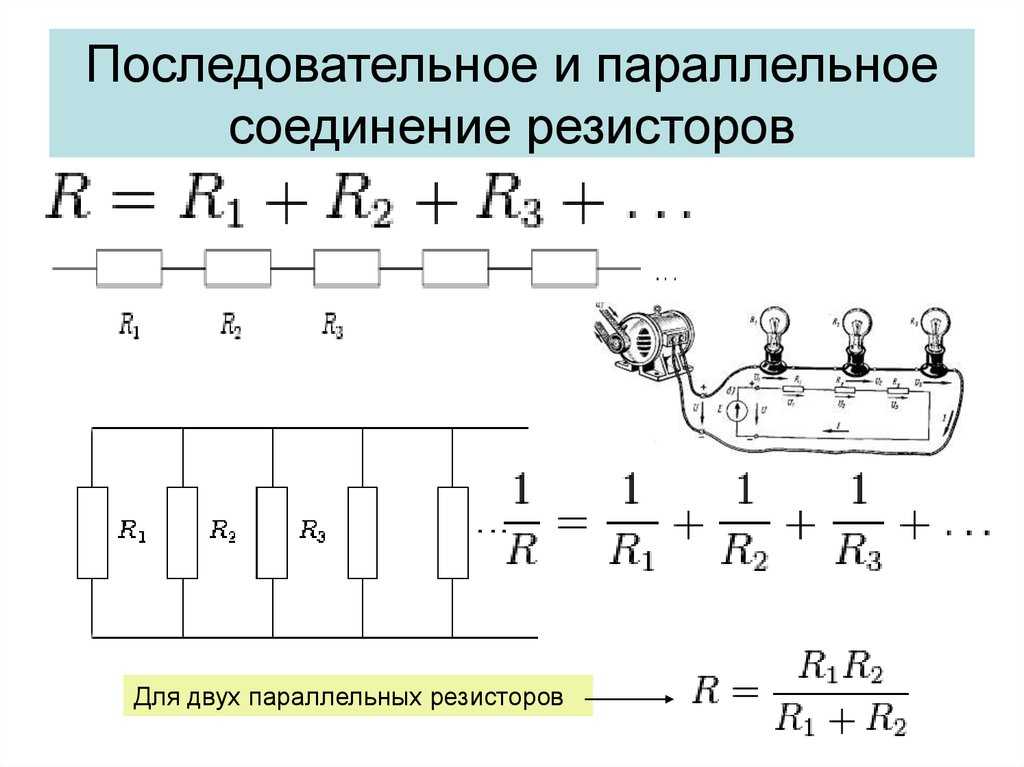 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - электродвижущая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- разность потенциалов. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Series Circuits. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Параллельные цепи. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Комбинированные цепи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 2 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.
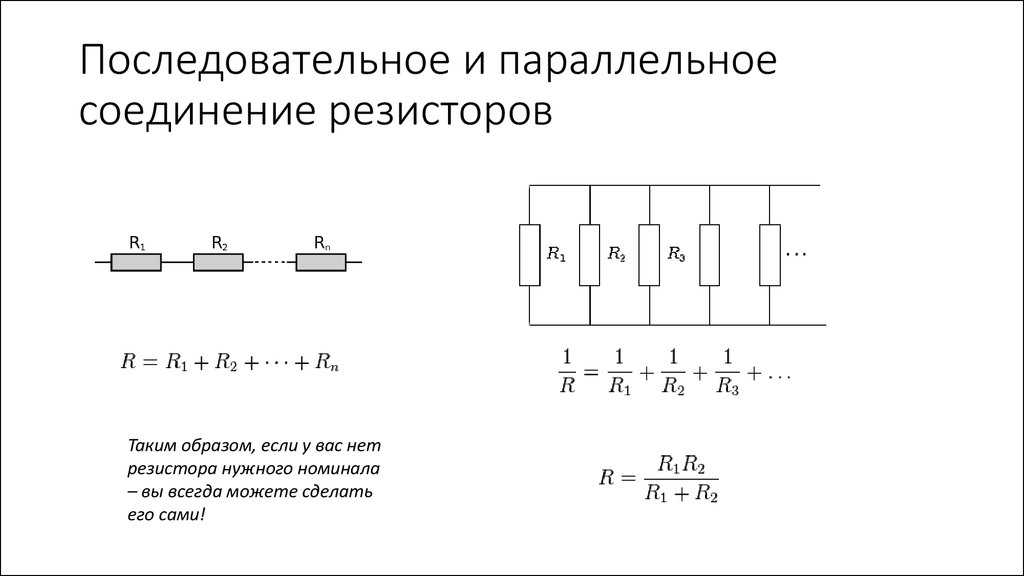 org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Лицензия : CC BY: Attribution - Резисторы. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- OpenStax College, College Physics. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 7 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 7 ноября 2012 г. Предоставлено : OpenStaxCNX.
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution
и параллельные резисторные схемы
Электронные компоненты соединяются разными способами. Две простейшие формы соединений — последовательное и параллельное. соединения.
Если компоненты соединены в цепи последовательно, то цепь называется последовательной. Если резисторы соединены последовательно в цепи, то цепь называется цепью последовательного резистора.
Если компоненты соединены в цепи параллельно, то цепь называется параллельной. Если резисторы соединены в цепи параллельно, то цепь называется параллельной цепью резисторов.
Серийный резистор цепь
А
Цепь последовательного резистора представляет собой электронную схему, в которой все
резисторы подключены один за другим по одному и тому же пути
чтобы через каждый и
каждый резистор.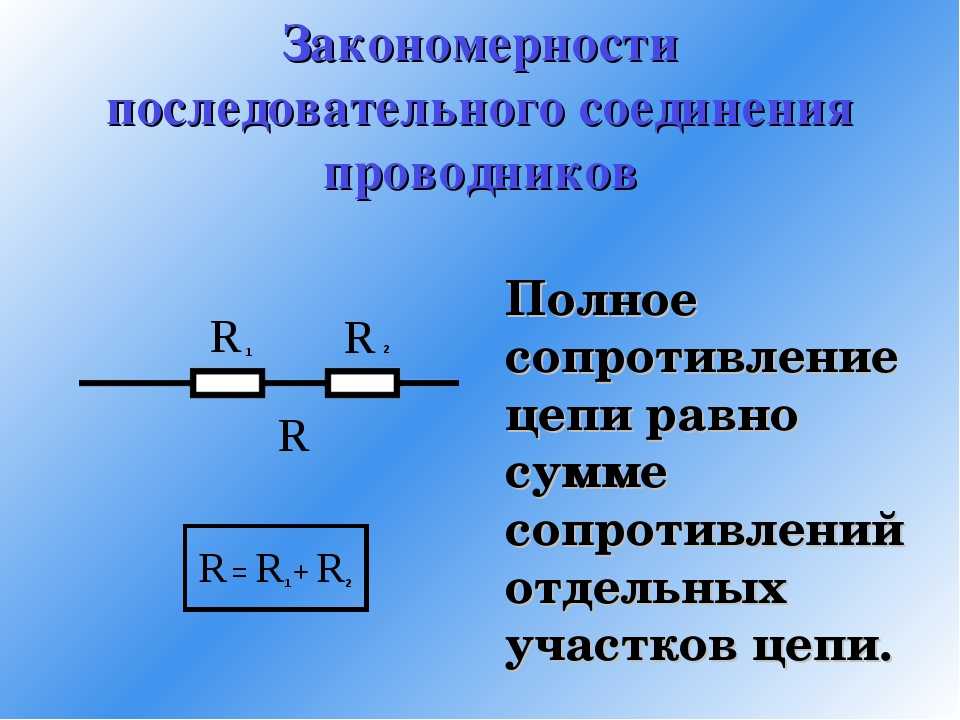
полное сопротивление такой цепи получается просто суммирование значений сопротивления отдельных резисторов.
Р Т = Р 1 + Р 2 + Р 3 + Р 4 ……..и т. д.
Для Например, если пять резисторов соединены последовательно. Затем полное сопротивление цепи равно:
Р Т = Р 1 + Р 2 + Р 3 + Р 4 + R 5
Все ток, протекающий через первый резистор, не имеет другого путь идти. Следовательно, он также должен пройти через второй резистор, третий резистор, четвертый резистор и так далее.
Пример:
А
Схема последовательного резистора показана на рисунке ниже. Этот
схема состоит из пяти резисторов, соединенных
последовательно и источник постоянного напряжения.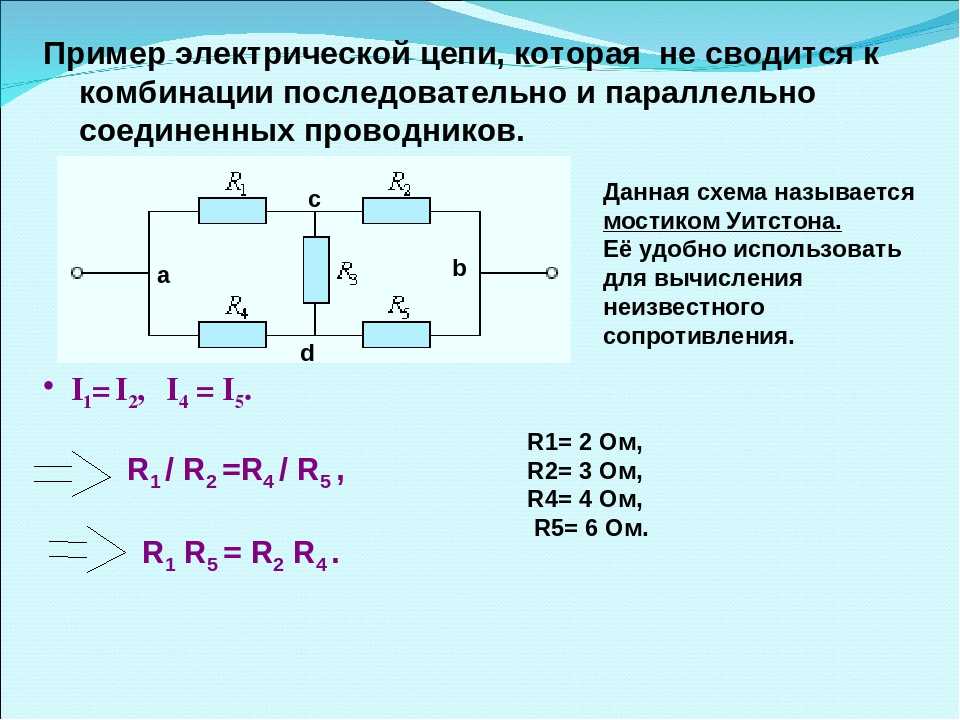
Если значения пяти резисторов: R 1 = 4 Ом, R 2 = 4 Ом, R 3 = 2 Ом, R 4 = 2 Ом, R 5 = 3 Ом и батарея постоянного тока = 15 В, тогда
Общее сопротивление р т = Р 1 + Р 2 + Р 3 + Р 4 + R 5 = 4 + 4 + 2 + 2 + 3 = 15 Ом.
Вспомните формулу закона Ома, V = I R
Зная любые две переменные в приведенное выше уравнение, мы можем легко найти оставшееся неизвестное переменная.
Нам известно общее значение сопротивления Т.е. R T = 15 Ом и значение напряжения I.e. V = 15 В
Теперь нужно найти оставшееся неизвестное значение тока I.
Текущий ток
через каждый резистор будет 1 А.
Напряжение на каждый резистор в последовательной цепи отличается. Если все резисторы в последовательной цепи имеют одинаковое значение сопротивления тогда напряжение через каждый резистор одинаковый. С другой стороны, если каждый резистор имеет другое значение сопротивления, то напряжение на каждом резисторе разный.
Напряжение на резистор (R 1 ) есть В 1 = I × R 1 = 1 × 4 = 4 В
Напряжение на резистор (R 2 ) равен В 2 = I × R 2 = 1 × 4 = 4 В
Напряжение на резистор (R 3 ) равен В 3 = I × R 3 = 1 × 2 = 2 В
Напряжение на резистор (R 4 ) составляет В 4 = I × R 4 = 1 × 2 = 2 В
Напряжение на резистор (R 5 ) равен В 5 = I × R 5 = 1 × 3 = 3 В
Общее напряжение в последовательная цепь равна сумме всех отдельных суммарные напряжения
Т. е. В Т = В 1
+ В 2 + В 3 + В 4 + ……….+В N
е. В Т = В 1
+ В 2 + В 3 + В 4 + ……….+В N
В нашей схеме общее напряжение равно сумме разностей потенциалов по Р 1, , Р 2 , Р 3 , R 4 и R 5 .
Т.е. В Т = В 1 + В 2 + В 3 + В 4 + В 5 = 4 + 4 + 2 + 2 + 3 = 15 В.
Параллельно цепь резистора
А
Цепь параллельных резисторов представляет собой электронную схему, в которой
все резисторы соединены рядом в разные
пути, чтобы один и тот же ток не протекал через каждый
резистор. Параллельная схема показывает несколько путей к
протекать электрический ток.
ток в параллельной цепи распадается, при этом некоторый ток
протекающие по каждой параллельной ветви и воссоединяющиеся, когда
ветви встречаются снова.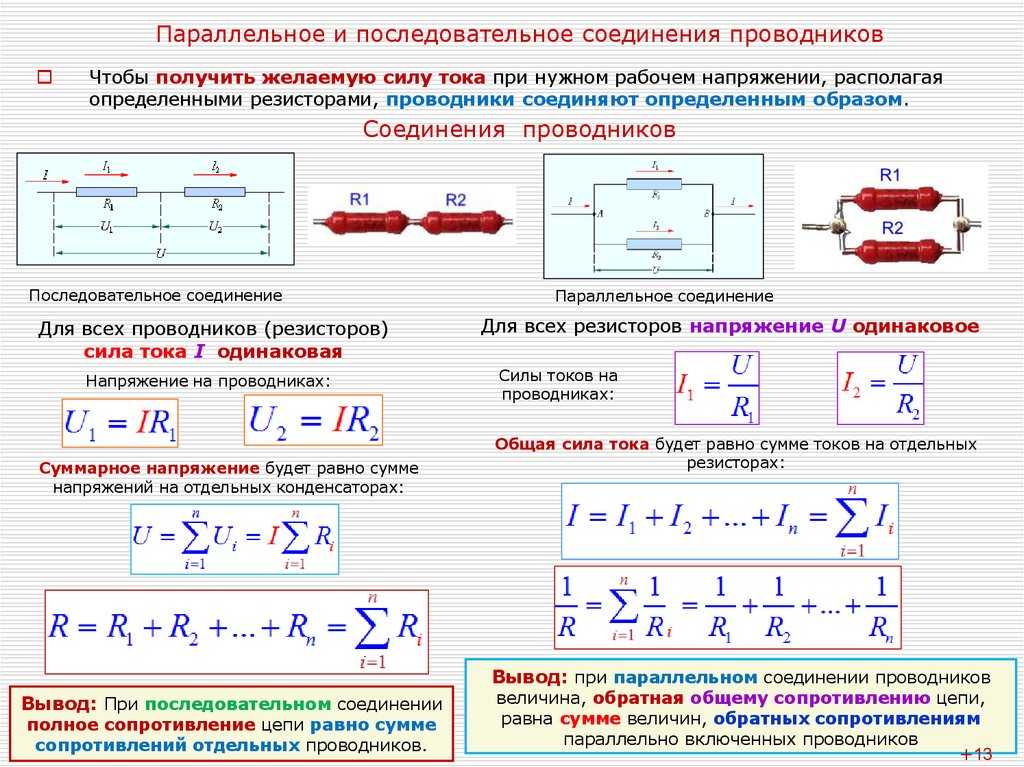 Следовательно, электрический ток через
каждый резистор будет другим. Однако напряжение на
каждый резистор одинаковый.
Следовательно, электрический ток через
каждый резистор будет другим. Однако напряжение на
каждый резистор одинаковый.
полное сопротивление параллельной цепи резистора получается по формуле суммируя обратные величины (1/R) значений сопротивления отдельные резисторы, а затем взяв обратную величину общий.
Для Например, если три резистора соединены параллельно. затем общее сопротивление цепи
Пример:
А
Схема параллельного резистора показана на рисунке ниже. Этот
схема состоит из трех резисторов, соединенных
параллельно и источник постоянного напряжения.
Если значения трех резисторов: R 1 = 8 Ом, R 2 = 8 Ом, R 3 = 4 Ом и батарея постоянного тока = 14 В, затем
общее сопротивление
Суммарный ток течет по цепи
Как
напряжение на каждом резисторе параллельно
схема, мы можем использовать омы
закон
найти ток отдельной ветви следующим образом.
ток через резистор (R 1 ) is I 1 = V / R 1 = 14 / 8 = 1,75 А
ток через резистор (R 2 ) это я 2 = В / Р 2 = 14 / 8 = 1,75 А
ток через резистор (R 3 ) is I 3 = В / Р 3 = 14 / 4 = 3.5 А
Тогда сумма
ток равен сумме токов отдельных ветвей
т.е. Я Т = Я 1 + I 2 + I 3 = 1,75 + 1,75 + 3,5 = 7 А
21.1 Резисторы, включенные последовательно и параллельно — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте цепь с параллельными и последовательными резисторами.

- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
Большинство цепей имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением. Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рис. 21.2. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Рисунок 21,2 а) последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Резисторы серии
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно.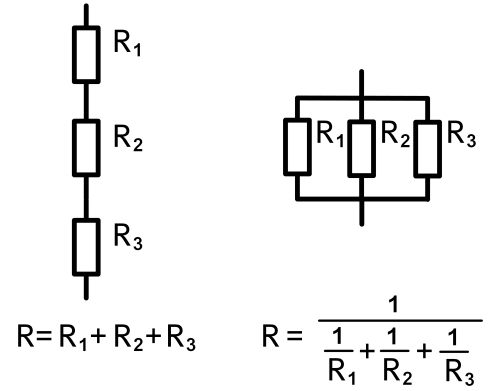 Например, если ток течет через человека, держащего отвертку, в землю, то R1R1 на рис. 21.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, а R4R4 — сопротивлением стержня отвертки. сопротивление ее обуви.
Например, если ток течет через человека, держащего отвертку, в землю, то R1R1 на рис. 21.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, а R4R4 — сопротивлением стержня отвертки. сопротивление ее обуви.
На рис. 21.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.)
Рисунок
21,3
Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения, в каждом резисторе на рис. 21.3.
В соответствии с законом Ома падение напряжения VV на резисторе при протекании через него тока рассчитывается по уравнению V=IRV=IR, где II равен току в амперах (А), а RR — сопротивление в омах. Ом. Другой способ представить это так: VV — это напряжение, необходимое для протекания тока II через сопротивление RR.
Таким образом, падение напряжения на R1R1 равно V1=IR1V1=IR1, на R2R2 V2=IR2V2=IR2, а на R3R3 V3=IR3V3=IR3. Сумма этих напряжений равна выходному напряжению источника; то есть
В=В1+В2+В3.В=В1+В2+В3.
21.1
Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением PE=qVPE=qV, где qq — электрический заряд, а VV — напряжение. Таким образом, энергия, подаваемая источником, равна qVqV, а энергия, рассеиваемая резисторами, равна
Таким образом, энергия, подаваемая источником, равна qVqV, а энергия, рассеиваемая резисторами, равна
qV1+qV2+qV3.qV1+qV2+qV3.
21,2
Связи: законы сохранения
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равными, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, qV=qV1+qV2+qV3qV=qV1+qV2+qV3. Заряд qq компенсируется, что дает V=V1+V2+V3V=V1+V2+V3, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется. )
)
Теперь подстановка значений отдельных напряжений дает
V=IR1+IR2+IR3=I(R1+R2+R3).V=IR1+IR2+IR3=I(R1+R2+R3).
21,3
Обратите внимание, что для эквивалентного последовательного сопротивления RsRs мы имеем
V=IRs.V=IRs.
21,4
Это означает, что общее или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs=R1+R2+R3Rs=R1+R2+R3.
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, общее сопротивление RsRs последовательного соединения равно
Rs=R1+R2+R3+…,Rs=R1+R2+R3+…,
21,5
как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 21.1
Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис.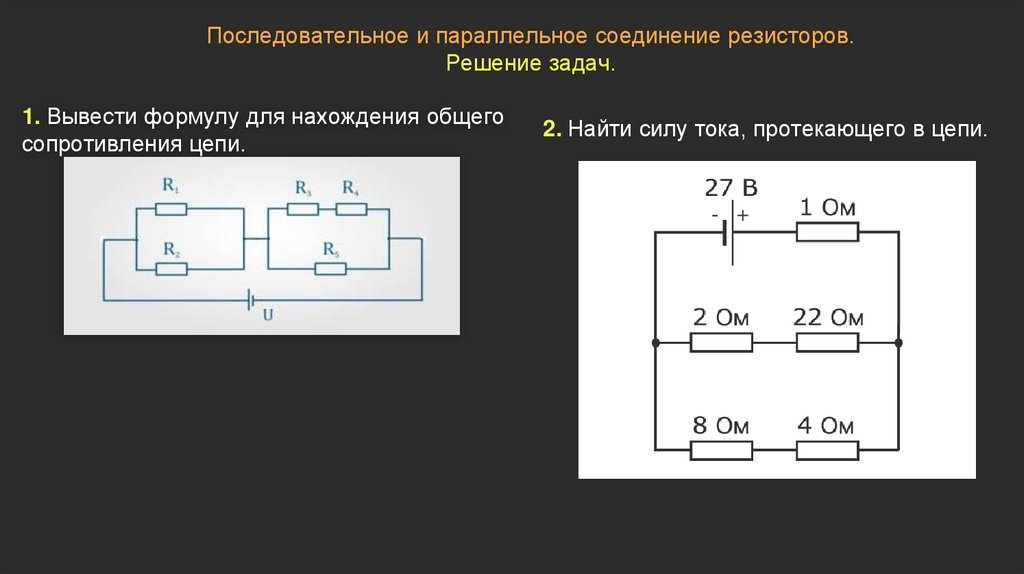 =6,00 Ом, R2=6,00 Ом и R3=13,0 Ом, R3=13,0 Ом. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
=6,00 Ом, R2=6,00 Ом и R3=13,0 Ом, R3=13,0 Ом. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:
Rs=R1+R2+R3=1,00 Ом+6,00 Ом+13,0 Ом=20,0 Ом .Rs=R1+R2+R3=1,00 Ом+6,00 Ом+13,0 Ом=20,0 Ом.
21,6
Стратегия и решение для (b)
Ток определяется по закону Ома, V=IRV=IR. Ввод значения приложенного напряжения и полного сопротивления дает ток для цепи:
I=VRs=12,0 В20,0 Ом=0,600 A.I=VRs=12,0 В20,0 Ом=0,600 А.
21,7
Стратегия и решение для (c)
Падение напряжения или IRIR падения на резисторе определяется законом Ома.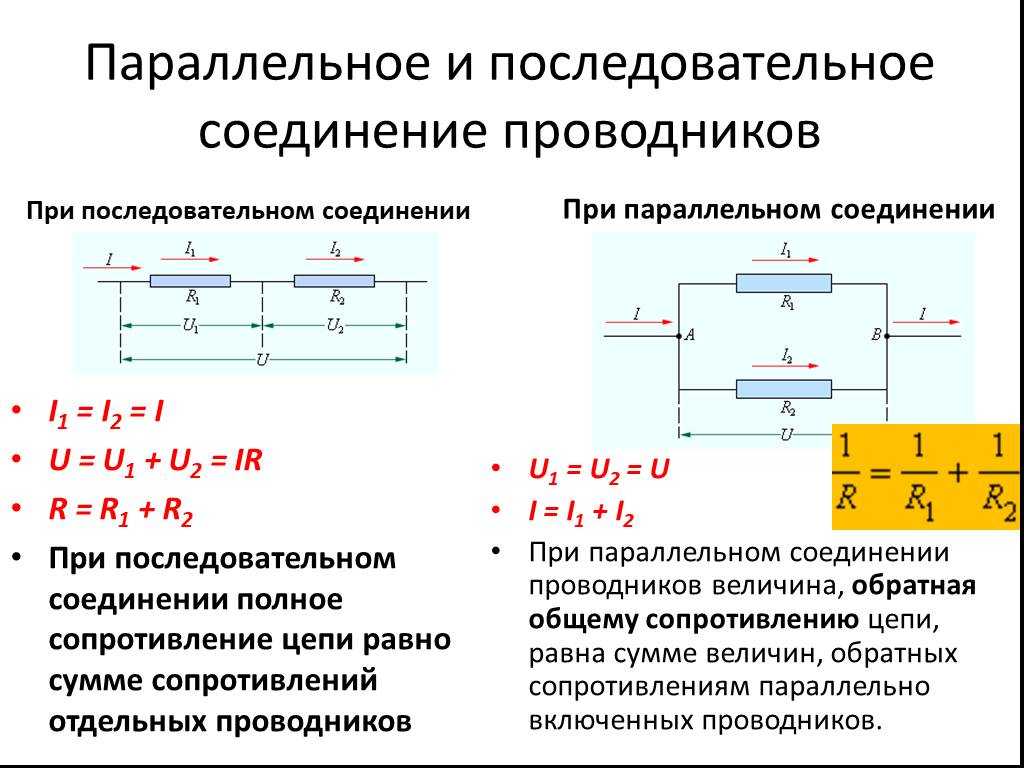 Ввод тока и значения первого сопротивления дает
Ввод тока и значения первого сопротивления дает
V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.
21,8
Аналогично,
V2=IR2=(0,600 А)(6,0 Ом)=3,60 VV2=IR2=(0,600 А)(6,0 Ом)=3,60 В
21,9
и
V3=IR3=(0,600 А)( 13,0 Ом)=7,80 В. V3=IR3=(0,600 А)(13,0 Ом)=7,80 В.
21.10
Обсуждение для (c)
Три капли IRIR добавляют к 12,0 В12,0 В, как и прогнозировалось:
V1+V2+V3=(0,600+3,60+7,80)V=12,0 В.V1+V2+ V3=(0,600+3,60+7,80)V=12,0 В.
21,11
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, состоит в использовании Закон Джоуля, P=IVP=IV, где PP – электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.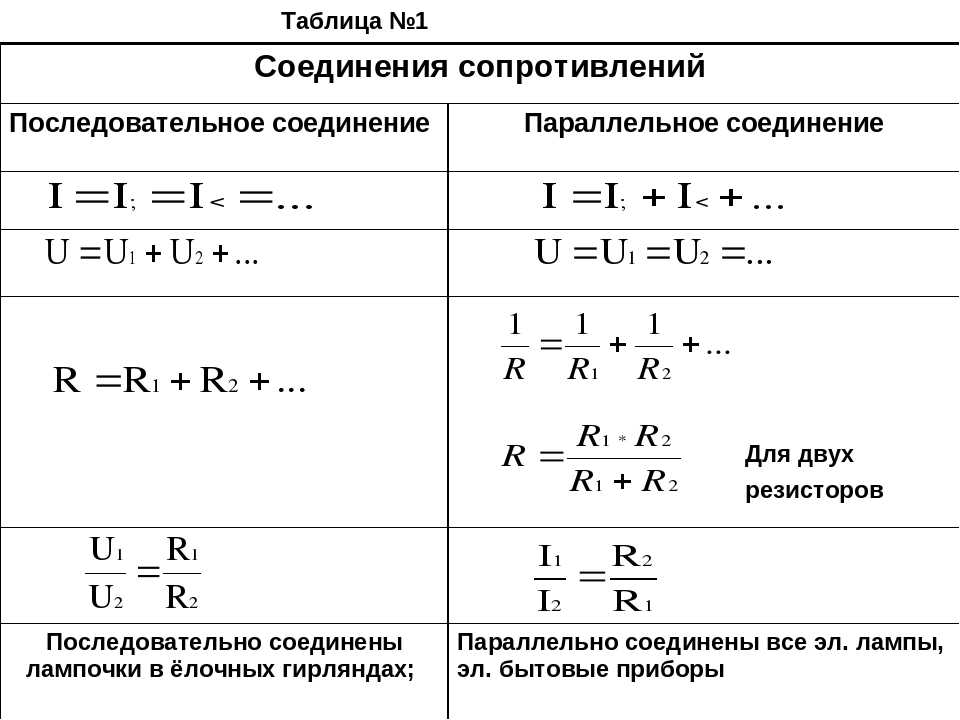 Подставив закон Ома V=IRV=IR в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как
Подставив закон Ома V=IRV=IR в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как
P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт.P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт. 0,600 А)2(6,00 Ом)=2,16 WP2=I2R2=(0,600 А)2(6,00 Ом)=2,16 Вт
21,13
и
P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт .P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.
21,14
Обсуждение для (d)
Мощность также можно рассчитать, используя либо P=IVP=IV, либо P=V2RP=V2R, где VV — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P=IVP=IV, где VV — напряжение источника. Это дает
P=(0,600 А)(12,0 В)=7,20 Вт.P=(0,600 А)(12,0 В)=7,20 Вт. рассеиваемая резисторами также составляет 7,20 Вт, столько же, сколько мощность, выдаваемая источником.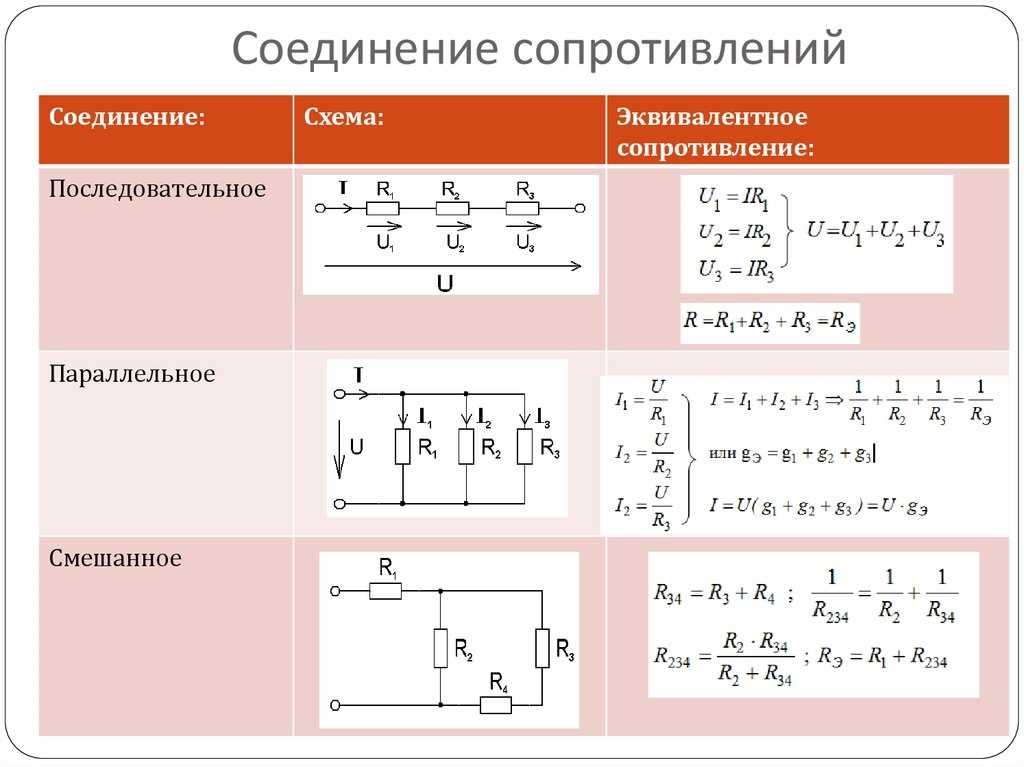 То есть
То есть
P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт.P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт.
21.16
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии необходимо, чтобы выходная мощность источника равнялась общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов в серии
- Дополнительные резисторы: Rs=R1+R2+R3+….Rs=R1+R2+R3+….
- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
Резисторы параллельно
На рис. 21.4 показаны резисторы, подключенные параллельно к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление.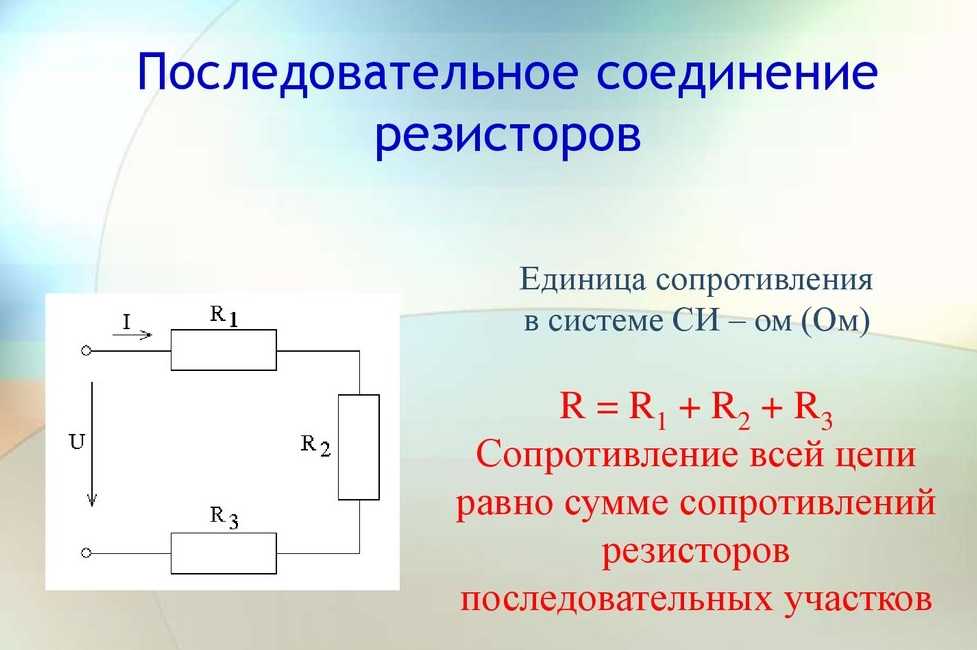 Таким образом, к каждому резистору приложено полное напряжение источника.
Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 21.4(б).)
Рисунок 21,4 (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одинарное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления RpRp, давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны I1=VR1I1=VR1, I2=VR2I2=VR2 и I3=VR3I3=VR3. Сохранение заряда подразумевает, что полный ток II, производимый источником, представляет собой сумму этих токов:
Сохранение заряда подразумевает, что полный ток II, производимый источником, представляет собой сумму этих токов:
I=I1+I2+I3.I=I1+I2+I3.
21,17
Подстановка выражений для отдельных токов дает
I=VR1+VR2+VR3=V1R1+1R2+1R3.I=VR1+VR2+VR3=V1R1+1R2+1R3.
21,18
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
I=VRp=V1Rp.I=VRp=V1Rp.
21.19
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление RpRp параллельного соединения связано с отдельными сопротивлениями как 9.0005
1Rp=1R1+1R2+1R.3+….1Rp=1R1+1R2+1R.3+….
21,20
Это соотношение приводит к тому, что общее сопротивление RpRp меньше наименьшего из индивидуальные сопротивления. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример 21,2
Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис. 21.4 такие же, как и при последовательном соединении, рассмотренном ранее: V=12,0 VV=12,0 В, R1=1,00 Ом R1=1,00 Ом, R2=6,00 Ом R2=6,00 Ом, а R3=13,0 Ом R3=13,0 Ом. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает
1Rp=1R1+1R2+1R3=11,00 Ом+16,00 Ом+113,0 Ом. 1Rp=1R1+1R2+1R3=11,00 Ом+16,00 Ом+113,0 Ом.
1Rp=1R1+1R2+1R3=11,00 Ом+16,00 Ом+113,0 Ом.
21,21
Таким образом,
1Rp=1,00 Ом+0,1667 Ом+0,07692 Ом=1,2436 Ом.1Rp=1,00 Ом+0,1667 Ом+0,07692 Ом=1,2436 Ом.
21,22
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти общее сопротивление RpRp. Это дает
Rp=11,2436 Ом=0,8041 Ом. Rp=11,2436 Ом=0,8041 Ом.
21,23
Общее сопротивление с правильным количеством значащих цифр равно Rp=0,804 Ом. Rp=0,804 Ом.
Обсуждение для (a)
RpRp, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив RpRp вместо полного сопротивления. Это дает
I=VRp=12,0 В0,8041 Ом=14,92 A.I=VRp=12,0 В0,8041 Ом=14,92 А.
21,24
Обсуждение для (b) устройства, соединенные последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
I1=VR1=12,0 В1,00 Ом=12,0 A.I1=VR1=12,0 В1,00 Ом=12,0 А. VR2=12,0 В6,00 Ом=2,00 А
21,26
и
I3=VR3=12,0 В13,0 Ом=0,92 А.I3=VR3=12,0 В13,0 Ом=0,92 А. для (c)
Общий ток представляет собой сумму отдельных токов:
I1+I2+I3=14,92 А. I1+I2+I3=14,92 А.
21,28
Это соответствует закону сохранения заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Будем использовать P=V2RP=V2R, так как на каждый резистор подается полное напряжение. Таким образом,
Будем использовать P=V2RP=V2R, так как на каждый резистор подается полное напряжение. Таким образом,
P1=V2R1=(12,0 В)21,00 Ом=144 Вт.P1=V2R1=(12,0 В)21,00 Ом=144 Вт.
21,29
Ом=24,0 WP2=V2R2=(12,0 В)26,00 Ом=24,0 Вт
21,30
и
P3=V2R3=(12,0 В)213,0 Ом=11,1 Вт.P3=V2R3=(12,0 В)213,0 Ом=11,1 Вт. при параллельном подключении выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор P=IVP=IV и ввод общего тока дает
P=IV=(14,92 А)(12,0 В)=179 W.P=IV=(14,92 А)(12,0 В)=179Вт.
21,32
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
P1+P2+P3=144 Вт+24,0 Вт+11,1 Вт=179 Вт. P1+P2+P3=144 Вт +24,0Вт+11,1Вт=179Вт.
P1+P2+P3=144 Вт +24,0Вт+11,1Вт=179Вт.
21.33
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
Основные характеристики резисторов, включенных параллельно
- Параллельное сопротивление получается из 1Rp=1R1+1R2+1R3+…1Rp=1R1+1R2+1R3+…, и оно меньше любого отдельного сопротивления в комбинации.
- К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они его делят.
Комбинации серий и параллелей
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединений можно привести к одному эквивалентному сопротивлению с помощью метода, показанного на рис. 21.5. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 21,5 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 21.6, является также наиболее поучительной, поскольку она встречается во многих приложениях. Например, R1R1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, включенным параллельно. R2R2 и R3R3 могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Например, R1R1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, включенным параллельно. R2R2 и R3R3 могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 21,3
Расчет сопротивления, падения IRIR, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рис. 21.6 показаны резисторы из двух предыдущих примеров, соединенные другим способом — комбинация последовательного и параллельного соединения. Мы можем рассматривать R1R1 как сопротивление проводов, ведущих к R2R2 и R3R3. а) Найдите полное сопротивление. (b) Каково падение IRIR в R1R1? (c) Найдите ток I2I2 через R2R2. г) Какую мощность рассеивает R2R2?
Рисунок
21,6
Эти три резистора подключены к источнику напряжения так, что R2R2 и R3R3 параллельны друг другу, а эта комбинация последовательно с R1R1.
Стратегия и решение для (a)
Чтобы найти общее сопротивление, заметим, что R2R2 и R3R3 соединены параллельно, а их комбинация RpRp последовательно с R1R1. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
Rtot=R1+Rp.Rtot=R1+Rp.
21,34
Сначала находим RpRp, используя уравнение для параллельных резисторов и вводя известные значения:
1Rp=1R2+1R3=16,00 Ом+113,0 Ом=0,2436 Ом.1Rp=1R2+1R3=16,00 Ом+113,0 Ом=0,2436 Ом.
21,35
Инвертирование дает
Rp=10,2436 Ом=4,11 Ом. Rp=10,2436 Ом=4,11 Ом.
21,36
Таким образом, общее сопротивление равно
Rtot=R1+Rp=1,00Ω+4,11 Ω=5,11 Ω.Rtot=R1+Rp=1,00Ω+4,11 Ω=5,11 Ω.
21,37
Обсуждение для (a)
Суммарное сопротивление этой комбинации является промежуточным между чисто последовательным и чисто параллельным значениями (20,0 Ом, 20,0 Ом и 0,804 Ом, 0,804 Ом соответственно), найденными для тех же резисторов в два предыдущих примера.
Стратегия и решение для (b)
Чтобы найти падение IRIR в R1R1, заметим, что полный ток II протекает через R1R1. Таким образом, его падение IRIR равно
V1=IR1.V1=IR1.
21,38
Мы должны найти II, прежде чем мы сможем вычислить V1V1. Полный ток II находится по закону Ома для цепи. То есть
I=VRtot=12,0 В5,11 Ом=2,35A.I=VRtot=12,0 В5,11 Ом=2,35A.
21,39
Подставив это в выражение выше, получим
V1=IR1=(2,35 А)(1,00 Ом)=2,35 В. V1=IR1=(2,35 А)(1,00 Ом)=2,35 В.
21.40
Обсуждение для (b)
Напряжение, подаваемое на R2R2 и R3R3, меньше общего напряжения на величину V1V1. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R2R2 и R3R3.
Стратегия и решение для (c)
Чтобы найти ток через R2R2, мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение VpVp, потому что оно подается на параллельную комбинацию резисторов. Напряжение, подаваемое как на R2R2, так и на R3R3, уменьшается на величину V1V1, поэтому оно равно
Мы называем это напряжение VpVp, потому что оно подается на параллельную комбинацию резисторов. Напряжение, подаваемое как на R2R2, так и на R3R3, уменьшается на величину V1V1, поэтому оно равно
Vp=V−V1=12,0 В−2,35 В=9,65 В.Vp=V−V1=12,0 В−2,35 В=9,65 В.
21,41
Теперь ток I2I2 через сопротивление R2R2 находится по закону Ома:
I2=VpR2=9,65 V6,00 Ом=1,61 A.I2=VpR2=9,65 V6,00 Ом=1,61 А.
21,42
Обсуждение для (c)
через R2R2, когда он был подключен параллельно к батарее в предыдущем примере с параллельной схемой.
Стратегия и решение для (d)
Мощность, рассеиваемая резистором R2R2, определяется как
P2=(I2)2R2=(1,61 А)2(6,00 Ом)=15,5 Вт.P2=(I2)2R2=(1,61 А)2(6,00 Ом)=15,5 Вт.
21,43
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемая этим резистором при параллельном подключении к источнику 12,0 В.
Практические выводы
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IRIR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рис. 21.7. Устройство, представленное R3R3, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IRIR в проводах, представленных R1R1, уменьшая напряжение на лампочке (которая является R2R2), которая затем заметно тускнеет.
Рисунок 21,7 Почему гаснет свет при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IRIR в проводах и снижает напряжение на светильнике.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.
Решение
Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного соединения, включая петли и соединения. В таких случаях правила Кирхгофа, которые будут представлены в Правилах Кирхгофа, позволят вам проанализировать схему.
Стратегии решения проблем для последовательных и параллельных резисторов
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения.
 Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме. - Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах. Особое примечание: при нахождении
RpRp, к взаимному нужно относиться с осторожностью.

- Проверьте, разумны ли и последовательны ли ответы. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
Резисторы, соединенные последовательно: цепь, уравнение, напряжение, примеры
В электрической цепи инженеры соединяют компоненты внутри последовательно или параллельно, чтобы создать ряд полезных цепей. При этом мы можем рассчитать напряжение, ток и сопротивление в цепях. Говорят, что эти резисторы соединены «голова к хвосту» при последовательном соединении, а эквивалентное общее сопротивление представляет собой сумму значений отдельных сопротивлений. В этой статье вы узнаете о схеме, уравнении, напряжении, приложениях и некоторых примерах резисторов, соединенных последовательно.
Читать Подробнее: различные типы резисторов
Содержание
- 1 Резисторы в серии
-
- 1,0,1 Диаграмма серийных резисторов:
-
- 2 Applications of Series .
- 4 Уравнение последовательного уравнения
- 5 Напряжение последовательных резисторов
- 5.1 Подпишитесь на нашу рассылку новостей
- 5.1.1 Посмотрите видео ниже, чтобы узнать больше о последовательном соединении резисторов:
- 5.1 Подпишитесь на нашу рассылку новостей
- 6 Заключение
- 6.1 Пожалуйста, поделитесь!

Резисторы, соединенные последовательно
Резисторы называются последовательными, если они расположены в одну линию. В результате через них проходит общий ток. Здесь отдельные резисторы могут быть соединены вместе либо последовательно. Параллельное соединение или комбинации последовательного и параллельного соединения могут быть использованы для создания более сложной цепи резисторов. В связи эквивалентное сопротивление представляет собой математическую комбинацию отдельных резисторов, соединенных вместе.
Обратите внимание, что резистор — это не только основной электронный компонент, используемый для преобразования напряжения в ток или тока в напряжение. Однако, правильно отрегулировав его значение, преобразованному току и/или напряжению можно присвоить другой вес. Вот почему его можно использовать в схемах опорного напряжения и приложениях. Резисторы в последовательном соединении или сложные резисторные цепи могут быть заменены одним эквивалентным резистором R EQ или импедансом Z EQ . Вы должны знать, что независимо от комбинации или сложности цепи резисторов, все резисторы подчиняются одним и тем же основным правилам, как указано в законе Ома и законах цепей Кирхгофа.
Однако, правильно отрегулировав его значение, преобразованному току и/или напряжению можно присвоить другой вес. Вот почему его можно использовать в схемах опорного напряжения и приложениях. Резисторы в последовательном соединении или сложные резисторные цепи могут быть заменены одним эквивалентным резистором R EQ или импедансом Z EQ . Вы должны знать, что независимо от комбинации или сложности цепи резисторов, все резисторы подчиняются одним и тем же основным правилам, как указано в законе Ома и законах цепей Кирхгофа.
Кроме того, при токе, проходящем через цепь, ток, протекающий через резисторы, является общим. Это связано с тем, что ток, протекающий через один резистор, должен также протекать через другие, поскольку он протекает только по одному пути. Тогда мы можем сказать, что величина тока, протекающего через набор последовательно соединенных резисторов, одинакова во всех точках последовательно соединенной резисторной сети.
Подробнее: Понимание резисторов
Например, резисторы R 1 , R 2, и R 3 соединены последовательно между точками А и В с общим током I, протекающим через них.
Схема последовательных резисторов:
Применение последовательных резисторов
Применение последовательных резисторов на печатной плате очень обширно, поскольку они могут использоваться для создания различных напряжений на самих себе. Эти типы резисторных цепей также полезны для создания цепей делителей напряжения. Если один из резисторов в цепи делителя напряжения заменить датчиком, например термистором, светозависимым резистором (LDR) или переключателем, преобразование измеряемой аналоговой величины в подходящий электрический сигнал, который может быть измерено.
Цепь последовательного резистора
Как упоминалось ранее, поскольку резисторы соединены последовательно, через каждый резистор в цепи проходит один и тот же ток. Общее сопротивление R T цепи должно быть равно сумме всех различных сопротивлений, сложенных вместе. Взяв отдельные номиналы резисторов, общее эквивалентное сопротивление R EQ можно определить как:
R EQ = R 1 + R 2 + R 3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Подробнее: Значение резистора с проволочной обмоткой
Теперь вы видите, как три отдельных резистора можно заменить одним эквивалентным резистором номиналом 9 кОм.
В случае, когда четыре, пять или более резисторов соединены вместе в последовательной цепи, общее или эквивалентное сопротивление цепи RT по-прежнему будет суммой всех отдельных резисторов, соединенных вместе, и чем больше резистор добавлен к серии, тем больше эквивалентное сопротивление. Эквивалентное сопротивление обычно известно как полное сопротивление, и его можно определить как «одно значение сопротивления, которое может заменить любое количество последовательно соединенных резисторов без изменения значений тока или напряжения в цепи.
Уравнение последовательного уравнения
Приводится уравнение для расчета полного сопротивления цепи при последовательном соединении резисторов:
R всего = R 1 + R 2 + R 6 90 065 3 90 065 3 90 065 R n и т. д.
Следует знать, что полное или эквивалентное сопротивление R T оказывает такое же влияние на цепь, как и исходная комбинация резисторов. Это потому, что это алгебраическая сумма отдельных сопротивлений. Если два последовательных сопротивления или импеданса равны и имеют одинаковое значение, то общее или эквивалентное сопротивление равно удвоенному значению одного резистора. Другими словами, оно равно 2R, а для трех одинаковых резисторов, включенных последовательно, 3R и т. д.
Это потому, что это алгебраическая сумма отдельных сопротивлений. Если два последовательных сопротивления или импеданса равны и имеют одинаковое значение, то общее или эквивалентное сопротивление равно удвоенному значению одного резистора. Другими словами, оно равно 2R, а для трех одинаковых резисторов, включенных последовательно, 3R и т. д.
Подробнее: Понятие светозависимого резистора LDR
Кроме того, если два последовательно соединенных резистора или импеданса неодинаковы и имеют разные значения, то общее или эквивалентное сопротивление R T равно математической сумме двух сопротивлений. . Это равно R 1 + R 2 . Если последовательно соединены три и более неодинаковых (или одинаковых) резистора, то эквивалентное сопротивление равно R1 + R2 + R3 +… и т. д.
Напряжение последовательных резисторов
В последовательно соединенных резисторах напряжение на каждом из них подчиняется правилам, отличным от правил последовательного тока. Мы понимаем, что общее напряжение питания на резисторах равно сумме разностей потенциалов на R 1 , R 2 , и R 3 .
Мы понимаем, что общее напряжение питания на резисторах равно сумме разностей потенциалов на R 1 , R 2 , и R 3 .
В AB = В R1 + В R2 + В R3 = 9В.
Подпишитесь на нашу рассылку новостей
Используя закон Ома, напряжение на отдельных резисторах можно рассчитать как:
напряжение через r 1 = IR 1 = 1MA x 1Kω = 1 В
напряжение через R 2 = IR 2 = 1MA X 2Kω = 2V
Voltage через R 3 = IR 3 В 2020.
Учитывая общее напряжение В AB (1 В + 2 В + 6 В) = 9 В, что равно значению напряжения питания. при этом сумма разностей потенциалов на резисторах равна полной разности потенциалов на комбинации и 9V. Уравнение для расчета полного напряжения в последовательной цепи, которое представляет собой сумму всех отдельных напряжений, сложенных вместе, имеет следующий вид: + …+ V N
Подробнее: Понимание термистора
При этом цепи последовательных резисторов также можно рассматривать как «делители напряжения», а цепь последовательных резисторов имеет N резистивных компонентов будет иметь N-разное напряжение через него и все еще поддерживать общий ток. Используя закон Ома, можно легко найти ток или сопротивление любой последовательно соединенной цепи. Кроме того, резистор последовательной цепи можно поменять местами, не влияя на общее сопротивление, ток или мощность каждого резистора.
Используя закон Ома, можно легко найти ток или сопротивление любой последовательно соединенной цепи. Кроме того, резистор последовательной цепи можно поменять местами, не влияя на общее сопротивление, ток или мощность каждого резистора.
Посмотрите видео ниже, чтобы узнать больше о резисторах, соединенных последовательно:
Подробнее: Понимание резисторов из углеродного состава
Заключение
Резисторы называются последовательными, если они расположены в одну линию. В результате через них проходит общий ток. Отдельные резисторы могут быть соединены вместе в любом последовательном соединении. Это все для этой статьи, где схема, уравнение, напряжение, приложения и некоторые примеры резисторов приведены последовательно.
Я надеюсь, что вы получили много полезного от чтения, если да, пожалуйста, поделитесь с другими студентами. Спасибо за чтение, увидимся!
Цепи постоянного тока серии— цепи постоянного тока
Цепи постоянного тока
Цепь серии определяется как цепь, содержащая только один путь для текущего потока. Чтобы сравнить базовую схему и более сложная последовательная цепь, на рисунке ниже показаны две цепи. Основная схема имеет только одна лампа, а в последовательной цепи три лампы соединены последовательно.
Сравнение основных и последовательных цепей.
Сопротивление в последовательной цепи
Ссылаясь на рисунок выше, ток в последовательной цепи должен протекать через
каждая лампа для завершения электрического пути в цепи. Каждая дополнительная лампа
оказывает дополнительное сопротивление. В последовательной цепи
полное сопротивление цепи R t равно сумме
индивидуальные сопротивления .
В виде уравнения:
Примечание. Нижний индекс n обозначает любое количество дополнительных сопротивлений, может быть в уравнении.
Пример: На рисунке ниже последовательная цепь, состоящая из трех резисторов: показаны один из 10 Ом, один из 15 Ом и один из 30 Ом. Источник напряжения дает 110 В. Чему равно полное сопротивление?
Расчет полного сопротивления в последовательной цепи.
Дано:
R 1 = 10 Ом, R 2 = 15 Ом, R 3 = 30 Ом
Решение:
В некоторых схемах общее сопротивление известно, а значение необходимо определить один из резисторов цепи. Уравнение R t = R 1 + R 2 + R 3 можно транспонировать, чтобы найти значение неизвестного сопротивления.
Пример:
На рисунке ниже полное сопротивление цепи
с тремя резисторами составляет 40 Ом. Два резистора цепи
10 Ом каждый. Рассчитайте номинал третьего резистора ( Р 3 ).
Два резистора цепи
10 Ом каждый. Рассчитайте номинал третьего резистора ( Р 3 ).
Расчет значения одного сопротивления в последовательной цепи.
Дано:
R t = 40 Ом, R 1 = 10 Ом, R 2 = 10 Ом,
Ч 3 = ?
Решение:
Вычитание ( R 1 + R 2 ) с обеих сторон уравнение
Ток в последовательной цепи
Так как в последовательной цепи ток проходит только один путь, то один и тот же ток должен протекать через каждый компонент цепи. Чтобы определить ток в последовательной цепи, только ток через один из компоненты должны быть известны.
Тот факт, что один и тот же ток протекает через каждый компонент серии
цепь можно проверить, вставив счетчики в цепь в различных точках,
как показано на рисунке ниже. Если бы это было сделано, каждый метр
окажется, что они указывают на одно и то же значение тока.
Ток в последовательной цепи.
Напряжение в последовательной цепи
Падение напряжения на резисторе в цепи, состоящей из одного резистор и источник напряжения — это общее напряжение в цепи, равное равно приложенному напряжению. Полное напряжение в последовательной цепи, которое состоит из более чем одного резистора и равно приложенному напряжению, но состоит из суммы падений напряжения на отдельных резисторах. В любой серии цепи сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рис. рисунок ниже.
Расчет отдельных падений напряжения в последовательной цепи.
В этой цепи сброшен потенциал источника ( В t ) 20 В. через последовательную цепь, состоящую из двух резисторов по 5 Ом. Общая сопротивление цепи ( R t ) равно сумме два отдельных сопротивления или 10 Ом. По закону Ома схема ток можно рассчитать следующим образом:
Дано: В t = 20 В, R t = 10 Ом
Решение:
Поскольку известно, что номинал резисторов равен 5 Ом каждый, а
ток через резисторы равен 2 А, напряжение на них падает
резисторы можно рассчитать. Напряжение ( В 1 )
через R 1 поэтому:
Напряжение ( В 1 )
через R 1 поэтому:
Дано: I 1 = 2 А, R 1 = 5 Ом
Решение:
Осмотрев схему, можно увидеть, что R 2 то же омическое значение как R 1 и несет такой же ток. Напряжение падение на R 2 поэтому также равно 10 В. Сложение этих двух 10-вольтовых падений вместе дает общее падение 20 В, точно равно приложенному напряжению. Тогда для последовательной цепи:
Пример: Последовательная цепь состоит из трех резисторов со значениями 20 Ом, 30 Ом и 50 Ом соответственно. Найдите прикладной напряжение, если ток через резистор 30 Ом равен 2 А.
Для решения задачи сначала рисуется и маркируется принципиальная схема (рисунок ниже).
Расчет приложенного напряжения в последовательной цепи.
Дано: R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 50 Ом, I = 2 А
Решение: поскольку задействованная цепь представляет собой последовательную цепь, те же 2 А
ток течет через каждый резистор. По закону Ома напряжение падает на
каждый из трех резисторов может быть рассчитан и составляет:
По закону Ома напряжение падает на
каждый из трех резисторов может быть рассчитан и составляет:
Когда известны отдельные капли, их можно сложить, чтобы найти общее количество. или приложенное напряжение:
Примечание. Когда вы используете закон Ома, величины для уравнения должны быть равны . взято из той же части схемы. В приведенном выше примере напряжение на R 2 было рассчитано с использованием тока через R 2 и сопротивление R 2 .
Величина падения напряжения на резисторе определяется приложенным напряжения и пропорциональна сопротивлениям цепи. Напряжение падает которые возникают в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток. чем больше омическое сопротивление резистора, тем больше падение напряжения на нем.
Параллельная цепь и последовательная цепь — разница и сравнение
Компоненты электрической цепи или электронной схемы могут быть соединены разными способами. Два простейших из них называются последовательными и параллельными и встречаются часто. Компоненты, соединенные последовательно, соединяются по одному пути, поэтому через все компоненты протекает один и тот же ток. Компоненты, соединенные параллельно, соединяются несколькими путями, поэтому на каждый компонент подается одинаковое напряжение.
Два простейших из них называются последовательными и параллельными и встречаются часто. Компоненты, соединенные последовательно, соединяются по одному пути, поэтому через все компоненты протекает один и тот же ток. Компоненты, соединенные параллельно, соединяются несколькими путями, поэтому на каждый компонент подается одинаковое напряжение.
Цепь, состоящая исключительно из компонентов, соединенных последовательно, называется последовательной цепью; аналогично, полностью параллельное соединение называется параллельной цепью.
Сравнительная таблица
| Параллельная цепь | Серийная цепь | |
|---|---|---|
| Введение | Цепь, состоящая из компонентов, соединенных полностью параллельно. | Цепь, состоящая исключительно из компонентов, соединенных последовательно. |
| Проволока | Для изготовления требуется сравнительно больше проволоки. | Для его изготовления требуется сравнительно меньше проволоки. |
| Ток | Ток цепи от батареи до достижения любого компонента представляет собой сумму всех токов компонентов в цепи после прохождения через нее. | Ток всех компонентов цепи одинаков. |
| Напряжение | Напряжение всех компонентов цепи одинаково. | Напряжение батареи представляет собой сумму всех напряжений компонентов в цепи. |
| Функциональность | Компоненты работают, даже если любой из других компонентов поврежден. | Компоненты не работают, если какой-либо из компонентов поврежден из-за нарушения протекания тока. |
Общие сведения о последовательных и параллельных цепях
В последовательной цепи ток через каждый из компонентов одинаков, а напряжение в цепи представляет собой сумму напряжений на каждом компоненте. В параллельной цепи напряжение на каждом из компонентов одинаково, а общий ток равен сумме токов через каждый компонент.
Видео на YouTube ниже предлагает хорошее объяснение последовательных и параллельных цепей и того, как расположение влияет на величину тока, протекающего по цепям в соответствии с законом Ома (хотя миниатюра создает впечатление, что видео может быть повреждено, это еще работает):
Напряжение
В последовательной цепи напряжение является суммой всех элементов напряжения.
- В = В 1 + В 2 + .
 .. + В n
.. + В n
В параллельной цепи напряжение одинаково для всех элементов.
- V = V 1 = V 2 = … = V n
Current
In a series circuit, the current is the same for все элементы.
В параллельной цепи ток в каждом отдельном резисторе рассчитывается по закону Ома.
- .
Резисторы
Сопротивление и проводимость в последовательных цепях
Общее сопротивление в последовательной цепи представляет собой просто сумму сопротивлений отдельных резисторов.
Проводимость обратно пропорциональна сопротивлению. Таким образом, общая проводимость последовательной цепи рассчитывается по следующему уравнению:
- .
Сопротивление и проводимость в параллельных цепях
Общее сопротивление в параллельной цепи рассчитывается как проводимость в последовательной цепи:
- .

Проводимость в параллельной цепи представляет собой просто сумму проводимостей отдельных элементов:n:
- .
Переключатели
Два или более последовательно соединенных переключателя выполняют логическую операцию И. Цепь пропускает ток, только если все переключатели замкнуты (вкл.). Но в параллельной схеме два или более переключателя образуют логический элемент ИЛИ. Ток течет до тех пор, пока любой из переключателей замкнут.
Каталожные номера
- Последовательные и параллельные цепи — Википедия
- Введение в схемы: параллельные и последовательные схемы — YouTube
- Подписаться
- Поделиться
- Укажите
- Авторы
Поделитесь этим сравнением:
Если вы дочитали до этого места, подписывайтесь на нас:
«Параллельная цепь против последовательной цепи». Diffen.com.

 Что может привести к возгоранию. И не будет нам ни чая, ни взбитого теста для блинчиков, ни тостов.
Что может привести к возгоранию. И не будет нам ни чая, ни взбитого теста для блинчиков, ни тостов.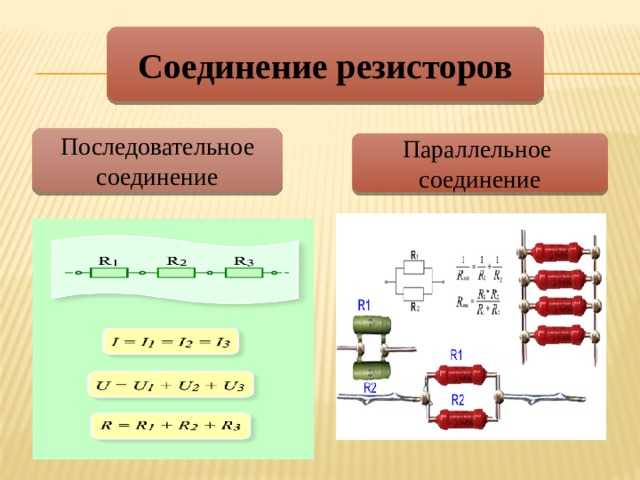 Сопротивление участка станет равным нулю, как показано на рисунке:
Сопротивление участка станет равным нулю, как показано на рисунке: