Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Какие формулы используются для вычисления эквивалентного сопротивления цепи. Чем отличаются последовательное и параллельное соединения резисторов.
Последовательное соединение проводников: основные характеристики
При последовательном соединении проводников они подключаются один за другим, образуя единую неразветвленную цепь. Основные особенности такого соединения:
- Сила тока одинакова во всех участках цепи
- Общее напряжение равно сумме напряжений на отдельных проводниках
- Общее сопротивление цепи равно сумме сопротивлений отдельных проводников
Формула расчета сопротивления при последовательном соединении
Для расчета общего сопротивления цепи при последовательном соединении используется формула:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.

Параллельное соединение проводников: ключевые особенности
При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Основные характеристики:
- Напряжение одинаково на всех параллельных участках
- Общий ток равен сумме токов в отдельных ветвях
- Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям отдельных проводников
Формула для вычисления сопротивления при параллельном соединении
Общее сопротивление при параллельном соединении рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных проводников.
Чем отличается последовательное соединение от параллельного?
Основные отличия последовательного и параллельного соединений:
- При последовательном соединении общее сопротивление увеличивается, при параллельном — уменьшается
- В последовательной цепи ток одинаков, а напряжение делится. В параллельной — напряжение одинаково, а ток делится между ветвями
- Формулы для расчета общего сопротивления различаются
Практическое применение последовательного и параллельного соединений
Последовательное и параллельное соединения проводников широко применяются в электротехнике и электронике:

- Последовательное соединение используется для увеличения общего сопротивления цепи
- Параллельное соединение применяется для уменьшения общего сопротивления
- В бытовых электрических сетях потребители подключаются параллельно
- В электронных схемах часто используются комбинации последовательных и параллельных соединений
Как рассчитать сопротивление при смешанном соединении проводников?
При смешанном (последовательно-параллельном) соединении для расчета общего сопротивления необходимо:
- Разбить схему на участки с последовательным и параллельным соединением
- Рассчитать эквивалентное сопротивление для каждого участка по соответствующим формулам
- Объединить полученные значения, используя формулы последовательного или параллельного соединения
Примеры расчета сопротивления для разных типов соединений
Рассмотрим несколько примеров вычисления общего сопротивления цепи:
Последовательное соединение
Даны три резистора: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом.
R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
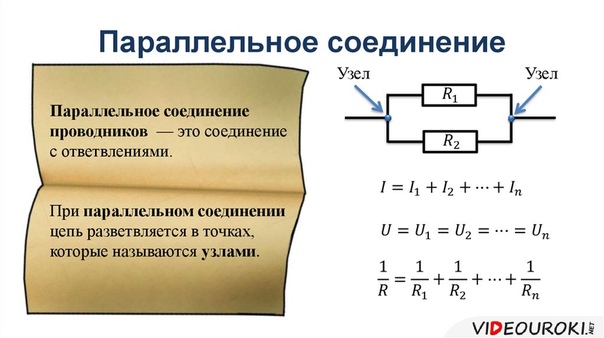
Параллельное соединение
Даны два резистора: R1 = 6 Ом, R2 = 3 Ом.
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 2 Ом
Смешанное соединение
Дана схема: R1 = 10 Ом последовательно с параллельным соединением R2 = 20 Ом и R3 = 30 Ом.
- Рассчитаем параллельное соединение R2 и R3:
1/Rпар = 1/20 + 1/30 = 5/60
Rпар = 12 Ом
- Теперь имеем последовательное соединение R1 и Rпар:
R = R1 + Rпар = 10 + 12 = 22 Ом
Ключевые моменты при расчете сопротивления электрических цепей
При вычислении общего сопротивления важно помнить:
- Для последовательного соединения сопротивления складываются
- Для параллельного соединения складываются величины, обратные сопротивлениям
- Общее сопротивление параллельного соединения всегда меньше наименьшего из сопротивлений
- В сложных схемах нужно последовательно упрощать цепь, заменяя участки их эквивалентными сопротивлениями
Заключение: важность понимания принципов соединения проводников
Знание формул и принципов расчета сопротивления при различных соединениях проводников крайне важно для:

- Проектирования электрических цепей
- Анализа работы электронных устройств
- Расчета параметров электрических сетей
- Обеспечения безопасности при работе с электрооборудованием
Правильное применение этих знаний позволяет эффективно решать разнообразные задачи в области электротехники и электроники.
Последовательное и параллельное соединение проводников — урок. Физика, 8 класс.
В быту и в промышленности в электрическую цепь соединяются сразу несколько потребителей электрической энергии. Различают три вида соединения сопротивлений (резисторов):
- последовательное соединение проводников
- параллельное соединение проводников
- смешанное соединение проводников
Последовательное соединение проводников
Схема соединения выглядит следующим образом:
Обрати внимание!
При последовательном соединении все входящие в него проводники соединяются друг за другом, т.е. конец первого проводника соединяется с началом второго.
Опыт показывает:
Сила тока в любых частях цепи одна и та же (об этом свидетельствуют показания амперметров): I=I1=I2.
Если выкрутить одну лампу, то цепь разомкнётся, а другая лампа тоже погаснет.
Опыт показывает следующее:
При последовательном соединении сопротивлений результирующее напряжение равно сумме напряжений на участках: U=U1+U2.
Результирующее сопротивление последовательно соединённых потребителей равно сумме сопротивлений потребителей: R=R1+R2.
Для проверки данного утверждения можно использовать омметр. При подключении омметра ключ должен быть разомкнут!
Омметр подключают по очереди к каждому потребителю, а потом к обоим одновременно.
Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз больше сопротивления одной лампы: \(R\) = R1* \(n\).
Параллельное соединение проводников
Схема соединения выглядит следующим образом:
Обрати внимание!
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом — к другой точке В.
Опыт доказывает:
Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках.
Об этом свидетельствуют показания амперметров: I=I1+I2.
Если выкрутить одну лампу, то другая лампа продолжает гореть. Это свойство используют для подключения бытовых приборов в помещении.
Опыт свидетельствует, что:
Напряжение на участке цепи АВ и на концах всех параллельно соединённых проводников одно и то же.
Об этом свидетельствуют показания вольтметров:U=U1=U2.
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле:
1R=1R1+1R2.
Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников.
Для проверки формулы можно использовать омметр. При подключении омметра ключ должен быть разомкнут!
Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз меньше сопротивления одной лампы: \(R\) = R1/ \(n\).
Источники:
http://files. school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
http://files.school-collection.edu.ru/dlrstore/669ba074-e921-11dc-95ff-0800200c9a66/3_18.swf
http://class-fizika.narod.ru/8_33.htm
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:R = R1 + R2.
Это справедливо и для большего количества соединённых последовательно резисторов:
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Параллельное соединение резисторов (формула)
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
| Сопротивление из двух резисторов: |
R = | R1 × R2 |
| R1 + R2 |
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
Сопротивление параллельных резисторов
| 1 | = | 1 | + | 1 | + | 1 |
+ . .. .. |
| R | R1 | R2 | R3 |
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее.
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Например: десять резисторов номиналом 1 КОм и мощностью 1 Вт каждый, соединённые параллельно будут иметь общее сопротивление 100 Ом и мощность 10 Вт.
При последовательном соединении мощность резисторов также складывается. Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.
Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.
Физическая формула расчета (определения) эквивалентного сопротивления в цепи
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.
Метод свёртывания цепи
Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.
Последовательное соединение элементовВ случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).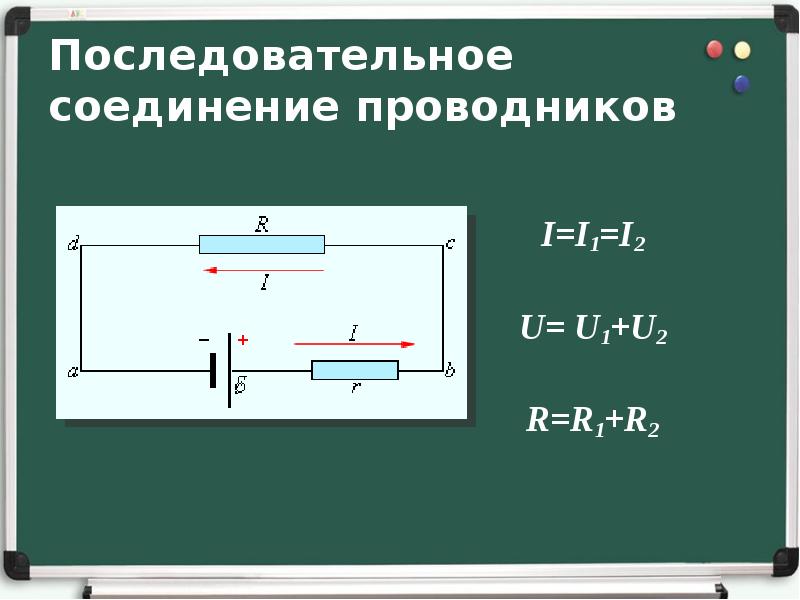
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Расчёт при смешанном соединении устройствВ случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.
При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.
Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:
- R1 = 1Ом,
- R2 = 2Ом,
- R3 = 3Ом,
- R4 = 6Ом,
- R5 = 9Ом,
- R6 = 18Ом,
- R7 = 2,8Ом,
- U = 32В.
Электрическая схема
Из закона Ома имеем:
I = U/R,
где R – суммарное сопротивление всех приборов.
Его будем находить, воспользовавшись методом сворачивания цепи.
Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:
R2,3= R2·R3 / (R2+R3).
R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:
1/R4,5,6 = 1/R4+1/R5+1/R6.
Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.
Эквивалентная схема
Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.
Rобщ может быть найдено по формуле:
Rобщ = R1 + R2,3 + R4,5,6 + R7.
Подставляем числовые значения и рассчитываем R для определённых участков:
- R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
- 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
- R4,5,6 = 3Ом,
- Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.
Теперь, после того, как нашли Rэкв, можно вычислять значение I:
I = 32В / 8Ом = 4А.
После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.
Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:
I1 = I2,3 = I4,5,6 = I7 = I = 4А.
На участке R2,3 напряжение находим по формуле:
- U2,3 = I2,3·R2,3,
- U2,3 = 4А·1,2Ом = 4,8В.
Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:
- I2 = U2 / R2,
- I2 = 4,8В / 2Ом = 2,4А,
- I3 = U3 / R3,
- I3 = 4,8В / 3Ом = 1,6А.
Проверяем правильность решения:
- I2,3 = I2 + I3,
- I2,3 = 2,4А + 1,6А = 4А.
На участке R4,5,б напряжение также находим, исходя из закона Ома:
- U4,5,6 = I4,5,6·R4,5,6,
- U4,5,6 = 4А·3Ом = 12В.
Так как R4, R5, Rб подключены параллельно друг к другу, то:
U4,5,6 = U4 = U5 = U6 = 12В.
Вычисляем I4, I5, I6:
- I4 = U4 / R4,
- I4 = 12В / 6Ом = 2А,
- I5 = U5 / R5,
- I5 = 12В / 9Ом » 1,3А,
- I6 = U6 / R6,
- I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:
I4,5,6 = 2А + 1,3А + 0,7А = 4А.
Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.
Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.
Видео Оцените статью:Как найти параллельное сопротивление формула
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.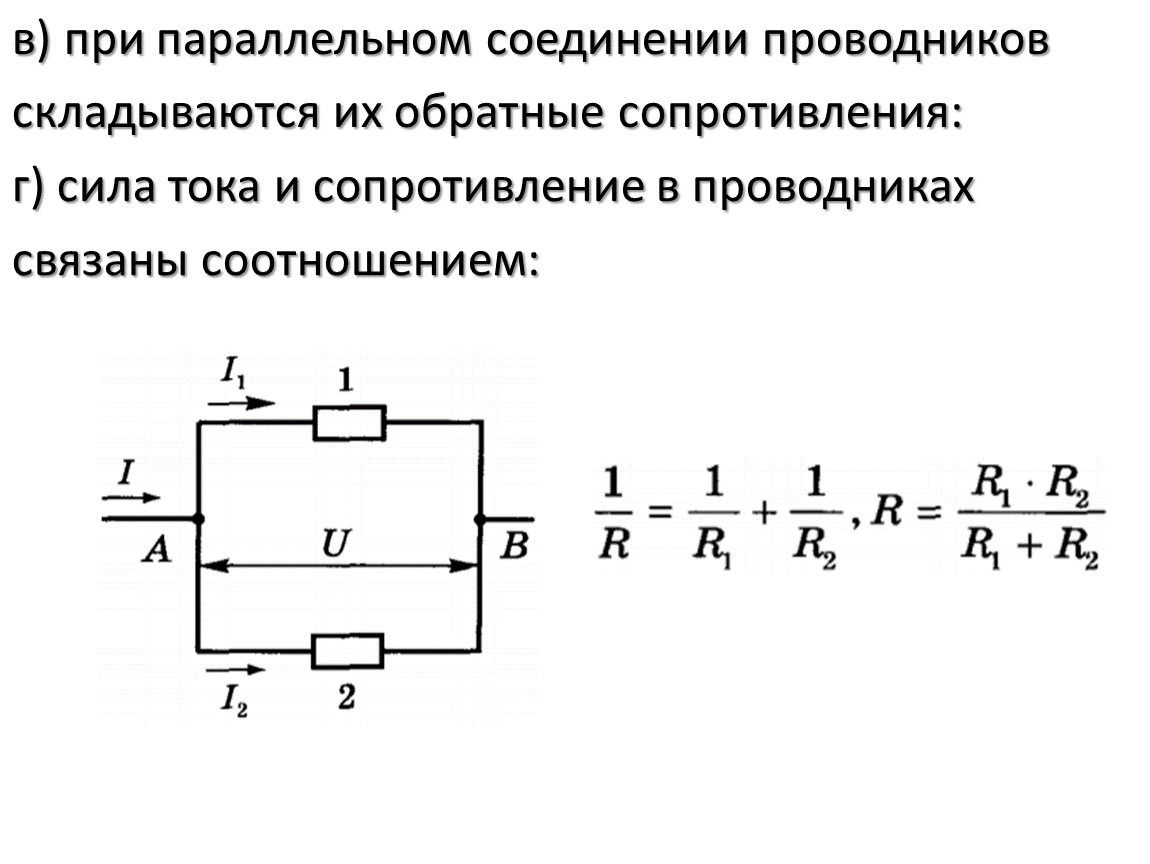
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.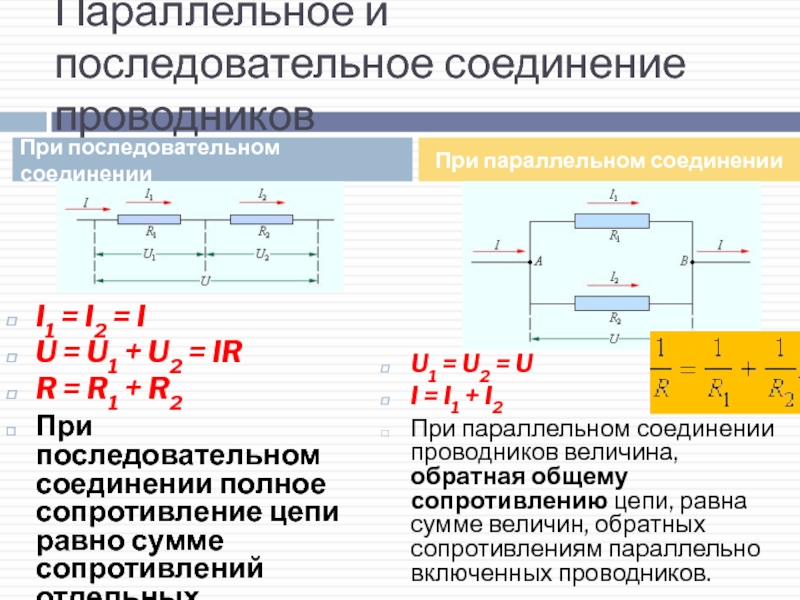
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Сопротивление при параллельном соединении, формула для расчета сопротивления при параллельном соединении
В этой статье мы разберем, как посчитать общее сопротивление при параллельном соединении сопротивлений. Параллельным соединением сопротивлений называется соединение (рисунок ниже), при котором один зажим каждого из сопротивлений присоединяется к одной точке (узлу) электрической цепи, а другой зажим каждого из тех же сопротивлений присоединяется к другой точке электрической цепи. Таким образом, между двумя точками (узлами) электрической цепи включается несколько сопротивлений, образующих параллельные ветви.
При этом напряжение между концами всех ветвей будет одним и тем же, а токи в отдельных ветвях определяются по закону Ома:
I1 = U / r1 ; I2 = U / r2 ; I3 = U / r3.
Напряжение U между узлами (А и Б):
U = I1r1 = I2r2 = I3r3,
откуда
I1 / I2 = R2 / R1 и I2 / I3 = R3 / R2,
т. е.
Токи в параллельных ветвях распределяются обратно пропорционально их сопротивлениям.
Согласно первому правилу Кирхгофа,
I = I1 + I2 + I3
или
U / Rсум = U / R1 + U / R2 + U / R2 = U (1 / R1 + 1 / R2 + 1 / R3).
Произведя сокращение на U, получим:
1 / Rсум = 1 / R1 + 1 / R2 + 1 / R3
или
g = g1 + g2 + g3 ,
где R и g—сопротивление и проводимость разветвленной цепи или, как их часто называют, общие сопротивление и проводимость цепи.
Из полученной формулы следует, что
Общая проводимость разветвленной цепи равна сумме проводимостей отдельных ветвей.
Формула
1 / Rсум = 1 / R1 + 1 / R2 + 1 / R3
дает возможность определить общее сопротивление цепи. Например, для трех параллельно соединенных сопротивлений, приведя правую часть уравнения к общему знаменателю, получим:
1 / Rсум = R2R3 + R1R3 + R1R2 / R1R2R3
откуда
Rсум = R1R2R3 / R2R3 + R1R3 + R1R2
Если сопротивления R1 = R2 = R3, то общее сопротивление цепи:
Rсум = R1 / 3,
а в общем случае при n параллельных ветвях с равными сопротивлениями R1 :
Rсум = R1 / n
В случае двух параллельных ветвей:
1 / Rсум = 1 / R1 + 1 / R2
откуда
Rсум = R1R2 / R2R3 + R1R3
При параллельном соединении приемников энергии все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Совершенно иначе обстоит дело при последовательном соединении приемников, при котором изменение сопротивления одного из них тотчас же приводит к изменению напряжения на других, последовательно соединенных с ним. Поэтому электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, включаются параллельно. Одинаковые электрические лампы иногда соединяются последовательно. Пусть, например, напряжение сети U, а напряжение лампы U0 < U Тогда n ламп соединяются цепочкой друг за другом, причем n > U / U0
Такое соединение ламп можно встретить, например, в трамваях, метро и других случаях.
Пример 1:
К сети с напряжением 220 в параллельно подключены двигатель мощностью 1,1 квт и 11 ламп, каждая мощностью 40 вт. Определить ток в главных (подводящих) проводах
Ток двигателя
I1 = P1 / U = 1100 / 220 = 5a.
Ток ламп
I2 = P2 / U = 11 x 40 / 220 = 2a.
Ток в подводящих проводах
I = I1 + I2 = 5 + 2 = 7a.
Пример 2:
Определить общее сопротивление десяти параллельно включенных ламп накаливания, если каждая из них 240 ом:
R = Rл / n = 240 / 10 = 24ом.
последовательное, параллельное, смешанное соединение. Расчет сопротивления
Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.
Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I1+I2+..In
С учетом этого имеем:
- I=U/R
- I1=U/R1
- I2=U/R2
- In=U/Rn
- U/R=U/R1+U/R2+…U/Rn
- 1/R=1/R1+1/R2+…1/Rn
Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно: R=(R1*R2)/(R1+R2).
Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R1=R2) их общее сопротивление будет вдвое меньше любого из них. Это полезно помнить.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:
- U=I*R
- I=I1=I2=…In
- U=U1+U2+…Un
- I*R=I*R1+I*R2+…I*Rn
- R=R1+R2+…Rn
То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.
СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.3).
Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:
- последовательное сопротивление резисторов Rпосл=R1+R2
- параллельное соединение R=(Rпосл*R3)/(Rпосл+R3)
Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.
Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:
- Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.
Например, для рисунка 3.a, если фактическая погрешность R1 составляет +10%, а R2 имеет +15%, то для Rпосл она будет +25%.
Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.
- Необходимость получить большую мощность.
Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.
Про мощность и номиналы резисторов можно почитать здесь.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Физическая формула расчета эквивалентного сопротивления в цепи
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).
Эквивалентное сопротивление резисторов
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
Последовательное включение резисторов
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Параллельное включение резисторов
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Способ расчёта при смешанном соединении
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
резисторов последовательно и параллельно
Резисторы серии
Общее сопротивление в цепи с последовательно включенными резисторами равно сумме отдельных сопротивлений.
Цели обучения
Рассчитайте общее сопротивление в цепи с последовательно включенными резисторами
Основные выводы
Ключевые моменты
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: [латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N} [/ latex].
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
Обзор
Большинство схем имеет более одного компонента, называемого резистором, который ограничивает поток заряда в цепи.Мера этого предела для потока заряда называется сопротивлением. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Цепи серии : Краткое введение в анализ последовательных и последовательных цепей, включая закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Резисторы серии
Резисторы включены последовательно, когда заряд или ток должны проходить через компоненты последовательно.
Резисторы в серии : Эти четыре резистора подключены последовательно, потому что, если бы ток подавался на один конец, он бы протекал через каждый резистор последовательно до конца.
показывает резисторы, последовательно подключенные к источнику напряжения. Общее сопротивление в цепи равно сумме отдельных сопротивлений, поскольку ток должен проходить через каждый резистор последовательно через цепь.
Резисторы, подключенные последовательно. : Три резистора, подключенные последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Использование закона Ома для расчета изменений напряжения в резисторах серии
Согласно закону Ома падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR, где I — ток в амперах (A), а R — сопротивление в омах (Ω). .
Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , на R 2 составляет В 2 = IR 2 , а на R 3 составляет В 3 = IR 3 .Сумма напряжений будет равна: V = V 1 + V 2 + V 3 , исходя из сохранения энергии и заряда. Если подставить значения отдельных напряжений, получим:
[латекс] \ text {V} = \ text {IR} _1 + \ text {IR} _2 + \ text {IR} _3 [/ latex]
или
[латекс] \ text {V} = \ text {I} (\ text {R} _1 + \ text {R} _2 + \ text {R} _3) [/ латекс]
Это означает, что полное сопротивление в серии равно сумме отдельных сопротивлений. Следовательно, для каждой цепи с Н количество резисторов, включенных последовательно:
[латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N }.[/ латекс]
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, и последовательно соединенные сопротивления просто складываются.
Поскольку напряжение и сопротивление имеют обратную зависимость, отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Об этом свидетельствует пример, когда две лампочки соединены в последовательную цепь с аккумулятором. В простой схеме, состоящей из одной батареи 1,5 В и одной лампочки, падение напряжения на лампе будет равно 1.5V через него. Однако, если бы две лампочки были соединены последовательно с одной и той же батареей, на каждой из них было бы падение напряжения 1,5 В / 2 или 0,75 В. Это будет очевидно по яркости света: каждая из двух последовательно соединенных лампочек будет в два раза слабее, чем одиночная лампочка. Следовательно, резисторы, соединенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия распределяется между резисторами в зависимости от их сопротивлений.
Параллельные резисторы
Общее сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.
Цели обучения
Рассчитайте общее сопротивление в цепи с резисторами, включенными параллельно
Основные выводы
Ключевые моменты
- Общее сопротивление в параллельной цепи меньше наименьшего из отдельных сопротивлений.
- Каждый резистор, включенный параллельно, имеет то же напряжение, что и приложенный к нему источник (напряжение в параллельной цепи постоянно).
- Не каждый параллельный резистор получает полный ток; они делят его (ток зависит от номинала каждого резистора и общего количества резисторов в цепи).
Ключевые термины
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
Обзор
Резисторы в цепи могут быть включены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Параллельные схемы : Краткий обзор анализа параллельных цепей с использованием таблиц VIRP для студентов-физиков средней школы.
Параллельные резисторы
Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельное соединение резисторов : Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
ЗаконОм и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны [латекс] \ text {I} _1 = \ frac {\ text {V}} {\ text {R} _1} [/ latex], [latex] \ text {I} _2 = \ frac {\ text {V}} {\ text {R} _2} [/ latex] и [latex] \ text {I} _3 = \ frac {\ text {V}} {\ text {R} _3} [/ латекс].Сохранение заряда подразумевает, что полный ток равен сумме этих токов:
Параллельные резисторы : Три резистора, подключенные параллельно батарее, и эквивалентное одиночное или параллельное сопротивление.
[латекс] \ text {I} = \ text {I} _1 + \ text {I} _2 + \ text {I} _3. [/ Latex]
Подстановка выражений для отдельных токов дает:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R} _1} + \ frac {\ text {V}} {\ text {R} _2} + \ frac {\ текст {V}} {\ text {R} _3} [/ latex]
или
[латекс] \ text {I} = \ text {V} (\ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} + \ frac {1} { \ text {R} _3}) [/ latex]
Это означает, что полное сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.Следовательно, для каждой цепи с числом [latex] \ text {n} [/ latex] или параллельно подключенных резисторов —
[латекс] \ text {R} _ {\ text {n} \; (\ text {parallel})} = \ frac {1} {\ text {R} _1} + \ frac {1} {\ text { R} _2} + \ frac {1} {\ text {R} _3}… + \ frac {1} {\ text {R} _ \ text {n}}. [/ Latex]
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет такое же полное напряжение источника, как на него, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с аккумулятором на 1,5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию обеими лампочками.В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.
Комбинированные схемы
Комбинированная цепь может быть разбита на аналогичные части, которые работают последовательно или параллельно.
Цели обучения
Описать расположение резисторов в комбинированной цепи и его практическое значение
Основные выводы
Ключевые моменты
- Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного.
- Различные части комбинированной схемы могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
- Сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление в проводах относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными и повлиять на выходную мощность в бытовые приборы.
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- Комбинированная схема : электрическая цепь, содержащая несколько резисторов, которые соединены как последовательным, так и параллельным соединением.
Комбинированные схемы
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Это часто встречается, особенно если учитывать сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная цепь может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на схеме. На рисунке общее сопротивление может быть рассчитано путем соединения трех резисторов друг с другом последовательно или параллельно. R 1 и R 2 соединены параллельно друг другу, поэтому мы знаем, что для этого подмножества сопротивление, обратное сопротивлению, будет равно:
Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Комбинированные схемы : Два параллельных резистора, соединенные последовательно с одним резистором.
[латекс] \ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} [/ latex] или [латекс] \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} [/ latex]
R 3 соединены последовательно с как R 1 , так и R 2 , поэтому сопротивление будет рассчитываться как:
[латекс] \ text {R} = \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} + \ text {R} _3 [/ латекс ]
Сложные комбинированные схемы
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление, как показано на.На этом рисунке комбинация из семи резисторов была идентифицирована как включенные последовательно или параллельно. На исходном изображении две обведенные кружком секции показывают резисторы, включенные параллельно.
Сокращение комбинированной схемы : Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до достижения единого эквивалентного сопротивления.
Уменьшение этих параллельных резисторов до одного значения R позволяет нам визуализировать схему в более упрощенном виде.На верхнем правом изображении мы видим, что обведенная кружком часть содержит два последовательно соединенных резистора. Мы можем дополнительно уменьшить это до другого значения R, добавив их. Следующий шаг показывает, что два обведенных резистора включены параллельно. Уменьшение тех ярких моментов, что последние два соединены последовательно и, таким образом, могут быть уменьшены до одного значения сопротивления для всей цепи.
Практическое применение комбинированной схемы состоит в том, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Комбинированная цепь может быть преобразована в последовательную цепь на основе понимания эквивалентного сопротивления параллельных ветвей комбинированной цепи. Последовательная цепь может использоваться для определения общего сопротивления цепи. По сути, сопротивление провода является последовательным с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение ИК-излучения в проводах также может быть значительным.
Зарядка аккумулятора: последовательные и параллельные ЭДС
При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; параллельно они остаются прежними.
Цели обучения
Сравнить сопротивления и электродвижущие силы для источников напряжения, подключенных с одинаковой и противоположной полярностью, последовательно и параллельно
Основные выводы
Ключевые моменты
- ЭДС, соединенные последовательно с одинаковой полярностью, являются аддитивными и приводят к более высокой общей ЭДС.
- Две ЭДС, соединенные последовательно с противоположной полярностью, имеют общую ЭДС, равную разнице между ними, и могут использоваться для зарядки источника более низкого напряжения.
- Два источника напряжения с идентичными ЭДС, соединенные параллельно, имеют чистую ЭДС, эквивалентную одному источнику ЭДС, однако чистое внутреннее сопротивление меньше и, следовательно, дает более высокий ток.
Ключевые термины
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- серия : ряд элементов, которые следуют одно за другим или соединяются одно за другим.
Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно, аналогично резисторам в цепи.Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила или ЭДС складываются алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Фонарик и лампочка : Последовательное соединение двух источников напряжения в одном направлении. Эта схема представляет собой фонарик с двумя последовательно включенными ячейками (источниками напряжения) и одной лампочкой (сопротивление нагрузки).
Батарея представляет собой соединение нескольких гальванических элементов. Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы должны добавить как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, у вас будет такая же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу, например, когда одна вставляется в прибор задом наперед, общая ЭДС меньше, так как это алгебраическая сумма отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство : представляет два источника напряжения, соединенных последовательно с противоположными ЭДС. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений.(Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем батарея, чтобы через него протекал обратный ток.
Когда два источника напряжения с идентичными ЭДС соединены параллельно и также подключены к сопротивлению нагрузки, общая ЭДС равна индивидуальной ЭДС. Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Две идентичные ЭДС : Два источника напряжения с идентичными ЭДС (каждый помечен буквой E), соединенные параллельно, создают одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и напряжение на клеммах
Выходное напряжение или напряжение на клеммах источника напряжения, такого как аккумулятор, зависит от его электродвижущей силы и внутреннего сопротивления.
Цели обучения
Выразите взаимосвязь между электродвижущей силой и напряжением на клеммах в форме уравнения
Основные выводы
Ключевые моменты
- Электродвижущая сила (ЭДС) — это разность потенциалов источника при отсутствии тока.
- Напряжение на клеммах — это выходное напряжение устройства, измеренное на его клеммах.
- Напряжение на клеммах рассчитывается по формуле V = ЭДС — Ir.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- напряжение на клеммах : выходное напряжение устройства, измеренное на его клеммах.
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
Когда вы забываете выключить автомобильные фары, они постепенно тускнеют по мере разрядки аккумулятора. Почему они просто не мигают, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных или перегруженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС — это вообще не сила; это особый тип разности потенциалов источника при отсутствии тока. Единицы измерения ЭДС — вольты.
Электродвижущая сила напрямую связана с источником разности потенциалов, например, с конкретной комбинацией химических веществ в батарее.Однако при протекании тока ЭДС отличается от выходного напряжения устройства. Напряжение на выводах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно падает дальше, когда батарея разряжается или разряжается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для сильно разряженной батареи).
Напряжение на клеммах
представляет схематическое изображение источника напряжения.Выходное напряжение устройства измеряется на его выводах и называется напряжением на выводах В . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения : Любой источник напряжения (в данном случае углеродно-цинковый сухой элемент) имеет ЭДС, связанную с источником разности потенциалов, и внутреннее сопротивление r, связанное с его конструкцией. (Обратите внимание, что сценарий E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V.Поскольку V = ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
[латекс] \ text {V} = \ text {emf} — \ text {Ir} [/ latex],
, где r — внутреннее сопротивление, а I — ток, протекающий во время измерения.
I является положительным, если ток течет от положительного вывода. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора. По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \).В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)). В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков.В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора. Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе.(b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.Резисторы серии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \). Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке \ (\ PageIndex {2} \) ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков. Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор.Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается с использованием уравнения \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \). N V_i = 0.\]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов.
Эквивалентное сопротивление в последовательной цепи
Любое количество резисторов может быть подключено последовательно. Если \ (N \) резисторы соединены последовательно, эквивалентное сопротивление равно
. N R_i.\ label {серия эквивалентных сопротивлений} \]Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
- Ответ
-
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере прохождения зарядов от батареи часть заряда проходит через резистор \ (R_1 \), а часть — через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Общий ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
-
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет равен \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельное соединение. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Решение
-
Река, текущая горизонтально с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Не каждый параллельный резистор получает полный ток; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, из раздела о емкости мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть уменьшены до одного эквивалентного сопротивления, используя технику, показанную на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти с помощью закона Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Общая энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в цепь, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какая мощность рассеивается \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Решение
-
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, поэтому вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии двери.Обычно у холодильника есть только один шнур для подключения к стене. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2,00 \, A (25,00 \, \ Omega) = 50,00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и авторство
-
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения. Когда все устройства в цепи соединены последовательными соединениями, тогда схема называется последовательной схемой.Когда все устройства в цепи соединены параллельными соединениями, тогда схема называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно.Это пример комбинированной схемы .
При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям. Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии - Ток одинаков на всех резисторах; этот ток равен току в батарее.
- Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи.
- Общее сопротивление набора резисторов равно сумме отдельных значений сопротивлений,
Параллельные схемы - Падение напряжения одинаково на каждой параллельной ветви.
- Сумма тока в каждой отдельной ветви равна току вне ветвей.
- Эквивалентное или полное сопротивление набора резисторов определяется уравнением 1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 …
Каждое из вышеперечисленных понятий имеет математическое выражение.Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных схемОсновная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом.Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно.Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи.Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
. R до = 1 R 2 + 3 +…Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.
Пример 1:Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление.Цель анализа — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 .Таким образом, общее сопротивление составляет
. R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR до = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (60 В) / (15 Ом)I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи.При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
I до = I 1 = I 4 = 4 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению.Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 А.
I 2 = I 3 = 2 АТеперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)
ΔV 1 = 20 В
ΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 В
ΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 В
ΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое значение сопротивления. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …1 / R экв = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 3 Ом + R 4 = 5 Ом + 3 Ом + 8 ОмR до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (24 В) / (16 Ом)I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)
ΔV 1 = 7,5 В
ΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и R 4 . Таким образом,
ΔV 2 = V 3 = 4,5 ВЗная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)
I 2 = 1,125 А
I 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 А
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегииДва приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, потратьте время на ее создание. Используйте условные обозначения, такие как те, что показаны в примере выше.
- При решении проблемы, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например, I — , I 1 , R 3 , ΔV 2 и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (по вашему мнению) параллельную секцию одним резистором, значение сопротивления которого равно эквивалентному сопротивлению параллельной секции.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) току в точке B.
г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.
г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) току в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.
3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.
5. Обращаясь к диаграмме в вопросе №4, определите …
а. … номинальная мощность резистора 4.
г. … скорость, с которой энергия потребляется резистором 3.
Серияи параллельные резисторы
- Изучив этот раздел, вы должны уметь:
- Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
- • Вычисление суммы обратных величин.
- • Произведение над суммой.
- Рассчитайте значения общего сопротивления в последовательной / параллельной сети.
Расчеты в последовательно- и параллельных резисторных цепях
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но различная разность потенциалов (напряжение) может существовать на каждом из них.
ПАРАЛЛЕЛЬНО, так что одинаковая разность потенциалов (напряжение) существует на всех компонентах, но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы серии
Рис. 4.2.2 Параллельные резисторы
В любом случае (для резисторов) полное сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.
Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных схем с использованием относительно простых методов.Это очень полезно при поиске неисправностей.
ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНОСТЬЮ ПОПРОБУЙТЕ ИСПОЛЬЗУЙТЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов в серии:
Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов, включенных параллельно:
Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.
Обратите внимание, однако, что эта формула НЕ дает вам общего сопротивления R TOT . Это дает вам ВЗАИМОДЕЙСТВИЕ R TOT или:
Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, деленный на TOT . Чтобы получить правильное значение для TOT рэндов (которое будет обратным 1/ TOT , т. Е. TOT /1, просто нажмите соответствующую клавишу на вашем калькуляторе (отмеченную 1 / x или x-1) .
Другой способ расчета параллельных цепей.
Суммарное сопротивление двух резисторов, включенных параллельно , которое не включает обратных, равно:
Эту формулу часто называют «произведение над суммой».
Рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и сделайте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.
О, еще кое-что, что нужно помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это ДО того, как использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.
Подсказки
Использование обратного метода
Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину. 1 / R1 + 1 / R2 + 1 / R3 = 1 / R TOT и чтобы найти R TOT , вы должны найти обратную величину 1 / R TOT .
Упрощающие схемы
Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, по которой можно найти R TOT .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто определите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .
Теперь вы можете использовать первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.
Когда все параллельные резисторы одинакового номинала.
Если несколько одинаковых параллельных резисторов подключены, общее сопротивление будет равно номиналу резистора, умноженному на обратную величину количества резисторов.
, т. Е. Два параллельных резистора 12 кОм имеют общее сопротивление
.12K x 1/2 = 6K
Три параллельно включенных резистора 12 кОм имеют суммарное сопротивление
12K x 1/3 = 4K и т. Д.
Проверяю ответ
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Серияи параллельная комбинация
Попробуйте несколько вычислений, основанных на последовательной и параллельной цепях резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Прежде чем начать, подумайте об этих нескольких советах. Они упростят задачу, если вы будете внимательно им следовать.
1. Разработайте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой работаете.
2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу (например.грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.
3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.
Пример последовательной и параллельной цепей.
Хорошо, здесь есть что вспомнить, так почему бы не попробовать несколько практических вопросов в модуле резисторов 4.5 по определению общего сопротивления некоторых цепей резисторов?
Резисторы— learn.sparkfun.com
Добавлено в избранное Любимый 48 Серияи параллельные резисторы
Резисторы постоянно соединяются вместе в электронике, обычно в последовательной или параллельной схеме.Когда резисторы объединяются последовательно или параллельно, они создают общее сопротивление , которое можно рассчитать с помощью одного из двух уравнений. Знание того, как объединяются значения резисторов, пригодится, если вам нужно создать конкретное значение резистора.
Резисторы серииПри последовательном соединении значения резисторов просто складываются.
Н резисторов последовательно. Общее сопротивление — это сумма всех последовательных резисторов.
Так, например, если у вас всего , должно быть из 12.33к & Ом; резистор, найдите некоторые из наиболее распространенных номиналов резисторов 12 кОм; и 330 Ом, и соединить их последовательно.
Параллельные резисторы
Определить сопротивление параллельно включенных резисторов не так-то просто. Общее сопротивление резисторов N , включенных параллельно, является обратной суммой всех обратных сопротивлений. Это уравнение может иметь больше смысла, чем последнее предложение:
Н резисторов параллельно. Чтобы найти общее сопротивление, инвертируйте каждое значение сопротивления, сложите их, а затем инвертируйте.
(Сопротивление, обратное сопротивлению, на самом деле называется проводимостью , поэтому короче: проводимость параллельных резисторов является суммой каждой из их проводимости).
В качестве частного случая этого уравнения: если у вас только два резистора , подключенных параллельно, их полное сопротивление можно рассчитать с помощью этого чуть менее инвертированного уравнения:
Как еще , более частный случай этого уравнения, если у вас есть два параллельных резистора с одинаковым значением , общее сопротивление составляет половину их значения.Например, если два 10k & ohm; резисторы включены параллельно, их полное сопротивление 5кОм.
Сокращенно сказать, что два резистора подключены параллельно, можно с помощью оператора параллельности: || . Например, если R 1 находится параллельно с R 2 , концептуальное уравнение может быть записано как R 1 || R 2 . Намного чище и скрывает все эти неприятные фракции!
Резисторные сети
В качестве специального введения в вычисление полного сопротивления, учителя электроники любят подвергать своих учеников поиску сумасшедших, запутанных сетей резисторов.
Приручить резисторный сетевой вопрос может быть что-то вроде: «какое сопротивление между выводами A, и B в этой цепи?»
Чтобы решить такую проблему, начните с задней части схемы и упростите ее к двум клеммам. В этом случае R 7 , R 8 и R 9 идут последовательно и могут складываться вместе. Эти три резистора включены параллельно с R 6 , поэтому эти четыре резистора можно превратить в один с сопротивлением R 6 || (R 7 + R 8 + R 9 ).Делаем нашу схему:
Теперь четыре крайних правых резистора можно упростить еще больше. R 4 , R 5 и наш конгломерат R 6 — R 9 все последовательно и могут быть добавлены. Тогда все эти последовательные резисторы подключены параллельно с R 3 .
И это всего лишь три последовательных резистора между клеммами A и B . Добавьте их! Таким образом, полное сопротивление этой цепи составляет: рэнд 1 + р 2 + р 3 || ( р + р 5 + р 6 || ( 7 + р ) 8 + R 9 )).
← Предыдущая страница
Номинальная мощностьКалькулятор параллельного и последовательного сопротивления
Параллельный и последовательный
СопротивлениеПараллельное сопротивление XXXX Ом Сопротивление серии XXXX Ом
Рассчитать Прозрачный
⚠️ Сообщить о проблемеСопротивление — это электрический элемент, который не позволяет легко протекать через него току.В нашей повседневной жизни сопротивление используется во многих электрических цепях и устройствах. Внутри этих электрических устройств сопротивления расположены в различных конфигурациях.
Вы также, должно быть, наблюдали, выполняя соединения на макетной плате в своей лаборатории электроники, как резисторы подключаются по-разному. В зависимости от способа соединения их концов различают два основных типа цепей сопротивления:
- Цепи серии
- Параллельные схемы
По мере продвижения в этом посте мы будем понимать работу, сравнение, вычисления и различия между этими последовательными цепями и параллельными цепями.
Цепи серииДва или более резистора считаются подключенными последовательно, если ток, протекающий через них, одинаков. Другими словами, ток, исходящий от источника, или общий ток не будут разветвляться по какому-либо другому пути, а будут двигаться только по одному прямому пути.
При последовательном соединении сопротивлений чистое сопротивление цепи является суммой всех сопротивлений цепи.
На следующей принципиальной схеме показаны три последовательно соединенных сопротивления R 1 , R 2 и R 3 .Чистое сопротивление этой последовательной цепи составляет R нетто = 1 R + 2 R + 3 R.
Как правило, если «n» сопротивлений соединены последовательно, общее сопротивление составляет R net = R 1 + R 2 +…. Р н .
Например, если в цепи есть три последовательно соединенных резистора по 10 Ом, и источник напряжения 30 В, то ток, протекающий в цепи и через каждый из них, определяется выражением I = V / R = 10/30 = 0. .33 А.
Параллельные цепи
Два или более резистора считаются подключенными параллельно, если они соединены головками на одной стороне и выводами на другой стороне цепи. В параллельной цепи ток, исходящий от источника, или полный ток будет ветвиться в месте соединения, где головки сопротивлений встречаются, а затем течет в разных количествах в каждом резисторе, а затем снова объединяется в точке встречи хвостов резисторы и течет в сторону начала координат.
При параллельном соединении сопротивлений сопротивление цепи, обратное сопротивлению цепи, является суммой значений, обратных сопротивлению всех сопротивлений цепи.
На следующей принципиальной схеме показаны три параллельно включенных сопротивления R 1 , R 2 и R 3 . Общее сопротивление этой параллельной цепи составляет 1 / R net = 1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3 .
Как правило, если «n» сопротивлений подключены параллельно, общее сопротивление составляет:
1 / R net = 1 / R = 1 / R + 1 / R 2 + 1 / R 3 +….+ 1 / R n
Например, если три резистора 4 Ом, 8 Ом и 8 Ом подключены параллельно в цепи с питанием 10 В, то общее сопротивление цепи определяется как: 1 / Rnet = 1/4 + 1/8 + 1/8 = ½ или Rnet = 2 Ом
Тогда ток, протекающий по цепи, равен V / I = 10/2 = 5 ампер.
Если вы хотите рассчитать ток в каждом резисторе, вы можете использовать закон Ома:
Ток через резистор 4 Ом I 1 = 10/4 = 2.5 А
Ток через резистор 8 Ом I 1 = 10/8 = 1,25 A
Ток через резистор 4 Ом I 1 = 10/8 = 1,25 A
Обратите внимание, что если вы сложите отдельные токи через каждый резистор, вы получите общий ток, протекающий в цепи.
Комбинация последовательных и параллельных резисторов
Если вы найдете схему, в которой резисторы включены последовательно и параллельно, то вам нужно решить комбинацию резисторов шаг за шагом, учитывая, находятся ли они последовательно или параллельно с соседними, и затем прийти к окончательному сопротивлению цепи.
Баллов о последовательном и параллельном соединении резисторов:
- Эффективное сопротивление последовательной цепи всегда больше, чем сопротивление каждого резистора в цепи.
- Эффективное сопротивление параллельной цепи всегда меньше, чем сопротивление каждого резистора в цепи.
- Ток в каждом из последовательно соединенных резисторов одинаков, а напряжение на каждом параллельном резисторе одинаково.
- В цепи последовательных резисторов, если одно сопротивление повреждается, вся цепь разрывается и ведет себя как разомкнутая цепь.
- В схеме параллельных резисторов, если один резистор поврежден, ток продолжает течь в других резисторах, и схема будет продолжать работать, но с другим значением сопротивления цепи.
Как вам помогает калькулятор последовательного и параллельного сопротивления CalculatorHut?
В нашей повседневной жизни мы сталкиваемся с последовательным и параллельным сочетанием резисторов во многих местах. Например, для цепей освещения мы используем параллельное соединение, а для приборов, которые работают непосредственно от сети, дается последовательное соединение.
CalculatorHut, универсальный центр научных и ненаучных онлайн-калькуляторов, предлагает бесплатный онлайн-калькулятор последовательного и параллельного сопротивления, который решит все ваши потребности в онлайн-калькуляторе бесплатно. Вы можете рассчитать до десяти резисторов, которые подключены последовательно или параллельно, с помощью этого удобного онлайн-калькулятора последовательного и параллельного сопротивления. Это очень удобный инструмент для студентов, который помогает им проверить правильность расчетов сопротивления.
CalculatorHut также предлагает широкий выбор из более 100 калькуляторов по различным темам — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные онлайн-калькуляторы для научных расчетов.
Наши читатели также могут получить бесплатный виджет любого калькулятора из нашего широкого спектра калькуляторов для встраивания в качестве виджетов на свои веб-сайты. Для этого они могут написать нам по адресу [адрес электронной почты]
.Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста, дайте нам знать.Мы будем более чем счастливы удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно и всегда!
Вот еще одна фантастическая новость! Вы можете бесплатно носить с собой в кармане наш широкий ассортимент онлайн-калькуляторов. Да! Бесплатное приложение CalculatorHut — ваш друг, который упрощает и упрощает любые вычисления! Удачных расчетов!
Сопротивление серии— Inst Tools
Общее сопротивление в последовательной цепи равно сумме всех частей этой цепи, как показано в уравнении ниже.
R
T = R1 + R2 + R3… и т. Д., где
R T = общее сопротивление
R1, R2 и R3 = последовательное сопротивлениеПример:
В последовательной цепи последовательно подключены резисторы 60 Ом, 100 Ом и 150 Ом (Рисунок 18). Какое полное сопротивление цепи?
Рисунок 18 Сопротивление в последовательной цепи
Решение:
РТ = R1 + R2 + R3
РТ = 60 + 100 + 150
RT = 310 Ом
Общее напряжение в последовательной цепи равно сумме напряжений на каждом резисторе в цепи (рисунок 19), как показано в уравнении ниже.
VT = V1 + V2 + V 3… и т. Д.
где
VT = общее напряжение
V1 = напряжение на R1
V2 = напряжение на R2
V3 = напряжение на R3
Рисунок 19 Падения напряжения в последовательной цепи
Теперь законОма может применяться ко всей последовательной цепи или к отдельным ее составным частям. При использовании на отдельных компонентах напряжение на этой части равно току, умноженному на сопротивление этой части.Для схемы, показанной на рисунке 20, напряжение можно определить, как показано ниже.
V1 = IR1
V2 = IR2
V3 = IR3VT = V1 + V2 + V3
VT = 10 В + 24 В + 36 В
VT = 70 ВРисунок 20 Суммарное напряжение в последовательной цепи
Чтобы найти полное напряжение в последовательной цепи, умножьте ток на общее сопротивление, как показано в уравнении ниже.
В
Т = I. Р тгде
VT = общее напряжение
I = ток
R T = общее сопротивлениеПример 1:
В последовательной цепи последовательно подключены резисторы 50 Ом, 75 Ом и 100 Ом (Рисунок 21).Найдите напряжение, необходимое для получения тока 0,5 ампер.
Рисунок 21 Пример 1 последовательной цепи
Решение:
Шаг 1: Найдите ток в цепи. Как мы уже знаем, ток в последовательной цепи один и тот же, он уже составляет 0,5 ампер.
Шаг 2: Найдите R T
РТ = R1 + R2 + R3
RT = 50 Ом + 75 Ом + 100 Ом
RT = 225 Ом
Шаг 3: Найдите VT.
Используйте закон Ома. В Т = I. Р т
VT = 0,5 x 225
VT = 112,5 вольт
Пример 2:
Батарея на 120 В соединена последовательно с тремя резисторами: 40 Ом, 60 Ом и 100 Ом (Рисунок 22). Найдите напряжение на каждом резисторе.
Рисунок 22 Пример 2 последовательной цепи
Решение:
Шаг 1: Найдите полное сопротивление.
РТ = R1 + R2 + R3
RT = 40 Ом + 60 Ом + 100 Ом
RT = 200 Ом
Шаг 2: Найдите ток в цепи (I).
Используйте закон Ома. В Т = I. Р т
Решение для I
I = V T / R T
I = 120/200 = 0,6 ампер
Шаг 3: Найдите напряжение на каждом компоненте.
-

