Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы использовать для вычислений. Как изменяются ток и напряжение в цепи при разных способах соединения. Примеры расчетов с пошаговым решением.
Основные принципы соединения резисторов
Резисторы в электрических цепях могут соединяться двумя основными способами:
- Последовательное соединение
- Параллельное соединение
Каждый способ соединения имеет свои особенности и применяется для решения различных задач. Рассмотрим подробнее каждый из них.
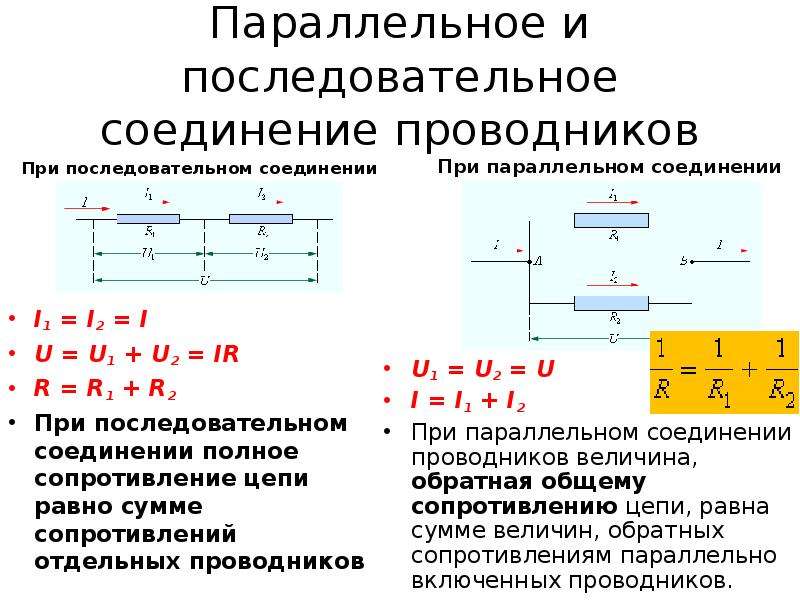
Последовательное соединение резисторов
При последовательном соединении резисторы включаются один за другим, образуя единую цепь. Ток проходит через все резисторы поочередно.
Основные характеристики последовательного соединения:
- Общее сопротивление равно сумме сопротивлений всех резисторов
- Сила тока одинакова во всех участках цепи
- Напряжение распределяется между резисторами пропорционально их сопротивлениям
Формула для расчета общего сопротивления:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Как рассчитать общее сопротивление при последовательном соединении.
Чтобы найти общее сопротивление последовательно соединенных резисторов, нужно сложить их номиналы. Например:
Дано: R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом
Решение: R = R1 + R2 + R3 = 100 + 200 + 300 = 600 Ом
Общее сопротивление цепи составит 600 Ом.
Параллельное соединение резисторов
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Ток разветвляется между резисторами.
Основные характеристики параллельного соединения:
- Общее сопротивление всегда меньше сопротивления любого из резисторов
- Напряжение на всех резисторах одинаковое
- Общий ток равен сумме токов через отдельные резисторы
Формула для расчета общего сопротивления:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Как рассчитать общее сопротивление при параллельном соединении.
Чтобы найти общее сопротивление параллельно соединенных резисторов, нужно:
- Найти обратные величины сопротивлений
- Сложить их
- Найти обратную величину от полученной суммы
Например:
Дано: R1 = 100 Ом, R2 = 200 Ом
Решение:
- 1/R1 = 1/100 = 0.01, 1/R2 = 1/200 = 0.005
- 1/R = 0.01 + 0.005 = 0.015
- R = 1/0.015 ≈ 66.7 Ом
Общее сопротивление цепи составит примерно 66.7 Ом.
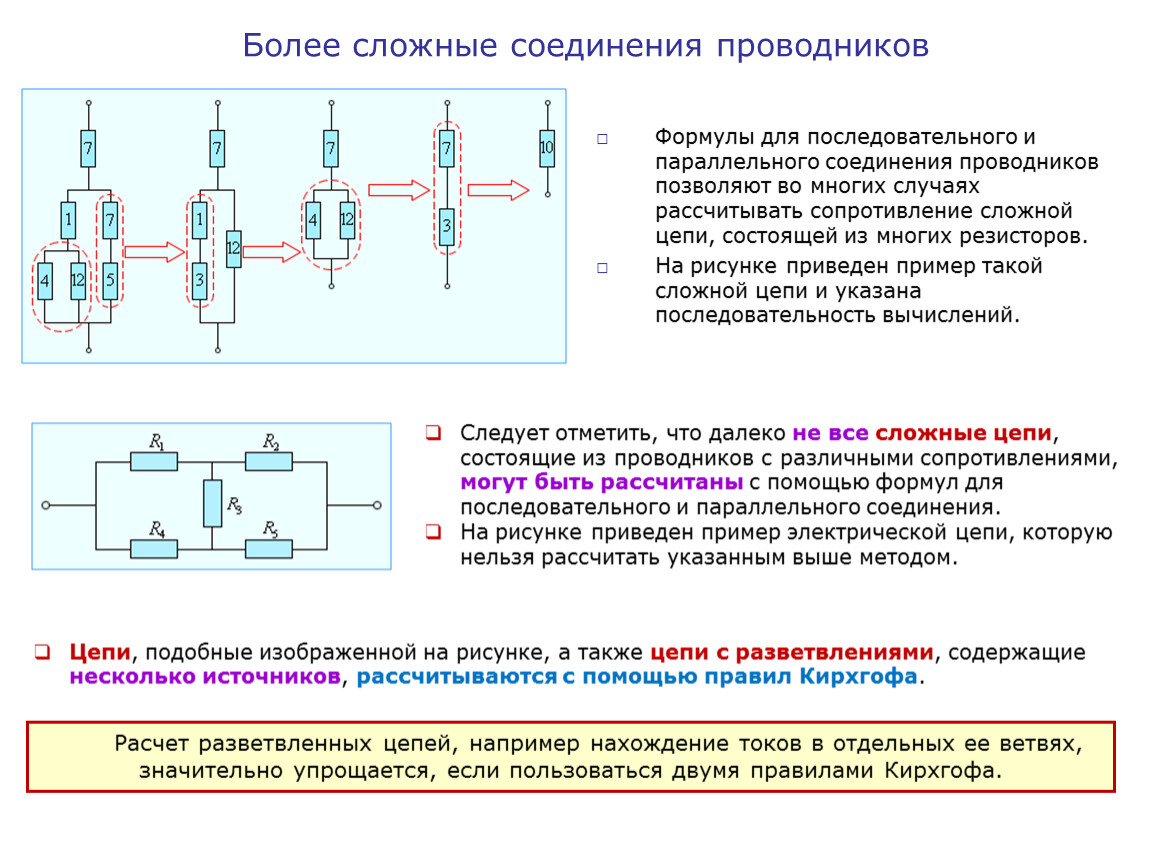
Смешанное соединение резисторов
В реальных схемах часто встречается комбинация последовательного и параллельного соединения резисторов. Такое соединение называется смешанным.
Для расчета общего сопротивления при смешанном соединении:
- Разбейте схему на группы последовательно и параллельно соединенных резисторов
- Рассчитайте сопротивление каждой группы по соответствующим формулам
- Объедините полученные результаты
Применение различных способов соединения резисторов
Где используется последовательное соединение:
- Для увеличения общего сопротивления цепи
- В делителях напряжения
- Для ограничения тока в цепи
Где применяется параллельное соединение:
- Для уменьшения общего сопротивления
- Для увеличения мощности рассеивания
- В схемах суммирования токов
Примеры расчетов
Пример 1: Последовательное соединение
Задача: Рассчитать общее сопротивление цепи, состоящей из трех последовательно соединенных резисторов: 100 Ом, 220 Ом и 330 Ом.

Решение:
R = R1 + R2 + R3 = 100 + 220 + 330 = 650 Ом
Ответ: Общее сопротивление цепи составляет 650 Ом.
Пример 2: Параллельное соединение
Задача: Найти общее сопротивление двух параллельно соединенных резисторов 100 Ом и 200 Ом.
Решение:
- 1/R = 1/R1 + 1/R2 = 1/100 + 1/200 = 0.01 + 0.005 = 0.015
- R = 1/0.015 ≈ 66.7 Ом
Ответ: Общее сопротивление цепи приблизительно равно 66.7 Ом.
Часто задаваемые вопросы
Как изменяется общее сопротивление при последовательном соединении резисторов.
При последовательном соединении общее сопротивление всегда увеличивается. Оно будет больше, чем сопротивление любого отдельного резистора в цепи.
Как меняется напряжение на резисторах при параллельном соединении.
При параллельном соединении напряжение на всех резисторах одинаковое и равно напряжению источника питания.
Почему параллельное соединение используется для увеличения мощности рассеивания.
При параллельном соединении ток распределяется между резисторами, что позволяет каждому из них рассеивать меньшую мощность. Это позволяет использовать резисторы меньшей мощности или увеличить общую рассеиваемую мощность.
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.
Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
формула сопротивление проводникаρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
 обозначение резистора на схемах
обозначение резистора на схемах
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
 последовательное соединение резисторов
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что
 формула при последовательном соединении резисторов
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
 сила тока через последовательное соединение проводников
сила тока через последовательное соединение проводников
Получается, что
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
 параллельное соединение резисторов
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:

Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Похожие статьи по теме “последовательное и параллельное соединение”
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
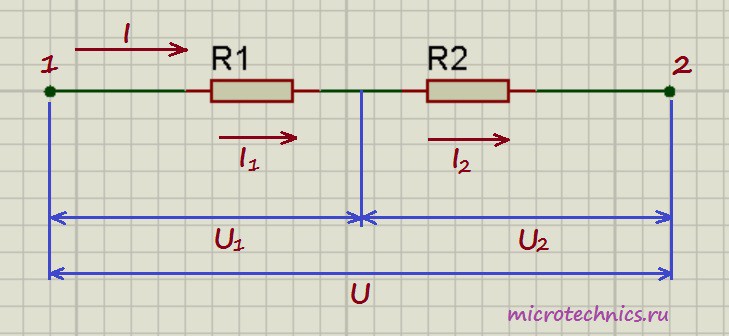
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
I = I_1 = I_2
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
U = U_1 + U_2
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
U_1 = I_1R_1 = IR_1
U_2 = I_2R_2 = IR_2
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжение также справедлив закон Ома:
U = IR_0
Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
R_0 = R_1 + R_2
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
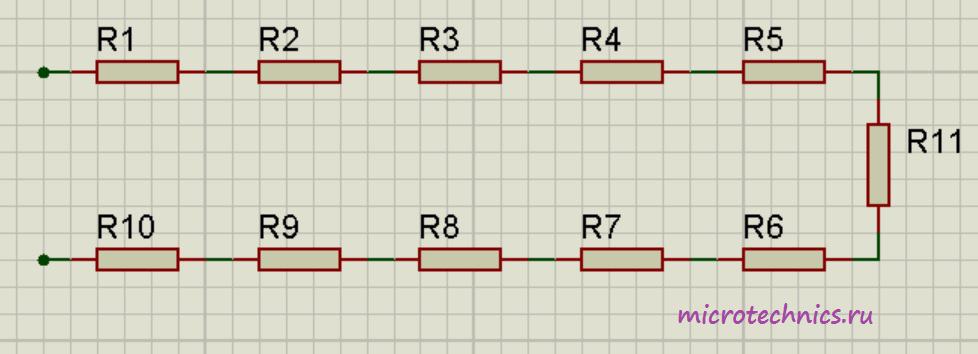
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:
R_0 = nR
В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
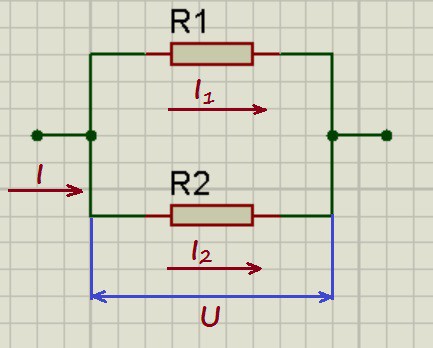
При параллельном соединении напряжения на проводниках равны:
U_1 = U_2 = U
А для токов справедливо следующее выражение:
I = I_1 + I_2
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}
I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}
Подставим эти выражения в формулу общего тока:
I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})
А по закону Ома ток:
I = \frac{U}{R_0}
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}
Данную формулу можно записать и несколько иначе:
R_0 = \frac{R_1R_2}{R_1 + R_2}
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
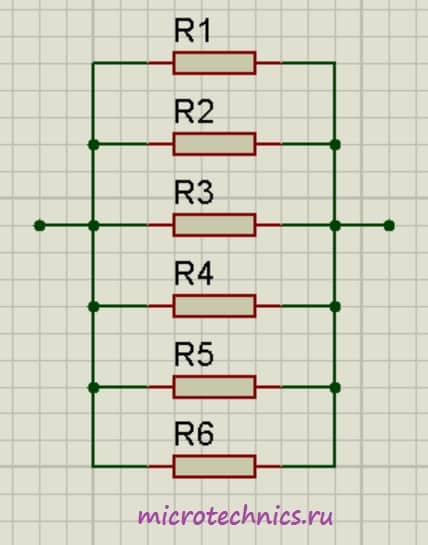
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
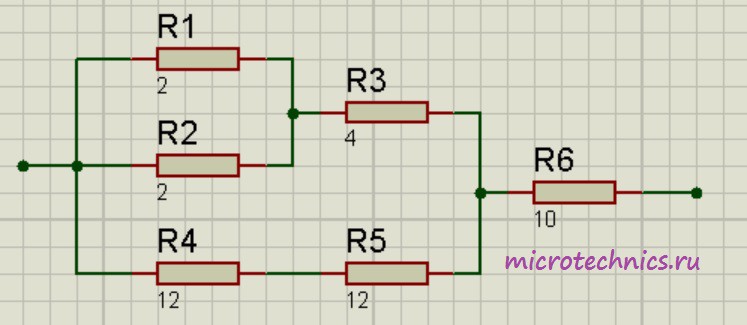
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:
R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1
Теперь у нас образовались две группы последовательно соединенных резисторов:
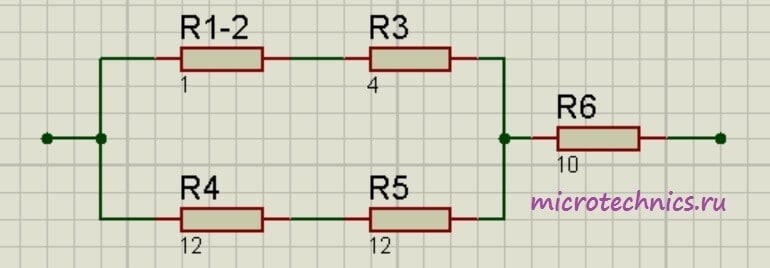
Заменим эти две группы двумя резисторами, сопротивление которых равно:
R_{1-2-3} = R_{1-2} + R_3 = 5
R_{4-5} = R_4 + R_5 = 24
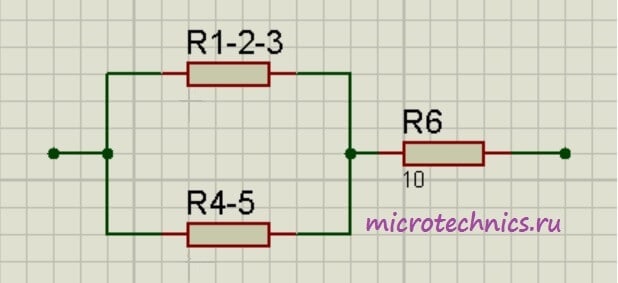
Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:
R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4.14
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
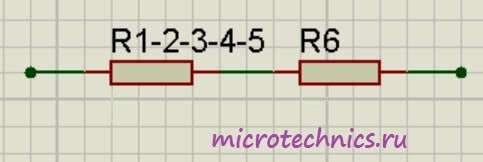
Общее сопротивление цепи получилось равным:
R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.
Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:
R = R1 + R2 + R3
То есть, в нашем случае общее сопротивление цепи будет равно:
R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.
Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.
Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).
Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:
Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.
В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
Необходимо рассчитать падение напряжения на выводах «А» и «В»:
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Резистор и сопротивление [База знаний]
Резистор и сопротивление
Теория
КОМПОНЕНТЫ
ARDUINO
ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ
Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.
Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:
1 кОм = 1000 Ом,1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
Ниже на рисунке видна маркировка резисторов на схемах:
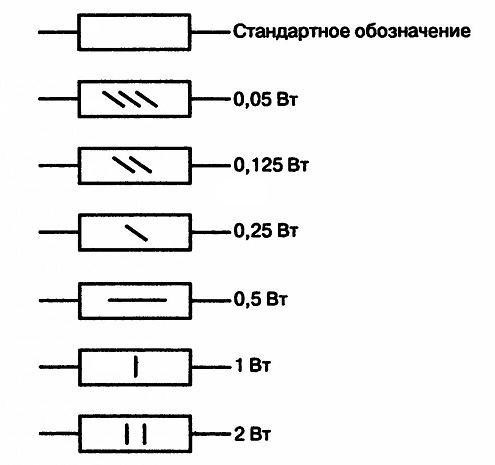
Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.
Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Последовательное соединение резисторов
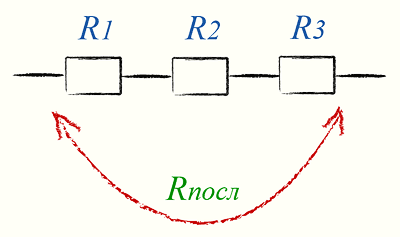 Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
Rобщ = R1 + R2
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
Rобщ = R1 + R2
Это справедливо и для большего количества соединённых последовательно резисторов:
Rобщ = R1 + R2 + R3 + … + RnЦепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200 + 100 + 51 + 39 = 390 Ом 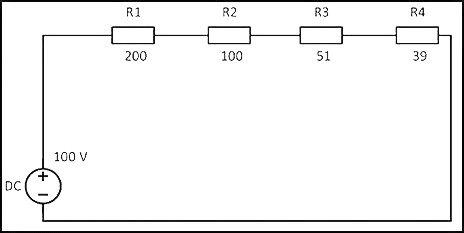
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 AНа основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I2 x R = 0,2562 x 390 = 25,55 ВтТаким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
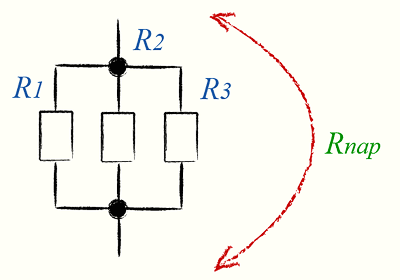 Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Rобщ = (R1 × R2) / (R1 + R2)Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
1 / Rобщ = 1 / R1 + 1 / R2 + … + 1 / RnСопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же. 1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 ОмR = 1 / 0,06024 ≈ 16,6 Ом
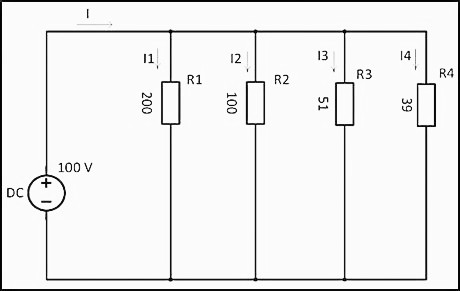
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 AЗная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I2 x R = 6,0242 x 16,6 = 602,3 ВтРасчет силы тока для каждого резистора выполняется по формулам:
I1 = U/R1 = 100/200 = 0,5 A;I2 = U/R2 = 100/100 = 1 A;
I3 = U/R3 = 100/51 = 1,96 A;
I4 = U/R4 = 100/39 = 2,56 A
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U2/R1 = 1002/200 = 50 Вт;P2 = U2/R2 = 1002/100 = 100 Вт;
P3 = U22/R3 = 1002/51 = 195,9 Вт;
P4 = U22/R4 = 1002/39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Калькулятор
Цветовая маркировка резисторов
Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.
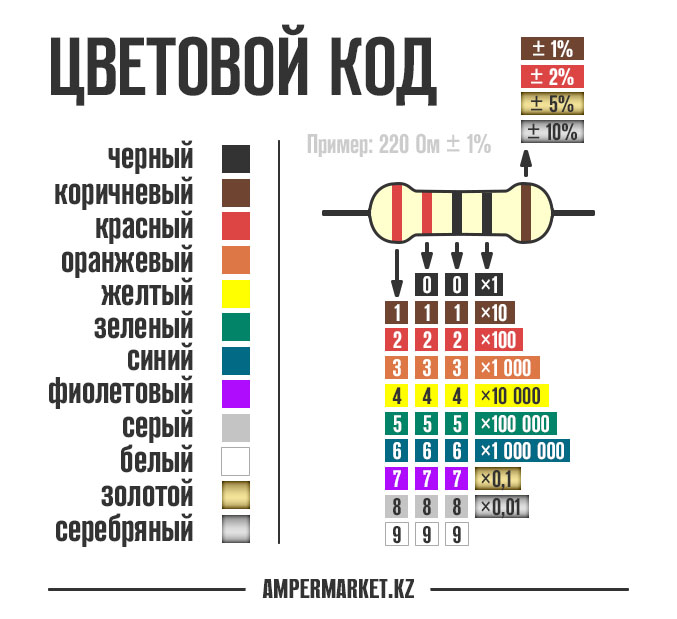
Калькулятор цветовой маркировки резисторов
Основные характеристики
| Сопротивление (номинал) | R | Ом |
| Точность (допуск) | ± | % |
| Мощность | P | Ватт |
Переменный резистор
Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:

На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.
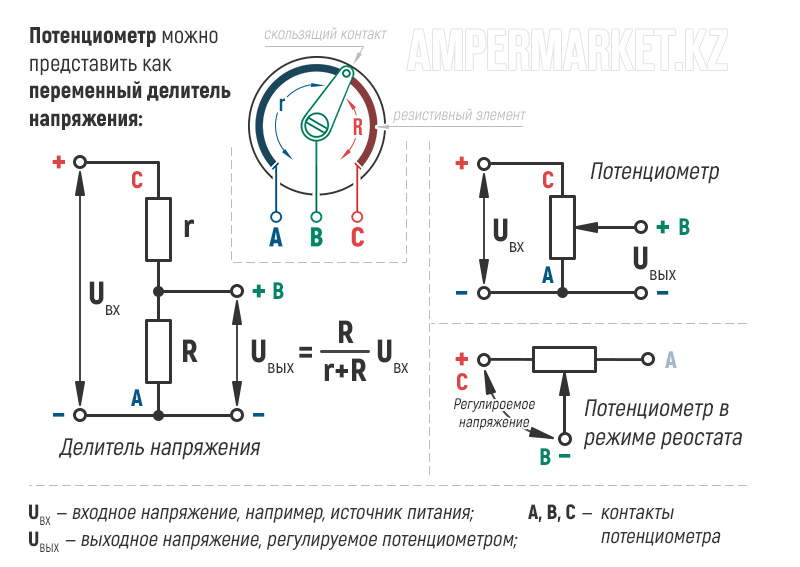
Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.

Термисторы, варисторы и фоторезисторы
Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.

В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:
Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.

На схемах варисторы обозначаются так:
В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.
А на схемах изображаются так:
Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
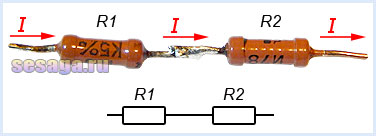
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
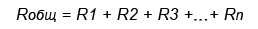
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
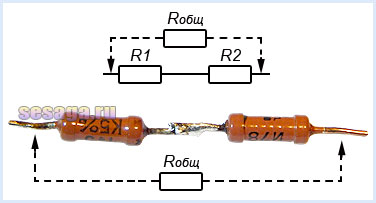
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Параллельное соединение резисторов
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
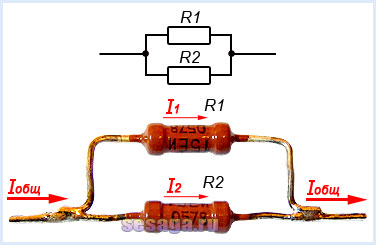
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
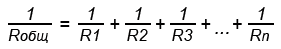
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:
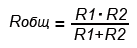
При включении трех резисторов расчет общего сопротивления будет таким:
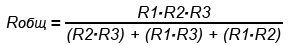
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.
На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
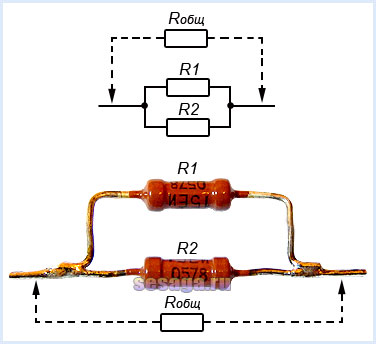
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
При последовательном соединении резисторов конец одного из них соединяется с началом следующего. В такой схеме через все резистивные элементы протекает одинаковый ток I, но падение напряжения на каждом из них пропорционально величине сопротивления. Для расчета электрических величин в схемах используется сложение сопротивлений всех элементов в последовательной цепи для получения суммарной величины, как показано на рисунке:
 Последовательное соединение резисторов
Последовательное соединение резисторов
Данный онлайн калькулятор позволяет выполнять расчет суммарного сопротивления для последовательно соединенных элементов цепи.
Чтобы воспользоваться калькулятором расчета вам необходимо:
- В окошке «количество резисторов» укажите число последовательно соединенных элементов, в данном случае, в схеме представлено три резистора, но может быть и другое количество;
- После этого в поле ниже появится несколько окошек, в которые вам необходимо внести значение сопротивления каждого резистора, к примеру, 10, 20 и 45 Ом;
- Нажмите кнопку «рассчитать» и в окошке «сопротивление» вы получите значение сопротивления в 75 Ом.
Для перехода к расчету следующей цепи или при необходимости подобрать другие элементы, нажмите кнопку «сбросить», чтобы обнулить значение последовательно включенных элементов калькулятора.
В работе калькулятора для определения сопротивления цепи последовательно соединенных резисторов используется принцип арифметического сложения. Поэтому формулу для определения суммарного значения можно представить следующим образом:
Rсум = R1 + R2 + R3 +…+ Rn
Где,
- Rсум — суммарное сопротивление последовательно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.
Так как в рассматриваемом примере включено только три элемента, то формула примет такой вид:
Rсум = R1 + R2 + R3
Подставив значение омического сопротивления каждого из элементов, получим:
Rсум = 10 + 20 + 45 = 75 Ом
Использование калькулятора для вычисления суммарного сопротивления в цепи последовательно соединенных резисторов наиболее актуально для схем с большим количеством элементов и дробными величинами.
90000 List of Factors affecting resistance 90001 90002 90003 Resistance is the property of the material that restricts the flow of electrons. There are four factors affecting resistance which are Temperature, Length of wire, Area of the cross-section of wire, and nature of the material. 90004 When there is current in a conductive material, the free electrons move through the material and occasionally collide with atoms. These collisions cause the electrons to lose some of their energy, and thus their movement is restricted.This restriction varies and is determined by the type of material. The property of a material that restricts the flow of electrons is called resistance. 90004 When there is current through any material that has resistance, heat is produced by the collisions of free electrons and atoms. Therefore, wire, which typically has a very small resistance, becomes warm when there is sufficient current through it. 90004 See Also: Types of electric charge 90004 90008 What is the unit of resistance? 90009 90004 Resistance, R, is expressed in ohms and is symbolized by the Greek letter omega (Ω).90004 «One ohm (1Ω) of resistance exists if there is one ampere (1A) of current in a material when one volt (1V) is applied across the material.» 90004 90008 What is conductance? 90009 90004 The reciprocal of resistance is conductance, symbolized by G.It is a measure of the ease with which current is established. The formula is: 90016 90002 G = 1 / R 90016 90002 The unit of conductance is the Siemens, abbreviated S.Foe example, the conductance of a 22KΩ resister is G = 1 / 22KΩ = 45.5μs. Occasionally, the obsolete unit of mho is still used for conductance.90004 See Also: Coulomb’s law 90016 90022 List of Factors affecting resistance 90023 90002 Resistance decreases with an increase in temperature. The thermistor is a temperature-dependent resistor and its resistance decreases as temperature rises. The thermistor is used in a circuit that senses temperature change. There are four factors on which resistance depends. 90016 90026 90027 Length (L) 90028 90027 it’s cross-sectional area (A) 90028 90027 the type of material 90028 90027 nature of material 90028 90035 90002 The resistance of a wire depends both on the cross-sectional area and length of the wire and on the nature of the material of the wire.Thick wires have less resistance than thin wires. Longer wires have more resistance than short wires. Copper wire has less resistance thin steel wire of the same size. Electrical resistance also depends on temperature. At a certain temperature and for a particular substance. 90016 90038 How does the length of the wire affect resistance? 90039 90002 The resistance R of the wire is directly proportional to the length of the wire: 90016 90002 R α L … .. (1) 90016 90002 It means, if we double the length of the wire, its resistance will also be doubled, and if its length is halved, its resistance would become one half.90016 90046 Relation of resistance with area: 90047 90002 The resistance R of a wire is inversely proportional to the area of cross-section A of the wire as: 90016 90002 R α 1 / A …… (2) 90016 90002 It means that a thick wire would have smaller resistance than a thin wire. After combining the equations (1) and (2) we get; 90016 90002 R α L / A 90016 90002 R = ρL / A …. (3) 90016 90002 Where ρ is the constant of proportionality, known as specific resistance. Its value depends upon the nature of conductor i.e copper, iron, tin, and silver would each have different values of ρ. From equation (3) we have; 90016 90002 ρ = R A /L….(4) 90016 90002 If L = 1m, A = 1m² then ρ = R.Thus the equation (4) gives the definition. 90004 See also: Difference between Voltage and current 90016 90022 90008 What is specific resistance? 90009 90023 90002 The resistance of a one-meter cube of a substance is equal to its specific resistance. The unit of ρ is ohm-meter (Ωm) .Below given table of some metals with specific resistance: 90016 90046 Metal specific resistance (10-8Ω) 90047 90026 90027 silver 1.7 90028 90027 Copper 1.69 90028 90027 Aluminum 2.75 90028 90027 Tungsten 5.25 90028 90027 Platinum 10.6 90028 90027 Iron 9.8 90028 90027 Ni-chrome 100 90028 90027 Graphite 3500 90028 90035 90002 90008 What are conductors? 90009 90004 A material or an object that conducts heat, electricity, light or sound is called conductors.Metal wires are good conductors of electricity and offer less resistance to the flow of current.Why metals conduct electricity? … Metals like silver and copper have an excess of free electrons which are not held strongly with any particular atom of metals. These free electrons move randomly in all directions inside metals. When we apply external field these electrons can easily move in a specific direction. 90004 This movement of free electrons in a particular direction under the influence of an external field causes the flow of current in metal wires. 90016 90038 How does resistance increase with temperature? 90039 90002 The conductors have a low value of resistance.The resistance of conductors increases with an increase in temperature. This is due to an increase in the number of collisions of electrons with themselves and with the atoms of the metals. Gold, silver, copper, aluminum, and other metals are good examples of conductors. Earth is also a very good and big conductor. 90004 90008 What are insulators? 90009 90004 A material that does not easily transmit energy, such as electric current or heat is called insulators. why insulators do not conduct electricity ?.All materials contain electrons. The electrons in insulators, like rubber, however, are not free to move. They are tightly bound inside atoms. Hence, current can not flow through an insulator because they are no free electrons for the flow of current. Insulators have a very large value of resistance.Glass, wood, plastic, fur, silk, etc. 90016 90022 Combinations of resistance in the electric circuit 90023 90002 There are two possible combinations of resistance in electric circuits: 90016 90026 90027 90046 Series combination 90047 90028 90027 90046 Parallel combination 90047 90028 90035 90119 90027 90038 Series combination: 90039 90028 90124 90002 In series combinations , resistors are connected end to end and electric current has a single path through the circuit.This means that the current passing through each resistor is the same. 90126 90004 The current is the same through all points in the series circuit. The current through each resistor in a series circuit is the same as the current through all the resistors that are in series with it. In the above figure, three resistors are connected in series to a DC voltage source. 90004 At any point in this circuit, the current into that point must equal the current out of that point. Notice also that the current out of each resistor must equal the current into each resistor because there is no place where part of the current can branch-off and go somewhere else.90004 Therefore, the current in each section of the circuit is the same as the current in all other sections. It has only one path going from the positive (+) side of the source to the negative (_) side. 90016 90046 Total series resistance: 90047 90133 90002 The total series resistance of a series circuit is equal to the sum of the resistance of each individual series resistor. When resistors are connected in series, the resistor values add because each resistor offers opposition to the current in the direct proportion to its resistance.A greater number of resistors connected in series creates more opposition to current. More opposition to current implies a higher value of resistance. Thus, every time a resistor is added in series, the total resistance increases. 90004 See also: Types of electric charge 90016 90046 Formula of total resistance in series combination: 90047 90002 For any number of individual resistors connected in series, the total resistance is the sum of each of the individual values. 90016 90002 Rt = R1 + R2 + R3 + R4 + ……….. + Rn 90016 90002 Where Rt is the total resistance and Rn is the last resistor in the series string. For example, if there are 3 resistors in series .the total resistance formula will be 90016 90002 Rt = R1 + R2 + R3 90016 90002 If there are six resistors in series (n = 6), the total resistance formula will be: 90016 90002 Rt = R1 + R2 + R3 + R4 + R5 + R6 90016 90038 2: Parallel combination: 90039 90002 When two or more resistors are individually connected between the same two separate points, they are in parallel with each other.A parallel circuit provides more than one path for current. 90154 90016 90002 Each current path is called a 90008 branch 90009. A 90159 parallel 90160 circuit 90159 90160 is one more that has more than one branch. Three resistors are connected in parallel shown in the above figure. When resistors are connected in parallel, the current has more than one path. The number of current paths is equal to the number of parallel branches. 90016 90046 Formula for total parallel resistance: 90047 90002 Since Vs is the voltage across each of the parallel resistors in the above figure, by 90008 Ohm’s law 90009 I = Vs / R 90008: 90009 90016 90002 Vs / Rt = Vs / R1 + Vs / R2 + Vs / R3 …….(1) 90016 90002 The term Vs can be factored out of the right side of the equation and canceled with Vs on the left side, leaving only the resistance terms. 90016 90002 1 / Rt = 1 / R1 + 1 / R2 + 1 / R3 …… (2) 90016 90002 Recall that the reciprocal of resistance (1 / R) is called 90008 conductance 90009, which is 90008 90009 symbolized by G.The unit of conductance is the Siemens (s). Equation (2) can be expressed in terms of conductance as: 90016 90002 Gt = G1 + G2 + G2 90016 90002 Solve for Rt in equation (2) by taking the reciprocal of that is inverting both sides of the equation.90016 90002 Rt = 1 / (1 / R1) + (1 / R2) + (1 / R3) 90016 90002 90008 Related topics: 90009 90016.90000 Resistance Formula 90001 90002 Electrical resistance is a property of materials that allow electric current to flow. Resistance opposes the flow of current. The unit of resistance is Ohms, which is represented with the Greek uppercase letter omega: Ω. Resistors are components of electric circuits. The resistance depends on the voltage across the resistor, and the current flowing through it. 90003 90002 90005 90003 90002 90008 90003 90002 R = resistance (Ohms, Ω) 90003 90002 V = voltage difference between the two ends of a resistor (Volts, 90013 V 90014) 90003 90002 I = the current flowing through a resistor (Amperes, A) 90003 90002 Resistance Formula Questions: 90003 90002 1) In an electric circuit, a current of 3.00 90013 A 90014 is flowing through a resistor. The voltage drop from one end of the resistor to the other is 120 V. What is the value of the resistance? 90003 90002 Answer: 90003 The resistance can be found using the formula: 90002 90008 90003 90002 90030 90003 90002 R = 40.0 Ω 90003 90002 The resistance of the resistor in the circuit is 40.0 Ω. 90003 90002 2) A certain resistor in a circuit has a resistance of 300.0 90013 kΩ 90014. If the voltage difference across this resistor is 1500 V, how much electric current is flowing through the resistor? 90003 90002 Answer: 90003 The resistance is given in units of 90013 kΩ 90014, meaning kilo-Ohms.One kilo-Ohm is equal to one thousand Ohms: 1 90013 kΩ 90014 = 1000 Ω. The resistance is therefore: 90002 90047 90003 R = 300000 Ω The current can be found by rearranging the formula: 90002 90050 90003 90002 90053 90003 90002 90056 90003 90002 I = 0.0050 90013 A 90014 90003 90002 The current flowing through the resistor is 0.0050 90013 A 90014. This can also be stated in milli-Amperes. One milli-Ampere is equal to one one-thousanth of an Ampere: 1 mA = 1/1000 90013 A 90014 = 0.001 90013 A 90014. In these units, the current is: 90003 90002 90071 90003 I = 5.0 90013 mA 90014 The current flowing through the resistor is 0.0050 A, which is equal to 5.0 90013 mA 90014. .90000 Resistance in Series — Explanation, Formula and Numericals 90001 90002 Last updated at April 28, 2020 by Teachoo 90003 90002 In this type of combination, different resistors are joined end to end. (One after the another) 90003 90002 Example 90003 90002 90009 90003 90002 90003 90002 This is done to Increase Resistance of Circuit 90003 90002 In this case Total Resistance of circuit is equal to sum of Individual Resistance of the Resistors 90003 90002 R = R 90018 1 90019 + R 90018 2 90019 + R 90018 3 90019 90003 90002 90003 90002 Example 90003 90002 Suppose Resistance of 2 resistors are 20 Ω and 30 Ω 90003 90002 Hence, R 90018 1 90019 = 20 Ω and R 90018 2 90019 = 30 Ω 90003 90002 Total Resistance = R 90018 1 90019 + R 90018 2 90019 = 20 + 30 = 50 Ω 90003 90043 90044 90043 IMPORTANT POINTS 90044 90047 When 2 Resistors are Connected in Series 90048 90049 90050 Same Current flows throughout the circuit in all resistors Let it be denoted by I 90051 90050 Potential Difference across combination of Resistors is equal to total Potential Difference of Each Resistor 90053 Suppose 3 Different Resistors have Potential Difference of V 90018 1 90019 , V 90018 2 90019 and V 90018 3 90053 90019 Total Potential Difference V = V 90018 1 90019 + V 90018 2 90019 + V 90018 3 90053 90019 Hence, Total Potential Difference is equal to voltage of the battery 90051 90050 Total Resistance is equal to Individual Resistance of each Resistor Hence R = R 90018 1 90019 + R 90018 2 90019 + R 90018 3 90019 90051 90077 90047 90048 90047 How is the Resistance formula Derived — for series circuits? 90048 90002 90083 90003 90002 90086 90003 90002 90003 90002 Resistance of first resistor + second resistor + third resistor = Total Resistance 90003 90002 Hence we can say that sum of Individual Resistance of 3 resistors is equal to Total Resistance 90003 90002 So more than one resistors are combined together to increase resistance of the circuit 90003 90002 More the Resistance, less the current flows through circuit 90003 90002 Hence, this method is used to reduce current flow in circuit 90003 90002 90003 90102 90002 90104 Note -: 90105 In case of series, the total resistance is always greater than the resistance of the resistors.90053 The resistance produced is highest when resistors are connected in series. 90003 90108 90002 90003 90102 90002 90104 Note -: 90105 An ammeter is connected in series in a circuit so that it can detect the net current flowing in a circuit. 90003 90108 90043 90044 90043 Questions 90044 90002 90104 Q1 Page 213 — 90105 Draw a schematic diagram of a circuit consisting of a battery of three cells of 2V each, a 5Ω resistor, an 8 Ω resistor, and a 12 Ω resistor.And a plug key, all connected in series. 90003 90002 View Answer 90003 90002 90003 90002 90104 Q2 Page 213 90105 — Redraw the circuit of Question 1, putting in an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the 12 Ω resistor. What would be the readings in the ammeter and the voltmeter? 90003 90002 View Answer 90003 90002 90003 90002 90003 90002 90104 Example 12.7 — 90105 An electric lamp, whose resistance is 20 Ω, and a conductor of 4 Ωresistance are connected to a 6 V battery (Fig.12.9). Calculate 90053 (a) the total resistance of the circuit, 90053 (b) the current through the circuit, and 90053 (c) the potential difference across the electric lamp and conductor. 90003 90002 View Answer 90003 90002 90104 90105 90003 90002 90104 Question 4 — 90105 What is the maximum resistance which can be made using five 90003 90002 (A) 1/5 Ω 90003 90002 (B) 10 Ω 90003 90002 (C) 5 Ω 90003 90002 (D) 1 Ω 90003 90002 View Answer 90003 90002 90003 90002 90104 Question 9 — 90105 A cell, a resistor, a key and ammeter are arranged as shown in the circuit diagrams below.The current recorded in the ammeter will be 90003 90002 (A) maximum in (i) 90003 90002 (B) maximum in (ii) 90003 90002 (C) maximum in (iii) 90003 90002 (D) the same in all the cases 90003 90002 View Answer 90003 90002 90003 90002 90104 Question 11 — 90105 Why does Ammeter have low resistance? Given reason 90003 90002 Why does Voltmeter have high resistance? 90003 90002 View Answer 90003 90002 90003 90002 90003 90102 90002 Subscribe to our Youtube Channel — https: // you.tube / teachoo 90003 90108 .90000 Series Resistance | PVEducation 90001 Skip to main content 90002 90003 90004 Menu 90005 90006 90002 90004 Instructions 90005 90004 1. Introduction 90002 90004 1. Introduction 90005 90004 Introduction 90005 90004 Solar Energy 90005 90004 The Greenhouse Effect 90005 90006 90005 90004 2. Properties of Sunlight 90002 90004 2. Properties of Sunlight 90005 90004 2.1. Basics of Light 90005 90004 Properties of Light 90005 90004 Energy of Photon 90005 90004 Photon Flux 90005 90004 Spectral Irradiance 90005 90004 Radiant Power Density 90005 90038 2.2. Blackbody Radiation 90005 90004 2.3. Solar Radiation 90005 90004 The Sun 90005 90004 Solar Radiation in Space 90005 90004 2.4. Terrestrial Solar Radiation 90005 90004 Solar Radiation Outside the Earth’s Atmosphere 90005 90004 Atmospheric Effects 90005 90004 Air Mass 90005 90004 Motion of the Sun 90005 90004 Solar Time 90005 90004 Declination Angle 90005 90004 Elevation Angle 90005 90004 Azimuth Angle 90005 90004 The Sun’s Position 90005 90004 Sun Position Calculator 90005 90004 Sun’s Position to High Accuracy 90005 90004 Solar Radiation on a Tilted Surface 90005 90004 Arbitrary Orientation and Tilt 90005 90004 2.5. Solar Radiation Data 90005 90004 Calculation of Solar Insolation 90005 90004 Measurement of Solar Radiation 90005 90004 Analysis of Solar Irradiance Data Sets 90005 90004 Typical Meteorological Year Data (TMY) 90005 90004 Making Use of TMY Data 90005 90004 Average Solar Radiation 90005 90004 Isoflux Contour Plots 90005 90004 Sunshine Hour Data 90005 90004 Cloud Cover Data 90005 90004 Satellite Irradiance 90005 90006 90005 90004 3. Semiconductors & Junctions 90002 90004 3. Semiconductors & Junctions 90005 90004 Introduction 90005 90004 3.1. Basics 90005 90004 Semiconductor Materials 90005 90004 Semiconductor Structure 90005 90004 Conduction in Semiconductors 90005 90004 Band Gap 90005 90004 Intrinsic Carrier Concentration 90005 90004 Doping 90005 90004 Equilibrium Carrier Concentration 90005 90004 3.2. Generation 90005 90004 Absorption of Light 90005 90004 Absorption Coefficient 90005 90004 Absorption Depth 90005 90004 Generation Rate 90005 90004 3.3. Recombination 90005 90004 Types of Recombination 90005 90004 Lifetime 90005 90004 Diffusion Length 90005 90004 Surface Recombination 90005 90004 3.4. Carrier Transport 90005 90004 Movement of Carriers in Semiconductors 90005 90004 Diffusion 90005 90004 Drift 90005 90004 3.5. P-n Junctions 90005 90004 Formation of a PN-Junction 90005 90004 PN Junction Diodes 90005 90004 Bias of PN Junctions 90005 90004 Diode Equation 90005 90004 3.6. Diode Equations for PV 90005 90160 Ideal Diode Equation Derivation 90005 90004 Basic Equations 90005 90004 Applying the Basic Equations to a PN Junction 90005 90004 Solving for Depletion Region 90005 90004 Solving for Quasi Neutral Regions 90005 90004 Finding Total Current 90005 90004 90005 90006 90005 90006.Следует отметить, если вам известно омическое сопротивление каждого элемента в разных единицах измерения (Ом, кОм, МОм), то их следует привести к одной, к примеру, к Омам, так как калькулятор выполняет расчет для всех резисторов в одинаковой единице.
