Постоянное магнитное поле. Влияние постоянного магнитного поля на костную ткань: эффекты и применение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как постоянное магнитное поле воздействует на костную ткань. Какие эффекты оказывает магнитное поле на состояние костей. Где применяется магнитотерапия для лечения заболеваний костной системы.

Содержание

Что такое постоянное магнитное поле и как оно влияет на организм

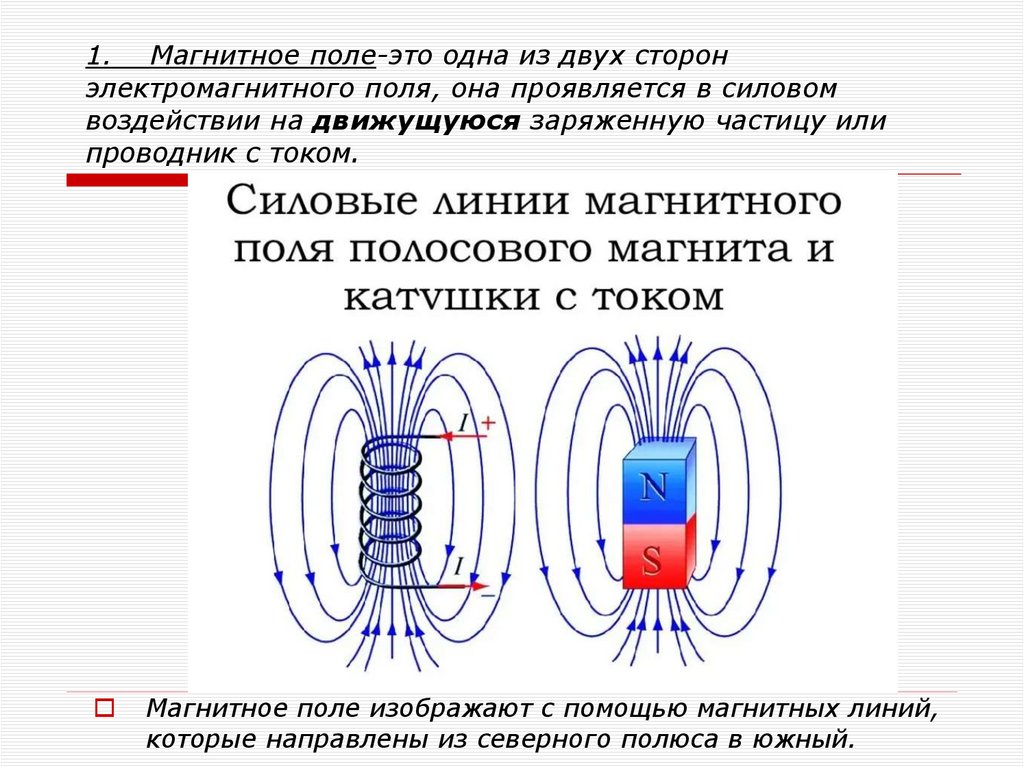
Постоянное магнитное поле — это магнитное поле, не изменяющееся во времени. Основные источники постоянного магнитного поля:

Постоянные магниты
Электромагниты, питаемые постоянным током
Магнитное поле Земли

При воздействии на организм постоянное магнитное поле оказывает следующие эффекты:

Улучшает микроциркуляцию крови
Оказывает противовоспалительное и обезболивающее действие
Стимулирует регенерацию тканей
Нормализует обменные процессы
Повышает иммунитет

Эти свойства делают постоянное магнитное поле перспективным для применения в медицине, в том числе для лечения заболеваний костной системы.

Влияние магнитного поля на костную ткань

Исследования показывают, что воздействие постоянного магнитного поля на костную ткань вызывает следующие эффекты:

Стимулирует активность остеобластов — клеток, образующих костную ткань
Усиливает синтез коллагена и минерализацию костного матрикса
Улучшает кровоснабжение костной ткани
Ускоряет регенерацию костной ткани при переломах
Замедляет процессы резорбции (разрушения) костной ткани

Таким образом, магнитное поле способствует укреплению костей и может применяться для профилактики и лечения остеопороза и других заболеваний, связанных с потерей костной массы.

Применение магнитотерапии при заболеваниях костной системы

На основе положительного влияния магнитного поля на костную ткань разработаны методы магнитотерапии, которые применяются в следующих случаях:

Лечение переломов костей — для ускорения срастания
Остеопороз — для замедления потери костной массы

Остеоартроз — для уменьшения воспаления и боли в суставах
Остеохондроз позвоночника
Травмы и заболевания связочного аппарата

Магнитотерапия может проводиться с помощью стационарных аппаратов в медицинских учреждениях или портативных устройств для домашнего использования. Курс обычно составляет 10-15 процедур длительностью 15-30 минут.

Механизмы воздействия магнитного поля на костную ткань

Основные механизмы влияния постоянного магнитного поля на костную ткань включают:

Усиление локального кровотока и микроциркуляции в костной ткани
Активация ферментов, участвующих в костном метаболизме
Стимуляция синтеза белков и нуклеиновых кислот в костных клетках
Повышение активности остеобластов и торможение активности остеокластов
Усиление поглощения кальция костной тканью

Эти процессы в совокупности приводят к усилению образования костной ткани и замедлению ее резорбции, что способствует укреплению костей.

Экспериментальные исследования влияния магнитного поля на кости

Многочисленные эксперименты на животных подтверждают положительное влияние постоянного магнитного поля на состояние костной ткани:

У крыс с экспериментальным остеопорозом магнитное поле предотвращало потерю костной массы
При переломах костей у животных наблюдалось более быстрое образование костной мозоли под действием магнитного поля
Магнитное поле усиливало пролиферацию и дифференцировку остеобластов в клеточных культурах
Отмечалось увеличение минеральной плотности костной ткани у животных, подвергавшихся воздействию магнитного поля

Эти данные свидетельствуют о перспективности применения магнитотерапии для укрепления костной ткани и лечения костных заболеваний.

Применение постоянных магнитов для терапии костно-суставной системы

Помимо аппаратной магнитотерапии, для воздействия на костно-суставную систему применяются постоянные магниты небольшой мощности:

Магнитные браслеты и повязки
Магнитные стельки для обуви
Магнитные аппликаторы
Магнитные матрацы

Их применяют при остеохондрозе, артрозах, травмах суставов и связок. Постоянные магниты создают локальное магнитное поле, которое улучшает кровообращение, уменьшает воспаление и боль в области воздействия.

Противопоказания к применению магнитотерапии

Несмотря на безопасность и эффективность, магнитотерапия имеет ряд противопоказаний:

Наличие кардиостимулятора или других электронных имплантов
Беременность
Онкологические заболевания
Эпилепсия
Тяжелые нарушения сердечного ритма
Гипертоническая болезнь III стадии

Перед применением магнитотерапии необходимо проконсультироваться с врачом, особенно при наличии хронических заболеваний.

Заключение

Постоянное магнитное поле оказывает многостороннее положительное влияние на костную ткань, стимулируя образование костной ткани и замедляя процессы ее резорбции. Это делает магнитотерапию перспективным методом профилактики и лечения остеопороза, ускорения заживления переломов и лечения других заболеваний костно-суставной системы. Однако необходимы дальнейшие клинические исследования для определения оптимальных параметров воздействия и разработки эффективных схем лечения.

Постоянное магнитное поле и его влияние на организм человека

Постоянное магнитное поле (далее – ПМП) – это одна из форм электромагнитного поля. Источниками ПМП являются постоянные магниты, электромагниты, сильноточные системы постоянного тока. Постоянные магниты широко используются в приборостроении и при устройствах динамиков, магнитных сепараторов, устройств для магнитной обработки воды, магнито-гидродинамических генераторах, установках ядерного магнитного резонанса, электронного парамагнитного резонанса и пр. Наиболее чувствительными к воздействию ПМП являются системы, выполняющие регуляторные функции (нервная, сердечно-сосудистая, нейроэндокринная и др.) в организме человека. У работающих с источниками ПМП наиболее часто встречаются изменения в здоровье в форме вегетодистоний, астеновегетативного и периферического вазовегетативного синдромов или их сочетания. Периферический вазовегетативный синдром характеризуется вегетативными, сенситивными расстройствами (атаксия — нарушение походки и координации движений в результате поражения путей глубокой мышечно-суставной чувствительности. У больного исчезает представление о направлении и объеме движений, он не ощущает, как располагаются в пространстве части его тела).

Кровь достаточно устойчива к воздействию ПМП. Отмечается лишь тенденция к снижению количества эритроцитов и содержания гемоглобина, а также умеренный лейко- и лимфоцитоз. Поэтому под воздействием ПМП улучшается циркуляции крови, а также изменяется прохождение нервных импульсов, увеличивается содержание кислорода в крови и увеличивается щелочной состав физиологических жидкостей, магнитное влияние на движущиеся ионы, уменьшаются отложения на стенках кровеносных сосудов и др.

Существует широкий круг медицинских приборов и устройств, методов диагностики и лечения, способов борьбы с различными медицинскими проблемами человека, в которых магнитные явления и свойства магнитных материалов не только с успехом используются, но их применение является научно оправданным.

В перечень исследуемых физических факторов отделения гигиены физических факторов входит проведение инструментальных измерений уровня постоянного магнитного поля.

Постоянное магнитное поле

Источниками этого поля являются постоянные электрические токи, движущиеся электрические заряды (телами и частицами), намагниченные тела, переменные электрические поля. Источниками постоянного магнитного поля являются постоянные токи.

Свойства магнитного поля

Во времена, когда изучение магнитных явлений только началось, исследователи особенное внимание уделяли тому, что существуют полюса в намагниченных брусках. В них магнитные свойства проявлялись особенно ярко. При этом четко было видно, что полюса магнита различны. Разноименные полюса притягивались, а одноименные отталкивались. Гильберт высказал идею о существовании «магнитных зарядов». Эти представление подержал и развил Кулон. На основе опытов Кулона силовой характеристикой магнитного поля стала сила, с которой магнитное поле действует на магнитный заряд, равный единице. Кулон же обратил внимание на существенные различия между явлениями в электричестве и магнетизме. Различие проявляется уже в том, что электрические заряды можно разделить и получить тела с избытком положительного или отрицательного заряда, тогда как невозможно разделить северный и южный полюса магнита и получить тело только с одним полюсом. Из невозможности деления магнита на исключительно «северный» или «южный» Кулон решил, что два эти вида зарядов неразрывны в каждой элементарной частице намагничивающего вещества. Так, было признано, что каждая частица вещества — атом, молекула или их группа — есть нечто вроде микро магнита с двумя полюсами. Намагничивание тела при этом — процесс ориентации его элементарных магнитов под влиянием внешнего магнитного поля (аналог поляризации диэлектриков).

Взаимодействие токов реализуется посредством магнитных полей. Эрстед обнаружил, что магнитное поле возбуждается током и оказывает ориентирующее действие на магнитную стрелку. У Эрстеда проводник с током был расположен над магнитной стрелкой, которая могла вращаться. Когда ток шел в проводнике, стрелка поворачивалась перпендикулярно проволоке. Смена направления тока вызывало переориентацию стрелки. Из опыта Эрстеда следовало, что магнитное поле имеет направление и должно характеризоваться векторной величиной. Эту величину назвали магнитной индукцией и обозначили: $\overrightarrow{B}.2}\left(2\right),\]

где$\ \overrightarrow{r}$- радиус-вектор, проведенный из элемента тока в рассматриваемую точку, $\overrightarrow{dl}$- элемент проводника с током (направление задано направление тока), $\vartheta$ — угол между $\overrightarrow{dl}$ и $\overrightarrow{r}$. Направление вектора $\overrightarrow{dB}$ — перпендикулярно к плоскости, в которой лежат $\overrightarrow{dl}$ и $\overrightarrow{r}$. Определяется правилом правого винта.

Для магнитного поля выполняется принцип суперпозиции:

\[\overrightarrow{B}=\sum{{\overrightarrow{B}}_i\left(3\right),}\]

где ${\overrightarrow{B}}_i$ — отдельные поля, которые порождаются движущимися зарядами, $\overrightarrow{B}$ — суммарная индукция магнитного поля.

Пример 1

Задание: Найдите отношение сил магнитного и кулоновского взаимодействия двух электронов, которые движутся с одинаковыми скоростями $v$ параллельно. Расстояние между частицами постоянно.

Решение:

Будем считать, что один электрон поле создает (и магнитное и электрическое), а другой в нем движется.2}2\pi R=\frac{{\mu }_0}{2}\frac{I}{R}.\]

Ответ: $B$=$\frac{{\mu }_0}{2}\frac{I}{R}.$

Постоянное магнитное поле и его физиотерапевтическое воздействие на организм

Что такое физиотерапия?

Не всегда даже медики – профессионалы четко понимают, что такое физиотерапия. Физис – природа, т.е. использование природных факторов в лечебных, профилактических и реабилитационных целях.

А что такое природные или физические факторы? Вы хорошо их знаете. Они делятся на так называемые естественные – это солнце, воздух, вода, лечебные грязи и вторую часть – это преформированные (т.е. видоизмененные) – по сути это те же природные факторы, но они видоизменены при помощи аппаратов. Это — электрическая энергия, магнитные поля, все это есть в природе, та же световая энергия, но при помощи аппарата они подводятся к человеку, это составляет второй раздел физиотерапии – аппаратная физиотерапия, которая и используется в кабинетах физиотерапии каждой поликлиники. 115 лет назад профессором Штанге была создана Санкт-Петербургская кафедра физиотерапии. Сразу хочу обратить внимание, что наряду с тем, что физиотерапия это была медицинская специальность, всегда существовала домашняя физиотерапия. Хотя, по большому счету, домашняя физиотерапия присутствовала у человечества всегда: во-первых, это лёд, который прикладывали к ушибам и травмам, это и грелки для прогревания. Естественно, с развитием цивилизации, под влиянием технического прогресса появилась аппаратная физиотерапия и для домашнего применения. Человек дома всегда использовал методы физиотерапии и знал, что это поможет. Кстати, очень важный вопрос: «А это поможет?» Вроде дозы такие небольшие. Вы должны четко понимать: «Да, это поможет.»

Это связано с жизнью в целом. Дело в том, что Вы хорошо знаете, что человек живет в различных условиях от Сахары до Арктики. Наш организм всегда подвергается воздействию всевозможных факторов: то дождь льет, то жара, то холод и пр. Это очень серьёзная нагрузка на защитные силы организма. Несмотря на это, мы живы и наш организм нормально работает в пределах каких-то величин. У нас постоянная температура тела, постоянное давление (у здоровых, конечно), нормально работает желудок. Т.е. организм работает в системе, какого-то постоянства. Это состояние было названо гомеостазом. Гомеостаз — это постоянство каких-то величин, которые позволяют организму существовать независимо от того, что происходит в окружающей среде, а иногда и внутри организма.

Как же организм приспосабливается, в результате чего? Дело в том, что приспособиться можно по-разному. Эволюция, т.е. развитие, привела к тому, что наш организм приспосабливается по-разному. Во-первых, можно просто не реагировать на изменения. Но все живые организмы, ткани выбрали другое направление — это реагирование и настройка на изменяющиеся условия. Наверное, самая интересная реакция живого организма на внешние какие-то раздражители была открыта доктором Селье в 1932 году. Он обратил внимание, что первая реакция организма практически на любые раздражители — это реакция стресса.

Кто из нас не знает, что все болезни от стрессов? И действительно, стресс крайне важная реакция организма. Но она возникает на мощные раздражители, воздействующие на нас. При этом стресс бывает также и хроническим, если раздражители не только сильные, но и продолжительные. Наша жизнь, её темп, мы должны всё успеть. Как Вы понимаете, это как раз и способствует такому состоянию. Мы сидим за компьютерами, пользуемся мобильными телефонами и смотрим телевизор. И всё это время на нас действуют электромагнитные поля. Особенно интенсивные поля на нас действуют в метрополитене, там доза электромагнитных излучений превышает норму на 500 пдн. Организм, естественно, реагирует на такое воздействие и реакция — это стресс. Стресс протекает фазно, и при этом происходят различные изменения в организме, причем некоторые приводят к разрушениям тканей. При начальной фазе могут возникать даже язвы в желудочно-кишечном тракте, что в дальнейшем может привести к тяжелым заболеваниям. Нашими отечественными специалистами в 69-м году были выделены другие системы реакции организма. Такими системами является реакция на малые раздражители. Это так называемая реакция тренировки. И на раздражители средней степени – это реакции активации. Я бы хотела обратить внимание на реакцию тренировки, т.е. ответ организма на раздражения малой силы по своей величине.

А стоит ли использовать раздражения малой величины? А зачем они нам нужны? Так вот, нашими исследователями, физиологами было доказано, что даже на малые раздражители организм реагирует. Причем он тоже реагирует, как и на стресс – есть три стадии. Первое, что организм всегда спрашивает: «А что это такое?», т.е. стадия ориентировки, он должен сориентироваться в этот момент. Как и при стрессе у нас немного увеличивается щитовидная железа, изменяется соотношение в крови форменных элементов, но все эти изменения не выходят за пределы нормы. При настоящем стрессе все показатели далеко выходят за рамки нормы, а здесь они всего лишь достигают верхних границ нормы. Меняется соотношение в гормональной системе, но эти изменения незначительны. Если слабый фактор действует на протяжении нескольких дней, то организм, разобравшись, что ничего страшного не происходит, просто перестаёт реагировать. Если же этот слабый фактор каждый день действует, но чуть выше, т.е. сегодня в одной дозе воздействует, а завтра чуть в большей дозе. Что происходит? Возникает реакция тренированности для организма. Эту стадию назвали стадией тренировки, организм на этой стадии начинает функционировать на чуть более высоком физиологическом уровне.

Что же меняется? Повышается устойчивость защитных сил организма к неблагоприятным условиям, а их у нас более чем достаточно. Вот на этом принципе и основано наше так называемое профилактическое направление физиотерапии, т.е. закаливание организма. И неважно чем закаливаться, можно холодной водой, можно заниматься на тренажерах. Однако при всей видимой простоте кто из нас выполняет эти нехитрые процедуры? Мы предлагаем Вам проводить тренировки с помощью магнитного поля аппликатора магнитостимулирующего НЕВОТОН.

Магнитное поле.

Почему именно магнитное поле? Дело в том, что именно магнитное поле наиболее близко нам по своей природе и его воздействие максимально физиологично. Что же такое магнитное поле, и как оно возникает? Многие из Вас, так или иначе, связаны с техникой и знают, что там, где есть электрические заряды, там есть электрический ток и, соответственно, электромагнитное поле. Но это искусственно созданное магнитное поле. С другой стороны, наша Земля также обладает магнитным полем и имеет соответственно Северный и Южный полюса. Мы с Вами живём в своеобразной электромагнитной колыбели, и если вдруг человеческий организм или любую живую клетку лишить этой колыбели, она перестает функционировать и погибает достаточно быстро. Магнитное поле Земли чутко реагирует на все изменения, происходящие в космосе. Так называемые вспышки на Солнце становятся причиной электромагнитных бурь на Земле. Эти бури становятся настоящим врагом для не очень здоровых людей. На сегодняшний день известно, что в дни магнитных бурь резко ухудшается самочувствие, особенно у тех, кто страдает заболеваниями сердечно-сосудистой системы. В частности, было установлено, что накануне магнитных бурь происходит смена погоды, резко увеличивается количество гипертонических кризов, инфарктов миокарда, кровоизлияний, легочных кровотечений, нарушается реакция вегетативной нервной системы, т.е. той нервной системы, которая осуществляет регуляцию работы всех внутренних органов. Вегетативная система обеспечивает всю нашу жизнедеятельность. Таким образом, перед нами встает необходимость постоянно поддерживать и усиливать устойчивость организма к неблагоприятным факторам внешней среды.

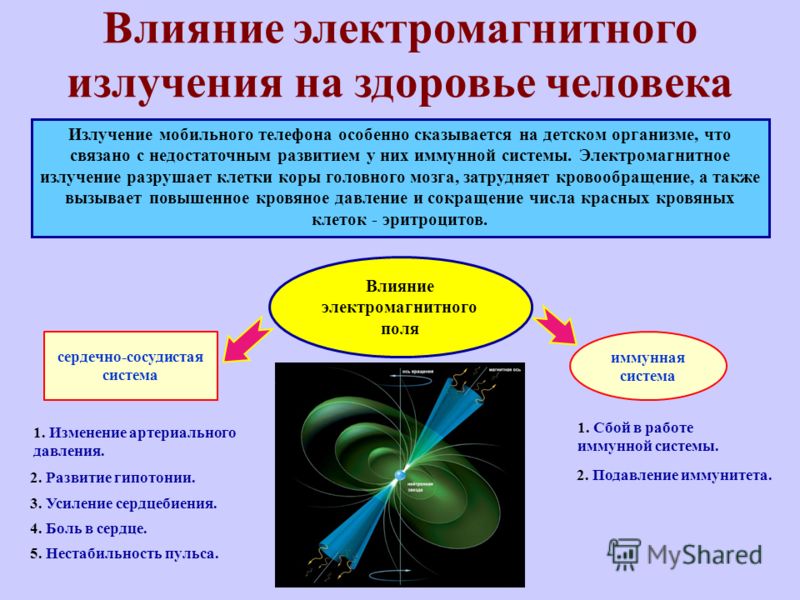
Воздействие магнитного поля на организм.

Я недаром Вам рассказывала про реакции тренировки. Повышать устойчивость организма можно большим количеством способов. Однако на сегодняшний день современная жизнь не позволяет нам уделять много времени на здоровье, а молодым и красивым хочется быть всегда. В этом отношении магнитное поле, создаваемое приборами, позволяет восстановить нарушенные функции организма. Почему? Потому что было установлено, что магнитное поле, влияя на организм, вызывает в нём те же самые физические и химические процессы. Когда магнитное поле проникает в ткани человека, оно вызывает упорядочивание движения электрически заряженных частиц в жидких средах. Меняются свойства крови, она становится более текучей, перераспределяются форменные элементы: эритроциты и лейкоциты, тромбоциты. Меняется так называемая реология крови, и это, по существу, профилактика ИБС и прочих сердечно-сосудистых заболеваний, бронхитов, тромбозов и т.д. Одновременно с изменениями крови в клетках тканей происходят удивительные процессы: меняется соотношение ядерного вещества, ферментов, активнее начинают работать митохондрии (так называемые энергетические станции клетки), меняется проницаемость клеточной оболочки, и соответственно, газообмен, и обмен веществ клетки. Особенно подвержены воздействию магнитного поля центральная и периферическая нервная система.

Что это даёт? В нервном волокне улучшается проведение нервного импульса, человек легче реагирует на всевозможные изменения окружающей среды. Улучшение работы головного мозга, прежде всего, выражается в своевременном проявлении важной реакции торможения. Реагируя на всевозможные воздействия, человек приходит в состояние возбуждения. И длительное пребывание в этом состоянии приводит к серьёзному истощению организма. Становится очевидно, что реакция торможения жизненно необходима для нормального функционирования организма. И именно эту реакцию восстанавливает и усиливает магнитное поле, т.е. поддерживает жизненные силы организма и защищает от истощения.

Хотелось бы также обратить внимание на то, что магнитное поле благотворно влияет на саму сосудистую стенку, повышает ее тонус. В зоне действия поля в активный кровоток включаются резервные сосуды и капилляры, просвет сосудов расширяется, и кровоснабжение тканей значительно увеличивается.

Этим свойством нередко пользуются косметологи, они говорят: «Хотите быть красивой?» Что надо для этого сделать? Чтобы личико всегда имело здоровый розовый цвет, необходимо улучшить кровоток в тканях лица. Таким образом, обеспечивается доставка питательных веществ, кислорода и в итоге усиливаются обменные процессы, накапливается белок в тканях, т.е. строительный материал для молодых клеток. По этому же принципу осуществляется лечение магнитным полем трофических язв, дряблости кожи и пр. Кстати, существуют методики электромагнитного стимулирования по формированию красивых, рельефных мышц. В то же время наблюдается противовоспалительный эффект магнитного поля. Однако в первую очередь магнитное поле влияет на форменные элементы крови. Ведь именно они и создают так называемый иммунитет. Причиной нарушений в иммунной системе организма являются нехватка форменных элементов крови, их плохое функционирование. Форменные элементы крови вырабатываются стволовыми клетками, которые располагаются в костях. В силу разных причин у каждого человека возникают проблемы с иммунитетом, а воздействие магнитным полем на области стволовых клеток позволяют увеличить количество вырабатываемых лимфоцитов и, следовательно, повысить иммунологический ответ организма. Расположение прибора в медальонной зоне, в месте традиционной китайской точки, которая ответственна за кроветворение, повышает иммунологическую реактивность. В чем же феномен этой зоны? Дело в том, что в медальонной зоне находится грудина. Это губчатая кость, где формируется большое количество стволовых клеток. Поэтому, воздействуя на эту зону, мы непосредственно стимулируем кроветворение и, соответственно, иммунитет.

Хочу обратить Ваше внимание, что при любом физиотерапевтическом воздействии крайне важна дозировка, т.к. результаты могут быть не только положительные, но и разрушительные для организма.

Для постоянного магнитного поля показательной величиной является напряженность порядка 1 мТл. 1 мТл – это та величина, которая уже вызывает значимые лечебные изменения на уровне тканей нашего организма, т.е. улучшения со стороны кроветворения, проведения нервных импульсов и пр. В изделиях фирмы НЕВОТОН напряженность магнитного поля составляет 12 мТл. Эта величина появилась не случайно. Т.к. напряженность магнитного поля падает пропорционально квадрату расстояния от прибора, то для локального воздействия она оптимальна. Официально Минздравом РФ разрешено применение гражданами в домашних условиях без контроля врача магнитных полей до 30 мТл. Однако, чем больше напряженность, тем более внимательно нужно следить за дозировкой. 12 мТл – это та величина, которая позволяет применение аппликатора без опасности передозировки: она не окажет повреждающего воздействия на человека, поле проникает в глубину в пределах нескольких сантиметров. Естественно, что при применении такого мягкого воздействия максимальный лечебный эффект проявится при воздействии на самые чувствительные точки, т.е. точки акупунктуры. Хотелось бы подчеркнуть мысль о том, что при воздействии слабым фактором организм к нему привыкает и перестает на него реагировать. Чтобы этого не происходило, чтобы организм постоянно реагировал на воздействие надо постоянно повышать дозу. Что такое доза? Это сила воздействия и время. Т.к. силу воздействия изменить мы не можем, увеличение дозировки производится за счет увеличения времени проведения процедуры. В нашем случае применение НЕВОТОНА мы рекомендуем начинать с 1,5 – 2 часов, через два-три дня увеличить дозу до 3-4 часов и т.д. Однако, когда проблема стоит остро, к примеру сильные боли, то аппликатор закрепляется на длительный срок 5-12 часов и боль проходит. Как долго необходимо пользоваться прибором? Реакция тренировки может формироваться в течение 15-20 процедур, максимум 25, поэтому постоянно носить аппарат нет необходимости. Через 20-30 дней обычно проводят повторный курс. При решении более сложных проблем курс лечения подобран для каждого заболевания индивидуально и указан в подробной инструкции. Поскольку применение НЕВОТОНА выполняет как профилактические, так и лечебные функции, то пользоваться прибором можно практически всю жизнь.

Постоянное электромагнитное поле

Постоянным электромагнитным полем мы называем поле, не зависящее от времени. Очевидно, что потенциалы постоянного поля можно выбрать так, чтобы они были функциями только от координат, но не от времени. Постоянное магнитное поле по-прежнему равно H=rotA. Постоянное же электрическое поле

E = − grad φ. (19.1)

Таким образом, постоянное электрическое поле определяется только скалярным потенциалом, а магнитное — векторным потенциалом.

Мы видели в предыдущем параграфе, что потенциалы поля определены не однозначно. Легко, однако, убедиться в том, что если описывать постоянное электромагнитное поле с помощью не зависящих от времени потенциалов, то к скалярному потенциалу можно прибавить, не изменяя поля, лишь произвольную постоянную (не зависящую ни от координат, ни от времени). Обычно на φ накладывают еще дополнительное условие, требуя, чтобы он имел определенное значение в определенной точке пространства; чаще всего выбирают φ так, чтобы он был равен нулю на бесконечности. Тогда и упомянутая произвольная постоянная становится определенной, и скалярный потенциал постоянного поля, таким образом, становится вполне однозначным.

Напротив, векторный потенциал по-прежнему не однозначен даже для постоянного электромагнитного поля; к нему можно прибавить градиент любой функции координат.

Определим, чему равна энергия заряда в постоянном электромагнитном поле. Если поле постоянно, то и функция Лагранжа для заряда не зависит явно от времени. Как известно, в этом случае энергия сохраняется, совпадая с функцией Гамильтона.

Согласно (16.6) имеем

= + eφ. (19.2)

Таким образом, вследствие наличия поля к энергии частицы прибавляется член eφ — потенциальная энергия заряда в поле. Отметим существенное обстоятельство, что энергия зависит только от скалярного, но не от векторного потенциала. Другими словами, магнитное поле не влияет на энергию зарядов; энергию частицы может изменить только электрическое поле. Это связано с тем, что магнитное поле, в противоположность электрическому, не производит над зарядом работы.

Если напряженность поля во всех точках пространства одинакова, то поле называют однородным. Скалярный потенциал однородного электрического поля может быть выражен через напряженность поля согласно равенству

φ = −Er. (19.3)

Действительно, при E=const имеем grad(Er)=(E)r=E.

Векторный же потенциал однородного магнитного поля выражается через напряженность этого поля H в виде

A = [Hr]. (19.4)

Действительно, при H=const находим с помощью известных формул векторного анализа:

rot [Hr] = H div r − (H)r − 2H

(напомним, что div r=3).

Векторный потенциал однородного магнитного поля можно выбрать и иначе, например, в виде

A_x = −Hy, A_y = A_z = 0 (19.5)

(ось z выбрана вдоль направления H). Легко убедиться, что и при таком выборе A имеет место равенство H=rotA. В соответствии с формулами преобразования (18.3) потенциалы (19.4) и (19.5) отличаются друг от друга градиентом некоторой функции: (19.5) получается из (19.4) прибавлением f, где f=−xyH/2.

ВЛИЯНИЕ ПОСТОЯННОГО МАГНИТНОГО ПОЛЯ НА СОСТОЯНИЕ КОСТНОЙ ТКАНИ КРЫС С ПОВЫШЕННЫМ УРОВНЕМ РЕЗОРБЦИИ

Подковкин В.Г. Иванов Д.Г. Иванов Г.А.

Исследовано влияние постоянного магнитного поля на морфо-функциональное состояние костной ткани крыс в условиях повышенной резорбции. Показано, что воздействие на животных постоянным магнитным полем 9 мТл предотвращает деградацию коллагена и потерю костной массы у крыс, подвергавшихся действию высокой температуры, и не влияет на состояние костной ткани интактных животных.

Введение

В условиях современного производства и при эксплуатации технических аппаратов человек сталкивается с действием повышенных температур и магнитных полей различной напряженности. В этих условиях возрастает напряжение систем, обеспечивающих адаптацию организма к внешним факторам [2, 12]. Особую опасность для человека представляет действие экстремальных факторов, результатом которого может быть развитие различного рода патологий. Это обусловливает необходимость исследования эффекта указанных факторов на живые организмы с целью исследования и прогнозирования последствий их действия.

С другой стороны магнитные поля способны стимулировать репаративные процессы костной ткани [8,14]. В работе [15] показана возможность предотвращения потери костной массы у овариоэктомированных крыс путем экспозиции животных в магнитном поле.

В наших исследованиях было обнаружено, что эффект магнитного поля на активацию процессов костной резорбции у крыс, подвергающихся действию повышенной температуры среды, зависит от индукции поля и периода между действием на животных термического и магнитного факторов [3,4].

В настоящей работе мы поставили цель оценить защитное действие постоянного магнитного поля на морфо-функциональное состояние костной ткани крыс с повышенным уровнем костной
резорбции.

Материалы и методы

Эксперимент был проведен на 32 беспородных крысах-самцах массой 120-180 грамм. Все манипуляции с животными проводились по международным правилам и нормам [13].

Согласно экспериментальным условиям животные были разделены на четыре группы. Группы животных формировались методом аналогов [9].

Первую группу составляли животные с повышенным уровнем костной резорбции. Активацию процессов резорбции костной ткани вызывали при помощи гипертермии, по методике, описанной ранее [5]. Крысы помещались на 10 минут в камеру с температурой воздуха 70⁰С ежедневно в течение 7 суток.

Ко второй группе были отнесены животные с повышенным уровнем костной резорбции, на которых воздействовали постоянным магнитным полем с индукцией 9 мТл. Воздействие магнитным полем производили на оригинальной установке УМ-7 через 30 минут после термического воздействия. Градиент индукции по продольной оси соленоида составляет 0,02±0,005 мТл/см. Одновременно в соленоид помещали 6-8 крыс. Продолжительность экспозиции в магнитном поле составляла 8 минут.

Животные третьей группы подвергались изолированному действию постоянного магнитного поля с индукцией 9 мТл по схеме описанной выше, но без активации костной резорбции с помощью гипертермии.

Группа, состоящая из интактных крыс, служила контролем.

Животных выводили из эксперимента путем декапитации. У животных вычленяли бедренные кости, очищали их от мягких тканей и взвешивали. Массу бедренной кости представляли в процентах от массы тела животного.

Оценивали отношение массы кости к диаметру диафиза бедренной кости измеренному по середине. Такой показатель имел размерность г/мм.

Объем бедренной кости определяли по объему вытесненной жидкости. По результатам замеров рассчитывали плотность кости. Для каждого животного определяли среднее значение показателей бедренной кости, состоящее из значений полученных для правой и левой бедренной кости.

О метаболизме коллагена костной ткани судили по уровню свободного и белковосвязанного оксипролина в плазме крыс. Плазму крови собирали у декапитированных животных, в качестве антикоагулянта использовали 5% раствор трилона Б. Свободный и белковосвязанный оксипролин определяли по реакции с п-диметиламинобензальдегидом [10].

Полученные результаты были подвергнуты стандартной статистической обработке с использованием t-критерия Стьюдента [9].

Результаты исследования

Проведенные исследования обнаружили усиление процессов деградации костного коллагена у крыс, подвергающихся действию термического фактора, что выражалось в значимом увеличении содержания свободного оксипролина в крови этих животных (табл. 1).

Воздействие магнитного поля 9 мТл на животных, через 30 минут после действия термического фактора предотвращало распад коллагена, индуцированный действием повышенной температуры. Изолированное действие магнитного поля не изменяло уровня обмена костного коллагена.

Таблица 1. Содержание свободного и белковосвязанного оксипролина в крови крыс под действием повышенной температуры и постоянного магнитного поля

Способ воздействия	Содержание свободного оксипролина, мкг/мл	Содержание белковосвязанного оксипролина, мкг/мл
Контроль	3,00±0,57#	90,12±12,83#
70 ⁰С, 10 мин.	5,73±0,83*	149,11±16,66*
70 ⁰С, 10 мин.; 9 мТл, 8 мин.	1,67±0,38#	56,26±13,65#
9 мТл, 8 мин.	2,69±0,24#	56,82±11,24#

* — отличие от контроля статистически значимо (р<0.05),

# — отличие от результатов группы крыс, подвергавшихся термическому воздействию, статистически значимо (р<0.05).

Необходимо отметить, что наряду с усилением распада коллагена, действие термического фактора активировало процессы синтеза костного матрикса у крыс, что обнаруживалось в виде повышения белковосвязанного оксипролина в крови животных. Этот эффект термического фактора не обнаруживался, в случае, когда на животных действовало постоянное магнитное поле.

Изменение интенсивности обмена коллагена сопровождалось изменением биометрических характеристик бедренной кости животных. Как видно из данных, представленных в таблице 2, под действием термического фактора происходило снижение относительной массы кости крыс и уменьшение ее плотности.

Таблица 2. Биометрические характеристики бедренной кости крыс под действием повышенной температуры и постоянного магнитного поля

Способ воздействия	Относительная масса бедренной кости, %	Отношение массы бедренной кости к диаметру диафиза, г/мм	Плотность кости, г/см³
Контроль	0,33±0,03#	0,21±0,01#	1,40±0,02#
70 ⁰С, 10 мин.	0,25±0,01*	0,16±0,01*	1,29±0,04*
70 ⁰С, 10 мин.; 9 мТл, 8 мин.	0,32±0,01#	0,20±0,01#	1,38±0,07
9 мТл, 8 мин.	0,37±0,02#	0,22±0,02#	1,33±0,05

* — отличие от контроля статистически значимо (р<0.05),

Вместе с массой кости под действием повышенной температуры у крыс снижалось отношение массы к диаметру ее диафиза. Действие магнитного поля предотвращало изменение биометрических характеристик бедренной кости, вызванных влиянием термического фактора.

Действие магнитного поля на интактных крыс не изменяло биометрические характеристики бедренной кости.

Обсуждение

Деградация костного коллагена, сопровождающаяся повышением содержания свободного оксипролина в крови крыс, под действием термического фактора связана с напряжением адаптационных систем животных, и в частности активацией оси гипоталамус-гипофиз-кора надпочечников [5]. На морфологических препаратах подвздошной кости крысы наблюдается снижение количества остеобластов, повышение активности остеокластов и истончение костных балок в период от третьих до седьмых суток термического воздействия [6]. В результате этого снижается масса кости. Биометрические характеристики бедренной кости под действием термического фактора изменяются медленнее массы тела животного, поэтому отношение массы кости к ее линейным размерам или объему часто является более информативным по сравнению с относительной массой кости.

В работах [7,11] показано действие магнитного поля на гипоталамус с последующей активацией функции коры надпочечников. На основании этих данных можно полагать, что магнитные поля с низкой индукцией действуют на организм, затрагивая гипоталамо-гипофизарно-надпочечниковую систему. При этом их действие вызывает неспецифическую реакцию, отличную от стрессовой, но имеющую адаптационное значение для организма [1]. Вероятно, воздействие магнитного поля на организм, согласно режиму, применяемому в данной работе, снижает возбудимость и реактивность центральной нервной системы, предотвращая активацию гипоталамо-гипофизарно-надпочечниковой оси при влиянии термического фактора и, как следствие, активацию процессов костной резорбции в результате повышения уровня глюкокортикоидов в крови. При этом изолированное действие магнитного фактора не оказывает влияние на состояние костной ткани у животных по предположенному механизму.

Заключение

Таким образом, в работе наблюдалось снижение активности процессов костной резорбции, индуцированных гипертермией у крыс в результате ежедневного восьмиминутного воздействия постоянным магнитным полем с индукцией 9 мТл. При этом изолированное действие магнитного поля не оказывало существенного влияния на морфо-функциональное состояние костной ткани крыс, что позволяет рекомендовать предложенный способ снижения костной резорбции для испытания в клинической практике.

СПИСОК ЛИТЕРАТУРЫ:

Гаркави Л.Х., Квакина Е.Б., Коробейникова Е.П. и др. // Электромагнитные поля в биосфере. Т.2: Биологическое действие электромагнитных полей. М.: Наука, 1984. С. 46.
Григорьев Ю.Г. Космическая радиобиология. М.: Энергоатомиздат, 1982. — 176 с.
Иванов Д.Г. // Окружающая природная среда и экологическое образование и воспитание. Пенза, 2007. С.34.
Иванов Д.Г., Подковкин В.Г. // Экологические проблемы современности. Пенза, 2007. С.21.
Подковкин В.Г., Иванов Д.Г. // Вестник Самарского государственного университета. Естественнонаучная серия, 2006. — №9. С.237.
Подковкин В.Г., Иванов Д.Г. // Наука. Творчество: Коняевские чтения. Т.2. Самара, 2007. С.369.
Подковкин В.Г., Слободянюк И.Л., Углова М.В. Влияние электромагнитных полей окружающей среды на системы гомеостаза Самара: Издательство «Самарский университет», 2000. — 108 с.
Савельев В.И., Муравьев М.Ф. // Применение магнитных полей в клинике: Тез. докл. Куйбышевской обл. конф. Куйбышев, 1976. С. 151.
Спетлиев Д. Статистические методы в научных медицинских исследованиях. М.: Медицина, 1968. — 419с.
Современные методы в биохимии / Под ред. В.Н. Ореховича. М.: Медицина, 1977. — 392 с.
Холодов, Ю.А. Мозг в электромагнитных полях. М.: Наука, 1982. — 120с.
Чвырев, В.Г., Ажаев А.Н., Новожилов Г.Н. Тепловой стресс: руководство для врачей. М.: Медицина,
2000. — 296с.
Guide for the сare and use of laboratory animals. Washington, D.C.: National Academy Press, 1996. — 128 p.
Botticelli A.R., Caielli D., Fraticelli D., et al. // Electro- and Magnetobiology, 1998. — V. 17. No. 1. P. 87.
Taniguchi, N., Kanai S. // eCAM, 2007. — V. 4(1). P. 99.

Библиографическая ссылка

Подковкин В.Г., Иванов Д.Г., Иванов Г.А. ВЛИЯНИЕ ПОСТОЯННОГО МАГНИТНОГО ПОЛЯ НА СОСТОЯНИЕ КОСТНОЙ ТКАНИ КРЫС С ПОВЫШЕННЫМ УРОВНЕМ РЕЗОРБЦИИ // Успехи современного естествознания. – 2008. – № 7. – С. 13-16;
URL: https://natural-sciences.ru/ru/article/view?id=10195 (дата обращения: 13.08.2021).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Устройство и классификация МР-томографов

Устройство МР-томографа

Любой МР-томографа состоит из:

магнита, создающего постоянное магнитное поле, в которое помещают пациента;
градиентных катушек, создающих слабое переменное магнитное поле в центральной части основного магнита. Это поле называют градиентным. Оно позволяет выбрать область исследования части тела пациента;
передающих и принимающих радиочастотных катушек; передающие, используются для создания возбуждения в теле пациента, приемные — для регистрации ответа возбужденных участков;
компьютера, управляющего работой катушек, регистрирацией, обработкой измеренных сигналов, реконструкцией МР-изображений.

Радиочастотные катушки для различных отделов тела необходимы для получения качественного изображения.

Магнитное поле характеризуется индукцией магнитного поля, единицей измерения является Тл (тесла) по имени сербского учёного Николы Теслы.

Различают несколько типов томографов (зависит от величины постоянного магнитного поля):

0,01 Тл — 0,1 Тл → со сверхслабым полем;
0,1 — 0,5 Тл → со слабым полем;
0,5 — 1.0 Тл → со средним полем;
1.0 — 2,0 Тл → с сильным полем;
>2,0 Тл → со сверхсильным полем.

Существует три вида магнитов для мр-томографа: резистивные, постоянные и сверхпроводящие.

Томографы с полем до 0,3 Тл чаще всего имеют резистивные или постоянные магниты, выше 3,0 Тл — сверхпроводящие.

Оптимальная напряженность магнитного поля является постоянным предметом дискуссий среди специалистов.

Более 90% магнитно-резонансных томографов составляют модели со сверхпроводящими магнитами (0,5 — 1,5 Тл). Томографы со сверхсильным полем (выше 3,0 Тл) очень дороги в эксплуатации. Постоянные магниты напротив, дёшевы и просты в эксплуатации.

Открытый и закрытый тип МР-томографа.

Резистивные магниты

Магнитное поле создается с помощью электрического тока, который проходит через катушку. МР-томографы с резистивными магнитами требуют большого количества электроэнергии, которая сильно нагревает магнит, что необходимо для получения сильных магнитных полей. Такая система вырабатывает поле с напряженностью до 0,3 Тесла.

Резистивные магниты были первыми применены в клинической практике. Они просты в изготовлении, стоят дешевле сверхпроводящих или постоянных. При этом они требуют мощного и стабильного источника питания, системы водоохлаждения с качественной очисткой воды. Уровень магнитного поля в них ограничен величиной 0.3Т, при котором отношение сигнал/шум еще не достаточно высоко. По качеству и времени сканирования они уступают томографам с более сильными полями. В настоящее время этот тип магнита практически не используется, и весь современный парк томографов состоит из приборов с постоянными и сверхпроводящими магнитами.

Постоянные магниты

Магнитное поле этого типа не требует высоких эксплуатационных расходов на электроэнергию и криогенные материалы. Главным недостатком постоянных магнитов являет то, что они генерируют слабое поле с напряженностью до 0,3 Тесла. Кроме того, такие томографы обладают большой массой, так же у них отсутствует функция аварийного снижения магнитного поля. Часто томографы с постоянными магнитами имеют «открытый» тип конструкции, постоянными магнитами обычно комплектуются небольшие приборы для специализированных исследований отдельных частей тела, например, суставов конечностей.

Сверхпроводящие магниты

В таких магнитах используется свойство сверхпроводимости, которое присуще некоторым материалам при очень низких температурах, близких к абсолютному нулю. Сверхпроводящий материал не требует энергетических затрат, потому что практически не имеет электрического сопротивления. Однако для создания температуры, близкой к абсолютному нулю, необходимы криогенные материалы (жидкий гелий). Сверхпроводящие магниты создают магнитные поля высокой напряженности 1,0-3,0 Тесла и более. Они являются наиболее дорогими, но, благодаря высокому уровню поля и наилучшему соотношению сигнал/шум, обеспечивают наилучшее качество изображения. Не случайно наибольший прогресс в совершенствовании магнитных томографов наблюдается в области сверхпроводящих магнитов. Сегодня они покрывают более 80% рынка МР-томографов. Относительно низкий расход жидкого гелия у современных моделей, высокая скорость исследования и качество изображения делают их максимально привлекательными для потребителя.

В настоящее время изготавливаются магнитно-резонансные томографы двух типов: закрытого и открытого типа. Открытый тип томографа удобен для проведения различных манипуляций, поскольку обеспечивает более свободный доступ к пациенту. Преимуществом таких томографов является отсутствие замкнутого пространства, что актуально для пациентов страдающих клаустрофобией. Нужно учитывать, что при всех удобствах, отрытую конструкцию чаще имеют аппараты с низкой и средней напряжённостью магнитного поля, а большая часть томографов с мощными полями и наилучшим качеством изображения имеют туннельный тип.

Регулируемые источники постоянного магнитного поля большой интенсивности

В данных генераторах магнитного поля использован принцип дипольной Хальбах-структуры. В рабочем объеме цилиндрической формы создается высокоинтенсивное магнитное поле поперечного направления. Оригинальная конструкция устройства позволяет, используя в качестве привода шаговый двигатель, изменять величину поля от – В_max до + В_max; при этом сохраняется направление вектора поля, а также его однородность в пределах ± 0.5 %.

Источник магнитного поля может быть подключен к компьютеру или другому управляющему устройству, что позволяет задавать различные режимы изменения поля. Важно отметить, что с помощью перестраиваемых источников поля на постоянных магнитах удается достигать весьма высоких скоростей изменения магнитного поля – до 10 Тл/с.

Пример конструкции регулируемого источника магнитного поля.

В тех случаях, когда не требуется высокая однородность магнитного поля и высокая скорость его изменения, мы можем предложить различные варианты несложных устройств, в частности, показанную на рисунке систему с симметричным линейным перемещением магнитных полюсов.

Источник магнитного поля с диапазоном изменения поля в центре рабочего зазора от 0,1 Тл до 1.0 Тл.

Основные характеристики:
Размер полюсов:	40 × 60 мм
Минимальное межполюсное расстояние:	10 мм

С дополнительной информацией о регулируемых источниках постоянного магнитного поля большой интенсивности можно ознакомиться в статье «Highly intensive magnetic systems», подготовленной AMT&C для журнала «Magnetics Technology International Journal».

магнитное поле | Определение и факты

Наблюдайте за действием магнитного поля и взаимодействием между магнитными полюсами

Узнайте о магнитных полях и взаимодействиях между магнитными полюсами.

Encyclopædia Britannica, Inc. Посмотреть все видео по этой статье

магнитное поле , векторное поле в окрестности магнита, электрический ток или изменяющееся электрическое поле, в котором наблюдаются магнитные силы. Магнитные поля, такие как у Земли, заставляют стрелки магнитного компаса и другие постоянные магниты выстраиваться в линию в направлении поля.Магнитные поля заставляют электрически заряженные частицы двигаться по круговой или винтовой траектории. Эта сила, действующая на электрические токи в проводах в магнитном поле, лежит в основе работы электродвигателей. (Для получения дополнительной информации о магнитных полях, см. магнетизм.

Вокруг постоянного магнита или провода, по которому проходит постоянный электрический ток в одном направлении, магнитное поле является стационарным и называется магнитостатическим полем. В любой заданной точке его величина и направление остается прежним.Магнитное поле вокруг переменного или постоянного тока постоянно меняет свою величину и направление.

Подробнее по этой теме

Магнетизм: основы

Основными для магнетизма являются магнитное поле с и их влияние на материю, как, например, отклонение движущихся зарядов …

Магнитные поля могут быть представлены непрерывными силовыми линиями или магнитным потоком, которые исходят из магнитных полюсов, направленных на север, и входят в магнитные полюсы, направленные на юг.Плотность линий указывает величину магнитного поля. Например, на полюсах магнита, где сильное магнитное поле, силовые линии сжимаются или становятся более плотными. Дальше, где магнитное поле слабое, они разветвляются, становясь менее плотными. Однородное магнитное поле представлено параллельными прямыми, расположенными на одинаковом расстоянии друг от друга. Направление потока — это направление, в котором указывает северный полюс небольшого магнита. Линии потока непрерывны, образуя замкнутые контуры.Для стержневого магнита они выходят из северного полюса, расходятся веером, входят в магнит на южном полюсе и проходят через магнит к северному полюсу, где снова появляются. Единицей измерения магнитного потока в системе СИ является вебер. Количество веберов — это мера общего количества линий поля, пересекающих данную область.

Магнитные поля могут быть представлены математически величинами, называемыми векторами, которые имеют направление, а также величину. Два разных вектора используются для представления магнитного поля: один, называемый плотностью магнитного потока или магнитной индукцией, обозначается как B ; другой, называемый напряженностью магнитного поля или напряженностью магнитного поля, обозначается как H .Магнитное поле H можно рассматривать как магнитное поле, создаваемое протеканием тока в проводах, а магнитное поле B — как полное магнитное поле, включая также вклад, вносимый магнитными свойствами материалов в поле. Когда ток течет в проволоке, намотанной на цилиндр из мягкого железа, намагничивающее поле H довольно слабое, но фактическое среднее магнитное поле ( B ) внутри утюга может быть в тысячи раз сильнее, поскольку B значительно усилен выравниванием бесчисленных крошечных естественных атомных магнитов железа в направлении поля. См. Также магнитная проницаемость.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Что такое магнетизм? | Магнитные поля и магнитная сила

Магнетизм — это один из аспектов комбинированной электромагнитной силы. Это относится к физическим явлениям, возникающим из-за силы, вызванной магнитами, объектами, которые создают поля, которые притягивают или отталкивают другие объекты.

Согласно веб-сайту HyperPhysics Университета штата Джорджия, магнитное поле воздействует на частицы в поле за счет силы Лоренца.Движение электрически заряженных частиц порождает магнетизм. Сила, действующая на электрически заряженную частицу в магнитном поле, зависит от величины заряда, скорости частицы и силы магнитного поля.

Все материалы обладают магнетизмом, некоторые сильнее, чем другие. Постоянные магниты, сделанные из таких материалов, как железо, испытывают сильнейшее воздействие, известное как ферромагнетизм. За редким исключением, это единственная форма магнетизма, достаточно сильная, чтобы ее могли почувствовать люди.

Противоположности притягиваются

Магнитные поля генерируются вращающимися электрическими зарядами, согласно HyperPhysics. Все электроны обладают свойством углового момента или спина. Большинство электронов имеют тенденцию образовывать пары, в которых один из них имеет «спин вверх», а другой — «спин вниз», в соответствии с принципом исключения Паули, который гласит, что два электрона не могут находиться в одном и том же энергетическом состоянии одновременно. В этом случае их магнитные поля направлены в противоположные стороны, поэтому они компенсируют друг друга.Однако некоторые атомы содержат один или несколько неспаренных электронов, спин которых может создавать направленное магнитное поле. По данным Ресурсного центра неразрушающего контроля (NDT), направление их вращения определяет направление магнитного поля. Когда значительное большинство неспаренных электронов выровнены своими спинами в одном направлении, они объединяются, чтобы создать магнитное поле, достаточно сильное, чтобы его можно было почувствовать в макроскопическом масштабе.

Источники магнитного поля биполярные, с северным и южным магнитными полюсами.По словам Джозефа Беккера из Университета Сан-Хосе, противоположные полюса (северный и южный) притягиваются, а подобные полюса (северный и северный, или южный и южный) отталкиваются. Это создает тороидальное поле или поле в форме пончика, поскольку направление поля распространяется наружу от северного полюса и входит через южный полюс.

Земля сама по себе является гигантским магнитом. Согласно HyperPhysics, планета получает свое магнитное поле от циркулирующих электрических токов внутри расплавленного металлического ядра. Компас указывает на север, потому что маленькая магнитная стрелка в нем подвешена, так что он может свободно вращаться внутри своего корпуса, выравниваясь с магнитным полем планеты.Как ни парадоксально, то, что мы называем Северным магнитным полюсом, на самом деле является южным магнитным полюсом, потому что он притягивает северные магнитные полюса стрелок компаса.

Ферромагнетизм

Если выравнивание неспаренных электронов сохраняется без приложения внешнего магнитного поля или электрического тока, образуется постоянный магнит. Постоянные магниты — результат ферромагнетизма. Приставка «ферро» относится к железу, потому что постоянный магнетизм впервые наблюдался в форме естественной железной руды, называемой магнетитом, Fe ₃ O ₄.Кусочки магнетита можно найти разбросанными на поверхности земли или вблизи нее, и иногда они намагничиваются. Эти встречающиеся в природе магниты называются магнитными камнями. «Мы до сих пор не уверены в их происхождении, но большинство ученых считают, что магнитный камень — это магнетит, в который попала молния», — говорится в сообщении Университета Аризоны.

Вскоре люди узнали, что можно намагнитить железную иглу, поглаживая ее магнитным камнем, в результате чего большинство неспаренных электронов в игле выстраиваются в одном направлении.По данным НАСА, примерно в 1000 году нашей эры китайцы обнаружили, что магнит, плавающий в чаше с водой, всегда выстраивался в направлении север-юг. Таким образом, магнитный компас стал огромным помощником в навигации, особенно днем и ночью, когда звезды были скрыты облаками.

Было обнаружено, что другие металлы, помимо железа, обладают ферромагнитными свойствами. К ним относятся никель, кобальт и некоторые редкоземельные металлы, такие как самарий или неодим, которые используются для создания сверхпрочных постоянных магнитов.

Другие формы магнетизма

Магнетизм принимает множество других форм, но, за исключением ферромагнетизма, они обычно слишком слабы, чтобы их можно было наблюдать за исключением чувствительных лабораторных приборов или при очень низких температурах. Диамагнетизм был впервые открыт в 1778 году Антоном Бругнамсом, который использовал постоянные магниты в поисках материалов, содержащих железо. По словам Джеральда Кюстлера, широко публикуемого независимого немецкого исследователя и изобретателя, в его статье «Диамагнитная левитация — исторические вехи», опубликованной в Румынском журнале технических наук, Бругнамс заметил: «Только темный и почти фиолетовый висмут проявлял конкретное явление в исследовании; когда я положил его кусок на круглый лист бумаги, плавающий на воде, он оттолкнулся обоими полюсами магнита.

Было установлено, что висмут обладает самым сильным диамагнетизмом из всех элементов, но, как обнаружил Майкл Фарадей в 1845 году, это свойство всей материи отталкиваться магнитным полем.

Диамагнетизм вызван орбитальным движением электронов, создающих крошечные токовые петли, которые создают слабые магнитные поля, согласно HyperPhysics. Когда к материалу прикладывается внешнее магнитное поле, эти токовые петли имеют тенденцию выравниваться таким образом, чтобы противостоять приложенному полю.Это заставляет все материалы отталкиваться постоянным магнитом; однако результирующая сила обычно слишком мала, чтобы быть заметной. Однако есть некоторые заметные исключения.

Пиролитический углерод, вещество, похожее на графит, демонстрирует даже более сильный диамагнетизм, чем висмут, хотя и только вдоль одной оси, и фактически может подниматься над сверхсильным редкоземельным магнитом. Некоторые сверхпроводящие материалы демонстрируют еще более сильный диамагнетизм ниже своей критической температуры, поэтому над ними можно левитировать редкоземельные магниты.(Теоретически из-за их взаимного отталкивания один может левитировать над другим.)

Парамагнетизм возникает, когда материал временно становится магнитным при помещении в магнитное поле и возвращается в свое немагнитное состояние, как только внешнее поле удаляется. При приложении магнитного поля некоторые из неспаренных электронных спинов выравниваются с полем и преодолевают противоположную силу, создаваемую диамагнетизмом. Однако, по словам Дэниела Марша, профессора физики Южного государственного университета Миссури, эффект заметен только при очень низких температурах.

Другие, более сложные формы включают антиферромагнетизм, при котором магнитные поля атомов или молекул выстраиваются рядом друг с другом; и поведение спинового стекла, которое включает как ферромагнитные, так и антиферромагнитные взаимодействия. Кроме того, ферримагнетизм можно рассматривать как комбинацию ферромагнетизма и антиферромагнетизма из-за множества общих черт между ними, но, по данным Калифорнийского университета в Дэвисе, он все же имеет свою уникальность.

Электромагнетизм

Когда провод перемещается в магнитном поле, поле индуцирует в проводе ток.И наоборот, магнитное поле создается движущимся электрическим зарядом. Это соответствует закону индукции Фарадея, который лежит в основе электромагнитов, электродвигателей и генераторов. Заряд, движущийся по прямой линии, как по прямому проводу, создает магнитное поле, которое вращается вокруг провода по спирали. Когда этот провод превращается в петлю, поле приобретает форму пончика или тора. Согласно Руководству по магнитной записи (Springer, 1998) Marvin Cameras, это магнитное поле можно значительно усилить, поместив ферромагнитный металлический сердечник внутрь катушки.

В некоторых приложениях постоянный ток используется для создания постоянного поля в одном направлении, которое можно включать и выключать вместе с током. Это поле может затем отклонить подвижный железный рычаг, вызывая слышимый щелчок. Это основа телеграфа, изобретенного в 1830-х годах Сэмюэлем Ф. Б. Морзе, который позволял осуществлять связь на большие расстояния по проводам с использованием двоичного кода, основанного на импульсах большой и малой длительности. Импульсы посылались опытными операторами, которые быстро включали и выключали ток с помощью подпружиненного переключателя с мгновенным контактом или ключа.Другой оператор на принимающей стороне затем переводил слышимые щелчки обратно в буквы и слова.

Катушку вокруг магнита также можно заставить двигаться по шаблону с изменяющейся частотой и амплитудой, чтобы индуцировать ток в катушке. Это основа для ряда устройств, в первую очередь для микрофона. Звук заставляет диафрагму двигаться внутрь и наружу с волнами переменного давления. Если диафрагма соединена с подвижной магнитной катушкой вокруг магнитопровода, она будет производить переменный ток, аналогичный падающим звуковым волнам.Затем этот электрический сигнал может быть усилен, записан или передан по желанию. Крошечные сверхсильные магниты из редкоземельных металлов теперь используются для изготовления миниатюрных микрофонов для сотовых телефонов, сообщил Марш Live Science.

Когда этот модулированный электрический сигнал подается на катушку, он создает колеблющееся магнитное поле, которое заставляет катушку двигаться внутрь и наружу по магнитному сердечнику по той же схеме. Затем катушка прикрепляется к подвижному диффузору динамика, чтобы он мог воспроизводить слышимые звуковые волны в воздухе.Первым практическим применением микрофона и динамика был телефон, запатентованный Александром Грэмом Беллом в 1876 году. Хотя эта технология была усовершенствована и усовершенствована, она все еще является основой для записи и воспроизведения звука.

Применения электромагнитов почти бесчисленны. Закон индукции Фарадея формирует основу для многих аспектов нашего современного общества, включая не только электродвигатели и генераторы, но и электромагниты всех размеров. Тот же принцип, который используется гигантским краном для подъема старых автомобилей на свалку металлолома, также используется для выравнивания микроскопических магнитных частиц на жестком диске компьютера для хранения двоичных данных, и каждый день разрабатываются новые приложения.

Штатный писатель Таня Льюис внесла свой вклад в этот отчет.

Дополнительные ресурсы

Магнитное поле токоведущего провода

Темы и файлы

E&M Тема

Электромагнетизм, магнитное поле в катушке

Напильник Capstone

Список оборудования

Введение

Цель этого упражнения — измерить магнитное поле, создаваемое токоведущим проводом в форме катушки.Используйте усилитель мощности для создания и измерения тока в катушке и используйте датчик магнитного поля для измерения напряженности магнитного поля в катушке. Используйте Capstone для записи и отображения данных. Рассчитайте проницаемость свободного пространства ( μ ₀) на основе размера и количества витков в катушке, измеренного тока и измеренного магнитного поля.

Фон

Токоведущий провод испытывает магнитную силу при помещении в магнитное поле, создаваемое внешним источником, например постоянным магнитом.Токоведущий провод также создает собственное магнитное поле. Ганс Кристиан Эрстед (1777–1851) впервые обнаружил этот эффект в 1820 году, когда заметил, что провод с током влияет на ориентацию расположенной рядом стрелки компаса. Стрелка компаса выравнивается с чистым магнитным полем, создаваемым током и землей. Открытие Эрстеда, связавшее движение электрических зарядов с созданием магнитного поля, положило начало важной дисциплине под названием электромагнетизм.Экспериментально установлено, что величина B магнитного поля, создаваемого длинным прямым проводом, прямо пропорциональна току I и обратно пропорциональна радиальному расстоянию r от провода, как показано ниже. Константа пропорциональности преобразует выражение в уравнение, которое дает величину магнитного поля вокруг длинного прямого провода. Константа « μ ₀» известна как проницаемость свободного пространства, и ее значение показано ниже.

(3)

мкм ₀ = 4 π × 10 ⁻⁷ Т · м / А

Если токопроводящий провод согнут в круговую петлю, силовые линии магнитного поля вокруг петли будут иметь рисунок, подобный тому, что и вокруг стержневого магнита. В центре петли радиусом R магнитное поле перпендикулярно плоскости петли и имеет значение, показанное в уравнении ниже, где I обозначает ток в петле. Часто петля состоит из N витков провода, намотанных так близко друг к другу, что они образуют плоскую катушку с одной петлей.В этом случае магнитные поля отдельных витков складываются, чтобы получить результирующее поле, которое в Н в раз больше, чем у одиночной петли. Для такой катушки магнитное поле в центре зависит от количества петель, тока и радиуса петли, как показано в уравнении ниже.

(PDF) Влияние постоянного магнитного поля на электроосаждение металлов, сплавов, проводящих полимеров и органические реакции

17.Кодзука Т., Хонда Х, Фукуда С., Кавахара М. Влияние магнитного поля

на свойства анодирования металла. 8-я Международная

конференция по электромагнитной обработке материалов, 2015,

Канны, Франция

18. Хайндс Дж., Коуи Дж. М. Д., Лион MEG (1998) Магнитоэлектролиз меди

. J Appl Phys 83 (11): 6447–6449. https://doi.org/10.1063/1.

367734

19. Coey JMD, Hinds G (2001) Магнитное электроосаждение. Дж. Сплавы

Ср. 326 (1-2): 238–245.https://doi.org/10.1016/S0925-8388(01)

01313-5

20. Matsushima H, Bund A, Plieth W., Kikuchi S, Fukunaka Y (2007)

Электроосаждение меди в магнитном поле . Электрохим Acta

53 (1): 161–166. https://doi.org/10.1016/j.electacta.2007.01.043

21. Coey JMD, Hinds G, Lyons MEG (1999) Эффекты магнитного поля на фрактальных электроосаждениях

. Europhys Lett 47 (2): 267–272. https: // doi.

org / 10.1209 / epl / i1999-00382-3

22.Rhen FMF, Hinds G, Coey JMD (2004) Влияние магнитного поля на потенциал покоя цинка

. Electrochem Commun 6 (4): 413–416. https: //

doi.org/10.1016/j.elecom.2004.02.014

23. Heresanu V, Bodea S, Ballou R, Molho P (2003) Влияние магнитного поля

на рост электроосажденного цинка и железа arbores-

центов. https://www.electrochem.org/dl/ma/203/pdfs/0640.pdf

Доступ 17 сентября 2017 г.

24. Aaboubi O, Douglade J (2013) Применение магнитного поля для управления процессом массового транспорта

при цементации серебра на меди.

J Electroanal Chem 693: 42–50. https://doi.org/10.1016/j.jelechem.

2013.01.006

25. Джокич С.С. (2010) Электроосаждение: теория и практика. Springer,

Нью-Йорк. https://doi.org/10.1007/978-1-4419-5589-0

26. Левентис Н., Чен М., Гао Х, Каналас М., Чжан П. (1998)

Электрохимия с неподвижным диском и кольцом-диском миллиэлектроды

в магнитных полях. J. Phys Chem B 102 (18): 3512–3522. https: // doi.

орг / 10.1021 / jp980498f

27. Любашевский О., Кац Э., Виллнер И. (2004) Влияние магнитного поля на электрохимические процессы

: теоретическая гидродинамическая модель. J

Phys Chem B 108 (18): 5778–5784. https://doi.org/10.1021/

jp037785q

28. Aogaki R, Fueki K, Mukaibo T (1976) Процесс диффузии в вязком потоке раствора электролита

в электроды магнитогидродинамического насоса

. Денки Кагаку (в настоящее время — Электрохимия)

44 (2): 89–94

29.Судибьо, Азиз Н. (2015) Разработка полуэмпирического уравнения

предельного тока для магнитоэлектроосаждения свинца (Pb).

Химия процедур 16: 1–7. https://doi.org/10.1016/j.proche.2015.

12.001

30. Элиаз Н., Гилеади Э. (2008) Индуцированное соосаждение сплавов вольфрама-

, молибдена и рения с переходными металлами. Modern

Aspect Electrochem 42: 191–301

31. Цинцару Н., Цесиулис Х., Донтен М., Сорт Дж., Пеллисер Э, Подлаха

Мерфи Э.Дж. (2012) Современные тенденции в электроосаждении вольфрамовых сплавов —

с группой железа металлы.Surf Eng Appl Electrochem 48 (6): 491–

520. https://doi.org/10.3103/S1068375512060038

32. Соча Дж., Вебер Дж. (2001) Основы электролитического осаждения металлических сплавов

. Институт точной механики, Варшава

33. Узир М.Х., Судибио Н., Азиз М., Отман Р. (2015) Магнито-электро

осаждение дендритов олова. Surf Coat Tech 264: 66–71. https: // doi.

org / 10.1016 / j.surfcoat.2015.01.018

34. Ганеш В., Виджаярагхаван Д., Лакшминараян В. (2005) Мелкий рост зерен

никелевого электроосаждения: влияние приложенного магнитного поля

во время осаждения.Appl Surf Sci 240 (1-4): 286–295. https: //

doi.org/10.1016/j.apsusc.2004.06.139

35. Bund A, Ispas A, Mutschke G (2008) Влияние магнитного поля на электрохимические осаждения металлов

. Sci Technol Adv Mater 9 (2):

024208. https://doi.org/10.1088/1468-6996/9/2/024208

36. Мацусима Х, Нохира Т., Моги I, Ито И (2004) Влияние магнитных полей

на электроосаждение железа. Surf Coat Tech 179 (2-3): 245–251.

https://doi.org/10.1016 / S0257-8972 (03) 00860-0

37. Коза Дж., Улеманн М., Геберт А., Шульц Л. (2008) Влияние магнитных полей

на электроосаждение железа. J Solid State

Electrochem 12 (2): 181–192. https://doi.org/10.1007/s10008-007-

0379-0

38. Краузе А., Улеманн М., Геберт А., Шульц Л. (2004) Влияние магнитных полей

на электроосаждение кобальта. Электрохим Acta

49 (24): 4127–4134. https://doi.org/10.1016/j.electacta.2004.04.006

39. Мацусима Х., Испас А., Бунд А, Плиет В., Фукунака Ю. (2007)

Влияние магнитного поля на микроструктурные вариации электроосажденных пленок кобальта. J Solid State Electrochem 11 (6): 737–743. https: //

doi.org/10.1007/s10008-006-0210-3

40. Devos O, Aaboubi O, Chopart JP, Olivier A (2000) Есть ли влияние магнитного поля на электрохимическую кинетику? ? J Phys Chem A

104 (7): 1544–1548. https://doi.org/10.1021 / jp993696v

41. Gao F, Yin Q, Wang J, Zhou G, Gu Z (2016) 66

Electronic

Конференция по компонентам и технологиям, синтез и характеристики —

ization одномерного Cu — Диффузионные пары нанопроволоки SN для сборки и соединения нанопроволок

, https: //www.deepdyve.

com / LP / Institute-of-Electric-and-Electronics-Engineering / Synthesis-

и-характеристика-одномерная-cu-sn-nanowire-

bIRN2Xzj8x

42.Molin S, Sabato AG, Bindi M, Leone P, Cempura G, Salvo M,

Cabanas Polo S, Boccaccini AR, Smeacetto F (2017)

Микроструктурные и электрические характеристики шпинели Mn-Co

. межсоединения оксидных ячеек. J Europ Ceram

Soc 37 (15): 4781–4791. https://doi.org/10.1016/j.jeurceramsoc.

2017.07.011

43. Зелински М. (2013) Влияние постоянного магнитного поля на реакции троосаждения электроосаждения и структуру сплава кобальт-вольфрам.Мат

Chem Phys 141 (1): 370–377. https://doi.org/10.1016/j.

matchemphys.2013.05.025

44. Зелински М. (2013) Влияние постоянного магнитного поля на электроосаждение

кобальта и кобальтовых сплавов. Int J Electrochem

Sci 8 (11): 12192–12204

45. Зелински М., MiękośE (2008) Влияние постоянного магнитного поля

на электроосаждение Co – Mo – валлоев. J Appl Electrochem

38 (12): 1771–1778. https: // doi.org / 10.1007 / s10800-008-9628-x

46. Ispas A, Matsushima H, Plieth W., Bund A (2007) Влияние магнитного поля

на электроосаждение сплавов никель-железо.

Electrochim Acta 52 (8): 2785–2795. https://doi.org/10.1016/j.

electacta.2006.10.064

47. Рао В.Р., Бангера К.В., Читхаранджан Хегде А. (2013) Электроосаждение покрытий из сплава Zn – Ni с помощью магнитного поля

и их коррозионное поведение. J Magn Magn Mat 345: 48–54.https://doi.org/10.

1016 / j.jmmm.2013.06.014

48. Рао В.Р., Читараджан Хегде А (2014) Магнитно-индуцированное

соосаждение покрытий из сплава Ni – Cd для лучшей защиты от коррозии. Ind Eng Chem Res 53 (13): 5490–5497. https://doi.org/10.

1021 / ie403639z

49. Aaboubi O (2011) Активность выделения водорода из покрытия Ni – Mo

, электроосажденного под контролем магнитного поля. Int J Hydrog Energy

36 (8): 4702–4709.https://doi.org/10.1016/j.ijhydene.2011.01.035

50. Lou C, Kou Y, LyuX, Zhang W (2015) Электроосаждение тонкой пленки Sm-Fe

в водном растворе под сильным магнитным полем. поле. Int J

Electrochem Sci 10 (1): 9687–9694

51. Koza JA, Uhlemann M, Gebert A, Schultz L (2008) Влияние магнитных полей

на электроосаждение сплавов CoFe.

Electrochim Acta 53 (16): 5344–5353. https://doi.org/10.1016/j.

electacta.2008.02.082

52. Zieliński M, MiękośE, Szczukocki D, Dałkowski R, Leniart A,

Krawczyk B, Juszczak R (2015) Влияние постоянного магнитного поля

на электроосаждение сплава Co-W-Cu. Int J Electrochem Sci 10 (5):

4146–4154

1646 J Solid State Electrochem (2018) 22: 1629–1647

Содержание предоставлено Springer Nature, применяются условия использования. Права защищены.

Непостоянное магнитное поле Земли | Управление научной миссии

Непостоянство Земли
Магнитное поле

Магнитное поле нашей планеты находится в постоянном изменении, говорят исследователи, которые начинают понимать, как оно ведет себя и почему.

Послушайте эту историю с помощью потокового аудио, загружаемого файла или обратитесь за помощью.

29 декабря 2003 г .: Каждые несколько лет ученый Ларри Ньюитт из Геологической службы Канады отправляется на охоту. Он хватает перчатки, куртку, модный компас, садится в самолет и летит над канадской Арктикой. Среди разбросанных островов и морского льда не так много шевелений, но жертва Ньюитта всегда там — всегда движущаяся, подвижная, неуловимая.

Его добыча — северный магнитный полюс Земли.

В настоящее время он расположен на севере Канады, примерно в 600 км от ближайшего города: Резольют-Бэй, население 300, где на популярной футболке написано: «Резольют-Бэй — это не конец света, но вы можете увидеть это отсюда. . » Ньюитт останавливается там, чтобы перекусить и купить припасы, а также убежище в плохую погоду. «Что часто бывает», — говорит он.

Справа: Движение северного магнитного полюса Земли через канадскую Арктику, 1831-2001 гг.Предоставлено: Геологическая служба Канады. [подробнее]

Ученым давно известно, что магнитный полюс движется. Джеймс Росс впервые обнаружил полюс в 1831 году после изнурительного арктического путешествия, во время которого его корабль застрял во льдах на четыре года. Никто не вернулся до следующего столетия. В 1904 году Роальд Амундсен снова нашел полюс и обнаружил, что он переместился — по крайней мере, на 50 км со времен Росса.

Подпишитесь на рассылку EXPRESS SCIENCE NEWS

Полюс продолжал двигаться в течение 20-го века на север со средней скоростью 10 км в год, а в последнее время ускоряется «до 40 км в год», — говорит Ньюитт.Такими темпами он выйдет из Северной Америки и через несколько десятилетий достигнет Сибири.

Отслеживание северного магнитного полюса — работа Ньюитта. «Обычно мы выходим и проверяем его местонахождение раз в несколько лет», — говорит он. «Теперь, когда он движется так быстро, нам придется совершить больше поездок».

Магнитное поле Земли изменяется и по другим причинам: например, стрелки компаса в Африке смещаются примерно на 1 градус за десятилетие. А в глобальном масштабе с 19 века магнитное поле ослабло на 10%.Когда об этом упомянули исследователи на недавнем заседании Американского геофизического союза, многие газеты опубликовали эту историю. Типичный заголовок: «Магнитное поле Земли коллапсирует?»

Наверное, нет. Какими бы замечательными ни были эти изменения, «они мягкие по сравнению с тем, что магнитное поле Земли делало в прошлом», — говорит профессор Калифорнийского университета Гэри Глатцмайер.

Иногда поле полностью переворачивается. Северный и южный полюса меняются местами. Такие инверсии, зафиксированные в магнетизме древних горных пород, непредсказуемы.Они приходят с нерегулярными интервалами, в среднем около 300 000 лет; последний был 780 000 лет назад. Мы просрочили еще один? Никто не знает.

Слева: Магнитные полосы вокруг срединно-океанических хребтов раскрывают историю магнитного поля Земли на протяжении миллионов лет. Изучение прошлого магнетизма Земли называется палеомагнетизмом. Изображение предоставлено: USGS. [подробнее]

По словам Глатцмайера, продолжающееся падение на 10% не означает, что разворот неизбежен. «Поле постоянно увеличивается или уменьшается», — говорит он.«Мы знаем это из исследований палеомагнитной записи». Современное магнитное поле Земли на самом деле намного сильнее обычного. Дипольный момент, мера напряженности магнитного поля, теперь равен 8 × 10 ²² ампер × м ². Это вдвое больше, чем в среднем за миллион лет 4 × 10 ²² ампер × м ².

Чтобы понять, что происходит, говорит Глатцмайер, мы должны совершить путешествие … к центру Земли, где создается магнитное поле.

В центре нашей планеты лежит твердый железный шар, горячий, как поверхность Солнца.Исследователи называют это «внутренним ядром». Это действительно мир в мире. Внутреннее ядро на 70% меньше ширины Луны. Он вращается со своей собственной скоростью, на целых 0,2 ° долготы в год быстрее, чем Земля над ним, и у него есть свой собственный океан: очень глубокий слой жидкого железа, известный как «внешнее ядро».

Справа: схематическая диаграмма недр Земли. Внешнее ядро является источником геомагнитного поля.

Магнитное поле Земли исходит из этого океана железа, который представляет собой электропроводящую жидкость, находящуюся в постоянном движении.Находясь на горячем внутреннем ядре, жидкое внешнее ядро бурлит и бурлит, как вода в кастрюле на горячей плите. Во внешнем ядре также есть «ураганы» — водовороты, приводимые в действие силами Кориолиса вращения Земли. Эти сложные движения создают магнетизм нашей планеты посредством процесса, называемого динамо-эффектом.

Используя уравнения магнитогидродинамики, раздела физики, имеющего дело с проводящими жидкостями и магнитными полями, Глатцмайер и его коллега Пол Робертс создали суперкомпьютерную модель недр Земли.Их программное обеспечение нагревает внутреннее ядро, перемешивает металлический океан над ним, а затем вычисляет результирующее магнитное поле. Они запускают свой код в течение сотен тысяч смоделированных лет и смотрят, что происходит.

То, что они видят, имитирует реальную Землю: магнитное поле нарастает и ослабевает, полюса дрейфуют, а иногда и меняются местами. Изменения — это нормально, они научились. И неудивительно. Источник поля, внешнее ядро, само по себе бурлит, кружится, бурлит. «Там внизу хаос, — отмечает Глатцмайер.Изменения, которые мы обнаруживаем на поверхности нашей планеты, являются признаком этого внутреннего хаоса.

Они также узнали, что происходит во время магнитного переворота. Для завершения инверсии требуется несколько тысяч лет, и за это время — вопреки распространенному мнению — магнитное поле не исчезает. «Все становится еще сложнее, — говорит Глатцмайер. Магнитные силовые линии у поверхности Земли скручиваются и запутываются, а магнитные полюса появляются в непривычных местах. Южный магнитный полюс может появиться, например, над Африкой, или северный полюс над Таити.Странный. Но это все еще планетарное магнитное поле, и оно по-прежнему защищает нас от космической радиации и солнечных бурь.

Вверху: Суперкомпьютерные модели магнитного поля Земли. Слева — нормальное дипольное магнитное поле, типичное для долгих лет между сменами полярности. Справа — вид сложного магнитного поля Земли во время переворота инверсии. [подробнее]

И, как бонус, Таити может быть отличным местом, чтобы увидеть северное сияние.В такое время работа Ларри Ньюитта была бы другой. Вместо того, чтобы дрожать в заливе Резольют, он мог наслаждаться теплым южным Тихим океаном, прыгая с острова на остров, охотясь за магнитными полюсами, в то время как полярные сияния танцевали над головой.

Иногда, может быть, небольшое изменение может быть хорошим делом.

Решение теории поля струн, соответствующее постоянному фоновому магнитному полю | Успехи теоретической и экспериментальной физики

Следуя методу, недавно предложенному Эрлером и Маккаферри, мы строим решения уравнения движения теории поля кубической струны Виттена, которые описывают фон постоянного магнитного поля.Мы изучаем операторы изменения граничных условий, относящиеся к такому фону, и вычисляем их операторные разложения. Получены решения, классическое действие которых совпадает с действием Борна – Инфельда.

1. Введение

С момента открытия тахионного вакуумного решения [1] классические решения теории поля кубической струны [2] изучаются достаточно активно [3–21]. В недавней статье Эрлер и Маккаферри [22] дали возможность реализовать любую граничную конформную теорию поля (BCFT) как решение уравнения движения.

С помощью метода Эрлера и Маккаферри теперь можно изучать различные фоны открытых струн с точки зрения теории поля струн. Уже много лет известно, что теория открытых струн на фоне постоянного магнитного поля [23] имеет ряд интересных особенностей. Он соответствует точно решаемой BCFT, и действие задается действием Борна – Инфельда. Некоммутативная геометрия появляется в теории открытых струн на заднем плане [24,25].

В этой статье мы хотели бы построить решение Эрлера – Маккаферри, соответствующее постоянному магнитному фону.Мы начинаем с теории поля струны, связанной с D-браной с исчезающим фоном калибровочного поля, и хотели бы реализовать постоянный магнитный фон как решение уравнения движения. Для этого мы изучаем операторы изменения граничных условий (BCC), которые изменяют граничное условие открытой струны с одного фона на другое. ¹

Данный документ организован следующим образом. В разд. В разделе 2 мы кратко рассмотрим решения Эрлера – Маккаферри.В разд. В разделе 3 изучаются операторы BCC, необходимые для построения нашего решения. Мы исследуем состояния открытой струны, соответствующие этим операторам, вычисляем их корреляционные функции и, наконец, получаем их операторные разложения. В разд. В разделе 4 мы строим решения уравнения движения теории поля струн, используя операторы ОЦК, изученные в разд. 3. Раздел 5 посвящен выводам и обсуждениям. В приложениях представлены подробности расчетов операторов BCC.

2. Решения Эрлера – Маккаферри

Сначала объясним, как построить решения Эрлера – Маккаферри уравнения движения теории поля кубической струны Виттена. Здесь предположим, что решение Ψ = 0 соответствует граничной конформной теории поля BCFT0⁠. Мы хотели бы обсудить решение, связанное с другой граничной конформной теорией поля BCFT * ⁠. Решение строится из полей струн. Поля K⁠, B⁠, c — это те поля, которые играют решающую роль в построении классических решений теории поля кубических струн [1,28] и удовлетворяют так называемой алгебре KBc:

B2 = c2 = 0, [K, B] = 0, Bc + cB = 1, QK = 0, QB = K, Qc = c∂c.

(2.2) Здесь произведение строковых полей — это звездное произведение, а Q (⋅) обозначает вариацию BRST. Строковые поля σ, σ¯ — это те поля, которые могут быть выражены как где I — единичное строковое поле, а σ (s), σ¯ (s) — операторы BCC, такие что σ (s) изменяет граничное условие открытой строки с поле, соответствующее BCFT *, соответствует BCFT0⁠, и σ¯ (s) изменяется в обратном порядке, как показано на рис. 1. Мы предполагаем, что σ (s), σ¯ (s) являются первичными полями материи с весом 0 и удовлетворяют операторному разложению (OPE)

σ¯ (s) σ (0) ∼1, σ (s) σ¯ (0) ∼g * g0

(2.3) для s> 0⁠, где g * — это статистическая сумма диска BCFT *, а g0 — функция BCFT0⁠. Имеем следующие алгебраические соотношения, включающие σ, σ¯⁠:

[σ, c] = 0, [σ, ∂c] = 0, [σ, B] = 0, [σ¯, c] = 0, [σ ¯, ∂c] = 0, [σ¯, B] = 0, Qσ = c∂σ, Qσ¯ = c∂σ¯, σ¯σ = 1, σσ¯ = g * g0.

(2,4)

Рис. 1.

σ (z), σ¯ (z) ⁠. Граница слева от σ на вещественной оси соответствует граничному условию BCFT0, а граница справа соответствует граничному условию BCFT * ⁠, и наоборот для σ¯⁠.Порядок звездного произведения и порядок на рисунке совпадают, если мы возьмем направление действительной оси, как указано выше [4].

Рис. 1.

σ (z), σ¯ (z) ⁠. Граница слева от σ на вещественной оси соответствует граничному условию BCFT0, а граница справа соответствует граничному условию BCFT * ⁠, и наоборот для σ¯⁠. Порядок звездного произведения и порядок на рисунке совпадают, если мы возьмем направление действительной оси, как указано выше [4].

Со всеми этими строковыми полями можно построить решение Ψ, задаваемое формулой где Ψtv — решение Эрлера – Шнабла [4] для тахионного вакуума, а Σ, Σ¯ — строковые поля

Σ = QΨtv (11 + KBσ11 + K), Σ¯ = QΨtv (11 + KBσ¯11 + K)

(2.6) с использованием формулы, которая может быть получена из уравнений. Используя уравнения (2.2), (2.4) и (2.6), можно вычислить энергию и калибровочно-инвариантную наблюдаемую [29–33] как

E = 1Vol (X0) (- g02π2 + g * 2π2), TrV [ Ψ] = 14πi (〈V | c0− | B0〉 — 〈V | c0− | B *〉).

Из этих результатов следует, что решение соответствует граничной конформной теории поля BCFT * ⁠. Следовательно, чтобы построить решение, соответствующее BCFT * ⁠, нам нужно построить примарные поля σ (s), σ¯ (s) веса 0, удовлетворяющий ОПЕ (2.3). Эрлер и Маккаферри рассмотрели случай не зависящих от времени решений, и σ (s), σ¯ (s) выражаются как

σ (s) = σ * eihX0 (s), σ¯ (s) = σ¯ * e − ihX0 (s).

Здесь σ * (s), σ¯ * (s) — операторы BCC веса h, удовлетворяющие

σ¯ * (s) σ * (0) ∼s − 2h, σ * (s) σ¯ * ( 0) ∼g * g0s − 2h

(2.7) для s> 0⁠, и они действуют как тождественный оператор во временном направлении.

3. Операторы ОЦК для постоянного фонового магнитного поля

Мы хотим построить решение уравнения движения (2.1), которое соответствует фону постоянного магнитного поля. Здесь мы рассматриваем теорию бозонных струн в 26-мерном пространстве-времени Минковского и берем BCFT0 как обычную для Dp-браны, т.е.е. Граничные условия Неймана для Xμ (μ = 0,…, p) и граничные условия Дирихле для XI (I = p + 1,…, 25) ⁠. В качестве BCFT * выберем BCFT с постоянным магнитным полем, а именно с F0μ = 0⁠. Наша цель — изучить операторы BCC в этой установке и вычислить OPE, которые необходимы для построения решения Эрлера – Маккаферри.

3.1. Каноническое квантование

Операторы BCC соответствуют состояниям открытых цепочек, один конец которых удовлетворяет граничному условию BCFT0, а другой конец — граничному условию BCFT *.Следовательно, можно вывести свойства операторов BCC, изучая состояния открытой струны в таких секторах. Рассмотрим теорию мирового листа открытой струны, которая задается конформной теорией поля (CFT) на полосе, где граничные условия Неймана накладываются при σ = 0, а другая граница при σ = π связана с электромагнитными полями как В данном случае у нас есть постоянное магнитное поле (3.1), и мы берем Поскольку Fμν — действительный антисимметричный тензор с F0μ = 0⁠, мы можем повернуть его, чтобы преобразовать его в блочно-диагональную форму:

Fμν = (00F12− F1200F34 − F340⋱).

(3.4) Мы концентрируемся на одном из блоков и вводим комплексные координаты X = (X1 + iX2) / 2 и X˜ = (X1 − iX2) / 2⁠ в этих двух измерениях. Граничные условия для этих переменных оказываются равными

X ′ = 0, X˜ ′ = 0 (σ = 0),

(3.5)

X ′ = — i2πα′F12X˙, X˜ ′ = i2πα′F12X˜ ( σ = π).

(3.6) Теория открытых струн с такими граничными условиями изучается в [3]. [23], результаты которого рассмотрены в Приложении A. Разложения по модам X и X˜ задаются выражением

X (z, z¯) = x + iα′2∑k = −∞∞1k + λ (z −k − λ + z¯ − k − λ) αk + λ,

(3.7)

X˜ (z, z¯) = x˜ + iα′2∑k = −∞∞1k − λ (z − k + λ + z¯ − k + λ) α˜k − λ,

(3.8 ), где z = eτ + iσ, а λ связано с магнитным полем как 2πα′F12 = tanπλ (0≤λ <1) ⁠. Чтобы X1, X2 были действительными, (αk + λ) † = α˜ − k − λ и (x) † = x˜⁠. αk + λ⁠, α˜k − λ⁠, x⁠ и x˜ удовлетворяют коммутационным соотношениям

[αk + λ, α˜k′ − λ] = (k + λ) δk + k ′, 0,

( 3.9)

[αk + λ, αk ′ + λ] = [α˜k − λ, α˜k′ − λ] = 0, [x, x˜] = — 1F12 = −2πα′tanπλ.

(3.10) Уравнение (3.10) означает, что некоммутативное пространство возникает из-за фонового калибровочного поля. Тензор энергии-импульса задается формулой

T (z) = limz ′ → z [−2α′∂X (z) ∂X ˜ (z ′) — 1 (z − z ′) 2],

(3.11) и получаем генераторы Вирасоро

Ln = ∑k = −∞∞: αk + λα˜n − k − λ: + 12λ (1 − λ) δn, 0,

(3.12) где: ⋅: обозначает нормальную заказ. Мы строим базис пространства Фока с помощью осцилляторов αk + λ, α˜k − λ⁠. Каждому кет-состоянию соответствует оператор BCC, который можно использовать для построения решения Эрлера – Маккаферри. В этой статье для простоты мы ограничимся операторами BCC, соответствующими основным состояниям. Из уравнения. (3.12), мы видим, что эти операторы являются примарными полями с конформным весом. Основное состояние может быть выражено как линейная комбинация, удовлетворяющая

αk + λ | y〉 = 0 (k≥0), α˜k + 1− λ | y〉 = 0 (k≥0), 12i (x − x˜) | y〉 = y | y〉, 〈y | y ′〉 = δ (y − y ′).

(3.13) Мы можем определить операторы BCC σ * y, σ¯ * y такие, что

| y〉 = σ * y (0) | 0〉, 〈y | = limz → ∞ 〈0 | zλ (1 − λ ) σ¯ * y (z).

Другой выбор базиса основных состояний дается собственными состояниями оператора F12xx˜, который входит в угловой момент J, связанный с симметрией вращения X → eiΦX, X˜ → e − iΦX˜⁠:

J = F12x˜ x − 12 − ∑k = 0∞ (1k + λα˜ − k − λαk + λ − 1k − λ + 1α − k + λ − 1α˜k − λ + 1),

(3.14) где нормальная константа порядка определяется четностью по направлению x2. ² Поскольку нулевые моды удовлетворяют x † = x˜ и уравнению.(3.10) оператор F12x˜x является своего рода оператором подсчета чисел, и его математическое ожидание должно быть положительно или отрицательно определенным, в зависимости от сигнатуры F12⁠. Таким образом, оператор x рассматривается как оператор уничтожения, а x˜ — как оператор создания, если −F12> 0⁠, а роли x и x˜ меняются, если −F12 <0⁠. Следовательно, вакуум определяется как x | Ω〉 = 0 для −F12> 0 или x˜ | Ω〉 = 0 для −F12 <0⁠. Мы можем определить операторы BCC σ * Ω, σ¯ * Ω такие, что

| Ω〉 = σ * Ω (0) | 0〉, 〈Ω | = limz → ∞ 〈0 | zλ (1 − λ) σ¯ * Ω (z).

Собственное состояние углового момента задается как x˜n | Ω〉 (n = 0,1,2,…) для −F12> 0, а его собственные значения равны J = — (n + 1/2) ⁠. Для −F12 <0⁠ xn | Ω〉 является собственным состоянием J, соответствующим собственному состоянию n + 1 / 2⁠. Классически это интерпретируется как круговое движение в направлении вращения для фиксированного направления магнитного поля, и квантово-механический момент его углового момента дискретизируется.

3.2. Тороидально компактифицированная теория

Мы можем следовать той же процедуре, что и выше, и иметь дело со случаем, когда направления X1, X2 тороидально компактифицированы как

X1∼X1 + 2πR1, X2∼X2 + 2πR2.

(3.15) Получаем такие же разложения по модам (3.7), (3.8) и коммутационные соотношения (3.10), (3.10). В этом случае нам нужно ввести два унитарных оператора

U = exp (ix1R1), V = exp (ix2R2)

(3.16) с

x1 = 12 (x + x˜), x2 = 12i (x − x˜)

, чтобы получить представление алгебры нулевых мод (3.10), согласованное с периодичностью (3.15). Поскольку квантование Дирака подразумевает для некоторого целого числа N⁠, мы можем видеть, что U, V удовлетворяют соотношению

UV = ei2πNVU, (N = ± 1, ± 2,…).

(3.18) Хорошо известно, что алгебра (3.18) имеет | N | -мерное представление. При | N | = 1⁠ можно взять U = V = 1⁠. Для | N | ≠ 1⁠, если мы диагонализуем оператор V⁠, представление будет явно дано в матричной форме как

U = [01 ⋯ 0 ⋮ 01 ⋮⋮ ⋱⋱000110 ⋯⋯ 0], V = [1ωω2⋱ω | N | −1], (ω = ei2πN).

(3.19) Пусть | k〉 — собственное состояние V, соответствующее собственному значению ωk (k∈ℤ, | k | ≤ | N | 2) ⁠. Мы нормализуем собственные состояния как Мы можем определить операторы BCC σ * k, σ¯ * k так, чтобы

| k〉 = σ * k (0) | 0〉, 〈k | = limz → ∞ 〈0 | zλ (1− λ) σ¯ * k (z).

Теория, обсуждаемая в предыдущем пункте, соответствует пределу R1, R2, | N | → ∞ с фиксированным. Состояния | y〉, определенные в формуле. (3.13) может быть задано пределом

| y〉 = lim (| N | 2πR2 | k〉),

(3.21) с фиксированным.

3.3. Корреляционные функции

Для построения решений Эрлера – Маккаферри необходимо получить OPE операторов BCC. Мы вычисляем трехточечные и четырехточечные корреляционные функции операторов BCC и выводим из них OPE.

Рассмотрим сначала теорию в компактифицированном пространстве (3.15) и изучим трехточечную функцию вида

〈σ¯ * l (∞) eip⋅X (z, z¯) σ * k (0)〉,

, который может быть выражен на языке оператора. Как показано в Приложении B, эта корреляционная функция может быть оценена с помощью формул. (3.8), (3.9) и (3.10), и мы получаем

〈σ¯ * l (∞) eip⋅X (z, z¯) σ * k (0)〉 = {δ − α′p22 | z | α′p2 〈l | ei (px˜ + p˜x) | k〉 (z> 0) δ − α′p22cos2πλ | z | α′p2cos2πλ 〈l | ei (px˜ + p˜x) | k〉 (z <0).

(3.22) Для

pi = niRi (i = 1,2, ni∈ℤ),

получаем

〈l | ei (px˜ + p˜x) | k〉 = e − iπn1n2N 〈l | Un1Vn2 | k 〉 = Ωn1n22 + n2lδk − l, n1 (modN).

С трехточечной функцией (3.22) ОПЕ операторов σ * k, σ¯ * l получаются как

σ * k (s) σ¯ * l (0) ∼1g0∑n1, n2 〈σ¯ * l (∞) eip⋅X (1,1) σ * k (0)〉 s − λ (1 − λ) + α′p2e − ip⋅X (0), σ¯ * l (s) σ * k (0) ∼1g * ∑n1, n2 〈σ¯ * l (∞) eip⋅X (−1, −1) σ * k (0)〉 s − λ (1 − λ) + α′p2cos2πλe − ip⋅ X (0)

(3.23) для s> 0⁠. g0 равен объему (2π) 2R1R2 двумерного пространства, и все, что нам нужно сделать, это получить g * ⁠, которое может быть получено из четырехточечной функции. Четырехточечные функции операторов BCC вычислены в Приложении C, и мы имеем

〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 = 1 ( 2π) 2R1R2x − λ (1 − λ) (1 − x) −λ (1 − λ) 1F (λ, 1 − λ, 1; x) δj − i, l − k (modN) × ∑n, mω ( j − l) mexp [−πα′sinπλF (λ, 1 − λ, 1; 1 − x) F (λ, 1 − λ, 1; x) {(j − i + nN) 2R12 + m2R22}].

(3.24) Чтобы оценить g * ⁠, исследуем предел x → 1−0⁠, который можно изучить, переписав его в виде

〈σ * j (0) σ¯ * i (x) σ * k (1) σ¯ * l (∞)〉 = | cosπλ | (2π) 2R1R2x − λ (1 − λ) (1 − x) −λ (1 − λ) 1F (λ, 1 − λ, 1; 1 −x) δj − i, l − k (modN) × ∑n, mω (i − j) nexp [−πα′sinπλcos2πλF (λ, 1 − λ, 1; x) F (λ, 1 − λ, 1; 1 − x) {(i − k + mN) 2R12 + n2R22}]

(3.25) с использованием формулы пересуммирования Пуассона

∑m = −∞∞ei2πN (j − l) me − am2 = πa∑m = −∞∞ e − π2N2a (j − l + mN) 2, ∑n = −∞∞e − a (j − i + nN) 2 = 1 | N | πa∑n = −∞∞ei2πN (i − j) ne − π2N2an2 .

Из уравнения. (3.25) находим, что для x∼1⁠

〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 ∼ | cosπλ | (2π) 2R1R2∑p → ωn1n2 + n2 (i − l) δk − i, n1 (modN) δl − j, n1 (modN) δ − α′p2 (1 − x) −λ (1 − λ) + α′p2cos2πλ.

Сравнивая это с формулой. (3.23) получаем и ОПЕ

σ * k (s) σ¯ * l (0) ∼1 (2π) 2R1R2s − λ (1 − λ) ∑n1, n2 (sδ − 12) α ′ (( n1R1) 2+ (n2R2) 2) × ωn1n22 + n2lδk − l, n1 (modN) e − i (n1R1X1 + n2R2X2) (0), σ¯ * l (s) σ * k (0) ∼ | cosπλ | ( 2π) 2R1R2s − λ (1 − λ) ∑n1, n2 (sδ − 12) α ′ ((n1R1) 2+ (n2R2) 2) cos2πλ × ωn1n22 + n2lδk − l, n1 (modN) e − i (n1R1X1 + n2R2X2) (0).

(3.27) Поскольку

1 | cosπλ | = 1 + tan2πλ = 1 + (2πα′F12) 2,

(3.28) g * может быть выражено как

g * = (2π) 2R1R2det (12πα′F122πα′F211) = ∫d2xdet (12πα′F122πα′F211),

, что совпадает с вкладом в действие Борна – Инфельда от двух рассматриваемых нами измерений.Точно так же можно поступить и с некомпактным корпусом. Трехточечная функция и четырехточечная функция σΩ, σ¯Ω могут быть вычислены как

〈σ * Ω (∞) eip⋅X (z, z¯) σ¯ * Ω (0)〉 = {δ −α′p22 | z | α′p2exp (−p24 | F12 |) (z> 0) δ − α′p22cos2πλ | z | α′p2cos2πλexp (−p24 | F12 |) (z <0),

(3,29)

〈σ¯ * Ω (0) σ * Ω (x) σ¯ * Ω (1) σ * Ω (∞)〉 = x − λ (1 − λ) (1 − x) −λ (1 − λ) 1F (λ, 1 − λ, 1; x) × ∫d2p (2π) 2exp [−πα ′ | tanπλ | p2 − πα′sinπλF (λ, 1 − λ, 1; 1 − x) F (λ, 1− λ, 1; x) p2] = | cosπλ | x − λ (1 − λ) (1 − x) −λ (1 − λ) 1F (λ, 1 − λ, 1; 1 − x) × ∫d2p ( 2π) 2exp [−πα ′ | tanπλ | p2 − πα′sinπλcos2πλF (λ, 1 − λ, 1; x) F (λ, 1 − λ, 1; 1 − x) p2].

(3.30) Для z∈ℝ⁠ двухточечные функции BCFT0 на верхней полуплоскости нормированы как

〈eip⋅X (z, z¯) eip′⋅X (0,0)〉 BCFT0 = ( 2π) 2δ2 (p + p ′) | z | −2α′p2,

(3.31), а для BCFT * должны быть

〈eip⋅X (z, z¯) eip′⋅X (0,0)〉 BCFT * = 1 | cosπλ | (2π) 2δ2 (p + p ′) | z | −2α′p2cos2πλ.

(3.32) Из уравнений (3.31) и (3.32) следует

g0 = 〈1〉 BCFT0 = (2π) 2δ2 (p + p ′) | p = p ′ = 0 = ∫d2x, g * = 〈1〉 BCFT * = ∫d2xdet (12πα′F122πα′F211),

, хотя и g0, и g * бесконечны. Мы можем вывести ОПЕ

(3.33) при s> 0⁠. Они задаются как интеграл экспоненциального оператора по непрерывным импульсам, и на их основе сложно построить операторы ОЦК, удовлетворяющие (2.3). ОПЕ для σ * y, σ¯ * y можно получить либо вычислением корреляционных функций, либо просто переходя к пределу (3.21) уравнения. (3.27). Получаем

σ * y (s) σ¯ * y ′ (0) ∼s − λ (1 − λ) | tanπλ | 2πα′∫dp2 (2π) 2 (sδ − 12) α ′ ((tanπλ2πα ′ (y −y ′)) 2+ (p2) 2) × eip2y + y′2e − i (tanπλ2πα ′ (y − y ′) X1 + p2X2) (0), σ¯ * y ′ (s) σ * y (0 ) ∼s − λ (1 − λ) | sinπλ | 2πα′∫dp2 (2π) 2 (sδ − 12) α ′ ((tanπλ2πα ′ (y − y ′)) 2+ (p2) 2) cos2πλ × eip2y + y′2e − i (tanπλ2πα ′ (y − y ′) X1 + p2X2) (0)

(3.34) при s> 0⁠.

4. Классические решения для постоянного магнитного поля

Используя OPE (3.27), (3.33) и (3.34), полученные в предыдущем разделе, мы можем построить решение Эрлера – Маккаферри, соответствующее фону постоянного магнитного поля. Все, что нам нужно сделать, это найти операторы ОЦК σ *, σ¯ *, удовлетворяющие уравнению. (2.7).

4.1. Тороидально компактифицированная теория

В случае теории в тороидально компактифицированном пространстве легко построить σ *, σ¯ * ⁠.Поскольку уравнение Из (3.27) следует

σ * k (s) σ¯ * l (0) ∼1 (2π) 2R1R2s − λ (1 − λ) δk, l, σ¯ * l (s) σ * k (0) ∼ | cosπλ | (2π) 2R1R2s − λ (1 − λ) δk, l

для малых положительных s⁠ можно взять

σ * (s) = (2π) 2R1R2 | cosπλ | σ * k (s), σ¯ * (s) = (2π) 2R1R2 | cosπλ | σ¯ * k (s)

(4.1) для некоторого k (| k | ≤ | N | 2), удовлетворяющего ОПЕ (2.7), при

h = 12λ (1 −λ), g * g0 = 1 | cosπλ |.

Из них можно построить решение Эрлера – Маккаферри (2.5), которое описывает D-браны с калибровочной напряженностью поля F12⁠. Из уравнения. Из (3.28) видно, что действие фона определяется разностью между действием Борна – Инфельда и натяжением D-браны.Также возможно построить решения, соответствующие решениям кратных бран с фоном F12, рассматривая

σ *, k (s) = (2π) 2R1R2 | cosπλ | σ * k (s), σ¯ *, l (s) = (2π) 2R1R2 | cosπλ | σ¯ * l (s),

(4.2), из которых мы можем построить строковые поля Σk, Σ¯l аналогично уравнению. (2.6) удовлетворяет так, что

Ψ = Ψtv − ∑k = 1MΣkΨtvΣ¯k

(4.4) дает решение для 0 3 M не может быть больше | N | поскольку BCC-операторы, которые мы рассматриваем в этой статье, соответствуют основным состояниям пространства Фока в разд.3.1. Должна быть возможность иметь дело с более общими случаями, вводя операторы BCC, соответствующие другим состояниям.

Также возможно построить решения с общим Fμν вида (3.4), рассматривая тензорное произведение операторов BCC (4.2), по одному для каждого блока. Несложно показать, что энергия решения определяется разностью действия Борна – Инфельда и натяжения D-браны.

4.2. Некомпактный корпус

В отличие от компактифицированного случая (3.34) и (3.33) включают дополнительную lns-зависимость для малых положительных s⁠, и поэтому мы не можем выбрать σ * y, σ¯ * y или σ * Ω, σ¯ * Ω в качестве σ *, σ¯ *, удовлетворяющих OPE ( 2.7). Один несколько искусственный способ построения таких операторов BCC состоит в том, чтобы составить следующие линейные комбинации σ * y, σ¯ * y⁠:

σ * (s) ≡ (2π) 2aα ′ | sinπλ | ∑n = −∞∞σ * na (s), σ¯ * (s) ≡ (2π) 2aα ′ | sinπλ | ∑n = −∞∞σ * na (s)

для a> 0⁠. Из (3.34) легко получить следующие ОПЕ для s> 0:

σ¯ * (s) σ * (0) ∼s − λ (1 − λ), σ * (s) σ¯ * (0) ∼1 | cosπλ | s − λ (1 − λ).

Из σ *, σ¯ * ⁠ мы можем построить решения, соответствующие D-бране с фоном Fμν, как описано в предыдущем пункте. Аналогично, взяв различные линейные комбинации σ * y, σ¯ * y⁠, например

σ *, k (s) ≡ (2π) 2Maα ′ | sinπλ | ∑n = −∞∞σ * (nM + k) a (s), σ¯ *, l (s) ≡ (2π) 2Maα ′ | sinπλ | ∑n = −∞∞σ * (nM + l) a (s)

(⁠M∈ℕ; k, l = 0,1,…, M − 1⁠) имеем

σ¯ *, k (s) σ *, l (0) ∼s − λ (1 − λ) δk, l, σ *, k (s) σ¯ *, l (0) ∼1 | cosπλ | s − λ (1 − λ) δk, l

для s> 0, и по ним можно построить решения, соответствующие кратным D-бранам с Fμν.

5. Заключительные замечания

В этой статье мы построили решения Эрлера – Маккаферри, соответствующие конфигурациям постоянного магнитного поля на D-бранах. Для этого мы вычислили корреляционные функции операторов BCC и получили их OPE в случаях теорий в тороидально компактифицированном и некомпактном пространстве. Мы показали, что действие Борна – Инфельда появляется как действие для таких фонов.

В решениях, полученных в этой статье, необходимо изучить несколько важных моментов.В случае тороидально компактифицированного пространства число Черна калибровочного поля U (1) не обращается в нуль. Поэтому конфигурация должна быть топологически нетривиальной с точки зрения низких энергий. Возникает вопрос, как такие конфигурации реализованы как конфигурации строкового поля. Такой вопрос можно изучить, исследуя пространственный профиль калибровочного поля, как это было сделано в [4]. [22]. Из ОПЕ операторов σ *, σ¯ * ⁠ можно вычислить профиль, который, как легко видеть, является периодической функцией координат x1, x2⁠.Поэтому можно ожидать, что профиль калибровочного поля будет иметь скачкообразные разрывы в зависимости от x1, x2, чтобы конфигурация была топологически нетривиальной. ⁴ Оставляем это на будущее.

С помощью решения, построенного в этой статье, мы сможем вывести все интересные особенности теории открытых струн вокруг фона. В частности, связь с некоммутативной геометрией следует увидеть при анализе решения. Одна вещь, которую можно сделать, — это получить связь между переменными мирового листа BCFT0 и BCFT *, используя технику теории поля струн.В исх. В [22] указывается, что соответствие между состояниями в BCFT0 и BCFT * может быть задано строковыми полями Σ⁠, Σ¯⁠. Было бы интересно изучить такое соответствие и сравнить с тем, что дано в работах. [34,35].

Благодарности

Мы благодарим T. Erler, M. Kudrna, C. Maccaferri и M. Schnabl за полезные комментарии. Мы также хотели бы поблагодарить организаторов «VIII семинара по теории поля струн и связанных с ней аспектах» в Сан-Паулу, особенно Н.Берковиц, за гостеприимство. Эта работа была частично поддержана JSPS Grant-in-Aid for Scientific Research (C) (JP25400242), JSPS Grant-in-Aid for Young Scientists (B) (JP25800134) и JSPS Grant-in-Aid for Scientific Research ( C) (JP15K05056).

Финансирование

Финансирование открытого доступа: SCOAP ³.

Приложение A. Первое квантование открытых струн в фоновом калибровочном поле

В этом приложении мы обсуждаем первое квантование открытых струн в фоновых калибровочных полях.Об этом говорилось в [5]. [23], и мы приводим их результаты здесь, чтобы исправить наши обозначения.

Давайте рассмотрим теорию мирового листа переменных X, X˜, определенных в разд. 3.1. Здесь мы исследуем общий случай, когда заряды на концах струн равны q1, q2⁠. Действие равно

S = 12πα′∫dtdσ (X˙X˜˙ − X′X˜ ′) — iθ4πα′∫dt [q1 (XX˜˙ − X˜X˙) | σ = 0 + q2 (XX˜˙ −X˜X˙) | σ = π],

(A.1) где θ = −2πα′F12⁠. Система, обсуждаемая в разд. 3.1 соответствует случаю q1 = 0, q2 = 1⁠. Канонический импульс определяется как

P (t, σ) = ∂L∂X˙ = 12πα′X˜˙ + iθ4πα ′ {q1δ (σ) + q2δ (π − σ)} X˜,

(A.2)

P˜ (t, σ) = ∂L∂X˜˙ = 12πα′X˙ − iθ4πα ′ {q1δ (σ) + q2δ (π − σ)} X,

(A.3), и они удовлетворяют условию канонические коммутационные соотношения

[X (t, σ), P (t, σ ′)] = [X˜ (t, σ), P˜ (t, σ ′)] = iδ (σ − σ ′),

( A.4) с исчезновением всех остальных коммутаторов. Граничные условия задаются формулами

X ′ = — iq1θX˙ (σ = 0), X ′ = iq2θX˙ (σ = π),

(A.5)

X˜ ′ = iq1θX˜˙ (σ = 0), X˜ ′ = — iq2θX˜˙ (σ = π).

(П.6) Сначала рассмотрим случай q1 + q2 ≠ 0⁠. Переменные X, X˜ можно разложить как

X (t, σ) = x + i2α′∑k = −∞∞1k + λ1 + λ2αk + λ1 + λ2ψk (t, σ),

(.7)

X˜ (t, σ) = x˜ + i2α′∑k = −∞∞1k − λ1 − λ2α˜k − λ1 − λ2ψ − k * (t, σ),

(A.8) где qiθ = −tanπλi (i = 1,2) ⁠. ψk (t, σ) — модовые функции, которые являются решениями волнового уравнения с граничными условиями (A.5):

ψk (t, σ) = e − i (k + λ1 + λ2) tcos [(k + λ1 + λ2) σ − πλ1].

(A.9) Их комплексно сопряженные ψk * (t, σ) удовлетворяют граничным условиям (A.6). Поскольку X˜ эрмитово сопряжение X⁠, операторы x⁠, x˜⁠, αk + λ1 + λ2⁠ и α˜k + λ1 + λ2 подчиняются

x † = x˜, (αk + λ1 + λ2) † = α˜ − k − λ1 − λ2.

(A.10) Соотношения ортогональности задаются формулой

∫0πdσψk * (t, σ) Dψl (t, σ) = π (k + λ1 + λ2) δk, l,

(A.11) где D = i∂t → −i∂t ← + q1θδ (σ) + q2θδ (π − σ). Поскольку ψk (t, σ) и постоянная мода образуют полный набор, операторы x⁠, x˜⁠, αk + λ1 + λ2⁠ и α˜k + λ1 + λ2 выражаются как

αk + λ1 + λ2 = 12α′πi∫0πdσψk * [2πα′iP˜ + {k + λ1 + λ2 + q1θ2δ (σ) + q2θ2δ (π − σ)} X],

(A.13)

α˜k − λ1 − λ2 = 12α ′ Πi∫0πdσψ − k [2πα′iP + {k − λ1 − λ2 − q1θ2δ (σ) −q2θ2δ (π − σ)} X˜],

(A.14)

x = 1 (q1 + q2) θ∫ 0πdσ [2πα′iP˜ + {q1θ2δ (σ) + q2θ2δ (π − σ)} X],

(A.15)

x˜ = 1 (q1 + q2) θ∫0πdσ [−2πα′iP + {q1θ2δ ( σ) + q2θ2δ (π − σ)} X˜].

(A.16) Из этих выражений и канонических коммутационных соотношений следует, что

[αk + λ1 + λ2, α˜l − λ1 − λ2] = (k + λ1 + λ2) δk + l, 0, [x , x˜] = 2πα ′ (q1 + q2) θ.

(A.17) Тензор энергии-импульса определяется как

T (z) = limz ′ → z [−2α′∂X (z) ∂X˜ (z ′) — 1 (z − z ′) 2]. ,

и получаем генератор Вирасоро

Ln = ∑k = −∞∞: αn − k + λ1 + λ2α˜k − λ1 − λ2: +12 (λ1 + λ2) (1 − λ1 − λ2) δn, 0.

Обратимся к случаю q1 + q2 = 0⁠, что соответствует нейтральной струне. Легкий способ справиться с этим случаем — взять предел λ1 = −λ + ϵ, λ2 = λ + ϵ, ϵ → 0 приведенных выше результатов. Хотя предел нулевых мод требует некоторой осторожности, в итоге мы получаем разложения по модам

X (t, σ) = x0 + 2α′α0 {tcosπλ − i (σ − π2) sinπλ} + i2α′∑n ≠ 01nαne − intcos (nσ + πλ),

(А.18)

X˜ (t, σ) = x˜0 + 2α′α˜0 {tcosπλ + i (σ − π2) sinπλ} + i2α′∑n ≠ 01nα˜ne − intcos (nσ − πλ)

(A .19) и коммутационные соотношения

[x0, α˜0] = [x˜0, α0] = i2α′cosπλ, [αm, α˜m] = nδn + m, 0,

(A.20) со всеми другие коммутаторы исчезают. Генераторы Вирасоро задаются формулой. Вакуум Фока | p →〉 можно определить так, чтобы выполнялось

α0 | p →〉 = 2α′pcosπλ | p →〉, α˜0 | p →〉 = 2α′p˜cosπλ | p →〉 .

| p →〉 соответствует первичному полю eip → ⋅X → (z, z¯) = ei (p˜X + pX˜) (z, z¯) с весом α′p2cos2πλ⁠,

| p →〉 = eip → ⋅X → (0,0) | 0〉.

Оператор eip → ⋅X → (0,0) здесь нормально упорядочен и может быть выражен более точно как

eip → ⋅X → (0,0) = limϵ → 0 {exp [iπ∫0πdθ (pX˜ (ϵeiθ , ϵe − iθ) + p˜X (ϵeiθ, ϵe − iθ))] × exp [−α′pp˜π2∫0πdθ∫0πdθ ′ (ln | ϵeiθ − ϵeiθ ′ | + (cos2πλ) ln | ϵeiθ − ϵe− iθ ′ |)]}.

(A.21) Здесь для регуляризации мы заменяем локальный оператор X (z, z¯) интегралом по малому контуру вокруг z = 0⁠. Переходя к пределу ϵ → 0 с множителем во второй строке уравнения. (.21) получаем нормально упорядоченный оператор eip → ⋅X → (0,0). Это выражение полезно при вычислении трехточечных функций.

Приложение Б. Трехточечные функции

В этом приложении мы покажем, как вычислить корреляционные функции вида

〈| eip → ⋅X → (z, z¯) | 〉 ′

(Б.1) для z∈ℝ⁠, которые играют решающую роль в выводе OPE операторов BCC в разд. 3.3. Здесь | 〉 ′, 〈| состояния в пространстве Фока, определенные в разд. 3.1 и 3.2, и удовлетворяют условию

αk + λ | 〉 ′ = 0, α˜k + 1 − λ | 〉 ′ = 0, 〈| α − k − 1 + λ = 0, 〈| α˜ − k − λ = 0

(B.2) для k≥0⁠. Такие корреляционные функции могут быть оценены, по существу, следуя методу, описанному в [5]. [36]. Для z> 0⁠ возьмем примарное поле eip → ⋅X → в уравнении. (B.1) должно соответствовать нормированному основному состоянию дельта-функции в BCFT0⁠.Поэтому он должен совпадать с формулой. (П.21) в случае λ = 0, и мы получаем

〈| eip → ⋅X → (z, z¯) | 〉 ′ = Limϵ → 0 {〈| Rexp [iπ∫0πdθ (pX˜ (z + ϵeiθ, z¯ + ϵe − iθ) + p˜X (z + ϵeiθ, z¯ + ϵe − iθ))] | 〉 ′ × exp [−α′pp˜π2∫0πdθ∫0πdθ ′ (ln | ϵeiθ − ϵeiθ ′ | + ln | ϵeiθ − ϵe − iθ ′ |)]},

(B.3) где R [⋯] обозначает радиальное упорядочение. Подставляя модовые разложения (3.7), (3.8) в уравнение. (B.3) легко вычислить математическое ожидание в правой части уравнения. (B.3) и получаем

〈| Rexp [iπ∫0πdθ (pX˜ (z + ϵeiθ, z¯ + ϵe − iθ) + p˜X (z + ϵeiθ, z¯ + ϵe − iθ))] | 〉 ′ = Exp [−α′pp˜4π2∫0πdθ∫0πdθ ′ (1λ (w′w) λF (λ, 1,1 + λ; w′w) + 1λ (w¯′w) λF (λ, 1 , 1 + λ; w¯′w) + 1λ (w′w¯) λF (λ, 1,1 + λ; w′w¯) + 1λ (w¯′w¯) λF (λ, 1,1 + λ; w¯′w¯) + 11 − λ (ww ′) 1 − λF (1 − λ, 1,2 − λ; ww ′) + 11 − λ (w¯w ′) 1 − λF (1 − λ , 1,2 − λ; w¯w ′) + 11 − λ (ww¯ ′) 1 − λF (1 − λ, 1,2 − λ; ww¯ ′) + 11 − λ (w¯w¯ ′) 1 − λF (1 − λ, 1,2 − λ; w¯w¯ ′))] × 〈| ei (px˜ + p˜x) | 〉 ′

(Б.4) где F (α, β, γ; z) — гипергеометрическая функция ⁵ и

w = z + ϵeiθ, w ′ = z + ϵeiθ ′.

По формуле [37]

F (α, β, α + β; z) = Γ (α + β) Γ (α) Γ (β) ∑n = 0∞ (α) n (β) n (n !) 2 {2ψ (n + 1) −ψ (n + α) −ψ (n + β) −ln (1 − z)} (1 − z) n = Γ (α + β) Γ (α) Γ (β) {- ln (1 − z) + 2ψ (1) −ψ (α) −ψ (β)} + ⋯.

для | arg (1 − z) | <π, | 1 − z | <1⁠, правая часть уравнения. (B.3) оценивается как

δ − α′p22 | z | α′p2 〈| ei (px˜ + p˜x) | 〉 ′,

, где

lnδ = 2ψ (1) −ψ (λ) −ψ (1 − λ),

(B.5) и ψ (x) — дигамма-функция. точечная функция (Б.1) можно вычислить таким же образом, используя

〈| eip → ⋅X → (z, z¯) | 〉 ′ = Limϵ → 0 {〈| Rexp [iπ∫0πdθ (pX˜ (z + ϵeiθ, z¯ + ϵe − iθ) + p˜X (z + ϵeiθ, z¯ + ϵe − iθ))] | 〉 ′ × exp [−α′pp˜π2∫0πdθ∫0πdθ ′ (ln | ϵeiθ − ϵeiθ ′ | + (cos2πλ) ln | ϵeiθ − ϵe − iθ ′ |)]}

(B.6) и уравнение. (Б.4) с z = eπi | z | ⁠. В итоге получаем

〈| eip → ⋅X → (z, z¯) | 〉 ′ = {Δ − α′p22 | z | α′p2 〈| ei (px˜ + p˜x) | 〉 ′ (Z> 0) δ − α′p22cos2πλ | z | α′p2cos2πλ 〈| ei (px˜ + p˜x) | 〉 ′ (Z <0).

Приложение C. Корреляционные функции четырех операторов BCC

Четырехточечные функции операторов ОЦК

〈σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l (x4)〉

могут быть вычислены с использованием техники, развитой в орбифолде ЦФТ [38,39].Корреляционная функция может быть задана как

〈σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l (x4)〉 = ∑p → Cp → 〈σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l (x4)〉 p →,

где 〈σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l ( x4)〉 p → — конформный блок, определяемый импульсами p → операторов, которые входят в ОПЕ операторов σ¯ * j (x1) и σ * i (x2) ⁠. Рассмотрим следующее соотношение корреляционных функций, определенных на верхней полуплоскости со вставками операторов ОЦК при x1 G˜p → (z, w, xi) = 〈∂X (z) ∂X˜ (w) σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l (x4)〉 p → 〈σ¯ * j (x1) σ * i (x2) σ¯ * k (x3) σ * l (x4)〉 p →.

(C.1) Как функция z, w⁠, G˜p → (z, w, xi) может быть аналитически определена на всей комплексной плоскости, которая соответствует дублю мирового листа. Поскольку G˜p → (z, w, xi) является 1-формой на сфере относительно переменных z, w⁠, она ведет себя как ∼O (z − 2) (z∼∞) и ∼O (w− 2) (w∼∞) ⁠. Из ОПЕ ∂X и ∂X˜⁠ следует, что

G˜p → (z, w, xi) = — α ′ / 2 (z − w) 2 + конечный (z∼w).

(C.2) Из OPE между ∂X, ∂X˜ и операторами BCC мы получаем

G˜p → (z, w, xi) ∼ {(z − xi) — (1 − λ) (z ∼xi, i = 1,3) (z − xi) −λ (z∼xi, i = 2,4) (w − xi) −λ (w∼xi, i = 1,3) (w − xi) — (1 − λ) (w∼xi, i = 2,4).

(C.3) Используя все эти условия, G˜p → (z, w, xi) фиксируется как

G˜p → (z, w; xi) = — α′2ω (z) ω˜ (w) [(1 − λ) (z − x1) (z − x3) (w − x2) (w − x4) (z − w) 2 + λ (z − x2) (z − x4) (w − x1) ( w − x3) (z − w) 2 + A (xi)],

где функции ω (z) и ω˜ (w) имеют вид

ω (z) = (z − x1) −1 + λ ( z − x2) −λ (z − x3) −1 + λ (z − x4) −λ,

(C.4)

ω˜ (w) = (w − x1) −λ (w − x2) −1 + λ (w − x3) −λ (w − x4) −1 + λ,

(C.5) и A (xi) — мероморфная функция, которая остается неопределенной. Мы можем использовать преобразование SL (2, R), чтобы зафиксировать x1 = 0⁠, x2 = x⁠, x3 = 1⁠ и x4 → ∞⁠, и G˜ (z, w; x) преобразуется в

G˜p → ( z, w; x) = — α′2ω (z) ω˜ (w) [(1 − λ) z (z − 1) (w − x) (z − w) 2 + λ (z − x) w (w − 1) (z − w) 2 + A (x)],

(С.6) где ω (z) = z − 1 + λ (z − x) −λ (z − 1) −1 + λ и ω˜ (w) = w − λ (w − x) −1 + λ (w −1) −λ⁠.A (x) можно зафиксировать с помощью условий

∮dz∂X = 2πα′p, ∮dz∂X˜ = 2πα′p˜,

(C.7) где контуры интегрирования вокруг ветви, разрезанной на отрезке (0, x) ⁠. p и p˜ — импульсы операторов, входящих в ОПЕ операторов σ¯ * j (0) и σ * i (x) ⁠. Интегрируя (C.6) вокруг сечения ветви на отрезке (0, x) и используя условие (C.7), получаем

∮dzG˜p → (z, w, x) = 2ieπiλsinπλ∫0xdzG˜p → (z, w, x) = 2πα′p 〈∂X˜ (w) σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 p → 〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 p →.

(C.8) Количество в правой части уравнения. (C.8) можно увидеть пропорционально ω˜ (w) ⁠, а коэффициент пропорциональности можно определить, наложив уравнение. (С.7) еще раз. В результате получаем

∫0xdzG˜p → (z, w; x) = π2α′2p22sin2πλω˜ (w) ∫0xdwω˜ (w).

(C.9) Переходя к пределу w → ∞⁠, находим, что A (x) задается формулой

A (x) = — λ∫0xdz (z − x) ω (z) ∫0xdzω (z) −π2α ′ P2sin2πλ1∫0xdzω (z) ∫0xdwω˜ (w).

(C.10) Все интегралы, которые появляются в правой части, могут быть выражены через гипергеометрическую функцию:

∫0xdzω (z) = — πsinπλF (λ, 1 − λ, 1; x),

( С.11)

∫0xdwω˜ (w) = — πsinπλF (λ, 1 − λ, 1; x),

(C.12)

∫0xdz (z − x) ω (z) = πλsinπλx (1 − x) ddxF (λ, 1 − λ, 1; x),

(C.13)

1∫0xdzω (z) ∫0xdwω˜ (w) = — sinπλπx (1 − x) ddxF (λ, 1 − λ, 1; 1) −x) F (λ, 1 − λ, 1; x).

(C.14) Здесь мы использовали следующую формулу для гипергеометрической функции: Ref. [37],

F (α, β, γ; z) = Γ (γ) Γ (β) Γ (γ − β) ∫01tβ − 1 (1 − t) γ − β − 1 (1 − tz) — αdt,

(C.15)

ddz [(1 − z) α + β − γF (α, β, γ; z)] = (γ − α) (γ − β) γ (1 − z) α + β − γ − 1F (α, β, γ + 1; z),

(C.16)

ddz [zγ − 1F (α, β, γ; z)] = (γ − 1) zγ − 2F (α , β, γ − 1; z),

(С.17)

ddz [F (α, 1 − α, 1; 1 − z) F (α, 1 − α, 1; z)] = — sinπαπz − 1 (1 − z) −1F (α, 1 − α , 1; z) 2.

(C.18) Таким образом, мы в конечном итоге находим

G˜p → (z, w; x) = — α′2ω (z) ω˜ (w) [(1 − λ) z (z − 1) (w −x) (z − w) 2 + λ (z − x) w (w − 1) (z − w) 2 + x (1 − x) ddxlnF (λ, 1 − λ, 1; x) + πα ′ p2sinπλx (1 − x) ddxF (λ, 1 − λ, 1; 1 − x) F (λ, 1 − λ, 1; x)].

(C.19) Из этой корреляционной функции мы можем вывести

〈T (z) σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 p → 〈 σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 p → = 12λ (1 − λ) (1z + 1z − 1−1z − x) 2 + x (1 − x) z (z − 1) (z − x) ddx [lnF (λ, 1 − λ, 1; x) + πα′p2sinπλF (λ, 1 − λ, 1; 1 − x) F (λ , 1-λ, 1; x)]

с использованием уравнения.(3.11). Учитывая предел z → x⁠, получаем

ddxln 〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 p → = −λ (1 − λ) (1x + 1x − 1) −ddx [lnF (λ, 1 − λ, 1; x) + πα′p2sinπλF (λ, 1 − λ, 1; 1 − x) F (λ, 1 − λ, 1; x )].

Следовательно, мы находим, что четырехточечная функция может быть выражена как

〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 = ∑p → Cp → x − λ (1 − λ) (1 − x) −λ (1 − λ) 1F (λ, 1 − λ, 1; x) exp [−πα′sinπλp2F (λ, 1 − λ, 1; 1 − x ) F (λ, 1 − λ, 1; x)],

(C.20), где постоянная Cp → определяется переходом к пределу x → 0 в уравнении. (С.20). Переходя к пределу правой части уравнения. (C.20), получаем

〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 ∼∑p → Cpδ − α′p2x − λ (1 −λ) + α′p2,

(С.21), где δ — тот, который фигурирует в формуле. (В.5). С другой стороны, используя ОПЕ (3.23), получаем

〈σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 ∼1 (2π) 2R1R2x− λ (1 − λ) ∑n1, n2 (xδ − 12) α ′ ((n1R1) 2+ (n2R2) 2) ωn1n22 + n2jδi − j, n1 (modN) 〈σ¯ * k | e − ip⋅X ( 1,1) | σ * l〉,

(C.22), где pi = ni / Ri (⁠i = 1,2⁠). Подставляя уравнение. (3.22) в уравнение. (C.22) и сравнивая его с формулой. (C.21), мы можем получить

Cp = 1 (2π) 2R1R2ωn1n2 + n2 (j − k) δi − j, n1 (modN) δl − k, −n1 (modN)

(C.23) и

〈 σ¯ * j (0) σ * i (x) σ¯ * k (1) σ * l (∞)〉 = 1 (2π) 2R1R2x − λ (1 − λ) (1 − x) −λ (1− λ) 1F (λ, 1 − λ, 1; x) δj − i, l − k (modN) × ∑n, mω (j − l) mexp [−πα′sinπλF (λ, 1 − λ, 1; 1 −x) F (λ, 1 − λ, 1; x) {(j − i + nN) 2R12 + m2R22}].

(C.24) Здесь суммы по n, m соответствуют суммам по импульсам в направлениях x1 и x2. Импульсы в этих направлениях трактуются асимметрично из-за выбора состояний, соответствующих операторам ОЦК.

То же самое и с некомпактным корпусом. Сумма по промежуточным импульсам в уравнении. (C.20) становится интегралом по ним, и мы получаем Ур. (3.30).

Список литературы

[2]

Witten

Nucl.Phys. В

268

253

(

1986

). [23]

Abouelsaood

Callan

C. G.

Jr. $$$

Наппи

C. R.

Йост

S. A.

Nucl. Phys. В

280

599

(

1987

). [27]

de Groot

Mansfield

Phys. Lett. В

231

245

(

1989

).[37]

Милтон Абрамовиц

I. A. S.

Справочник по математическим функциям с формулами, графиками и математическими таблицами

(

Dover Publications

New York

1965

). [38]

Dixon

L. J.

Friedan

Martinec

E.J.

Shenker

S. H.

Nucl. Phys. В

282

(

1987

Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинал работа правильно процитирована. Финансируется SCOAP ³

Введение в магнитные поля

Основы магнитного поля

В этом разделе представлена справочная информация о магнитных полях применительно к электронным микроскопам и аналогичным приборам.Магнитные поля создаются электрическими токами в пространстве вокруг них. Токи, которые не меняются со временем (называемые постоянными токами или постоянным током), создают постоянные магнитные поля, которые мы называем полями постоянного тока. Постепенное изменение постоянного тока создает соответствующее постепенное изменение в поле постоянного тока. По соглашению мы называем неизменяющиеся поля и поля, которые изменяются таким медленным непериодическим образом, полями постоянного тока.

Токи, которые регулярно меняют знак со временем, называются переменными токами или переменным током и вызывают соответствующие переменные магнитные поля.

Наиболее распространенные поля переменного тока создаются линиями электропередач и обычно имеют основные частоты 50 или 60 Гц (называемые «линейной частотой»), часто с гармониками до примерно 5 кГц. Поля переменного тока на других частотах могут создаваться вращающимися машинами, содержащими постоянные магниты. Примерами являются магнитные мешалки и машины для плазменного травления, которые могут создавать поля с частотой около 0,3 Гц.

Для измерения магнитных полей используются следующие единицы …
Единица измерения напряженности магнитного поля в СИ: Ампер / метр (А / м)
Единица плотности магнитного потока в СИ: Тесла (Тл)
Единица плотности магнитного потока в системе СИ : Гаусс (G)

Единицы СИ являются современными единицами, но старая единица СГС, Гаусс, до сих пор так широко используется, что осталась в системах Spicer Consulting.Старая единица измерения напряженности магнитного поля CGS, Эрстед, сейчас используется редко.

Блок ампер / метр обычно используется в электроэнергетике, поскольку он напрямую связан с токами, которые создают магнитное поле. Тесла и Гаусс — единицы плотности потока, создаваемого магнитным полем, и являются наиболее распространенными единицами измерения полей. Соотношение между единицами измерения (в воздухе или в космосе) следующее …
1 Ампер / метр = 1,257 микротесла = 12.57 миллиГаусс

Магнитное поле Земли

Планета Земля окружена постоянным магнитным полем, которое создается постоянным током, протекающим в расплавленном ядре Земли. Ток и магнитное поле поддерживаются эффектом «динамо». Магнитное поле — это векторная величина, то есть имеет величину и направление. Величина поля Земли составляет около 0,5 Гаусс (50 микротесла). Направление вектора магнитного поля приблизительно вертикально на северном и южном полюсах и горизонтально (указывает на север) на экваторе.

Поле Земли претерпевает значительные изменения (включая смену знака) довольно случайным образом в масштабе времени в тысячи лет. Также есть небольшие изменения от 1 до 5 мГс в день, которые, как считается, связаны с взаимодействием солнечного ветра с ионосферой Земли. На рисунке ниже представлена диаграмма, в которой записаны изменения поля Земли за трехдневный период, измеренные в нашей лаборатории Стюартби. с помощью датчика магнитного поля SC20 / DCMR. Ось Y датчика совмещена с магнитным севером, ось X указывает на восток, а ось Z — вертикально.

Электронные микроскопы

Электронные микроскопы контролируют движение своих электронов с помощью электрических и магнитных полей внутри части прибора, называемой «колонкой». Системы сфокусированного ионного пучка аналогичны. Колонна обычно состоит из набора электронно-оптических компонентов, «линз» для фокусировки электронного луча и «дефлекторов» для позиционирования луча. Колонка в основном сделана из ферромагнитного железа, которое служит магнитопроводом для линз и механической структурой колонки.Магнитные поля внутри некоторых линз могут достигать 10 000 Гаусс (1,0 Тесла), то есть в 20 000 раз больше поля Земли. Железная структура колонны служит частичным барьером для магнитных полей, проникающих в колонну извне, и утечки больших внутренних полей линзы.

Окружающие магнитные поля проникают в столб электронного луча извне (в некоторой степени) и добавляют к магнитным полям в линзах и дефлекторах. Поля переменного тока и поля постоянного тока, которые меняются во время работы микроскопа, могут ухудшить характеристики микроскопа.Обычно поля постоянного тока проникают в столбец больше, чем поля переменного тока. Это связано с тем, что поля переменного тока также ослабляются механизмом, называемым «вихретоковым экранированием».

Изменяющиеся поля постоянного тока, которые вызывают проблемы для электронных микроскопов, могут быть созданы стальными объектами, движущимися и локально искажающими поле земли. Примеры включают дверцы шкафов, стулья, автомобили и лифты (лифты). Сильные изменяющиеся поля постоянного тока могут создаваться электрическими трамваями и электричками, которые потребляют постоянный ток от контактного провода, возвращая его по рельсам.Сверхпроводящие магниты в исследовательских центрах также не являются хорошей новостью для электронных микроскопов, потому что они могут излучать большие поля постоянного тока на расстояния в десятки метров.

Магнитное поле Земли также проникает через столб электронного луча, но для большинства электронных микроскопов его можно считать постоянным, поскольку оно изменяется медленно по сравнению со временем, требуемым для микрофотографии. Его эффект регулируется с помощью органов управления прибора во время повседневной работы микроскопа, и оператор обычно не замечает его присутствие.Для машин электронно-лучевой литографии, используемых для записи сеток для микросхем IC (или для записи непосредственно на кремниевой пластине), изменения магнитного поля Земли во время записи (несколько часов) могут значительно ухудшить точность записанного рисунка. Некоторые производители литографических машин EBeam теперь указывают максимальное изменение поля в 0,1 мГс. Поскольку в обычный день поле Земли изменяется намного больше, чем это, необходимо для этих машин, чтобы они соответствовали техническим требованиям, подавление магнитного поля.

Электронные микроскопы формируют свое изображение либо путем проецирования (ПЭМ), либо путем сканирования для формирования изображения, подобного телевизору (ПЭМ, СТЭМ). Влияние полей постоянного или переменного тока на проецируемые изображения заключается в перемещении всего изображения, что приводит к потере разрешения на экране изображения. Влияние полей постоянного или переменного тока на сканированные изображения заключается в перемещении частей изображения. Поля линии переменного тока обычно образуют волнистые края на изображении, которые часто называют «разрывом края» или «рваным краем». Поля постоянного тока могут вызвать неоднородность изображения и сделать прямые края похожими на горные хребты.

Что такое постоянное магнитное поле и как оно влияет на организм

Влияние магнитного поля на костную ткань

Применение магнитотерапии при заболеваниях костной системы

Механизмы воздействия магнитного поля на костную ткань

Экспериментальные исследования влияния магнитного поля на кости

Применение постоянных магнитов для терапии костно-суставной системы

Противопоказания к применению магнитотерапии

Заключение

Постоянное магнитное поле и его влияние на организм человека

Постоянное магнитное поле

Свойства магнитного поля

Постоянное магнитное поле и его физиотерапевтическое воздействие на организм

Что такое физиотерапия?

Магнитное поле.

Воздействие магнитного поля на организм.

Постоянное электромагнитное поле

ВЛИЯНИЕ ПОСТОЯННОГО МАГНИТНОГО ПОЛЯ НА СОСТОЯНИЕ КОСТНОЙ ТКАНИ КРЫС С ПОВЫШЕННЫМ УРОВНЕМ РЕЗОРБЦИИ

Библиографическая ссылка

Устройство и классификация МР-томографов

Резистивные магниты

Постоянные магниты

Сверхпроводящие магниты

Регулируемые источники постоянного магнитного поля большой интенсивности

магнитное поле | Определение и факты

Что такое магнетизм? | Магнитные поля и магнитная сила

Противоположности притягиваются

Ферромагнетизм

Другие формы магнетизма

Электромагнетизм

Магнитное поле токоведущего провода

Темы и файлы

E&M Тема

Напильник Capstone

Список оборудования

Введение

Фон

(PDF) Влияние постоянного магнитного поля на электроосаждение металлов, сплавов, проводящих полимеров и органические реакции

Непостоянное магнитное поле Земли | Управление научной миссии

Решение теории поля струн, соответствующее постоянному фоновому магнитному полю | Успехи теоретической и экспериментальной физики

1. Введение

2. Решения Эрлера – Маккаферри

3. Операторы ОЦК для постоянного фонового магнитного поля

3.1. Каноническое квантование

3.2. Тороидально компактифицированная теория

3.3. Корреляционные функции

4. Классические решения для постоянного магнитного поля

4.1. Тороидально компактифицированная теория

4.2. Некомпактный корпус

5. Заключительные замечания

Благодарности

Финансирование

Приложение A. Первое квантование открытых струн в фоновом калибровочном поле

Приложение Б. Трехточечные функции

Приложение C. Корреляционные функции четырех операторов BCC

Список литературы

Введение в магнитные поля

Основы магнитного поля

Магнитное поле Земли

Электронные микроскопы

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ