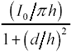Поверхностный эффект и эффект близости в электротехнике: причины, влияние и применение

Что такое поверхностный эффект в проводниках с переменным током. Как проявляется эффект близости при протекании тока по соседним проводникам. Какое влияние оказывают эти эффекты на распределение тока и сопротивление проводников. Где используются поверхностный эффект и эффект близости на практике.

Что такое поверхностный эффект и почему он возникает

Поверхностный эффект — это явление неравномерного распределения переменного электрического тока по сечению проводника. При протекании переменного тока плотность тока оказывается наибольшей у поверхности проводника и уменьшается по мере приближения к его центру.

Основные причины возникновения поверхностного эффекта:

• Переменное магнитное поле, создаваемое током в проводнике
• Явление электромагнитной индукции
• Вихревые токи, возникающие в проводнике

Переменный ток, протекающий по проводнику, создает вокруг него переменное магнитное поле. Это поле индуцирует в проводнике вихревые токи, которые стремятся противодействовать изменению основного тока. В результате происходит вытеснение тока к поверхности проводника.

Как проявляется эффект близости при протекании тока по соседним проводникам

Эффект близости — это явление взаимного влияния соседних проводников с переменным током друг на друга. Он приводит к еще большей неравномерности распределения тока по сечению проводников, чем при поверхностном эффекте.

Основные особенности проявления эффекта близости:

• Усиление концентрации тока на обращенных друг к другу поверхностях проводников при противоположных направлениях токов
• Вытеснение тока на внешние поверхности при одинаковых направлениях токов
• Увеличение эффекта с ростом частоты тока и уменьшением расстояния между проводниками

Эффект близости объясняется взаимодействием переменных магнитных полей соседних проводников. Это приводит к перераспределению плотности тока и дополнительному вытеснению тока к определенным участкам поверхности.

Влияние поверхностного эффекта и эффекта близости на параметры проводников

Неравномерное распределение тока по сечению проводников оказывает существенное влияние на их электрические параметры:

• Увеличение активного сопротивления проводников переменному току
• Уменьшение эффективного сечения проводников
• Рост потерь энергии в проводниках
• Изменение индуктивности проводников

Степень влияния этих эффектов зависит от частоты тока, размеров и формы сечения проводников, их взаимного расположения, свойств материала. Для количественной оценки используется понятие глубины проникновения тока.

Способы уменьшения негативного влияния поверхностного эффекта

Для снижения негативного влияния поверхностного эффекта и эффекта близости применяются следующие методы:

• Использование проводников из немагнитных материалов (медь, алюминий)
• Применение проводников с большим удельным сопротивлением
• Разделение проводников на отдельные изолированные жилы
• Транспозиция (перекрещивание) проводников
• Применение специальных профилей сечения проводников

Выбор конкретных способов зависит от назначения и условий работы электротехнического устройства. Например, в трансформаторах часто используют обмотки из тонких изолированных проводников, соединенных параллельно.

Практическое применение поверхностного эффекта и эффекта близости

Несмотря на негативное влияние в некоторых случаях, поверхностный эффект и эффект близости находят полезное применение в электротехнике:

• Высокочастотная закалка металлических деталей
• Индукционный нагрев в промышленности
• Экранирование электромагнитных полей
• Создание высокочастотных трансформаторов
• Разработка датчиков и измерительных приборов

Например, при высокочастотной закалке используется концентрация тока в поверхностном слое детали для ее быстрого нагрева. А в экранах используется вытеснение электромагнитного поля из внутренней области проводящей оболочки.

Особенности проявления эффектов в проводниках различной формы

Характер распределения тока существенно зависит от формы сечения проводника:

• В круглых проводниках ток вытесняется к поверхности равномерно по периметру
• В прямоугольных шинах наблюдается концентрация тока в углах
• В полых трубчатых проводниках ток протекает преимущественно по внешней поверхности
• В многожильных кабелях происходит вытеснение тока в наружные повивы

Учет этих особенностей позволяет оптимизировать конструкцию проводников для конкретных условий применения. Например, для уменьшения потерь на высоких частотах используют полые трубчатые проводники.

Методы расчета и моделирования поверхностного эффекта

Для количественного анализа поверхностного эффекта и эффекта близости применяются различные методы:

• Аналитические расчеты на основе уравнений Максвелла
• Численное моделирование методом конечных элементов
• Упрощенные инженерные методики с использованием эмпирических коэффициентов
• Экспериментальные исследования на физических моделях

Выбор метода зависит от требуемой точности, сложности геометрии проводников и диапазона частот. Для простых конфигураций часто используются приближенные аналитические формулы. Сложные системы проводников обычно рассчитываются численными методами.

Поверхностный эффект и эффект близости

Сопротивление проводника неизменному току определяется по известной формуле rо=ρl/S.

Это сопротивление можно также найти, зная величину неизменного тока Iо и мощность Ро:

rо = Pо / Iо²

Оказывается, что в цепи переменного тока сопротивление r такого же проводника больше сопротивления постоянному току: r > rо

Это сопротивление r в отличие от сопротивления неизменному току rо и носит заглавие активного сопротивления. Повышение сопротивления проводника разъясняется тем, что при переменном токе плотность тока не схожа в разных точках поперечного сечения проводника. Уповерхности проводника плотность тока выходит больше, чем при неизменном токе, а и центре меньше.

При высочайшей частоте неравномерность проявляется так резко, что плотность тока в значимой центральной чисти сечения проводника фактически равна нулю, ток проходит исключительно в поверхностном слое, отчего это явление и получило заглавие поверхностного эффекта.

Таким макаром, поверхностный эффект приводит к уменьшению сечения проводника, по которому проходит ток (активного сечения), и, как следует, к повышению его сопротивления по сопоставлению с сопротивлением неизменному току.

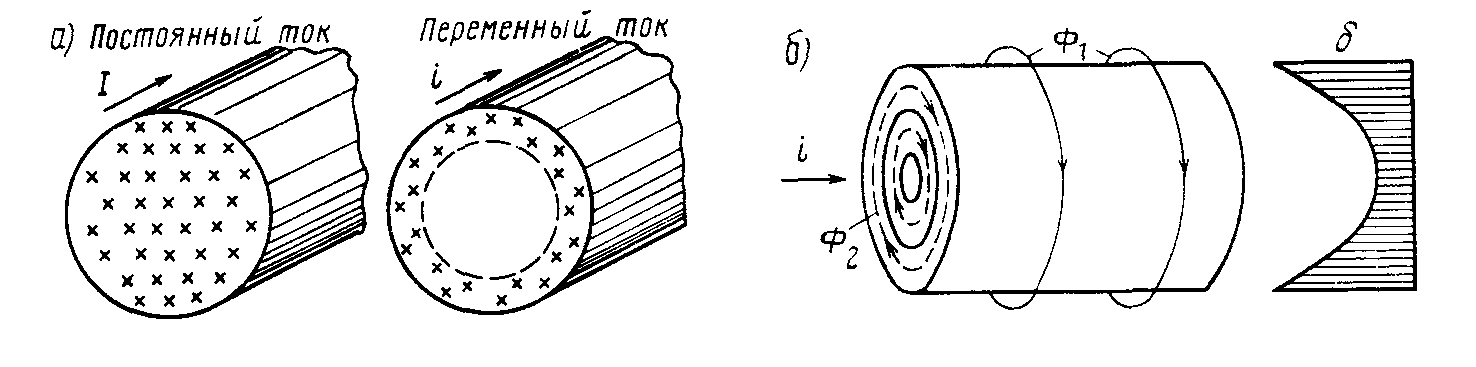
Для разъяснения предпосылки появления поверхностного эффекта представим цилиндрический провод (рис. 1) состоящим из большего числа простых проводников схожего сечения, прилегающих впритирку друг к другу и расположенных концентрическими слоями.

Сопротивления этих проводников неизменному току, отысканные по формуле ρl/S будут схожи.

Рис. 1. Магнитное поле цилиндрического проводника.

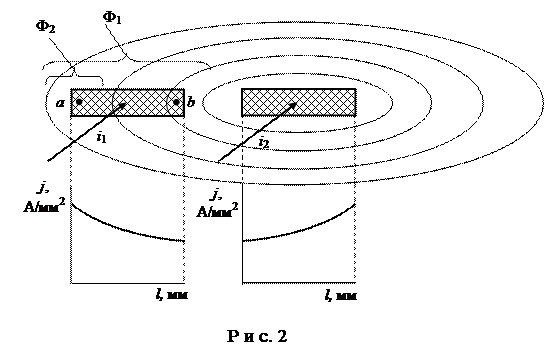
При переменном электронном токе вокруг каждого проводника создается переменное магнитное поле (рис. 1). Разумеется, простый проводник, расположенный поближе к оси, охватывается огромным магнитным потоком проводник, расположенный у поверхности провода, потому 1-ый обладает большей индуктивностью и индуктивным сопротивлением, чем 2-ой.

При схожем напряжении на концах простых проводников длиной l, расположенных у оси и у поверхности, плотность тока в первых меньше, чем во вторых.

Разница в плотностях тока у оси и на периферии провода растет с повышением поперечника провода d, проводимости материала γ, магнитной проницаемости материала μ и частоты переменного токаf.

Отношение активного сопротивления проводника r к его сопротивлению при. неизменном, токе rо именуется коэффициентом поверхностного эффекта и обозначается буковкой ξ (кси), как следует, коэффициент ξ можно найти по графику рис. 2, на котором представлена зависимость ξ от произведения d и √γμμоf.

Рис. 2. График для определения коэффициента поверхностного эффекта.

При вычислении этого произведения следует выражать d в см, γ — в 1/ом-см, μо — в гн/см и f = в гц.

Пример. Нужно найти коэффициент поверхностного эффекта для медного проводника поперечником d= 11,3 мм (S = 100 мм2) при частоте f = 150 гц.

Произведение d√γμоf.

По графику на рис. 2 находим ξ = 1,03

Неодинаковая плотность тока в проводе выходит также из-за воздействия токов в примыкающих проводах. Это явление именуется эффектом близости.

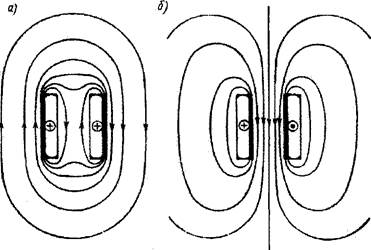
Рассматривая магнитное поле токов одною направления в 2-ух параллельно расположенных проводах, просто показать, что те простые проводники, принадлежащие различным проводам, которые более удалены друг от друга, сцеплены с минимальным магнитным потоком, как следует, плотность тока в их большая. Если токи в параллельных проводах имеют, различные направления, то можно показать, что большая плотность тока наблюдается в тех простых проводниках, принадлежащих различным проводам, которые более сближены вместе.

Школя для электрика -http://electricalschool.info/

Поверхностный эффект и эффект близости — Студопедия

Сопротивление проводника постоянному току определяется по известной формуле rо=ρl/S.

Это сопротивление можно также определить, зная величину постоянного тока Iо и мощность Ро:

rо = Pо / Iо²

Оказывается, что в цепи переменного тока сопротивление r того же проводника больше сопротивления постоянному току: r > rо

Это сопротивление r в отличие от сопротивления постоянному току rо и носит название активного сопротивления. Увеличение сопротивления проводника объясняется тем, что при переменном токе плотность тока не одинакова в различных точках поперечного сечения проводника. У поверхности проводника плотность тока получается больше, чем при постоянном токе, а и центре меньше.

При высокой частоте неравномерность проявляется так резко, что плотность тока в значительной центральной чисти сечения проводника практически равна нулю, ток проходит только в поверхностном слое, отчего это явление и получило название поверхностного эффекта.

Таким образом, поверхностный эффект приводит к уменьшению сечения проводника, по которому проходит ток (активного сечения), и, следовательно, к увеличению его сопротивления по сравнению с сопротивлением постоянному току.

Для объяснения причины возникновения поверхностного эффекта представим цилиндрический провод (рис. 1) состоящим из большего числа элементарных проводников одинакового сечения, прилегающих вплотную друг к другу и расположенных концентрическими слоями.

Сопротивления этих проводников постоянному току, найденные по формуле ρl/S будут одинаковы.

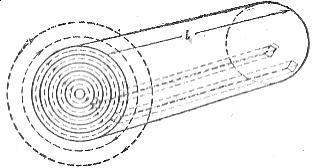
Рис. 1. Магнитное поле цилиндрического проводника.

При переменном электрическом токе вокруг каждого проводника создается переменное магнитное поле (рис. 1). Очевидно, элементарный проводник, расположенный ближе к оси, охватывается большим магнитным потоком проводник, расположенный у поверхности провода, поэтому первый обладает большей индуктивностью и индуктивным сопротивлением, чем второй.

При одинаковом напряжении на концах элементарных проводников длиной l, расположенных у оси и у поверхности, плотность тока в первых меньше, чем во вторых.

Разница в плотностях тока у оси и на периферии провода возрастает с увеличением диаметра провода d, проводимости материала γ, магнитной проницаемости материала μ и частоты переменного токаf.

Отношение активного сопротивления проводника r к его сопротивлению при. постоянном, токе rо называется коэффициентом поверхностного эффекта и обозначается буквой ξ (кси), следовательно, коэффициент ξ можно определить по графику рис. 2, на котором представлена зависимость ξ от произведения d и √γμμоf.

Рис. 2. График для определения коэффициента поверхностного эффекта.

При вычислении этого произведения следует выражать d в см, γ — в 1/ом-см, μо — в гн/см и f = в гц.

Пример. Необходимо определить коэффициент поверхностного эффекта для медного проводника диаметром d= 11,3 мм (S = 100 мм2) при частоте f = 150 гц.

Произведение d√γμоf.

По графику на рис. 2 находим ξ = 1,03

Неодинаковая плотность тока в проводе получается также из-за влияния токов в соседних проводах. Это явление называется эффектом близости.

Рассматривая магнитное поле токов одною направления в двух параллельно расположенных проводах, легко показать, что те элементарные проводники, принадлежащие разным проводам, которые наиболее удалены друг от друга, сцеплены с наименьшим магнитным потоком, следовательно, плотность тока в них наибольшая. Если токи в параллельных проводах имеют, разные направления, то можно показать, что большая плотность тока наблюдается в тех элементарных проводниках, принадлежащих разным проводам, которые наиболее сближены друг с другом.

5.5. Электрический поверхностный эффект в плоской шине. Эффект близости

Рассмотрим явление поверхностного эффекта при прохождении переменного синусоидального тока частотой w вдоль пластины (шины) (рис. 5.7). Предположим, что обратная шина (обратный проводник) находится настолько далеко, что влиянием магнитного потока, вызванного током в ней, на распределение тока в исследуемой шине можно пренебречь.

В этом случае поле внутри пластины определяется по формулам:

Сопротивление единицы длины шины

(5.8)

Здесь – комплексные амплитуды напряженности электрического и магнитного поля на поверхности шины (z = 0).

На рис. 5.8 приведены кривые B_m/B_me и E_m/E_me в функции от z для следующих параметров: m = 1000m₀; g = 10⁷ См/м; f = 500 Гц; d = 2 мм. Эти зависимости определяются формулами:

Как видно из рисунка, неравномерность распределения напряженности электрического поля (а значит, и плотности тока) довольно значительная. Так, напряженность поля в середине шины почти в десять раз меньше, чем на поверхности. В этом и заключается электрический поверхностный эффект.

Если в непосредственной близости друг от друга расположено несколько проводников с переменными токами и каждый из них находится не только в собственном переменном магнитном поле, но и в магнитном поле других проводников, то распределение в каждом проводнике будет несколько отличаться от того, которое имело бы место, если бы этот проводник был уединен. Этот эффект носит наименование эффекта близости. Он приводит к дополнительному увеличению активного сопротивления проводников.

В случае двухпроводной линии передачи, в проводах которой токи протекают в противоположных направлениях, эффект близости приводит к тому, что плотность тока на сторонах проводников, обращенных друг к другу, оказывается большей, чем на противоположных сторонах.

В качестве иллюстрации рассмотрим двухпроводную линию в виде двух параллельных близко расположенных плоских шин (рис. 5.9), по которым протекает в противоположных направлениях синусоидальный ток.

Поместим начало декартовой системы координат в средней плоскости левой шины и примем размеры d << h и 2b << h. В этом случае, с учетом того, что слева от левой шины напряженность магнитного поля Н = 0, а в пространстве между шинами Н = I/h (согласно закону полного тока), получим следующие формулы для определения Н и Е в левой шине:

На рис. 5.10 приведены кривые Н_m/Н_me и E_m/E_me в функции от z для тех же параметров, что и в предыдущем примере. Здесь Н_me и E_me – значение наряженности магнитного и электрического поля на правой поверхности левой шины (z = 0.5d).

Как видно из рис. 5.10, в данном случае распределение напряженности электрического поля и напряженности магнитного поля (кривые практически совпадают) существенно отличаются от соответствующего распределения для одиночной шины (рис. 5.9).

Поверхностный эффект и эффект близости широко используют при поверхностной закалке стальных изделий индукционным методом.

Так, если поднести плоский контур, по которому протекает ток высокой частоты, к плоской поверхности стального тела, то в этом теле вблизи его поверхности возникнут индуктированные токи. Эти токи и нагревают поверхностный слой тела напротив контура.

Поверхностный эффект и его влияние на нагрев

Поверхностный эффект – это эффект оттеснения переменного электрического тока, протекающего через проводник, к его периферии, вызванный переменным магнитным полем, создаваемым этим током.

Механизм возникновения поверхностного эффекта стоит рассмотреть на примере проводника круглого сечения, по которому протекает переменный электрический ток.

Протекание электрического тока вдоль проводника приводит к возникновению магнитного поля, силовые линии которого изображены на рисунке. Вектор индукции магнитного поля B при этом всегда направлен по касательной к силовой линии магнитного поля. Поскольку ток j, протекающий через проводник является переменным, вектор индукции магнитного поля также изменяет свой модуль и направление в каждой точке силовой линии в противоположные стороны, а вектор его производной по времени коллинеарен вектору индукции магнитного поля (т.е. векторы могут быть либо сонаправлены либо противонаправлены в каждый момент времени).

Наличие ненулевой первой производной по времени вектора магнитной индукции приводит, в соответствии с законом Фарадея, к возникновению вектора напряженности электрического поля E, ротор которого определяется согласно уравнению Максвелла.

Физически это можно представить как возникновение дополнительной электродвижущей силы, сонаправленной с направлением протекания тока вблизи периферии проводника и противонаправленной вблизи его оси.

Этот эффект приводит к неравномерному распределению протекающего электрического тока в проводнике, при котором большая часть тока протекает в его поверхностном слое.

График распределения тока представлен на рисунке. Распределение имеет экспоненциальный характер, поэтому для упрощения расчетов в первом приближении принято считать, что электрический ток протекает равномерно только в поверхностном слое толщиной Δ, называемым скин-слоем, а в остальном сечении проводника — отсутствует.  Действительная величина плотности тока на глубине скин-слоя в 2,7 раза меньше плотности тока на поверхности проводника, однако в связи с экспоненциальной характеристикой затухания, на глубине 2Δ плотность тока незначительна, а выделяемая мощность практически равна нулю.

Поверхностный эффект характерен только для протекания переменного тока: при протекании постоянного тока, ток распределяется равномерно по всему сечению проводника. Толщина скин-слоя сильно зависит от частоты, электрического сопротивления материала и его магнитной проницаемости: она уменьшается с увеличением частоты переменного тока и магнитной проницаемости материала и увеличивается с ростом удельного сопротивления согласно соотношению.

Ярко выраженное изменение толщины скин-слоя происходит при нагреве сплавов на основе железа при переходе температуры точки Кюри: толщина скин-слоя при этом увеличивается на порядок, при этом визуально наблюдается увеличение области нагрева.

Поверхностный эффект имеет огромное значение в индукционном нагреве, поскольку с его помощью можно концентрировать выделение тепловой энергии в определенной области заготовки. Это связано с тем, что нагрев производится вихревыми токами внутри детали в области их протекания, а эта область и, следовательно, область нагрева определяется поверхностным эффектом. Это широко используется, например, при поверхностной закалке, когда необходимо закалить только поверхность изделия, не изменяя структуры металла на большей глубине.

Использование частот, при которых толщина скин-слоя намного меньше нагреваемой области возможно, однако в этом случае за счет того, что энергия выделяется в тонком поверхностном слое, нагрев более глубоких зон будет производится слой за слоем за счет теплопроводности металла, что увеличивает длительность нагрева, снижает общий КПД системы, а также не обеспечивает равномерности нагрева.

Таким образом, для глубинного равномерного нагрева крупных стальных заготовок следует использовать более низкие частоты, в то время как для нагрева небольших деталей, для поверхностной закалки или для нагрева немагнитных металлов необходимы ТВЧ преобразователи с частотами на порядок выше.

Для ориентировочного расчета толщины скин-слоя нескольких основных материалов рекомендуется использовать следующие соотношения.

виды и группы, ГОСТы, принцип работы, преимущества

Высокочастотная сварка представляет собой способ контактной сварки, нагревание металла при котором происходит с применением переменного тока частоты 10 кГц и более. Подача энергии происходит через механические контакты или способом наведения в детали.

Общая информация

Способ включает использование законов и явлений физики.

Законы:

• электромагнитной индукции;
• полного тока.

Явления:

• эффекта близости;
• возникновения электромагнитных сил;
• поверхностного эффекта;
• влияния на распределение тока в проводнике медных экранов и магнитопроводов;
• катушечного или кольцевого эффекта;
• изменения свойств металлов при изменении напряженности магнитного поля и температуры.

При высокочастотном нагревании основная роль отводится явлению поверхностного эффекта и эффекта близости.

Поверхностный эффект

Заключается в неравномерности распространения переменного тока по профилю проводника (глубина проникновения тока). У внешней поверхности плотность тока наибольшая и постепенно уменьшается по мере удаления вглубь. В центре тела она минимальна.

Благодаря поверхностному эффекту, в наружных слоях происходит концентрирование выделения энергии и быстрый нагрев металла. Эффект близости также способствует этому проявлению.

Эффект близости

Заявляет о себе путем прохождения в системе проводников переменного тока. На каждый из проводников при этом распространяется влияние как собственного переменного магнитного поля, так и поля других проводников.

Чем меньше расстояние, отделяющее проводники друг от друга, и выше частота тока, тем сильнее эффект близости.

Это явление способствует усилению концентрации энергии во внешнем слое металла, подвергаемому нагреву. Таким образом, выделение тепловой энергии происходит непосредственно в толще металла, обеспечивая быстрый нагрев в сварочной зоне и высокую эффективность способа нагрева.

Виды и группы

Высокочастотная сварка в зависимости от способа передачи энергии кромкам классифицируется на виды:

1. Контактный. На свариваемые кромки накладываются контакты, к которым подводится ток высокой частоты.
2. Индукционный. Нагревание происходит с помощью индуктора, при протекании через который переменного тока возникает магнитное поле. При помещении металлической детали в середину индуктора переменным магнитным потоком будет вызван индукционный ток, и выполнено нагревание в заданной зоне.

Процессы сварки ТВЧ подразделяются на 3 группы:

1. Давлением с оплавлением. Механизм заключается в предварительном нагреве соединяемых поверхностей и их местного расплавления. Расплавленный материал удаляется из сварочной зоны при осадке. Шов образуется между деталями в твердом состоянии.
2. Давлением без оплавления. Свариваемые поверхности предварительно нагреваются до температуры, значение которой ниже точки плавления металла, подвергаемого процессу.
3. Плавлением без давления. Нагрев элементов осуществляется до оплавления. Сварная ванна металла застывает, шов образуется без приложения давления.

ГОСТы

Информация, относящаяся к высокочастотной сварке, изложена в ГОСТах, которые необходимо выполнять.

ГОСТ Р ИСО 857-1-2009 содержит:

• формулировку термина «высокочастотная сварка»;
• информацию о принадлежности метода по виду энергоносителя к классу «Электрический ток».

Другой стандарт:

• процессы сварки: ГОСТ Р ИСО 4063-2010 – список общепринятых сокращений высокочастотной сварки.

Принцип работы

Соединяемые заготовки изделия установлены под небольшим углом с образованием щели между соединяемыми кромками. Ток высокой частоты к кромкам подводится одним из способов – индуктором или через скользящие контакты и проходит от одной кромки к другой через зону их схождения. Высокая концентрация энергии в этой зоне достигается в результате действия проявлений поверхностного эффекта и близости.

При соприкосновении кромок в рабочей зоне происходит интенсивный нагрев металла и его расплавление. В результате сдавливания обжимными роликами металл осаживается, образуется прочное соединение.

Процесс высокочастотной сварки труб

Положительные качества

Достоинства способа:

• возможность бесконтактного нагрева заготовки;
• высокая степень локализации энергии;
• широкая возможность изменения параметров сварки;
• отсутствие ограничений по скорости процесса;
• невысокая энергоемкость работ.

Где применяется

Метод эффективен при непрерывном процессе массового изготовления изделий простой конфигурации.

Высокочастотная сварка находит применение в производстве:

• прямошовных и спиральношовных труб из цветных и черных металлов;
• тавровых и двутавровых балок в судостроении;
• оболочек электрических кабелей.

Способ используют при изготовлении профилей, приварке ребер.

4. Исследование поверхностного эффекта и эффекта близости

4.1. Общие сведения

Переменный ток распределяется по сечению массивных проводников (шин) неравномерно вследствие поверхностного эффекта и эффекта близости. Наибольшая плотность тока наблюдается на поверхности шины и уменьшается к центру поперечного сечения (рис.4.1.а). В двух близко расположенных шинах с противоположным направлением токов, кроме того, происходит вытеснение токов на поверхности шин обращённые друг к другу (рис.4.1 6). При одинаковых направлениях токов в двух таких шинах вытеснение токов происходит на внешние поверхности.

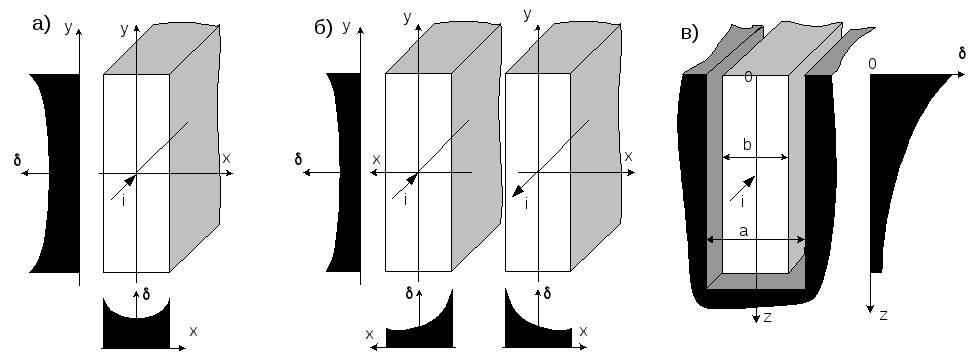
а) б) в)

Рисунок 4.1. Исследование поверхностного эффекта и эффекта близости

В проводнике, уложенном в ферромагнитный паз ротора или статора электрической машины происходит вытеснение тока на открытую поверхность проводника (рис. 4.1 в).

Неравномерное распределение тока по сечению проводников приводит к увеличению их активных сопротивлений, что необходимо учитывать при проектировании электрических машин и токопроводов.

Наиболее простым для математического описания является проводник, уложенный в ферромагнитный паз. При достаточной высоте паза можно пренебречь отражённой электромагнитной волной от его дна. Тогда распределение действующего значения плотности тока по высоте паза (вдоль оси z) может быть описано следующей формулой [1]:

(4.1)

, где 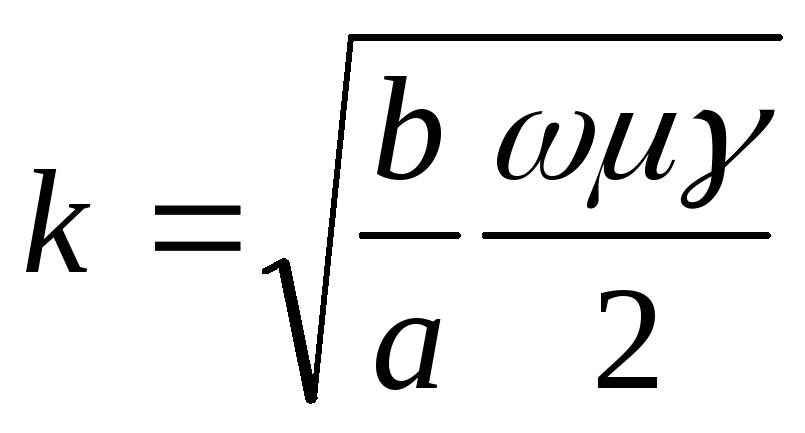— коэффициент затухания и коэффициент фазы;

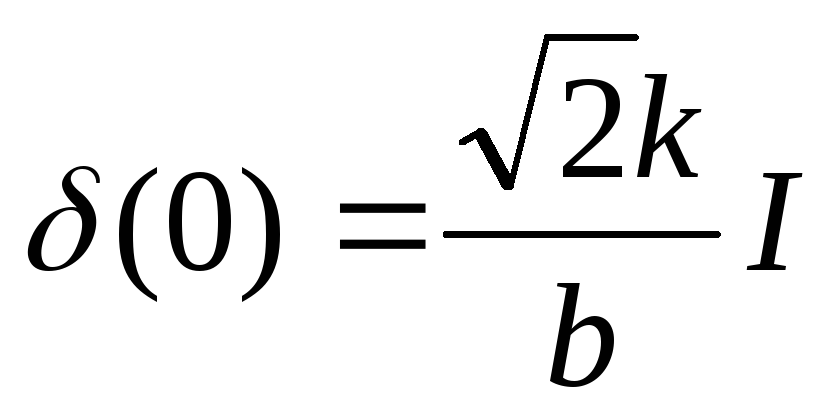— действующее значение плотности тока на открытой поверхности проводника;

В этих формулах:

I -действующее значение тока в проводнике;

w — круговая частота переменного тока;

 и  — магнитная проницаемость и проводимость проводника;

а = 2 мм — ширина паза;

b = 0,35 мм — толщина проводящей шины.

Согласно этим формулам, плотность тока уменьшается вдоль оси z по экспоненциальному закону (множитель 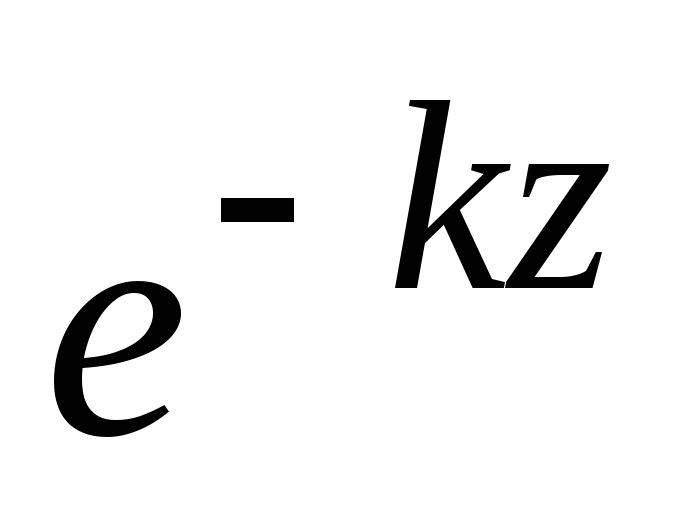). Начальная фаза плотности тока на поверхности проводник равна 45^О и с увеличением координаты z изменяется по фазе в сторону отставания (ц = 45^О – kz).

Глубина, на которой плотность тока в е = 2,718 раз меньше, чем на поверхности проводника, называется глубиной проникновения электромагнитной волны  = 1/к. Глубина проникновения уменьшается с увеличением частоты переменного тока, магнитной проницаемости и проводимости проводника.

В данной работе исследуется распределение тока в ленточных медных проводниках толщиной 0.35 мм и шириной 25 мм при их различном взаимном расположении (рис.4.2).

Рисунок 4.2. Ленточный медные проводники

Первый вариант расположения проводников (см. рис. 4.2 а) позволяет экспериментально исследовать распределение тока вдоль ширины (ось у) двух близко расположенных прямоугольных шин, показанных на рис. 4.1 б.

Во втором случае (рис. 4.2 б) опыт может быть выполнен при двух значениях расстояния между шинами: d = 63 мм и d =3 мм.

При большом расстоянии между ленточными проводниками, распределение тока в них аналогично распределению тока в одном из горизонтальных слоёв прямоугольной шины, показанной на рис. 4.1 а (вдоль оси х). Эффект близости сказывается здесь незначительно.

При малом расстоянии между ленточными проводниками их можно рассматривать как один из горизонтальных слоёв двух близко расположенных шин, показанных на рис. 4.1 б. Вдоль горизонтальной оси (оси х) здесь сильно проявляется эффект близости.

В третьем случае (рис. 4.2 в.) медная лента охвачена с трёх сторон ферромагнитным экраном и распределение тока в ней примерно такое же, как в проводнике, уложенном в паз электрической машины (рис.4.1 .в).

Проводящие ленты для каждого из описанных четырёх вариантов смонтированы на стеклотекстолитовых платах и образуют замкнутые контуры. Электрический ток к ним подводится через понижающий трансформатор, вторичной обмоткой которого является сам контур из проводящих лент и соединительных шин (один виток).

Лабораторная установка с одним из вариантов проводящего контура схематично показана на рис. 4.3.

Для её сборки необходимо сначала установить в левой верхней части наборной панели катушку трансформатора 170 витков вместе с нижней U-образной частью разъёмного сердечника, затем надеть на катушку один из исследуемых проводящих контуров и закрепить его над наборной панелью, пользуясь соединительными вилками со средним выводом, как подставками. Подставки необходимы для увеличения расстояния между исследуемыми проводниками и металлической поверхностью наборной панели. Иначе наводимые в ней вихревые токи существенно изменят распределение тока в исследуемых проводниках.

Рисунок 4.3. Лабораторная установка

После этого нужно вставить в катушку вторую половинку разъёмного сердечника и скрепить две половинки сердечника резиновым кольцом.

Для измерения падения напряжения вдоль нити тока в проводящей ленте служит датчик напряжения, также изображённый на рис. 4.3. Он представляет собой пластинку из стеклотекстолита, в которую вмонтированы два миниатюрных контакта. Провода от контактов проходят вдоль нити тока в исследуемом проводнике до середины пластинки, затем они поворачивают на 90° и проходят вместе сквозь ручку к усилителю напряжения. При прижатии контактов к исследуемой поверхности, соединительные провода датчика оказываются расположенными почти вплотную к этой поверхности. В результате, магнитный поток, сцеплённый с контуром измерительной цепи, оказывается близким к нулю и на вход усилителя подводится активная составляющая напряжения, пропорциональная плотности тока:

(4.2)

где

U — напряжение между контактами датчика,

Е — тангенциальная составляющая напряжённости электрического поля,

L — расстояние между контактами датчика, равное 0,1 м.

 = 55 м/(Ом·м²) — удельная проводимость медного проводника.

Для измерения тока в исследуемых проводниках используется трансформатор тока с коэффициентом трансформации 100. Он имеет один первичный виток и расположен непосредственно на соединительной шине (рис. 4.3).

Потери в проводниках и деталях электрических аппаратов, поверхностный эффект и эффект близости

НАГРЕВ ЭЛЕКТРИЧЕСКИХ АППАРАТОВ

Нагрев электрических аппаратов

2.1 Потери в проводниках и деталях электрических аппаратов, поверхностный эффект и эффект близости.

2.2 Отдача теплоты нагретым телом, коэффициент теплообмена.

2.3 Нагрев и охлаждение однородного проводника по времени: уравнение теплового баланса, нагрев и расчет сечения при длительном режиме с постоянной нагрузкой, выбор сечения по таблицам ПУЭ.

При протекании тока в проводниках и деталях электрических аппаратов возникают потери электрической энергии в виде тепла. Тепловая энергия расходуется частично на нагрев аппарата и частично рассеивается в окружающую среду. Подсчитано, что ≈5% электроэнергии теряется, чтобы подвести электрическую энергию от электрических станций к потребителям на уровне напряжения 10,0 кВ.

Потери в проводниках и деталях электрических аппаратов

Мощность, теряемая в проводнике

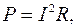(1)

где I – действующий ток проводника, R – сопротивление проводника.

Сопротивление при постоянном токе

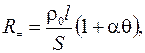(2)

где ρ₀ – удельное сопротивление, l – длина, S – сечение, α — температурный коэффициент сопротивления, θ – температура проводника.

Активное сопротивление и потери при переменном токе будут больше из – за дополнительных потерь

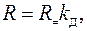(3)

где k_Д – коэффициент дополнительных потерь, который равен

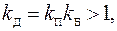(4)

где k_П – коэффициент поверхностного эффекта, k_Б – коэффициент эффекта близости.

Поверхностный эффект

Переменное магнитное поле, охватывающее проводник, обтекаемый переменным током, индуцирует в этом проводнике ЭДС, которая создаёт ток, направленные, согласно правилу Ленца, навстречу приложенному напряжению и основному току.

Центральные слои проводника пересекаются большим магнитным потоком, чем наружные,

Ф₁ > Ф₂

(рис. 1) и наводимая в них противо – ЭДС больше.

Это приводит к вытеснению тока к поверхности проводника, уменьшению плотности тока в центре и увеличению у поверхности, что будет восприниматься как увеличение активного сопротивления.

Чем больше частота f и больше диаметр проводника d_ПР, тем больше k_П.

Эффект близости

Магнитное поле соседнего проводника пересекает данный проводник и наводит в нем ЭДС. Эта ЭДС создает ток в теле проводника, который геометрически складывается с основным током. В результате ток по течению распределяется неравномерно.

На рис. 2 приведены две шины, токи направлены в одном направлении.

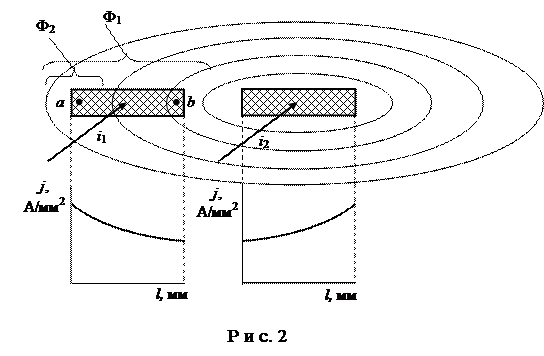Ближние слои в шине с током i₁ охватываются большим магнитным потоком Ф₁, созданным током i₂ соседней шины, и противо ЭДС в них больше, а плотность тока меньше (рис.2). Если токи в противоположных направлениях, то в ближних слоях плотность тока больше. Эффект близости также может приводить к увеличению потерь в проводнике.

На рис. 2 приведена упрощенная схема. В действительности первой шиной также создаётся магнитный поток и образуется результирующее магнитное поле.

Потери в магнитных материалах

В магнитных материалах под действием переменного магнитного поля в элементарных цилиндрических слоях появляются ЭДС и вихревые токи таких направлений, которые противодействуют изменению основного потока (правило Ленца). Помимо потерь на вихревые токи Р_В существуют потери, обусловленные гистерезисом Р_Г.

Полные потери в стали магнитопровода

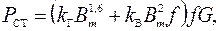(5)

где k_Г=1,9–2,6; k_В=0,4–1,2 – коэффициенты потерь на гистерезис и вихревые токи, они зависят от материала сердечника (толщины пластин и др.), B_m – максимальное значение индукции в сердечнике,

G – масса магнитопровода, f – частота тока.

Для снижения этих потерь сердечники изготавливают шихтованные из магнитомягкого материала.

Удельные потери в различной стали сердечников при частоте 50,0 Гц приведены в приложении П1.

Вывод. За счет указанных потерь электрические аппараты нагреваются и отдают тепло в окружающую среду. Нагрев происходит также в местах контактирования поверхностей за счет переходного сопротивления контактов.

Что такое эффект близости? Определение и факторы, влияющие на него

Определение: Когда проводники несут высокое переменное напряжение, тогда токи неравномерно распределяются по площади поперечного сечения проводника. Этот эффект называется эффектом близости. Эффект близости приводит к увеличению кажущегося сопротивления проводника из-за наличия поблизости от него других проводников, по которым проходит ток.

Когда два или более проводника расположены рядом друг с другом, их электромагнитные поля взаимодействуют друг с другом.Благодаря этому взаимодействию ток в каждом из них перераспределяется таким образом, что большая плотность тока сосредоточена в той части жилы, которая наиболее удалена от мешающего проводника.

Если проводники переносят ток в одном направлении, то магнитное поле половин проводников, которые расположены близко друг к другу, нейтрализует друг друга, и, следовательно, ток не течет через эту половинную часть проводника. Ток скапливается в удаленной половине проводника.

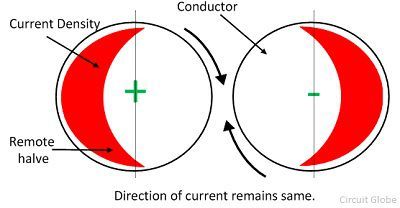
Когда по проводникам переносится ток в противоположном направлении, то закрытая часть проводника переносится, тем больше ток и магнитное поле удаленной половины проводника компенсируют друг друга. Таким образом, в удаленной половине проводника ток равен нулю, а в ближайшей части проводника происходит скопление.

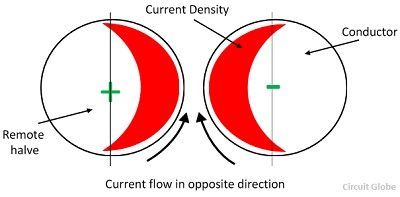
Если постоянный ток течет по поверхности проводника, то ток равномерно распределяется по площади поперечного сечения проводника.Следовательно, на поверхности проводника не возникает эффекта близости.

Эффект близости важен только для проводов сечением более 125 мм. ² . Чтобы учесть этот факт, необходимо применять поправочные коэффициенты.

Если R _dc — нескорректированный уровень постоянного тока в сердечнике
Y _s — коэффициент скин-эффекта, т.е. дробное приращение сопротивления с учетом скин-эффекта.
y _p — коэффициент эффекта близости, т.е. дробное приращение сопротивления учету скин-эффекта.
R _e — эффективное или скорректированное омическое сопротивление жилы.
С учетом эффекта близости сопротивление проводника переменному току становится равным
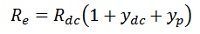Сопротивление R _{постоянного тока} известно из многожильных таблиц.

Факторы, влияющие на эффект близости

Эффект близости в основном зависит от таких факторов, как материал проводника, диаметр проводника, частота и структура проводника. Факторы подробно описаны ниже

1. Частота — Близость увеличивается с увеличением частоты.
2. Диаметр — Эффект близости усиливается с увеличением проводника.
3. Структура — Этот эффект больше для сплошного проводника по сравнению с многожильным проводником (например, ASCR), потому что площадь поверхности многожильного проводника меньше, чем у сплошного проводника.
4. Материал — Если материал состоит из высокоферромагнитного материала, то эффект близости больше проявляется на их поверхности.

Как уменьшить эффект близости?

Эффект близости можно уменьшить, используя провод ACSR (алюминиевый сердечник, армированный сталью).В проводнике ACSR сталь помещается в центре проводника, а алюминиевый проводник располагается вокруг стальной проволоки.

Сталь увеличивала прочность проводника, но уменьшала площадь поверхности проводника. Таким образом, ток течет в основном во внешнем слое проводника, а в центре проводника ток не проходит. Таким образом снижается влияние близости на проводник.

.

Эффект близости | Параметры линии передачи

Высокочастотный ток в круглом проводе течет в основном по поверхности провода, но не равномерно по периметру. Магнитные поля от провода и связанный с ним обратный ток распределяют ток по периметру несколько неравномерно (рис. 2.19), что, в свою очередь, увеличивает кажущееся сопротивление проводников сверх того, что можно было бы ожидать от воздействия кожи. только эффект.В параллельных проводниках мы называем это дополнительное увеличение сопротивления эффектом близости.

Рисунок 2.19. Эффект близости перераспределяет высокочастотный ток по периметру проводника.

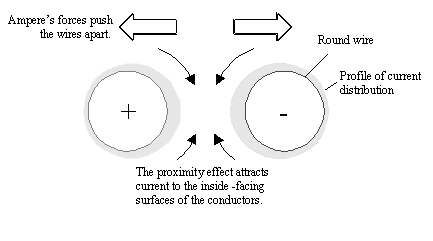
Эффект близости отличается от скин-эффекта, который удерживает высокочастотный ток в неглубокой полосе глубиной d по периметру проводника (см. Предыдущий раздел). Эффект близости также отличается от открытия Ампера о том, что соседние провода, несущие противоположные токи постоянного тока, отталкиваются.В то время как силы Ампера раздвигают структуру атомной решетки двух проводов, и скин-эффект плотно связывает ток с поверхностью, эффект близости просто перераспределяет плотность переменного тока по периметру двух проводов. Эффект близости не оказывает на провода чистой механической силы.

Эффект близости — это индуктивный механизм, вызванный изменением магнитных полей. Это мешает протеканию высокочастотных токов. Он игнорирует установившиеся токи, которые создают статические магнитные поля.Выше той частоты, на которой имеет место эффект близости, распределение тока по периметру проводника достигает конфигурации с минимальной индуктивностью и больше не изменяется с частотой (пока вы не достигнете начала не-ТЕМ режимов распространения).

На рис. 2.12 показаны магнитные поля внутри одиночного проводника, показывающие, как самоиндуцированные вихревые токи ограничивают протекание тока неглубокой полосой непосредственно под поверхностью проводника. Эффект близости действует по аналогичному механизму.В случае эффекта близости магнитные поля от первого провода индуцируют вихревые токи на втором проводе, перераспределяя ток по поверхности второго проводника (рисунок 2.20). Ток на втором проводе все еще плотно связан с неглубокой полосой прямо под поверхностью за счет собственного внутреннего скин-эффекта, но эффект близости перераспределяет ток по периметру второго проводника.

Рисунок 2.20. Изменяющееся магнитное поле от первого проводника индуцирует вихревые токи на поверхности второго проводника, изменяя его распределение тока.

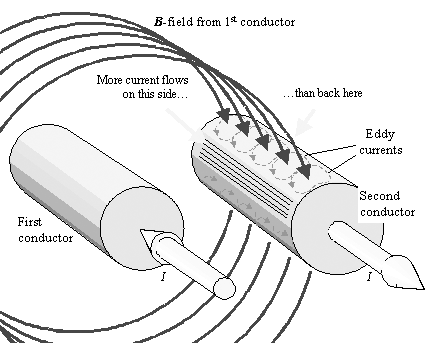
На схеме показаны вихревые токи, циркулирующие вокруг магнитного поля, проникающие через верхнюю часть второго проводника, и большее количество вихревых токов, циркулирующих в нижней части, где выходят магнитные силовые линии. Общий эффект этих вихревых токов заключается в концентрации большего тока на обращенных внутрь поверхностях проводников и меньшем — на обращенных наружу сторонах. Для хорошего проводника на частотах, превышающих w d, концентрация увеличивается до тех пор, пока магнитное поле не перестанет проникать во второй проводник.

Скин-эффект и эффект близости — два проявления одного и того же принципа: магнитные линии потока не могут проникать через хороший проводник. Разница между эффектами заключается в том, что скин-эффект — это реакция на магнитные поля, создаваемые током, протекающим внутри затронутого проводника, в то время как эффект близости — это реакция на магнитные поля, создаваемые током, текущим в других проводниках. Оба эффекта действуют по одному и тому же руководящему принципу, а именно, что никакие высокочастотные магнитные поля не должны проникать через проводник.Таким образом, частота, при которой имеет место эффект близости, совпадает с частотой w d, на которой имеет место скин-эффект. На рис. 2.21 показан рисунок магнитных силовых линий, окружающих два круглых проводника с частотой значительно выше w d. Как видите, силовые линии магнитного поля касаются поверхностей проводников.

Рисунок 2.21. Этот вид в разрезе магнитного поля вблизи двух круглых проводников показывает, что магнитные силовые линии касаются поверхностей проводников.Возмущения гладкости магнитных силовых линий являются артефактами пространственного квантования, используемого решателем поля для создания этой диаграммы

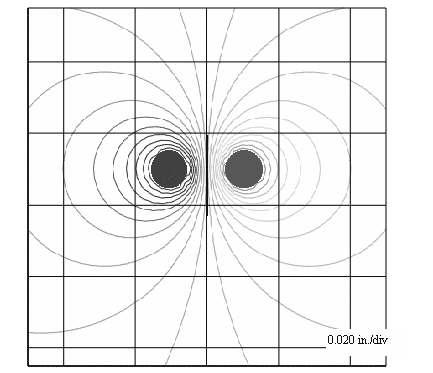
В любом двумерном изображении магнитного поля плотность магнитных силовых линий указывает на силу магнитного поля. По периметру проводников плотность тока в определенной точке на поверхности профиля проводника пропорциональна магнитному полю в этой точке. На рисунке 2.21 магнитные силовые линии явно лежат ближе друг к другу на обращенных внутрь сторонах двух проводников, что указывает на преобладание напряженности поля и, следовательно, тока на обращенных внутрь сторонах проводников.

2.10.1 Коэффициент близости

Коэффициент близости представляет собой увеличение кажущегося сопротивления проводов по переменному току сверх того, что можно было бы ожидать от действия только скин-эффекта. Фактор близости появляется в уравнении для сопротивления переменному току (см. Раздел 2.6, «Кожный эффект»):

Уравнение 2.63

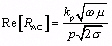
где	k p — поправочный коэффициент, определяемый эффектом близости,
	поправочный коэффициент для эффекта шероховатости игнорируется (см. Раздел 2.11, «Шероховатость поверхности»),
	Вт — частота работы (рад / с),
	Re [R AC] — последовательное сопротивление проводника с учетом скин-эффекта и эффекта близости (Вт / м) и при условии, что w >> w d,
	р — периметр поперечного сечения сигнального проводника (м),
	м — магнитная проницаемость проводника (Гн / м), а
	с — удельное сопротивление провода (См / м).
Для отожженной меди s = 5,800 · 10 7 См / м.
Для немагнитных материалов m = 4 · 10 “7 Гн / м.

Фактор k p технически определяется как отношение (1) фактического сопротивления переменному току к (2) сопротивлению, вычисленному при условии равномерного распределения тока по периметру сигнального проводника и игнорирования сопротивления обратного проводника.

Общее поведение k p следующее.

• Любой проводник, хорошо отделенный от обратного пути с низким сопротивлением, имеет k p 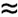1.
• Дифференциальные конфигурации имеют k p 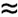2 (а также k a 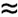2).
• По мере сближения проводника и его обратного пути k p увеличивается.
• Каким бы ни было значение k p, на частотах ниже w d оно не влияет на реакцию передачи; только сопротивление постоянному току имеет значение на частотах ниже w d.

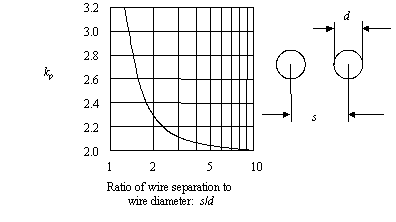
Для пары круглых проводов величина коэффициента близости k p определяется отношением s / d, где s — расстояние между центрами проводов, а d — диаметр проволоки, как показано на рисунке 2.22. При больших отношениях s / d коэффициент близости асимптотически приближается к 2, что соответствует тому факту, что в кабеле с витой парой последовательное сопротивление всегда в два раза больше сопротивления одного провода. При соотношении s / d = 2,0, что примерно соответствует типичной конфигурации кабеля витой пары на 100 Ом, коэффициент близости для круглых проводов равен 2.30. Фактор близости резко возрастает, когда два провода почти соприкасаются.

Рисунок 2.22. Коэффициент близости для круглых проводов увеличивается по мере их соединения. (По материалам Frederick Terman, Radio Engineer’s Handbook, McGraw-Hill, New York, 1943, стр. 43).

На рис. 2.13 для различных проводников показана частота, на которой проявляются скин-эффекты и эффекты близости. Для проводника, работающего ниже своей начальной частоты, магнитные силы из-за изменения токов в проводнике слишком малы по сравнению с силами сопротивления, чтобы влиять на схему протекания тока.Таким образом, ток низкой частоты следует по пути наименьшего сопротивления. Путь наименьшего сопротивления заполняет объем каждого проводника, равномерно протекая по поперечному сечению проводника.

Выше начальной частоты магнитные силы, которые растут пропорционально частоте, превышают силы сопротивления, поэтому именно магнитный (индуктивный) эффект определяет путь тока. Выше начальной частоты ток течет по пути наименьшей индуктивности.

Общие принципы протекания высокочастотного тока следующие:

• Ток в проводнике на высоких частотах распределяется, нейтрализуя все внутренние магнитные силы.
• На высоких частотах магнитные силовые линии не проникают через проводящую поверхность.
• На высоких частотах линии магнитного поля касаются каждой проводящей поверхности.
• Говоря техническим языком, составляющая магнитного поля, нормальная к (хорошей) проводящей поверхности, равна (почти) нулю.
• Ток на высоких частотах распределяется по схеме, которая сводит к минимуму общую потенциальную энергию, запасенную в магнитном поле, окружающем проводники.
• Ток на высоких частотах распределяется по схеме, которая минимизирует общую индуктивность контура, образованного исходящим и возвращаемым токами.
• Если есть выбор, ток обратного сигнала предпочитает течь рядом с трактом исходящего сигнала.
• В высокоскоростной печатной плате со сплошной контрольной плоскостью обратный ток для каждого сигнала течет на нижележащую контрольную плоскость, следуя близко под дорожкой сигнала.

Все приведенные выше точки зрения верны и эквивалентны.Эффективное последовательное сопротивление проводника в зоне намного выше w d обычно определяется с помощью инструмента, называемого двумерным решателем электромагнитного поля. Такие инструменты рассчитывают эффект близости для проводников произвольной формы. Некоторые подсказки о работе этого класса инструментов приведены в Разделе 2.10.4.2, «Решатели 2-D квазистатических полей».

Точное взаимодействие между скин-эффектом и эффектом близости трудно смоделировать вблизи начальной области. Большинство программ для двухмерного моделирования работает намного ниже начальной частоты, когда имеет значение только сопротивление постоянному току.Он также работает значительно выше начальной частоты, когда имеют значение только периметр, глубина скин-фактора и коэффициент близости k p. Рядом с начальной областью программное обеспечение использует общую функцию микширования для постепенного перехода от одного режима к другому. Модель неточна вблизи переходной области. При моделировании типичных конфигураций печатных плат эта неточность не имеет большого значения, потому что интересные проблемы обычно возникают намного выше начальной частоты. Различия между функциями смешивания обсуждаются в разделе 2.8.1, «Практическое моделирование внутреннего импеданса».

2.10.2 Эффект близости для коаксиальных кабелей

Коаксиальные кабели из-за концентричности их проводников демонстрируют очень простое распределение высокочастотного тока. Вокруг центрального проводника ток равномерно распределяется. Вокруг экрана он также равномерно распределен, хотя и с меньшей плотностью тока, связанной с соотношением диаметра центрального проводника и диаметра экрана.

При расчете k p учитывается сумма последовательных сопротивлений сигнального проводника и экрана:

Уравнение 2.64

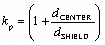
где	d ЦЕНТР — это внешний диаметр центрального проводника (м), а
	d SHIELD — это внутренний диаметр проводника экрана (м).

2.10.3 Эффект близости для микрополосковых и полосковых схем

Микрополосковые и полосковые цепи подвержены воздействию эффекта близости так же, как и круглые проводники.Эффект близости притягивает ток сигнала к стороне трассы (микрополосковой или полосковой), обращенной к плоскости отсчета, и одновременно концентрирует ток возвращаемого сигнала на плоскости отсчета, формируя его в узкую полосу, которая течет по плоскости, в основном оставаясь под след сигнала.

Главы 5 и 6 содержат таблицы коэффициентов близости как для несимметричных, так и для дифференциальных конфигураций.

2.10.4 Последние слова об эффекте близости

Я закрою этот раздел двумя краткими статьями об эффекте близости.В первой статье описывается один алгоритм вычисления эффекта близости. Этот алгоритм может быть реализован в любой математической таблице общего назначения. Вторая статья касается общих ограничений, применимых ко всем двухмерным симуляторам.

2.10.4.1 Эффект близости II

Информационный бюллетень по высокоскоростному цифровому дизайну, том 4, выпуск 3 Билл Стутц пишет Я читаю вашу замечательную книгу и хотел бы задать пару вопросов, связанных с проблемой возврата, представленной в томе.3, № 11 вашего информационного бюллетеня. Есть ли у вас какие-либо ссылки, касающиеся эффекта близости более подробно (кроме Термана) и, в частности, с распределением плотности тока в заземляющем слое под трассой высокочастотного сигнала? Меня интересует как численный расчет распределения, так и использование дифференциальных уравнений в частных производных для непосредственного получения формы решения. Заранее благодарим за ответ.

Ответить Благодарим за интерес к высокоскоростному цифровому дизайну. Чтобы ответить на оба вопроса, я должен указать вам направление литературы по моделированию электромагнитного поля. Оба эффекта являются следствием уравнений Максвелла. И то, и другое можно наблюдать, моделируя различные картины поля. Для любого эффекта нет простого и правильного объяснения, кроме как просто представить в поведенческом смысле то, что имеют тенденцию делать токи. Хорошие ссылки на поведение в полевых условиях E&M включают [24] и [5]. ВНИМАНИЕ: оба они очень математичны. Здесь я опишу один метод моделирования полей для задачи эффекта близости, в надежде, что вы сможете почерпнуть из этого метода некоторое понимание того, как токи текут в твердых проводниках. Мой метод состоит в том, чтобы сначала смоделировать поверхность каждого проводника, вовлеченного в проблему. Поскольку скин-эффект вызывает протекание высокочастотных токов только вблизи поверхности каждого проводника, модель только для поверхности должна быть подходящей для большинства проблем с линией передачи.Кроме того, если мы предположим, что следы проходят в направлении z и что распределение тока по окружности каждого проводника является постоянным с линейным положением z, нам нужно только смоделировать вид в поперечном сечении x-y поверхности каждого проводника. Итак, я начинаю с рисования линии вокруг поперечного сечения каждого проводника (дорожек и плоскостей) и разбиения этой линии на последовательность маленьких отрезков. Я предполагаю, что плотность тока по каждому элементу постоянна. [изд. примечание: «Значительное усовершенствование вышеупомянутой техники линейно интерполирует плотность тока между точками, расположенными по периметру проводника.В любом случае эффективная плотность тока определяется только одним значением на сегмент.] Теперь я могу представить проблему как задачу нахождения тока для каждого маленького элемента, который удовлетворяет ряду ограничений: Сумма всех токов в сигнальном проводнике равна I, Сумма всех токов в обратном проводнике (ах) равна «I, . На поверхности сигнального проводника общий магнитный поток, проникающий в каждый сегмент, равен нулю (верно, если потенциал напряжения по всей поверхности проводника остается постоянным, что в значительной степени и происходит для хорошего проводника), и На поверхности обратного проводника (ов) полный магнитный поток, проникающий через каждый сегмент, равен нулю. Другой способ сформулировать ограничения 3 и 4 — сказать, что магнитное поле параллельно проводящим поверхностям во всех точках (или что составляющая магнитного поля, перпендикулярная поверхностям, должна быть равна нулю). С точки зрения алгоритма решения, если у вас есть N сегментов проводника, было бы удобно работать с ровно N ограничениями. Мы знаем, что 1 и 2 вместе составляют ровно два ограничения, поэтому для ограничений 3 и 4 обычно нужно выбрать в общей сложности N «2 точек для оценки этих ограничений.Теперь у вас есть N переменных и N ограничений, и существует одно уникальное решение. Одна простая процедура решения вычисляет перпендикулярное магнитное поле в каждой точке ограничения как линейную функцию токов на всех других сегментах, строит большую матрицу, представляющую все ограничения, а затем инвертирует ее, чтобы найти окончательное решение. Это не самый эффективный и не самый точный метод решения, но его легче всего визуализировать. Если вы знаете, как написать выражение для магнитного поля, окружающего один элемент (длинный прямой провод), вы можете запрограммировать это в MathCad. Другой способ найти решение — это угадать некоторое основное распределение токов и затем вычислить магнитные поля. Если бы эта схема тока существовала в природе, то везде, где перпендикулярное магнитное поле между двумя соседними элементами тока не равно нулю, это привело бы к увеличению тока в одном элементе и уменьшению в другом. Сделайте соответствующие корректировки. Затем пересчитайте шаблоны полей и снова отрегулируйте. Итерируйте, пока не придете к окончательному решению.Вот как природа решает проблему. Любой из подходов приводит к выводу, что для случая небольшого тонкого следа, расположенного около твердой плоскости отсчета, правильное распределение токов на твердой плоскости определяется выражением Уравнение 2,65 где I = общий ток сигнала в амперах. ч = высота следа примерно ближайшей опорной плоскости, а также d = расстояние по горизонтали от центральной линии следа. Это соотношение является основой для моих простых оценок перекрестных помех (и особенно вывода о том, что, если d намного больше, чем h, перекрестные помехи уменьшаются на 1 / d 2).Вывод [2.65] в закрытом виде появляется в моем информационном бюллетене, том 4, № 8, Эффект близости III. Моделирование следа realistic- размера над твердой плоскостью, вы обнаружите, что плотность тока немного больше на опорной плоскости стороне трассы, чем на обратной стороне. Это явление иногда называют эффектом близости. То же самое происходит с двумя тонкими проводами, расположенными в непосредственной близости: ток имеет тенденцию концентрироваться на двух обращенных друг к другу поверхностях. Эффект близости — простое проявление общего правила, согласно которому при выборе высокоскоростной ток имеет тенденцию концентрироваться вблизи своего обратного пути. Я представил только схему процедуры моделирования. Если вам нужны более подробные сведения, еще одно хорошее место для поиска — это Руководство по вычислительному моделированию EMI / EMC [23]. Предлагаю вам начать свое исследование там.

2.10.4.2 2-D квазистатические решатели поля

Статья впервые опубликована в журнале EDN Magazine 27 сентября 2001 г. Мне нравятся симуляторы целостности сигнала.К сожалению, они не всегда дают правильные ответы. Например, большинство пакетов программного обеспечения для проверки целостности сигналов рассчитывают импеданс и потери в линиях передачи с использованием 2-мерного квазистатического решателя дискретного поля. Решатель поля зависит от шести важных предположений. Если ваша система нарушает любое из этих предположений, симулятор выдаст неверные ответы. Предположение о поле боя Решатели двумерных полей не вычисляют краевые поля на концах проводников.Это упущение кажется разумным, пока основные эффекты в середине линии значительно превышают эффекты краевого поля на концах. Чтобы удовлетворить это требование, длина линии передачи должна значительно превышать расстояние между ее проводниками. Симуляторы не всегда дают правильные ответы. Для типичных размеров следа печатной платы предположение о граничном поле остается в силе. Например, 2,5 см (1 дюйм.) линия передачи, расположенная на 125 мм (0,005 дюйма) над плоскостью отсчета, имеет отношение длины к разделению от 200 до 1. В этих условиях конечные эффекты, вероятно, имеют менее 1% общего влияния на поведение линии. . Предположение о единообразии Если линия передачи помимо того, что она длинная, имеет одинаковое поперечное сечение, вы можете предположить, исходя из симметрии, что в каждом двумерном сечении линии значения R, L, G на единицу длины и C одинаковы.Затем программное обеспечение может выполнить анализ импеданса и перекрестных помех только один раз для одного двумерного поперечного сечения. Предположение о единообразии снижает сложность задачи моделирования от задачи полного трехмерного моделирования до задачи, включающей только одно сечение (двумерная проблема). Любые дефекты в процентах или колебания ширины и высоты линии напрямую влияют на точность модели. Например, если ширина вашего следа указана как 3 мил (± 1), ошибка моделирования может достигать ± 33%. Квазистатическое допущение Когда ваш симулятор вычисляет распределение тока (или заряда) по поверхности одного конкретного двумерного среза линии передачи, он игнорирует фазу. Квазистатический анализ предполагает, что фаза тока одинакова во всем срезе. Квазистатическое допущение работает только тогда, когда волны линии передачи распространяются в ТЕМ (поперечном электромагнитном) режиме, который требует, чтобы длина волны сигнала значительно превышала расстояние между проводниками. Типичные дорожки печатной платы на частотах менее 10 ГГц соответствуют квазистатическому предположению. Например, полосковая линия FR-4, расположенная на 125 мм (0,005 дюйма) над ближайшей плоскостью отсчета, имеет отношение длины волны к разделению на частоте 10 ГГц лучше 100: 1. В этих условиях любое квазистатическое поведение, вероятно, будет иметь общее влияние на поведение линии менее 1%. Предположение малой глубины Индуктивность линии передачи незначительно изменяется на частотах, близких к началу скин-эффекта.Чтобы избежать необходимости учитывать изменяющиеся по частоте значения для индуктивности, большинство программ предполагают, что ваша конструкция работает на частоте, намного превышающей начало скин-эффекта, так что изменения индуктивности становятся несущественными. На такой высокой частоте толщина скин-слоя мала, поэтому ток течет только в неглубокой полосе прямо под поверхностью каждого проводника, а не посередине проводника. Допущение малой глубины скин-слоя позволяет программному обеспечению вычислять значения распределения тока только по периметру (1-D) каждого проводника в конкретном двумерном срезе вместо вычисления точного распределения по всему (2-D) тело двухмерного среза.Это предположение снижает сложность моделирования с двумерной задачи до одномерной. Для прямоугольных дорожек при размерах печатной платы w = 0,008 дюйма и t = 0,00065 дюйма (½-OZ меди) возникновение скин-эффекта происходит со следующей частотой: Уравнение 2.66 На частотах, значительно превышающих начало скин-глубины, расчет периметра (1-D) дает правильный ответ.Кроме того, стандартные предположения о том, как работает скин-эффект, разумно экстраполируют изменения индуктивности на более низких частотах. Однако, если вы моделируете проводники на частотах, близких к частоте возникновения скин-эффекта, может потребоваться более полное 2-мерное моделирование полного распределения тока. Дискретное предположение 2-мерный решатель квазистатического поля представляет периметр каждого проводника в 2-мерном сечении в виде набора коротких линейных сегментов.Он представляет плотность тока по периметру как одномерный вектор, причем каждый элемент вектора определяет плотность тока в одном сегменте. Симуляторы делают разные предположения об интерполяции значений тока при перемещении внутри сегмента и между сегментами по периметру проводника. Очевидно, этот дискретный подход к проблеме работает только тогда, когда размер дискретных сегментов мал по сравнению с кривизной проводников.Коммерческие симуляторы редко описывают в полной мере степень несовершенства, которую вносят их дискретные приближения. Допущение за круглым углом Полевые тренажеры выдают несколько ошибочные результаты на углах. Большинство из них дают более привлекательные результаты (с меньшим количеством ложных выступов на углах), если вы закругляете углы проводников перед выполнением вычислений, потому что это снижает кривизну моделируемой конструкции.Однако, если ваши углы не закруглены в реальном мире, вы можете задаться вопросом, как искусственное закругление влияет на точность результатов. Я делаю. Для дальнейшего чтения см. [23], [24] и [5].

ЧТО НАПОМИНАТЬ

• Эффект близости распределяет переменный ток неравномерно по периметру проводника.
• Фактор близости увеличивает кажущееся сопротивление проводника по переменному току сверх того, что можно было бы ожидать от действия только скин-эффекта.
• Выше той частоты, на которой имеет место эффект близости, распределение тока по периметру проводника достигает конфигурации с минимальной индуктивностью и больше не изменяется с частотой.
• Скин-эффект и эффект близости — два проявления одного и того же принципа: магнитные линии потока не могут проникать через хороший проводник.
• Полевые тренажеры основывают свои расчеты на многих предположениях и не всегда дают правильные ответы.

.

Что такое эффект свободной поверхности и как его уменьшить

Прочтите о влиянии свободной поверхности в сосудах и методах, используемых для его уменьшения. Если эффект свободной поверхности не исправить, то он представляет большую угрозу для устойчивости корабля. У танкеров в основном проблемы с этим типом эффекта.

Давайте посмотрим, что это такое и как мы справляемся в реальных сценариях.

Концепция эффекта свободной поверхности

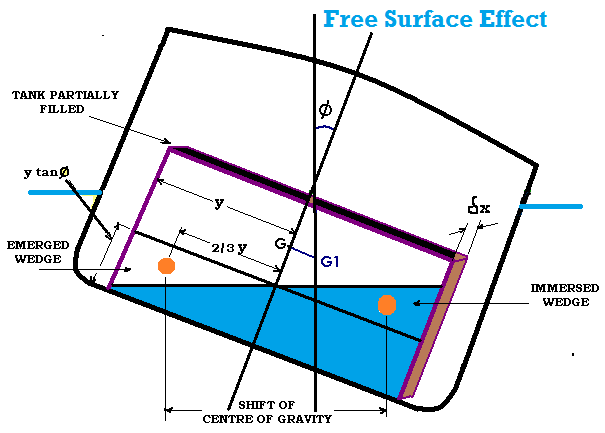
Когда резервуар на центральной линии судна не полностью заполнен жидкостью, и судно кренится, жидкость в резервуаре движется поперек резервуара в том же направлении, что и направление крена.Из-за этого эффекта центр тяжести корабля смещается от осевой линии, что уменьшает восстанавливающий рычаг «GZ» и высоту метацентра, что еще больше увеличивает угол крена. Этот эффект известен как эффект свободной поверхности.

Рассмотрим резервуар, частично заполненный водой на корабле водоизмещением ‘∆’ и наклоненный под некоторым углом ‘’. Центр тяжести корабля сместится от «G» к «G1», поскольку клин жидкости перемещается по резервуару.

Насколько нам известно, см. Диаграмму.

Момент смещения плавучести судна = момент от смещения клина плавучести.

∆ x GG1 = m x gg1

м x gg1

GG1 = ………………… ..

∆

v x ρ x gg1

GG1 = ……………… .. = это смещение C.G. …… .. (1)

▼ x ρ1

Значение терминов:

v = объем клина, ρ = плотность клина, ρ1 = плотность морской воды

▼ = Объем вытеснения.m = Масса клина

Теперь, когда клин жидкости имеет треугольную форму и предполагается, что он разделен на тонкие полоски длиной «δx».

Объем полосы клина = ½ x y x ytanǾ x δx

= ½ y2 tanǾ x δx Масса полосы клина = ρ x ½ y2 tanǾ x δx Момент перехода полосы клина

= (4 / 3y) x ρ x ½ y2 tanǾ x δx

= ρ tanǾ x 2/3 y3 δx

Момент передачи общей клин

=
ρ tanǾ x Σ (2/3 y3 δx) …………………………….. (2)

Также момент передачи общей клин будет

= v x ρ x gg1 …………………………… .. (3) Мы получим из уравнений (2) И (3)

vx ρ x gg1 = ρ tanǾ x Σ (2/3 y3 δx) …………………………… ..
(4) Теперь, когда клин жидкости имеет треугольную форму и предполагается, что он разделен на на тонкие полоски длиной ‘δx’.

Объем полосы клина = ½ x y x ytanǾ x δx

=
½ y2 tanǾ x δx

Масса полосы клина = ρ x ½ y2 tanǾ x δx

Момент передачи полосы клина

= (4 / 3y) x ρ x ½ y2 tanǾ x δx

= ρ tgǾ x 2/3 y3 δx Момент переноса всего клина

= ρ tanǾ
x Σ (2/3 y3 δx) …………………………….. (2)

Также момент передачи общей клин

= v x ρ x gg1 …………………………… .. (3) Из уравнений 2 и 3 получим

v x ρ x gg1
= ρ tanǾ x Σ (2/3 y3 δx) …………………………… .. (4)

Но, как мы знаем,

Σ (2/3 y3 δx) = 2-й момент площади свободной поверхности относительно средней линии резервуара

= Ixx = (1/12 xlxb) ……………………………… ..
(5) Мы получим из уравнений (3) и
(5), vx ρ x gg1 = ρ tanǾ x Ixx …………………………….. (6)

из пунктов (1) и (6)

ρ tanǾ x Ixx

GG1
= …………………………… .. = смена C.G. …………………………… .. (7)

▼ x ρ1

В результате этого перемещения (смещения) центра тяжести корабля с g на G1 восстанавливающий рычаг «GZ» понижается до «G1Z»

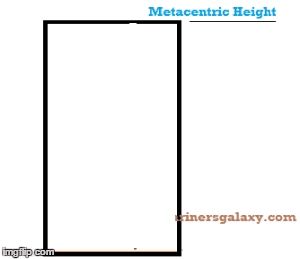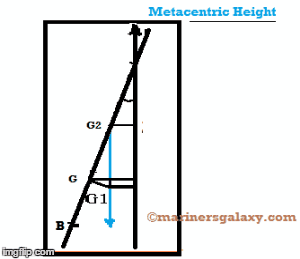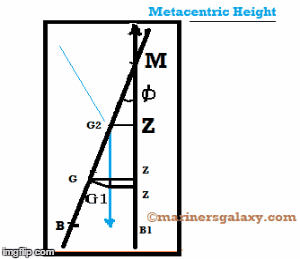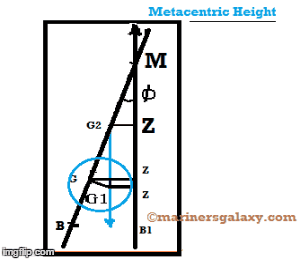
Уменьшение восстанавливающего рычага из-за влияния свободной поверхности будет = G1Z = G2Z = G2M sinǾ

Теперь из треугольника «GG1G’2»

GG1

——
= загарǾ

GG2

GG2 = уменьшение метацентрической высоты

GG1

= …………………………… 8)

tanǾ Следовательно, из (7) и (8)

ρ tanǾ x Ixx 1

GG2
= ……………… x ………………

▼ x ρ1 тангенс

И будет уменьшение грамма за счет этого эффекта свободной поверхности

ρ x Ixx

=
GG2 = ……………… (9)

▼ x ρ1

Методы уменьшения эффекта свободной поверхности

1) Использование танковых дивизий

На танкерах это первый метод.Эффект свободной поверхности жидкости может быть наиболее опасным в сосуде с малой метацентрической высотой и может даже привести к нестабильности сосуда. На таких судах резервуары, в которых должна находиться жидкость, должны быть плотно прижаты. Если судно изначально было нестабильным и кренилось влево или вправо, необходимо соблюдать осторожность, поскольку любая попытка наполнения водяного балласта еще больше снизит остойчивость и, таким образом, повлияет на остойчивость. Поэтому перед балластировкой следует попытаться снизить центр тяжести судна, надавливая вверх существующие цистерны и уменьшая массу судна.Рассмотрим прямоугольный резервуар
длиной «l» и шириной «b», частично заполненный жидкостью, как показано на рисунке.

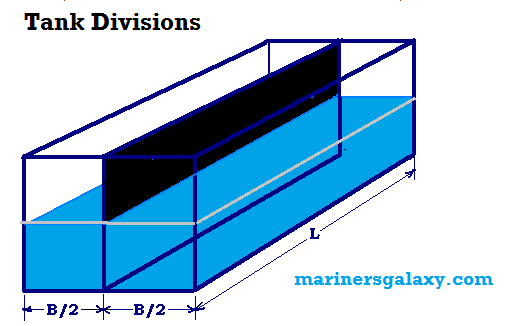
ρ x Ixx

GG2 = ———–

▼ x ρ1

Ixx

=
……………… (AS ρ = ρ1)

▼

1/12 x Д x В3

= ………………

▼

л B3

GG2 = ……………… (1)

12 ▼

ρ x Ixx

GG2
= ……………… & ρ = ρ1

▼ x ρ1

Только один резервуар

1 В

Ixx =
—– x L x (—–) 3

12 2

для двух цистерн

1
Б

Ixx =
….x L x (…) 3 X 2

12
2

1 1

=
… x ……… L B3

4 12

1 x
LB3

GG2 = (………) ……………… (2)

4
x 12 ▼

Из уравнения № (1), (2) и (3) наблюдается, что эффект свободной поверхности уменьшается за счет введения продольных перегородок пластин, образующих резервуары одинакового размера.

1 л B3

(n + 1) 2 12 ▼

Судно с наибольшим эффектом свободной поверхности — это нефтяной танкер, так как в баках должно быть оставлено место для расширения масла. Первоначально было построено
танкера с центральной переборкой и расширительными баками. Затем были введены сдвоенные продольные переборки без расширительных баков, которые оказались успешными, поскольку конструкция учитывает потерю метацентрической высоты из-за эффекта свободной поверхности.Невозможно спроектировать сухогруз таким же образом, поскольку положение центра тяжести судна значительно зависит от характера размещения груза.

Они ограничивают движение воды в резервуаре, тем самым уменьшая эффект свободной поверхности.

Они отклоняют движение воды, и в результате вода достигает другого конца через много времени.

Таким образом, они не контролируют непосредственно эффект свободной поверхности, они уменьшают прокатку и, следовательно, существующую прокатку.Это из статьи Что такое эффект свободной поверхности и как его уменьшить.

.

Эффект близости (электромагнетизм) — Википедия повторно опубликована // WIKI 2

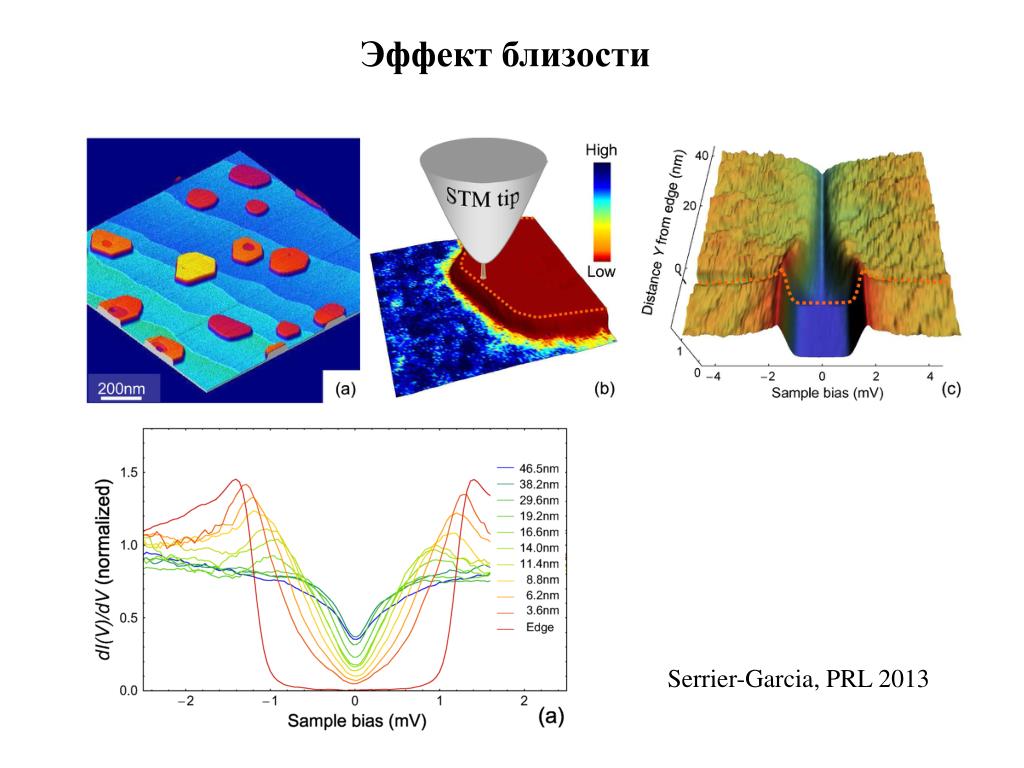
Величина плотности тока в обмотках трансформатора 20 кГц.

В проводнике, несущем переменный ток, если токи протекают через один или несколько других соседних проводников, например, в тесно намотанной катушке провода, распределение тока внутри первого проводника будет ограничиваться меньшими областями. Возникающая в результате нынешняя скученность называется эффектом близости .Это скопление приводит к увеличению эффективного сопротивления цепи, которое увеличивается с увеличением частоты.

Энциклопедия YouTube

• 1/3

  Просмотры:

  4229

  376948

  5 949

• ✪ Детали эффекта близости на хинди Электрическая капсула

• ✪ Что такое эффект Холла и как работают датчики на эффекте Холла

• ✪ AV Genius «Как смешивать» — Эффект близости

Содержание

Пояснение

Изменяющееся магнитное поле будет влиять на распределение электрического тока, протекающего в электрическом проводнике, посредством электромагнитной индукции.Когда переменный ток (AC) протекает через проводник, он создает вокруг него соответствующее переменное магнитное поле. Переменное магнитное поле индуцирует вихревые токи в соседних проводниках, изменяя общее распределение тока, протекающего через них. В результате ток концентрируется в областях проводника, наиболее удаленных от соседних проводников, по которым ток проходит в том же направлении.

Эффект близости может значительно увеличить сопротивление переменного тока соседних проводников по сравнению с его сопротивлением постоянному току.Эффект увеличивается с частотой. На более высоких частотах сопротивление проводника переменному току может легко в десять раз превышать его сопротивление постоянному току.

Пример

Например, если два провода, по которым проходит один и тот же переменный ток, лежат параллельно друг другу, как в катушке, используемой в индукторе или трансформаторе, магнитное поле одного провода будет индуцировать продольные вихревые токи в соседнем проводе, которые текут. в длинных петлях вдоль провода в том же направлении, что и основной ток на стороне провода, обращенной от другого провода, и обратно в противоположном направлении на стороне провода, обращенной к другому проводу.Таким образом, вихревой ток будет усиливать основной ток на стороне, обращенной от первого провода, и противодействовать основному току на стороне, обращенной к первому проводу. В результате ток в поперечном сечении провода перераспределяется в тонкую полосу на стороне, противоположной другому проводу. Поскольку ток сосредоточен в меньшей площади провода, сопротивление увеличивается.

Точно так же в двух соседних проводниках, по которым проходят переменные токи, текущие в противоположных направлениях, например, в силовых кабелях и парах шин, ток в каждом проводе концентрируется в полосе на стороне, обращенной к другому проводнику.

Эффекты

Дополнительное сопротивление увеличивает потери мощности, которые в силовых цепях могут вызывать нежелательный нагрев. Близость и скин-эффект значительно усложняют конструкцию эффективных трансформаторов и катушек индуктивности, работающих на высоких частотах, используемых, например, в импульсных источниках питания.

В радиочастотных схемах, используемых в радиооборудовании, потери на близость и скин-эффект в катушке индуктивности снижают добротность, расширяя полосу пропускания. Чтобы минимизировать это, в радиочастотных индукторах используется особая конструкция.Обмотка обычно ограничивается одним слоем, и часто витки разнесены для разделения проводников. В многослойных катушках последовательные слои намотаны крест-накрест, чтобы провода не лежали параллельно друг другу; их иногда называют катушками «корзиночного плетения» или «сотами». Поскольку ток течет по поверхности проводника, высокочастотные катушки иногда покрывают серебром или делают из литц-проволоки.

Метод Дауэля для определения потерь

Этот одномерный метод для трансформаторов предполагает, что провода имеют прямоугольное поперечное сечение, но его можно приблизительно применить к круглому проводу, рассматривая его как квадрат с такой же площадью поперечного сечения.

Обмотки разделены на «части», каждая часть представляет собой группу слоев, которая содержит одну позицию нулевого MMF. Для трансформатора с раздельными первичной и вторичной обмотками каждая обмотка является частью. Для трансформатора с чередующимися (или секционированными) обмотками каждая внутренняя и внешняя секции являются одной частью, в то время как другие секции каждая разделена на две части в точке, где возникает нулевое значение m.m.f.

Общее сопротивление части определяется выражением RAC = RDC (Re (M) + (m2−1) Re (D) 3) {\ displaystyle R_ {AC} = R_ {DC} {\ bigg (} Re (M) + {\ frac {(m ^ { 2} -1) Re (D)} {3}} {\ bigg)}}

Отношение сопротивления постоянному и переменному току для части ленточной обмотки на разных частотах (δ — глубина скин-слоя).Видно, что увеличение количества слоев резко увеличивает сопротивление на высоких частотах.

R _DC — сопротивление части постоянного тока

Re (.) — действительная часть выражения в скобках

м количество слоев в участке, это должно быть целое число

M знак равно αhcoth⁡ (αh) {\ Displaystyle M = \ альфа h \ coth (\ alpha h) \,}

D знак равно 2αhtanh⁡ (αh / 2) {\ displaystyle D = 2 \ alpha h \ tanh (\ alpha h / 2) \,}

α знак равно jωμ0ηρ {\ displaystyle \ alpha = {\ sqrt {\ frac {j \ omega \ mu _ {0} \ eta} {\ rho}}}}

ω {\ displaystyle \ omega} Угловая частота тока

ρ {\ displaystyle \ rho} удельное сопротивление материала проводника

η знак равно Nlab {\ displaystyle \ eta = N_ {l} {\ frac {a} {b}}}

Н _л Количество витков на слой

ширина квадратного проводника

b ширина намоточного окна

h Высота квадратного проводника

Метод производной квадратного поля

Может использоваться для трансформаторов с круглым или многопроволочным проводом или индукторов с несколькими обмотками произвольной геометрии с произвольными формами колебаний тока в каждой обмотке.Диаметр каждой пряди должен быть меньше 2 δ. Также предполагается, что магнитное поле перпендикулярно оси провода, что имеет место в большинстве конструкций.

• Найдите значения поля B для каждой обмотки отдельно. Это можно сделать с помощью простой магнитостатической модели FEA, в которой каждая обмотка представлена ​​как область постоянной плотности тока, без учета отдельных витков и гибких жил.
• Создайте матрицу D из этих полей. D зависит от геометрии и не зависит от формы сигнала тока.{4}} {64 \ rho _ {c}}}}

  Nj {\ displaystyle N_ {j}} — это количество витков в обмотке j, для гибкого провода это произведение количества витков и жил на виток.

  lt, j {\ displaystyle l_ {t, j}} — средняя длина поворота.

  dc, j {\ displaystyle d_ {c, j}} — диаметр проволоки или пряди

  ρc {\ displaystyle \ rho _ {c}} — удельное сопротивление провода

  • Потери мощности переменного тока во всех обмотках можно найти с помощью D и выражений для мгновенного тока в каждой обмотке:

  P = [di1dtdi2dt] D [di1dtdi2dt] ¯ {\ displaystyle P = {\ overline {{\ begin {bmatrix} {\ frac {di_ {1}} {dt}} {\ frac {di_ {2}} {dt }} \ end {bmatrix}} \ mathbf {D} {\ begin {bmatrix} {\ frac {di_ {1}} {dt}} \\ {\ frac {di_ {2}} {dt}} \ end { bmatrix}}}}}

  • Общая потеря мощности в обмотке затем определяется путем объединения этого значения с потерями постоянного тока, Irms2 × RDC {\ displaystyle I_ {rms} ^ {2} \ times R_ {DC}}

  Метод может быть обобщен на несколько обмоток. .

  См. Также

  Внешние ссылки

  Ссылки

  Эта страница последний раз была отредактирована 22 февраля 2020 в 21:21 .