Правило ома – Закон Ома. Формула Закона Ома

Закон Ома. Формула Закона Ома

Нужна помощь в написании работы?

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Георг Симон Ом

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока — ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].

Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Нужна помощь в написании работы?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Нужна помощь в написании работы?

zakon-oma.ru

формулы и определения / Блог

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

 

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=\frac{U}{R}
2. U — напряжение (в системе СИ измеряется — Вольт)
3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
   • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
   • Формула R=\frac{U}{I}

 

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).

 

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

 

Формула I=\frac{\varepsilon}{R+r}

• \varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

 

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

 

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

---

 

Смотри также:

 

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

bingoschool.ru

Закон Ома для участка цепи простым языком для чайников

Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.

Диаграмма, упрощающая запоминание

Классическая формулировка

Этот простой вариант трактовки, известный нам со школы.


Однородный открытый участок электроцепи

Формула в интегральной форме будет иметь следующий вид:

Формула в интегральной форме

То есть, поднимая напряжение, мы тем самым увеличиваем  ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I».  Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.

В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.

Принятые единицы измерения

Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:

• напряжение – в вольтах;
• ток в амперах
• сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.

Формулировка для полной цепи

Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.

Схема с подключенным с источником

Учитывая «r» ЭДС, формула предстанет в следующем виде:



Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.

Напряжение будет  меньше ЭДС, определить его можно по формуле:



Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.

Неоднородный участок цепи постоянного тока

Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.

Схема неоднородного участка

Формула для такого участка (обобщенный закон) будет иметь следующий вид:

Формула для неоднородного участка цепи

Переменный ток

Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:



Где «Z» представляет  собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.

Практическое использование

Видео: Закон Ома для участка цепи — практика расчета цепей.


Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.


Применяем закон к любому участку цепи

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

Преобразуем исходные данные:
• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление.

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров.

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Вывод

Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.

Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.

Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.

Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.

www.asutpp.ru

Онлайн калькулятор закона Ома для участка цепи

Рад приветствовать тебя, дорогой читатель, в этой первой статье моего блога! Ее я посвятил самому основному закону, который должен хорошо понимать современный человек, работающий с электричеством.

Мой онлайн калькулятор закона Ома создан для участка цепи. Он значительно облегчает электротехнические расчеты в домашней проводке, подходит для цепей переменного и постоянного тока.

Им просто пользоваться: прочти правила ввода данных и работай!

Содержание статьи

Правила работы на калькуляторе

В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:

1. напряжение;
2. ток;
3. сопротивление;
4. или мощность.

Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.

Будь внимательным, чтобы не допустить ошибки.

Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.

Осуществить переход к ним тебе поможет наглядная таблица.

Онлайн калькулятор закона Ома

Простые примеры расчета

Бытовая сеть переменного тока

Пример №1. Проверка ТЭНа.

В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления.
По мощности рассчитываем ток и сопротивление.

I = 1250 / 220 = 5,68 А; R = 220 / 5,68 = 38,7 Ом.

Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.

Пример №2. Проверка сопротивления двигателя

Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:

I = 1600 / 220 = 7,3 А.

Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:

• сопротивление двигателя — 30,1 Ома;
• мощность 1600 ватт.

Цепи постоянного тока

Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.

Считаем ток:

I = 55 / 12 = 4,6 А.

Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:

• сопротивление 2,6 ома.
• мощность 5 ватт.

Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже.

Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.

Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.

Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.

В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.

При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.

Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.

Полезная информация для начинающего электрика

Как использовать закон Ома на практике

Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.

Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.

Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.

Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:

1. значения приложенного к цепи напряжения;
2. сопротивления среды, по которой движется ток.

Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.

Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.

Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.

Примеры из жизни

№1: выключатель освещения разрывает цепь электрических проводов, по которым напряжение добирается до лампочки.

Между контактами образуется воздушный зазор. Он отличный изолятор, исключающий движение тока по осветительному прибору.

№2: клеммы розетки, как источника напряжения, замкнули между собой без сопротивления короткой проволокой. В этой ситуации создается короткое замыкание.

Ток КЗ способен сжечь электропроводку, вызвать пожар в квартире. Поэтому от таких ситуаций существует только одно спасение: использование защит, способных максимально быстро отключить питающее напряжение.

Для бытовой сети это функция автоматических выключателей или предохранителей, о работе которых я буду рассказывать в других статьях.

Используя сопротивление, следует понимать, что оно, само по себе, не вечно: обладая резервом противостояния приложенной энергии, оно может его израсходовать, не справиться со своей задачей и сгореть.

Поэтому для сопротивления вводится понятие мощности рассеивания, которая надежно отводится во внешнюю среду. Если тепловая энергия, развиваемая прохождением тока, превышает эту величину, то сопротивление сгорает.

Напряжение и сопротивление в комплексе формируют электрические процессы. Онлайн калькулятор закона Ома позволяет оптимально рассчитать величину тока, необходимую для совершения полезной работы.

Что такое участок цепи

Рассмотрим самую простую электрическую схему, состоящую из батарейки, лампочки и проводов. В ней циркулирует электрический ток.

Представленная схема или полная цепь состоит из двух контуров:

1. Внутреннего источника напряжения.
2. Внешнего участка: лампочки с подключенными проводами.

Те процессы, которые происходят внутри батарейки, нас интересуют в основном как познавательные. Их мы можем только ухудшить при неправильной эксплуатации.

Например, приходящая в квартиру электрическая энергия от трансформаторной подстанции нам не подвластна. Мы ей просто пользуемся. От неисправностей и аварийных режимов нас защищают автоматические выключатели, УЗО, реле РКН, ограничители перенапряжения или УЗИП, другие современные модули защит.

Внешний же, подключенный к источнику напряжения контур, является участком цепи, в котором мы, используя закон Ома, совершаем полезную для себя работу.

Как использовать треугольник закона Ома

Простое мнемоническое правило представлено тремя составляющими в виде частей треугольника. Оно позволяет легко запомнить взаимосвязи между током, сопротивлением и напряжением.

Вверху всегда стоит напряжение. Ток и сопротивление снизу. Когда вычисляем какую-то одну величину по двум другим, то ее изымаем из треугольника и выполняем арифметическое действие: деление или умножение.

Шпаргалка электрика для новичков

Треугольник закона Ома легко запоминается, но он не позволяет учитывать мощность потребления электроприбора. Этот четвертый параметр, важный для любого домашнего электрика, всегда надо учитывать. .

На всех бытовых электрических приборах указывают мощность потребления электрической энергии в ваттах или киловаттах. Ее формулы, совместно с предыдущими величинами, можно брать со следующей картинки.

Такая шпаргалка электрика позволяет делать простые вычисления в уме или на бумаге. Формулы из нее заложены в алгоритм, по которому работает мой онлайн калькулятор закона Ома.

Предлагаю провести одинаковые вычисления обоими методами и сравнить полученные результаты. Если вдруг найдете расхождения, то укажите в комментариях. Это будет ваша помощь моему проекту.

Я постарался кратко и просто рассказать о принципах работы закона Ома применительно к задачам, решаемым домашним мастером. Считаю, что это достаточно и не рассматриваю закон Ома для полной цепи в обычной форме, комплексных числах, или ином виде.

Если же вы хотите просмотреть видеоурок по этой теме, то воспользуйтесь материалами владельца Физика-Закон Ома.

Возможно, у вас остались вопросы о работе калькулятора? Задавайте. Я на них отвечу. Воспользуйтесь разделом комментариев.

Напоследок напоминаю, что у вас сейчас самое благоприятное время поделиться этим материалом с друзьями в соц сетях и подписаться на рассылку сайта. Тогда вы сможете своевременно получать информацию о новых публикуемых статьях.

electrikblog.ru

2. Закон Ома для участка и полной цепи

Закон Ома для участка цепи: сила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

Формула закона: I=. Отсюда запишем формулыU= IR и R =.

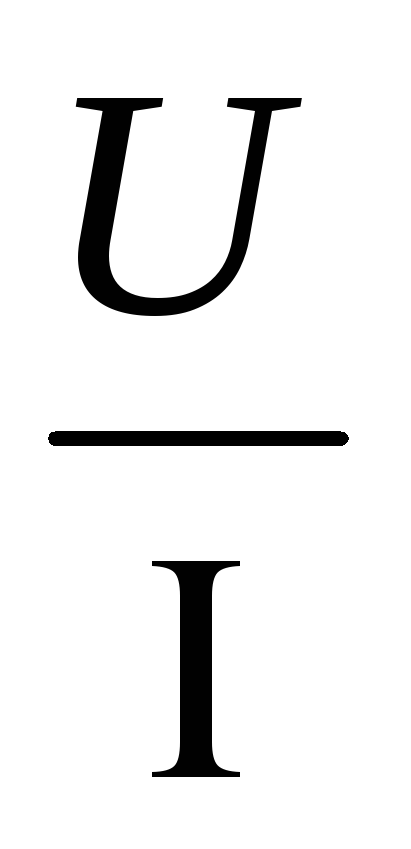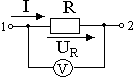Рис.1.Участок цепи Рис.2.Полная цепь

Закон Ома для полной цепи: сила тока I полной электрической цепи равна ЭДС (электродвижущей силе) источника тока Е, деленной на полное сопротивление цепи (R + r). Полное сопротивление цепи равно сумме сопротивлений внешней цепи R и внутреннего r источника тока. Формула закона I = 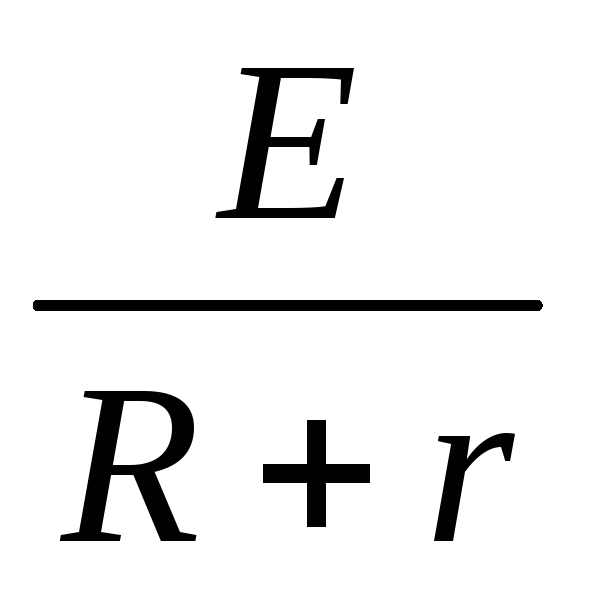. На рис. 1 и 2 приведены схемы электрических цепей.

3. Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно. Смешанное соединение сочетает оба эти соединения.

Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением этих проводников.

Последовательное соединение

Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.

Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).

1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I₁ = I₂ =  I₃ = I

Рис. 1. Последовательное соединение двух проводников.

2. Согласно закону Ома, напряжения U₁ и U₂ на проводниках равны U₁ = IR₁,  U₂ = IR₂, U₃ = IR₃.

Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.

U = U₁ + U₂ + U₃

По закону Ома, напряжения U_1,U₂на проводниках равны U₁ = IR₁,  U₂ = IR₂, В соответствии вторым правилом Кирхгофа напряжение на всем участке:

U = U₁ + U₂ = IR₁+ IR₂ = I(R₁+ R₂)= I·R. Получаем: R = R₁ + R₂ 

Общее напряжение U на проводниках равно сумме напряжений U₁, U_{2 ,}U₃ равно: U = U₁ + U₂ + U₃ = I·(R₁ + R₂ + R₃)  = IR

где R_ЭКВ – эквивалентное сопротивление всей цепи. Отсюда: R_ЭКВ = R₁ + R₂ + R₃

При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R _ЭКВ= R₁ + R₂ + R₃+…

Этот результат справедлив для любого числа последовательно соединенных проводников.

Из закона Ома следует: при равенстве сил тока при последовательном соединении:

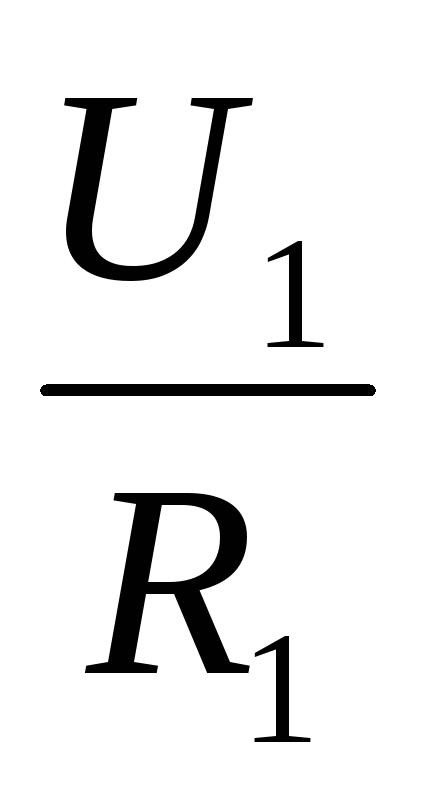I = ,I = 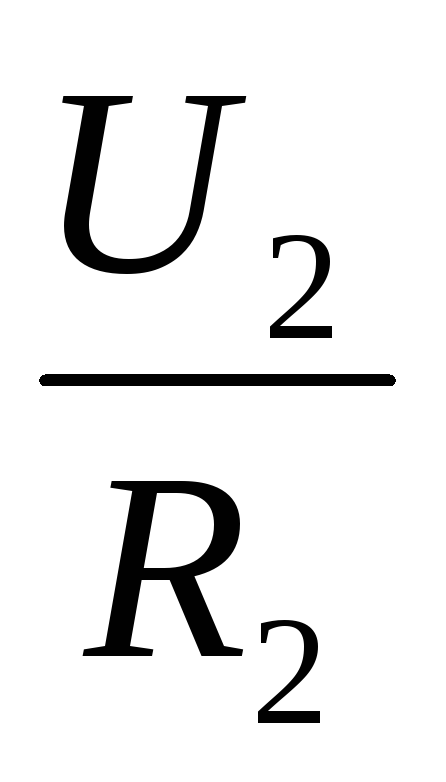. Отсюда 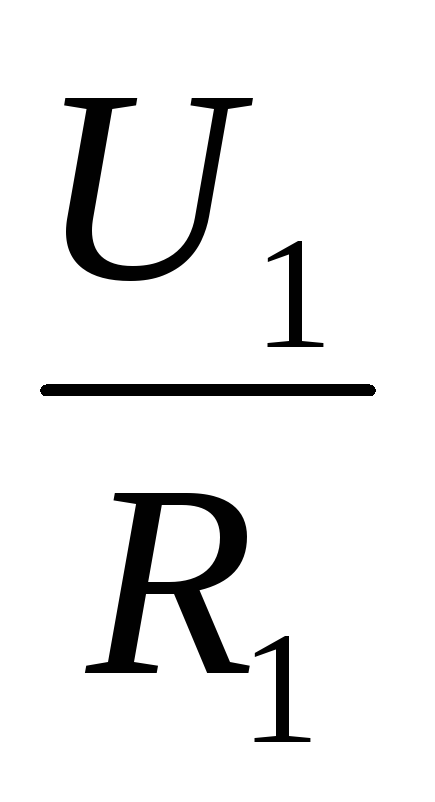= 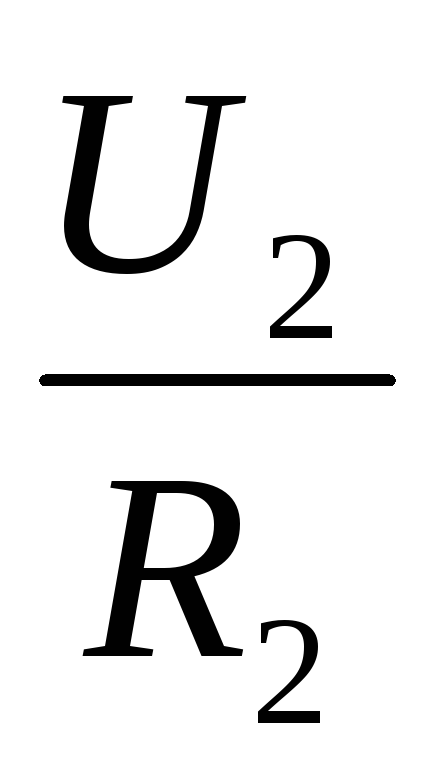или =, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.

При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U₁ на их количество n:

U_ПОСЛЕД= n ·U₁. Аналогично для сопротивлений: R_ПОСЛЕД = n· R₁

При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.

studfile.net

Закон Ома для участка цепи и полной цепи: формулы и объяснение

Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.

Историческая справка

Год открытия Закон Ома  — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.

Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.

Закон Ома для участка цепи

Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:

I=U/R

Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.

Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.

Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.

Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

f(x) = ky или f(u) = IR или f(u)=(1/R)*I

Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:

I=12 В/6 Ом=2 А

Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.

Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.



Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:

R_провод=ρ(L/S)

Где ρ – удельное сопротивление в Ом*мм²/м, L – длина в м, S – площадь поперечного сечения.

Закон Ома для параллельной и последовательной цепи

В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:

I=I1=I2

U=U1+U2

R=R1+R2

Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:

U_эл=I*R_{элемента}

Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:

I=I1+I2

U=U1=U2

1/R=1/R1+1/R2

Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.



Закон Ома для полной цепи

Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:

• напряжение, если это источник ЭДС;
• силу тока, если это источник тока;

Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.



Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:

I=ε/(R+r)

Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.

На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.

Закон Ома в дифференциальной и интегральной форме

Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.



Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.



В интегральной форме:



Закон Ома для переменного тока

При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R_a и реактивное сопротивление X (или R_r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:

1. Ток в цепи с индуктивностью не может измениться мгновенно.
2. Напряжение в цепи с ёмкостью не может измениться мгновенно.

Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.

U=I*Z



X_L и X_C – это реактивные составляющие нагрузки.

В связи с этим вводится величина cosФ:



Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.

Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.

При этом сопротивление представляют в комплексной форме:



Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.

Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».

Как запомнить закон Ома

Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:

Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.

Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.



Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:



Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.



Напоследок рекомендуем просмотреть полезное видео, в котором простыми словами объясняется Закон Ома и его применение:

Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить амперы в киловатты или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома». И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.

samelectrik.ru

Закон Ома — Вікіпедія



Зако́н О́ма — це твердження про пропорційність сили струму в провіднику прикладеній напрузі.

Закон Ома справедливий для металів і напівпровідників при не надто великих прикладених напругах. Якщо для елемента електричного кола справедливий закон Ома, то говорять, що цей елемент має лінійну вольт-амперну характеристику.

Фізична природа закону[ред. | ред. код]

Закон Ома справедливий для провідників, виготовлених із матеріалів, у яких є вільні носії заряду: електрони провідності, дірки або іони. Якщо до таких провідників прикласти напругу, то в провідниках виникає електричне поле, що змушуватиме носії заряду рухатися. Під час цього руху носії заряду розганяються і збільшують свою кінетичну енергію. Проте зростання енергії носіїв заряду обмежене зіткненнями між собою, зі зміщеними з положень рівноваги, внаслідок теплового руху, атомами матеріалу. Під час таких зіткнень, надлишкова кінетична енергія носіїв струму передається коливанням кристалічної ґратки, та виділяється у вигляді тепла.

В середньому, носії заряду мають швидкість, яка визначається частотою зіткнень. Математичною характеристикою таких зіткнень є час розсіяння і зв’язана із ним довжина вільного пробігу носіїв заряду. Обчислення показують, що середня швидкість носіїв заряду пропорційна прикладеному електричному полю, а отже й напрузі.

Таким чином, у матеріалах із вільними носіями заряду сила струму пропорційна напруженості електричного поля. Проходження струму крізь матеріал супроводжується виділеннями тепла. Докладніше про це — у статті закон Джоуля-Ленца.

У сильних електричних полях закон Ома часто не справджується навіть для гарних провідників, оскільки фізична картина розсіювання носіїв заряду змінюється. Розігнаний до великої швидкості носій заряду може іонізувати нейтральний атом, породжуючи нові носії заряду, які теж у свою чергу вносять вклад в електричний струм. Електричний струм різко, іноді лавиноподібно, зростає.

У деяких матеріалах за низьких температур процеси розсіювання носіїв заряду гасяться завдяки особливій взаємодії між ними та коливаннями кристалічної ґратки — фононами. В такому разі виникає явище надпровідності.

Математичне формулювання[ред. | ред. код]

В електротехніці прийнято записувати закон Ома в інтегральному вигляді

U=I∗R{\displaystyle U=I*R}

де U — прикладена напруга, I — сила струму, R — електричний опір провідника.

I=U/R U=I×R R=U/I

Проте опір є характеристикою провідника, а не матеріалу, й залежить від довжини та поперечного перерізу провідника. Тому в фізиці застосовують закон Ома у диференціальному вигляді:

j=σ⋅E{\displaystyle \mathbf {j} =\sigma \cdot \mathbf {E} }

де j — густина струму, σ — питома провідність матеріалу, E — напруженість електричного поля.

Питома провідність залежить від кількості вільних носіїв заряду в провіднику і від їхньої рухливості.

Еквівалентність двох форм запису[ред. | ред. код]

Різниця потенціалів (напруга) на кінцях провідника довжиною l{\displaystyle l} з постійною напруженістю електричного поля E{\displaystyle E} дорівнює

U=Δφ=El{\displaystyle U=\Delta \varphi =El}

Якщо провідник має площу перерізу S, то сила струму в ньому зв’язана з густиною сили струму формулою:

I=jS{\displaystyle I=jS}.

Виходячи із закону Ома в формі

j=σE{\displaystyle j=\sigma E}

і, підставляючи значення j=I/S{\displaystyle j=I/S} та E=U/l{\displaystyle E=U/l}, отримуємо рівняння

IS=σUl{\displaystyle {\frac {I}{S}}=\sigma {\frac {U}{l}}},

або

U=lσSI=RI{\displaystyle U={\frac {l}{\sigma S}}I=RI},

де опір R{\displaystyle R} визначається через питому провідність формулою

R=lσS=ρlS{\displaystyle R={\frac {l}{\sigma S}}=\rho {\frac {l}{S}}}.

Тут ρ=1/σ{\displaystyle \rho =1/\sigma } — питомий опір.

У випадку змінного струму закон Ома можна розширити, включивши в розгляд також елементи електричного кола, які характеризуються ємністю й індуктивністю. Змінний струм проходить крізь конденсатор, та випереджає за фазою напругу. В індуктивності змінний струм відстає за фазою від напруги. Проте в обох випадках амплітуда змінного струму пропорційна амплітуді прикладеної змінної напруги. Математично це можна описати, ввівши комплексні опори (імпеданси).

Тоді можна записати

U=I⋅Z{\displaystyle U=I\cdot Z}

де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.

Закон Ома для повного кола[ред. | ред. код]

В повному колі окрім опору навантаження є ще джерело живлення, яке має власний внутрішній опір. Сила струму в ньому визначається формулою

I=ER+r{\displaystyle I={\frac {\mathcal {E}}{R+r}}}

де E{\displaystyle {\mathcal {E}}} — електрорушійна сила, R{\displaystyle R} — опір навантаження, r{\displaystyle r} — внутрішній опір джерела струму.

Георг Ом проводив дослідження протікання струму в електричному колі на початку XIX століття. На шляху до встановлення закономірності йому довелося подолати чимало перешкод. Для проведення досліджень і встановлення закономірності необхідно було мати вимірювальні прилади, джерела струму із стандартними властивостями, що не змінювалися б з часом, стандартні провідники. Усе це довелося створити або вдосконалити.

Було добре відомо, що магнітна дія струму змінюється при зміні елементів замкнутого кола: джерела електричного струму та провідників, які з’єднують полюси джерела. Чи існує закономірність, яка пов’язує магнітну дію струму з величинами, які характеризують елементи замкнутого кола? Мабуть, таке питання виникало у багатьох дослідників.

Легко уявити обставини, в яких почалися пошуки інтуїтивно відчуваної закономірності. Поняття напруги, спаду напруги, електрорушійної сили ще не були сформульовані. Точаться суперечки щодо механізму дії гальванічних елементів, незрозуміле взаємовідношення електростатичних сил та сил, які виникають при протіканні струму; нарешті невідомо що таке рухома електрика та електрика в спокої. Ом, наприклад, називає в своїх перших працях електричний струм «контактною електрикою».

Ом керувався наступною ідеєю. Якщо над провідником, яким проходить струм, підвісити на пружній нитці магнітну стрілку, то кут повороту стрілки дасть інформацію про струм, точніше про його зміни при варіаціях елементів замкнутого кола. Ом повернувся до ідеї Кулона й сконструював крутильні терези. Магнітна стрілка виявилась точним і чуттєвим гальванометром.

В перших дослідах, результати яких Ом опублікував у 1825 році, спостерігалась «втрата сили» (зменшення кута відхилення стрілки) із збільшенням довжини провідника, підключеного до полюсів вольтового стовпа (поперечний переріз провідника був постійним). Оскільки не було одиниць вимірювання, довелося вибрати еталон — «стандартний дріт». Як залежна змінна фігурувало зменшення сили, що діяла на магнітну стрілку. Досліди виявили закономірне зменшення цієї сили при збільшенні довжини провідника. Функція отримала аналітичний вираз, але Ом не претендував на встановлення закономірності тому, що гальванічний елемент не давав постійної електрорушійної сили (е.р.с.).

Ом ще не розумів значення внутрішнього опору джерела струму. Вольтів стовп, з яким він експериментував, мав внутрішній опір, який значно перевищував зовнішній. Щоб отримати показники, достатні для оцінки відхилення магнітної стрілки «гальванометра», звичайно ж доводилося зводити до мінімуму опір зовнішньої частини кола, який визначався, по суті, коротким відрізком металевого провідника. Зрозуміло, що в такій ситуації точність встановлення залежності сили струму від опору металевих провідників була недостатньою. До того ж внутрішній опір вольтового стовпа був далеко не постійним.

Звичайно ж потрібно дивуватися тому, що закономірність для описаної ситуації була отримана вірно, хоча б у першому наближенні. Проте до встановлення закону було ще далеко.

Успіх наступних експериментів Ома вирішило відкриття термоелектрики. Німецький фізик Томас Йоганн Зеєбек (1770 —†1831) брав участь у великій дискусії між прихильниками хімічної та контактної теорії. Він дотримувався думки Вольта, що е.р.с. виникає при контакті речовини незалежно від наявності хімічного реагенту, та шукав доказів. У 1822 році Зеебек виготовив спіраль з мідної смужки, всередині якої закріпив компас. Це був по-сучасному гальванометр з невеликим внутрішнім опором. Кінці спіралі приєднувались до різних металевих пластинок. Коли було взято бісмутовий диск і покладено на мідний, магнітна стрілка здригнулася. Ефекту не було, якщо диск брали не рукою, а за допомогою предмета, який мав кімнатну температуру.

Врешті-решт Зеебек з’ясував, що ефект пропорційний різниці температур двох контактів.

Одним з найважливіших чинників відкриття було те, що в руках експериментаторів з’явилося джерело, е.р.с. якого можна було плавно регулювати і підтримувати постійною.

Ом використав термопару бісмут-мідь, один спай поміщався в лід, інший — у окріп. Чутливість гальванометра довелося звичайно ж збільшити. Процес вимірів являв собою наступне : 8 експериментальних провідників почергово вмикалися в коло. В кожному випадку фіксувалося відхилення магнітної стрілки. Результат досліду Ом виразив такою формулою:

X=ab+x{\displaystyle X={\frac {a}{b+x}}}, де

• Х — сила магнітної дії провідника,
• а — стала, яка визначала е.р.с. термопари,
• х — довжина провідника.
• b — константа, яка визначала провідність всього кола.

Це був другий крок. Тут ще немає звичних нам понять сили струму, е.р.с., зовнішнього, внутрішнього опору. Вони відграняться поступово.

В наступній праці (1826 рік) Ом вводить поняття «електроскопічної сили», користується поняттям сили струму та записує закон для ділянки кола вже у формі, дуже близькій до сучасної:

X=kwal{\displaystyle X={\frac {kwa}{l}}}, де

• Х — сила струму,
• k — провідність,
• w — поперечний переріз провідника,
• а — електроскопічна сила,
• l — довжина провідника.

Незважаючи на переконливі дані експериментів та чіткі теоретичні основи, закон Ома протягом майже десяти років лишався маловідомим. Достатньо сказати, що Фарадей також не підозрював про існування закону; при описанні дослідів він був змушений звертатися до перечислення даних про елементи кола: кількість пластин в батареях, їхні розміри, склад електроліту, довжина, діаметр та матеріал дроту.

Омові довгий час безуспішно доводилося доводити місцевим вченим, що ним відкрито важливу істину. Ввести закон в фізику виявилося набагато складніше, ніж відкрити. І це закономірно. Фізичне мислення на той час було ще не готовим до сприйняття загальної закономірності (тим більше з рук провінційного вчителя).

Перевірка закону Ома тривала впродовж майже всього XIX століття. В 1876 році спеціальний комітет Британської асоціації провів точну перевірку, вказану Максвеллом. Справедливість закону Ома для рідких провідників було підтверджено Коном, Фітцтжеральдом та Троутоном.

• І.М. Кучерук, І.Т. Горбачук, П.П. Луцик (2006). Загальний курс фізики: Навчальний посібник у 3-х т. Т.2. Електрика і магнетизм. Київ: Техніка. 
• С.Е. Фріш і А.В. Тіморєва (1953). Курс загальної фізики. Том II. Електричні і електромагнітні явища. Київ: Радянська школа. 
• Сивухин Д.В. (1977). Общий курс физики. т III. Электричество. Москва: Наука. 

uk.wikipedia.org