При параллельном соединении напряжение равно. Последовательное и параллельное соединение проводников: особенности, формулы расчета и примеры

Как рассчитать сопротивление при последовательном и параллельном соединении проводников. Какие основные формулы используются для расчетов. Каковы особенности распределения тока и напряжения при разных типах соединений. Где на практике применяются различные виды соединений проводников.

Виды соединений проводников в электрических цепях

В электротехнике выделяют три основных способа соединения проводников:

• Последовательное соединение
• Параллельное соединение
• Смешанное соединение

Каждый из этих видов соединений имеет свои особенности и применяется для решения различных технических задач. Рассмотрим подробнее особенности и формулы расчета для последовательного и параллельного соединений.

Последовательное соединение проводников

При последовательном соединении проводники соединяются друг за другом, образуя единую неразветвленную цепь. Ток в такой цепи проходит через все элементы поочередно.

Особенности последовательного соединения:

• Сила тока одинакова во всех элементах цепи
• Общее напряжение равно сумме напряжений на отдельных участках
• Общее сопротивление равно сумме сопротивлений всех элементов

Формулы для расчета параметров последовательной цепи:

Общее сопротивление: R = R1 + R2 + R3 + … + Rn

Общее напряжение: U = U1 + U2 + U3 + … + Un

Сила тока: I = U / R (одинакова для всех участков)

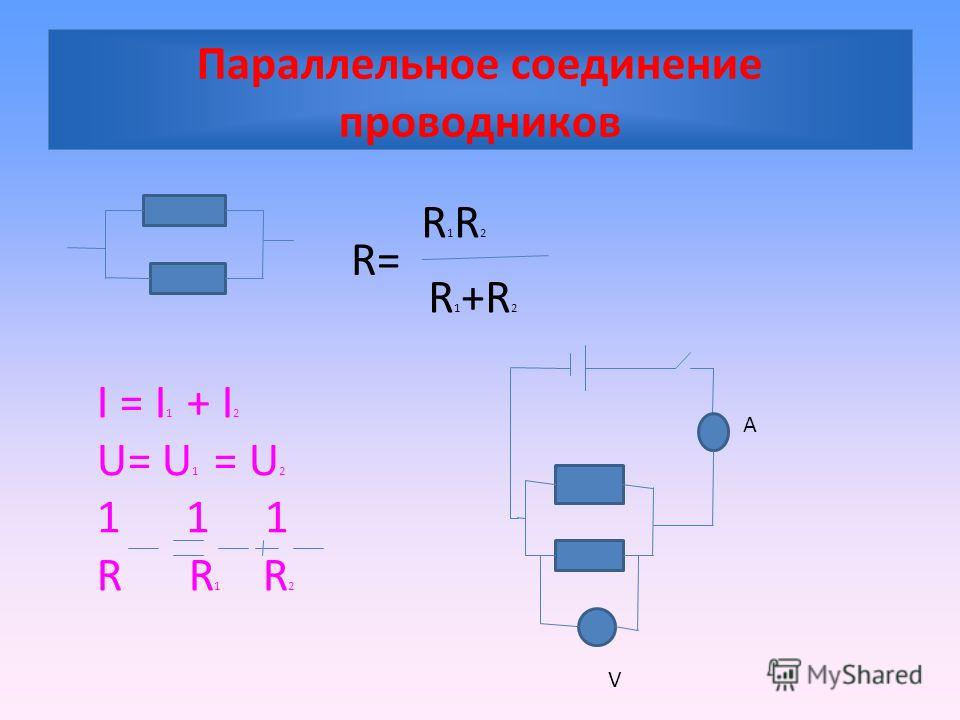
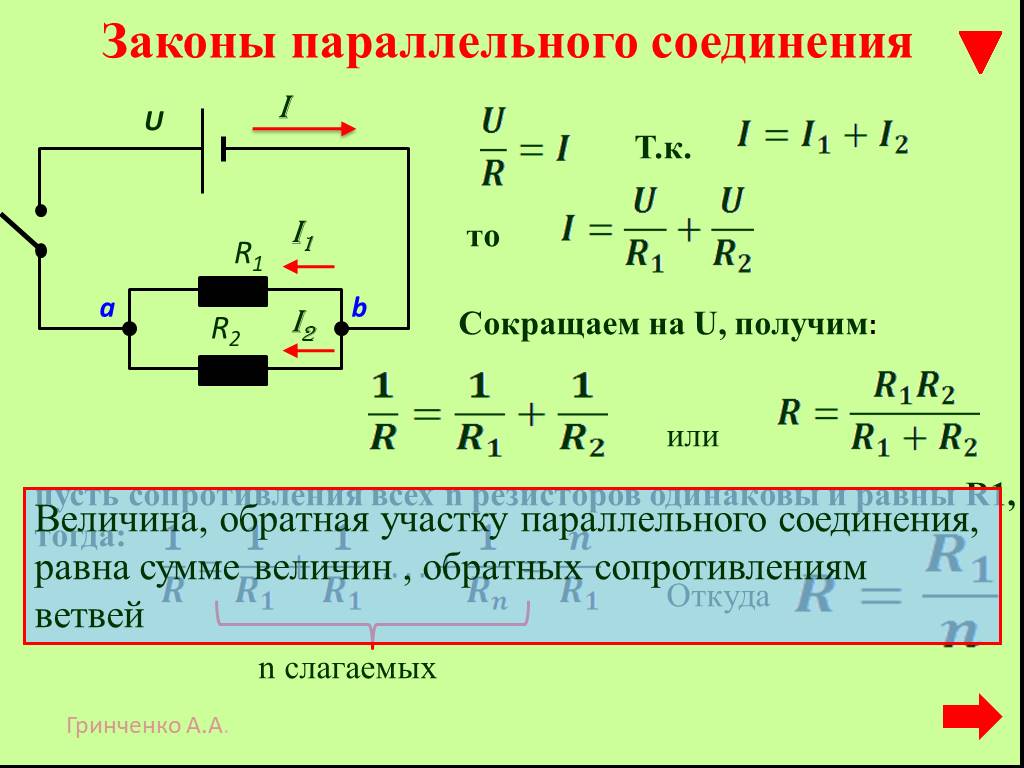
Параллельное соединение проводников

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи, образуя разветвление тока.

Основные характеристики параллельного соединения:

• Напряжение одинаково на всех параллельных участках
• Общий ток равен сумме токов в отдельных ветвях
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений ветвей

Формулы для расчета параметров параллельной цепи:

Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Общий ток: I = I1 + I2 + I3 + … + In

Напряжение: U = U1 = U2 = U3 = … = Un (одинаково для всех ветвей)

Сравнение последовательного и параллельного соединений

Чем отличаются последовательное и параллельное соединения проводников?

• При последовательном соединении общее сопротивление увеличивается, а при параллельном — уменьшается
• В последовательной цепи ток везде одинаков, а в параллельной — разветвляется
• В параллельной цепи напряжение на всех ветвях одинаково, а в последовательной — распределяется по участкам

Практическое применение различных соединений проводников

Где на практике применяются последовательное и параллельное соединения?

Применение последовательного соединения:

• Елочные гирлянды
• Предохранители в электрических цепях
• Реостаты для регулировки силы тока

Применение параллельного соединения:

• Подключение бытовых электроприборов в квартире
• Соединение аккумуляторов для увеличения емкости
• Шунты в измерительных приборах

Выбор типа соединения зависит от конкретной задачи и требуемых параметров электрической цепи.

Расчет сопротивления при смешанном соединении проводников

Как рассчитать общее сопротивление при смешанном соединении проводников? Это более сложная задача, требующая поэтапного подхода:

1. Разбить схему на участки с последовательным и параллельным соединением
2. Рассчитать сопротивление для каждого участка по соответствующим формулам
3. Заменить рассчитанные участки эквивалентными сопротивлениями
4. Повторять процесс, пока вся схема не сведется к одному эквивалентному сопротивлению

Пример расчета смешанного соединения:

Допустим, у нас есть схема с тремя резисторами: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом. R1 и R2 соединены параллельно, а их общее сопротивление последовательно с R3.

1. Рассчитаем сопротивление параллельного участка R1,2: 1/R1,2 = 1/R1 + 1/R2 = 1/10 + 1/20 = 3/20 R1,2 = 20/3 ≈ 6,67 Ом
2. Теперь схема сводится к последовательному соединению R1,2 и R3: R общее = R1,2 + R3 = 6,67 + 30 = 36,67 Ом

Таким образом, общее сопротивление смешанной цепи составляет примерно 36,67 Ом.

Влияние изменения сопротивления на работу электрической цепи

Как изменение сопротивления одного элемента влияет на работу всей цепи? Это зависит от типа соединения:

При последовательном соединении:

• Увеличение сопротивления одного элемента увеличивает общее сопротивление цепи
• Это приводит к уменьшению общего тока в цепи
• Напряжение на измененном элементе возрастает, а на остальных — уменьшается

При параллельном соединении:

• Увеличение сопротивления одной ветви незначительно влияет на общее сопротивление
• Ток в измененной ветви уменьшается, а в остальных — немного возрастает
• Общий ток цепи слегка уменьшается

Понимание этих закономерностей важно для проектирования и анализа электрических цепей.

Законы Кирхгофа в разветвленных электрических цепях

Как применяются законы Кирхгофа в разветвленных цепях? Эти законы являются фундаментальными для анализа сложных электрических схем:

Первый закон Кирхгофа (закон токов):

Алгебраическая сумма токов в узле равна нулю. Это означает, что сумма входящих в узел токов равна сумме выходящих из него токов.

Второй закон Кирхгофа (закон напряжений):

В любом замкнутом контуре электрической цепи алгебраическая сумма напряжений на всех участках этого контура равна нулю.

Применение этих законов позволяет составить систему уравнений для нахождения токов и напряжений в сложных разветвленных цепях.

Расчет мощности в электрических цепях

Как рассчитать мощность в электрических цепях с различными соединениями проводников?

Формулы для расчета мощности:

• P = U * I (мощность равна произведению напряжения на ток)
• P = I^2 * R (мощность равна квадрату тока, умноженному на сопротивление)
• P = U^2 / R (мощность равна квадрату напряжения, деленному на сопротивление)

Особенности расчета мощности при разных соединениях:

• При последовательном соединении общая мощность равна сумме мощностей отдельных элементов
• При параллельном соединении общая мощность также равна сумме мощностей ветвей

Расчет мощности важен для определения энергопотребления устройств и выбора компонентов электрической цепи.

Расчет сопротивления параллельного соединения. Расчет сопротивления при параллельном соединении. Смешанное соединение проводников

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

1. Постоянные.
2. Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

1. Последовательное.
2. Параллельное.
3. Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи.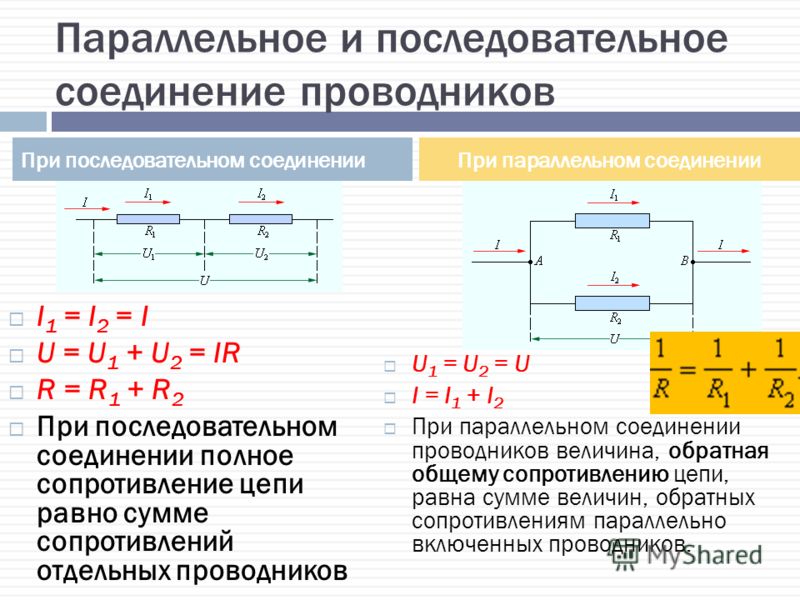 То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.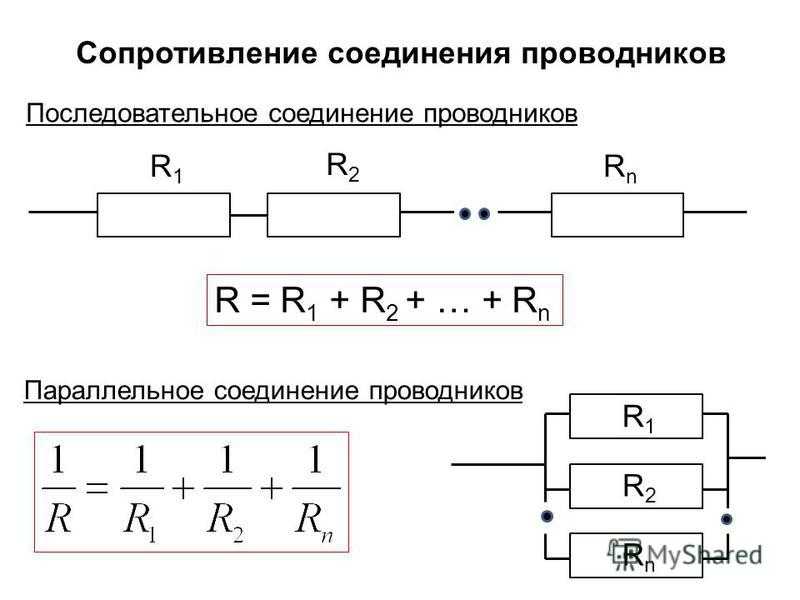

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения.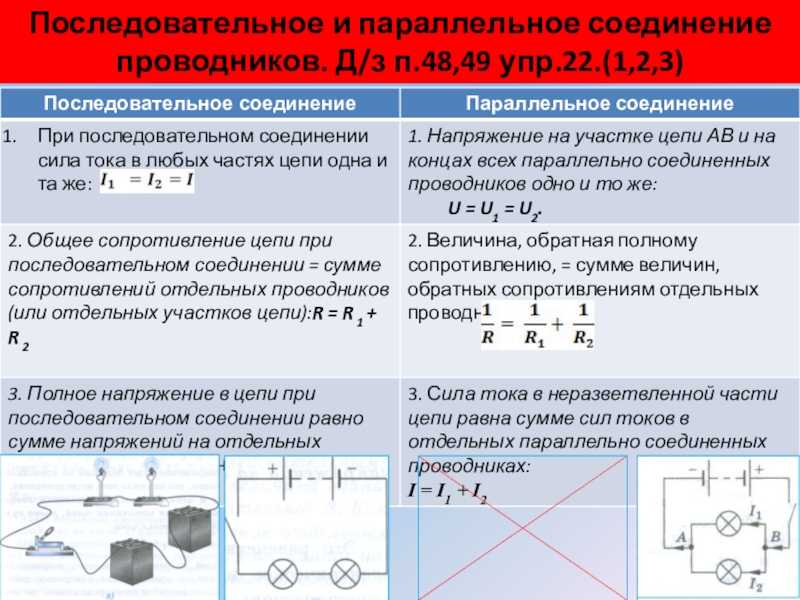 При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.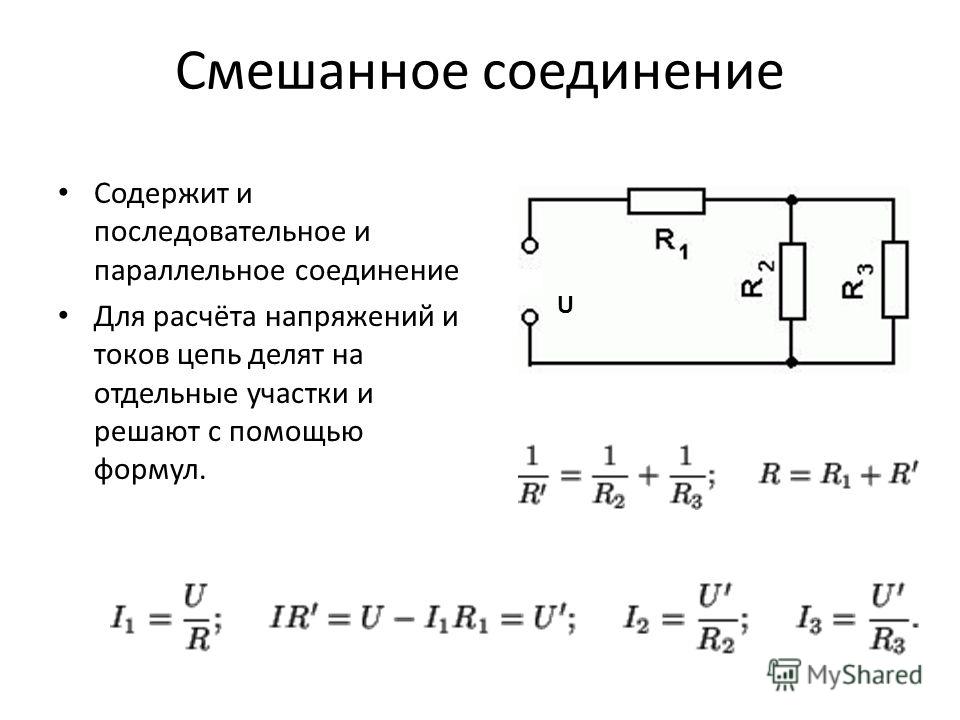

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Основы электроники и электротехники — Лабораторная работа №4

Исследование сопротивлений проводников при смешанном соединении.

 

1. Цель работы.

 

Получение  навыков  сборки  электрических  цепей,  измерений  токов  и напряжений  на  отдельных  участках  электрической  цепи;  убедиться  в соблюдении  законов Кирхгофа в разветвленной линейной электрической цепи; научиться  применять  законы  Кирхгофа  в  графическом  виде.  Исследовать особенности  смешанного  соединения  элементов  в  электрических  цепях постоянного тока.

 

2. Краткие теоретические  сведения.

 

Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д.     

 

Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений. 
Rобщ. =R1+R2+R3 
Rобщ=5ом+10ом+25ом=40ом 

 

        Величина тока в последовательной цепи.

 

         Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени, в любой точке цепи будет одинаковым. 
         Следовательно, во всех точках последовательной цепи величина тока одинакова. 

     Эти четыре амперметра покажут одинаковые величины тока. Поэтому при последовательном соединении  для измерения тока достаточно включать один амперметр на любом участке цепи. 

 

Распределение напряжения в последовательной цепи.

 

         Напряжение источника тока, приложенное к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. 

 

 

 

Напряжение приложенное к каждому из этих резисторов определяется по формуле:

 

  Так как ток в последовательной цепи везде одинаков значит действительно напряжение на ее участках зависит от сопротивления чем больше сопротивление тем большее напряжение приложено к данному участку.  

 

Сумма напряжений на участках последовательной цепи равна напряжению источника тока:

 

 

 Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.

 

Общее сопротивление параллельно включенных сопротивлений определяется по формуле:

 

  Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. 

 

 На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.

 

Первый частный случай:  Если параллельно включено только два резистора  то их общее сопротивление можно определить по формуле:

 

 

 

 Второй частный случай: Если параллельно включено любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить  если сопротивление одного резистора разделить на количество резисторов.  

 

 

 

Распределение токов и напряжения в параллельных ветвях.

 

Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками. 

 

 

Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

 

 

 

 Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника. 

 

 

 

   Второе свойство цепи с параллельным соединением  заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям. 

 

Это значит что, чем больше сопротивление, тем меньше по нему пойдет ток. 

 

 

 

Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее: 

 

 

 

Следовательно, третье свойство параллельного соединения может сформулирована так: Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях. 

 

3. Порядок выполнения работы.

 

3.1.  Собрать цепь со смешанным соединением резисторов (рис. 1). Собрать

 

цепь со смешанным соединением резисторов, выбрав элементы цепи  и величину напряжения  питания  в  соответствии  с  заданным  вариантом (табл. 1).

 

Таблица 1

 

Варианты	1	2	3	4	5	6
Е2, В	12	10	8	12	10	8
R1	R2	R3	R2	R3	R2	R3
R2	R4-1	R4-1	R4-1	R4-2	R4-2	R4-3
R3	R7	R7	R7	R9	R9	R9

 

 

 

3. 2.  После проверки схемы преподавателем -включить источник питания Е2, установить  заданное  значение  величины  напряжения  питания  и  измерить напряжения на входе цепи U и на всех  участках  цепи (U1 и U2), а также  все  токи (I1,I2 и I3).  Результаты занести в табл. 2.  

 

3.3.  С помощью соответствующего тумблера установить новое значение резистора R2 и снова  измерить напряжения и токи в цепи. Выключить источник питания Е2. По результатам измерений вычислить мощность каждого участка цепи Р1, Р2, Р3 и всей цепи Р, определить эквивалентное сопротивление цепи RЭ, Результаты вычислений занести в табл. 2. Выключить электропитание. 

 

3.4. Проанализировать  влияние  изменения  величины  сопротивления резистора  R2 на  режим  работы  всей  цепи  и  отдельных  потребителей. Объяснить, почему это имеет место. 

 

Таблица 2.

 

№ опыта	Измерено						Вычислено
	U	U1	U2. 3	I1	I2	I3	P1	P2	P3	P	Rэк
	В	В	В	А	А	А	Вт	Вт	Вт	Вт	Ом
1
2
3

 

 

 

3. 5. Проверить выполнение баланса мощностей.

 

3.6. Включить  электропитание.  Плавно  изменяя  величину  входного напряжения с помощью потенциометра, измерить значения напряжения и токов на  всех  участках  цепи  при  трех  различных  значениях  входного  напряжения. Результаты измерений занести в табл. 3. Выключить электропитание. 

 

Таблица 3.

 

№ опыта	U	U1	U2.3	I1	I2	I3
	В	В	В	А	А	А
1
2
3

 

 

 

3. 7. По результатам измерений построить  в  одной  координатной системе  вольтамперные характеристики  резисторов R1, R2, R3. Пользуясь ими, построить вольтамперную  характеристику всей  цепи  Uвх = f(I1)  и  по  ней определить  эквивалентное  сопротивление  цепи  Rэкв.  Здесь  же  построить экспериментальную вольтамперную характеристику цепи Uвх = f(I1), сравнить её  с  расчетной  вольтамперной  характеристикой  всей  цепи

 

 

 

4. Содержание отчета 

 

 Отчет по работе должен содержать:

 

а) наименование работы и цель работы;

 

б) схемы экспериментов и таблицы полученных экспериментальных данных;

 

в) результаты расчетов;

 

г) выводы по работе.

 

 

 

 5. Контрольные вопросы

 

1. Как по показаниям амперметра и вольтметра можно определить величину сопротивления  участка  электрической  цепи  постоянного  тока  и  потребляемую им мощность?

 

2. Нарисуйте схемы для измерения методом амперметра и вольтметра больших и малых электрических сопротивлений.

 

3. Как определить величину эквивалентного сопротивления для исследуемой цепи?

 

5. Как по вольтамперной характеристике определить величину сопротивления цепи? 

 

Параллельное подключение различных источников напряжения

спросил 3 года, 7 месяцев назад

Изменено 7 месяцев назад

Просмотрено 36 тысяч раз

\$\начало группы\$

Я понимаю, что параллельное соединение двух разных источников напряжения является противоречием (в идеальной схеме). Но если бы я подключил это на практике и измерил напряжение в точках А и В, какое значение напряжения он показал бы? И какой ток будет потреблять батарея 5V? (Не идеальные условия)

• напряжение
• параллельный
• цепи

\$\конечная группа\$

7

\$\начало группы\$

Это полностью зависит от внутренних резисторов источников напряжения.

^{смоделируйте эту цепь – Схема создана с помощью CircuitLab}

Затем вы можете использовать принцип суперпозиции и рассчитать уровень напряжения в верхней части цепи.

Итак, если оба внутренних резистора имеют одинаковое значение, напряжение V_out будет 7,5 В. При других номиналах резисторов напряжение может варьироваться от 5В до 10В.

\$\конечная группа\$

\$\начало группы\$

Многое зависит от используемых источников питания.

Вы не можете сделать это с теоретически идеальными источниками напряжения, так как любая разница напряжений приведет к бесконечным циркулирующим токам, протекающим от источника с более высоким напряжением к источнику с более низким напряжением.

---

В реальном мире наиболее вероятные сценарии:

• Для большинства типичных настольных блоков питания они могут только отдавать ток, а не потреблять ток. Например, если я попытаюсь сделать это с настольными источниками питания, которые есть в моей лаборатории, я настрою их на одинаковое напряжение. Тот, у которого немного более высокое напряжение, обеспечивает весь ток, пока не достигнет предела тока. Напряжение немного падает, и оба блока питания работают. Если я установлю их на заметно разные напряжения, то одно, установленное выше, обеспечивает весь ток, а другое отображает неисправность. Только источник более высокого напряжения обеспечивает какой-либо ток для нагрузки, если она существует. Источник с более низким напряжением уже воспринимает выходное напряжение как максимально высокое и не обеспечивает ток.

• Некоторые блоки питания не любят, когда их подключают параллельно, поэтому сначала сверьтесь с руководством или обратитесь к производителю. Например, замыкание на выходе одного источника питания для OVP может привести к протеканию очень высоких токов, что может привести к выходу из строя одного или обоих источников питания.

• Некоторые блоки питания предназначены для разделения тока. Один из способов — обеспечить определенное последовательное сопротивление, хотя это часто имитируется, чтобы избежать потери мощности. Другой способ заключается в обеспечении общего сигнала распределения тока между источниками питания.

\$\конечная группа\$

1

\$\начало группы\$

Некоторые источники питания имеют нерегулируемый источник последовательно со схемой регулирования. Если эта схема регулирования имеет низкое сопротивление от точки измерения до выхода, это может привести к тому, что цепь регулирования «нижнего» источника будет потреблять ток до тех пор, пока что-то не даст.

\$\конечная группа\$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 9Серия 0000 и параллельные цепи в источниках питания

Пожалуйста, включите Javascript в вашем браузере для лучшего взаимодействия с пользователем.

Фотогальванические модули и батареи являются строительными блоками системы. Хотя каждый модуль или батарея имеют номинальное напряжение или силу тока, их также можно соединить вместе, чтобы получить желаемое системное напряжение.

1. Последовательные цепи

Последовательные соединения проводки выполняются от положительного (+) конца одного модуля к отрицательному (-) концу другого модуля. Когда нагрузки или источники питания соединены последовательно, напряжение увеличивается. Последовательное подключение не увеличивает производимую силу тока. На изображении справа показаны два последовательно соединенных модуля, что дает 24 В и 3 А. 9Схемы серии 0005

также можно проиллюстрировать с помощью батареек для фонарей.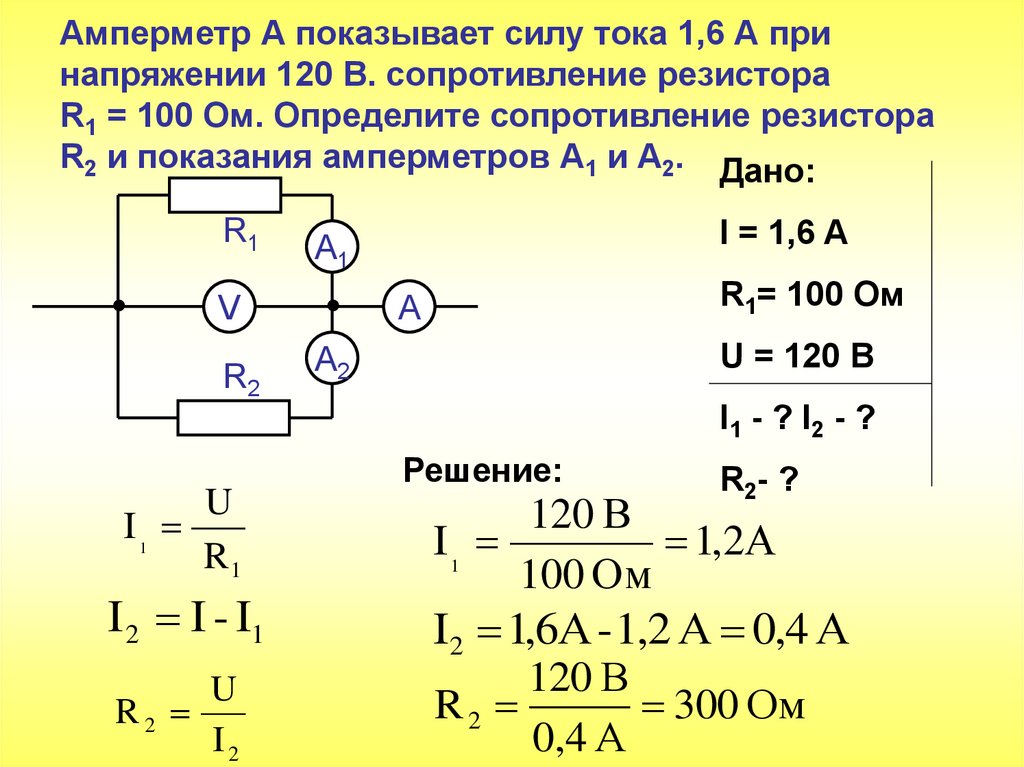 Аккумуляторы фонарика часто соединяют последовательно для увеличения напряжения и питания лампы с более высоким напряжением, чем одна батарея может питать в одиночку.

Вопрос: Когда четыре батареи постоянного тока 1,5 В соединены последовательно, каково итоговое напряжение?

Ответ: 6 вольт

2. Параллельные цепи

Параллельные соединения выполняются от положительной (+) к положительной (+) клемме и отрицательной (-) к отрицательной (-) клеммам между модулями. Когда нагрузки или источники подключены параллельно, токи складываются, а напряжение одинаково во всех частях цепи. Чтобы увеличить силу тока системы, источники напряжения должны быть подключены параллельно. На изображении справа показаны фотоэлектрические модули, соединенные параллельно, чтобы получить систему на 12 В и 6 ампер. Обратите внимание, что параллельное соединение увеличивает производимый ток, но не увеличивает напряжение.

Батареи также часто подключаются параллельно для увеличения общего количества ампер-часов, что увеличивает емкость аккумулятора и продлевает время работы. получить необходимые напряжения и силы тока. На изображении справа показаны четыре модуля на 3 А и 12 В постоянного тока, соединенные последовательно и параллельно. Строки из двух модулей соединены последовательно, увеличивая напряжение до 24В. Каждая из этих цепочек подключена параллельно цепи, увеличивая силу тока до 6 ампер. В результате получается 6-амперная система с напряжением 24 В постоянного тока.

4. Батареи в последовательном и параллельном соединении

Преимущества параллельной схемы можно проиллюстрировать, наблюдая, как долго будет работать фонарь, прежде чем батареи полностью разрядятся. Чтобы фонарик работал в два раза дольше, необходимо удвоить емкость аккумулятора.

На рисунке слева ряд из четырех батарей добавлен параллельно другому ряду из четырех батарей для увеличения емкости (ампер-часы). Новая цепочка батарей подключается параллельно, что увеличивает доступный ампер-час, тем самым добавляя дополнительную емкость и увеличивая время использования. Вторую цепочку нельзя было добавить последовательно, потому что общее напряжение было бы 12 вольт, что несовместимо с 6-вольтовой лампой.

5. Высоковольтные фотоэлектрические батареи

До сих пор в этой главе мы обсуждали только входные напряжения до номинального значения 24 В. Сегодня большинство безбатарейных сетевых инверторов, представленных на рынке, требуют высокого напряжения на входе постоянного тока. Это входное окно обычно находится в диапазоне от 350 до 550 В постоянного тока. Из-за требований инвертора к высокому входному напряжению фотоэлектрические модули должны быть соединены последовательно, чтобы достаточно увеличить напряжение.

6. Примеры последовательного и параллельного подключения и инструкции

1. Соедините фотогальванические модули (массив) последовательно или параллельно, чтобы получить требуемое системное напряжение.

2. Рассчитать общий выход модуля для вольт и ампер.

3. Подключите массив к контроллеру заряда.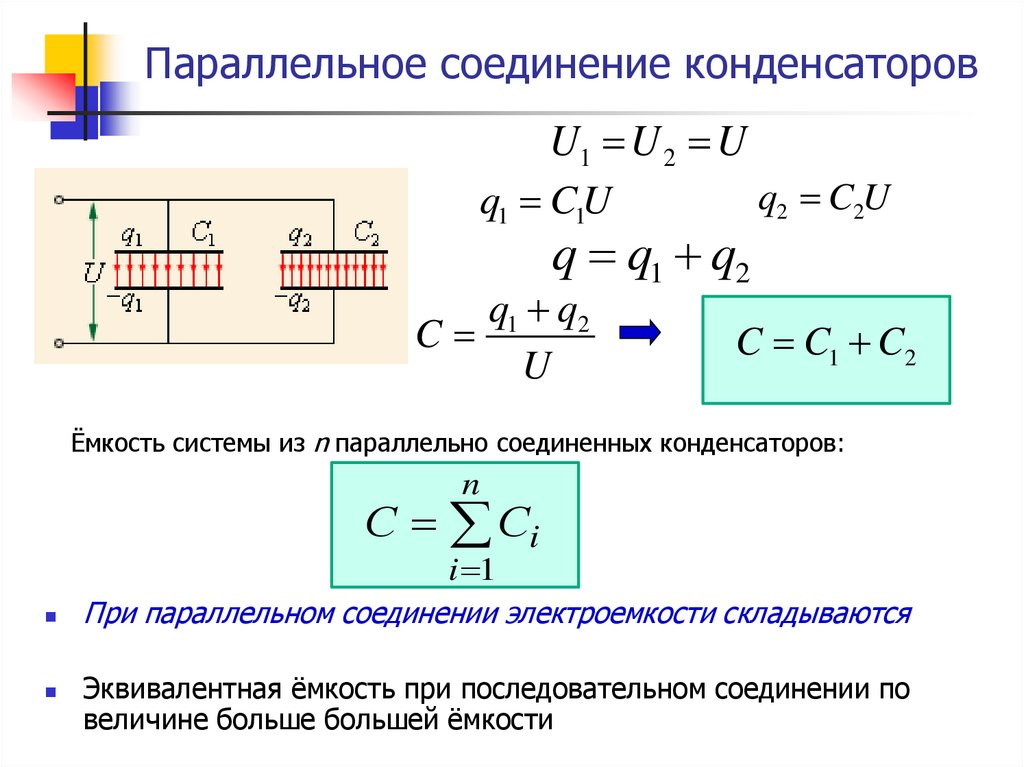

4. Подсоедините аккумуляторы последовательно или параллельно, чтобы получить требуемое системное напряжение.

5. Рассчитайте общее напряжение батареи и емкость в ампер-часах.

6. Подключите аккумуляторную батарею к контроллеру заряда.

Источник : «ФОТОЭЛЕКТРИЧЕСКАЯ СИСТЕМА — Руководство по проектированию и установке» компании Solar Energy International.

Сертификационное обучение солнечной энергии от профессиональных установщиков солнечной энергии

18 сертифицированных IREC-ISPQ инструкторов по солнечной фотоэлектрической энергии и 24 сертифицированных NABCEP монтажников солнечной фотоэлектрической энергии — больше, чем любая другая организация по обучению солнечной энергии — опытная команда Solar Energy International находится в авангарде обучения возобновляемым источникам энергии. Если вы ищете онлайн-обучение по солнечной энергии или личное лабораторное обучение для экзамена начального уровня NABCEP или сертификации установщика NABCEP, почему бы не получить образование у команды самых опытных специалистов по установке солнечной энергии в отрасли? Многие инструкторы SEI участвовали в самых известных солнечных установках в своих сообществах в США и в развивающихся странах.