При параллельном соединении сопротивление равно. Последовательное и параллельное соединение проводников: формулы, закономерности и примеры расчетов

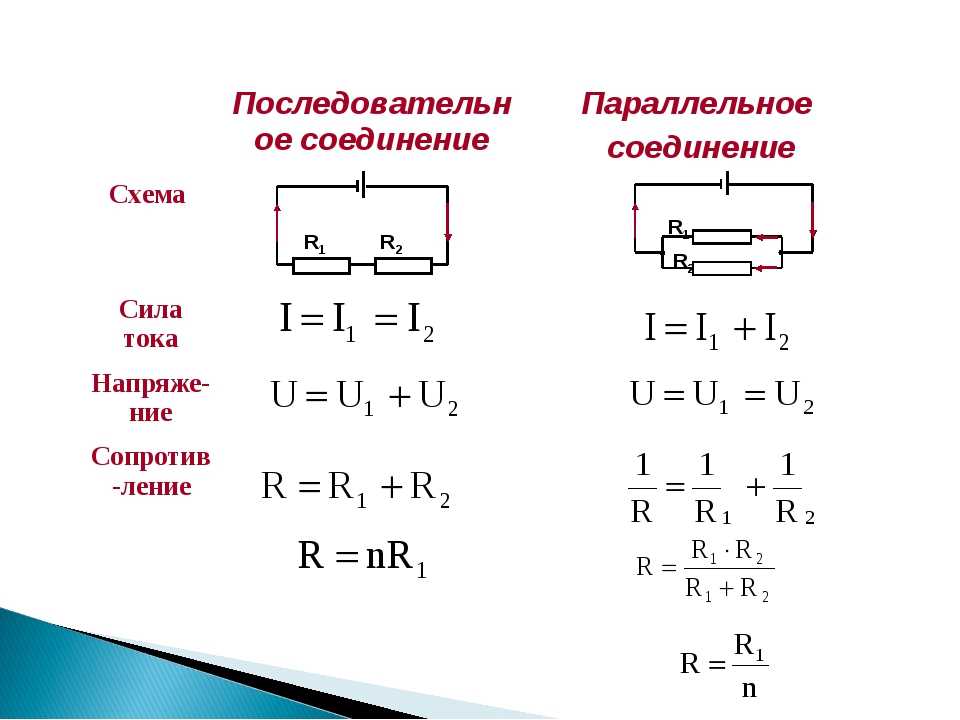
Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Почему при параллельном соединении напряжение на всех участках одинаково. Какие формулы применяются для расчета параметров электрической цепи при различных соединениях.

Основные закономерности последовательного соединения проводников

При последовательном соединении проводников наблюдаются следующие закономерности:

• Сила тока во всех проводниках одинакова: I = I1 = I2 = … = In
• Общее напряжение равно сумме напряжений на отдельных проводниках: U = U1 + U2 + … + Un
• Общее сопротивление равно сумме сопротивлений отдельных проводников: R = R1 + R2 + … + Rn

Эти закономерности вытекают из того, что при последовательном соединении проводники образуют единую неразветвленную цепь, по которой течет один и тот же ток.

Расчет параметров цепи при последовательном соединении

Для расчета параметров электрической цепи при последовательном соединении применяются следующие формулы:

• Общее сопротивление: R = R1 + R2 + … + Rn
• Сила тока: I = U / R, где U — общее напряжение
• Напряжение на каждом проводнике: U1 = I * R1, U2 = I * R2 и т.д.

Зная эти формулы, можно легко рассчитать любые параметры цепи при последовательном соединении проводников.

Особенности параллельного соединения проводников

При параллельном соединении проводников наблюдаются следующие основные закономерности:

• Напряжение на всех параллельно соединенных участках одинаково: U = U1 = U2 = … = Un
• Общий ток равен сумме токов в отдельных ветвях: I = I1 + I2 + … + In
• Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям отдельных проводников: 1/R = 1/R1 + 1/R2 + … + 1/Rn

Почему напряжение одинаково при параллельном соединении?

Многих учащихся смущает тот факт, что при параллельном соединении напряжение на всех участках одинаково, независимо от их сопротивления. Это объясняется следующим образом:

1. Все параллельно соединенные участки подключены к одним и тем же точкам цепи
2. Разность потенциалов между этими точками одинакова для всех участков
3. Напряжение и есть разность потенциалов между точками подключения
4. Поэтому напряжение на всех параллельных участках будет одинаковым

При этом ток в каждой ветви будет разным, в соответствии с законом Ома: I = U / R. Чем меньше сопротивление участка, тем больший ток по нему протекает при одинаковом напряжении.

Формулы для расчета параметров при параллельном соединении

Для расчета параметров электрической цепи при параллельном соединении применяются следующие основные формулы:

• Общее сопротивление: 1/R = 1/R1 + 1/R2 + … + 1/Rn
• Сила тока в каждой ветви: I1 = U / R1, I2 = U / R2 и т.д.
• Общий ток: I = I1 + I2 + … + In

Зная эти формулы, можно рассчитать любые параметры цепи при параллельном соединении проводников.

Пример расчета параметров цепи при последовательном соединении

Рассмотрим пример расчета параметров цепи при последовательном соединении двух резисторов:

• Сопротивление первого резистора R1 = 100 Ом
• Сопротивление второго резистора R2 = 200 Ом
• Напряжение источника U = 12 В

Необходимо рассчитать:

1. Общее сопротивление цепи
2. Силу тока в цепи
3. Напряжение на каждом резисторе

Решение:

1. Общее сопротивление: R = R1 + R2 = 100 Ом + 200 Ом = 300 Ом
2. Сила тока: I = U / R = 12 В / 300 Ом = 0.04 А
3. Напряжение на первом резисторе: U1 = I * R1 = 0.04 А * 100 Ом = 4 В
4. Напряжение на втором резисторе: U2 = I * R2 = 0.04 А * 200 Ом = 8 В

Проверка: U1 + U2 = 4 В + 8 В = 12 В, что равно общему напряжению источника.

Пример расчета параметров цепи при параллельном соединении

Рассмотрим пример расчета параметров цепи при параллельном соединении двух резисторов:

• Сопротивление первого резистора R1 = 30 Ом
• Сопротивление второго резистора R2 = 60 Ом
• Напряжение источника U = 12 В

Необходимо рассчитать:

1. Общее сопротивление цепи
2. Силу тока в каждой ветви
3. Общий ток в неразветвленной части цепи

Решение:

1. Общее сопротивление: 1/R = 1/R1 + 1/R2 = 1/30 + 1/60 = 3/60 = 1/20 R = 20 Ом
2. Сила тока в первой ветви: I1 = U / R1 = 12 В / 30 Ом = 0.4 А
3. Сила тока во второй ветви: I2 = U / R2 = 12 В / 60 Ом = 0.2 А
4. Общий ток: I = I1 + I2 = 0.4 А + 0.2 А = 0.6 А

Проверка: I = U / R = 12 В / 20 Ом = 0.6 А, что совпадает с рассчитанным значением.

Применение знаний о соединениях проводников на практике

Понимание принципов последовательного и параллельного соединения проводников имеет большое практическое значение:

• При проектировании электрических цепей для достижения нужных параметров
• При расчете и подборе элементов электрических схем
• При анализе работы электрических устройств
• При поиске и устранении неисправностей в электрических цепях

Зная закономерности различных соединений, можно грамотно рассчитывать и собирать электрические цепи для решения различных технических задач.

Ключевые отличия последовательного и параллельного соединения

Подведем итог основным отличиям последовательного и параллельного соединения проводников:

Параметр	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова во всех элементах	Различна в разных ветвях
Напряжение	Сумма напряжений на элементах	Одинаково на всех элементах
Сопротивление	Сумма сопротивлений элементов	Меньше наименьшего из сопротивлений

Понимание этих ключевых отличий позволяет правильно анализировать работу электрических цепей и решать задачи, связанные с расчетом их параметров.

Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.

Комментарии преподавателя

Закон Ома для участка цепи

Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.

Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.

Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.

Из математической записи закона Ома:

 

можно выразить напряжение :

и сопротивление проводника:

.

Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.

Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.

Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.

где l-длина проводника, s-его площадь поперечного сечения.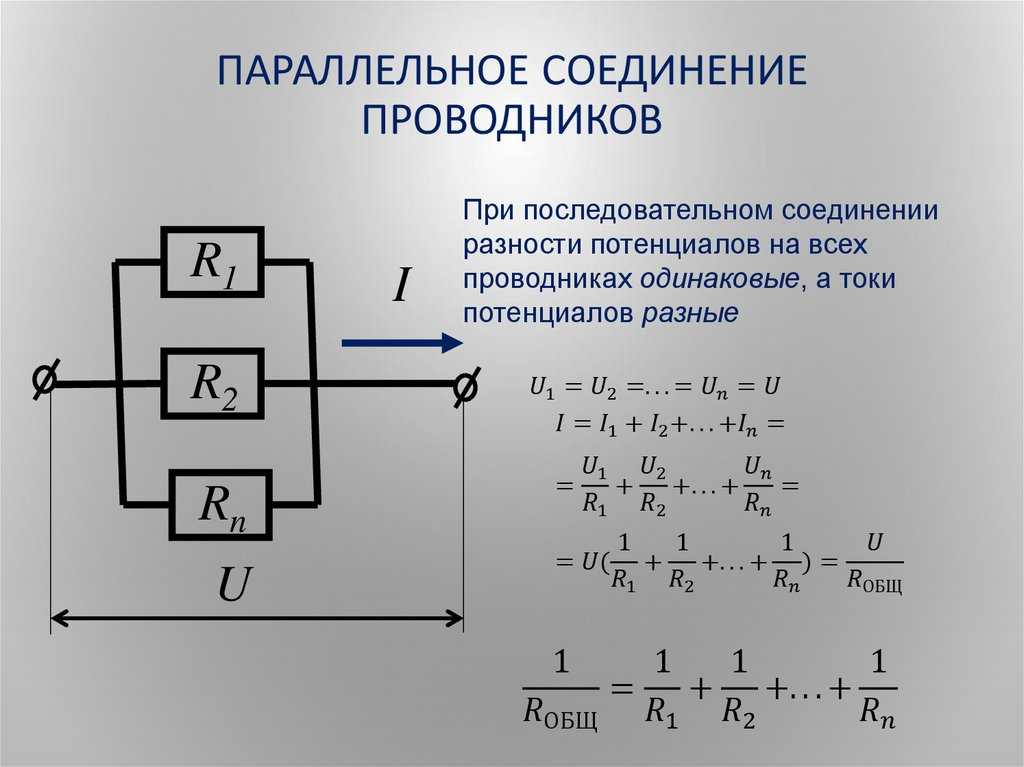

ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.

Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .

Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения

при вычислении площадь поперечного сечения проводника следует выражать в мм2.

В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.

Последовательное соединение проводников

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. Последовательное включение лампочек и источников питания

Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.

I = I1 = I2

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Последовательное соединение проводников

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

R = R1 + R2

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U1 = IR1, U2 = IR2.

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

U = U1 + U2.

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.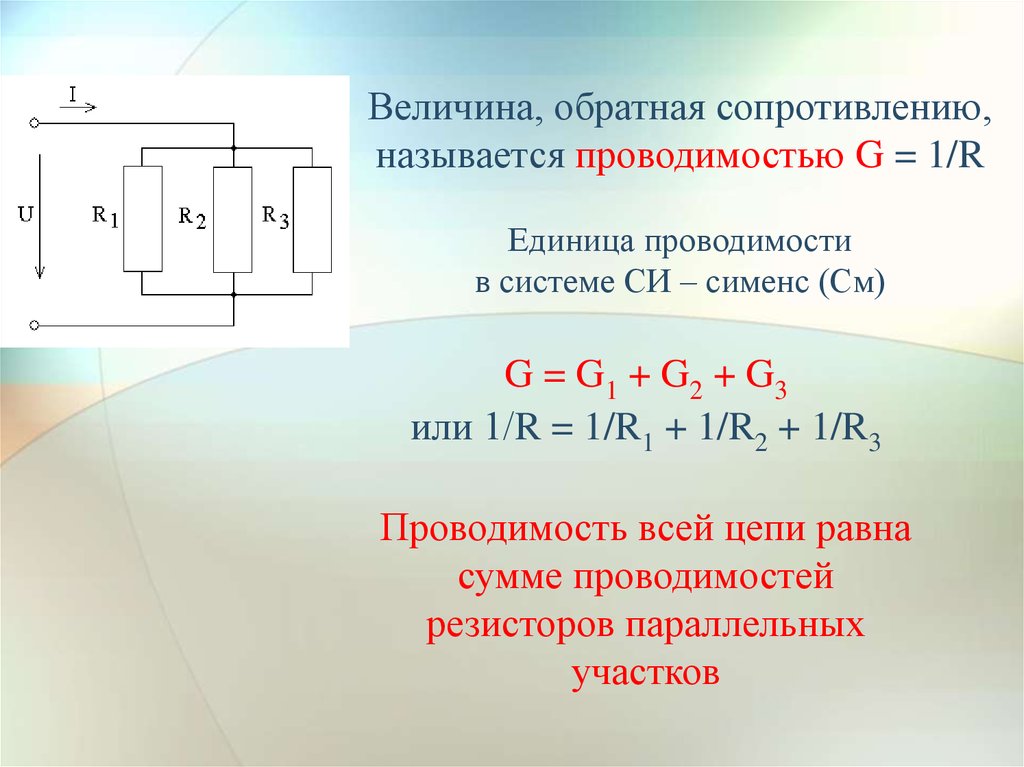

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

Расчет параметров электрической цепи
при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R — сопротивление проводника,
1/R — электрическая проводимость проводника)

Если в цепь включены параллельно только два сопротивления, то:

( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений

)

4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:

A=A1+A2

5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:

P=P1+P2

Для двух сопротивлений:

т.е. чем больше сопротивление, тем меньше в нём сила тока.

Домашняя работа.

Задание 1. Ответить на вопросы.

1. Какое соединение проводников называют последовательным? Изобразите его на схеме.
2. Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
4. Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
5. Какое соединение проводников называют параллельным? Изобразите его на схеме.
6. Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
7. Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
8. Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
9. Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?

Задание 2.Решите задачи.

1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.

2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.

К занятию прикреплен файл  «Это интересно». Вы можете скачать файл в любое удобное для вас время.

Использованные источники:

• http://www.tepka.ru/
• http://class-fizika.narod.ru
• http://www.youtube.com/watch?v=cVKE9NItreo
• http://znaika.ru/catalog/10-klass/physics/
• http://www.youtube.com/watch?v=NB7hOVYe7h0
• https://www.youtube.com/watch?v=cVKE9NItreo
• https://www.youtube.com/watch?v=0hFWeR8ybxs
• http://www.youtube.com/watch?v=EDI8DzWSSWY
• http://www.youtube.com/watch?v=bH_-qGnjJqc
  
   

 

 

 

Урок 28. Лекция 28-2 (продолжение) ЭДС источника. Соединения проводников и источников.

Начало лекции 28 ЭДС источника. Соединения проводников и источников.

Проводники в электрических цепях тоже могут соединяться последовательно и параллельно.

1. При последовательном соединении проводников

1. Сила тока во всех проводниках одинакова:

I₁ = I₂ = I

2.   Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂ на каждом проводнике:

U = U₁ + U₂

3. По закону Ома, напряжения U₁ и U₂ на проводниках равны U₁ = IR₁,   U₂ = IR₂ а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда  IR = IR₁ + IR_2.Отсюда следует

R = R₁ + R₂

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

2. При параллельном соединении проводников

1. Напряжения U₁ и U₂на обоих проводниках одинаковы

U₁ = U₂ = U

2. Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

I = I₁ + I₂

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно, I = I₁ + I₂.

3. Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

или    

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).

 

На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже  соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.

При последовательном соединении два соседних источника соединяются разноименными полюсами.

Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.

Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.

1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε₁ + ε₂ + ε₃

2. Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r_{батареи}= r₁ + r₂ + r₃

Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε_1, а сопротивление r_{батареи}= nr₁

3. Сила тока в такой цепи по закону Ома 

При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.

Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).

Параллельно соединяют только источники с одинаковой ЭДС. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.

 

1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε₁= ε₂ = ε₃

2. Сопротивление батареи меньше, чем сопротивление одного источника r_{батареи}= r₁/n
3. Сила тока в такой цепи по закону Ома 

Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.

Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.

электрических цепей — Почему напряжение на резисторах, соединенных параллельно, одинаково?

Задавать вопрос

спросил 1 год, 10 месяцев назад

Изменено 1 год, 10 месяцев назад

Просмотрено 806 раз

$\begingroup$

Допустим, у меня есть цепь и три резистора, соединенные параллельно. Затем, если я хочу рассчитать эквивалентное сопротивление, я использую закон Ома (V = IR). Назовите три резистора R1, R2, R3 и ток, проходящий через них, как I1, I2, I3 соответственно. Теперь в моем учебнике это было дано отсюда следующим образом: —

Пусть I=I1+I2+I3, что является полным током, проходящим через резистор. По закону Ома

V/R = (V/R1)+(V/R2)+(V/R3)

Таким образом, эквивалентное сопротивление равно сумме обратных величин каждого резистора. Меня смутило то, почему разность потенциалов одинакова для всех трех резисторов, соединенных параллельно? Меня смущает тот факт, что если сопротивление меняется, то и напряжение должно изменяться (по закону Ома), то почему здесь это не так?

• электрические цепи
• электрические токи
• электрические сопротивления
• напряжения

$\endgroup$

2

$\begingroup$

В цепи постоянного тока, когда два резистора соединены параллельно:

Резисторы по определению подключаются непосредственно к клеммам батареи.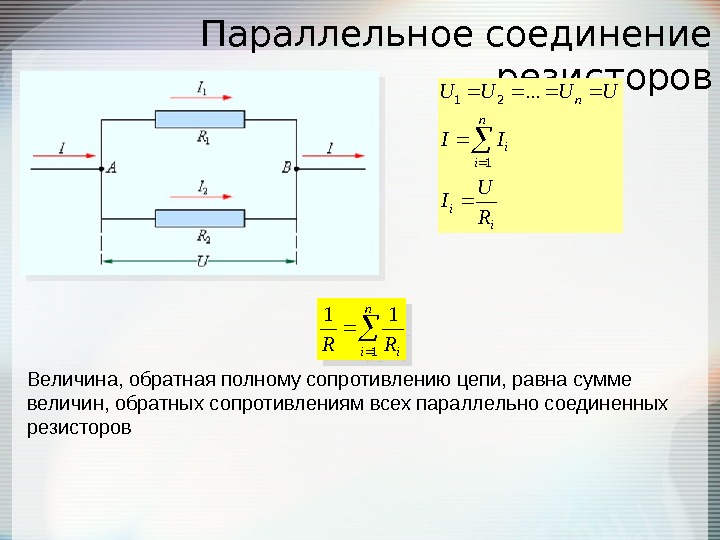 Следовательно, разности потенциалов на резисторах одинаковы: $$\Delta V = \Delta V_1 = \Delta V_2$$ По закону Ома имеем $\Delta V = IR$, поэтому, несмотря на то, что резисторы имеют разное сопротивление, ток, протекающий через резисторы, изменяется обратно пропорционально сопротивлению (больше тока течет по ветви с меньшим сопротивлением и наоборот), поэтому дать одинаковую разность потенциалов (напряжение)

Надеюсь, это поможет.

$\endgroup$

$\begingroup$

Это не вопрос физики, это вопрос определений.

Напряжение в цепи измеряется между двумя узлами. «Параллельно», по определению, означает, что все резисторы подключены между одними и теми же двумя узлами. Когда вы измеряете напряжение на любом из резисторов, вы по определению, измеряете напряжение между теми же двумя узлами.

$\endgroup$

$\begingroup$

Во-первых, когда любые две точки соединяются проводом с меньшим сопротивлением, их потенциалы становятся равными. Это можно доказать следующим образом. Предположим, что A и B соединены проводом с меньшим сопротивлением. Тогда разность потенциалов между A и B определяется законом Ома как: $$V_{AB} = ИР$$ Но поскольку R равно нулю, $V_{AB}$ (разность потенциалов между A и B) также равна нулю, т. е. обе точки имеют одинаковый потенциал.

Пусть теперь потенциал катода в ячейке равен v, а потенциал анода равен $0$. Поскольку точки D,E,F соединены с катодом проводом без сопротивления, их потенциалы также равны v.

Также, поскольку точки A,B,C соединены с анодом проводом без сопротивления, потенциалы этих точек равны нулю.

Итак, на каждом резисторе есть разность потенциалов $v-0=v$.

Следовательно, эквивалентное сопротивление имеет разность потенциалов v.

Теперь, чтобы ответить на ваш вопрос, почему разность потенциалов не меняется при изменении значения сопротивления, напомню вам закон Ома:

$$V = IR$$

Когда эквивалентное сопротивление становится половиной значения любого компонента сопротивления, то ток через эквивалентное сопротивление становится вдвое больше тока через сопротивление компонента, поэтому чистое значение разности потенциалов на эквивалентном сопротивлении остается таким же, как и у резистора компонента.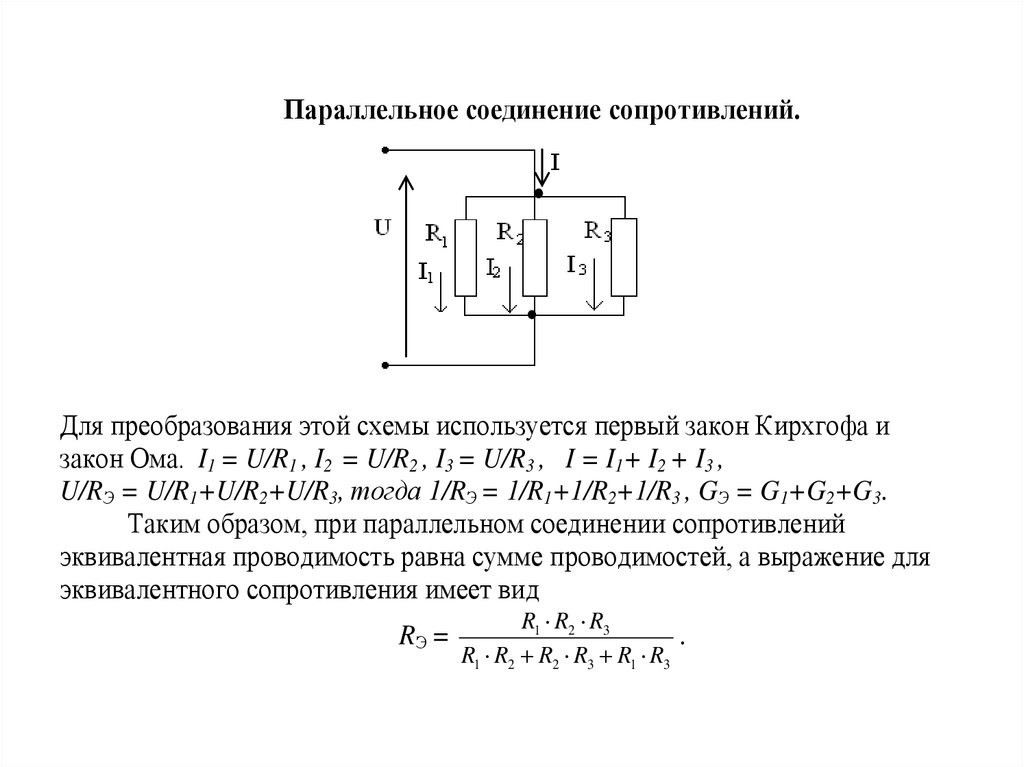

$\endgroup$

$\begingroup$

Возможно, вы не обратили внимания на основное уравнение, т.к. $$ В = ИК $$ Таким образом, в некоторых параллельных ветвях при изменении R ток, протекающий через эту ветвь, изменится настолько обратно пропорционально, что произведение $IR$ останется постоянным. Как вы можете видеть на практике, напряжение зависит от источника питания (или энергии), такого как батарея, а не от сопротивления проводника.

Например, два резервуара с водой, расположенные на разной высоте и соединенные двумя трубами (две трубы на одной высоте), перетекание воды из более высокого в нижний будет вызвано гравитационным потенциалом. Который не будет зависеть от того, насколько велики или малы (по сравнению с размером сопротивления в проводах) трубы. (Хотя это повлияет на расход аналог тока в электрических цепях)

$\endgroup$

Когда два резистора с сопротивлением R1 и R2 соединены параллельно, результирующее сопротивление составляет 3 Ом.

При последовательном соединении. Его значения 16 Ом. Рассчитайте значение R1 и R2.

Вопрос

Обновлено:08.05.2021

СОВРЕМЕННЫЕ ПУБЛИКАЦИИ-ЭЛЕКТРИЧЕСТВО-УПРАЖНЕНИЯ

20 видео

РЕКЛАМА

Ответ

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

---

Похожие видео

Когда два резистора с сопротивлением R1 и R2 соединены параллельно, общее сопротивление составляет 3 Ом. При последовательном соединении его значение равно 16 Ом. Рассчитайте значения R1 и R2.

11760263

Два сопротивления R_1 = (16 +- 0,3) Ом и R_2 = (48 +- 0,5) Ом соединены параллельно. Найдите общее сопротивление комбинации и максимальную процентную ошибку.

11761737

Два сопротивления r_1 = (100,0+- 0,3) Ом и r_2 = (150,0+- 0,5) Ом соединены последовательно. Рассчитайте комбинированное сопротивление с пределами погрешности.

11761866

्रतिरोध R1 और R2 हों, तो उनका समतुल्य प्रतिरोध Rp

8

4 резисторы сопротивлений R_1 и R_2 (R_2

460658460

Текст Решение

Неизвестное сопротивление R_1 есть соединены последовательно с сопротивлением 10 Ом. Эта комбинация подключена к одному зазору метрового моста, а сопротивление R_2 подключено к другому зазору. Точка баланса находится на 50 см. Теперь, когда сопротивление 10 Ом удалено, точка баланса смещается до 40 см. Значение R_1 составляет (в Ом)

474051044

Если R_1 и R_2 представляют собой два последовательно соединенных резистора, каково их эффективное сопротивление?

643215156

Текст Решение

Два сопротивления R1 и R2 имеют эффективное сопротивление Rs при последовательном соединении и Rp при параллельном соединении. Если RsRp=16 и R1/R2=4, рассчитайте значения R1 и R2 (в единицах сопротивления).

643265759

При параллельном соединении двух резисторов с сопротивлениями R_1 и R_2 их общее сопротивление будет ______.