Как распределяется напряжение при последовательном соединении проводников. Почему ток одинаков во всех элементах последовательной цепи. Какие закономерности наблюдаются при последовательном соединении резисторов.
Основные характеристики последовательного соединения проводников
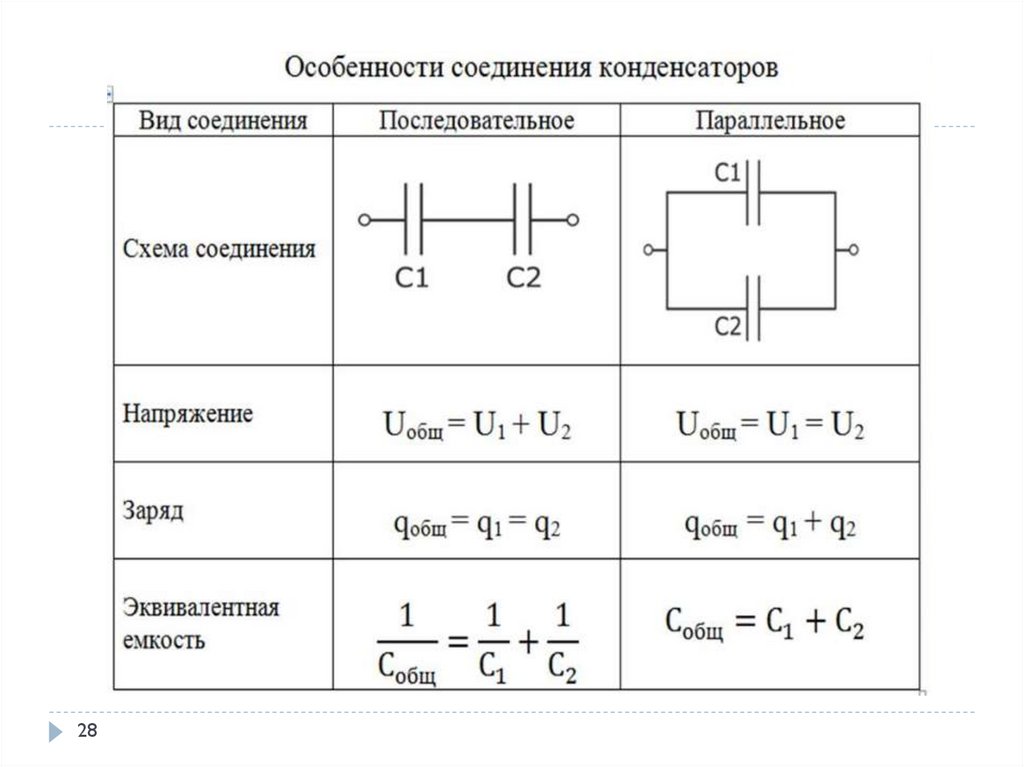
Последовательное соединение проводников — это такое соединение, при котором элементы цепи соединены друг за другом, образуя единую неразветвленную цепь. При этом конец одного элемента соединяется с началом следующего. Такой тип соединения имеет ряд важных особенностей:
- Ток во всех элементах цепи одинаков
- Общее напряжение равно сумме напряжений на отдельных элементах
- Общее сопротивление цепи равно сумме сопротивлений отдельных элементов
Рассмотрим подробнее каждую из этих характеристик и их физическое обоснование.
Распределение тока в последовательной цепи
Одной из ключевых особенностей последовательного соединения является то, что сила тока одинакова во всех участках цепи. Это объясняется законом сохранения электрического заряда — количество электронов, проходящих через любое сечение проводника за единицу времени, должно быть одинаковым.
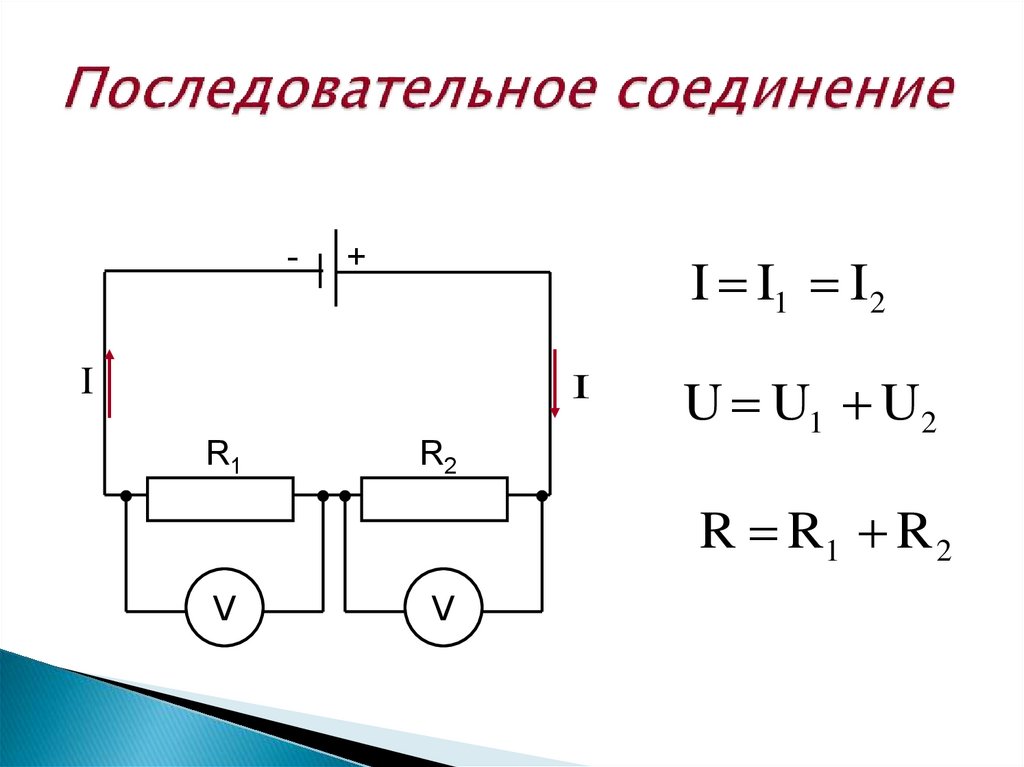
Почему ток в последовательной цепи везде одинаков? Это связано с тем, что заряды не могут накапливаться в каких-либо участках цепи. Сколько электронов вошло в начало цепи, столько же должно выйти в конце. Если бы в каком-то месте ток был меньше, это означало бы накопление заряда, чего в установившемся режиме не происходит.
Пример с последовательно соединенными лампочками
Наглядно это можно продемонстрировать на примере гирлянды из последовательно соединенных лампочек. Если одна лампочка перегорает, вся гирлянда гаснет. Это происходит потому, что ток прерывается во всей цепи — он не может «обойти» перегоревшую лампочку, так как нет другого пути.
Распределение напряжения в последовательной цепи
В отличие от тока, напряжение в последовательной цепи распределяется между элементами. Общее напряжение на концах цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 + … + Un
Это связано с тем, что напряжение характеризует работу электрического поля по перемещению заряда. При прохождении через каждый элемент цепи часть энергии расходуется, что и выражается в падении напряжения на этом элементе.

Зависимость падения напряжения от сопротивления
Важно отметить, что падение напряжения на каждом элементе пропорционально его сопротивлению. Это следует из закона Ома:
U = I * R
Так как ток I одинаков во всей цепи, то напряжение U будет больше на тех элементах, где больше сопротивление R.
Эквивалентное сопротивление последовательной цепи
Общее сопротивление последовательной цепи равно сумме сопротивлений всех ее элементов:
R = R1 + R2 + R3 + … + Rn
Это свойство позволяет заменить несколько последовательно соединенных резисторов одним эквивалентным, что упрощает расчеты в сложных цепях.
Физическое обоснование суммирования сопротивлений
Почему сопротивления при последовательном соединении складываются? Это можно объяснить тем, что каждый резистор создает дополнительное препятствие для движения электронов. Чем больше препятствий на пути тока, тем больше общее сопротивление цепи.
Практическое применение последовательного соединения
Последовательное соединение проводников широко используется в различных электрических устройствах и системах. Вот несколько примеров практического применения:

- Делители напряжения
- Предохранители и автоматические выключатели
- Резисторы в электронных схемах для ограничения тока
- Соединение батарей для увеличения напряжения
- Рождественские гирлянды
Каждое из этих применений основано на уникальных свойствах последовательного соединения.
Расчет параметров последовательной цепи
Для расчета параметров последовательной цепи используются следующие формулы:
- Общее сопротивление: R = R1 + R2 + R3 + … + Rn
- Сила тока: I = U / R, где U — общее напряжение, R — общее сопротивление
- Напряжение на отдельном элементе: Ui = I * Ri
- Общее напряжение: U = U1 + U2 + U3 + … + Un
Эти формулы позволяют решать различные задачи, связанные с последовательными цепями.
Пример расчета последовательной цепи
Рассмотрим пример: В цепи последовательно соединены три резистора с сопротивлениями 2 Ом, 3 Ом и 5 Ом. Общее напряжение на концах цепи 20 В. Найдем ток в цепи и напряжение на каждом резисторе.
- Общее сопротивление: R = 2 + 3 + 5 = 10 Ом
- Ток в цепи: I = U / R = 20 В / 10 Ом = 2 А
- Напряжение на резисторах: U1 = I * R1 = 2 А * 2 Ом = 4 В U2 = I * R2 = 2 А * 3 Ом = 6 В U3 = I * R3 = 2 А * 5 Ом = 10 В
Проверка: U1 + U2 + U3 = 4 В + 6 В + 10 В = 20 В, что соответствует общему напряжению.
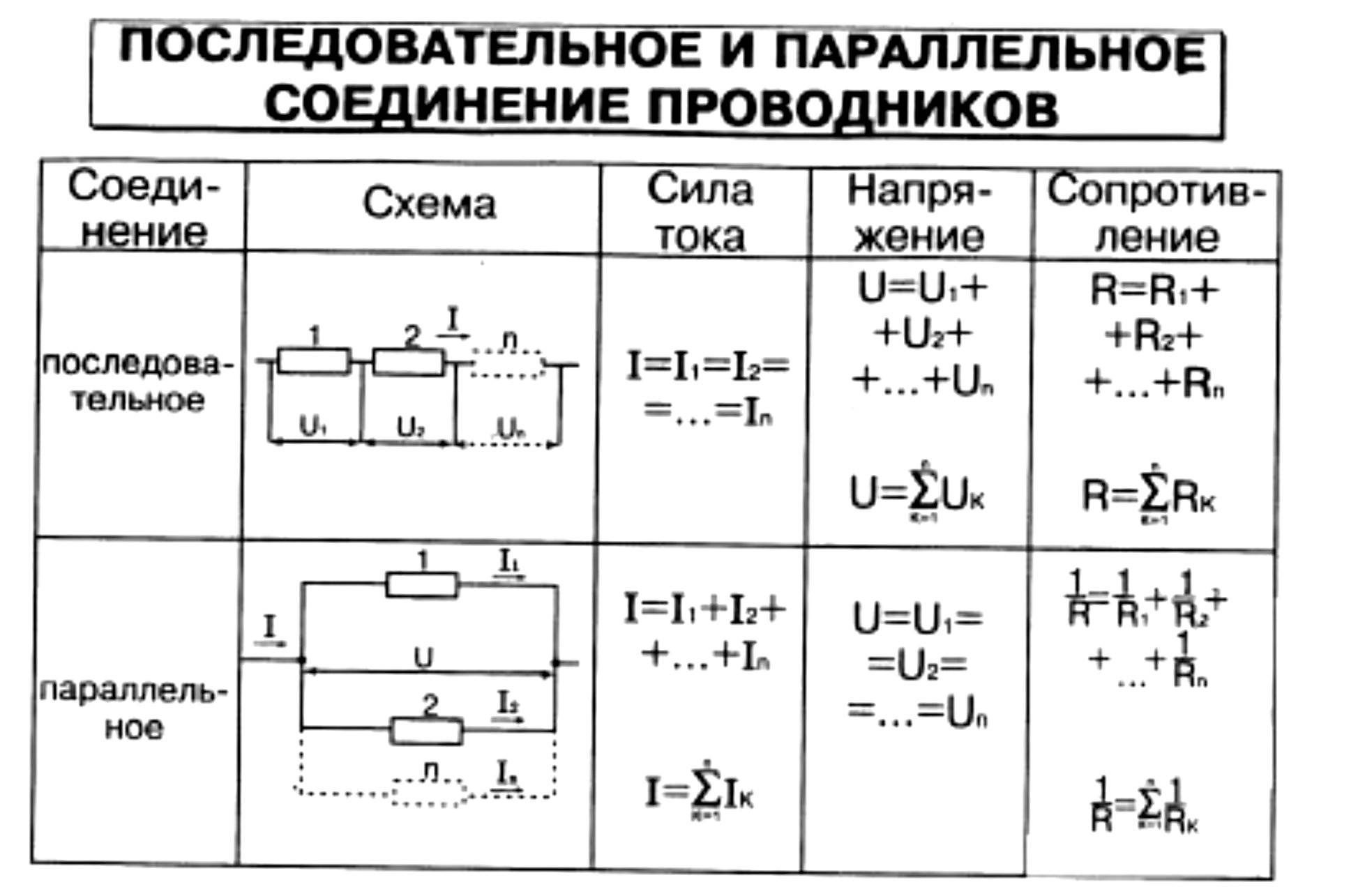
Сравнение последовательного и параллельного соединения
Для полного понимания особенностей последовательного соединения полезно сравнить его с параллельным:
| Характеристика | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Ток | Одинаков во всех элементах | Разный в разных ветвях |
| Напряжение | Сумма напряжений на элементах | Одинаково на всех элементах |
| Сопротивление | Сумма сопротивлений элементов | Меньше наименьшего из сопротивлений |
Эти различия определяют области применения каждого типа соединения в электротехнике и электронике.
Преимущества и недостатки последовательного соединения
Как и любой метод соединения элементов в электрической цепи, последовательное соединение имеет свои плюсы и минусы:
Преимущества:
- Простота соединения элементов
- Возможность легко увеличить общее сопротивление цепи
- Удобство для создания делителей напряжения
- Одинаковый ток во всех элементах, что важно для некоторых приложений
Недостатки:
- При выходе из строя одного элемента прерывается вся цепь
- Сложнее обеспечить одинаковое напряжение на разных элементах
- Общее сопротивление всегда больше сопротивления любого отдельного элемента
Понимание этих особенностей помогает правильно выбирать тип соединения для конкретных задач.

5.3. Ток и напряжение при последовательном соединении r, l, с
Пусть в схеме рис.5.3, состоящей из последовательно соединенных сопротивления R, индуктивности L, емкости С, известен ток При последовательном соединении сопротивлений ток, протекающий через каждый элемент, имеет одно и то же значение.
Подставим значение тока в это уравнение
Из полученных выражений для ur, uL, uC видно, что напряжение на сопротивлении r совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол /2, а напряжение на емкости отстает по фазе от тока на угол /2.
На
рис. 5.4 показаны кривые мгновенных
значений тока и напряжений для частного
случая, когда амплитуда напряжения та
катушке
больше амплитуды напряжения на
конденсаторе
иi
> 0. Синусоида иr
совпадает по фазе с синусоидой тока, а
синусоиды иL
и иС
сдвинуты относительно тока на угол /2
соответственно влево (опережение) и
вправо (отставание). Ордината кривой
напряжения
состоит из суммы ординат кривых
иr
+ иL
+ иC
= и.
Запишем комплекс действующего значения
тока и комплексы действующих значений
напряжений на основании выражений для
мгновенного тока и мгновенных напряжений:
где
действующее Значение тока
Синусоида иr
совпадает по фазе с синусоидой тока, а
синусоиды иL
и иС
сдвинуты относительно тока на угол /2
соответственно влево (опережение) и
вправо (отставание). Ордината кривой
напряжения
состоит из суммы ординат кривых
иr
+ иL
+ иC
= и.
Запишем комплекс действующего значения
тока и комплексы действующих значений
напряжений на основании выражений для
мгновенного тока и мгновенных напряжений:
где
действующее Значение тока
В выражениях для иучтено, что
Сумме синусоидальных напряжений соответствует сумма изображающих их векторов или комплексов их действующих значений напряжений
Это
соотношение представляет собой уравнение
по второму закону Кирхгофа, записанное
в комплексной или векторной форме.
Представим его на векторной диаграмме
рис. 5.5. Напряжение ur
соответствует по фазе с током
i,
поэтому вектор
изобразим одинаково направленным с
вектором.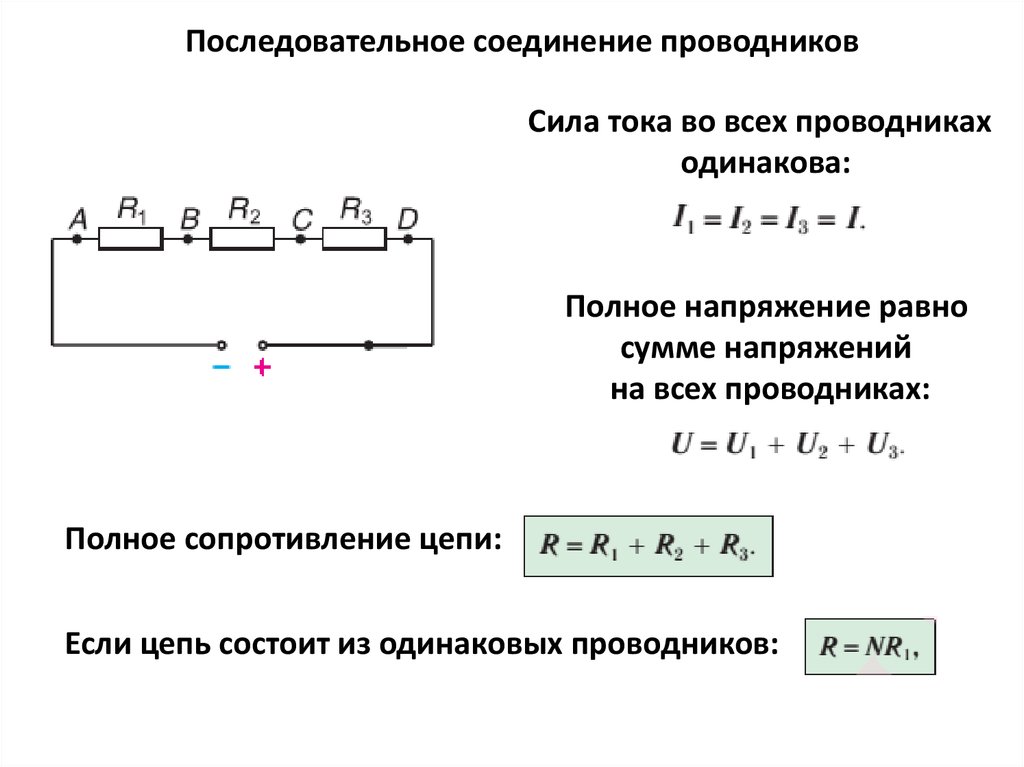 Напряжение
Напряжение
Действительно,
вектор
получается умножениемна вещественную величинуr.
Аргумент комплексной величины
такой же, как комплексного тока,
поэтому направление векторасовпадает с направлением вектора.
Вектор
получается умножениемна
.
Умножение
тока
на вещественную величину
не изменяет аргумента, а умножение на
увеличивает аргумент на /2.
Следовательно, вектор
повернут относительно векторана угол/2
«вперед». Вектор
получается делениемна
.
Деление комплексной величины на
не изменяет аргумента, а деление на
j,
что равносильно умножению на
,
уменьшает аргумент на /2.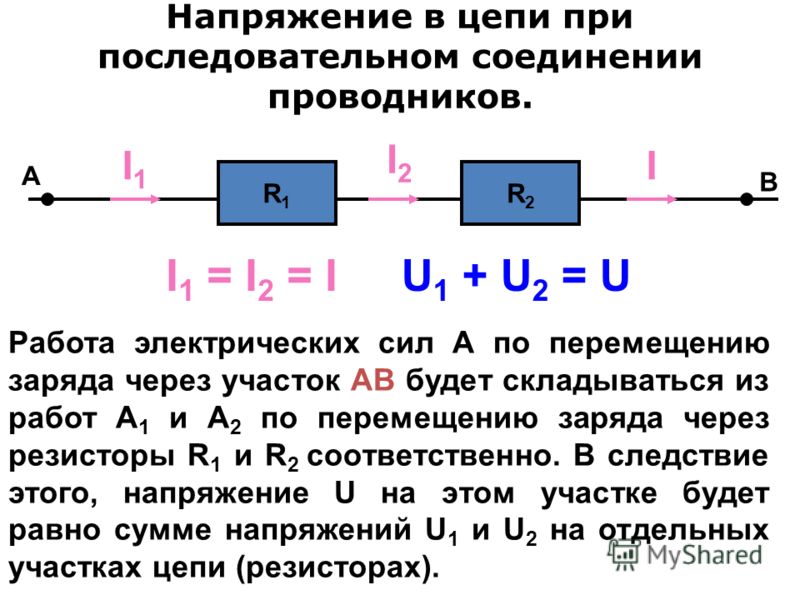 Следовательно, вектор
повернут относительно векторана угол/2
«назад».
Следовательно, вектор
повернут относительно векторана угол/2
«назад».
Так как умножение и деление вектора на j приводят к повороту вектора на /2 соответственно «вперед» и «назад», то множитель j часто называют оператором поворота на /2. Сложив векторы , и , получим вектор. Его длина определяет действующее напряжение, а положение относительно координатных осей – начальную фазу u.
Решим, ту же задачу аналитически. Напомним, что был задан ток . На основании последних выкладок можно записать:
Или
где – комплексное сопротивление.
Это соотношение между комплексными напряжениями и током называют законом Ома в комплексной форме. Записав комплексные величины в показательной форме, имеем
Где
Получаем
Заметим
Так как ито
Таким образом, амплитуда Um и начальная фаза u напряжения на зажимах цепи определены, и можно записать выражение для мгновенного напряжения
электрических цепей — Как происходит падение напряжения при последовательном соединении?
Часть 0 — резисторы
Да, резисторы создают падение напряжения, «локально» замедляя электроны, так что им приходится «тратить» часть энергии на преодоление препятствия — это вызывает падение напряжения. Вы можете думать о них как о «лестницах» в напряжении.
Вы можете думать о них как о «лестницах» в напряжении.
Часть первая — падение напряжения — удельное сопротивление — идеальные цепи
Причина в том, что мы идеализируем «соединения» как имеющие нулевое сопротивление, т.е. две точки в цепи без сопротивления между ними будут иметь одинаковое напряжение. Кроме того, мы предполагаем, что существует устойчивое состояние, так что «начальным» потоком электронов внутри цепи можно пренебречь, и мы сосредоточимся на том, когда система течет без изменений во времени. Это идеализация.
Если подумать, тот факт, что кабели не имеют сопротивления, должен быть ложным, потому что в противном случае короткое замыкание цепи (т. е. соединение двух полюсов батареи напряжением $V$ без какого-либо сопротивления между ними) приведет к к току $I=V/R$, где сопротивление $R=0$, так что это привело бы к бесконечному току $I=\infty$.
В действительности кабели имеют некоторое сопротивление $r$. Мы можем смоделировать это как кусок кабеля длиной $dx$ с сопротивлением $$r=\rho dx$$, то есть $\rho$ — это сопротивление на единицу длины. Будем считать его постоянным.
Будем считать его постоянным.
В этом случае, если вы измерите напряжение между двумя точками цепи на расстоянии $L$ без какого-либо сопротивления между ними, вы измерите падение напряжения, зависящее от расстояния $$\Delta V = -\rho L I$ $ где $I$ — испытательный ток.
Однако это падение, как правило, очень мало по сравнению с напряжением $V$ батареи, и им обычно пренебрегают. Однако иногда необходимо это учитывать!
Итак, если у вас есть цепь длиной $L_{tot}$ с батареей в точке $\ell=0$ (где $\ell$ — длина цепи), то (точечный) «нормальный» сопротивление $R$ при $\ell=\ell_0$ и снова батарея при $\ell=L_{tot}$ у вас будет падение напряжения $V(\ell)$
$$ V(\ell)= \begin{случаи} -I\rho\ell, & \text{if}\ \ell<\ell_0 \\ -I\rho\ell-RI, &\ell>=\ell_0 \end{случаи} $$
, который зависит от длины.
Обратите внимание, что вы всегда можете аппроксимировать это идеальной схемой с сопротивлением $r=\rho L$, включенным последовательно с «нормальным» сопротивлением $R$ — это, конечно, если вы действительно не интересуетесь пространственным значением. напряжения $V(\ell)$.
напряжения $V(\ell)$.
Исходя из тех же соображений, вместо того, чтобы моделировать сопротивление $R$ как точечный объект, можно предположить, что оно имеет расширение $L_0$ с сопротивлением на единицу длины $r_0=R/L_0$, так что теперь напряжение зависит от того, где вы измеряете вдоль сопротивления с $\Delta V= -r_0 x I$ с $x$ положением вдоль сопротивления.
В схеме, которую вы нарисовали, это как $\rho=0$, а затем два точечных резистора номиналом $R$, которые должны обеспечить необходимое падение напряжения, и они «делят» его, так как они равны. Но вы также можете видеть его как один большой конденсатор с общим сопротивлением $2R$ и длиной $2L$, так что он имеет $\rho_0=(2R)/(2L)$, так что через расстояние $L$ (эквивалентное одному резистору ) падение напряжения составляет $\Delta V_1=(2R/2L)*L*I=R*I$, что эквивалентно одному полному резистору. Потому что в вашем случае ток I составляет 100 В/2 R$ (общее напряжение, деленное на общее сопротивление), и вы получаете $$\Дельта V_1=R*100В/(2R) = 100В/2 = 50В$$
Вы также можете моделировать кабели в виде трехмерных цилиндров с удельным сопротивлением на единицу объема и т. д. — чтобы узнать больше: удельное сопротивление
д. — чтобы узнать больше: удельное сопротивление
Часть вторая — начальные моменты времени — что-то вроде
Теперь мы моделируем цепь в начальные моменты времени. Чтобы сделать это должным образом, нам понадобился бы конденсатор и дифференциальное уравнение, но я думаю, что сейчас это было бы слишком сложно. Я попробую другой подход.
Предположим, у нас есть кабель с общим сопротивлением $R$, и мы разделили его на $N$ частей с сопротивлением $r=R/N$. У нас есть батарея, и кабели соединяют две части батареи. В начальный момент все находится под напряжением $V=0$, кроме точки, где находится батарея, имеющая напряжение $V$. Вначале электроны видят небольшой участок цепи с сопротивлением $r$, разностью потенциалов $V$ и испускают ток $i_1=V/r$. Теперь они видят другой резистор и испускают ток $i_2=V/(2r)$. (Это потому, что они видят резистор $r$ при напряжении $V$ и затем следуют закону Ома).
Если раньше падение напряжения на первом резисторе было $V_1(0)=i_2*r=V$, так как полное «напряжение» должно было снижаться через первый резистор, то теперь напряжение делится между двумя резисторы, так что падение напряжения на первом равно $V_1(1)=i_2 r=V/(2r) * r= V/2$.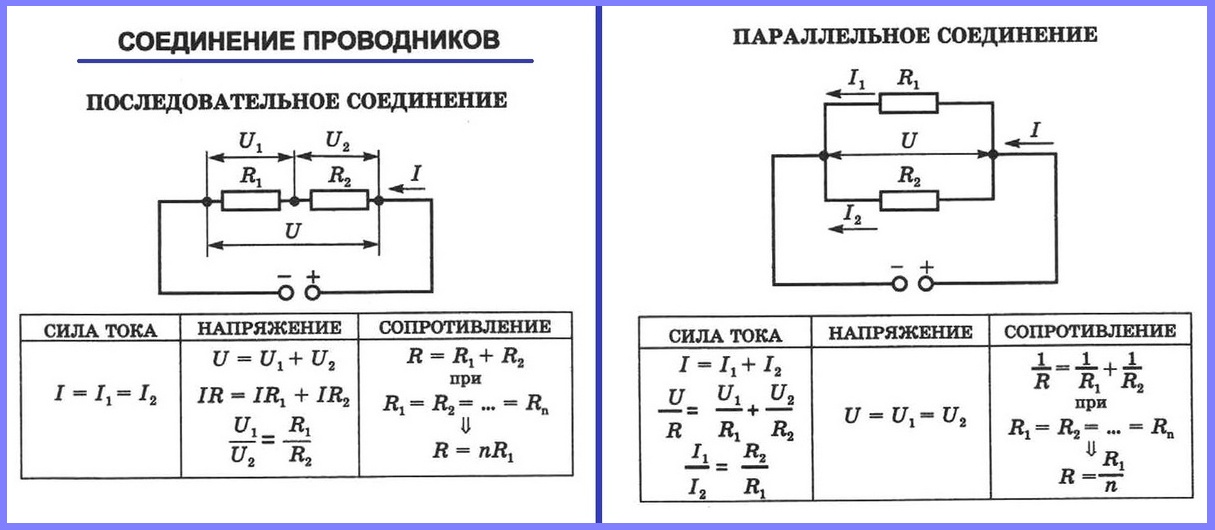
И так далее, чтобы когда электроны пересекли $n$ резисторов, падение напряжения на первом было $$V_1(n)=V/n$$
Если время прохождения электронов через резистор равно $\tau$, то мы получаем, что $n=t/\tau$ (т.е. через время $10\ tau$ мы пересекли $n=10$ резисторов), так что
$$V_1(t)=V/n={V\over(t/\tau)}={V\tau\over t}$$ действительно для $t При этом ток уходит от 0 (при присоединении цепи ток отсутствует ) до $$i_n=V/(nr)={V\over(t/\tau)r}={V\tau\over nt}$$, которое также уменьшается до конечного значения $I=V/(Nr )=V/R$. Итак, в момент времени $t=0$ где происходит всплеск тока через первый резистор, который затем уменьшается до конечного значения по мере того, как электроны «исследуют» наличие новых резисторов и уточняют их средний конечный ток. То же самое относится и к напряжению. Автор Kaushikee Banerjee Напряжение на каждом резисторе в последовательной цепи отличается в зависимости от значения сопротивления. Мы используем слово «постоянный», чтобы указать фиксированное значение количества, которое остается неизменным. Напряжение никогда не может быть постоянным параметром в любой электрической цепи. Каждый резистор имеет разное падение напряжения на них при последовательном соединении. Следовательно, напряжение в последовательных цепях не одинаково и не постоянно. Когда мы подключаем несколько резисторов или параметров импеданса в линию один за другим, это называется последовательной цепью. При последовательном соединении ток во всей цепи одинаков. Эквивалентное сопротивление в последовательном соединении представляет собой сумму всех индивидуальных импедансов. Падение напряжения на всех резисторах суммируется до общего напряжения. Подробнее о….функция последовательной цепи Вышеприведенная схема изображает простую последовательную цепь с тремя резисторами 5 Ом, 10 Ом и 20 Ом. Наша цель — найти падения напряжения на них. Сначала найдем эквивалентное сопротивление. Эквивалентное сопротивление R= R 1 +R 2 +R 3 = 5+20+10= 35 Ом Итак, полный ток= полное напряжение / эквивалентное сопротивление = 10/35= 0,29 Напряжение через резистор 5 Ом = 5*0,29= 1,45 В Напряжение через резистор 10 Ом = 10*0,29= 2,9 В Напряжение через резистор 20 Ом = 20*0,29= 5,8 В Постоянно ли напряжение в последовательной цепи: 3 Важные пояснения —
 Таким образом, последовательное напряжение непостоянно. Только одинаковые резисторы могут давать одинаковое падение напряжения.
Таким образом, последовательное напряжение непостоянно. Только одинаковые резисторы могут давать одинаковое падение напряжения.
Что такое последовательная цепь? Объясните ток и эквивалентное сопротивление в последовательных цепях. 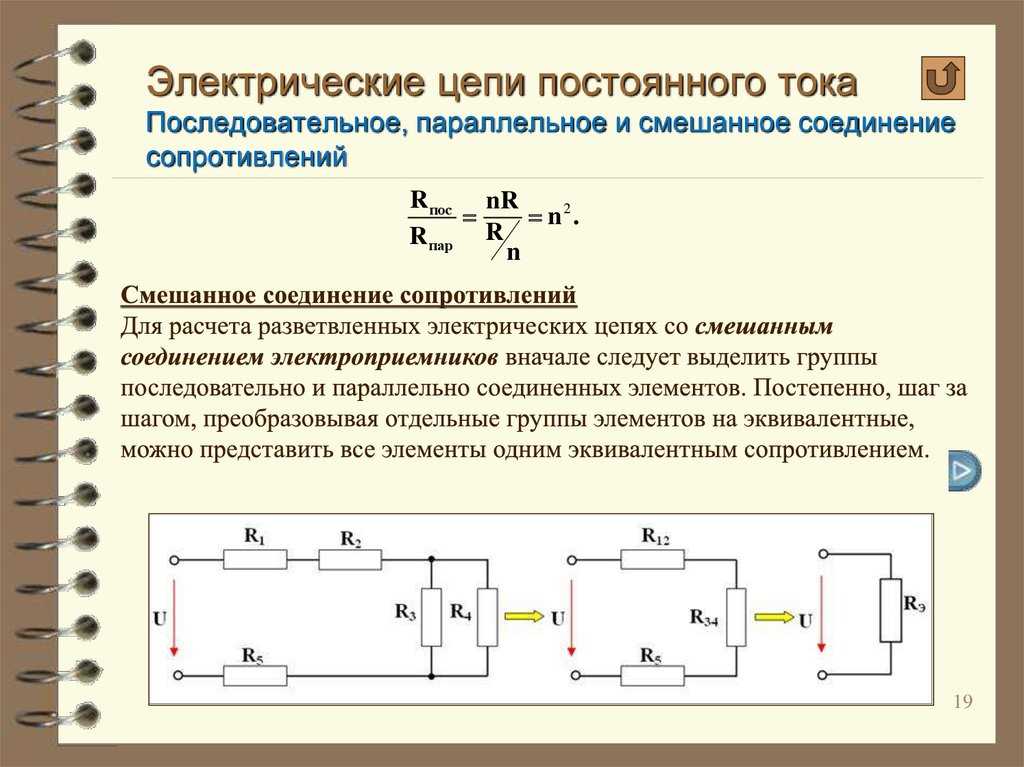 Падение напряжения на каждом компоненте цепи различно. Эти падения напряжения рассчитываются путем умножения общего тока на номинал резистора.
Падение напряжения на каждом компоненте цепи различно. Эти падения напряжения рассчитываются путем умножения общего тока на номинал резистора.
Как рассчитать напряжение в последовательной цепи? Объясните на числовом примере.
Как напряжение влияет на ток в последовательных цепях?
Каждый резистор в последовательной цепи получает одинаковый ток при последовательном соединении. Рассчитаем падение напряжения на них, используя известные номиналы резисторов.
Рассчитаем падение напряжения на них, используя известные номиналы резисторов.
Последовательная цепь представляет собой соединение нескольких элементов сопротивления. Таким образом, если цепь в любой момент разорвется, вся цепь выйдет из строя, и ток не будет течь. Очень распространенным примером этого является последовательное соединение лампочек разной светимости. Если мы продолжим добавлять больше лампочек, яркость со временем упадет.
Рассчитайте общее напряжение V в последовательной цепи, показанной ниже.
Схема, изображенная выше, состоит из четырех резисторов, соединенных последовательно. В цепи присутствует батарея с неизвестным напряжением V. Течет ток 0,25 ампер. Нам нужно узнать значение V.
Падение напряжения на резисторе 6 Ом= 6*0,25= 1,5 В
Падение напряжения на резисторе 8 Ом= 8*0,25= 2 В
Падение напряжения на резисторе 10 Ом= 10*0,25= 2,5 В
Падение напряжения на резисторе 12 Ом = 12*0,25= 3 Вольта
Следовательно, общее напряжение батареи = V=1,5+2+2,5+3 = 9 Вольт
Каково применение последовательного напряжения?
Последовательные и параллельные схемы считаются строительными блоками схемотехники.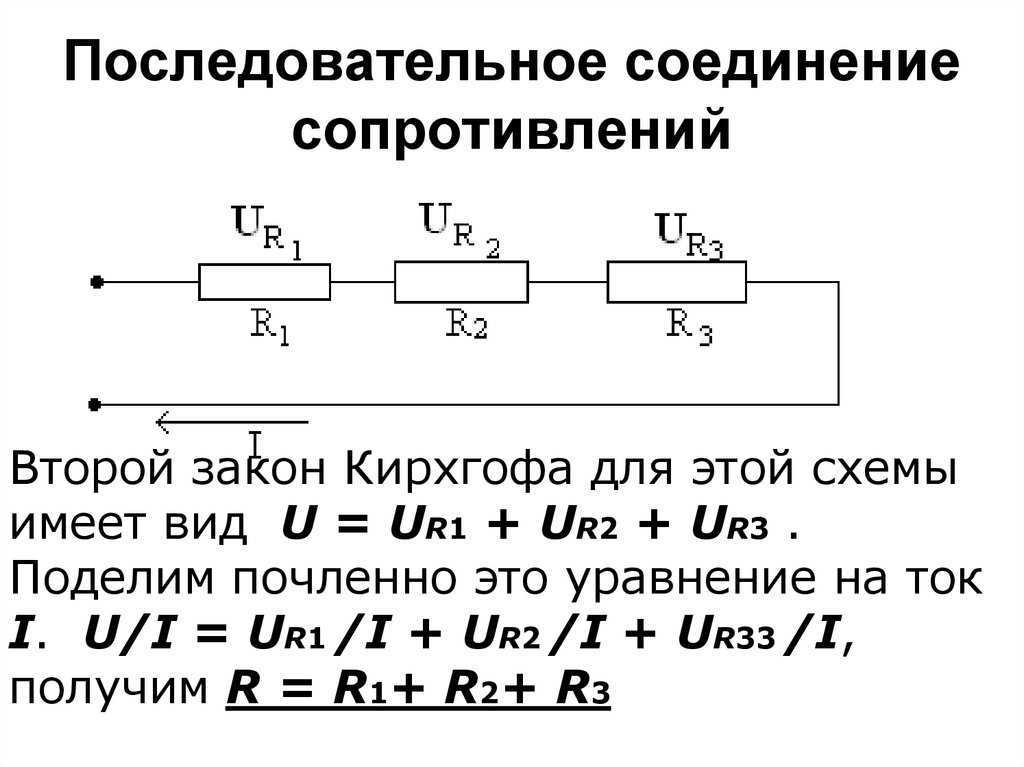 Они обычно используются для многих приложений ограничения тока, таких как деление напряжения, смещение транзисторов и т. д.
Они обычно используются для многих приложений ограничения тока, таких как деление напряжения, смещение транзисторов и т. д.
Напряжение в последовательной цепи имеет различные применения. Some common applications of the voltage in series are-
- Voltage divider circuits
- TV remote batteries
- Fire alarm
- Analog filters
- Resonant circuits
- Power-line фильтры
- Ленты светодиодных ламп
- Внутренние компоненты автомобилей
Как найти отдельные напряжения в последовательной цепи?
Индивидуальные напряжения резисторов в последовательной цепи получаются путем умножения общего тока на номинал резистора.
Предположим, есть два резистора R 1 и R 2 , соединенные последовательно с батареей V. Следовательно, эквивалентное сопротивление R eq равно R 1 +R 2 . Таким образом, напряжение на любом резисторе = сопротивление резистора x общий ток
Следовательно, эквивалентное сопротивление R eq равно R 1 +R 2 . Таким образом, напряжение на любом резисторе = сопротивление резистора x общий ток
The voltage across R 1 = V 1 = V.R 1 / R 1 +R 2 Volt
The voltage across R 2 = V 2 = V.R 2 / R 1 +R 2 Вольт
Одинаково ли напряжение последовательно?
Напряжение в последовательной цепи не одинаковое и не постоянное. Падение напряжения на каждом резисторе различно во всех случаях, кроме случая, когда все резисторы в последовательной сети имеют одинаковое значение.
Когда резисторы в цепи одинакового номинала, то одинаковыми будут только падения напряжения на всех резисторах. Предположим, что в цепи, содержащей три резистора, все резисторы имеют сопротивление ом. Эквивалентное значение сопротивления = R+R+R = 3R.