Принцип работы полосового фильтра. Полосно-заграждающий фильтр: принцип работы, характеристики и применение

Что такое полосно-заграждающий фильтр. Как работает полосно-заграждающий фильтр. Какие бывают виды полосно-заграждающих фильтров. Где применяются полосно-заграждающие фильтры. Как рассчитать параметры полосно-заграждающего фильтра.

Что такое полосно-заграждающий фильтр и как он работает

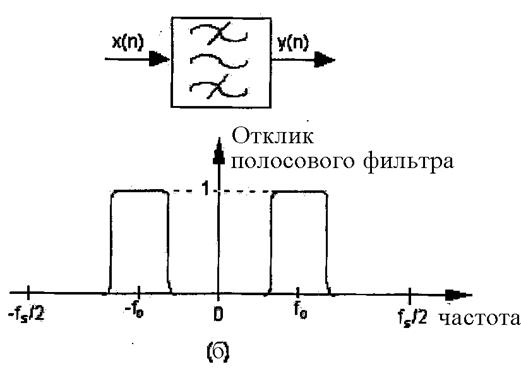
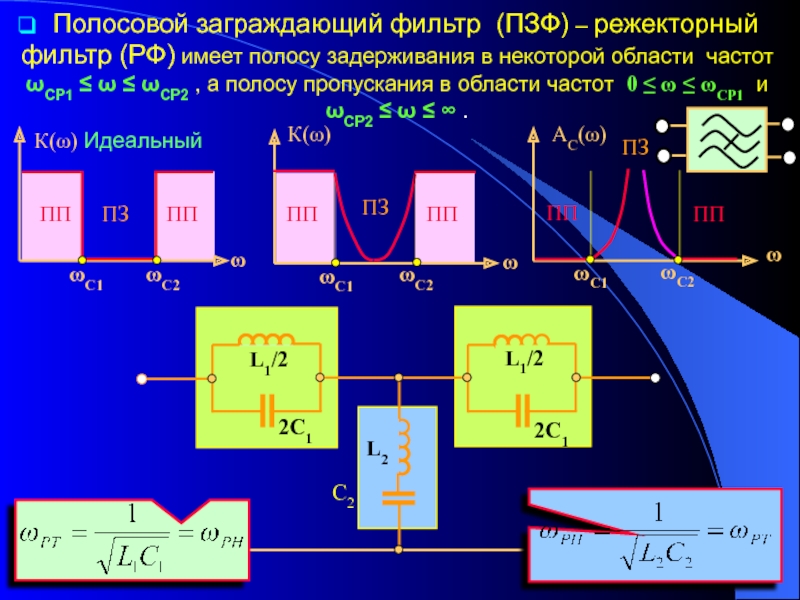
Полосно-заграждающий фильтр (также называемый режекторным фильтром или фильтром-пробкой) — это электронное устройство, которое пропускает большинство частот без изменений, но ослабляет или подавляет частоты в определенном диапазоне до очень низкого уровня. Это противоположно работе полосового фильтра, который пропускает только частоты в заданном диапазоне.

Принцип работы полосно-заграждающего фильтра основан на явлении резонанса в электрических цепях. Фильтр содержит резонансный контур, настроенный на центральную частоту полосы заграждения. На этой частоте и в узком диапазоне вокруг нее контур имеет очень высокое сопротивление, что приводит к подавлению сигнала.

Основные характеристики полосно-заграждающих фильтров

Ключевыми параметрами, определяющими свойства полосно-заграждающего фильтра, являются:

• Центральная частота (f0) — частота максимального подавления сигнала
• Полоса заграждения (BW) — диапазон частот, в котором происходит подавление
• Глубина подавления — степень ослабления сигнала в полосе заграждения
• Добротность (Q) — отношение центральной частоты к полосе заграждения
• Крутизна срезов — скорость изменения АЧХ на границах полосы заграждения

Виды полосно-заграждающих фильтров

Существует несколько основных типов полосно-заграждающих фильтров:

Пассивные LC-фильтры

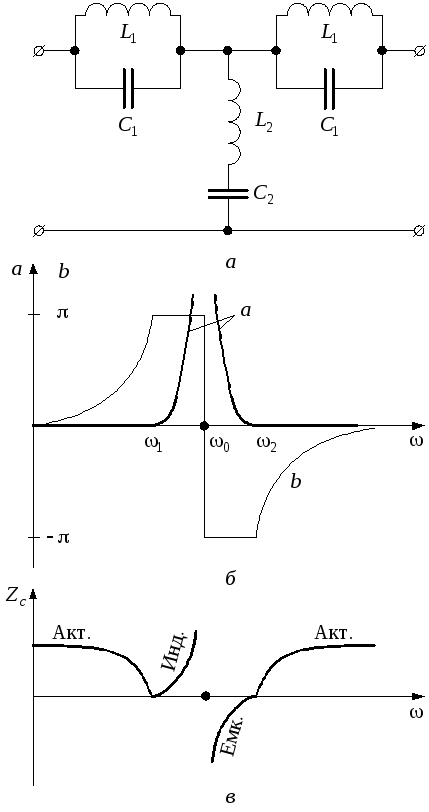
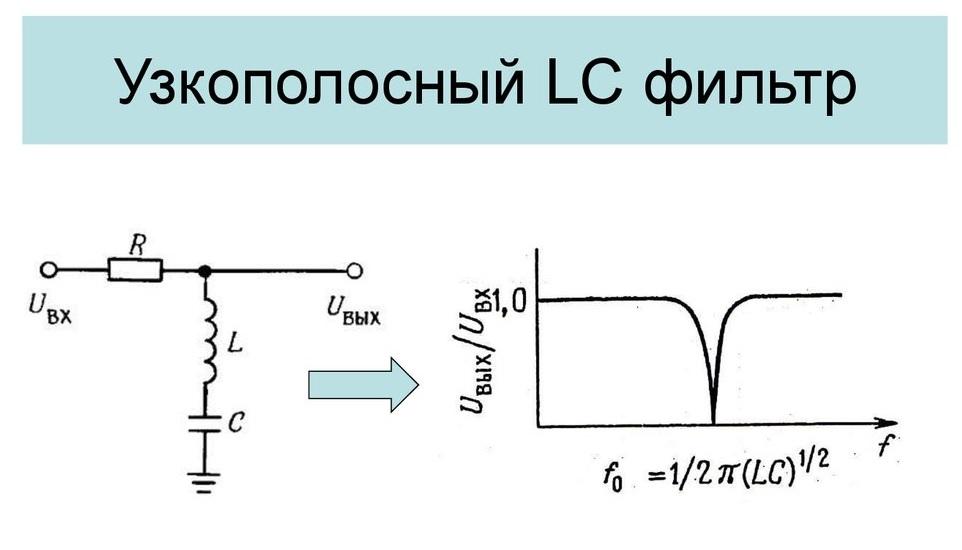
Простейший вид полосно-заграждающих фильтров на основе катушек индуктивности и конденсаторов. Имеют невысокую добротность и ограниченную глубину подавления.

Активные RC-фильтры

Используют операционные усилители и RC-цепи. Позволяют получить более высокую добротность и глубину подавления по сравнению с пассивными фильтрами.

Цифровые фильтры

Реализуются программно на цифровых сигнальных процессорах. Обеспечивают высокую гибкость настройки параметров и стабильность характеристик.

Области применения полосно-заграждающих фильтров

Полосно-заграждающие фильтры находят широкое применение в различных областях:

• Подавление сетевых помех в аудиоаппаратуре
• Фильтрация нежелательных сигналов в радиоприемниках
• Устранение наводок в измерительных приборах
• Выделение полезных сигналов на фоне помех в системах связи
• Коррекция АЧХ в эквалайзерах и аудиопроцессорах

Расчет параметров полосно-заграждающего фильтра

При проектировании полосно-заграждающего фильтра необходимо рассчитать его основные параметры. Рассмотрим пример расчета простого LC-фильтра:

1. Выбираем центральную частоту f0 и полосу заграждения BW
2. Рассчитываем добротность Q = f0 / BW
3. Выбираем значение емкости конденсатора C
4. Вычисляем индуктивность катушки L = 1 / (4π²f0²C)
5. Рассчитываем сопротивление R = Q√(L/C)

Для более сложных фильтров расчет производится с помощью специализированных программ.

Преимущества и недостатки полосно-заграждающих фильтров

Полосно-заграждающие фильтры имеют ряд достоинств и ограничений:

Преимущества:

• Эффективное подавление узкополосных помех
• Возможность точной настройки на заданную частоту
• Минимальное влияние на полезный сигнал вне полосы заграждения

Недостатки:

• Сложность реализации фильтров с высокой добротностью
• Возможность возникновения паразитных резонансов
• Зависимость параметров от температуры и старения компонентов

Сравнение полосно-заграждающих и полосовых фильтров

Полосно-заграждающие фильтры часто сравнивают с полосовыми фильтрами, так как они имеют противоположные функции:

Параметр	Полосно-заграждающий фильтр	Полосовой фильтр
Полоса пропускания	Все частоты, кроме заданного диапазона	Только заданный диапазон частот
Применение	Подавление помех и нежелательных сигналов	Выделение полезного сигнала
АЧХ	Имеет провал в полосе заграждения	Имеет пик в полосе пропускания

Практические рекомендации по применению полосно-заграждающих фильтров

При использовании полосно-заграждающих фильтров следует учитывать несколько важных моментов:

• Правильно выбирайте центральную частоту и полосу заграждения в соответствии с характеристиками подавляемой помехи
• Учитывайте возможное влияние фильтра на фазовые характеристики сигнала
• При каскадном включении нескольких фильтров следите за их взаимным влиянием
• Для повышения эффективности используйте комбинацию аналоговой и цифровой фильтрации

Перспективы развития технологий полосно-заграждающих фильтров

Развитие технологий полосно-заграждающих фильтров идет в нескольких направлениях:

• Создание адаптивных фильтров, автоматически подстраивающихся под изменяющиеся характеристики помех
• Разработка миниатюрных фильтров на основе МЭМС-технологий для применения в мобильных устройствах
• Использование новых материалов для повышения добротности и стабильности параметров фильтров
• Интеграция полосно-заграждающих фильтров в системы искусственного интеллекта для оптимизации их работы

Полосно-заграждающие фильтры остаются важным инструментом в обработке сигналов и борьбе с помехами. Их дальнейшее совершенствование позволит повысить качество работы различных электронных устройств и систем.

Полосно-заграждающий фильтр — принцип работы, характеристики, схемы, формулы — Кови

Полосный фильтр, известный также как Notch Filter и Band Stop Filter, блокирует и отклоняет частоты, лежащие между двумя точками частоты среза, пропускает все частоты, находящиеся по обе стороны от этого диапазона.

Комбинируя основной RC-фильтр низких частот с RC-фильтром высоких частот, мы можем сформировать простой полосовой фильтр, который будет пропускать диапазон или полосу частот по обе стороны от двух точек среза. Но мы также можем объединить эти секции фильтра низких и высоких частот для создания другого типа RC-фильтра, называемого полосовым фильтром, который может блокировать или, по крайней мере, сильно ослабить диапазон частот в пределах этих двух точек среза.

Полосовой стоп-фильтр (BSF) — это еще один тип частотно-избирательной схемы, которая функционирует прямо противоположно полосовому проходному фильтру, который мы рассматривали ранее. Полосовой фильтр, также известный как полосовой отклоняющий фильтр, пропускает все частоты, за исключением тех, которые находятся в определенной полосе пропускания и сильно ослаблены.

Если эта полоса очень узкая и сильно ослаблена на несколько герц, то полосовой фильтр чаще называют фильтром с засечками, так как его частотная характеристика имеет вид глубокой засечки с высокой избирательностью (крутая кривая), а не уплощенной широкой полосы.

Также, как и полосовой пропускной фильтр, полосовой стоп-фильтр (полосовой отклоняющий фильтр или фильтр с засечками) — это фильтр второго порядка (двухполюсный), имеющий две частоты среза, обычно называемые точками -3 дБ или точками половинной мощности, с широкой полосой пропускания между этими двумя точками -3 дБ.

Тогда функция полосового фильтра заключается в том, чтобы пропускать все частоты от нуля (DC) до первой (нижней) точки частоты среза ƒL, и пропускать все частоты выше второй (верхней) частоты среза ƒH, но блокировать или отклонять все частоты между ними. Тогда полоса пропускания фильтра, BW, определяется как: (ƒH — ƒL).

Таким образом, для широкополосного фильтра фактическая полоса пропускания лежит между нижней и верхней точками -3 дБ, поскольку он ослабляет или отклоняет любую частоту между этими двумя частотами среза.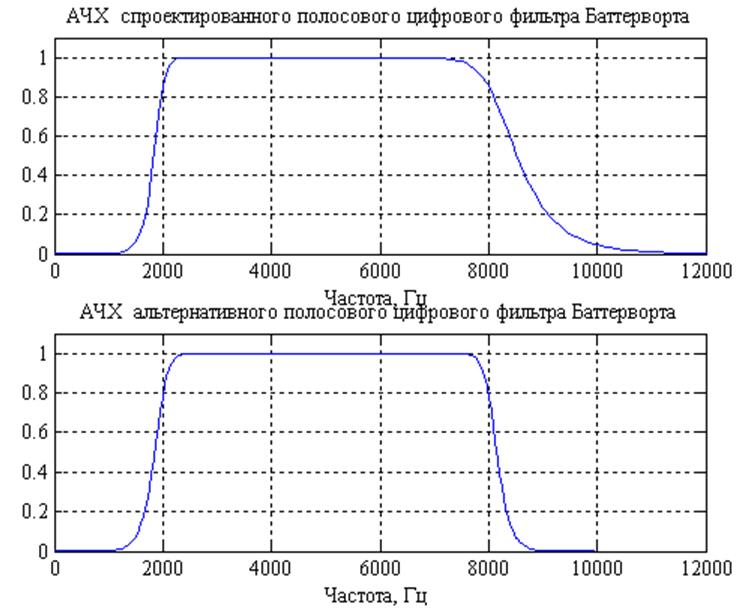 Поэтому кривая частотной характеристики идеального полосового стоп-фильтра имеет вид:

Содержание

Отклик фильтра с полосовой остановкой

Из вышеприведенных кривых амплитуды и фазы для полосового пропускающего контура видно, что величины ƒL, ƒH и ƒC совпадают с теми, которые используются для описания поведения полосового фильтра. Это объясняется тем, что полосовой фильтр является просто инвертированной или дополненной формой стандартного полосового фильтра. На самом деле определения, используемые для полос пропускания, полосы пропускания, полосы остановки и центральной частоты, такие же, как и раньше, и мы можем использовать те же формулы для расчета полосы пропускания, BW, центральной частоты, ƒC, и коэффициента качества, Q.

Идеальный полосовой фильтр имеет бесконечное затухание в своей полосе пропускания и нулевое затухание в любой из полос пропускания. Переход между двумя полосами пропускания и полосой остановки будет вертикальным (кирпичная стена). Существует несколько способов создания «полосового стоп-фильтра», и все они преследуют одну и ту же цель.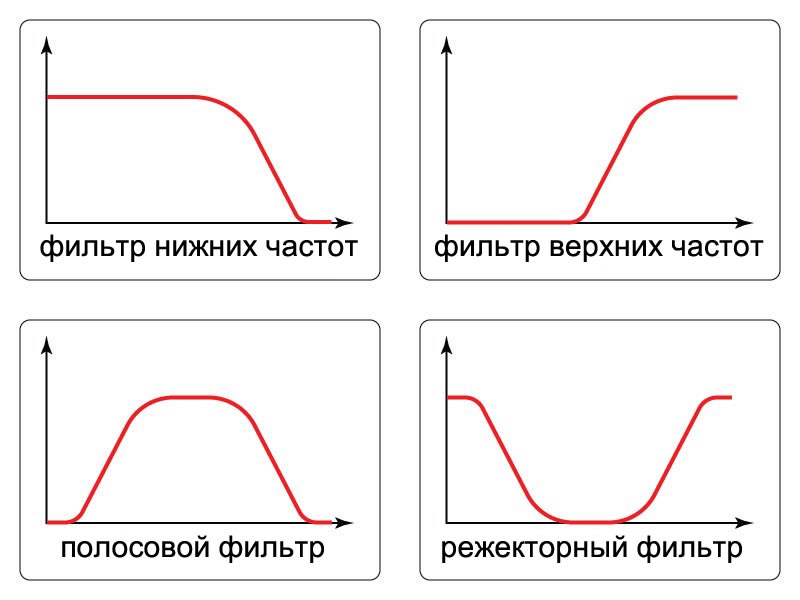

Как правило, полосовые фильтры создаются путем объединения фильтра низких частот (LPF) последовательно с фильтром высоких частот (HPF). Полосно-задерживающие фильтры создаются путем объединения секций фильтра низких и высоких частот в «параллельную» конфигурацию, как показано на рисунке.

Типичная конфигурация фильтра остановки полосы пропускания

Суммирование фильтров высоких и низких частот означает, что их частотные характеристики не перекрываются, в отличие от полосового фильтра. Это связано с тем, что их начальная и конечная частоты находятся в разных частотных точках. Например, предположим, что у нас есть фильтр низких частот первого порядка с частотой среза ƒL 200 Гц, соединенный параллельно с фильтром высоких частот первого порядка с частотой среза ƒH 800 Гц. Поскольку два фильтра соединены параллельно, входной сигнал подается на оба фильтра одновременно, как показано выше.

Все входные частоты ниже 200 Гц будут пропущены фильтром низких частот без затухания на выход.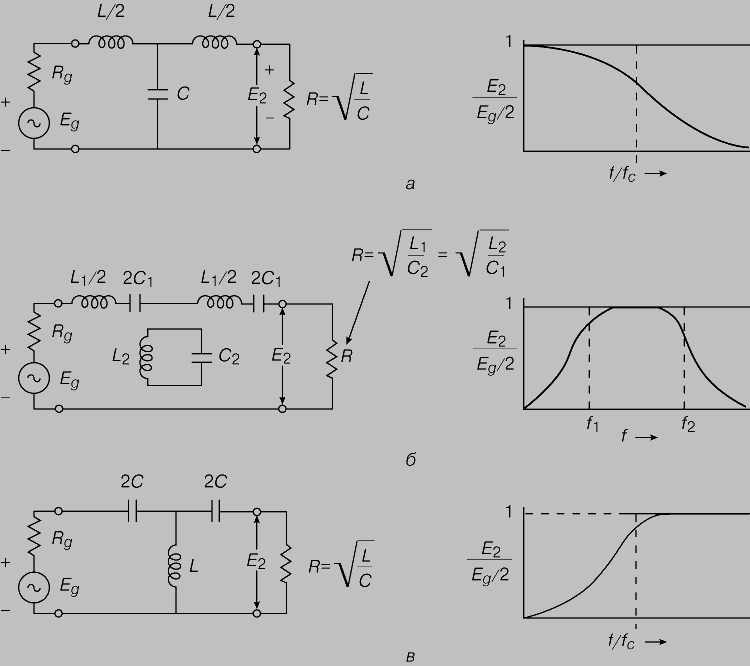 Аналогично, все входные частоты выше 800 Гц будут пропущены без ослабления на выход фильтром высоких частот. Однако частоты входного сигнала между этими двумя точками среза 200 Гц и 800 Гц, то есть от ƒL до ƒH, будут отклонены любым из фильтров, образуя зазубрину в выходной характеристике фильтров.

Другими словами, сигнал с частотой 200 Гц или меньше и 800 Гц и выше пройдет без помех, но сигнал с частотой, скажем, 500 Гц будет отклонен, поскольку он слишком высок, чтобы быть пропущенным фильтром низких частот, и слишком низок, чтобы быть пропущенным фильтром высоких частот. Мы можем показать эффект этой частотной характеристики ниже.

Характеристики фильтра остановки полосы пропускания

Преобразование этой характеристики фильтра может быть легко реализовано с помощью одной схемы фильтра низких и высоких частот, изолированной друг от друга неинвертирующим последователем напряжения (Av = 1). Выходные сигналы этих двух схем фильтра затем суммируются с помощью третьего операционного усилителя, подключенного в качестве лепестка напряжения (сумматора), как показано на рисунке.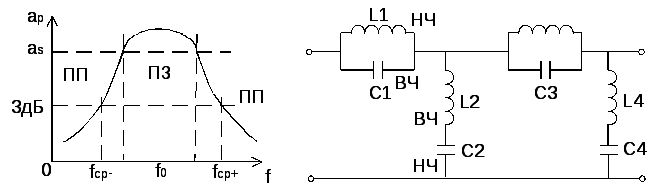

Схема полосового фильтра

Использование операционных усилителей в конструкции полосового ограничительного фильтра также позволяет нам ввести коэффициент усиления по напряжению в базовую схему фильтра. Два неинвертирующих последователя напряжения могут быть легко преобразованы в базовый неинвертирующий усилитель с коэффициентом усиления Av = 1 + Rƒ/Rin путем добавления входных резисторов и резисторов обратной связи, как показано в нашем учебнике по неинвертирующим операционным усилителям.

Также если нам требуется, чтобы полосовой фильтр имел точки среза -3 дБ, скажем, на частотах 1 кГц и 10 кГц и коэффициент усиления полосы -10 дБ между ними, мы можем легко разработать фильтр низких частот и фильтр высоких частот с такими требованиями и просто соединить их вместе, чтобы сформировать нашу конструкцию широкополосного полосового фильтра.

Теперь мы понимаем принцип работы полосового фильтра, давайте спроектируем его, используя предыдущие значения частоты среза.

Пример No1

Разработайте базовый широкополосный RC-полосный фильтр с нижней частотой среза 200 Гц и верхней частотой среза 800 Гц. Найдите геометрическую центральную частоту, полосу пропускания -3 дБ и Q схемы.

Верхнюю и нижнюю точки частоты среза для полосового фильтра можно найти по той же формуле, что и для фильтров низких и высоких частот, как показано на рисунке.

Предполагая, что значение конденсатора C для обеих секций фильтра составляет 0,1 мкФ, значения двух определяющих частоту резисторов RL и RH рассчитываются следующим образом.

Секция фильтра низких частот

Секция фильтра высоких частот

Исходя из этого, мы можем рассчитать частоту геометрического центра, ƒC как:

Теперь, когда мы знаем значения компонентов для двух ступеней фильтра, мы можем объединить их в одну схему сумматора напряжения для завершения нашей конструкции фильтра. Величина и полярность выходного сигнала сумматора в любой момент времени будет равна алгебраической сумме двух его входов.

Если мы сделаем резистор обратной связи оп-ампа и два его входных резистора одинаковыми, скажем, 10kΩ, то инвертирующая суммирующая схема обеспечит математически правильную сумму двух входных сигналов с нулевым коэффициентом усиления напряжения.

Тогда окончательная схема для нашего примера полосового фильтра будет выглядеть следующим образом:

Проектирование полосового задерживающего фильтра

Мы видели выше, что простые полосовые фильтры могут быть изготовлены с использованием фильтров низких и высоких частот первого или второго порядка вместе с неинвертирующей суммирующей схемой операционного усилителя для отклонения широкого диапазона частот. Но мы также можем разработать и сконструировать полосовые фильтры для получения гораздо более узкой частотной характеристики для устранения определенных частот путем увеличения избирательности фильтра. Этот тип конструкции фильтра называется «Notch Filter».

Фильтры с засечкой

Фильтры с засечками — это высокоселективная форма полосового стоп-фильтра с высокой добротностью, которая может использоваться для отсеивания одной или очень маленькой полосы частот, а не целого диапазона различных частот. Например, может потребоваться отклонить или ослабить определенную частоту, генерирующую электрический шум (например, сетевой гул), который был наведен в цепи индуктивной нагрузкой, такой как двигатели или балластное освещение, или удалить гармоники и т.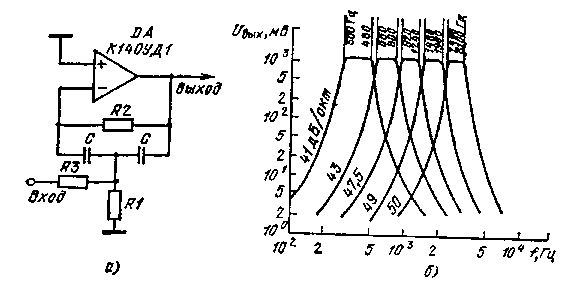 д.

Но помимо фильтрации, фильтры с переменной насечкой также используются музыкантами в звуковом оборудовании, таком как графические эквалайзеры, синтезаторы и электронные кроссоверы, для борьбы с узкими пиками в акустическом отклике музыки. Таким образом, мы видим, что фильтры с насечками широко используются примерно так же, как низкочастотные и высокочастотные фильтры.

По своей конструкции фильтры с насечками имеют очень узкую и очень глубокую полосу пропускания вокруг своей центральной частоты, причем ширина насечки описывается ее избирательностью Q точно так же, как пики резонансной частоты в RLC-цепях.

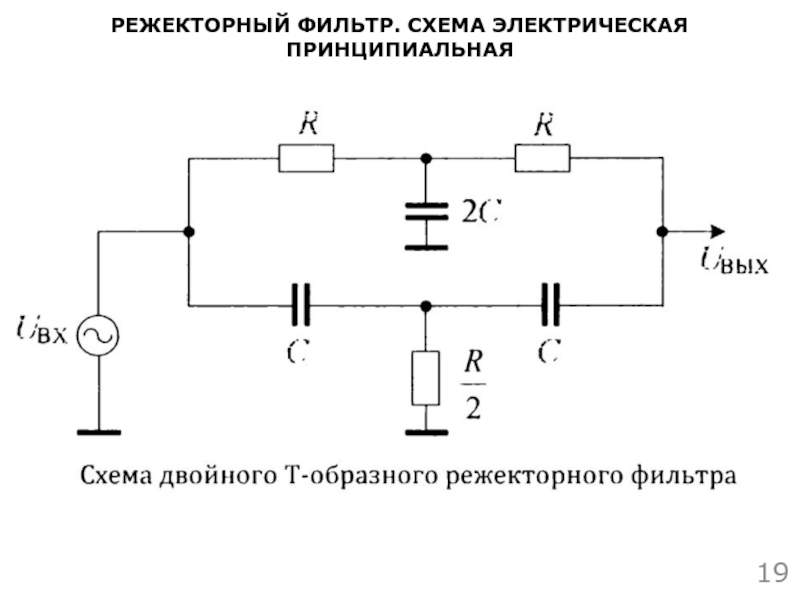
Наиболее распространенной конструкцией фильтров с засечками является сеть фильтров с засечками типа Twin-T. В своей базовой форме конфигурация twin-T, также называемая параллельным тройником, состоит из двух RC-ветвей в виде двух тройников, в которых используются три резистора и три конденсатора с противоположными и противоположными R и C элементами в тройниковой части конструкции, как показано на рисунке, что создает более глубокую засечку.

Базовая конструкция фильтра с двумя зубцами

Верхняя Т-образная конфигурация из резистора 2R и конденсатора 2C образует секцию фильтра низких частот, а нижняя Т-образная конфигурация из конденсатора C и резистора R — секцию фильтра высоких частот. Частота, на которой эта базовая конструкция фильтра с двумя Т-образными засечками обеспечивает максимальное затухание, называется «частотой засечки», ƒN, и определяется как:

Уравнение фильтра с двумя зубцами

Будучи пассивной RC-сетью, одним из недостатков этой базовой конструкции сдвоенного Т-образного режекторного фильтра является то, что максимальное значение выходного сигнала (Vout) ниже частоты режекции обычно меньше, чем максимальное значение выходного сигнала выше частоты режекции, частично из-за того, что два последовательных сопротивления (2R) в секции фильтра нижних частот имеют большие потери, чем реактивное сопротивление двух последовательных конденсаторов (C) в секции высоких частот.

Помимо неравномерного усиления по обе стороны от частоты засечки, еще одним недостатком этой базовой конструкции является то, что она имеет фиксированное значение Q, равное 0,25, порядка -12 дБ. Это происходит потому, что на частоте засечки реактивное сопротивление двух последовательных конденсаторов равно сопротивлению двух последовательных резисторов, в результате чего токи, протекающие в каждой ветви, расходятся по фазе на 180o.

Мы можем улучшить эту ситуацию, сделав фильтр с засечками более избирательным с помощью положительной обратной связи, подключенной к центру двух опорных ножек. Вместо того чтобы соединять спай R и 2C с землей (0 В), вместо этого подключите его к центральному выводу сети делителя напряжения, питаемого выходным сигналом. Величина обратной связи, задаваемая коэффициентом делителя напряжения, определяет значение Q, которое, в свою очередь, в некоторой степени определяет глубину засечки.

Однотактный фильтр с двумя T-образными засечками

Здесь выход из секции сдвоенного Т-образного режекторного фильтра изолирован от делителя напряжения одним неинвертирующим буфером операционного усилителя. Выход с делителя напряжения подается обратно на точку «земли» R и 2C. Величина обратной связи сигнала, известная как доля обратной связи k, задается соотношением резисторов и имеет вид:

Значение Q определяется соотношением резисторов R3 и R4, но если бы мы хотели сделать Q полностью регулируемым, мы могли бы заменить эти два резистора обратной связи одним потенциометром и подать его на другой буфер оп-ампа для увеличения отрицательного усиления. Кроме того, для получения максимальной глубины засечки на заданной частоте, резисторы R3 и R4 можно исключить, а соединение R и 2C подключить непосредственно к выходу.

Пример No2
Разработайте узкополосный RC-фильтр с двумя ОУ с центральной частотой среза ƒN 1 кГц и полосой пропускания -3 дБ 100 Гц. Используйте в конструкции конденсаторы 0.1uF и рассчитайте ожидаемую глубину засечки в децибелах.

Приведенные данные: ƒN = 1000 Гц, BW = 100 Гц и C = 0,1 мкФ.

1. Рассчитайте значение R для заданной емкости 0,1uF.

2. Рассчитайте значение Q

3. Рассчитайте значение доли обратной связи k

4. Вычислите значения резисторов R3 и R4

5. Рассчитайте ожидаемую глубину надреза в децибелах, дБ

Проектирование фильтров с насечками

Краткое описание полосового стоп-фильтра

Мы видели, что идеальный полосовой фильтр имеет частотную характеристику, обратную полосовому фильтру. Полосовые фильтры блокируют или «отклоняют» частоты, лежащие между двумя точками среза (ƒL и ƒH), но пропускают все частоты по обе стороны от этого диапазона. Диапазон частот выше ƒL и ниже ƒH называется полосой останова.

Фильтры остановки полосы достигают этого путем суммирования выходов фильтра высоких частот и фильтра низких частот (особенно для широкополосной конструкции), при этом выход фильтра является разностью. Конструкцию полосового фильтра с широкой полосой пропускания также называют полосовым отклоняющим фильтром, а конструкцию полосового фильтра с узкой полосой пропускания — полосовым фильтром. В любом случае, полосовые фильтры являются фильтрами второго порядка.

Фильтры с засечками предназначены для обеспечения высокого затухания на одной частоте и вблизи нее при незначительном или нулевом затухании на всех остальных частотах. Для получения глубокой зазубрины в фильтрах с зазубринами используется параллельная сеть сопротивления-емкости (RC) в виде двойного тройника. Более высокие значения Q можно получить, подавая часть выходного сигнала на соединение двух тройников.

Чтобы сделать фильтр с засечками более избирательным и с регулируемыми значениями Q, можно соединить стык сопротивления и емкости в двух тройниках с центральной точкой делителя напряжения, подключенного к выходному сигналу фильтра. Правильно спроектированный фильтр с засечками может давать затухание более -60 дБ на частоте засечки.

Фильтры с засечками имеют множество применений в электронике и коммуникационных схемах, и, как мы видели здесь, они могут использоваться для удаления полосы нежелательных частот из системы, позволяя другим частотам проходить с минимальными потерями. Фильтры с насечками могут быть высокоселективными и могут быть разработаны для отклонения или ослабления определенной частоты или гармоник, создающих электрический шум, например, сетевой гул в цепи.

Видеообзор: Полосно-заграждающий фильтр

Полосовой фильтр — frwiki.wiki

Изображение, к которому был применен полосовой фильтр (результат справа)

Полосовой фильтр представляет собой фильтр , позволяя только полосу или интервал частот , чтобы пройти между низким отсечения частоты и высокой частоты среза фильтра.

Концепция полосового фильтра — это математическое преобразование, применяемое к данным (сигналу). Полосовой фильтр можно реализовать в цифровом виде или с помощью электронных компонентов. Функция этого преобразования заключается в ослаблении частот за пределами полосы пропускания , интервала частот между частотами среза. Таким образом, только частоты, включенные в этот интервал, остаются нетронутыми или с небольшим затуханием.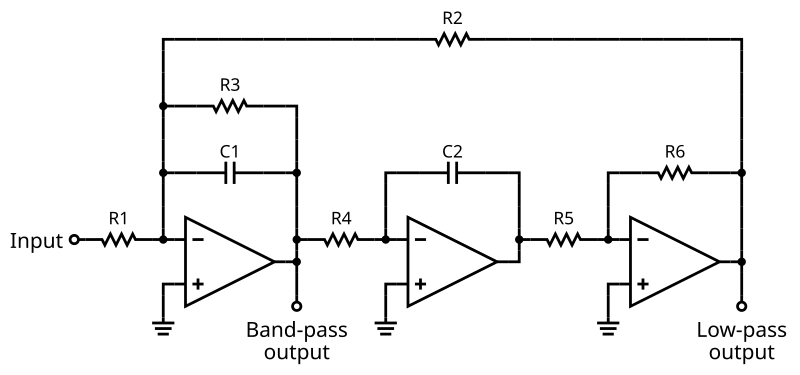

Резюме

• 1 Идеальный фильтр
• 2 Аналоговый полосовой фильтр
  • 2.1 Полосовой фильтр второго порядка
• 3 Пропускная способность
• 4 Использование в электронике
  • 4.1 Схема RLC и диаграмма Боде
• 5 Использование с механическими волнами
• 6 Статьи по теме

Идеальный фильтр

Идеальный полосовой фильтр имеет постоянное усиление в полосе пропускания и нулевое усиление в полосе среза. Переход между двумя состояниями происходит мгновенно. В действительности, фильтр имеет на своей частоте среза усиление Gmax -3  дБ, а затем уменьшает усиление на -20  дБ на декаду (т. Е. -6  дБ на октаву) (фильтр 1- ^го  порядка).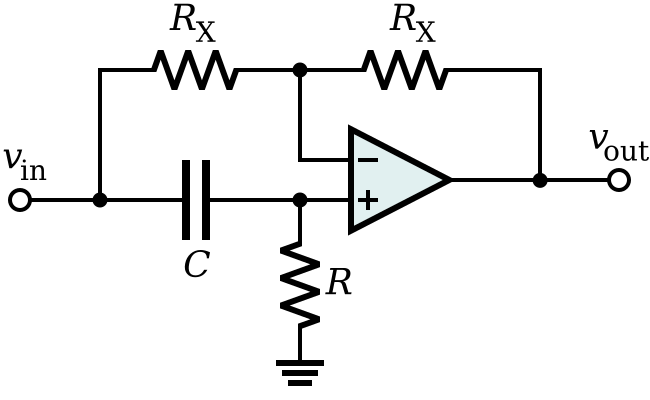

Аналоговый полосовой фильтр

Полосовой фильтр может быть реализован аналогично электронным компонентам. Следовательно, этот вид фильтра применяется к непрерывным сигналам в реальном времени. Компоненты и конфигурация схемы будут фиксировать различные характеристики фильтра , такие как порядок, частоты среза и его диаграмма Боде . Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта , Чебышева , Бесселя , эллиптические и др. Реализация фильтров одного и того же семейства обычно выполняется с использованием одной и той же конфигурации схемы, и они имеют одинаковую форму передаточной функции, но изменяются ее параметры, следовательно, значение компонентов передаточной функции. .

Полосовой фильтр второго порядка

Передаточная функция второго порядка полосового фильтра записывается в виде :, с A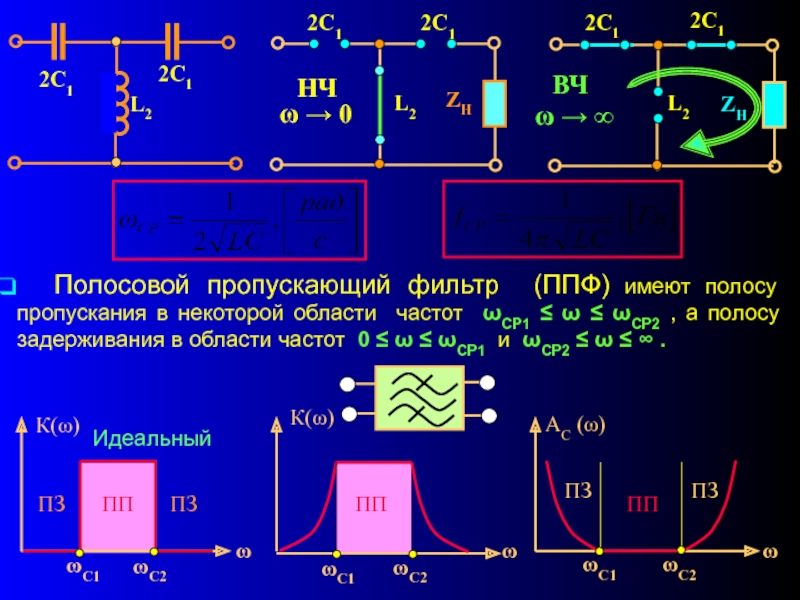

0 коэффициент усиления; и ( сокращенная переменная ). А Q — добротность. час(jш)знак равноВ01+j⋅Q⋅(Икс-1Икс){\ displaystyle h (jw) = {\ frac {A_ {0}} {1 + j \ cdot Q \ cdot (x — {\ frac {1} {x}})}}}Иксзнак равноωω0{\ displaystyle x = {\ frac {\ omega} {\ omega _ {0}}}}

Пропускная способность

Полоса пропускания BP полосового фильтра — это интервал импульсов [ω _c1 , ω _c2 ], который соответствует таким импульсам, что коэффициент усиления не более чем на 3 децибела ниже максимального усиления (здесь 0 дБ).

G (ω _ci ) = G (ω ₀ ) -3,

а также

BP = [ω _c1 , ω _c2 ]

Эти импульсы отсечки таковы, что

|час(jωпротив1)|знак равно|час(jωпротив2)|знак равночасмвИкс2{\ displaystyle | час (j \ omega _ {c1}) | = | h (j \ omega _ {c2}) | = {\ frac {h _ {\ mathrm {max}}} {\ sqrt {2}} }}

(так как20бревно⁡12≈-3){\ displaystyle \ left ({\ text {car}} \ quad 20 \ log {\ frac {1} {\ sqrt {2}}} \ приблизительно -3 \ right)}

Использование в электронике

Есть много приложений в электронике . Полосовая схема может использоваться для удаления шума из сигнала , если известно, что сигнал имеет частоты в пределах указанного диапазона частот. Это также полосовая схема, которая позволяет при радиосвязи выбирать радиочастоту для прослушивания.

Схема RLC и диаграмма Боде

Схема полосового фильтра RLC

Пассивный полосовой фильтр можно получить с помощью схемы RLC, описанной на диаграмме напротив. Затем мы находим следующую передаточную функцию:

час(jш)знак равно11+j(Lрω-1рПРОТИВω){\ displaystyle h (jw) = {\ frac {1} {1 + j \ left ({\ frac {L} {R}} \ omega — {\ frac {1} {RC \ omega}} \ right)} }}

который имеет вид: час(jИкс)знак равно11+jQ(Икс-1Икс){\ displaystyle h (jx) = {\ frac {1} {1 + jQ \ left (x — {\ frac {1} {x}} \ right)}}}

с участием:

Иксзнак равноωω0{\ displaystyle x = {\ frac {\ omega} {\ omega _ {0}}}}

ω0знак равно1LПРОТИВ{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}}}

Qзнак равно1рLПРОТИВ{\ displaystyle Q = {\ frac {1} {R}} {\ sqrt {\ frac {L} {C}}}}

Таким образом, мы имеем:

час(jω)знак равно11+jQ(ωω0-ω0ω){\ displaystyle h (j \ omega) = {\ frac {1} {1 + jQ \ left ({\ frac {\ omega} {\ omega _ {0}}} — {\ frac {\ omega _ {0}) } {\ omega}} \ right)}}}

Мы делаем вывод, что:

|час(jω)|знак равно11+Q2(ωω0-ω0ω)2{\ displaystyle | час (j \ omega) | = {\ frac {1} {\ sqrt {1 + Q ^ {2} \ left ({\ frac {\ omega} {\ omega _ {0}}} — { \ frac {\ omega _ {0}} {\ omega}} \ right) ^ {2}}}}}

аргумент⁡(час(jω))знак равно-арктан⁡(Q(Икс-1Икс)){\ displaystyle \ arg (час (j \ omega)) = — \ arctan \ left (Q \ left (x — {\ frac {1} {x}} \ right) \ right)}

Использование с механическими волнами

В акустике можно использовать полосовой фильтр, чтобы ослабить некоторые неприятные или даже вредные звуки , пропуская при этом «полезные» звуки (голос, предупреждающий сигнал).

В механике полосовой фильтр может позволить ослабить мешающие или даже вредные вибрации или колебания, сохраняя при этом определенную гибкость системы: система может деформироваться и, следовательно, адаптироваться к условиям, она имеет возвратную силу. до исходных размеров, но он не очень чувствителен к внешним воздействиям, имеющим быструю или медленную частоту. В случае измерения ( микрофон , сейсмограф и т. Д.) Такой фильтр также позволяет выбрать диапазон регистрируемых волн.

Статьи по Теме

• Режекторный фильтр, фильтр, принцип действия которого противоположен принципу полосового фильтра.
• Фильтр высоких частот
• Фильтр низких частот
• Фильтр (электронный)

Фильтры
Типы фильтров	Фильтр низких частот  · High Pass Filter  · полосовой фильтр  · режекторный фильтр
линейные фильтры	Фильтр Бесселя  · Фильтр Баттерворта  · Фильтр Чебышева  · Фильтр эллиптический
цифровые фильтры	Конечная импульсная характеристика  · фильтр бесконечной импульсной характеристики

<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Что такое полосовые фильтры и почему они важны?

COVID-19 Обновление:

Компания Envin Scientific открыта для бизнеса во всех областях своей продукции, таких как оптические фильтры и средства обнаружения и контроля газов.

Прочтите заявление

Оптические полосовые фильтры — это фильтры, которые позволяют свету определенного спектра проходить через подложку, блокируя при этом нежелательные частоты за счет поглощения, отражения или того и другого.

Они могут использоваться для передачи сигналов в определенном диапазоне частот, от очень узкого диапазона до очень широкого диапазона.

Envin Scientific производит заказные оптические полосовые фильтры с очень специфическими характеристиками, чтобы решать и преодолевать широкий спектр электрооптических задач.

Что такое оптический полосовой фильтр?

Оптические полосовые фильтры пропускают (или «пропускают») определенный диапазон (или «диапазон») частот. Это может включать видимый свет, а также невидимые длины волн в инфракрасном и ультрафиолетовом диапазонах спектра.

Результатом является вывод, который содержит только желаемые частоты и длины волн, а нежелательные части спектра заблокированы.

В Envin Scientific стандартный диапазон длин волн, которые могут блокироваться и передаваться нашими высокоточными оптическими фильтрами, составляет от 175-200 нм до 8 микрон.

Как работают оптические полосовые фильтры?

Полосовые фильтры работают, поглощая или отражая нежелательные длины волн и пропуская только желаемые части спектра видимого света.

Их можно определить с помощью ряда характеристик:

• Уровень блокировки: Насколько эффективно устраняются нежелательные длины волн.
• Пиковая передача: насколько эффективно передается падающий свет.
• Центральная длина волны: Длина волны в центре профиля передачи.
• Полная ширина на половине максимума: пределы полосы пропускания, между которыми передается 50% или более света.

Например, очень высокое пропускание во всем диапазоне FWHM с крутым спадом и очень низким пропусканием за пределами этого диапазона является признаком высокоэффективного фильтра с очень небольшим «шумом» на выходе.

Как изготавливаются оптические полосовые фильтры?

Оптические полосовые фильтры могут быть изготовлены несколькими способами:

• Тонкопленочные фильтры и фильтры с покрытием изготавливаются путем вакуумного напыления многослойных диэлектрических покрытий на подложку.
• Спектральные и абсорбционные фильтры изготавливаются комбинацией ламинирования, склеенных слоев и тонкопленочного покрытия.

Комбинируя фильтры и методы, можно производить однослойные полосовые фильтры с очень специфическими и сложными свойствами для достижения всех видов электрооптических применений.

Хотя существуют некоторые ограничения на то, насколько тонким может быть полосовой фильтр, оптические тонкопленочные фильтры Envin Scientific имеют толщину от 0,1 мм до нескольких сантиметров и могут быть размером от 1 мм до более 100 мм.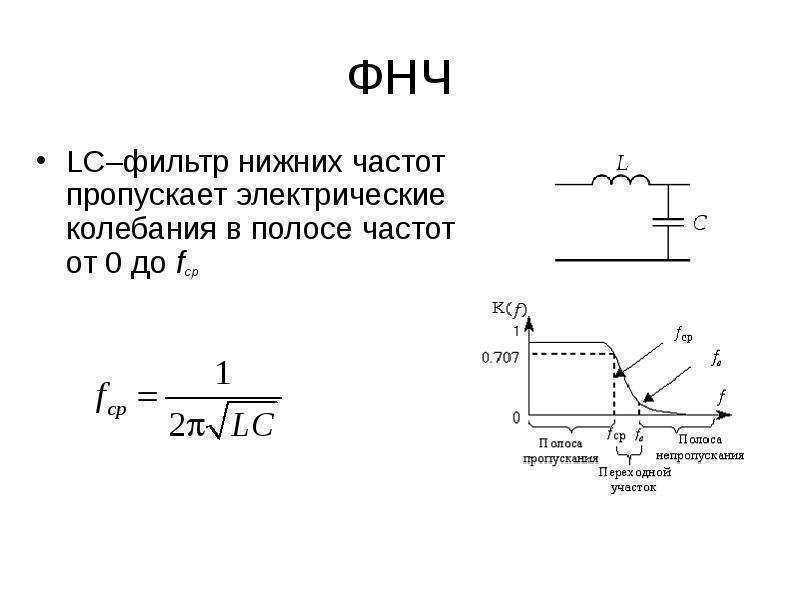

Пользовательские оптические фильтры могут иметь круглую, квадратную/прямоугольную или другую форму в соответствии с вашими требованиями.

Для чего используются оптические полосовые фильтры?

В зависимости от диапазона передаваемых длин волн оптические полосовые фильтры могут использоваться для невероятно разнообразных приложений, включая, например:

• Антибликовое и антибликовое покрытие
• Химический анализ
• Диэлектрические зеркала и высокие отражатели
• Флуоресцентные фильтры
• Инфракрасные (ИК) приложения
• Лазерные оптические фильтры
• Длинноволновый проход (передает только длинные волны)
• Коротковолновый проход (передает только короткие волны)
• Телекоммуникации и оптоволокно
• Ультрафиолетовое (УФ) применение

Мы приветствуем все запросы, касающиеся изготовленных на заказ полосовых фильтров для всех видов оптических применений, и можем посоветовать наиболее подходящие подложки, тонкие пленки и другие методы изготовления необходимых оптических полосовых фильтров.

Свяжитесь с нашими специалистами сегодня по телефону 01829771792 или свяжитесь с нами через Интернет.

Схема, типы, работа и ее применение

Во время обработки сигнала необходимо устройство, называемое полосовым фильтром или полосовым фильтром, чтобы обеспечить определенный диапазон требуемых частот и избежать нежелательных частотных диапазонов или компонентов. С помощью этой фильтрации шумовой сигнал может быть уменьшен за счет исключения частот, которые не требуются. Различные типы фильтров, такие как линейные и нелинейные, аналоговые, цифровые, активные и пассивные и т. д., доступны для использования в зависимости от требований. В этой статье обсуждается обзор полосового фильтра.

Полосовой фильтр определяется как устройство, которое пропускает частоты, находящиеся в требуемом частотном диапазоне, и подавляет оставшиеся частоты, которые не входят в этот конкретный диапазон. Что касается фильтра верхних частот, этот фильтр будет ослаблять сигналы с частотой ниже частоты среза, а фильтр нижних частот будет ослаблять сигналы с частотами выше частоты среза. Но если нам нужен только определенный диапазон частот и мы хотим исключить частоты, выходящие за пределы этого диапазона, другой фильтр может быть сформирован путем каскадирования фильтра верхних частот и фильтра нижних частот, который можно назвать полосовым фильтром.

В этом полосовом фильтре есть две частоты среза, одна из фильтра верхних частот и его верхняя частота среза. Это будет самый высокий частотный предел этого диапазона. Существует еще одна частота среза фильтра нижних частот и его вторая частота среза, известная как нижняя частота среза, которая определяет низкочастотный диапазон этой полосы.

Этот полосовой фильтр пропускает только определенный диапазон и ослабляет все оставшиеся сигналы выше или ниже этих частот среза.

Цепь полосового фильтра

Это принципиальная схема пассивного полосового фильтра RC.

Полосовой фильтр

Каскадирование или комбинация фильтра верхних частот и фильтра нижних частот образует полосовой фильтр, поскольку он пропускает определенную полосу частот и ослабляет сигналы выше и ниже частот среза. Этот полосовой фильтр позволит подавать входные сигналы без искажений и шумов. Ширина этой полосы частот называется пропускной способностью. Чтобы четко определить полосу пропускания, это конкретный диапазон частот, который находится между двумя точками отсечки, то есть высокой частотой отсечки и низкой частотой отсечки.

Bw= fH – fL

Разница между самой низкой частотой среза и самой высокой частотой среза называется полосой пропускания.

Чтобы быть идеальным полосовым фильтром, фильтр должен фильтровать или ослаблять определенные частоты, которые даже лежат в пределах полосы, чтобы устранить шум. Полосовые фильтры также известны как фильтры второго порядка из-за наличия двух конденсаторов, реактивных компонентов в одной цепи. Один конденсатор в цепи верхних частот и другой конденсатор в цепи нижних частот.

Перейдите по этой ссылке для получения информации о полосовых фильтрах MCQ

Различные типы полосовых фильтров

Эти полосовые фильтры в основном подразделяются на два типа фильтров.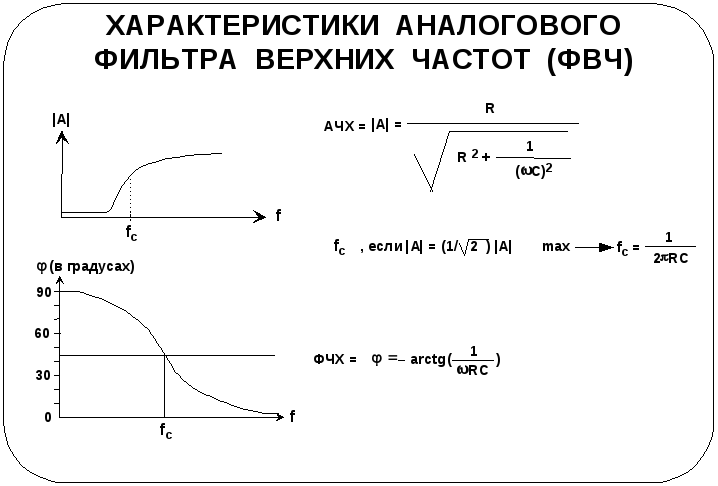 Это

• Широкополосный фильтр
• Узкополосный фильтр

Широкополосный фильтр

Принципиальная схема широкополосного фильтра показана ниже. В этой схеме широкополосного фильтра существует несколько практических схем. Как мы уже говорили, этот широкополосный фильтр может быть сформирован путем каскадирования двух секций, т. е. фильтра верхних и нижних частот.

Широкополосный фильтр

Для формирования полосового фильтра + или – 20 дБ/декада две секции секции верхних частот первого порядка и секции нижних частот первого порядка каскадируются таким же образом для формирования + или – 4odb /decade полосовой фильтр второго порядка секция верхних частот и секция нижних частот второго порядка соединены. Это означает, что порядок фильтров нижних и верхних частот будет определять порядок полосового фильтра.

Характеристики полосового фильтра

На изображении выше показаны характеристики полосового фильтра. Здесь на рисунке показан широкополосный фильтр, состоящий из фильтра верхних частот первого порядка и фильтра нижних частот первого порядка.

Узкополосный фильтр

На этой диаграмме показан узкополосный фильтр, использующий несколько обратных связей. В этом фильтре используется только один операционный усилитель. По сравнению с другими фильтрами, этот фильтр имеет несколько уникальных функций, которые очень полезны.

Узкий BPF

• Он называется фильтром с множественной обратной связью из-за наличия двух путей обратной связи.
• Существовавший здесь операционный усилитель используется в инвертирующем режиме
• На рисунке выше мы можем видеть частотную характеристику узкополосного фильтра. Проектирование узкополосного фильтра выполняется для конкретных значений fc или Q и BW.

For the calculation purpose

C1 = C2 = C

R1 =Q/2π fc CAf

R2= Q/2πfc C(2Q2-Af) &

R3= Q/πfc C

Здесь коэффициент усиления на центральной частоте определяется как Af

Af=R3/2R1

Fc может быть изменен на fc’ без изменения полосы пропускания или коэффициента усиления. Его можно получить, просто заменив R2 на R2′

R’2= R2[fc/f’c]2

Расчет калькулятора полосового фильтра

Это схема пассивного полосового фильтра, и расчеты полосы пропускания могут быть выполнены с помощью этой схемы.

Расчет BPF

Используя формулу, мы можем узнать необходимую частоту в этом пассивном полосовом фильтре.

Для высокой частоты среза = 1/2ΠR1C1

Для низкой частоты среза = 1/2ΠR2C2

Даже мы можем рассчитать требуемые частоты для различных полосовых фильтров, таких как активный инвертирующий операционный усилитель BPF и активный неактивный инвертирующий ОУ BPF

Применение полосового фильтра

Полосовой фильтр имеет широкий спектр применения

• Он используется в оптике, такой как LIDARS, LASER и т. д.
• Эти фильтры широко используются в беспроводных передатчиках и приемниках.
• В обработке аудиосигнала эти полосовые фильтры играют жизненно важную роль, пропуская определенные частоты и удаляя нежелательные.