Расчет базы биполярного транзистора: Расчет тока базы транзистора — RadioRadar

Расчет смещения (биполярные транзисторы)

Добавлено 23 октября 2017 в 00:45

Сохранить или поделиться

Хотя транзисторные коммутационные схемы работают без смещения, для аналоговых схем работать без смещения – это необычно. Одним из немногих примеров является радиоприемник на одном транзисторе в разделе «Радиочастотные схемы» главы 9 с усиливающим АМ (амплитудная модуляция) детектором. Обратите внимание на отсутствие резистора смещения базы в этой схеме. В этом разделе мы рассмотрим несколько базовых схем смещения, которые могут устанавливать выбранное значение тока эмиттера I_Э. Учитывая величину тока эмиттера I_Э, которую необходимо получить, какие потребуются номиналы резисторов смещения, R_Б, R_Э и т.д.

Схема смещения с фиксированным током базы

В простейшей схеме смещения применяется резистор смещения базы между базой и батареей базы V_смещ. Использовать существующий источник V_пит, вместо нового источника смещения, – очень удобно. Пример данной схемы смещения показан в каскаде аудиоусилителя в детекторном приемнике в разделе «Радиочастотные схемы» главы 9. Обратите внимание на резистор между базой и клеммой батареи. Подобная схема показана на рисунке ниже.

Напишите уравнение закона напряжений Кирхгофа для контура, включающего в себя батарею, R_Б и падение напряжения V_БЭ на переходе транзистора, на рисунке ниже. Обратите внимание, что мы используем обозначение V_смещ, хотя на самом деле это V_пит. Если коэффициент β велик, мы можем сделать приближение, что I_К = I_Э. Для кремниевых транзисторов V_БЭ ≅ 0.7 В.

Схема смещения с фиксированным током базы

\[V_{смещ} — I_Б R_Б — V_{БЭ} = 0\]

\[V_{смещ} — V_{БЭ} = I_Б R_Б\]

\[I_Б = { V_{смещ} — V_{БЭ} \over R_Б }\]

\[I_Э = (\beta + 1)I_Б \approx \beta I_Б\]

\[I_Э = { V_{смещ} — V_{БЭ} \over R_Б / \beta }\]

Коэффициент β малосигнальных транзисторов, как правило, лежит в диапазоне 100–300. Предположим у нас есть транзистор β=100, какое номинал резистора смещения базы потребуется, чтобы достичь тока эмиттера 1 мА?

Решение уравнения I_Э для определения R_Б и подстановка значений β, V_смещ, V_БЭ и I_Э дадут результат 930 кОм. Ближайший стандартный номинал равен 910 кОм.

\(\beta = 100 \qquad V_{смещ} = 10 В \qquad I_К \approx I_Э = 1 мА \)

\[R_Б = { V_{смещ} — V_{БЭ} \over I_Э / \beta } = { 10 — 0,7 \over 1 мА / 100 } = 930 кОм \]

Чему будет равен ток эмиттера при резисторе 910 кОм? Что случится с током эмиттера, если мы заменим транзистор на случайный с β=300?

\(\beta = 100 \qquad V_{смещ} = 10 В \qquad R_Б = 910 кОм \qquad V_{БЭ} = 0,7 В\)

\[I_Э = { V_{смещ} — V_{БЭ} \over R_Б / \beta } = { 10 — 0,7 \over 910 кОм / 100 } = 1,02 мА \]

\(\beta = 300 \)

\[I_Э = { 10 — 0,7 \over 910 кОм / 300 } = 3,07 мА \]

При использовании резистора стандартного номинала 910 кОм ток эмиттера изменится незначительно. Однако при изменении β со 100 до 300 ток эмиттера утроится. Это неприемлемо для усилителя мощности, если мы ожидаем, что напряжение на коллекторе будет изменяться от почти V_пит до почти земли. Тем не менее, для сигналов низкого уровня от микровольт до примерно вольта точка смещения может быть отцентрирована для β, равного квадратному корню из (100·300), что равно 173. Точка смещения будет по-прежнему дрейфовать в значительном диапазоне. Однако сигналы низкого уровня не будут обрезаны.

Схема смещения с фиксированным током базы по своей природе не походит для больших токов эмиттера, которые используются в усилителях мощности. Ток эмиттера в схеме смещения с фиксированным током базы не стабилен по температуре. Температурный уход – это результат большого тока эмиттера, который вызывает повышение температуры, которое вызывает увеличение тока эмиттера, что еще больше повысит температуру.

Схема автоматического смещения (с обратной связью с коллектором)

Изменения смещения из-за температуры и коэффициента бета могут быть уменьшены путем перемещения вывода резистора смещения с источника напряжения V_смещ на коллектор транзистора, как показано на рисунке ниже. Если ток эмиттера будет увеличиваться, увеличится падение напряжения на R_К, что уменьшит напряжение V_К, что уменьшит I_Б, подаваемый обратно на базу. Это в свою очередь уменьшит ток эмиттера, корректируя первоначальное увеличение.

Напишем уравнение закона напряжений Кирхгофа для контура, включающего в себя батарею, R_К, R_Б и падение напряжения V_БЭ. Заменим I_К≅I_Э и I_Б≅I_Э/β. Решение для I_Э дает формулу I_Э для схемы автоматического смещения при обратной связи с коллектором. Решение для R_Б дает формулу R_Б для схемы автоматического смещения при обратной связи с коллектором.

Схема автоматического смещения при обратной связи с коллектором

\[I_К = \beta I_Б \qquad I_К \approx I_Э \qquad I_Э \approx \beta I_Б \]

\[V_{пит} — I_К R_К — I_Б R_Б -V_{БЭ} = 0\]

\[V_{пит} — I_Э R_К — (I_Э/ \beta) R_Б -V_{БЭ} = 0\]

\[V_{пит} -V_{БЭ} = I_Э R_К + (I_Э/ \beta) R_Б\]

\[V_{пит} -V_{БЭ} = I_Э (( R_Б / \beta) + R_К)\]

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К }\]

\[R_Б = \beta \left[ {V_{пит} -V_{БЭ} \over I_Э } — R_К \right] \]

Найдем необходимый резистор смещения при обратной связи с коллектором для тока эмиттера 1 мА, резистора нагрузки коллектора 4,7 кОм и транзистора с β=100. Найдем напряжение коллектора V_К. Оно должно быть примерно посередине между V_пит и корпусом.

\(\beta = 100 \qquad V_{пит} = 10 В \qquad I_К \approx I_Э = 1 мА \qquad R_К = 4,7 кОм \)

\[R_Б = \beta \left[ {V_{пит} — V_{БЭ} \over I_Э } — R_К \right] = 100 \left[ {10 — 0,7 \over 1 мА } — 4,7 кОм \right] = 460 кОм \]

\[ V_К = V_{пит} — I_К R_К = 10 — (1 мА) (4,7 кОм) = 5,3 В \]

Ближайший стандартный номинал к резистору 460 кОм для автоматического смещения при обратной связи с коллектором равен 470 кОм. Найдем ток эмиттера I_Э для резистора 470 кОм. Пересчитаем ток эмиттера для транзисторов с β=100 и β=300.

\(\beta = 100 \qquad V_{пит} = 10 В \qquad R_К = 4,7 кОм \qquad R_Б = 470 кОм \)

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К } = {10 -0,7 \over 470 кОм / 100 + 4,7 кОм } = 0,989 мА \]

\(\beta = 300 \)

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К } = {10 -0,7 \over 470 кОм / 300 + 4,7 кОм } = 1,48 мА \]

Мы видим, что по мере того как коэффициент бета изменяется от 100 до 300, ток эмиттера увеличивается с 0,989 мА до 1,48 мА. Это лучше, чем в предыдущей схеме смещения с фиксированным током базы, где ток эмиттера увеличился с 1,02 мА до 3,07 мА. При изменении коэффициента бета смещение с обратной связью с коллектором в два раза стабильнее, чем смещение с фиксированным током базы.

Смещение эмиттера

Вставка резистора R_Э в схему эмиттера, как показано на рисунке ниже, вызывает уменьшение уровня сигнала на выходе, также известное как отрицательная обратная связь. Она препятствует изменениям тока эмиттера I_Э из-за изменений температуры, допустимых отклонений номиналов резисторов, изменений коэффициента бета или допустимых отклонений напряжения питания. Типовые допуски составляют: сопротивление резисторов – 5%, бета – 100-300, источник питания – 5%. Почему резистор эмиттера может стабилизировать изменение тока? Полярность падения напряжения на R_Э обусловлена V_пит на батарее коллектора. Полярность на выводе резистора, ближайшем к (-) клемме батареи, равна (-), а на выводе, ближайшем к клемме (+), равна (+). Обратите внимание, что (-) вывод R_Э подключен к базе через батарею V_смещ и R_Б. Любое увеличение тока через R_Э увеличит величину отрицательного напряжения, приложенного к цепи базы, уменьшая ток базы, что уменьшает ток эмиттера. Это уменьшение тока эмиттера частично компенсирует первоначальное увеличение.

Смещение эмиттера

\[V_{смещ} — I_Б R_Б — V_{БЭ} — I_Э R_Э = 0\]

\[I_Э = (\beta+1)I_Б \approx \beta I_Б\]

\[V_{смещ} — (I_Э / \beta) R_Б — V_{БЭ} — I_Э R_Э = 0\]

\[V_{смещ} — V_{БЭ} = I_Э ((R_Б / \beta) +R_Э)\]

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э }\]

\[R_Б / \beta +R_Э = {V_{смещ} — V_{БЭ} \over I_Э }\]

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right]\]

Обратите внимание, что на рисунке выше для смещения базы, вместо V_пит, используется батарея базы V_смещ. Позже мы покажем, что смещение эмиттера более эффективно с меньшей батареей смещения базы. Между тем, напишем уравнение закона напряжений Кирхгофа для контура цепи базы-эмиттера, обращая внимание на полярности компонентов. Подставим I_Б≅I_Э/β и решим уравнение для тока эмиттера I_Э. Это уравнение может быть решено для R_Б (смотрите выше).

Прежде чем применять формулы R_Б и I_Э (смотрите выше), нам нужно выбрать значения резисторов R_К и R_Э. R_К зависит от источника питания коллектора V_пит и тока коллектора, который мы хотим получить, и который, как мы предполагаем, приблизительно равен току эмиттера I_Э. Обычно точка смещения для V_К устанавливается равно половине V_пит. Хотя ее можно было бы установить и выше для компенсации падения напряжения на резисторе эмиттера R_Э. Ток коллектора – это то, что нам необходимо. Он варьируется от микроампер до ампер в зависимости от приложения и параметров транзистора. Мы выберем I_К = 1 мА, типовое значение для транзисторной схемы для малых сигналов. Мы вычисляем значение R_К и выбираем ближайшее стандартное значение. Как правило, хорошо подходит резистор эмиттера, который составляет 10-50% от резистора нагрузки коллектора.

\[V_К = V_{пит} / 2 = 10/2 = 5 В \]

\[R_К = V_К / I_К = 5/1 мА = 5 кОм \quad \text{(стандартный номинал 4,7 кОм)} \]

\[R_Э = 0,1 R_К = 0,1 (4,7 кОм) = 470 Ом \]

В нашем первом примере используем источник смещения с высоким напряжением V_смещ = V_пит = 10 В, чтобы показать, почему желательно более низкое напряжение. Определим стандартный номинал резистора. Рассчитаем ток эмиттера для β=100 и β=300. Сравним стабилизацию тока с предыдущими схемами смещения.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = V_{смещ} = 10 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {10 — 0,7 \over 0,001 } — 470 \right] = 883 кОм\]

Для рассчитанного сопротивления резистора R_Б 883 кОм ближайшим стандартным номиналом является 870 кОм. При β=100 ток эмиттера I_Э равен 1,01 мА.

\(\beta = 100 \qquad R_Б = 870 кОм \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {10 — 0,7 \over 870кОм / 100 + 470 } = 1,01 мА\]

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {10 — 0,7 \over 870кОм / 300 + 470 } = 2,76 мА\]

Токи эмиттера показаны в таблице ниже.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА

В приведенной выше таблице показано, что для V_смещ = 10 В смещение эмиттера не очень хорошо помогает стабилизировать ток эмиттера. Пример со смещением эмиттера лучше, чем предыдущий пример смещения базы, но не намного. Ключом к эффективности смещения эмиттера является снижение напряжения смещения базы V_смещ ближе к величине смещения эмиттера.

Какую величину смещения эмиттера мы сейчас имеем? Округляя, ток эмиттера, умноженный на сопротивление резистора эмиттера: I_ЭR_Э = (1 мА)(470) = 0,47 В. Кроме того, нам необходимо превысить V_БЭ = 0,7 В. Таким образом, на необходимо напряжение V_смещ > (0.47 + 0.7) В или > 1.17 В. Если ток эмиттера изменяется, это число изменится по сравнению с фиксированным напряжение смещения базы V_смещ, что приведет к коррекции тока базы I_Б и тока эмиттера I_Э. Нам подойдет V_Б > 1.17 В, равное 2 В.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 470 \right] = 83 кОм\]

Рассчитанный резистор базы 83 кОм намного меньше, чем предыдущий 883 кОм. Мы выбираем 82 кОм из списка стандартных номиналов. Токи эмиттера при R_Б = 82 кОм и коэффициентах β=100 и β=300 равны:

\(\beta = 100 \qquad R_Б = 82 кОм \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 82 кОм / 100 + 470 } = 1,01 мА\]

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 82 кОм / 300 + 470 } = 1,75 мА\]

Сравнение токов эмиттера для смещения эмиттера при V_смещ = 2 В и коэффициентах β=100 и β=300 с предыдущими примерами схем смещения показано в таблице ниже. И здесь мы видим значительное улучшение при 1,75 мА, хотя и не так хорошо, как 1,48 мА при обратной связи с коллектором.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В	1,01 мА	1,75 мА

Как мы можем улучшить эффективность смещения эмиттера? Либо увеличить резистор эмиттера R_Э или уменьшить напряжение источника смещения V_смещ, или и то, и другое. В качестве примера удвоим сопротивление резистора эмиттера до ближайшего стандартного значения 910 Ом.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 910 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 910 \right] = 39 кОм\]

Рассчитанное сопротивление R_Б = 39 кОм совпадает с одним из значений из стандартного списка номиналов. Пересчитывать I_Э для β = 100 нет необходимости. Для β=300 ток эмиттера равен:

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 39 кОм / 300 + 910 } = 1,25 мА\]

Эффективность схемы смещения эмиттера с резистором эмиттера 910 Ом намного лучше. Смотрите таблицу ниже.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 470 Ом	1,01 мА	1,75 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 910 Ом	1,00 мА	1,25 мА

В качестве упражнения изменим пример смещения эмиттера, вернув резистор эмиттера на 470 Ом, и уменьшив напряжение источника смещения до 1,5 В.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 1,5 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {1,5 — 0,7 \over 0,001 } — 470 \right] = 33 кОм\]

Рассчитанное сопротивление R_Б = 33 кОм совпадает с одним из значений из стандартного списка номиналов. Поэтому пересчитывать I_Э для β = 100 нет необходимости. Для β=300 ток эмиттера равен:

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {1,5 — 0,7 \over 33 кОм / 300 + 470 } = 1,38 мА\]

В таблице ниже приведено сравнение результатов 1 мА и 1,38 мА с предыдущими примерами.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 470 Ом	1,01 мА	1,75 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 910 Ом	1,00 мА	1,25 мА
Смещение эмиттера, Vсмещ = 1,5 В, RЭ = 470 Ом	1,00 мА	1,38 мА

Формулы для смещения эмиттера были повторены ниже с учетом внутреннего сопротивления эмиттера для лучшей точности. Внутреннее сопротивление эмиттера представляет собой сопротивление в цепи эмиттера внутри корпуса транзистора. Это внутреннее сопротивление r_Э оказывает большое влияние, когда (внешний) резистор эмиттера R_Э мал или даже равен нулю. Значение внутреннего сопротивления эмиттера является функцией тока эмиттера I_Э. Формула приведена ниже.

\[ r_Э = KT/I_Э m \]

где

• K=1.38×10^-23 Дж·К⁻¹ – постоянная Больцмана;
• T – температура в Кельвинах, берем ≅300;
• I_Э – ток эмиттера;
• m – для кремния изменяется от 1 до 2.

\[ r_Э = 0,026 В/I_Э = 26 мВ/I_Э \]

Ниже приведен вывод формул с учетом r_Э.

Схема смещения эмиттера с учетом внутреннего сопротивления r_Э

Более точные формулы смещения эмиттера могут быть получены при написании уравнения закона напряжений Кирхгофа для контура цепи базы-эмиттера. В качестве альтернативы, начнем с формулы I_Э, а затем перейдем в к формуле R_Б, заменив R_Э на r_Э + R_Э. Результаты показаны ниже.

\[V_{смещ} — I_Б R_Б — V_{БЭ} — I_Э r_Э — I_Э R_Э = 0\]

\[I_Э = (\beta+1)I_Б \approx \beta I_Б\]

\[V_{смещ} — (I_Э / \beta) R_Б — V_{БЭ} — I_Э r_Э — I_Э R_Э = 0\]

\[V_{смещ} — V_{БЭ} = I_Э (R_Б / \beta) + I_Э r_Э + I_Э R_Э\]

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta + r_Э +R_Э }\]

\[R_Б / \beta + r_Э +R_Э = {V_{смещ} — V_{БЭ} \over I_Э }\]

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — r_Э — R_Э \right]\]

\[r_Э = 26 мВ / I_Э \]

Повторим расчет R_Б из предыдущего примера, но уже с учетом r_Э, и сравним результаты.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 470 Ом \)

\( r_Э = 26 мВ / 1 мА = 26 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — r_Э — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 26 — 470 \right] = 80,4 кОм\]

Включение в расчеты r_Э приводит к более низкому значению сопротивления резистора базы R_Б, как показано в таблице ниже. Это значение находится ниже стандартного номинала 82 кОм, а не выше его.

Эффект от учета r_Э на расчет R_Б

rЭ?	Значение RБ
Без учета rЭ	83 кОс
С учетом rЭ	80,4 кОм

Конденсатор обхода R

_Э

Одна из проблем смещения эмиттера заключается в том, что значительная часть выходного сигнала падает на резисторе эмиттера R_Э (рисунок ниже). Это падение напряжения на резисторе эмиттера находится в последовательном соединении с базой и обладает полярностью, противоположной полярности входного сигнала. (Это похоже на схему с общим коллектором с коэффициентом усиления по напряжению < 1). Это уменьшение уровня сигнала сильно снижает коэффициент усиления по напряжению от базы до коллектора. Решение для усилителей сигналов переменного тока заключается в обходе резистора эмиттера с помощью конденсатора. Это восстанавливает усиление переменного напряжения, поскольку конденсатор для сигналов переменного тока представляет собой короткое замыкание. Постоянный ток эмиттера всё еще будет уменьшаться на резисторе эмиттера, таким образом, стабилизация постоянного тока сохранится.

Конденсатор обхода требуется для предотвращения уменьшения усиления сигнала переменного напряжения

Какая величина емкости должна быть у конденсатора обхода? Она зависит от самой низкой частоты усиливаемого сигнала. Для радиочастот C_обхода может быть небольшим. Для аудиоусилителя с нижней частотой 20 Гц этот конденсатор будет большим. «Эмпирическое правило» для конденсатора обхода состоит в том, что реактивное сопротивление должно составлять 1/10 или меньше от сопротивления резистора эмиттера. Конденсатор должен быть выбран таким образом, чтобы поддерживать самую низкую частоту усиливаемого сигнала. Конденсатор для аудиоусилителя 20 Гц – 20 кГц равен:

\[X_C = { 1 \over 2 \pi f C }\]

\[C = { 1 \over 2 \pi f X_C }\]

\[C = { 1 \over 2 \pi 20 (470/10) } = 169 мкФ\]

Обратите внимание, что внутреннее сопротивление эмиттера r_Э не обходится конденсатором обхода.

Смещение делителем напряжения

Устойчивое смещение эмиттера требует низковольтного источника смещения базы (рисунок ниже). Альтернативой источнику базы V_смещ является делитель напряжения, питаемый источником питания коллектора V_пит.

Смещение делителем напряжения заменяет источник напряжения базы на делитель напряжения

Технология проектирования заключается в том, чтобы сначала разработать схему смещения эмиттера, затем преобразовать ее в схему смещения базы с помощью делителя напряжения, используя теорему Тевенина. Этапы графически показаны на рисунке ниже. Нарисуем делитель напряжения, не присваивая номиналов резисторов. Отделите делитель от базы (база транзистора является его нагрузкой). Примените теорему Тевенина, чтобы получить эквивалентные одно сопротивление Тевенина R_Тев и один источник напряжения V_Тев.

Теорема Тевенина преобразует делитель напряжения в один источник напряжения V_Тев и одно сопротивление R_Тев

Эквивалентное сопротивление Тевенина – это сопротивление от точки нагрузки (стрелка) при уменьшении напряжения батареи (V_пит) до 0 (земля). Другими словами, R1 || R2. Эквивалентное напряжение Тевенина представляет собой напряжение разомкнутой цепи (снятая нагрузка). Этот расчет осуществляется методом коэффициента деления делителя напряжения. R1 получается путем исключения R2 из пары формул для R_Тев и V_Тев. Ниже приведена формула расчета R1, исходя из значений R_Тев, V_Тев и V_пит. Обратите внимание, что R_Тев представляет собой R_Б, резистор смещения из схемы смещения эмиттера. Также ниже приведена формула расчета R2, исходя из значений R1 и R_Тев.

\[R_{Тев} = R1 || R2\]

\[{ 1 \over R_{Тев} } = { 1 \over R1} + { 1 \over R2}\]

\[V_{Тев} = V_{пит} \left[ {R2 \over R1+R2} \right]\]

\[\text f = { V_{Тев} \over V_{пит} }= \left[ {R2 \over R1+R2} \right]\]

\[{ 1 \over R_{Тев} } = { R2 + R1 \over R1 \cdot R2 } = { 1 \over R1 } \left[ { R2 + R1 \over R2 } \right] = { 1 \over R1 } \cdot { 1 \over \text f }\]

\[R1 = { R_{Тев} \over \text f } = R_{Тев} { V_{пит} \over V_{Тев}}\]

\[{ 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1}\]

Преобразуем предыдущий пример смещение эмиттера в смещение с помощью делителя напряжения.

Пример смещения эмиттера, преобразованный в смещение с помощью делителя напряжения

Эти значения были ранее выбраны или расчитаны для примера смещения эмиттера.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 1,5 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {1,5 — 0,7 \over 0,001 } — 470 \right] = 33 кОм\]

Подстановка значений V_пит, V_смещ и R_Б даст в результате значения R1 и R2 для схемы смещения с делителем напряжения.

\[V_Б = V_{Тев} = 1,5 В \]

\[R_Б = R_{Тев} = 33 кОм \]

\[R1 = R_{Тев} { V_{пит} \over V_{Тев}} = 33 кОм { 10 \over 1,5} = 220 кОм \]

\[{ 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1} = { 1 \over 33 кОм} — { 1 \over 220 кОм} \]

\[R2 = 38,8 кОм \]

Значение R1 равно стандартному значению 220 кОм. Ближайшее стандартное значение для R2, равного 38,8 кОм, рано 39 кОм. Это не сильно изменить I_Э, чтобы его рассчитывать.

Задача: Рассчитаем резисторы смещения для каскодного усилителя на рисунке ниже. V_Б2 – это напряжение смещения каскада с общим эмиттером. V_Б1 – это довольно высокое напряжение 11,5 В, потому что мы хотим, чтобы каскад с общей базой удерживал напряжение на эмиттере на уровне 11,5 – 0,7 = 10,8 В, примерно 11 В. (Это будет 10 В после учета падения напряжения на R_Б1.) То есть, каскад с общей базой является нагрузкой, заменяющей резистор, коллектора каскада с общим эмиттером. На нужен ток эмиттера 1 мА.

Смещение для каскодного усилителя

\( V_{пит} = 20 В \qquad I_Э = 1 мА \qquad \beta = 100 \qquad V_A = 10 В \qquad R_{нагр} = 4,7 кОм \)

\( V_{смещ1} = 11,5 В \qquad V_{смещ2} = 1,5 В \)

\[ I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } \]

\[R_{Б1} = { V_{смещ} — V_{БЭ} \over I_Э / \beta } = { (V_{смещ1} — V_A) — V_{БЭ} \over I_Э / \beta } = { (11,5 — 10) — 0,7 \over 1 мА / 100 } = 80 кОм\]

\[R_{Б2} = { V_{смещ2} — V_{БЭ} \over I_Э / \beta } = { (1,5) — 0,7 \over 1 мА / 100 } = 80 кОм\]

Задача: Преобразуем резисторы смещения базы в каскодном усилителе в резисторы схемы смещения с делителем напряжения, питающимся от V_пит 20 В.

\[ R_{смещ1} = 80 кОм \]

\[ V_{смещ1} = 11,5 В \]

\[ V_{смещ} = V_{Тев} = 11,5 В \]

\[ R_Б = R_{Тев} = 80 кОм \]

\[ R1 = R_{Тев} { V_{пит} \over V_{Тев}} \]

\[ R1 = 80 кОм { 20 \over 11,5} = 139,1 кОм \]

\[ { 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1} \]

\[ { 1 \over R2 } = { 1 \over 80 кОм} — { 1 \over 139,1 кОм} \]

\( R2 = 210 кОм \)

\[ V_{пит} = V_{Тев} = 20 В \]

\[ R_{смещ2} = 80 кОм \]

\[ V_{смещ2} = 1,5 В \]

\[ V_{смещ} = V_{Тев} = 1,5 В \]

\[ R_Б = R_{Тев} = 80 кОм \]

\[ R3 = R_{Тев} { V_{пит} \over V_{Тев}} \]

\[ R3 = 80 кОм { 20 \over 1,5} = 1,067 МОм \]

\[ { 1 \over R4 } = { 1 \over R_{Тев}} — { 1 \over R3} \]

\[ { 1 \over R4 } = { 1 \over 80 кОм} — { 1 \over 1067 кОм} \]

\( R4 = 86,5 кОм \)

Окончательная схема показана в главе 9 «Практические аналоговые схемы» в разделе «Радиочастотные схемы» под названием «Каскодный усилитель класса A…».

Подведем итоги:

• Посмотрите на рисунок ниже.
• Выберите схему смещения.
• Выберите R_К и I_Э для вашего приложения. Значения R_К и I_Э обычно должны устанавливать напряжение коллектора V_К на 1/2 от V_пит.
• Рассчитайте резистор базы R_Б, чтобы получить необходимый ток эмиттера.
• Если необходимо, пересчитайте ток эмиттер I_Э для стандартных номиналов резисторов.
• Для схемы смещения с делителем напряжения выполните сначала расчет смещения эмиттера, а затем определите R1 и R2.
• Для усилителей переменного тока: конденсатор обхода, параллельный R_Э, улучшает усиление по переменному напряжению. Выберите X_C≤0,10R_Э для самой низкой частоты.

Формулы расчета смещения (вкратце)

Оригинал статьи:

Теги

Автоматического смещение с обратной связью с коллекторомБиполярный транзисторНапряжение смещенияОбучениеСмещение делителем напряженияСмещение с фиксированным током базыСмещение транзистораСмещение эмиттераЭлектроника

Сохранить или поделиться

Общий расчёт структуры биполярного транзистора — Студопедия

Практическая работа №2. Проектирование и расчёт биполярного транзистора.

План практической работы

1. Общий расчёт структура биполярного транзистора.

2. Выбор концентрации примеси в эпитаксиальном слое коллектора.

3. Расчёт профиля легирования.

4. Расчёт удельных поверхностных сопротивлений базового и эмиттерного слоёв.

5. Контрольные задания.

Общий расчёт структуры биполярного транзистора.

Для расчёта всей структуры биполярного транзистора, изображённой на рис. 2.1., необходимы следующие исходные данные для расчета: глубина коллекторного перехода и концентрация примеси на поверхности пассивной базы.

Рис. 2.1. Структура биполярного транзистора.

Расчет выполняют в такой последовательности:

1. По заданному максимально допустимому напряжению определяют пробивное напряжение , которое должно быть хотя бы на 20% больше , т.е. . Пробивное напряжение коллекторного p-n-перехода выбирают с коэффициентом запаса 2…3.

По графику зависимости (рис. 2.2.), где – концентрация примесей на высокоомной стороне p-n-перехода, находят . Удельное сопротивление коллекторного перехода при рассчитывают по формуле:

Подвижности при заданной концентрации примесей находят из рис. 2.3.

Рис. 2.2. График зависимости пробивного напряжения от концентрации носителей.

Рис. 2.3. Зависимости подвижности носителей от концентрации примесей в полупроводнике.

2. Определяют характеристическую длину в распределении примесей акцепторов и характеристическую длину в распределении доноров :

3. Для расчёта ширины объёмного заряда на коллекторном и эмиттерном переходах предварительно вычисляют потенциал:

контактную разность потенциалов на коллекторном переходе:

где – тепловой потенциал, равный 0,026 В при ; — концентрация собственных носителей заряда в кремнии ( ).

Контактная разность потенциалов на эмиттерном переходе определяется аналогично .

4. Рассчитывают ширину области объёмного заряда, распространяющуюся в сторону базы и в сторону коллектора при максимальном смещении коллекторного перехода :

5. Выбирают ширину технологической базы, которая должна быть больше ширины слоя объемного заряда на коллекторном переходе , так как последний будет иметь максимальную ширину при :

6. Ширину высокоомного коллектора под коллекторным переходом выбирают больше ширины слоя объемного заряда на коллекторном переходе, распространяющейся в сторону коллектора при максимальном обратном смещении: . Полная толщина коллекторного слоя

7. Определяют концентрацию акцепторов на эмиттерном переходе:

8. В результате высокой степени легирования эмиттера область объёмного заряда на эмиттерном переходе в основном будет сосредоточена в базе. Приближённо можно считать, что , где:

Ширина базы была определена без учета и может оказаться заниженной; в свою очередь, величина тоже может быть меньше действительной, а ширина объемного заряда – больше. Однако превышение незначительно и приведет только к тому, что технологическая ширина базы будет выбрана с некоторым запасом.

9. Корректируют технологическую базу:

10. Для определения размеров активной базы рассчитывают ширину области объемного заряда и при прямом смещении эмиттерного и обратном смещении коллекторного переходов.

11. Определяют активную ширину базы:

12. Находят размеры коллекторов, имеющего квадратную форму со стороной:

где – площадь коллектора, которую рассчитывают по известной емкости коллекторного перехода при заданном смещении , принимая емкость коллектора :

13. Площадь эмиттера можно определить исходя из допустимой плотности тока эмиттера , при которой коллекторный переход находится при нулевом смещении, когда транзистор еще не вошел в режим насыщения:

где

Минимальное напряжение на участке эмиттер-коллектор транзистора рассчитывают по максимальной мощности на p-n переходе и максимальному току коллектора :

Размеры остальных областей транзистора, а также его общая площадь могут быть определены исходя из известной площади эмиттера , минимальной ширины контактов, минимального расстояния между контактами и других конструктивно технологических ограничений, принятых для данной технологии изготовления полупроводниковой ИМС.

Для определённого типа микросхем применяют и другие конструкции интегральных транзисторных структур. В логических микросхемах широко используется многоэмиттерный транзистор (МЭТ), типовая структцра которого приведена на рис. 2.4.

Рис. 2.4. Многоэмиттерный транзистор.

МЭТ представляет собой совокупность нескольких n-p-n транзисторов. Такая структура имеет общую базу и коллектор. Число эмиттеров может быть равным 5..8. Активные базовые области, находящиеся под эмиттерными переходами, объединяются между собой с помощью пассивной области базы. Особенностью МЭТ является наличие паразитного транзистора эмиттер – база – эмиттер. Действие паразитного межэмиттерного транзистора существенно для структур, у которых расстояние между эмиттерами соизмеримо с расстоянием от эмиттера до коллектора. Для уменьшения паразитных токов через эмиттеры искусственно увеличивают сопротивление пассивной области базы.

Расчёт транзисторных каскадов по схемам с общей базой (ОБ) и общим коллектором (ОК)

Онлайн калькулятор номиналов элементов схем ОБ и ОК, построенных на
биполярных транзисторах.

Усилительные каскады, выполненные по схеме с общим эмиттером, мы рассмотрели на прошлой странице, осталось всего-то ничего: усилительный каскад с общей базой (ОБ) и каскад с общим коллектором (ОК) — он же эмиттерный повторитель, он же повторитель напряжения. .

1. Каскад на транзисторе с общей базой (ОБ).

Рис.1 Рис.2

На Рис.1 изображена схема ОЭ с предыдущей страницы.
Если верхний вывод блокирующей ёмкости Сэ оторвать от эмиттера и подключить к базе транзистора, а входной сигнал через разделительный конденсатор Ср1 подать на освободившийся эмиттер (Рис.2), то каскад ОЭ преобразуется в классическую

схему каскада с общей базой (ОБ).
Расчёт схемы с ОБ по постоянному току производится точно также, как мы это делали на предыдущей странице для каскада ОЭ:
1. I_б = (U_б — U_бэ)/[(R_э + r_э) x (1 + β)] , где Uбэ фиксируется подбором номиналов резисторов делителя Rб1 и Rб2 ,
2. I_делит = (3…10)I_б ;
3. I_к = I_б x β ;
4. U_к = E_к — I_к x R_к ;
5. R_вых = R_к ll (r_э + r_к ) ;
6. U_э = (0,1…0,2)E_к — для достижения приемлемого эффекта термостабилизации.

А вот по переменному току каскады имеют существенные различия. Схема каскада с общей базой (ОБ), изображённая на Рис.2, обладает следующими характеристиками по переменному току:

7. R_вх = r_э , где r_э (Ом) = 25,6/I_э (мА) — активное сопротивление эмиттера ;
8. K_i = β / (β +1) ;
9. K_u ≈ R_к x β / [r_э x (β +1)] ;

Итак, подытожим основные отличия данного каскада ОБ от каскадов ОЭ:
1. Усилительные каскады на транзисторе с общей базой не инвертируют сигнал;
2. Коэффициент передачи по току каскада c ОБ меньше единицы;
3. Входное сопротивление каскада ОБ значительно ниже входного сопротивления каскада ОЭ.

Крайне низкое входное сопротивление транзисторного каскада с общей базой Rвх (единицы — десятки Ом) уже не позволяет пренебрежительно относиться к выходному сопротивлению предыдущего каскада Rист. К тому же, если данный резистор выполнить внешним, появляется возможность гибкой регулировки усиления каскада.

Формула для коэффициента передачи схемы каскада ОБ с учётом выходного сопротивления источника сигнала (либо внешнего резистора), принимает следующий вид:

9. K_u ≈ R_к x β / [(r_э + R_и ) x (β +1)] ;

2. Каскад на транзисторе с общим коллектором (ОК) — эмиттерный повторитель.

Главным отличительным свойством каскада с ОК являются: высокое входное и низкое выходное сопротивления. Основная его область применения — согласование источника с высоким импедансом с низкоомной нагрузкой. Исходя из этого, было бы не очень правильно упускать из расчётов выходное сопротивление источника сигнала.
На Рис.3 изображена схема эмиттерного повторителя.

Рис.3

Приведём формулы: Rвх = [(Rэ + rэ) x (1 + β)] ll Rб1 ll Rб2 ; Iб = (Uб — Uбэ)/[(Rэ1 + rэ) x (1 + β)] , где Uб фиксируется подбором номиналов резисторов делителя Rб1 и Rб2, а Uбэ = 0,6…0,7В для кремниевого транзистора и 0,3…0,4 — для германиевого; Uэ = Uб — Uбэ ; Iделит = (3…10)Iб ; Rвых = rэ +Rист / (1 + β) ; Ku = Rэ / [ Rэ + rэ + Rист /(1 + β)] ; Ki = β +1 .

Итак, что мы имеем? Эмиттерный повторитель не инвертирует сигнал, коэффициент передачи по напряжению каскада меньше единицы, усиление происходит только по току.
Ну и по традиции калькулятор.

РАСЧЁТ КАСКАДОВ ОБ и ОК НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ.

Коэффициент передачи тока h31э не постоянен и имеет сложную зависимость от частоты и тока коллектора. В зависимости от типа транзистора максимум коэффициента передачи может наступать при токах коллектора: от 1-2 мА для маломощных транзисторов, до нескольких сотен миллиампер — для мощных.

Расчёт разделительных ёмкостей Сp1 и Сp2, а также блокирующей емкости Сб производится точно также, как в случае с каскадами ОЭ.
Т.е. следует задаться номиналами их реактивных сопротивлений Xс = 1/2πƒС (на минимальной рабочей частоте), как минимум, в 10 раз (а лучше в 100) меньшими, чем значения приведённых ниже величин:
X_Cp1вх , где Rвх — входное сопротивление каскада, посчитанное в калькуляторе,
X_Cp2вх посл , где Rвх посл — входное сопротивление последующего каскада,
X_Cбэ .

И ещё раз повторю калькулятор для расчёта характеристического сопротивления конденсатора.

 

Расчет биполярного транзистора КТ501А Введение

Расчёт состоит из следующих этапов:

1) расчёт примесного профиля структуры транзистора;

2) приближённый расчёт статического коэффициента передачи тока базы;

3) расчёт толщины эпитаксиального (высокоомного) слоя коллектора;

4) проверка ширины базы на граничную частоту и прокол;

5) расчёт топологии кристалла;

6) расчёт барьерных емкостей, сопротивлений слоёв и граничной частоты;

7) расчёт напряжения насыщения;

8) расчёт статического коэффициента передачи тока базы с учётом эффектов высокого уровня легирования и Кирка;

9) расчёт семейства выходных характеристик транзистора;

10) расчёт импульсных характеристик транзистора;

Проведём расчёт в среде MathCad кремниевого биполярного p-n-p транзистора КТ501А. Допустим, что он должен иметь следующие параметры [5]:

· Статический коэффициент передачи тока в схеме с общим эмиттером при U_кб = 1 В, I_э = 30 мА равен 40.

· Граничная частота коэффициента передачи тока в схеме с общим эмиттером f_гр = 5 МГц.

· Напряжение насыщения коллектор-эмиттер при I_к = 0,3 А, I_б = 0,06 А не более 0,4 В.

· Обратный ток коллектора при не более 1 мкА.

· Ёмкость коллекторного перехода при U_кб = 10 В не более 50 пФ.

· Ёмкость эмиттерного перехода при U_бэ = 0,5 В не более 100 пФ.

Транзистор должен иметь следующие предельные эксплуатационные данные.

· Постоянное напряжение коллектор-база U_кб = 15 В.

· Постоянное напряжение коллектор-эмиттер при R_бэ <10 кОм, U_кэ = 15 В.

· Постоянное напряжение база-эмиттер U_бэ = 10 В.

· Постоянный ток коллектора 0,3 А.

· Импульсный ток коллектора I_ик = 0,5 А.

· Постоянный ток базы 0,1 А.

· Постоянная рассеиваемая мощность коллектора — 0,35 Вт.

· Диапазон температур окружающей среды -60…+125 oС (213…398 К).

Введем константы:

— постоянная Больцмана;

— диэлектрическая постоянная вакуума;

— диэлектрическая проницаемость кремния;

— заряд электрона;

— собственная концентрация носителей в кремнии при 300 К;

— температура кристалла;

— тепловой потенциал;

— ширина запрещенной зоны при температуре Tn;

Введем значения параметров, которым должен соответствовать рассчитываемый транзистор в соответствии с заданием [5]:

— граничная частота;

— наибольшее обратное постоянное напряжение база-эмиттер;

— напряжение коллектор-база, при котором определяется граничная частота;

— максимальное напряжение на коллекторном переходе;

— ёмкость коллекторного перехода при = 5 В;

— постоянный ток коллектора;

— постоянный ток коллектора, при котором определяется граничная частота;

— постоянный ток коллектора, при котором определяется напряжение насыщения коллектор-эмиттер;

— постоянный ток базы, при котором определяется напряжение насыщения коллектора-эмиттер;

— постоянный ток коллектора, при котором определяется время включения транзистора;

— постоянный ток базы, при котором определяется время включения транзистора.

Порядок расчета цепей смещения биполярных транзисторов: Исходные данные для проведения расчетов

В предыдущих разделах мы представили и теоретически обосновали достаточно много способов схемотехнической реализации цепей смещения (т.е. способов задания и стабилизации исходной рабочей точки по постоянному току) в каскадах с биполярными транзисторами. Однако для практического использования при самостоятельной разработке электронных схем такой вид подачи информации явно неудобен. Более полезным оказывается иметь в своем распоряжении четкие правила, описывающие по шагам порядок действий разработчика (не менее важным представляется наличие окончательных формул или таблиц, из которых при подстановке известных справочных данных можно получить все необходимые значения для параметров и номиналов применяемых компонентов). Сразу отметим, что само по себе наличие указанных правил не обеспечивает гарантированный успех при практической разработке разнообразной аппаратуры. Разработчик по-прежнему должен очень четко понимать суть всех процессов, происходящих в цепях, и по мере надобности обращаться к теории. В приложении к рассматриваемой здесь задаче расчета цепей смещения это выражается в следующем. Умение правильно рассчитать номиналы элементов цепей смещения ни в коей мере не помогает в процессе выбора самого способа схемотехнической реализации этих цепей смещения. Т.е. мы приводим здесь только алгоритмы и формулы, позволяющие выбрать номиналы элементов в разнообразных схемах задания смещения, но обходим стороной вопрос — в каком случае применение той или иной схемы является оправданным (оптимальным). Заметим также, что в реальных усилительных устройствах цепи задания и стабилизации исходной рабочей точки по постоянному току могут в довольно причудливой форме переплетаться с цепями, оказывающими влияние только на переменные сигналы. Поэтому следует понимать, что все приводимые здесь схемы (даже и те, в которых указаны номиналы элементов) на практике обычно видоизменяются, дополняясь множеством компонентов, обеспечивающих их надлежащие характеристики в рабочем диапазоне частот. В следующем разделе мы вернемся к этому вопросу и приведем некоторые примеры реальных схем, тем не менее читатель должен иметь достаточно четкое представление о том, какое влияние на постоянные и переменные токи и напряжения оказывают различные электрические цепи. В этом случае проблем с применением описываемых в данном разделе схем смещения в реальных транзисторных усилителях возникать не должно.   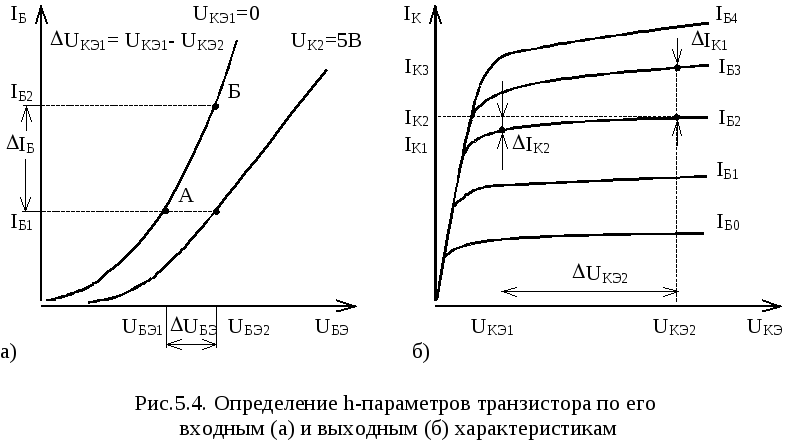Исходные данные для проведения расчетов В качестве исходных данных при расчете цепей смещения транзисторных каскадов в общем случае могут выступать различные наборы параметров. Мы не будем пытаться охватить абсолютно все случаи, а ограничимся только одним, имеющим наибольшее распространение на практике. Итак, в первую очередь разработчик должен однозначно определиться с типономиналом применяемого в схеме транзистора. Более того, в некоторых случаях необходимо определиться даже с конкретным экземпляром прибора, поскольку в рамках одной серии может существовать существенный разброс параметров, влияющих на номиналы элементов в цепях смещения. Параллельно выбирается режим работы транзистора по постоянному току (т.е. определяется положение исходной рабочей точки). Выше мы нарисовали очень красивые графики, в которых исходная рабочая точка выбиралась при графическом анализе статических характеристик транзистора. Однако на практике в большинстве случаев у нас нет всех этих характеристик, поскольку они не приводятся в стандартных справочных данных на транзистор. Конечно, мы могли бы снять их экспериментально, но обычно можно воспользоваться другим методом. В большинстве справочников при описании параметров транзисторов приводятся значения для постоянных составляющих тока коллектора \({I_К}_0\) (или тока эмиттера \({I_Э}_0\)) и напряжения коллектор—эмиттер \({U_{КЭ}}_0\), которые соответствуют оптимальному режиму работы транзистора по какому-либо из параметров, характеризующих его усилительные свойства (минимальный коэффициент шума, максимальный коэффициент усиления по мощности, максимальный коэффициент передачи тока эмиттера и т.п.). Иногда оптимальные значения \({I_К}_0\) и \({U_{КЭ}}_0\) могут быть найдены из графиков зависимостей, связывающих различные параметры транзистора, которые также часто имеются в справочниках. Разработчику обычно остается только определиться с тем, какие из усилительных характеристик транзистора он считает наиболее важными и соответствующим образом выбрать конкретные величины \({I_К}_0\) и \({U_{КЭ}}_0\). Безусловно, встречаются ситуации, когда необходимо учитывать очень большое количество факторов и процесс выбора исходной рабочей точки по постоянному току выглядит гораздо сложнее. С другой стороны, бывает и так, что рабочую точку выбирают, просто разделив пополам параметры предельно допустимого режима выбранного транзистора (это особенно популярно в низкочастотных усилителях при высоких уровнях сигналов). Так или иначе, мы будем предполагать, что конкретные величины \({I_К}_0\) и \({U_{КЭ}}_0\) нам известны. Помимо параметров коллекторной цепи для расчета некоторых схем смещения может понадобиться и знание постоянной составляющей напряжения на переходе база—эмиттер транзистора \({U_{БЭ}}_0\). Эта величина также берется из справочных данных или находится по входным характеристикам транзистора. Если же ее не удается определить по справочнику, то не будет большой ошибкой для маломощных транзисторов принимать \({U_{БЭ}}_0 = {0,6…1,1 В}\) — для кремниевых транзисторов и \({U_{БЭ}}_0 = {0,2…0,6 В}\) — для германиевых транзисторов. При разработке электронных устройств важным вопросом является обеспечение правильного питания. Тут возможны различные методики работы. По одной из них все параметры цепей питания определяются после расчета основных каскадов и подгоняются под них. Однако на практике обычно используется несколько иной способ. А именно, напряжение источника питания задается еще на начальном этапе (в большинстве случаев это не вызывает никаких проблем), а расчет остальных каскадов производится уже исходя из этой заданной величины. Остается только отследить соответствие мощности потребления схемы возможностям использованного источника питания. Мы будем придерживаться второй более практичной методики, т.е. \(U_П\) во всех случаях полагается известным. Одним из важнейших параметров транзистора является статический коэффициент передачи тока базы \(\beta_{СТ}\). Суть этого параметра мы уже объясняли достаточно подробно в разделе 2.5. Здесь же отметим, что большинство транзисторов может иметь довольно широкий разброс значений \(\beta_{СТ}\) внутри одной серии (партии). Т.е. для точного расчета цепей смещения может оказаться недостаточным наличие очень расплывчатых справочных данных (в справочниках обычно указывается диапазон возможных значений \(\beta_{СТ}\) для определенного транзистора в определенном режиме) — требуется экспериментальное измерение данного параметра для конкретного экземпляра транзистора, использование которого предполагается в схеме. Однако следует понимать, что необходимость таких измерений продиктована не только наличием в некоторых формулах величины \(\beta_{СТ}\), но и тем влиянием, которое эта величина оказывает на результат вычислений. Выяснить степень данного влияния на практике проще всего непосредственным вычислением, подставляя в формулу различные (вероятные для используемого транзистора) значения \(\beta_{СТ}\) и проверяя, насколько при этом меняется результат. Если изменение результата относительно невелико, то и в точном измерении \(\beta_{СТ}\) нет необходимости — можно обойтись справочными данными (в справочниках часто приводится т.н. типовое значение \(\beta_{СТ}\), если же его нет, то берут среднее значение приведенного диапазона). Еще раз обращаем внимание читателя на то, что речь здесь идет именно о статическом коэффициенте передачи \(\beta_{СТ}\) (в системе статических \(H\)-параметров он может обозначаться как \(h_{21Э}\)), а не о коэффициенте передачи тока базы в режиме малого сигнала (\(\beta\) или \(h_{21э}\)), значения которого также часто указываются в справочной документации на транзисторы. У большинства современных маломощных биполярных транзисторов величина \(\beta_{СТ}\) лежит в пределах 50…250, так что довольно часто при проведении расчетов не будет ошибкой принимать \(\beta_{СТ} \approx {100}\). Далее при рассмотрении конкретных схем мы столкнемся с необходимостью предварительного (до начала расчетов) задания и еще некоторых величин. Причем не всегда эти величины могут быть выражены в цифрах. Например, нам может понадобиться знание глубины обратной связи по току или напряжению, реализовать которую мы намереваемся в каскаде. Напомним, что обратная связь позволяет улучшить стабильность исходной рабочей точки по постоянному току при воздействии внешних дестабилизирующих факторов. Учитывая, что реальный транзистор — прибор в значительной степени нелинейный, а также помня о влиянии цепей обратной связи по постоянному току на сигналы и параметры каскада в рабочей полосе частот, мы не можем в рамках данной главы описать критерии, по которым разработчик должен выбирать точную величину глубины внутрикаскадных ООС в различных ситуациях. Вообще говоря, и во всей данной книге недостаточно информации для полного решения этого вопроса (не хватает подробного описания нелинейных свойств транзисторов). Поэтому в дальнейшем при проведении расчетов мы будем полагать, что требуемая глубина ООС заранее известна, а в то, откуда она взялась, вникать не будем. Большой выбор схем при реализации цепей смещения обусловлен наличием множества внешних факторов, которые в различных устройствах могут учитываться по-разному и иметь значительный разброс по степени важности их учета разработчиком. Одним из основных таких показателей является температурная стабильность каскада. Для оценки этого параметра применяется т.н. коэффициент нестабильности тока коллектора \({S_I}_К\), который определяется как отношение допустимого изменения коллекторного тока транзистора \(\Delta {I_К}_0\) к вызвавшему его изменению обратного тока коллекторного перехода \(\Delta I_{КБ обр}\): \({S_I}_К = \cfrac{\Delta {I_К}_0}{\Delta I_{КБ обр}}\). Здесь следует заметить, что обратный ток коллектора — один из наиболее температурно-зависимых параметров транзистора. Именно его колебания во многом определяют температурные изменения статических характеристик транзистора, показанные на рис. 3.16. Таким образом, коэффициент нестабильности отражает степень смещения исходной рабочей точки по постоянному току (вернее, только одного из показателей, задающих эту рабочую точку, — тока коллектора) при колебаниях температуры. Чем более устойчива схема к колебаниям температуры, тем ближе к единице оказывается коэффициент нестабильности \({S_I}_К\). Иногда при проектировании схемы обеспечение надлежащей температурной стабильности является одним из основных требований. Это может выражаться в задании некоторого числового значения коэффициента нестабильности, которому должна удовлетворять схема (т.е. \({S_I}_К\) становится одним из исходных параметров расчетов). Не всегда удается достичь заданного показателя только лишь правильным выбором номиналов элементов (тем не менее там, где это возможно, пригодятся приводимые далее формулы) — может оказаться, что выбранная схема цепей смещения не обеспечивает нужного уровня температурной стабилизации рабочей точки или при вычисленных номиналах элементов значительно (выше разумного предела) деградируют другие важные показатели каскада (потребляемый ток, входное сопротивление и т.п.). В таком случае разработчику необходимо изменять схемотехнику цепей смещения, переходя к использованию более стабильных решений. Мы везде будем приводить формулы, позволяющие вычислить коэффициент нестабильности \({S_I}_К\) рассматриваемой схемы при известных номиналах некоторых ее элементов. Перед тем как перейти наконец к описанию конкретных схем и методик расчета, отметим еще один момент, касающийся воплощения полученных результатов на практике. Естественно, что числовые значения номиналов резисторов, рассчитываемые по приводимым далее формулам, оказываются дробными. На практике мы вынуждены использовать сопротивления с номиналами, близкими к расчетным. Также и сама теоретическая модель, из которой выводятся формулы, не всегда достаточно точно отражает реальные физические процессы в транзисторе. Все это приводит к тому, что при практическом исполнении вроде бы корректно рассчитанной схемы реальные токи и напряжения в цепях могут значительно отклониться от тех значений, которые мы хотели бы там видеть. В этом случае требуется экспериментальный подбор номиналов некоторых элементов схемы. Далее на принципиальных схемах мы будем указывать резисторы (звездочкой у обозначения резистора), подбором которых осуществляется точная установка выбранной исходной рабочей точки по постоянному току. В реальных устройствах иногда оказывается удобным вместо подбора резистора установить на его место подстроечный резистор и осуществлять регулировку без перепайки. Пунктирная линия на наших схемах будет указывать на параметр (в данном случае это везде ток коллектора \({I_К}_0\)), который устанавливается регулировкой данного резистора.     < Предыдущая   Следующая >

Расчет статического режима работы биполярного транзистора по постоянному току (расчет рабочей точки)

Анализ технического задания.

В современной радиоэлектронной аппаратуре используются усилители. Усилитель осуществляет увеличение энергии управляющего сигнала за

счет энергии вспомогательного источника. Входной сигнал является как бы шаблоном, в соответствии с которым регулируется поступление энергии от источника к потребителю усиленного сигнала. Усилители делятся [1]:

1) По способности усиливать постоянные и переменные сигналы :

· Усилители постоянного тока

· Усилители переменного тока

2) По виду сигналов, для которых предназначен усилитель:

· Усилители гармонических сигналов

· Усилители импульсных сигналов

3) По диапазону частот, на которые рассчитан усилитель:

· Усилители низкой частоты (предназначены для усиления частот звукового диапазона 0,01…20кГц)

· Усилители высокой частоты (предназначены для усиления сигналов в радиочастотном диапазоне)

4) По усиливаемому электрическому показателю:

· Усилители напряжения

· Усилители тока

· Усилители мощности

Существует понятие коэффициента передачи усилителя – это функция, определяемая как отношение выходного сигнала усилителя к его входному сигналу.

В современных транзисторах используется коэффициент α=0,9÷0,999 Данная величина всегда меньше единицы, но близка к ней.[2]

Параметры рассчитываемого усилителя близки к параметрами, предложенным в задании к курсовой работе. Исходя из этого, можно сделать вывод, что используя современную элементную базу, можно реализовать данную курсовую работу.

Выбор транзистора и элементной базы.

Для расчета усилителя я выбираю транзистор КТ201А. Это отечественный маломощный биполярный транзистор n-p-n структуры. Он предназначен для применения в усилителях низкой частоты. Выпускается в металлостеклянном корпусе с гибкими выводами.

Общеизвестно, что техника может работать в предельном режиме, но надежность и срок службы оборудования уменьшается. Поэтому необходимо выбрать транзистор исходя из условия, что . Это означает, что необходимо выбрать транзистор с максимальным напряжением не менее 20 В. В задании указана верхняя граничная частота не менее 210 кГц. Для того чтобы упростить расчет АЧХ необходимо выбрать транзистор с граничной частотой превышающей это значение. Это позволит считать транзистор частотно-независимым. Таким образом, верхняя граничная частота транзистора должна быть не менее 1МГц. В задании указан температурный диапазон (-20-+80⁰С), который должен выдерживать выбранный транзистор.

На основе вышеизложенного для реализации технического задания подойдет транзистор КТ201А. Параметры транзистора приведены ниже:

******

Расчет статического режима работы биполярного транзистора по постоянному току (расчет рабочей точки).

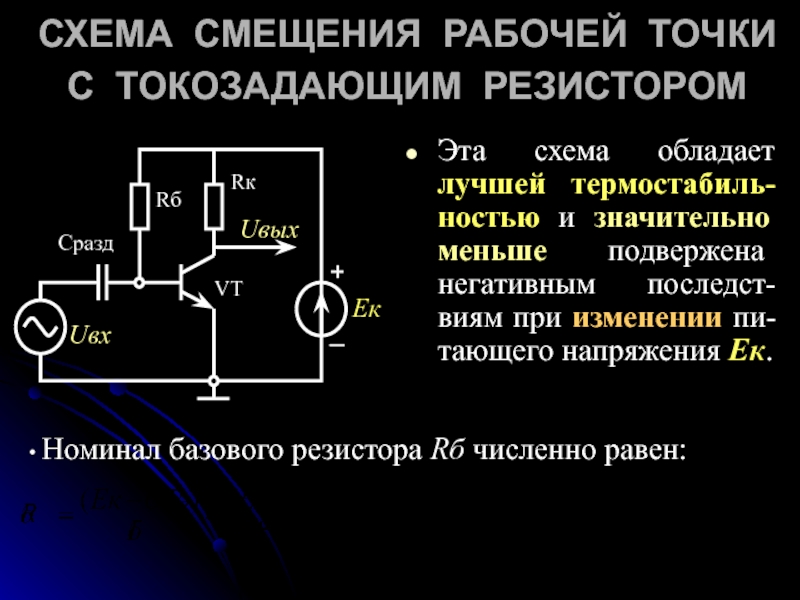
Для обеспечения надежной работы при широком разбросе параметров транзистора и изменения условий окружающей среды рассчитаем рабочую точку с помощью H смещения.

Зададим . Ток коллектора рассчитывается по формуле: ,

при условии выбора рабочей точки в середине нагрузочной прямой. Выражаем из этой формулы : . Округляем резистор до значения соответствующего ряду ***. Выбираем .

Теперь рассчитаем исходя из формулы для коэффициента усиления каскада: . Отсюда . Округляем резистор до значения соответствующего ряду ***. Выбираем .

Рассчитаем ток базы: ,

где — коэффициент усиления ока базы в схеме с ОЭ.

Для задания рабочей точки транзистора необходимо зафиксировать напряжение на базе с помощью делителя напряжения. Ток через резисторы и делителя напряжения должен быть много больше тока базы для обеспечения режима источника ЭДС. Возьмем ток делителя в 10 раз больше тока базы, т. е. . Тогда .

Рассчитаем напряжение на базе транзистора по формуле: .

Рассчитаем сопротивление резисторов и делителя напряжения по формулам:

.

Округляем резистор до значения соответствующего ряду ***. Выбираем .

Округляем резистор до значения соответствующего ряду ***. Выбираем

Заменим делитель напряжения и источником напряжения и внутренним сопротивлением .

Рассчитаем по формуле

.

А теперь рассчитаем коэффициент нестабильности схемы с Н смещением:

Список используемой литературы.

[1]- А. А. Ровдо «Схемотехника усилительных каскадов на биполярных транзисторах» 188 с.

[2]- http://fn.bmstu.ru/electro

Стационарные режимы усиления биполярных транзисторов Текст научной статьи по специальности «Физика»

УДК 621.38

DOI: 10.17586/0021-3454-2015-58-5-372-379

СТАЦИОНАРНЫЕ РЕЖИМЫ УСИЛЕНИЯ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ

Б. И. Григорьев

Университет ИТМО, 197101, Санкт-Петербург, Россия E-mail: a.a.rassadina@gmail. com

Рассматривается решение краевой задачи, корректно отражающей стационарные режимы усиления р—п—р- и п—р—п-биполярных транзисторов в широких диапазонах изменения плотности коллекторного тока. Получены выражения коэффициентов усиления по току, а также коэффициентов инжекции, переноса и передачи неосновных носителей заряда при высоких уровнях инжекции в базовых областях биполярного транзистора. Рассмотрены основные физические механизмы, определяющие как рост, так и уменьшение коэффициента усиления при увеличении тока коллектора от минимально возможных значений до максимально допустимых. Приведен сравнительный анализ теоретических и экспериментальных результатов.

Ключевые слова: биполярные транзисторы, ток коллектора, напряжение коллектор—эмиттер, коэффициент усиления по току, коэффициент инжекции, время жизни носителей в базе, эмиттер, база, комбинированные полупроводниковые приборы.

Введение. Основное назначение биполярного транзистора (БТ) как усилителя электрического тока реализуется при его включении по схеме с общим эмиттером и характеризуется коэффициентом усиления по току

Р = (/к /!б) = а/(1 -а),

где /к и ¡б — токи коллектора и базы, а = yh и h — коэффициенты передачи и переноса неосновных носителей заряда в базе, у — коэффициент инжекции эмиттерного р—п-перехода БТ.

В общем случае зависимость коэффициента Р от тока /к для всех германиевых и кремниевых транзисторов имеет вид, представленный на рис. 1, что обусловлено влиянием на значение Р ряда физических процессов, протекающих в областях полупроводниковой структуры и на поверхности эмиттера БТ.

Физические механизмы, предположительно определяющие зависимость Р (1к), в достаточно полном объеме представлены и проанализированы в работах [1, 2]. К этим механизмам относятся поверхностная рекомбинация, рекомбинация Шокли — Рида — Холла (ШРХ) и

Оже-рекомбинация, сужение ширины запрещенной зоны в эмиттере, оттеснение тока к краю эмиттера, расширение базы (эффект Кирка) и сужение базы (эффект Эрли).

В настоящее время не существует единого мнения относительно значимости влияния на значение Р каждого из перечисленных механизмов [2]. Действительно, поверхностная рекомбинация оказывает существенное влияние на Р только при низких уровнях инжекции в области токов, существенно меньших /к0, и только в БТ с малыми размерами кристалла полупроводника [3]; влияние Оже-рекомбинации, когда она накладывается на эффект сужения запрещенной зоны, наблюдается только в приборах с мелкими эмиттерами с глубиной залегания 1 мкм и менее. Следовательно, эти механизмы рекомбинации необходимо учитывать при разработке и изготовлении низковольтных БТ микроэлектроники [4]. Оттеснение тока к краю эмиттера может приводить к снижению значения Р с увеличением тока коллектора /к, но лишь при очень больших его значениях, находящихся за пределами максимально допустимых. Среди всех эффектов, рассмотренных в работах [1, 2], только в процессе рекомбинации ШРХ время жизни неосновных носителей заряда (ННЗ) в базе БТ увеличивается с ростом /к, определяя возрастание коэффициента И и, следовательно, коэффициента Р в области токов коллектора /к < /к0. При /к > /к0 доминирующим механизмом снижения Р является уменьшение коэффициента у.

Зависимость Р ( /к ) во всем диапазоне изменения тока коллектора, в основу модели которой положена поверхностная рекомбинация, впервые была исследована Вебстером [5]. Основной параметр этой модели — скорость поверхностной рекомбинации — для кремниевых БТ составляет 200 — 2000 см/с [4], трудно поддается экспериментальному определению и существенно ограничивает применимость модели даже к БТ с низкими напряжениями коллектор—база. В последующих публикациях исследовалась только часть зависимости Р ( /к ) в области токов /к > /к0 . Так, в работе [6] эта зависимость объясняется в предположении, что при увеличении /к снижается коэффициент переноса из-за уменьшения времени жизни ННЗ в

базе БТ при высоких уровнях инжекции. Это предположение противоречит рекомбинацион-ной теории ШРХ, согласно которой время жизни может только возрастать, достигая своего максимального значения. Теория рекомбинации ШРХ экспериментально подтверждена в ряде публикаций, в том числе, и в работе [7]. Уменьшение коэффициента Р с ростом тока можно проанализировать, используя модель контролируемого заряда Гуммеля — Пуна [8], учитывающую снижение коэффициента инжекции у при больших токах. В этой области токов модель обладает высокой точностью, но для ее описания требуется достоверная информация о 25 электрофизических параметрах БТ [1]. Модель, основанная на так называемом эффекте Кирка [1, 2], базируется на предположении, что время жизни ННЗ и коэффициенты диффузии в металлургической базе и приколлекторной области одинаковы; в общем случае это не так, и при более точном анализе следует учитывать их различие.

Резюмируя вышеизложенное, с высокой степенью вероятности можно утверждать, что доминирующим механизмом, определяющим зависимость Р (/к) при /к < /к0 , является рекомбинация ШРХ, а при /к > /к0 — уменьшение коэффициента инжекции эмиттерного

р—п-перехода БТ. Эти механизмы положены в основу представленной в настоящей статье физико-математической модели зависимости коэффициента усиления по току биполярного транзистора от тока коллектора, где, кроме того, учтен эффект Эрли — зависимость Р от напряжения коллектор—база. Предложенная модель пригодна для расчета устройств на основе как дискретных БТ, так и комбинированных полупроводниковых приборов, например составных транзисторов.

Постановка задачи и ее анализ. Рассмотрим стационарный режим усиления БТ со структурой п+—р—п—П-типа в схеме с общим эмиттером (рис. 2), концентрация легирующей примеси в базе которого на 2-3 порядка ниже, чем в эмиттере, и настолько же выше, чем в п-коллекторе. При анализе будем полагать, что в базе БТ реализуется высокий уровень ин-жекции, а в эмиттере — низкий. Кроме того, будем считать значение приложенного к БТ напряжения коллектор—эмиттер достаточным для того, чтобы коллекторный переход БТ оставался смещенным в обратном направлении.

+ П р П + П

1и

-юэ

0

Юб

Рис.бТб / (Ъ +1)] 2, Аб и Тб — концентрация, плотность тока, диффузионная длина, коэффициент диффузии и время жизни электронов в базе; Ъ — 2,7 — отношение

подвижностей электронов и дырок; рэ (х), 7рэ (х), Ьэ — (Аэтэ )1/2 , А, и тэ — те же параметры.

но дырок в эмиттере; q — заряд электрона, у — уэ —

плотность тока в коллекторе.

Граничные условия определяются выражениями

Пб (Юб )- 0,

плотность тока в эмиттере, 7 — ук

-П1

(Юб )—«

7к

(3)

V — (4)

-х 2qDб

Рэ (-Юэ )- 0, (5)

Рэ (0) Мэ — Пб2(0). (6)

Условия (3) и (4) отражают тот факт, что в рассматриваемой задаче коллекторный переход БТ смещен в обратном направлении и протекающий через него ток чисто электронный. Условие (5) справедливо в предположении бесконечной на границе х — -юэ скорости рекомбинации, а условие (6) — при равенстве произведений концентраций электронов и дырок по обе стороны от эмиттерного перехода, где Мэ — концентрация легирующей примеси в эмиттере. Краевая задача (1)—(6) сформулирована в одномерном приближении, оправданном тем, что в современных БТ, имеющих гребенчатую конфигурацию эмиттера и работающих при плотности коллекторного тока, не превышающей нескольких десятков ампер на сантиметр в квадрате, неодномерный эффект (оттеснение тока к краю эмиттера) выражен слабо. Из выражений (1) и (3)—(5) следует, что

Пб (х)-тАк 8Ь ((б — Хб ) и Рэ (х)-

(

7 к Ьб

2qDб

■иШа

8Ь(Жэ + Xэ )

(7)

I.0б) 1, Кэ = Д, (эNШЖ,) 1, — площадь коллектора, равная эффективной площади эмиттера.

Коэффициент инжекции эмиттерного п+—р-перехода, коэффициенты переноса и передачи электронов в базе, составляющие коэффициент усиления по току БТ, определяются как

]пб (0) = еЬЖб + /к В /(Ъ +1)

У =

Лб (°) + jp3 (0)

chW6 + IK B

(10)

h = jn6 (®б) / jn6 (0) = [ch W + IKB / (b +1)]

\-i

-1

(11)

а = уИ = (Жб +/к В). (12)

Для подавляющего большинства существующих БТ справедливо приближение тонкой базы [1, 2]. Полагая в выражении (9) Жб <<1, преобразуем его к виду

(

Р =

b +1 © 2b Тб

Л

-1

+ Iк B

(13)

У

где B = (b +1) ©бKэ / 2bqD6SK, ©б = raj2 / 2D6 — время пролета электронов в базе.

Согласно рекомбинации ШРХ параметр Тб в области токов 0 < IK < IKo возрастает с увеличением !к от практически нулевого значения до близкого к максимальному Тб max в соответствии с эмпирическим выражением [9]

Тб = сТб max /(1 + c), (14)

где c = Пб (0)/ Мб — параметр, характеризующий уровень инжекции в базе БТ, Мб — концентрация легирующей примеси в базе.

2b Тб max У

выразить из уравнения (16) коэффициент B и преобразовать выражение (15) в следующее:

(16)

Р =

b +1 ©б

2b т

б max

I н + I к

V Ас

I н I к

к0 У

-1

Рассмотрим, далее, эффект влияния на значение Р напряжения коллектор—эмиттер икэ (эффект Эрли), для чего заменим в выражении (17) параметр шб на эффективную толщину базы:

ш

бэф — шб(1_d6 /шбХ

(18)

1/2

где йб = (2в80икэ / дЫб ) — толщина области пространственного заряда в базе БТ, в = 12 —

диэлектрическая проницаемость кремния, во = 8,9-10-14 Ф/см — электрическая постоянная [10].н1к

Л

L

I

к0 У

(19)

Строго говоря, напряжение икэ влияет не только на время пролета электронов в базе, но и на значение параметра /н. Однако, как показали расчеты, зависимость /н от икэ практически не сказывается на значении Р .

Установим связь параметра /н с постоянной нарастания тока коллектора, которую легко определить экспериментальным путем. Из решения нестационарного уравнения непрерывности для электронов в базе, выполненного в приближении квазистационарного эмиттера, следует, что при любом уровне инжекции постоянная нарастания

( 1 .. Л-1

тн — тб

1 _ Y 1 + 2-!- тб

©б б

(20)

Раскроем уравнение (20) с помощью (10) и (14), приняв в полученном выражении постоянной нарастания сЬ^б + /к В = 1, после чего уравнение (20) преобразуем к следующему:

тн -т

( 2b т V1

1н + 1к + —^^ Bll

б max ^к 1н + ^к + 7—7 В1к • (21)

I b+1 ©б У

Согласно выражению (16) и уравнению (21), справедливому при 1к = 1ко, искомая связь параметра 1н c постоянной нарастания тока коллектора определяется как

/н — 0,5 (Тб max/ Тн _1) ^ (22)

Из уравнения (21) следует, что постоянная тн зависит от 1к, поэтому ее экспериментальное определение необходимо проводить при токах 1к, близких к значению 1ко .

Таким образом, решением поставленной задачи, определяющей зависимость коэффициента усиления по току БТ от тока коллектора, является уравнение (19), параметр 1н в котором рассчитывается по выражению (22). Очевидно, что уравнение (19) определяет зависимость Р (1к ) и для БТ со структуройp+—n—p- типа.

В уравнении (19) все электрофизические и геометрические параметры, определяющие Р, являются известными технологическими параметрами БТ, а ток 1ко — параметром, известным из справочных данных, который, кроме того, можно рассчитать по выражению (22). Вместе с тем количественная информация об этих параметрах, кроме 1ко, в справочниках по БТ не приводится. Поэтому возможности использования зависимости Р (1к) в виде уравнения (19), полезной для разработчиков БТ, ограничены при ее применении разработчиками аппаратуры на основе дискретных БТ и, особенно, устройств на базе комбинированных полупро-

водниковых приборов, например составных транзисторов. [11], который легко определить экспериментальным путем.

Приняв в выражении (17) Р = Р0 и 1к = 1ко, выделим составляющую

п-1

Ъ +1 0

б

2Ъ 1,

б тах

(

Ро

2 +1

1к0

Л

У.

после чего преобразуем уравнение (17) к следующему:

Р = Рс

V 1кО

• + 1

А, + 1 к + 1н1к

N-1

I к

I

(23)

кО У

1к = 1ко и йб = 0, выделим из него со-

где Ро — значение Р , соответствующее заданному значению напряжения и. Г

&е

1н + 1к + 1н 1к

1к

I,

кО У

(24)

где Р1рр — значение Р, соотвествующее напряжению коллектор—база икб = 0, т.е. значению напряжения икэ = ибэ.

Выражение (23) позволяет рассчитать зависимость Р (1к) в широких диапазонах изменения тока коллектора п—р—п- и р—п—р-БТ и содержит минимальное число параметров полупроводниковой структуры БТ, каждый из которых может быть определен экспериментально, что выгодно отличает данное выражение от модельных представлений, развитых в более ранних публикациях. Из уравнений (23) и (24) следует, что

С

Р = Р1

гр

1 —

Л

-2

&е

(25)

Эксперимент. = 29, ш8 = 13 мкм, измерены с использованием методов, изложенных в работах [7, 11, 12], параметр 1к0 = 1 А определен непосредственно по графику экспериментальной кривой, а среднее значение концентрации легирующей примеси в базе Мб = 1016 см-3 задано как наиболее вероятное [2] для транзисторов КТ808. Для того чтобы исключить возможное влияние слаболегированного п-коллектора и температуры на значение Р , измерения проведены импульсным методом при икэ = 15 В. Отметим, что значение параметра 1к0 изначально является заданным, так как практически для каждого из типов и видов БТ приведено в справочниках. Анализ рис. 3 показывает, что расчетная и экспериментальная зависимости Р (1к) удовлетворительно согласуются во всем

рабочем диапазоне изменения тока коллектора не только качественно, но и количественно с

Указанная погрешность обусловлена, главным образом, погрешностями измерения и определения электрофизических параметров БТ, входящих в выражение (24).

Влияние эффекта Эрли на коэффициент усиления по току проиллюстрировано на рис. 4, где приведены зависимости Р (икэ ), рассчитанные по выражениям (24) и (25).

Представленные зависимости удовлетворительно согласуются с результатами эксперимента, а относительное увеличение ß с ростом UK3 практически в точности совпадает со справочными данными на транзистор КТ808 [13], по крайней мере, в диапазоне изменения напряжения коллектор—эмиттер от 1 до 15 В.

Заключение. В результате исследований, представленных в настоящей статье, предложена достаточно простая и достоверная модель зависимости коэффициента усиления по току биполярного транзистора от тока коллектора во всем рабочем диапазоне его изменения. Модель базируется на теории рекомбинации Шокли — Рида —Холла и эффекте снижения инжекционной способности эмиттера транзистора с ростом тока, учитывает эффект сужения базы при увеличении напряжения коллектор—эмиттер, применима к n—p—n- и p—n—р-транзисторам и может быть использована разработчиками аппаратуры на основе не только дискретных, но и комбинированных полупроводниковых приборов, например составных транзисторов. Помимо электрических, модель содержит минимальное число электрофизических параметров транзистора, каждый из которых можно определить экспериментальным путем. Все это выгодно отличает ее от результатов, полученных ранее ведущими в области полупроводникового приборостроения зарубежными специалистами.

СПИСОК ЛИТЕРАТУРЫ

1. Зи С. Физика полупроводниковых приборов. М.: Мир, 1984. Т. 1.

2. Блихер А. Физика силовых биполярных и полевых транзисторов. Л.: Энергоатомиздат, 1986.

3. Пасынков В. В., Чиркин Л. К., Шинков А. Д. Полупроводниковые приборы. М.: Высш. школа, 1981.

4. Крутякова М. Г., Чарыков Н. А., Юдин В. В. Полупроводниковые приборы и основы их проектирования. М.: Радио и связь, 1983.

5. Webster W. M. On the variation of junction transistors current amplification factor with emitter current // Proc. IRE. 1954. Vol. 42. P. 914—922.

6. ClarkL. E. High current-density beta dimination // IEEE Trans. Electron Devices. 1970. Vol. ED-17, N 9. P. 661—666.

7. Григорьев Б. И., Рудский В. А., Тогатов В. В. Измерение времени жизни неосновных носителей заряда в высокоомных слоях транзисторных структур // Радиотехника и электроника. 1981. Т. 26, № 7. С. 1514—1521.

8. Gummel H. K., Poon H. C. An integral charge control model of bipolar transistors // Bell System. Techical Journal. 1970. Vol. 49. P. 827—834.

9. Шокли В., Рид В. Статистика рекомбинации дырок и электронов. Полупроводниковые приборы. М.: Изд-во иностр. лит., 1953.

10. Блихер А. Физика тиристоров. Л.: Энергоатомиздат, 1981.

11. Григорьев Б. И. Граничные коэффициенты усиления по току силового высоковольтного транзистора // Изв. вузов. Приборостроение. 2000. Т. 43, № 4. С. 35—39.

12. Григорьев Б. И., Резанов Ю. В., Семенов В. Т. Постоянные времени мощных высоковольтных транзисторов // Электронная техника. Сер. 2. Полупроводниковые приборы. 1986. Вып. 2(181). С. 42—47.

13. Бородин Б. А., Ломакин В. М., Мокряков В. В, Петухов В. М., Хрулев А. К. Мощные полупроводниковые приборы. Транзисторы. М.: Радио и связь, 1985.

Сведения об авторе

Борис Иванович Григорьев — канд. техн. наук, доцент; Униаерситет ИТМО, кафедра электроники

E-mail: [email protected]

Рекомендована кафедрой Поступила в редакцию

электроники 27.10.14 г.

Ссылка для цитирования: Григорьев Б. И. Стационарные режимы усиления биполярных транзисторов // Изв. вузов. Приборостроение. 2015. Т. 58, № 5. С. 372—379.

STATIONARY GAIN MODES OF BIPOLAR TRANSISTORS

B. I. Grigoryev

ITMO University, 197101, Saint Petersburg, Russia E-mail: [email protected]

The boundary value problem describing adequately the stationary gain modes of р—n—р- and n—р—n-bipolar transistors in a wide range of the collector current density is formulated and solved. Expressions for current gain, as well as for injection efficiency, minority carriers transfer coefficient at high injection levels in the basic areas of bipolar transistor are derived and analyzed. The basic physical mechanisms responsible for increase as well as for decrease in gain with increased collector current from the lowest possible up to the maximal allowable values are considered. Comparative analysis of the obtained theoretical results with experiments data is presented.

Keywords: bipolar transistor, collector current, collector—emitter current gain, injection rate, carrier lifetime in the base, emitter, base, combined semiconductors.

Data on author

Boris I. Grigoryev — PhD, Associate Professor; ITMO University, Department of Electronics;

E-mail: [email protected]

Reference for citation: Grigoryev B. I. Stationary gain modes of bipolar transistors // Izvestiya Vysshikh Uchebnykh Zavedeniy. Priborostroenie. 2015. Vol. 58, N 5. P. 372—379 (in Russian).

DOI: 10.17586/0021-3454-2015-58-5-372-379

Расчеты смещения транзистора

| Биполярные переходные транзисторы

Хотя схемы переключения транзисторов работают без смещения, для аналоговых схем необычно работать без смещения. Один из немногих примеров — «TR One, одно транзисторное радио» TR One, Ch 9 с усиленным детектором AM (амплитудной модуляцией). Обратите внимание на отсутствие резистора смещения на базе в этой схеме. В этом разделе мы рассмотрим несколько основных схем смещения, которые могут установить выбранный IE тока эмиттера. При желаемом токе эмиттера IE, какие номиналы резисторов смещения требуются, RB, RE и т. Д.?

Базовый резистор смещения

В простейшем смещении используется резистор смещения базы между базой и базовой батареей V BB . Удобно использовать существующий источник питания VCC вместо нового источника напряжения смещения. Примером каскада аудиоусилителя, использующего смещение базы, является «Кристаллический радиоприемник с одним транзистором. . . Кристалл радиоприемника, Ch 9. Обратите внимание на резистор от базы до клеммы аккумулятора. Аналогичная схема изображена на рисунке ниже. Напишите уравнение KVL (закон напряжения Кирхгофа) для контура, содержащего батарею, RB и падение диода VBE на транзисторе, как показано на рисунке ниже. Обратите внимание, что мы используем VBB для базового питания, хотя на самом деле это VCC.Если β велико, мы можем сделать приближение IC = IE. Для кремниевых транзисторов ВБЭ≅0,7В.

Базовое смещение

Кремниевые малосигнальные транзисторы обычно имеют β в диапазоне 100–300.

Пример расчета:

Предполагая, что у нас есть транзистор с β = 100, какое значение резистора смещения базы требуется, чтобы обеспечить ток эмиттера 1 мА? Решение уравнения базового смещения IE для RB и замена β, VBB, VBE и IE дает 930 кОм.Ближайшее стандартное значение — 910 кОм.

Какой ток эмиттера с резистором 910 кОм? Каков ток эмиттера, если мы случайно получим транзистор β = 300?

Ток эмиттера мало изменяется при использовании резистора стандартного номинала 910 кОм. Однако при изменении β от 100 до 300 ток эмиттера утроился. Это неприемлемо для усилителя мощности, если мы ожидаем, что напряжение коллектора будет колебаться от около VCC до около земли. Однако для сигналов низкого уровня от микровольт до примерно вольт точка смещения может быть центрирована для β квадратного корня из (100 · 300) = 173.Точка смещения все равно будет сильно смещаться. Однако сигналы низкого уровня не будут обрезаться.

Базовое смещение не подходит для высоких эмиттерных токов, используемых в усилителях мощности. Смещенный к базе эмиттерный ток нестабилен по температуре.

Термический выход из строя является результатом высокого эмиттерного тока, вызывающего повышение температуры, которое вызывает увеличение эмиттерного тока, что еще больше увеличивает температуру.

Смещение обратной связи коллектора

Вариации смещения из-за температуры и бета можно уменьшить, переместив конец VBB резистора смещения базы к коллектору, как показано на рисунке ниже.Если ток эмиттера увеличится, падение напряжения на RC увеличится, уменьшится VC и уменьшится IB, возвращаемый на базу. Это, в свою очередь, уменьшает ток эмиттера, корректируя первоначальное увеличение.

Напишите уравнение KVL для контура, содержащего батарею, RC, RB и каплю VBE. Заменить IC≅IE и IB≅IE / β. Решение IE дает уравнение смещения IE CFB. Решение IB дает уравнение IB CFB-bias.

Смещение обратной связи коллектора.

Пример расчета:

Найдите требуемый резистор смещения обратной связи коллектора для тока эмиттера 1 мА, a 4.Коллекторный нагрузочный резистор 7К, а транзистор с β = 100. Найдите напряжение коллектора VC. Это должно быть примерно посередине между VCC и землей.

Ближайшее стандартное значение резистора смещения обратной связи коллектора 460 кОм составляет 470 кОм. Найдите ток эмиттера IE с резистором 470 кОм. Пересчитайте ток эмиттера для транзистора с β = 100 и β = 300.

Мы видим, что при изменении бета от 100 до 300 ток эмиттера увеличивается с 0,989 мА до 1.48 мА. Это улучшение по сравнению с предыдущей схемой базового смещения, которая увеличилась с 1,02 мА до 3,07 мА. Смещение обратной связи коллектора в два раза стабильнее, чем базовое смещение по отношению к бета-вариации.

Эмиттер-смещение

Вставка резистора RE в схему эмиттера, как показано на рисунке ниже, вызывает вырождение , также известное как отрицательная обратная связь . Это препятствует изменению тока эмиттера IE из-за изменений температуры, допусков резистора, бета-изменения или допуска источника питания.Типовые допуски следующие: резистор — 5%, бета — 100-300, блок питания — 5%. Почему эмиттерный резистор может стабилизировать изменение тока? Полярность падения напряжения на RE обусловлена ​​коллекторной батареей VCC. Конец резистора, ближайший к (-) клемме батареи, — (-), конец, ближайший к клемме (+), — это (+). Обратите внимание, что (-) конец RE подключен через батарею VBB и RB к базе. Любое увеличение тока, протекающего через RE, увеличит величину отрицательного напряжения, приложенного к цепи базы, уменьшив ток базы, уменьшив ток эмиттера.Этот уменьшающийся ток эмиттера частично компенсирует первоначальное увеличение.

Эмиттер-смещение

Обратите внимание, что батарея смещения базы VBB используется вместо VCC для смещения базы на рисунке выше. Позже мы покажем, что смещение эмиттера более эффективно при использовании батареи с более низким базовым смещением. Между тем, мы пишем уравнение КВЛ для контура через цепь база-эмиттер, обращая внимание на полярность компонентов. Подставляем IB≅IE / β и решаем ток эмиттера IE.Это уравнение может быть решено для RB, уравнение: RB emitter-bias, рисунок выше.

Перед применением уравнений: RB emitter-bias и IE emitter-bias, рисунок выше, нам нужно выбрать значения для RC и RE. RC связан с питанием коллектора VCC и желаемым током коллектора IC, который, как мы предполагаем, приблизительно равен току эмиттера IE.

Обычно точка смещения для VC устанавливается равной половине VCC. Однако его можно установить выше, чтобы компенсировать падение напряжения на эмиттерном резисторе RE.Ток коллектора — это то, что мы требуем или выбираем. Он может варьироваться от микроампер до ампер в зависимости от приложения и номинала транзистора. Выбираем IC = 1 мА, что типично для схемы на малосигнальном транзисторе.

Пример расчета:

Рассчитываем значение RC и выбираем близкое стандартное значение. Эмиттерный резистор, который составляет 10-50% резистора нагрузки коллектора, обычно работает хорошо.

Для RB был рассчитан резистор 883 кОм, выбрано 870 кОм.При β = 100 IE составляет 1,01 мА.

Для β = 300 токи эмиттера показаны в таблице ниже.

Сравнение тока эмиттера для β = 100, β = 300.

Цепь смещения	IC β = 100	IC β = 300
базовое смещение	1,02 мА	3,07 мА
смещение обратной связи коллектора	0,989 мА	1,48 мА
эмиттер-смещение, В BB = 10 В	1.01 мА	2,76 мА

Таблица выше показывает, что для VBB = 10 В смещение эмиттера не очень хорошо стабилизирует ток эмиттера. Пример смещения эмиттера лучше, чем предыдущий пример смещения базы, но не намного. Ключом к эффективному смещению эмиттера является снижение базового напряжения VBB ближе к величине смещения эмиттера.

Округление, равное умножению тока эмиттера на резистор эмиттера: IERE = (1 мА) (470) = 0,47 В. Кроме того, нам нужно преодолеть VBE = 0.7В. Таким образом, нам нужен VBB> (0,47 + 0,7) В или> 1,17 В. Если ток эмиттера отклоняется, это число изменится по сравнению с фиксированным базовым питанием VBB, вызывая корректировку базового тока IB и эмиттерного тока IE. Хорошее значение для VB> 1,17 В — 2 В.

Расчетный базовый резистор 83 кОм намного ниже, чем у предыдущего 883 кОм. Выбираем 82к из списка стандартных значений. Токи эмиттера с РБ 82 кОм для β = 100 и β = 300 составляют:

Сравнивая токи эмиттера для смещения эмиттера с VBB = 2 В при β = 100 и β = 300 с предыдущими примерами схемы смещения в таблице ниже, мы видим значительное улучшение при 1.75 мА, однако, не так хорошо, как 1,48 мА обратной связи коллектора.

Сравнение тока эмиттера для β = 100, β = 300.

Цепь смещения	IC β = 100	IC β = 300
базовое смещение	1,02 мА	3,07 мА
смещение обратной связи коллектора	0,989 мА	1,48 мА
эмиттер-смещение, В BB = 10 В	1,01 мА	2.76 мА
эмиттер-смещение, В BB = 2 В	1,01 мА	1,75 мА

Чтобы улучшить характеристики эмиттерного смещения, либо увеличьте эмиттерный резистор RE, либо уменьшите подачу базового смещения VBB, либо и то, и другое.

В качестве примера мы удвоим резистор эмиттера до ближайшего стандартного значения 910 Ом.

Вычисленное RB = 39 кОм — резистор стандартного номинала. Нет необходимости пересчитывать IE для β = 100. Для β = 300 это:

Характеристики цепи эмиттерного смещения с эмиттерным резистором 910 значительно улучшены.См. Таблицу ниже.

Сравнение тока эмиттера для β = 100, β = 300.

Цепь смещения	IC β = 100	IC β = 300
базовое смещение	1,02 мА	3,07 мА
смещение обратной связи коллектора	0,989 мА	1,48 мА
эмиттер-смещение, В BB = 10 В	1,01 мА	2,76 мА
эмиттер-смещение, В BB = 2 В, R E = 470	1.01 мА	1,75 мА
эмиттер-смещение, В BB = 2 В, R E = 910	1,00 мА	1,25 мА

В качестве упражнения переработайте пример смещения эмиттера с резистором эмиттера, возвращенным обратно на 470 Ом, а напряжение смещения базы уменьшено до 1,5 В.

Базовый резистор 33 кОм — стандартное значение, ток эмиттера при β = 100 в порядке. Ток эмиттера при β = 300 составляет:

В таблице ниже сравниваются результаты упражнений 1 мА и 1.38 мА к предыдущим примерам.

Сравнение тока эмиттера для β = 100, β = 300.

Цепь смещения	IC β = 100	IC β = 300
базовое смещение	1,02 мА	3,07 мА
смещение обратной связи коллектора	0,989 мА	1,48 мА
эмиттер-смещение, В BB = 10 В	1,01 мА	2,76 мА
эмиттер-смещение, В BB = 2 В, R B = 470	1.01 мА	1,75 мА
эмиттер-смещение, В BB = 2 В, R B = 910	1,00 мА	1,25 мА
эмиттер-смещение, В BB = 1,5 В, R B = 470	1,00 мА	1,38 мА

Уравнения смещения эмиттера повторены на рисунке ниже с включенным внутренним сопротивлением эмиттера для большей точности. Внутреннее сопротивление эмиттера — это сопротивление в цепи эмиттера внутри корпуса транзистора.Это внутреннее сопротивление rEE является значительным, когда (внешний) эмиттерный резистор RE мал или даже равен нулю. Значение внутреннего сопротивления REE является функцией тока эмиттера IE, таблица ниже.

Получение r _EE

 r  EE  = KT / I  E  m где: K = 1,38 × 10 -23  ватт-сек /  o  C, постоянная Больцмана T = температура в Кельвинах ≅300. I  E  = ток эмиттера m = изменяется от 1 до 2 для кремния r  EE  ≅ 0.026V / I  E  = 26 мВ / I  E  

Для справки приближение 26 мВ указано как уравнение rEE на рисунке ниже.

Уравнения смещения эмиттера с внутренним сопротивлением эмиттера rEE.

Более точные уравнения смещения эмиттера на рисунке выше могут быть получены путем записи уравнения KVL. В качестве альтернативы, начните с уравнений IE emitter-bias и RB emitter-bias на рисунке выше, заменив RE на rEE + RE. Результатом являются уравнения IE EB и RB EB соответственно на рисунке выше.

Повторите вычисление RB в предыдущем примере смещения эмиттера с включением rEE и сравните результаты.

Включение rEE в расчет приводит к более низкому значению базового резистора RB, как показано в таблице ниже. Он падает ниже стандартного значения резистора 82 кОм, а не выше него.

Влияние включения РЭЭ на расчетную РБ

r EE ?	r EE Значение
Без r EE	83к
С r EE	80.4к

Байпасный конденсатор для RE

Одна из проблем со смещением эмиттера заключается в том, что значительная часть выходного сигнала пропускается через резистор эмиттера RE (рисунок ниже). Это падение напряжения на эмиттерном резисторе идет последовательно с базой и имеет противоположную полярность по сравнению с входным сигналом. (Это похоже на обычную конфигурацию коллектора с коэффициентом усиления <1). Это ухудшение сильно снижает коэффициент усиления от базы к коллектору. Решением для усилителей сигналов переменного тока является обход эмиттерного резистора с помощью конденсатора.Это восстанавливает усиление переменного тока, поскольку конденсатор не подходит для сигналов переменного тока. Постоянный ток эмиттера все еще испытывает вырождение в эмиттерном резисторе, таким образом, стабилизируя постоянный ток.

Cbypass требуется для предотвращения снижения усиления переменного тока.

Величина байпасного конденсатора зависит от самой низкой частоты, которую нужно усилить.

Для радиочастот Cbpass было бы мало. Для аудиоусилителя с диапазоном частот до 20 Гц он будет большим.«Практическое правило» для байпасного конденсатора состоит в том, что реактивное сопротивление должно быть 1/10 сопротивления эмиттера или меньше. Конденсатор должен быть спроектирован таким образом, чтобы выдерживать самую низкую усиливаемую частоту. Конденсатор для аудиоусилителя с диапазоном частот от 20 Гц до 20 кГц будет:

.

Обратите внимание, что внутреннее сопротивление эмиттера rEE не обходится байпасным конденсатором.

Смещение делителя напряжения

Для стабильного смещения эмиттера требуется источник смещения базы низкого напряжения, как показано на рисунке ниже.Альтернативой базовому источнику питания VBB является делитель напряжения, основанный на питании коллектора VCC.

Делитель напряжения смещения заменяет базовую батарею делителем напряжения.

Методика проектирования состоит в том, чтобы сначала разработать схему смещения эмиттера, а затем преобразовать ее в конфигурацию смещения делителя напряжения с помощью теоремы Тевенина. [TK1] Шаги графически показаны на рисунке ниже. Изобразите делитель напряжения без назначения значений. Отсоедините перегородку от основания.(База транзистора — это нагрузка.) Примените теорему Тевенина, чтобы получить одно эквивалентное сопротивление Тевенина Rth и источник напряжения Vth.

Теорема Тевенина преобразует делитель напряжения на однополярное питание Vth и сопротивление Rth.

Эквивалентное сопротивление Тевенина — это сопротивление от точки нагрузки (стрелка) с аккумулятором (VCC), уменьшенным до 0 (земля). Другими словами, R1 || R2. Эквивалентное напряжение Тевенина — это напряжение холостого хода (нагрузка снята). Этот расчет выполняется методом коэффициента делителя напряжения.R1 получается путем исключения R2 из пары уравнений для Rth и Vth. Уравнение R1 выражается в известных величинах Rth, Vth, Vcc. Обратите внимание, что Rth — это RB, резистор смещения из конструкции эмиттерного смещения. Уравнение для R2 выражается через R1 и Rth.

Преобразуйте этот предыдущий пример смещения эмиттера в смещение делителя напряжения.

Пример преобразования эмиттерного смещения в смещение делителя напряжения.

Эти значения были ранее выбраны или рассчитаны для примера смещения эмиттера

Замена VCC, VBB, RB дает R1 и R2 для конфигурации смещения делителя напряжения.

R1 — стандартное значение 220К. Ближайшее стандартное значение для R2, ​​соответствующее 38,8k, составляет 39k. Это не меняет IE настолько, чтобы мы могли его вычислить. Примеры проблем 1. Рассчитайте резисторы смещения для каскодного усилителя, показанного на рисунке ниже. VB2 — напряжение смещения для каскада с общим эмиттером. VB1 — это довольно высокое напряжение на уровне 11,5, потому что мы хотим, чтобы каскад с общей базой удерживал на эмиттере 11,5-0,7 = 10,8 В, около 11 В. (Это будет 10 В с учетом падения напряжения на RB1.) То есть каскад с общей базой является нагрузкой, заменяющей резистор, для коллектора каскада с общим эмиттером. Нам нужен ток эмиттера 1 мА.

Смещение для каскодного усилителя.

2. Преобразуйте базовые резисторы смещения для каскодного усилителя в резисторы смещения делителя напряжения, управляемые напряжением VCC 20 В.

Окончательная принципиальная схема показана в главе «Практические аналоговые схемы», «Каскодный усилитель класса А. . . ”Каскод, гл. 9.

ОБЗОР:

• См. Рисунок ниже.
• Выбор конфигурации цепи смещения
• Выберите RC и IE для предполагаемого приложения. Значения RC и IE обычно должны устанавливать напряжение коллектора VC равным 1/2 от VCC.
• Рассчитайте базовый резистор RB для достижения желаемого тока эмиттера.
• При необходимости пересчитайте ток эмиттера IE для резисторов стандартного номинала.
• Для смещения делителя напряжения сначала выполните расчеты смещения эмиттера, а затем определите R1 и R2.
• Для усилителей переменного тока байпасный конденсатор, включенный параллельно с RE, улучшает усиление переменного тока.Установите XC≤0,10RE для минимальной частоты.

Сводка уравнений смещения.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Калькулятор базового резистора транзистора

Чтобы использовать калькулятор для значений резистора базы транзистора, ВАЖНО, чтобы вы прочитали следующее.

Таблица значений транзистора

• Сначала вычислите ток, который вам нужно пройти через транзистор, когда он включен, то есть ток коллектора .
• Во-вторых, найдите коэффициент усиления по току , бета, Hfe . Эти значения указаны в таблице данных для конкретного транзистора. Для расчета наихудшего случая используйте минимальное значение Hfe или правильное значение для необходимого вам тока коллектора.
• Напряжение Vce — это напряжение на коллекторе и эмиттере.
• Базовое напряжение — это напряжение, которое вы используете для управления базой транзистора.
• Падение напряжения — это значение Vbe (sat) , вы получите его из таблицы данных, глядя на график Vbe и Vce (sat) vs.коллекторный ток.

Чтобы получить наилучший результат, рассмотрите следующие

• Чтобы обеспечить полное включение транзистора, вы можете удвоить значение тока коллектора. В результате вы получите номинал базового резистора, равный половине того, что дает вам этот калькулятор.
• Например, здесь он дается для максимального тока коллектора и коэффициента усиления наихудшего случая, Hfe. Значения для вашей схемы могут отличаться, обязательно вводите значения для своих нужд.
• Для расчета для транзистора PNP введите отрицательные числа в ток коллектора, напряжение базы и падение напряжения.

Чтобы помочь вам запомнить распиновку транзисторов NPN и PNP:

Транзистор NPN и транзистор PNP с базовым резистором

Примеры приведены для транзисторов NPN 2N2222, 2N3055, 2N3904, BC547, TIP31, TIP31A, TIP31C, TIP41, TIP41A, TIP41C и транзисторов PNP 2N3906.

Формулы и математика, используемые для расчета резистора базы транзистора

Закон Ом: Базовый резистор = (Напряжение питания — Падение напряжения) / (Ток коллектора / Бета)

Необходимыми электронными компонентами являются 5-полосный резистор с обычной цветной полосой, полосы представляют величину сопротивления, допуск резистора и, в некоторых случаях, температурный коэффициент.

транзисторов — Расчет базового тока Байт

Сначала попробуйте прочитать это

Транзистор, переходящий в насыщение, не является свойством сам транзистор, но вместо этого свойство окружающей цепи транзистор и транзистор, как его часть.

Вопрос о Vce NPN BJT в области насыщения

Для этой схемы с идеальным транзистором (источник тока с регулируемым током CCCS) любой базовый ток больше:

\ $ \ Large I_B> \ frac {\ frac {V_ {cc}} {R_c}} {\ beta} \ $ пропитает BJT.

Но в реальной жизни идеальных транзисторов не существует. Для любого реального транзистора β не является постоянным. β изменяется в зависимости от Ic, Vce, температуры. И что еще хуже, каждый транзистор будет иметь разное значение бета, и бета также будет меняться для разных условий эксплуатации. Также в насыщении не держатся \ $ I_C = I_B * β \ $.

Итак, чтобы преодолеть эту проблему с бета и насыщением, мы вынуждены использовать уловку « overdrive factor » или « Forced Beta ».

Мы просто увеличиваем базовый ток намного выше \ $ I_B> \ frac {\ frac {V_ {cc}} {R_C}} {\ beta} \ $.

Мы делаем это, чтобы убедиться, что у нас достаточно тока базы, чтобы перевести транзистор в состояние насыщения при любых условиях в нашей схеме.

Кроме того, большинство поставщиков BJT определяют область насыщения, когда Ic / Ib = 10 (так называемая Forced Beta ). И самый технический паспорт показывает Vce_sat для Ic / Ib = 10

Итак, чтобы быть на сто процентов уверенным, что ваш BJT будет в области насыщения, вы должны использовать эту так называемую технику принудительного бета-тестирования при выборе номинала базового резистора.

$$ \ frac {I_C} {I_B} = 10 $$

$$ R_B = \ frac {V_ {IN} — V_ {BE}} {0,1 * I_C} $$

$$ R_C = \ frac {V_ {CC} — V_ {CE_ {sat}}} {I_C} $$

Или мы можем использовать KVL и решить для \ $ R_B \ $

$$ I_B = \ frac {V_ {IN} — V_ {BE}} {R_B} $$

$$ V_ {CE} = V_ {CC} — I_C * R_C = V_ {CC} — \ beta * I_B * R_C = V_ {CC} — \ beta \ frac {V_ {IN} — V_ {BE}} { R_B} * R_C $$ Решение для \ $ R_B \ $

$$ R_B \ leqslant \ frac {V_ {IN_ {min}} — V_ {BE}} {V_ {CC} — V_ {CE_ {sat}}} * \ frac {\ beta_ {min}} {K} * R_C $$

и К = 3…10 — коэффициент повышающей передачи

(PDF) Метод извлечения базовых последовательных сопротивлений биполярного транзистора при наличии тока скопления

ЖУРНАЛ ТВЕРДОТЕЛЬНЫХ ЦЕПЕЙ IEEE, VOL. 31, NO. 1, ЯНВАРЬ 1996 135

Рис. 4. Зависимость от смещения эмиттер / база для извлеченного сопротивления основного листа

(полная линия). Дается сравнение с зависимым от положения листовым сопротивлением

(пунктирные линии), рассчитанным из 2-D смоделированных распределений потенциала и тока

с помощью (13).

Рис. 5. Зависимость полного сопротивления базы от ширины эмиттера для различных напряжений эмиттер / база

. Сплошные линии соответствуют результатам метода экстракции. Пунктирные линии

являются эталонным расчетом, полученным путем интегрирования (12) с использованием

2-мерных смоделированных распределений потенциала и тока.

Максимальная относительная погрешность, определяемая методом измерения

, остается ниже 5% на высоте

м во всем диапазоне напряжений базы / эмиттера

.

В. C

ВКЛЮЧЕНИЕ

Был описан простой аналитический метод определения сопротивлений базовой серии

. Эти извлеченные величины

были тщательно проверены путем прямого сравнения с их аналогами

, интегрированными с использованием внутренних распределений тока и напряжения

, полученных из 2-D моделирования устройств. Этот метод

имеет следующие преимущества перед большинством существующих методов измерения

:

1) индивидуальная оценка внешнего, внутреннего и основного

листовых сопротивлений

2) простое аналитическое определение общего сопротивления

при происходит текущая скученность.

Относительная ошибка, сделанная для самых больших окон эмиттера и

базовых / эмиттерных напряжений, оказалась в пределах 5%. Это остаточное несоответствие

, вероятно, можно отнести к неравномерному падению напряжения

в эмиттерной области. Таким образом, настоящая методика извлечения

может быть улучшена путем введения эффекта сглаживания

из-за структуры эмиттера из поликремния. Из-за сложности дифференциального уравнения

, описывающего

вкладов как эмиттерной, так и базовой скученности, аналитическая обработка

, используемая в этом методе, в этом случае должна быть заменена более сложной численной обработкой

.

A

ЗНАНИЕ

Авторы выражают признательность М. Браулту и Дж. Лебайли

из компании Philips Components, Кан, за предоставленные образцы процесса

QUBiC и ценные обсуждения.

R

ЭФЕРЕНЦИИ

[1] К. Х. Ван и Й. ван дер Фельден, «Технология однополигонального BiCMOS

с биполярной частотой 30 ГГц

» в BCTM Tech. Dig., Октябрь 1994, с. 234–237.

[2] Х. Накадзима, Н. Ито, К. Иноу, Т.Иинума, С. Мацуда, К. Йошино, Ю.

Кацумата и Х. Иваи, «Технология кремниевых биполярных транзисторов 0,5 мм

для аналоговых приложений», в BCTM Tech. Dig., Октябрь 1994, с. 213–216.

[3] Т. Ямагути, Т. М. Арчер, Р. Э. Джонстон и Дж. С. Ли, «Оптимизация процессов и устройств

для аналоговой комплементарной биполярной ИС

с 5,5 ГГц транзистором

PNP», IEEE Trans. Электронные устройства, т.

41, стр. 1019–1026, июнь 1994 г.

[4] Д. Д. Танг и П. М. Соломон, «Конструкция биполярного транзистора для оптимизированных логических схем

задержки мощности», IEEE J. Solid-State Circuits, vol. 14, pp.

679–684, август 1979 г.

[5] С. Дж. Прасад, «Метод измерения сопротивления базы и эмиттера

HBT AlGaAs / GaAs», в BCTM Tech. Dig., Октябрь 1992 г., стр. 204–207.

[6] А. Нойгрошель, «Измерение слаботочных сопротивлений базы и эмиттера

биполярных транзисторов», IEEE Trans.Электронные устройства, т.

34, стр. 817–822, апрель 1987 г.

[7] WM Sansen и RG Meyer, «Определение характеристик и измерение

сопротивлений базы и эмиттера биполярного транзистора», IEEE J. Solid-State

Схемы, т. 7, pp. 492–498, декабрь 1972 г.

[8] С. Т. Хсу, «Шум в транзисторах с высоким коэффициентом усиления и его применение для измерения

определенных параметров транзисторов», IEEE Trans. Электрон

Приборы, т. 18, стр. 425–431, июль 1971 г.

[9] Х. К. де Граафф и Ф. М. Клаассен, «Компактное моделирование транзисторов

для проектирования схем», Вычислительная микроэлектроника, Под ред. S. Selberherr,

Вена, Нью-Йорк: Springer-Verlag.

[10] Т. Х. Нинг и Д. Д. Тан, «Метод определения последовательного сопротивления эмиттера и базы

биполярных транзисторов», IEEE Trans. Электрон

Приборы, т. 31, pp. 409–412, Apr. 1984.

[11] Дж. Венг, Дж. Хольц и Т. Ф. Мейстер, «Новый метод определения базового сопротивления

биполярных транзисторов», IEEE Electron Device Lett., т. 13,

pp. 158–160, Mar. 1992.

[12] Дж. Лебайи и М. Браулт, «Схема потокового процесса QUBiC», частное сообщение.

[13] Дж. Р. Хаузер, «Влияние распределенного базового потенциала на плотность инжектируемого тока эмиттера

и эффективное сопротивление базы для полосковых транзисторов

геометрии», IEEE Trans. Электронные устройства, т. ED-11, pp. 238–242,

May 1964.

[14] Э. Дюбуа, Дж. Л. Коппи, Б. Баккус и Д.Коллард, «Исследование электрических характеристик

изоляционных конструкций», IEEE Trans. Электрон

Приборы, т. 37, pp. 1477–1486, June 1990.

[15] E. Dubois, P.-H. Брикау и Э. Робиллиарт, «Точность схем экстракции последовательного сопротивления для биполярных транзисторов из поликремния», в BCTM

Tech. Dig., Pp. 148–151, Oct. 1994.

% PDF-1.3 % 36 0 объект > эндобдж xref 36 237 0000000016 00000 н. 0000005089 00000 н. 0000006668 00000 н. 0000006823 00000 н. 0000007106 00000 н. 0000007450 00000 н. 0000007748 00000 н. 0000007998 00000 н. 0000008312 00000 н. 0000008636 00000 н. 0000008951 00000 п. 0000009397 00000 н. 0000009885 00000 н. 0000010169 00000 п. 0000010433 00000 п. 0000010731 00000 п. 0000011036 00000 п. 0000011329 00000 п. 0000011606 00000 п. 0000011996 00000 п. 0000012224 00000 п. 0000012545 00000 п. 0000012867 00000 п. 0000013135 00000 п. 0000013507 00000 п. 0000013765 00000 п. 0000014029 00000 п. 0000014417 00000 п. 0000014754 00000 п. 0000015040 00000 п. 0000015355 00000 п. 0000015406 00000 п. 0000015706 00000 п. 0000016014 00000 п. 0000016283 00000 п. 0000016596 00000 п. 0000016907 00000 п. 0000017178 00000 п. 0000017359 00000 п. 0000017620 00000 н. 0000017829 00000 п. 0000018163 00000 п. 0000018471 00000 п. 0000018644 00000 п. 0000018837 00000 п. 0000019081 00000 п. 0000019356 00000 п. 0000019603 00000 п. 0000019918 00000 п. 0000020257 00000 п. 0000020575 00000 п. 0000021004 00000 п. 0000021170 00000 п. 0000021432 00000 п. 0000021598 00000 п. 0000021861 00000 п. 0000022125 00000 п. 0000022331 00000 п. 0000022642 00000 п. 0000022905 00000 п. 0000023059 00000 п. 0000023323 00000 п. 0000023584 00000 п. 0000023822 00000 п. 0000024168 00000 п. 0000024470 00000 п. 0000024748 00000 п. 0000025027 00000 н. 0000025079 00000 п. 0000025218 00000 п. 0000025449 00000 п. 0000025705 00000 п. 0000025929 00000 п. 0000025981 00000 п. 0000026018 00000 п. 0000026070 00000 п. 0000026135 00000 п. 0000026303 00000 п. 0000026403 00000 п. 0000026665 00000 п. 0000026907 00000 п. 0000027169 00000 н. 0000027458 00000 п. 0000027688 00000 н. 0000027878 00000 н. 0000028178 00000 п. 0000028476 00000 п. 0000028788 00000 п. 0000029155 00000 п. 0000029410 00000 п. 0000029718 00000 п. 0000030025 00000 п. 0000030250 00000 п. 0000030550 00000 п. 0000030757 00000 п. 0000031029 00000 п. 0000031269 00000 п. 0000031436 00000 п. 0000031488 00000 п. 0000031750 00000 п. 0000031984 00000 п. 0000032210 00000 п. 0000032467 00000 п. 0000032704 00000 п. 0000032947 00000 п. 0000033207 00000 п. 0000033424 00000 п. 0000033768 00000 п. 0000034004 00000 п. 0000034239 00000 п. 0000034517 00000 п. 0000034774 00000 п. 0000035091 00000 п. 0000035332 00000 п. 0000035648 00000 п. 0000035945 00000 п. 0000036245 00000 п. 0000036488 00000 п. 0000036743 00000 п. 0000036795 00000 п. 0000036965 00000 п. 0000037333 00000 п. 0000037577 00000 п. 0000037931 00000 п. 0000038136 00000 п. 0000038322 00000 п. 0000038692 00000 п. 0000038744 00000 п. 0000038913 00000 п. 0000039163 00000 п. 0000039381 00000 п. 0000039516 00000 п. 0000039727 00000 н. 0000040048 00000 н. 0000040361 00000 п. 0000040738 00000 п. 0000040955 00000 п. 0000041216 00000 п. 0000041382 00000 п. 0000041681 00000 п. 0000041943 00000 п. 0000042191 00000 п. 0000042495 00000 п. 0000042757 00000 п. 0000043067 00000 п. 0000043461 00000 п. 0000043502 00000 п. 0000043803 00000 п. 0000044059 00000 п. 0000044326 00000 п. 0000044579 00000 п. 0000044888 00000 н. 0000045212 00000 п. 0000045560 00000 п. 0000045912 00000 п. 0000046214 00000 п. 0000046469 00000 п. 0000046787 00000 п. 0000047071 00000 п. 0000047362 00000 п. 0000047687 00000 п. 0000047972 00000 п. 0000048245 00000 п. 0000048523 00000 п. 0000048922 00000 н. 0000049101 00000 п. 0000049367 00000 п. 0000049634 00000 п. 0000050014 00000 п. 0000050290 00000 н. 0000050554 00000 п. 0000050779 00000 п. 0000051049 00000 п. 0000051243 00000 п. 0000051459 00000 п. 0000051768 00000 п. 0000051996 00000 п. 0000052313 00000 п. 0000052573 00000 п. 0000052812 00000 п. 0000053074 00000 п. 0000053355 00000 п. 0000053687 00000 п. 0000053865 00000 п. 0000054091 00000 п. 0000054358 00000 п. 0000054684 00000 п. 0000054924 00000 п. 0000055240 00000 п. 0000055552 00000 п. 0000055811 00000 п. 0000056004 00000 п. 0000056308 00000 п. 0000056429 00000 п. 0000056963 00000 п. 0000057015 00000 п. 0000057323 00000 п. 0000057585 00000 п. 0000057763 00000 п. 0000058029 00000 п. 0000058289 00000 п. 0000058590 00000 п. 0000059387 00000 п. 0000059625 00000 п. 0000059896 00000 п. 0000060105 00000 п. 0000060372 00000 п. 0000060623 00000 п. 0000060843 00000 п. 0000061106 00000 п. 0000061366 00000 п. 0000061673 00000 п. 0000061965 00000 п. 0000062250 00000 п. 0000062475 00000 п. 0000062702 00000 п. 0000062960 00000 п. 0000065279 00000 п. 0000065539 00000 п. 0000065604 00000 п. 0000065780 00000 п. 0000066056 00000 п. 0000066108 00000 п. 0000066382 00000 п. PDj0Yb! YiPN * u! 5j9 :: = /

Основная идея о том, как рассчитать базовый ток и входное напряжение встроенного транзистора резистора смещения (BRT) | Toshiba Electronic Devices & Storage Corporation

BRT обычно используются в качестве переключателей.В идеале их напряжение в открытом состоянии (напряжение коллектор-эмиттер, В _CE ) должно быть как можно ближе к нулю.
Для достижения этого условия следует учитывать базовый ток.
Чтобы минимизировать V _CE , BRT используются в области насыщения, показанной на рисунке 1. Обычно считается, что биполярные транзисторы обеспечивают h _FE , равное 100. Однако, поскольку BRT работают в области насыщения, необходимо предположить что они обеспечивают h _FE от 10 до 20.Это означает, что ток базы должен составлять от 1/10 до 1/20 тока коллектора.

Предположим, что нам нужны V _CE на 0,2 В и I _C на 10 мА. Здесь RN1402 (с R ₁ = R ₂ = 10 кОм) используется в качестве BRT. Посмотрите на кривые V _{CE (sat)} — I _C , показанные в таблице данных RN1402 (рисунок 3). Когда h _FE ＝ I _C / I _B ＝ 20, V _{CE (sat)} можно прочитать как от 0,05 В до 0,06 В при I _C = 10 мА.Итак, предположим эти условия.

Внутренний базовый ток (I _b ) базовой цепи BRT, показанной на рисунке 2, составляет:
I _b ＝ I _C / ч _FE = 10 мА / 20 = 0,5 мА
Для простоты предположим, что внутреннее базовое напряжение (V _будет ) равно обычно используемому значению 0,7 В. Тогда I _R2 , протекающий через R ₂ , вычисляется следующим образом:
I _R2 = 0,7 В / 10 кОм = 0.07 мА
Следовательно, центральное значение базового тока BRT (I _B ) составляет:
I _B = I _b + I _R2 = 0,57 мА
Входное напряжение (В _I ), обеспечивающее I _B 0,57 мА, рассчитывается следующим образом:
V _I = R ₁ * I _B + V _be = 10 кОм * 0,57 мА + 0,7 = 6,4 В

Таким образом, можно считать, что V _CE 0,2 В и I _C 10 мА можно получить, подав входное напряжение 6.4 В или выше, хотя необходимо учитывать вариации устройства и температурные характеристики.

На практике входное напряжение (V _I ) выше 6,4 В должно подаваться на клемму B. В следующих параграфах описывается работа BRT, когда V _I > 6,4 В.

Как рассчитать значение Vce в транзисторе

Транзисторы — это строительные блоки современной электронной эры. Они работают как небольшие усилители, которые усиливают электрические сигналы по мере необходимости для облегчения работы схемы.Транзисторы состоят из трех основных частей: базы, коллектора и эмиттера. Параметр транзистора «Vce» означает напряжение, измеренное между коллектором и эмиттером, что чрезвычайно важно, поскольку напряжение между коллектором и эмиттером является выходным сигналом транзистора. Более того, основная функция транзистора заключается в усилении электрических сигналов, и Vce представляет результаты этого усиления. По этой причине Vce является наиболее важным параметром при проектировании схем транзисторов.

Найдите значение напряжения коллектора (Vcc), резисторов смещения (R1 и R2), резистора коллектора (Rc) и резистора эмиттера (Re). Используйте схему транзистора на веб-странице Learning About Electronics (см. Ссылку в разделе Ресурсы) в качестве модели того, как эти параметры схемы подключаются к транзистору. Обратитесь к электрической схеме вашей транзисторной схемы, чтобы найти значения параметров. Для наглядности предположим, что ваш Vcc составляет 12 вольт, R1 — 25 кОм, R2 — 15 кОм, Rc — 3 кОм и Re — 7 кОм.

Найдите значение бета для вашего транзистора. Бета — это текущий коэффициент усиления или коэффициент усиления транзистора. Он показывает, насколько транзистор усиливает базовый ток, то есть ток, который появляется на базе транзистора. Бета — это константа, которая для большинства транзисторов находится в диапазоне от 50 до 200. См. Паспорт транзистора, предоставленный производителем. Найдите в таблице данных фразу «усиление по току», «коэффициент передачи по току» или переменную «hfe». При необходимости обратитесь к производителю транзистора для получения этого значения.Для наглядности предположим, что бета равно 100.

Рассчитайте номинал базового резистора Rb. Базовый резистор — это сопротивление, измеренное на базе транзистора. Это комбинация R1 и R2, как указано в формуле Rb = (R1) (R2) / (R1 + R2). Используя числа из предыдущего примера, уравнение работает следующим образом:

Rb = [(25) (15)] / [(25 + 15)] = 375/40 = 9,375 кОм.

Рассчитайте базовое напряжение Vbb, которое представляет собой напряжение, измеренное на базе транзистора.Используйте формулу Vbb = Vcc * [R2 / (R1 + R2)]. Используя числа из предыдущих примеров, уравнение работает следующим образом:

Vbb = 12 * [15 / (25 + 15)] = 12 * (15/40) = 12 * 0,375 = 4,5 вольт.

Рассчитайте ток эмиттера, то есть ток, протекающий от эмиттера к земле. Используйте формулу Ie = (Vbb — Vbe) / [Rb / (Beta + 1) + Re], где Ie — это переменная для тока эмиттера, а Vbe — это напряжение от базы к эмиттеру.