Расчет цепи онлайн. Закон Ома для цепей постоянного и переменного тока: формулы, расчеты, онлайн-калькулятор

03.09.201826.07.2020 alexxlabРазное

Что такое закон Ома и как он применяется в электротехнике. Как рассчитать ток, напряжение и сопротивление по закону Ома. Особенности закона Ома для цепей переменного тока. Онлайн-калькулятор для расчетов по закону Ома.

Содержание

Что такое закон Ома и его основная формула

Закон Ома является фундаментальным законом электротехники, который устанавливает связь между силой тока, напряжением и сопротивлением в электрической цепи. Основная формула закона Ома для участка цепи выглядит следующим образом:

I = U / R

где:

I — сила тока в амперах (А)
U — напряжение в вольтах (В)
R — сопротивление в омах (Ом)

Эта формула позволяет рассчитать любую из трех величин, если известны две другие. Из нее также можно вывести следующие производные формулы:

U = I * R — для расчета напряжения
R = U / I — для расчета сопротивления

Применение закона Ома для расчета электрических цепей

Закон Ома имеет широкое практическое применение при расчете и проектировании электрических цепей:

Определение тока в цепи при известном напряжении и сопротивлении
Расчет необходимого сопротивления для ограничения тока до требуемого значения
Определение падения напряжения на участке цепи
Расчет параметров источников питания
Проверка работоспособности электроприборов

Рассмотрим несколько примеров применения закона Ома на практике.

Примеры расчетов по закону Ома

Пример 1. Расчет тока через лампу накаливания

Дано: лампа накаливания мощностью 60 Вт подключена к сети 220 В.

Требуется определить ток, протекающий через лампу.

Решение:

Рассчитаем сопротивление лампы: R = U^2 / P = 220^2 / 60 = 806 Ом
По закону Ома находим ток: I = U / R = 220 / 806 = 0,27 А

Ответ: через лампу протекает ток 0,27 А.

Пример 2. Определение напряжения на резисторе

Дано: через резистор сопротивлением 1 кОм протекает ток 5 мА.

Требуется найти напряжение на резисторе.

Решение:

По закону Ома: U = I * R = 0,005 * 1000 = 5 В

Ответ: напряжение на резисторе составляет 5 В.

Закон Ома для полной цепи

Для полной электрической цепи, содержащей источник ЭДС, закон Ома записывается в виде:

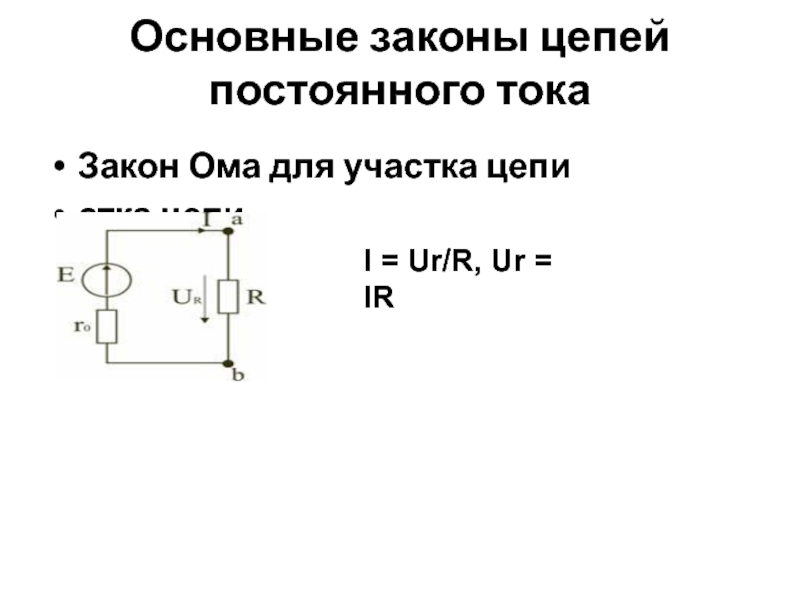
I = E / (R + r)

где:

E — электродвижущая сила источника
R — сопротивление внешней цепи
r — внутреннее сопротивление источника

Эта формула учитывает влияние внутреннего сопротивления источника на ток в цепи.

Особенности закона Ома для цепей переменного тока

В цепях переменного тока закон Ома сохраняет свою силу, но имеет некоторые особенности:

Вместо сопротивления R используется полное сопротивление цепи Z
Z учитывает активное, индуктивное и емкостное сопротивления
Расчет ведется по действующим значениям тока и напряжения

Формула закона Ома для переменного тока:

I = U / Z

где Z = √(R^2 + (X_L — X_C)^2)

X_L = ωL — индуктивное сопротивление

X_C = 1 / (ωC) — емкостное сопротивление

ω = 2πf — угловая частота

Онлайн-калькулятор для расчетов по закону Ома

Для удобства расчетов по закону Ома предлагаем воспользоваться онлайн-калькулятором. Введите известные значения, а калькулятор автоматически рассчитает остальные параметры.

«` import React, { useState } from ‘react’; import { Input, Button } from ‘@/components/ui/input’; const OhmsLawCalculator = () => { const [voltage, setVoltage] = useState(»); const [current, setCurrent] = useState(»); const [resistance, setResistance] = useState(»); const [result, setResult] = useState(»); const calculate = () => { if (voltage && current) { setResistance((parseFloat(voltage) / parseFloat(current)).toFixed(2)); setResult(`Сопротивление: ${(parseFloat(voltage) / parseFloat(current)).toFixed(2)} Ом`); } else if (voltage && resistance) { setCurrent((parseFloat(voltage) / parseFloat(resistance)).toFixed(2)); setResult(`Ток: ${(parseFloat(voltage) / parseFloat(resistance)).toFixed(2)} А`); } else if (current && resistance) { setVoltage((parseFloat(current) * parseFloat(resistance)).toFixed(2)); setResult(`Напряжение: ${(parseFloat(current) * parseFloat(resistance)).toFixed(2)} В`); } else { setResult(‘Пожалуйста, введите любые два значения’); } }; return (

Калькулятор закона Ома

setVoltage(e.target.value)} /> setCurrent(e.target.value)} />

setResistance(e.target.value)} />

{result}

); }; export default OhmsLawCalculator; «`

Этот калькулятор позволяет быстро произвести расчеты по закону Ома, введя любые два известных параметра.

Практические применения закона Ома

Закон Ома находит широкое применение в различных областях электротехники и электроники:

Проектирование электрических сетей
Расчет параметров электронных схем
Выбор предохранителей и автоматических выключателей
Определение сечения проводов
Диагностика неисправностей электрооборудования

Понимание и умение применять закон Ома — необходимый навык для любого специалиста, работающего с электрическими системами.

Ограничения закона Ома

Несмотря на свою универсальность, закон Ома имеет некоторые ограничения:

Не применим к нелинейным элементам (диоды, транзисторы)
Не учитывает температурную зависимость сопротивления
Не работает для сверхпроводников
Имеет ограничения при очень высоких частотах

В этих случаях требуются более сложные модели и расчеты.

Заключение

Закон Ома — фундаментальный закон электротехники, позволяющий рассчитывать основные параметры электрических цепей. Его понимание необходимо для эффективной работы с электрическими системами. Использование онлайн-калькуляторов значительно упрощает расчеты и помогает быстро получить нужные результаты.

Расчёт электрических цепей онлайн | FaultAn.ru

На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий момент реализованы методы расчёта по законам Ома и по законам Кирхгофа. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта.

Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.

В боковой панели доступны следующие элементы с задаваемыми параметрами:

Инструкция по применению программы приведена здесь.

Методы расчёта

После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.

Расчёт по закону Ома

Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.

Пример схемы и расчёт:

Исходные данные и схема:

E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
R1:
- Номер элемента: 1
- Сопротивление, Ом: 1

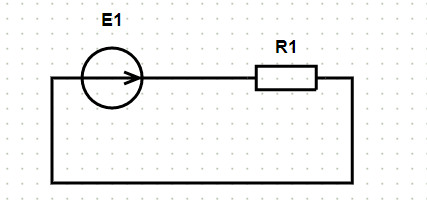
После нажатия кнопки «Расчёт» формируется решение:

В исходной схеме только один контур. Рассчитаем её по закону Ома.

Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ \underline{I} $ направление источника ЭДС $ \underline{E}_{1} $:

$$ R_{1}\cdot \underline{I} = \underline{E}_{1} $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ 1.0\cdot \underline{I}=100 $$

Отсюда искомый ток в цепи равен

$$ \underline{I} = 100\space \textrm{А}$$

Расчёт по законам Кирхгофа

Для многоконтурных схем расчёт осуществляется по законам Кирхгофа. Используемая методика расчёта приведена здесь.

Пример схемы и расчёт:

Исходные данные и схема:

E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
C1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:

Рассчитаем схему по законам Кирхгофа.

В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.

Произвольно зададим направления токов в ветвях и направления обхода контуров.

Принятые направления токов:

Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.

Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке.
Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке.

Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».

Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у} − 1 $, где $ N_\textrm{у} $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.

Составим уравнение для узла №1:

$$ \underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 $$

Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.

Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в} − N_\textrm{у} + 1 $, где $ N_\textrm{в} $ — число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.

Составим уравнение для контура №1:

$$ R_{1}\cdot \underline{I}_{1} + jX_{L1}\cdot \underline{I}_{2}=\underline{E}_{1} $$

Составим уравнение для контура №2:

$$ jX_{L1}\cdot \underline{I}_{2} − (−jX_{C1})\cdot \underline{I}_{3}=0 $$

Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:

$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I}_{1}+jX_{L1}\cdot \underline{I}_{2} = \underline{E}_{1} \\ jX_{L1}\cdot \underline{I}_{2}−(−jX_{C1})\cdot \underline{I}_{3} = 0 \\ \end{cases} $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3}=0 \\ \underline{I}_{1}+ j \cdot \underline{I}_{2}=100 \\ j \cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$

Решим систему уравнений и получим искомые токи:

$$ \underline{I}_{1} = 0 $$
$$ \underline{I}_{2} = −100j $$
$$ \underline{I}_{3} = 100j $$

Если вам нравится наш контент, помогите в развитии сайта.

1. EasyEDA — дизайн электронной цепи, моделирование цепи и PCB дизайн:

EasyEDA — удивительный бесплатный онлайн симулятор электроцепи, который очень подходит для тех, кто любит электронную схему. EasyEDA команда стремится делать сложную программу дизайна на веб-платформе в течение нескольких лет, и теперь инструмент становится замечательным для пользователей. Программная среда позволяет тебя сам проектировать схему. Проверить операцию через симулятор электроцепи. Когда вы убедитесь функцию цепи хорошо, вы будете создавать печатную плату с тем же программным обеспечением.

Есть более 70,000+ доступных диаграмм в их веб-базах данных вместе с 15,000+ Pspice программами библиотеки. На сайте вы можете найти и использовать множество проектов и электронных схем, сделанные другими, потому что они являются публичными и открытыми аппаратными оснащениями. Он имеет некоторые довольно впечатляющие варианты импорта (и экспорта). Например, вы можете импортировать файлы в Eagle, Kikad, LTspice и Altium проектант, и экспортировать файлы в .PNG или .SVG. Есть много примеров на сайте и полезных программ обучения, которые позволяют людей легко управлять.

Circuit Sims

2. Circuit Sims: Это был один из первых вебов исходя из эмуляторов электроцепи с открытым кодом я тестировал несколько лет назад. Разработчикам не удалось повысить качество и увеличить графический интерфейс пользователя.

DcAcLab

3. DcAcLab имеет визуальные и привлекательные графики, но ограничивается моделированием цепи. Это несомненно отличная программа для обучения, очень проста в использовании. Это делает вас видеть компоненты, как они сделаны. Это не позволит вам проектировать схему, но только позволит сделать практику.

EveryCircuit

4. EveryCircuit представляет собой электронный эмулятор онлайн с хорошими сделанными графиками. Когда вы входите в онлайн программу, и она будет просить вас создать бесплатный счет, чтобы вы можете сохранить ваши проекты и иметь ограниченную часть площади рисовать вашу схему. Чтобы использовать его без ограничений, требующих годовой взнос в размере $ 10. Он можно скачивать и использоваться на платформах Android и iTunes. Компоненты имеют ограниченную способность имитировать с небольшими минимальными параметрами. Очень просто в использовании, он имеет прекрасную систему электронного дизайна. Она позволяет вам включать (вставлять) моделирование в ваши веб-страницы.

DoCircuits

5.DoCircuits: Хотя она оставляет людям первое впечатление от путаницы о сайте, но она дает много примеров о том, как работает программа, можно видеть себя на видео «будет начать в пять минут». Измерения параметров электронной схемы продемонстрируют с реалистичными виртуальными инструментами.

PartSim

6. PartSim электронный симулятор схемы онлайн. Он был способным к моделированию. Вы можете рисовать электрические схемы и протестировать их. Он еще новый симулятор, так что есть несколько компонентов, чтобы сделать моделирования для выбора.

123DCircuits

7. 123DCircuits Активная программа разработана AutoDesk, она позволяет вам создавать схему, можно увидеть её на макетной плате, использовать платформу Arduino, имитировать электронную схему и окончательно создать PCB. Компоненты продемонстрируются в 3D в их реальной форме. Вы можете запрограммировать Arduino непосредственно из этой программы моделирования, (она) действительно производит глубокое впечатление.

TinaCloud

8. TinaCloud Эта программа моделирования имеет усовершенствованные возможности. Она позволяет вам моделировать, в дополнение к обычным схемам со смешанными сигналами, и микропроцессорами, VHDL, SMPS поставки электричества и радио частотных цепей. Расчеты для электронного моделирования выполняются непосредственно на сервере компании и позволяют отличную скорость моделирования

Spicy schematics

9.Spicy schematics является программой формы cross-plat, все формы платформы можно поддерживать, в том числе iPad.

Gecko simulations

10. Gecko simulations представляет собой программу моделирования, специализирующуюся на открытом исходном коде и питания цепей. С помощью этой программы вы также можете измерить потребляемую энергию схемы. Это программа является клоном программы ETH (ETH Zurich).

Импеданс. Расчёт

Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.

Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора U_R = IR; на выводах конденсатора U_C = IX_C; на выводах катушки U_L = IX_L.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах U_X = U_L — U_C .
Пропорционально напряжению, получим общее реактивное сопротивление X = X_L — X_C .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , U_R и U_X представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = U_R² + U_X² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

X_L = ωL = 2πfL — реактивное сопротивление индуктивности.
X_C = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:

Z = R + jX

Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:

Z = |Z|e^jargZ = Ze^jφ

Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.

Параллельное соединение

Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.

y = 1/Z = √(G² + b²)

Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:

Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:

Y = G — jb

Либо в показательной форме:

Y = |Y|e^-jφ = ye^-jφ

Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.

Онлайн-калькулятор расчёта импеданса и угла сдвига фаз

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Последовательное соединение
Z = √(R²+(XL-Xc)²)

Параллельное соединение
Z = 1/√(1/R²+(1/XL-1/Xc)²)

Похожие страницы с расчётами:

Реактивное сопротивление. Расчёт.
Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для:
участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
элементами.

— А любите ли Вы закон Ома так, как люблю его я? — спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, — Всеми силами души Вашей, со всем энтузиазмом и исступлением, к которому только способна пылкая молодость, — никак не угомонялся он, сверкая из-под очков пытливым взглядом.
— Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая «Калинку-Малинку» в направлении ближайшего супермаркета — не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

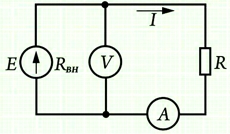где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками:

С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
1В=1000мВ=1000000мкВ;
1А=1000мА=1000000мкА;
1Ом=0.001кОм=0.000001МОм;
1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

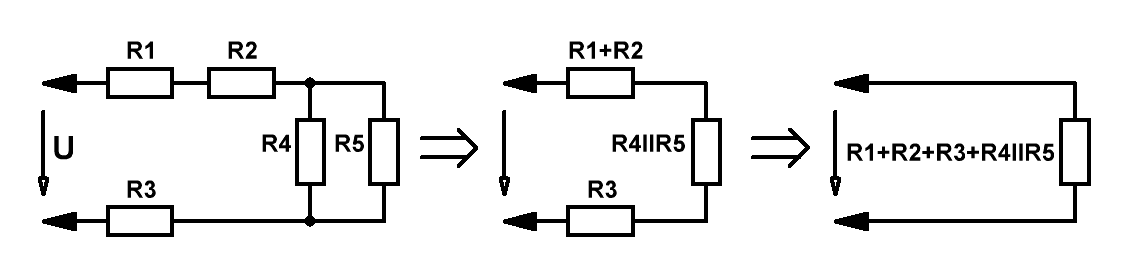
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

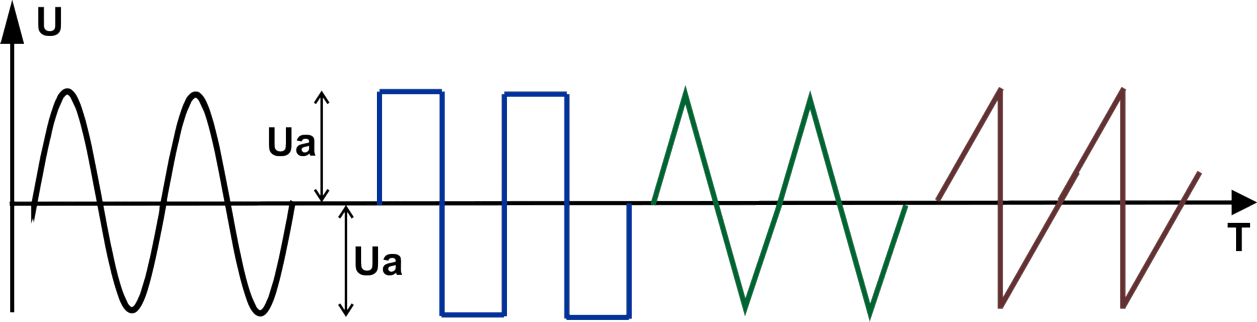
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

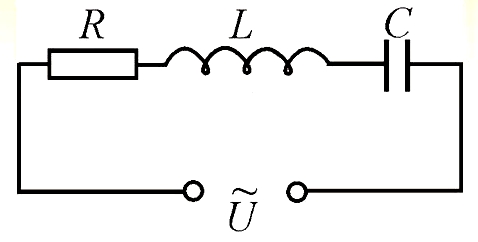
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:
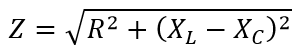
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: X_C = 1/(2πƒС) , X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

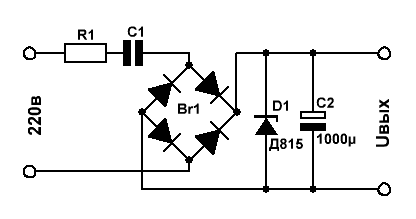
Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Онлайн калькулятор закона Ома для участка цепи

Рад приветствовать тебя, дорогой читатель, в этой первой статье моего блога! Ее я посвятил самому основному закону, который должен хорошо понимать современный человек, работающий с электричеством.

Мой онлайн калькулятор закона Ома создан для участка цепи. Он значительно облегчает электротехнические расчеты в домашней проводке, подходит для цепей переменного и постоянного тока.

Им просто пользоваться: прочти правила ввода данных и работай!

Содержание статьи

Правила работы на калькуляторе

В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:

напряжение;
ток;
сопротивление;
или мощность.

Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.

Будь внимательным, чтобы не допустить ошибки.

Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.

Осуществить переход к ним тебе поможет наглядная таблица.

Онлайн калькулятор закона Ома

Простые примеры расчета

Бытовая сеть переменного тока

Пример №1. Проверка ТЭНа.

В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления.
По мощности рассчитываем ток и сопротивление.

I = 1250 / 220 = 5,68 А; R = 220 / 5,68 = 38,7 Ом.

Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.

Пример №2. Проверка сопротивления двигателя

Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:

I = 1600 / 220 = 7,3 А.

Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:

сопротивление двигателя — 30,1 Ома;
мощность 1600 ватт.

Цепи постоянного тока

Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.

Считаем ток:

I = 55 / 12 = 4,6 А.

Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:

сопротивление 2,6 ома.
мощность 5 ватт.

Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже.

Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.

Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.

Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.

В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.

При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.

Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.

Полезная информация для начинающего электрика

Как использовать закон Ома на практике

Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.

Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.

Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.

Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:

значения приложенного к цепи напряжения;
сопротивления среды, по которой движется ток.

Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.

Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.

Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.

Примеры из жизни

№1: выключатель освещения разрывает цепь электрических проводов, по которым напряжение добирается до лампочки.

Между контактами образуется воздушный зазор. Он отличный изолятор, исключающий движение тока по осветительному прибору.

№2: клеммы розетки, как источника напряжения, замкнули между собой без сопротивления короткой проволокой. В этой ситуации создается короткое замыкание.

Ток КЗ способен сжечь электропроводку, вызвать пожар в квартире. Поэтому от таких ситуаций существует только одно спасение: использование защит, способных максимально быстро отключить питающее напряжение.

Для бытовой сети это функция автоматических выключателей или предохранителей, о работе которых я буду рассказывать в других статьях.

Используя сопротивление, следует понимать, что оно, само по себе, не вечно: обладая резервом противостояния приложенной энергии, оно может его израсходовать, не справиться со своей задачей и сгореть.

Поэтому для сопротивления вводится понятие мощности рассеивания, которая надежно отводится во внешнюю среду. Если тепловая энергия, развиваемая прохождением тока, превышает эту величину, то сопротивление сгорает.

Напряжение и сопротивление в комплексе формируют электрические процессы. Онлайн калькулятор закона Ома позволяет оптимально рассчитать величину тока, необходимую для совершения полезной работы.

Что такое участок цепи

Рассмотрим самую простую электрическую схему, состоящую из батарейки, лампочки и проводов. В ней циркулирует электрический ток.

Представленная схема или полная цепь состоит из двух контуров:

Внутреннего источника напряжения.
Внешнего участка: лампочки с подключенными проводами.

Те процессы, которые происходят внутри батарейки, нас интересуют в основном как познавательные. Их мы можем только ухудшить при неправильной эксплуатации.

Например, приходящая в квартиру электрическая энергия от трансформаторной подстанции нам не подвластна. Мы ей просто пользуемся. От неисправностей и аварийных режимов нас защищают автоматические выключатели, УЗО, реле РКН, ограничители перенапряжения или УЗИП, другие современные модули защит.

Внешний же, подключенный к источнику напряжения контур, является участком цепи, в котором мы, используя закон Ома, совершаем полезную для себя работу.

Как использовать треугольник закона Ома

Простое мнемоническое правило представлено тремя составляющими в виде частей треугольника. Оно позволяет легко запомнить взаимосвязи между током, сопротивлением и напряжением.

Вверху всегда стоит напряжение. Ток и сопротивление снизу. Когда вычисляем какую-то одну величину по двум другим, то ее изымаем из треугольника и выполняем арифметическое действие: деление или умножение.

Шпаргалка электрика для новичков

Треугольник закона Ома легко запоминается, но он не позволяет учитывать мощность потребления электроприбора. Этот четвертый параметр, важный для любого домашнего электрика, всегда надо учитывать. .

На всех бытовых электрических приборах указывают мощность потребления электрической энергии в ваттах или киловаттах. Ее формулы, совместно с предыдущими величинами, можно брать со следующей картинки.

Такая шпаргалка электрика позволяет делать простые вычисления в уме или на бумаге. Формулы из нее заложены в алгоритм, по которому работает мой онлайн калькулятор закона Ома.

Предлагаю провести одинаковые вычисления обоими методами и сравнить полученные результаты. Если вдруг найдете расхождения, то укажите в комментариях. Это будет ваша помощь моему проекту.

Я постарался кратко и просто рассказать о принципах работы закона Ома применительно к задачам, решаемым домашним мастером. Считаю, что это достаточно и не рассматриваю закон Ома для полной цепи в обычной форме, комплексных числах, или ином виде.

Если же вы хотите просмотреть видеоурок по этой теме, то воспользуйтесь материалами владельца Физика-Закон Ома.

Возможно, у вас остались вопросы о работе калькулятора? Задавайте. Я на них отвечу. Воспользуйтесь разделом комментариев.

Напоследок напоминаю, что у вас сейчас самое благоприятное время поделиться этим материалом с друзьями в соц сетях и подписаться на рассылку сайта. Тогда вы сможете своевременно получать информацию о новых публикуемых статьях.

Расчет электрической цепи: онлайн кальлкулятор

Студенты, которые проходят курс ТОЭ или практикующие инженеры так или иначе должны знать, как рассчитать электрическую цепь. Это несложный, но кропотливый процесс, который требует повышенной внимательности, ведь нужно учесть множество формул, знаков и размерностей. К тому же метод расчета зависит от рода тока, наличия нелинейных элементов или реактивных мощностей. Давайте рассмотрим, что нужно для самостоятельных вычислений, а также как выполнить расчет электрической цепи, используя онлайн калькулятор.

В простейшем случае результатом расчетов является вычисление электрической мощности и её коэффициента (cos Ф). Однако иногда необходимо знать эквивалентное сопротивление элементов нагрузки, эти данные вы можете получить онлайн с помощью нашего калькулятора, когда известно напряжение:

Рассмотрим, как рассчитать электрическую цепь. Для начала нужно вспомнить законы или правила Кирхгофа:

Сумма токов в узле цепи равна нулю. Простыми словами — сколько электричества вошло, столько и вышло через точку соединения нескольких ветвей.
Сумма ЭДС равна сумме падений напряжения в замкнутом контуре.

Кроме этого нам понадобится Закон Ома, базовые сведения о работе с комплексными числами, понятия активного и реактивного сопротивления и мощности. Комплексные числа в теоретических основах электротехники занимают значимое место во многих задачах, и если нет специализированных калькуляторов, то работа с ними очень затруднительна.

Также полезно знать о том, что работу любой элетросхемы можно представить в виде векторной диаграммы, тогда углы отклонения токов и напряжений зависят от рода нагрузки. При резистивной они направлены в одну сторону, а при индуктивной, емкостной или смешанной — отклонены друг от друга. Угол отклонения используется при вычислении коэффициентов мощности.

Надеемся, предоставленный онлайн калькулятор для расчета электроцепи был для вас полезным! Если возникли вопросы, задавайте их в комментариях под статьей.

Онлайн программа Расчёт размера длины цепи

	Нашли ошибку? Пожалуйста сообщите
Укажите значения по документации (умолчанию / СТОК) или же значения которые установлены сейчас на мотоцикле
Выберите шаг цепи (тип цепи)	тип: 530 шаг: 15.875 тип: 215 шаг: 7 тип: 219 шаг: 7.774 тип: 350 шаг: 9.525 тип: 415 шаг: 12.7 тип: 420 шаг: 12.7 тип: 428 шаг: 12.7 тип: 520 шаг: 15.875 тип: 525 шаг: 15.875 тип: 530 шаг: 15.875 тип: 630 шаг: 19.05 тип: 632 шаг: 19.05
Размер передней звезды (кол-во зубов)	15891011121314151617181920212223242526272829
Размер задней звезды (кол-во зубов)	49222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119
Количество звеньев цепи	104161820222426283032343638404244464850525456586062646668707274767880828486889092949698100102104106108110112114116118120122124126128130132134136138140142144146148150152154156158160162164166168170172174176178180182184186188190192194196198200202204206208210212214216218220222224226228230232234236238240242244246248250252254256258260262264266268270272274276278280282284286288290292294296298
Укажите желаемые / подбираемые / новые значения
Выберите шаг цепи (тип цепи)	тип: 530 шаг: 15.875 тип: 215 шаг: 7 тип: 219 шаг: 7.774 тип: 350 шаг: 9.525 тип: 415 шаг: 12.7 тип: 420 шаг: 12.7 тип: 428 шаг: 12.7 тип: 520 шаг: 15.875 тип: 525 шаг: 15.875 тип: 530 шаг: 15.875 тип: 630 шаг: 19.05 тип: 632 шаг: 19.05
Размер передней звезды (кол-во зубов)	17891011121314151617181920212223242526272829
Размер задней звезды (кол-во зубов)	52222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119

Сетевой симулятор и редактор схем

«Попробуйте — это отличная идея».

EDN

«Удивительно удобный и простой в освоении даже начинающий любитель».

«Симулятор цепи на основе браузера может похвастаться множеством функций».

«Умные провода» Технология:
Создайте свою схему быстрее, чем когда-либо прежде, с помощью нашей уникальной интеллектуальной технологии Smart Wires для подключения клемм и перестановки компонентов.

Патентованный симулятор :
Ядро числового решателя с повышенной точностью и усовершенствованный механизм моделирования, управляемый событиями в смешанном режиме, позволяют быстро запускать моделирование.

Схема представления качества:
Печатайте четкие, красивые векторные PDF-файлы ваших схем, а также экспортируйте их в PNG, EPS или SVG для включения схем в проектную документацию или результаты поставки.

Мощный двигатель печати:
Простая работа с несколькими сигналами с помощью настраиваемых окон печати, вертикальных и горизонтальных маркеров и расчетов по сигналам. Экспорт сюжетных изображений для включения в проектную документацию.

,Резонансный частотный калькулятор

| LC Calculator

Этот калькулятор резонансной частоты использует значения емкости (C) и индуктивности (L) LC-контура (также известный как резонансный контур, контур бака или настроенный контур) для определения его резонансной частоты (f).

Вы можете использовать калькулятор в три простых шага:

Введите любые два параметра для резонансного контура.
Выберите единицы измерения, которые вы хотите использовать.
Нажмите «Рассчитать», и калькулятор резонансной частоты вычислит третий отсутствующий параметр.

Ссылка

В области электроники схема LC используется либо для генерации сигналов на определенной частоте, либо для выбора одного сигнала из более сложного сигнала на конкретной частоте. Цепи LC играют фундаментальную роль в работе многих электронных устройств, включая радиооборудование, и используются в таких цепях, как фильтры, генераторы, тюнеры и смесители частот.

Цепи

LC состоят из двух соединенных электронных компонентов: катушки индуктивности (L) и конденсатора (C).

Когда L и C размещены параллельно или последовательно, они имеют резонансную частоту. Эта резонансная частота представлена следующим уравнением:

f = 1 / (2π √L C)

Где: f — резонансная частота в герцах (Гц), L — индуктивность в Генри (H), C — емкость в Фарадах (F), π — постоянная (3.141592654…)

Пример расчета резонансной частоты

Допустим, мы хотим определить резонансную частоту LC-цепи, которая имеет индуктивность 3 мГн и конденсатор 3 мкФ.(-6)))

f = 1677,64 Гц ≈ 1,687 кГц.

формул

Этот калькулятор резонансной частоты использует следующие формулы:

f = 1 / (2π √L C) Резонансная частота [Гц]

L = 1 / (4π ² f ² C) Индуктивность [H]

C = 1 / (4π ² f ² L) Емкость [F]

Вас также может заинтересовать наш бесплатный калькулятор кроссовера

Калькулятор падения напряжения

Это калькулятор для оценки падения напряжения в электрической цепи на основе размера провода, расстояния и ожидаемого тока нагрузки. Обратите внимание, этот калькулятор предполагает, что схема работает в нормальных условиях — температура в помещении с нормальной частотой. Фактическое падение напряжения может варьироваться в зависимости от состояния провода, используемого трубопровода, температуры, разъема, частоты и т. Д. Рекомендуется, чтобы падение напряжения не превышало 5% при условии полной нагрузки.

Основной закон падения напряжения

В _{падение} = ИК

где:
I: ток через объект, измеренный в амперах
R: сопротивление проводов, измеряется в омах

Типичные размеры проволоки AWG

AWG	Диаметр		витка провода		Площадь		Медное сопротивление		NEC медная проволока с изоляцией 60/75/90 ° C (A)	Прибл. Метрический эквивалент
AWG	дюймов	мм	на дюйм	на см	тыс. Куб. М.	мм ²	O / км	O / KFT	NEC медная проволока с изоляцией 60/75/90 ° C (A)	Прибл. Метрический эквивалент
0000 (4/0)	0.4600	11,684	2,17	0,856	212	107	0,1608	0,04901	195/230/260
000 (3/0)	0,4096	10,404	2,44	0,961	168	85,0	0,2028	0,06180	165/200/225
00 (2/0)	0.3648	9,266	2,74	1,08	133	67,4	0,2557	0,07793	145/175/195
0 (1/0)	0,3249	8,252	3,08	1,21	106	53,5	0,3224	0,09827	125/150/170
1	0.2893	7,348	3,46	1,36	83,7	42,4	0,4066	0,1239	110/130/150
2	0,2576	6,544	3,88	1,53	66,4	33,6	0,5127	0,1563	95/115/130
3	0.2294	5,827	4,36	1,72	52,6	26,7	0,6465	0,1970	85/100/110	196 / 0,4
4	0,2043	5,189	4,89	1,93	41,7	21,2	0,8152	0,2485	70/85/95
5	0.1819	4,621	5,50	2,16	33,1	16,8	1,028	0,3133		126 / 0,4
6	0,1620	4,115	6,1723	2,43	26,3	13,3	1,296	0,3951	55/65/75
7	0.1443	3,666	6,93	2,73	20,8	10,5	1,634	0,4982		80 / 0,4
8	0,1285	3,264	7,78	3,06	16,5	8,37	2,061	0,6282	40/50/55
9	0.1144	2,906	8,74	3,44	13,1	6,63	2,599	0,7921		84 / 0,3
10	0,1019	2,588	9,81	3,86	10,4	5,26	3,277	0,9989	30/35/40	84 / 0,3
11	0.0907	2,305	11,0	4,34	8,23	4,17	4,132	1,260		56 / 0,3
12	0,0808	2,053	12,4	4,87	6,53	3,31	5,211	1,588	25/25/30 (20)
13	0.0720	1,828	13,9	5,47	5,18	2,62	6,571	2,003		50 / 0,25
14	0,0641	1,628	15,6	6,14 923	4.11	2,08	8,286	2,525	20/20/25 (15)
15	0.0571	1,450	17,5	6,90	3,26	1,65	10,45	3,184		30 / 0,25
16	0,0508	1,291	19,7	7,75	2,58	1,31	13.17	4,016	— / — / 18 (10)	30 / 0,25
17	0.0453	1,150	22,1	8,70	2,05	1,04	16,61 923	5,064		32 / 0,2
18	0,0403	1,024	24,8	9,77	1,62	0,823	20,95	6,385	— / — / 14 (7)	24/0.2
19	0,0359	0,912	27,9	11,0	1,29	0,653	26,42	8,051		24/0.2
20	0,0320	0,812	31,3	12,3	1,02	0,518	33,31 923	10.15		16 / 0,2
21	0,0285	0,723	35,1	13,8	0,810	0,410	42,00	12.80		13 / 0,2
22	0,0253	0,644	39,5	15.5	0,642	0,326	52,96	16,14		7 / 0,25
23	0,0226	0,573	44,3	17,4	0,509	0,258	66,79	20,36
24	0.0201	0,511	49,7	19,6	0,404	0,205	84.22	25,67		1 / 0,5, 7 / 0,2, 30 / 0,1
25	0,0179	0,455	55,9	22,0	0,320	0,162	106,2	32,37
26	0.0159	0,405	62,7	24,7	0,254	0,129	133,9	40,81		7 / 0,15
27	0,0142	0,361	70,4	27,7	0,202	0,102	168,9	51,47
28	0.0126	0,321	79,1	31,1	0,160	0,0810	212,9	64.90
29	0,0113	0,286	88,8	35,0	0,127	0,0642	268,5	81,84
30	0.0100	0,255	99,7	39,3	0,101	0,0509	338,6	103,2		1 / 0,25, 7 / 0,1
31	0,00893	0,227	112	44,1	0,0797	0,0404	426,9	130,1
32	0.00795	0,202	126	49,5	0,0632	0,0320	538,3	164,1		1 / 0,2, 7 / 0,08
33	0,00708	0,180	141	55,6	0,0501	0,0254	678,8	206,9
34	0.00630	0,160	159	62,4	0,0398	0,0201	856,0	260,9
35	0,00561	0,143	178	70,1	0,0315	0,0160	1079	329,0
36	0.00500	0,127	200	78,7	0,0250	0,0127	1361	414,8
37	0,00445	0,113	225	88,4	0,0198	0,0100	1716	523,1
38	0.00397	0,101	252	99,3	0,0157	0,00797	2164	659,6
39	0,00353	0,0897	283	111	0,0125	0,00632	2729	831,8
40	0.00314	0,0799	318	125	0,00989	0,00501	3441	1049

Когда электрический ток проходит через провод, он должен превышать определенный уровень противоположного давления. Если ток переменный, такое давление называется импедансом. Импеданс — это вектор или двумерная величина, состоящая из сопротивления и реактивного сопротивления (реакция накопленного электрического поля на изменение тока).Если ток постоянный, давление называется сопротивлением.

Все это звучит ужасно абстрактно, но на самом деле мало чем отличается от воды, протекающей через садовый шланг. Требуется определенное давление, чтобы протолкнуть воду через шланг, что похоже на напряжение для электричества. Ток похож на воду, текущую через шланг. И шланг вызывает определенный уровень сопротивления, в зависимости от его толщины, формы и т. Д. То же самое относится и к проводам, так как их тип и размер определяют уровень сопротивления.

Чрезмерное падение напряжения в цепи может вызвать мерцание или тусклое освещение, нагреватели плохо нагреваться и двигатели работать горячее, чем обычно, и перегорать. Это условие заставляет нагрузку работать с меньшим напряжением, подталкивающим ток.

Эксперты говорят, что падение напряжения никогда не должно превышать 3 процентов. Это можно сделать, выбрав правильный размер провода и позаботившись об использовании удлинителей и подобных устройств.

Существует четыре основных причины падения напряжения.

Первый — это выбор материала, используемого для проволоки. Медь — лучший проводник, чем алюминий, и при данной длине и размере провода падение напряжения будет меньше, чем у алюминия. Электричество, которое движется по медному проводу, на самом деле представляет собой группу электронов, на которые воздействует напряжение. Чем выше напряжение, тем больше электронов, которые могут быть отправлены, протекают через провод.

Амплитуда относится к максимальному количеству электронов, которое может быть выдвинуто за один раз — слово амплитуда является сокращением от амперной емкости.

Размер провода является еще одним важным фактором в определении падения напряжения. При больших размерах провода (с большим диаметром) падение напряжения будет меньше, чем при меньших размерах провода той же длины. В американском измерительном приборе каждое уменьшение на 6 проводов дает удвоение диаметра проволоки, а каждое уменьшение на 3 проводника удваивает площадь поперечного сечения провода. В метрической шкале калибр в 10 раз больше диаметра в миллиметрах, поэтому метрическая проволока 50 калибра будет иметь диаметр 5 мм.

Еще одним критическим фактором падения напряжения является длина провода.У более коротких проводов будет меньшее падение напряжения, чем у более длинных проводов для провода того же размера (диаметра). Падение напряжения становится важным, когда длина провода или кабеля становится очень большой. Обычно это не проблема в цепях внутри дома, но может стать проблемой при подключении провода к хозяйственной постройке, скважинному насосу и т. Д.

Чрезмерное падение напряжения может привести к потере эффективности при работе света, двигателей и приборов. Это может привести к тусклому освещению и двигателям или приборам, срок службы которых сокращается.Поэтому важно использовать правильный калибр провода при прокладке проводов на большое расстояние.

Наконец, величина передаваемого тока может влиять на уровни падения напряжения. Падение напряжения на проводе увеличивается с увеличением тока, протекающего через провод. Пропускная способность по току равна амплитуде.

Емкость провода зависит от ряда факторов. Провода покрыты изоляцией, и это может привести к повреждению, если температура провода станет слишком высокой. Основной материал, из которого сделана проволока, является, конечно, важным ограничивающим фактором.Если переменный ток посылается через провод, скорость чередования может влиять на амплитуду. Температура, при которой используется провод, также может влиять на амплитуду.

Кабели

часто используются в жгутах, и при их соединении общее количество выделяемого тепла влияет на амплитуду и падение напряжения. Существуют строгие правила в отношении комплектации кабелей, которые необходимо соблюдать по этой причине.

Выбор кабеля руководствуется двумя основными принципами. Во-первых, кабель должен выдерживать текущую нагрузку на него без перегрева.Он должен быть в состоянии сделать это в самых экстремальных условиях, с которыми он сталкивается в течение срока службы. Во-вторых, он должен обеспечивать достаточно надежное заземление, чтобы (i) ограничить напряжение, до которого люди подвергаются безопасному уровню, и (ii) позволить току короткого замыкания отключить предохранитель за короткое время.

Это важные соображения безопасности. В течение 2005-2009 гг. В среднем происходило 373900 пожаров в год, вызванных плохой электроустановкой. Выбор правильного кабеля для работы является важной мерой безопасности.

Crossover Calculator — Хорошие калькуляторы

Этот калькулятор кроссовера можно использовать для расчета пассивных фильтров (первого, второго, третьего и четвертого порядка) в двухсторонних и трехсторонних кроссоверных сетях. Он также создаст принципиальную схему и предоставит требуемые значения компонентов.

Инструкции: Выберите тип кроссовера (двухсторонний или трехсторонний), значения входного сопротивления для твитера, низкочастотного динамика и средних частот (с сетью кроссовера с тремя путями), выберите порядок / тип фильтра, введите кроссовер частоту и нажмите на кнопку «Рассчитать».Затем калькулятор предоставит значения компонентов, необходимые для выбранного вами типа кроссовера.

Калькулятор кроссовера использует следующие формулы:

Формулы проектирования двухстороннего кроссовера

	1-й заказ Butterworth	1-й заказ Solen Split -6 дБ
C1 =	.159 / R _H f	.1125 / (R _H f)
L1 =	R _L/6.28f	.2251R _L / f

	2-й заказ Bessel	2-й заказ Butterworth	2-й заказ Чебышев	2-й заказ Линквитц-Райли
C1 =	.0912 / (R _H f)	.1125 / (R _H f)	.1592 / (R _H f)	.0796 / (R _H е)
C2 =	.0912 / (R _L f)	.1125 / (R _L f)	.1592 / (R _L f)	.0796 / (R _L f)
L1 =	.2756R _H / f	.2251R _H / f	.1592R _H / f	.3183R _H / f
L2 =	.2756R _L / f	.2251R _L / f	.1592R _L / f	.3183R _L / f

	3-й Заказать Баттерворт	3-й Заказать Бессель
C1 =	.1061 / (R _H f)	.0791 / (R _H f)
C2 =	.3183 / (R _H f)	.3953 / (R _H f)
C3 =	.2122 / (R _L f)	.1897 / (R _L f)
L1 =	.1194R _H / f	.1317R _H / f
L2 =	.2387R _L / f	.3294R _L / f
L3 =	.0796R _L / ф	.0659R _L / ф

	4-й заказ Бессель	4-й заказ Butterworth	4-й заказ Гауссовская
C1 =	.0702 / (R _H f)	.1040 / (R _H f)	.0767 / (R _H f)
C2 =	.0719 / (R _H f)	.1470 / (R _H f)	.1491 / (R _H f)
C3 =	.2336 / (R _L f)	.2509 / (R _L f)	.2235 / (R _L f)
C4 =	.0504 / (R _L f)	.0609 / (R _L f)	.0768 / (R _L f)
L1 =	.0862R _H / f	.1009R _H / f	.1116R _H / f
L2 =	.4983R _H / f	.4159R _H / f	.3251R _H / f
L3 =	.3583R _L / f	.2437R _L / f	.3253R _L / f
L4 =	.1463R _L / f	.1723R _L / f	.1674R _L / f

	4-й заказ Legendre	4-й заказ Линейная фаза	4-й заказ Линквитц-Райли
C1 =	.1104 / (R _H f)	.0741 / (R _H f)	.0844 / (R _H f)
C2 =	.1246 / (R _H f)	.1524 / (R _H f)	.1688 / (R _H f)
C3 =	.2365 / (R _L f)	.255 / (R _L f)	.2533 / (R _L f)
C4 =	.0910 / (R _L f)	.0632 / (R _L f)	.0563 / (R _L f)
L1 =	.1073R _H / f	.1079R _H / f	.1000R _H / f
L2 =	.2783R _H / f	.3853R _H / f	.4501R _H / f
L3 =	.2294R _L / f	.3285R _L / f	. 3000R _L / f
L4 =	.2034R _L / f	.1578R _L / f	.1500R _L / f

Примечание. Значения приведены в Фарадах (C1 — Cn), Генри (L1 — Ln), Герцах (f) и Ом (R _H, R _L).

Формула проектирования трехстороннего кроссовера

	Нормальная полярность 1-го порядка f _H / f _L = 10	Нормальная полярность 1-го порядка f _H / f _L = 8
C1 =	.1590 / (R _H f _H)	.1590 / (R _H f _H)
C2 =	.5540 / (R _M f _M)	.5070 / (R _M f _M)
L1 =	.0458R _М / ф _М	.0500R _М / ф _М
L2 =	.1592R _L / f _L	.1592R _L / f _L

	2-го порядка (обратная полярность среднего диапазона) f _H / f _L = 10	2-го порядка (обратная полярность среднего диапазона) f _H / f _L = 8
C1 =	.0791 / (R _H f _H)	.0788 / (R _H f _H)
C2 =	.3236 / (R _M f _M)	.3046 / (R _M f _M)
C3 =	.0227 / (R _M f _M)	.0248 / (R _M f _M)
C4 =	.0791 / (R _L f _L)	.0788 / (R _L f _L)
L1 =	.3202R _H / f _H	.3217R _H / f _H
L2 =	1.0291R _М / ф _М	.9320R _М / ф _М
L3 =	.0837R _М / ф _М	.0913R _М / ф _М
L4 =	.3202R _L / f _L	.3217R _L / f _L
	Полоса пропускания = 2.08 дБ	Полоса пропускания = 2,45 дБ

	3-й порядок нормальной полярности f _H / f _L = 10	3-й порядок нормальной полярности f _H / f _L = 8
C1 =	.1138 / (R _H f _H)	.1158 / (R _H f _H)
C2 =	.2976 / (R _H f _H)	.2927 / (R _H f _H)
C3 =	.0765 / (R _M f _M)	.0884 / (R _M f _M)
C4 =	.3475 / (R _M f _M)	.3112 / (R _M f _M)
C5 =	1,068 / (R _M f _M)	,9667 / (R _M f _M)
С6 =	.2127 / (R _L f _L)	.2130 / (R _L f _L)
L1 =	.1191R _H / f _H	.1189R _H / f _H
L2 =	.0598R _М / ф _М	.0634R _М / ф _М
L3 =	.0253R _М / ф _М	.0284R _М / ф _М
L4 =	.3789R _М / ф _М	.3395R _М / ф _М
L5 =	.2227R _L / f _L	.2187R _L / f _L
L6 =	.0852R _L / f _L	.0866R _L / f _L
	Усиление полосы пропускания = .85 дБ	Усиление полосы пропускания = .99 дБ

	3-го порядка (обратная полярность среднего диапазона) f _H / f _L = 10	3-го порядка (обратная полярность среднего диапазона) f _H / f _L = 8
C1 =	.0995 / (R _H f _H)	.0980 / (R _H f _H)
C2 =	.3402 / (R _H f _H)	.3459 / (R _H f _H)
C3 =	.0683 / (R _M f _M)	.0768 / (R _M f _M)
C4 =	.3128 / (R _M f _M)	.2793 / (R _M f _M)
C5 =	1.148 / (R _M f _M)	1,061 / (R _M f _M)
C6 =	.2126 / (R _L f _L)	.2129 / (R _L f _L)
L1 =	.1191R _H / f _H	.1190R _H / f _H
L2 =	.0665R _М / ф _М	.0711R _М / ф _М
L3 =	.0233R _М / ф _М	.0254R _М / ф _М
L4 =	.4285R _М / ф _М	.3951R _М / ф _М
L5 =	.2546R _L / f _L	.2586R _L / f _L
L6 =	.0745R _L / f _L	.0732R _L / f _L
	Полоса пропускания = 1.6 дБ	Полоса пропускания = 2,1 дБ

	Четвертый порядок нормальной полярности f _H / f _L = 10	Четвертый порядок нормальной полярности f _H / f _L = 8
C1 =	.0848 / (R _H f _H)	.0849 / (R _H f _H)
C2 =	.1686 / (R _H f _H)	.1685 / (R _H f _H)
C3 =	.3843 / (R _M f _M)	.3774 / (R _M f _M)
C4 =	.5834 / (R _M f _M)	.5332 / (R _M f _M)
C5 =	.0728 / (R _M f _M)	.0799 / (R _M f _M)
С6 =	.0162 / (R _M f _M)	.0178 / (R _M f _M)
C7 =	.2523 / (R _L f _L)	.2515 / (R _L f _L)
C8 =	.0567 / (R _L f _L)	.0569 / (R _L f _L)
L1 =	.1004R _H / f _H	.1007R _H / f _H
L2 =	.4469R _H / f _H	.4450R _H / f _H
L3 =	.2617R _М / ф _М	.2224R _М / ф _М
L4 =	1.423R _М / ф _М	1.273R _М / ф _М
L5 =	.0939R _М / ф _М	.1040R _М / ф _М
L6 =	.0445R _М / ф _М	0404R _М / ф _М
L7 =	.2987R _L / f _L	.2983R _L / f _L
L8 =	.1502R _L / f _L	.1503R _L / f _L
	Полоса пропускания = 2,28 дБ	Полоса пропускания = 2,84 дБ

Примечание. Значения приведены в Фарадах (C1 — Cn), Генри (L1 — Ln), Герцах (f _H, f _M, f _L) и Ом (R _H, R _M , R _{, L}).f _M = (f _H × f _L) ^1/2

Ссылка: Дикасон, Вэнс. (2006). Поваренная книга по дизайну громкоговорителей. 7-е издание. Аудио Любительская Пресса. с. 163 — 169