Расчет частоты и периода колебаний: формулы, калькуляторы и примеры

Как рассчитать частоту по периоду колебаний. Как найти период по частоте. Формулы и онлайн калькуляторы для расчета частоты и периода. Примеры решения задач на нахождение частоты и периода колебаний.

Что такое частота колебаний и как ее рассчитать

Частота колебаний — это физическая величина, которая показывает, сколько колебаний совершается за единицу времени. Частота обозначается буквой f и измеряется в герцах (Гц). 1 Гц равен 1 колебанию в секунду.

Основная формула для расчета частоты:

f = 1 / T

где f — частота, T — период колебаний.

Период колебаний — это время, за которое совершается одно полное колебание. Период измеряется в секундах.

Формулы для расчета частоты колебаний

Существует несколько формул для расчета частоты в зависимости от известных параметров колебательного процесса:

• f = 1 / T — через период колебаний
• f = ν / λ — через скорость волны и длину волны
• f = ω / 2π — через циклическую частоту

Где:

• f — частота (Гц)
• T — период колебаний (с)
• ν — скорость волны (м/с)
• λ — длина волны (м)
• ω — циклическая частота (рад/с)

Онлайн калькулятор для расчета частоты и периода

Для быстрого расчета частоты и периода колебаний можно воспользоваться онлайн калькулятором:

[Здесь может быть размещен встроенный калькулятор для расчета частоты и периода]

Калькулятор позволяет рассчитать:

• Частоту по периоду
• Период по частоте
• Частоту по длине волны и скорости
• Длину волны по частоте и скорости

Примеры решения задач на расчет частоты и периода

Задача 1. Расчет частоты по периоду

Дано: период колебаний T = 0,5 с.

Найти: частоту колебаний f.

Решение:

Используем формулу f = 1 / T

f = 1 / 0,5 = 2 Гц

Ответ: частота колебаний равна 2 Гц.

Задача 2. Расчет периода по частоте

Дано: частота колебаний f = 440 Гц (частота ноты ля первой октавы).

Найти: период колебаний T.

Решение:

Используем формулу T = 1 / f

T = 1 / 440 ≈ 0,00227 с

Ответ: период колебаний равен 0,00227 с.

Применение расчетов частоты в различных областях

Расчеты частоты и периода колебаний широко применяются в различных областях науки и техники:

• Акустика — расчет частот звуковых волн
• Радиотехника — настройка радиоприемников и передатчиков
• Оптика — определение частот световых волн
• Механика — анализ колебаний механических систем
• Электротехника — расчет параметров переменного тока

Связь частоты с другими характеристиками колебаний

Частота колебаний тесно связана с другими характеристиками колебательных и волновых процессов:

• Длина волны λ = v / f, где v — скорость волны
• Циклическая частота ω = 2πf
• Энергия фотона E = hf, где h — постоянная Планка

Как мы видим, частота является ключевым параметром для описания любых периодических процессов. Понимание связи частоты с другими характеристиками позволяет проводить комплексный анализ колебательных систем.

Частотные диапазоны в природе и технике

В природе и технике мы сталкиваемся с колебаниями различных частотных диапазонов:

• Инфразвук: до 20 Гц
• Звуковой диапазон: 20 Гц — 20 кГц
• Ультразвук: свыше 20 кГц
• Радиоволны: от 3 кГц до 3000 ГГц
• Оптический диапазон: около 10^14 — 10^15 Гц
• Рентгеновское излучение: 10^16 — 10^19 Гц
• Гамма-излучение: свыше 10^19 Гц

Каждый частотный диапазон имеет свои особенности и области применения. Например, радиоволны используются для передачи информации, а рентгеновское излучение — в медицинской диагностике.

Особенности расчета частоты в различных системах

При расчете частоты в различных физических системах необходимо учитывать их специфику:

Механические колебания

Для механических колебаний (например, маятника) частота зависит от параметров системы:

f = (1 / 2π) * √(k / m)

где k — жесткость пружины, m — масса груза.

Электромагнитные колебания

В колебательном контуре частота определяется формулой Томсона:

f = 1 / (2π√(LC))

где L — индуктивность, C — емкость.

Квантовые системы

В квантовых системах частота излучения или поглощения связана с разницей энергетических уровней:

f = (E2 — E1) / h

где E2 и E1 — энергии уровней, h — постоянная Планка.

Методы измерения частоты

Существует несколько методов измерения частоты колебаний:

• Осциллографический метод — анализ формы сигнала на экране осциллографа
• Резонансный метод — использование явления резонанса
• Цифровой метод — подсчет числа колебаний за заданный интервал времени
• Гетеродинный метод — сравнение с опорной частотой

Выбор метода зависит от диапазона частот и требуемой точности измерений.

Заключение

Расчет частоты и периода колебаний является важной задачей в различных областях физики и техники. Понимание связи между частотой и другими характеристиками колебательных процессов позволяет анализировать и проектировать сложные системы — от механических до квантовых. Использование онлайн калькуляторов и знание основных формул существенно упрощает решение практических задач, связанных с расчетом частотных характеристик.

Расчёт частоты электрического сигнала по переходу через ноль

Для некоторых функций релейной защиты и автоматики необходима информация о частоте наблюдаемого напряжения или тока. В дополнение к ранее опубликованной статье, в которой были приведены наиболее оптимальные сигналы, по которым следует рассчитывать частоту сети, рассмотрим вариант расчёта частоты электрического сигнала по переходу через ноль.

Рассмотрим синусоидальный сигнал, например, напряжения сети (рис. 1). На рисунке отмечен период сигнала T. Частота f является величиной, обратной периоду, т.е. f = 1 / T.

Рис. 1. Пример синусоидального сигнала

Таким образом, для того, чтобы определить частоту сигнала, необходимо рассчитать его период. В идеальном случае для этого достаточно определить соседние моменты времени, в которых наблюдаемый сигнал переходит нулевое значение в одном и том же направлении (например, из области отрицательных значений в область положительных значений сигнала). Однако в цифровой релейной защите наблюдаемые сигналы дискретизированы (т.е. значения наблюдаемого сигнала фиксируются в определённые дискретные моменты времени с определённой частотой дискретизации f_д через равные промежутки времени τ, называемые интервалом дискретизации), в связи с чем возникает проблема определения момента перехода через ноль.

В качестве возможного решения указанной проблемы применяется линейная интерполяция наблюдаемого сигнала в те моменты времени, в которые исследуемый сигнал не регистрируется. На рис. 2 показана иллюстрация данного подхода.

Рис. 2. Линейная интерполяция дискретизированного сигнала

Составим алгоритм определения расчётного момента времени перехода через ноль сигнала (по рисунку 2):

1. Определяем дискретный момент времени k₂, когда наблюдаемый сигнал переходит из области отрицательных значений в области положительных значений (или наоборот).
2. Фиксируем значения сигнала A₁ и A₂
   в дискретные моменты времени k₁ и k₂ соответственно.
3. Рассчитываем значение m исходя из уравнения прямой, проходящей через 2 точки.

Учитывая, что (k₂ – k₁) = 1, значение m определяется по следующему выражению:

$$ m = \frac{\lvert A_1 \rvert}{\lvert A_1 \rvert + A_2} $$

После определения соседних моментов времени перехода через ноль рассчитывается период сигнала. Рассмотрим сигнал по рис. 3.

Рис. 3. Рассматриваемый сигнал

Для данного сигнала с принятыми обозначениями период сигнала будет определяться по следующему выражению

$$ T = (k_j + m_2- k_i- m_1) \cdot \tau, $$

где $ \tau $ — интервал дискретизации сигнала.

После появления очередного перехода через производится перерасчёт частоты в соответствии с указанным выше алгоритмом. Приведённый в статье алгоритм расчёта частоты по переходу через ноль приведён в приложенном файле программы в среде Matlab: freq_calc.m.

На рис. 4 приведен результат расчёта частоты модельного сигнала, содержащего переходный процесс.

Рис. 4. Исходный сигнал и результаты расчёта частоты данного сигнала

Из результатов видно, что расчёт частоты по переходу через ноль обладает большой погрешностью в переходном режиме. Для уменьшения данной погрешности, к примеру, используют усреднение значения на нескольких периодах.

Примеры формул для расчета частоты повторений в Excel

Квартили являются популярным инструментом служащим для деления данных на равные диапазоны. Поэтому Excel предлагает специально предназначенную функцию для этой цели – КВАРТИЛЬ. Однако иногда приходится разделять данные на самостоятельно определенные диапазоны. Функция ЧАСТОТА позволяет сегментировать данные в Excel на любое количество сегментов и долей по условию пользователя.

Как посчитать частоту в Excel по формуле

Ниже на рисунке представлен список фактур с их целыми числовыми значениями сумм. Допустим, что в данном примере нам необходимо проверить: как часто клиенты делают покупки на суммы в границах от 1 и до 100, от 101 и до 200 и т.

д.

Функция ЧАСТОТА считает все фактуры, которые содержат значения, определенные в диапазоне:

Функция ЧАСТОТА является массивной функцией. Это значит, что, вводя ее в строку формул, необходимо для подтверждения ввода нажать комбинацию клавиш CTRL+SHIFT+Enter, а не просто клавишу Enter как обычно. Excel помещает тогда формулу внутрь фигурных скобок ({}), которые означают что введена формула массива.

Функция ЧАСТОТА имеет 2 аргумента:

1. Массив данных – исходный диапазон ячеек для разделения на части.
2. Массив интервалов – диапазон чисел, определяющих верхние границы для этих же частей.

Сначала введите в столбец E границы пределов. Значения в столбце D не имеют влияние на результат вычисления формулы. Они необходимы лишь для того, чтобы было наглядно видно где находиться нижние границы частей делений данных.

Чтобы ввести функцию ЧАСТОТА в столбце F, сначала выделите диапазон ячеек F2:F11. Не снимая выделения вводите формулу. Несмотря на то, что формула будет введена только в одной ячейке, нажатие на комбинацию клавиш CTRL+SHIFT+Enter позволит заполнить все выделенные ячейки диапазона формулой массива.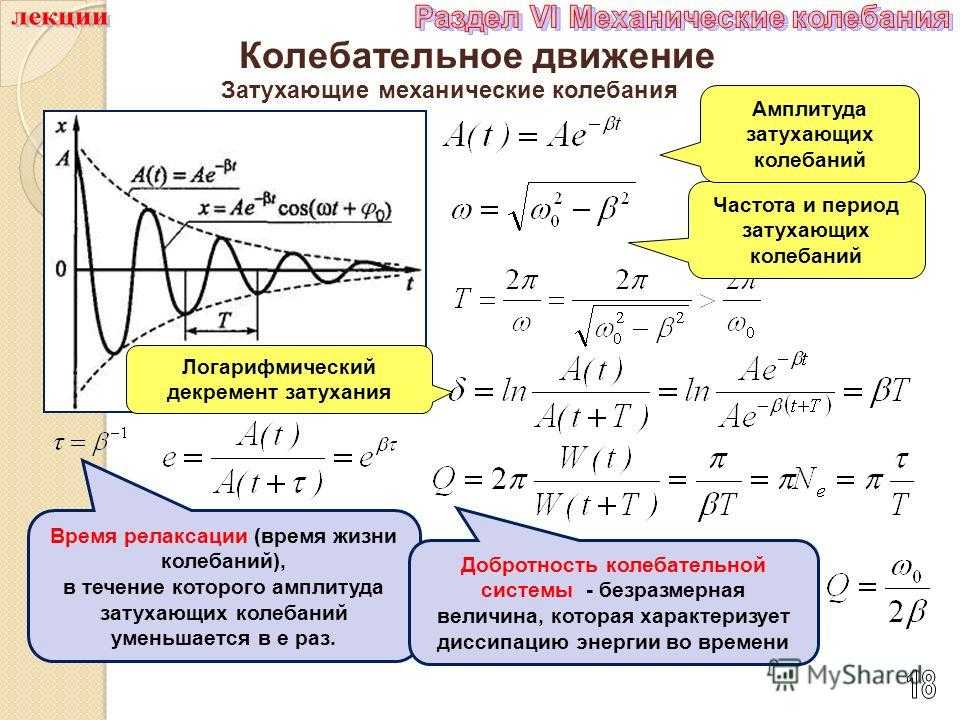

Результат возвращаемый с помощью функции ЧАСТОТА отображает, что большая часть клиентов совершает покупки на сумму в границах от 200 и до 300 во время одного визита.

Если попробовать убрать одну с ячеек в диапазоне, в котором введена функция ЧАСТОТА, Excel выдаст сообщение «Нельзя изменять часть массива». Excel воспринимает эти и другие функции массива в диапазоне ячеек как одно целое. Можно изменять диапазон целиком, но не его отдельные ячейки. Если нужно изменить границы делений данных придется удалить и заново ввести формулу всю массива.



Расчет частоты в Excel с помощью функции СЧЁТЕСЛИМН

Для создания графика частот можно воспользоваться функцией СЧЁТЕСЛИМН. Данная функция не является массивной, поэтому введение изменений для границ диапазона, а также увеличение или уменьшение их количества будет простым заданием. В случае с данными представленными на рисунке ранее функция СЧЁТЕСЛИМН используется в следующей формуле:

В отличии от функции ЧАСТОТА функция СЧЁТЕСЛИМН требует указать нижнюю границу предела (столбец D) и считает все значения, которые больше чем нижняя граница и меньше от верхнего предела или равно ему.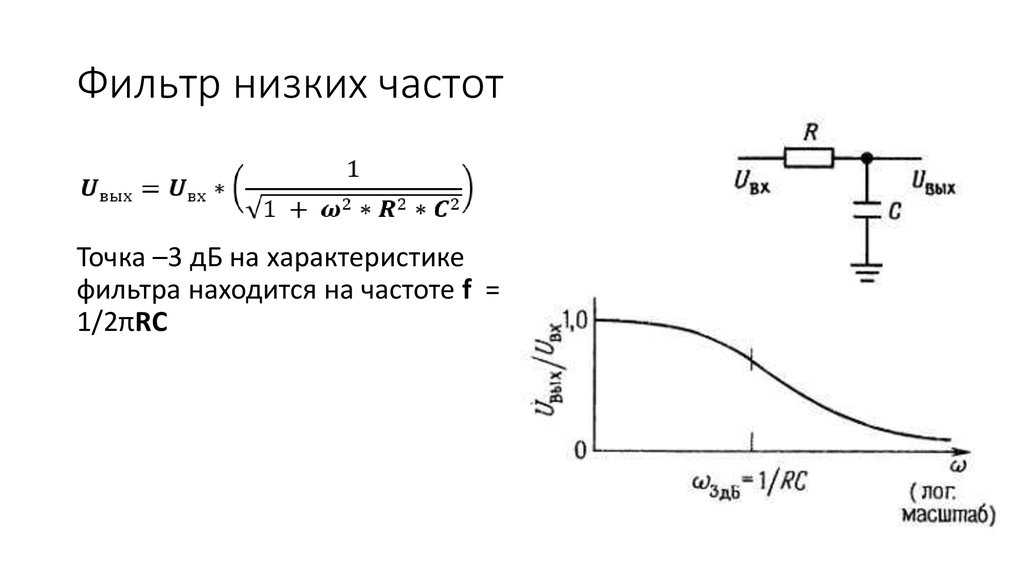 Данную функцию не нужно вводить как формулу массива. Достаточно лишь скопировать ее в очередные нижние ячейки ровно столько раз сколько есть определенных пределов границ.

Частотная формула — что такое частотная формула? Примеры

Частотная формула используется для определения частоты волны. Частота определяется как количество циклов, совершаемых в единицу времени. Он также говорит о том, сколько гребней проходит через фиксированную точку в единицу времени. Иногда его называют обратным времени. Частота выражается в герцах (Гц). Частотная формула используется для определения частоты волны. Давайте лучше поймем это на решенных примерах.

Что такое формула частоты?

Частота — это общее количество повторений повторяющегося события в единицу заданного времени. Существуют различные частотные формулы для расчета частоты в зависимости от известных величин. Формула частоты волны используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ). 1 Герц относится к одному циклу в секунду.

Формула частоты

Формула частоты дается как,

Формула 1: Формула частоты по времени дается как:

f = 1/T

где

• f — частота в герцах, измеренная в м/с, а
• T — время выполнения одного цикла в секундах

Формула 2: Формула частоты для длины волны и скорости волны задается следующим образом:

λ — длина волны в м

Формула 3:  Частота с точки зрения угловой частоты выражается как,

f = ω/2π

, где ω — угловая частота

Давайте лучше поймем формулу частоты на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Примеры с использованием формулы частоты

Пример 1: Используя формулу частоты, найдите частоту волны, один цикл которой завершается за 0,5 с.
Решение:

, чтобы найти: частота

Дано:

Время = 0,5S

с использованием частоты формулы

F = 1 / T

F = 1 / 0,5

F = 2

Ответ: Ответ: Ответ:: Частота 2Гц.

Пример 2: Найдите частоту световой волны, если длина волны света равна 600 нм.
Решение:     

Найти: Частоту

Дано: Длина волны = 600 нм = 600 × 10 ^-9 м

= 6 × 10 ^-7 м

Мы знаем, что скорость света = 3 × 10 ⁸  м/с

Используя формулу частоты

/ λ00

f = F = 3 × 10 ⁸ /6 × 10 ^-7

F = 5 × 10 ¹⁴ СЕД ^-1

Ответ: частота 5 × 10 ¹⁴ Гц.

Пример 3: Определите частоту маятника, совершающего один оборот за 4 секунды.
Решение:

, чтобы найти: частота

Дано:

Время = 4S

Использование частоты Формулы

F = 1 / T

F = 1/4

F = 0,25

Ответ: Частота. составляет 0,25 Гц.

Часто задаваемые вопросы о частоте

Что такое формула частоты?

Формула частоты определяется как формула для определения частоты волны. Формула частоты используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ).

Каковы применения формулы частот?

Применение формулы частоты:

• Частота считается важным параметром в области науки и техники, как и формула частоты.
• Формула для частоты используется для определения скорости колебательных и вибрационных явлений, в основном механических колебаний, звуковых сигналов (звука), радиоволн и световых волн.
• Формула частоты используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ), а также для получения других связанных формул.

Как формула частоты применяется для заданных значений?

Процентная формула представлена ​​в следующем виде:

• Частотная формула в единицах времени представлена ​​в виде: f = 1/T, где f — частота в герцах, а T — время, необходимое для завершения одного цикла в секундах
• Формула частоты для длины волны и скорости волны задается следующим образом: f = 𝜈/λ, где 𝜈 – скорость волны, а λ – длина волны
• Формула частоты в терминах угловой частоты задается как f = ω/2π, где ω – угловая частота

Что такое «T» в частотной формуле?

В частотной формуле f = 1/T, T — период времени. T – время выполнения одного цикла (в секундах). Период времени обратно пропорционален частоте.

Калькулятор частоты | Period to Frequency and More

Создано Rita Rain

Отзыв от Dominik Czernia, PhD и Jack Bowater

Последнее обновление: 21 декабря 2022 г.

Содержание:

• Определение частоты и формула частоты
• Частотное уравнение для длины волны
• Как пользоваться частотным калькулятором?
• Пример: Как рассчитать частоту по периоду?
• Пример: Как найти частоту волны?
• Реальное применение
• Часто задаваемые вопросы

Калькулятор частоты позволит вам найти частоту волны по заданной длине волны и ее скорости или периоду в кратчайшие сроки. Вы можете выбрать скорость волны из предустановленного списка, так что вам не нужно запоминать.

В тексте вы также найдете определение частоты , две формулы частоты (отношение периода к частоте и длины волны к частоте) и несколько примеров, показывающих, как вычислять частоту.

Если вы хотите узнать больше о волнах, воспользуйтесь калькулятором длины волны, а если вы хотите узнать частоту музыкальных нот, воспользуйтесь калькулятором частоты нот.

Определение частоты и формула частоты

Посмотрите на следующую модель волны; это поможет вам понять термины, используемые в приведенном ниже определении частоты.

Источник: Британская энциклопедия

Частота — это количество полных циклов волны в секунду . Другими словами, частота говорит нам, сколько гребней волны проходит данную точку за секунду.

Это определение частоты приводит нас к простейшей частотной формуле :

f=1Tf=\frac{1}{T}f=T1​

fff обозначает частоту, а TTT обозначает время, необходимое для завершения одного волновой цикл измеряется в секундах.

Единицей частоты SI является Герц (Гц) , что равно 1/с (один цикл в секунду). Другие единицы частоты включают миллигерц (мГц), килогерц (кГц), мегагерц (МГц), гигагерц (ГГц) и терагерц (ТГц).

Частотное уравнение от длины волны

Посмотрите на другую картинку, которая позволит нам увидеть связь между частотой и длиной волны. Длина волны — это расстояние между двумя соседними гребнями (или впадинами). Другими словами — это длина одного волнового цикла. Чем длиннее длина волны, тем ниже частота :

Источник: Encyclopedia Britannica

Еще один факт, который нам нужен — скорость распространения волн (скорость волн) определяет, сколько из них пройдет заданную точку в секунду. Это означает , что чем выше скорость волны, тем выше частота .

Эти два соотношения между частотой и длиной волны (λ\lambdaλ) и между частотой и скоростью (vvv) приводят нас к следующему частотному уравнению :

f=vλf=\frac{v}{\lambda}f=λv​

Как пользоваться частотным калькулятором?

Наш калькулятор частоты включает вышеупомянутые формулы частоты. Таким образом, вы можете использовать его в качестве калькулятора периода для частоты или калькулятора длины волны для частоты.

Как использовать его в качестве калькулятора преобразования периода в частоту? (Как найти частоту, если известен период?)

1. Введите время, в течение которого происходит один цикл волны ( период ). Калькулятор определит частоту.

2. Вы можете использовать этот калькулятор для определения периода, если знаете его частоту.

Как использовать его в качестве калькулятора преобразования длины волны в частоту? (Как рассчитать частоту по длине волны?)

1. Введите скорость волны во второе поле или выберите тип волны и ее среду из списка в первом поле. По умолчанию у нас установлено значение свет в вакууме .

2. Введите длину волны, появится значение частоты.

Так что, в принципе, можно ввести любые две переменные, и тут же появится третья 😀

Пример: Как рассчитать частоту по периоду?

Чтобы развеять сомнения, как рассчитать частоту по периоду, разберем несколько простых примеров. Во-первых, вспомним частотное уравнение:

f=1Tf=\frac{1}{T}f=T1​

Пример 1:

Как найти частоту волны, в которой один цикл завершается за 0,25 s:

f=1T=10,25 s=4×1s\begin{align*} f&=\frac{1}{T}\\[1.2em] &=\frac{1}{0,25\ \text{s}}\\[1,2em] &= 4\times\frac{1}{\text{s}} \end{align*}f​=T1​=0,25 s1​=4×s1​​

Не забудьте преобразовать 1s\frac{1}{\text{s}}s1​ в единицу измерения частоты:

f=4 Hzf = 4\ \text{Hz}f=4 Hz

Пример 2:

Как найти частоту волны, в которой за 1 минуту происходит 360 циклов:

f=3601 m=36060 s=6s=6 Hz\begin{align*} f&=\frac{360}{1\ \text{m}}\\[1.2em] &=\frac{360}{60\ \text{s}}\\[1.2em] &= \frac{6}{\text{s}}\\[1.2em] &= 6\ \text{Гц} \end{align*}f​=1 m360​=60 s360​=s6​=6 Hz​

Пример: Как найти частоту волны?

На этот раз мы хотим узнать, как найти частоту волны, если известны скорость и длина волны. Вам необходимо использовать следующую формулу частоты:

f=vλf=\frac{v}{\lambda}f=λv​

Пример 1:

Скорость волны равна 320 м/с, а длина волны равна 8 м. Найдя его частоту, имеем:

f=vλ=320 мс8 m=40с≈40 Гц\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &=\frac{320\\tfrac{\text{m}}{\text{s}}}{8\ \text{m}}\\[1.2em] &= \frac{40}{\text{s}}\\[1.2em] &\около 40\ \text{Гц} \end{align*}f​=λv​=8 м320 см​=s40​≈40 Гц​

Пример 2:

Найдите частоту света, если длина волны равна 3000 км. Скорость волны равна скорости света в вакууме примерно равна 300 000 км300,\hspace{-0,05 см}000\ \tfrac{\text{км}}{\text{s}}300 000 скм​. Используя формулу частоты, получаем:

f=vλ=300 000 км3 000 км=100 с≈100 Гц\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &=\frac{300,\hspace{-0,05см}000\ \tfrac{\text{км}}{\text{s}}}{3,\hspace{-0,05cm}000\ \text{км} }\\[1.2em] &= \frac{100}{\text{s}}\\[1.2em] &\примерно 100\\текст{Гц} \end{align*}f​=λv​=3000 км300 000 skm​=s100​≈100 Гц​

Реальное приложение

В беспроводной связи у нас есть объем эллипсоида между антенной передатчика и антенной приемника . Эта область определяется расстоянием между антеннами и частотой беспроводной волны. Она называется Зона Френеля и выглядит так:

Из основной формулы зоны Френеля мы делаем вывод, что чем выше частота, тем меньший объем эллипсоида должен быть свободен для правильной беспроводной связи. Наоборот, для низкой частоты мы получаем большую зону Френеля, которую здания или деревья могут легко блокировать и, таким образом, создавать нестабильную беспроводную связь.

💡 Вы можете узнать больше о зоне Френеля, посмотрев наш Калькулятор зоны Френеля.

Волны с разной частотой вызывают биения и задаются вопросом, как рассчитать частоту биений, а объем камеры сильно влияет на частоту резонанса Гельмгольца.

FAQ

Как рассчитать частоту?

Вам необходимо знать либо длину волны и скорость, либо период волны (время, необходимое для завершения одного цикла волны). Если вы знаете период:

1. Преобразуйте в секунды, если нужно, и разделите 1 на период .
2. Результатом будет частота , выраженная в Герцах .

Если вы хотите рассчитать частоту по длине волны и скорости волны:

1. Убедитесь, что имеют одинаковые единицы измерения длины.
2. Разделите скорость волны на длину волны .
3. Преобразование результата в герцы. 1/с равняется 1 Герцу.

Как определить длину волны по частоте?

1. Определить скорость волны.
2. Определить частоту.
3. Преобразовать герц в 1/с.
4. Убедитесь, что скорость волны и частота имеют одну и ту же единицу времени.
5. Разделите скорость волны на частоту.

Какая связь между частотой и длиной волны?

Частота равна скорости волны, деленной на длину волны. Следовательно, чем длиннее длина волны, тем ниже частота, а чем короче длина волны, тем выше частота. Другими словами, 9Частота 0015 обратно пропорциональна длине волны .

В чем измеряется частота?

Частота волны измеряется в Герцах . 1 герц равен 1/с — один цикл в секунду. Связанные единицы включают миллигерц (одна тысячная герца), килогерц (тысяча герц), мегагерц (миллион герц) и гигагерц (миллиард герц). Единица названа в честь Генриха Рудольфа Герца, физика, доказавшего существование электромагнитных волн.

Как найти частоту волны?

1. Определить скорость волны.
2. Определить длину волны.
3. Убедитесь, что скорость волны и длина волны имеют одну и ту же единицу длины, например, если скорость выражается в метрах в секунду, длина волны должна быть выражена в метрах.
4. Разделите скорость волны на длину волны.
5. Преобразование результата в герцы. Один герц равен 1/с — один цикл в секунду.

Какая частота у 5G?

5G, который является технологическим стандартом пятого поколения для сотовых сетей, работает в различных диапазонах частот, которые попадают в два частотных диапазона. Диапазон частот 1 — от 450 МГц до 6 ГГц , а диапазон частот 2 — от 24,25 ГГц до 52,6 ГГц .

Какой цвет имеет самую высокую частоту?

Фиолетовый — это цвет с самой высокой частотой , которая колеблется от 670 до 750 терагерц. На другой стороне спектра находится красный цвет с частотой от 430 до 480 терагерц.

Какая связь между частотой и энергией?

Энергия прямо пропорциональна частоте . Другими словами, чем выше частота, тем больше энергия. Связь между частотой и энергией описывается следующей формулой для энергии фотона:

E = h × f

«E» — символ энергии, «h» — постоянная Планка, а «f» обозначает частоту.

Какая волна имеет самую высокую частоту?

Гамма-лучи — это электромагнитные волны с наивысшей частотой , то есть более 10 ¹⁹ Гц.